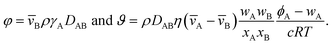Equilibration times in viscous and viscoelastic aerosol particles†
Received
5th June 2022
, Accepted 5th September 2022
First published on 7th September 2022
Abstract
Secondary organic aerosol (SOA) particles in Earth's atmosphere can exist in phase states where mass transport and chemical transformations are greatly impeded. Gas-particle partitioning in both semi-solid and solid (e.g. glassy phase state) SOA particles can be kinetically limited, and these equilibration timescales are often evaluated using a Fickian model with a concentration-dependent diffusivity. Within that framework, particles are considered to be inviscid fluids and thus their rheology is ignored. In this work, rheological properties are not neglected and particle equilibration is investigated using both a viscous model (an incompressible Newtonian fluid) and a viscoelastic model (a Maxwell material). We derive analytic expressions for gas-particle equilibration times in viscous and viscoelastic aerosol particles and compare these times to the well-known Fickian equilibration time. These expressions are then applied to the important example of the equilibration of atmospheric aerosol particles with the surrounding relative humidity (i.e. water uptake and loss). The two systems studied here are aqueous sucrose, which is often used as a surrogate for secondary organic material found in the atmosphere, and aqueous oxidized α-pinene, which is an atmospherically relevant secondary organic material. We show that viscous effects (i) are likely unimportant in single particle experiments, except under very dry conditions, and (ii) can result in water vapor equilibration times of minutes to hours at any altitude in the troposphere for accumulation mode particles.
Environmental significance
The analytic equations derived here allow for both viscosity and viscoelasticity to be included in calculations of the gas-particle equilibration timescale. In the atmospheric aerosol, this is relevant to our understanding of how high viscosity secondary organic aerosol particles equilibrate with their surroundings. We show that, for sub-100 nm particles, timescales that include viscosity can be several orders of magnitude greater than those calculated within a purely Fickian framework. The consequences of this are that water vapor equilibration times for accumulation mode particles can be minutes to hours longer in situations where it was previously reported that equilibrium can always be assumed, e.g. the planetary boundary layer and middle troposphere.
|
1 Introduction
Binary diffusion in the liquid state is generally well-described by Fick's laws of diffusion. When assessing the timescale for establishing gas-particle equilibrium, a characteristic equilibration time, τD, based on the Fickian model is often used in atmospheric aerosol science. For a particle with a binary (Fickian) diffusivity, DAB, in the condensed phase and radius, s, the equilibration timescale is| | 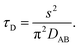 | (1) |
This equation has been applied to a variety of mass transport calculations where gas-particle partitioning is limited by condensed phase diffusion, such as equilibration in aqueous droplets1–3 and mixing in high viscosity secondary organic aerosol (SOA) particles.4,5
For SOA particles, eqn (1) is commonly used to make arguments concerning the validity of the homogeneous mixing assumption in the atmosphere; e.g. are equilibration timescales long enough to inhibit cloud condensation nuclei (CCN) activation or impact ice nucleation pathways?6–9 Depending on composition, temperature, and relative humidity (RH), the phase state of SOA particles can be a low viscosity liquid, but solid and semi-solid phase states are also possible.10–12 These non-liquid states can have very high viscosities.13,14 For instance, glassy states that form in the SOA condensed phase can have viscosities on the order of 1012 Pa s.10 Therefore, one would anticipate that a Fickian framework, which treats the condensed phase as being an inviscid fluid insofar as mass transport is concerned, would eventually become inaccurate. Certainly, decades of work on sorption in glassy materials has already demonstrated that understanding non-Fickian behaviour is crucial to accurate mass transport calculations.15–21 In these high viscosity systems, viscoelastic or purely viscous effects can readily dominate Fickian diffusion and very often cannot be ignored.22 However, it would be difficult to directly apply this previous research to SOA particles as it has almost exclusively focused on polymer-penetrant systems where physical quantities are determined using models appropriate for polymer solutions.19
Fig. 1 presents laboratory measurements of diffusivity and viscosity for two well-studied systems across a large range of water activities. Fig. 1a shows measurements for sucrose, a common surrogate for SOA material in laboratory-based studies,13,23–32 and Fig. 1b shows measurements for SOA material produced by the oxidation of α-pinene.7,33–38 Here, the Stokes–Einstein (SE) relation is used to convert diffusivity to viscosity or vice versa. Two trends are immediately apparent from Fig. 1. First, both viscosity and diffusivity vary by orders of magnitude across atmospherically relevant water activities. Second, the discrepancy between diffusivity (viscosity) predicted by the SE relation using viscosity (diffusivity) measurements can be quite large. At lower water activities, the predictions from the SE relation can be off by several orders magnitude. For instance, for aqueous sucrose at a water activity of 0.25, viscosity and diffusivity predicted using the SE relation differ by a factor of 8.2 × 105 from their measured values. In addition to the breakdown of the SE relation, it is also clear from Fig. 1 that there will be a large range of water activities where the equilibrated condensed phase will not be a low-viscosity liquid. Typically, liquids have viscosities less than 102 Pa s and the phase state between 102 to 1012 Pa s is characterized as a semi-solid.12 In both panels of Fig. 1, this semi-solid region covers a significant portion of atmospherically relevant water activities.
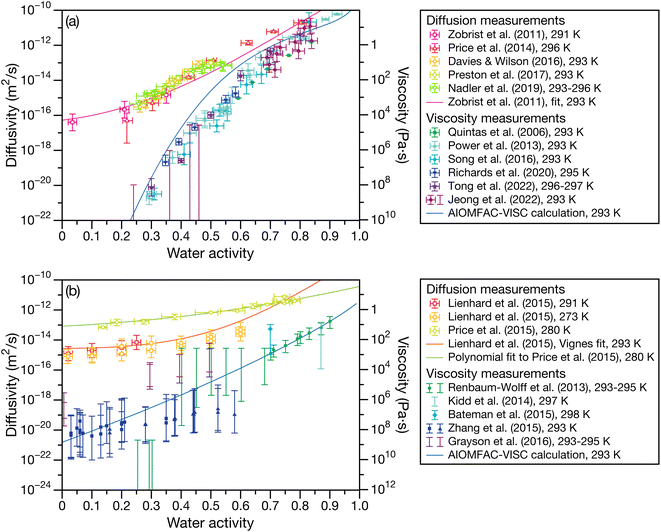 |
| | Fig. 1 Experimental measurements of diffusivity and viscosity for (a) aqueous sucrose13,23–32 and (b) aqueous oxidized α-pinene secondary organic material.7,33–38 Conversions from diffusivity to viscosity or vice versa were calculated using the SE relation with a temperature of 293 K and a molecular radius of 0.2 nm.60 Diffusivity measurements were performed on either binary (H2O + solute) or ternary (H2O + D2O + solute) systems. See referenced papers for details. | |
In the current work, we study the influence of fluid rheology on the characteristic equilibration time of aerosol particles with their surroundings. We consider both viscous and viscoelastic fluids as models for phase states relevant to atmospheric aerosol particles. These two models differ from the Fickian framework as viscosity is no longer zero during mass transport. The main question that we are concerned with is: How do the rheological properties of these phase states impact gas-particle partitioning? This is answered by deriving expressions for the characteristic equilibration time, analogous to eqn (1), for both viscous and viscoelastic spherical particles. The resulting expressions, given in eqn (29) and (35), are found to predict equilibration times that are several orders of magnitude greater than the Fickian equilibration time for a range of atmospherically relevant particle sizes and conditions. We discuss the implications for single particle experiments and also examine timescales for representative conditions that exist in the planetary boundary layer, middle troposphere and upper troposphere.
2 Theory
2.1 Mass transport in a viscous and viscoelastic binary system
Mass transport of species α in a non-reacting solution is written using the convection–diffusion equation with no source term| | 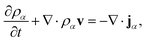 | (2) |
where ρα is the mass concentration of species α, v is the mass average velocity, and jα is the mass flux of species α.
For a solution containing N components, we can express the mass density of the solution, ρ, with the partial specific volumes, ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) α, and mass fractions, wα, of species α using
α, and mass fractions, wα, of species α using
| | 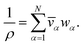 | (3) |
We have previously shown that, when ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) α are constant, the mass average velocity can be expressed in terms of mass fluxes according to39
α are constant, the mass average velocity can be expressed in terms of mass fluxes according to39
| | 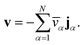 | (4) |
This equation allows for the mass average velocity to be eliminated from eqn (2). For a binary system (N = 2) with species A and B, eqn (4) along with the relation jA = −jB can be applied to eqn (2) to yield
| | 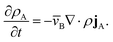 | (5) |
Therefore, to calculate the rate of change of the mass concentration in a binary system, what is now required is an expression for jA. For binary diffusion in the absence of temperature gradients and forced diffusion, the generalized Maxwell–Stefan (MS) equation40 simplifies to
| | 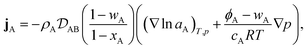 | (6) |
where, for species A,
xA is the mole fraction,
aA =
γAxA is the activity,
γA is the activity coefficient,
cA =
xAc is the molar concentration,
ϕA =
ρA![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A
A is the volume fraction,
c is the total molar concentration,
R is the universal gas constant,
T is the temperature,
p is the local pressure, and
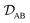
is the binary MS diffusivity. As indicated in
eqn (6), the gradient of the natural logarithm of
aA is evaluated at a constant
T and
p.
In a binary system, the MS diffusivity and the Fickian diffusivity, DAB, are related through41
| | 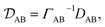 | (7) |
where
ΓAB is the thermodynamic factor for the binary system and is defined as
| | 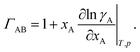 | (8) |
Therefore, when γA is constant (e.g. for an ideal solution where it would be equal to one), we will have 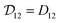 and the two diffusivities are identical.
and the two diffusivities are identical.
The pressure gradient in eqn (6) is determined by using the equation of motion
| | 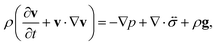 | (9) |
where
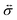
is the stress tensor, and
g is the external force per unit mass. For simplicity, we ignore the effects of inertia by setting the left-hand side of
eqn (9) to zero. As we will only consider cases where
g = 0,
eqn (9) simplifies to
| | 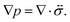 | (10) |
A viscoelastic stress–strain relationship will be used to describe the stress in eqn (10). The standard Maxwell model42 is chosen here. In this linear model of viscoelasticity, the fluid consists of a spring and a dashpot in series19
| | 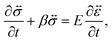 | (11) |
where
E is the Young's modulus,
β =
E/
η is the ratio of the elasticity to viscosity,
η is the concentration-dependent viscosity of the dashpot in the Maxwell model,
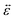
is the infinitesimal strain tensor, and
| | 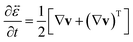 | (12) |
is the rate-of-strain tensor. A relaxation time can be defined as
τl = 1/
β =
η/
E.
We will restrict our analysis to spherical coordinates with radial symmetry. Eqn (10) will be
| | 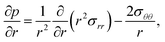 | (13) |
and the non-zero components of the rate-of-strain tensor are
| | 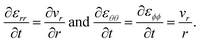 | (14) |
The solution to eqn (11) when η and E depend on the concentration of A for a system that is initially unstressed (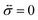 at t = 0) is
at t = 0) is
| | 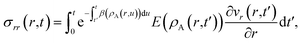 | (15) |
| | 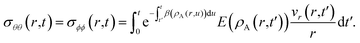 | (16) |
In these equations, the concentration history of the system, extending back to the initial unstressed state at t = 0, influences the stresses at the current time, t. The origin of this memory effect in a viscoelastic system is the presence of a finite relaxation time (τl > 0).
In addition to the viscoelastic model, we will also consider a viscous model. When E → ∞, the Maxwell model (eqn (11)) reduces to
| | 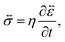 | (17) |
which is identical to the description of stress that is found using an incompressible Newtonian fluid (when the term with dilatational viscosity is set to zero, see p. 241 from ref.
40). The non-zero components of the stress tensor will simply be
| | 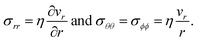 | (18) |
In the viscous model, only the current state of the system determines the stress. The memory effect seen in the solution to the viscoelastic model is absent as relaxation is now instantaneous (τl = 0).
We now proceed in our analysis by considering the case where only small changes in species A and B occur during the mass transport process (this is sometimes referred to as differential sorption).17 We will linearize equations by assuming that the coefficients that appear in them are constant. When eqn (13) is inserted into eqn (6), the mass flux of species A can be written as
| | 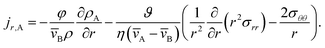 | (19) |
where
Eqn (5) and (19) along with the appropriate stress expressions can be used to determine governing partial differential equations for both viscous and viscoelastic mass transport during differential sorption. For the viscous model, the governing equation can be found by inserting eqn (18) into (19) and then using eqn (4) to eliminate vr from the resulting equation. All of the fluxes, jr,A, and their partial derivatives can then be replaced through the application of eqn (5) and its partial derivatives. This yields
| | 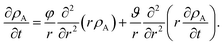 | (20) |
The governing equation for the viscoelastic model is determined as follows. First, we recognize that for constant η and E, eqn (15) and (16) simplify to
| | 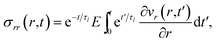 | (21) |
| | 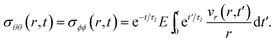 | (22) |
These two equations are then inserted into eqn (19) and then eqn (4) is used to eliminate vr. The result will be an equation that contains integrals over the interval of 0 to t. If the partial derivative with respect to time is applied to both sides of this equation, the resulting equation will contain no integrals. Then, just like the viscous case, application of eqn (5) and its partial derivatives can be used to replace all fluxes with partial derivatives of concentrations. When this is done, the viscoelastic governing equation is found to be
| | 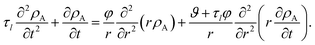 | (23) |
It is clear from inspection that when the relaxation time goes to zero (τl → 0), the viscoelastic governing equation (eqn (23)) reduces to the viscous governing equation (eqn (20)).
2.2 Characteristic equilibration times
The viscous and viscoelastic equilibration times for the binary system where species A is the gas-phase species/penetrant and species B is the condensed/particle phase species can be found by solving the linear boundary problem with the appropriate boundary conditions. At the centre of the particle we have the usual symmetry condition| | 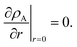 | (24) |
For nanometer-sized particles with low condensed phase diffusivity, it is usually an excellent approximation to assume that the concentration of A at the surface can be fixed at its final value.5,43,44 Therefore, in this particle-diffusion limited case, the boundary condition at the particle surface will be
where
ρA,∞ is the bulk gas-phase mass concentration of species A in the condensed-phase. We remark that the approximation that yields
eqn (25) has only been validated within a Fickian framework.
5,43,44
The particle radius is assumed to be constant here so that we do not have a moving boundary problem. The initial condition for the problem will be
where
ρA,0 is the concentration of species A in the particle at
t = 0.
For the viscous case, we can solve the boundary-value problem using separation of variables to get
| | 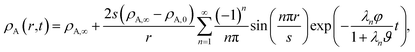 | (27) |
where the eigenvalues are
| | 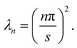 | (28) |
The characteristic equilibration time, τN, for the viscous incompressible Newtonian fluid is then
| | 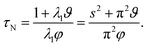 | (29) |
For the case when ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A =
A = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B there is no viscous flow and τN will reduce to the Fickian equilibration time (eqn (1)), provided that the solution is ideal (γA = 1). However, if
B there is no viscous flow and τN will reduce to the Fickian equilibration time (eqn (1)), provided that the solution is ideal (γA = 1). However, if ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A ≠
A ≠ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B then τN will not reduce to τD, even if the viscosity is zero. This occurs because the typical Fickian treatment neglects convective mass transport due to density changes. Also, we see that for s2 ≫ π2ϑ, the viscous pressure gradients will not significantly affect the equilibration time. Fig. 2 shows concentration profiles calculated using eqn (27) during both uptake and loss in the case when Fickian diffusion dominates (a and c) and viscous effects dominate (b and d). In panels b and d, the concentration of A is always uniform (except near r = s) and equilibration is determined by material response during swelling or shrinkage (rheological limitations).
B then τN will not reduce to τD, even if the viscosity is zero. This occurs because the typical Fickian treatment neglects convective mass transport due to density changes. Also, we see that for s2 ≫ π2ϑ, the viscous pressure gradients will not significantly affect the equilibration time. Fig. 2 shows concentration profiles calculated using eqn (27) during both uptake and loss in the case when Fickian diffusion dominates (a and c) and viscous effects dominate (b and d). In panels b and d, the concentration of A is always uniform (except near r = s) and equilibration is determined by material response during swelling or shrinkage (rheological limitations).
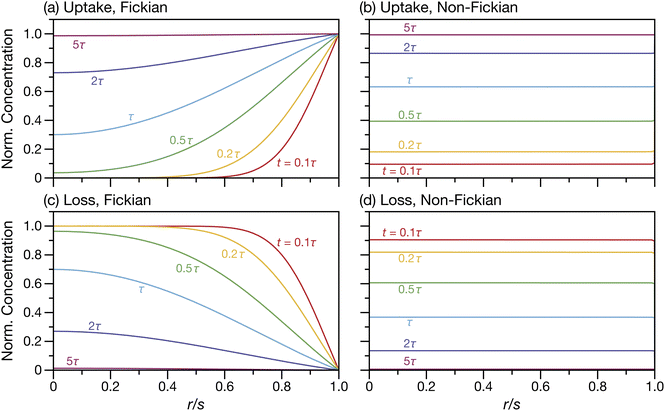 |
| | Fig. 2 Concentration profiles for species A during uptake (a and b) and loss (c and d) calculated using eqn (27). In panels (a) and (c) s2 ≫ π2ϑ and transport is dominated by Fickian diffusion. In panels (b) and (d) s2 ≪ π2ϑ and transport is dominated by non-Fickian effects (which are viscous in this case). | |
An approximate expression for τN that is more straightforward to apply in many situations of interest, and also useful in terms of physical insight, can be obtained through the following assumptions: the solution is ideal, wA ≪ wB, and the s2/π2φ term can be replaced by τD. Then, eqn (29) becomes
| | 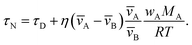 | (30) |
In Fig. 3, eqn (29) and (30) are compared across a range of water activities and radii for the system of aqueous sucrose. Even when the condition wA ≪ wB is no longer true, the accuracy of eqn (30) does not begin to deteriorate. This is because τD will dominate in that case, so the second term on right-hand side of eqn (30) is negligible. Aside from being slightly simpler than eqn (29), one other advantage of eqn (30) is that MB is not needed if wA is already known. So, for instance, in a calculation involving water transport in SOA material, the molar mass of the SOA, which is typically defined as an average, will not be required.
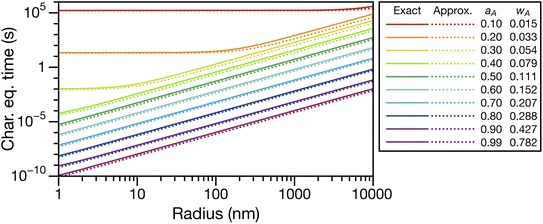 |
| | Fig. 3 Comparison between the viscous characteristic equilibration time calculated using the exact (eqn (29)) and approximate (eqn (30)) equations as a function of radius at several different activities, aA (or mass fractions wA). Species A is water and species B is sucrose. Parameters for aqueous sucrose at T = 293 K were used for the calculations. | |
For the viscoelastic case, we require a second initial condition to formulate the boundary-value problem due to the second order time derivative in eqn (23). We will use
| | 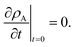 | (31) |
With this additional condition, the solution to the viscoelastic boundary-value problem is
| | 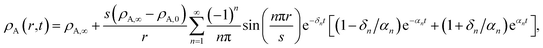 | (32) |
where
| | 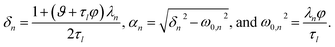 | (33) |
The parameters ϑ, φ, and λn have the same definitions as in the viscous case. The difference between the viscous and viscoelastic solutions is that the time-dependent part of eqn (32) in the viscoelastic solution is that of a damped harmonic oscillator whereas the viscous solution was that of a homogeneous first-order differential equation. Therefore, δn is the damping parameter and ω0,n is the natural frequency. As should be expected, in the limit where τl → 0, eqn (32) reduces to the time-dependent viscous concentration profile (eqn (27)).
For large t in the overdamped case (δn2 > ω0,n2), eqn (32) can be approximated as
| | 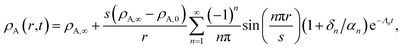 | (34) |
where
Λn =
δn −
αn.
Fig. 4 shows the parameters
δ12 and
ω0,12 across an activity range of zero to one for the model system of aqueous sucrose at several different radii. In all cases, the overdamped condition is satisfied. We will therefore assume that the overdamped solution is the only one that is relevant for atmospheric systems and that the characteristic time,
τV, for the viscoelastic fluid can subsequently be written as
| | 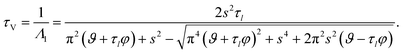 | (35) |
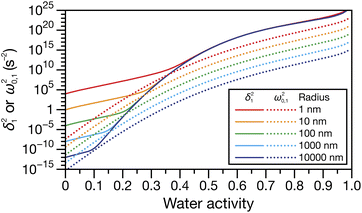 |
| | Fig. 4 Viscoelastic parameters δ12 and ω0,12 as a function of water activity. Eqn (33) and parameters for aqueous sucrose at T = 293 K were used for the calculations. | |
The viscoelastic equilibration time given here does not exactly reduce to the viscous equilibration time (eqn (29)) when the relaxation time goes to zero due to the approximations used to arrive at eqn (35).
3 Results
3.1 Calculated characteristic equilibration times
Fig. 5 shows the characteristic equilibration times for aqueous sucrose particles calculated across a range of water activities and radii using the expressions for viscous and viscoelastic equilibration times found in Section 2.2. Although the equilibration times were evaluated from 10 μm down to 1 nm, it should be anticipated that as this lower size limit is approached, the continuum assumption used throughout this work will fail. The Fickian equilibration time (eqn (1)) is also presented for comparison. The parameterizations for diffusivity and activity for aqueous sucrose were taken from ref. 23 and viscosity was calculated using AIOMFAC-VISC.45,46 For the Young's modulus, a value of 33 GPa was used in all calculations, which is representative of reported measurements for sucrose crystals at room temperature.47,48 Note that regardless of particle size and water activity, there will always be a small difference between the Fickian equilibration time and the other two equilibration times because ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A ≠
A ≠ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B and γA ≠ 1 in the viscous and viscoelastic calculations. The origin of this discrepancy was discussed in Section 2.2.
B and γA ≠ 1 in the viscous and viscoelastic calculations. The origin of this discrepancy was discussed in Section 2.2.
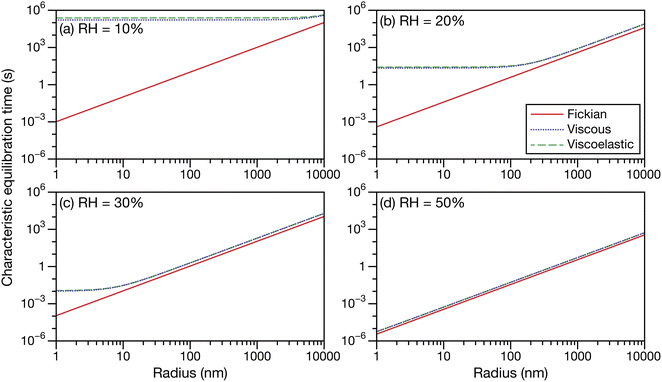 |
| | Fig. 5 The Fickian (eqn (1)), viscous (eqn (29)), and viscoelastic (eqn (35)) characteristic equilibration time as a function of radius for an aqueous sucrose particle at a RH of (a) 10%, (b) 20%, (c) 30%, and (d) 50%. Parameters for aqueous sucrose at T = 293 K were used for the calculations. | |
In Fig. 5 we see that at lower RHs (drier conditions), the radius at which noticeable separation between the three curves first appears becomes larger. The most significant difference across all panels is always between the Fickian curve and the viscous and viscoelastic curves. In the driest example shown (panel a), the Fickian times are several orders of magnitude faster than the viscous or viscoelastic times across sizes that would be relevant to atmospheric SOA (e.g. size distributions that are peaked below 100 nm (ref. 49–51)). In contrast, both the viscous and viscoelastic curves are qualitatively similar. Even quantitatively, the difference between the two curves is small. As the Young's modulus is always positive, the viscoelastic equilibration time will always be greater than the viscous equilibration time. Overall, as the RH increases, the region where this difference occurs moves to lower radii. At the highest RH (panel d), the three curves are nearly indistinguishable from each other over the plotted range of radii.
The often large difference between the Fickian curve and the other two curves in Fig. 5 can be understood by comparing the expression for the Fickian equilibration time (eqn (1)) to the expression for the viscous equilibration time (eqn (29)). When it is no longer true that s2 ≫ π2ϑ, then viscous pressure gradients play a significant role during equilibration. For a non-zero viscosity, this can always be achieved by either (i) decreasing the particle radius or (ii) increasing ϑ. In the approximate equation for the viscous equilibration time (eqn (30)), the viscous equilibration time is separated into a sum of the Fickian equilibration time and a product involving the viscosity. It is apparent that simply increasing the viscosity does not guarantee that viscous effects will dominate, as the SE relation states that the diffusivity will simultaneously decrease (resulting in the Fickian equilibration time increasing). If the SE relation is perfectly satisfied, increasing the viscosity will not affect the difference between the viscous and Fickian times for radii greater than 1 nm in the case of aqueous sucrose. However, as was discussed in Section 1, the SE relation is often inaccurate for lower water activities. In Fig. 1 it is clear that as water activity decreases (and thus viscosity increases), deviations from the SE relation become more significant. The measured viscosity becomes orders of magnitude larger than that predicted from the diffusivity using the SE relation. Therefore, the breakdown of the SE relation provides an explanation as to why the radius at which deviations begin to occur is larger for lower water activities.
In Fig. 6 and 7 the calculations from Fig. 5 are repeated but using parameters for aqueous oxidized α-pinene particles. Viscosity was calculated with AIOMFAC-VISC using a system of 15 SOA surrogate components. Tabulated AIOMFAC-VISC calculations are provided in the ESI.† As there are no measurements of the Young's modulus for oxidized α-pinene, only viscous and Fickian calculations are shown here. To our knowledge, there are only two activity-dependent diffusivity data sets for oxidized α-pinene (with the data set from ref. 7 also being temperature-dependent). Both sets of measurements along with their fits are shown in Fig. 1b, where it can be seen that, at lower water activities, the discrepancy between the two data sets is around one to two orders of magnitude. This type of difference is not seen with any of the five aqueous sucrose data sets shown in Fig. 1a. The most straightforward explanation as to why there are such large differences between the oxidized α-pinene measurements is that the oxidation products in the two cases are significantly different. The chemical composition of the oxidized α-pinene products is sensitive to the conditions under which they are produced,38 and the two samples were generated under very different conditions; e.g. the samples in ref. 7 were produced using oxidation with OH radicals, while the samples in ref. 33 were produced using O3 oxidation. This cannot be neglected, as it can be seen that the choice of the diffusivity for oxidized α-pinene has a significant impact on the calculated equilibration times: at a radius of 100 nm the Fickian and viscous times are nearly identical in every panel in Fig. 6, whereas in Fig. 7, large differences are seen in both panels (a) and (b). The implications of this will be discussed in Section 3.3.
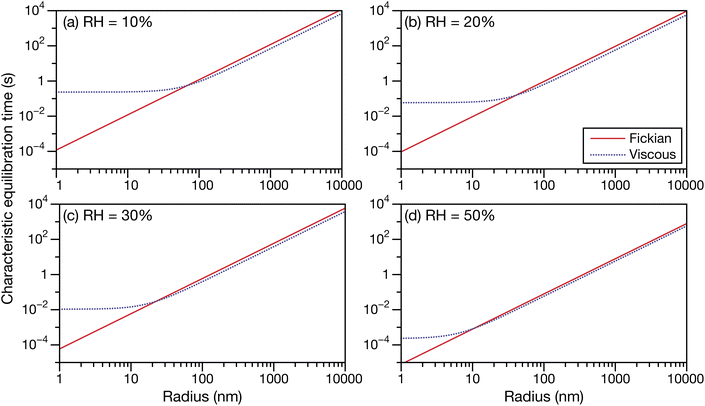 |
| | Fig. 6 The Fickian (eqn (1)) and viscous (eqn (29)) characteristic equilibration time as a function of radius for an aqueous oxidized α-pinene particle at a RH of (a) 10%, (b) 20%, (c) 30%, and (d) 50%. Parameters for aqueous oxidized α-pinene at T = 293 K were used for the calculations, with the diffusivity being calculated using the parameterization from ref. 7. | |
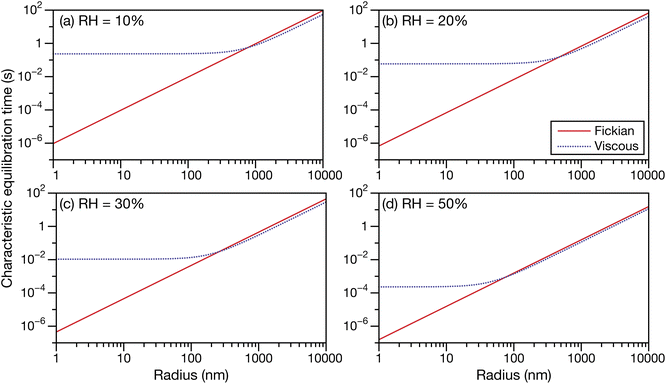 |
| | Fig. 7 The Fickian (eqn (1)) and viscous (eqn (29)) characteristic equilibration time as a function of radius for an aqueous oxidized α-pinene particle at a RH of (a) 10%, (b) 20%, (c) 30%, and (d) 50%. Parameters for aqueous oxidized α-pinene at T = 280 K were used for the calculations, with the diffusivity being calculated using a polynomial fit to the measurements from ref. 33. | |
3.2 Implications for single particle measurements
For more than a decade, single particle measurements have been used to determine the condensed phase diffusivity in aerosol particles. Six of the eight diffusivity data sets presented in Fig. 1 were measured by holding a particle in an electrodynamic balance or with optical tweezers (the other two data sets used a liquid disk on a hydrophobic slide). In all cases, the dimensions of the particles were on the order of microns. Analysis in these previous experiments was always performed within the Fickian framework. From Section 3.1, we see that such an approach should be satisfactory as, for particles in this size regime, viscous and viscoelastic effects will not affect water transport and can be safely neglected for all but the driest conditions.
3.3 Atmospheric implications
The calculations in Fig. 5–7 demonstrate that treating SOA particles, especially those with sizes in the sub-100 nm size regime (e.g. glass formers), as inviscid fluids can potentially result in a many orders of magnitude error in the characteristic equilibration time. The implications of this result to Earth's atmosphere are explored by calculating characteristic equilibration times for particles with the surrounding RH using simulated RHs and temperatures from the global chemistry climate model EMAC52 at the Earth's surface, 850 hPa (∼1.35 km), and 500 hPa (∼5.5 km). The RH and temperature data that was used is plotted in the ESI.†
Fig. 8 shows the Fickian and viscous equilibration times for aqueous sucrose and Fig. 9 shows the Fickian and viscous equilibration times for aqueous oxidized α-pinene. Viscoelastic equilibration times were not calculated as there is no temperature-dependent measurements of the Young's modulus available for either substance. However, based on calculations in Fig. 5, viscoelastic times should not differ significantly from viscous times. A particle radius of 100 nm was chosen as being representative of accumulation mode particles. Prior to our discussion, we note that sharp decreases in viscosity have been predicted for radii below 50 nm.53 While this effect will not impact the calculations shown in this section, a viscosity decrease would certainly need to be considered for smaller radii.
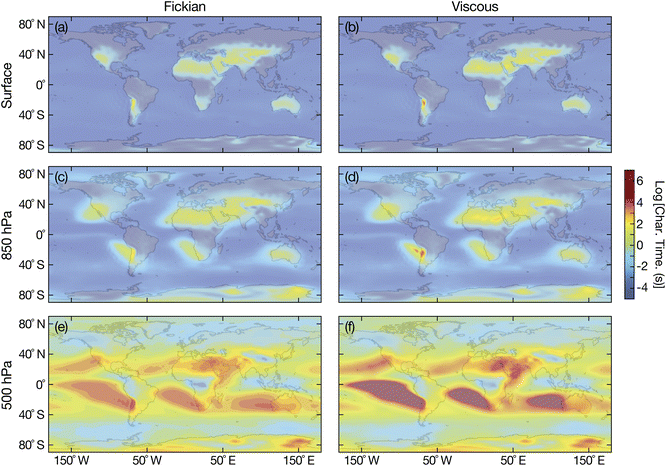 |
| | Fig. 8 Characteristic equilibration time for an aqueous sucrose particle with a radius of 100 nm with the surrounding RH at (a and b) the Earth's surface, (c and d) 850 hPa, and (e and f) 500 hPa. Fickian equilibration times (a, c and e) were calculated using eqn (1) and viscous equilibration times (b, d and f) were calculated using eqn (29). Parameters for aqueous sucrose were used for the calculations. RHs and temperatures that were used as input for these calculations were taken from the global chemistry climate model EMAC,52 and are identical to those used in ref. 8. | |
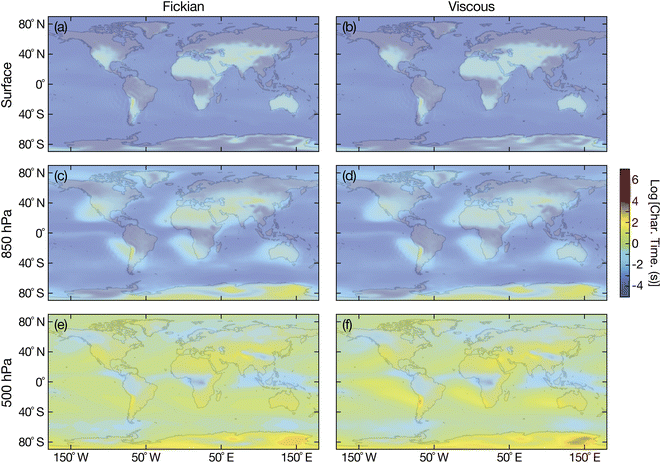 |
| | Fig. 9 Characteristic equilibration time for an aqueous oxidized α-pinene particle with a radius of 100 nm with the surrounding RH at (a and b) the Earth's surface, (c and d) 850 hPa, and (e and f) 500 hPa. Fickian equilibration times (a, c and e) were calculated using eqn (1) and viscous equilibration times (b, d and f) were calculated using eqn (29). Parameters for aqueous oxidized α-pinene were used for the calculations, with the diffusivity being calculated using the parameterization from ref. 7. RHs and temperatures that were used as input for these calculations were taken from the global chemistry climate model EMAC,52 and are identical to those used in ref. 8. | |
For the surrogate system of aqueous sucrose particles, shown in Fig. 8, the Fickian model never predicts equilibration times of more than a few minutes at the surface or 850 hPa. This is consistent with earlier calculations using the same Fickian model and similar parameters,8 where longer times (tens of minutes or hours) were only found to occur at 500 hPa. In contrast to the Fickian calculations, the viscous model predicts equilibration times of several hours for certain locations at both the surface and 850 hPa. The implications of these longer equilibration timescales for water uptake and loss are the following: Predictions concerning heterogeneous chemistry will be affected as the particle's phase state may not be that which is found by assuming equilibrium with the surrounding RH.4,54,55 This also applies to calculations of equilibrium particle size and the partitioning of semivolatile organics into the condensed phase.56,57 The phase state of the particle is also key to ice nucleation pathways. In typical adiabatic updrafts of 0.1 m s−1, glassy or solid-containing aerosol particles with equilibration times that exceed several minutes (longer than typical CCN activation time periods), may initiate ice nucleation heterogeneously under sufficiently cold conditions.6,9
Unlike aqueous sucrose particles, the equilibration times from both the Fickian and viscous calculations for aqueous oxidized α-pinene particles, shown in Fig. 9, are indistinguishable from each other at the surface and 850 hPa and are always less than a few minutes. Here, timescales longer than several minutes only occurs at 500 hPa. The similarity between Fickian and viscous times for aqueous oxidized α-pinene was anticipated based on Fig. 6, where the two times were nearly identical at a radius of 100 nm for all RHs that were shown. Of course, as the products of oxidized α-pinene can vary significantly depending on the conditions under which the oxidation takes place, it is not possible to state that the results in Fig. 9 will apply to all oxidized α-pinene particles. In Section 3.1 we discussed how oxidized α-pinene generated under different conditions can have viscous times that are much longer than Fickian times for radii of 100 nm; i.e. the results shown in Fig. 7. However, the diffusivity function used in that example does not have a temperature dependence (it is only valid for 280 K) and cannot be used in the atmospheric calculations performed here.
It appears that the answer to the question of whether or not viscous effects can significantly effect the equlibration of SOA particles with surrounding water vapor is dependent on the organic material that forms particles. In Fig. 8, the effect of viscosity was significant and equilibration times much longer than Fickian ones were observed at both the surface and 850 hPa. In contrast, in Fig. 9, the difference between the viscous and Fickian times was small everywhere except for a few locations at 500 hPa. Unfortunately, there is currently a dearth of temperature-dependent diffusivity measurements of oxidized aqueous organic material. More laboratory-based studies will be required to determine whether the situation in Fig. 8 or 9 is dominant in the atmosphere.
Finally, although the calculations here were restricted to binary systems consisting of water and an organic solute, inorganic species can also be a significant component of organic aerosol.58 One model ternary system of atmospheric relevance where equilibration times have been measured is water + citric acid + ammonium sulfate.59 In that case, the Fickian equilibration time initially increased as ammonium sulfate was added to the mixture of water and citric acid. For RH between 10 and 40%, it was only after a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of ammonium sulfate to citric acid was exceeded that the Fickian equilibration time became faster than that of the binary case of water and citric acid. For RH between 10 and 40%, AIOMFAC-VISC calculations for this ternary system predict only a decrease in viscosity with the addition of ammonium sulfate. Therefore, for this system, eqn (30) predicts that the viscous effects become less important as an inorganic solute is added to the organic and water mixture.
1 molar ratio of ammonium sulfate to citric acid was exceeded that the Fickian equilibration time became faster than that of the binary case of water and citric acid. For RH between 10 and 40%, AIOMFAC-VISC calculations for this ternary system predict only a decrease in viscosity with the addition of ammonium sulfate. Therefore, for this system, eqn (30) predicts that the viscous effects become less important as an inorganic solute is added to the organic and water mixture.
4 Summary
The main results from this work were the formulation and solution to the problem of mass transport in both a viscous and viscoelastic spherical particle. The derived analytic expressions for gas-particle equilibration times in viscous (eqn (29)) and viscoelastic (eqn (35)) particles can potentially have a broad range of applications beyond those discussed here (e.g. differential sorption in polymer spheres). When applied to systems of atmospheric relevance, it was shown that viscous and viscoelastic effects will be unimportant in laboratory-based studies of water transport involving super-micron particles. In contrast, in the sub-micron regime, and in particular below 100 nm, the effects become significant and both the viscous and viscoelastic equilibration times can be several orders of magnitude slower than the Fickian time for the same environmental conditions. For the model system of aqueous sucrose, this result was demonstrated to have significant implications for the equilibration with water vapor in the atmosphere. However, for aqueous oxidized α-pinene, the viscous equilibration time showed little difference from the Fickian equilibration time.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
T. C. P. and A. Z. acknowledge support from the Fonds de Recherche du Québec – Nature et Technologies (FRQNT). The authors wish to thank Prof. Manabu Shiraiwa for providing the simulated RH and temperature data from ref. 8 and Dr Ulrich Krieger for providing the activity and temperature-dependent parameterization for aqueous oxidized α-pinene from ref. 7.
References
- S. E. Schwartz and J. E. Freiberg, Mass-transport limitation to the rate of reaction of gases in liquid droplets: Application to oxidation of SO2 in aqueous solutions, Atmos. Environ., 1981, 15, 1129–1144 CrossRef CAS.
- S. Kumar, The characteristic time to achieve interfacial phase equilibrium in cloud drops, Atmos. Environ., 1989, 23, 2299–2304 CrossRef CAS.
- B. Shi and J. H. Seinfeld, On mass transport limitation to the rate of reaction of gases in liquid droplets, Atmos. Environ., 1991, 25A, 2371–2383 CrossRef CAS.
- M. Shiraiwa, M. Ammann, T. Koop and U. Pöschl, Gas uptake and chemical aging of semisolid organic aerosol particles, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11003–11008 CrossRef CAS PubMed.
- H. Mai, M. Shiraiwa, R. C. Flagan and J. H. Seinfeld, Under What Conditions Can Equilibrium Gas–Particle Partitioning Be Expected to Hold in the Atmosphere?, Environ. Sci. Technol., 2015, 49, 11485–11491 CrossRef CAS PubMed.
- T. Berkemeier, M. Shiraiwa, U. Pöschl and T. Koop, Competition between water uptake and ice nucleation by glassy organic aerosol particles, Atmos. Chem. Phys., 2014, 14, 12513–12531 CrossRef.
- D. M. Lienhard, A. J. Huisman, U. K. Krieger, Y. Rudich, C. Marcolli, B. P. Luo, D. L. Bones, J. P. Reid, A. T. Lambe, M. R. Canagaratna, P. Davidovits, T. B. Onasch, D. R. Worsnop, S. S. Steimer, T. Koop and T. Peter, Viscous organic aerosol particles in the upper troposphere: diffusivity-controlled water uptake and ice nucleation?, Atmos. Chem. Phys., 2015, 15, 13599–13613 CrossRef CAS.
- M. Shiraiwa, Y. Li, A. P. Tsimpidi, V. A. Karydis, T. Berkemeier, S. N. Pandis, J. Lelieveld, T. Koop and U. Pöschl, Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- D. A. Knopf, P. A. Alpert and B. Wang, The Role of Organic Aerosol in Atmospheric Ice Nucleation: A Review, ACS Earth Space Chem., 2018, 2, 168–202 CrossRef CAS.
- B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Do atmospheric aerosols form glasses?, Atmos. Chem. Phys., 2008, 8, 9263–9321 CrossRef.
- A. Virtanen, J. Joutsensaari, T. Koop, J. Kannosto, P. Yli-Pirilä, J. Leskinen, J. M. Mäkelä, J. K. Holopainen, U. Pöschl, M. Kulmala, D. R. Worsnop and A. Laaksonen, An amorphous solid state of biogenic secondary organic aerosol particles, Nature, 2010, 467, 824–827 CrossRef CAS.
- T. Koop, J. Bookhold, M. Shiraiwa and U. Pöschl, Glass transition and phase state of organic compounds: dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 2011, 13, 19238 RSC.
- R. M. Power, S. H. Simpson, J. P. Reid and A. J. Hudson, The transition from liquid to solid-like behaviour in ultrahigh viscosity aerosol particles, Chem. Sci., 2013, 4, 2597 RSC.
- J. P. Reid, A. K. Bertram, D. O. Topping, A. Laskin, S. T. Martin, M. D. Petters, F. D. Pope and G. Rovelli, The viscosity of atmospherically relevant organic particles, Nat. Commun., 2018, 9, 1–14 CAS.
- T. Alfrey, E. F. Gurnee and W. G. Lloyd, Diffusion in Glassy Polymers, J. Polym. Sci., Part C: Polym. Symp., 1966, 12, 249–261 CrossRef.
- N. L. Thomas and A. H. Windle, A theory of case II diffusion, Polymer, 1982, 23, 529–542 CrossRef CAS.
- C. J. Durning, J. L. Spencer and M. Tabor, Differential sorption and permeation
in viscous media, J. Polym. Sci., Polym. Lett. Ed., 1985, 23, 171–181 CrossRef CAS.
- D. Jou, J. Camacho and M. Grmela, On the nonequilibrium thermodynamics of non-Fickian diffusion, Macromolecules, 1991, 24, 3597–3602 CrossRef CAS.
- J. C. Wu and N. A. Peppas, Modeling of penetrant diffusion in glassy polymers with an integral sorption Deborah number, J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 1503–1518 CrossRef CAS.
- J. C. Wu and N. A. Peppas, Numerical simulation of anomalous penetrant diffusion in polymers, J. Appl. Polym. Sci., 1993, 49, 1845–1856 CrossRef CAS.
- D. De Kee, Q. Liu and J. Hinestroza, Viscoelastic (Non-Fickian) Diffusion, Can. J. Chem. Eng., 2005, 913–929 CAS.
- D. A. Edwards and D. S. Cohen, A mathematical model for a dissolving polymer, AIChE J., 1995, 41, 2345–2355 CrossRef CAS.
- B. Zobrist, V. Soonsin, B. P. Luo, U. K. Krieger, C. Marcolli, T. Peter and T. Koop, Ultra-slow water diffusion in aqueous sucrose glasses, Phys. Chem. Chem. Phys., 2011, 13, 3514–3526 RSC.
- H. C. Price, B. J. Murray, J. Mattsson, D. O'Sullivan, T. W. Wilson, K. J. Baustian and L. G. Benning, Quantifying water diffusion in high-viscosity and glassy aqueous solutions using a Raman isotope tracer method, Atmos. Chem. Phys., 2014, 14, 3817–3830 CrossRef.
- J. F. Davies and K. R. Wilson, Raman spectroscopy of isotopic water diffusion in ultraviscous, glassy, and gel states in aerosol by use of optical tweezers, Anal. Chem., 2016, 88, 2361–2366 CrossRef CAS PubMed.
- T. C. Preston, J. F. Davies and K. R. Wilson, The frequency-dependent response of single aerosol particles to vapour phase oscillations and its application in measuring diffusion coefficients, Phys. Chem. Chem. Phys., 2017, 19, 3922–3931 RSC.
- K. A. Nadler, P. Kim, D.-L. Huang, W. Xiong and R. E. Continetti, Water diffusion measurements of single charged aerosols using H2O/D2O isotope exchange and Raman spectroscopy in an electrodynamic balance, Phys. Chem. Chem. Phys., 2019, 21, 15062–15071 RSC.
- M. Quintas, T. R. S. Brandão, C. L. M. Silva and R. L. Cunha, Rheology of supersaturated sucrose solutions, J. Food Eng., 2006, 77, 844–852 CrossRef CAS.
- Y.-C. Song, A. E. Haddrell, B. R. Bzdek, J. P. Reid, T. Bannan, D. O. Topping, C. Percival and C. Cai, Measurements and Predictions of Binary Component Aerosol Particle Viscosity, J. Phys. Chem. A, 2016, 120, 8123–8137 CrossRef CAS PubMed.
- D. S. Richards, K. L. Trobaugh, J. Hajek-Herrera and R. D. Davis, Dual-Balance Electrodynamic Trap as a Microanalytical Tool for Identifying Gel Transitions and Viscous Properties of Levitated Aerosol Particles, Anal. Chem., 2020, 92, 3086–3094 CrossRef CAS PubMed.
- Y.-K. Tong, Y. Liu, X. Meng, J. Wang, D. Zhao, Z. Wu and A. Ye, Relative humidity-dependent viscosity of single quasi aerosol particle and possible implications for atmospheric aerosol chemistry, Phys. Chem. Chem. Phys., 2022, 10514–10523 RSC.
- R. Jeong, J. Lilek, A. Zuend, R. Xu, M. N. Chan, D. Kim, H. G. Moon and M. Song, Viscosity and physical state of sucrose mixed with ammonium sulfate droplets, Atmos. Chem. Phys., 2022, 22, 8805–8817 CrossRef CAS.
- H. C. Price, J. Mattsson, Y. Zhang, A. K. Bertram, J. F. Davies, J. W. Grayson, S. T. Martin, D. O'Sullivan, J. P. Reid, A. M. J. Rickards and B. J. Murray, Water diffusion in atmospherically relevant α-pinene secondary organic material, Chem. Sci., 2015, 6, 4876–4883 RSC.
- L. Renbaum-Wolff, J. W. Grayson, A. P. Bateman, M. Kuwata, M. Sellier, B. J. Murray, J. E. Shilling, S. T. Martin and A. K. Bertram, Viscosity of α-pinene secondary organic material and implications for particle growth and reactivity, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8014–8019 CrossRef CAS PubMed.
- C. Kidd, V. Perraud, L. M. Wingen and B. J. Finlayson-Pitts, Integrating phase and composition of secondary organic aerosol from the ozonolysis of α-pinene, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 7552–7557 CrossRef CAS PubMed.
- A. P. Bateman, A. K. Bertram and S. T. Martin, Hygroscopic influence on the semisolid-to-liquid transition of secondary organic materials, J. Phys. Chem. A, 2015, 119, 4386–4395 CrossRef CAS PubMed.
- Y. Zhang, M. S. Sanchez, C. Douet, Y. Wang, A. P. Bateman, Z. Gong, M. Kuwata, L. Renbaum-Wolff, B. B. Sato, P. F. Liu, A. K. Bertram, F. M. Geiger and S. T. Martin, Changing shapes and implied viscosities of suspended submicron particles, Atmos. Chem. Phys., 2015, 15, 7819–7829 CrossRef CAS.
- J. W. Grayson, Y. Zhang, A. Mutzel, L. Renbaum-Wolff, O. Böge, S. Kamal, H. Herrmann, S. T. Martin and A. K. Bertram, Effect of varying experimental conditions on the viscosity of α-pinene derived secondary organic material, Atmos. Chem. Phys., 2016, 16, 6027–6040 CrossRef CAS.
- T. C. Preston, Non-Fickian diffusion in viscous aerosol particles, Can. J. Chem., 2022, 100, 168–174 CrossRef CAS.
-
R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport Phenomena, John Wiley & Sons, 2nd edn, 2006 Search PubMed.
-
R. Taylor and R. Krishna, Multicomponent Mass Transfer, John Wiley & Sons, 1993 Search PubMed.
-
R. M. Christensen, Theory of Viscoelasticity, Academic Press, New York, 1971 Search PubMed.
- K. Fowler, P. J. Connolly, D. O. Topping and S. O'Meara, Maxwell–Stefan diffusion: a framework for predicting condensed phase diffusion and phase separation in atmospheric aerosol, Atmos. Chem. Phys., 2018, 18, 1629–1642 CrossRef CAS.
- A. Moridnejad and T. C. Preston, Models of isotopic water diffusion in spherical aerosol particles, J. Phys. Chem. A, 2016, 120, 9759–9766 CrossRef CAS PubMed.
- N. R. Gervasi, D. O. Topping and A. Zuend, A predictive group-contribution model for the viscosity of aqueous organic aerosol, Atmos. Chem. Phys., 2020, 20, 2987–3008 CrossRef CAS.
- J. Lilek and A. Zuend, A predictive viscosity model for aqueous electrolytes and mixed organic-inorganic aerosol phases, Atmos. Chem. Phys., 2022, 22, 3203–3233 CrossRef CAS.
- W. C. Duncan-Hewitt and G. C. Weatherly, Evaluating the hardness, Young's modulus and fracture toughness of some pharmaceutical crystals using microindentation techniques, J. Mater. Sci. Lett., 1989, 8, 1350–1352 CrossRef CAS.
- K. J. Ramos and D. F. Bahr, Mechanical behavior assessment of sucrose using nanoindentation, J. Mater. Res., 2011, 22, 2037–2045 CrossRef.
- B. Bonn and G. K. Moortgat, New particle formation during α- and β-pinene oxidation by O3, OH and NO3, and the influence of water vapour: Particle size distribution studies, Atmos. Chem. Phys., 2002, 2, 183–196 CrossRef CAS.
- I. Riipinen, T. Yli-Juuti, J. R. Pierce, T. Petäjä, D. R. Worsnop, M. Kulmala and N. M. Donahue, The contribution of organics to atmospheric nanoparticle growth, Nat. Geosci., 2012, 5, 1–6 CrossRef.
- R. A. Zaveri, J. E. Shilling, A. Zelenyuk, J. Liu, D. M. Bell, E. L. D'Ambro, C. J. Gaston, J. A. Thornton, A. Laskin, P. Lin, J. Wilson, R. C. Easter, J. Wang, A. K. Bertram, S. T. Martin, J. H. Seinfeld and D.
R. Worsnop, Growth kinetics and size distribution dynamics of viscous secondary organic aerosol, Environ. Sci. Technol., 2018, 52, 1191–1199 CrossRef CAS PubMed.
- P. Jöckei, H. Tost, A. Pozzer, C. Brühl, J. Buchholz, L. Ganzeveld, P. Hoor, A. Kerkweg, M. G. Lawrence, R. Sander, B. Steil, G. Stiller, M. Tanarhte, D. Taraborrelli, J. Van Aardenne and J. Lelieveld, The atmospheric chemistry general circulation model ECHAM5/MESSy1: Consistent simulation of ozone from the surface to the mesosphere, Atmos. Chem. Phys., 2006, 6, 5067–5104 CrossRef.
- M. Petters and S. Kasparoglu, Predicting the influence of particle size on the glass transition temperature and viscosity of secondary organic material, Sci. Rep., 2020, 10, 15170 CrossRef CAS PubMed.
- M. Shiraiwa, C. Pfrang and U. Pöschl, Kinetic multi-layer model of aerosol surface and bulk chemistry (KM-SUB): The influence of interfacial transport and bulk diffusion on the oxidation of oleic acid by ozone, Atmos. Chem. Phys., 2010, 10, 3673–3691 CrossRef CAS.
- F. H. Marshall, R. E. H. Miles, Y.-C. Song, P. B. Ohm, R. M. Power, J. P. Reid and C. S. Dutcher, Diffusion and reactivity in ultraviscous aerosol and the correlation with particle viscosity, Chem. Sci., 2016, 7, 1298–1308 RSC.
- Q. Ye, E. S. Robinson, X. Ding, P. Ye, R. C. Sullivan and N. M. Donahue, Mixing of secondary organic aerosols versus relative humidity, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12649–12654 CrossRef CAS.
- P. Liu, Y. J. Li, Y. Wang, M. K. Gilles, R. A. Zaveri, A. K. Bertram and S. T. Martin, Lability of secondary organic particulate matter, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12643–12648 CrossRef CAS.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Evolution of organic aerosols in the atmosphere, Science, 2009, 326, 1525–1529 CrossRef CAS.
- B. J. Wallace, C. L. Price, J. F. Davies and T. C. Preston, Multicomponent diffusion in atmospheric aerosol particles, Environ. Sci.: Atmos., 2021, 1, 45–55 CAS.
- D. L. Bones, J. P. Reid, D. M. Lienhard and U. K. Krieger, Comparing the mechanism of water condensation and evaporation in glassy aerosol, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11613–11618 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab and
Andreas
Zuend
*ab and
Andreas
Zuend
 a
a
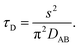

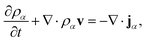
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) α, and mass fractions, wα, of species α using
α, and mass fractions, wα, of species α using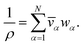
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) α are constant, the mass average velocity can be expressed in terms of mass fluxes according to39
α are constant, the mass average velocity can be expressed in terms of mass fluxes according to39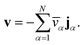
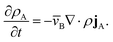
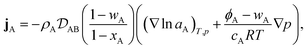
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A is the volume fraction, c is the total molar concentration, R is the universal gas constant, T is the temperature, p is the local pressure, and
A is the volume fraction, c is the total molar concentration, R is the universal gas constant, T is the temperature, p is the local pressure, and 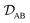 is the binary MS diffusivity. As indicated in eqn (6), the gradient of the natural logarithm of aA is evaluated at a constant T and p.
is the binary MS diffusivity. As indicated in eqn (6), the gradient of the natural logarithm of aA is evaluated at a constant T and p.
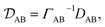
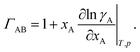
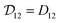 and the two diffusivities are identical.
and the two diffusivities are identical.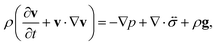
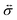 is the stress tensor, and g is the external force per unit mass. For simplicity, we ignore the effects of inertia by setting the left-hand side of eqn (9) to zero. As we will only consider cases where g = 0, eqn (9) simplifies to
is the stress tensor, and g is the external force per unit mass. For simplicity, we ignore the effects of inertia by setting the left-hand side of eqn (9) to zero. As we will only consider cases where g = 0, eqn (9) simplifies to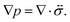
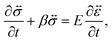
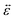 is the infinitesimal strain tensor, and
is the infinitesimal strain tensor, and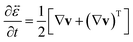
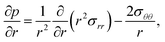
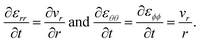
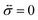 at t = 0) is
at t = 0) is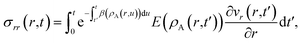
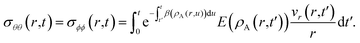
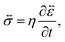
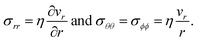
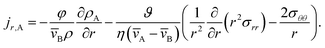
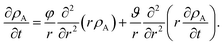
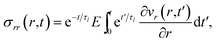
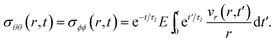
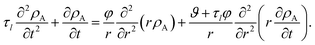
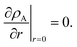
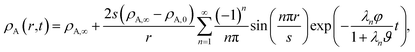
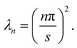
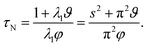
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A =
A = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B there is no viscous flow and τN will reduce to the Fickian equilibration time (eqn (1)), provided that the solution is ideal (γA = 1). However, if
B there is no viscous flow and τN will reduce to the Fickian equilibration time (eqn (1)), provided that the solution is ideal (γA = 1). However, if ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A ≠
A ≠ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B then τN will not reduce to τD, even if the viscosity is zero. This occurs because the typical Fickian treatment neglects convective mass transport due to density changes. Also, we see that for s2 ≫ π2ϑ, the viscous pressure gradients will not significantly affect the equilibration time. Fig. 2 shows concentration profiles calculated using eqn (27) during both uptake and loss in the case when Fickian diffusion dominates (a and c) and viscous effects dominate (b and d). In panels b and d, the concentration of A is always uniform (except near r = s) and equilibration is determined by material response during swelling or shrinkage (rheological limitations).
B then τN will not reduce to τD, even if the viscosity is zero. This occurs because the typical Fickian treatment neglects convective mass transport due to density changes. Also, we see that for s2 ≫ π2ϑ, the viscous pressure gradients will not significantly affect the equilibration time. Fig. 2 shows concentration profiles calculated using eqn (27) during both uptake and loss in the case when Fickian diffusion dominates (a and c) and viscous effects dominate (b and d). In panels b and d, the concentration of A is always uniform (except near r = s) and equilibration is determined by material response during swelling or shrinkage (rheological limitations).
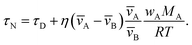

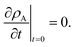
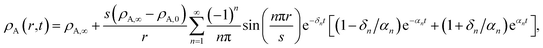
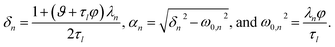
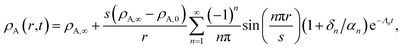
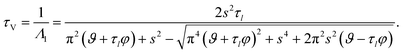

![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) A ≠
A ≠ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) B and γA ≠ 1 in the viscous and viscoelastic calculations. The origin of this discrepancy was discussed in Section 2.2.
B and γA ≠ 1 in the viscous and viscoelastic calculations. The origin of this discrepancy was discussed in Section 2.2.





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of ammonium sulfate to citric acid was exceeded that the Fickian equilibration time became faster than that of the binary case of water and citric acid. For RH between 10 and 40%, AIOMFAC-VISC calculations for this ternary system predict only a decrease in viscosity with the addition of ammonium sulfate. Therefore, for this system, eqn (30) predicts that the viscous effects become less important as an inorganic solute is added to the organic and water mixture.
1 molar ratio of ammonium sulfate to citric acid was exceeded that the Fickian equilibration time became faster than that of the binary case of water and citric acid. For RH between 10 and 40%, AIOMFAC-VISC calculations for this ternary system predict only a decrease in viscosity with the addition of ammonium sulfate. Therefore, for this system, eqn (30) predicts that the viscous effects become less important as an inorganic solute is added to the organic and water mixture.