Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluation of local measurement-driven adjustments of modelled cloud-free atmospheric photolysis rate coefficients†
Hannah L.
Walker
ab,
Mathew R.
Heal
 *a,
Christine F.
Braban
b,
Lisa K.
Whalley
cd and
Marsailidh M.
Twigg
b
*a,
Christine F.
Braban
b,
Lisa K.
Whalley
cd and
Marsailidh M.
Twigg
b
aSchool of Chemistry, University of Edinburgh, David Brewster Road, Edinburgh, EH9 3FJ, UK
bUK Centre for Ecology & Hydrology, Bush Estate, Penicuik, Edinburgh, EH26 0QB, UK
cSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK
dNational Centre for Atmospheric Science, University of Leeds, Leeds, LS2 9JT, UK
First published on 30th August 2022
Abstract
Photolysis rate constants (j-values) play a crucial role in atmospheric chemistry modelling, but capturing the variability in local conditions needed for their accurate simulation is computationally challenging. One approach is to adjust modelled clear-sky estimates using ratios of measured-to-modelled j-values of a reference photolysis, typically j(NO2) or j(O1D). However, application of such adjustments to other photolysis reactions introduces uncertainty. Using spectral radiometer data from the UK, this study examines how hourly measurement driven adjustment factors (MDAF) across a set of 12 photolysis reactions group together using cluster analysis, and evaluates the uncertainties in using j(NO2) and j(O1D)-derived MDAF values to adjust modelled j-values of other photolysis reactions. The NO2-MDAF reference is suitable for adjusting photolysis reactions that absorb at λ > 360 nm (HONO, methylglyoxal, ClNO2, ClONO2 → Cl), which are largely independent of solar zenith angle and total ozone column (<31% error). In particular, NO2-MDAF is a good reference for j(HONO) and j(ClNO2). The O1D-MDAF performed better at adjusting modelled j-values for species that predominantly photodissociate at λ < 350 nm, such as HNO3, H2O2, CH3CHO, HCHO → H, HCHO → H2 and ClONO2 → ClO (errors ≤ 30%). However, j(O1D) radiometers require more data processing to account for local conditions. The maximum error determined using NO2-MDAF was within a factor of two (91% for j(H2O2)), which may still be acceptable in some instances. It is important that MDAFs are used to improve accuracy and uncertainty in simulated j-values caused by variation in local conditions.
Environmental significanceAtmospheric chemistry is driven by solar photolysis reactions so accurate values of photolysis rate constants (j-values) are essential for accurate modelling of air quality. But these vary with local meteorological conditions such as cloud cover that models cannot readily simulate. Instruments that measure j(NO2) and j(O1D) have been used as local references to adjust modelled cloud-free j-values of other photolysis reactions but this introduces error. Using spectral radiometer data from a site in the UK, we assess the errors associated with use of j(NO2) and j(O1D) measurement-driven adjustment factors to adjust the j-values of 10 other photolysis reactions. It is important that appropriate adjustments for local solar flux conditions are used to reduce uncertainty in local air quality modelling. |
1 Introduction
Atmospheric chemistry is driven by reactive radicals produced in solar photolysis reactions.1 Consequently, inaccurate values for photolysis rate constants in models of atmospheric processes contribute uncertainty in model simulations of both primary and secondary pollutant concentrations, in the same way as inaccuracies in standard thermal rate constants.2 The photolysis rate constant, or j-value, is defined as follows,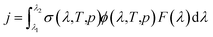 | (1) |
In respect of representation of j-values in models, the Master Chemical Mechanism (MCM) parameterises all its j-values as a function of solar zenith angle (SZA).9,10 Chemical Transport Models (CTMs) are often coupled with radiative transfer models like the Tropospheric Ultraviolet and Visible radiation model (TUV),11 or the Fast-J subroutine,12 which resolve the path of radiation from the top of the atmosphere, accounting for absorption and scattering of radiation by atmospheric components including clouds, aerosols and stratospheric ozone.13–15 Different cloud conditions can reduce16 or enhance17 the magnitude of shortwave radiation and hence the j-values at the surface. However, it is challenging to create model representations of these conditions with high accuracy without becoming computationally demanding, due to the inhomogeneity and variability in meteorological conditions with respect to location and time.18 The EMEP CTM, for example, uses the two-stream PHODIS routine19 to calculate photolysis rate constants, which are then compiled into look-up tables (of 10° latitude and 1° SZA resolution at each model height)20 for three predefined conditions: clear sky, light cloud and dense cloud.21 It is possible to incorporate Fast-J into global CTMs to determine hourly j-values, but this is still limited by model representation of spatial and temporal variation in cloud and aerosol cover, and by the uniformity imposed throughout a given model grid.
Photolysis rate constants simulated in models are often not verified beyond an initial intercomparison with measurements. Short-term campaigns have constrained model j-values based on spectral radiometer measurements,22 or adjusted for local conditions using some form of scaling factor. Kanaya et al.23 suggested that a single transmission factor, defined as the ratio of actinic flux in cloudy versus clear conditions at the same wavelength, could be used as a linear scaling factor to calculate any j-value under cloudy conditions at the same SZA, within 15%. Ratios of measured to modelled photolysis rate constants for reference species have been used more often in subsequent years. The usual reference is j(NO2),24–26 associated with (R1), due to the simplicity and long-term stability of its measurement with a filter radiometer.3
| NO2 + hν (λ ≤ 420 nm) → NO + O(3P) | (R1) |
Measurements of j(O1D) (R2) have also been used where this reaction pathway is studied specifically.22,27 Measurement of j(O1D) can be made by spectral or filter radiometer, but the latter is more difficult since instrument outputs require corrections to account for SZA, total ozone column, and temperature.28,29
| O3 + hν (λ ≤ 330 nm) → O(1D) + O2 | (R2) |
Ratios derived from j(NO2) measurements have been used to scale modelled j(O1D), despite the lack of overlap in wavelengths of actinic flux contributing to photolysis.30,31 The use of a single reference species assumes that all wavelengths of actinic flux respond linearly to changes in meteorological conditions (e.g. clouds and aerosols), which has been demonstrated as invalid for the photolysis of NO2 and O3.32 In clear-sky conditions, Rayleigh scattering is dominant, and its proportionality to λ−4 causes more efficient scattering of shorter wavelengths and more diffuse solar radiation at the surface relative to direct radiation. The quantity of diffuse light is therefore greater at higher SZA due to the longer radiation path length (greater number of scatterers in the path). The presence of clouds and aerosols produce comparatively less dependence on wavelength33 and consequently affect j(NO2) at the surface to a greater extent than j(O1D),34 since the difference with clear skies is greater.
Studies such as Dusanter et al.35 and Stone et al.36 have recognised this and used a mixture of j(NO2)- and j(O1D)-derived adjustment factors, where each photolysis rate constant is scaled according to the wavelengths relevant to the photolysis reaction under consideration. Photolysis rate constants for reactions which take place more in the UVB region (280–315 nm) use a j(O1D)-derived adjustment factor, and vice versa. However, the impact of this mixed approach for deriving adjustment factors for other species has not yet been explored. Therefore, the overall aim of the work presented here was to investigate reaction-specific measurement-driven adjustment factors (MDAFs) for a set of 12 atmospheric photodissociation reactions. The specific objectives were to determine how the MDAF values across a set of photolysis reactions group together and to evaluate the uncertainty that arises from using MDAF values derived from j(NO2) or j(O1D) to adjust other modelled j-values. The dataset comprises time series of spectral radiometer measurements from Chilbolton Observatory in southern UK. The ten photolysis reactions included in addition to (R1) and (R2) are listed in Table 1. Hierarchical cluster analysis was used to cluster these photolysis reactions into groups, and to investigate the applicability of j(NO2)- and j(O1D)-derived reference MDAF values on the j-values of other species. The difference in these scaling factors was demonstrated through calculations of the production rate of OH radicals from the photolysis of O3 (p(OH)O3). The implications for use of MDAFs for quantifying local air quality are discussed.
| Photolysis reaction | j-Value & MDAF label | Molecular-specific parameter references | ||
|---|---|---|---|---|
| Spectral radiometer | TUV model | |||
| a Quantum yield of unity used for all wavelengths considered. b Evaluation of these references by Madronich as specified in the TUV v5.3 model code.43 | ||||
| NO2 + hν → NO + O(3P) | j(NO2) | σ | Mérienne et al.60 | Vandaele et al.61 |
| NO2-MDAF | ϕ | Gardner et al.62 | Roehl et al.63 corrected by Troe64 | |
| O3 + hν → O(1D) + O2 | j(O1D) | σ | Molina et al.65 | Molina and Molina45 |
| O1D-MDAF | ϕ | Matsumi et al.57 | ||
| H2O2 + hν → 2OH | j(H2O2) | σ | Burkholder et al.46 | De More et al.66,67 |
| H2O2-MDAF | ϕ | Atkinson et al.68,a | Assumed to be 1a | |
| HONO + hν → OH + NO | j(HONO) | σ | Bongartz et al.69,70 | Bongartz et al.69 |
| HONO-MDAF | ϕ | Burkholder et al.46,a | Sander et al.50,a | |
| HNO3 + hν → OH + NO2 | j(HNO3) | σ | Burkholder et al.44 | Molina et al.45 |
| HNO3-MDAF | ϕ | Atkinson et al.68,a | Assumed to be 1a | |
| HCHO + hν → H + HCO | j(HCHO)–H | σ | Meller and Moortgat71 | |
| HCHO–H-MDAF | ϕ | Smith et al.72 | Horowitz and Calvert;73 Moortgat et al.74,b | |
| HCHO + hν → H2 + CO | j(HCHO)–H2 | σ | Meller and Moortgat71 | |
| HCHO–H2-MDAF | ϕ | Moortgat et al.74 | Horowitz and Calvert;73 Moortgat et al.74,b | |
| CH3CHO + hν → CH3 + HCO | j(CH3CHO) | σ | Martinez et al.75 | Sander at al50 |
| CH3CHO-MDAF | ϕ | Meyrahn et al.76 | Horowitz and Calvert77 | |
| CH3COCHO + hν → CH3CO + HCO | j(MGLY) | σ | Meller et al.;78 Staffelbach et al.79 | Sander at al50 |
| MGLY-MDAF | ϕ | Chen et al.80 | ||
| ClNO2 + hν → Cl + NO2 | j(ClNO2) | σ | Ghosh et al.47 | Illies and Takacs;48 Furlan et al.49 |
| ClNO2-MDAF | ϕ | Assumed to be 1a | ||
| ClONO2 + hν → Cl + NO3 | j(ClONO2)–Cl | σ | Burkholder et al.81 | |
| ClONO2–Cl-MDAF | ϕ | Atkinson et al.;82 Sander et al.50 | ||
| ClONO2 + hν → ClO + NO2 | j(ClONO2)–ClO | σ | Burkholder et al.81 | |
| ClONO2–ClO-MDAF | ϕ | ϕ ClONO2–ClO(λ) = 1 − ϕClONO2–Cl(λ) | ||
2 Methods
2.1 Measured j-values
Radiation measurements were made at Chilbolton Observatory, a rural background air quality monitoring station ∼100 km south-west of London (51°09′N, 1°26′W, altitude: 78 m; Fig. 1). It is located in the grounds of Chilbolton Atmospheric Observatory (CAO), which makes long-term meteorological observations for the study of clouds, rainfall and boundary-layer processes.37 The site is also the UK's southern EMEP level II supersite,38 incorporating instruments for a variety of different air pollutant monitoring networks.39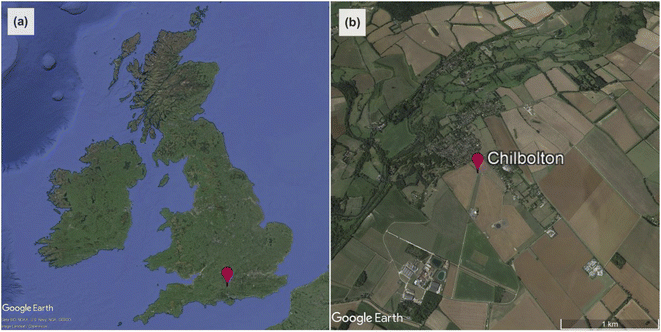 | ||
| Fig. 1 (a) The location of Chilbolton Observatory in the UK. (b) Satellite image of the area surrounding Chilbolton Observatory to ∼1 km in all directions (from Google Earth83). | ||
Spectral actinic flux was measured between 280–750 nm (∼1 nm resolution) using a spectrometer with a back-thinned CCD detector (Ocean Optics QE65000, USA) coupled with a fibre-optic cable to a 2π quartz receiver optic (Meteorologie Consult GmbH, DE). This is the UK's National Atmospheric Facility radiometer, as used, for example, in the Clean Air for London project.22,40 The radiometer was located on the north side of the CAO site, mounted ∼6.5 m above ground level on black-painted railings of a cabin roof. The ground beneath the cabin is predominantly short grass, surrounded by homogeneous arable farmland. The immediate area within the view of the 2π sr optical inlet is clear, and the majority of the site is approximately 500 m south of the cabin. The radiometer was available between 17 December 2020 and 19 March 2021 and was calibrated prior to deployment against a 1000 W tungsten–halogen lamp of standard spectral irradiance (OL FEL-A; Gooch & Housego, USA).
Photolysis rate constants for the reactions considered here were derived using IUPAC-recommended literature values of absorption cross-sections and quantum yields (Table 1), interpolated to the wavelength resolution of the measurements. Time resolution of estimated photolysis rate constants was 1 min. Raw signals measured by the spectrometer were corrected by subtracting both the dark signal and the estimated contribution of stray light. The dark signal was acquired from spectra measured during the night, whilst stray light was determined following published procedure41 by extrapolating a curve fit where no solar light is observed to all measured wavelengths where solar and stray light both contribute. Previous deployments of this spectrometer against a double monochromator spectrometer in London confirm the robustness of these stray light corrections,22 as concluded also by Bohn and Lohse.41
The SZA was determined for each scan from latitude, longitude, date and time in UTC.42 As spectral radiometer calibration was for SZAs up to 86°, measurements at SZA > 86° were excluded from further analysis.
The clearest day in the dataset was identified as 9 March 2021 from the smoothest curves of 1 min measurements for all j-values (collectively covering the full wavelength range; see ESI Fig. S1†). All spectra of photodissociation rate coefficients, and corresponding hierarchical clustering, utilise data collected at solar noon on this day.
2.2 Modelled j-values
Modelled j-values for the 12 reactions were determined for cloud-free conditions at the location and altitude of the radiometer inlet using the Tropospheric Ultraviolet and Visible radiative transfer model (TUV v5.3)11,43 and the σ and ϕ values detailed in Table 1. Calculations were undertaken for downwelling radiation (direct and diffuse) and for SZAs 40°–90°, in intervals of 0.5°, for the TUV default wavelength grid between 250 and 700 nm.The σ and ϕ values used in the TUV model derive mostly from the JPL recommendations while those used for spectral radiometer calculations are from IUPAC. These agree to ≤10%, with a few exceptions. The IUPAC recommended σ(HNO3) values44 match those used in the TUV model45 to ≤15% for wavelengths ≤310 nm,46 but differences increase to ∼50% at 330 nm. Similarly, the σ(ClNO2) values agree well for λ ≤ 310 nm, but deviations from the more recent IUPAC recommended values47 occur for λ > 320 nm. The values used in the TUV model are an averaged combination of Illies and Takacs48 and Furlan et al.,49 which reach a maximum difference of 45% and 70% smaller, respectively, than those of Ghosh et al.47 However, the largest discrepancies occur at the smallest values of σ(ClNO2) (at 400 nm), so consequently have little impact on total calculated j(ClNO2). Although some values of the variables have been updated in more recent JPL and IUPAC recommendations – for example, the JPL 2011 values of σ(HCHO)50 have been scaled up by 8% in JPL 2020 recommendations46 – this study proceeded with the values used in TUV v5.3 (and MCM v3.3), as specified in Table 1.
The ozone column, air temperature and aerosol optical depth (AOD) measurements used as model input were daily averages, with linear interpolation across data gaps. The ozone column data were obtained from the OMI instrument on NASA's Earth Observing System's (EOS) Aura satellite.51 Air temperature and AOD were measured on-site. The former was measured with a Vaisala HMP155A humidity and temperature probe, and the latter with an AERONET (AErosol RObotic NETwork) Cimel Sunphotometer.52 AOD at 550 nm was obtained from linear interpolation of AOD measured at 340, 380, 440, 500, 675, 870 and 1020 nm on each day, and scaled in the model by altitude using the US Standard Atmosphere profile.53 The aerosol single scattering albedo (SSA) was set to 0.99. High values of SSA denote a highly scattering atmosphere in the model (1 = purely scattering, 0 = purely absorbing), and small changes can lead to a larger difference in transmission of diffuse radiation, e.g. 300–360 nm region reported by Michalsky et al.54 In this model set-up, a decrease in SSA of 0.1 resulted in approx. 6% decrease in downwelling j(NO2). It is expected that the SSA will be >0.8 for aerosols,42 resulting in a maximum potential uncertainty of <12%.
2.3 Measurement-driven adjustment factor
An hourly averaged measurement-driven adjustment factor (MDAF) for each photolysis reaction X was derived as the ratio of the measured to modelled j-values (eqn (2)).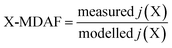 | (2) |
There are no MDAF values for SZA > 86° because these measured j(X) values were excluded. Where multiple photolysis channels are considered (e.g. for j(HCHO) and j(ClONO2)), the MDAF labels for the separate channels are presented in Table 1.
2.4 Hierarchical cluster analysis of j-values
The extent of similarity amongst the studied set of j-values was investigated using hierarchical cluster analysis of the time series of hourly MDAF values derived from the measurements. In hierarchical cluster analysis (HCA), each observation initially comprises its own cluster. The distances between clusters are computed, and the two nearest (most similar) clusters are merged together. This is repeated until all clusters are merged into one containing all observations. The hierarchy of similarity between the observations is visualised using a dendrogram. The HCA was performed in R,55 and presented using the openair package.563 Results and discussion
3.1 Variation in j-value MDAFs
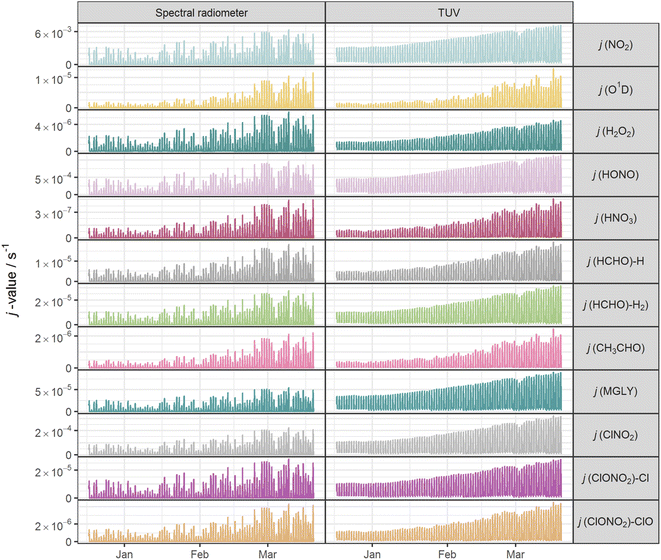
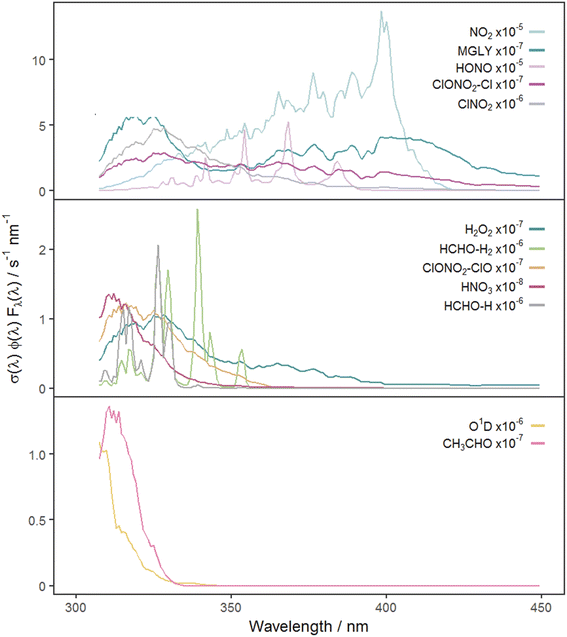
Fig. 2 shows the time series of hourly j-values determined from measured actinic flux and from the TUV model for the 12 photolysis reactions. As expected, all j-values follow broadly the same variation over the full time series of measurements, driven by seasonality and the prevailing synoptic meteorology. Fig. 3 shows the photolysis action spectra (the product of absorption cross section, quantum yield and actinic flux at each wavelength) for the 12 reactions. These spectra were calculated using actinic flux measured at solar noon on the clearest day (9 March 2021), for which SZA ∼ 55°. The set of measured diurnal j-values on this day are shown in ESI Fig. S1.†Variations in the modelled cloud-free j-values for a given photolysis reaction are driven by changes in aerosol optical depth (AOD; 550 nm) and the ozone column. In this study, daily mean AOD ranges from 0.035–0.43 (mean 0.082), while total ozone column shows a broadly increasing trend between December and March, within the range 258–424 DU (mean 318 DU) (ESI Fig. S2†). The total ozone column has negligible impact on photodissociations dominated by longer wavelengths (e.g. NO2, Fig. 3) since O3 does not absorb at these wavelengths. The primary influences on these j-values in cloudless conditions are SZA and AOD. This is illustrated during the period of maximum AOD (>0.1; 1–3 March 2021) in the time series of modelled j-values (Fig. 2), where modelled j-values decrease from the otherwise upwards trend in time. No other factors cause significant variations in j-values for photodissociations that predominantly occur in the UVA region. However, photodissociations that occur further into the UVB region (such as the O(1D) channel of O3, Fig. 3) are affected by SZA, AOD and total ozone column (Rayleigh scattering is also greater at shorter wavelengths), and therefore have more variation in simulated cloud-free j-values. Since the impact of total ozone column is intrinsically linked to SZA (via the slant ozone column, which is proportional to 1/cos(SZA)), modelled diurnal variation for the photolyses absorbing in the UVB are influenced by the ozone column density. Where the total ozone column is higher, predicted j-values are smaller, particularly at high SZA (such as sunrise or sunset), resulting in a narrower diurnal cycle than for the predominantly UVA-dependent photodissociations: for example, for the diurnal cycle of j(O1D) compared with j(NO2) shown in ESI Fig. S1.†
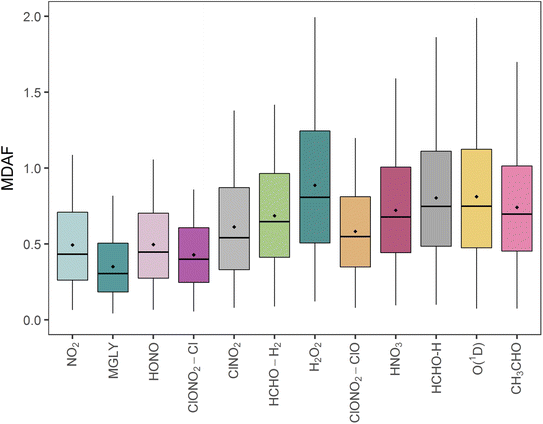
The mean measured and modelled j-values for the full period, and the ratio between them, are presented in Table 2. This ratio of long-term j-value means is closest to unity for j(H2O2) (0.88) and furthest from unity for j(MGLY) (0.38). However, what is relevant to atmospheric chemistry is how this ratio varies on short timescales, so Fig. 4 presents box plots of the hourly MDAF values for each photolysis reaction. The mean and standard deviation of the hourly MDAF values are summarised in Table 3. These data again pick out j(H2O2) as having mean MDAF closest to unity (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.89), followed by O1D-MDAF (
= 0.89), followed by O1D-MDAF (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.81), HNO3-MDAF (
= 0.81), HNO3-MDAF (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.80) and CH3CHO-MDAF (
= 0.80) and CH3CHO-MDAF (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.74), whilst mean MGLY-MDAF is furthest from unity (
= 0.74), whilst mean MGLY-MDAF is furthest from unity (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.35), followed by ClNO2-MDAF (
= 0.35), followed by ClNO2-MDAF (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.43), NO2-MDAF (
= 0.43), NO2-MDAF (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.49) and HONO-MDAF (
= 0.49) and HONO-MDAF (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 0.50).
= 0.50).
| Photolysis rate constant | Mean/s−1 | Ratio measured/modelled | |
|---|---|---|---|
| Measured | Modelled | ||
| j(NO2) | 1.7 × 10−3 | 3.3 × 10−3 | 0.52 |
| j(O1D) | 1.8 × 10−6 | 2.3 × 10−6 | 0.78 |
| j(H2O2) | 1.5 × 10−6 | 1.7 × 10−6 | 0.88 |
| j(HONO) | 2.6 × 10−4 | 5.1 × 10−4 | 0.51 |
| j(HNO3) | 6.2 × 10−8 | 7.8 × 10−8 | 0.79 |
| j(HCHO)–H | 4.3 × 10−6 | 6.0 × 10−6 | 0.72 |
| j(HCHO)–H2 | 7.2 × 10−6 | 1.2 × 10−5 | 0.60 |
| j(CH3CHO) | 4.0 × 10−7 | 5.5 × 10−7 | 0.73 |
| j(MGLY) | 1.5 × 10−5 | 3.9 × 10−5 | 0.38 |
| j(ClNO2) | 5.7 × 10−5 | 1.3 × 10−4 | 0.44 |
| j(ClONO2)–Cl | 7.4 × 10−6 | 1.3 × 10−5 | 0.57 |
| j(ClONO2)–ClO | 1.0 × 10−6 | 1.4 × 10−6 | 0.71 |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) and standard deviation (σ) of hourly X-MDAF measurements over the full dataset. The same is presented for the ratio of X-MDAF to NO2-MDAF and the ratio of X-MDAF to O1D-MDAF. Also presented are the relative standard deviation (RSD, %) and the overall error (in %) in the ratios, the latter of which represents the sum in quadrature of the RSD and the absolute percentage difference between the mean X-MDAF/NO2-MDAF or X-MDAF/O1D-MDAF and unity
) and standard deviation (σ) of hourly X-MDAF measurements over the full dataset. The same is presented for the ratio of X-MDAF to NO2-MDAF and the ratio of X-MDAF to O1D-MDAF. Also presented are the relative standard deviation (RSD, %) and the overall error (in %) in the ratios, the latter of which represents the sum in quadrature of the RSD and the absolute percentage difference between the mean X-MDAF/NO2-MDAF or X-MDAF/O1D-MDAF and unity
| HCA group | Photolysis reaction (X) | X-MDAF | X-MDAF/NO2-MDAF | X-MDAF/O1D-MDAF | |||||
|---|---|---|---|---|---|---|---|---|---|
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
σ |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
σ (RSD) | Overall error |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
σ (RSD) | Overall error | ||
| 1 | NO2 | 0.49 | 0.3 | — | — | — | 0.60 | 0.1 (17%) | 43% |
| MGLY | 0.35 | 0.2 | 0.71 | 0.02 (3%) | 29% | 0.43 | 0.09 (21%) | 61% | |
| HONO | 0.50 | 0.3 | 1.0 | 0.04 (4%) | 4% | 0.61 | 0.1 (16%) | 42% | |
| ClONO2–Cl | 0.61 | 0.3 | 1.3 | 0.03 (2%) | 30% | 0.75 | 0.2 (26%) | 36% | |
| ClNO2 | 0.43 | 0.2 | 0.91 | 0.08 (9%) | 13% | 0.54 | 0.09 (17%) | 49% | |
| 2 | H2O2 | 0.89 | 0.5 | 1.9 | 0.2 (11%) | 91% | 1.1 | 0.2 (18%) | 21% |
| HCHO–H2 | 0.58 | 0.3 | 1.3 | 0.1 (8%) | 31% | 0.74 | 0.1 (14%) | 30% | |
| ClONO2–ClO | 0.69 | 0.3 | 1.5 | 0.2 (13%) | 52% | 0.86 | 0.1 (12%) | 18% | |
| HNO3 | 0.80 | 0.4 | 1.7 | 0.3 (18%) | 72% | 1.0 | 0.09 (9%) | 9% | |
| HCHO–H | 0.72 | 0.3 | 1.6 | 0.2 (13%) | 61% | 0.92 | 0.1 (11%) | 14% | |
| 3 | O(1D) | 0.81 | 0.4 | 1.7 | 0.4 (24%) | 74% | — | — | — |
| CH3CHO | 0.74 | 0.4 | 1.6 | 0.3 (19%) | 63% | 0.93 | 0.07 (8%) | 11% | |
Although mean X-MDAF values for all photolysis reactions are less than unity, the hourly MDAF values show considerable variation (large standard deviations in Table 3), extending from almost zero to a maximum value of 2.0 observed for one measurement hour for O1D-MDAF (Fig. 4). In general, the MDAF values closest to unity have the largest variation, as illustrated by the spread of the box plots in Fig. 4. The common feature between these photolysis reactions is that they occur at shorter wavelengths compared to those with a lower mean MDAF value (e.g., NO2). As a result, during the lowest light levels (highest SZA), these MDAF values are more sensitive to differences between measured and modelled j-values.
3.2 Groupings of j-value MDAFs
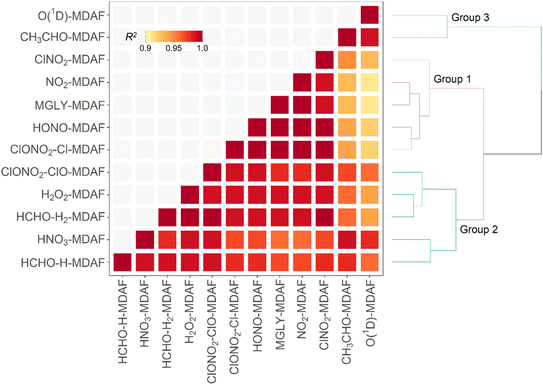
The focus of this study is on how the MDAFs across a set of photolysis reactions group together, and on investigating the magnitude of uncertainty that arises from using MDAFs derived from one photolysis reaction (typically j(NO2) and j(O1D)) to adjust the modelled j-values of another photolysis reaction. Fig. 5 shows the correlations and associated agglomerative hierarchical clustering derived from the time series of the hourly MDAFs of the 12 photolysis reactions considered here. They divide into the following three groups.• Group 1: nitrogen dioxide (NO2), methyl glyoxal (MGLY), nitrous acid (HONO), Cl-channel of chlorine nitrate (ClONO2–Cl) and nitryl chloride (ClNO2).
• Group 2: hydrogen peroxide (H2O2), nitric acid (HNO3), H2-channel of formaldehyde (HCHO–H2), H-channel of formaldehyde (HCHO–H) and ClO-channel of chlorine nitrate (ClONO2–ClO).
• Group 3: ozone (O1D) and acetaldehyde (CH3CHO).
Although the hierarchical clustering requires some choices on clustering algorithm, exploration of other clustering options (e.g., distance matrix), led to similar clustering.
Reference to Fig. 3 shows that these groupings derive from similar broad features in the photolysis action spectra, in particular the wavelengths of principal absorption. This is because fluctuations in actinic flux due to variation in clouds, aerosols and ozone column are different for wavelengths in the UVA and UVB regions.34 The mean X-MDAF values shown in Table 3 are presented in the same groups in order to highlight the different magnitudes of measurement-driven adjustment of modelled j-values across the three groups.
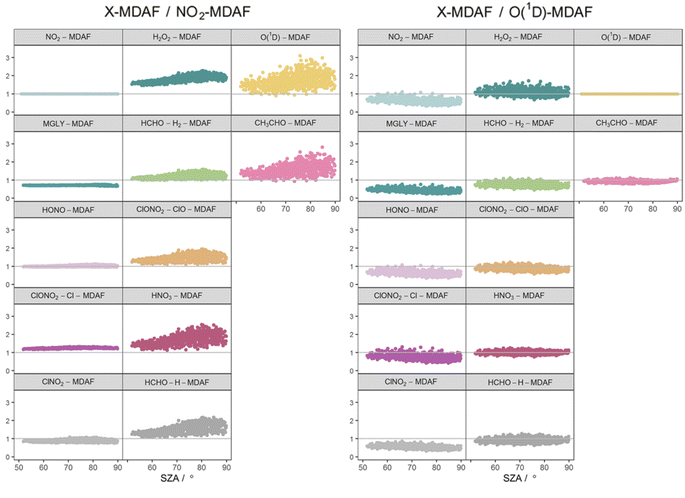
The photolysis reactions in group 1 [j(NO2), j(HONO), j(MGLY), j(ClNO2) and j(ClONO2–Cl)] are characterised by absorption across a broad band of wavelengths, but particularly by absorptions at wavelengths within the upper limit of the UVA (>370 nm) and into the visible regions (>400 nm) (Fig. 3). As such, variation in the j-values for these reactions behave similarly to j(NO2), and are primarily affected by SZA and AOD. The MDAF values for each photolysis in this group lie in ranges that are invariant with SZA (Fig. 6). Similarly, their MDAF values lie in ranges that are invariant with slant ozone column (ESI Fig. S3†). There is little absorption by the ozone column at wavelengths relevant to the action spectra for these photolyses. As a result, the quantity of actinic flux reaching the point of observation has a larger relative decrease when measurements are impacted by clouds. This large impact of cloud cover on measurements relative to the cloud-free model estimate means this group of photolysis reactions have the largest differences between measured and modelled values, i.e., the smallest average values of X-MDAF (0.35–0.61; Table 3).
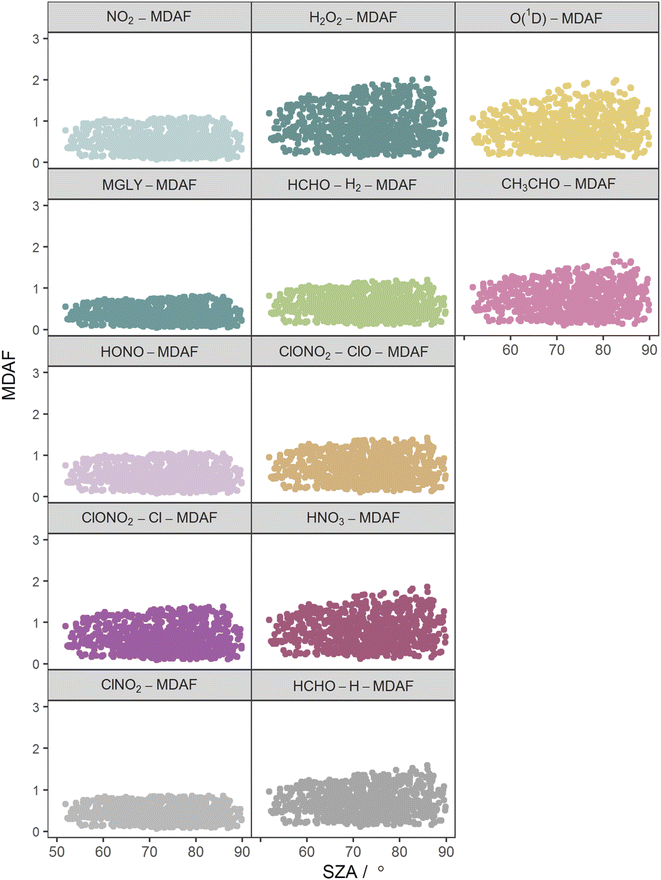 | ||
| Fig. 6 Hourly MDAF values for each photolysis reaction as a function of SZA. The panels are arranged into the three groups derived from hierarchical clustering of the MDAF time series. | ||
In contrast, the action spectra of the two photolysis reactions in group 3 [j(O1D) and j(CH3CHO)] are characterised by photodissociation in the UVB region and complete absence of absorption at λ > ∼330 nm. This indicates that a lack of photodissociation at longer wavelengths is a more significant influence on the MDAFs for these photolyses than photodissociation at shorter wavelengths. Stronger Rayleigh scattering and greater absorption by the ozone column at larger SZA and longer atmospheric path-lengths result in less relative difference in actinic flux between cloudy and cloud-free conditions. Consequently, average MDAF values are closer to unity for photolysis reactions in group 3 (mean O1D-MDAF = 0.81 and mean CH3CHO-MDAF = 0.74; Table 3) than in group 1.
The MDAF values of photolysis reactions in group 2 [j(HNO3), j(HCHO–H), j(HCHO–H2), j(H2O2) and j(ClONO2–ClO)] lie between these two extremes. Their action spectra are characterised by absorptions in the 330–370 nm region across both UVA and UVB, but no absorptions at λ > ∼370 nm at which the group 1 reactions photolyse. The MDAF values demonstrate some dependence on SZA (Fig. 6) but show more within-group variation. The H2O2-MDAF and HNO3-MDAF values have the greatest ranges with SZA, because of the considerable absorption at shorter wavelengths demonstrated by the broad peaks in Fig. 3.
The MDAF values associated with j(H2O2) cluster into a different group than for j(ClNO2) and j(NO2) (Fig. 5) despite superficially appearing to have quite similar profiles of absorption with wavelength in their action spectra (Fig. 3). However, the magnitudes of the MDAF values for these photolysis reactions are quite different (Fig. 4), and the much greater magnitudes of σ(ClNO2) and σ(NO2) compared with σ(H2O2) at longer wavelengths (λ > 340 nm),45,47 as shown in the different y-axis scales in Fig. 3, means the photolyses of ClNO2 and NO2 at longer wavelengths are an order of magnitude greater than for H2O2. (ϕ is the same (unity) at all wavelengths for all these species.) This causes ClNO2 and NO2 to group together separately from the photolyses in group 2.
Temperature can influence modelled j-values through both σ and ϕ. For example, there is a 13% increase in j(O1D), although only a 1% increase in j(ClNO2), between 273 and 298 K.28,29,47,57 In this study, the range of daily average temperature was relatively small (14 K; 271–285 K), which led to a difference of approximately 7.5% for j(O1D), and a negligible effect on j(ClNO2). Temperature therefore has less impact on j-value estimates than either AOD or total ozone column.
3.3 Impact of using a reference species to scale other photodissociation rate constants
The photolysis of NO2 appears in group 1. Therefore, as would be expected, ratios of X-MDAF to NO2-MDAF are closest to unity for the rest of the photolysis reactions in group 1 (Table 3). These reactions all have significant photolysis at longer wavelengths. HONO-MDAF has the best agreement with NO2-MDAF with a mean ratio of 1.0 ± 0.04 (Table 3), and essentially no dependence on SZA (Fig. 7) or on slant ozone column (Fig. 8). This is consistent with the high correlation observed between j(NO2) and j(HONO) observed by Kraus and Hofzumahaus.58 Values of ClNO2-MDAF also demonstrate good agreement with NO2-MDAF (mean ratio 0.91 ± 0.08, Table 3), albeit with more uncertainty at all SZAs in this dataset (55–86°). Therefore, using NO2-MDAF values to derive locally appropriate j(HONO) and j(ClNO2) values should not introduce significant errors. Relying solely on the TUV model estimations of these j-values results in a modelled overestimation of approximately a factor of 2 for each photolysis reaction (Table 3).
 | ||
| Fig. 7 Ratios of derived MDAF values for each photolysis reaction relative to an NO2-MDAF reference (left) and an O(1D)-MDAF reference (right), as a function of SZA. The panels are arranged into the three groups derived from hierarchical clustering of the MDAF time series, and the same positions as Fig. 6. | ||
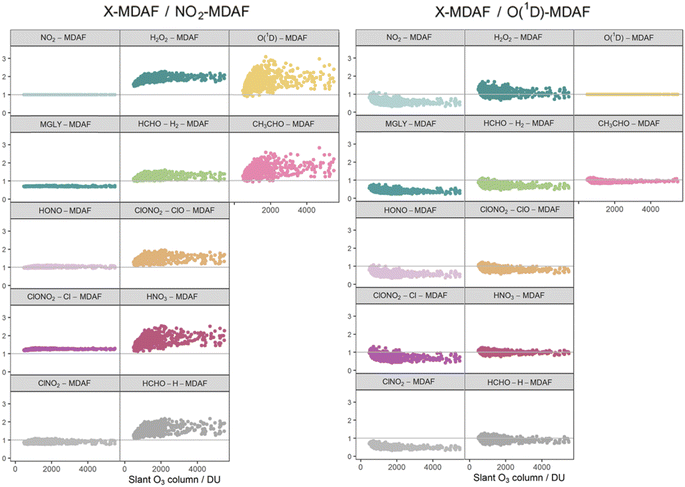 | ||
| Fig. 8 Ratios of derived MDAF values for each photolysis reaction relative to an NO2-MDAF reference (left) and an (O1D)-MDAF reference (right), as a function of the slant ozone column. The panels are arranged into the three groups derived from hierarchical clustering of the MDAF time series, and the same positions as Fig. 6. | ||
The MDAF values of the remainder of the photolysis reactions in group 1 (MGLY and ClONO2–Cl) also have very good linearity with NO2-MDAF for the full range of observed SZA (Fig. 7) and slant ozone column (Fig. 8). However, the mean values of the ratios of MGLY-MDAF and ClONO2–Cl-MDAF to NO2-MDAF are approximately 30% above and below unity, respectively (0.71 ± 0.02 and 1.3 ± 0.03, Table 3). Since the j-values of both the measured and modelled data are calculated with the same molecule-specific parameters, the difference in ratio to NO2-MDAF is a consequence of j(MGLY) and j(ClONO2–Cl) being approximately two orders of magnitude smaller than j(NO2) (Fig. 2). The absolute differences between the cloud-free modelled and cloud-inclusive measured j(MGLY) are larger than j(NO2), while those of j(ClONO2–Cl) are smaller. Ultimately, this increases the potential uncertainty of applying an NO2-MDAF metric to these modelled j-values to around 30%, but this could be reduced to an uncertainty closer to the RSD estimates (4% and 2%, respectively) by using another adjustment factor to scale the NO2-MDAF ratio for each photolysis reaction.
As expected, given the groupings, O1D-MDAF and CH3CHO-MDAF exhibit the most variation in their ratios to NO2-MDAF across all SZA (Fig. 7) and slant ozone columns (Fig. 8). This large deviation from NO2-MDAF is due to these photolyses occurring at shorter wavelengths (Fig. 3).
Photolysis reactions in group 2 have more variation in the X-MDAF/NO2-MDAF ratios (RSD ≥ 8%) than those in group 1 (Table 3). The X-MDAF/NO2-MDAF relationships are mostly constant at lower SZA (≤60°; Fig. 7) but increase in both magnitude and scatter at SZA > 60°. A similar observation is apparent in Fig. 8, where the ratio of X-MDAF to NO2-MDAF increases rapidly at similar slant ozone column, demonstrating the importance of the total ozone column abundance when considering reactions which photolyse at shorter wavelengths. HCHO–H2-MDAF has the most similarities to NO2-MDAF, being near unity and constant at the smaller observed SZA (approx. <65°). This can be attributed to a larger peak in the action spectra of HCHO–H2 at around 340 nm, compared to its smaller peaks in the UVB region (<315 nm) (Fig. 3), which could be driving the increased scatter at larger SZA. The relative standard deviation (8%) and overall error (31%) of using an NO2-MDAF reference to adjust j(HCHO)–H2 is similar to using NO2-MDAF for the photolysis reactions in group 1 (Table 3). HNO3-MDAF shows the weakest consistency with NO2-MDAF (RSD = 18%) in group 2 and is more similar in characteristics to those in group 3.
The largest overall discrepancy for adjustment with NO2-MDAF is for H2O2-MDAF, but it is still within a factor of 2 (1.9 ± 0.2, Table 3). The main constituent of this error is the difference in MDAF magnitudes, rather than in the spread (or imprecision) of the values (RSD = 11%). Since the TUV model simulates similar values of j(H2O2) to those measured on average, H2O2-MDAF has the largest mean MDAF (0.89). This is likely contributed in part by the temperature dependence of σ(H2O2) used by the model (but not the spectral radiometer) which decreases modelled j(H2O2) by around 8% at the ambient temperatures in this study.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 relationship (overall errors of 43, 49 and 61%, respectively and mean ratios of 0.43–0.75).
1 relationship (overall errors of 43, 49 and 61%, respectively and mean ratios of 0.43–0.75).
Table 3 shows that the mean X-MDAF/NO2-MDAF ratio is larger than that of X-MDAF/O(1D)-MDAF, in part because measured changes in ozone column abundance are considered in the model input, and because absorption of short wavelengths (UVB) by the ozone column accounts for a large reduction in actinic flux. Therefore, the difference between cloud-free and cloudy conditions is not as great as observed for j(NO2), which photodissociates at longer wavelengths. This is observed in Fig. 8 where the magnitude of the ratio of X-MDAF to O(1D)-MDAF for group 1 species increases at slightly shorter slant ozone columns. It is due to variation in measured ozone column abundance at similar SZA driving the variation in modelled j(O1D) compared with the j-values for photolyses in group 1.
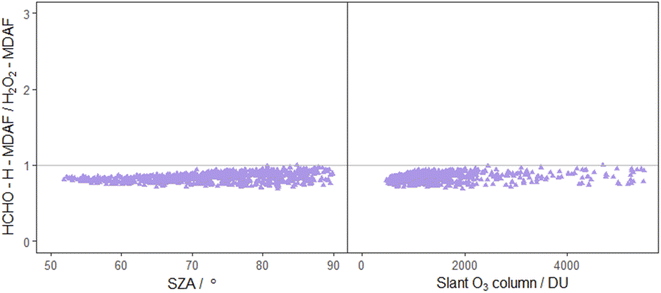 | ||
| Fig. 9 Ratio of HCHO–H-MDAF to H2O2-MDAF as a function of SZA (left) and slant ozone column (right). The combination of j(HCHO)–H and j(H2O2) was suggested by Kraus and Hofzumahaus58 based on the high correlation of their spectroradiometer measurements. Other pairing of j-values also suggested by these authors are j(HONO) with j(NO2), and j(CH3CHO) with j(O1D), which are presented in both Fig. 7 and 8. | ||
In contrast, application of NO2-MDAF to the O(1D) photolysis channel of O3 (e.g. Sörgel et al.30) results in substantial error. This bias will propagate through model simulations, as illustrated via the calculation using eqn (3) of the rate of production of OH from the photolysis of O3 (Fig. 10). (More detail on this calculation is given in the ESI.†)
| p(OH)O3 = 2 × f × j(O1D) × [O3] | (3) |
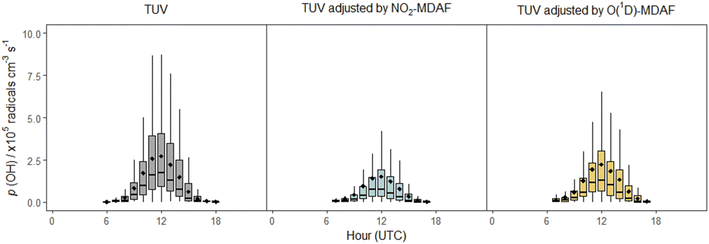 | ||
| Fig. 10 Box plots of diel cycles for the production rate of OH from the photolysis of O3 at Chilbolton Observatory between 17 December 2020 and 19 March 2021, calculated using eqn (3). Plots show data calculated using cloud-free TUV-modelled j(O1D) values (left, grey), using TUV-modelled j(O1D) values adjusted using NO2-MDAF (middle, blue) and using TUV-modelled j(O1D) values adjusted using O(1D)-MDAF (right, yellow). The horizontal lines and diamonds show the median and mean OH production rates each hour, boxes show the upper and lower quartiles, and whiskers indicate the 5–95% range. | ||
In this equation, f is the fraction of O(1D) atoms that react with water vapour to form OH, as opposed to their quenched removal by N2 or O2 molecules, which for this study was 4.7 ± 1% (based on hourly values). For this time series, use of the cloud-free TUV model output for j(O1D) results in mean p(OH)O3 estimations at solar noon approximately 1.3 × 105 cm−3 s−1 (86%) greater than when j(O1D) is adjusted with NO2-MDAF, and 6 × 104 cm−3 s−1 (26%) greater than when adjusted with O1D-MDAF (Fig. 10). The difference between these two OH production rates for the two different MDAF values used to account for local changes in meteorology is 7 × 104 radicals cm−3 s−1 (or 32%). This variation in the rate of production of OH with choice of O1D j-value demonstrates how uncertainty can propagate through chemical mechanisms and ultimately lead to significant uncertainty in modelled pollutant concentrations. For example, modelled daily maximum O3 concentrations in East Asia increased by up to 25% after updating j-values (via σ and ϕ) in RADM2 and RACM.2 These sorts of corrections may be even more important in locations with high aerosol loadings, such as during biomass burning season in South Asia.59
However, if available, MDAF values derived from measurements of j(O1D) can be applied with relatively little error (≤30% in this analysis) to adjust modelled j-values of other photolysis reactions in groups 2 (HNO3, HCHO–H, HCHO–H2, H2O2, ClONO2–ClO) and 3 (CH3CHO). These are photolysis reactions whose action spectra are predominantly at λ < ∼360 nm. For these photolyses, this study demonstrates that a lower propagated error for local j(X) will be achieved when using O1D-MDAFs rather than NO2-MDAFs to correct the cloud-free j(X) value for local meteorological conditions.
4 Conclusions
Accurate local air quality modelling requires accurate photolysis rate constants. The most accurate j-values for a model domain would derive from calibrated spectral radiometer measurements at the locality, but this is not practical for the whole suite of atmospheric photolysis reactions. Using spectral radiometer data from Chilbolton Observatory, southern England, measurement-driven adjustment factors (MDAF) that adjust model-derived cloud-free j-values according to local atmospheric conditions were investigated for 12 photodissociation reactions important in air quality and chemical transport models. A previously used NO2-MDAF and a new O1D-MDAF were tested.The 12 photolysis reactions separated into three groups on the basis of how the hourly ratios of their measured-to-modelled j-values responded to local conditions of solar zenith angle, aerosol optical depth and ozone column. The first group contained the photolysis of NO2, along with the photolyse of HONO, MGLY, ClNO2 and the Cl channel of ClONO2. Although these photodissociations require the largest adjustments of cloud-free values, errors in applying NO2-MDAFs to their modelled j-values were ≤30%. NO2-MDAFs constitutes a good reference for HONO and ClNO2 in particular. It appears the presence of significant photodissociation at longer wavelengths is more influential on this grouping than the presence or not of absorptions in the UVB region. Consequently, it is assumed that NO2-MDAFs would be suitable reference for other photolysis reactions where the significant dissociation absorptions are at λ > ∼360 nm.
The O1D-MDAF performed better than NO2-MDAF at adjusting modelled j-values for species that predominantly photodissociate at λ < 330 nm, such as CH3CHO, as well as those that photodissociate at slightly longer wavelengths <350 nm, such as HNO3, H2O2, the H and H2 channels of HCHO and the ClO channel of ClONO2 (errors ≤ 30%). Therefore, for photolysis reactions occurring predominantly at wavelengths <350 nm, O1D-MDAF is preferable. (However, the maximum error determined from the application of NO2-MDAF to any of the included photolyses was within a factor of 2, which may still be acceptable for some modelling.) There is more variability in the adjustments of these j-values due to stronger scattering and absorption of solar radiation at the relevant wavelengths. Variability is greatest at higher SZA and ozone column abundances due to the longer atmospheric slant path length.
It is important that MDAFs are used to improve accuracy and uncertainty in simulated j-values caused by variation in local conditions. Errors in photolysis rate constants propagate through mechanism calculations and lead to uncertainty in estimated pollutant concentrations. This study has highlighted that modelled j-values need to be calibrated and validated against local measurements to ensure confidence in atmospheric models. This is particularly critical where these are used to assess public health and support policy makers in developing mitigation strategies. Use of filter/spectral radiometers to provide NO2- and O1D-MDAFs would improve estimation of the impact (and uncertainty) on j-values of variation in local conditions in model domains, without requiring computationally-intensive model approaches for their prediction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
HLW acknowledges studentship funding from the UK Centre for Ecology & Hydrology (CEH) co-funding of Environment Agency Contract grant NEC05967 and the University of Edinburgh, School of Chemistry. The authors acknowledge Darcy Ladd (STFC) for setting up and hosting the spectral radiometer at Chilbolton Observatory, and Judith Jeffery (STFC) for providing meteorological measurements at the site. The authors also acknowledge the UK Department for Environment, Food and Rural Affairs (Defra) and the Devolved Administrations for maintaining instrument operations (ECM48524).References
- P. S. Monks, Gas-phase radical chemistry in the troposphere, Chem. Soc. Rev., 2005, 34, 376–395, 10.1039/B307982C.
- C.-H. Chen, T.-F. Chen, S.-P. Huang and K.-H. Chang, Comparison of the RADM2 and RACM chemical mechanisms in O3 simulations: effect of the photolysis rate constant, Sci. Rep., 2021, 11, 5024, DOI:10.1038/s41598-021-84629-4.
- B. Bohn, G. K. Corlett, M. Gillmann, S. Sanghavi, G. Stange, E. Tensing, M. Vrekoussis, W. J. Bloss, L. J. Clapp, M. Kortner, H. P. Dorn, P. S. Monks, U. Platt, C. Plass-Dülmer, N. Mihalopoulos, D. E. Heard, K. C. Clemitshaw, F. X. Meixner, A. S. H. Prevot and R. Schmitt, Photolysis frequency measurement techniques: results of a comparison within the ACCENT project, Atmos. Chem. Phys., 2008, 8, 5373–5391, DOI:10.5194/acp-8-5373-2008.
- E. Gerasopoulos, S. Kazadzis, M. Vrekoussis, G. Kouvarakis, E. Liakakou, N. Kouremeti, D. Giannadaki, M. Kanakidou, B. Bohn and N. Mihalopoulos, Factors affecting O3 and NO2 photolysis frequencies measured in the eastern Mediterranean during the five-year period 2002–2006, J. Geophys. Res., 2012, 117, D22305, DOI:10.1029/2012JD017622.
- J. N. Crowley, N. Pouvesle, G. J. Phillips, R. Axinte, H. Fischer, T. Petäjä, A. Nölscher, J. Williams, K. Hens, H. Harder, M. Martinez-Harder, A. Novelli, D. Kubistin, B. Bohn and J. Lelieveld, Insights into HOx and ROx chemistry in the boreal forest via measurement of peroxyacetic acid, peroxyacetic nitric anhydride (PAN) and hydrogen peroxide, Atmos. Chem. Phys., 2018, 18, 13457–13479, DOI:10.5194/acp-18-13457-2018.
- G. D. Edwards and P. S. Monks, Performance of a single-monochromator diode array spectroradiometer for the determination of actinic flux and atmospheric photolysis frequencies, J. Geophys. Res.: Atmos., 2003, 108, 8546, DOI:10.1029/2002JD002844.
- C. Topaloglou, S. Kazadzis, A. F. Bais, M. Blumthaler, B. Schallhart and D. Balis, NO2 and HCHO photolysis frequencies from irradiance measurements in Thessaloniki, Greece, Atmos. Chem. Phys., 2005, 5, 1645–1653, DOI:10.5194/acp-5-1645-2005.
- R. Sommariva, L. R. Crilley, S. M. Ball, R. L. Cordell, L. D. J. Hollis, W. J. Bloss and P. S. Monks, Enhanced wintertime oxidation of VOCs via sustained radical sources in the urban atmosphere, Environ. Pollut., 2021, 274, 116563, DOI:10.1016/j.envpol.2021.116563.
- S. M. Saunders, M. E. Jenkin, R. G. Derwent and M. J. Pilling, Protocol for the development of the master chemical mechanism, MCM v3 (part A): tropospheric degradation of non-aromatic volatile organic compounds, Atmos. Chem. Phys., 2003, 3, 161–180 CrossRef CAS.
- R. Sommariva, S. Cox, C. Martin, K. Borońska, J. Young, P. K. Jimack, M. J. Pilling, V. N. Matthaios, B. S. Nelson, M. J. Newland, M. Panagi, W. J. Bloss, P. S. Monks and A. R. Rickard, AtChem (version 1), an open-source box model for the master chemical mechanism, Geosci. Model Dev., 2020, 13, 169–183, DOI:10.5194/gmd-13-169-2020.
- S. Madronich, Photodissociation in the atmosphere: 1. actinic flux and the effects of ground reflections and clouds, J. Geophys. Res.: Atmos., 1987, 92, 9740–9752, DOI:10.1029/JD092iD08p09740.
- O. Wild, X. Zhu and M. J. Prather, Fast-J: Accurate Simulation of In- and Below-Cloud Photolysis in Tropospheric Chemical Models, J. Atmos. Chem., 2000, 37, 245–282, DOI:10.1023/A:1006415919030.
- X. Tie, S. Madronich, S. Walters, R. Zhang, P. Rasch and W. Collins, Effect of clouds on photolysis and oxidants in the troposphere, J. Geophys. Res., 2003, 108, 4642, DOI:10.1029/2003JD003659.
- A. Voulgarakis, N. H. Savage, O. Wild, G. D. Carver, K. C. Clemitshaw and J. A. Pyle, Upgrading photolysis in the p-TOMCAT CTM: model evaluation and assessment of the role of clouds, Geosci. Model Dev., 2009, 2, 59–72, DOI:10.5194/gmd-2-59-2009.
- O. A. Søvde, M. J. Prather, I. S. A. Isaksen, T. K. Berntsen, F. Stordal, X. Zhu, C. D. Holmes and J. Hsu, The chemical transport model Oslo CTM3, Geosci. Model Dev., 2012, 5, 1441–1469, DOI:10.5194/gmd-5-1441-2012.
- S. R. Hall, K. Ullmann, M. J. Prather, C. M. Flynn, L. T. Murray, A. M. Fiore, G. Correa, S. A. Strode, S. D. Steenrod, J. F. Lamarque, J. Guth, B. Josse, J. Flemming, V. Huijnen, N. L. Abraham and A. T. Archibald, Cloud impacts on photochemistry: building a climatology of photolysis rates from the atmospheric tomography mission, Atmos. Chem. Phys., 2018, 18, 16809–16828, DOI:10.5194/acp-18-16809-2018.
- N. H. Schade, A. Macke, H. Sandmann and C. Stick, Enhanced solar global irradiance during cloudy sky conditions, Meteorol. Z., 2007, 16, 295–303 CrossRef.
- H. Mao, W.-C. Wang, X.-Z. Liang and R. W. Talbot, Global and seasonal variations of O3 and NO2 photodissociation rate coefficients, J. Geophys. Res., 2003, 108, 4216, DOI:10.1029/2002JD002760.
- A. Kylling, K. Stamnes and S. C. Tsay, A reliable and efficient two-stream algorithm for spherical radiative transfer: documentation of accuracy in realistic layered media, J. Atmos. Chem., 1995, 21, 115–150, DOI:10.1007/BF00696577.
- EMEP MSC-W, Open Source EMEP/MSC-W Model rv4.36 (202011), DOI:10.5281/zenodo.4230110, accessed June 2021.
- D. Simpson, A. Benedictow, H. Berge, R. Bergström, L. D. Emberson, H. Fagerli, C. R. Flechard, G. D. Hayman, M. Gauss, J. E. Jonson, M. E. Jenkin, A. Nyiri, C. Richter, V. S. Semeena, S. Tsyro, J. P. Tuovinen, A. Valdebenito and P. Wind, The EMEP MSC-W chemical transport model - technical description, Atmos. Chem. Phys., 2012, 12, 7825–7865 CrossRef CAS.
- L. K. Whalley, D. Stone, R. Dunmore, J. Hamilton, J. R. Hopkins, J. D. Lee, A. C. Lewis, P. Williams, J. Kleffmann, S. Laufs, R. Woodward-Massey and D. E. Heard, Understanding in situ ozone production in the summertime through radical observations and modelling studies during the Clean air for London project (ClearfLo), Atmos. Chem. Phys., 2018, 18, 2547–2571, DOI:10.5194/acp-18-2547-2018.
- Y. Kanaya, Y. Kajii and H. Akimoto, Solar actinic flux and photolysis frequency determinations by radiometers and a radiative transfer model at Rishiri Island: comparisons, cloud effects, and detection of an aerosol plume from Russian forest fires, Atmos. Environ., 2003, 37, 2463–2475, DOI:10.1016/S1352-2310(03)00183-3.
- Y. F. Elshorbany, J. Kleffmann, A. Hofzumahaus, R. Kurtenbach, P. Wiesen, T. Brauers, B. Bohn, H.-P. Dorn, H. Fuchs, F. Holland, F. Rohrer, R. Tillmann, R. Wegener, A. Wahner, Y. Kanaya, A. Yoshino, S. Nishida, Y. Kajii, M. Martinez, D. Kubistin, H. Harder, J. Lelieveld, T. Elste, C. Plass-Dülmer, G. Stange, H. Berresheim and U. Schurath, HOx budgets during HOxComp: A case study of HOx chemistry under NOx-limited conditions, J. Geophys. Res., 2012, 117, D03307, DOI:10.1029/2011JD017008.
- T. J. Bannan, A. Bacak, M. Le Breton, M. Flynn, B. Ouyang, M. McLeod, R. Jones, T. L. Malkin, L. K. Whalley, D. E. Heard, B. Bandy, M. A. H. Khan, D. E. Shallcross and C. J. Percival, Ground and Airborne U.K. Measurements of Nitryl Chloride: An Investigation of the Role of Cl Atom Oxidation at Weybourne Atmospheric Observatory, J. Geophys. Res., 2017, 122, 11154–11165, DOI:10.1002/2017JD026624.
- C. Xue, C. Zhang, C. Ye, P. Liu, V. Catoire, G. Krysztofiak, H. Chen, Y. Ren, X. Zhao, J. Wang, F. Zhang, C. Zhang, J. Zhang, J. An, T. Wang, J. Chen, J. Kleffmann, A. Mellouki and Y. Mu, HONO Budget and Its Role in Nitrate Formation in the Rural North China Plain, Environ. Sci. Technol., 2020, 54, 11048–11057, DOI:10.1021/acs.est.0c01832.
- D. E. Heard, L. J. Carpenter, D. J. Creasey, J. R. Hopkins, J. D. Lee, A. C. Lewis, M. J. Pilling, P. W. Seakins, N. Carslaw and K. M. Emmerson, High levels of the hydroxyl radical in the winter urban troposphere, Geophys. Res. Lett., 2004, 31, L18112, DOI:10.1029/2004GL020544.
- B. Bohn, A. Kraus, M. Müller and A. Hofzumahaus, Measurement of atmospheric O3 → O(1D) photolysis frequencies using filterradiometry, J. Geophys. Res., 2004, 109, D10S90, DOI:10.1029/2003JD004319.
- B. Bohn, D. E. Heard, N. Mihalopoulos, C. Plass-Dülmer, R. Schmitt and L. K. Whalley, Characterisation and improvement of j(O1D) filter radiometers, Atmos. Meas. Tech., 2016, 9, 3455–3466, DOI:10.5194/amt-9-3455-2016.
- M. Sörgel, E. Regelin, H. Bozem, J. M. Diesch, F. Drewnick, H. Fischer, H. Harder, A. Held, Z. Hosaynali-Beygi, M. Martinez and C. Zetzsch, Quantification of the unknown HONO daytime source and its relation to NO2, Atmos. Chem. Phys., 2011, 11, 10433–10447, DOI:10.5194/acp-11-10433-2011.
- M. M. Lew, P. S. Rickly, B. P. Bottorff, E. Reidy, S. Sklaveniti, T. Léonardis, N. Locoge, S. Dusanter, S. Kundu, E. Wood and P. S. Stevens, OH and HO2 radical chemistry in a midlatitude forest: measurements and model comparisons, Atmos. Chem. Phys., 2020, 20, 9209–9230, DOI:10.5194/acp-20-9209-2020.
- P. S. Monks, A. R. Rickard, S. L. Hall and N. A. D. Richards, Attenuation of spectral actinic flux and photolysis frequencies at the surface through homogenous cloud fields, J. Geophys. Res., 2004, 109, D17206, DOI:10.1029/2003JD004076.
- A. R. Webb, A. F. Bais, M. Blumthaler, G. P. Gobbi, A. Kylling, R. Schmitt, S. Thiel, F. Barnaba, T. Danielsen, W. Junkermann, A. Kazantzidis, P. Kelly, R. Kift, G. L. Liberti, M. Misslbeck, B. Schallhart, J. Schreder and C. Topaloglou, Measuring Spectral Actinic Flux and Irradiance: Experimental Results from the Actinic Flux Determination from Measurements of Irradiance (ADMIRA) Project, J. Atmos. Ocean. Technol., 2002, 19, 1049–1062, DOI:10.1175/1520-0426(2002)019<1049:MSAFAI>2.0.CO;2.
- R. McKenzie, P. Johnston, A. Hofzumahaus, A. Kraus, S. Madronich, C. Cantrell, J. Calvert and R. Shetter, Relationship between photolysis frequencies derived from spectroscopic measurements of actinic fluxes and irradiances during the IPMMI campaign, J. Geophys. Res., 2002, 107, D5, DOI:10.1029/2001JD000601.
- S. Dusanter, D. Vimal, P. Stevens, R. Volkamer, L. Molina, A. Baker, S. Meinardi, D. Blake, P. Sheehy, A. Merten, R. Zhang, J. Zheng, E. Fortner, W. Junkermann, M. Dubey, T. Rahn, B. Eichinger, P. Lewandowski, J. Prueger and H. Holder, Measurements of OH and HO2 concentrations during the MCMA-2006 field campaign - part 2: model comparison and radical budget, Atmos. Chem. Phys., 2009, 9, 6655–6675 CrossRef CAS.
- D. Stone, M. J. Evans, R. Commane, T. Ingham, C. F. A. Floquet, J. B. McQuaid, D. M. Brookes, P. S. Monks, R. Purvis, J. F. Hamilton, J. Hopkins, J. Lee, A. C. Lewis, D. Stewart, J. G. Murphy, G. Mills, D. Oram, C. E. Reeves and D. E. Heard, HOx observations over West Africa during AMMA: impact of isoprene and NOx, Atmos. Chem. Phys., 2010, 10, 9415–9429, DOI:10.5194/acp-10-9415-2010.
- Centre for Environmental Data Analysis and Chilbolton Atmospheric Observatory (CAO), https://catalogue.ceda.ac.uk/uuid/0d60dd064b6449b09f5c7fd4c41bd693.
- H. L. Walker, M. R. Heal, C. F. Braban, S. Ritchie, C. Conolly, A. Sanocka, U. Dragosits and M. M. Twigg, Changing supersites: assessing the impact of the southern UK EMEP supersite relocation on measured atmospheric composition, Environ. Res. Commun., 2019, 1, 041001, DOI:10.1088/2515-7620/ab1a6f.
- Defra, Department for Environment, Food and Rural Affairs, UK AIR: Site Information for Chilbolton Observatory, https://uk-air.defra.gov.uk/networks/site-info?site_id=CHBO, accessed 10 January 2021 Search PubMed.
- J. D. Lee, L. K. Whalley, D. E. Heard, D. Stone, R. E. Dunmore, J. F. Hamilton, D. E. Young, J. D. Allan, S. Laufs and J. Kleffmann, Detailed budget analysis of HONO in central London reveals a missing daytime source, Atmos. Chem. Phys., 2016, 16, 2747–2764 CrossRef CAS.
- B. Bohn and I. Lohse, Calibration and evaluation of CCD spectroradiometers for ground-based and airborne measurements of spectral actinic flux densities, Atmos. Meas. Tech., 2017, 10, 3151–3174, DOI:10.5194/amt-10-3151-2017.
- S. Madronich, in Environmental UV Photobiology, ed. A. R. Young, J. Moan, L. O. Björn and W. Nultsch, Springer US, Boston, MA, 1993, pp. 1–39, DOI:10.1007/978-1-4899-2406-3_1.
- NCAR, Tropospheric Ultraviolet and Visible (TUV) Radiation Model v5.3, National Centre for Atmospheric Research (NCAR), available at: https://www2.acom.ucar.edu/modeling/tropospheric-ultraviolet-and-visible-tuv-radiation-model Search PubMed.
- J. B. Burkholder, R. K. Talukdar, A. R. Ravishankara and S. Solomon, Temperature dependence of the HNO3 UV absorption cross sections, J. Geophys. Res., 1993, 98, 22937–22948, DOI:10.1029/93JD02178.
- L. T. Molina and M. J. Molina, UV absorption cross sections of HO2NO2 vapor, J. Photochem., 1981, 15, 97–108, DOI:10.1016/0047-2670(81)85002-2.
- J. B. Burkholder, J. P. D. Abbatt, C. Cappa, T. S. Dibble, C. E. Kolb, V. L. Orkin, D. M. Wilmouth, S. P. Sander, J. R. Barker, J. D. Crounse, R. E. Huie, M. J. Kurylo, C. J. Percival and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies – Evaluation Number 19, JPL Publication 19-5, https://jpldataeval.jpl.nasa.gov/, 2020 Search PubMed.
- B. Ghosh, D. K. Papanastasiou, R. K. Talukdar, J. M. Roberts and J. B. Burkholder, Nitryl Chloride (ClNO2): UV/Vis Absorption Spectrum between 210 and 296 K and O(3P) Quantum Yield at 193 and 248 nm, J. Phys. Chem. A, 2012, 116, 5796–5805, DOI:10.1021/jp207389y.
- A. J. Illies and G. A. Takacs, Gas phase ultra-violet photoabsorption cross-sections for nitrosyl chloride and nitryl chloride, J. Photochem., 1976, 6, 35–42, DOI:10.1016/0047-2670(76)87005-0.
- A. Furlan, M. A. Haeberli and J. R. Huber, The 248 nm Photodissociation of ClNO2 Studied by Photofragment Translational Energy Spectroscopy, J. Phys. Chem. A, 2000, 104, 10392–10397, DOI:10.1021/jp000792j.
- S. P. Sander, R. R. Friedl, J. R. Barker, D. M. Golden, M. J. Kurylo, P. H. Wine, J. P. D. Abbatt, J. B. Burkholder, C. E. Kolb, G. K. Moortgat, R. E. Huie and V. L. Orkin, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies – Evaluation Number 17, PL Publication 10-6, Pasadena CA, 2011 Search PubMed.
- NOAA ESRL, National Oceanic and Atmospheric Administration Earth System Research Laboratory Global Monitoring Division (NOAA-ESRL-GMD) OMI Satellite Level 3e Daily Averaged Ozone Data Gridded at 0.25 × 0.25 degrees, https://www.esrl.noaa.gov/gmd/grad/neubrew/SatO3DataTimeSeries.jsp, accessed 20 March 2021 Search PubMed.
- AERONET, D. Ladd and E. Rumi, NASA AERONET (AErosol RObotic NETwork): Chilbolton, https://aeronet.gsfc.nasa.gov/cgi-bin/data_display_aod_v3?site=Chilbolton%26nachal=2%26level=3%26place_code=10, accessed 20 March 2021 Search PubMed.
- L. Elterman, UV, Visible, and IR Attenuation for Altitudes to 50 km, Air Force Cambridge Research Laboratories (AFCRL), Cambridge, MA, 1968 Search PubMed.
- J. J. Michalsky and P. W. Kiedron, Comparison of UV-RSS spectral measurements and TUV model runs for clear skies for the May 2003 ARM aerosol intensive observation period, Atmos. Chem. Phys., 2008, 8, 1813–1821, DOI:10.5194/acp-8-1813-2008.
- R Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/, 2021 Search PubMed.
- D. C. Carslaw and K. Ropkins, openair - an R package for air quality data analysis, Environ. Model. Softw., 2012, 27–28, 52–61 CrossRef.
- Y. Matsumi, F. J. Comes, G. Hancock, A. Hofzumahaus, A. J. Hynes, M. Kawasaki and A. R. Ravishankara, Quantum yields for production of O(1D) in the ultraviolet photolysis of ozone: recommendation based on evaluation of laboratory data, J. Geophys. Res., 2002, 107, D3, DOI:10.1029/2001JD000510.
- A. Kraus and A. Hofzumahaus, Field Measurements of Atmospheric Photolysis Frequencies for O3, NO2, HCHO, CH3CHO, H2O2, and HONO by UV Spectroradiometry, J. Atmos. Chem., 1998, 31, 161–180, DOI:10.1023/A:1005888220949.
- V. Kumar, B. P. Chandra and V. Sinha, Large unexplained suite of chemically reactive compounds present in ambient air due to biomass fires, Sci. Rep., 2018, 8, 626, DOI:10.1038/s41598-017-19139-3.
- M. F. Mérienne, A. Jenouvrier and B. Coquart, The NO2 absorption spectrum. I: absorption cross-sections at ambient temperature in the 300–500 nm region, J. Atmos. Chem., 1995, 20, 281–297, DOI:10.1007/BF00694498.
- A. C. Vandaele, C. Hermans, P. C. Simon, M. Carleer, R. Colin, S. Fally, M. F. Mérienne, A. Jenouvrier and B. Coquart, Measurements of the NO2 absorption cross-section from 42000 cm−1 to 10000 cm−1 (238–1000 nm) at 220 K and 294 K, J. Quant. Spectrosc. Radiat. Transfer, 1998, 59, 171–184, DOI:10.1016/S0022-4073(97)00168-4.
- E. P. Gardner, P. D. Sperry and J. G. Calvert, Primary quantum yields of NO2 photodissociation, J. Geophys. Res., 1987, 92, 6642–6652, DOI:10.1029/JD092iD06p06642.
- C. M. Roehl, J. J. Orlando, G. S. Tyndall, R. E. Shetter, G. J. Vazquez, C. A. Cantrell and J. G. Calvert, Temperature-Dependence of the Quantum Yields for the Photolysis of NO2 Near the Dissociation Limit, J. Phys. Chem., 1994, 98, 7837–7843 CrossRef CAS.
- J. Troe, Are Primary Quantum Yields of NO2 Photolysis at λ ≤ 398 nm Smaller than Unity?, Z. Phys. Chem., 2000, 214, 573–581, DOI:10.1524/zpch.2000.214.5.573.
- L. T. Molina and M. J. Molina, Absolute absorption cross sections of ozone in the 185- to 350-nm wavelength range, J. Geophys. Res., 1986, 91, 14501–14508, DOI:10.1029/JD091iD13p14501.
- W. B. De More, S. P. Sander, D. M. Golden, R. F. Hampson, M. J. Kurylo, C. J. Howard, A. R. Ravishankara, C. E. Kolb and M. J. Molina, Chemical Kinetics and Photochemical Data for Use in Stratospheric Modelling, Report 11, Pasadena, 1994 Search PubMed.
- W. B. De More, S. P. Sander, D. M. Golden, R. F. Hampson, M. J. Kurylo, C. J. Howard, A. R. Ravishankara, C. E. Kolb and M. J. Molina, Chemical Kinetics and Photochemical Data for Use in Stratospheric Modeling, Evaluation Number 12, JPL Publication 97-4, Pasadena CA, 1997 Search PubMed.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Evaluated kinetic and photochemical data for atmospheric chemistry: volume I - gas phase reactions of Ox, HOx, NOx and SOx species, Atmos. Chem. Phys., 2004, 4, 1461–1738, DOI:10.5194/acp-4-1461-2004.
- A. Bongartz, J. Kames, F. Welter and U. Schurath, Near-UV absorption cross sections and trans/cis equilibrium of nitrous acid, J. Phys. Chem., 1991, 95, 1076–1082, DOI:10.1021/j100156a012.
- A. Bongartz, J. Kames, U. Schurath, C. George, P. Mirabel and J. L. Ponche, Experimental determination of HONO mass accommodation coefficients using two different techniques, J. Atmos. Chem., 1994, 18, 149–169, DOI:10.1007/BF00696812.
- R. Meller and G. K. Moortgat, Temperature dependence of the absorption cross sections of formaldehyde between 223 and 323 K in the wavelength range 225–375 nm, J. Geophys. Res., 2000, 105, 7089–7101, DOI:10.1029/1999JD901074.
- G. D. Smith, L. T. Molina and M. J. Molina, Measurement of Radical Quantum Yields from Formaldehyde Photolysis between 269 and 339 nm, J. Phys. Chem. A, 2002, 106, 1233–1240, DOI:10.1021/jp013180n.
- A. Horowitz and J. G. Calvert, Wavelength dependence of the quantum efficiencies of the primary processes in formaldehyde photolysis at 25 °C, Int. J. Chem. Kinet., 1978, 10, 805–819, DOI:10.1002/kin.550100803.
- G. K. Moortgat, W. Seiler and P. Warneck, Photodissociation of HCHO in air: CO and H2 quantum yields at 220 and 300 K, J. Chem. Phys., 1983, 78, 1185–1190, DOI:10.1063/1.444911.
- R. D. Martinez, A. A. Buitrago, N. W. Howell, C. H. Hearn and J. A. Joens, The near UV absorption spectra of several aliphatic aldehydes and ketones at 300 K, Atmos. Environ., Part A, 1992, 26, 785–792, DOI:10.1016/0960-1686(92)90238-G.
- H. Meyrahn, G. K. Moortgat and P. Warneck, The photolysis of acetaldehyde under atmospheric conditions, presented at the 15th Informal Conference on Photochemistry, Stanford, CA, June 27–July 1, 1982 Search PubMed.
- A. Horowitz and J. G. Calvert, Wavelength dependence of the primary processes in acetaldehyde photolysis, J. Phys. Chem., 1982, 86, 3105–3114, DOI:10.1021/j100213a011.
- R. Meller, W. Raber, J. N. Crowley, M. E. Jenkin and G. K. Moortgat, The UV-visible absorption spectrum of methylglyoxal, J. Photochem. Photobiol., A, 1991, 62, 163–171, DOI:10.1016/1010-6030(91)87017-P.
- T. A. Staffelbach, J. J. Orlando, G. S. Tyndall and J. G. Calvert, The UV-visible absorption spectrum and photolysis quantum yields of methylglyoxal, J. Geophys. Res., 1995, 100, 14189–14198 CrossRef.
- Y. Chen, W. Wang and L. Zhu, Wavelength-Dependent Photolysis of Methylglyoxal in the 290–440 nm Region, J. Phys. Chem. A, 2000, 104, 11126–11131, DOI:10.1021/jp002262t.
- J. B. Burkholder, R. K. Talukdar and A. R. Ravishankara, Temperature-dependence of the ClONO2 UV absorption spectrum, Geophys. Res. Lett., 1994, 21, 585–588 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Evaluated kinetic and photochemical data for atmospheric chemistry: volume III - gas phase reactions of inorganic halogens, Atmos. Chem. Phys., 2007, 7, 981–1191, DOI:10.5194/acp-7-981-2007.
- Google Earth, Satellite Imagery of the United Kingdom, 2021, https://earth.google.com/web, accessed 6 May 2021 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ea00072e |
| This journal is © The Royal Society of Chemistry 2022 |