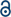 Open Access Article
Open Access ArticleThe driving effects of common atmospheric molecules for formation of prenucleation clusters: the case of sulfuric acid, formic acid, nitric acid, ammonia, and dimethyl amine†
Conor J.
Bready
 ,
Vance R.
Fowler
,
Leah A.
Juechter
,
Luke A.
Kurfman
,
Grace E.
Mazaleski
and
George C.
Shields
,
Vance R.
Fowler
,
Leah A.
Juechter
,
Luke A.
Kurfman
,
Grace E.
Mazaleski
and
George C.
Shields
 *
*
Department of Chemistry, Furman University, Greenville, South Carolina 29613, USA. E-mail: george.shields@furman.edu
First published on 3rd October 2022
Abstract
How secondary aerosols form is critical as aerosols' impact on Earth's climate is one of the main sources of uncertainty for understanding global warming. The beginning stages for formation of prenucleation complexes, that lead to larger aerosols, are difficult to decipher experimentally. We present a computational chemistry study of the interactions between three different acid molecules and two different bases. By combining a comprehensive search routine covering many thousands of configurations at the semiempirical level with high level quantum chemical calculations of approximately 1000 clusters for every possible combination of clusters containing a sulfuric acid molecule, a formic acid molecule, a nitric acid molecule, an ammonia molecule, a dimethylamine molecule, and 0–5 water molecules, we have completed an exhaustive search of the DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G** Gibbs free energy surface for this system. We find that the detailed geometries of each minimum free energy cluster are often more important than traditional acid or base strength. Addition of a water molecule to a dry cluster can enhance stabilization, and we find that the (SA)(NA)(A)(DMA)(W) cluster has special stability. Equilibrium calculations of SA, FA, NA, A, DMA, and water using our quantum chemical ΔG° values for cluster formation and realistic estimates of the concentrations of these monomers in the atmosphere reveals that nitric acid can drive early stages of particle formation just as efficiently as sulfuric acid. Our results lead us to believe that particle formation in the atmosphere results from the combination of many different molecules that are able to form highly stable complexes with acid molecules such as SA, NA, and FA.
Environmental significanceUnderstanding how secondary aerosols form is extremely important as aerosols' impact on Earth's climate is one of the main sources of uncertainty for understanding global warming. The beginning stages for the formation of prenucleation complexes, that eventually lead to larger aerosols, cannot currently be investigated experimentally. We have determined the lowest Gibbs free energy clusters using robust computational chemistry methods, which allows for the prediction of the equilibrium concentrations of the sulfuric acid–formic acid–nitric acid–ammonia–dimethylamine–water system. Optimal pathways were mapped out and revealed that nitric acid could initiate new particle formation just as well as sulfuric acid under certain conditions, particularly with water. This indicates that particle growth in the atmosphere likely results from many unique molecules producing clusters stabilized with acids. |
1. Introduction
Aerosols affect the climate through light scattering, absorbing and emitting radiation, and by serving as cloud condensation nuclei (CCN).1 They exert a substantial influence on the microphysical properties of water and ice clouds, thereby affecting the processes that lead to the formation of various forms of precipitation.2 Secondary aerosol particles form from atmospheric gases and are predicted to make up 50% or more of global CCN.3,4 The precise way that gaseous vapor comes together to form prenucleation complexes, which eventually build to aerosols, and thus form CCN, is a very active area of research.3,5–74 Much of this activity is driven by the uncertainty in how much aerosols and clouds will impact global warming.75,76 While it is thought that in general more aerosols will lead to a cooling effect, the uncertainty in our knowledge exceeds the actual size of the predicted cooling.75 Aerosols promote photochemical reactions at their surfaces and amplification of light within aerosols accelerates photochemistry.77–81 In addition, nanodroplets and microdroplets catalyze chemical reactions at the air–water interface.82–91Current instrumentation is capable of examining the various stages of aerosol formation, but no single instrument can concurrently analyze data from the sub-nanometer size regime to the 10 nm size regime, leading to gaps in our knowledge about initial aerosol formation.67 Meanwhile accurate calculations of the Gibbs free energy for cluster formation (ΔG°) requires both a comprehensive exploration of the potential energy surfaces for each possible cluster along with high-level quantum chemical calculations on all the lowest free energy structures.55,92 In this study we have used robust computational chemistry methods to determine the ΔG° values for every possible cluster that can be formed in the sulfuric acid–nitric acid–formic acid–ammonia–dimethylamine–water system from monomers of each molecule along with 0–5 waters. This is the first study to probe three different acid molecules and two different bases to date, and adds to the insights obtained from previous work.
2. Methodology
Configurational sampling of every possible combination of sulfuric acid (SA), formic acid (FA), nitric acid (NA), ammonia (A), dimethylamine (DMA), and 0–5 water (W) molecules was performed with a genetic-algorithm-based protocol using the OGOLEM program93,94 and semiempirical methods. This algorithm takes an initial pool of randomly generated configurations and changes them according to an evolutionary algorithm to produce a final set of converged structures. We typically used a pool size of 1000 and set the number of global optimizations to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Two different semiempirical methods were used, PM7,95 and GFN2,96–98 to calculate approximately 1000 final structures for each system. These geometries were then used for DFT geometry optimizations with the Gaussian 16 Rev. B01 program99 using either the M08-HX100 or ωB97X-D101,102 functionals. Clusters containing SA, FA, A, and W were previously optimized with the M08-HX functional and the MG3S basis set.68,100 All of these M08-HX geometries were re-optimized with ωB97X-D using the 6-31++G** basis set103–106 to obtain a final set of consistent geometries. The electronic energies of all structures within 8 kcal mol−1 of the ωB97X-D global minimum for each system were recomputed using the domain-based local pair natural orbital coupled-cluster (DLPNO-CCSD(T)) method107–120 with single, double, and semi-canonical perturbative triple excitations with three Dunning basis sets, cc-pVnZ (n = D, T, Q),121–124 using the ORCA 5.0.1 program.125,126 The ωB97X-D frequencies were scaled by 0.971 to partially correct for anharmonicity127 and used to estimate the thermodynamic corrections for H°, S°, and G° at a standard state of 1 atm pressure and temperatures of 217.65, 273.15, and 298.15 K using the THERMO.pl script128 from the National Institute of Science and Technology. The three CCSD(T) electronic energies were used in a 4–5 inverse polynomial complete basis set (CBS) extrapolation129 and combined with the scaled ωB97X-D thermodynamic corrections to obtain the final set of ΔG° values for every system. For the tetramers of two acids and two bases and the pentamer systems, we include a comparison of the cc-pVnZ and aug-cc-pVnZ (n = D, T, Q) for the dry clusters. Additionally, we show the difference between using the cc-pVnZ versus the aug-cc-pVnZ basis sets in the ESI (Table S1),† as well as a comparison of using scaled vs. unscaled frequencies for the calculation of ΔE° and ΔG° values (Table S2†). The rate-limiting step in our computational methodology is the DFT geometry optimizations from the initial set of PM7 or GFN2 structures produced from the genetic algorithm. Semiempirical methods have long been known to do a better job at predicting structures for hydrogen-bonded clusters than energies.130,131 Because of this the PM7 and GFN2 potential energy surfaces are quite flat, such that we cannot rely on a cut-off in energy to select the lowest energy ensemble of structures, but must optimize every semiempirical structure. Switching to the ωB97X-D functional and the smaller 6-31++G** basis set has sped up this rate-limiting step.54,55,61 Further details on methodology are presented in our previous works57–59,68 and a summary of the most effective methodology is presented in Fig. 1. This methodology allows for the determination of accurate ΔG° values for every possible combination of our monomers SA, FA, NA, A, DMA, and up to five waters. An example of how to calculate all possible stepwise energies is shown in the ESI.† Assuming a closed system, we can then calculate the equilibrium concentrations for all possible clusters from the ΔG° values and initial concentrations of the monomers.58,68 We note that two big caveats about our methodology are that (a) no search routine based on lower level methods can possibly find every final minimum energy cluster, and (b) that any combination of electronic energy theory such as CCSD(T) with DFT geometries like ωB97X-D means that the electronic energy theory is calculated on the DFT PES. Both of these uncertainties will produce ΔG° values that are more positive than the values one would obtain if (a) a lower energy conformer is obtained, or (b) the PES is improved to be closer to the electronic energy method used in the calculation.
000. Two different semiempirical methods were used, PM7,95 and GFN2,96–98 to calculate approximately 1000 final structures for each system. These geometries were then used for DFT geometry optimizations with the Gaussian 16 Rev. B01 program99 using either the M08-HX100 or ωB97X-D101,102 functionals. Clusters containing SA, FA, A, and W were previously optimized with the M08-HX functional and the MG3S basis set.68,100 All of these M08-HX geometries were re-optimized with ωB97X-D using the 6-31++G** basis set103–106 to obtain a final set of consistent geometries. The electronic energies of all structures within 8 kcal mol−1 of the ωB97X-D global minimum for each system were recomputed using the domain-based local pair natural orbital coupled-cluster (DLPNO-CCSD(T)) method107–120 with single, double, and semi-canonical perturbative triple excitations with three Dunning basis sets, cc-pVnZ (n = D, T, Q),121–124 using the ORCA 5.0.1 program.125,126 The ωB97X-D frequencies were scaled by 0.971 to partially correct for anharmonicity127 and used to estimate the thermodynamic corrections for H°, S°, and G° at a standard state of 1 atm pressure and temperatures of 217.65, 273.15, and 298.15 K using the THERMO.pl script128 from the National Institute of Science and Technology. The three CCSD(T) electronic energies were used in a 4–5 inverse polynomial complete basis set (CBS) extrapolation129 and combined with the scaled ωB97X-D thermodynamic corrections to obtain the final set of ΔG° values for every system. For the tetramers of two acids and two bases and the pentamer systems, we include a comparison of the cc-pVnZ and aug-cc-pVnZ (n = D, T, Q) for the dry clusters. Additionally, we show the difference between using the cc-pVnZ versus the aug-cc-pVnZ basis sets in the ESI (Table S1),† as well as a comparison of using scaled vs. unscaled frequencies for the calculation of ΔE° and ΔG° values (Table S2†). The rate-limiting step in our computational methodology is the DFT geometry optimizations from the initial set of PM7 or GFN2 structures produced from the genetic algorithm. Semiempirical methods have long been known to do a better job at predicting structures for hydrogen-bonded clusters than energies.130,131 Because of this the PM7 and GFN2 potential energy surfaces are quite flat, such that we cannot rely on a cut-off in energy to select the lowest energy ensemble of structures, but must optimize every semiempirical structure. Switching to the ωB97X-D functional and the smaller 6-31++G** basis set has sped up this rate-limiting step.54,55,61 Further details on methodology are presented in our previous works57–59,68 and a summary of the most effective methodology is presented in Fig. 1. This methodology allows for the determination of accurate ΔG° values for every possible combination of our monomers SA, FA, NA, A, DMA, and up to five waters. An example of how to calculate all possible stepwise energies is shown in the ESI.† Assuming a closed system, we can then calculate the equilibrium concentrations for all possible clusters from the ΔG° values and initial concentrations of the monomers.58,68 We note that two big caveats about our methodology are that (a) no search routine based on lower level methods can possibly find every final minimum energy cluster, and (b) that any combination of electronic energy theory such as CCSD(T) with DFT geometries like ωB97X-D means that the electronic energy theory is calculated on the DFT PES. Both of these uncertainties will produce ΔG° values that are more positive than the values one would obtain if (a) a lower energy conformer is obtained, or (b) the PES is improved to be closer to the electronic energy method used in the calculation.
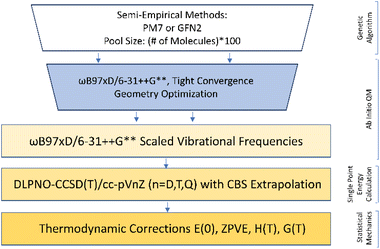 | ||
| Fig. 1 Computational methodology employed to obtain the minimum free energy structures and ΔG° values. | ||
3. Results and discussion
3.1 Monomer and dimer systems
All of the monomer and dimer systems researched have been well examined prior to this study. Therefore, all of the structures and corresponding energies are presented in the ESI (Fig. S1–S6 and Tables S3–S8).† Our results are consistent with previous studies of these clusters, with some new structures designated as the minimum due to level of theory differences from past studies.4,28,33,37,48,50,61,65,66,68,87,127–137 In these systems, no minimum energy clusters undergo proton transfers. This is unlike two-acid dimer systems such as (SA)2(W)0–5, which have been found to undergo proton transfers in the 3–5 water range.16,54,132Additional studies of these smaller systems have been performed experimentally. For example, rapid growth of new atmospheric particles through condensation of NA and A has been observed in the CLOUD chamber at CERN to produce particles as small as a few nm in diameter.53 This same system has been studied in a flow tube and NA–DMA particles were detected with diameters of 9–30 nm in dry and humid conditions.48 The NA/DMA ratio remained close to one, and modeling predicted that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 clusters had smaller evaporation rates, resulting in the most favorable thermodynamic pathway for growth.48
1 clusters had smaller evaporation rates, resulting in the most favorable thermodynamic pathway for growth.48
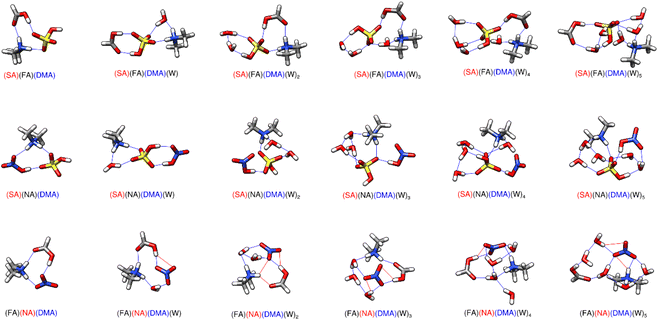
3.2 Trimers of a single acid and two bases
The structures and ΔG° values for formation of clusters consisting of the sequential hydration of one acid (SA, NA, or FA alone) and both bases (A and DMA), are listed in the ESI (Fig. S7 and Table S9)† as our results reveal they are less likely to be atmospherically relevant at any temperature (see Section 3.8). However, these systems do demonstrate the clear relationship that the strongest acid, sulfuric, which is a known driver of CCN formation,133–138 forms more negative ΔG° clusters with bases than either nitric or formic acid. The ΔG° of formation for the dry formic acid cluster with the two bases is roughly 0 kcal mol−1 at 298 K. The dry nitric acid and sulfuric acid with two base clusters are more stable, with ΔG° values of −5 and −15 kcal mol−1 respectively. This decrease in cluster formation Gibbs free energy likely results from the proton transfer from the acid to DMA. Even though nitric acid donates its proton and forms the same number of hydrogen bonds as sulfuric acid (Fig. S7†), the (NA)(A)(DMA) cluster is still roughly 10 kcal mol−1 higher in energy, demonstrating the importance of sulfuric acid in prenucleation cluster formation. For all of the one acid–two base hydrated clusters, the acid always acts as a bridge between the two bases such that the bases are on opposite sides of the clusters. The (FA)(A)(DMA)(W)0–2 clusters consist of neutral molecules, but in every other case one acid–two base cluster the acid always transfers its proton to the dimethylamine. In the unique case of (SA)(A)(DMA)(W)5, the sulfuric acid becomes a sulfate anion, with proton transfers forming both the protonated dimethyl amine and ammonium moieties. (This is the only instance where a sulfate anion was part of the lowest free energy cluster for any of the trimers and smaller systems in this work.) However, even with the additional proton transfer, the five-water cluster is still uphill in free energy compared to (SA)(A)(DMA)(W)4 at 298 K (Table S9†).3.3 Trimers of two acids and one base
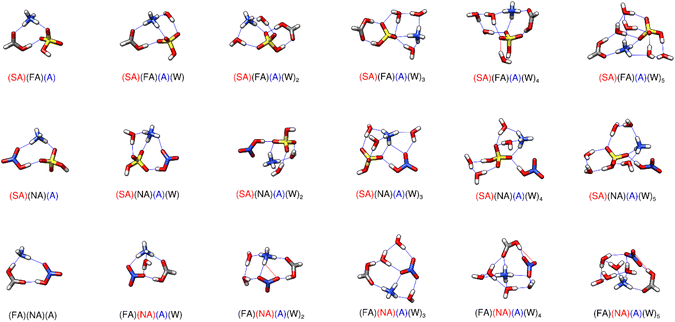
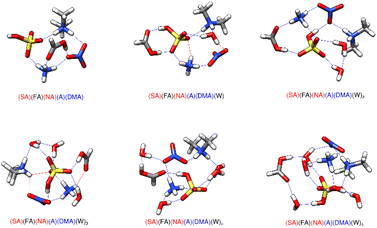
In our figures we have denoted strong hydrogen bonds, which have hydrogen-bonded distances less than 2.2 Å and hydrogen bond angles between 140° and 180°, with blue lines. We have used red lines to denote other van der Waals forces where the bond angle is less than 140° and/or the putative hydrogen bond distance is greater than 2.2 Å. The clusters consisting of two acids paired with one base allow for an easy comparison of the strength of the driving force between the two bases. Prior studies have investigated the stabilities of sulfuric-acid based clusters with ammonia versus amines such as methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA).24,25,28,37,50,61,63,92,139–145 Overall, the more substituted amines, specifically DMA and TMA, tend to be better nucleators with SA,145,146 with A forming the least stable complexes. However, the 2–3 orders of magnitude higher concentration of ammonia may compensate for the lower stabilities. When ammonia and amines are both present together, the effects are synergistic, with nucleation increasing by nearly a thousand-fold.50,138,139,143,147–152 As seen from Tables 1 and 2, substituting DMA for A decreases the ΔG° for formation of the dry clusters by roughly 6–8 kcal mol−1, further supporting the idea that DMA is a better nucleator. As all of these clusters contain three strong hydrogen bonds (Fig. 2 and 3), and all except (FA)(NA)(A) transfer a proton from the stronger acid to the base, the stronger base DMA forms more stable hydrogen bonds than ammonia. This view is consistent with past results.92| Cluster | 216.65 K | 273.15 K | 298.15 K |
|---|---|---|---|
| SA + FA + A ⇌ (SA)(FA)(A) | −17.13 | −13.39 | −11.74 |
| (SA)(FA)(A) + W ⇌ (SA)(FA)(A)(W) | −4.65 | −2.76 | −1.93 |
| (SA)(FA)(A)(W) + W ⇌ (SA)(FA)(A)(W)2 | −3.19 | −1.36 | −0.55 |
| (SA)(FA)(A)(W)2 + W ⇌ (SA)(FA)(A)(W)3 | −3.23 | −1.42 | −0.62 |
| (SA)(FA)(A)(W)3 + W ⇌ (SA)(FA)(A)(W)4 | 0.43 | 2.07 | 2.79 |
| (SA)(FA)(A)(W)4 + W ⇌ (SA)(FA)(A)(W)5 | −3.58 | −1.11 | −0.01 |
| SA + NA + A ⇌ (SA)(NA)(A) | −15.74 | −11.99 | −10.40 |
| (SA)(NA)(A) + W ⇌ (SA)(NA)(A)(W) | −5.73 | −4.04 | −3.23 |
| (SA)(NA)(A)(W) + W ⇌ (SA)(NA)(A)(W)2 | −3.83 | −2.13 | −1.38 |
| (SA)(NA)(A)(W)2 + W ⇌ (SA)(NA)(A)(W)3 | −3.15 | −1.51 | −0.79 |
| (SA)(NA)(A)(W)3 + W ⇌ (SA)(NA)(A)(W)4 | −1.07 | 0.85 | 1.71 |
| (SA)(NA)(A)(W)4 + W ⇌ (SA)(NA)(A)(W)5 | −3.87 | −2.27 | −1.56 |
| FA + NA + A ⇌ (FA)(NA)(A) | −8.42 | −5.25 | −3.87 |
| (FA)(NA)(A) + W ⇌ (FA)(NA)(A)(W) | −2.79 | −0.32 | 0.78 |
| (FA)(NA)(A)(W) + W ⇌ (FA)(NA)(A)(W)2 | −2.84 | −0.96 | −0.18 |
| (FA)(NA)(A)(W)2 + W ⇌ (FA)(NA)(A)(W)3 | −0.80 | 0.69 | 1.40 |
| (FA)(NA)(A)(W)3 + W ⇌ (FA)(NA)(A)(W)4 | −1.55 | 0.67 | 1.65 |
| (FA)(NA)(A)(W)4 + W ⇌ (FA)(NA)(A)(W)5 | −0.07 | 1.78 | 2.60 |
| Cluster | 216.65 K | 273.15 K | 298.15 K |
|---|---|---|---|
| SA + FA + DMA ⇌ (SA)(FA)(DMA) | −26.08 | −22.19 | −20.48 |
| (SA)(FA)(DMA) + W ⇌ (SA)(FA)(DMA)(W) | −3.31 | −1.57 | −0.80 |
| (SA)(FA)(DMA)(W) + W ⇌ (SA)(FA)(DMA)(W)2 | −1.93 | 0.00 | 0.85 |
| (SA)(FA)(DMA)(W)2 + W ⇌ (SA)(FA)(DMA)(W)3 | −1.21 | 0.50 | 1.25 |
| (SA)(FA)(DMA)(W)3 + W ⇌ (SA)(FA)(DMA)(W)4 | −1.74 | 0.23 | 1.08 |
| (SA)(FA)(DMA)(W)4 + W ⇌ (SA)(FA)(DMA)(W)5 | 0.05 | 2.01 | 2.91 |
| SA + NA + DMA ⇌ (SA)(NA)(DMA) | −25.19 | −21.37 | −19.69 |
| (SA)(NA)(DMA) + W ⇌ (SA)(NA)(DMA)(W) | −3.60 | −1.66 | −0.89 |
| (SA)(NA)(DMA)(W) + W ⇌ (SA)(NA)(DMA)(W)2 | −2.95 | −1.24 | −0.42 |
| (SA)(NA)(DMA)(W)2 + W ⇌ (SA)(NA)(DMA)(W)3 | −2.35 | −0.62 | 0.16 |
| (SA)(NA)(DMA)(W)3 + W ⇌ (SA)(NA)(DMA)(W)4 | 0.68 | 3.11 | 4.19 |
| (SA)(NA)(DMA)(W)4 + W ⇌ (SA)(NA)(DMA)(W)5 | −2.90 | −1.29 | −0.58 |
| FA + NA + DMA ⇌ (FA)(NA)(DMA) | −15.58 | −11.46 | −9.65 |
| (FA)(NA)(DMA) + W ⇌ (FA)(NA)(DMA)(W) | −2.34 | −0.71 | 0.00 |
| (FA)(NA)(DMA)(W) + W ⇌ (FA)(NA)(DMA)(W)2 | −1.42 | 0.34 | 1.12 |
| (FA)(NA)(DMA)(W)2 + W ⇌ (FA)(NA)(DMA)(W)3 | −1.66 | 0.31 | 1.18 |
| (FA)(NA)(DMA)(W)3 + W ⇌ (FA)(NA)(DMA)(W)4 | −0.92 | 0.98 | 1.82 |
| (FA)(NA)(DMA)(W)4 + W ⇌ (FA)(NA)(DMA)(W)5 | 0.72 | 2.47 | 3.25 |
While the dry cluster with DMA is a lot more stable than with A, adding waters to the ammonia clusters tends to yield lower ΔG° values than adding to the dimethyl amine clusters (Tables 1 and 2). This is because ammonium is able to form more hydrogen bonds than the dimethyl ammonium ion. The ammonium ion remains near the middle of large clusters to donate three or four hydrogen bonds to the surrounding molecules, while protonated DMA can only donate two. This is in line with previous work where it was found that for small clusters, like the dry clusters reported here, the gas phase basicity determines gas phase base strength: DMA is a much stronger gas phase base than A and is better able to promote proton transfer. On the other hand, as a cluster is hydrated and grows in size, ammonia is better able to bind multiple molecules together in larger clusters.92 The general trend is that ammonium will be located between waters, whereas DMA tends to remain on the outside of the cluster. One effect of this is that the DMA clusters tend to have spines of hydration, as can be seen for the (SA)(FA)(DMA)(W)4, (SA)(NA)(DMA)(W)4, and (FA)(NA)(DMA)(W)3,4 structures in Fig. 2.
Previous work on SA–FA–A reveals that FA is geometrically suited to form a stable hydrogen bonded complex with SA, and that hydrogen bond topology is sometimes more important than acid/base strength.68 The weak acid FA can form structures with SA with the same strength as structures of SA with the base A. Structures (SA)(FA)(A)(W)2 and (SA)(FA)(A)(W)3 in Fig. 3 illustrate the SA–FA hydrogen-bonded dimer.
Recent DFT work by Li et al. on SA–FA–A and SA–FA–DMA reveal that although amines are generally confirmed to be more active than A as stabilizers of binary clusters, in some cases mixed trimers containing A are more stable thermodynamically than those containing DMA.144 In addition they studied the interactions of SA with A, amines, and 14 organic acids, and they show that (SA)(FA)(A) and (SA)(FA)(DMA) trimers are more stable than (SA)2(A) and (SA)2(DMA) trimers.144
3.4 Trimers of three acids
The system composed of all three acids (SA, FA, and NA) together with up to five waters is shown in Fig. S8 with energies in Table S10.† Comparing this system's dry energies of formation with those of the other trimer systems, one will notice that even without a base present, this system is more stable than any other trimer without SA except for (FA)(NA)(DMA) (Tables 1, 2, S7 and S8†). With multiple strong acids, a proton transfer might be expected with the first available water molecule, as it can act as a base. However, proton transfer only occurs when there are three or more waters present. The proton transfer is always from the sulfuric acid to one of the waters, forming the bisulfate anion and a hydronium cation. The proton transfer occurring only from 3–5 waters is consistent with the results from Rasmussen et al., who studied (SA)3(W)n for n = 0–5.54 Addition of acetic acid to the (SA)2(W)n system results in proton transfer with two waters.132 Our SA–NA–FA–(W)n system as well as the Rasmussen et al. (SA)3(W)n were both calculated using ωB97X-D for the geometry optimizations and DLPNO-CCSD(T) for the single-point energy calculations while the Zhu et al. (SA)2(acetic acid)(W)n system was calculated using PW91PW91 for both geometries and energies. Differences in these methodologies could explain the discrepancy for when ionization occurs in these systems, as quite often the DLPNO-CCSD(T)/CBS minimum differs from the DFT minimum for atmospheric clusters.58,59,683.5 Tetramers of three acids and one base
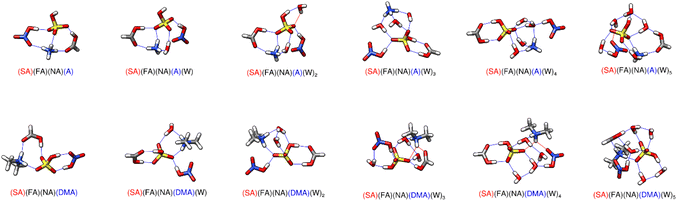
The energies of formation and sequential hydration of the tetramer systems containing SA, FA, NA and either A or DMA are listed in Table 3, with the corresponding minimum energy structures shown in Fig. 4. Forming the dry cluster with DMA is roughly 8.5 kcal mol−1 lower in free energy than forming the dry cluster with ammonia at all three temperatures. While part of this is likely because of DMA's ability to form more stable clusters, it could also be due to the strength of the hydrogen bonds. Both clusters contain 5 strong hydrogen bonds; however, the cluster with ammonia has three of the type N–H⋯O, whereas the cluster with DMA only has two of these. Since oxygen is more electronegative, this difference in the strength of the hydrogen bond could also play a role in the extra stability of the dry cluster with DMA.| Cluster | 216.65 K | 273.15 K | 298.15 K |
|---|---|---|---|
| SA + FA + NA + A ⇌ (SA)(FA)(NA)(A) | −24.77 | −18.82 | −16.28 |
| (SA)(FA)(NA)(A) + W ⇌ (SA)(FA)(NA)(A)(W) | −3.77 | −2.38 | −1.71 |
| (SA)(FA)(NA)(A)(W) + W ⇌ (SA)(FA)(NA)(A)(W)2 | −2.81 | −1.14 | −0.40 |
| (SA)(FA)(NA)(A)(W)2 + W ⇌ (SA)(FA)(NA)(A)(W)3 | −0.98 | 0.86 | 1.68 |
| (SA)(FA)(NA)(A)(W)3 + W ⇌ (SA)(FA)(NA)(A)(W)4 | −2.23 | −0.16 | 0.75 |
| (SA)(FA)(NA)(A)(W)4 + W ⇌ (SA)(FA)(NA)(A)(W)5 | −1.80 | 0.56 | 1.60 |
| SA + FA + NA + DMA ⇌ (SA)(FA)(NA)(DMA) | −33.41 | −27.50 | −24.90 |
| (SA)(FA)(NA)(DMA) + W ⇌ (SA)(FA)(NA)(DMA)(W) | −2.39 | −0.48 | 0.36 |
| (SA)(FA)(NA)(DMA)(W) + W ⇌ (SA)(FA)(NA)(DMA)(W)2 | −1.81 | −0.01 | 0.78 |
| (SA)(FA)(NA)(DMA)(W)2 + W ⇌ (SA)(FA)(NA)(DMA)(W)3 | −0.87 | 0.82 | 1.57 |
| (SA)(FA)(NA)(DMA)(W)3 + W ⇌ (SA)(FA)(NA)(DMA)(W)4 | −1.79 | 0.21 | 1.11 |
| (SA)(FA)(NA)(DMA)(W)4 + W ⇌ (SA)(FA)(NA)(DMA)(W)5 | −0.77 | 1.54 | 2.57 |
In all of these tetramer systems, a proton transfer occurs between the sulfuric acid and the base. Similar to smaller clusters, the energy of formation for the SA–FA–NA-base dry cluster has a more positive free energy for ammonia than for dimethylamine, but the sequential hydration energies decrease more rapidly for A than for DMA. This is because the ammonium cation usually donates three or four hydrogen bonds as the cluster is hydrated, whereas the dimethyl ammonium ion can only donate two in any system. The bisulfate anion is in the middle of these clusters which maximizes hydrogen bonding interactions, but this leaves NA on the outside where it can donate only one hydrogen bond and accept at most one hydrogen bond.
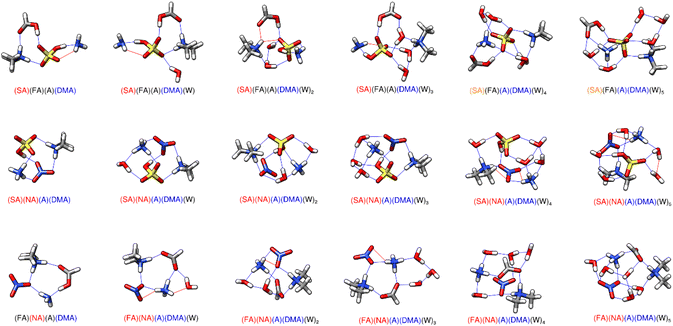
3.6 Tetramers of two acids and two bases
The interactions between the two acid and two base systems are shown in Fig. 5, with the energies corresponding to their formation listed in Table 4. Sulfuric acid has a strong driving effect, accounting for more than 10 kcal mol−1 of stabilization for the dry clusters with either acid and the two bases at all three temperatures. The two dry clusters SA–FA–A–DMA, and SA–NA–A–DMA are only 2–3 kcal mol−1 different in free energy (Table 4). The extra stabilization for the NA cluster stems from the additional proton transfer from the nitric acid to one of the bases, forming an overall tetra-ionic cluster, resulting in a strong hydrogen bond between the two ions.| Cluster | 216.65 K | 273.15 K | 298.15 K |
|---|---|---|---|
| SA + FA + A + DMA ⇌ (SA)(FA)(A)(DMA) | −30.63 (−29.82) | −24.98 (−24.17) | −22.49 (−21.68) |
| (SA)(FA)(A)(DMA) + W ⇌ (SA)(FA)(A)(DMA)(W) | −2.25 | −0.50 | 0.27 |
| (SA)(FA)(A)(DMA)(W) + W ⇌ (SA)(FA)(A)(DMA)(W)2 | −1.07 | 1.10 | 1.99 |
| (SA)(FA)(A)(DMA)(W)2 + W ⇌ (SA)(FA)(A)(DMA)(W)3 | −2.05 | −0.48 | 0.28 |
| (SA)(FA)(A)(DMA)(W)3 + W ⇌ (SA)(FA)(A)(DMA)(W)4 | −2.10 | 0.17 | 1.18 |
| (SA)(FA)(A)(DMA)(W)4 + W ⇌ (SA)(FA)(A)(DMA)(W)5 | −2.83 | −0.93 | −0.09 |
| SA + NA + A + DMA ⇌ (SA)(NA)(A)(DMA) | −33.31 (−32.14) | −27.23 (−26.06) | −24.55 (−23.38) |
| (SA)(NA)(A)(DMA) + W ⇌ (SA)(NA)(A)(DMA)(W) | −6.79 | −4.84 | −3.99 |
| (SA)(NA)(A)(DMA)(W) + W ⇌ (SA)(NA)(A)(DMA)(W)2 | −1.60 | 0.48 | 1.40 |
| (SA)(NA)(A)(DMA)(W)2 + W ⇌ (SA)(NA)(A)(DMA)(W)3 | −1.62 | 0.22 | 1.04 |
| (SA)(NA)(A)(DMA)(W)3 + W ⇌ (SA)(NA)(A)(DMA)(W)4 | −0.35 | 1.39 | 2.16 |
| (SA)(NA)(A)(DMA)(W)4 + W ⇌ (SA)(NA)(A)(DMA)(W)5 | −1.67 | 0.52 | 1.48 |
| FA + NA + A + DMA ⇌ (FA)(NA)(A)(DMA) | −19.35 (−16.67) | −13.94 (−11.26) | −11.57 (−8.88) |
| (FA)(NA)(A)(DMA) + W ⇌ (FA)(NA)(A)(DMA)(W) | −2.16 | −0.32 | 0.50 |
| (FA)(NA)(A)(DMA)(W) + W ⇌ (FA)(NA)(A)(DMA)(W)2 | −1.82 | 0.38 | 1.36 |
| (FA)(NA)(A)(DMA)(W)2 + W ⇌ (FA)(NA)(A)(DMA)(W)3 | −2.73 | −1.23 | −0.66 |
| (FA)(NA)(A)(DMA)(W)3 + W ⇌ (FA)(NA)(A)(DMA)(W)4 | −0.52 | 1.95 | 3.14 |
| (FA)(NA)(A)(DMA)(W)4 + W ⇌ (FA)(NA)(A)(DMA)(W)5 | −0.74 | 0.85 | 1.55 |
The addition of water molecules has some interesting effects on these systems. The (SA)(FA)(A)(DMA)(W)n system remains mostly di-ionic, only undergoing two proton transfers to form a tetra-ionic system when four or five waters are added. In this case sulfuric acid loses both its protons and the bisulfate dianion is complexed with the protonated bases and a neutral formic acid (Fig. 5). In contrast, the (SA)(NA)(A)(DMA)(W)n system is tetra-ionic for n = 0–5, with the sulfuric acid and nitric acid both losing one proton. The addition of one water molecule greatly stabilizes the dry tetra-ionic cluster, as both acids bridge the two bases together in (SA)(NA)(A)(DMA)(W)1, resulting in a stepwise ΔG° value of −6.8 kcal mol−1 at 217 K and −4.0 kcal mol−1 at 298 K. This is the most negative drop in free energy for the addition of any water in all of the reported structures, such that the (SA)(NA)(A)(DMA)(W)1 cluster has an outsized effect on the results of the simulation reported in Section 3.8. The water appears to greatly stabilize this tetra-ionic structure. The (FA)(NA)(A)(DMA)(W)n clusters became tetra-ionic with the addition of one water. Unlike the (SA)(FA)(A)(DMA)(W)4–5 structures, in this case formic acid does lose its proton. However, this additional proton transfer does not account for a lot of stability, as the ΔG° value at 298 K is still positive (0.50 kcal mol−1). These results are mostly consistent with our knowledge of acid strength. However, HSO4− is a weak acid, and yet it loses a proton to become SO42− while formic acid remains neutral in the (SA)(FA)(A)(DMA)(W)4–5 systems. This is probably because hydrogen bonding topology is more important than acid/base strength,68,70 and the details of the hydrogen-bonded structure in the gas phase govern the overall free energy change. For all of the clusters that contain a proton transferred to ammonia, the ammonium cation donates at least three hydrogen bonds and resides near the middle of the cluster.
3.7 Pentamers of three acids and two bases
The system containing all five molecules along with zero to five waters is depicted in Fig. 6, and the respective energies for formation of the clusters are in Table 5. The system remains tetra-ionic at all stages of hydration, with the sulfuric acid and nitric acid donating their protons to the two bases.| Cluster | 216.65 K | 273.15 K | 298.15 K |
|---|---|---|---|
| SA + FA + NA + A + DMA ⇌ (SA)(FA)(NA)(A)(DMA) | −39.56 (−37.78) | −31.53 (−29.75) | −28.00 (−26.22) |
| (SA)(FA)(NA)(A)(DMA) + W ⇌ (SA)(FA)(NA)(A)(DMA)(W) | −4.13 | −2.15 | −1.27 |
| (SA)(FA)(NA)(A)(DMA)(W) + W ⇌ (SA)(FA)(NA)(A)(DMA)(W)2 | −4.07 | −2.06 | −1.17 |
| (SA)(FA)(NA)(A)(DMA)(W)2 + W ⇌ (SA)(FA)(NA)(A)(DMA)(W)3 | 1.16 | 3.17 | 4.05 |
| (SA)(FA)(NA)(A)(DMA)(W)3 + W ⇌ (SA)(FA)(NA)(A)(DMA)(W)4 | −2.62 | −0.84 | −0.06 |
| (SA)(FA)(NA)(A)(DMA)(W)4 + W ⇌ (SA)(FA)(NA)(A)(DMA)(W)5 | −4.47 | −2.85 | −2.12 |
Without any water present, the pentamer system forms a tetra-ionic species with SA and NA donating protons to A and DMA. These four molecules make a ring with both A (1.70 Å, 170°; 1.78 Å, 145°) and DMA (1.69 Å, 173°; 1.77 Å, 164°) donating a hydrogen bond to each strong acid. The FA receives a strong hydrogen bond from the A (1.78 Å, 166°) and donates one to the NA (1.64 Å, 175°), making a triangular structure between those three molecules.
Upon the addition of one water, FA and SA form the strong SA–FA dimer (1.68 Å, 173°; 1.67 Å, 178°).68 The SA then receives an additional three strong hydrogen bonds: (1.85 Å, 149°) from the A, (1.99 Å, 146°) from the W, and (1.83 Å, 158°) from DMA, as well as forming a weaker van der Waals interaction with A (2.22 Å, 118°). The DMA donates another strong hydrogen bond to the water (1.70 Å, 166°), bridging it to the two strong acids through a strong bond to the SA and a van der Waals interaction with NA (2.04 Å, 134°). The NA also receives a strong bond from the A (1.58 Å, 167°), resulting in a total of seven strong hydrogen bonds and two weaker van der Waals interactions.
When a second water is added, the A donates a strong hydrogen bond to all three acids present (1.76 Å, 157°; 1.79 Å, 162°; 1.72 Å, 175°). The SA receives from the FA (1.64 Å, 172°) and donates to the NA (1.62 Å, 171°), making a loop on either side of the SA between the A, SA, and NA. The SA also receives a hydrogen bond from both of the two waters (1.88 Å, 162°; 1.81 Å, 160°), which bond to each other to form a water dimer (1.85 Å, 154°). The DMA bridges the NA (1.76 Å, 169°) to the one water (1.66 Å, 179°) through two strong hydrogen bonds. Overall, the structure has 10 hydrogen bonds.
The three-water cluster is the only pentamer cluster in which the A appears to donate all four hydrogens. These four link to a water (1.74 Å, 165°), SA (1.88 Å, 167°), NA (1.97 Å, 141°), and FA (2.09 Å, 124°); we classify the A–FA contact as a weaker van der Waals force. That singular water molecule only donates one hydrogen bond, which is to the SA (1.90 Å, 154°). The FA donates from its singular proton to the SA (1.72 Å, 172°). The other two waters form a dimer (1.88 Å, 153°) with both waters donating to the SA (1.88 Å, 166°; 1.95 Å, 150°) and the DMA donating to one of the waters (1.68 Å, 173°). This same bonding pattern is present in the two-water cluster. However, the DMA does not form a second strong hydrogen bond but instead forms two weak van der Waals interactions: one to the NA (2.05 Å, 128°) and one to the SA (2.18 Å, 132°). The SA uses its singular proton to donate a strong hydrogen bond to the NA (1.55 Å, 172°). Overall, this structure forms 10 strong hydrogen bonds with three weak van der Waals interactions. Interestingly, this three-water pentamer cluster is less stable than the two-water cluster by 4 kcal mol−1 at 298 K (Table 5). The three-water system is also the only pentamer system in which another structure was identified within 1 kcal mol−1 of the DLPNO-CCSD(T)/CBS//ωB97X-D/6-31++G**Gibbs free energy minimum. The next lowest three-water cluster is 0.42 kcal mol−1 higher in free energy than the minimum. In this cluster, the SA donates both of its protons to A and DMA, forming the sulfate anion, while NA and FA both remain neutral. In this cluster, A forms three strong hydrogen bonds with SA (1.82 Å, 148°), FA (1.82 Å, 162°), and a water molecule (1.86 Å, 155°), with the fourth donor site forming two weak interactions with SA (2.08 Å, 128°) and NA (2.29 Å, 120°) respectively. The NA forms another weak interaction with the first water molecule (1.95 Å, 139°), and donates a strong hydrogen bond to SA (1.45 Å, 178°). FA donates a strong hydrogen bond to SA as well (1.57 Å, 163°). Again, the pattern appears of a water dimer (1.89 Å, 151°) where each water donates a hydrogen bond to SA (1.74 Å, 171°; 1.93 Å, 147°) and one receives a hydrogen bond from DMA (1.69 Å, 170°). DMA also donates a hydrogen bond to SA (1.66 Å, 175°) for a total of 10 hydrogen bonds and 3 weak interactions.
The four-water cluster reverts to the A only donating three hydrogen bonds, to the SA (1.73 Å, 167°), NA (1.79 Å, 172°), and one of the waters (1.80 Å, 156°). That one water donates one bond to the SA (1.73 Å, 170°), forming a ring. On the other side of the SA, it receives hydrogen bonds (1.92 Å, 166°; 1.73 Å, 170°) from each W in a water dimer, although this dimer itself is weakly bound (2.28 Å, 125°). The DMA again donates to the one water in the dimer (1.83 Å, 173°). Here, the DMA also donates to the NA (1.79 Å, 160°), similar to the two-water structure. The NA receives from the last water molecule (1.75 Å, 168°), which receives from the FA (1.58 Å, 179°). The other end of the FA receives from the SA (1.63 Å, 177°). Overall, this structure has 11 strong hydrogen bonds, and one weak van der Waals force holding it together.
When 5 waters are present, there are two water dimers around the three SA oxy groups. The waters in the first dimer (1.84 Å, 159°) each donate to an oxy group in SA (1.79 Å, 170°; 1.92 Å, 158°). In the second dimer (1.93 Å, 154°), one water donates to the same oxy group as the first dimer (1.90 Å, 156°), and the other donates to the third oxy group in SA (1.76 Å, 169°). The A connects these two dimers together by donating to one water molecule in each (1.69 Å, 165°; 1.68 Å, 167°). The A also donates to the NA (1.83 Å, 160°), which receives from the second of the waters in the second dimer (2.00 Å, 144°) and the DMA (1.73 Å, 180°). The DMA donates its second hydrogen bond to the SA (1.75 Å, 173°). SA donates one proton to the last water molecule (1.61 Å, 178°), which donates to the FA (1.77 Å, 170°). The FA donates to the same water that bonds to the NA (1.62 Å, 171°), resulting in that one water having four hydrogen bonds. Overall, the structure has 15 strong hydrogen bonds.
3.8 Equilibrium concentrations and optimal pathways
To calculate the equilibrium concentrations of the clusters, equilibrium constants were calculated using the ΔG° values at 217 and 298 K. For each temperature, a system of 186 equations was created according to Odbadrakh et al.,57 using the equilibrium constants, with 5 equations representing mass balances for the 5 monomers and 181 equations for the reactions. This system of equations solves for the thermodynamics and does not completely account for the kinetics. The ratio of each equilibrium constant is of course the ratio of the forward and reverse reaction of each elementary clustering reaction. However, the results would likely change when accounting for the collision and evaporation rates of these clusters in the atmosphere. The system of equations was solved simultaneously to predict the equilibrium cluster concentrations assuming initial starting concentrations of 5 × 107 cm−3 for SA, 2 × 1011 cm−3 for FA, 9.8 × 1010 cm−3 for NA, 2 × 1011 cm−3 for A, and 2 × 109 cm−3 for DMA at 298 K. These concentrations were picked as they are atmospherically relevant over continents, typically near urban areas.16,133,153–156 To account for the decrease in monomeric concentrations with an increase in altitude, the initial concentrations were decreased by three orders of magnitude at 217 K. We chose a water concentration of 7.7 × 1017 cm−3 at 298 K and 9.9 × 1014 cm−3 at 217 K, which corresponds to 100% humidity at the bottom and top of the troposphere.133 The results are shown in Table 6. We only populated Table 6 with clusters that exceeded 1 cm−3 at either 217 or 298 K. While most monomers remain close to their starting concentrations, sulfuric acid is almost completely used up at 217 K. In urban areas where the DMA concentration is high, the rates of new particle formation are also quite high.143,152,157 Interestingly, although ammonia has an initial concentration two orders of magnitude greater than DMA, clusters with DMA are still more common and typically are present in higher equilibrium concentrations, supporting the idea that DMA is a stronger driver for prenucleation than ammonia.145,146 Using these concentrations, the optimal pathways for forming clusters can be mapped out by finding which smaller clusters have the highest equilibrium concentrations and sequentially adding monomers until the larger cluster is formed. From this, the three best pathways for forming the dry pentamer at both 217 and 298 K are shown in Table 7. While forming the (SA)(DMA) cluster first is optimal at both temperatures, starting with NA instead of SA will also lead to good cluster growth. In five of the six pathways, SA or NA first forms a dimer with a base, and then a second acid is added to form a trimer, and then the third acid is added to form a tetramer. The best pathway at 217 and 298 K forms the (SA)(FA)(NA)(DMA) tetramer. Of these six possible pathways for growing the dry pentamer, the only pathway that forms the (SA)(NA)(A)(DMA) tetramer is the second best at 298 K. Thus, the three acids tend to preferentially build up these clusters.| Cluster | 216.65 K | 298.15 K |
|---|---|---|
| SA | 2.87 × 101 | 1.48 × 107 |
| FA | 2.00 × 108 | 1.99 × 1011 |
| NA | 9.77 × 107 | 9.62 × 1010 |
| A | 2.00 × 108 | 2.00 × 1011 |
| DMA | 1.95 × 106 | 1.98 × 109 |
| SA–FA | 3.79 × 10−2 | 1.03 × 103 |
| SA–NA | 6.29 × 10−6 | 2.10 × 100 |
| SA–A | 9.29 × 10−2 | 5.98 × 103 |
| SA–DMA | 2.42 × 104 | 1.14 × 107 |
| FA–NA | 3.40 × 101 | 1.76 × 104 |
| FA–A | 4.85 × 10−4 | 2.90 × 101 |
| FA–DMA | 6.04 × 10−1 | 5.00 × 102 |
| NA–A | 2.71 × 102 | 2.15 × 105 |
| NA–DMA | 1.87 × 102 | 2.23 × 104 |
| SA–FA–DMA | 2.00 × 103 | 9.85 × 103 |
| SA–NA–DMA | 1.22 × 102 | 1.26 × 103 |
| SA–A–DMA | 2.44 × 10−3 | 1.05 × 100 |
| SA–W1 | 2.42 × 101 | 1.50 × 107 |
| SA–W2 | 3.31 × 100 | 2.90 × 106 |
| SA–W3 | 7.26 × 10−2 | 1.45 × 105 |
| SA–W4 | 3.19 × 10−3 | 1.19 × 104 |
| SA–W5 | 4.39 × 10−7 | 1.82 × 101 |
| FA–W1 | 1.92 × 105 | 1.13 × 109 |
| FA–W2 | 1.07 × 103 | 1.99 × 107 |
| FA–W3 | 1.80 × 10−1 | 5.22 × 104 |
| FA–W4 | 2.57 × 10−6 | 7.25 × 100 |
| NA–W1 | 3.18 × 105 | 1.73 × 109 |
| NA–W2 | 3.03 × 102 | 1.33 × 107 |
| NA–W3 | 3.13 × 10−2 | 1.50 × 104 |
| NA–W4 | 2.35 × 10−6 | 1.16 × 101 |
| A–W1 | 6.52 × 103 | 3.79 × 108 |
| A–W2 | 5.59 × 10−2 | 4.52 × 104 |
| A–W3 | 1.89 × 10−5 | 1.03 × 102 |
| DMA–W1 | 1.84 × 102 | 5.00 × 106 |
| DMA–W2 | 1.04 × 10−2 | 3.76 × 103 |
| DMA–W3 | 2.46 × 10−6 | 5.54 × 100 |
| SA–FA–W1 | 1.13 × 10−2 | 3.79 × 102 |
| SA–FA–W2 | 4.57 × 10−4 | 2.71 × 101 |
| SA–NA–W1 | 6.85 × 10−6 | 2.13 × 100 |
| SA–A–W1 | 6.44 × 10−3 | 5.61 × 102 |
| SA–A–W2 | 8.70 × 10−1 | 1.29 × 104 |
| SA–A–W3 | 3.72 × 10−4 | 6.30 × 101 |
| SA–A–W4 | 1.48 × 10−5 | 2.76 × 100 |
| SA–DMA–W1 | 2.27 × 104 | 5.41 × 106 |
| SA–DMA–W2 | 7.12 × 102 | 3.06 × 105 |
| SA–DMA–W3 | 7.68 × 101 | 4.30 × 104 |
| SA–DMA–W4 | 7.75 × 10−3 | 2.12 × 101 |
| SA–DMA–W5 | 3.48 × 10−4 | 1.26 × 100 |
| FA–NA–W1 | 6.88 × 10−3 | 5.38 × 101 |
| FA–A–W1 | 2.63 × 10−3 | 4.56 × 101 |
| FA–DMA–W1 | 3.56 × 10−3 | 1.12 × 101 |
| NA–A–W1 | 9.58 × 10−3 | 1.28 × 102 |
| NA–DMA–W1 | 6.67 × 100 | 1.42 × 103 |
| NA–DMA–W2 | 1.37 × 10−1 | 6.54 × 101 |
| NA–DMA–W3 | 1.24 × 10−3 | 3.39 × 100 |
| SA–FA–DMA–W1 | 1.28 × 102 | 1.19 × 103 |
| SA–FA–DMA–W2 | 3.28 × 10−1 | 8.87 × 100 |
| SA–NA–DMA–W1 | 1.51 × 101 | 1.77 × 102 |
| SA–NA–DMA–W2 | 4.18 × 10−1 | 1.12 × 101 |
| SA–NA–A–DMA–W1 | 2.34 × 101 | 9.79 × 10−1 |
| 216.65 K | 298.15 K | |
|---|---|---|
| Optimal pathway | SA + DMA ⇌ (SA)(DMA) + FA ⇌ (SA)(FA)(DMA) + NA ⇌ (SA)(FA)(NA)(DMA) + A ⇌ (SA)(FA)(NA)(A)(DMA) | SA + DMA ⇌ (SA)(DMA) + FA ⇌ (SA)(FA)(DMA) + NA ⇌ (SA)(FA)(NA)(DMA) + A ⇌ (SA)(FA)(NA)(A)(DMA) |
| 2nd best pathway | NA + A ⇌ (NA)(A) + FA ⇌ (FA)(NA)(A) + SA ⇌ (SA)(FA)(NA)(A) + DMA ⇌ (SA)(FA)(NA)(A)(DMA) | NA + A ⇌ (NA)(A) + SA ⇌ (SA)(NA)(A) + DMA ⇌ (SA)(NA)(A)(DMA) + FA ⇌ (SA)(FA)(NA)(A)(DMA) |
| 3rd best pathway | NA + DMA ⇌ (NA)(DMA) + SA ⇌ (SA)(NA)(DMA) + FA ⇌ (SA)(FA)(NA)(DMA) + A ⇌ (SA)(FA)(NA)(A)(DMA) | NA + DMA ⇌ (NA)(DMA) + SA ⇌ (SA)(NA)(DMA) + FA ⇌ (SA)(FA)(NA)(DMA) + A ⇌ (SA)(FA)(NA)(A)(DMA) |
For all of the hydrated and dehydrated tetramer and pentamer clusters, the only one that appears in an equilibrium concentration above 1 cm−3 is (SA)(NA)(A)(DMA)(W). This individual cluster, which was identified with exceptional stability in Section 3.6, demonstrates the synergistic effects between the two bases when there are also at least the same number of acids present. For this reason, the three best pathways to forming this cluster have been identified in Table 8. Interestingly, the second and third pathways are different at the two temperatures. Additionally, these clusters tend to add in SA later, preferring early growth with NA. In every pathway except the second best at 217 K, where the water adds second to form the trimer, the water adds first to form the dimer, likely caused by the extreme amount of water present in the atmosphere. In four of these six pathways, the tetramer consists of SA, NA, DMA, and W. In the third best pathway at 217 K, A replaces DMA. The only pathway where one acid, both bases, and a water form a tetramer is for the second-best pathway at 298 K, where the (SA)(A)(SMA)(W) tetramer is predicted to form along this pathway, with NA adding last to form the final (SA)(NA)(A)(DMA)(W) cluster.
| 216.65 K | 298.15 K | |
|---|---|---|
| Optimal pathway | NA + W ⇌ (NA)(W) + DMA ⇌ (NA)(DMA)(W) + SA ⇌ (SA)(NA)(DMA)(W) + A ⇌ (SA)(NA)(A)(DMA)(W) | NA + W ⇌ (NA)(W) + DMA ⇌ (NA)(DMA)(W) + SA ⇌ (SA)(NA)(DMA)(W) + A ⇌ (SA)(NA)(A)(DMA)(W) |
| 2nd best pathway | SA + DMA ⇌ (SA)(DMA) + W ⇌ (SA)(DMA)(W) + NA ⇌ (SA)(NA)(DMA)(W) + A ⇌ (SA)(NA)(A)(DMA)(W) | A + W ⇌ (A)(W) + SA ⇌ (SA)(A)(W) + DMA ⇌ (SA)(A)(DMA)(W) + NA ⇌ (SA)(NA)(A)(DMA)(W) |
| 3rd best pathway | A + W ⇌ (A)(W) + NA ⇌ (NA)(A)(W) + SA ⇌ (SA)(NA)(A)(W) + DMA ⇌ (SA)(NA)(A)(DMA)(W) | SA + W ⇌ (SA)(W) + DMA ⇌ (SA)(DMA)(W) + NA ⇌ (SA)(NA)(DMA)(W) + A ⇌ (SA)(NA)(A)(DMA)(W) |
Unlike the other molecules in our experiment, DMA is believed to have a very short lifetime in the atmosphere, of only 1–2 hours above coastal areas and 5–10 hours over other parts of populated continents.158 Because of this, we have also performed the calculations where the concentration of DMA was decreased further. When the concentration of DMA remained above the concentration of SA, there were nearly no changes in the results. However, as soon as the concentration of DMA dropped below that of SA, the results changed drastically, with the DMA being depleted in place of the SA. As the DMA concentration was continually lowered, the system converged towards one more like that shown by Harold et al., where the clusters containing acids and ammonia had the highest concentrations (Tables S11–S13†).68
4. Conclusions
This is the first study to probe three different acid molecules and two different bases to date, and adds to the insights obtained from previous work. Accurate ΔG° values for the formation of every possible cluster that can be formed from a sulfuric acid molecule, a formic acid molecule, a nitric acid molecule, an ammonia molecule, a dimethylamine molecule, and 0–5 water molecules were determined from a comprehensive search of the PM7, GFN2, and ωB97X-D potential energy surfaces combined with DLPNO-CCSD(T)/CBS electronic energy calculations on the DFT geometries. The detailed geometries of each minimum free energy cluster are more important than traditional acid or base strength in many cases. Addition of a water molecule to a dry cluster can enhance stabilization of that cluster. Dimethylamine forms stronger clusters than ammonia in the absence of water, but as waters are added, the ammonium cation is able to donate more hydrogen bonds than the dimethyl ammonium cation, increasing the stability of the ammonium–water clusters relative to DMA. Results presented here reveal that the (SA)(NA)(A)(DMA)(W) cluster has special stability. Equilibrium concentrations were then calculated and used to map out the optimal pathways for forming the dry pentamer and this especially stable (SA)(NA)(A)(DMA)(W) cluster. The pathways indicate that NA could initiate new particle formation just as efficiently as SA, especially in the presence of water. This suggests that particle growth in the atmosphere results from the combination of many different molecules that are able to form highly stable complexes with nitric, formic, and sulfuric acids. Pathways that lead to tetramers with all three acids and one base are predicted to be important in the growth of mixed acid/base clusters.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the reviewers and Ali Afzalifar for helpful advice, and Togo Odbadrakh and Sara Vanovac for technical help. Funding for this work was provided by grants CHE-1229354, CHE-16626238, CHE-1903871, and CHE-2018427 from the National Science Foundation (GCS), the Arnold and Mabel Beckman Foundation Beckman Scholar Award (CJB), and the Barry M. Goldwater Scholarship (CJB). High-performance computing resources were provided by the Research Corporation for Science Advancement (27446) and the MERCURY Consortium (https://www.mercuryconsortium.org).159,160 Molecular graphics and analyses performed with UCSF Chimera, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from NIH P41-GM103311.References
- K. A. Prather, C. D. Hatch and V. H. Grassian, Analysis of atmospheric aerosols, Annu. Rev. Anal. Chem., 2008, 1, 485–514 CrossRef CAS PubMed.
- M. O. Andreae and D. Rosenfeld, Aerosol–cloud–precipitation interactions. Part 1. The nature and sources of cloud-active aerosols, Earth-Sci. Rev., 2008, 89(1), 13–41 CrossRef.
- J. Kontkanen, D. Stolzenburg, T. Olenius, C. Yan, L. Dada, L. Ahonen, M. Simon, K. Lehtipalo and I. Riipinen, What controls the observed size-dependency of the growth rates of sub-10 nm atmospheric particles?, Environ. Sci.: Atmos., 2022, 2(3), 449–468 CAS.
- A. A. Nair and F. Q. Yu, Quantification of Atmospheric Ammonia Concentrations: A Review of Its Measurement and Modeling, Atmosphere, 2020, 11(10), 1092 CrossRef CAS.
- J. N. Smith, K. F. Moore, P. H. McMurry and F. L. Eisele, Atmospheric Measurements of Sub-20 nm Diameter Particle Chemical Composition by Thermal Desorption Chemical Ionization Mass Spectrometry, Aerosol Sci. Technol., 2004, 38(2), 100–110 CrossRef CAS.
- J. L. Jimenez, M. R. Canagaratna, N. M. Donahue, A. S. Prevot, Q. Zhang, J. H. Kroll, P. F. DeCarlo, J. D. Allan, H. Coe, N. L. Ng, A. C. Aiken, K. S. Docherty, I. M. Ulbrich, A. P. Grieshop, A. L. Robinson, J. Duplissy, J. D. Smith, K. R. Wilson, V. A. Lanz, C. Hueglin, Y. L. Sun, J. Tian, A. Laaksonen, T. Raatikainen, J. Rautiainen, P. Vaattovaara, M. Ehn, M. Kulmala, J. M. Tomlinson, D. R. Collins, M. J. Cubison, E. J. Dunlea, J. A. Huffman, T. B. Onasch, M. R. Alfarra, P. I. Williams, K. Bower, Y. Kondo, J. Schneider, F. Drewnick, S. Borrmann, S. Weimer, K. Demerjian, D. Salcedo, L. Cottrell, R. Griffin, A. Takami, T. Miyoshi, S. Hatakeyama, A. Shimono, J. Y. Sun, Y. M. Zhang, K. Dzepina, J. R. Kimmel, D. Sueper, J. T. Jayne, S. C. Herndon, A. M. Trimborn, L. R. Williams, E. C. Wood, A. M. Middlebrook, C. E. Kolb, U. Baltensperger and D. R. Worsnop, Evolution of organic aerosols in the atmosphere, Science, 2009, 326, 1525–1529 CrossRef CAS PubMed.
- J. N. Smith and G. J. Rathbone, Carboxylic acid characterization in nanoparticles by thermal desorption chemical ionization mass spectrometry, Int. J. Mass Spectrom., 2008, 274(1–3), 8–13 CrossRef CAS.
- J. N. Smith, K. C. Barsanti, H. R. Friedli, M. Ehn, M. Kulmala, D. R. Collins, J. H. Scheckman, B. J. Williams and P. H. McMurry, Observations of aminium salts in atmospheric nanoparticles and possible climatic implications, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(15), 6634–6639 CrossRef CAS PubMed.
- T. E. Morrell and G. C. Shields, Atmospheric implications for formation of clusters of ammonium and 1–10 water molecules, J. Phys. Chem. A, 2010, 114(12), 4266–4271 CrossRef CAS PubMed.
- J. Herb, A. B. Nadykto and F. Yu, Large ternary hydrogen-bonded pre-nucleation clusters in the Earth's atmosphere, Chem. Phys. Lett., 2011, 518, 7–14 CrossRef CAS.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of density functional theory in predicting structures and free energies of reaction of atmospheric prenucleation clusters, J. Chem. Theory Comput., 2012, 8(6), 2071–2077 CrossRef CAS PubMed.
- C. Kuang, M. Chen, J. Zhao, J. Smith, P. H. McMurry and J. Wang, Size and time-resolved growth rate measurements of 1 to 5 nm freshly formed atmospheric nuclei, Atmos. Chem. Phys., 2012, 12(7), 3573–3589 CrossRef CAS.
- P. M. Winkler, J. Ortega, T. Karl, L. Cappellin, H. R. Friedli, K. Barsanti, P. H. McMurry and J. N. Smith, Identification of the biogenic compounds responsible for size-dependent nanoparticle growth, Geophys. Res. Lett., 2012, 39(20), L20815 CrossRef.
- D. E. Husar, B. Temelso, A. L. Ashworth and G. C. Shields, Hydration of the bisulfate ion: atmospheric implications, J. Phys. Chem. A, 2012, 116(21), 5151–5163 CrossRef CAS PubMed.
- B. Temelso, T. E. Morrell, R. M. Shields, M. A. Allodi, E. K. Wood, K. N. Kirschner, T. C. Castonguay, K. A. Archer and G. C. Shields, Quantum mechanical study of sulfuric acid hydration: atmospheric implications, J. Phys. Chem. A, 2012, 116(9), 2209–2224 CrossRef CAS PubMed.
- B. Temelso, T. N. Phan and G. C. Shields, Computational study of the hydration of sulfuric acid dimers: implications for acid dissociation and aerosol formation, J. Phys. Chem. A, 2012, 116(39), 9745–9758 CrossRef CAS PubMed.
- J. Almeida, S. Schobesberger, A. Kurten, I. K. Ortega, O. Kupiainen-Maatta, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppa, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petaja, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Trostl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamaki and J. Kirkby, Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 2013, 502, 359–363 CrossRef CAS PubMed.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petaja, M. Sipila, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Jarvinen, M. Aijala, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkila, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin 3rd, J. Duplissy, H. Vehkamaki, J. Back, A. Kortelainen, I. Riipinen, T. Kurten, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. Lehtinen, A. Laaksonen, V. M. Kerminen and D. R. Worsnop, Direct observations of atmospheric aerosol nucleation, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- Y. Zhang, I. R. Turkmen, B. Wassermann, A. Erko and E. Ruhl, Structural motifs of pre-nucleation clusters, J. Chem. Phys., 2013, 139(13), 134506 CrossRef CAS PubMed.
- J. Elm, M. Bilde and K. V. Mikkelsen, Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445 RSC.
- J. Elm, M. Fard, M. Bilde and K. V. Mikkelsen, Interaction of glycine with common atmospheric nucleation precursors, J. Phys. Chem. A, 2013, 117(48), 12990–12997 CrossRef CAS PubMed.
- J. Elm, P. Norman, M. Bilde and K. V. Mikkelsen, Computational study of the Rayleigh light scattering properties of atmospheric pre-nucleation clusters, Phys. Chem. Chem. Phys., 2014, 16(22), 10883–10890 RSC.
- J. Elm, T. Kurtén, M. Bilde and K. V. Mikkelsen, Molecular interaction of pinic acid with sulfuric acid: exploring the thermodynamic landscape of cluster growth, J. Phys. Chem. A, 2014, 118(36), 7892–7900 CrossRef CAS PubMed.
- J. Elm and K. V. Mikkelsen, Computational approaches for efficiently modeling of small atmospheric clusters, Chem. Phys. Lett., 2014, 615, 26–29 CrossRef CAS.
- D. J. Bustos, B. Temelso and G. C. Shields, Hydration of the sulfuric acid-methylamine complex and implications for aerosol formation, J. Phys. Chem. A, 2014, 118(35), 7430–7441 CrossRef CAS PubMed.
- K. Lehtipalo, L. Rondo, J. Kontkanen, S. Schobesberger, T. Jokinen, N. Sarnela, A. Kurten, S. Ehrhart, A. Franchin, T. Nieminen, F. Riccobono, M. Sipila, T. Yli-Juuti, J. Duplissy, A. Adamov, L. Ahlm, J. Almeida, A. Amorim, F. Bianchi, M. Breitenlechner, J. Dommen, A. J. Downard, E. M. Dunne, R. C. Flagan, R. Guida, J. Hakala, A. Hansel, W. Jud, J. Kangasluoma, V. M. Kerminen, H. Keskinen, J. Kim, J. Kirkby, A. Kupc, O. Kupiainen-Maatta, A. Laaksonen, M. J. Lawler, M. Leiminger, S. Mathot, T. Olenius, I. K. Ortega, A. Onnela, T. Petaja, A. Praplan, M. P. Rissanen, T. Ruuskanen, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Simon, J. N. Smith, J. Trostl, G. Tsagkogeorgas, A. Tome, P. Vaattovaara, H. Vehkamaki, A. E. Vrtala, P. E. Wagner, C. Williamson, D. Wimmer, P. M. Winkler, A. Virtanen, N. M. Donahue, K. S. Carslaw, U. Baltensperger, I. Riipinen, J. Curtius, D. R. Worsnop and M. Kulmala, The effect of acid-base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 2016, 7, 11594 CrossRef CAS PubMed.
- J. Trostl, W. K. Chuang, H. Gordon, M. Heinritzi, C. Yan, U. Molteni, L. Ahlm, C. Frege, F. Bianchi, R. Wagner, M. Simon, K. Lehtipalo, C. Williamson, J. S. Craven, J. Duplissy, A. Adamov, J. Almeida, A. K. Bernhammer, M. Breitenlechner, S. Brilke, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, M. Gysel, A. Hansel, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, H. Keskinen, J. Kim, M. Krapf, A. Kurten, A. Laaksonen, M. Lawler, M. Leiminger, S. Mathot, O. Mohler, T. Nieminen, A. Onnela, T. Petaja, F. M. Piel, P. Miettinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, K. Sengupta, M. Sipila, J. N. Smith, G. Steiner, A. Tome, A. Virtanen, A. C. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, K. S. Carslaw, J. Curtius, J. Dommen, J. Kirkby, M. Kulmala, I. Riipinen, D. R. Worsnop, N. M. Donahue and U. Baltensperger, The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 2016, 533, 527–531 CrossRef CAS PubMed.
- J. Elm, C. N. Jen, T. Kurtén and H. Vehkamäki, Strong hydrogen bonded molecular interactions between atmospheric diamines and sulfuric acid, J. Phys. Chem. A, 2016, 120(20), 3693–3700 CrossRef CAS PubMed.
- F. Bianchi, J. Trostl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kurten, H. E. Manninen, S. Munch, O. Perakyla, T. Petaja, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, New particle formation in the free troposphere: a question of chemistry and timing, Science, 2016, 352, 1109–1112 CrossRef CAS PubMed.
- H. Gordon, K. Sengupta, A. Rap, J. Duplissy, C. Frege, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Trostl, T. Nieminen, I. K. Ortega, R. Wagner, E. M. Dunne, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. S. Craven, A. Dias, S. Ehrhart, L. Fischer, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, J. Kirkby, M. Krapf, A. Kurten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, S. A. Monks, A. Onnela, O. Perakyla, F. Piel, T. Petaja, A. P. Praplan, K. J. Pringle, N. A. Richards, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, S. Sharma, M. Sipila, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tome, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, J. Curtius and K. S. Carslaw, Reduced anthropogenic aerosol radiative forcing caused by biogenic new particle formation, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12053–12058 CrossRef CAS PubMed.
- J. Kirkby, J. Duplissy, K. Sengupta, C. Frege, H. Gordon, C. Williamson, M. Heinritzi, M. Simon, C. Yan, J. Almeida, J. Trostl, T. Nieminen, I. K. Ortega, R. Wagner, A. Adamov, A. Amorim, A. K. Bernhammer, F. Bianchi, M. Breitenlechner, S. Brilke, X. Chen, J. Craven, A. Dias, S. Ehrhart, R. C. Flagan, A. Franchin, C. Fuchs, R. Guida, J. Hakala, C. R. Hoyle, T. Jokinen, H. Junninen, J. Kangasluoma, J. Kim, M. Krapf, A. Kurten, A. Laaksonen, K. Lehtipalo, V. Makhmutov, S. Mathot, U. Molteni, A. Onnela, O. Perakyla, F. Piel, T. Petaja, A. P. Praplan, K. Pringle, A. Rap, N. A. Richards, I. Riipinen, M. P. Rissanen, L. Rondo, N. Sarnela, S. Schobesberger, C. E. Scott, J. H. Seinfeld, M. Sipila, G. Steiner, Y. Stozhkov, F. Stratmann, A. Tome, A. Virtanen, A. L. Vogel, A. C. Wagner, P. E. Wagner, E. Weingartner, D. Wimmer, P. M. Winkler, P. Ye, X. Zhang, A. Hansel, J. Dommen, N. M. Donahue, D. R. Worsnop, U. Baltensperger, M. Kulmala, K. S. Carslaw and J. Curtius, Ion-induced nucleation of pure biogenic particles, Nature, 2016, 533, 521–526 CrossRef CAS PubMed.
- J. Elm, Elucidating the limiting steps in sulfuric acid-base new particle formation, J. Phys. Chem. A, 2017, 121, 8288–8295 CrossRef CAS PubMed.
- J. Elm, N. Myllys, T. Olenius, R. Halonen, T. Kurtén and H. Vehkamäki, Formation of atmospheric molecular clusters consisting of sulfuric acid and C8H12O6 tricarboxylic acid, Phys. Chem. Chem. Phys., 2017, 19(6), 4877–4886 RSC.
- J. Elm, M. Passananti, T. Kurten and H. Vehkamaki, Diamines can initiate new particle formation in the atmosphere, J. Phys. Chem. A, 2017, 121, 6155–6164 CrossRef CAS PubMed.
- H.-B. Xie, J. Elm, R. Halonen, N. Myllys, T. Kurtén, M. Kulmala and H. Vehkamäki, The atmospheric fate of monoethanolamine: enhancing new particle formation of sulfuric acid as an important removal process, Environ. Sci. Technol., 2017, 51(15), 8422–8431 CrossRef CAS PubMed.
- J. V. Kildgaard, K. V. Mikkelsen, M. Bilde and J. Elm, Hydration of atmospheric molecular clusters: a new method for systematic configurational sampling, J. Phys. Chem. A, 2018, 122(22), 5026–5036 CrossRef CAS PubMed.
- H. Chen, S. Chee, M. J. Lawler, K. C. Barsanti, B. M. Wong and J. N. Smith, Size resolved chemical composition of nanoparticles from reactions of sulfuric acid with ammonia and dimethylamine, Aerosol Sci. Technol., 2018, 52(10), 1120–1133 CrossRef CAS.
- H. Chen, A. L. Hodshire, J. Ortega, J. Greenberg, P. H. McMurry, A. G. Carlton, J. R. Pierce, D. R. Hanson and J. N. Smith, Vertically resolved concentration and liquid water content of atmospheric nanoparticles at the US DOE Southern Great Plains site, Atmos. Chem. Phys., 2018, 18(1), 311–326 CrossRef CAS.
- M. J. Lawler, M. P. Rissanen, M. Ehn, R. L. Mauldin, N. Sarnela, M. Sipilä and J. N. Smith, Evidence for diverse biogeochemical drivers of boreal forest new particle formation, Geophys. Res. Lett., 2018, 45(4), 2038–2046 CrossRef.
- L. Pichelstorfer, D. Stolzenburg, J. Ortega, T. Karl, H. Kokkola, A. Laakso, K. E. J. Lehtinen, J. N. Smith, P. H. McMurry and P. M. Winkler, Resolving nanoparticle growth mechanisms from size- and time-dependent growth rate analysis, Atmos. Chem. Phys., 2018, 18(2), 1307–1323 CrossRef CAS.
- N. Myllys, T. Ponkkonen, M. Passananti, J. Elm, H. Vehkamäki and T. Olenius, Guanidine: a highly efficient stabilizer in atmospheric new-particle formation, J. Phys. Chem. A, 2018, 122(20), 4717–4729 CrossRef CAS PubMed.
- S. E. Waller, Y. Yang, E. Castracane, E. E. Racow, J. J. Kreinbihl, K. A. Nickson and C. J. Johnson, The interplay between hydrogen bonding and coulombic forces in determining the structure of sulfuric acid-amine clusters, J. Phys. Chem. Lett., 2018, 9, 1216–1222 CrossRef CAS PubMed.
- Y. Yang, S. E. Waller, J. J. Kreinbihl and C. J. Johnson, Direct link between structure and hydration in ammonium and aminium bisulfate clusters implicated in atmospheric new particle formation, J. Phys. Chem. Lett., 2018, 9, 5647–5652 CrossRef CAS PubMed.
- Y. Yang and C. J. Johnson, Hydration motifs of ammonium bisulfate clusters of relevance to atmospheric new particle formation, Faraday Discuss., 2019, 217, 47–66 RSC.
- J. Elm, An atmospheric cluster database consisting of sulfuric acid, bases, organics, and water, ACS Omega, 2019, 4(6), 10965–10974 CrossRef CAS.
- F. Ma, H.-B. Xie, J. Elm, J. Shen, J. Chen and H. Vehkamäki, Piperazine enhancing sulfuric acid-based new particle formation: implications for the atmospheric fate of piperazine, Environ. Sci. Technol., 2019, 53(15), 8785–8795 CrossRef CAS PubMed.
- J. Shen, H. B. Xie, J. Elm, F. Ma, J. Chen and H. Vehkamaki, Methanesulfonic acid-driven new particle formation enhanced by monoethanolamine: a computational study, Environ. Sci. Technol., 2019, 53(24), 14387–14397 CrossRef CAS PubMed.
- S. Chee, N. Myllys, K. C. Barsanti, B. M. Wong and J. N. Smith, An Experimental and Modeling Study of Nanoparticle Formation and Growth from Dimethylamine and Nitric Acid, J. Phys. Chem. A, 2019, 123(26), 5640–5648 CrossRef CAS PubMed.
- X. Li, S. Chee, J. Hao, J. P. D. Abbatt, J. Jiang and J. N. Smith, Relative humidity effect on the formation of highly oxidized molecules and new particles during monoterpene oxidation, Atmos. Chem. Phys., 2019, 19(3), 1555–1570 CrossRef CAS.
- N. Myllys, S. Chee, T. Olenius, M. Lawler and J. Smith, Molecular-level understanding of synergistic effects in sulfuric acid-amine-ammonia mixed clusters, J. Phys. Chem. A, 2019, 123, 2420–2425 CrossRef CAS PubMed.
- N. Myllys, J. Kubečka, V. Besel, D. Alfaouri, T. Olenius, J. N. Smith and M. Passananti, Role of base strength, cluster structure and charge in sulfuric-acid-driven particle formation, Atmos. Chem. Phys., 2019, 19, 9753–9768 CrossRef CAS.
- N. Myllys, T. Ponkkonen, S. Chee and J. Smith, Enhancing potential of trimethylamine oxide on atmospheric particle formation, Atmosphere, 2019, 11, 35 CrossRef.
- M. Wang, W. Kong, R. Marten, X. C. He, D. Chen, J. Pfeifer, A. Heitto, J. Kontkanen, L. Dada, A. Kurten, T. Yli-Juuti, H. E. Manninen, S. Amanatidis, A. Amorim, R. Baalbaki, A. Baccarini, D. M. Bell, B. Bertozzi, S. Brakling, S. Brilke, L. C. Murillo, R. Chiu, B. Chu, L. P. De Menezes, J. Duplissy, H. Finkenzeller, L. G. Carracedo, M. Granzin, R. Guida, A. Hansel, V. Hofbauer, J. Krechmer, K. Lehtipalo, H. Lamkaddam, M. Lampimaki, C. P. Lee, V. Makhmutov, G. Marie, S. Mathot, R. L. Mauldin, B. Mentler, T. Muller, A. Onnela, E. Partoll, T. Petaja, M. Philippov, V. Pospisilova, A. Ranjithkumar, M. Rissanen, B. Rorup, W. Scholz, J. Shen, M. Simon, M. Sipila, G. Steiner, D. Stolzenburg, Y. J. Tham, A. Tome, A. C. Wagner, D. S. Wang, Y. Wang, S. K. Weber, P. M. Winkler, P. J. Wlasits, Y. Wu, M. Xiao, Q. Ye, M. Zauner-Wieczorek, X. Zhou, R. Volkamer, I. Riipinen, J. Dommen, J. Curtius, U. Baltensperger, M. Kulmala, D. R. Worsnop, J. Kirkby, J. H. Seinfeld, I. El-Haddad, R. C. Flagan and N. M. Donahue, Rapid growth of new atmospheric particles by nitric acid and ammonia condensation, Nature, 2020, 581(7807), 184–189 CrossRef CAS PubMed.
- F. R. Rasmussen, J. Kubečka, V. Besel, H. Vehkamäki, K. V. Mikkelsen, M. Bilde and J. Elm, Hydration of atmospheric molecular clusters III: procedure for efficient free energy surface exploration of large hydrated clusters, J. Phys. Chem. A, 2020, 124(25), 5253–5261 CrossRef CAS PubMed.
- J. Elm, J. Kubečka, V. Besel, M. J. Jääskeläinen, R. Halonen, T. Kurtén and H. Vehkamäki, Modeling the formation and growth of atmospheric molecular clusters: a review, J. Aerosol Sci., 2020, 149, 105621 CrossRef CAS.
- A. Leonardi, H. M. Ricker, A. G. Gale, B. T. Ball, T. T. Odbadrakh, G. C. Shields and J. G. Navea, Particle formation and surface processes on atmospheric aerosols: a review of applied quantum chemical calculations, Int. J. Quantum Chem., 2020, 120(20), e26350 CrossRef CAS.
- T. T. Odbadrakh, A. G. Gale, B. T. Ball, B. Temelso and G. C. Shields, Computation of atmospheric concentrations of molecular clusters from ab initio thermochemistry, J. Visualized Exp., 2020, 158, e60964 Search PubMed.
- B. T. Ball, S. Vanovac, T. T. Odbadrakh and G. C. Shields, Monomers of Glycine and Serine Have a Limited Ability to Hydrate in the Atmosphere, J. Phys. Chem. A, 2021, 125(38), 8454–8467 CrossRef CAS PubMed.
- L. A. Kurfman, T. T. Odbadrakh and G. C. Shields, Calculating Reliable Gibbs Free Energies for Formation of Gas-Phase Clusters that Are Critical for Atmospheric Chemistry: (H2SO4)3, J. Phys. Chem. A, 2021, 125(15), 3169–3176 CrossRef CAS PubMed.
- J. J. Kreinbihl, N. C. Frederiks and C. J. Johnson, Hydration motifs of ammonium bisulfate clusters show complex temperature dependence, J. Chem. Phys., 2021, 154, 014304 CrossRef CAS PubMed.
- J. Elm, Clusteromics I: Principles, Protocols, and Applications to Sulfuric Acid-Base Cluster Formation, ACS Omega, 2021, 6(11), 7804–7814 CrossRef CAS PubMed.
- J. Elm, Clusteromics II: Methanesulfonic Acid-Base Cluster Formation, ACS Omega, 2021, 6(26), 17035–17044 CrossRef CAS PubMed.
- H.-B. Xie and J. Elm, Tri-Base Synergy in Sulfuric Acid-Base Clusters, Atmosphere, 2021, 12(10), 1260 CrossRef CAS.
- S. H. Jathar, C. D. Cappa, Y. He, J. R. Pierce, W. Chuang, K. R. Bilsback, J. H. Seinfeld, R. A. Zaveri and M. Shrivastava, A computationally efficient model to represent the chemistry, thermodynamics, and microphysics of secondary organic aerosols (simpleSOM): model development and application to α-pinene SOA, Environ. Sci.: Atmos., 2021, 1(6), 372–394 CAS.
- S. Chee, K. Barsanti, J. N. Smith and N. Myllys, A predictive model for salt nanoparticle formation using heterodimer stability calculations, Atmos. Chem. Phys., 2021, 21(15), 11637–11654 CrossRef CAS.
- N. Myllys, D. Myers, S. Chee and J. N. Smith, Molecular properties affecting the hydration of acid-base clusters, Phys. Chem. Chem. Phys., 2021, 23, 13106–13114 RSC.
- J. N. Smith, D. C. Draper, S. Chee, M. Dam, H. Glicker, D. Myers, A. E. Thomas, M. J. Lawler and N. Myllys, Atmospheric clusters to nanoparticles: recent progress and challenges in closing the gap in chemical composition, J. Aerosol Sci., 2021, 153, 105733 CrossRef CAS.
- S. E. Harold, C. J. Bready, L. A. Juechter, L. A. Kurfman, S. Vanovac, V. R. Fowler, G. E. Mazaleski, T. T. Odbadrakh and G. C. Shields, Hydrogen-Bond Topology Is More Important Than Acid/Base Strength in Atmospheric Prenucleation Clusters, J. Phys. Chem. A, 2022, 126(10), 1718–1728 CrossRef CAS PubMed.
- R. Zhang, J. Shen, H.-B. Xie, J. Chen and J. Elm, The role of organic acids in new particle formation from methanesulfonic acid and methylamine, Atmos. Chem. Phys., 2022, 22, 2639–2650 CrossRef CAS.
- C. J. Bready, S. Vanovac, T. T. Odbadrakh and G. C. Shields, Amino Acids Compete with Ammonia in Sulfuric Acid-Based Atmospheric Aerosol Prenucleation: The Case of Glycine and Serine, J. Phys. Chem. A, 2022, 126(31), 5195–5206 CrossRef CAS PubMed.
- A. Afzalifar, G. C. Shields, V. R. Fowler and R. H. A. Ras, Probing the Free Energy of Small Water Clusters: Revisiting Classical Nucleation Theory, J. Phys. Chem. Lett., 2022, 13(34), 8038–8046 CrossRef CAS PubMed.
- Y. Liu, H. B. Xie, F. F. Ma, J. W. Chen and J. Elm, Amine-Enhanced Methanesulfonic Acid-Driven Nucleation: Predictive Model and Cluster Formation Mechanism, Environ. Sci. Technol., 2022, 56(12), 7751–7760 CrossRef CAS PubMed.
- Z. H. Fu, H. B. Xie, J. Elm, Y. Liu, Z. Q. Fu and J. W. Chen, Atmospheric Autoxidation of Organophosphate Esters, Environ. Sci. Technol., 2022, 56(11), 6944–6955 CrossRef CAS PubMed.
- J. Elm, Clusteromics III: Acid Synergy in Sulfuric Acid-Methanesulfonic Acid-Base Cluster Formation, ACS Omega, 2022, 7(17), 15206–15214 CrossRef CAS PubMed.
- IPCC, Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2021 Search PubMed.
- M. E. Gonzalez, A. F. Corral, E. Crosbie, H. Dadashazar, G. S. Diskin, E.-L. Edwards, S. Kirschler, R. H. Moore, C. E. Robinson, J. S. Schlosser, M. Shook, C. Stahl, K. L. Thornhill, C. Voigt, E. Winstead, L. D. Ziemba and A. Sorooshian, Relationships between supermicrometer particle concentrations and cloud water sea salt and dust concentrations: analysis of MONARC and ACTIVATE data, Environ. Sci.: Atmos., 2022, 2, 738–752 CAS.
- J. M. Anglada, M. T. C. Martins-Costa, J. S. Francisco and M. F. Ruiz-López, Photoinduced Oxidation Reactions at the Air–Water Interface, J. Am. Chem. Soc., 2020, 142(38), 16140–16155 CrossRef CAS PubMed.
- M. F. Ruiz-Lopez, J. S. Francisco, M. T. C. Martins-Costa and J. M. Anglada, Molecular reactions at aqueous interfaces, Nat. Rev. Chem., 2020, 4, 459–475 CrossRef CAS.
- K. J. Kappes, A. M. Deal, M. F. Jespersen, S. L. Blair, J. F. Doussin, M. Cazaunau, E. Pangui, B. N. Hopper, M. S. Johnson and V. Vaida, Chemistry and photochemistry of pyruvic acid at the air-water interface, J. Phys. Chem. A, 2021, 125, 1036–1049 CrossRef CAS PubMed.
- S. Banerjee, E. Gnanamani, X. Yan and R. N. Zare, Can all bulk-phase reactions be accelerated in microdroplets?, Analyst, 2017, 142(9), 1399–1402 RSC.
- P. C. Arroyo, G. David, P. A. Alpert, E. A. Parmentier, M. Ammann and R. Signorell, Amplification of light within aerosol particles accelerates in-particle photochemistry, Science, 2022, 376(6590), 293–296 CrossRef CAS PubMed.
- C. M. Dobson, G. B. Ellison, A. F. Tuck and V. Vaida, Atmospheric aerosols as prebiotic chemical reactors, Proc. Natl. Acad. Sci. U. S. A., 2000, 97(22), 11864–11868 CrossRef CAS PubMed.
- V. Vaida, Perspective: water cluster mediated atmospheric chemistry, J. Chem. Phys., 2011, 135, 020901 CrossRef PubMed.
- E. C. Griffith, A. F. Tuck and V. Vaida, Ocean-atmosphere interactions in the emergence of complexity in simple chemical systems, Acc. Chem. Res., 2012, 45(12), 2106–2113 CrossRef CAS PubMed.
- E. C. Griffith and V. Vaida, In situ observation of peptide bond formation at the water-air interface, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15697–15701 CrossRef CAS PubMed.
- V. Vaida, Prebiotic phosphorylation enabled by microdroplets, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 12359–12361 CrossRef CAS PubMed.
- A. M. Deal, R. J. Rapf and V. Vaida, Water-air interfaces as environments to address the water paradox in prebiotic chemistry: a physical chemistry perspective, J. Phys. Chem. A, 2021, 125, 4929–4942 CrossRef CAS PubMed.
- T. Müller, A. Badu-Tawiah and R. G. Cooks, Accelerated Carbon-Carbon Bond-Forming Reactions in Preparative Electrospray, Angew. Chem., Int. Ed., 2012, 51(47), 11832–11835 CrossRef PubMed.
- R. M. Bain, C. J. Pulliam and R. G. Cooks, Accelerated Hantzsch electrospray synthesis with temporal control of reaction intermediates, Chem. Sci., 2015, 6(1), 397–401 RSC.
- A. G. Gale, T. T. Odbadrakh, B. T. Ball and G. C. Shields, Water-mediated peptide bond formation in the gas phase: A model prebiotic reaction, J. Phys. Chem. A, 2020, 124(20), 4150–4159 CrossRef CAS PubMed.
- A. G. Gale, T. T. Odbadrakh and G. C. Shields, Catalytic activity of water molecules in gas-phase glycine dimerization, Int. J. Quantum Chem., 2020, 120, e26469 CrossRef CAS.
- B. Temelso, E. F. Morrison, D. L. Speer, B. C. Cao, N. Appiah-Padi, G. Kim and G. C. Shields, Effect of mixing ammonia and alkylamines on sulfate aerosol formation, J. Phys. Chem. A, 2018, 122(6), 1612–1622 CrossRef CAS PubMed.
- J. M. Dieterich and B. Hartke, OGOLEM: global cluster structure optimisation for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach, Mol. Phys., 2010, 108(3–4), 279–291 CrossRef CAS.
- B. Hartke, Global optimization, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(6), 879–887 CAS.
- J. J. P. Stewart, Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters, J. Mol. Model., 2013, 19(1), 1–32 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB-An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions, J. Chem. Theory Comput., 2019, 15, 1652–1672 CrossRef CAS PubMed.
- S. Grimme, Exploration of chemical compound, conformer, and reaction space with meta-dynamics simulations based on tight-binding quantum chemical calculations, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22(14), 7169–7192 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, Gaussian 16 Rev. B.01, Wallingford, CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Exploring the limit of accuracy of the global hybrid meta density functional for main-group thermochemistry, kinetics, and noncovalent interactions, J. Chem. Theory Comput., 2008, 4(11), 1849–1868 CrossRef CAS PubMed.
- J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. D. Chai and M. Head-Gordon, Systematic optimization of long-range corrected hybrid density functionals, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- F. Neese, Prediction of molecular properties and molecular spectroscopy with density functional theory: from fundamental theory to exchange-coupling, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- F. Neese, A. Hansen and D. G. Liakos, Efficient and accurate approximations to the local coupled cluster singles doubles method using a truncated pair natural orbital basis, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- F. Neese, F. Wennmohs and A. Hansen, Efficient and accurate local approximations to coupled-electron pair approaches: an attempt to revive the pair natural orbital method, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- A. Hansen, D. G. Liakos and F. Neese, Efficient and accurate local single reference correlation methods for high-spin open-shell molecules using pair natural orbitals, J. Chem. Phys., 2011, 135, 214102 CrossRef PubMed.
- D. G. Liakos and F. Neese, Improved correlation energy extrapolation schemes based on local pair natural orbital methods, J. Phys. Chem. A, 2012, 116, 4801–4816 CrossRef CAS PubMed.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- D. G. Liakos and F. Neese, Is it possible to obtain coupled cluster quality energies at near density functional theory cost? Domain-based local pair natural orbital coupled cluster vs. modern density functional theory, J. Chem. Theory Comput., 2015, 11, 4054–4063 CrossRef CAS PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. Martin and F. Neese, Exploring the accuracy limits of local pair natural orbital coupled-cluster theory, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, SparseMaps – a systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- F. Pavosevic, C. Peng, P. Pinski, C. Riplinger, F. Neese and E. F. Valeev, SparseMaps – a systematic infrastructure for reduced-scaling electronic structure methods. V. Linear scaling explicitly correlated coupled-cluster method with pair natural orbitals, J. Chem. Phys., 2017, 146(17), 174108 CrossRef PubMed.
- M. Sparta, M. Retegan, P. Pinski, C. Riplinger, U. Becker and F. Neese, Multilevel approaches within the local pair natural orbital framework, J. Chem. Theory Comput., 2017, 13, 3198–3207 CrossRef CAS PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: an improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- A. Altun, F. Neese and G. Bistoni, Extrapolation to the limit of a complete pair natural orbital space in local coupled-cluster calculations, J. Chem. Theory Comput., 2020, 16(10), 6142–6149 CrossRef CAS PubMed.
- D. G. Liakos, Y. Guo and F. Neese, Comprehensive benchmark results for the domain based local pair natural orbital coupled cluster method (DLPNO-CCSD(T)) for closed- and open-shell systems, J. Phys. Chem. A, 2020, 124, 90–100 CrossRef CAS PubMed.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- K. A. Peterson, D. E. Woon and T. H. Dunning, Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H+H2→H2+H reaction, J. Chem. Phys., 1994, 100, 7410–7415 CrossRef CAS.
- A. K. Wilson, T. van Mourik and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. VI. Sextuple zeta correlation consistent basis sets for boron through neon, J. Mol. Struct.: THEOCHEM, 1996, 388, 339–349 CrossRef CAS.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- S. Kanchanakungwankul, J. L. Bao, J. Zheng, I. M. Alecu, B. J. Lynch and D. G. Truhlar, Database of Frequency Scale Factors for Electronic Model Chemistries – Version 5, 2021 Search PubMed.
- K. K. Irikura, THERMO.PL, NIST, 2002 Search PubMed.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- M. W. Jurema, K. N. Kirschner and G. C. Shields, Modeling of magic water clusters (H2O)20 and (H2O)21H+ with the PM3 quantum-mechanical method, J. Comput. Chem., 1993, 14(11), 1326–1332 CrossRef CAS.
- M. W. Jurema and G. C. Shields, Ability of the PM3 quantum-mechanical method to model intermolecular hydrogen bonding between neutral molecules, J. Comput. Chem., 1993, 14(1), 89–104 CrossRef CAS.
- Y.-P. Zhu, Y.-R. Liu, T. Huang, S. Jiang, K.-M. Xu, H. Wen, W.-J. Zhang and W. Huang, Theoretical Study of the Hydration of Atmospheric Nucleation Precursors with Acetic Acid, J. Phys. Chem. A, 2014, 118(36), 7959–7974 CrossRef CAS PubMed.
- J. H. Seinfeld and S. N. Pandis, in Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, Wiley, 3rd edn, 2016 Search PubMed.
- R. J. Weber, J. J. Marti, P. H. McMurry, F. L. Eisele, D. J. Tanner and A. Jefferson, Measured Atmospheric New Particle Formation Rates: Implications for Nucleation Mechanisms, Chem. Eng. Commun., 1996, 151(1), 53–64 CrossRef CAS.
- R. J. Weber, J. J. Marti, P. H. McMurry, F. L. Eisele, D. J. Tanner and A. Jefferson, Measurements of new particle formation and ultrafine particle growth rates at a clean continental site, J. Geophys. Res.: Atmos., 1997, 102(D4), 4375–4385 CrossRef CAS.
- L. M. Brown, N. Collings, R. M. Harrison, A. D. Maynard, R. L. Maynard, P. H. McMurry, K. S. Woo, R. Weber, D.-R. Chen and D. Y. H. Pui, Size distributions of 3–10 nm atmospheric particles: implications for nucleation mechanisms, Philos. Trans. R. Soc. London, Ser. A, 2000, 358(1775), 2625–2642 CrossRef.
- T. Berndt, O. Boge, F. Stratmann, J. Heintzenberg and M. Kulmala, Rapid formation of sulfuric acid particles at near-atmospheric conditions, Science, 2005, 307(5710), 698–700 CrossRef CAS PubMed.
- M. Sipila, T. Berndt, T. Petaja, D. Brus, J. Vanhanen, F. Stratmann, J. Patokoski, R. L. Mauldin 3rd, A. P. Hyvarinen, H. Lihavainen and M. Kulmala, The role of sulfuric acid in atmospheric nucleation, Science, 2010, 327, 1243–1246 CrossRef.
- T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia, Atmos. Chem. Phys., 2008, 8(14), 4095–4103 CrossRef.
- H. R. Leverentz, J. I. Siepmann, D. G. Truhlar, V. Loukonen and H. Vehkamaki, Energetics of atmospherically implicated clusters made of sulfuric acid, ammonia, and dimethyl amine, J. Phys. Chem. A, 2013, 117, 3819–3825 CrossRef CAS PubMed.
- T. Olenius, O. Kupiainen-Määttä, I. K. Ortega, T. Kurtén and H. Vehkamäki, Free energy barrier in the growth of sulfuric acid–ammonia and sulfuric acid–dimethylamine clusters, J. Chem. Phys., 2013, 139(8), 084312 CrossRef CAS PubMed.
- C. N. Jen, P. H. McMurry and D. R. Hanson, Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.: Atmos., 2014, 119(12), 7502–7514 CrossRef CAS.
- H. Li, A. Ning, J. Zhong, H. Zhang, L. Liu, Y. Zhang, X. Zhang, X. C. Zeng and H. He, Influence of atmospheric conditions on sulfuric acid-dimethylamine-ammonia-based new particle formation, Chemosphere, 2020, 245, 125554 CrossRef CAS PubMed.
- Y. Li, H. Zhang, Q. Zhang, Y. Xu and A. B. Nadykto, Interactions of sulfuric acid with common atmospheric bases and organic acids: thermodynamics and implications to new particle formation, J. Environ. Sci., 2020, 95, 130–140 CrossRef.
- R. Cai, C. Yan, D. Yang, R. Yin, Y. Lu, C. Deng, Y. Fu, J. Ruan, X. Li, J. Kontkanen, Q. Zhang, J. Kangasluoma, Y. Ma, J. Hao, D. R. Worsnop, F. Bianchi, P. Paasonen, V. M. Kerminen, Y. Liu, L. Wang, J. Zheng, M. Kulmala and J. Jiang, Sulfuric acid–amine nucleation in urban Beijing, Atmos. Chem. Phys., 2021, 21(4), 2457–2468 CrossRef CAS.
- J. Brean, M. Dall'Osto, R. Simó, Z. Shi, D. C. S. Beddows and R. M. Harrison, Open ocean and coastal new particle formation from sulfuric acid and amines around the Antarctic Peninsula, Nat. Geosci., 2021, 14(6), 383–388 CrossRef CAS.
- V. Loukonen, T. Kurtén, I. K. Ortega, H. Vehkamäki, A. A. H. Pádua, K. Sellegri and M. Kulmala, Enhancing effect of dimethylamine in sulfuric acid nucleation in the presence of water – a computational study, Atmos. Chem. Phys., 2010, 10(10), 4961–4974 CrossRef CAS.
- A. B. Nadykto, J. Herb, F. Yu and Y. Xu, Enhancement in the production of nucleating clusters due to dimethylamine and large uncertainties in the thermochemistry of amine-enhanced nucleation, Chem. Phys. Lett., 2014, 609, 42–49 CrossRef CAS.
- T. Olenius, T. Kurten, O. Kupiainen-Maatta, H. Henschel, I. K. Ortega and H. Vehkamaki, Effect of hydration and base contaminants on sulfuric acid diffusion measurement: a computational study, Aerosol Sci. Technol., 2014, 48(6), 593–603 CrossRef CAS.
- W. A. Glasoe, K. Volz, B. Panta, N. Freshour, R. Bachman, D. R. Hanson, P. H. McMurry and C. Jen, Sulfuric acid nucleation: an experimental study of the effect of seven bases, J. Geophys. Res.: Atmos., 2015, 120(5), 1933–1950 CrossRef CAS.
- J. M. Thomas, S. He, C. Larriba-Andaluz, J. W. DePalma, M. V. Johnston and C. J. Hogan Jr, Ion mobility spectrometry-mass spectrometry examination of the structures, stabilities, and extents of hydration of dimethylamine-sulfuric acid clusters, Phys. Chem. Chem. Phys., 2016, 18, 22962–22972 RSC.
- L. Yao, O. Garmash, F. Bianchi, J. Zheng, C. Yan, J. Kontkanen, H. Junninen, S. B. Mazon, M. Ehn, P. Paasonen, M. Sipilä, M. Wang, X. Wang, S. Xiao, H. Chen, Y. Lu, B. Zhang, D. Wang, Q. Fu, F. Geng, L. Li, H. Wang, L. Qiao, X. Yang, J. Chen, V.-M. Kerminen, T. Petäjä, D. R. Worsnop, M. Kulmala and L. Wang, Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 2018, 361(6399), 278–281 CrossRef CAS PubMed.
- S. Aloisio, P. E. Hintze and V. Vaida, The hydration of formic acid, J. Phys. Chem. A, 2002, 106(2), 363–370 CrossRef CAS.
- K. Acker, D. Möller, R. Auel, W. Wieprecht and D. Kalaß, Concentrations of nitrous acid, nitric acid, nitrite and nitrate in the gas and aerosol phase at a site in the emission zone during ESCOMPTE 2001 experiment, Atmos. Res., 2005, 74(1–4), 507–524 CrossRef CAS.
- X. Ge, A. S. Wexler and S. L. Clegg, Atmospheric amines – part I. A review, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS.
- X. Ge, A. S. Wexler and S. L. Clegg, Atmospheric amines – part II. Thermodynamic properties and gas/particle partitioning, Atmos. Environ., 2011, 45, 561–577 CrossRef CAS.
- L. Liu, F. Yu, L. Du, Z. Yang, J. S. Francisco and X. Zhang, Rapid sulfuric acid-dimethylamine nucleation enhanced by nitric acid in polluted regions, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(35), e2108347118 Search PubMed.
- F. Yu and G. Luo, Modeling of gaseous methylamines in the global atmosphere: impacts of oxidation and aerosol uptake, Atmos. Chem. Phys., 2014, 14(22), 12455–12464 CrossRef.
- G. C. Shields, The Molecular Education and Research Consortium in Undergraduate computational chemistry (MERCURY): twenty years of exceptional success supporting undergraduate research and inclusive excellence, Scholarship and Practice of Undergraduate Research, 2019, 3, pp. 5–15 Search PubMed.
- G. C. Shields, Twenty years of exceptional success: the molecular education and research consortium in undergraduate computational chemistry (MERCURY), Int. J. Quantum Chem., 2020, 120, e26274 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ea00087c |
| This journal is © The Royal Society of Chemistry 2022 |