Open Access Article
Open Access ArticleAtomic-scale structures and dynamics at the growing calcite step edge investigated by high-speed frequency modulation atomic force microscopy
Kazuki
Miyata
 abc,
Yuta
Kawagoe
b,
Naoyuki
Miyashita
b,
Tomoki
Nakagawa
c and
Takeshi
Fukuma
abc,
Yuta
Kawagoe
b,
Naoyuki
Miyashita
b,
Tomoki
Nakagawa
c and
Takeshi
Fukuma
 *abc
*abc
aNano Life Science Institute (WPI-NanoLSI), Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan. E-mail: fukuma@staff.kanazawa-u.ac.jp; Fax: +81-76-234-4632; Tel: +81-76-234-4847
bDivision of Electrical Engineering and Computer Science, Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan
cDivision of Frontier Engineering, Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan
First published on 18th November 2021
Abstract
We have investigated the calcite growth mechanism by directly imaging atomic-scale structural changes at the growing step edges with high-speed frequency modulation atomic force microscopy (HS-FM-AFM). We compared the results with those previously obtained during dissolution, where a transition region (TR) consisting of a Ca(OH)2 monolayer was found to be formed along the step edges as an intermediate state. We found that the TR is created not only during dissolution but also during the growth process. Steps with and without a TR coexist with a ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in both dissolution and growth, implying that their primary reaction pathways should involve TR formation. While all the dissolving steps show a linear shape, the growing steps additionally present a complex non-linear shape with many kinks. The TRs formed along the linear steps present a fixed and uniform width, while those along the complex steps present a non-uniform and dynamically varying width. The acute and obtuse steps show similar TR formation probability, TR width, and step velocity during growth, while a TR is preferentially formed along an acute step during dissolution. For both step types, TRs during growth are wider than those during dissolution. Based on these findings, we present possible reaction pathways triggered by the adsorption of either CO2 or HCO3− for the elementary steps in calcite growth.
3 in both dissolution and growth, implying that their primary reaction pathways should involve TR formation. While all the dissolving steps show a linear shape, the growing steps additionally present a complex non-linear shape with many kinks. The TRs formed along the linear steps present a fixed and uniform width, while those along the complex steps present a non-uniform and dynamically varying width. The acute and obtuse steps show similar TR formation probability, TR width, and step velocity during growth, while a TR is preferentially formed along an acute step during dissolution. For both step types, TRs during growth are wider than those during dissolution. Based on these findings, we present possible reaction pathways triggered by the adsorption of either CO2 or HCO3− for the elementary steps in calcite growth.
1 Introduction
Calcite is the most abundant carbonate mineral on the Earth, and its growth and dissolution play critical roles in the global carbon cycle.1–3 In addition, calcite has attracted much attention due to its importance in biomineralization,4,5 carbon sequestration,6,7 and optical engineering.8,9 Thus, the mechanism of calcite growth and dissolution has intensively been studied by various methods.10–20 In particular, atomic force microscopy (AFM)21 has been a powerful tool for visualizing atomistic step flows, which has helped us to understand the nanoscale behaviors of the calcite growth and dissolution processes.10,11,16,22–24In the growth process, screw dislocations serve as the source of the steps.25 The created steps take a spiral shape near the center of the dislocation and are transformed into a linear shape as they propagate away from the center (Fig. 1b).11 Meanwhile, the dissolution is initiated by forming small rectangular pits followed by propagation of the four linear steps surrounding the pits.23,24 These basic behaviors have successfully been reproduced by kinetic Monte Carlo simulations, typically with empirically determined activation energy values for the different step edge structures (i.e., acute and obtuse steps shown in Fig. 1c and d)26 and solution conditions (e.g., pH, degree of supersaturation, and various additives).14,27,28 However, it is essential to understand the atomistic behaviors at the step edges to understand the origin of these different activation energies.
Compared with the nanoscale step flow behaviors, the atomistic events at the step edges have not been well understood due to the difficulties in their direct observation. So far, AFM observations of the step flow with varying pH and Ca2+/CO32− ratios have been performed to obtain insights into the chemical reactions associated with the adsorption or desorption of ions at the step edges.15,17 Meanwhile, molecular dynamics (MD) simulations were performed to investigate the free energy landscape for Ca2+ and CO32− and the stability of water near the step edges.19,20,29 Based on these results, a possible model for the atomistic kink formation was proposed.20 However, direct observations of atomistic events are strongly demanded to validate the mechanisms suggested by these previous experiments and simulations.
We have recently developed high-speed frequency modulation AFM (HS-FM-AFM) to solve such problems.30 The developed system allows in-liquid atomic-resolution imaging at ∼0.5 s per frame.31 With this technique, we previously performed direct imaging of the atomistic events at the step edges during the calcite dissolution in water.30 The obtained images revealed the existence of a layer-like structure, the “transition region (TR)”, along the step edges. The TR typically has a width of a few nanometers and a height of 0.1–0.2 nm. This height is lower than the atomistic step (0.304 nm) at the calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface. With the help of MD simulations, we attributed the TRs to a Ca(OH)2 monolayer formed as an intermediate state during the dissolution. Furthermore, we also reported their statistical properties,31 behaviors in a small etch pit,32 and possible roles in the step dissolution kinetics.32 However, the method has not been applied to studies on the calcite growth process. Thus, the existence of the TR and its possible roles in the growth process remain unclear.
4) surface. With the help of MD simulations, we attributed the TRs to a Ca(OH)2 monolayer formed as an intermediate state during the dissolution. Furthermore, we also reported their statistical properties,31 behaviors in a small etch pit,32 and possible roles in the step dissolution kinetics.32 However, the method has not been applied to studies on the calcite growth process. Thus, the existence of the TR and its possible roles in the growth process remain unclear.
In this study, we have investigated the atomic-scale mechanism of the calcite growth process by directly imaging atomistic events at the growing step edges in a supersaturated solution. The obtained images confirm the existence of TRs in the growth process. Their structures and dynamics are clarified and compared with those observed during the dissolution. Based on these findings, we present possible models to explain the atomic-scale growth mechanism at the step edges.
2 Experimental
2.1 Sample preparation
In this study, we used a calcite single crystal (Crystal Base Co, Ltd.) with a size of 5 × 5 × 2 mm3. This crystal was fixed onto a sample holder for our AFM system with epoxy glue. The fixed crystal was cleaved by a razor blade. Immediately after the cleavage, 50 μl solution was dropped onto the sample surface to perform AFM experiments in the deposited liquid.The calcite supersaturated solution used for the AFM imaging of the growth process was prepared as follows. We prepared an 11.6 mM CaCl2 solution by dissolving its powder form (10043-52-4, FUJIFILM Wako Pure Chemical) into Milli-Q water. In the same way, we prepared 11.6 mM NaHCO3 solution from its powder form (31212-25, Nacalai Tesque). These two solutions and Milli-Q water were mixed with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 to prepare the supersaturated solution with a relative supersaturation (σ) of 21. σ is defined by (C − Ceq)/Ceq, where C and Ceq denote the real and saturated calcite concentrations, respectively. For this solution, C (=1.3 mM) is 22 times higher than Ceq (=58 μM).10
7 to prepare the supersaturated solution with a relative supersaturation (σ) of 21. σ is defined by (C − Ceq)/Ceq, where C and Ceq denote the real and saturated calcite concentrations, respectively. For this solution, C (=1.3 mM) is 22 times higher than Ceq (=58 μM).10
1.3 mM HCO3−, produced by the ionization of the dissolved NaHCO3, should be subject to the following equilibrium reactions.
| CO2 + H2O ⇌ H+ + HCO3−, | (1) |
| HCO3− ⇌ H+ + CO32−. | (2) |
The ionization constants of reactions (1) and (2) are Ka1 = 4.25 × 10−7 M and Ka2 = 5.6 × 10−11 M, respectively. From these parameters, the pH can be calculated to be 8.3. This pH is slightly higher than the experimentally measured value (∼7.8) due to the dissolution of CO2 from the air. By taking into account this carbon increase, we expect that the solution should contain 2.6 mM Cl−, 1.3 mM Ca2+, Na+, and HCO3−, 60 μM CO2, and 3.6 μM CO32−.
2.2 AFM experiments
We used a custom-built HS-FM-AFM with a low-noise cantilever deflection sensor,33–35 highly stable photothermal cantilever excitation system,35,36 high-speed scanner,37,38 and low-latency wideband PLL and FM-AFM controller.39–41 Details of the design and performance of this system were reported previously.30All the HS-FM-AFM imaging was performed in the constant frequency shift (Δf) mode at room temperature. The growth process was imaged in the supersaturated solution (σ = 21), while the dissolution process was imaged in Milli-Q water. We used commercially available silicon cantilevers (AC55, Olympus) with a typical spring constant k, quality factor Q, and resonance frequency f0 in an aqueous environment of 80 N m−1, 10 and 1.5 MHz, respectively. The AFM tip was coated with a 15 nm silicon film by a dc sputter coater (K575XD, Emitech) for cleaning and stabilizing the tip surface.42
3 Results and discussion
3.1 HS-FM-AFM imaging
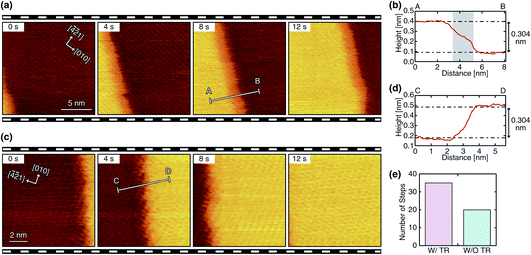
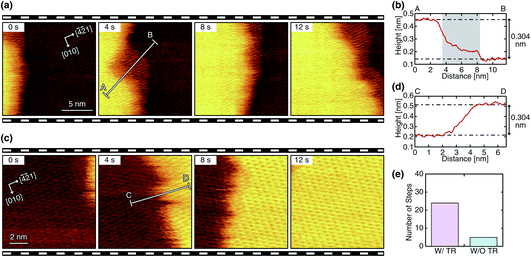
We performed HS-FM-AFM imaging of the growing steps on the calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface in the supersaturated solution. The obtained images reveal the variations in the step edge structure and dynamics. Among the 84 steps observed in this study, 55 steps (65%) show a linear edge with a small number of kinks, as shown in Fig. 2a and c. Meanwhile, 29 steps (35%) show a complex non-linear edge with many kinks, as shown in Fig. 3a and c. Thus, the linear ones seem to be more common. Both linear and complex steps were imaged with and without a TR, which demonstrates that a TR can be formed even during the growth process. Fig. 2 and 3 show typical HS-FM-AFM images of these different types of steps. These images demonstrate that HS-FM-AFM successfully visualizes atomic-scale structural changes near the step edge during the calcite growth.
4) surface in the supersaturated solution. The obtained images reveal the variations in the step edge structure and dynamics. Among the 84 steps observed in this study, 55 steps (65%) show a linear edge with a small number of kinks, as shown in Fig. 2a and c. Meanwhile, 29 steps (35%) show a complex non-linear edge with many kinks, as shown in Fig. 3a and c. Thus, the linear ones seem to be more common. Both linear and complex steps were imaged with and without a TR, which demonstrates that a TR can be formed even during the growth process. Fig. 2 and 3 show typical HS-FM-AFM images of these different types of steps. These images demonstrate that HS-FM-AFM successfully visualizes atomic-scale structural changes near the step edge during the calcite growth.
The height profiles measured across the four different types of steps (Fig. 2b, d and 3b, d) show that the height difference between the upper and lower terraces corresponds to the single molecular step height (∼0.304 nm). Thus, the steps shown in these figures should be monomolecular ones. For the steps with a TR, the height profiles (Fig. 2b and 3b) show a plateau or a shoulder between the upper and lower terraces with a medium height of 0.1–0.2 nm and a width of 1–10 nm. Because of the similarity in these structural features, the observed layer-like structures should correspond to the TRs previously observed during dissolution (i.e., a Ca(OH)2 monolayer formed as an intermediate state). As indicated in Fig. 2e and 3e, the steps with a TR were more often observed than those without a TR, implying that the growth process involving the TR formation should be the primary pathway under these experimental conditions. The same trend was previously confirmed in the dissolution process.31
The linear steps typically propagate in one direction with little change in the edge structure (Fig. 2a and c). The TRs formed at these steps also show a linear edge and an almost constant width. This behavior is similar to that observed during dissolution. In contrast, the complex steps and the associated TRs show dynamic changes in their edge structure during their propagation (Fig. 3a and c). In this case, the width of the TRs is not uniform and dynamically changes in the range of 0 to 10 nm. Furthermore, the direction of the step propagation is not necessarily constant but varies during the growth. Such dynamic changes in the step edge structure and the TR width are not observed during dissolution.
In general, the linear step edge structure suggests preferred adsorption of the growth unit to the kinks over the step edges. Thus, there must be a reason to locally weaken such a preference at the location where the complex step edges are formed. One possible reason is the distortion of the crystal lattice caused by defects or dislocations. For example, curved steps are often formed around a screw dislocation to form a spiral step arrangement during the growth process,10 while linear steps are created around a rectangular pit from the very beginning of the dissolution.32 Such a difference in the step flow behavior may account for the observed difference in the atomic-scale structures. In addition, local enhancement of the solute concentration may induce adsorption to the step edges. Such variation may occur if the step density is non-uniform.
3.2 Analysis of the TR properties
During calcite growth and dissolution, steps propagate in four different crystallographic orientations (Fig. 1b). Among them, the [48![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]− and [
]− and [![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 41]− steps are known as acute steps (Fig. 1c), while the [48
41]− steps are known as acute steps (Fig. 1c), while the [48![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ]+ and [
]+ and [![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 41]+ steps are known as obtuse steps (Fig. 1d). Previous studies have revealed that these two types of steps show different step flow behaviors.11–13,15,16,20,43–45 To understand the correlation between such a nanoscale step flow behavior and atomic-scale step edge structures, we compare TR properties between obtuse and acute steps and growth and dissolution. Note that the dissolution data was adapted from our previous report.31
41]+ steps are known as obtuse steps (Fig. 1d). Previous studies have revealed that these two types of steps show different step flow behaviors.11–13,15,16,20,43–45 To understand the correlation between such a nanoscale step flow behavior and atomic-scale step edge structures, we compare TR properties between obtuse and acute steps and growth and dissolution. Note that the dissolution data was adapted from our previous report.31
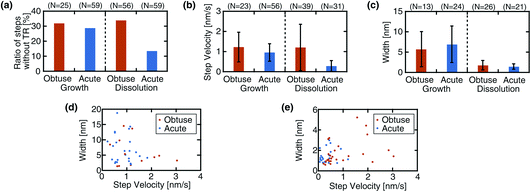
Fig. 4a shows a comparison of the ratios of the steps without a TR. For the growth process, the acute steps show a slightly lower ratio (29%) than the obtuse steps (32%), although the difference is minor. For the dissolution process, the same relationship is observed but with a much more significant difference. These results suggest that the TR formation does not show a strong preference for the step type in the growth process, while it is preferentially formed at the acute steps in the dissolution.
Fig. 4b shows a comparison of the step velocity. The obtuse steps move slightly faster (1.22 ± 0.736 nm s−1) than the acute steps (0.95 ± 0.43 nm s−1) in the growth process. The same relationship was observed in the dissolution, yet the difference is more evident than that in the growth. As for the dissolution, previous AFM studies have consistently reported a faster velocity for the obtuse steps under various solution conditions.31,46,47 Meanwhile, this relationship is valid for the growth process only at high supersaturation and is suppressed or even inverted as the supersaturation is reduced.11,12 While the Ca2+ concentration (1.3 mM) in the solution used for this growth experiment is sufficiently high, the CO32− concentration (3.6 μM) is relatively low. This low concentration may explain the small difference between the obtuse and acute step velocities in the growth process.
Fig. 4c shows a comparison of the TR width. A significant difference is found not between the acute and obtuse steps but between the growth and dissolution processes: the growing steps present a much broader TR than the dissolving steps. This difference is observed for both linear and complex steps. Fig. 4d and e show the correlations between the velocity and width for the growth and dissolution, respectively. For the growth process, there may be a weak trend that a narrow TR is formed along a fast step while a wide TR is formed along a slow step. Otherwise, no strong correlation is found between the two parameters.
Although the mechanism of the TR formation is not fully understood, one possible explanation was suggested by the previous MD simulation.30,31 According to this simulation, the hydration structure formed on the upper terrace almost seamlessly extends over the TR. Such an extended hydrogen-bonding network may explain the energetic merit to form a TR as an intermediate state during the dissolution or growth. If this model is correct, the wider TR width observed in the growth process may suggest that an extended hydration structure may be more easily formed during the growth process. However, more accurate discussions should require atomic-scale simulations with a model taking into account the TR formation.
3.3 Atomic-scale growth mechanism
This study found that the step edge reaction involving the TR formation is the most favorable pathway in both dissolution and growth. Here, we briefly overview the previously proposed dissolution mechanism and then discuss possible models for the growth mechanism. In the previously proposed model, the dissolution is triggered by the dissociative adsorption of water to the CO32− vacancy at the step edge, which produces an ion pair of CaOH+ and HCO3−, as described by| CaCO3 + H2O → CaOH+ + HCO3−. | (3) |
The produced ion pairs can form a mobile adsorption layer only when trapped inside a nanoscale pit.32 Otherwise, the ion pair is soon subject to the following reaction to form a TR consisting of a Ca(OH)2 monolayer.
| CaOH+ + HCO3− → Ca(OH)2 + CO2. | (4) |
As for the growth process, an atomistic model was proposed by the recent simulation study.20 In the proposed model, CO32− first adsorbs at the step edge, which induces the subsequent adsorption of Ca2+. Such a model should explain the growth mechanism without involving the TR formation. However, the growth mechanism involving the TR formation has not been investigated by simulation yet, making it difficult to determine the reaction pathway uniquely. Thus, here we only present a few possible reaction pathways that can explain the observed phenomena.
The growth process involves reactions not only at the step edges but also at the TR edges. At the growing edge of a TR, the following reaction should form Ca(OH)2.
| Ca2+ + 2OH− → Ca(OH)2. | (5) |
This reaction does not progress in a bulk neutral solution. However, the growth of the TR edges observed in this study (Fig. 2a and 3a) suggests that this reaction can progress at the TR edges. This argument is partially supported by our previous MD simulation study,30 where we confirmed the stable adsorption of a Ca(OH)2 monolayer at the step edge.
As for the reactions at the upper terrace edges, a few different pathways are conceivable. One of them is the inverse reactions of the dissolution process, as described by
| Ca(OH)2 + CO2 → CaOH+ + HCO3−, | (6) |
| CaOH+ + HCO3− → CaCO3 + H2O. | (7) |
These reactions correspond to reactions (i) and (ii) in Fig. 5b, respectively. Alternatively, these reactions may take place in one step (Fig. 5b(iii)):
| Ca(OH)2 + CO2 → CaCO3 + H2O. | (8) |
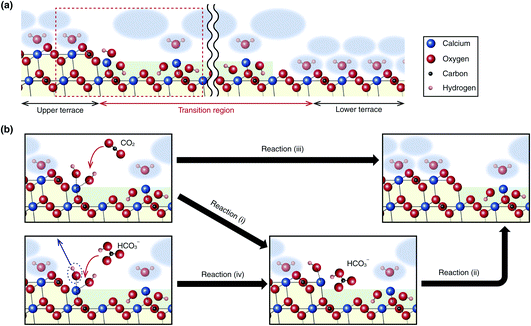 | ||
Fig. 5 (a) Atomic-scale model of a step edge with a TR on the calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface. (b) Possible chemical reaction pathways for the calcite growth process at the step edge. 4) surface. (b) Possible chemical reaction pathways for the calcite growth process at the step edge. | ||
Instead of the adsorption of a CO2, the growth reaction may be driven by the replacement of a surface OH− with an adsorbed HCO3−, as described by
| Ca(OH)2 + HCO3− → CaOH+ + HCO3− + OH−. | (9) |
This reaction corresponds to reaction (iv) in Fig. 5b. Afterward, reaction (ii) should progress to produce a CaCO3.
The concentration of HCO3− (1.3 mM) is much higher than that of CO32− (3.6 μM) in the solution used for this experiment, which suggests that reaction (iv) followed by reaction (ii) may be the major pathway under these experimental conditions. However, a more reliable analysis should require an atomic-level simulation study.
4 Conclusions
In this study, we have investigated the atomic-scale calcite growth mechanism by HS-FM-AFM. We succeeded in the atomic-resolution HS-FM-AFM imaging of structural changes at the growing calcite step edges at 2 s per frame on the calcite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 4) surface. We compared the results with those previously obtained in the dissolution process and clarified the following points.
4) surface. We compared the results with those previously obtained in the dissolution process and clarified the following points.
Monomolecular steps with and without a TR coexist with a ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in both the dissolution and growth processes. While all the dissolving steps show a linear shape, the growing steps additionally show a complex non-linear shape with many kinks. The TRs formed along the linear steps present a fixed and uniform width, while those along the complex steps present a non-uniform and dynamically varying width. The acute and obtuse steps show similar TR formation probability, TR width, and step velocity in the growth process, while a TR is preferentially formed along an acute step in the dissolution. For both step types, TRs during growth are much wider than those during dissolution. Based on these findings, we have presented possible reaction pathways for the elementary steps in calcite growth. One of them is the inverse of the dissolution reactions and is triggered by adsorption of CO2 to react with surface Ca(OH)2. In addition, we presented another possible pathway triggered by a replacement of the surface OH− with an adsorbed HCO3−.
3 in both the dissolution and growth processes. While all the dissolving steps show a linear shape, the growing steps additionally show a complex non-linear shape with many kinks. The TRs formed along the linear steps present a fixed and uniform width, while those along the complex steps present a non-uniform and dynamically varying width. The acute and obtuse steps show similar TR formation probability, TR width, and step velocity in the growth process, while a TR is preferentially formed along an acute step in the dissolution. For both step types, TRs during growth are much wider than those during dissolution. Based on these findings, we have presented possible reaction pathways for the elementary steps in calcite growth. One of them is the inverse of the dissolution reactions and is triggered by adsorption of CO2 to react with surface Ca(OH)2. In addition, we presented another possible pathway triggered by a replacement of the surface OH− with an adsorbed HCO3−.
So far, the atomic-scale calcite growth mechanism has been mostly investigated with an assumption of the direct adsorption of the growth units to the step edge. However, our HS-FM-AFM observations strongly suggest that the primary growth pathway should involve the formation of a TR as an intermediate state. This finding should improve the accuracy of the initial structure assumed in simulation studies, and lead to a better understanding of the atomistic calcite growth mechanism.
Author contributions
K. M. and T. F. conceptualized the study and designed the experiments. K. M., Y. K., N. M. and T. N. performed the high-speed FM-AFM experiments. T. F. prepared the first draft of the manuscript but all the authors contributed to the data analyses, establishment of the growth model, and the preparation of the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the World Premier International Research Center Initiative (WPI), MEXT, Japan, and JSPS KAKENHI grant numbers JP20H00345 and JP20H05212.Notes and references
- R. J. Reeder, in Carbonates, Mineralogy, and Chemistry: Reviews in Mineralogy, ed. R. J. Reederi, Mineralogical Society of America, 1983 Search PubMed.
- D. M. Sigman and E. A. Boyle, Nature, 2000, 407, 859–869 CrossRef CAS PubMed.
- J. Sarmiento and N. Gruber, Ocean Biogeochemical Dynamics, Princeton University Press, 2006 Search PubMed.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970 CrossRef CAS.
- S. A. G. Falini, S. Weiner and L. Addadi, Science, 1996, 271, 67–69 CrossRef.
- M. L. Druckenmiller and M. M. Maroto-Valer, Fuel Process. Technol., 2005, 86, 1599–1614 CrossRef CAS.
- E. H. Oelkers, S. R. Gislason and J. Matter, Elements, 2008, 4, 333–337 CrossRef CAS.
- R. R. Alfano and S. L. Shapiro, Phys. Rev. Lett., 1970, 24, 592–594 CrossRef CAS.
- G. Ghosh, Opt. Commun., 1999, 163, 95–102 CrossRef CAS.
- A. J. Gratz, P. E. Hillner and P. K. Hansma, Geochim. Cosmochim. Acta, 1993, 57, 491–495 CrossRef CAS.
- H. H. Teng, P. M. Dove and J. J. D. Yoreo, Geochim. Cosmochim. Acta, 2000, 64, 2255–2266 CrossRef CAS.
- L. E. Wasylenki, P. M. Dove and J. J. D. Yoreo, Geochim. Cosmochim. Acta, 2005, 69, 4227–4236 CrossRef CAS.
- G. Nehrke, G. J. Reichart, P. Van Cappellen, C. Meile and J. Bijma, Geochim. Cosmochim. Acta, 2007, 71, 2240–2249 CrossRef CAS.
- J. J. De Yoreo, L. A. Zepeda-Ruiz, R. W. Friddle, S. R. Qiu, L. E. Wasylenki, A. A. Chernov, G. H. Gilmer and P. M. Dove, Cryst. Growth Des., 2009, 9, 5135–5144 CrossRef CAS.
- K. Larsen, K. Bechgaard and S. L. S. Stipp, Geochim. Cosmochim. Acta, 2010, 74, 2099–2109 CrossRef CAS.
- A. G. Stack and M. C. Grantham, Cryst. Growth Des., 2010, 10, 1409–1413 CrossRef CAS.
- E. Ruiz-Agudo, C. V. Putnis, C. Rodriguez-Navarro and A. Putnis, Geochim. Cosmochim. Acta, 2011, 75, 284–296 CrossRef CAS.
- M. P. Andersson, S. Dobberschutz, K. K. Sand, D. J. Tobler, J. J. De Yoreo and S. L. Stipp, Angew. Chem., Int. Ed., 2016, 55, 11086–11090 CrossRef CAS PubMed.
- M. De La Pierre, P. Raiteri and J. D. Gale, Cryst. Growth Des., 2016, 16, 5907 CrossRef CAS.
- M. De La Pierre, P. Raiteri, A. G. Stack and J. D. Gale, Angew. Chem., Int. Ed., 2017, 56, 8464–8467 CrossRef CAS PubMed.
- G. Binnig, C. F. Quate and C. Gerber, Phys. Rev. Lett., 1986, 56, 930 CrossRef PubMed.
- P. E. Hillner, A. J. Gratz, S. Manne and P. K. Hansma, Geology, 1992, 20, 359–362 CrossRef CAS.
- Y. Liang, D. R. Baer, J. M. McCoy, J. E. Amonette and J. P. Lafemina, Geochim. Cosmochim. Acta, 1996, 60, 4883–4887 CrossRef CAS.
- R. S. Arvidson, I. E. Ertan, J. E. Amonette and A. Luttge, Geochim. Cosmochim. Acta, 2003, 67, 1623–1634 CrossRef CAS.
- W. K. Burton, N. Cabrera and F. C. Frank, Philos. Trans. R. Soc. London, Ser. A, 1951, 243, 299–358 CrossRef.
- I. Kurganskaya and A. Luttge, J. Phys. Chem. C, 2016, 120, 6482–6492 CrossRef CAS.
- J. M. McCoy and J. P. LaFemina, Surf. Sci., 1997, 373, 288–299 CrossRef CAS.
- I. Kurganskaya and S. V. Churakov, J. Phys. Chem. C, 2018, 122, 29285–29297 CrossRef CAS.
- D. Spagnoli, S. Kerisit and S. C. Parker, J. Cryst. Growth, 2006, 294, 103–110 CrossRef CAS.
- K. Miyata, J. Tracey, K. Miyazawa, V. Haapasilta, P. Spijker, Y. Kawagoe, A. S. Foster, K. Tsukamoto and T. Fukuma, Nano Lett., 2017, 17, 4083–4089 CrossRef CAS PubMed.
- K. Miyata, Y. Kawagoe, J. Tracey, K. Miyazawa, A. S. Foster and T. Fukuma, J. Phys. Chem. C, 2019, 123, 19786–19793 CrossRef CAS.
- K. Miyata, K. Takeuchi, Y. Kawagoe, P. Spijker, J. Tracey, A. S. Foster and T. Fukuma, J. Phys. Chem. Lett., 2021, 12, 8039–8045 CrossRef CAS PubMed.
- T. Fukuma, M. Kimura, K. Kobayashi, K. Matsushige and H. Yamada, Rev. Sci. Instrum., 2005, 76, 053704 CrossRef.
- T. Fukuma and S. P. Jarvis, Rev. Sci. Instrum., 2006, 77, 043701 CrossRef.
- T. Fukuma, Rev. Sci. Instrum., 2009, 80, 023707 CrossRef PubMed.
- T. Fukuma, K. Onishi, N. Kobayashi, A. Matsuki and H. Asakawa, Nanotechnology, 2012, 23, 135706 CrossRef CAS PubMed.
- K. Miyata, S. Usho, S. Yamada, S. Furuya, K. Yoshida, H. Asakawa and T. Fukuma, Rev. Sci. Instrum., 2013, 84, 043705 CrossRef PubMed.
- S. M. R. Akrami, K. Miyata, H. Asakawa and T. Fukuma, Rev. Sci. Instrum., 2014, 85, 126106 CrossRef PubMed.
- Y. Mitani, M. Kubo, K. Muramoto and T. Fukuma, Rev. Sci. Instrum., 2009, 80, 083705 CrossRef PubMed.
- K. Miyata, H. Asakawa and T. Fukuma, Appl. Phys. Lett., 2013, 103, 203104 CrossRef.
- K. Miyata and T. Fukuma, Beilstein J. Nanotechnol., 2018, 9, 1844–1855 CrossRef CAS PubMed.
- S. M. R. Akrami, H. Nakayachi, T. Watanabe-Nakayama, H. Asakawa and T. Fukuma, Nanotechnology, 2014, 25, 455701 CrossRef CAS PubMed.
- M. Xu, X. Hu, K. G. Knauss and S. R. Higgins, Geochim. Cosmochim. Acta, 2010, 74, 4285–4297 CrossRef CAS.
- M. Xu and S. R. Higgins, Geochim. Cosmochim. Acta, 2011, 75, 719–733 CrossRef CAS.
- M. E. Smith, K. G. Knauss and S. R. Higgins, Chem. Geol., 2013, 360–361, 10–21 CrossRef CAS.
- R. Shiraki, P. A. Rock and W. Casey, Aquat. Geochem., 2000, 6, 87–108 CrossRef CAS.
- G. D. Giudici, Am. Mineral., 2002, 87, 1279–1285 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |