Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multiple pathways in NaCl homogeneous crystal nucleation†
Aaron R.
Finney
 * and
Matteo
Salvalaglio
* and
Matteo
Salvalaglio
 *
*
Thomas Young Centre and Department of Chemical Engineering, University College London, London WC1E 7JE, UK. E-mail: a.finney@ucl.ac.uk; m.salvalaglio@ucl.ac.uk
First published on 16th December 2021
Abstract
NaCl crystal nucleation from metastable solutions has long been considered to occur according to a single-step mechanism where the growth in the size and crystalline order of the emerging nuclei is simultaneous. Recent experimental observations suggest that significant ion–ion correlations occur in solution and that NaCl crystals can emerge from disordered intermediates which is seemingly at odds with this established view. Here, we performed biased and unbiased molecular dynamics simulations to analyse and characterise the pathways to crystalline phases from solutions far into the metastable region. We find that large liquid-like NaCl clusters emerge as the solution concentration is increased and a wide distribution of crystallisation pathways are observed with two-step nucleation pathways—where crystalline order emerges in dense liquid NaCl regions—being more dominant than one-step pathways to phase separation far into the metastable region. Analyses of cluster size populations and the ion pair association constant show that these clusters are transient, unlike the thermodynamically stable prenucleation cluster solute species that were suggested in other mineralising systems. A Markov state model was developed to analyse the mechanisms and timescales for nucleation from unbiased molecular dynamics trajectories in a reaction coordinate space characterising the dense regions in clusters and crystalline order. This allowed calculation of the committor probabilities for the system to relax to the solution or crystal states and to estimate the rate of nucleation, which shows excellent agreement with literature values. From a fundamental nucleation perspective, our work highlights the need to extend the attribute ‘critical’ to an ensemble of clusters which can display a broad range of structures and include sizeable disordered domains depending upon the reaction conditions. Moreover, our recent simulation studies demonstrated that carbon surfaces catalyse the formation of liquid-like NaCl networks which, combined with the observations here, suggests that alternative pathways beyond the single-step mechanism can be exploited to control the crystallisation of NaCl.
Introduction
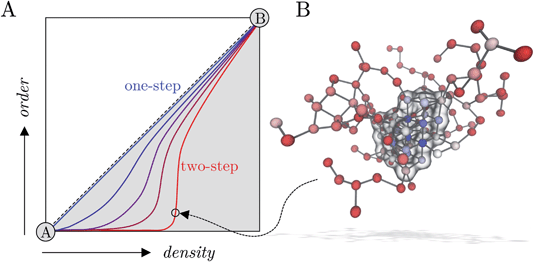
Many pathways to crystals have been observed in a range of systems that seemingly deviate from the single-step crystal nucleation mechanism from a parent solution phase that is predicted by classical nucleation theory (CNT).1,2 It was shown some time ago in simulations of spherical particles with short-ranged interactions that, under appropriate conditions, liquid-like intermediates precede the formation of crystals and the rate for crystal nucleation increases.3 Experiments were later presented that support these observations in systems containing proteins4,5 and small organic molecules.6,7 The nucleation of crystals from supersaturated solutions was therefore described as ‘two-step’8 in light of findings such as these.Evidence was presented for hydrous mineral dense liquid phases which precede the precipitation of amorphous solid and crystalline phases at room temperature,9–14 demonstrating how multi-step crystallisation pathways are a common feature in a range of crystallising systems. In principle, this observation does not negate CNT as an adequate framework to predict the rates for phase separation in mineralising solutions.15,16 Indeed, it should be noted at the outset that a two-step pathway can be described using thermodynamic concepts consistent with CNT17 adopting a core–shell composite cluster model.18,19 Furthermore, observation of amorphous intermediates alone does not confirm their direct role in crystallisation i.e., crystal nuclei could form in a single-step via stochastic density fluctuations of the dissociated ions in the surrounding lean solution in quasi-equilibrium with amorphous states. An alternative to the pathway described by CNT posits that liquid-like microscopic associates are thermodynamically stable species with respect to dissociated ions and are present even in undersaturated solutions; these were described as ‘prenucleation clusters’ on the basis that they purportedly represent the solute species directly involved in nucleation.20–23 The prenucleation cluster pathway was described as a paradigmatic example of ‘nonclassical’ nucleation because here, aggregation of the stable clusters is the limiting step to phase separation.14,20,24
In NaCl(aq), which is arguably the simplest mineralising solution, computer simulations have been and continue to be instrumental for our understanding of crystal nucleation.25–35 Molecular dynamics simulations using the classical force field of Joung and Cheatham36 identified that the nominal equilibrium molality for a saturated NaCl(aq) solution at ambient temperature and pressure was 3.7 m (ref. 37–42) (where m refers to mol kg−1 units) and the limit of solution stability was identified at 15 m.26 This provides a relatively wide range of concentrations where the solution is metastable and crystal nucleation is favoured but does not occur spontaneously.
In metastable NaCl(aq) solutions at T = 298 K, crystal nucleation rates were determined using seeded molecular dynamics simulations and classical nucleation theory (CNT).27,28,34 The rates calculated by Lamas et al. were found to match well with those calculated from forward flux sampling (FFS), with both sets of computed rates deviating from the experimentally determined values.25,34 Zimmermann et al. showed that the rates from seeded MD simulations can be aligned to the experimental data by adopting suitable criteria for the identification of ions belonging to the crystal phase.28 These results thus indicate that CNT provides a consistent model for determining the nucleation kinetics in metastable NaCl(aq) solutions. At the limit of solution stability, however, simulations identified that, before crystal nucleation, NaCl clusters with minimal crystalline order display large fluctuations in size.26 This informed a two-step description for nucleation of NaCl at and beyond the spinodal, which marks the transition for a change in the type of nucleation mechanism.26,34 The recent experimental observation and characterisation of hydrated dense liquid NaCl domains in supersaturated solutions puts this schematic picture into question. In ref. 43, Hwang et al. measured long-lived liquid-like nanometre-sized ion domains in levitated droplets by in situ X-ray and Raman spectroscopy, and further supported their findings with results from molecular dynamics (MD) simulations. The formation of these domains at high supersaturations was described as a possible first step in a two-step nucleation process.
Direct observation of amorphous NaCl intermediates to crystal nucleation was obtained in studies of NaCl(aq) confined to aminated carbon nanotubes performed using transmission electron microscopy after removal of the solvent from the samples.44 Before the nucleation of a nanocrystal, disordered NaCl clusters emerge and dissipate multiple times. The nucleation step involved the formation of a (NaCl)50 nanocrystal from a semi-ordered precursor. While this process appears compatible with a two-step mechanism, the drying of the samples in vacuo, presence of the (vibrating) carbon nanotube wall and confinement means that the mechanism exposed here is not directly applicable to the case of crystal nucleation in metastable bulk solutions. Amorphous NaCl nanoparticles have been stabilised over long times by spray–drying;45 the mechanism of nanoparticle formation here is not clear and, given the method of preparation, kinetically arrested amorphous structures could well result from spinodal decomposition.
Here, we employed swarms of MD simulations, seeded MD simulations and swarms of well-tempered metadynamics46 simulations to study the pathways associated with crystal nucleation in highly supersaturated, metastable NaCl(aq) solutions at room temperature and pressure. We analyse and discuss speciation in solution and the role of liquid-like clusters in order to characterise nucleation mechanisms in the context of those described above and identify the signature for multi-step nucleation in this regime.
Computational methods
MD simulations of solutions
A series of MD simulations were performed to investigate the structure and dynamics of ions in bulk NaCl(aq) solutions. The molality of these solutions was 2, 3, 4, 5.1, 6.1, 7.1, 8.1, 9, 10, 11.1, 12.5, 13.7, 15 and 16 m which provided supersaturation ratios, S = 0.5–4.3, defined as S = b(NaCl)/beq(NaCl) and where beq(NaCl) = 3.7 m.42 At the lowest concentrations (2–5 m) ions and 4000 water molecules were randomly placed into a cubic simulation cell; the number of NaCl ion pairs increased from 145 to 370 over this molality range. In the remaining simulations, the number of ions was fixed at 370 NaCl and the number of water molecules decreased from 4000 to 1280 to achieve the desired molality. Ions and water molecules were assigned random initial positions (ensuring no overlap between atoms) in a cubic simulation cell. A short 0.5 ns simulation was then performed in the (N, p, T) ensemble to relax the simulation cell volume and system potential energy, before a minimum of 10 ns of production runs were performed at each S. In order to account for slower relaxation times at higher concentrations the simulation time was increased to 20 ns beyond 9 m and 50 ns beyond 11.1 m. In this set of simulations, 13.7 m represents a special case as it is at this molality where nucleation pathways were evaluated and, hence, the MD simulation time here was substantially extended, reaching 300 ns.Simulations at S = 3.7
Two approaches were taken to prepare input configurations for simulations at b(NaCl) = 13.7 m (S = 3.7) initiated from either a homogeneous solution phase (solution) or crystalline seeds (seeded) in solution. In the first case, cubic simulation cells were randomly populated with ions and water molecules as described above; ten configurations in total were prepared in this manner. For seeded simulations, crystalline seeds were extracted from a rock salt supercell. Pseudo-spherical crystals with diameter d = 0.6–2.4 nm (in 0.2 nm increments) and containing N = 7 to 341 ions were cut from the bulk crystal where no constraint was placed on the charge of the resulting nanocrystals. The smallest seed was comprised of an octahedral [NaCl6]+ complex and, hence, carried a high charge density. The absolute excess charge density (ρex) in seeds decayed rapidly as the number of ions in the seed (N) increased, and this can be reasonably approximated by ρex = 1.4N−0.6e per atom. The crystalline seeds were subsequently immersed in a solution such that b(NaCl) = 13.7 m according to the total number of ions the simulation box. All systems were relaxed during 0.5 ns (N, p, T) MD simulations in which the ions in crystalline seeds were fixed to their initial positions. This was followed by 300 ns production runs, where all ions were mobile except for one cation at the centre of the crystal which was fixed to the centre of the simulation cell. These initial configurations (both solutions and seeds) were also used to perform well-tempered metadynamics simulations, as described in the following section.Simulation details
In line with other recent simulation studies of NaCl nucleation,25–28 ions in solution were modelled using the Joung and Cheatham force field36 which adopts the SPC/E model47 for water. The geometry of water molecules was constrained using the LINCS algorithm.48 MD simulations were performed using GROMACS 2018.6 (ref. 49) and the leapfrog time integration algorithm with a 1 fs timestep. The temperature and pressure of the system were held constant at 298 K and 1 bar, respectively, within statistical fluctuations using the Bussi–Donadio–Parrinello thermostat50 and the barostat of Berendsen et al.51 Particle Mesh Ewald summation52 was adopted to compute the energies and forces on atoms arising from electrostatic interactions. As three-dimensional periodic boundary conditions were used throughout, the real-space contributions to the Ewald sum were computed for atoms within 0.9 nm, and Lennard-Jones interactions were truncated at 0.9 nm with a dispersion correction added to the energies of short-range intermolecular interactions.Collective variables
We analysed pathways from solutions to crystals on a two-dimensional reaction coordinate space characterised by the collective variables (CVs) n and n(q6) which quantify the total size of high ion density regions and crystalline regions in NaCl clusters, respectively. These calculations were performed using PLUMED (version 2.5).53 Here, we determined the coordination between ions according to a smoothly varying geometric criterion: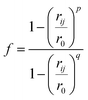 | (1) |
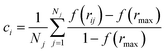 | (2) |
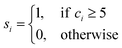 | (3) |
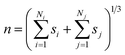 | (4) |
The spatial distribution of s, ξ(s), was calculated in order to identify ions as a function of distance, r, from the centre of the cubic simulation cell:
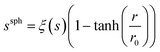 | (5) |
Together with CVs n and nsph, which inform about regions of high local ion density, we also determined the degree of crystallinity in these regions. To this aim, we calculated a local average of the sixth order Steinhardt bond-orientational order parameter54 defined according to:
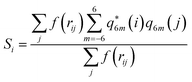 | (6) |
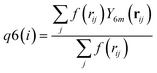 | (7) |
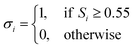 | (8) |
Well-tempered metadynamics
Well-tempered metadynamics46 was adopted in this work to enhance the sampling of local fluctuations of the ion density by biasing nsph on the fly during MD simulations using PLUMED.53 During the simulations, an artificial bias potential, V, was evolved over time by the iterative deposition of Gaussian contributions to V every 1 ps with σn = 0.01, initial height, wn = 2.5 kJ mol−1, and bias factor, γ = 200. The bias in n was stored on a grid with limits −1 to 10 (bin width = 0.002). Metadynamics simulations were performed for around 500 ns initiated from twenty independent configurations obtained from either a solution or crystal seed in solution at S = 3.7, providing a total of ∼10 μs of simulation time.Relative free energies between states can be calculated according to:
F = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(p) ln(p) | (9) |
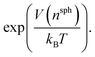 Metadynamics simulations that failed to sample both the solution and crystalline states and transition states between them were neglected, and the remaining 14 data sets were aligned such that the average p(nsph, n, n(q6)) for the solution phase was equal within noise. The relative free energy was then calculated according to the weighted average:
Metadynamics simulations that failed to sample both the solution and crystalline states and transition states between them were neglected, and the remaining 14 data sets were aligned such that the average p(nsph, n, n(q6)) for the solution phase was equal within noise. The relative free energy was then calculated according to the weighted average: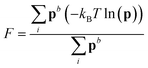 | (10) |
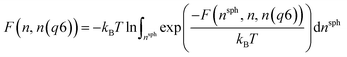 | (11) |
Umbrella Sampling
To investigate ion association, we performed Umbrella Sampling simulations in solutions approaching the limit of infinite dilution. Here, one Na+, one Cl− and 4000 water molecules were inserted into a cubic simulation cell which was relaxed in (N, p, T) simulations for 0.5 ns. A total of 20 (N, p, T) simulations (windows) followed, where the distance between ions was restrained at r0Na–Cl = 0.25–1 nm in 0.025 nm increments by the introduction of a time-independent harmonic bias potential: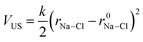 | (12) |
Ion clusters and diffusion
A depth first search algorithm56 was used to determine the cluster size distribution according to a continuous but sharp definition of ion coordination in the first sphere using eqn (2) and (1) where r0 = 0.355 nm, rmax = 0.36 nm, p = 6 and q = 12. In addition, self-diffusion coefficients, D, for ions and water were calculated from the mean squared displacement of ions according to D = limt→∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d〈(r(t) − r(0))2〉/6dt, where r(t) are the atom positions at time t. A correction was applied to account for the finite size of the simulation cell57 and here the shear viscosity of the adopted water model was taken from ref. 58.
d〈(r(t) − r(0))2〉/6dt, where r(t) are the atom positions at time t. A correction was applied to account for the finite size of the simulation cell57 and here the shear viscosity of the adopted water model was taken from ref. 58.
Markov state model construction
All unbiased simulations, totalling more than 20 μs, were used to inform Markov State Models (MSMs) in the reaction coordinate space defined by CVs n and n(q6), as well as by their localised counterparts nsph and nsph(q6). MSM construction and analyses were implemented using PyEMMA 2.5.6.59 The two-dimensional reaction coordinate spaces were partitioned into discrete sets of states via regular space clustering,60,61 leading to sets of approximately 100 states in both (n, n(q6)) and (nsph, nsph(q6)) which are fully connected to one another via intermediate states. MSMs constructed from these sets showed a convergent behavior for the slowest implied timescale for lag-times τ > 50 ps (see Fig. S3 and S4 in ESI†).62 Bayesian MSMs were therefore employed to estimate the average and 95% confidence interval of the slowest implied timescale using τ = 100 ps, and to estimate the equilibrium probability distribution.63 Using discrete transition path theory (TPT),64,65 the MSMs were used to compute the committor probability, as well as the state-to-state probability flux and the mean first passage time associated with the nucleation process. This analysis, further described in the Results and discussion section, provides quantitative information on the pathways connecting the liquid and crystal states.Results and discussion
Solution speciation
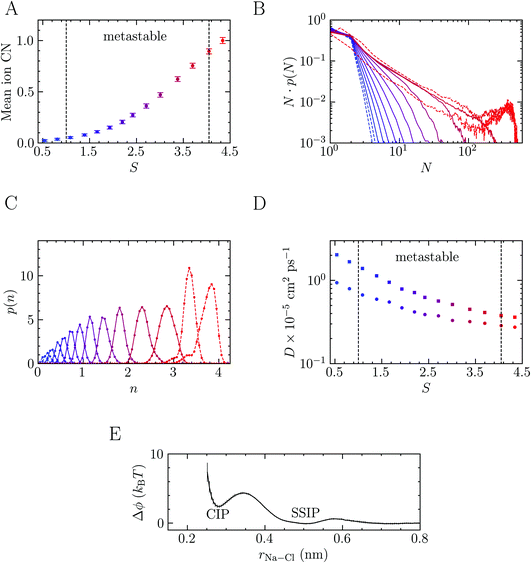
Before discussing NaCl crystallisation pathways from solution, we analyse the ionic species characterising a stable (S ≤ 1) and metastable (S > 1) solution at the steady state, i.e. for timescales significantly shorter than the characteristic nucleation times. The solution achieves a quasi-equilibrium within such timescales; thus, ensemble averages pertaining to pre-critical species in solution can be directly computed via brute-force sampling. To this aim, a series of MD simulations were performed where NaCl molality (b) was 2–13.7 m and S = 0.5–3.7. We also performed simulations at and beyond the limit of solution stability (S = 4.1)26 where b = 15 and 16 m (S = 4.1 and 4.3). Fig. S1 in ESI† indicates how the supersaturation levels targeted in this work compare to other computational studies and recent experiments from the literature. Fig. 1 shows how the non-ideality of the solution increases as the system is progressively brought further into the metastable region (1 < S < 4.1). The average ion coordination number in Fig. 1A increases from a value of around zero (i.e., indicating that ions are completely solvated by water molecules in the first coordination sphere) to 0.75 when S = 3.7. Across the same range of molality, the maximum coordination number increases from 1.1 ± 0.2 to 3.2 ± 0.2. In the stable solution when S = 0.5, the maximum coordination number is 0.7 ± 0.2, while at S = 4.3, this is 3.6 ± 0.2 (albeit with a conservative definition of ion coordination; see Methods). The increased ion–ion coordination, and partial dehydration across the metastable region, leads to clustering and the formation of extended ionic networks. This observation is in very good agreement with results from recent experiments and simulations that showed the presence of extended Na–Cl ionic networks when S is greater than 1.3.43The extent to which clusters can grow is highlighted by the number-weighted cluster size probability distributions in Fig. 1B, representing the probability of finding an ion within a cluster of size N. All distributions below the limit of solution stability show a rapid decay with respect to N; indeed, at the lowest concentration in the metastable region, an exponentially decaying function (N·p(N) ∝ exp(−1.8N)) can be fitted to the data. The complexity of the solution structure increases with concentration and large clusters emerge (the largest of which contain 8–18% of the simulated ions at S = 3.7). We anticipate a system size dependence on the extent to which clusters can grow; both due to the number of ions available to form clusters in finite sized simulations66,67 and the size of the cluster domain with respect to the simulation cell geometry. While Lamas et al.34 observed crystal nucleation in much larger brute force simulations when S = 3.8 (b = 14 m i.e., close to the limiting case of S = 3.7 in the metastable region studied here), we did not observe spontaneous crystal nucleation (by monitoring n(q6)) in brute force simulations in the metastable region. To verify this, we performed nine additional 300 ns MD simulations at S = 3.7, where the initial solution configurations were generated independently, none of which crystallised. Based on the rate for nucleation calculated in this work (3.5 × 1031 s−1 m−3, see below), the timescale for nucleation in this system is around 500 ns.
On crossing the spinodal, the cluster size distributions show markedly different behaviour (see the dashed curves in Fig. 1B where S = 4.1 and 4.3), with additional peaks in N·p(N) highlighting the spontaneous phase separation associated with large fluctuations of the local ion densities that occurs at these supersaturations. The probability for the smallest clusters at the highest concentrations tends to decrease over time, concomitant with an increase in the size of the largest clusters. This indicates that, beyond the limit of solution stability, the timescale for phase separation is comparable with the length of our simulations and it is likely that the curves in Fig. 1B for these cases would continue to evolve beyond the 50 ns used in our analyses. At the end of these trajectories we also observed crystalline regions which develop spontaneously in the clusters, in agreement with simulations reported elsewhere.25,26,31,32,34
Further insight into the coordination environment in clusters can be gained by considering p(n) which is correlated to the number of ions in the clusters with particularly high local ion density. The variable n, defined in the Methods section, represents the cubic root of the number of ions possessing a five-fold or higher ion coordination. In the calculation of n, the function, f, describing coordination goes smoothly from one to zero over a distance 0.38–1 nm. Fig. 1C shows well-defined monomodal distributions for p(n) which shift to larger values of n as the concentration of ions increases. Together with Fig. 1A and B, this shows that in a relatively lean metastable solution the ionic species present before nucleation are predominantly dissociated ions. As the system explores further into the metastable region, the large clusters which form contain regions of high ion density accounting for 0.1–0.3 of the total fraction of ions in the clusters. Phase separation, which occurs spontaneously at the spinodal point, increases the likelihood of these dense regions, which is shown by a shifting to larger n and the appearance of a shoulder in the peaks (see the dashed curves in Fig. 1C) averaged over the entire MD simulation.
Finally, we investigated how ion clustering affects the dynamics of ions and water in solutions crossing the spinodal. Fig. 1D shows a slowing of the diffusion of all solution species as the concentration increases. However, the observed decay is monotonic, as also shown elsewhere,26 and the data does not provide clear evidence for a dynamic arresting of ions in the clusters. Furthermore, as for the mean ionic coordination number, no discernible discontinuity in the diffusion of solution species is detected when crossing the spinodal, at least on the timescale of ∼101 ns. The self-diffusion coefficients, D, for Na+ and water can be accurately determined as 7 × 10−6S−0.66 and 1.5 × 10−5S−0.96 cm2 ps−1, respectively for the range of S sampled here. With only limited reduction to the dynamics of ions, it is not surprising that, in experiments, dehydration and reorganisation of ions in dense regions to the crystal coordination geometry occur over very short timescales; hence, special techniques such as rapid drying must be used to avoid NaCl crystallisation in the production of amorphous NaCl nanoparticles.45
The presence of extended ionic networks with relatively high and low regions of ion density raises questions about their potential role in nucleation. In the context of characterising nucleation pathways, it is also useful to consider whether ion association is thermodynamically favoured, as this could indicate nucleation via the prenucleation cluster (PNC) pathway.20 The mechanism for precipitation along this pathway involves the association of PNCs during a microscopic liquid–liquid phase transition with a slowing of the solution dynamics in the proceeding liquid intermediate which can undergo further transformations to amorphous solids or crystals.14,20,22 A significant debate has surrounded the role of PNCs in nucleation and even their existence.13,15,16,68,69 In the case of calcium carbonate, PNCs are described as dynamically ordered polymeric species.21 The thermodynamic stability of the PNCs, relative to free ions in solution, is ascribed to a strongly exergonic ion association reaction where KMa—the molar equilibrium ion association constant—is independent of cluster size i.e., for (AX)n + (AX) ⇌ (AX)n+1, where A, X and AX represent anions, cations and ion pairs, respectively, the free energy change for the forward reaction is a constant value independent of n. If KMa > 1, then according to a multiple binding model, it was argued that a (meta)stable PNC population should exist in solution, regardless of the value of S.69
To calculate KMa, we performed Umbrella Sampling simulations to evaluate the potential of mean force for ion pairing, ϕ, in a system that approached the limit of infinite dilution following the method described in detail in the work of Chialvo et al.70 Δϕ(r) is provided in Fig. 1E and shows excellent agreement with studies elsewhere.71 This indicates that the contact ion pair (CIP; rNa–Cl = 0.28 nm) is less stable than the solvent shared ion pair (SSIP; rNa–Cl = 0.5 nm). Under these conditions,
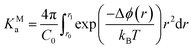 | (13) |
Perhaps a better indicator for ion association in solution is the equilibrium constant for the formation of a CIP from a SSIP, which can be calculated according to:
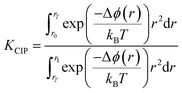 | (14) |
Sampling nucleation events using metadynamics
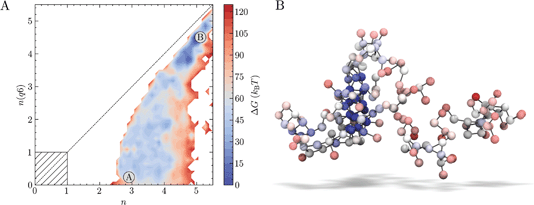
Well-tempered metadynamics (WTmetaD) simulations were initiated both from homogeneous supersaturated solutions and from crystals of various sizes immersed in solution (see Methods) to analyse the pathways for crystallisation when S = 3.7, i.e., a supersaturation far into the metastable region. 10 μs total simulation time was generated from 20 individual simulations. The added bias potential (V(nsph)) in WTmetaD enhances the sampling of the high ion density regions in the clusters within a spherical volume in the simulation cell (see Methods). Localising the enhancement of ion density fluctuations triggered by the bias is necessary at high S to limit the number of crystal nucleation events leading to the formation of structures stabilised by periodic boundary conditions. No constraint was applied to the position of the nuclei emerging from solution, however, and these can translate outside of the spherical volume. We therefore post-process the trajectories (see Methods) to calculate the probability density of states in the space n, n(q6). Calculating the forces on atoms from the derivatives of the bias in n(q6) is computationally very expensive, which makes biasing this CV in simulations intractable for the adopted system size and simulation times. This offers an advantage in that by introducing bias only to increase the fluctuations in local density, we avoid forcing the system to adopt any particular crystalline structure. However, since fluctuations in the CVs defining the energy landscape were not directly enhanced during the sampling, some regions of the reaction coordinate are less well converged than others; indeed, out of the 20 WTmetaD simulations, four failed to visit both the solution and crystalline states (and transition states between them) and were therefore discarded in subsequent analyses.The free energy landscape in Fig. 2A indicates that a wide range of states with minimal crystalline order corresponding to small values of n(q6) are accessible. The minimum accessible n is around 2.5 when n(q6) = 0, in agreement with our unbiased simulations. A value of n = 2.5 indicates that around 15 ions in solution have high ion coordination and form partially dehydrated ion clusters. The configuration in Fig. 2B provides an example of an ion cluster which emerged in MD simulations of NaCl(aq) solutions when S = 3.7; the colours for the ions indicate their relative coordination number for the case where n = 2.8, n(q6) = 0. Our MD simulations indicated that the average number of ions in the largest cluster at S = 3.7 was 100 ± 40. It is clear that non-uniform chemical ordering occurs in the ion clusters: high density regions, shown by the blue spheres in Fig. 2B, are surrounded by extended ionic networks where ion coordination is much lower, and where the geometry and connectivity of the cluster evolves rapidly during the simulations. The energy landscape generated using WTmetaD indicates that n states beyond the maximum found in MD simulations, up to n ≈ 4, are accessible in the long time limit. The molality of ions in the high density regions when S = 3.7, therefore, is around 0.6 m, but this can increase by several m as the system explores n.
As the degree of crystalline order increases, the accessible region in n narrows significantly. Up to n(q6) ≈ 2, the range of accessible n states is largely independent of n(q6), but it is around this point that the accessible states converge towards a limiting case for crystallisation on the diagonal, where the size of the dense and crystalline regions increase simultaneously. The crystal basin is observed beyond n = 5 and n(q6) = 4.5. Although the definition of n(q6) was able to correctly identify crystal ions at rock salt planar surfaces, the rough crystal nanoparticle surfaces found in solution limits the accessibility of states on the diagonal to systems which contain particularly large crystals. From the minimum corresponding to the metastable solution and labelled ‘A’, lowest energy pathways to the crystal, ‘B’, were calculated using nudged elastic band (NEB) calculations.76 While these correctly identified the crystal as the most stable state, the profiles were noisy and no clear transition state for crystallisation was identifiable with confidence. Nevertheless, WTmetaD was instrumental to obtain an extensive sampling of configurations spanning the entire reaction coordinate space which are inaccessible to sub-μs seeded MD or solution simulations.
Nucleation pathways in unbiased simulations
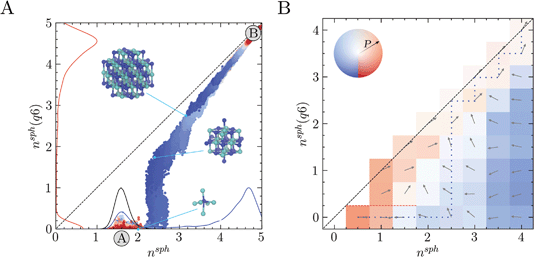
Two approaches were taken to investigate diffusive fluxes in the reaction coordinate space. In the first of these, 10 crystalline seeds of various sizes were simulated in solution for 300 ns and their growth or dissolution was monitored by tracing trajectories in nsph, nsph(q6). Fig. 2A shows that, depending on the size of the initial crystal seed, systems consistently relax to either the solution (A) or crystal states (B). Overlapping multiple seeded trajectories provides a representation of the path between these states in the two-dimensional reaction coordinate space nsph, nsph(q6). While the smallest and largest crystal seeds dissolved and grew, respectively, seeds with diameters in the range 0.8–1 nm relaxed to states which were opposite to this general trend, as shown in ESI Fig. S2.† A seed containing 19 ions where nsph(q6) = 1.3, and which was highly faceted, grew in solution; whereas, a seed containing 27 ions with perfectly planar surfaces, and where nsph(q6) = 1.5 (since in both seeds only one ion has complete rock salt coordination geometry), dissolved. Ion coordination between seeds and other liquid-like clusters occurred readily at the beginning of the simulations and ion exchange with the surrounding ionic networks ultimately consumed these less dense regions of the clusters when the seeds were post-critical. The probability densities shown in Fig. 2A indicate that the pathway to bulk crystals involves increasing the density in ion clusters in a first step to crystal nucleation: a departure from the mean nsph in solutions at the steady state (see the black curve) occurs before crystalline order emerges, when nsph(q6) > 0, in a second step. This is particularly significant as it indicates that crystallisation occurs in regions where relatively high levels of ion–ion coordination, and therefore low levels ion solvation, are observed compared to the homogeneous solution state. The minimum in the probability density in nsph(q6) is 0.5–0.6; here, n = 2 indicating at least eight ions—on average—in the subspace with an ion rich first coordination sphere. The rate limiting step to crystallisation, therefore, is the reordering of ions in the dense liquid domains to a geometry which begins to resemble that of the crystalline phase.
Further support for the two-step pathway to phase separation is gained from our second approach to investigate diffusive flux in the reaction coordinate space. Here, the nsph, nsph(q6) space was discretised into 0.5 × 0.5 bins. Swarms of MD simulations were initiated in each bin where the initial configurations for the simulations were extracted from MD simulations of solutions and from the WTmetaD simulations already described. Initial configurations were selected randomly, ensuring that no two initial starting points were correlated. At least 40 independent 2.5 ns simulations were initiated in each bin which was increased to ∼100 simulations in regions of the configuration space where diffusion is particularly slow. Fig. 3B shows the direction of flux for the average trajectory initialised in each bin. Using this coarse-grained representation of the flux of configurations in the reaction coordinate space, the two-step nucleation pathway spontaneously emerges, and is clearly apparent. This is highlighted by the most probable pathway which propagates the system beyond previously visited states in the solution phase to the crystal based on the transitions between adjacent bins, as shown by the blue dotted line in Fig. 3B. Here, nsph(q6) initially increases when nsph = 2.5 until the system approaches and follows the diagonal beyond nsph = 2.5, nsph(q6) = 2.5, in close agreement with the pathway identified in Fig. 3A. Furthermore, the qualitative features here are in good agreement with the free energy landscape provided in Fig. 2A.
Systems where nsph(q6) = 0 and nsph is particularly small diffuse rapidly to states where the ion density in clusters increases and there was zero probability of transition from bins where nsph < 2 and nsph(q6) = 0 to those where nsph(q6) > 0 during the 2.5 ns timescale. When nsph > 2.5 and nsph(q6) = 0, the system tends to diffuse towards nsph = 1.5–2.5, with the probability of transitions (highlighted by the opacity of the colours in the figure) increasing with nsph. This provides confidence to the qualitative assessment regarding the accessibility of states with increased ion coordination relative to the most probable state for a homogeneous solution. It is notable too that the direction of the mean path when nsph = 1, nsph(q6) = 1 indicates concerted growth in the reaction space variables. A pathway along the diagonal from nsph = 1, nsph(q6) = 1 could be consistent with single-step nucleation occurring via the addition of single monomers to growing crystal nuclei; although technically, these nuclei could still reside within a liquid-like cluster. Therefore, while the most likely pathway under these conditions appears consistent with two-step nucleation, multiple, coexisting pathways may contribute to phase separation.
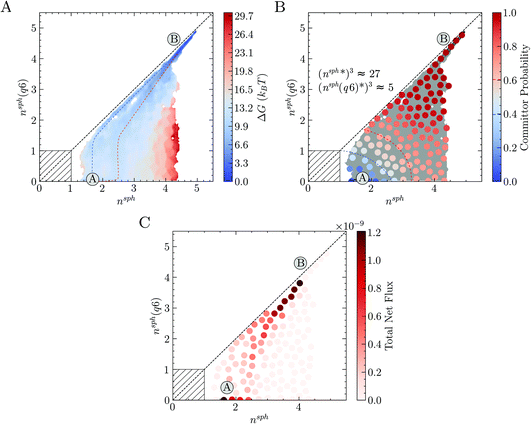
The free energy landscape in Fig. 4A shows two basins for the solution and crystal states (labelled A and B, respectively) and again confirms the wide distribution of accessible nsph states corresponding to clusters with negligible crystalline order. Following the two-step pathway already identified in Fig. 3, the barrier to crystallisation (extracted from nudged elastic band calculations along the most probably pathway) is 7 kBT, in reasonable agreement with the barrier determined elsewhere by interpolating the data from Umbrella Sampling simulations and mean first passage time in forward flux sampling.26 An alternative pathway exists from the solution basin to nsph = nsph(q6) = 1, and which subsequently follows closely to the diagonal towards the crystal basin, is also evident in the energy landscape; this is captured due to the finer partitioning of states here compared to the coarse approach taken in Fig. 3A. The barrier for crystal nucleation along this pathway is 9 kBT, which further supports the notion that multiple pathways for nucleation are available to the system far into the metastable region. The energy landscape in Fig. 4A is compatible with those theorised using a general framework to describe two-step nucleation pathways (using CNT concepts) recently proposed by Kashchiev.17 Both one- and two-step pathways to crystal nucleation are predicted by this framework when the maximum in the free energy landscape—characterised by cluster size and crystalline order—is associated with a large amorphous cluster (see ref. 17 and Fig. 3A). The distinction between the pathways identified in Fig. 4A tends to fade when the free energy in the space n, n(q6) is analysed (see Fig. S4C in ESI†), due to the noise associated with n fluctuations in the entire simulation cell.
A committor analysis was performed to calculate the probability for partitioned states (associated with the MSM) in the reaction coordinate space to relax to either the solution or crystal basins. This analysis (see Fig. 4B and S4D†) revealed that the transition state ensemble, identified here by states with committor probability values of 0.4–0.6, spans a wide range of cluster configurations including both fully ordered and completely disordered ones. Indeed, even for the largest clusters with no apparent crystalline order (i.e., when nsph is beyond 2 and nsph(q6) is zero), the committor is larger than 0.5, indicating their post-critical nature, i.e., they display a greater likelihood to crystallise than to dissolve. This observation is evidence for the coexistence of multiple pathways from the solution to crystal states and introduces the necessity of generalising the concept of a critical nucleus, to that of a critical ensemble of nuclei. Our simulations indicate that, within the critical ensemble, the average cluster contains around 27 ions with five-fold coordination or more, 5 of which have rock salt crystal coordination geometries.
The MSM provides quantitative estimates for the kinetics associated with state-to-state dynamics. By interpreting the slowest implied timescale as the time for relaxation of the system between states A and B (Fig. 4A–C), we obtain a nucleation rate of 3.5 × 1031 m−3 s−1 (95% confidence interval: 2.7 × 1031 to 5.1 × 1031 m−3 s−1). Alternatively, the nucleation rate has been computed from the mean first passage time between two metastable states identified using the robust Perron cluster analysis77 as 6.0 × 1031 m−3 s−1. Both estimates are in excellent agreement with the rates determined elsewhere using alternative methods.26,34
Finally, we project the total current of reactive trajectories in state space, defined for state i as 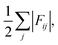 where Fij is the current of reactive trajectories between states i and j. This provides a quantitative analysis of the transition mechanism between states A and B, which further supports the emergent picture for phase separation described so far. In particular, analysis of the high current trace between states, shown in Fig. 4C, indicates the presence of a main reaction channel corresponding to the most probable pathway identified by seeded simulations (Fig. 3A), and by analysing the flux of configurations directly obtained from swarms of short MD simulations (Fig. 3B). Interestingly, a secondary channel, closer to the definition of a one-step mechanism and associated to lower values of the net flux can be identified, quantitatively supporting the co-existence of multiple pathways from solution to crystals in the metastable region.
where Fij is the current of reactive trajectories between states i and j. This provides a quantitative analysis of the transition mechanism between states A and B, which further supports the emergent picture for phase separation described so far. In particular, analysis of the high current trace between states, shown in Fig. 4C, indicates the presence of a main reaction channel corresponding to the most probable pathway identified by seeded simulations (Fig. 3A), and by analysing the flux of configurations directly obtained from swarms of short MD simulations (Fig. 3B). Interestingly, a secondary channel, closer to the definition of a one-step mechanism and associated to lower values of the net flux can be identified, quantitatively supporting the co-existence of multiple pathways from solution to crystals in the metastable region.
Jiang et al.26 sampled similar reaction coordinate spaces using forward flux sampling simulations and brute force simulations. They find that the nucleation pathway below the spinodal (when S = 2.7 and 3.2) occurs in a single-step through correlated fluctuations in the density and crystallinity of emerging clusters. Beyond the spinodal (when S = 4.3), the phase separation mechanism was consistent with two-step nucleation, where a wide distribution in the size of amorphous clusters was observed before the formation of crystalline regions (as we also observed in MD simulations at this molality). It is possible then that, on moving the system far into the metastable region, there is a transition in the most probable pathway from one- to two-step nucleation and this may occur in the window S = 3.2–3.7. Multiple accessible pathways to crystals allow for greater control of the nucleation process, as was shown mechanistically for the case of urea.78,79
Conclusions
In this work, homogeneous NaCl nucleation mechanisms from solutions far into the metastable region were analysed in detail. To this aim, an extensive set of molecular trajectories obtained using different computational methods, including biased and unbiased dynamics, was generated. In our analyses we explicitly considered nucleation as a process evolving along a multidimensional reaction coordinate space where both the size for ion dense regions and crystalline order in emerging nuclei evolve along pathways connecting metastable solutions and crystalline phases. An analysis of the cluster size populations in this work shows that ion clusters are apparent in solutions at all concentrations in the metastable region at the steady state (before nucleation), in line with experiments;43 although no special thermodynamic status can be attributed to these species, as was suggested in other mineralising systems.69 In metastable solutions, the clusters emerge through density fluctuations and are unstable with respect to dissociated ions; however, beyond the spinodal, aggregation leads to extended amorphous clusters during a spontaneous phase separation. Both the average size for the largest clusters and the size of high ion density regions in the clusters (where there is a significant level of dehydration) increase as the system explores further into the metastable solution region.Inspired by the recent approach of Kashchiev17 to provide a thermodynamic and kinetic framework for two-step nucleation, we analysed free energy landscapes characterising the size of the dense cluster regions and the degree of crystalline order in clusters (see the schematic in Fig. 5A). These show that multiple nucleation pathways are available to the system when b(NaCl(aq)) = 13.7 m and S = 3.7, and we identified the lowest energy one- and two-step routes to crystals from the range of possible pathways, beginning from the solution phase (see Fig. 5A). Two-step nucleation is the most probable of these pathways to phase separation under the conditions studied, and a wide range of states are accessible where clusters which contain regions of high ion density (compared to lower ion density clusters on average in solution) are completely amorphous; indeed, committor probabilities computed via the construction of a MSM showed that a critical ensemble of nuclei exist, and that even large amorphous clusters tend to relax to a crystal rather than dissolving. The activation energy for crystallisation along the one-step pathway we identify is greater than in the case of two-step nucleation by 2 kBT, and a single thermodynamic barrier separates the solution and crystal basins. It is important to note that nucleation in a single step, defined in terms of the reaction space variables n and n(q6), could occur by direct association of dissociated ions into a crystal nucleus or by concerted increases to the density and crystalline order of ions already present in liquid-like clusters in solution. From an experimental perspective, distinguishing these types of one-step nucleation mechanisms would be challenging, particularly at large values of S. Fig. 5B shows a pre-critical cluster along the two step pathway which contained around 100 ions. Crystal nucleation occurs in the high density region of the cluster shown by the blue spheres and highlighted by the transparent surface in the image. The kinetics of nucleation computed here, explicitly acknowledging the complexity of the configuration space, showed excellent agreement with those calculated elsewhere.26,34
Given the finding that crystal nucleation in NaCl(aq) solutions occurs via a single-step pathway when b(NaCl(aq)) = 12 m,26 we hypothesise that the transition from predominantly one- to two-step nucleation occurs in the metastable region at S = 3.2–3.7; however, we predict that large amorphous clusters with high density ion regions could still provide pathways to crystals within this range of supersaturation. In other mineralising systems, amorphous mineral phases are observed during two-step nucleation from solutions.9,10,13,14 On the other hand, amorphous NaCl phases are only stabilised using special preparation techniques.45 The difference here may simply be due to undersaturation of the solutions with respect to a dense liquid (if one exists) or amorphous solid NaCl phase; nonetheless, this scenario could still lead to a two-step nucleation pathway,17 where nascent amorphous clusters rapidly transform to crystals. It is possible that kinetic stabilisation of the amorphous phase occurs in other systems, where the energetic barriers associated with translating bulkier anions to their crystalline geometries results in longer-lived amorphous precipitates.
Recently, we showed that surfaces catalyse the formation of large liquid-like NaCl clusters in solutions where the chemical potential is held constant in CμMD simulations.80,81 Both the size and density of ions in the clusters were increased in the presence of graphite surfaces. Within the context of CNT, interfaces reduce the surface energies of emerging nuclei and therefore the thermodynamic barriers to nucleation. Given the pivotal role of dense clusters in the two-step nucleation pathway, it may also be the case that surfaces catalyse a change in the nucleation mechanism from predominantly one-step to two-step in the metastable region, at lower supersaturations than those analysed here. This observation opens up new avenues to experimentally validate the mechanistic picture emerging from simulations, and to exploit surfaces to control nucleation.
Data availability
PLUMED input files used in this work are available via PLUMED-NEST (https://www.plumed-nest.org),82 the public repository for the PLUMED consortium, using the project ID: plumID:21.044.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from an EPSRC Programme Grant (Grant EP/R018820/1) which funds the Crystallization in the Real World consortium. The authors acknowledge the use of the UCL Myriad High Throughput Computing Facility (Myriad@UCL), and associated support services, in the completion of this work.References
- J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Crystallization by particle attachment in synthetic, biogenic, and geologic environments, Science, 2015, 349, aaa6760 CrossRef PubMed.
- J. De Yoreo, in ACS Symposium Series, ed. X. Zhang, American Chemical Society, Washington, DC, 2020, vol. 1358, pp. 1–17 Search PubMed.
- P. R. Ten Wolde and D. Frenkel, Enhancement of Protein Crystal Nucleation by Critical Density Fluctuations, Science, 1997, 277, 1975–1978 CrossRef CAS PubMed.
- O. Galkin and P. G. Vekilov, Control of protein crystal nucleation around the metastable liquid-liquid phase boundary, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 6277–6281 CrossRef CAS PubMed.
- O. Galkin, K. Chen, R. L. Nagel, R. E. Hirsch and P. G. Vekilov, Liquid-liquid separation in solutions of normal and sickle cell hemoglobin, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 8479–8483 CrossRef CAS PubMed.
- B. A. Garetz, J. Matic and A. S. Myerson, Polarization Switching of Crystal Structure in the Nonphotochemical Light-Induced Nucleation of Supersaturated Aqueous Glycine Solutions, Phys. Rev. Lett., 2002, 89, 175501 CrossRef PubMed.
- P. E. Bonnett, K. J. Carpenter, S. Dawson and R. J. Davey, Solution crystallisation via a submerged liquid–liquid phase boundary: oiling out, Chem. Commun., 2003, 698–699 RSC.
- P. G. Vekilov, The two-step mechanism of nucleation of crystals in solution, Nanoscale, 2010, 2, 2346 RSC.
- M. Faatz, F. Gröhn and G. Wegner, Amorphous Calcium Carbonate: Synthesis and Potential Intermediate in Biomineralization, Adv. Mater., 2004, 16, 996–1000 CrossRef CAS.
- S. E. Wolf, J. Leiterer, M. Kappl, F. Emmerling and W. Tremel, Early Homogenous Amorphous Precursor Stages of Calcium Carbonate and Subsequent Crystal Growth in Levitated Droplets, J. Am. Chem. Soc., 2008, 130, 12342–12347 CrossRef CAS PubMed.
- X. Wang, I.-M. Chou, W. Hu and R. C. Burruss, In situ observations of liquid–liquid phase separation in aqueous MgSO4 solutions: Geological and geochemical implications, Geochim. Cosmochim. Acta, 2013, 103, 1–10 CrossRef CAS.
- M. A. Bewernitz, D. Gebauer, J. Long, H. Cölfen and L. B. Gower, A metastable liquid precursor phase of calcium carbonate and its interactions with polyaspartate, Faraday Discuss., 2012, 159, 291–312 RSC.
- P. J. M. Smeets, A. R. Finney, W. J. E. M. Habraken, F. Nudelman, H. Friedrich, J. Laven, J. J. De Yoreo, P. M. Rodger and N. A. J. M. Sommerdijk, A classical view on nonclassical nucleation, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E7882–E7890 CrossRef CAS PubMed.
- J. T. Avaro, S. L. P. Wolf, K. Hauser and D. Gebauer, Stable Prenucleation Calcium Carbonate Clusters Define Liquid–Liquid Phase Separation, Angew. Chem., Int. Ed., 2020, 59, 6155–6159 CrossRef CAS PubMed.
- Q. Hu, M. H. Nielsen, C. L. Freeman, L. M. Hamm, J. Tao, J. R. I. Lee, T. Y. J. Han, U. Becker, J. H. Harding, P. M. Dove and J. J. De Yoreo, The thermodynamics of calcite nucleation at organic interfaces: Classical vs. non-classical pathways, Faraday Discuss., 2012, 159, 509 RSC.
- A. Carino, A. Testino, M. R. Andalibi, F. Pilger, P. Bowen and C. Ludwig, Thermodynamic-Kinetic Precipitation Modeling. A Case Study: The Amorphous Calcium Carbonate (ACC) Precipitation Pathway Unravelled, Cryst. Growth Des., 2017, 17, 2006–2015 CrossRef CAS.
- D. Kashchiev, Classical nucleation theory approach to two-step nucleation of crystals, J. Cryst. Growth, 2020, 530, 125300 CrossRef CAS.
- M. Iwamatsu, Free-energy landscape of nucleation with an intermediate metastable phase studied using capillarity approximation, J. Chem. Phys., 2011, 134, 164508 CrossRef PubMed.
- M. Iwamatsu, Nucleation pathway of core-shell composite nucleus in size and composition space and in component space, Phys. Rev. E, 2012, 86, 041604 CrossRef PubMed.
- D. Gebauer, A. Völkel and H. Cölfen, Stable Prenucleation Calcium Carbonate Clusters, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Stable prenucleation mineral clusters are liquid-like ionic polymers, Nat. Commun., 2011, 2, 590 CrossRef PubMed.
- F. Sebastiani, S. L. P. Wolf, B. Born, T. Q. Luong, H. Cölfen, D. Gebauer and M. Havenith, Water Dynamics from THz Spectroscopy Reveal the Locus of a Liquid-Liquid Binodal Limit in Aqueous CaCO3 Solutions, Angew. Chem., Int. Ed., 2017, 56, 490–495 CrossRef CAS PubMed.
- J. Scheck, B. Wu, M. Drechsler, R. Rosenberg, A. E. S. Van Driessche, T. M. Stawski and D. Gebauer, The Molecular Mechanism of Iron(III) Oxide Nucleation, J. Phys. Chem. Lett., 2016, 7, 3123–3130 CrossRef CAS PubMed.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Pre-nucleation clusters as solute precursors in crystallisation, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC.
- H. Jiang, A. Haji-Akbari, P. G. Debenedetti and A. Z. Panagiotopoulos, Forward flux sampling calculation of homogeneous nucleation rates from aqueous NaCl solutions, J. Chem. Phys., 2018, 148, 044505 CrossRef PubMed.
- H. Jiang, P. G. Debenedetti and A. Z. Panagiotopoulos, Nucleation in aqueous NaCl solutions shifts from 1-step to 2-step mechanism on crossing the spinodal, J. Chem. Phys., 2019, 150, 124502 CrossRef PubMed.
- N. E. R. Zimmermann, B. Vorselaars, D. Quigley and B. Peters, Nucleation of NaCl from Aqueous Solution: Critical Sizes, Ion-Attachment Kinetics, and Rates, J. Am. Chem. Soc., 2015, 137, 13352–13361 CrossRef CAS PubMed.
- N. E. R. Zimmermann, B. Vorselaars, J. R. Espinosa, D. Quigley, W. R. Smith, E. Sanz, C. Vega and B. Peters, NaCl nucleation from brine in seeded simulations: Sources of uncertainty in rate estimates, J. Chem. Phys., 2018, 148, 222838 CrossRef PubMed.
- J. Alejandre and J.-P. Hansen, Ions in water: From ion clustering to crystal nucleation, Phys. Rev. E, 2007, 76, 061505 CrossRef PubMed.
- F. Giberti, G. A. Tribello and M. Parrinello, Transient Polymorphism in NaCl, J. Chem. Theory Comput., 2013, 9, 2526–2530 CrossRef CAS PubMed.
- G. Lanaro and G. N. Patey, Birth of NaCl Crystals: Insights from Molecular Simulations, J. Phys. Chem. B, 2016, 120, 9076–9087 CrossRef CAS PubMed.
- D. Chakraborty and G. N. Patey, How Crystals Nucleate and Grow in Aqueous NaCl Solution, J. Phys. Chem. Lett., 2013, 4, 573–578 CrossRef CAS PubMed.
- D. Zahn, Atomistic Mechanism of NaCl Nucleation from an Aqueous Solution, Phys. Rev. Lett., 2004, 92, 040801 CrossRef PubMed.
- C. P. Lamas, J. R. Espinosa, M. M. Conde, J. Ramírez, P. Montero de Hijes, E. G. Noya, C. Vega and E. Sanz, Homogeneous nucleation of NaCl in supersaturated solutions, Phys. Chem. Chem. Phys., 2021, 23, 26843–26852 RSC.
- T. Karmakar, P. M. Piaggi and M. Parrinello, Molecular Dynamics Simulations of Crystal Nucleation from Solution at Constant Chemical Potential, J. Chem. Theory Comput., 2019, 15, 6923–6930 CrossRef CAS PubMed.
- I. S. Joung and T. E. Cheatham, Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- F. Moučka, I. Nezbeda and W. R. Smith, Molecular simulation of aqueous electrolytes: Water chemical potential results and Gibbs-Duhem equation consistency tests, J. Chem. Phys., 2013, 139, 124505 CrossRef PubMed.
- F. Moučka, I. Nezbeda and W. R. Smith, Chemical Potentials, Activity Coefficients, and Solubility in Aqueous NaCl Solutions: Prediction by Polarizable Force Fields, J. Chem. Theory Comput., 2015, 11, 1756–1764 CrossRef PubMed.
- Z. Mester and A. Z. Panagiotopoulos, Mean ionic activity coefficients in aqueous NaCl solutions from molecular dynamics simulations, J. Chem. Phys., 2015, 142, 044507 CrossRef PubMed.
- Z. Mester and A. Z. Panagiotopoulos, Temperature-dependent solubilities and mean ionic activity coefficients of alkali halides in water from molecular dynamics simulations, J. Chem. Phys., 2015, 143, 044505 CrossRef PubMed.
- A. L. Benavides, J. L. Aragones and C. Vega, Consensus on the solubility of NaCl in water from computer simulations using the chemical potential route, J. Chem. Phys., 2016, 144, 124504 CrossRef CAS PubMed.
- J. R. Espinosa, J. M. Young, H. Jiang, D. Gupta, C. Vega, E. Sanz, P. G. Debenedetti and A. Z. Panagiotopoulos, On the calculation of solubilities via direct coexistence simulations: Investigation of NaCl aqueous solutions and Lennard-Jones binary mixtures, J. Chem. Phys., 2016, 145, 154111 CrossRef CAS PubMed.
- H. Hwang, Y. C. Cho, S. Lee, Y.-H. Lee, S. Kim, Y. Kim, W. Jo, P. Duchstein, D. Zahn and G. W. Lee, Hydration breaking and chemical ordering in a levitated NaCl solution droplet beyond the metastable zone width limit: evidence for the early stage of two-step nucleation, Chem. Sci., 2021, 12, 179–187 RSC.
- T. Nakamuro, M. Sakakibara, H. Nada, K. Harano and E. Nakamura, Capturing the Moment of Emergence of Crystal Nucleus from Disorder, J. Am. Chem. Soc., 2021, 143, 1763–1767 CrossRef CAS PubMed.
- E. Amstad, M. Gopinadhan, C. Holtze, C. O. Osuji, M. P. Brenner, F. Spaepen and D. A. Weitz, Production of amorphous nanoparticles by supersonic spray-drying with a microfluidic nebulator, Science, 2015, 349, 956–960 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: New feathers for an old bird, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Bond-orientational order in liquids and glasses, Phys. Rev. B, 1983, 28, 784–805 CrossRef CAS.
- A. Grossfield, WHAM: the weighted histogram analysis method, http://membrane.urmc.rochester.edu/wordpress/?page_id=126 Search PubMed.
- G. A. Tribello, F. Giberti, G. C. Sosso, M. Salvalaglio and M. Parrinello, Analyzing and Driving Cluster Formation in Atomistic Simulations, J. Chem. Theory Comput., 2017, 13, 1317–1327 CrossRef CAS PubMed.
- I.-C. Yeh and G. Hummer, System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- M. A. González and J. L. F. Abascal, The shear viscosity of rigid water models, J. Chem. Phys., 2010, 132, 096101 CrossRef PubMed.
- M. K. Scherer, B. Trendelkamp-Schroer, F. Paul, G. Pérez-Hernández, M. Hoffmann, N. Plattner, C. Wehmeyer, J.-H. Prinz and F. Noé, PyEMMA 2: A software package for estimation, validation, and analysis of Markov models, J. Chem. Theory Comput., 2015, 11, 5525–5542 CrossRef CAS PubMed.
- J.-H. Prinz, H. Wu, M. Sarich, B. Keller, M. Senne, M. Held, J. D. Chodera, C. Schütte and F. Noé, Markov models of molecular kinetics: Generation and validation, J. Chem. Phys., 2011, 134, 174105 CrossRef PubMed.
- J. A. Hartigan, Clustering Algorithms, John Wiley & Sons Inc., New York, NY, 1975 Search PubMed.
- G. R. Bowman, V. S. Pande and F. Noé, An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation, Springer Science & Business Media, 2013, vol. 797 Search PubMed.
- B. Trendelkamp-Schroer, H. Wu, F. Paul and F. Noé, Estimation and uncertainty of reversible Markov models, J. Chem. Phys., 2015, 143, 174101 CrossRef PubMed.
- P. Metzner, C. Schütte and E. Vanden-Eijnden, Transition path theory for Markov jump processes, Multiscale Model. Simul., 2009, 7, 1192–1219 CrossRef CAS.
- F. Noé, C. Schütte, E. Vanden-Eijnden, L. Reich and T. R. Weikl, Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 19011–19016 CrossRef PubMed.
- J. Wedekind, D. Reguera and R. Strey, Finite-size effects in simulations of nucleation, J. Chem. Phys., 2006, 125, 214505 CrossRef PubMed.
- M. Salvalaglio, P. Tiwary, G. M. Maggioni, M. Mazzotti and M. Parrinello, Overcoming time scale and finite size limitations to compute nucleation rates from small scale well tempered metadynamics simulations, J. Chem. Phys., 2016, 145, 211925 CrossRef PubMed.
- K. Henzler, E. O. Fetisov, M. Galib, M. D. Baer, B. A. Legg, C. Borca, J. M. Xto, S. Pin, J. L. Fulton, G. K. Schenter, N. Govind, J. I. Siepmann, C. J. Mundy, T. Huthwelker and J. J. D. Yoreo, Supersaturated calcium carbonate solutions are classical, Sci. Adv., 2018, 4, eaao6283 CrossRef PubMed.
- D. Gebauer, P. Raiteri, J. D. Gale and H. Cölfen, On classical and non-classical views on nucleation, Am. J. Sci., 2018, 318, 969–988 CrossRef CAS.
- A. A. Chialvo, P. T. Cummings, H. D. Cochran, J. M. Simonson and R. E. Mesmer, Na+–Cl− ion pair association in supercritical water, J. Chem. Phys., 1995, 103, 9379–9387 CrossRef CAS.
- C. Zhang, F. Giberti, E. Sevgen, J. J. de Pablo, F. Gygi and G. Galli, Dissociation of salts in water under pressure, Nat. Commun., 2020, 11, 3037 CrossRef CAS PubMed.
- P. C. Ho, D. A. Palmer and R. E. Mesmer, Electrical conductivity measurements of aqueous sodium chloride solutions to 600°C and 300 MPa, J. Solution Chem., 1994, 23, 997–1018 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters, J. Phys. Chem. B, 2009, 113, 13279–13290 CrossRef CAS PubMed.
- A. F. Wallace, L. O. Hedges, A. Fernandez-Martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Microscopic Evidence for Liquid-Liquid Separation in Supersaturated CaCO3 Solutions, Science, 2013, 341, 885–889 CrossRef CAS PubMed.
- U. Rana, C. P. Brangwynne and A. Z. Panagiotopoulos, Phase separation vs. aggregation behavior for model disordered proteins, J. Chem. Phys., 2021, 155, 125101 CrossRef CAS PubMed.
- G. Henkelman and H. Jonsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- S. Röblitz and M. Weber, Fuzzy spectral clustering by PCCA+: application to Markov state models and data classification, Adv. Data Anal. Classif., 2013, 7, 147–179 CrossRef.
- M. Salvalaglio, M. Mazzotti and M. Parrinello, Urea homogeneous nucleation mechanism is solvent dependent, Faraday Discuss., 2015, 179, 291–307 RSC.
- M. Salvalaglio, C. Perego, F. Giberti, M. Mazzotti and M. Parrinello, Molecular-dynamics simulations of urea nucleation from aqueous solution, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E6–E14 CrossRef CAS PubMed.
- A. R. Finney, I. J. McPherson, P. R. Unwin and M. Salvalaglio, Electrochemistry, ion adsorption and dynamics in the double layer: a study of NaCl(aq) on graphite, Chem. Sci., 2021, 12, 11166–11180 RSC.
- A. R. Finney and M. Salvalaglio, Bridging the gap between mesoscopic and molecular models of solid/liquid interfaces out-of-equilibrium, arXiv, 2021, preprint, arXiv:2109.00568 Search PubMed.
- The PLUMED consortium, Promoting transparency and reproducibility in enhanced molecular simulations, Nat. Methods, 2019, 16, 670–673 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures. See DOI: 10.1039/d1fd00089f |
| This journal is © The Royal Society of Chemistry 2022 |