Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Off-stoichiometry in I–III–VI2 chalcopyrite absorbers: a comparative analysis of structures and stabilities†
Kostiantyn V.
Sopiha
 *,
Jes K.
Larsen
*,
Jes K.
Larsen
 ,
Jan
Keller
,
Jan
Keller
 ,
Marika
Edoff
,
Marika
Edoff
 ,
Charlotte
Platzer-Björkman
,
Charlotte
Platzer-Björkman
 and
Jonathan J. S.
Scragg
and
Jonathan J. S.
Scragg

Division of Solar Cell Technology, Department of Materials Science and Engineering, Uppsala University, Sweden. E-mail: kostiantyn.sopiha@gmail.com
First published on 30th May 2022
Abstract
Chalcopyrite Cu(In,Ga)Se2 (CIGSe) solar absorbers are renowned for delivering high solar power conversion efficiency despite containing high concentration of lattice defects amounting to copper deficiencies of several atomic percent. The unique ability to incorporate this deficiency without triggering decomposition (i.e. “tolerance to off-stoichiometry”) is viewed by many as the key feature of CIGSe. In principle, this property could benefit any solar absorber, but remarkably little attention has been paid to it so far. In this study, we assess the tolerance to off-stoichiometry of thin-film photovoltaic materials by carrying out ab initio analysis of group-I-poor ordered defect compounds (ODCs) in the extended family of I–III–VI systems (where I = Cu, Ag, III = Al, Ga, In, and VI = S, Se, Te). We analyze convex hulls and structural evolution with respect to group-I content, link them with experimental phase diagrams, and determine two empirical principles for the future identification of solar energy materials with high tolerance to off-stoichiometry. Practical implications for the deposition of I–III–VI absorbers are also discussed in light of our computational results and recent experimental findings.
Introduction
Recent years have seen a surge in effort devoted to the identification of new thin-film solar absorbers.1–4 This exploration relies on knowledge gained from studying the few well-established high-performance absorber materials, most notably CdTe and CIGSe, but even these have not yet revealed all their secrets. One unresolved question is why Cu-deficient CIGSe absorbers, which typically have a [Cu]/([In] + [Ga]) ratio as low as 0.8, demonstrate such a good or even superior solar cell performance.5 The explanation might be rooted in the unusual ability of CIGSe to accommodate large off-stoichiometry, which, jointly with its high defect tolerance,6 make CIGSe forgiving of unintentional compositional perturbations and imperfections. Previously, off-stoichiometry had been tacitly assumed to result from high concentrations of isolated point defects or compensated (2VCu + InCu) defect complexes, with phase separation into ordered defect compounds (ODCs) occurring in extreme cases. However, in our recent study,7 we found that Cu deficiency in CIGSe is enabled by a hitherto unknown series of stable ODCs with zinc-blende-derived lattice and cation vacancies arranged in various 2D and 3D conformations. These compounds span a wide range of compositions and can therefore form to facilitate a range of off-stoichiometries, all the while being nearly invisible to X-ray diffraction (XRD). Consequently, a revised model of off-stoichiometry in CIGSe was proposed and verified against the existing experimental evidence, resolving crucial contradictions and proving obsolete the classical model of isolated point defects and complexes. In light of these findings, it is important to understand how common the discovered behavior is and how significant its role is in making a good solar absorber.As the first step towards answering these questions, we extend our previous analysis to a broader family of I–III–VI systems. All of them form chalcopyrite I–III–VI2 compounds, many of which are already employed or have been intensively investigated for multijunction photovoltaics,8–14 thermoelectrics,15 light emitting diodes,16 water splitting devices,17–20etc. Some other I–III–VI2 compounds have shown great promise for improving performance in traditional single-junction photovoltaics, both theoretically2 and experimentally.21,22 Despite their superficial similarity, the observed response to the off-stoichiometry of I–III–VI2 chalcopyrites was at times highly divergent from the expectations elicited from CIGSe processing. For instance, AgGaSe2 and CuInS2 are known to have relatively narrow homogeneity (i.e. single-phase chalcopyrite) regions in the phase diagrams,8,23,24 which complicates the absorber deposition, post-deposition processing, and storage.8,9,25–31 Therefore, the extended family of I–III–VI systems, while being technologically important for thin-film photovoltaics, is also well-suited for a comparative study, with opportunities for experimental verification. Our results indicate that only a third of all considered I–III–VI systems exhibit tolerance to off-stoichiometry at a level comparable to that in CIGSe. All of them contain Cu as the group-I cation. We found that their common feature is the existence of stable ODC structures with lattice constants similar to those in the respective chalcopyrite compound. In an attempt to generalize these findings, we propose that high tolerance to off-stoichiometry is more likely if (i) the compound of interest has a lattice closely related by symmetry with a neighboring phase and (ii) the difference in their lattice parameters is sufficiently small. We believe that these simple principles can serve as a convenient jumping -off point for future high-throughput materials exploration and the growth of high-quality absorbers.
Methods
All calculations were performed using the Vienna Ab initio Simulation Package (VASP)32–34 employing the projector augmented wave (PAW)35,36 formalism within density functional theory (DFT). As a default, total energies were computed using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional37 and cut-off energy of 350 eV. Pseudopotentials with the following valence electron configurations were selected: Cu 3d104s1, Ag 4d105s1, Al 3s23p1, Ga 4s24p1, In 5s25p1, S 3s23p4, Se 4s24p4, Te 5s25p4. Reciprocal space integration was done over the Brillouin zones approximated by Γ-centred Monkhorst–Pack grids38 with a density of about 2500 k-points per reciprocal atom. The cell geometries and ionic positions were optimized simultaneously until all forces decreased below a threshold of 10 meV Å−1. Since no magnetic moment was expected in the I–III–VI compounds, all calculations were performed in the non-spin-polarized regime. Data processing was facilitated by the use of the pymatgen (Python Materials Genomics) library39 and the structures were visualized by the Visualization for Electronic and STructural Analysis (VESTA) software.40The vast majority of I–III–VI structures analysed here were obtained via the isovalent substitution of atoms in the Cu–In–Se structures generated and analysed in our previous study.7 Therein, a large set of Cu–In–Se structures with different compositions were created by filling all cationic sites in various supercells of the zinc-blende unit cell with either Cu, In, or a vacancy, while keeping the anionic sublattice fully occupied by Se atoms. Only those structures that fell on the pseudo-binary In2Se3–CuInSe2 tie-line were considered, and only in the case when they exhibited a small deviation from the octet rule – a well-known prerequisite of low energy structures.41–43 The search for stable ODCs was further facilitated by the use of the cluster expansion formalism for a quick on-the-fly energy pre-assessment. More details can be found in our previous work.7 In total, 3174 structures containing up to 64 atomic sites (counting vacancies) were investigated using DFT in every I–III–VI system without Al or Te. The estimated number of inequivalent structures analysed using cluster expansion is of the order of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 in every I–III–VI. A smaller subset of 755 structures containing up to 40 atomic sites was studied using DFT for systems with Al or Te – such a subset was found to be representative of other I–III–VI systems. Moreover, a series of literature structures were taken from earlier publications,44–48 the Materials Project repository,49 and the Inorganic Crystal Structure Database (ICSD)50 – all modified by isovalent replacement to generate isomorphs for all I–III–VI systems.
000 in every I–III–VI. A smaller subset of 755 structures containing up to 40 atomic sites was studied using DFT for systems with Al or Te – such a subset was found to be representative of other I–III–VI systems. Moreover, a series of literature structures were taken from earlier publications,44–48 the Materials Project repository,49 and the Inorganic Crystal Structure Database (ICSD)50 – all modified by isovalent replacement to generate isomorphs for all I–III–VI systems.
For convenience, the I–III–VI compounds are referred to by the numbers in their empirical formulae, i.e. 1:1:2 for I–III–VI2, 1:5:8 for I–III5–VI8, 2:4:7 for I2–III4–VI7, and so on. The term “ODC” is broadly applied to all structures with a zinc-blende-derived lattice and composition distinct from 1:1:2. These are important to differentiate from stable non-ODC compounds with the same compositions (e.g. CuIn5S8) that do exist and are discussed in comparison with their unstable ODC polymorphs below.
Results
Convex hull analysis
Convex hulls for several representative systems are shown in Fig. 1 and for the extended I–III–VI family in Fig. S1.† The enthalpies are depicted by green markers if they correspond to ODCs identified as ground states for Cu–In–Se, by red markers if the structures were extracted from the literature, and by blue markers if the structures were generated and found to be unstable in the Cu–In–Se system in our previous work.7 Clearly, the convex hulls differ greatly even within such a narrow materials family and, based on the observed behavior, three categories can be distinguished. The first (type-I) category is recognized when a system has a series (or rather a continuum) of ODCs on the convex hull. This behavior is exemplified by Cu–Ga–Se in Fig. 1a, but it is also observed for most Cu-based I–III–VI systems. Type-II is ascribed to a system when at least one non-ODC compound falls on the convex hull and, thus, greatly destabilizes the ODCs. A good example of a type-II system is Cu–In–S, which forms a stable thio-spinel CuIn5S8 structure that makes all ODCs highly unstable (see Fig. 1b). Type-II behavior is seen for four systems, all of which are sulfides with III = Al or In. Finally, the third (type-III) category is characterized by “intermediate” ODCs (like 2:4:7, 3:5:9, etc.) being unstable with respect to a mixture of chalcopyrite 1:1:2 and conventional ODC (i.e. either 1:3:5 or 1:5:8). This behavior is common for Ag-based I–III–VI systems, although details of the convex hull are found to differ on a case-to-case basis. For instance, the instability of intermediate ODCs is more severe for Ag–Ga–Se (see Fig. 1c) as compared to Ag–In–Te (see Fig. 1d), with the 1:5:8 ODC being expected to form alongside AgGaSe2 (as opposed to the 1:3:5 ODC alongside AgInTe2) in the group-I-poor materials. More examples and peculiarities of convex hulls for other systems can be found in Fig. S1.†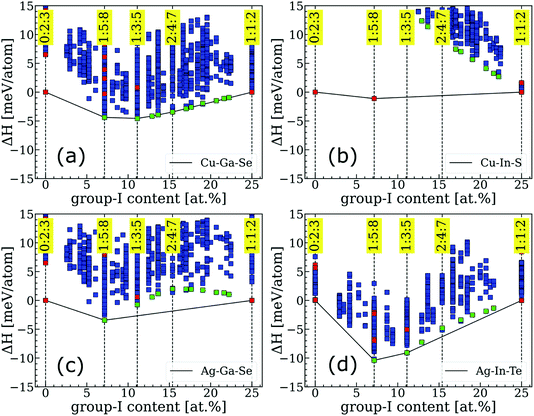 | ||
| Fig. 1 Examples of convex hulls from different categories: (a) type-I for Cu–Ga–Se, (b) type-II for Cu–In–S, and type-III for (c) Ag–Ga–Se and (d) Ag–In–Te. The ordinate axis (ΔH) is the formation enthalpy relative to the mixture of terminal phases (i.e. 1:1:2 and 0:2:3). Convex hulls for other I–III–VI systems are presented in Fig. S1.† | ||
The proposed classification is useful because it groups I–III–VI systems based on their tolerance to off-stoichiometry. Specifically, the continuum of stable ODCs in type-I systems means that they can accommodate an overall group-I deficiency without causing thermodynamic instability. Chalcopyrite phases in such systems are anticipated to have wide single-phase regions, i.e. high tolerance to off-stoichiometry. On the contrary, the severe instability of ODCs in type-II systems means that the global energy minimum is achieved when the group-I deficiency segregates into a non-ODC phase co-existing with stoichiometric 1:1:2 chalcopyrite. A very narrow single-phase chalcopyrite region is thus anticipated for type-II systems. Finally, type-III systems are expected to exhibit some limited tolerance to off-stoichiometry because the enthalpy of the ODCs with near-1:1:2 composition, despite being positive with respect to the convex hull, can still be overcome by the entropy contribution at elevated temperatures. While the exact single-phase region extension is difficult to predict from these ground-state calculations, it is still possible to conclude that the existence of non-ODC phases (as in type-II systems), whether they are predicted to fall on the convex hull in calculations or observed alongside group-I-poor chalcopyrite 1:1:2 phase in experiment, is an indication of poor tolerance to off-stoichiometry. This principle can thus be employed in high-throughput searches for solar absorbers in the future.
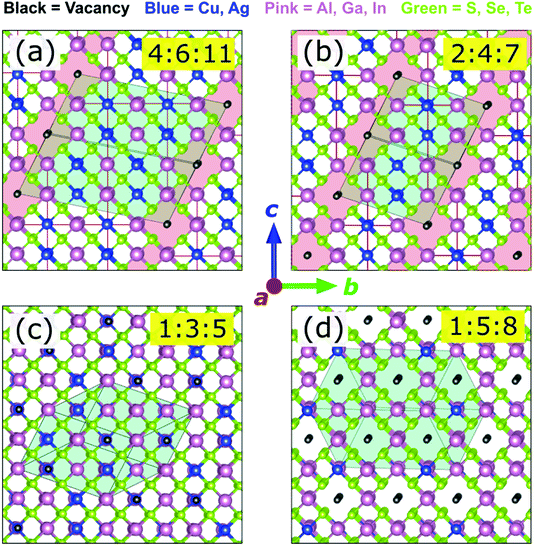
Representative ODC structures
For the convenience and simplicity of further analysis, a smaller but representative set of ODCs can be compiled. In our previous work, all stable structures with 0.5 ≤ [I]/[III] < 1.0 in CIGSe were found to consist of chalcopyrite-like domains separated by Cu-free regions.7 This structural motif is confirmed for the extended family of I–III–VI herein. The [I]/[III] ratio of ODCs in this composition range is thus determined by the volume fraction of (or spatial separation between) the group-I-free domains, as exemplified for 2:4:7 and 4:6:11 in Fig. 2a and b. Due to the structural similarity, these two ODCs were considered sufficient to represent the entire series of ODCs in the composition range 0.5 ≤ [I]/[III] < 1.0.Next, as evidenced from the convex hulls in Fig. S1,† a number of low-energy 1:5:8 structures have enthalpies slightly (within 1 meV per atom) above the ground state in most I–III–VI systems. For CIGSe, a common motif containing (001) vacancy planes has been identified before.7 This motif is found to be common for the extended family of I–III–VI systems. In fact, out of the 18 systems considered, 14 have the same lowest-enthalpy 1:5:8 ODC structure (see Fig. 2d). For the remaining four, it falls within 0.5 meV per atom above the convex hull. This structure was thus included as the 1:5:8 ODC reference in the smaller ODC set.
Furthermore, the same 1:3:5 ODC structure (shown in Fig. 2c) was found on the convex hulls in many I–III–VI systems. The representative ODC set was thus complemented with this 1:3:5 ODC. Chalcopyrite 1:1:2 and defected zinc-blende 0:2:3 ODC (obtained by isovalent replacement in β-Ga2Se3)51 were added for completeness. The compiled set of six compounds (i.e. 1:1:2, 4:6:11, 2:4:7, 1:3:5, 1:5:8, and 0:2:3) was thus adopted for further analysis, which was performed with higher accuracy (k-point grids with a density of 4000 points per reciprocal atom, 550 eV energy cut-off, and 5 meV Å−1 force threshold). Note that some ODCs from the smaller set are unstable in some I–III–VI systems, but their enthalpies are always the lowest (or close to the lowest) among all zinc-blende-derived structures considered.
Evolution of lattice geometries with off-stoichiometry
The key to understanding the difference between type-I and type-III convex hulls lies in how the lattice geometry changes with respect to the off-stoichiometry, which is quantified here by two parameters: (i) per-anion volume of the ODC normalized by the corresponding value for the 1:1:2 phase, V/V0, and (ii) tetragonal distortion defined as a ratio of the lattice constants, η = c/(a + b), in analogy to the classical definition of η = c/2a for ideal chalcopyrites.52,53 The need to distinguish between a and b vectors stems from the fact that lattices of ODCs with 0.5 ≤ [I]/[III] < 1.0 are not tetragonal. The directions of the a, b, and c vectors are selected based on the orientation of the chalcopyrite-like domains in ODCs. To deduce the parameters of interest, large rectangular supercells were created to match the directions of the chalcopyrite basis and then the supercell parameters were divided by the number of repeating zinc-blende units. The computed values for different I–III–VI systems are summarized in Fig. 3.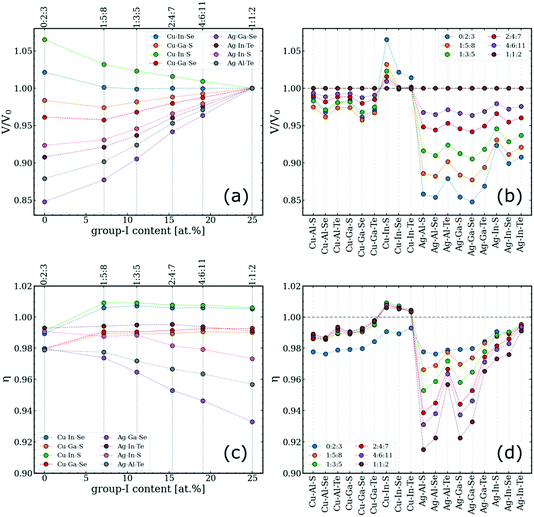 | ||
| Fig. 3 Analysis of the computed lattice geometries of ODCs in different I–III–VI systems. (a and b) Per-anion lattice volumes of ODCs normalized by the per-anion volume of the corresponding chalcopyrite compound. (c and d) Tetragonal distortions of the same structures. The quantities are given versus (a and c) group-I content (for eight arbitrary systems) and (b and d) type of system for the entire I–III–VI family considered. The corresponding trends for the individual lattice parameters are given in Fig. S2.† | ||
It is observed that most I–III–VI systems exhibit gradual lattice contraction with decreasing group-I content. This trend could be expected considering that the evolution is mediated by the incorporation of vacancies. A curious exception here is Cu–In–S, in which ODCs have slightly larger volumes than that of the chalcopyrite 1:1:2 phase. The key finding from Fig. 3a and b is that the changes for ODCs in Ag-based I–III–VI are much greater than for their Cu-based counterparts. Specifically, the cumulative volume change for Cu–III–VI (comparing 1:1:2 vs. 0:2:3) is below 5% for all the systems except Cu–In–S, whereas the lattice compression for Ag–III–VI is at the level of 10%. The overall maximum is 15% in the Ag–Ga–Se system.
The lattice relaxation is generally not uniform, however, as evidenced from the changes in the computed tetragonal distortion in Fig. 3c and d. For the Cu-based I–III–VI systems, in which the 1:1:2 phase has a nearly ideal tetragonal cell geometry (η in the range of 0.98–1.01), the off-stoichiometry alters the cell proportions only slightly, maintaining η at roughly the same level. The datapoints for 0:2:3 compounds notably fall off the trend, presumably due to the unique coordination (this is the only stable structure with anions coordinated by two group-III elements and two cation vacancies).7 In contrast, a systematic increase in η with lowering [I]/[III] is evident for Ag-based I–III–VI. A conclusion can therefore be drawn that group-I off-stoichiometry effectively reduces tetragonal distortion by relaxing the lattice more along the a and b vectors than along vector c (see Fig. S2† for the trends in each lattice vector separately).
The explanation for these relaxation trends is rooted in ionic sizes. The effective ionic radius of Cu (RCu = 0.60 Å; all values are for four-coordinated ions according to Shannon)54 is not far from those of group-III cations (RAl = 0.39 Å, RGa = 0.47 Å, RIn = 0.62 Å), whereas Ag ions are much larger (RAg = 1.00 Å). The greater difference in sizes of group-I and group-III cations produces greater disproportionality between the I–VI and III–VI bonds in Ag–III–VI, resulting in higher distortion values. Consequently, when the Ag content decreases with off-stoichiometry in the ODCs, the disproportionality is reduced, the lattice symmetry is increased, and the η values shift towards unity, as reflected in Fig. 3c and d.
Correlation between enthalpy and relaxation
Despite being a purely geometric parameter, tetragonal distortion has been previously linked to various phase transitions in I–III–VI systems. Specifically, the magnitude of η was suggested to correlate with the order–disorder transition temperature24 and the extension of the single-phase chalcopyrite region.25,55–57 The latter hypothesis is particularly relevant for this work, and thus we put it to the test using our computed data.As discussed above, the single-phase region width is determined by the enthalpy of ODCs with near-1:1:2 composition, which have the same structural motif as the 2:4:7 and 4:6:11 ODCs depicted in Fig. 2a and b. The enthalpy of these ODCs relative to the convex hulls can thus be used as a convenient quantification parameter for the tolerance to off-stoichiometry. The enthalpy values computed for the different I–III–VI systems are plotted in Fig. 4a. Note that compounds with other lattices (e.g. spinel 1:5:8) were not included in these calculations. On the surface, the data seems to confirm the hypothesis about the importance of η because the enthalpies are higher for Ag-based I–III–VI (which have lower η for 1:1:2) as compared to those of the Cu-based systems.52 However, when the enthalpies are plotted versus the computed tetragonal distortion, little-or-no correlation is distinguished (see Fig. S3†). This result means that the significance of η with regard to off-stoichiometry has been overstated. The conclusion is not particularly surprising, considering that doubts about the correlation in question are almost as old as the original hypothesis.56
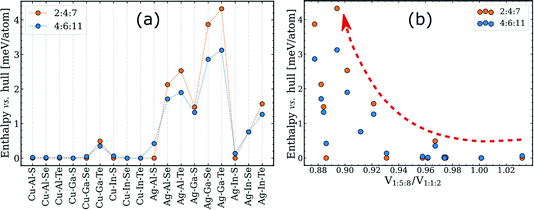 | ||
| Fig. 4 Enthalpies of 2:4:7 and 4:6:11 ODCs above the simplified convex hull (consisting of six representative zinc-blende derived structures, see text for details). The enthalpies are presented (a) for different I–III–VI systems and (b) versus the ratio of the per-anion volume of 1:5:8 ODC to that of the 1:1:2 phase. The red dashed arrow in (b) is drawn to guide the eye. The corresponding plots for the 1:3:5 ODC are given in Fig. S4.† | ||
On the other side, the knowledge of the structural motif provides guidance to more descriptive structural parameters. As noted earlier,7 intermediate ODC structures can be represented as mixtures of 1:1:2- and 1:5:8-like domains and, thus, their enthalpies might correlate with the mismatch between the lattices of 1:1:2 and 1:5:8 ODC. Ignoring the different domain orientations, and neglecting the relaxation anisotropy described above, the lattice mismatch can be expressed via the ratio of per-anion volumes of 1:1:2 and 1:5:8 ODC. The computed enthalpies above the hull for the representative intermediate ODCs (i.e. 2:4:7 and 4:6:11) are plotted versus this ratio in Fig. 4b. As one can see, the quantities indeed correlate but loosely, presumably due to different bond stretching force constants and the employed model approximations. A better correlation might be found in the future, but it can already be stated that a large difference in the lattice parameters of the 1:5:8 ODC and 1:1:2 compound is a prerequisite for a high enthalpy for the intermediate ODCs and, thus, poor tolerance to off-stoichiometry in I–III–VI2 chalcopyrite absorbers.
Competition between spinel and zinc-blende-derived phases
To explore the origins of the type-II convex hull behavior, a closer inspection of the 1:5:8 and 0:2:3 phases is carried out. The primary endpoint for this analysis is the difference in enthalpies of zinc-blende-derived ODCs and spinel structures, the sign of which determines if the system in question belongs to the type-II category. All other compositions and symmetries were excluded because they were found to be unstable or otherwise irrelevant for the type-II systems. Fig. 5 depicts the computed data. As one can see, four systems – Cu–In–S, Ag–In–S, Cu–Al–S, and Ag–Al–S – have negative enthalpy difference values, although for Ag–Al–S, the spinel structure is found to be more stable for 0:2:3 only. The fact that all four systems are sulfides suggests that the spinel lattice might be unable to incorporate larger anions. It is, however, surprising that the spinel structures are unstable for systems with Ga, which in the periodic table is sandwiched between Al and In, as reflected in the ionic radii (RAl < RGa < RIn). The reason for this lack of correlation is currently unclear, but it certainly has nothing to do with the type of group-I cation, since the enthalpy trends for 0:2:3 and 1:5:8 are identical. The explanation might be found in more complex structural factors for the spinel lattice,58–60 but no attempts to pinpoint it have been made in this work, in order to retain the focus on the tolerance to off-stoichiometry.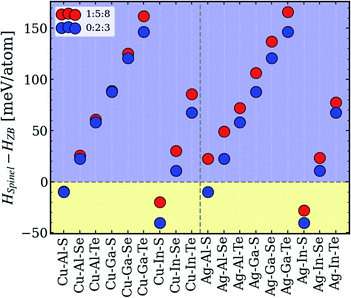 | ||
| Fig. 5 Relative enthalpies of spinel vs. zinc-blende-derived 1:5:8 and 0:2:3 structures in different I–III–VI systems. | ||
Predicted tolerance to off-stoichiometry
A convenient summary of the tolerance to off-stoichiometry, ascribed based on the computed convex hulls with the inclusion of literature structures, is presented color-coded in Fig. 6. The green and red colors here mark type-I and type-II systems, respectively, whereas type-III systems are highlighted by either orange or yellow depending on whether the enthalpy above the hull for the 2:4:7 ODC exceeds an arbitrary threshold of 1.5 meV per atom. As one can see, only a third of I–III–VI systems belong to the type-I category and, thus, are expected to exhibit high tolerance to off-stoichiometry (single-phase region width is comparable to that of CIGSe). Note that all systems in green are Cu-based, all systems in orange are Ag-based, and all systems in red are sulfides, which stems from the trends in stability of spinel compounds and structural relaxations described above.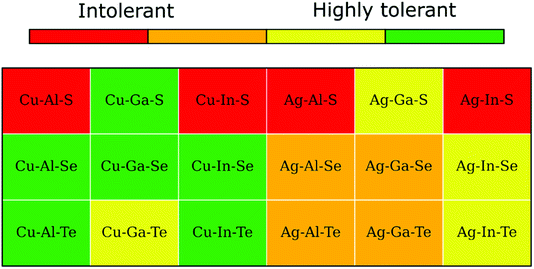 | ||
| Fig. 6 Tolerance to off-stoichiometry for I–III–VI systems ascribed based on the computed enthalpies above the hull for the 2:4:7 and 1:5:8 ODCs (see text for details). | ||
Discussion
Comparison with experiment
The predicted tolerance to off-stoichiometry can further be verified against the single-phase region width in pseudo-binary I2VI–III2VI3 phase diagrams. Our summary of the literature data is presented in Table 1. Unfortunately, the experimental data is lacking or incomplete for many of the I–III–VI systems considered, and in some cases the values could only be estimated from phase diagrams sketched based on limited experimental evidence. A further complication is that phase boundaries are temperature-dependent. In any case, the values in Table 1 are deemed useful for qualitative comparison. For details on the phase diagrams, the authors recommend the following handbooks: ref. 57 and 61, and the other sources cited in Table 1.| System | Single-phase region width (mol% of III2VI3) | Notable group-I-poor compounds | References |
|---|---|---|---|
| Cu–Al–S | 49.5–50.3% at 800 °C | CuAl5S8 (spinel or other cubic) | 64 and 65 |
| Cu–Al–Se | 44–46% at 800 °C | No ODCs (Al2Se3 segregation) | 66 and 67 |
| Spinel CuAl5Se8 at high pressure | |||
| Cu–Al–Te | 47.4–54.4% at 400 °C | No ODCs (Al2Te3 segregation) | 68 |
| Cu–Ga–S | 50–52% at RT | 1:5:8 ODC, 1:3:5 ODC (1:3:6-like ODC suggested in ref. 69) | 70–72 |
| 51–56% at 1050 °C | |||
| Cu–Ga–Se | 50–58% at RT | 1:5:8 ODC, 1:3:5 ODC | 57, 73, and 74 |
| 50–60% at 950 °C | |||
| Cu–Ga–Te | 52–62% at RT | ODC series – 1:3:5, 2:4:7, 3:5:9 | 57 |
| Cu–In–S | 48.5–52% at RT | CuIn5S8 (spinel) | 24, 56, 75, and 76 |
| 50–52% at RT (or narrower) | |||
| Cu–In–Se | 50–52.5% at RT | ODC series – 1:3:5, 1:5:8, 2:4:7, 3:5:9 | 57, 77, and 78 |
| 50–52% at 327 °C | |||
| 47.5–55% at 750 °C | |||
| Cu–In–Te | 51–59% at 400 °C | ODC series – 1:5:8, 1:3:5, 2:4:7, 3:5:9 | 57 and 79 |
| Ag–Al–S | Not indicated | AgAl5S8 (cubic) | 62 and 63 |
| Ag–Ga–S | 50–52% at 900 °C | Ag2Ga20S31 (zinc-blende or wurtzite-derived) | 50, 55, 57, 80, and 81 |
| Ag–Ga–Se | 50–52% at 700 °C (or narrower) | 1:7:11 ODC, 1:5:8 ODC | 8, 23, and 57 |
| Ag–Ga–Te | 51–52% at RT | 1:5:8 ODC | 57, 61, and 82 |
| 50–56% at 600 °C | |||
| Ag–In–S | Line phase | AgIn5S8 (spinel) | 57, 83, and 84 |
| Ag–In–Se | 48.5–52% at 800 °C (or narrower) | 1:5:8 ODC, 3:5:9 ODC | 57 and 85–87 |
| Ag–In–Te | 50–52% at RT | ODC series – 1:5:8, 1:3:5, 2:4:7, 4:10:17, 2:8:13 | 57, 88, and 89 |
| 50–58% at 400 °C | |||
| 50–62% at 600 °C |
Comparing the literature data with our predictions in Fig. 6, one can notice decent (but not perfect) agreement. CuAlS2, CuInS2, and AgInS2 are indeed intolerant to off-stoichiometry and form stable thio-spinel 1:5:8 compounds in the group-I-poor regime, in accordance with the predicted type-II character. The type-II behavior, however, could not be confirmed for AgAlS2 because the relevant data for Ag–Al–S is currently lacking. Still, the phase diagrams sketched in ref. 62 and 63 imply the coexistence of chalcopyrite AgAlS2 with cubic (most likely spinel) AgAl5S8, as opposed to Al2S3 predicted by our calculations. Yet, the limitations of the literature data do not allow us to exclude the possibility of misidentification for the Ag–Al–S system.
The majority of other Cu-based systems form several stable ODCs and exhibit broad single-phase regions, in accordance with the predominant type-I character. The exceptions here are Cu–Al–Se and Cu–Al–Te, which do not form any ODCs predicted by the calculations. The homogeneity region of CuAlSe2 is also reportedly narrower than expected for a type-I system. A part of the problem here might again be the relative scarcity and shortcomings of experimental studies of the Cu–Al–VI systems.
Experimental reports also indicate narrower single-phase regions for Ag-based systems compared to their Cu-based analogues, in compliance with the predicted type-III behavior. A major discrepancy exists, however, with regard to the homogeneity regions of AgInTe2 and AgGaTe2, which in both cases are found to be much wider in the experimental phase diagrams than predicted. We find no credible explanation for this result at present and call on the reader for further investigation.
Implications for the fabrication of chalcopyrite-based solar cells
Our results prove that the response to off-stoichiometry of Cu-poor CIGSe cannot be simply extrapolated to other chalcopyrite materials. For Ag-based I–III–VI systems, in order to stay in the single-phase 1:1:2 region, the chalcopyrite phase must contain a higher, and in some cases perfectly stoichiometric [I]/[III] ratio. In type-III systems, if not enough of the group-I element is being provided, a mixture of 1:1:2 chalcopyrite and 1:3:5/1:5:8 ODC becomes the most energetically favorable configuration. Depending on the processing route, this can prevent intermixing (e.g. producing coexisting 1:1:2 and 1:3:5/1:5:8 ODC grains in CIGSe heavily co-alloyed with Ag and Ga)8,9,25 or trigger the segregation of ODCs upon cooling (has not been reported so far, but is expected based on the narrowing of the single-phase region upon cooling).23 Although the impact of ODC precipitates on the absorber is not completely clear,9,25 it is hard to conceive of any benefit for the device. Beyond hitting the perfect stoichiometry, a possible strategy to increase the tolerance to off-stoichiometry in type-III systems is alloying with other elements, like alkalis. In particular, alkali elements are known to accumulate in the ODCs,25,90 which may enhance the stabilities of the intermediate ODCs (i.e. 2:4:7 and 4:6:11), converting the I–III–VI of interest into a type-I system. This prospect is supported by the expansion of the single-phase 1:1:2 region for CIGSe observed with Na addition,91 as well as the reported variance in ODC content with respect to the type and concentration of alkali impurities.8,92–95 However, the proposed solution remains hypothetical until verification is provided.On the other hand, the addition of alkalis has little chance of changing the character of type-II systems because a much larger enthalpy difference (between the spinel and tetragonal 1:5:8 ODC phases) would need to be compensated for. A practical solution here may instead lie in the modification of the deposition protocol and/or post-deposition treatments to account for the peculiarities of the growth kinetics. For example, three-stage elemental co-evaporation – a standard method of CIGSe deposition – yields a bi-layer film morphology for sulfide Cu(In,Ga)S2 due to the segregation of a spinel CuIn5S8-like layer with low [Ga]/[In] and a tetragonal Cu(In,Ga)S2-like layer with high [Ga]/[In] during the second (Cu-rich) deposition stage.30 The fundamental reason is that the type-II Cu–In–S system cannot incorporate Cu deficiency into the chalcopyrite phase (a miscibility gap exists between CuInS2 and CuIn5S8), whereas the type-I Cu–Ga–S system can do so readily without breaking the lattice (hence, a continuum of ODCs is observed). This discrepancy leads to a miscibility gap between spinel CuIn5S8 and Cu-poor tetragonal Cu1−xGa1+x/3S2 (where 0 < x ≤ 0.75), with both phases being able to accept only a small concentration of the other group-III element. At the same time, stoichiometric CuInS2 and CuGaS2 are known to exhibit full miscibility,18,26,96 and therefore Cu(In,Ga)S2 alloys can form readily when [Cu]/[III] ≥ 1. Thus, a modified strategy for the co-evaporation growth of Cu–(In,Ga)–S films could attempt to first grow Cu1−xGa1+x/3S2 and start adding indium only when [Cu]/[Ga] exceeds unity (i.e. by depositing Ga and In during the first and third co-evaporation stages, respectively). A more straightforward but practically challenging solution could be to maintain [Cu]/[III] = 1 throughout the deposition while varying [Ga]/[In], if band gap grading is intended. One can try fine-tuning the composition by depositing a sacrificial CuxS layer on top of slightly Cu-deficient Cu(In,Ga)S2, followed by annealing and KCN etching. The intended benefit of such post-deposition treatment over the simple KCN etching of Cu-rich Cu(In,Ga)S2 film is that CuxS would be confined to the film surface, allowing it to be readily and effectively removed. Unfortunately, the above recommendations are not universal and should be adjusted to every I–III–VI system or alloy individually.
In a broader context
The practical examples discussed above illustrate that low tolerance to off-stoichiometry can preclude intermixing and promote the segregation of secondary phases. The resulting morphologies are likely to induce additional losses due to unfavorable band alignment, reduction in the active absorber volume, accumulation of recombination centers at interfaces, and so on. The possibility of mechanical failures and thermal instabilities should be expected to increase as well. Therefore, the benefit of high tolerance to off-stoichiometry is practical – it allows the loosening of the composition control requirements during synthesis without triggering the segregation of secondary phases – but it does not make the main absorber phase better by itself. Intrinsic point defects are present in bulk either way and, thus, defect tolerance is still necessary to avoid the formation of recombination centers. In other words, defect tolerance and tolerance to off-stoichiometry are complementary features that manifest themselves at different defect concentrations. Specifically, the equilibrium point defect concentration of 1020 cm−3 is huge when talking about intrinsic defects, but the off-stoichiometry it produces is below the detection limit for most (if not all) material characterization tools. From the other side, the experimentally measured off-stoichiometry cannot plausibly be accommodated by isolated point defects because interaction and clustering cannot be avoided at such small distances (at most 10 Å separation between defect complexes in CIGSe at [Cu]/[In] = 0.8, assuming that they form a uniform 3D grid).Our conclusion that only one-third of I–III–VI2 chalcopyrites considered can accept group-I deficiency suggests that tolerance to off-stoichiometry is not defined by the lattice symmetry and can vary greatly even within a narrow family of isomorphic materials. Instead, judging by the trends for I–III–VI systems, we suggest that high tolerance to off-stoichiometry is more probable for a compound meeting two simple conditions. First, it should have a closely related lattice symmetry with the phase it coexists in the equilibrium (i.e. forming a two-phase region). Second, the lattice constants of these two phases should be sufficiently similar. Both conditions sound intuitive, consistent with classical examples of non-stoichiometric compounds, and potentially useful for high-throughput materials screening. For instance, the future identification of novel solar absorbers with a practically favorable high tolerance to off-stoichiometry could be done by analyzing the experimental lattice geometries of all known compounds in the investigated system. However, we must acknowledge that the proposed indicators must be taken with a pinch of salt until the correlation is proven valid for a wider range of materials systems.
Conclusions
When noticing the structural similarities of I–III–VI2 isomorphs, one might be forgiven for projecting the behavior of CIGSe onto the entire family of I–III–VI compounds. It might be a reasonable guess for ideal 1:1:2 chalcopyrites, but it is certainly invalid for off-stoichiometric materials. Our stability analysis reveals three types of material response to group-I deficiency. Crucially, only a third of all I–III–VI systems investigated are predicted to demonstrate tolerance to off-stoichiometry at the level of that in CIGSe. This is unfortunate because the possibility of depositing a homogeneous single-phase absorber without the need for precise composition control is favorable for the device. One way that things can go wrong in a I–III–VI system is when a spinel 1:5:8 or 0:2:3 phase has a much lower enthalpy than its zinc-blende-derived ODC counterpart, resulting in a narrow one-phase chalcopyrite region that causes troubles for the absorber deposition and processing. This problem is predicted for four sulfide I–III–VI systems with the group-III element being either In or Al, while the systems with III = Ga are surprisingly devoid of this issue, in spite of the trend in ionic radii dictating otherwise. A similar but less severe issue emerges when ODCs with 0.5 < [I]/[III] < 1.0 are destabilized and shifted above the convex hull. In the analyzed chalcopyrite family, this primarily happens due to the replacement of smaller copper with larger silver ions. The lattice relaxation is emblematical of these changes and it can therefore serve as an indicator of solar absorber materials tolerant to off-stoichiometry. Specifically, a compound is deemed to have a greater chance of being tolerant to off-stoichiometry if: (i) its lattice exhibits a close symmetry relationship with the phase it coexists with in the two-phase region of the phase diagram and (ii) lattice constants of these phases are sufficiently close. These simple principles can be integrated into high-throughput screening and ultimately accelerate the discovery of materials for next-generation photovoltaics and beyond.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was made possible by funding provided by the Swedish Foundation for Strategic Research (grant no. RMA15-0030). The computations and data handling were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC), partially funded by the Swedish Research Council through grant agreement no. 2018-05973. The corresponding author is also infinitely grateful to the Armed Forces of Ukraine for protecting peaceful skies over the head during the preparation of this manuscript.References
- R. Woods-Robinson, Y. Han, H. Zhang, T. Ablekim, I. Khan, K. A. Persson and A. Zakutayev, Chem. Rev., 2020, 120, 4007–4055 CrossRef CAS PubMed.
- L. Yu and A. Zunger, Phys. Rev. Lett., 2012, 108, 068701 CrossRef PubMed.
- Z. Huo, S.-H. Wei and W.-J. Yin, J. Phys. D: Appl. Phys., 2018, 51, 474003 CrossRef.
- K. Kuhar, M. Pandey, K. S. Thygesen and K. W. Jacobsen, ACS Energy Lett., 2018, 3, 436–446 CrossRef CAS.
- S. Siebentritt, L. Gütay, D. Regesch, Y. Aida and V. Deprédurand, Sol. Energy Mater. Sol. Cells, 2013, 119, 18–25 CrossRef CAS.
- J. Pohl and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245203 CrossRef.
- K. Sopiha, C. Persson, M. Edoff, C. Platzer-Björkman and J. J. S. Scragg, 2022, submitted.
- J. K. Larsen, O. Donzel-Gargand, K. V. Sopiha, J. Keller, K. Lindgren, C. Platzer-Björkman and M. Edoff, ACS Appl. Energy Mater., 2021, 4, 1805–1814 CrossRef CAS.
- J. Keller, P. Pearson, N. S. Nilsson, O. Stolt, L. Stolt and M. Edoff, Sol. RRL, 2021, 5, 2100403 CrossRef CAS.
- E. Rudigier, T. Enzenhofer and R. Scheer, Thin Solid Films, 2005, 480–481, 327–331 CrossRef CAS.
- H. Hiroi, Y. Iwata, S. Adachi, H. Sugimoto and A. Yamada, IEEE J. Photovoltaics, 2016, 6, 760–763 Search PubMed.
- S. Shukla, M. Sood, D. Adeleye, S. Peedle, G. Kusch, D. Dahliah, M. Melchiorre, G.-M. Rignanese, G. Hautier, R. Oliver and S. Siebentritt, Joule, 2021, 5, 1816–1831 CrossRef CAS.
- N. Barreau, A. Thomere, D. Cammilleri, A. Crossay, C. Guillot-Deudon, A. Lafond, N. Stéphant, D. Lincot, M. T. Caldes, R. Bodeux and B. Bérenguier, in 47th IEEE Photovoltaic Specialists Conference (PVSC), IEEE, 2020, pp. 1715–1718 Search PubMed.
- S. Merdes, R. Sáez-Araoz, A. Ennaoui, J. Klaer, M. C. Lux-Steiner and R. Klenk, Appl. Phys. Lett., 2009, 95, 213502 CrossRef.
- F.-J. Fan, L. Wu and S.-H. Yu, Energy Environ. Sci., 2014, 7, 190–208 RSC.
- B. V. Korzun, A. A. Fadzeyeva, K. Bente, W. Schmitz and G. Kommichau, Phys. Status Solidi B, 2005, 242, 1581–1587 CrossRef CAS.
- N. Gaillard, Appl. Phys. Lett., 2021, 119, 090501 CrossRef CAS.
- N. Gaillard, D. Prasher, M. Chong, A. Deangelis, K. Horsley, H. A. Ishii, J. P. Bradley, J. Varley and T. Ogitsu, ACS Appl. Energy Mater., 2019, 2, 5515–5524 CrossRef CAS.
- N. Gaillard, Wide Band Gap Chalcopyrite Photoelectrodes for Direct Water Splitting, Univ. of Hawaii, Honolulu, HI (United States), 2019 Search PubMed.
- D. Huang and C. Persson, Chem. Phys. Lett., 2014, 591, 189–192 CrossRef CAS.
- J. H. Kim, S. T. Kim, L. Larina, B. T. Ahn, K. Kim and J. H. Yun, Sol. Energy Mater. Sol. Cells, 2018, 179, 289–296 CrossRef CAS.
- C. P. Muzzillo, W. E. Klein, Z. Li, A. D. DeAngelis, K. Horsley, K. Zhu and N. Gaillard, ACS Appl. Mater. Interfaces, 2018, 10, 19573–19579 CrossRef CAS PubMed.
- J. C. Mikkelsen, Mater. Res. Bull., 1977, 12, 497–502 CrossRef CAS.
- J. J. M. Binsma, L. J. Giling and J. Bloem, J. Cryst. Growth, 1980, 50, 429–436 CrossRef CAS.
- J. Keller, L. Stolt, K. V. Sopiha, J. K. Larsen, L. Riekehr and M. Edoff, Sol. RRL, 2020, 4, 2000508 CrossRef CAS.
- F. Khavari, J. Keller, J. K. Larsen, K. V. Sopiha, T. Törndahl and M. Edoff, Phys. Status Solidi A, 2020, 217, 2000415 CrossRef CAS.
- F. Khavari, N. Saini, J. Keller, J. K. Larsen, K. V. Sopiha, N. M. Martin, T. Törndahl, C. P. Björkman and M. Edoff, Phys. Status Solidi A, 2022, 219, 2100441 CrossRef CAS.
- J. K. Larsen, J. Keller, O. Lundberg, T. Jarmar, L. Riekehr, J. J. S. Scragg and C. Platzer-Björkman, IEEE J. Photovoltaics, 2018, 8, 604–610 Search PubMed.
- J. Keller, O. V. Bilousov, E. Wallin, O. Lundberg, J. Neerken, S. Heise, L. Riekehr, M. Edoff and C. Platzer-Björkman, Phys. Status Solidi A, 2019, 216, 1900472 CrossRef CAS.
- A. Thomere, N. Barreau, N. Stephant, C. Guillot-Deudon, E. Gautron, M. T. Caldes and A. Lafond, Sol. Energy Mater. Sol. Cells, 2022, 237, 111563 CrossRef CAS.
- J. Larsen, K. Sopiha, C. Persson, C. Platzer-Björkman and M. Edoff, Adv. Sci., 2022, 2200848 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- S.-H. Wei, L. G. Ferreira and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 2533–2536 CrossRef CAS PubMed.
- S.-H. Wei, S. B. Zhang and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, R2478–R2481 CrossRef CAS.
- S. B. Zhang, S.-H. Wei and A. Zunger, Phys. Rev. Lett., 1997, 78, 4059–4062 CrossRef CAS.
- X. Chen, W. Liu and Y. Duan, J. Phys.: Condens. Matter, 2021, 33, 075401 CrossRef CAS PubMed.
- W. Liu, H. Liang, Y. Duan and Z. Wu, Phys. Rev. Mater., 2019, 3, 125405 CrossRef CAS.
- A. Sharan, F. P. Sabino, A. Janotti, N. Gaillard, T. Ogitsu and J. B. Varley, J. Appl. Phys., 2020, 127, 065303 CrossRef CAS.
- C. D. R. Ludwig, T. Gruhn, C. Felser and J. Windeln, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174112 CrossRef.
- S. B. Zhang, S.-H. Wei, A. Zunger and H. Katayama-Yoshida, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 9642–9656 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- M. Hellenbrandt, Crystallogr. Rev., 2004, 10, 17–22 CrossRef CAS.
- D. Lübbers and V. Leute, J. Solid State Chem., 1982, 43, 339–345 CrossRef.
- A. Zunger, Appl. Phys. Lett., 1987, 50, 164–166 CrossRef CAS.
- J. E. Jaffe and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 1882–1906 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- G. Brandt and V. Krämer, Mater. Res. Bull., 1976, 11, 1381–1388 CrossRef CAS.
- A. W. Verheijen, L. J. Giling and J. Bloem, Mater. Res. Bull., 1979, 14, 237–240 CrossRef CAS.
- V. B. Lazarev, Z. Z. Kish, E. Y. Peresh and E. E. Semrad, Complex Chalcogenides in AI–BIII–CVI Systems, Metallurgy, Moscow, 1993 (in Russian) Search PubMed.
- R. J. Hill, J. R. Craig and G. V. Gibbs, Phys. Chem. Miner., 1979, 4, 317–339 CrossRef CAS.
- K. Kugimiya and H. Steinfink, Inorg. Chem., 1968, 7, 1762–1770 CrossRef CAS.
- M. G. Brik, A. Suchocki and A. Kamińska, Inorg. Chem., 2014, 53, 5088–5099 CrossRef CAS PubMed.
- J. L. Shay and J. H. Wernick, Ternary Chalcopyrite Semiconductors: Growth, Electronic Properties, and Applications: International Series of Monographs in the Science of the Solid State, Elsevier, 2017, vol. 7 Search PubMed.
- E. E. Hellstrom and R. A. Huggins, J. Solid State Chem., 1980, 35, 207–214 CrossRef CAS.
- M. Guittard, C. Alain and F. Jean, C. R. Hebd. Seances Acad. Sci., 1981, 293, 661–663 CAS.
- D. Máuhl, J. Pickardt and B. Reuter, Z. Anorg. Allg. Chem., 1982, 491, 203–207 CrossRef.
- B. V. Korzun, K. Bente, R. R. Mianzelen, T. Doering, G. Kommichau, W. Schmitz and A. A. Fadzeyeva, J. Mater. Sci.: Mater. Electron., 2005, 16, 25–28 CrossRef CAS.
- B. V. Korzoun, L. A. Makovetskaya, V. A. Savchuk, V. A. Rubtsov, G. P. Popelnyuk and A. P. Chernyakova, J. Electron. Mater., 1995, 24, 903–906 CrossRef CAS.
- K.-J. Range, G. Engert and M. Zabel, Z. Naturforsch. B, 1974, 29, 807–808 CrossRef CAS.
- B. V. Korzun, A. A. Fadzeyeva, K. Bente and T. Doering, J. Mater. Sci.: Mater. Electron., 2008, 19, 255–260 CrossRef CAS.
- T. Ueno, K. Nagasaki, T. Horikawa, M. Kawakami and K. Kondo, Can. Mineral., 2005, 43, 1653–1661 CrossRef CAS.
- A. Thomere, C. Guillot-Deudon, M. T. Caldes, R. Bodeux, N. Barreau, S. Jobic and A. Lafond, Thin Solid Films, 2018, 665, 46–50 CrossRef CAS.
- M. Kokta, J. R. Carruthers, M. Grasso, H. M. Kasper and B. Tell, J. Electron. Mater., 1976, 5, 69–89 CrossRef CAS.
- T. Maeda, Y. Yu, Q. Chen, K. Ueda and T. Wada, Jpn. J. Appl. Phys., 2017, 56, 04CS12 CrossRef.
- J. C. Mikkelsen, J. Electron. Mater., 1981, 10, 541–558 CrossRef CAS.
- O. M. Strok, I. D. Olekseyuk, O. F. Zmiy, I. A. Ivashchenko and L. D. Gulay, J. Phase Equilib. Diffus., 2013, 34, 94–103 CrossRef CAS.
- S. Fiechter, Y. Tomm, M. Kanis, R. Scheer and W. Kautek, Phys. Status Solidi B, 2008, 245, 1761–1771 CrossRef CAS.
- H. Migge and J. Grzanna, J. Mater. Res., 1994, 9, 125–131 CrossRef CAS.
- U.-C. Boehnke and G. Kühn, J. Mater. Sci., 1987, 22, 1635–1641 CrossRef CAS.
- O. F. Zmiy, I. A. Mishchenko and I. D. Olekseyuk, J. Alloys Compd., 2004, 367, 49–57 CrossRef CAS.
- E. M. Kadykalo, L. P. Marushko, I. A. Ivashchenko, O. F. Zmiy and I. D. Olekseyuk, J. Phase Equilib. Diffus., 2013, 34, 221–228 CrossRef CAS.
- R. S. Feigelson and R. K. Route, Opt. Eng., 1987, 26, 262113 CrossRef.
- E. F. Sinyakova, V. I. Kosyakov and K. A. Kokh, Inorg. Mater., 2009, 45, 1217 CrossRef CAS.
- V. Krämer, H. Hirth, M. Hofherr and H.-P. Trah, Thermochim. Acta, 1987, 112, 88–94 CrossRef.
- R. S. Roth, H. S. Parker and W. S. Brower, Mater. Res. Bull., 1973, 8, 333–338 CrossRef CAS.
- V. P. Sachanyuk, G. P. Gorgut, V. V. Atuchin, I. D. Olekseyuk and O. V. Parasyuk, J. Alloys Compd., 2008, 452, 348–358 CrossRef CAS.
- S. Chen, J. Chang, S. Tseng, L. Chang and J. Lin, J. Alloys Compd., 2016, 656, 58–66 CrossRef CAS.
- I. D. Olekseyuk and O. V. Krykhovets, J. Alloys Compd., 2001, 316, 193–202 CrossRef CAS.
- I. A. Ivashchenko, I. V. Danyliuk, I. D. Olekseyuk and V. V. Halyan, J. Solid State Chem., 2014, 210, 102–110 CrossRef CAS.
- Z. Bahari, J. Rivet, B. Legendre and J. Dugué, J. Alloys Compd., 1999, 282, 164–174 CrossRef CAS.
- P.-W. Chiang, D. F. O’Kane and D. R. Mason, J. Electrochem. Soc., 1967, 114, 759 CrossRef CAS.
- A. Stokes, M. Al-Jassim, A. Norman, D. Diercks and B. Gorman, Progr. Photovolt.: Res. Appl., 2017, 25, 764–772 CrossRef CAS.
- R. Herberholz, U. Rau, H. W. Schock, T. Haalboom, T. Gödecke, F. Ernst, C. Beilharz, K. W. Benz and D. Cahen, Eur. Phys. J.: Appl. Phys., 1999, 6, 131–139 CrossRef CAS.
- D. Güttler, A. Chirila, S. Seyrling, P. Blösch, S. Buecheler, X. Fontané, V. Izquierdo-Roca, L. Calvo-Barrio, A. Peréz-Rodriguez, J. R. Morante, A. Eicke and A. N. Tiwari, in 35th IEEE Photovoltaic Specialists Conference, IEEE, 2010, pp. 003420–003424 Search PubMed.
- K. V. Sopiha, J. K. Larsen, O. Donzel-Gargand, F. Khavari, J. Keller, M. Edoff, C. Platzer-Björkman, C. Persson and J. J. Scragg, J. Mater. Chem. A, 2020, 8, 8740–8751 RSC.
- T. Tanaka, Y. Demizu, T. Yamaguchi and A. Y. A. Yoshida, Jpn. J. Appl. Phys., 1996, 35, 2779 CrossRef CAS.
- T. Tanaka, Y. Demizu, A. Yoshida and T. Yamaguchi, J. Appl. Phys., 1997, 81, 7619–7622 CrossRef CAS.
- T. Maeda, R. Nakanishi, M. Yanagita and T. Wada, Jpn. J. Appl. Phys., 2020, 59, SGGF12 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2fd00105e |
| This journal is © The Royal Society of Chemistry 2022 |