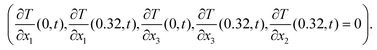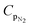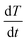Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental and numerical evaluation of the effect of micro-aeration on the thermal properties of chocolate
D.
Bikos
 *a,
G.
Samaras
a,
M. N.
Charalambides
a,
P.
Cann
a,
M.
Masen
a,
C.
Hartmann
b,
J.
Vieira
c,
A.
Sergis
a and
Y.
Hardalupas
*a
*a,
G.
Samaras
a,
M. N.
Charalambides
a,
P.
Cann
a,
M.
Masen
a,
C.
Hartmann
b,
J.
Vieira
c,
A.
Sergis
a and
Y.
Hardalupas
*a
aDepartment of Mechanical Engineering, Imperial College London, UK. E-mail: d.bikos17@imperial.ac.uk; y.hardalupas@imperial.ac.uk
bNestlé Research Lausanne, UK
cNestlé Product Technology Centre, York, UK
First published on 4th April 2022
Abstract
Thermal properties, such as thermal conductivity, specific heat capacity and latent heat, influence the melting and solidification of chocolate. The accurate prediction of these properties for micro-aerated chocolate products with varying levels of porosity ranging from 0% to 15% is beneficial for understanding and control of heat transfer mechanisms during chocolate manufacturing and food oral processing. The former process is important for the final quality of chocolate and the latter is associated with sensorial attributes, such as grittiness, melting time and flavour. This study proposes a novel multiscale finite element model to accurately predict the temporal and spatial evolution of temperature across chocolate samples. The model is evaluated via heat transfer experiments at temperatures varying from 16 °C to 45 °C. Both experimental and numerical results suggest that the rate of heat transfer within the micro-aerated chocolate is reduced by 7% when the 15% micro-aerated chocolate is compared to its solid counterpart. More specifically, on average, the thermal conductivity decreased by 20% and specific heat capacity increased by 10% for 15% micro-aeration, suggesting that micro-pores act as thermal barriers to heat flow. The latter trend is unexpected for porous materials and thus the presence of a third phase at the pore's interface is proposed which might store thermal energy leading to a delayed release to the chocolate system. The developed multiscale numerical model provides a design tool to create pore structures in chocolate with optimum melting or solidifying response.
1. Introduction
Chocolate is a popular food product, which has a complex behaviour due to its multiphase nature. Chocolate consists of hard particles such as sugar crystals, cocoa solids and fat crystals dispersed in a soft continuous matrix, the cocoa butter.1 There is extensive literature investigating the effects of chocolate composition on material properties such as rheological effects, and on consumer perception.2–6 The importance of material properties has been thoroughly reported and linked to flow processes,2,7 oral processes4,8 and cooling processes.9–11 Carvalho da Silva12 highlighted that the melting behaviour of chocolate plays a determinant role in the final quality of the chocolate.Thermal properties, such as specific heat capacity, thermal conductivity and latent heat, affect the melting and solidification/crystallisation behaviour of chocolate13,14 and therefore, the accurate measurement and prediction of these thermal properties is crucial. These include the cooling stage during manufacturing, which is important for the final product quality, and the consumer experience during consumption or oral processing of the chocolate, where melting is associated with several sensorial attributes, such as melting time and flavour intensity.15 These thermal properties have been evaluated experimentally and numerically.
Amongst others, Le Reverend et al.13 highlighted the importance of developing a numerical model that considers the thermal properties of chocolate, coupled with the phase transformation kinetics of fat crystals, to predict the crystallisation evolution during the cooling stage of chocolate. This can ultimately be used to control and improve the cooling process during chocolate manufacturing, ensuring the formation of the desired crystal form. Several computational modelling studies simulate the cooling process during chocolate tempering or before demoulding.14,16,17
In addition, Haedelt, Beckett, and Niranjan15 reported a link between melting behaviour of chocolate during oral processing and sensory properties for different porous chocolate products with different pore sizes through a series of in vivo sensory tests. Ziegler, Mongia, and Hollender18 reported similar findings and highlighted the effect of melting time on the release of flavour attributes: the slow melting of porous chocolate will release flavour attributes more intensely compared to solid chocolate, which melts rapidly. However, no studies are available that explain the mechanisms relating the effect of porosity or pore size to the melting behaviour of chocolate and consequently to consumer perception. Oral processing of chocolate lasts approximately 20 seconds19 and within this timeframe all processes change dynamically. Chocolate melting assists the release of all flavour attributes captured inside the chocolate and is related to textural attributes such as moistness, melting time and grittiness.
Thus, the accurate prediction of the thermal properties is required to understand and control both the cooling stage during manufacturing and the melting behaviour during food oral processing. Even though the importance of the thermal properties to the crystallisation of chocolate and to the cooling stage during the manufacturing process has been highlighted previously and thorough investigation has been performed, this is not true in the case of the melting process during oral process. To the authors’ knowledge, there is no literature that systematically tackles this topic in an analogous way as has been done for the cooling process.
Material properties are strongly dependent on the chocolate recipe and composition. This is the reason why thermal property values for different chocolates slightly deviate across literature.13,14,20,21 Across the literature, differential scanning calorimetry (DSC) devices are commonly used to investigate the crystallisation form of chocolate and measure the latent heat and the specific heat capacity against temperature and rate of heating or cooling.13,17,22–24 Unfortunately, such instruments are not able to provide measurements of the thermal conductivity, at least directly. Commercially available instruments or methods to measure thermal conductivity, such as the hot wire method (HWM) and the laser flash method (LFM), exhibit limitations when applied to materials which are not solid and exhibit low melting temperature points, such as chocolate. These techniques provide more accurate results when a large temperature testing range can be employed, which produces an additional limitation to their implementation in the study of chocolate. However, there are some studies that report thermal conductivity measurements on chocolate using custom-designed experimental setups coupled with numerical modelling methods calibrated on these experimental setups.13,14,17
Literature typically only refers to non-aerated chocolate, either milk or dark and does not address the thermal properties of micro-aerated chocolates. Micro-aeration has been utilised in chocolate systems as a method to modify textural attributes such as hardness, crumbliness, grittiness, and stickiness.8,15 The micro-pores inside the chocolate system are found to have an average diameter of 40 μm, which is of the same scale as other ingredients found in chocolate such as cocoa solids and sugar particles. A micro-pore suspension is developed inside the chocolate by injecting gaseous N2 before the moulding process, when the chocolate is already tempered. It has been shown that micro-aeration of chocolate significantly affects mechanical properties such as Young's modulus, fracture toughness, and friction coefficient4,8 but there is no data available that relates the thermal properties of chocolate, such as thermal conductivity, latent heat, and specific heat capacity to the level of micro-aeration of the chocolate. These thermal properties are important parameters to determine the chocolate thermal response under transient thermal loading conditions.
A review on porous foods by Dadmohammadi and Datta25 reported the significance of investigating the link between the porous structure of the resulting food product and its quality, both in terms of material properties and texture. The pores can significantly influence the microstructure of the food and therefore affect processes such as cooking, drying and freezing. In literature, experimental, numerical, and analytical approaches have been employed to investigate the thermal behaviour of porous foods.26–28
Many analytical models have been developed to predict the effective thermal properties of foods.27,29–31 These analytical models employ a range of assumptions for the porous microstructure (such as the distribution and shape of pores etc.) to devise a relationship associating the thermal properties of the mixture and the thermal properties of the constituents and porosity. Semi-empirical analytical models31 that employ additional fitting parameters – often without any physical justification – also exist, which are not considered in the current work. Despite the large number of proposed analytical models, there is yet no conclusive model to accurately predict the effective thermal properties of multiphase foods. Therefore, the need for a conclusive and accurate model to describe the complex multiphase microstructure and behaviour of food materials remains.
Numerical modelling is an attractive approach to simulate the engineering of foods, due to the high versatility of the methods, low costs and quick result turnarounds.26–28,32 The ability to change parameters such as environmental (temperature, moisture content etc.)27,28,33 and geometrical (size, and shape)27,34 conditions and record parameters that are otherwise impossible to extract from in vivo tests (e.g. simulation of chewing), constitutes this method a powerful design tool for the food industry. However, despite the extensive use of such models, they fail to describe all the physical mechanisms taking place inside these materials. For example, no studies have been presented showing the heat transfer in porous foodstuff at the microscale and the resulting consequences on the averaged thermal properties of the bulk material.
Our recent work on the effect of micro-aeration on chocolate structure, mechanical, and sensory properties during oral processing highlighted the importance of heat transfer and chocolate melting on the structural breakdown during mastication that is expected to alter its’ perceived consumer experience.35 It was found that the combined action of heat transfer and fragmentation guides chocolate oral processing after the first bite. The need to compute the true properties of the micro-porous chocolate under thermal conditions relevant to oral processing remained as previous work only used macroscale analytical models to predict the effects of micro-aeration on the thermal properties of chocolate rather than an extensive micro-FEM calculation, i.e. the focus of the current paper. The Finite Element Model of the current work may prove a useful design tool to create chocolate products with controlled sensorial attributes.
The aim of this study is to investigate the thermal behaviour of three milk chocolates with varying levels of micro-aeration: one non-aerated and two micro-aerated with 10% and 15% porosity. This work targets to develop a multiscale model which can simulate the unsteady heat transfer phenomena within the chocolate. The unsteady heat transfer effects are important for the oral processing of chocolate. This effort reflects food industry's needs to investigate how small structural changes, such as low levels of porosity, can change material and sensorial properties of chocolate during oral processing that affect the consumer experience.35 Measurements on a novel heat transfer rig and a commercially available DSC instrument are coupled to a multiscale finite element model to predict the thermal temporal response produced by these different porous structures. The multiscale numerical model is composed of a heat transfer model at the microscale to compute the average (effective) thermal properties of the resulting porous material which are then used in a heat transfer model at the macroscale to predict the experimental results. This multiscale numerical model can be utilised as a design tool to optimise the microstructural parameters, such as porosity level, pore size, pore distribution, to adjust the melting or solidifying behaviour of chocolate in a time and cost effective way.
The paper is structured as follows; section 2 summarises the experimental, numerical, and analytical methods used. Section 3 presents and discusses the results obtained using these methods. The paper ends with a summary of the findings.
2. Materials & methods
2.1. Materials
Three types of milk chocolates with different porosity levels of 0%, 10% and 15% were provided by Nestlé Product Technology Centre in York, UK and used for the heat transfer experiments. These samples consisted of 44 wt% sugar particles, 27 wt% cocoa fat, 10 wt% whole milk powder and 6 wt% non-fat cocoa solids. The initial geometry of the chocolate is a rectangular beam with a length of 80 mm, a width of 15 mm, and a height of 8 mm. For a detailed description of the manufacturing process and the micro-aeration process, the reader is referred to Bikos et al. 2021.8 The chocolate geometries were further modified using a razor saw to a final dimension of 50 mm length (L), and 8 mm in width (W) and height (H), as shown in Fig. 1. Blind holes of 0.6 mm diameter with a depth of up to half of the height (H) were created using the tip of a needle. | ||
| Fig. 1 (a): Non-aerated chocolate used for the heat transfer experiments. (b) Non-aerated chocolate placed in the thermally insulated sample holder. | ||
Cocoa butter samples were manufactured to be tested in the DSC tests to assess the specific heat capacity of cocoa butter. Refined, untempered cocoa butter was provided by Nestlé Product Technology Centre in York which was tempered using a custom designed double bath to ensure the relatively slow and controlled heating of the material. Following the heating-cooling protocol the commonly used seeding method was employed to temper the cocoa butter, as described by Beckett.36 After the tempering process the cocoa butter mass was deposited into cylindrical moulds of 25 mm diameter and height.
2.2. Experimental methods
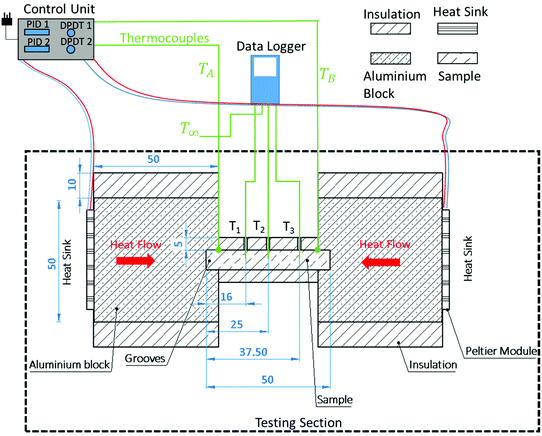
A heat transfer rig was developed which was able to heat or cool the ends of the beam-shaped chocolate samples independently and record the spatial and temporal temperature profile. As shown in Fig. 2, the heat transfer rig consisted of the testing section, the control unit and a data logger, which recorded the temperature evolution at three locations across the chocolate sample. The testing section was the part of the rig where the chocolate samples were actively heated or cooled. The control unit consisted of a combination of two PID controllers (CN142 Omega Ltd, UK). The temperature profiles were recorded using an 8-channel thermocouple data logger (OM-HK-EH-TC Omega Ltd, UK) at different locations in the chocolate sample T1, T2, and T3, (see Fig. 2) placed in the centre of the sample (H/2).The ends of the chocolate samples were inserted into square-shaped grooves of size 5 mm length, height, and width. The groves were machined into the side surface of the aluminium blocks as shown in Fig. 2. The aluminium blocks had a size of 50 mm length, 50 mm height, and 40 mm width (width is not shown in Fig. 2) and used to support the chocolate samples and ensure that the heat transfer was uniform over the area inside the grooves. As shown in Fig. 2, on the opposite side of each of the aluminium blocks, Peltier Modules (ET-161-12-14-E, Adaptive Thermal Management, UK) with a maximum power of 62.3 W were placed to apply or remove heat to/from the sample. On the other side of the Peltier modules, two Aluminium heatsinks (LAM 4 Fischer Elektronic, Germany) with a thermal resistance of 0.4 °C W−1 ventilated by standard computer axial fans (Multifan S5 AC Infinity Inc., USA) were used to ensure that sufficient heat was dissipated/absorbed by the Peltier module exhausts. The fans were only used in the case where the Peltier modules were cooling the chocolate due to the required, relatively high, energy dissipation for the Peltier modules to provide effective cooling.
The Peltier modules were each controlled by individual PID controllers to ensure a constant set temperature of the sample ends when placed inside the aluminium grooves. This was achieved by monitoring the temperature of each groove using a thermocouple connected to each of the two PID controllers, see thermocouples TA and TB in Fig. 2. The PID controllers were modulating the power delivery to the Peltier modules according to the target temperature and actual readings of the groove thermocouples. Using a double pole double throw switch (DPDT) for each Peltier module, as shown in Fig. 2, the polarity of the Peltier module could be reversed to either heat or cool the samples. An example of the direction of heat flow inside the aluminium block and, by extend, the chocolate sample is shown in Fig. 2 for one of the scenaria investigated (i.e. scenaria 1 and 2 are explained below, see Table 1). The aluminium block and chocolate sample were insulated using 3D-printed custom sleeves in order to limit heat losses. The material used for the insulation was ABS with micro-pores in the shape of honeycomb to increase thermal insulation performance.
| Scenario | T left, °C | T right, °C |
|---|---|---|
| 1 | 35 | 35 |
| 2 | 45 | 45 |
| 3 | 16 | 16 |
| 4 | 45 | 16 |
The temperature of the core of the chocolate specimen was recorded at three different locations T1, T2, and T3, which corresponded to distances of 16 mm, 25 mm, and 37.5 mm, using k-type thermocouples. Four different thermal loading scenaria were implemented, three within the melting temperature range of the chocolate and one outside. Scenario 1 represented heating to a constant temperature of 35 °C on both sides, scenario 2 rapid heating to a constant temperature of 45 °C on both sides, scenario 3 cooling to a constant temperature of 16 °C on both sides, and scenario 4 rapid heating to a constant temperature of 45 °C at the left side and cooling to a constant temperature of 16 °C at the right side of the testing section. The ambient temperature and relative humidity for all experiments was controlled and set to 23 °C and 50% respectively. The boundary conditions of all scenaria are summarised in Table 1. Three repeats were performed for each loading scenario. The uncertainties of the thermocouple measurements were estimated to be approximately 0.1 °C or 1% of the measured value and the sampling period was 5 s.
Preliminary experiments were performed, using the thermal rig shown in Fig. 2, on aluminium specimens of known physical and thermal properties and same geometries as the chocolate samples. The experiments were used to validate the experimental setup and calibrate the boundary conditions at the interface of the tested sample and the aluminium block and the boundary conditions at the insulated surfaces which are required for the numerical model of section 2.3.1.
Standard differential scanning calorimetry (DSC) experiments were conducted on all three types of chocolate (DSC Q2000, TA Instruments, USA) as follows. All tests were performed at a temperature range between 12 °C and 45 °C at two linear rates of 1 °C min−1 (the lowest possible rate for the instrument) and 10 °C min−1. Each test was performed twice for each type of chocolate. These tests were also performed for cocoa butter to provide initial indications on the specific heat capacity of the material that forms the chocolate matrix. Helium was selected as a purge gas for the calorimetric chamber. The heat flow rate data obtained from the DSC tests were then converted into specific heat capacity measurements using eqn (1):
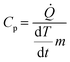 | (1) |
![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) is the heat flow rate into the chocolate measured by the DSC, m is the mass of the DSC test sample, and
is the heat flow rate into the chocolate measured by the DSC, m is the mass of the DSC test sample, and 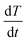 is the applied heating rate.
is the applied heating rate.
The DSC instrument measures the heat flow rate ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) for a given temperature and produces a
for a given temperature and produces a ![[Q with combining dot above]](https://www.rsc.org/images/entities/i_char_0051_0307.gif) – temperature graph, which in turn, can be converted into a Cp – temperature curve using eqn (1). The area underneath a Cp – temperature curve, at the part of the curve where the phase occurs (discontinuity in the curve), represents the latent heat of the chocolate. The latent heat values ΔH were measured using the TA Universal Analysis software (TA Instruments, USA).
– temperature graph, which in turn, can be converted into a Cp – temperature curve using eqn (1). The area underneath a Cp – temperature curve, at the part of the curve where the phase occurs (discontinuity in the curve), represents the latent heat of the chocolate. The latent heat values ΔH were measured using the TA Universal Analysis software (TA Instruments, USA).
2.3. Numerical methods
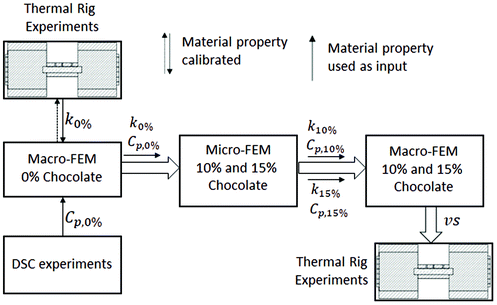
In this section, the methodology of the numerical steady-state and unsteady heat transfer models at the microscale (micro-FEM) and the unsteady heat transfer model at the macroscale (macro-FEM) will be presented. The calculation of the effective material properties, such as specific heat capacity, thermal conductivity, density and thermal diffusivity, in relation to porosity will be presented using micromechanical modelling (micro-FEM). These material properties will then be used as input parameters for a macro-FEM to simulate the experimental conditions of the two porous chocolate samples. The sequence of the numerical studies is summarised in Fig. 3 and used as follows; the macro-FEM model was initially introduced for non-aerated chocolate to calibrate the thermal conductivity based on the temperature-time data extracted from thermal rig experiments. The micro-FEM models were then followed to calculate the thermal properties as a function of porosity using the thermal properties of the solid chocolate. Finally, the macro-FEM model was re-employed, but this time for the micro-aerated chocolates. The results from the macro-FEM for all chocolate materials were compared against the experimental data from the thermal rig. In all numerical models, the commercially available software Abaqus37 and the Standard/Implicit Abaqus solver was used.An implicit transient uncoupled heat transfer step was selected in Abaqus to simulate the experimental conditions with the thermal test rig. The transient step in Abaqus follows the backward Euler method and does not exhibit any stability issues (e.g. mesh density or time increment) for problems when conduction is dominant.37 The time step was selected to be less than 1% of the relevant time scale observed during the heat transfer experiments. Therefore, a maximum time step of 1 s was selected for the macro-FEM model. The analysis was complete when a modelled time of 4000 s was reached, same as the overall time from the heat transfer experiments.
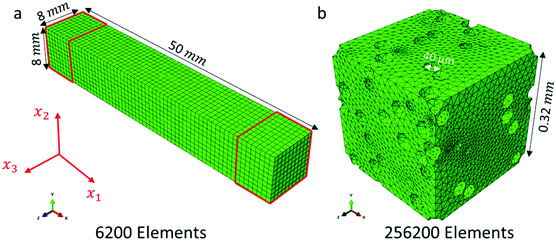
In Fig. 4a, the highlighted volume with red colour at both ends of the specimen indicates the volume in contact with the aluminium block, and, therefore, represents the volume of elements where the temperature boundary conditions were applied. The boundary conditions of the macro-FEM at the highlighted regions (Fig. 4a) together with ones at the insulated surfaces, which are required for the macro-FEM model, were calibrated based on the preliminary experiments, using the thermal rig of Fig. 2, on aluminium specimens. The need for these preliminary experiments was an unexpected mismatch between the applied temperature from the Peltier module and the target temperature of the grooves due to heat losses and thermal contact resistance at the contact surfaces between aluminium block and the tested sample. These preliminary experiments were employed for the four scenaria of Table 1. Using the unsteady heat transfer macro-FEM model described earlier but this time on the aluminium specimens with known material properties, the heat transfer coefficients at the boundary conditions at the aluminium block-sample interface, hp, and at the insulated surfaces, hins, were evaluated. The same boundary conditions hp and hins as evaluated from the preliminary tests on aluminium specimens were used for the non-aerated chocolate and two micro-aerated chocolates and shown in section 3.2.
Finally, the definition of the material properties of chocolates were required for the macro-FEM model. In the case of the non-aerated chocolate, the Cp and ΔH values were obtained from the DSC experiments described in section 2.2. The density of the non-aerated chocolate was calculated from the weight for a known volume. However, the thermal conductivity could not be extracted directly either from the thermal rig or the DSC experiments. Therefore, a starting value of 0.3 W m−1 K−1 for the thermal conductivity both at solid and liquid state was selected, which was within the range from commonly reported values in the literature (0.16 W m−1 K−1–10.7 W m−1 K−1).13,14,17 The thermal conductivity values at solid and liquid states were then adjusted using the macro-FEM model to match the experimental data. In a similar way to the DSC experiments, the thermal properties, such as thermal conductivity and specific heat capacity, were grouped to those for the solid state (temperatures lower than 28 °C) and liquid state (temperatures higher than 34 °C). During phase change of chocolate (temperatures between 28 °C and 34 °C), the process was driven by latent heat ΔH. In the case of the two micro-aerated products, the Cp and ΔH values were also computed from the DSC experiments and the density value was evaluated in the same way as the non-aerated chocolate. The effective thermal properties such as the thermal conductivity and the specific heat capacity were obtained from the micro-FEM.
A minimum volumetric size or representative volume element (RVE) with 30 pores is needed to achieve representative thermal results when periodic boundary conditions are used.38,39 The number of pores inside the RVE needs to be increased at least to 60 pores to ensure that the calculated effective thermal properties remain unaffected by the type of boundary conditions employed.40,41 Dirichlet boundary conditions (constant surface temperature) were used in the current work. Therefore, three different 3D RVEs with different pore arrangement were created with 100 pores dispersed within the structure to enable the estimation of representative values of the thermal conductivity and the specific heat capacity.
For an RVE with 10% porosity, an average number of 256![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 4-node linear heat transfer brick elements (DC3D4) was used for the heat transfer analysis at the microscale, as shown in Fig. 4b. In this case, the RVE had a length of approximately 0.32 mm. Due to the small pore diameters (i.e. 40 μm) present in the chocolate, the dominant mode of heat transfer is expected to be pure conduction, whilst convection and radiation can be neglected42–44 because closed pores smaller than 10 mm lead to a relatively small Rayleigh number (<1000), which suggests convection has only a minor effect. More specifically, the possibility of significant convection effects to be present within a pore is expressed in terms of the Rayleigh number, which is a function of the Prandtl and Grashof numbers, and gives details regarding the flow characteristics within the pore. A critical value of the Rayleigh number close to 1000 indicates that convection effects within the pore cannot be neglected. Based on Clyne et al.,43 for a spherical pore, this critical value is reached for a pore size of 10 mm, which is much larger than the sizes investigated in the current work (i.e. 10 s of microns). Based on the same studies, for temperature differences below 1000 °C, radiation can also be neglected. The thermal properties of the chocolate were selected to be the same as the unsteady macro-FEM.
200 4-node linear heat transfer brick elements (DC3D4) was used for the heat transfer analysis at the microscale, as shown in Fig. 4b. In this case, the RVE had a length of approximately 0.32 mm. Due to the small pore diameters (i.e. 40 μm) present in the chocolate, the dominant mode of heat transfer is expected to be pure conduction, whilst convection and radiation can be neglected42–44 because closed pores smaller than 10 mm lead to a relatively small Rayleigh number (<1000), which suggests convection has only a minor effect. More specifically, the possibility of significant convection effects to be present within a pore is expressed in terms of the Rayleigh number, which is a function of the Prandtl and Grashof numbers, and gives details regarding the flow characteristics within the pore. A critical value of the Rayleigh number close to 1000 indicates that convection effects within the pore cannot be neglected. Based on Clyne et al.,43 for a spherical pore, this critical value is reached for a pore size of 10 mm, which is much larger than the sizes investigated in the current work (i.e. 10 s of microns). Based on the same studies, for temperature differences below 1000 °C, radiation can also be neglected. The thermal properties of the chocolate were selected to be the same as the unsteady macro-FEM.
An implicit uncoupled steady-state and unsteady state heat transfer step was selected for the micro-FEM models to compute the keff and Cpeff respectively. A maximum time step of 0.01 s was selected for the unsteady micro-FEM model, which corresponded to 1% of the relevant time scale of the heat transfer within the RVE. The unsteady micro-FEM is simulated until a steady state solution is reached, which means that the temperature gradient is less than 10−5 °C s−1. Both models used the same RVE geometries, whilst the only differences were the actual step used in Abaqus and the applied boundary conditions at the surfaces. In addition, a mesh sensitivity analysis was performed both for the steady-state and unsteady steps to ensure representative results regardless of the mesh density of the model. Mesh independent results are achieved for mesh densities higher than 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 elements. However, in some RVEs, the mesh density was further increased to represent better the geometry of the pores within the RVE.
000 elements. However, in some RVEs, the mesh density was further increased to represent better the geometry of the pores within the RVE.
The relationship between heat flux and temperature is described by Fourier's law for steady-state heat conduction, see eqn (2):
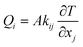 | (2) |
As boundary conditions, an arbitrary temperature difference ΔT of 10 °C between the bottom surface (x2 = 0) and top surface (x2 = 0.32 mm) was applied, whilst the other surfaces were thermally insulated 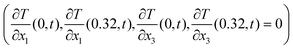 . The actual value of the input ΔT does not impact the resultant effective properties.
. The actual value of the input ΔT does not impact the resultant effective properties.
Under these boundary conditions and the assumption of an isotropic material (k11 = k22 = k33 = k, and kij = 0 when i ≠ j), the effective thermal conductivity of porous chocolate is given by the following relationship:
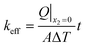 | (3) |
The two unknowns in eqn (3) are keff and Q|x2=0, which can be evaluated from the micro-FEM.
For the unsteady heat transfer analysis, the heat conduction equation is given by eqn (4):
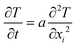 | (4) |
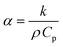 | (5) |
The unsteady heat transfer model was simulated similarly to a calorimetry experiment in order to measure the effective specific heat capacity of the RVE. Specifically, a pulse of heat with a total value of 0.5 mJ was applied at the bottom surface of the RVE along y-axis (Q|x2=0 = 0.5 mJ) for a duration of 1 s, subsequently the thermal load was removed and the surface was considered as thermally insulated. The other RVE surfaces were also thermally insulated.
The unsteady heat conduction equation of eqn (4) for a uniaxial heat transfer without heat losses, uniform temperature distribution within the material and boundary conditions described above can be simplified to eqn (6):
| Q|x2=0 = ρeffVCpΔT | (6) |
| ρeff = fρg + (1 − f)ρm | (7) |
Using the values of keff and Cpeff computed from the steady state and the transient (unsteady) micro-FEM, and the value of ρeff from eqn (7), the thermal diffusivity αeff of all chocolate materials can be determined through:
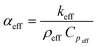 | (8) |
This thermal diffusivity can be plotted against porosity to determine the “speed of heat transfer” within the chocolate materials. This property is important to understand the material's heat transfer response.
The predicted values of keff and Cpeff from the micro-FEM and the ρeff from eqn (7) for 10% and 15% porosity will be used as input parameters into the unsteady heat transfer model at macroscale (macro-FEM) and will be compared with the temperature profiles of the micro-aerated chocolate of 10% and 15% porosity respectively for all four scenaria in Table 1.
2.4. Analytical methods
In this section, the analytical models for the effective thermal conductivity and specific heat capacity that are commonly used in the literature for foods and general porous materials are described. The porous chocolate studied in the current work is composed of two phases, the continuous chocolate matrix and the dispersed spherical N2 pores.Wiener bounds are the simplest models for isotropic materials when conduction is the dominant heat transfer mechanism.30,31,45,46 The models represent the case that the porous material is a mixture of horizontal (series model, SM) or vertical layers (parallel model, PM) of the two phases. The weighted average of the conductivities of the two phases in each case corresponds to the effective thermal conductivity of the mixture, as shown below for eqn (9) (PM) and eqn (10) (SM):
| keff = fkg + (1 − f)km | (9) |
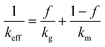 | (10) |
Similarly, the Hashin–Shtrikman bounds or commonly known as Maxwell–Eucken models also apply to isotropic materials and provide predictions for porous materials with porosity levels lower than 0.25.30,31,45 In contrast to the Wiener bounds, these models assume that the pores are spherical. The bounds of these models refer to the case where the pores are in a dispersed phase, MEM-1, (eqn (11)) or in a continuous phase, MEM-2, (eqn (12)). Eqn (11) is relevant to this study, where the N2 pores are dispersed in the chocolate matrix.
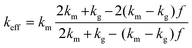 | (11) |
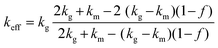 | (12) |
In the case of the effective medium theory model, EMT, (eqn (13)) both the pores and the matrix are mutually randomly dispersed implying a random distribution of both phases.31 reported that for closed-pore materials, such as the chocolate studied here, the thermal conductivity of the porous material should be between the predictions of MEM-1 and EMT.
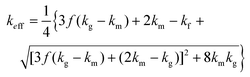 | (13) |
In comparison to the significant number of analytical models predicting the effective thermal conductivity, analytical models for the specific heat capacity are limited to the rule of mixtures, RoM, approximation.27,47,48 It is unclear, according to author's knowledge, why there are no other available analytical models for Cp,eff in the literature, whilst for keff there are plethora of analytical and semi-empirical models. One possible explanation could lie in the fact that most of the processes investigated for composites/porous materials in the literature regard heat transfer at steady state, hence the effects of specific heat capacity become irrelevant. The RoM assumes that the energy required to raise the temperature of a unit mass of the porous material corresponds to the weighted summation of the required energies from the two phases, as shown in eqn (14):
| Cpeff = wgCpg+ (1 − wg)Cpm | (14) |
The predictions from the analytical models for effective thermal conductivity and effective specific heat capacity will be compared against the results from the micro-FEM.
3. Results
3.1. Experimental results
The experimental results from the thermal rig, described in section 2.2, are summarised in Fig. 5. In this figure the temporal evolution of the thermocouple readings T1, T2, and T3 respectively are shown for the scenaria 1 (Fig. 5a), 2 (Fig. 5b), 3 (Fig. 5c), and 4 (Fig. 5d). The coloured scatter points represent the temperature response of the non-aerated chocolate (black) and the micro-aerated chocolate at 10% (red) and 15% (blue) porosity, respectively. The error bars in Fig. 5a, b and d are relatively small (<0.5%), whilst those for Fig. 5c are slightly larger (<1%) highlighting the reproducibility of the measurements. A possible source of added uncertainty for the cooling scenario shown in Fig. 5c is that the Peltier elements needed to be cooled using the axial fans, which may have resulted in air disturbance around the thermal rig.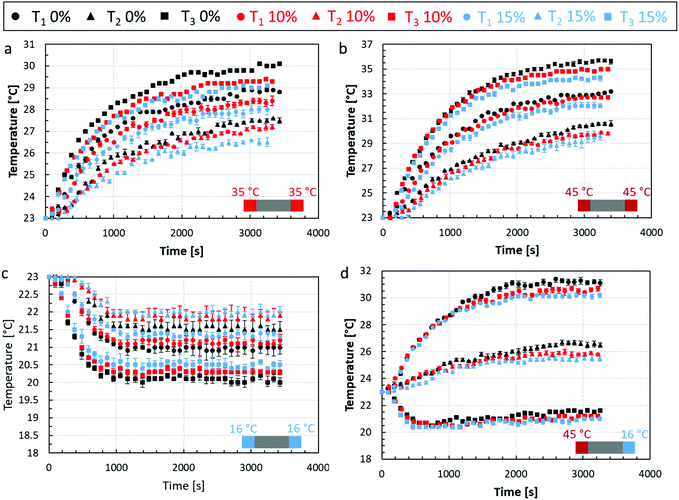 | ||
| Fig. 5 Temporal temperature evolution curves from heat transfer experiments for three chocolate types at three measurements locations (T1, T2, and T3) for: (a) scenario 1; (b) scenario 2; (c) scenario 3; (d) scenario 4 of Table 1. The schematic at the bottom right-hand corner for each graph shows the boundary conditions applied to the test section for each scenario. | ||
For all four scenaria, the micro-aerated chocolate showed an overall slower heat propagation than the non-aerated chocolate, except for the region corresponding to the first ∼1000 seconds, when all chocolate exhibited a similar response. The initial transient period before steady state behaviour can be assumed, is affected by both the thermal conductivity of the material and the specific heat capacity. Therefore, no conclusive arguments can be used at this region regarding the heat propagation between the three types of materials. However, when steady state is assumed in each scenario (because of the different applied thermal boundary condition scenaria 1, 2, and 4 equilibrate approximately after 3000 seconds and in scenario 3 after 1200 seconds), the heat transfer response is governed mainly by the thermal conductivity of the material. In addition, this is the region, where the maximum difference in the heat transfer behaviour is observed amongst the three chocolate products. This means that there is a difference between the values of thermal conductivity for each type of chocolate. This observation suggests that the dispersed micro-pores in the chocolate suspension may affect heat propagation. This argument will be also evaluated by the micro-FEM presented in the same section.
Based on Fig. 5a, the maximum temperature difference between the curves of the non-aerated chocolate and the 10% micro-aerated chocolate is 2.7% and is recorded by the thermocouple T2 at the centre of the sample. This difference increases to 4.3% when the non-aerated chocolate is compared to the 15% micro-aeration. For scenario 2, when the sample was heated to 45 °C the same comparison, i.e. 0% vs. 10% chocolate and 0% vs. 15% chocolate, leads to a maximum difference of 4.8% and 6.7% respectively. Similarly, for scenario 3, a maximum difference of 1.9% and 2.4% is observed when the non-aerated chocolate is compared to the micro-aerated chocolate samples of 10% and 15% porosity respectively. For the cooling scenario, Fig. 5c, all chocolate samples reach the steady state faster than in the other scenaria. This is attributed to the fact that the applied temperature i.e. 16 °C, is outside the phase change range (see Fig. 6), between 28 °C and 34 °C, of the chocolate and therefore no energy is used to melt the fat crystals.
Finally, Fig. 5d shows that when cooling one side and heating the other side, the temperature responses at the three locations T1, T2, ad T3 for the three types of chocolates, have a maximum difference of 0.8%, and 1.4% when the non-aerated chocolate is compared to the micro-aerated chocolates of 10% and 15% porosity respectively. After about 1000 s, the temperature from thermocouple T3, which is placed closer to the cooling side of the setup, starts to increase. This was consistent amongst all chocolate samples and was argued to be caused by the higher heat fluxes developed from the heated side, which eventually propagated to location T3 and increased the temperature. The temperature rise is due to an increased heat flux as the temperature difference between the ambient (23 °C) and the applied temperature at each side of the setup is larger between the heated (45 °C) rather than the cooled (16 °C) side. The maximum errors for all cases are summarised in Table 2.
| Scenario | ΔT [0% vs. 10%] | ΔT [0% vs. 5%] |
|---|---|---|
| 1 | 2.7% | 4.3% |
| 2 | 4.3% | 6.7% |
| 3 | 1.9% | 2.4% |
| 4 | 0.8% | 1.4% |
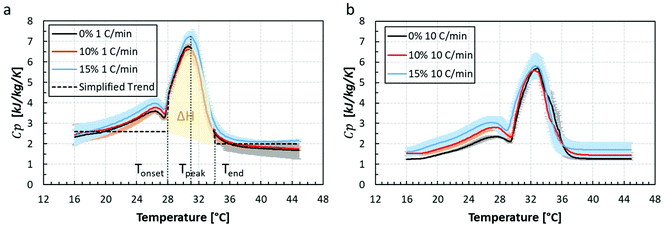
The specific heat capacity, Cp, extracted from the DSC experiments for all chocolate samples under two constant heating rates of 1 °C min−1 (Fig. 6a) and 10 °C min−1 (Fig. 6b) are summarised in Fig. 6. The black curves represent the Cp values of the non-aerated chocolate and the red and blue lines the Cp values of the micro-aerated chocolate of 10% and 15% porosity respectively. Comparing the Cp data for the two heating rates, a decrease in the Cp values with heating rate is observed for all chocolate samples. In addition, a decrease in the melting peak with the rate of heating is shown in Fig. 6, which is consistent with reports from the literature.13,14 However, no explanation is provided in these studies to the shift and decrease in Cp values with increasing heating rate. However, this dependency of the Cp data with the rate of heating has been reported for other composite polymers, such as PET, PTT, and PBT.49–51 Based on Elleithy et al. and Dhandapani, Nayak, and Mohanty, there is an association between crystallisation behaviour of the plastic nanocomposites and the heating rate, as shown by DSC measurements. A higher applied rate of heat transfer impacts the flexibility and the mobility of the polymeric chain of the material and by extend a shorter diffusing time is expected across the chain of molecules. This in turn would cause a faster crystallisation or melting. Similar for chocolates, the restricted mobility of the cocoa fat molecules might cause such shifting in the Cp data as well. The DSC data from the slower rate of heat transfer was eventually used for the models since this was more representative of the heat transfer rate found when both, the chocolate is orally processed as well as tested in the thermal experiments performed.
Based on Fig. 6a, the phase change for all chocolate types occurs between 28 °C (Tonset) and 34 °C (Tend) and the peak of the curves corresponds to a temperature of 31 °C (Tpeak. The phase change in the graph of Fig. 6b lies between 30 °C and 36 °C with a peak at 33 °C. Based on literature,13,14 the melting points of all crystal forms lie between 18 °C and 36 °C, thus it can be assumed that the chocolate is solid at temperatures lower than 18 °C and fully melted at temperatures higher than 36 °C. Based on this statement, the Cp values can be considered constant outside the 18 °C–36 °C range for both heating rates. This is found to be true for both figure for temperatures higher than Tend whilst a decreasing trend of Cp is observed at temperatures below 20 °C. In the data of Fig. 6, a local maximum peak is observed at temperatures between 24 °C and 28 °C implying the presence of fat crystals of other crystallisation form than V form. In this work the effect of different crystal forms of cocoa fat was not considered and the specific heat capacity value which corresponds to 18 °C is notated as Cpsolid and the value of specific heat capacity at 36 °C as Cpliquid. Therefore, a simplified Cp curve is created as shown by the dashed line in Fig. 6a. The melting parameters such as Cp and melting temperature for both cases are summarised in Tables 3 and 4.
| Sample | T onset, °C | T peak, °C | T end, °C | ΔH, kJ kg−1 | C psolid, kJ kg−1 K−1 | C pliquid, kJ kg−1 K−1 |
|---|---|---|---|---|---|---|
| 0% | | | | | | | 15 | 2.6 ± 0.1 | 2.0 ± 0.3 |
| 10% | 28 | 31 | 34 | 14 | 2.7 ± 0.2 | 2.1 ± 0.1 |
| 15% | | | | | | | 14 | 2.8 ± 0.3 | 2.3 ± 0.1 |
| Sample | T onset, °C | T peak, °C | T end, °C | ΔH, kJ kg−1 | C psolid, kJ kg−1 K−1 | C pliquid, kJ kg−1 K−1 |
|---|---|---|---|---|---|---|
| 0% | | | | | | | 16 | 1.5 ± 0.0 | 1.3 ± 0.1 |
| 10% | 30 | 33 | 36 | 14 | 1.7 ± 0.1 | 1.5 ± 0.1 |
| 15% | | | | | | | 15 | 2.0 ± 0.3 | 1.7 ± 0.4 |
Based on the Tables 3 and 4, the latent heat ΔH remains almost unaffected of porosity whilst the values of Cpsolid and Cpliquid slightly increased. Clearer increasing trends of specific heat capacity with porosity are observed when chocolate is at liquid state. This is true for both heating rates. This will be further discussed in the following section. Despite the significant rate dependent behaviour of specific heat capacity observed for all types of chocolates, the heating rate of interest, according to thermal rig experiments was found to be the slowest one, i.e. 1 °C min−1.
3.2. Numerical and analytical model results
This section is structured as follows; the boundary conditions of the macro-FEM model, which were calibrated by the thermal experiments on aluminium specimens of known materials properties are initially presented. Then, the calibrated thermal conductivity of non-aerated chocolate, using the macro-FEM model, is shown followed by the presentation of the effective thermal properties from the micro-FEM model and the analytical models, which are described in section 2.4. The comparison of the experimental data of all chocolate samples against the macro-FEM data is shown in the end of the section followed by the discussion of the importance of modelling the melting behaviour of chocolate.The calibrated boundary conditions from the macro-FEM model and the thermal rig experiments on aluminium specimens corresponded to a heat transfer coefficient of hp = 70 W m−2 K−1 at the interface inside the groove between the investigated sample and the aluminium block. This coefficient was found to be independent of loading scenario, i.e. 1, 2, 3 or 4. On the other hand, the heat transfer coefficient at the insulated surfaces was hins = 4 W m−2 K−1 for scenaria 1, 2, and 4 and hins = 8 W m−2 K−1 for scenario 3. The discrepancy in hins between scenaria 1, 2, and 4, and scenario 3 was attributed to the use of the double axial fans on both sides of the setup of scenario 3, which caused increased airflow disturbances around the thermal rig and increased the heat losses from the test samples to the ambient. When the double axial fans were also used for scenaria, 1, 2, and 4, the same value of hins = 8 W m−2 K−1 was found. The temperature values for aluminium block – chocolate interface regions were 35 °C, 45 °C, 16 °C depending on the loading scenario as shown in Table 1, whilst the temperature at the insulated sides was the same as the ambient temperature (23 °C). The same boundary conditions were also used for the macro-FEM model on chocolates.
The thermal properties of non-aerated chocolate, such as the thermal conductivity, which was calibrated from the macro-FEM model and the thermal rig experiments, the specific heat capacity and latent heat measured from the DSC tests are summarised in Table 5. The thermal conductivity of non-aerated chocolate was found to be 0.45 W m−1 K−1 and 0.55 W m−1 K−1 at the solid and liquid state respectively. These values are relatively within the range reported in the literature.13,14,20 In addition, the measured density of the non-aerated chocolate was found to be the same as the one reported in the literature.13
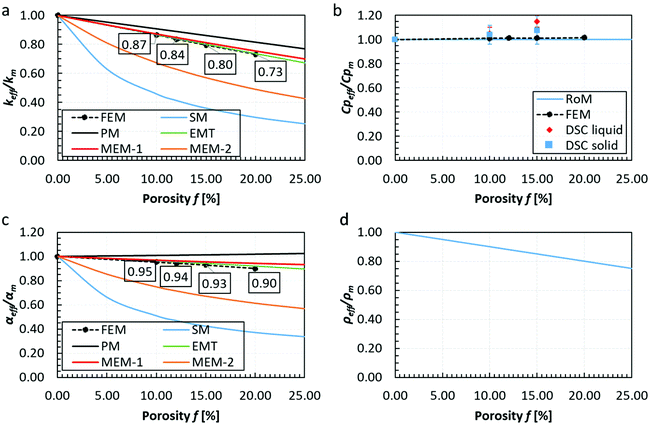
The results from the micromechanical FEM (micro-FEM) model of section 2.3 predicting the effective thermal properties, keff and Cpeff, together with the predictions from the analytical models as a function of porosity f, as described in section 2.4, are presented in Fig. 7. Each of the four plots of Fig. 7 will be discussed individually below.
In Fig. 7a, the normalised effective thermal conductivity keff is shown against porosity as predicted by the micro-FEM steady state and the analytical models. It is evident that the analytical models, such as the EMT and MEM-1, agree with the prediction from the FE-model. This finding is also in agreement with the literature for closed pore materials31 acting as independent validation of the micro-FEM presented in this study. Based on Fig. 7a, decreasing trends of the thermal conductivity are observed with porosity. Specifically, a decrease in thermal conductivity of the chocolate by 14% and 21% is observed for porosities 10% and 15% respectively.
These results agree with the experimental observations of section 3.1. It is evident, as discussed in section 3.1 and the reported temperature differences amongst all types of chocolate at stead-state that micro-pores act as thermal barriers to the heat flow leading to a decrease in the values of the thermal conductivity with increasing porosity. These findings are also in agreement with reports in the literature for other porous materials. Specifically, Smith et al.,44 Tavman,45 and Skibinski et al.46 reported decreasing trends with increasing porosity in materials, such as porous ceramics, granular materials, and porous copper. Similar reports were made by Carson et al.31 on porous foods, such as granular starch, milk powder, gels and cakes.
In Fig. 7b, the predictions of the specific heat capacity of chocolate against porosity are shown from the RoM analytical model and the micro-FEM. The results are in good agreement, suggesting that the specific heat capacity remains approximately the same at the investigated porosity range, i.e. less than 20% porosity. Specifically, the FE-model predicts a difference of 1% and 1.5% when the specific heat capacity of the non-aerated chocolate is compared to the specific heat capacity of the micro-aerated chocolate samples of 10% and 15% porosity respectively. Similar results have been reported for other porous materials.49 Based on these studies, weaker decreasing trends with increasing porosity were observed in the specific heat capacity values compared to the thermal conductivity for concrete and aluminium alloys.
The Cp data from the DSC experiments at a constant heating rate of 1 °C min−1, see Table 1, were also compared to the micro-FEM predictions of Fig. 7b. The comparison between the numerical model and the DSC experiments was limited to the slowest heating rate, because this rate was relevant to the heat transfer experiments of section 3.1, i.e. maximum heating rate of 0.7 °C min−1. Comparing the Cp data of the 10% and 15% micro-aerated chocolates obtained from the DSC experiments, see Table 3, to the predicted Cp values from the numerical models a significant difference is observed. This is caused by the fact that the DSC tests show a slight increase of the Cp, whilst for the numerical and the analytical models the specific heat capacity remains unaffected by porosity (an increase of 1% was estimated). Specifically, an increase of 4% and 5% in the values of Cp is observed between the non-aerated chocolate and the micro-aerated chocolate of 10% porosity at the solid and liquid state respectively, see Table 3. Similarly, for the micro-aerated chocolate of 15% porosity, a small increase in the average value of the specific heat capacity at the regions where the chocolate is solid (7%) and liquid (13%) is shown, see Table 3. It seems that there is an increasing trend of Cp with increasing porosity, which is unexpected for porous materials. Both the analytical models and the micro-FEM in this case do not show the same trends (micro-FEM only suggests a maximum of 1.5% increase).
One possible explanation of the increase of the specific heat capacity with increasing porosity from the DSC tests could potentially be a mechanism that causes an unexpected temperature change at the chocolate matrix and the pore interface that has not been captured by the simulation. This could for example be in the form of interfacial resistance between the pore and chocolate matrix or due to the presence of a third phase within the chocolate itself. In our previous work,8 a third “unknown” phase is reported at the interface of the chocolate matrix and the pore as evidenced by X-ray tomography images on micro-aerated chocolate of 15% porosity, which could be responsible for changes in the bulk thermal properties, such as the specific heat capacity observed by the DSC measurements.
The thermal diffusivity aeff of chocolate calculated from eqn (8) using different expressions for the effective thermal conductivity (see eqn (9)–(13)) and the RoM for the specific heat capacity (eqn (14)) are plotted against porosity in Fig. 7c. Based on the same graph, the EMT predicts most accurately the values of aeff amongst all other models based on the micro-FEM predictions. Based on Fig. 7c, the thermal diffusivity decreases with increasing porosity implying that a slower heat propagation is experienced in the case of the micro-aerated chocolate samples, when the samples are either heated or cooled. Specifically, based on the results of Fig. 7c, an average decrease of 5% in thermal diffusivity for the 10% micro-aerated chocolate and 7% decrease for the 15% micro-aerated chocolate are estimated. Similar findings were reported for concrete48 and porous aluminium alloys 56. The mass density values against porosity using eqn (7) are shown in Fig. 7d. Based on this figure, a linear decrease of the mass density of the micro-aerated chocolate with increasing porosity is estimated, as expected for porous materials.
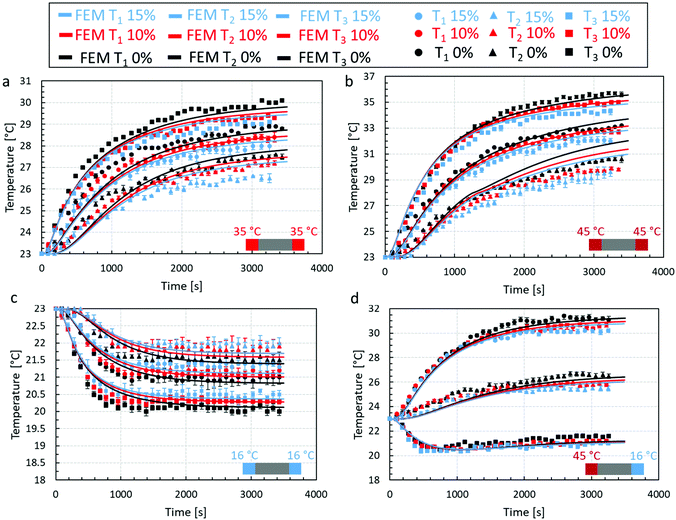
The temperature profiles recorded by the thermocouples at locations T1, T2, and T3 for all four scenaria and all types of chocolate are shown in Fig. 8, together with the predictions of the macro-FEM using the effective thermal properties presented in Fig. 7 from the micro-FEM. Overall, a reasonable agreement between the results from the macro-FEM model and the experimental results is observed for all types of chocolate and all four scenaria. The macro-FEM predicts accurately both the shape of the temperature recordings from the three thermocouples considering the melting behaviour of the chocolate but also the temperature of all chocolate materials during the unsteady and steady state regime. A slight overestimation of the temperature profiles in the case of the two micro-aerated chocolates was observed, which was attributed to microstructural findings reported in the literature8 at the pore-chocolate interface, as mentioned earlier in the section. As evidenced by Bikos et al.,8 there are unknown microscopic features at the chocolate-pore interface, which create a shell around the insulating gas pore. Assuming these regions are mainly or solely cocoa butter concentrated around the pore, the material at the pore interface is capable to store thermal energy due to the higher specific heat capacity of the cocoa butter compared to chocolate, as shown in Table 5, which could thereafter explain the increase in heat capacity of the material and eventual slower heat penetration observed for the aerated vs. non aerated samples. The possible presence of a cocoa butter shell around the otherwise low thermal capacity and thermal conductivity gas pore could promote heat storage within the shell. This could also result to significant discrepancies, which should not be neglected, close to the interface and in turn affect significantly the effective thermal properties and, by extent, the thermal processes for porous chocolates (such as the cooling time during manufacturing or melting time during oral processing). This hypothesis requires further investigation both, in terms of understanding the origin and nature of the material concentrated around the pore and its impact on the effective thermal properties of chocolates.
However, recent studies have shown that TAG polymorphs of high melting point, which are the same as the ones found in cocoa butter, are formed on the surface of a bubble creating a crystal coating54 around the bubble when crystallised. These studies have been performed on various edible oils, such as vegetable and rapeseed oil. In addition, similar evidence has been reported in whisked cocoa butter, where laminar shaped fat crystals are formed on the surface of the bubble.55 It is argued that it might be oriented parallel to the oil-fat interface to reduce the surface energy in that region.
Based on the results of Fig. 8a, the macro-FEM predicts reasonably accurate the temperature profiles at T1, T2, and T3 for all chocolate materials as evidenced by the thermal experiments. In the case of the non-aerated chocolate, a slight underestimation in temperature values is observed at location T3 with a maximum difference less than 2%, while at locations T1 and T3 slightly higher maximum differences are depicted of 3.6% and 4%. Similar trends are observed for the non-aerated and the micro-aerated chocolates of 10% and 15% porosity.
The temporal evolution of the temperature for scenario 2 (fast heating) at locations T1, T2, and T3 for all chocolate samples is shown in Fig. 8b. The maximum differences between the experimental readings and the numerical predictions increase to a maximum of 4.6%, 3.7%, and 4.8% for the non-aerated and micro-aerated chocolates of 10% and 15% porosity respectively.
For scenario 3, where the temperature profile is outside the melting range of the chocolate (see Fig. 8c), higher accuracy predictions are presented for all chocolate products. Specifically, a maximum difference of less than 2.5% is indicated in the case of the non-aerated chocolate, whilst a maximum 1.8% and 1.4% difference between the experimental and macro-FEM results are observed for the micro-aerated cases. Since no phase change occurs, the steady state is reached relatively fast after approximately 2000 seconds.
Although scenario 4 (see Fig. 8d), where the chocolate sample was heated from one side and cooled from the other, produced a more complex temperature profile across the samples, the macro-FEM estimates the temperature evolution for all three locations relatively accurate. In fact, the macro-FEM captured the increasing trends of the experimental data at location T3. Finally, the maximum differences between experiments and computations are within 3.6%, 2.4% and 3.3% for non-aerated chocolate and micro-aerated chocolate samples of 10% and 15% porosity respectively.
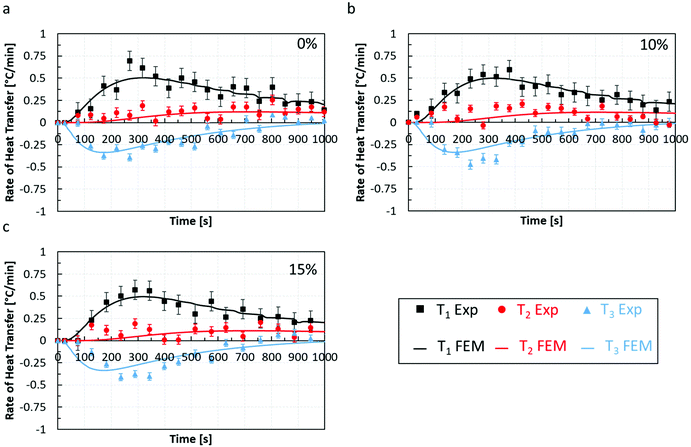
To assess the quality of the model predictions, a comparison between the rate of heat transfer, 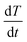 , measured from the heat transfer experiments using the thermal rig and the macro-FEM for all chocolate samples for scenario 4 is performed, as shown in Fig. 9. The
, measured from the heat transfer experiments using the thermal rig and the macro-FEM for all chocolate samples for scenario 4 is performed, as shown in Fig. 9. The 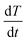 data obtained from the thermocouple measurements were averaged across twenty points, i.e. every 50 s, to minimise any random error from the thermocouple measurements and are shown Fig. 9 for all three materials. Based on the data of Fig. 9, a relatively good agreement between experiments and computations is observed, especially in predicting the shapes of the curves for all cases. Most changes occur in the first 1000 seconds and then both the experimental and numerical results approached zero rates. The largest uncertainties in the heat transfer rate were found at the early stages of the experiment (t = 250 s), as indicated in Fig. 9, mainly due to the temperature measurement uncertainty. This uncertainty is caused by the limited temperature resolution of the thermocouple measurements.
data obtained from the thermocouple measurements were averaged across twenty points, i.e. every 50 s, to minimise any random error from the thermocouple measurements and are shown Fig. 9 for all three materials. Based on the data of Fig. 9, a relatively good agreement between experiments and computations is observed, especially in predicting the shapes of the curves for all cases. Most changes occur in the first 1000 seconds and then both the experimental and numerical results approached zero rates. The largest uncertainties in the heat transfer rate were found at the early stages of the experiment (t = 250 s), as indicated in Fig. 9, mainly due to the temperature measurement uncertainty. This uncertainty is caused by the limited temperature resolution of the thermocouple measurements.
So far, the micro-FEM, experiments and analytical models have shown that micro-aeration significantly affects the thermal conductivity. It is believed that the role of micro-pores is to act as barriers to heat transfer, as evidenced by the decrease of thermal conductivity with increasing porosity. The predictions from the micro-FEM and the EMT analytical model suggest a weak or no dependency of the specific heat capacity on the porosity. However, the both the thermal rig and the DSC experiments implied increasing trends of specific heat capacity with increasing porosity, which is unexpected for porous materials.47,53 This may be explained by the presence of a third phase or a thermal mechanism, which increases the averaged specific heat capacity of the micro-porous chocolate. This mechanism cannot be solely explained by the presence of N2 in the pores due to the relatively low specific heat capacity and significantly lower density of N2 which means that the pores are not capable to store substantial energy. However, the presence of a cocoa butter shell around the pores could be responsible for such effects. Cocoa butter stores a higher amount of energy, as evidenced by its Cp (see Table 5), whilst recent studies54,55 have shown concentration of fat crystals on the interface of the chocolate matrix and the pore.
All these phenomena will play a determinant role in oral food processing. According to literature,12,15,18 the melting behaviour of chocolate affects a plethora of sensory properties, such as melting time, moistness, grittiness and overall flavour intensity. Melting is an important step of chocolate's oral processing transforming the continuous fat system into an oil–water suspension in presence of saliva, which in turn is linked with taste and flavour perception. It has been reported that melting is one of the main mechanisms which drives masticatory parameters such as the required number of chews and the chewing time.12 Our recent work has highlighted the need for coupling the mastication step with the thermal behaviour of chocolate in order to draw conclusive arguments regarding the chocolate's breakdown during oral processing.35 It is believed these processes together guide the chocolate's transition from solid to liquid phase and perhaps the final properties of the bolus. Understanding the effect of micro-aeration on the melting behaviour of chocolate will assist the design of food products with optimum sensorial properties.35
This work has presented a novel, and relatively inexpensive, experimental procedure, which can be used to accurately assess the effects of microscale structural changes in materials, such as low levels of porosity, to the macroscopic heat transfer behaviour of the material. The advantage of this setup over commercially available instruments is the ability of the method to accurately record the temperature response of complex materials under small temperature differences, something which is not possible in most commercial instruments that usually operate at higher temperature ranges.
A multiscale finite element model is proposed, which is calibrated using results obtained on the thermal rig. Effective material properties were validated using analytical models from literature and compared to the heat transfer measurements. The specific heat capacity values were also compared to DSC experiments. Combined, the experimental setup and the new multiscale model could provide a powerful tool to investigate the effects of material microstructure on the thermal properties of foods and optimise their thermal behaviour for various applications. One potential application is to use this model to optimise the temporal evolution of the melting behaviour of chocolate, porous or otherwise, and, for example, modify sweetness perception, while reducing sugar content, as required when developing foods with improved health characteristics.35 Future work will include the extension of the multiscale model to consider the presence of a third phase at the pore's interface between the chocolate matrix and the gas pore. The current suggestion that the third phase is in fact cocoa butter will be evaluated. The developed multiscale model can be expanded, in the future, to study the heat transfer response of porous chocolates at higher porosity levels than 15% and pore sizes higher than 40 μm.
4. Conclusions
Heat transfer experiments were performed on chocolate specimens with varying levels of porosity, using four different thermal loading scenaria. These experiments were accompanied by a multiscale Finite Element Model (FEM) to estimate the thermal response of chocolate. The main findings are summarised below:1. Micro-FEM steady-state predictions of the effective thermal conductivity of chocolate overlap with analytical models, such as Maxwell Eucken and effective medium theory.
2. The increasing trends of specific heat capacity with increasing porosity, as measured by DSC tests for porous materials, are opposed to the analytical and micro-FEM unsteady predictions. This observation suggests that a novel mechanism exists in the porous microstructure, which is able to store thermal energy. A concentration of material (as previously shown from XRT images8) at the pore's interface exists exhibiting higher specific heat capacity than chocolate. This material is believed to be cocoa butter, which exhibits approximately 1.3 times higher specific heat capacity than the non-aerated chocolate.
3. The developed multiscale model predictions are in good agreement (within 5%) with the measurements from the newly developed heat transfer experimental rig.
4. Compared to the non-aerated chocolate, the measurements showed that a 15% micro-aeration leads to an average reduction of 21% in thermal conductivity and increase of 21% in specific heat capacity. This results to a maximum 7% reduction in the rate of heat transfer.
This work assessed a method to quantify the change in melting behaviour of different types of chocolate with varying porosity, which in turn, can be used to design food structures with controlled sensorial attributes such as melting time, grittiness, flavour intensity, and sweetness.
Nomenclature
Abbreviations
| DPDT | Double pole double throw |
| DSC | Differential scanning calorimetry |
| EMT | Effective medium theory |
| FEM | Finite element model |
| HWM | Hot wire method |
| LFM | Laser flash method |
| macro-FEM | Macromechanical/macroscale finite element model |
| MEM | Maxwell Eucken model |
| micro-FEM | Micromechanical/microscale finite element model |
| PID | Proportional integral derivative |
| PM | Parallel model |
| RoM | Rule of mixtures |
| RVE | Representative volume element |
| SM | Series model |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Engineering and Physical Sciences Research Council (EPSRC) for the PhD studentship via the Centre for Doctoral Training – Theory and Simulation of Materials (CDT-TSM) and Nestlé PTC York for funding the project and providing the materials for testing. The authors would like also to acknowledge Ms Patricia Carry for technical guidance during the DSC experiments.Notes and references
- E. V. Gonçalves and S. C. da Silva Lannes, Cienc. Tecnol. Aliment., 2010, 30, 845–851 CrossRef.
- G. Mongia and G. R. Ziegler, Int. J. Food Prop., 2000, 137–147 CrossRef CAS.
- E. O. Afoakwa, A. Paterson, M. Fowler and J. Vieira, Int. J. Food Sci. Technol., 2009, 44, 111–119 CrossRef CAS.
- G. Samaras, D. Bikos, J. Vieira, Y. Hartmann, C. Charalambides, M. Hardalupas, M. Masen, P. Cann, C. Hartmann, M. Charalambides, Y. Hardalupas, M. Masen and P. Cann, Curr. Res. Food Sci., 2020, 3, 304–313 CrossRef PubMed.
- V. Glicerina, F. Balestra, M. Dalla Rosa and S. Romani, J. Food Eng., 2016, 169, 165–171 CrossRef.
- M. Owusu, M. A. Petersen and H. Heimdal, J. Food Sci. Technol., 2013, 50, 909–917 CrossRef CAS PubMed.
- T. A. L. Do, J. M. Hargreaves, B. Wolf, J. Hort and J. R. Mitchell, J. Food Sci., 2007, 72, 541–552 CrossRef PubMed.
- D. Bikos, G. Samaras, P. Cann, M. Masen, Y. Hardalupas, C. Hartmann, J. Vieira and M. Charalambides, Food Funct., 2021, 12, 4864–4886 RSC.
- E. L. Keijbets, J. Chen and J. Vieira, J. Food Eng., 2010, 98, 133–140 CrossRef.
- B. J. D. Le Révérend, I. Smart, P. J. Fryer and S. Bakalis, Chem. Eng. Sci., 2011, 66, 1077–1086 CrossRef.
- E. O. Afoakwa, A. Paterson, M. Fowler and J. Vieira, J. Food Eng., 2008, 89, 128–136 CrossRef.
- A. M. Carvalho-da-silva, I. van Damme, W. Taylor and B. Wolf, R. Soc. Chem., 2013, 4, 461–469 CAS.
- B. J. D. Le Reverend, P. J. Fryer and S. Bakalis, Soft Matter, 2008, 4, 1147–1150 RSC.
- H. Tewkesbury, A. G. F. Stapley and P. J. Fryer, Chem. Eng. Sci., 2000, 55, 3123–3132 CrossRef CAS.
- J. Haedelt, S. T. Beckett and K. Niranjan, J. Food Sci., 2007, 72, 138–142 CrossRef PubMed.
- L. Grob, K. Papadea, P. Braun and E. J. Windhab, Innovative Food Sci. Emerging Technol., 2021, 68 DOI:10.1016/j.ifset.2021.102629.
- F. Debaste, Y. Kegelaers, S. Liégeois, H. Ben Amor and V. Halloin, J. Food Eng., 2008, 88, 568–575 CrossRef.
- G. R. Ziegler, G. Mongia and R. Hollender, Int. J. Food Prop., 2001, 4, 353–370 CrossRef.
- A. M. Carvalho-da-silva, I. van Damme, B. Wolf and J. Hort, Physiol. Behav., 2011, 104, 929–933 CrossRef CAS PubMed.
- J. Engmann and M. R. Mackley, Food Bioprod. Process., 2006, 84, 102–108 CrossRef.
- E. O. Afoakwa, A. Paterson, M. Fowler and J. Vieira, Food Res. Int., 2008, 41, 751–757 CrossRef CAS.
- N. M. Coutinho, M. R. Silveira, T. C. Pimentel, M. Q. Freitas, J. Moraes, L. M. Fernandes, M. C. Silva, R. S. L. Raices, C. S. Ranadheera, F. O. Borges, R. P. C. Neto, M. I. B. Tavares, F. A. N. Fernandes, F. Nazzaro, S. Rodrigues and A. G. Cruz, LWT – Food Sci. Technol., 2019, 102, 324–329 CrossRef CAS.
- M. J. Smith, J. Chem. Educ., 2016, 93, 898–902 CrossRef CAS.
- M. Sarfarazi and M. Mohebbi, J. Food Meas. Charact., 2020, 14, 1568–1581 CrossRef.
- Y. Dadmohammadi and A. K. Datta, Food Rev. Int., 2020, 1–33 CrossRef.
- Z. G. Welsh, M. I. H. Khan and M. A. Karim, J. Food Eng., 2021, 292 DOI:10.1016/j.jfoodeng.2020.110252.
- L. Hou, X. Zhou and S. Wang, Int. J. Heat Mass Transfer, 2020, 154, 119704 CrossRef.
- F. Selimefendigil, S. Ö. Çoban and H. F. Öztop, Int. J. Therm. Sci., 2021, 162 DOI:10.1016/j.ijthermalsci.2020.106788.
- M. S. Rahman, M. M. Rashid and M. A. Hussain, Food Bioprod. Process., 2012, 90, 333–340 CrossRef.
- J. Wang, J. K. Carson, M. F. North and D. J. Cleland, Int. J. Heat Mass Transfer, 2006, 49, 3075–3083 CrossRef.
- J. K. Carson, S. J. Lovatt, D. J. Tanner and A. C. Cleland, J. Food Eng., 2006, 75, 297–307 CrossRef.
- Q. T. Ho, J. Carmeliet, A. K. Datta, T. Defraeye, M. A. Delele, E. Herremans, L. Opara, H. Ramon, E. Tijskens, R. van der Sman, P. van Liedekerke, P. Verboven and B. M. Nicolaï, J. Food Eng., 2013, 114, 279–291 CrossRef.
- R. G. M. van der Sman, Meat Sci., 2013, 95, 940–957 CrossRef CAS PubMed.
- S. Ahmad, G. V. Marson, W. Zeb, W. U. Rehman, M. Younas, S. Farrukh and M. Rezakazemi, Sep. Purif. Technol., 2020, 250 DOI:10.1016/j.seppur.2020.117209.
- D. Bikos, G. Samaras, P. Cann, M. Masen, Y. Hardalupas, M. N. Charalambides, C. Hartmann, J. German and J. Vieira, Food Struct., 2021, 31, 100244 CrossRef.
- S. T. Beckett, L. Info, M. Records and R. S. C. Read, Science of Chocolate, 2nd edn, 2008, pp. 240 Search PubMed.
- Simulia, Providence, DS SIMULIA Corp, RI, USA, 2017 Search PubMed.
- Y. Xu and K. Yagi, Comput. Mater. Sci., 2004, 30, 242–250 CrossRef.
- B. Mortazavi, M. Baniassadi, J. Bardon and S. Ahzi, Composites, Part B, 2013, 45, 1117–1125 CrossRef CAS.
- A. el Moumen, T. Kanit, A. Imad and H. el Minor, Comput. Mater. Sci., 2015, 97, 148–158 CrossRef.
- V. I. Kushch and A. G. Knyazeva, Acta Mech., 2016, 227, 113–126 CrossRef.
- S. Kang, J. Y. Choi and S. Choi, Polymers, 2019, 11(2) DOI:10.3390/polym11020221.
- T. W. Clyne, I. O. Golosnoy, J. C. Tan and A. E. Markaki, Philos. Trans. R. Soc., A, 2006, 364, 125–146 CrossRef CAS PubMed.
- D. S. Smith, A. Alzina, J. Bourret, B. Nait-Ali, F. Pennec, N. Tessier-Doyen, K. Otsu, H. Matsubara, P. Elser and U. T. Gonzenbach, J. Mater. Res., 2013, 28, 2260–2272 CrossRef CAS.
- I. H. Tavman, Int. Commun. Heat Mass Transfer, 1996, 23, 169–176 CrossRef CAS.
- J. Skibinski, K. Cwieka, S. H. Ibrahim and T. Wejrzanowski, Materials, 2019, 12(12) DOI:10.3390/ma12122017.
- Y. Zhao, J. Jiang, Y. Dai, L. Zhou and F. Ni, Appl. Sci., 2020, 10(5) DOI:10.3390/app10051671.
- H. G. Noh, J. H. Lee, H. C. Kang and H. S. Park, Nucl. Eng. Technol., 2017, 49, 459–465 CrossRef.
- R. H. Elleithy, M. E. Ali Mohsin, I. Ali and S. Al-Zahrani, in Annual Technical Conference - ANTEC, Conference Proceedings, 2012, vol. 3.
- Z. Yang, H. Peng, W. Wang and T. Liu, J. Appl. Polym. Sci., 2010, 116, 2658–2667 CAS.
- S. Dhandapani, S. K. Nayak and S. Mohanty, Polym. Sci., Ser. A, 2015, 57, 628–634 CrossRef CAS.
- P. Ottosem and G. Mannov, Thermal and mechanical properties of nitrogen, 1980 Search PubMed.
- A. M. Ramírez, F. J. E. Beltrán, J. M. Yáñez-Limón, Y. v. Vorobiev, J. González-Hernández and J. M. Hallen, J. Mater. Res., 1999, 14, 3901–3906 CrossRef.
- S. Mishima, A. Suzuki, K. Sato and S. Ueno, J. Am. Oil Chem. Soc., 2016, 93, 1453–1466 CrossRef CAS.
- B. P. Binks and I. Marinopoulos, Food Res. Int., 2017, 95, 28–37 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |