Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular behavior of fluid gels – the crucial role of edges and particle surface in macroscopic properties†
Marta
Ghebremedhin
 *a,
Sebastian
Seiffert
*a,
Sebastian
Seiffert
 b and
Thomas A.
Vilgis
b and
Thomas A.
Vilgis
 *a
*a
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: ghebre@mpip-mainz.mpg.de; vilgis@mpip-mainz.mpg.de
bDepartment of Chemistry, Johannes Gutenberg University Mainz, Duesbergweg 10–14, 55128 Mainz, Germany
First published on 16th May 2022
Abstract
Fluid gels exhibit unique properties during oral processing and thus are well known in gastronomy as well as for use in dysphagia patients. Agarose fluid gels, which are produced by gelation under shear, in particular, show elastic solid-like behavior at rest but a fluid-like behavior once critical stress is exceeded. In a previous study this special behavior is addressed to the “hairy” structure of the microgel particles – dangling gel parts and chains on the particle surface – which plays a crucial role in the rheological, mechanical and tribological properties of the gels. In this paper, atomic force microscopy (AFM) was used to investigate the underlying microscopic structures and develop a consistent physical model, which relates the irregular particle structures and their heterogonous shape to the experimental observation of the previous studies. One crucial point is the inner structure of the gel particles, which show a dense area in the center, whereas towards the periphery the network and thus the elastic properties change. Agarose gels by forming helices and meshes, which defines the basic length scale for their elastic response in bulk. These properties in turn depend on the concentration and preparation conditions. The present study is meant to address the still prevalent lack of understanding regarding a direct structure–property relationship of these novel fluid gels. Controlling the properties of such fluid gels may play a crucial role in the texture modification of foods and beverages for dysphagia.
1 Introduction
Biopolymers, such as thickening and gelling agents, are often used in various foods and personal care products to optimize and control their texture, oral processing properties, and flavor release. Some of these biopolymers can be used to produce fluid gels, which are particulate gel suspensions. These gels are produced by applying a shear field to a biopolymer solution during gelation.1–3 The irregularly shaped, elastic gel particles are immersed in the continuous water phase and exhibit novel flow properties, which result in unusual textural properties and an improved mouthfeel. Fluid gels show the properties of a shape-retaining elastic material, but exhibit liquid-like flow behavior when subjected to sufficient stress.3 Modifying the formulation of biopolymer-based products and creating a controlled microstructure enables a broader range of applications in food systems.1 In addition, fluid gels have also been extensively investigated in the pharmaceutical field for various pharmaceutical applications such as controlled drug delivery and drug release.4,5 The different shapes and sizes of the gel particles show distinct elasticity and lubrication properties, and thus impact the mouthfeel during consumption: during oral processing and swallowing, they are easily squeezed between the tongue and the palate, forcing the gel particles to mechanically interact with each other as well as with the oral surfaces.6 Furthermore, there is growing interest in fluid gels made from polysaccharides with unique physico–chemical properties such as agarose, which is spurring research into such novel edible soft matter systems to understand their basic properties and functions. Detailed knowledge of the rheological, mechanical and tribological behavior of such materials is necessary for understanding the process development and product formulation, especially in view of developing dysphagia food systems.7 To support these findings and investigate the underlying network structure, atomic force microscopy measurements were carried out in this study.Agarose, the main gelling agent of agar-agar extracted from red algae (Rhodophyceae), is a linear polymer composed of a (1–3)-linked agarobiose unit of β-D-galactopyranose (1–4)-linked to 3,6-anhydro-α-L-galactopyranose.8 Agarose solution undergoes a sol–gel transition very quickly on cooling due to its fast gelation kinetics, and forms a three-dimensional network due to its molecular structure and physicochemical properties.9 Beyond that, the transition from the coil to the helix of agarose polymer chains that occurs during cooling can be described by a mean field Zimm–Bragg approach.10–12 Furthermore, agarose gels tend to release water and are prone to syneresis. This effect increases with a decrease in concentration and has been studied and discussed in detail on quiescently cooled physical aqueous gels.13,14 This tendency to release water affects the texture properties and thus has an influence on the mouthfeel.9,15 Finally, due to the aggregation of double helices, agarose forms firm and slightly brittle gels when cooled under quiescent conditions, resulting in a poor mouthfeel. This behavior can be altered by manipulating the processing conditions, e.g. by applying different shear rates, concentration changes, or the use of biopolymers with different inherent molecular properties.
During gelation, as biopolymers are subjected to shear, a competing mechanism takes place between gelation by means of physical cross-linking via hydrogen bonds and their breaking by the induced shear force.16 Moreover, during gelation under shear, the resulting disordered network structure of the gel particles is subjected to the competition of two time scales: the shear rates on the one hand and the molecular dynamics of the polymer chains as expressed by the Rouse–Zimm model on the other hand both play a role in the growing cluster size inside of the forming gel particle.17 Since the cooling rate first affects the center of mass of the individual polymers and then that of the cluster, the dynamics of the cluster slows down with an increase in size, which also changes its shape.7 Thus, the order rate of the polymer is crucial for particle growth. In fact, the key requirement for a fundamental understanding of such fluid gels is the knowledge of particle growth of the network structure underlying the gelation mechanism of biopolymers under shear.
In one of the earliest studies on agarose fluid gels, confocal microscopy was used to reveal that fluid gels consist of highly concentrated, irregularly shaped gel particles suspended in a continuous water phase.3 These findings were supported by phase contrast micrographs, showing “hairy” particle structures.18,19 However, there are no publications yet on systematic investigations of the network structure at the molecular level of such fluid gels.
Moreover, particle size and particle volume fraction were found to depend on shear rate, temperature and concentration and determine the properties of the fluid gel.3,16 In earlier studies on agarose fluid gels, texture analysis was conducted on gels prepared under quiescent conditions and the obtained behavior was assumed to be that of individual gel particles of the fluid gels of the same concentration.6 In addition, the rheological properties of quiescently cooled agar gels have been compared with those of agar gels prepared under shear.2
Despite numerous studies on fluid gels, the exact gelation mechanism that occurs under shear and the resulting viscoelastic, textural and lubrication behavior is not yet understood on a molecular basis. Therefore, this study focuses on the characterization of fluid gels by establishing systematic fundamental relationships between the microstructure and bulk properties, in order to support the mechanical, tribological and textural properties based on the AFM findings. These investigations were motivated by gaining a deeper understanding of the concentration-dependent characteristics of agarose fluid gels, which in our previous work were found to be influenced by the size and shape of the gel particles.7 In addition, these findings were assisted by comparing the viscoelastic properties of gels prepared under quiescent conditions with those of fluid gels using rheology.
2 Materials and methods
2.1 Materials
The agarose [CAS: 9012-36-6] used in this work was purchased as a white powder with a number-average molar mass Mn of ≈74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 557.8 g mol−1, weight-average molar mass Mw of ≈213
557.8 g mol−1, weight-average molar mass Mw of ≈213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 949 g mol−1 and polydispersity index of 2.87 (Fig. S4†) from Fisher Scientific GmbH (Schwerte, Germany). According to the manufacturer, the gelling temperature is specified between 34 and 45 °C and the substance reaches a gel strength of >100 g cm−2. Furthermore, a sulfate content of 0.15% max was given.
949 g mol−1 and polydispersity index of 2.87 (Fig. S4†) from Fisher Scientific GmbH (Schwerte, Germany). According to the manufacturer, the gelling temperature is specified between 34 and 45 °C and the substance reaches a gel strength of >100 g cm−2. Furthermore, a sulfate content of 0.15% max was given.
2.2 Sample preparation
2.3 Rheological measurements
Dynamic viscoelastic measurements of different concentrations of the agarose fluid gels as well as the quiescent gels were performed on a Discovery HR-3 Rheometer (TA Instruments), by amplitude and temperature-dependent oscillatory measurements using a 40 mm diameter parallel plate with a pre-set distance of 500 μm and a solvent trap. All rheological measurements were performed in triplicate. The amplitude sweep test was performed to investigate and compare the viscoelastic properties of the gels prepared under shear with those of the gels prepared under quiescent conditions. Using this method, oscillatory deformation was applied and storage (G′) and loss (G′′) moduli were measured to describe the deformation behavior of the gel samples in the non-destructive range, which is defined as the linear-viscoelastic (LVE) range. All amplitude sweeps were carried out at a constant frequency ƒ = 1 Hz, and storage (G′) and loss (G′′) moduli were measured as a function of strain γ ranging from 0.001% to 1000% and at a temperature of 25 °C.2.4 Atomic force microscopy (AFM)
Atomic force microscopy measurements were conducted to examine the agarose polymer network structure at the periphery and the dangling chains formed by the aggregation of double-helical agarose molecules at the particle surface. This was done to gain insight into the effect of the microstructure of the gel particles on their texture and lubricating properties. The imaging was performed in tapping mode in air at ambient temperature using a Bruker Dimension Icon AFM with ScanAsyst. Standard tapping mode cantilevers VTESPA from Bruker with a resonance frequency of ƒ = 300 Hz, a spring constant of 42 N m−1 and a back side coating of reflective aluminum were used. All images were scanned at a resolution of 512 × 512 pixels and a scan rate of 0.698 Hz. For the topographical imaging, agarose fluid samples were diluted in Milli-Q water to a concentration of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 and pipetted onto a silicon wafer (1 cm × 1 cm) treated and cleaned with argon plasma for 10 minutes at a pressure of approximately 2 × 101 mbar (Harrick Plasma Cleaner/Sterilizer PDC-002, 200W, Harrick Scientific Corp., USA). We used silicon wafers instead of freshly cleaved mica because reflected light microscopy was performed on the same sample before AFM measurement, and silicon wafers proved to be suitable for using the same substrate for both reflected light microscopy for the preliminary investigation and subsequent AFM measurements, as suggested by Bertula et al.20 also. After carefully dropping about 3 μL of the samples onto the silicon wafer, they were allowed to dry under ambient temperature before scanning. Gwyddion,21 an open-source data analysis software for scanning probe microscopy (SPM), was used for flattening the images and for further image analysis.
100 and pipetted onto a silicon wafer (1 cm × 1 cm) treated and cleaned with argon plasma for 10 minutes at a pressure of approximately 2 × 101 mbar (Harrick Plasma Cleaner/Sterilizer PDC-002, 200W, Harrick Scientific Corp., USA). We used silicon wafers instead of freshly cleaved mica because reflected light microscopy was performed on the same sample before AFM measurement, and silicon wafers proved to be suitable for using the same substrate for both reflected light microscopy for the preliminary investigation and subsequent AFM measurements, as suggested by Bertula et al.20 also. After carefully dropping about 3 μL of the samples onto the silicon wafer, they were allowed to dry under ambient temperature before scanning. Gwyddion,21 an open-source data analysis software for scanning probe microscopy (SPM), was used for flattening the images and for further image analysis.
2.5 Scanning electron microscopy (SEM)
Scanning electron microscopy was implemented using a Leo Gemini 1530 microscope (Zeiss, Germany) with an acceleration voltage of 0.750 kV to examine the network structure of the gels cooled under quiescent conditions and of fluid gels, each at different concentrations. Gels which were stored at 4 °C for 24 h were cooled rapidly with liquid nitrogen before placing in a freeze dryer (Christ Alpha 1–2 LD plus). After drying overnight, the completely freeze-dried samples were stored at room temperature. For SEM measurements, the dried samples were not coated and were carefully placed on standard aluminum stubs (Plano GmbH, Wetzlar, Germany) attached with double sided adhesive carbon tapes (Plano) and transferred to a microscope.2.6 Statistical analysis
The experiments were performed in triplicate and reported as average values ± standard deviation (SD). The rheological data were statistically analyzed using the OriginPro 9.65 software (OriginLab Corporation, Northampton, MA, USA). One-way analysis of variance (ANOVA) was applied to determine the significant difference between gels in terms of rheological parameters and to compare the means with a significance level of p < 0.05.3 Results and discussion
3.1 AFM images of agarose fluid gels
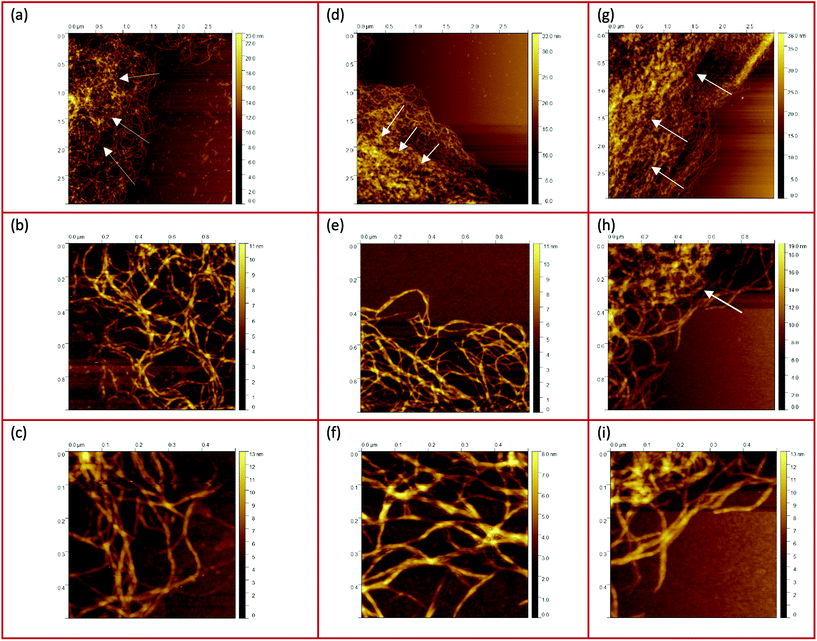
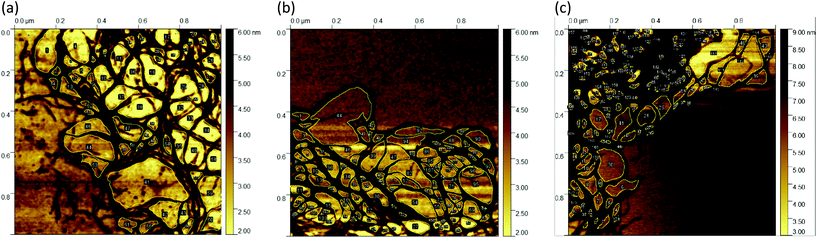
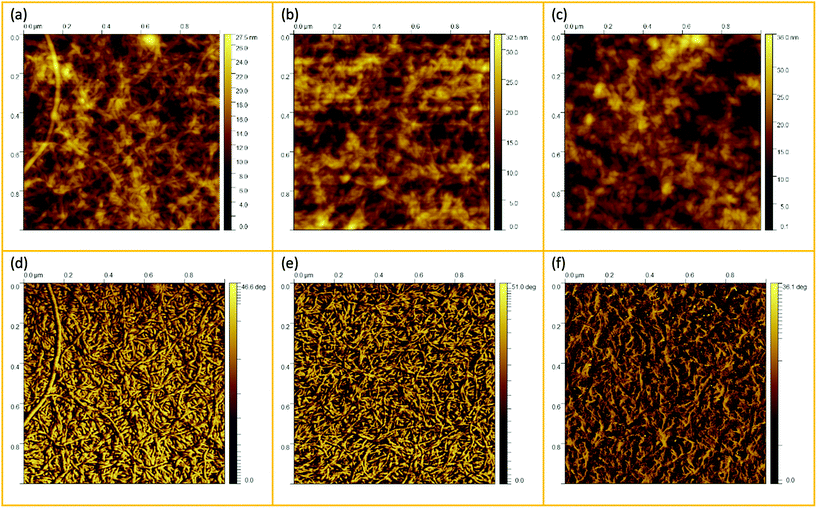
AFM scanning was performed to investigate the network structure of aggregated double-helical agarose polymer chains formed during cooling under shear. Fig. 1 illustrates a schematic experimental AFM setup in which different areas of the samples are scanned, both at the periphery and in the denser region at the center of a gel particle. As scanning was performed in tapping mode in air, the diluted fluid gels were dried beforehand on the silicon wafers as previously mentioned. This leads to the consideration that due to the adhesion of the agarose polymers on the silicon surface, the resulting network structures on the wafer seen in the AFM images are flattened from a 3D to a rather 2D + h surface after drying (where h is given by the layers of agarose bundles folded on top of each other). However, this in turn may cause the polymer molecules to become overstretched when adhering to the silicon wafer surface. Nevertheless, the typical characteristic structure formation, i.e. the association of single chains into double helices and their further aggregation, is preserved and provides a first insight into the structure of agarose molecules in fluid gels. On the other hand, it is also reported that the measurement of the height would be a more precise method to estimate the biopolymer diameters. This is because the measurement of width is considerably oversized not only due to the adhesion of the samples to the surface, leading to its overstretching but also due to the effect of probe broadening.22,23 Nevertheless, in order to correlate the microscopic and macroscopic properties, such a method allows for comparing the different three-dimensional scaffold network structures of the varied concentrations to different significant rheological, tribological and textural properties.Fig. 2 shows the AFM images of the particle gels of all three concentrations (0.5 wt%, 1 wt% and 2 wt%) taken at the center of the gel particles. At first glance, no distinct difference may be observed between the different concentrations. As mentioned in our previous publication,7 the micro-gel particles consist of a very dense region, the inner core with a dense cross-linked three-dimensional network of aggregated double helices of agarose polymer chains. This assertion can be illustrated by the height AFM images in Fig. 2(a–c). All three concentrations show very dense network structures, which are characterized by a blurred, not clearly distinguishable network due to the much higher concentration in the center, so that no aggregated conformation of the double helices can be identified and thus can only be assigned by considering the height bars. Accordingly, the maximum height is 27.5 nm for the 0.5 wt% sample, up to 32.5 nm for the 1 wt% sample, and a maximum height of 36 nm for the 2 wt% sample. On this basis, and taking into account that the width of an agarose double helix is between 1 and 2 nm,24,25 these images imply a multilayered cross-linked, stacked network of ordered agarose assemblies. Hence, the pictures show a three-dimensional network, although it turns out to be much flatter due to the drying process during sample preparation and consequently the adhesion to the silicon surface.
 | ||
| Fig. 2 AFM height (a–c) and phase (d–f) images taken from the center of the gel particles: (a and d) 0.5 wt%, (b and e) 1 wt%, and (c and f) 2 wt%. | ||
Fig. 2(d–f) shows the corresponding AFM phase micrographs, which give a better visual impression of the very densely packed agarose gel network structure. The phase mode allows the detection of single chains of multiple aggregated double helices of agarose molecules. While it is not possible to distinguish between the different concentrations of the samples using the height mode, the AFM phase images for the 0.5 wt% samples show a less densely packed network than for the 1 wt% sample. From the AFM phase image of the 0.5 wt% sample, more distinct and longer agarose strands can be seen than for the 1 wt% sample. The fact that the strands appear shorter and narrower on average in the image of the 1 wt% sample could be because the strands are so densely packed due to the higher concentration that too many strands are overlapped and thus appear shorter and narrower. Thus, for the 1 wt% sample, the length of the strands seen in total without being overlapped by other strands is shorter than for the 0.5 wt% sample, indicating that in three dimensions, before the gel dries, the mesh size is also smaller. The phase images of the network structure for the 2 wt% sample appear different and less clear, yet aggregated polymer chains can still be identified. An almost flat surface is seen here and yet it can be observed that the strands are much shorter until they are overlapped by another aggregated chain. This loss of quality in the case of Fig. 2(f) may be due to the artifacts caused by contamination of the cantilever tip with the gel samples, which in turn is due to the densely packed, highly concentrated core.
These phase micrographs of the densely cross-linked network in the particles are in agreement with the findings of not only the rheological (viscoelastic) and tribological (friction and lubrication) properties but also the textural (elasticity and plasticity) properties from previous work. It has been reported that an increase in agarose concentration leads not only to higher elasticity, as measured by texture analysis, and higher storage (G′) and loss (G′′) moduli, but also to a lower coefficient of friction in the boundary regime and to higher friction in the hydrodynamic regime of a Stribeck curve.7 This is explained by a denser cross-linked network in the particles, as a higher agarose concentration leads to a higher number of aggregated double helices, which in turn results in gel particles with more junction zones. This is substantiated by the well-known correlation between the mesh size ξ and the elastic modulus for permanently cross-linked gels, indicating the proportionality of the shear modulus G with the cube of the inverse mesh size of the gel (see eqn (1)).
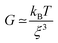 | (1) |
According to this scaling estimate eqn (1), the modulus of the gels is determined by the thermal energy kBT and the mean mesh size ξ of the network.26 Consequently, the modulus is determined by the mean distance between two adjacent cross-links (see Fig. 3).
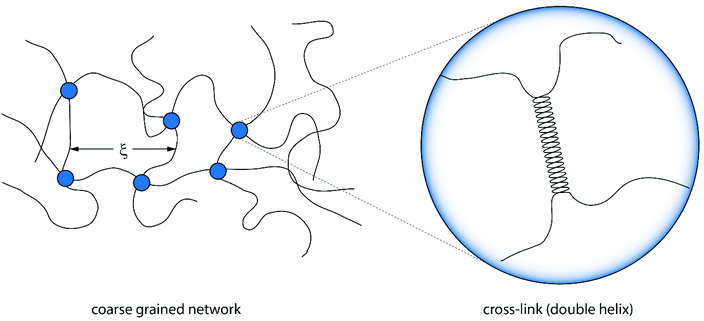 | ||
| Fig. 3 Illustration of a coarse grained version of an agarose gel connected by cross-links of polymers. The mean mesh size ξ is determined by the number of cross-links and thus the concentration.27 The cross-links themselves are formed by double helices. | ||
Despite the cross-links being formed by spatially extended double helices, a simple scaling relation can be applied to bulk agarose gels, too.28 The mesh size ξ depends strongly on the concentration and can be roughly estimated by ξ ∼ c−1/3. It is expected that these ideas lead also to a better understanding of the elasticity and dynamics of the fluid gel particles and will be proven in the next sections on experimental grounds.
Fluid gel particles consist of cross-linked cores and looser surfaces. The cross-link density of the core is expected to resemble the quiescent gel and shows a smaller mesh size ξ, whereas the outer arms and hairy parts are anticipated to show larger mesh sizes for the outer parts. These will be depending on the local concentration and, more importantly, on the competing timescales, defined by the shear rate and the molecular chain motions. Therefore the mesh size in the arms increases from the center to the periphery. It is also expected that the width of this transition region decreases with the increasing chain concentration: the higher the agarose concentration, the smaller the transition scale, and the “smoother” the surfaces, as has already been suggested by light microscopy earlier.7
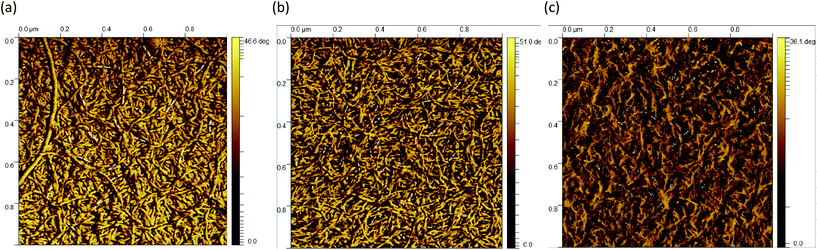
The AFM images of all three samples in Fig. 4 were taken in the region of interest at the periphery of the gel particle structure. All three fluid gel concentrations exhibit a network structure that becomes progressively less dense from the interior of the core to the exterior region of the core all the way to the periphery of the gel particle. Although it appears challenging to determine the exact mesh size, the AFM images do provide a substantial indication for the proposed specific model of the fluid gel particles and their aggregated agarose chains, referred to as the hairy structures at the periphery, along with their impact on the rheological, tribological and textural properties. When comparing the images of the different concentrations of 0.5 wt% (a), 1 wt% (d) and 2 wt% (g), it is interesting to note that the gradient of network density between the inner core and the periphery of the probed sample decreases with an increase in concentration.
Fig. 4(a) shows a loose network structure extending over a large area for the 0.5 wt% fluid gel. On the other hand, the network structure for 1 wt% shows a denser network towards the periphery in comparison to the 0.5 wt%, with a shorter distance and range until this network becomes compact towards the center. Images of the 2 wt% fluid gel sample reveal an even more densely packed network at the periphery, as already expected. When considering the physical gelation of biopolymer solution under shear, it here becomes apparent that the formation of gel particles is restricted by a competition between two processes: the aggregation of the agarose chains into increasing clusters on the one hand, and increasing hydrodynamic forces and shear forces, which increase with an increase in viscosity, on the other hand.16 Therefore, not only the shear rate but also the shear force exerted on the gelation of the polymer chains during shearing is directly related to their assembly and particle size. This leads to the fact that at a high concentration of 2 wt% in Fig. 4(g), at the edge a continuous network is no longer visible, but instead part of the network appears to be disrupted.
Furthermore, the figures with a higher magnification (b, e and h) show the trend more clearly. Again it can be seen that the network structure of the 0.5 wt% sample becomes looser towards the edge upon increasing the mesh size, while the structure of the 1 wt% sample shows a larger area with a dense three-dimensional network. Here, only a smaller area at the edge is visible where the network becomes looser but seems to be still denser than for the lower concentration. In Fig. 4(h), on the other hand, the 2 wt% sample again reveals an unevenly distributed, very dense network structure (indicated by a white arrow) surrounded by an even smaller area with a loosely formed network. Finally, the AFM images of the corresponding fluid gels in Fig. 4(c, f and i) at the highest magnification indicate that the gel particles of the different concentrations consist of single strands of presumably aggregated double helices of agarose polymers that associate to form further multiple aggregated helices upon further cooling.
For some exemplary cases, the AFM images shown in Fig. 4 are evaluated in more detail in the following section.
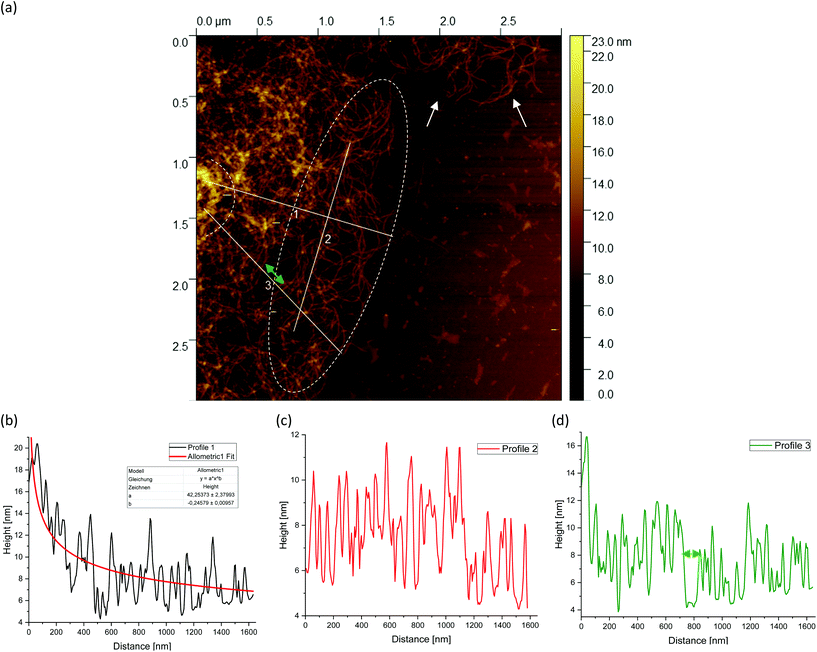
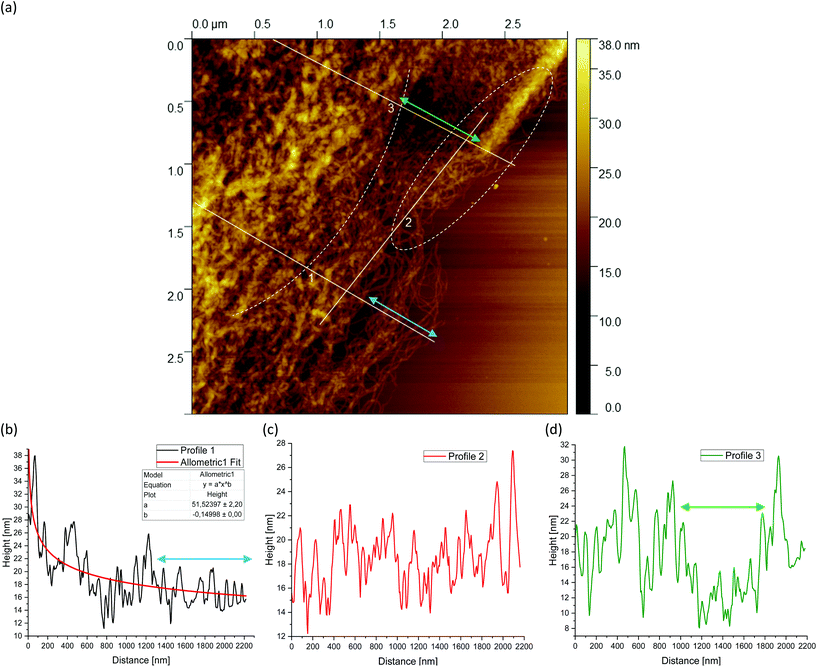
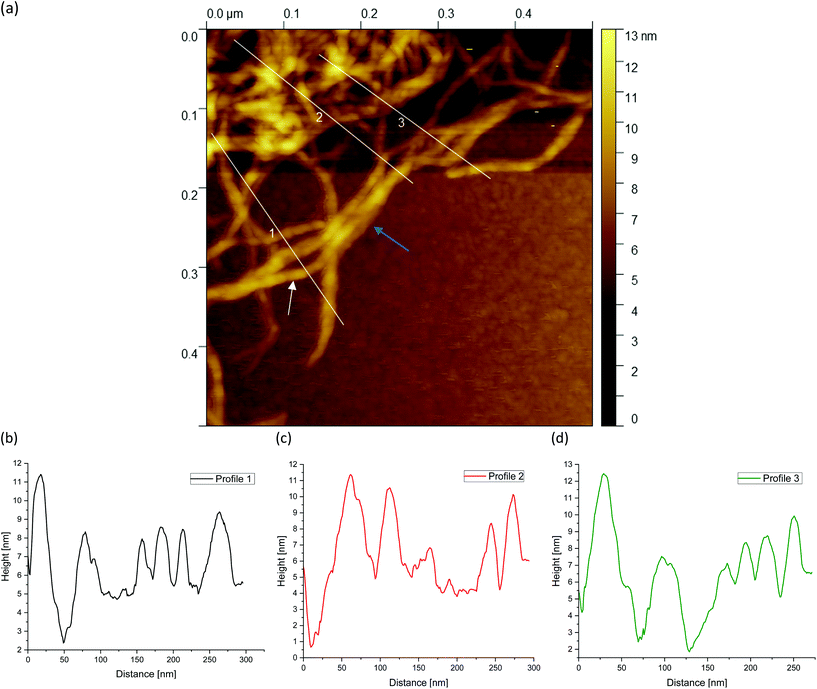
Fig. 5(a) shows a representative example of an AFM image for the 0.5 wt% sample, which is also shown in the overview AFM images in Fig. 4(a). In order to gain more insight into the structure of the gel particles, representative lines were drawn parallel and perpendicular to the surface in Fig. 5(a) and the profiles were evaluated (Fig. 5(b–d)). Furthermore, the inner core is indicated by the dashed semicircle whereas the outer core, i.e. periphery containing the dangling chains, is indicated by a dashed ellipse. In profile 1 (Fig. 5(b)), from the center to the periphery, it can be seen that the peaks representing aggregated double helices exhibit a characteristic trend. At a distance of about 60 nm, the highest peak can be taken at about 20 nm, followed by a continuous decrease in peak heights towards the outer periphery, until finally, the peaks towards the edge become smaller and more clearly distinguishable with an increase in distance, as the network becomes less dense. Furthermore, profile 1 (b) shows a fit based on a scaling estimate for a mesh size variation during gelation under shear from the core to the periphery, ξ(r) ∼ r−1/3, where r is the radial distance along line profile 1. The progression of the graph is to be expected when examining the corresponding AFM image in Fig. 5(a).
The higher value of the peaks in the interior of the gel particle can be explained by the fact that this area is denser and contains more material and an extended three-dimensional network. Furthermore, the peaks in the inner region show a larger width and become narrower towards the exterior, which can be attributed to a lower number of (aggregated) double helices. Thus, the decrease in peak heights and widths toward the outer region can eventually be attributed to a decrease in average density. The peak height in profile 2 (Fig. 5(c)) suggests an almost constant mesh size. The heights and widths of the peaks do not differ much from each other and are distributed evenly. This is due to the fact that the network is very loose due to the lower local concentrations in the outer regions of the gel particle. Profile 3 (Fig. 5(d)) shows a similar tendency to profile 1, although considerably less pronounced, with the highest peak of about 16 nm in the inner area at a distance of about 40 nm, which then declines directly. Again, the height and width of the peaks in the outer region are smaller and narrower and more clearly detectable. A typical example of a loose mesh can be seen in profile 3, which has a spacing of about 100 nm and is marked with a green double arrow both on the profile and in the AFM image in Fig. 5(a). In the radius of this region, however, more loose meshes can be seen, which also turn out to be larger. Comparing the number of peaks, it can be noted that the profile parallel to the edge has fewer peaks than the profiles perpendicular to it, which run from the inside of the core to the outside. This anisotropy results from the fact that the distances between the peaks are wider apart in the peripheral region, showing a lower density. The average distance between the peaks is about 57 nm and 59 nm for profiles 1 and 3, respectively, and 66 nm for profile 2. This suggests that the meshes are looser around the edges. The reason lies in the preparation process. As the gel particles are subjected to continuous shear during gelation, fewer agarose polymers aggregate outwards and the network becomes less dense towards the edge, resulting in wider meshes, as will be explained below. The network structure in Fig. 5(a) indicates a correlation between the core region in the AFM image and the junction zone i.e., the denser network region described in Ghebremedhin, Seiffert, and Vilgis.7 Indeed, it seems that the core region corresponds to the junction zones with its abundant bound water due to its higher water binding capacity and thus is consistent with the previous publication. Moreover, since the AFM image in Fig. 5(a) displays that the network density varies between the inner core and the periphery, it can be assumed that the mobility of the agarose chains and of the water molecules also varies. This seems to be in accordance with earlier studies on water properties in concentrated agarose gels by Watase, Nishinari, and Hatakeyama.29 In this work, these authors propose higher water binding capacity of the junction zones and that water molecules are less mobile in the junction zones, i.e. in the core region.
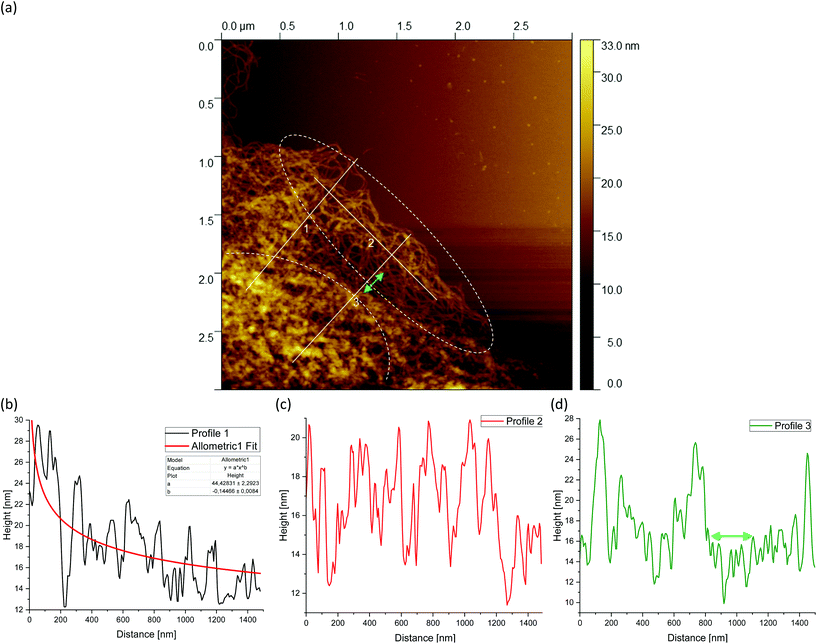
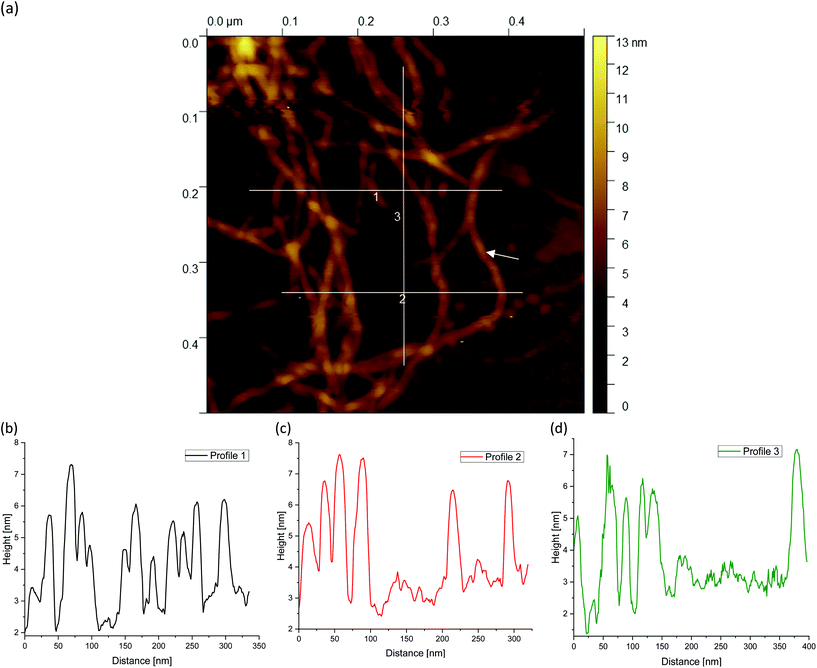
Fig. 6(a) shows an AFM image for the 1 wt% fluid gel samples shown previously in Fig. 4(d). Also in this AFM image, three white lines can be seen corresponding to the height profiles in Fig. 6(b–d). Line 2 runs parallel to the edge of the gel particle network and both lines 1 and 3 run perpendicular to it from the inner core of the network of gel particles outward to the periphery. Once again, the inner core is indicated by the dashed semicircle and the periphery regime by the dashed ellipse. For the 1 wt% sample, line 1 (Fig. 6(b)) shows a profile with a systematic decrease of the total height of the peaks. The highest peak lies at about 30 nm at a distance of about 55 nm and is higher than the highest peak value of the 0.5 wt% fluid gels in Fig. 5(b) due to the higher concentration. In addition, the trend of the peak heights shows a decreasing density distribution from the center to the outer periphery similar to profile 1 in Fig. 5(b). Similarly, the meshes and the average distance between the peaks increase outward. For line 2 (Fig. 6(c)), on the other hand, no continuous decrease in the peak height and density is observed over the entire drawn line. Looking at Fig. 6(a) and taking into account that it is a three-dimensional network structure, a thinning of the network and thus a decrease in density between the three lines and especially parallel to line 2 can be seen. By comparing the height profile of line 2 with that of line 3 (Fig. 6(d)) in the less dense network region, the latter (indicated by green double arrows) lies below that of line 2, but increases again in peak height and thus in density towards the edge. Such micro cracks are caused by the shear that takes place during gelation.
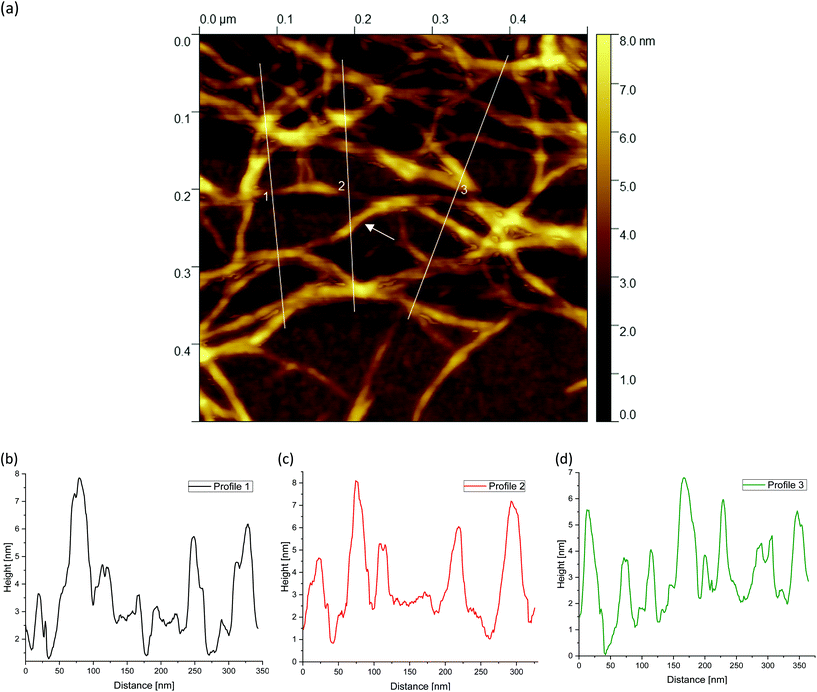
Fig. 7(a) shows the AFM images of the 2 wt% sample (as already shown in Fig. 4(g)). Again, line 2 is parallel to the edge of the gel particle network while both lines 1 and 3 are perpendicular to it starting from the inner core of the network of gel particles outwards to the periphery. Furthermore, the corresponding profiles of the diagrams are shown in Fig. 7(b–d). Profile 1 again shows a continuous decrease in peak height from the inner core of the gel network towards the periphery, with a highest peak of about 38 nm at a distance of around 68 nm, which is higher than the highest peak of the 0.5 wt% (Fig. 5(b)) and 1 wt% (Fig. 6(b)) fluid gel samples due to the higher concentration. In the area where line 3 runs, indicated by green double arrows in Fig. 7(a and d), a thinning of the three-dimensional network structure can be seen, similar to that already observed for the 1 wt% sample and interpreted as a microcrack. While the surface is smooth in the upper region at the edge, a ruptured network structure can be seen further down in Fig. 7(a), which runs parallel to the edge and is indicated by a blue double arrow. This network disruption can be explained by the fact that the gel particles tend to detach along the edge due to the high crosslinking of the 2 wt% sample under shear. It can be seen that a crack has formed and parts of the network have almost detached, although some connections to the core are still present. This area of loose network structure is similar to the network structure of the 0.5 wt% sample in Fig. 5(a).
The observed structures of the gel particles can be easily motivated by physical arguments: gel particles form when the temperature decreases below the concentration dependent critical value.7 The gelling temperature depends on the concentration. A crude two body interaction based argument suggests Tgel − T0 ∼ N(c − c0), where Tgel is the actual gelling temperature, T0 is the bulk gelling temperature, N is the degree of polymerization as before, c is the concentration, and c0 is the lowest concentration at which gelation occurs, which is obviously close to the overlap concentration, well known from the physics of polymer solution.26 Highly concentrated solutions can gel already at higher temperatures, meaning higher thermal and kinetic energy, than lower concentrated solutions. This aspect, which is trivial for gels cooled under quiscent conditions, becomes relevant for gelation under shear.
When small gel particles are formed under cooling and shear, growth can only take place at the surface. The surface shows a large number of dangling agarose chains, which can form helices with still freely dissolved chains when they come close to each other. Since the fluid is rotating with a constant shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , a time scale of τ = 1/
, a time scale of τ = 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is obtained, which competes with the time scales for gelling. Firstly, this leads to the finite particle size of the gel particles, estimated to be R ≃ (kBT/6πηsγ)1/3,16 secondly to a growing mesh size towards the periphery of the particles. Since the particles are rotating in a tumbling motion at different radii inside the rheometer tool, the local speed at the perimeter changes according to the shear rate
is obtained, which competes with the time scales for gelling. Firstly, this leads to the finite particle size of the gel particles, estimated to be R ≃ (kBT/6πηsγ)1/3,16 secondly to a growing mesh size towards the periphery of the particles. Since the particles are rotating in a tumbling motion at different radii inside the rheometer tool, the local speed at the perimeter changes according to the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The maximum local velocity v at the perimeter of a particle of size r is therefore ν(r) ∼
. The maximum local velocity v at the perimeter of a particle of size r is therefore ν(r) ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) r, which needs to be compared with the free chain (center of mass) diffusion following a Fick's law, yielding an (overestimated) scaling for the mesh size ξ(r) ∼ r−1/3, where r is the radial distance from the quiescent gel type cross-linked particle core to the periphery. Apparently, the mesh size parallel to the periphery, apart from statistical variations, does not change as observed in the AFM experiments.
r, which needs to be compared with the free chain (center of mass) diffusion following a Fick's law, yielding an (overestimated) scaling for the mesh size ξ(r) ∼ r−1/3, where r is the radial distance from the quiescent gel type cross-linked particle core to the periphery. Apparently, the mesh size parallel to the periphery, apart from statistical variations, does not change as observed in the AFM experiments.
As a result, shear has a more pronounced effect on the edge of the forming gel particle. This in turn means that gelation at the surface is hindered at this point and consequently there is an apparently lower concentration and thus a looser network structure in this area of the edge of the 2 wt% sample than in the interior of the gel particle. This loose network structure in Fig. 7(a) has a length of about 500–600 nm. Comparing this with the network structure of the 0.5 wt% sample in Fig. 5(a), this corresponds to a length of about 1500 nm and thus an extension of the loose network structure by a factor of 3.
This observation can be understood by considering again the competing time scales and molecular motions for concentrations larger than the overlap concentration. Thus, depending on the chain length, the molecules in these highly viscous solutions become increasingly entangled with higher concentrations. Consequently, the chain dynamics becomes slower.17 When chains move faster than the shear imposed time 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , they are able to form gels, comparable to the quiescent case. In concentrated polymer solutions the self-diffusion constant Ds of the polymer chains follows a reptation like motion, Ds ∼ kBT/(ζN2), where ζ is the monomer friction coefficient and N is the degree of polymerisation. The longest relaxation time scale is τR ∼ N3 and is much larger compared to 1/
, they are able to form gels, comparable to the quiescent case. In concentrated polymer solutions the self-diffusion constant Ds of the polymer chains follows a reptation like motion, Ds ∼ kBT/(ζN2), where ζ is the monomer friction coefficient and N is the degree of polymerisation. The longest relaxation time scale is τR ∼ N3 and is much larger compared to 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . In conclusion the core is densely cross-linked and reaches closer to the periphery of the particles for high agarose concentrations, but the particles remain smaller. They appear also much smoother compared to the surface particles generated at lower concentrations.
. In conclusion the core is densely cross-linked and reaches closer to the periphery of the particles for high agarose concentrations, but the particles remain smaller. They appear also much smoother compared to the surface particles generated at lower concentrations.
The fitting results deserve some attention. As mentioned already before, the power law (r) ∼ r−b, where b = 1/3 overestimates the decay of the cross-link density towards the periphery of the particles. The AFM results show clearly concentration dependent power laws, as shown in Table 1.
| c (wt%) | 0.5 | 1 | 2 |
|---|---|---|---|
| b | 0.25 | 0.14 | 0.15 |
These results suggest that the exponent b saturates with an increase in concentration, in other words with a higher overlap between the chains during the gelation process. Following the arguments of de Gennes26 the exponent b = 1/8, which is closer to the results for concentrations far below the overlap conditions. This assumes, however, that all pairs of the neighboring chains within a distance of ξ form cross-linking helices, which is questionable for gelation under steady state shear conditions.
Upon further comparison of the AFM images obtained for different concentrations, Fig. 5(a) shows loose dangling bundles or chain ends in the upper region marked with white arrows. This results from the fact that at the shear rate, due to the low concentration of 0.5 wt%, the chains cannot completely gel into a coherent network compared to the higher concentrations. These dangling ends do not appear to the same extent at the other concentrations. At the higher concentrations of 1 wt% (Fig. 6(a)) and 2 wt% (Fig. 7(a)) in the upper region parallel to the extended line 2, it can be seen that the agarose chains recede towards the core due to the high concentration and cross-linking at the periphery. It can be assumed that in the already disrupted network structure of the 2 wt% sample the agarose chains do not have much chance to cross-link further, because they do not find a second chain to form helices at appropriate time scales compared to 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
In Fig. 8, for concentrations of 0.5 wt% ((a), cf. Fig. 4(b)), 1 wt% ((b), cf. Fig. 4(e)), and 2 wt% ((c), cf. Fig. 4(h)) representative AFM images with higher magnifications are used to determine the mesh size. The mesh sizes of the different fluid gel concentrations were measured manually by evaluating the area using ImageJ. Here an attempt was made to choose closed meshes, as these mainly contribute to the elasticity. To determine the mesh size, the diameter was calculated from the area and assumed to be the distance length of the mesh.
The average mesh sizes for the respective fluid gel concentrations are given in Table 2, and it was found that the mesh sizes increase with a decrease in concentration as expected. However, as suggested in Fig. 8 the mesh sizes vary significantly and become larger towards the outer region of the fluid gel particles. The large variety of mesh sizes is therefore reflected in a large standard deviation. As mentioned in eqn (1), the modulus is mainly determined by the mesh size. By inserting the estimated mesh sizes into this equation, a theoretical modulus can be obtained in a highly simplified approximation, which is shown in Table 2. For comparison, the measured storage moduli at a strain of γ = 0.01% (LVE range) are given in Table 2. Comparing both the measured and estimated elastic moduli, it can be seen that the order of magnitude within the concentration is close. Indeed, the 2 wt%/1 wt% ratio for the elastic modulus is about 4.03 for the theoretically estimated value and 2.49 for the measured value, whereas the 1 wt%/0.5 wt% ratio is 2.82 for the theoretically estimated value and 2.79 for the measured value. This consistency supports the idea of using detailed information from AFM to gain a deeper fundamental understanding of fluid gels. Moreover, it supports and confirms the ideas proposed in the previous paper.7
| ξ c (FG) [nm] | G c (FG) [Pa] | G′m (FG) [Pa] | |
|---|---|---|---|
| 0.5 wt% | 83 ± 101 | 7.2 ± 26.4 | 132.5 ± 4.3 |
| 1 wt% | 59 ± 85 | 20.3 ± 88.6 | 369.6 ± 14.3 |
| 2 wt% | 37 ± 61 | 81.9 ± 406.7 | 920.2 ± 133.0 |
A further comparison of the mesh distribution in Fig. 8(a–c) shows that the loose meshes of the 0.5 wt% and 1 wt% samples extend over a wider area, while the 2 wt% sample shows only a small area of loose structures and a large part is dominated by the dense core.
Finally, Fig. 9(a), 10(a) and 11(a) (cf.Fig. 4(c, f and i)) show the AFM images for different agarose concentrations at the highest magnification. Again, the three lines indicate the paths for the height profiles in the corresponding Fig. 9, 10 and 11(b–d). It can be clearly seen here, once again, that the meshes increase on average with a decrease in concentration, whereas in the case of the 2 wt% sample, large meshes but also thick strands can be observed due to edge effects. The enlarged regions shown in the figures are of interest because the height profiles at this magnification allow clearer visualization and distinction of the peaks and thus the individual strands. It can be recognised that the different concentrations of agarose fluid gels have the same origin and are formed by single agarose chains associated with double helices, with the consequent aggregation of the double helices into multiple helices (indicated by white arrows). The profile height for the concentrations 0.5 wt% (Fig. 9(b–d)) and 1 wt% (Fig. 10(b–d)) showed an approximated measured value between 4 nm and 8 nm and a width range between 10 and 30 nm. If we assume that the width of a double helix is about 2 nm, we can assume about 10–30 agarose chains or 5–15 double helixes within such a broader peak. For the 2 wt% sample (Fig. 11(b–d)), the heights of the aggregated polymer chains are measured up to 12 nm, and the widths range up to a size of 40 and even 60 nm, whereby multiple aggregated helical strands are distinctly seen to form larger strands again.
The observations in Fig. 11 are consistent with the findings from the previous AFM images. At the periphery, several strands are present (indicated by a blue arrow) that actually intend to crosslink with the core. Due to the high concentration degree of crosslinking, multiple helical structures already aggregate at the periphery, but are prevented from further crosslinking with the core due to the imposed shear. With a shear rate of 400 s−1, the time during gelation is not enough for the molecules to assemble sufficiently, so only a few molecules are able to associate to form such a network structure. With respect to the location indicated by the blue arrow, with a width of about 40 nm, it is estimated that approx. 40 agarose polymer chains link to form assembled double helices.
The faster crosslinking time with respect to the inverse of the shear rate leads to these large aggregated agarose polymer chains at the periphery. As mentioned in the introduction, these aggregated chains diffuse much slower, which becomes even slower with further crosslinking of such chains i.e. the dynamics of the cluster slows down. As a result, the linkage to the gel core is no longer possible. As a result agarose chains and bundles remain unlinked with the cores of the gel particles.
The AFM micrographs offer additionally distinct structural elements, which contribute differently to the dynamics, i.e., elastic and loss moduli. Fig. 5(a), 8(a), and 9(a) of the 0.5 wt% samples (cf.Fig. 4(a, b and c)) show loose dangling chains at the periphery; these are no longer present for the 2 wt% sample in Fig. 7(a), 8(c), and 11(a) (cf.Fig. 4(g, h and i)). These detailed structural elements at the particle surfaces must be discussed together with the previous results of the rheology, especially with the frequency sweeps (see Fig. 12).7 For the 0.5 wt% sample, an increase in loss modulus (G′′) with an increase in frequency was observed which was due to the dangling chains but also their less dense volume fraction and mesh size. For the 2 wt% sample, the loss modulus remains constant up to 10 rad s−1 (see Fig. 12), which was attributed not only to the smooth and less irregularly “hairy” structure on the surface but also to the high volume fraction and dense packing. Moreover, the dense meshes contribute to the restriction and thus frequency-independent behavior of this sample.
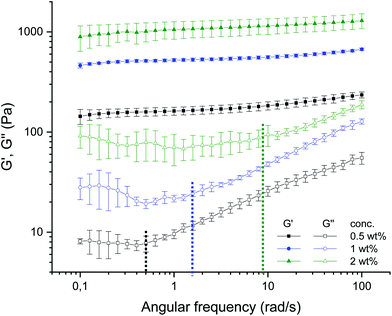 | ||
| Fig. 12 Frequency dependence of storage and loss moduli G′ (filled symbols), G′′ (empty symbols) at a constant strain (γ = 0.05%) and temperature (T = 25 °C) for agarose fluid gels with different concentrations 0.5 wt% (black), 1 wt% (blue) and 2 wt% (green). The dashed lines indicate the angular frequency (ωc) where G′′ starts to increase for the respective concentrations (reproduced from Ghebremedhin, Seiffert, and Vilgis7). | ||
The comparison of the measured height and width of the associated agarose strands of the different samples, which do not significantly differ from each other, further emphasizes how not only different textures but also rheological and tribological properties can arise from identical biopolymers simply by controlling the concentration and the process conditions, such as shear.7 Moreover, the processing conditions combined with the concentration of the biopolymers in use influence the formulated molecular network structure of the particulate gel suspension at the microscopic level. This in turn determines the macroscopic response of the material to external forces, leading to a unique change in biomaterial gel-based food products. In fact, shear rate-dependent gelation leads to specific network structures of gel particles which have a defined ratio between the network density of the inner core and the outer core as well as the size of the chains at the surface of the particles.
The very loose particle surface structure at low concentrations of 0.5 wt% requires a separate discussion. The corresponding time scales do not follow the predictions in the high concentration regimes, but can be estimated using a Rouse–Zimm model.17
The polymer chains diffuse to the nearest approximation before gelation begins, implying that the centre-of-mass diffusion constant DCM of the polymer chains in a good solvent behaves (apart from constant factors) as:
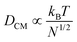 | (2) |
All these assumptions are in agreement with the findings of the AFM measurements in this work. Moreover, these results are additionally supported by the findings of the previous publication. It was proposed that the dangling chains, which were most pronounced in the 0.5 wt% samples, were responsible for a distinct increase in moduli during the frequency sweep.7Fig. 12 shows the frequency sweep of the resulting time-dependent behavior of the corresponding fluid gels at small oscillation strain. The observation is in agreement with the findings of the AFM images in this paper. It was suggested that the increase in G′ with an increase in frequency was due to the particle movement becoming faster, being pushed together and interfering with each other. The increase in G′′, on the other hand, was attributed to the flexible dangling chains on the particle surfaces, which show faster motion and were more pronounced for the 0.5 wt% sample compared to the 1 wt% and 2 wt% fluid gel samples. This is explained by the fact that with a decrease in concentration the aggregated chains present at the particle surface and the particle size increase, whereas the volume fraction and thus the percolation decrease. However, an extended LVE range during amplitude sweep was also attributed to these hairy structures on the particle surface. Furthermore, not only an increased coefficient of friction during tribological measurements, but also an increased viscosity during flow sweep measurements at small shear rates were attributed to the aggregated helical chains.7 Indeed, all these observations ascribed to the dangling ends and the higher proportion of the hairy structures could now be verified by AFM measurements.
More detailed knowledge of the loose surface structure allows the observations already made in Ghebremedhin, Seiffert, and Vilgis7 to be interpreted more accurately. As shown in Fig. 12, the frequency at which G′′ increases systematically depends on the concentration. Higher frequencies mean smaller time scales. However, this is precisely what suggests different surface structures. Assuming that the free ends behave in a first approximation according to the Rouse–Zimm model, relaxation times can be estimated with τ ∼ N3/2.17 The dangling parts are significantly longer at low agarose concentrations, so the time scales are longer. At high concentrations they are shorter. Consequently, the frequency at which the free ends of the external heavy movements can no longer follow the imposed oscillations increases. At these points, G′′ increases practically linearly with a slope, and their values are indicated in Fig. 12 by dashed lines for the frequency (ωc) for the respective concentrations. While the 0.5 wt% fluid gel sample shows an increase in loss modulus G′′ starting at a frequency of 0.5 rad s−1 with a slope of 0.387 ± 0.004, the 1 wt% sample exhibits an increase in G′′ starting at about 1.6 rad s−1 with a slope of 0.419 ± 0.007, whereas the 2 wt% sample displays an increase in G′′ starting at 9 rad s−1 with a slope of 0.347 ± 0.007.
The physical interpretation is quite striking. For low frequencies G′′ is not sensitive to frequency changes. The overdamped chain motion follows the imposed oscillatory shear from the rheometer. At higher frequencies the networks respond to their cross-link density accordingly. Assuming that the chain dynamics between two consecutive cross-links behaves close to a Rouse–Zimm-type motion, the frequency ωc, where G′′ starts to increase, is given by (ωcτR) ≈ 1. However, the relaxation time τR depends on the molecular weight of the mesh size roughly as ξ3 between two consecutive cross-links. Therefore ωc scales as 1/ξ3. This simple argument shows that ωc is shifted to larger values by decreasing the mesh size, and increasing the cross-link density. This trend can be seen by inserting the ratios of the mesh size at different concentrations (see Table 2) and calculating the shift factor of ωc as a function of the concentration. Hence, a determined ωc of 1.39 rad s−1 for the 1 wt% fluid gel sample and 6.5 rad s−1 for the 2 wt% fluid gel sample is obtained. Even considering the large standard deviations of the mesh size distribution, an agreement can be found with ωc given in Fig. 12. The slope of G′′ seems to vary only marginally in the measured frequency range, which indicates its origin from the peripheral chains as well. The frequency range where G′′ seems to increase linearly with the frequency may indicate the motion of the less restricted, loose and dangling network parts at the particle surfaces.
3.2 Comparison of the particle core with quiescent set gels
Another important question is whether the cross-link density of the gel core corresponds to the cross-link density of the quiescent set gels of the same concentration. In the previous sections it was assumed that the core gelation of the particles at time scales less than 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is compared directly to the quiescent gels. Consequently, the core shear modulus should be similar to the shear modulus of the bulk gel. This assumption can be attempted to be verified experimentally, as will be shown in the following paragraphs.
is compared directly to the quiescent gels. Consequently, the core shear modulus should be similar to the shear modulus of the bulk gel. This assumption can be attempted to be verified experimentally, as will be shown in the following paragraphs.
An amplitude sweep was performed to investigate and compare the viscoelastic properties of the hydrogels prepared under shear with those of the gels prepared under quiescent conditions.
This was done to gain a deeper understanding of the concentration-dependent characteristics of agarose fluid gels, which in our previous work were found to be influenced by the size and shape of the gel particles.7 Furthermore, in the course of these rheological measurements, together with the findings of atomic force microscopy, the aim is to achieve a better physical insight into the interaction between the gel particles.
The approach of directly comparing the properties of agar hydrogels prepared under shear with those prepared under quiescent conditions has also been carried out in previous work on rheological measurements.2 Furthermore, in other work on agarose fluid gels, texture analysis was performed on quiescently cooled agarose gels by assuming that the stress-deformation behavior exhibited corresponds to the behavior of individual particles.6 Thus, assuming that the number of crosslinks in the core of a fluid gel particle is the same as that of the corresponding unsheared gel, it seems apparent that this approach will be useful in understanding the network formation of the particles.
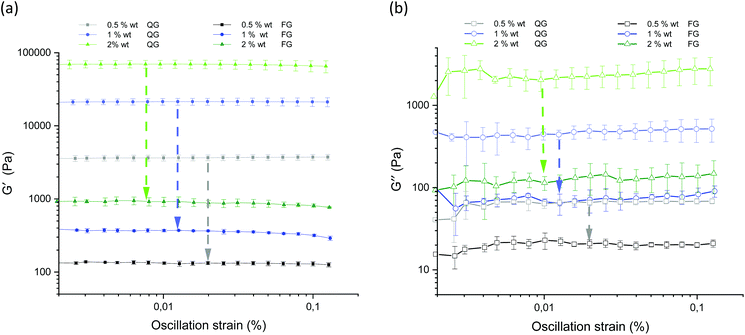
Fig. 13 displays the results of the amplitude sweep for different concentrations of the agarose fluid gels and the agarose gels prepared under quiescent conditions. The mean value and standard deviations of the elastic and viscous moduli are shown as a function of the strain. For all samples, storage (G′) and loss (G′′) moduli were specified within the linear-viscoelastic (LVE) range, thus describing the deformation behavior in the non-destructive range.
The limits of the LVE range and the characterization of the behavior after exceeding this range, which is called the non-linear viscoelastic range, have not been evaluated here. This has already been discussed in detail in the recent publication on fluid gels, where it was found that it is not the concentration and size of the particles but the structure that plays an important role in the mechanical properties, and is not relevant when comparing the fluid gels with the gels prepared under quiescent conditions.7
As expected, storage moduli (G′) (Fig. 13(a)) and loss moduli (G′′) (Fig. 13(b)) increase with an increase in agarose concentration, and it is also not surprising that both the moduli of the quiescently cooled gels increase by multiple orders of magnitude compared to those of the fluid gels. Such a strong decrease of the moduli for the differently prepared gels is indicated by arrows for the respective agarose concentrations. For easier comparison, Fig. 14 shows the mean and their standard deviations of the respective storage and loss moduli depending on the concentration at a strain of γ = 0.01%. When comparing the storage and loss moduli between different concentrations, the values are significantly different (p < 0.05) for both the fluid gels and quiescently cooled gels. For all gels, the corresponding mean values and their standard deviation are given in Table 3.
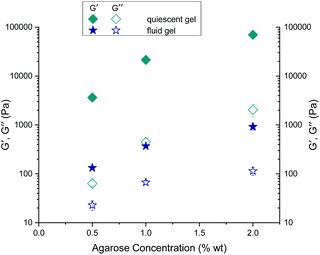 | ||
| Fig. 14 Comparison of the mean values of the storage (G′) and loss (G′′) moduli for the gels prepared under shear and non-sheared gels for different agarose concentrations at a strain of γ = 0.01%. | ||
| Gels | G′ [Pa] | G′′ [Pa] |
|---|---|---|
| 2 wt% QG | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888.3 ± 8819.7 888.3 ± 8819.7 |
2041.4 ± 566.2 |
| 2 wt% FG | 920.2 ± 133.0 | 114.3 ± 21.9 |
| 1 wt% QG | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.1 ± 2261.7 442.1 ± 2261.7 |
447.9 ± 68.9 |
| 1 wt% FG | 369.6 ± 14.3 | 66.9 ± 5.9 |
| 0.5 wt% QG | 3643.0 ± 333.6 | 63.6 ± 7.9 |
| 0.5 wt% FG | 132.5 ± 4.3 | 22.9 ± 5.2 |
As can be seen from Table 3, the 2 wt% fluid gels exhibit a storage modulus of 920 (± 133) Pa and a loss modulus of about 114 (± 21.9) Pa, while the quiescently cooled gel of the same concentration exhibits a much higher storage modulus by a factor of about 76, and a loss modulus higher by a factor of about 18. For the agarose concentration of 1 wt%, the fluid gels show a G′-value of about 369.6 (± 14.3) Pa and a G′′-value of 66.9 (± 5.9) Pa, whereas the corresponding quiescently cooled gel exhibits an increase in storage modulus by a factor of ∼58 and an increase in G′′ by a factor of ∼7. Finally, the 0.5 wt% fluid gel reveals a G′ of 132.5 (± 4.3) Pa and a G′′-value of 22.9 (± 5.2) Pa, where the corresponding quiescently cooled gel displays an increase in G′ by a factor of ∼28 and an increase in G′′ by a factor of ∼3.
These very high moduli of the gels cooled under quiescent conditions arise from the already mentioned fact that as a strong gelling polysaccharide, agarose forms firm and brittle gels. The agarose polymer chains, which form double helices via hydrogen bonding, aggregate into thick bundles of junction zones that lead to the formation of these strong gels.9 Consequently, according to the correlation between the mesh size and the elastic modulus for permanently cross-linked gels, an increase in the modulus with increasing agarose concentration is observed (see eqn (1)). Furthermore, for the fluid gels, storage and loss moduli increase with an increase in agarose concentration and the samples show an elastic dominated behavior i.e. a gel-like behavior, indicating an interconnected network of gel particles formed by a highly cross-linked agarose polymer.
By considering the decrease of the storage moduli of the fluid gels to those of the non-sheared gels and comparing them within the different concentrations, it can be observed that the increase from 0.5 wt% to 1 wt% gels is greater than the increase of the storage modulus from 1 wt% to 2 wt% samples. These observations no longer hold for the loss modulus (see Table 4). Thus, this observed trend is consistent with the assumption that the textural behavior of quiescently cooled gels is the same as that of the individual particles of the fluid gels of the same concentration.6 Furthermore it was assumed in earlier work that the moduli of the sheared agar gel would scale with the moduli of microgel particles, which correspond to the moduli of a quiescently cooled agar gel.2
| Gels | G′QG | G′′QG | G′FG | G′′FG |
|---|---|---|---|---|
| 2 wt%/1 wt% | 3.3 (± 3.9) | 4.6 (± 8.2) | 2.5 (± 9.3) | 1.7 ± (3.7) |
| 1 wt%/0.5wt% | 5.9 (± 6.8) | 7.1 ± (8.7) | 2.8 (± 3.3) | 2.9 ± (1.1) |
To compare the cross-link density of the gel core of the fluid gel particle corresponding to the cross-link density of the quiescently cooled gels of the same concentration, we consider the calculated mesh size estimated by the measured storage modulus of the quiescently cooled gel with the mesh size of the core of the fluid gel particle estimated by the AFM phase image in Fig. 2. According to eqn (1) and since kBT is given, ξ3 was computed by inserting the measured G′-value of the quiescently cooled gel (see Table 3).
Based on the AFM phase images in Fig. 2, one approach to estimating the mesh size would be to determine the distance of an agarose strand at the top level until it is overlapped by a next strand, either by entanglement or by cross-links. This means that this length corresponds to a distance between two cross-links i.e. junction zones, as already shown in Fig. 3. That is, if the length of the distinctly visible strands on the surface in Fig. 2 is shortened, it would imply a smaller mesh size. In fact, the distance between these cross-links would be the mesh size that determines the modulus. However, it should be noted that the distance ξ only applies in a good solvent. This is because the estimated mesh size in Fig. 2 corresponds to a gel that has been squeezed and shrunk into two dimensions by drying. Therefore, the distance in question should be multiplied by a factor of the water volume, which is thus the third root of the volume of the water fraction of the corresponding agarose gel concentration. The calculated mesh sizes from the storage moduli of the quiescently cooled gels measured by amplitude sweep (see Fig. 13 and Table 3) are given in Table 5.
| Gels | G′m (QG) [Pa] | ξ c (QG) [nm] | (ξc (QG) [nm]) × factor |
|---|---|---|---|
| 2 wt% QG | 69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 888.3 ± 8819.7 888.3 ± 8819.7 |
3.9 ± 0.1 | 17.9 ± 0.7 |
| 1 wt% QG | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 442.1 ± 2261.7 442.1 ± 2261.7 |
5.8 ± 0.2 | 26.7 ± 0.9 |
| 0.5 wt% QG | 3643.0 ± 333.6 | 10.4 ± 0.3 | 48.2 ± 1.5 |
By comparing the calculated mesh sizes of about 48 nm for the 0.5 wt% sample, 27 nm for the 1 wt% sample, and 18 nm for the 2 wt% sample of the quiescently cooled gels with the AFM phase images of the fluid gels in Fig. 2 and tracing these calculated values over such an undisturbed strand, it can be seen that the distances calculated here are somewhat shorter than those seen in the AFM phase images. Nevertheless, the magnitudes of the calculated ξ values agree with the lengths of the strands.
This is an indication of the fact that in the core of a fluid gel particle, the time scales of gel formation are faster than that of the imposed shear rate and therefore comparable gelling occurs as in a quiescently cooled gel. Indeed, this conclusion is consistent with the aforementioned assumption that when the chains move faster than the time 1/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) imposed by the shear, they are able to form gels comparable to the quiescent conditions.
imposed by the shear, they are able to form gels comparable to the quiescent conditions.
Fig. 15 shows the AFM phase images from Fig. 2 with the indicated lengths of the previously determined mesh size. This is to illustrate the extent to which the mesh size determined from the storage modulus approximates the lengths of the strands in the core of the AFM phase images. A total of 20 points were measured per concentration with an average of 56.1 ± 10.3 nm for 0.5 wt%, 29.7 ± 4.7 nm for 1 wt% and 22.2 ± 2.6 nm for 2 wt% fluid gel samples.
In previous work on fluid gels made of agar, the dependence on the concentration and method of preparation of sheared gels was compared with spherical microgel suspensions and also with gels prepared under quiescent conditions, all from the same material.2 They also found a dependence of the moduli on the concentration and more on the internal structure and particle shape.2
These results are in agreement with the findings of the AFM images shown here and with the assumption that the bulk rheology of the fluid gels is influenced by the particle shape, size and also elasticity. This in turn is governed by the elasticity of the higher network density in the inner core of the particles, which becomes less dense in the outer region. In addition, the chains on the particle surface play a role, which also depends on the agarose concentration.
3.3 Scanning electron microscopy (SEM)
Fig. 16 shows the SEM micrographs of the different concentrations of the fluid gels and the corresponding gels prepared under quiescent conditions. To provide supplemental structural information in addition to the results of the rheological properties, SEM was performed on all fluid gels prepared with the different concentrations and the corresponding quiescently cooled gels. The images for the fluid gels (a–c) show fibril-like microstructures formed by interconnected pores surrounding the fibers with a wide size distribution of up to several micrometers. Furthermore, it can be seen that as expected, a denser network forms with an increase in concentration. Thus, a densification of the network takes place.7 On the other hand the images of the gels prepared under quiescent conditions (d–f) display a completely different structure, namely a leaflet type structure. From the findings of the micrographs, the rheological and mechanical properties can be deduced, since the gel strength of the sample varies with the density of the network of structural patterns. Furthermore, the comparison of the SEM images of the different gels produced depicts how different properties can arise from identical biopolymers.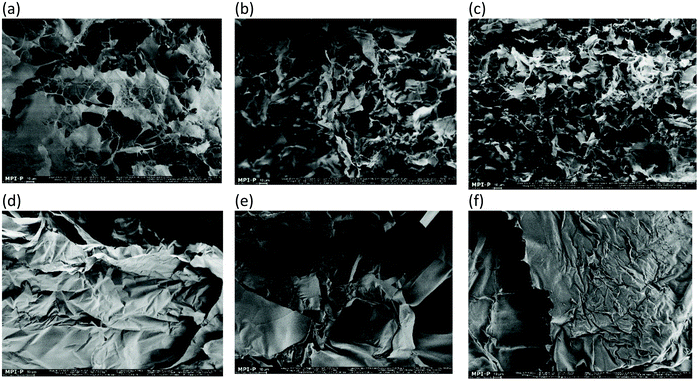 | ||
| Fig. 16 SEM images of the freeze dried fluid gels with (a) 0.5 wt%, (b) 1 wt%, and (c) 2 wt% agarose concentrations and gels cooled under quiescent conditions with (d) 0.5 wt%, (e) 1 wt% and (f) 2 wt% agarose concentrations. Scale bars are 10 μm. (a, b and c are reproduced from Ghebremedhin, Seiffert, and Vilgis7). | ||
4 Conclusion
In this work we have investigated the underlying physical and microscopic characteristics of fluid gels linked with their macroscopic properties. Agarose based fluid gels were prepared during gelation under shear, resulting in gel particles with various network structures that influence the macroscopic behavior. We used AFM measurements to investigate the network structure of the fluid gels. Representative examples of the AFM images of the network structures of the different agarose gel concentrations were analyzed. The height profiles and mesh sizes were determined to characterize and evaluate the AFM images. The focus of this work, however, was to determine the mesh size as this determines the structure and the elasticity as well as the dynamics that are reflected in G′ and G′′. In fact, these AFM images were intended to support the assumptions of the findings of our recent paper.It was found that the dense region of the network structure changed towards the periphery of the gel particles. Moreover, this network structure and its elasticity also changed with the concentration (0.5 wt%, 1 wt%, 2 wt%). In addition, the correlation that cracks at the edge of the network is more likely to occur at higher concentrations, as observed at concentrations of 1 wt% and 2 wt%, can be explained by the mechanism that takes place during the preparation of fluid gels. It was assumed that with a higher concentration, the probability of rapid gelation of agarose chains is higher because more chains are present that can associate to form double helices and subsequently aggregate. When this aggregated network forms, but at the same time, the gelation in the rheometer is subjected to shear, these cracks occur at the edge, and they are more pronounced the faster the gelation takes place since the probability of gelation is much higher. Furthermore, the peripheral region plays a crucial role in the interaction between the gel particles and contributes to defining the length scale for their elastic response in bulk. In fact, it can be deduced that near the surface of the gel particles, the elasticity and friction properties change as the ratio between the inner core and the outer core i.e. peripheral region changes. This is due to the fact that the mesh size shows a broader distribution from the center towards the periphery, depending on the concentration and competing time scales such as shear rate and molecular motion. Using oscillatory measurement the viscoelastic properties of the fluid gels were compared with gels prepared under quiescent conditions. With these measurements we could support the assumption that the textural behavior of quiescently cooled gels corresponds to that of the individual particles of the fluid gels of the same concentration. In addition, the assumption that the mesh size of the densely cross-linked core of the fluid gel particle is approximately the same as that in the quiescently cooled gel was confirmed. Accordingly, during gelation under shear, the molecules move faster on the time scale, than the shear imposed time due to concentration and temperature and associate into double helices and aggregate into larger clusters, resembling the quiescently cooled gels.
Finally, from the scanning electron microscopy (SEM) results, the result of rheological measurements could be deduced, showing that the viscoelastic properties of the gels vary with the density of the network of structural patterns.
Overall, this study illustrates the importance of understanding the interplay between the length and time scales of biopolymers during gelation under shear for the preparation of fluid gels in order to design fluid gels for tailored applications with specific viscoelastic, textural, and lubricating properties.
Author contributions
Marta Ghebremedhin: conceptualization, writing – original draft, methodology, investigation, validation, visualization, and data interpretation. Sebastian Seiffert: supervision and conceptualization. Thomas A. Vilgis: supervision, conceptualization, writing – review and editing, visualization, and interpretation.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors would like to thank Dr Rüdiger Berger and especially Helma Burg for the technical support with the atomic force microscopy measurements. Many thanks also to Gunnar Glaßer for recording the SEM images and Christine Rosenauer for the SEC measurements. Furthermore, we thank the members of the MPIP soft matter food science group for fruitful discussion and proofreading of the manuscript. Open Access funding was provided by the Max Planck Society.References
- I. F. Farrés, R. J. A. Moakes and I. T. Norton, Food Hydrocolloids Designing biopolymer fluid gels: A microstructural approach, Food Hydrocolloids, 2014, 42, 362–372, DOI:10.1016/j.foodhyd.2014.03.014.
- W. Frith, X. Garijo, T. Foster and I. Norton, Microstructural origins of the rheology of fluid gels, Special Publication, 2002 Search PubMed.
- I. T. Norton, D. A. Jarvis and T. J. Foster, A molecular model for the formation and properties of fluid gels, Int. J. Biol. Macromol., 1999, 26(4), 255–261, DOI:10.1016/S0141-8130(99)00091-4.
- M. H. Mahdi, B. R. Conway, T. Mills and A. M. Smith, Gellan gum fluid gels for topical administration of diclofenac, Int. J. Pharm., 2016, 515(1–2), 535–542 CrossRef CAS PubMed.
- M. H. Mahdi, B. R. Conway and A. M. Smith, Evaluation of gellan gum fluid gels as modified release oral liquids, Int. J. Pharm., 2014, 475(1–2), 335–343 CrossRef CAS PubMed.
- A. Gabriele, F. Spyropoulos and I. T. Norton, A conceptual model for fluid gel lubrication, Soft Matter, 2010, 6(17), 4205–4213, 10.1039/c001907k.
- M. Ghebremedhin, S. Seiffert and T. A. Vilgis, Physics of agarose fluid gels: Rheological properties and microstructure, Curr. Res. Food Sci., 2021, 4(December 2020), 436–448, DOI:10.1016/j.crfs.2021.06.003.
- A. Imeson, 3 Agar, Food stabilisers, Thick gelling agents, 2009, p. 31 Search PubMed.
- D. Nordqvist and T. A. Vilgis, Rheological Study of the Gelation Process of Agarose-Based Solutions, Food Biophys., 2011, 6(4), 450–460, DOI:10.1007/s11483-011-9225-0.
- C. Nowak and T. A. Vilgis, Rod-coil multiblock copolymers: Structure and stability, EPL (Europhys. Lett.), 2004, 68(1), 44 CrossRef CAS.
- T. A. Vilgis, Gels: Model systems for soft matter food physics, Curr. Opin. Food Sci., 2015, 3, 71–84, DOI:10.1016/j.cofs.2015.05.009.
- B. H. Zimm and J. K. Bragg, Theory of the phase transition between helix and random coil in polypeptide chains, J. Chem. Phys., 1959, 31(2), 526–535 CrossRef CAS.
- K. Nishinari and Y. Fang, Sucrose release from polysaccharide gels, Food Funct., 2016, 7(5), 2130–2146, 10.1039/c5fo01400j.
- K. Nishinari and Y. Fang, Relation between structure and rheological/thermal properties of agar. A mini-review on the effect of alkali treatment and the role of agaropectin, Food Struct., 2017, 13(September), 24–34, DOI:10.1016/j.foostr.2016.10.003.
- S. M. Fiszman and L. Duran, Effects of fruit pulp and sucrose on the compression response of different polysaccharides gel systems, Carbohydr. Polym., 1992, 17(1), 11–17 CrossRef.
- W D. Carvalho and M. Djabourov, Physical gelation under shear for gelatin gels, Rheol. Acta, 1997, 36(6), 591–609, DOI:10.1007/BF00367355.
- M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, (Clarendon) London, New York, 1986 Search PubMed.
- S. Holland, C. Tuck and T. Foster, Fluid Gels: a New Feedstock for High Viscosity Jetting, Food Biophys., 2018, 13(2), 175–185, DOI:10.1007/s11483-018-9523-x.
- A. L. Ellis, A. B. Norton, T. B. Mills and I. T. Norton, Stabilisation of foams by agar gel particles, Food Hydrocolloids, 2017, 73, 222–228, DOI:10.1016/j.foodhyd.2017.06.038.
- K. Bertula, L. Martikainen and P. Munne, et al., Strain-Stiffening of Agarose Gels, ACS Macro Lett., 2019, 8(6), 670–675, DOI:10.1021/acsmacrolett.9b00258.
- D. Nečas and P. Klapetek, Gwyddion, 2021, https://gwyddion.net/ (Accessed: 30th November 2021) Search PubMed.
- A. P. Gunning, A. R. Kirby, V. J. Morris, B. Wells and B. E. Brooker, Imaging bacterial polysaccharides by AFM, Polym. Bull., 1995, 34(5), 615–619 CrossRef CAS.
- V. J. Morris, A. R. Kirby and P. A. Gunning, Atomic Force Microscopy for Biologists, World Scientific, 2009 Search PubMed.
- M. Martínez-Sanz, A. Ström and P. Lopez-Sanchez, et al., Advanced structural characterisation of agar-based hydrogels: Rheological and small angle scattering studies, Carbohydr. Polym., 2020, 236(September 2019) DOI:10.1016/j.carbpol.2019.115655.
- S. A. Foord and E. D. Y. Atkins, New x–ray diffraction results from agarose: Extended single helix structures and implications for gelation mechanism, Biopolymers, 1989, 28(8), 1345–1365, DOI:10.1002/bip.360280802.
- P.-G. De Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- B. I. Zielbauer, N. Schönmehl, N. Chatti and T. A. Vilgis, Networks: From Rubbers to Food, in Designing of Elastomer Nanocomposites: From Theory to Applications, Springer, 2016, pp. 87–233 Search PubMed.
- N. Russ, B. I. Zielbauer, K. Koynov and T. A. Vilgis, Influence of nongelling hydrocolloids on the gelation of agarose, Biomacromolecules, 2013, 14(11), 4116–4124, DOI:10.1021/bm4012776.
- M. Watase, K. Nishinari and T. Hatakeyama, DSC study on properties of water in concentrated agarose gels, Food Hydrocolloids, 1988, 2(6), 427–438 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2fo00102k |
| This journal is © The Royal Society of Chemistry 2022 |