Study on the evaluation of the aging grade for industrial heat-resistant steel by laser-induced breakdown spectroscopy
Yongsheng
Zhang†
ac,
Meirong
Dong†
 *ac,
Junbin
Cai†
ac,
Yixiang
Chen†
ac,
Hongjie
Chen†
ac,
Chunyi
Liu†
b,
Jong H.
Yoo†
b and
Jidong
Lu†
*ac,
Junbin
Cai†
ac,
Yixiang
Chen†
ac,
Hongjie
Chen†
ac,
Chunyi
Liu†
b,
Jong H.
Yoo†
b and
Jidong
Lu†
 ac
ac
aSchool of Electric Power, South China University of Technology, Guangzhou, Guangdong 510640, China. E-mail: epdongmr@scut.edu.cn
bApplied Spectra, Inc., 46665 Fremont Blvd, Fremont, CA 94538, USA
cGuangdong Province Engineering Research Center of High Efficient and Low Pollution, Guangzhou, Guangdong 510640, China
First published on 17th November 2021
Abstract
Heat-resistant steel is widely used in various types of industrial pressure-bearing equipment, and the changes in the metallographic structure and properties of the steel are of great importance for the function and safety of this equipment. In this work, laser-induced breakdown spectroscopy (LIBS) was applied to estimate the aging grade of industrial heat-resistant steel. First, representative spectra of the metal matrix of an industrial pipe were obtained via depth profile analysis, and the effects of surface oxides on the matrix plasma parameters were evaluated and compared. The results indicated that correlation analysis of the emission intensities along the radial direction can accurately identify the boundary between the surface oxide and the matrix. The presence of surface oxides would decrease the plasma temperature and increase the electron density. Secondly, multiplicative scattering correction (MSC) was applied to correct for the interference of surface oxides, and K-fold-support vector machine-recursive feature elimination (K-SVM-RFE) was exploited to select the optimal spectral feature subset. Finally, estimation of the aging grade model was established based on the support vector machine (SVM) and the optimal feature subsets. The estimation accuracy of the validation set after spectral correction was improved from 80.56% to 84.72%, and the model exhibited similar capability for the industrial pipe and the corresponding samples with mechanical polishing to eliminate surface oxides. The work demonstrates that LIBS is suitable for the in situ estimation of steel aging grade for industrial pipe.
1. Introduction
With the continuous improvement in the degree and scale of industrialization, increasing amounts of high-temperature and pressure-bearing thermal equipment are in service in the electrical power, metallurgy, power machinery, petrochemical and other industries.1,2 During the entire service lifetime of the equipment, the microstructure of heat-resistant steel is constantly aging, and the macro-performance is gradually decreasing (i.e., steel aging),3 which can cause the possibility of burst-leak failure of the equipment and unplanned operational accidents.4–6 Therefore, it is critical to evaluate the steel aging grade to assess the operational safety and reliability of the equipment. The traditional evaluation method is based on off-line metallography inspection and assessment guidelines in which a specific part of the equipment must be cut off,7 which would cause irreversible damage to the equipment and increase the operating expenses. Hence, it is significant to develop an in situ, rapid and nondestructive technique to estimate the failure characteristics for stable production in various industries.Laser-induced breakdown spectroscopy (LIBS) is a rapid and in situ analysis technique based on atomic emission spectroscopy. It has the advantages of simultaneous multi-elemental analysis and low destructiveness and has been widely applied in quantitative analysis in various fields.8–11 This technique involves the focusing of a highly energetic laser pulse onto a sample surface to vaporize the source into a plasma that contains excited atoms, ions, and molecules. During plasma plume relaxation, the radiated energy can be spectrally resolved and detected by a spectrometer, and the emission lines can be used for quantitative analysis of the elements in the sample.12,13 The laser ablation process and plasma characteristics are affected by the matrix effects caused by the physical and chemical properties of the material. Therefore, properties and microstructure analysis such as hardness14 and alloy phase transformation,15 which are significant information for the safety assessment, can be distinguished according to the obtained spectra data. Delgado et al.16 identified the particular grades of steel at elevated temperature based on discriminant function analysis using LIBS. Nasrazadani et al.17 used linear correlation to distinguish iron oxide phases, and the results were found to be in good agreement with Fourier transform infrared (FTIR) analysis.
In our previous work, a series of studies fully verified the feasibility of estimating the failure characteristics of steel, such as surface hardness and aging grade. Yao et al.18 analyzed the plasma characteristics of 20 G steel with different metallurgical structures and found a correlation between the intensity ratios of the ionic to the atomic lines and tensile strength. Li et al.19 presented a correlation between the steel aging grade and the intensity ratios of Cr I/Fe I and Mo I/Fe I. Lu et al.20 explored the temporal and spatial evolution characteristics of T91 steel plasma with different aging degrees in order to reveal the mechanism of LIBS in the estimation of steel aging.
Although it has been confirmed that the materials characteristics such as mechanical properties and phase transformation can be reflected by spectral characteristics, it is still difficult to obtain precise aging estimation using conventional univariate models based on this correlation. Therefore, it is necessary to develop an effective multivariate analysis method that can employ the collective spectral information to establish a more reliable correlation. Lu et al.21,22 discussed the influence of feature selection methods on LIBS steel estimation models and evaluated the capability of models to handle the issues in measurement. Huang et al.23 established a model for the surface hardness of steel by analysing the correlation between emission line intensity and hardness. They then proposed a hybrid model combining wavelet transform and recursive feature elimination to estimate the different indicators of steel and an assessment matrix for evaluating the running state of steel, which was established using the indicators from the aging grade and hardness grade.24 However, the above achievements were mainly based on artificial specimens obtained from high-temperature and -stress aging treatment, which were sanded and polished to avoid surface oxides and foreign contaminants. In order to realize the in situ detection of heat-resistant steel, Cai et al.25 carried out some tentative work in the aging grade estimation for actual industrial T91 pipes using a new portable LIBS device, and different spectral pretreatment methods were compared to improve the prediction accuracy.
It is well known from our previous work that for the measurement of an actual pipeline, the surface characteristics of the sample have a great influence on the emission spectrum. Thus, it is necessary to obtain the spectra of the steel matrix under the surface oxide layer first. Actually, LIBS is an effective method for deposition and coating analysis.26,27 Hai et al.28 explored the depth profile of the deposited layer on the first wall of the Experimental and Advanced Superconducting Tokamak (EAST) by LIBS and identified the interface boundary between the deposition layer and the matrix. Xiao et al.29 evaluated the layer composition via the evolution of the spectral line intensities of W, Al, C and H. Balzer et al.30 measured the thickness of coated components precisely by calculating the coating thickness from the specific plasma signal in comparison to a reference measurement, and extended LIBS from a material analysis tool into the field of thickness measurement.
The aim of this work was to develop a method for the in situ estimation of the steel aging grade for industrial pipe. Representative spectra of the metal matrix were first obtained by a depth profile. Multiplicative scattering correction (MSC) was then applied to correct for the interference of surface oxides on the matrix spectrum. T91 specimens, including artificial specimens and industrial specimens of re-heaters obtained via mechanical polishing to eliminate surface oxides, were employed to establish a prediction model of the aging grade based on a subset of optimal features selected by K-fold-support vector machine-recursive feature elimination (K-SVM-RFE). Finally, the extension of the aging grade estimation from artificial specimens to industrial pipe is realized based on spectral correction.
2. Experimental
2.1 Specimen preparation
T91 steel (10Cr9Mo1VNbN) is a representative heat-resistant steel that is widely used in heat-exchange equipment such as superheaters, reheater tubes and boilers.31 The detailed treatment of the experimental specimens has been described in our previous work,20 which is briefly reviewed here. To acquire steel specimens with different aging degrees, an unused steel tube was designed and heated in various conditions involving a range of temperatures (from 600 °C to 700 °C) and stresses (from 35 MPa to 120 MPa) to provide artificial specimens. All the artificial specimens were obtained at four temperatures and placed on four black cylinders. They were heated under 10 different conditions to give 10 artificial specimens; these specimens are shown and labelled with “A”.In addition to these 10 artificial specimens, six industrial specimens cut from various re-heaters or super-heaters of a boiler were added as the experimental subjects to verify the practicability of the model, and were labelled with “I”. The surfaces of the 16 specimens were sanded with sandpaper at a gradient of about 200 mesh from 120 to 1200 and polished using 3.5 μm diameter diamond paste to remove the contaminants and oxide layers. In addition, there were also two industrial pipe samples whose surfaces were slightly smoothed with sandpaper, which were labelled with “P”. All the specimens were finally wiped with ethanol. The aging grade of the specimens can be determined by metallography with the DL/T 884-2004 criterion7 and are listed in Table 1. As the degree of microstructure aging increases, the carbide in the grain grows and moves to the boundaries of the grain, and the martensite orientation disperses gradually.
| Specimen | Aging grade | Assigned set |
|---|---|---|
| A-#1 | 2 | Training |
| A-#2 | 4 | Training |
| A-#3 | 3 | Training |
| A-#4 | 3 | Training |
| A-#5 | 5 | Training |
| A-#6 | 3 | Training |
| A-#7 | 1 | Training |
| A-#8 | 2 | Training |
| A-#9 | 2 | Testing |
| A-#10 | 3 | Training |
| I-#11 | 1 | Training |
| I-#12 | 2 | Training |
| I-#13 | 4 | Training |
| I-#14 | 5 | Testing |
| I-#15 | 1 | Testing |
| I-#16 | 3 | Testing |
| P-#17 | 1 | Testing |
| P-#18 | 3 | Testing |
2.2 LIBS setup
All the specimens were analyzed with the J200-LIBS system (Applied Spectra Inc., Fremont, CA).32 The system was equipped with a Q-switched Nd:YAG laser operated at 266 nm and a 4 ns pulse duration as an ablation source; the incident laser was reflected by a 45-degree laser line mirror and focused by a quartz lens on the sample surface. The focal lengths of the focusing and collection lenses used were 40 and 75 mm, respectively. The focus spot diameter was set to 120 μm. The laser was adjusted to 4.9 mJ operating with a 3 Hz repetition rate. A CMOS camera (Tucsen Photonics, ISH500, China) was mounted above the mirror to provide focus assistance and monitoring of the ablation position of the sample. The emission from the plasma plume was collected by a collimating lens at a 45° angle to the incident laser and transmitted by optic fiber to a six-channel spectrometer (Aurora, Fremont, CA). The delay time between the laser ablation and the scan of the spectrometer was set to 0.5 μs. All the experimental parameters (laser energy, laser spot size and gate delay) were optimized by orthogonal experimental design to obtain the best signal to noise ratio (SNR) and precision (% RSD) of the spectrum lines.The measurement scheme with a 12 position matrix was designed and implemented after the mechanical treatment of the specimen surface. For the samples labelled “A” and “I” with the oxide layer removed from the surface, 150 pulses were used to measure each position. For the industrial “P” samples, 550 pulses were applied at each position to ensure the removal of surface oxides. Auto-focus was performed before measurement at each measured position to prevent an inhomogeneous surface or curvature from interfering with the plasma characteristics.
3. Analytical methods
3.1 Multiplicative scattering correction (MSC)
Multiplicative scattering correction (MSC) is a preprocessing algorithm that uses a linear regression equation to fit each spectrum and ideal spectrum, and the fitting coefficients are then used to correct for the scattering effect of the raw spectrum.33,34 The process of linear regression and correction can be expressed as eqn (1) and (2), respectively:xi = ki![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) + bi + bi | (1) |
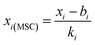 | (2) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) is the average representative spectrum at different locations of the same specimen, and xi(MSC) is the corrected spectrum. In this work, MSC was used to correct for the scattering effect caused by the inhomogeneous metal surface and non-uniform ablation craters.
is the average representative spectrum at different locations of the same specimen, and xi(MSC) is the corrected spectrum. In this work, MSC was used to correct for the scattering effect caused by the inhomogeneous metal surface and non-uniform ablation craters.
3.2 K-fold-support vector machine-recursive feature elimination (K-SVM-RFE)
The spectrum is represented by a vector in a multi-dimensional space whose components are the wavelength-specific intensities. Support vector machine (SVM) is used to map the spectrum intensity to a high-dimensional feature space and then construct a maximum margin hyperplane to solve the classification problem.35–37 The function expressing the hyperplane can be represented as eqn (3):| f(x) = wTx + b | (3) |
Support vector machine-recursive feature elimination (SVM-RFE) focuses on eliminating the irrelevant features using the weight vector of the SVM algorithm iteratively and obtaining the specified feature subset,38 and it is now beginning to be applied in various fields due to its excellent performance.39 In each iteration, the ranking of the features is obtained via SVM, and the feature with the minimum weight among the input subset features will be removed. The most important feature subset is selected according to the prediction performance of SVM with different subsets. However, SVM-RFE eliminates only one feature in each iteration, which is time-consuming, and the ranking of features is obtained within a fixed dataset without cross-validation in each iteration, which may affect the representativeness of the weight of the features.
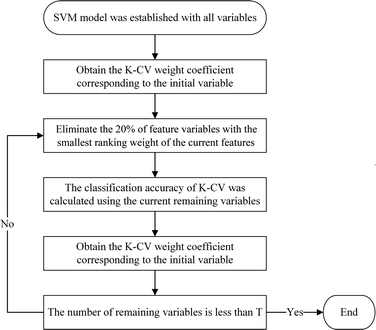
Therefore, a new improved approach, K-SVM-RFE, coupling cross-validation (CV) and SVM-RFE was proposed to build a robust classifier with the optimized feature subset. A logic flow chart of the K-SVM-RFE feature selection algorithm is shown in Fig. 1. The training set is randomly divided into K subsamples for cross-validation, a single subsample was retained as the validation data for testing the model, and the remaining K − 1 subsamples were used as training data using linear SVM. The statistical result (averaging each cross-validation model) of the weight matrix and prediction accuracy can then be obtained, and the 20% of spectral variables with the minimum weight are removed at each iteration, until the number of remaining variables less than the small value T. Finally, the optimal feature subset is obtained according to the internal cross-validation accuracy.
Generally, classification models are trained using several datasets with tuning of different parameters for best performance. However, as Nørgaard et al.40 discussed, it is necessary to ensure that all the local models have common parameter settings and then make the comparison possible. Therefore, in the iterative process of K-SVM-RFE, all the constructed models used the same parameter settings without individual fine tuning. The kernel function in SVM was set to the radial basis function (RBF), the penalty parameter was set to 0.1, and the kernel coefficient was set to 0.1.
3.3 Model evaluation
The classification accuracy of the testing set is selected as the figure of merit of model performance in this work, which is the rate of the number of spectral data correctly classified in the testing set to the total number of tested spectral data. It is worth mentioning that the processing and analysis of the data are carried out in Python 3.7, assisted by the open-source toolkit Scikit-learn.414. Results and discussion
4.1 Depth profile analysis of industrial pipe
In order to realize the in situ detection of industrial heat-resistant steel by LIBS, it is necessary to investigate the influence of the steel surface state on the spectral characteristics. To obtain the steel matrix spectrum, specimens with surface oxides and specimens from which surface oxides were removed by mechanical polishing were analyzed using depth profile analysis. Fig. 2 shows the variations in the line intensities of the matrix element Fe and alloying element Cr for specimen I-#15 (an industrial specimen with the surface oxide removed) along the depth profile. In the first five laser shots, changes in the line intensities are obvious, mainly due to the fact that the crater has not yet formed and the irregular profile of the surface. The intensities of Fe I (404.52 nm) and Cr I (425.44 nm) gradually decrease slightly during pulses 6–60; the downward trend can be explained by the geometrical effect of collecting a smaller amount of light as the number of laser shots increases and the plasma plunges into the crater. After that, the line intensities are relatively stable within a certain range. In addition, it is worth mentioning that using too many laser pulses to ablate the samples will have a negative effect on the evaluation of the steel aging grade;21 thus, the representative spectrum of each sample was obtained over an average of 61–100 pulses.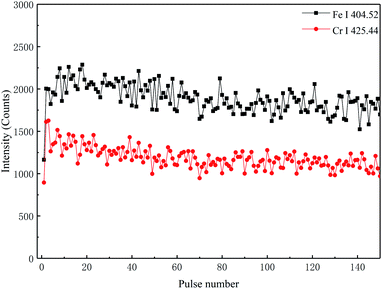 | ||
| Fig. 2 Emission intensity variations of the matrix element (Fe) and alloying element (Cr) along the depth profile for the specimen I-#15. | ||
Fig. 3 shows the emission intensity variations of the matrix element and alloying element along the radial direction for the specimen P-#17 (industrial pipe without surface oxide removal). The changing trend in the element content of the pipe along the radial direction can be represented by the change in the intensity of the element spectrum with the number of pulses. When the laser starts to ablate the pipe, the spectral line of alloying element Cr I (425.44 nm) is essentially not detected in the initial shots, and the characteristic spectral line of Fe is relatively stable. The main reason for this is that the surface oxide layer on the pipe is a multilayer structure, and the outer layer is mainly composed of porous Fe2O3 and Fe3O4, which essentially does not contain Cr.42,43 The inner layer consists of Cr-rich spinel and the Cr content is relatively high, so that the changes in the Fe and Cr content are always opposite.44 The laser initially ablates the outer oxide layer on the surface of the pipe, and as the number of laser pulses increases, the crater deepens. After the 100th laser pulse, the outer oxide layer is gradually broken down, and the laser starts to ablate the inner oxide layer. The closer the inner oxide layer is to the matrix, the higher the Cr content, and thus the characteristic spectral line intensity of Cr gradually increases. Finally, the inner oxide layer is broken down and the laser begins to ablate the steel matrix; as a result, the characteristic spectral line intensity tends to become stabilized. The Fe content of the outer oxide layer is often greater than that of the inner oxide layer, and the decrease in the Fe content of the inner oxide layer is often accompanied by an increase in the Cr content; thus, the characteristic line intensity of Fe gradually decreases during pulses 101–280. After 280 pulses, the intensities of the spectral lines are relatively stable, and the intensities of the Fe and Cr spectral lines of the specimen are greater than those of the specimen with surface oxides removed. In addition, the characteristic spectra of specimen P-#18 also had a similar trend along the radial direction.
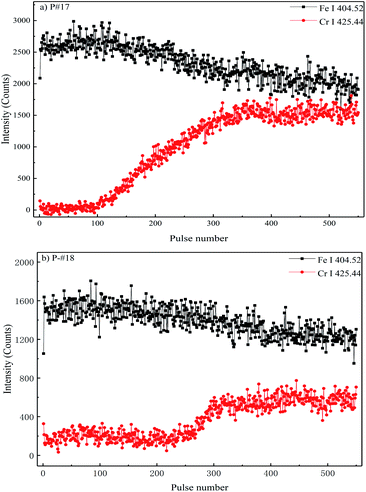 | ||
| Fig. 3 Emission intensity variations of the matrix element (Fe) and alloying element (Cr) along the radial direction for the specimens (a) P-#17 and (b) P-#18. | ||
In order to accurately identify the boundary between the surface oxides and the matrix to obtain the representative spectrum of the industrial pipe matrix, a linear correlation analysis between the representative spectrum with the surface oxide removed and the corresponding industrial pipe spectrum along the radial direction were carried out. The variations of the correlation coefficient were combined with the line intensities along the radial direction to accurately identify the boundary between the surface oxide and the matrix. The correlation coefficient can be calculated as shown in eqn (4):
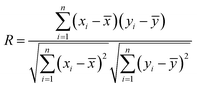 | (4) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) is the mean value of all xi, and ȳ is the average value of all yi.45 The value of R lies between −1 and +1, and can be used to indicate the correlation intensity between x and y. An R-value of near 1 corresponds to the positive correlation when the x and y spectra are from materials with similar chemical constitution. If the R value is near zero, then the x and y are uncorrelated.
is the mean value of all xi, and ȳ is the average value of all yi.45 The value of R lies between −1 and +1, and can be used to indicate the correlation intensity between x and y. An R-value of near 1 corresponds to the positive correlation when the x and y spectra are from materials with similar chemical constitution. If the R value is near zero, then the x and y are uncorrelated.
The results of the correlation along the radial direction of the pipe are shown in Fig. 4, and the correlation coefficient R is the mean value calculated at five different positions of the industrial pipe. It can be found that when the laser had just started to ablate the industrial pipe, the correlation between the spectrum data and the matrix spectrum was low due to the surface deposits, and the matrix composition is obviously different. As the pulse number increases, the deposits on the surface are gradually cleaned by the laser, and the laser starts to act on the outer oxide layer on the steel surface. It can be seen that there is a significant increase in the correlation. In the inner oxide layer, the correlation coefficient gradually increased. This is because the closer the inner layer is to the matrix, the more similar to the matrix the composition and structure become. In Fig. 4, the vertical blue line represents the location of the interface between the inner layer and outer layer, and the vertical red line represents the location of the interface between the oxide layer and matrix. The thickness and composition of the oxide layer are principally governed by the alloy composition, service temperature and time.46 For specimens P-#17 and P-#18, taking the spectra averaged from the 280th–320th and 350th–390th pulses as the representative spectrum of the matrix, their correlation coefficients are 0.89 and 0.88, respectively. The spectral average of the 40 pulses after the spectral line intensities reached a stable tendency were selected as the representative spectrum of the matrix. The results demonstrate that the R values can be used to easily distinguish the interface between the oxide and the matrix.
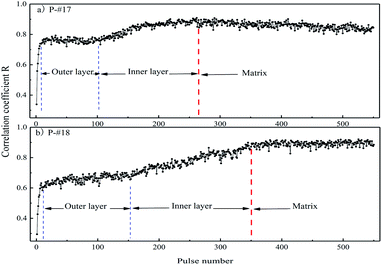 | ||
| Fig. 4 Correlation between the industrial pipe spectrum along the radial direction and the representative spectrum of the corresponding reference for (a) P-#17 and (b) P-#18. | ||
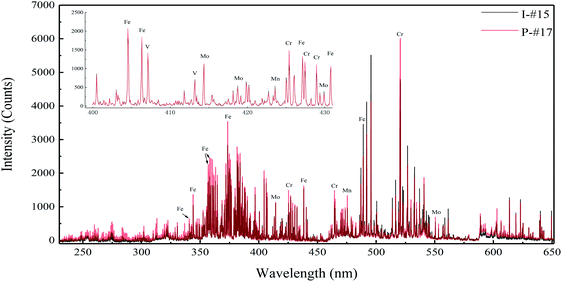
4.2 Spectral characteristics of different surface states
The representative spectra of different surface states of the superheater sample in the range of 230–650 nm are shown in Fig. 5. The black line is the representative spectrum of the I-#15 specimen with the surface oxide removed, and the red line is the representative spectrum of industrial pipe P-#17. The matrix element (Fe) and alloying elements (Cr, Mn, Mo) of the specimens can be well detected and resolved, and the spectra of the different surface states are generally in good agreement. The characteristic spectrum has a good consistency that can be clearly observed in the enlarged image of the 400–432 nm band in Fig. 5. However, there are still some differences in the spectra at some characteristic peaks and background signals, which are mainly attributed to the non-uniform ablation process and the redeposition of the ablated materials. The sample surface would be ablated to produce a conical crater due to the Gaussian energy distribution of the incident laser beam, and the ablated region spreads over the edge gradually. Therefore, the surface oxide layer will inevitably interfere with the spectral characteristics of the steel matrix.Generally, based on the assumption of local thermodynamic equilibrium (LTE) conditions, the integrated line intensity of a given elements can be represented as:
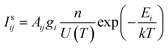 | (5) |
In order to investigate the interference of the oxide layer on the spectrum of the matrix, the plasma temperature and electron density were obtained from the specimens with and without the surface oxide. The plasma temperature was estimated using the Boltzmann plot approach, which has been described elsewhere.47,48 The spectral lines used for plasma temperature estimation are listed in Table 2. As shown in Fig. 6(a), the plasma temperature of I-#15 (with the surface oxide removed), P-#17 (with surface oxide interference) is 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431 K and 12
431 K and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 480 K, respectively; for I-#16 (with the surface oxide removed), P-#18 (with surface oxide interference), it is 13
480 K, respectively; for I-#16 (with the surface oxide removed), P-#18 (with surface oxide interference), it is 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571 K and 11
571 K and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 K, respectively.
460 K, respectively.
| NIST λ (nm) | A ij g i (s−1) | E i (eV) |
|---|---|---|
| Fe I 356.50 | 3.86 × 108 | 0.96 |
| Fe I 402.14 | 7.70 × 107 | 2.76 |
| Fe I 411.80 | 6.45 × 108 | 3.57 |
| Fe I 432.58 | 3.61 × 108 | 1.61 |
| Fe I 438.34 | 5.50 × 108 | 1.48 |
| Fe I 487.08 | 1.22 × 108 | 2.87 |
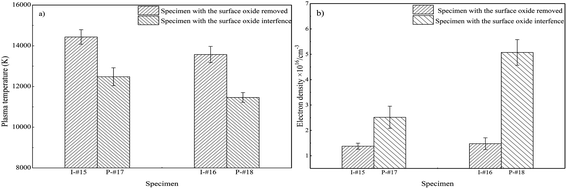 | ||
| Fig. 6 Plasma parameters of different surface states: (a) plasma temperature and (b) electron density. The error bars indicate the standard deviation of five measuring positions. | ||
The electron number density is calculated using the Stark broadening, and eqn (6) relates the full width at half maximum (FWHM) of a spectral line (Δλ1/2) with the electron number density Ne:49,50
Ne = [a0 + a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δλ1/2 + a2(ln Δλ1/2 + a2(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δλ1/2)2 + a3(ln Δλ1/2)2 + a3(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δλ1/2)3]Δλ1/23/21013 Δλ1/2)3]Δλ1/23/21013 | (6) |
It was found that the surface oxide layer decreased the plasma temperature of the matrix and increased the electron density. T and Ne show different trends for the same sample, which can be explained by the presence of an oxide layer on the metal surface due to the geometrical effect of collecting a smaller amount of light as the number of laser shots increases and the plasma plunges into the crater; T and Ne have different responses to this effect. Therefore, the influence of the surface oxide on the matrix plasma cannot be ignored. It is worth mentioning that the influence law of the surface oxide on the matrix plasma is the major concern, which allows a certain deviation in the calculated values of the plasma parameters.
4.3 Aging grade estimation based on spectrum correction
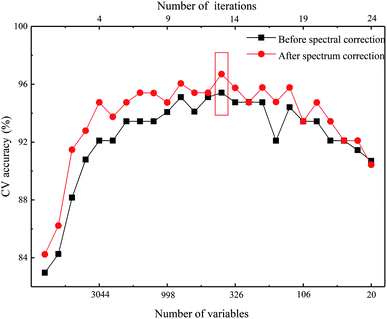
As mentioned above, the collected matrix spectrum will inevitably contain interference due to the laser cleaning of the surface oxides. In order to evaluate the aging grade of industrial pipes, it is necessary to correct for the interference of the surface oxides on the matrix spectrum. Before correcting for the oxide layer interference, to balance the relative importance of the spectral variables and rescale their range, the spectral data were preprocessed using standard normal variate (referred to as standardization, applied to each variable). It was found that the correlation coefficient between the representative spectrum of specimen P-#17 and the corresponding spectrum with the oxide interference removed increased from 0.89 to 0.91. The MSC method was then used to correct the representative spectra at different positions of the same specimen, and the correlation coefficient was increased to 0.94.There were 5944 features in the original spectra; thus, the algorithm was run for 25 iterations with K-SVM-RFE and the features were reduced from 5944 to 20 features. The five-fold CV accuracy of the training set with different feature subsets is shown in Fig. 7. To show the influence of spectrum correction on feature selection by K-SVM-RFE, the red corrected result curve and black original result curve are depicted and compared. It can be seen that the optimal feature subsets before and after the correction are obtained at iteration 14, the size of the feature subset is 776, and the CV accuracy of training set is 95.42% and 96.7% respectively. It should be pointed out that the feature subset with the best performance is determined by the highest point of the CV result curve. With regards to the resulting curves after spectrum correction, the CV accuracy is improved by gradually eliminating the irrelevant features before selecting the optimal feature subset. When the model further eliminated the irrelevant features of the subset after iteration 14, the CV accuracy steadily decreased. The results indicate that the model performance can be improved by spectrum correction within a certain range of selected variable number.
The results of the prediction models built with the selected features are shown in Table 3, which shows that the prediction accuracy of the SVM model testing samples is significantly improved (from 80.56% to 84.72%) after spectrum correction. Moreover, the classification accuracy of the data of the industrial pipe samples P-#16 and P-#18 after spectral correction is similar to the corresponding samples P-#15 and P-#17 with mechanical polishing to eliminate surface oxide interference. This indicates that MSC can effectively correct for the interference of the surface oxide layer of the steel on the spectrum of the matrix and improve the estimation of the steel aging grade.
| Spectral pretreatment | Prediction accuracy | Misclassification number of the testing samples |
|---|---|---|
| Before spectrum correction | 80.56% | #4 (1), #14 (2), #15 (2), #16 (4), #17 (2), #18 (3) |
| After spectrum correction | 84.72% | #4 (2), #14 (1), #15 (1), #16 (2), #17 (3), #18 (2) |
5. Conclusions
In this work, the representative spectra of the matrix were obtained by combining depth profiling analysis and correlation analysis, and the extension of the aging grade estimation from artificial specimens to industrial pipes was realized through spectral correction. It was found that the correlation analysis combined with line intensities along the radial direction can accurately identify the boundary between the surface oxide and the matrix, but the previously ablated layers influence the measurement by LIBS with successive laser ablation shots. The surface oxide on the steel decreased the plasma temperature of the matrix and increased the electron density. Therefore, the MSC was applied to correct for the interference of the surface oxide layer, and K-SVM-RFE was exploited to select the optimal feature subset. The estimation model of the aging grade was established with the corresponding optimal feature subsets, and the accuracy of the model was 84.72%. In addition, the estimation model of the aging grade performed similarly for the industrial pipe and the corresponding specimens with mechanical polishing to eliminate surface oxide. This evaluation method illustrates that LIBS can be exploited in the field of material damage diagnosis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Natural Science Foundation of China (No. 51976064), the Guangdong Basic and Applied Basic Research Foundation (2020A1515010646), and the Science and Technology Planning Project of Guangzhou (202102020726). We also acknowledge the support from the Guangdong Province Key Laboratory of Efficient and Clean Energy Utilization (2013A061401005).References
- S. V. Panin, P. O. Maruschak, I. V. Vlasov and B. B. Ovechkin, Theor. Appl. Fract. Mech., 2016, 83, 105–113 CrossRef CAS.
- R. Viswanathan, K. Coleman and U. Rao, Int. J. Pressure Vessels Piping, 2006, 83, 778–783 CrossRef CAS.
- B. Fournier, M. Sauzay, F. Barcelo, E. Rauch, A. Renault, T. Cozzika, L. Dupuy and A. Pineau, Metall. Mater. Trans. A, 2008, 40, 330–341 CrossRef.
- F.-s. Yin, W.-s. Jung and S.-h. Chung, Scr. Mater., 2007, 57, 469–472 CrossRef CAS.
- X. Wu, Y. Yang, Q. Zhan and Z. Hu, J. Mater. Eng. Perform., 1998, 7, 667–672 CrossRef CAS.
- Y. Chen, K. Sridharan and T. Allen, Corros. Sci., 2006, 48, 2843–2854 CrossRef CAS.
- N. D. A. R. China, DL/T 884-2004.
- T. Yuan, Z. Wang, S.-L. Lui, Y. Fu, Z. Li, J. Liu and W. Ni, J. Anal. At. Spectrom., 2013, 28, 1045–1053 RSC.
- M. O. Vieitez, J. Hedberg, O. Launila and L.-E. Berg, Spectrochim. Acta, Part B, 2005, 60, 920–925 CrossRef.
- E. Yang, W. Liao, Q. Lin, H. An, D. Li, F. Wei and Y. Duan, Anal. Chem., 2020, 92, 8090–8096 CrossRef CAS.
- L. Sun, H. Yu, Z. Cong, Y. Xin, Y. Li and L. Qi, Spectrochim. Acta, Part B, 2015, 112, 40–48 CrossRef CAS.
- Y. Zhang, M. Dong, L. Cheng, L. Wei, J. Cai and J. Lu, J. Anal. At. Spectrom., 2020, 35, 810–818 RSC.
- W. Li, M. Dong, S. Lu, S. Li, L. Wei, J. Huang and J. Lu, Anal. Methods, 2019, 11, 4471–4480 RSC.
- Z. A. Abdel-Salam, A. H. Galmed, E. Tognoni and M. A. Harith, Spectrochim. Acta, Part B, 2007, 62, 1343–1347 CrossRef.
- D. Bulajic, G. Cristoforetti, M. Corsi, M. Hidalgo, S. Legnaioli, V. Palleschi, A. Salvetti, E. Tognoni, S. Green, D. Bates, A. Steiger, J. Fonseca, J. Martins, J. McKay, B. Tozer, D. Wells, R. Wells and M. A. Harith, Spectrochim. Acta, Part B, 2002, 57, 1181–1192 CrossRef.
- T. Delgado, J. Ruiz, L. M. Cabalín and J. J. Laserna, J. Anal. At. Spectrom., 2016, 31, 2242–2252 RSC.
- S. Nasrazadani and H. Namduri, Spectrochim. Acta, Part B, 2006, 61, 565–571 CrossRef.
- S. Yao, J. Lu, K. Chen, S. Pan, J. Li and M. Dong, Appl. Surf. Sci., 2011, 257, 3103–3110 CrossRef CAS.
- J. Li, J. Lu, Y. Dai, M. Dong, W. Zhong and S. Yao, Appl. Surf. Sci., 2015, 346, 302–310 CrossRef CAS.
- S. Lu, M. Dong, Q. Chen, J. Huang, Y. Yu and J. Lu, Spectrochim. Acta, Part B, 2019, 151, 1–11 CrossRef CAS.
- S. Lu, M. Dong, J. Huang, W. Li, J. Lu and J. Li, Spectrochim. Acta, Part B, 2018, 140, 35–43 CrossRef CAS.
- S. Lu, S. Shen, J. Huang, M. Dong, J. Lu and W. Li, Spectrochim. Acta, Part B, 2018, 150, 49–58 CrossRef CAS.
- J. Huang, M. Dong, S. Lu, W. Li, J. Lu, C. Liu and J. H. Yoo, J. Anal. At. Spectrom., 2018, 33, 720–729 RSC.
- J. Huang, M. Dong, S. Lu, Y. Yu, C. Liu, J. H. Yoo and J. Lu, Analyst, 2019, 144, 3736–3745 RSC.
- J. Cai, M. Dong, Y. Zhang, Y. Chen, H. Chen, Y. Liang, W. Li and J. Lu, At. Spectrosc., 2021, 42, 43–50 CrossRef CAS.
- J. Karhunen, A. Hakola, J. Likonen, A. Lissovski, M. Laan and P. Paris, J. Nucl. Mater., 2015, 463, 931–935 CrossRef CAS.
- M. D. Mowery, R. Sing, J. Kirsch, A. Razaghi, S. Béchard and R. A. Reed, J. Pharm. Biomed. Anal., 2002, 28, 935–943 CrossRef CAS PubMed.
- R. Hai, N. Farid, D. Zhao, L. Zhang, J. Liu, H. Ding, J. Wu and G.-N. Luo, Spectrochim. Acta, Part B, 2013, 87, 147–152 CrossRef CAS.
- Q. Xiao, A. Huber, G. Sergienko, B. Schweer, P. Mertens, A. Kubina, V. Philipps and H. Ding, Fusion Eng. Des., 2013, 88, 1813–1817 CrossRef CAS.
- H. Balzer, S. Holters, V. Sturm and R. Noll, Anal. Bioanal. Chem., 2006, 385, 234–239 CrossRef CAS PubMed.
- M. Schütze, M. Schorr, D. P. Renusch, A. Donchev and J. P. T. Vossen, Mater. Res., 2004, 7, 111–123 CrossRef.
- M. Dong, L. Wei, J. Lu, W. Li, S. Lu, S. Li, C. Liu and J. H. Yoo, J. Anal. At. Spectrom., 2019, 34, 480–488 RSC.
- Y. W. Chu, S. S. Tang, S. X. Ma, Y. Y. Ma, Z. Q. Hao, Y. M. Guo, L. B. Guo, Y. F. Lu and X. Y. Zeng, Opt. Express, 2018, 26, 10119–10127 CrossRef CAS PubMed.
- H. Chen, Q. Song, G. Tang, Q. Feng and L. Lin, ISRN Spectrosc., 2013, 642190, 1–9 CAS.
- X. Li, T. Liu, P. Tao, C. Wang and L. Chen, Comput. Biol. Chem., 2015, 59, 95–100 CrossRef CAS.
- B. K. Li, Y. Cong, X. G. Yang, Y. Xue and Y. Z. Chen, Comput. Biol. Med., 2013, 43, 395–404 CrossRef CAS.
- M. Dong, L. Wei, J. J. Gonzalez, D. Oropeza, J. Chirinos, X. Mao, J. Lu and R. E. Russo, Anal. Chem., 2020, 92, 7003–7010 CrossRef CAS PubMed.
- S. Mishra and D. Mishra, Karbala Int. J. Mod. Sci., 2015, 1, 86–96 CrossRef.
- X. Lin, F. Yang, L. Zhou, P. Yin, H. Kong, W. Xing, X. Lu, L. Jia, Q. Wang and G. Xu, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2012, 910, 149–155 CrossRef CAS.
- L. Nørgaard, A. Saudland, J. Wagner, J. P. Nielsen, L. Munck and S. B. Engelsen, Appl. Spectrosc., 2000, 54, 413–419 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2012, 12, 2825–2830 Search PubMed.
- X. Zhong, X. Wu and E.-H. Han, J. Supercrit. Fluids, 2012, 72, 68–77 CrossRef CAS.
- A. M. Olmedo, M. G. Alvarez, G. Domínguez and R. Bordoni, Procedia Mater. Sci., 2012, 1, 543–549 CrossRef CAS.
- D. Laverde, T. Gómez-Acebo and F. Castro, Corros. Sci., 2004, 46, 613–631 CrossRef CAS.
- M. P. Mateo, G. Nicolas, V. Piñon and A. Yañez, Surf. Interface Anal., 2006, 38, 941–948 CrossRef CAS.
- R. Viswanathan, J. Sarver and J. M. Tanzosh, J. Mater. Eng. Perform., 2006, 15, 255–274 CrossRef CAS.
- P. Stavropoulos, C. Palagas, G. N. Angelopoulos, D. N. Papamantellos and S. Couris, Spectrochim. Acta, Part B, 2004, 59, 1885–1892 CrossRef.
- S. Rai, A. K. Rai and S. N. Thakur, Appl. Phys. B: Lasers Opt., 2008, 91, 645–650 CrossRef CAS.
- P. Boumans, Inductively Coupled Plasma Emission Spectroscopy, 1987 Search PubMed.
- R. Dai, J. Li, W. Li, X. Dong and J. Lu, Acta Photonica Sin., 2016, 45, 1–7 CrossRef.
Footnote |
| † Present address: No. 381 Wushan Road, Tianhe District, School of Electric Power, South China University of Technology, Guangzhou, Guangdong, 510640, China. |
| This journal is © The Royal Society of Chemistry 2022 |