Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrokinetic deterministic lateral displacement for fractionation of vesicles and nano-particles†
Richard J.
Gillams
 ab,
Victor
Calero
ab,
Victor
Calero
 ac,
Raul
Fernandez-Mateo
ac,
Raul
Fernandez-Mateo
 a and
Hywel
Morgan
a and
Hywel
Morgan
 *ab
*ab
aSchool of Electronics and Computer Science, University of Southampton, UK. E-mail: hm@ecs.soton.ac.uk
bInstitute for Life Sciences, University of Southampton, UK
cInternational Iberian Nanotechnology Laboratory (INL), Braga, Portugal
First published on 30th August 2022
Abstract
We describe fractionation of sub-micron vesicles and particles suspended in high conductivity electrolytes using an electrokinetically biased Deterministic Lateral Displacement (DLD) device. An optimised, asymmetric array of micron-sized pillars and gaps, with an AC electric field applied orthogonal to the fluid flow gives an approximately ten-fold reduction in the intrinsic critical diameter (Dc) of the device. The asymmetry in the device maximises the throughput. Fractionation of populations of 100 nm and 400 nm extruded vesicles is achieved in 690 mS m−1 KCl, and 100 nm, 200 nm and 500 nm polystyrene particles in 105 mS m−1 KCl. The electrokinetically biased DLD may provide solutions for simple and rapid isolation of extracellular vesicles.
Introduction
Nanoparticles play an important role in a wide range of industrial and healthcare applications. In the context of healthcare, extracellular vesicles (EVs) are of particular importance due to their role in inter-cellular communication,1–3 and are produced by a myriad of cells and organisms.4–6 EV isolation techniques have been developed for a broad variety of sample types, but processing large samples requires costly and time-consuming approaches. The ability to process small volumes rapidly will facilitate population level studies leading to a step change in the understanding of variation in EVs between individuals.The size of small extracellular vesicles is in the range of 30–250 nm diameter.7 Effective techniques for isolation of larger microvesicles have been developed,8,9 and there have been recent developments in methods for the isolation of extracellular vesicles.8,10,11 Due to the small size of EVs, a high level of precision is required for efficient separation. This often results in compromised volumetric throughput as seen with classical nanoscale Deterministic Lateral Displacement (DLD) devices.12 Miniaturisation enhances the control and selectivity, but narrow channels lead to high back pressure and low flow rates. An alternative is to redesign the system to enhance separation without constricting the flow of liquid through the device, either by optimising the channel geometry or by introducing external fields which influence the particle trajectory. This has been demonstrated for DLD devices where non-uniform electric fields are applied to the microfluidic channel.13–17
Deterministic lateral displacement (DLD) devices
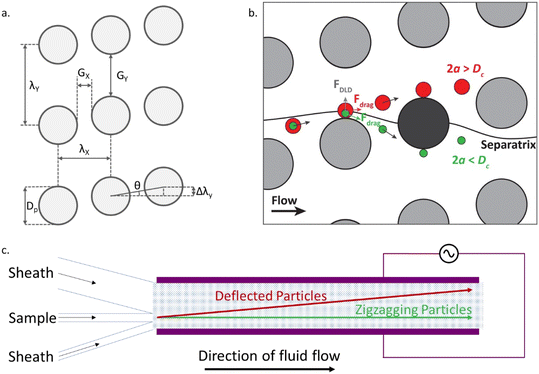
DLD devices comprise of an array of pillars within a fluidic channel as shown in Fig. 1(a). The geometrical arrangement of pillars includes a tilting angle θ, away from the direction of fluid flow, resulting in a lateral offset Δλy, between consecutive rows of pillars. The periodicity of the array, N = λy/Δλy, is defined such that with each set of N pillars the total lateral offset is equal to the lateral repeat distance λy. The devices used in the present work have a tilt angle (θ) of 2.15°.The fluid in the channel, constrained by the channel walls, flows in a zigzag fashion around the pillars, such that it maintains a straight net course. In the absence of other effects, the Stokes drag force moves particles along this liquid flow, causing particles to move through a downstream gap (Gx) once within each period of the array, as shown for the green particle in Fig. 1(b). To determine whether a particle can pass through the downstream gap, a flow line known as the separatrix is considered. The separatrix passes over a pillar and bisects the subsequent pillar. If a particle travels below the separatrix it will follow the zigzagging motion. However, particles with a size greater than a critical diameter Dc, are not able to pass through the downstream gap due to hydrodynamic forces. This causes the larger particles to be successively deflected, following the red particle trajectories shown in Fig. 1(b). The net effect of multiple successive deflections over the length of the channel leads to the formation of two distinct populations following the zigzagging (straight) or bumping (deflected) paths (Fig. 1(c)).
A simple DLD device design typically consists of a symmetric array of pillars, where Gx = Gy (Fig. 1a). Often the pillar diameter Dp, is also equal to the gap size. Symmetric designs have been well characterised, with an empirical formula to calculate the critical diameter Dc.18 In the work presented here, two enhancements are incorporated into the design. The first is the addition of an electric field across the channel and the second is an asymmetric pillar array, where Gx ≠ Gy. These two features work together leading to significant improvements in device performance. In particular the asymmetric design provides enhanced electrokinetic driven deflection due to the distortion of the electric field by the pillars.
Electrokinetic DLD
In the absence of an electric field, Dc is defined by the geometric design of the pillar array, and therefore it is fixed for a particular device. If an electric field is applied to the device this creates additional electrokinetic forces providing a way to tune the particle trajectories and induce deflection of particles smaller than the critical diameter across the DLD device.14,15,17 Recently Calero et al.13,17 characterised two distinct mechanisms that modify the trajectory of particles in two frequency regimes: low (<1 kHz) and high (>1 kHz) frequency.At low frequencies, there is a rich set of phenomena that depends on the surface conductance which include particle oscillations along the electric field lines due to electrophoresis (EP), and concentration-polarization electroosmosis (CPEO)19,20 which induce particle-wall repulsion.21 The combined action of these phenomena leads to new ways of enhancing the separation of particles in a DLD array.17,22 However, these effects are restricted to low conductivity electrolytes, since the relative importance of surface conductance, described by the Dukhin number (Du), diminishes at high conductivities and thus disappear at physiological conductivities.
At high frequencies particle behaviour is dominated by dielectrophoretic (DEP) forces. In this paper we exploit this phenomenon to achieve fractionation of nanoparticles in high conductivity electrolytes (necessary for processing biological samples). The DEP phenomenon occurs when a polarisable particle is exposed to a non-uniform electric field, defined by the following equation:
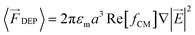 | (1) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) CM). If the particle is more polarisable than the medium Re [fCM] > 0, it is attracted towards the high electric field gradients and this is termed positive DEP (pDEP). On the contrary, if the particle is less polarisable than the medium Re [fCM] < 0, it is repelled from the high electric field gradients and this is termed negative DEP (nDEP).
CM). If the particle is more polarisable than the medium Re [fCM] > 0, it is attracted towards the high electric field gradients and this is termed positive DEP (pDEP). On the contrary, if the particle is less polarisable than the medium Re [fCM] < 0, it is repelled from the high electric field gradients and this is termed negative DEP (nDEP).
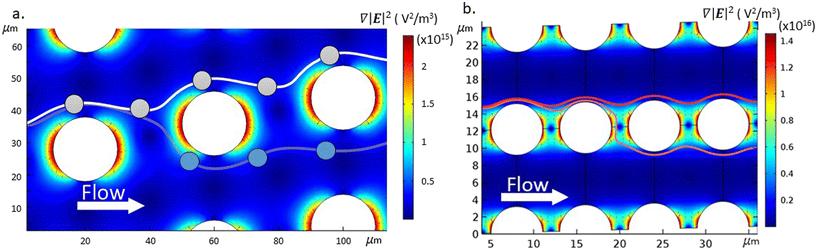
To introduce a DEP force into the DLD systems an electric field is applied orthogonal to the fluid flow using microfabricated planar electrodes (Fig. 1). The insulating pillars distort the electric field generating high field gradients in the horizontal gaps (Gx) between the pillars as shown in Fig. 2. Particles experiencing nDEP are repelled from these gaps as they travel along the channels. If the nDEP force is strong enough to overcome the fluid flow, the particles are prevented from zigzagging between the pillars and are forced to follow the deviation angle of the array. This effect only occurs for nDEP and is particularly suitable for high conductivity electrolytes where nDEP forces dominate across a wide range of frequencies. Furthermore, the use of high frequency AC signals minimises any by products from Faradaic reactions.
Materials and methods
Asymmetric DLD design
As shown by eqn (1), the DEP force scales with particle volume, which highlights the difficulty of using DEP to divert the trajectories of very small particles inside the DLD. Therefore, to increase the influence of the DEP force acting on the particles, the DLD micro-pillar array was designed to have small dimensions and asymmetric gaps (Gx ≠ Gy) and a small tilting angle. Asymmetric devices have previously been shown to enhance the separation of non-spherical particles.23The asymmetric design has a lateral gap Gy, and pillar diameter Dp of 6 μm, and a downstream gap Gx, of 2 μm. The critical diameter Dc was experimentally determined using spherical polystyrene beads to be between 1 μm and 1.5 μm. A schematic of the device is shown in Fig. 1(c) and consists of a channel with a pair of planar electrodes along either side. When a voltage is applied to these electrodes, an electric field is created across the channel, perpendicular to the direction of flow. The field is distorted by the presence of the insulating pillars of the DLD array. Thus when combined with an AC electric field, the benefits of the asymmetric pillar array are realised. The small downstream gap, Gx, produces a region of high electric field gradient, leading to stronger negative DEP forces, which can effectively block the zig-zag path.
Fig. 2 shows the regions of high electric field gradient on the upstream and downstream sides of the pillars, highlighting the benefits of the reduced downstream gap size.
Calculated trajectories of a 500 nm particle in the presence (red) and absence (magenta) of an electric field are superimposed on Fig. 2(b). With no electric field, as the 500 nm particle reaches the second pillar, the particle moves close to the pillar so that passing within the separatrix and following the fluid flow through the downstream gap between the pillars. However, in the presence of the electric field the particle experiences a nDEP force that deflects it, such that every time it passes a pillar it is above the separatrix and so bumps along the tilted array.
It is also important to consider the role of the tilt angle θ in DEP driven particle deflection in the DLD arrays.24 The small tilt angle for the DLD post arrays used in this work (θ = 2.15°) reduces the fluid drag that drive the particles to cross the downstream gap. Thus, the magnitude of the DEP force required to switch from zigzag to bumping mode decreases, reducing the minimum particle size that can be deflected in the channels for a given applied electric field.
Device fabrication
The devices were fabricated using standard photolithography. A 5 μm layer of photoresist (SU8-3005) was spun onto a silicon wafer and after baking exposed to UV light through a photomask to create a negative impression of the channel and pillar array. Devices were cast from this wafer in polydimethylsiloxane (PDMS). Electrodes were made from platinum on glass, and the PDMS channels were plasma bonded to this glass substrate ensuring correct alignment of the electrodes along the edge of the channel. The array is located in a channel which is 31.2 mm long with spacing between the electrodes of 1.1 mm. Prior to experiments, the device was primed with Pluronics® F-127 solution 0.1% (w/w) to avoid particles sticking to the PDMS/liquid interface.Polystyrene nanoparticle sample preparation
Suspensions of particles were prepared by diluting Fluoresbrite® YG carboxylate microspheres (Polysciences) in potassium chloride solutions with a conductivity of 105 mS m−1. The particles used were 100 nm (coefficient of variance (CV) = 10%), 200 nm (CV = 5%) and 500 nm (CV = 3%), diluted to 0.025% w/w suspensions.Lipid vesicle sample preparation
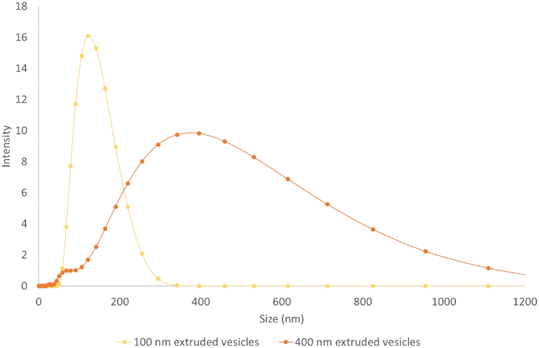
Lipid vesicles were prepared by dissolving a lipid mixture in chloroform and drying overnight before rehydrating with 690 mS m−1 KCl solution to a final lipid concentration of 1 mg mL−1. The main lipid component was the zwitterionic 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), doped with 2% (mol mol−1) fluorescently tagged 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt) (RhodPE) (Avanti Polar Lipids). After rehydration the lipids were periodically mixed for an hour before being extruded (11 passes) through a Nuclepore membrane nano-porous filter (Whatman). Two sizes of vesicle were produced for this work, by extruding through either a 100 nm pore filter or a 400 nm pore filter. The resulting vesicles were sized using a Zetasizer Nano ZS (Malvern Panalytical) and the size distributions are shown in Fig. 3.Experimental setup
The channel inlets (Fig. 1(c)) were connected to liquid reservoirs under positive pressure, with the pressure in each of the three reservoirs controlled independently using a pressure controller (Elveflow® OB1 MK3). The experiments described in this manuscript were run at 50 mbar, leading to residence times of the sample in the device of approximately 330 s. The estimated throughput under these conditions is 1.3 μL h−1. The outer inlets contain sheath fluid (electrolyte containing no particles) and the central inlet contains the sample. The geometry of the inlets and selected flow rates, cause the sample to enter the channel close to (but not in contact with) one of the electrodes. The array of pillars is such that in bumping mode, the particles will be laterally displaced across the channel. The degree of deflection was calculated through the analysis of microscope images collected near the outlet of the channel.A signal generator (TTi Inc TGA12104) and amplifier (Trek PZD700A) capable of providing a range of voltages up to 400 V peak to peak and a frequency up to 100 kHz, provide an AC voltage to the electrodes. A 10 μF capacitor was placed in series with the electrodes to remove any DC offset. The voltage and frequency were monitored with an oscilloscope (Agilent Technologies DSO3202A).
Results and discussion
The effects of the dielectrophoresis can be observed in the simplest case by placing a suspension of particles (in this case fluorescently labelled 160 nm DOPC/RhodPE vesicles in 105 mS m−1 KCl solution) in the channel in the absence of fluid flow.Fig. 4 shows quantitatively that the particles move away from the regions of highest electric field gradient identified in Fig. 2(b). In the absence of fluid flow and applied field, the particles are found evenly distributed throughout the channel, as seen in Fig. 4(a). Upon the application of the electric field (Fig. 4(b)) the vesicles are seen to move out of the small downstream gaps between the pillars and adopt positions in the larger lateral gaps. When considered in the context of the DLD device, this driving force moving particles away from the downstream gaps contributes towards the propensity for a particle to adopt the deflected trajectory. If the nDEP force is large enough relative to the fluid drag force, the particle will no longer pass through the downstream gap (once per array period) and so will not follow the zigzag path but the deviation angle.
In the absence of fluid flow, the nDEP forces are strong enough to overcome the Brownian motion and to confine the particles to areas of relatively low electric field gradient. As shown in Fig. 2(b) the areas between the pillars have high electric field gradient and so the vesicles are repelled from these regions. In the presence of fluid flow, the Stokes drag force combines with the DEP force to determine the particle trajectory. Under flow the DEP force alters the particle trajectory as the particles pass close to the pillars. Where the combined force causes successive bumping on pillars, the particles will be deflected across the channel.
At the outlet of the device, the channel was imaged using an inverted microscope (Zeiss Axiovert 200) and a camera (Hamamatsu ORCA-ER C4742-95) to quantify the deflection of the particles. The particles and vesicles studied here are significantly smaller than the critical diameter (Dc) of the pillar array and so in the absence of an applied electric field, the particles move along the zigzag trajectory. Given the period of the channel, N = 40, this trajectory involves the particles zigzagging once in every 40 pillars, leading to a net straight trajectory. As the electric field is applied, some particles will experience a strong enough nDEP force to decrease the frequency of the zigzagging events (passing through the downstream gap (Gx)). At high fields and for the largest particles, deflection is observed with every pillar interaction, leading to full displacement across the channel. The array straightens close to the electrode, such that the maximum possible deflection across the channel is approximately 1 mm.
The microscope images were analysed using code written in MATLAB (The MathWorks, Inc., Natick, Massachusetts, USA) to perform a background subtraction, identify the position of the particles and to characterise the distribution of particle positions within the channel. The deflection across the camera sensor in pixels was converted to μm. The results are shown in Fig. 5 and 7, where the data points indicate the centroid of the particle distribution and the error bars one standard deviation in the position.
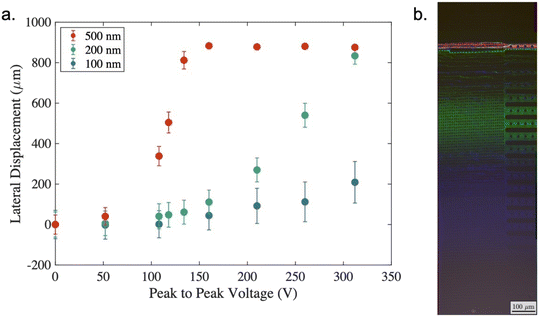
Fig. 5(a) shows results from a series of experiments in which polystyrene nanoparticles of different sizes (100, 200 and 500 nm diameter) were suspended in a solution of KCl with a conductivity of 105 mSm−1. In the absence of a field all three particle sizes adopt the zigzag trajectory as they are significantly below the critical diameter of the device. This is shown by the data at 0 V on the left-hand side of Fig. 5(a). Here, it is also possible to observe the effects of diffusion in the amplitude of the particle bands. The average displacement of a suspended colloid in one dimension is given by:
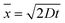 | (2) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /D (where U and
/D (where U and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) are characteristic velocities and lengths, respectively), which in our case, can be re-written as the ratio of the diffusion time to the convection time as:
are characteristic velocities and lengths, respectively), which in our case, can be re-written as the ratio of the diffusion time to the convection time as: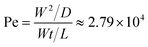 | (3) |
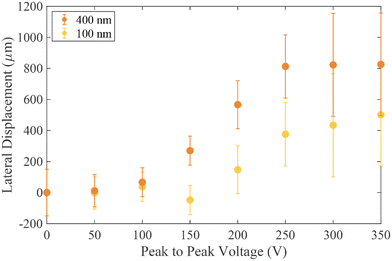
As the applied voltage is increased (with a fixed frequency of 100 kHz), the particle trajectory changes, such that the 500 nm particles (red) move to the deflected trajectory as the applied voltage reaches 100–150 V. At a higher voltage of approximately 250 V the 200 nm particles also change their trajectory and are deflected, however even for the largest voltage around 300 V it is only possible to induce a small deflection of the 100 nm particles. Of note in Fig. 5(a) is the effect observed when 250 Vpp was applied. At this point the 500 nm particles deflect approximately 900 μm, the 200 nm particles experience 540 μm deflection and the 100 nm particles around 100 μm. Microscope images taken under these conditions have been overlaid in Fig. 5(b) to demonstrate the separation. Even considering the distribution in deflection (denoted by the error bars) there is significant separation of the three populations, which enables collection of three distinct fractions.
In order to make these results applicable to the biological assays, the device was also evaluated with vesicles. These particles differ significantly from polystyrene particles. Rather than a solid electrical insulator, the vesicle interior has the same or very similar electrical properties to the external environment. The Clausius–Mossotti factor was calculated by considering the vesicles to be a spherical particle with a single shell (bilayer) with a surface conductance of 1nS.25Fig. 6 shows that the absolute value of the real part of the Clausius–Mossotti factor is very small for vesicles suspended in the KCl solution of 100 mSm−1, and it is not possible to generate significant DEP induced deflection at this conductivity.
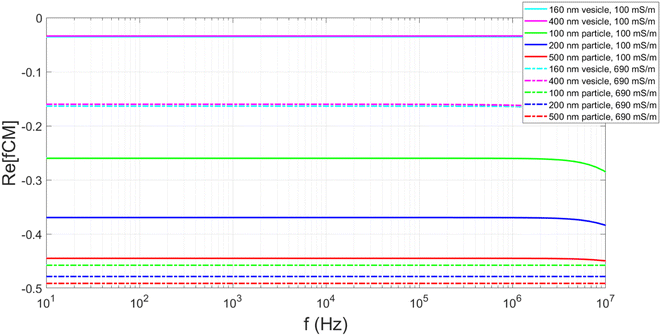 | ||
| Fig. 6 Plots showing the calculated real part of the Clausius–Mossotti factor for polystyrene particles and lipid vesicles suspended in both 100 and 690 mS m−1 KCl solution. Parameters used in the calculations shown in ESI.† | ||
Fig. 6 highlights that the conductivity of the media influences the Clausius–Mossotti factor. Vesicles produced in high conductivity media (690 mSm−1) are more representative of biological systems and calculations show these vesicles have a greater negative real part of the Clausius–Mossotti factor, and therefore experience a stronger nDEP. Fig. 7 summarises results for deflection of two different populations of vesicles in the DLD channel, produced using 100 nm and 400 nm pore sized filters. In the absence of an applied field, no deflection is observed, due to the vesicles being smaller than the Dc of the device. As the voltage is applied (at 100 kHz) and the electric field magnitude is increased, the larger of the two populations is deflected approximately the full width of the channel. The smaller vesicles are only displaced approximately halfway across the channel.
Despite the high conductivity used for these experiments, the effects of Joule heating were negligible and were not observed to alter the particle trajectories. Such effects are expected to be localised in the regions near the electrodes, far from where particles transit given the design of the device.
The vesicles have significant polydispersity in their measured diameters, with a large overlap of the two populations (see Fig. 3). Notwithstanding this, at a voltage of 200 V, two distinct positions are adopted by the 1σ distribution in the vesicle positions at the end of the channel, although not to the same level of separation as seen for the polystyrene particles- see Fig. 5(a). A comparison between Fig. 3 and 7 shows that the degree of deflection is closely matched with the diameter of the vesicle. This is corroborated with experimental observations that for vesicles in the same population, the brighter vesicles were seen to deflect further. The technique used to prepare the vesicles is expected to give a uniform distribution of dyed lipid, and as such the brighter vesicles are likely to be those with a larger diameter, which contain a larger number of lipid molecules and thus more dye. An analysis of the lateral displacement as a function of particle brightness is presented in the ESI.†
Conclusions and outlook
We have demonstrated electrokinetically induced separation of nanoparticle inside a microfluidic DLD device at high electrolyte conductivity and show the potential of this technique to sort nanovesicles. By adjusting the voltage applied across the device, tunable separation has been demonstrated for nanoparticles. At a voltage of 250 V (peak to peak) and a frequency of 100 kHz fractionation of nanoparticles is observed, with three distinct populations appearing at the exit of the channel. Importantly this separation is achieved using micron sized pillars and gaps, with a Dc of approximately 1 μm. The fabrication technique is simple and devices can be operated close to ambient pressure. Compared with other nanoscale DLD devices reported for nanoparticle separation, our technique delivers throughput orders of magnitude higher. Wunsch et al.12 demonstrated fractionation of vesicles and exosomes using a classical nanoDLD array fabricated using nano-lithography. The size of the pillars and gaps were as small as 42 nm. This leads to a very large back pressures (800 kPa) and low a volumetric flow rate (12 nL h−1). By contrast, our simple device uses an orthogonal electric field to decrease the critical diameter by a factor of ten using micron-sized pillars. It therefore has very low back pressure (160 times smaller), with 100 times higher throughput (for a single device). It is also easy to fabricate using standard lithography. Combining multiple device in parallel increases volumetric throughput, for example Smith et al. showed that integrating 1024 nanoDLD arrays in parallel increases the throughput substantially.26For the case of biological samples, vesicles are usually suspended in high salt concentration buffers, and can contain a variety of cargoes, including proteins and nucleic acids. This provides a significant challenge for electrokinetic separation methods. Nevertheless, here we have shown the potential of the electrokinetic actuated DLD to operate within this regime and achieve nanoparticle separation. The benefits of combining the asymmetric pillar array and the use of electrokinetics provides a highly flexible approach for fractionation of nano-bioparticles. With the emergence of low volume methods for analysing vesicle samples27,28 and developments in organ-on-chip technologies,29 such isolation methods will provide new opportunities for on-chip sample analysis.
Data accessibility
All data supporting this study are openly available from the University of Southampton repository at https://doi.org/10.5258/SOTON/D2347.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
RJG, RF-M and HM acknowledge funding from the evFOUNDRY project (H2020-FETOPEN-2016-2017—Project ID: 801367). The authors acknowledge Katie Chamberlain from the Centre of Hybrid Biodevices at the University of Southampton for her support in the fabrication of the devices.References
- L. Macia, R. Nanan, E. Hosseini-Beheshti and G. E. Grau, Int. J. Mol. Sci., 2020, 21 Search PubMed
.
- C. Admyre, S. M. Johansson, K. R. Qazi, J.-J. Filén, R. Lahesmaa, M. Norman, E. P. A. Neve, A. Scheynius and S. Gabrielsson, J. Immunol., 2007, 179, 1969–1978 CrossRef CAS
.
- L. A. Mulcahy, R. C. Pink and D. R. F. Carter, J. Extracell. Vesicles, 2014, 3 Search PubMed
.
- M. Valter, S. Verstockt, J. A. Finalet Ferreiro and I. Cleynen, Journal of Crohn's and Colitis, 2021, 15(3), 499–510 CrossRef CAS PubMed
.
- R. A. Acuña, M. Varas-Godoy, V. M. Berthoud, I. E. Alfaro and M. A. Retamal, Biomolecules, 2020, 10, 676 CrossRef PubMed
.
- V. Chatterjee, X. Yang, Y. Ma, M. H. Wu and S. Y. Yuan, Am. J. Physiol., 2020, 319, H1181–H1196 CAS
.
- S. Busatto, A. Zendrini, A. Radeghieri, L. Paolini, M. Romano, M. Presta and P. Bergese, Biomater. Sci., 2020, 8, 39–63 RSC
.
- K. Lee, H. Shao, R. Weissleder and H. Lee, ACS Nano, 2015, 9, 2321–2327 CrossRef CAS PubMed
.
- S. M. Santana, M. A. Antonyak, R. A. Cerione and B. J. Kirby, Biomed. Microdevices, 2014, 16, 869–877 CrossRef CAS PubMed
.
- C. Liu, J. Guo, F. Tian, N. Yang, F. Yan, Y. Ding, J. Wei, G. Hu, G. Nie and J. Sun, ACS Nano, 2017, 11, 6968–6976 CrossRef CAS PubMed
.
- Y. Wan, G. Cheng, X. Liu, S.-J. Hao, M. Nisic, C.-D. Zhu, Y.-Q. Xia, W.-Q. Li, Z.-G. Wang, W.-L. Zhang, S. J. Rice, A. Sebastian, I. Albert, C. P. Belani and S.-Y. Zheng, Nat. Biomed. Eng., 2017, 1, 0058 CrossRef CAS PubMed
.
- B. H. Wunsch, J. T. Smith, S. M. Gifford, C. Wang, M. Brink, R. L. Bruce, R. H. Austin, G. Stolovitzky and Y. Astier, Nat. Nanotechnol., 2016, 11, 936–940 CrossRef CAS PubMed
.
- V. Calero, P. Garcia-Sanchez, C. M. Fernandes Honrado, A. Ramos and H. Morgan, Lab Chip, 2019, 19, 1386–1396 RSC
.
- J. P. Beech, P. Jönsson and J. O. Tegenfeldt, Lab Chip, 2009, 9, 2698–2706 RSC
.
- J. P. Beech, K. Keim, B. D. Ho, C. Guiducci and J. O. Tegenfeldt, Adv. Mater. Technol., 2019, 4, 1–9 Search PubMed
.
- V. Calero, P. Garcia-Sanchez, A. Ramos and H. Morgan, Biomicrofluidics, 2019, 13, 054110 CrossRef PubMed
.
- V. Calero, P. García-Sánchez, A. Ramos and H. Morgan, J. Chromatogr. A, 2020, 1623, 461151 CrossRef CAS PubMed
.
-
J. A. Davis, Microfluidic Separation of Blood Components through Deterministic Lateral Displacement, PhD thesis, Princeton University, 2008 Search PubMed
.
- V. Calero, R. Fernández-Mateo, H. Morgan, P. Garciá-Sánchez and A. Ramos, Phys. Rev. Appl., 2021, 15, 1 Search PubMed
.
- R. Fernández-Mateo, P. García-Sánchez, V. Calero, H. Morgan and A. Ramos, J. Fluid Mech., 2021, 924, 1–11 Search PubMed
.
- R. Fernández-Mateo, V. Calero, H. Morgan, P. García-Sánchez and A. Ramos, Phys. Rev. Lett., 2022, 128, 74501 CrossRef PubMed
.
- B. D. Ho, J. P. Beech and J. O. Tegenfeldt, Micromachines, 2021, 12, 1–14 Search PubMed
.
- K. K. Zeming, T. Salafi, C.-H. Chen and Y. Zhang, Sci. Rep., 2016, 6, 22934 CrossRef CAS PubMed
.
-
V. Calero, Electrokinetic biased Deterministic Lateral Displacement for particle separation, PhD thesis, University of Southampton, 2021 Search PubMed
.
-
H. Morgan and N. G. Green, AC electrokinetics: colloids and nanoparticles, Research Studies Press, 2003 Search PubMed
.
- J. T. Smith, B. H. Wunsch, N. Dogra, M. E. Ahsen, K. Lee, K. K. Yadav, R. Weil, M. A. Pereira, J. V. Patel, E. A. Duch, J. M. Papalia, M. F. Lofaro, M. Gupta, A. K. Tewari, C. Cordon-Cardo, G. Stolovitzky and S. M. Gifford, Lab Chip, 2018, 18, 3913–3925 RSC
.
- S. Cheng, Y. Li, H. Yan, Y. Wen, X. Zhou, L. Friedman and Y. Zeng, Lab Chip, 2021, 21, 3219–3243 RSC
.
- S. Zhou, T. Hu, F. Zhang, D. Tang, D. Li, J. Cao, W. Wei, Y. Wu and S. Liu, Anal. Chem., 2020, 92, 1574–1581 CrossRef CAS PubMed
.
- E. Ferrari, C. Palma, S. Vesentini, P. Occhetta and M. Rasponi, Biosensors, 2020, 10, 110 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00583b |
| This journal is © The Royal Society of Chemistry 2022 |