Electric-field-based control of molecular magnetism in TMPc/Sc₂CO₂ van der Waals systems

Abstract

Controlling the magnetic states of molecular structures through electric fields is a major challenge in the area of electron spin manipulation, but it can be achieved upon utilizing the sensitivity of the electron distribution at a heterostructure interface. Here, we found that the magnetic states of a transition-metal phthalocyanine (TMPc) can be effectively controlled through switching the polarization state of monolayer Sc₂CO₂ to achieve a transition between the nonmagnetic and magnetic states of some TMPc molecules. Moreover, the magnetic moments of some structures can be regulated through applying an external vertical electric field. These novel characteristics are caused by the effects of an intrinsic or external electric field on the d-orbital electron transfer and orbital splitting of TMPc molecules. In addition, the p–d hybrid orbital in AgPc will also be affected by the external vertical electric field, ultimately changing the magnetic moment. Therefore, we are very interested in these different magnetic effects, and the fascinating phenomena seen in this study could guide the development of ferroelectric control for use in high-performance electronic memory writing, high-density magnetic memory reading, sensors, and other spintronic devices.

---

Introduction

The magnetoelectric effect refers to the coupling of ferroelectricity (FE) and ferromagnetism (FM), which has great potential for use in multifunctional devices.^1–3 It is an effective method for controlling the electron spin states of nanostructures using an electric field.^4,5 In general, there are two degenerate polarization states (P↑ and P↓) in two-dimensional ferroelectric materials, and the out-of-plane electric field depends on the polarization states; a polarized electric field can be used to effectively control the properties of magnetic materials. However, natural multiferroic materials are really rare and the magnetoelectric coupling is usually weak; on the other hand, traditional ferroelectric and ferromagnetic materials have different d-orbital electronic requirements.^6,7 Although there are materials that violate the d₀ rule,⁸ in many cases, it is still pretty challenging to find intense coupling between FE and FM.

In recent years, many two-dimensional (2D) FE materials have been widely studied, such as SnTe,⁹ In₂Se₃,^10,11 Sc₂CO₂,¹² AgBiP₂Se₆,¹³ CuInP₂S₆,^14,15 monolayer WTe₂,¹⁶ monolayer group IV chalcogenides,¹⁷ 2D honeycomb binary compounds,¹⁸ vertically polarized 2D ferroelectric BN, AlN, ZnO, MoS₂, GaSe,¹⁹ transition-metal dihalides,²⁰ and CrSnTe₃.²¹ In addition, theory predicts the existence of a variety of two-dimensional multiferrous materials with coexisting FE and FM, such as C₆N₈H organic networks,²² CrN,²³ Hf₂VC₂F₂,²⁴ and monolayer CrBr₃.²⁵

van der Waals heterostructures provide multiple possibilities for the development of artificial multiferroic materials, usually accompanied by novel physical phenomena and complex coupling principles. For example, the magnetic coupling of CrI₃ bilayers can be switched based on the Sc₂CO₂ polarization state,²⁶via tuning the ferroelectric polarization state in In₂Se₃/FeI₂, the FeI₂ monolayer transforms from ferromagnetic to antiferromagnetic,²⁷ and the polarization state of CuInP₂S₆ monolayers can be switched using an electric field.²⁸ These reports indicate that the use of vdW heterostructures provides a method for achieving artificial multiferroicity.²⁹

In this paper, a two-dimensional artificial multiferroic heterostructure is proposed, which is formed via vdW interactions between a transition-metal phthalocyanine molecule (TMPc) and monolayer Sc₂CO₂. Monolayer Sc₂CO₂ has out-of-plane electric polarization of 1.60 μC cm⁻³, and it has been studied in previous research;³⁰ the position of the carbon atom mainly determines the polarization state, and the energy barrier between up (P↑) and down (P↓) polarization is 0.52 eV per unit.³⁰ Besides, phthalocyanine has been widely used in chemical catalysis^31,32 and has been widely studied in spintronics.^33,34

We consider the case where the central atom of TMPc is a transition metal of the fourth or fifth period. Via first-principles calculations, we found that the magnetic state of TMPc can be switched through tuning the polarization state of the Sc₂CO₂ monolayer, the heterostructure can be switched from a magnetic state to a nonmagnetic state, and an external vertical electric field can control the magnetic moments of some heterostructures. Through further analysis, we know that the coupling variations between TMPc and Sc₂CO₂ are caused by a significant change in the structure arrangement and charge transfer between layers, mainly acting on the d and p orbitals. Moreover, an external electric field can further control charge transfer between layers so that the magnetic moment can be controlled. We also reveal the different origins of the magnetic variations of RuPc (P↑) and AgPc (P↑). Therefore, this research provides a novel method for designing artificial vdW multifunctional nanoelectronics and devices with strong magnetoelectric coupling.

Calculation methods

All the results are obtained based on VASP (the Vienna Ab initio Simulation Package).³⁵ We use the projector-augmented wave (PAW) method³⁶ to indicate the ion potential. For dealing with exchange–correlation effects between electrons, we chose the generalized gradient approximation (GGA) method established based on the Perdew–Burke–Ernzerhof (PBE) functional;³⁷ the Hubbard U correction describes the partial filling of d orbitals, where U_eff = U − J = 3 eV (U = 3, J = 0 eV),³⁸ and different U values do not affect the conclusions. The cutoff energy is 400 eV, and we use 25 Å vacuum space to minimize interactions between adjacent layers. In the relaxation structure, the convergence criterion is that the forces on all atoms are less than at least 0.02 eV Å⁻¹, and that energy variations are less than at least 10⁻⁵ eV. Grimme's zero damping DFT-D3 method³⁹ is used to describe the vdW effects of interlayers. We formed a 5 × 5 Sc₂CO₂ supercell to reduce the interactions of structures; the lattice parameter of Sc₂CO₂ is 3.37 Å, which is similar to previous studies,²⁶ and dipole correction is considered. The differential charge distribution was drawn using Vesta software,⁴⁰ and Bader⁴¹ is used for charge transfer analysis.

Results and discussion

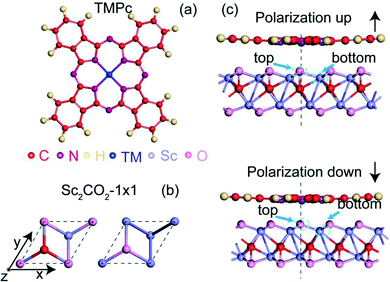
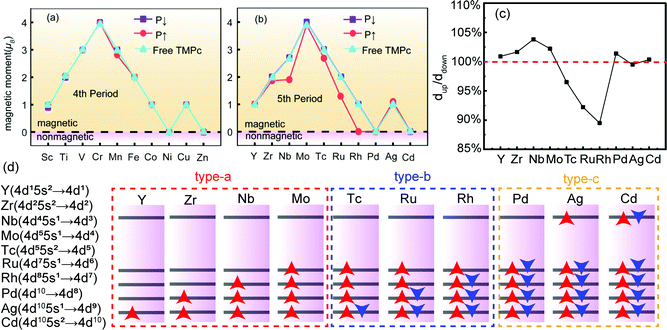
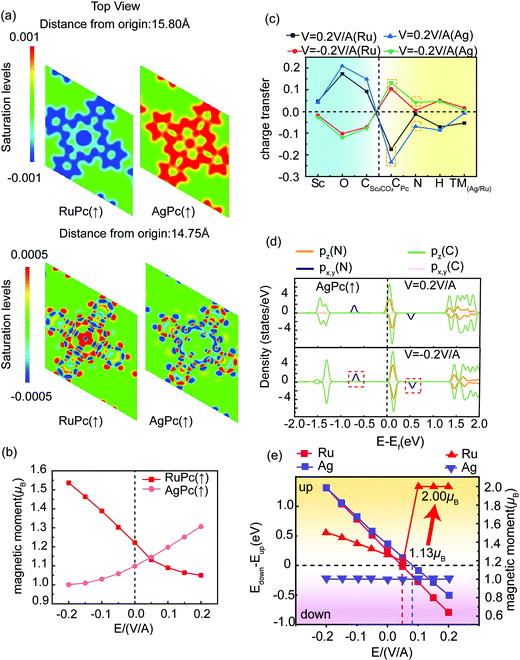
Firstly, we relax the structure to find the lowest-energy adsorption point of a TMPc molecule on Sc₂CO₂, as shown in Fig. 1(c). The TMPc and Sc₂CO₂ relative monolayer positions can be determined via referring to the oxygen atom in the nearest neighbor layer. The relative positions can be divided into top and bottom arrangements. Through rotation and translation, we find that system energy in the top position is lowest. The following research is based on this situation.

Fig. 1 (a and b) Top views of the metal phthalocyanine and a 1 × 1 cell of Sc₂CO₂. (c) Side views of the TMPc/Sc₂CO₂ system with the P↑ and P↓ configurations of the 5 × 5 Sc₂CO₂ supercell monolayer; the arrows point in the out-of-plane polarization direction.

As shown in Fig. 2(a and b), the transition metals of the fourth period show no evident magnetic moment variations on Sc₂CO₂; this may be due to the electronegativities of the fourth-period transition metals generally being weaker than those of the fifth-period transition metals. The energies of electrons occupying 4d and 5s orbitals are higher than those occupying 3d and 4s orbitals, and they can more easily participate in charge transfer processes. In terms of the D_4h symmetric ligand field structure of phthalocyanine, the magnetic variations can be explained based on the “4+1” splitting phenomenon.^42,43 TMPc with a central magnetic atom has four suborbitals of similar energy in its d orbital, while one has much higher energy. For example, the bonding of the central atom and ligands in VPc (3d³ 4s²) causes three electrons to be in close orbitals with lower energy, so the total magnetic moment is 3 μ_B, and with a further increase in d-orbital-filling electrons, such as in the case of MnPc (or with Fe, Co, Tc, Ru, and Rh), the electrons adopt opposite spin states, resulting in diminishing magnetic moments.

Fig. 2 (a and b) The effects of the substrate polarization direction on the magnetic moment when the central atom of the structure is a transition metal from the fourth or fifth period. (c) TMPc (↑) and TMPc (↓) layer distance ratios. (d) TMPc materials (fifth-period TMs) classified according to the change in magnetic moment.

For fifth-period transition-metal atoms, especially Nb, Ru, and Rh, Sc₂CO₂ (P↑) has a significant effect on the magnetic moment of the structure. In particular, the magnetic moment of the RuPc (P↑) structure is 0 μ_B, which means that the introduction of Sc₂CO₂ transforms the magnetic state of RhPc molecules. We mainly analyze the magnetic state transition of RhPc (P↑) and the magnetic moment variations of RuPc (P↑) in the following discussion. In order to explore changes in the interlayer spacing of the heterostructures after Sc₂CO₂ reversal, we plot the fifth-period interlayer spacing ratios in more detail, as shown in Fig. 2(c); systems that are significantly affected by the polarization of the ferroelectric layer show obvious changes in the interlayer spacing ratio, further affecting the electron density distribution and magnetic moment. We can divide the fifth-period systems into three types, the magnetic moment of a type-a material increases as the electrons occupy adjacent quadruple orbitals, while the magnetic moment of a type-b material decreases as the electrons occupy the opposite spin states of the quadruple orbitals. When the quadruple orbitals are fully occupied, the magnetic moment is 0 μ_B, and magnetic moment changes in type-c materials are only related to the electron occupancy of the highest energy suborbitals.

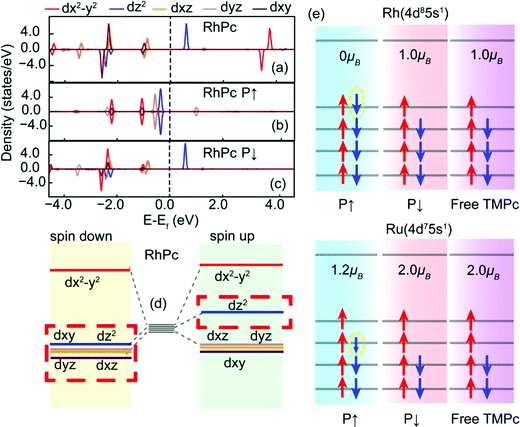
To further assess the magnetic contribution from each d-orbital sublayer in the RhPc system, we provide the following discussion. Fig. 3 illustrates the arrangements of the d-orbital sublayers. Based on similarities due to the “4+1” splitting phenomenon, the d_xz and d_yz orbitals of a pure RhPc molecule are degenerate. The two different spin states of the d_z² orbital are evidently split, mainly contributing to the magnetism. The energy level of the d_x²−y² orbital is significantly higher than those of d_xy, d_xz, d_yz, and d_z² orbitals. When the RhPc molecule is adsorbed on the Sc₂CO₂ monolayer, due to electrons migrating to the d_x²−y² orbital, the d_x²−y² orbital moves to a lower energy level and becomes degenerate with the d_xy orbital.

Fig. 3 (a) Density of states (DOS) and (d) energy levels of the d-orbital components of the TMPc central atom (Rh). (b and c) DOS of the d-orbital component of the TM atom (Rh) in two polarized structures. (e) The d-orbital electron arrangements of Rh and Ru in RhPc/Sc₂CO₂ and RuPc/Sc₂CO₂ (P↑ and P↓) and in RhPc and RuPc molecules without Sc₂CO₂.

As shown in Fig. 3(e), firstly, the outer electron distribution of Rh is 4d⁸ 5s¹; after bonding, the d orbital loses two electrons, then RhPc (P↑) obtains one electron from the interaction between the ligand and Sc₂CO₂, and the total magnetic moment is 0 μ_B. On the other hand, Rh does not obtain electrons in the P↓ structure and there is still electron mismatch in the 4d orbital; the total magnetic moment of the structure is 1 μ_B. Secondly, the outer electron arrangement of Ru is 4d⁷ 5s¹, and because the electronegativity of Ru is weaker than that of Rh, the number of electrons obtained in the P↑ structure is slightly less than one, so the total magnetic moment is more than 1 μ_B; the P↓ structure has two electrons which are unpaired, and the total magnetic moment of the structure is 2 μ_B.

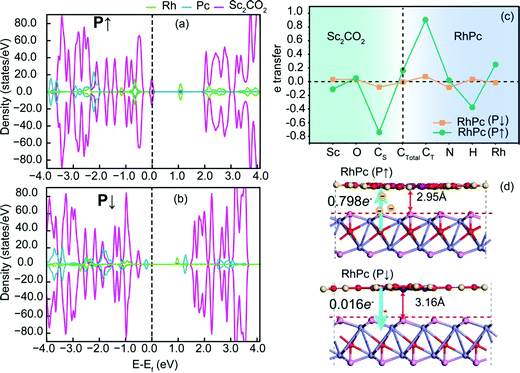
Further analysis of charge transfer in RhPc reveals the physical mechanism. This is illustrated via analyzing the density of states, charge transfer, and molecular structures of the two polarization situations. Fig. 4(a and b) shows the density distributions of electron states in RhPc (P↑) and RhPc (P↓). It can be seen that Sc₂CO₂ (P↑) transfers 0.798 electrons of charge to RhPc, which is much more than the 0.016 electrons of charge transferred from RhPc to Sc₂CO₂ (P↓); the Fermi level is lower for Sc₂CO₂ (P↑), showing a metallic state, which is different from the semiconductor state of Sc₂CO₂ (P↓). This transition differs from that of MPz/In₂Se₃²⁹ charge transfer, but it is essentially the transfer and redistribution of charge under the effects of a polarized electric field. Fig. 4(c) shows the internal transfer trend of electrons, where C_S refers to the carbon in Sc₂CO₂ and C_T refers to the carbon in TMPc, and C_Total = C_S + C_T. The number of electrons transferred has been subtracted from the intrinsic charges of the elements of TMPc and Sc₂CO₂; Rh gains more electrons in RhPc (P↑). According to Fig. 4(d), the interlayer distance in RhPc (P↑) is 2.95 Å, which is shorter than the distance of 3.12 Å between the layers in RhPc (P↓); this means that interactions between TMPc and Sc₂CO₂ are more intense in RhPc (P↑). The difference in interaction strengths leads to differences in charge transfer and orbital splitting, finally leading to the different magnetic states of TMPc in the two polarization situations.

Fig. 4 The effects of substrate polarization direction ((a) up and (b) down) on the DOS of the RhPc/Sc₂CO₂ structure. (c) The difference in charge transfer number between the RhPc/Sc₂CO₂ heterostructure and RhPc and Sc₂CO₂ pure molecules. (d) The interlayer distance between the two polarization directions of the heterostructures.

Based on the response of TMPc to the Sc₂CO₂ polarized electric field, it can be predicted that the external electric field has a significant effect on the charge transfer and distribution, then affecting the total magnetic moment of the system. For the P↑ situation, the interactions between TMPc and Sc₂CO₂ are more intense. Therefore, the electric field controls charge transfer more significantly.

Fig. 5(a) further explains the origin of the two different magnetic moments. At a position of 15.80 Å (above the Pc structure), the covalent bond between the Ag atom and the neighboring N atom is stronger. This is different from the almost complete lack of charge interaction between the Ru atom and the N atom. A more complex bond relationship can be seen at 14.75 Å. The main reason for the increase of the RuPc (P↑) magnetic moment is that the charge of the Ru d orbital decreases, increasing the net magnetic moment, while the change of the AgPc (P↑) magnetic moment is more sophisticated.

Fig. 5 (a) Differential charge distributions after switching the direction of the electric field when the magnetic moments of RuPc (P↑) and AgPc (P↑) increase (15.80 Å and 14.75 Å above Pc, respectively). (b) Magnetic moment variations of RuPc (P↑) and AgPc (P↑) in response to different electric fields. (c) Charge transfer between RuPc (P↑) and AgPc (P↑) in response to an electric field. (d) DOS of C and N in a AgPc molecule in different electric field directions. (e) The magnetic moment of RuPc is shown to significantly change due to the inversion of Sc₂CO₂ in response to a 0.05 V A⁻¹ electric field.

As seen in Fig. 5(b), the magnetic moments of AgPc (P↑) and RuPc (P↑) vary with the electric field, and it can be judged that the origins of the magnetic moment variations of the two structures are quite different according to the differential charge density variations. Fig. 5(c) illustrates charge transfer under an electric field (the charge without the electric field has been subtracted). In opposite electric field directions, Ru loses different numbers of electrons, which dominates the variation of the magnetic moment, while Ag loses few electrons in the different electric fields, and the main contribution to the magnetic moment from the structure is from N and C_Pc, which can be explained based on the magnetic nature of carbonitride;^44,45 as seen in Fig. 5(d), the p_x and p_y orbitals are degenerate, contributing part of the magnetic moment due to the asymmetry of electrons occupying spin-up and spin-down positions. AgPc (P↑) exhibits a semiconductor state in the reverse electric field direction and a half-metallic state in the forward electric field direction. The increase in magnetic moment mainly comes from the splitting of the p_z orbitals of C and N near the Fermi level, which is different from the physical mechanism involved in the case of RuPc/Sc₂CO₂ (P↑).

In order to further explore the influence of the intensity of the interlayer exchange effect on magnetic variations, we calculated the magnetic moment of the RuPc structure while changing the interlayer spacing of the heterostructure, as shown in Fig. 6; since there is no obvious difference in magnetic moments between the RuPc/Sc₂CO₂ (P↓) structure and RuPc molecule, we mainly study the RuPc/Sc₂CO₂ (P↑) structure, where E_Δ = E_d=2.2Å − E_d. d = 2.7 Å, marked in Fig. 6, is the optimized result for RuPc/Sc₂CO₂ (P↑) in this paper. When the interlayer spacing is too large, the result gradually approaches the behavior of two independent molecules in a vacuum. When the interlayer spacing is too small, the repulsion between electrons is strong, resulting in a drastic change in the structural distribution and the destruction of magnetism.

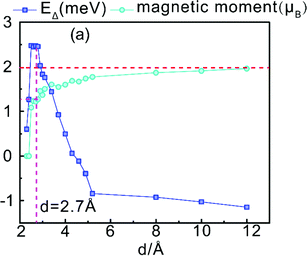Fig. 6 The effects of the distance d between heterostructure layers on the magnetic moment and energy of the system.

Conclusions

In summary, we propose and study two-dimensional van der Waals heterostructures composed of a transition metal phthalocyanine (TMPc) molecule and the ferroelectric monolayer Sc₂CO₂via first-principles calculations. The magnetic state of RhPc and the magnetic moments of NbPc and RuPc can be controlled through switching the polarization of Sc₂CO₂ using an electric field. The physical origin of this phenomenon is that ferroelectric interfacial polarization leads to charge transfer and redistribution, which is similar to the “4+1” splitting phenomenon. The variations of the magnetic moments of AgPc (P↑) and RuPc (P↑) under an external electric field are predicted, and the different physical mechanisms are revealed. For the AgPc (P↑) structure, carbon and nitrogen contribute to the magnetism and can be further regulated by the electric field. Therefore, our research provides a theoretical method for developing high-density nonvolatile magnetic memory and it may further accelerate research in related fields.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The calculations were carried out using supercomputers at the High Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures, the high-performance super-computing center of Nanjing University.

References

1. S. D. Bader and S. S. P. Parkin, Spintronics, Annu. Rev. Condens. Matter Phys., 2010, 1, 71–88.
2. J. T. Heron, et al., Deterministic Switching of Ferromagnetism at Room Temperature Using an Electric Field, Nature, 2014, 516, 370.
3. J. F. Scott, Data Storage – Multiferroic Memories, Nat. Mater., 2007, 6, 256–257.
4. S. E. Barnes, J. Ieda and S. Maekawa, Rashba Spin-Orbit Anisotropy and the Electric Field Control of Magnetism, Sci. Rep., 2014, 4, 4105.
5. S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnar, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Spintronics: A Spin-Based Electronics Vision for the Future, Science, 2001, 294, 1488–1495.
6. N. A. Hill and A. Filippetti, Why Are There Any Magnetic Ferroelectrics?, J. Magn. Magn. Mater., 2002, 242, 976–979.
7. K. F. Wang, J. M. Liu and Z. F. Ren, Multiferroicity: The Coupling between Magnetic and Polarization Orders, Adv. Phys., 2009, 58, 321–448.
8. H. X. Tan, M. L. Li, H. T. Liu, Z. R. Liu, Y. C. Li and W. H. Duan, Two-Dimensional Ferromagnetic-Ferroelectric Multiferroics in Violation of the D(0)Rule, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 195434.
9. K. Chang, et al., Discovery of Robust in-Plane Ferroelectricity in Atomic-Thick Snte, Science, 2016, 353, 274–278.
10. C. J. Cui, et al., Intercorrelated in-Plane and out-of-Plane Ferroelectricity in Ultrathin Two-Dimensional Layered Semiconductor In₂se₃, Nano Lett., 2018, 18, 1253–1258.
11. W. J. Ding, J. B. Zhu, Z. Wang, Y. F. Gao, D. Xiao, Y. Gu, Z. Y. Zhang and G. Zhu,W., Prediction of Intrinsic Two-Dimensional Ferroelectrics in In₂Se₃ and Other III2-VI3 van der Waals Materials, Nat. Commun., 2017, 8, 14956.
12. A. Chandrasekaran, A. Mishra and A. K. Singh, Ferroelectricity, Antiferroelectricity, and Ultrathin 2d Electron/Hole Gas in Multifunctional Monolayer Mxene, Nano Lett., 2017, 17, 3290–3296.
13. B. Xu, H. Xiang, Y. D. Xia, K. Jiang, X. G. Wan, J. He, J. Yin and Z. G. Liu, Monolayer Agbip₂se₆: An Atomically Thin Ferroelectric Semiconductor with out-Plane Polarization, Nanoscale, 2017, 9, 8427–8434.
14. A. Belianinov, Q. He, A. Dziaugys, P. Maksymovych, E. Eliseev, A. Borisevich, A. Morozovska, J. Banys, Y. Vysochanskii and S. V. Kalinin, Cuinp₂s₆ Room Temperature Layered Ferroelectric, Nano Lett., 2015, 15, 3808–3814.
15. M. W. Si, et al., Room-Temperature Electrocaloric Effect in Layered FerroelectricCuinp₂s₆ for Solid-State Refrigeration, ACS Nano, 2019, 13, 8760–8765.
16. Z. Y. Fei, W. J. Zhao, T. A. Palomaki, B. S. Sun, M. K. Miller, Z. Y. Zhao, Q. Yan,J., X. D. Xu and D. H. Cobden, Ferroelectric Switching of a Two-Dimensional Metal, Nature, 2018, 560, 336–339.
17. R. X. Fei, W. Kang and L. Yang, Ferroelectricity and Phase Transitions in Monolayer Group-IV Monochalcogenides., Phys. Rev. Lett., 2016, 117, 097601.
18. D. Di Sante, A. Stroppa, P. Barone, M. H. Whangbo and S. Picozzi, Emergence of Ferroelectricity and Spin-Valley Properties in Two-Dimensional Honeycomb Binary Compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 161401.
19. L. Li and M. H. Wu, Binary Compound Bilayer and Multilayer with Vertical Polarizations: Two-Dimensional Ferroelectrics, Multiferroics, and Nanogenerators, ACS Nano, 2017, 11, 6382–6388.
20. E. Bruyer, D. Di Sante, P. Barone, A. Stroppa, M. H. Whangbo and S. Picozzi, Possibility of Combining Ferroelectricity and Rashba-Like Spin Splitting in Monolayers of the 1t-Type Transition-Metal Dichalcogenides Mx2 (M = Mo, W; X = S, Se, Te), Phys. Rev. B, 2016, 94, 195402.
21. H. L. L. Zhuang, Y. Xie, P. R. C. Kent and P. Ganesh, Computational Discovery of Ferromagnetic Semiconducting Single-Layer Crsnte3., Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035407.
22. Z. Y. Tu, M. H. Wu and X. C. Zeng, Two-Dimensional Metal-Free Organic Multiferroic Material for Design of Multifunctional Integrated Circuits, J. Phys. Chem. Lett., 2017, 8, 1973–1978.
23. W. Luo, K. Xu and H. J. Xiang, Two-Dimensional Hyperferroelectric Metals: A Different Route to Ferromagnetic-Ferroelectric Multiferroics, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 235415.
24. J. J. Zhang, L. F. Lin, Y. Zhang, M. H. Wu, B. I. Yakobson and S. Dong, Type-Ii Multiferroic Hf2vc2f2 Mxene Monolayer with High Transition Temperature, J. Am. Chem. Soc., 2018, 140, 9768–9773.
25. C. X. Huang, Y. P. Du, H. P. Wu, H. J. Xiang, K. M. Deng and E. J. Kan, Prediction of Intrinsic Ferromagnetic Ferroelectricity in a Transition-Metal Halide Monolayer., Phys. Rev. Lett., 2018, 120.
26. Y. Lu, R. X. Fei, X. B. Lu, L. H. Zhu, L. Wang and L. Yang, Artificial Multiferroics and Enhanced Magnetoelectric Effect in van der Waals Heterostructures, ACS Appl. Mater. Interfaces, 2020, 12, 6243–6249.
27. W. Sun, W. Wang, D. Chen, Z. Cheng and Y. Wang, Valence Mediated Tunable Magnetism and Electronic Properties by Ferroelectric Polarization Switching in 2d Fei2/In₂se₃ van der Waals Heterostructures, Nanoscale, 2019, 11, 9931–9936.
28. L. Z. Li and B. Z. Zhou, Theoretical Investigation of Nonvolatile Electrical Control Behavior by Ferroelectric Polarization Switching in Two-Dimensional Mncl3/Cuinp₂s₆ van der Waals Heterostructures, J. Mater. Chem. C, 2020, 8, 4534–4541.
29. X. Tang, J. Shang, Y. D. Ma, Y. T. Gu, C. F. Chen and L. Z. Kou, Tuning Magnetism of Metal Porphyrazine Molecules by a Ferroelectric In₂se₃ Monolayer, ACS Appl. Mater. Interfaces, 2020, 12, 39561–39566.
30. A. Chandrasekaran, A. Mishra and A. K. Singh, Ferroelectricity, Antiferroelectricity, and Ultrathin 2d Electron/Hole Gas in Multifunctional Monolayer Mxene, Nano Lett., 2017, 17, 3290–3296.
31. N. B. McKeown, Phthalocyanine Materials: Synthesis, Structure, and Function, Cambridge University Press, Cambridge, UK, New York, 1998, vol. xvi, p. 193.
32. A. B. Sorokin, Phthalocyanine Metal Complexes in Catalysis, Chem. Rev., 2013, 113, 8152–8191.
33. L. Bogani and W. Wernsdorfer, Molecular Spintronics Using Single-Molecule Magnets, Nat. Mater., 2008, 7, 179–186.
34. Y. Shirota and H. Kageyama, Charge Carrier Transporting Molecular Materials and Their Applications in Devices, Chem. Rev., 2007, 107, 953–1010.
35. G. Kresse and J. Furthmuller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
36. P. E. Blochl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An Lsda+U Study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
39. S. Grimme, Semiempirical Gga-Type Density Functional Constructed with a Long- Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799.
40. K. Momma and F. Izumi, Vesta 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data., J. Appl. Crystallogr., 2011, 44, 1272–1276.
41. R. F. Bader, Atoms in Molecules, Acc. Chem. Res., 1985, 18, 9–15.
42. W. J. Cho, Y. Cho, S. K. Min, W. Y. Kim and K. S. Kim, Chromium Porphyrin Arrays as Spintronic Devices, J. Am. Chem. Soc., 2011, 133, 9364–9369.
43. M. S. Liao and S. Scheiner, Electronic Structure and Bonding in Metal Porphyrins, Metal = Fe, Co, Ni, Cu, Zn, J. Chem. Phys., 2002, 117, 205–219.
44. X. Li, J. Zhou, Q. Wang, Y. Kawazoe and P. Jena, Patterning Graphitic C–N Sheets into a Kagome Lattice for Magnetic Materials, J. Phys. Chem. Lett., 2013, 4, 259–263.
45. A. Du, S. Sanvito and S. C. Smith, First-Principles Prediction of Metal-Free Magnetism and Intrinsic Half-Metallicity in Graphitic Carbon Nitride, Phys. Rev. Lett., 2012, 108, 197207.

---