DOI:
10.1039/D1MA00912E
(Paper)
Mater. Adv., 2022,
3, 4170-4178
Rashba spin splitting and anomalous spin textures in the bulk ferroelectric oxide perovskite KIO3†
Received
30th September 2021
, Accepted 6th March 2022
First published on 8th March 2022
Abstract
The momentum-dependent Rashba and Dresselhaus spin splitting has gained much attention for its highly promising applications in spintronics. A non-centrosymmetric structure and the presence of spin–orbit coupling (SOC) lead to the momentum-dependent spin splitting of degenerate bands at non-time-reversal-invariant k-points. This lifts the Kramers degeneracy leading to Rashba and Dresselhaus splitting. In the search for new ferroelectric Rashba semiconductors, here we present ferroelectric oxide perovskite KIO3, where the presence of a heavy element (I), contributing to significant SOC and inversion asymmetric nature induces interesting band splitting. By employing the state-of-the-art density functional theory (DFT) with the semi-local and hybrid functional (HSE06) combined with SOC, we find non-negligible spin splitting effects at the conduction band minimum (CBm) and valence band maximum (VBM) for R3m and R3c phases. For a deeper understanding of the observed spin splitting, we have analyzed the spin textures within the combined framework of DFT and the k·p model Hamiltonian. Linear Rashba terms successfully explain splitting at the VBM. However, cubic terms become important in realizing spin-orientation near the CBm. In the R3c phase, the four-band k·p model Hamiltonian is needed to completely understand the anomalous nature of the spin textures, which is beyond the conventional linear Rashba and Dresselhaus splitting. Our results show the enhancement in Rashba parameters on tuning the epitaxial strain. Furthermore, we have observed a reversal of spin-orientation upon switching the direction of polarization.
1 Introduction
Ferroelectric Rashba semiconductors have recently created a huge sensation in the field of spintronics owing to their robust spontaneous electrical polarization.1–6 These materials find applications in spin field effect transistors, ferroelectric tunnel junctions, and storage and memory devices.7–12 The long-range order dipoles aligned in the same direction induce polarization in ferroelectric materials, leading to inversion asymmetry. Ferroelectric Rashba semiconductors interlink the phenomena of Rashba-type splitting and ferroelectricity, enabling the electric control of electron spin. In ferroelectric Rashba semiconductors, Rashba parameters can be enhanced via the application of ferroelectric (FE) polarization.
Ferroelectric materials, because of their robust spontaneous electrical polarization, are widely used in various applications. Interestingly, the spin-orientation can be inverted by reversing the direction of polarization using an external electric field.13 Electrical control of the spin degrees of freedom makes them suitable for spintronic devices. Some well known examples of ferroelectric Rashba semiconductors are KTaO3,14 BiAlO3,13 LiZnSb15 and FASnI3 (FA = formamidinium).16 GeTe was the first ferroelectric material, in which the Rashba effect was predicted theoretically17 and observed experimentally.18 However, it has a tendency to form Ge vacancies,19 which leads to p-type semiconducting behavior. This in turn poses a challenge to electric control of the spin. In this context, ferroelectric oxide perovskites such as KIO3 (KIO) show excellent piezoelectric, pyroelectric and non-linear optical properties.20,21 KIO, in particular, is experimentally synthesized at high temperature in a non-centrosymmetric rhombohedral phase with R3m space group symmetry.22 A thermodynamically favorable rhombohedral R3c phase was also theoretically predicted.21,23,24 In both phases, the distortion of the octahedra centered at the I-atom induces spontaneous FE polarization. Furthermore, the presence of a heavy element (I), contributing to significant spin–orbit coupling (SOC) and inversion asymmetric nature may induce interesting Rashba- and Dresselhaus-type band splitting.
Note that SOC and broken inversion symmetry play a pivotal role for the materials to exhibit Rashba and Dresselhaus effects.7, 12,25,26 In crystals lacking inversion symmetry, a relativistically moving electron experiences a Lorentz-transformed magnetic field due to a finite potential gradient. This results in spin-based splitting of degenerate bands at non-time-reversal-invariant k-points, which lifts the Kramers degeneracy leading to Rashba and Dresselhaus splitting. The spin-orientation is determined by the momentum-dependent spin–orbit field. For acentric non-polar crystals, Dresselhaus was the first to show band splitting, which shows a cubic dependence on momentum space for zinc blende-type crystal structures.27 For gyrotropic point group symmetries, linear Dresselhaus-type spin splitting can also be realized. In polar crystals and 2D electron gas, linear splitting terms are allowed as shown by Rashba and Bychkov.28–30 The SOC Hamiltonian HSO = Ω(k)·σ describes these effects, where σ is the Pauli matrix vector and Ω(k) is the spin–orbit field. The latter is odd in momentum space (i.e.Ω(−k) = −Ω(k)) to preserve the time-reversal symmetry of HSO. Ω(k) depends on the spatial symmetry of the system. For the simplest case, C2v point group symmetry Ω(k) can be written as a vector sum of linear Rashba (ΩR = αR(ky, −kx, 0)) and Dresselhaus (ΩD = αD(ky, kx, 0)) spin–orbit fields.31 Here, αR and αD are the Rashba and Dresselhaus coefficients, respectively. These coefficients mainly depend on the amount of SOC and the symmetry of the crystal.32 Energy eigenvalues corresponding to the linear Rashba Hamiltonian are given by E±(k) = ħ2k2/2m ± αRk. Rashba and Dresselhaus effects lead to the same type of band splitting. However, the type of splitting can be characterized by projection of the spin-orientation in Fourier space, usually referred to as the spin texture.33
In this article, we have studied the Rashba and Dresselhaus effects in R3m and R3c phases of FE oxide KIO using state-of-the-art density functional theory (DFT) and the symmetry adapted two-band k·p model Hamiltonian. Firstly, we have determined the FE polarization in both the phases. Subsequently, the crucial effect of SOC has been shown in the band structures. The Rashba spin splitting energy and offset momentum have been determined from the splitting at the valence band maximum (VBM) and conduction band minimum (CBm). Furthermore, the type of splitting has been characterized by plotting the spin texture. The Rashba and Dresselhaus parameters are determined after fitting the k·p model Hamiltonian to the DFT band structure. Finally, the effect of polarization on the aforementioned parameters has been investigated.
2 Methodology
The calculations are performed using the Vienna ab initio simulation package (VASP)34,35 within the framework of DFT using projector augmented wave (PAW)36 pseudopotentials. The Perdew–Burke–Ernzerhof (PBE)37 exchange–correlation (εxc) functional is used for DFT calculations. For better accuracy of excited state properties and validation of PBE results, the non-local Heyd–Scuseria–Ernzerhof (HSE06)38εxc functional is used. For an effective interpretation of results, the conventional hexagonal setting is also considered. A cutoff energy of 600 eV is used throughout the calculations. Both rhombohedral phases, R3c and R3m are fully relaxed (the lattice parameters as well as atomic coordinates) using the PBE εxc functional without including SOC with 9 × 9 × 4 and 9 × 9 × 8 k-grids, respectively, generated using the Monkhorst–Pack scheme.39 The insignificant role of SOC in relaxation is also verified by test calculations. The partial density of states (PDOS) and band structure calculations are done using a 12 × 12 × 6 k-grid. In structural optimization, the total energy difference between two ionic relaxation steps is set to be smaller than 10−5 eV and the tolerance on forces between two consecutive steps is set to 0.001 eV Å−1. The FE properties are calculated within the framework of Berry phase theory for polarization.40–42 We have conducted symmetry analysis using ref. 43, Findsym,44 Bilbao crystallographic server45 and SEEK-PATH.46 Finally, we have used Mathematica47 and PyProcar48 to plot spin textures and to solve the k·p model Hamiltonian. Spin textures are calculated using the expectation values of spin operators Si, given by| | 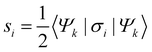 | (1) |
where σi are the Pauli matrices and Ψk is the spinor eigenfunction obtained from noncollinear spin calculations. Spin texture calculations are performed using a closely spaced 15 × 15 k-grid around a high symmetry point (HSP) within the kx − ky plane. The square region considered in the kx − ky plane is bound by |kx| ≤ 0.2 Å−1 and |ky| ≤ 0.2 Å−1. We have computed the k·p model band structures by minimizing the summation| | 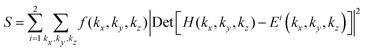 | (2) |
where f(kx, ky, kz) is the weight attached to (kx, ky, kz) point. We have used a normal distribution for f(kx, ky, kz) centered at the (kx, ky, kz) point to get a better fit near a HSP as used in ref. 49 and 50. The range of kx and ky used for fitting the DFT band structures is −0.125 to 0.125 Å−1. The coordinate convention used for calculating the band structures, spin textures and building the Hamiltonians is explained in Section I of the ESI.† For introducing the strain, the structural parameter c is varied with respect to equilibrium parameter c0 and the strain (ε) is calculated as| | 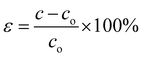 | (3) |
After introducing the respective strain, we have relaxed the atomic coordinates. We have varied the strain from −5% to +5%, where “−” and “+” represent the compressive and tensile strains, respectively.
3 Results and discussion
3.1 Structural and ferroelectric properties
KIO mainly exists in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, R3m and R3c space group symmetries. The Pm
m, R3m and R3c space group symmetries. The Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is centrosymmetric and contains an inversion center and therefore, does not show the Rashba-type splitting. Hence, we have studied the non-centrosymmetric rhombohedral phases R3m and R3c in detail for Rashba and Dresselhaus properties. The R3m phase is symmorphic as all generating symmetry operations leave one common point fixed, apart from the lattice translations. In contrast, R3c phase is non-symmorphic containing the glide planes. Fig. 1 shows the conventional hexagonal unit cells of the R3m and R3c phases of KIO. The lattice parameters of both phases are given in Table 1. The calculated lattice parameters of the R3m phase are well in agreement with experimental values (a = 6.34 Å, c = 7.94 Å).22 The lattice parameters of R3c phase coincide with the crystal structure already reported using DFT (a = 6.37 Å, c = 15.92 Å).23 At equilibrium (without considering the strain), the formation energy of the R3c phase is the lowest. Our calculated formation energy of the R3c phase is 18 meV f.u.−1 lower than that for the R3m phase. For the R3m phase, we have calculated the change in the ferroelectric polarization i.e., dipole moment per unit volume
m phase is centrosymmetric and contains an inversion center and therefore, does not show the Rashba-type splitting. Hence, we have studied the non-centrosymmetric rhombohedral phases R3m and R3c in detail for Rashba and Dresselhaus properties. The R3m phase is symmorphic as all generating symmetry operations leave one common point fixed, apart from the lattice translations. In contrast, R3c phase is non-symmorphic containing the glide planes. Fig. 1 shows the conventional hexagonal unit cells of the R3m and R3c phases of KIO. The lattice parameters of both phases are given in Table 1. The calculated lattice parameters of the R3m phase are well in agreement with experimental values (a = 6.34 Å, c = 7.94 Å).22 The lattice parameters of R3c phase coincide with the crystal structure already reported using DFT (a = 6.37 Å, c = 15.92 Å).23 At equilibrium (without considering the strain), the formation energy of the R3c phase is the lowest. Our calculated formation energy of the R3c phase is 18 meV f.u.−1 lower than that for the R3m phase. For the R3m phase, we have calculated the change in the ferroelectric polarization i.e., dipole moment per unit volume 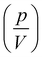 with respect to the centrosymmetric structure, of 41 μC cm−2 along the [0001] direction in a hexagonal setting (along the [111] direction in a rhombohedral setting). However, in the R3c phase, we have found a slightly smaller polarization of 29 μC cm−2 along the [0001] direction in a hexagonal setting. In previous studies on BiFeO3 thin films, it has been shown that FE polarization can be enhanced to be as large as 150 μC cm−2 using the strain.51–53 In view of this, we have also verified the enhancement in FE polarization of KIO on the application of strain (the calculated lattice parameters for different strained states are given in Section II of the ESI†). The FE polarization increases (decreases) under the application of tensile (compressive) strain and direction remains the same. The FE polarization has varied from 21 to 35 μC cm−2 and 29 to 50 μC cm−2 in R3m and R3c phases, respectively, on applying strain in the range of −5% to +5%.
with respect to the centrosymmetric structure, of 41 μC cm−2 along the [0001] direction in a hexagonal setting (along the [111] direction in a rhombohedral setting). However, in the R3c phase, we have found a slightly smaller polarization of 29 μC cm−2 along the [0001] direction in a hexagonal setting. In previous studies on BiFeO3 thin films, it has been shown that FE polarization can be enhanced to be as large as 150 μC cm−2 using the strain.51–53 In view of this, we have also verified the enhancement in FE polarization of KIO on the application of strain (the calculated lattice parameters for different strained states are given in Section II of the ESI†). The FE polarization increases (decreases) under the application of tensile (compressive) strain and direction remains the same. The FE polarization has varied from 21 to 35 μC cm−2 and 29 to 50 μC cm−2 in R3m and R3c phases, respectively, on applying strain in the range of −5% to +5%.
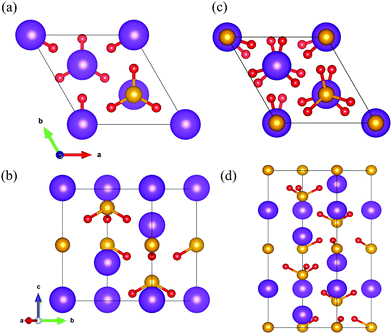 |
| | Fig. 1 Crystal structure of KIO3 in the (a) and (b) R3m phase and (c) and (d) R3c phase. The violet, orange and red balls denote the K, I and O ions, respectively. | |
Table 1 Lattice parameters and polarization for rhombohedral phases of KIO calculated using the PBE εxc functional
| Space group |
a (Å) |
c (Å) |
V (Å3) |
P (μC cm2) |
|
R3c |
6.37 |
15.91 |
558.6 |
29 |
|
R3m |
6.29 |
8.11 |
278.1 |
41 |
3.2 Electronic properties and spin splitting effects
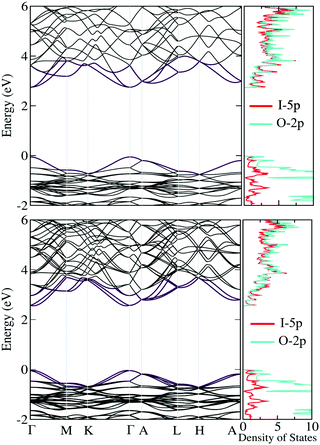
Fig. 2a shows the calculated band structure of the R3m phase without SOC along the high symmetry path in the first Brillouin zone (see the Fig. 2a inset for the high symmetry path). A direct band gap of 2.51 eV is observed at the k-point A. Since the Perdew–Burke–Ernzerhof (PBE)37εxc functional is known to underestimate the band gap, it is also calculated using a non-local HSE0638εxc functional. A larger direct band gap of 3.50 eV is observed at the k-point A. The uppermost valence band has a width of about 2.5 eV and the electronic states are mainly derived from O-2p orbitals (see the PDOS in Fig. 2). The lowest conduction band has a width of nearly 4 eV and the electronic states are mainly derived from equal contributions of I-5p and O-2p orbitals. Fig. 2b shows the calculated band structure and PDOS with the inclusion of SOC. The VBM and CBm shift from the k-point A towards L, which is known as the offset momentum (δk). The energy difference between the k-point A and extremum is known as the Rashba spin splitting energy (δE). A slightly indirect band gap of 2.24 and 3.27 eV is observed using PBE + SOC and HSE06 + SOC, respectively. Despite the underestimation of the band gap by PBE, the band dispersion around the HSP is known to be similar to HSE06.17 We have compared the band structures obtained using PBE + SOC and HSE06 + SOC and found that they are resulting in similar Rashba parameters (see Section III of the ESI†). Therefore, all the calculations are performed using PBE, since it is more cost effective. The presence of a large SOC is attributed to the heavy elements like I. A dominant spin splitting can be seen in the plane 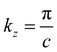 , which is perpendicular to the polarization axis (see Fig. 3a and b). In contrast, splitting is completely absent in the direction Γ–A, which is parallel to the polarization axis [0001]. It is consistent with the Rashba model, where splitting occurs in the direction perpendicular to the polarization axis. The δE for CB and VB is 27.3 and 18.1 meV, respectively. The δk for CB and VB is 0.047 and 0.054 Å−1, respectively. Within the linear approximation, these values lead to
, which is perpendicular to the polarization axis (see Fig. 3a and b). In contrast, splitting is completely absent in the direction Γ–A, which is parallel to the polarization axis [0001]. It is consistent with the Rashba model, where splitting occurs in the direction perpendicular to the polarization axis. The δE for CB and VB is 27.3 and 18.1 meV, respectively. The δk for CB and VB is 0.047 and 0.054 Å−1, respectively. Within the linear approximation, these values lead to 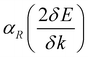 of 1.16 and 0.67 eV Å, respectively (see Section IV of the ESI†). We have observed a comparatively larger Rashba splitting at the CBm than at the VBM due to the higher contribution of I-5p orbitals at the CBm (see Fig. 2).
of 1.16 and 0.67 eV Å, respectively (see Section IV of the ESI†). We have observed a comparatively larger Rashba splitting at the CBm than at the VBM due to the higher contribution of I-5p orbitals at the CBm (see Fig. 2).
 |
| | Fig. 2 Band structure and PDOS for the R3m phase calculated using PBE (a) without SOC and (b) with SOC. The Fermi energy is set to the VBM. Here, the inset shows the first Brillouin zone for the hexagonal phase. | |
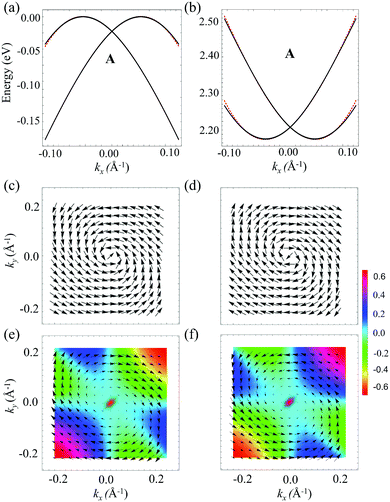 |
| | Fig. 3 (a) Valence bands and (b) conduction bands of KIO for the R3m phase with SOC along the A–L line (energy vs. kx). Here black solid lines and red dashed lines are obtained by DFT and parametrization of the model, respectively. (c) and (d) Spin textures of two upper most valence bands and (e) and (f) two lowest conduction bands. The arrows and color projection represent the in-plane and out-of-plane components of the spin texture with respect to the (kx– ky) plane. | |
In order to have a better understanding of the spin splitting nature, the spin texture is plotted near the VBM and CBm around the k-point A. The 2D spin texture is calculated by projecting the expectation values of σx, σy and σz in the Fourier plane (kx–ky). Fig. 3[(c), (d)] and [(e), (f)] show the calculated x-, y- and z-components of the spin texture near the VBM and CBm, respectively. The spin textures obtained using PBE and HSE06 are in close agreement (see Fig. S4 in the ESI†). Thus, we have further used PBE for computing spin textures. The in-plane spin components (Sx, Sy) show a helical nature with inner and outer bands having opposite orientations. This confirms the existence of Rashba-type splitting. A significant out of plane spin component can also be seen for the CBm, which is absent for the VBM. The out of plane spin component (Sz) has three-fold symmetry, which is in agreement with the three-fold rotation symmetry of the crystal. The spin splitting and textures can be explained by two-band effective Hamiltonian including only the spin degree of freedom. The little group of the k-point A is C3v, consisting of three-fold rotations C3, one reflection through vertical plane containing the z-axis (σxz) and two reflections through diagonal planes (Md1, Md2)54,55 (besides trivial identity operation). The band dispersion relation and spin texture around the k-point A in the plane orthogonal to the polar axis can be derived using all the symmetry-allowed terms such that O†H(k)O = H(k), where O is the symmetry operation belonging to the little group.13 The constructed two-band k·p Hamiltonian including linear and cubic Rashba terms satisfying the C3v symmetry near the k-point A takes the form56 (for more details see Section IV in the ESI†):
where,
| | | HSO = ασykx + βσxky + γσz[(kx3 + ky3) − 3(kxky2 + kykx2)] | (5) |
and
Ho(
k) is the free particle Hamiltonian.
α,
β are the coefficients of linear terms and
γ is the coefficient of the cubic term in the SOC Hamiltonian. The two energy eigenvalues of Hamiltonian are
| | 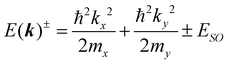 | (6) |
where,
mx and
my represent the effective masses in the
x and
y directions, respectively.
ESO is the energy eigenvalue of the SOC Hamiltonian given by
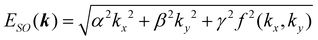
, where
f(
kx,
ky) = (
kx3 +
ky3) − 3(
kxky2 +
kykx2). Normalized spinor wavefunctions corresponding to energy eigenvalues are given by
| | 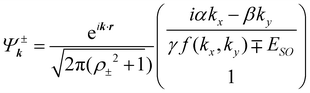 | (7) |
where
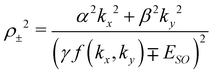
. The expectation values of spin operators are given by
| | 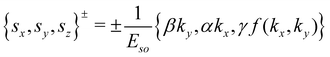 | (8) |
In-plane spin components are reproduced using α and β, whereas γ reproduces the out of plane spin component. For a specific k-point, the in-plane spin component is small as compared to out-of-plane if γf(kx,ky) is much larger than αkx and βky, and vice versa. Spin textures calculated using DFT satisfy the model Hamiltonian predictions. Three-fold degeneracy of the z-component of the spin is the consequence of the cubic nature of f(kx, ky) (see Section III in the ESI† for more details).
Fig. 3a and b show the comparison between the DFT and k·p model predicted band structures calculated using eqn (4) near the VBM and CBm, respectively, in the vicinity of the k-point A. The k·p model produces a band structure which is in close agreement with the DFT band structure. Near the k-point A, cubic terms have smaller energy contribution as compared to the linear terms in band structure calculations. In the range |ki| ≤ 0.125 Å−1 (i = x, y), the contribution coming from the cubic term is within 0.01 times the contribution coming from linear terms (note that the ratio of different contributions is a function of k). The energy eigenvalues of the Hamiltonian are given by 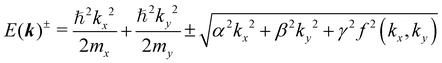 , which estimate only the magnitude of α, β and γ. The signs of α, β and γ are determined by the orientation of spins in Fourier space. Rashba and Dresselhaus coefficients are defined as
, which estimate only the magnitude of α, β and γ. The signs of α, β and γ are determined by the orientation of spins in Fourier space. Rashba and Dresselhaus coefficients are defined as 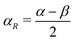 and
and 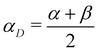 , respectively (the details can be seen in Section IV of ESI†). For the CB, α = 1.12 eV Å, β = −1.12 eV Å and γ = −21.70 eV Å3 reproduce the DFT band structure. These parameters lead to αR = 1.12 eV Å and αD = 0 eV Å, confirming that the splitting is coming mainly from the linear Rashba effect. For the VB, α = 0.63 eV Å, β = −0.63 eV Å and γ = −1.10 eV Å3 reproduce the DFT band structure leading to purely Rashba with αR = 0.63 eV Å apart from the negligible cubic contribution. The Rashba parameters calculated using the k·p model are listed in Table 2 and are fairly close to the DFT predictions.
, respectively (the details can be seen in Section IV of ESI†). For the CB, α = 1.12 eV Å, β = −1.12 eV Å and γ = −21.70 eV Å3 reproduce the DFT band structure. These parameters lead to αR = 1.12 eV Å and αD = 0 eV Å, confirming that the splitting is coming mainly from the linear Rashba effect. For the VB, α = 0.63 eV Å, β = −0.63 eV Å and γ = −1.10 eV Å3 reproduce the DFT band structure leading to purely Rashba with αR = 0.63 eV Å apart from the negligible cubic contribution. The Rashba parameters calculated using the k·p model are listed in Table 2 and are fairly close to the DFT predictions.
Table 2 Rashba parameters for band-splitting at the k-point A for R3m phase (note that β = −α in each case)
| Position |
m* (me) |
α (eV Å) |
γ (eV Å3) |
δE (meV) |
δk (Å−1) |
α
R
(eV Å) |
| VBM |
−0.72 |
0.63 |
−01.10 |
18.10 |
0.054 |
0.67 |
| CBm |
0.34 |
1.12 |
−21.70 |
27.30 |
0.047 |
1.16 |
Fig. 4a and b show the band structures and PDOS for the R3c phase without and with inclusion of SOC, respectively. It has a direct band gap of 2.86 eV at the k-point Γ without including SOC, which is 0.41 eV larger than for the R3m phase. The contribution of atomic orbitals in PDOS near the VBM and CBm for the R3c phase is nearly similar to the R3m phase. With the inclusion of SOC, the VBM and CBm shift towards the k-point K. A slightly indirect band gap of 2.65 eV on including SOC confirms the importance of SOC in the calculations. A larger band gap is calculated to be 3.80 eV using HSE06 + SOC. Spin splitting can be seen throughout the Brillouin zone except for Γ–A, which again confirms the polarization direction parallel to Γ–A (see Fig. 4b). A dominant spin splitting can be seen along the path Γ–M, Γ–K, A–L and A–H (see Fig. 4 and 5(a)–(d)). Fig. 5(e)–(h) show the plotted spin textures near the CBm and VBM, respectively, around the k-point Γ. Fig. 5(i)–(l) show the plotted spin textures for the lowest four conduction bands, around the k-point A. Near the k-point Γ, the in-plane spin textures form a helical-type spin texture with different orientations for inner and outer bands, confirming the Rashba-type splitting of degenerate levels. A significant out of plane spin component contribution can also be seen near the CBm, which is absent near the VBM. Near the k-point A, the spin splitting leads to novel spin textures, which are beyond the superposition of linear Rashba and Dresselhaus terms. These spin textures are completely different from those obtained using the two-band k·p model. These spin textures are a result of coupling between the orbital and spin degrees of freedom.49,57 The splitting near the k-point Γ can be explained by the two-band effective Hamiltonian, whereas the four-band Hamiltonian becomes important to understand the splitting near the k-point A. The little group of k-point Γ and A is the same, which is C3v. The model Hamiltonian given by eqn (4) can explain the band properties of the VBM and CBm near the k-point Γ. Fig. 5a and b show that DFT and k·p model predicted band structures near the k-point Γ are comparable. The Rashba spin splitting energy of 6.3 and 16.5 meV is obtained for VB and CB, respectively. The δk for CB and VB is 0.042 and 0.031 Å−1, respectively. From DFT, the value of αR is found to be 0.79 and 0.41 eV Å for CB and VB, respectively. For CB, fitted parameters of HSO are α =0.78 eV Å, β = −0.78 eV Å and γ = −13.3 eV Å3. These parameters lead to αR = 0.78 eV Å and αD = 0 eV Å. The corresponding parameters for VB are estimated as α = 0.40 eV Å, β = −0.40 eV Å and γ = −0.55 eV Å3 leading to a purely linear Rashba effect with αR = 0.40 eV Å with negligible cubic contribution. The Rashba coefficients calculated using the k·p model are fairly close to the DFT predictions and shown in Table 3. For splitting near k-point A, we have used the four-band model derived using method of invariants satisfying the C3v point group symmetry49 (see Section V of the ESI†):
| | 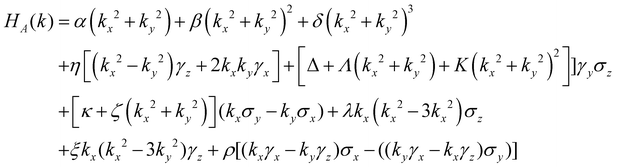 | (9) |
where both
γi and
σj are the Pauli matrices, denoting the orbital and spin degrees of freedom, respectively. Here,
γiσj represents the Kronecker delta product of matrices
γi and
σj.
γi and
σi denote
γiσ1and
γ1σi, where
γ1 and
σ1 are the identity matrices of dimension 2 × 2.
Fig. 5c shows the comparison between DFT and model predicted band structures for the lowest four conduction bands around the
k-point
A.
Fig. 5d shows the DFT (same as
Fig. 5c) and the modified model of
eqn (9) excluding the terms containing orbital degrees of freedom predicted band structures (see Section V in the ESI
†). The modified model band structure largely deviates from the DFT band structures. This confirms the significance of orbital degrees of freedom and four-band
k·
p Hamiltonian over the usual two-band
k·
p Hamiltonian to completely understand the spin splitting near the
k-point
A. We have observed the linear splitting of ∼0.64 and 0.45 eV Å for the bands around the
k-point
A (calculated using the expression
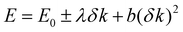
). The CBm and VBM are in the vicinity of the
k-point
A, which can be brought to the
k-point
A using the strain for possible applications of these novel spin textures. Rashba coefficients of some selected ferroelectric materials are compared with KIO in Section VI of the ESI.
†
 |
| | Fig. 4 Band structure and PDOS for R3c phase calculated using PBE (a) without SOC and (b) with SOC. The Fermi energy is set to the VBM. | |
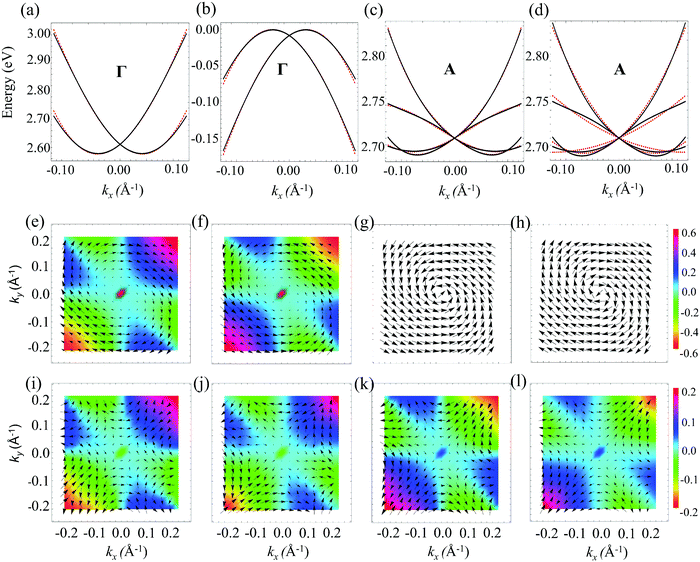 |
| | Fig. 5 (a) Valence bands and (b) conduction bands of KIO for the R3c phase with SOC along the Γ–M line (energy vs. kx). (c) The lowest four conduction bands around the k-point A with the full model are given in eqn (9) and (d) with the modified model excluding the terms containing the orbital degrees of freedom (obtained using η = ξ = Δ = Λ = K = ρ = 0 in eqn (9)). Here, black solid lines and red dashed lines are obtained by DFT and parametrization of the models using eqn (2), respectively. Spin textures of (e) and (f) two lowest conduction bands, (g) and (h) two uppermost valence bands around k-point Γ and (i)–(l) lowest four conduction bands around the k-point A. The arrows and color projection represent the in-plane and out of plane components of the spin texture with respect to the (kx–ky) plane. Our spin textures are prepared using the convention [(i)–(l) as examples] that if at the (kx, ky) point, energy eigenvalues associated with (i)–(l) are e1k, e2k, e3k, e4k, respectively, then e1k ≤ e2k ≤ e3k ≤ e4k. | |
Table 3 Rashba parameters for band-splitting at the k-point Γ for the R3c phase
| Position |
m* (me) |
α (eV Å) |
γ (eV Å3) |
δE (meV) |
δk (Å−1) |
α
R
(eV Å) |
| VBM |
−0.59 |
0.40 |
−0.55 |
6.30 |
0.031 |
0.41 |
| CBm |
0.41 |
0.78 |
−13.27 |
16.50 |
0.042 |
0.79 |
The experimental observations show that the electronic structure, ferroelectricity, and spin splitting in oxide perovskites are tunable using the strain.58 The polarization and Rashba splitting are sensitive to the uniaxial strain in oxide perovskites such as BiAlO3,13 KTaO359 and PbTiO3.60 In view of this, we have studied the strain dependence of δE, δk and αR in both the phases of KIO. We have considered the effect of strain within the (0001) plane on spin splitting and energy levels for both the phases around the VBM and CBm. Such a strain can be obtained by growing KIO films on top of hexagonal (0001) or cubic (111) substrates.61 The polarization direction remains along the [0001] direction throughout the full range of strain. Fig. 6 shows the change in the band gaps, δE and αR on application of strain. Band gap increases (decreases) under tensile (compressive) strain for R3m and R3c phases. δE decreases (increases) using the tensile (compressive) strain for conduction and valence bands. A linear trend is observed for spin splitting at the CBm and VBM in both phases. The amplitude of spin splitting can be tuned from 0.8 to 1.2 eV Å for the CBm in the R3m phase. It should be noted here that a more detailed analysis would be necessary to see if other states can be stabilized under the uniaxial strain. This can be done by calculating the total formation energy of structures with different space groups as a function of strain to know which one is the most stable at a particular strain.62
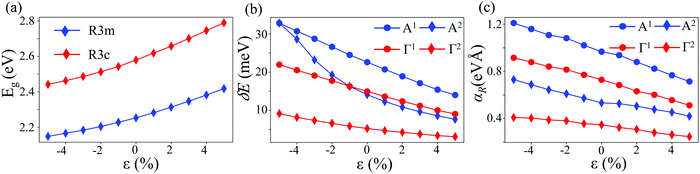 |
| | Fig. 6 (a) Band gap (Eg), (b) Rashba spin splitting energy (δE) and (c) Rashba coefficients (αR) as a function of strain (ε). The A1 and A2 show the information about splitting around the k-point A in the R3m phase around the CBm and VBM, respectively. In the same manner, Γ1 and Γ2 show splitting in the R3c phase around the k-point Γ. | |
The spin degeneracy can be restored when the structure is brought back to the parent centrosymmetric structure. The parent space group of R3m is R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, which is generated by the symmetry elements of R3m followed by an inversion. The polarization, Pz along the c-direction breaks the inversion symmetry. Thus, the R
m, which is generated by the symmetry elements of R3m followed by an inversion. The polarization, Pz along the c-direction breaks the inversion symmetry. Thus, the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is centrosymmetric and band splitting is absent. It is well known that in ferroelectric Rashba semiconductors, switching the direction of polarization leads to the reversal of the spin texture. The full reversal of the spin texture on reversing the direction of polarization is also observed in KIO. To switch the direction of polarization, transition state R
m phase is centrosymmetric and band splitting is absent. It is well known that in ferroelectric Rashba semiconductors, switching the direction of polarization leads to the reversal of the spin texture. The full reversal of the spin texture on reversing the direction of polarization is also observed in KIO. To switch the direction of polarization, transition state R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m has to be crossed, which defines the potential barrier. The parent centrosymmetric structure is generated using the program PSEUDO.63 The calculated potential barrier to switch the polarization through the R
m has to be crossed, which defines the potential barrier. The parent centrosymmetric structure is generated using the program PSEUDO.63 The calculated potential barrier to switch the polarization through the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is 135 meV f.u.−1 for R3m. Similarly, the potential barrier for the R3c phase is found to be 112 meV f.u.−1 The calculated potential barrier is comparable to 110 meV f.u.−1 of LaWN349 and is smaller than 130 meV f.u.−1 of LiNbO3.64 The Rashba parameters are larger for KIO than BAO, despite a significantly larger ferroelectric polarization in BAO. Therefore, we infer that larger ferroelectric polarization does not directly imply the larger splitting. A thorough analysis of the symmetry and electronic structure is always required.
m phase is 135 meV f.u.−1 for R3m. Similarly, the potential barrier for the R3c phase is found to be 112 meV f.u.−1 The calculated potential barrier is comparable to 110 meV f.u.−1 of LaWN349 and is smaller than 130 meV f.u.−1 of LiNbO3.64 The Rashba parameters are larger for KIO than BAO, despite a significantly larger ferroelectric polarization in BAO. Therefore, we infer that larger ferroelectric polarization does not directly imply the larger splitting. A thorough analysis of the symmetry and electronic structure is always required.
4 Conclusions
In summary, we have performed relativistic first-principles density functional theory calculations to study Rashba and Dresselhaus effects in ferroelectric rhombohedral phases of KIO with R3m and R3c space group symmetries. Ferroelectric and electronic properties are explored using DFT, which are also supported by the symmetry adapted k·p Hamiltonian. Near the VBM and CBm, states are mainly derived from I-5p and O-2p orbitals. A sufficiently wide and slightly indirect band gap is calculated for the R3m (2.24 (PBE + SOC), 3.27 eV (HSE06 + SOC)) and R3c (2.65 (PBE + SOC), 3.80 eV (HSE06 + SOC)) phases. Due to a significant amount of SOC, spin splitting effects are observed at both the VBM and CBm around k-points A and Γ for R3m and R3c phases, respectively. The helical-type in-plane spin texture confirms that the spin splitting mainly consists of Rashba-type splitting. The out of plane spin texture shows importance of cubic terms in the model Hamiltonian. The two-band k·p Hamiltonian satisfying C3v symmetry reproduces the band structure and spin texture near the CBm and VBM, that are well in agreement with the DFT results. In the R3c phase, the inclusion of four bands in the Hamiltonian incorporating orbital degrees of freedom becomes important for a complete analysis of spin splitting. Novel spin textures observed in the R3c phase are anomalous in the sense that they differ from usual spin textures and cannot be treated as linear Rashba, linear Dresselhaus or some unique combination of both. The largest Rashba coefficient is found for the CBm in the R3m phase. Furthermore, we have investigated the effect of strain on Rashba and Dresselhaus parameters and found that they increase linearly with strain. Control of spin-based properties using the external electric field makes it suitable for spintronics applications. The larger Rashba coefficient in comparison to that of other contemporary materials (viz. BAO and LaWN3) makes KIO a promising addition into this class of materials having Rashba-based applications.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
S. S. acknowledges CSIR, India, for the senior research fellowship [Grant No. 09/086(1432)/2019-EMR-I]. M. K. acknowledges CSIR, India, for the senior research fellowship [Grant No. 09/086(1292)/2017-EMR-I]. P. B. acknowledges UGC, India, for the senior research fellowship [1392/(CSIR-UGC NET JUNE 2018)]. S. B. acknowledges financial support from SERB under a core research grant (grant no. CRG/2019/000647) to set up his High Performance Computing (HPC) facility “Veena” at IIT Delhi for computational resources.
Notes and references
- L. W. Martin and A. M. Rappe, Nat. Rev. Mater., 2016, 2, 1–14 Search PubMed.
- Y. Ma, Y. Dai, N. Yin, T. Jing and B. Huang, J. Mater. Chem. C, 2014, 2, 8539–8545 RSC.
- B. Zhou, Nanoscale, 2020, 12, 5533–5542 RSC.
- X. Yang, X.-M. Li, Y. Li, Y. Li, R. Sun, J.-N. Liu, X. Bai, N. Li, Z.-K. Xie, L. Su, Z.-Z. Gong, X.-Q. Zhang, W. He and Z. Cheng, Nano Lett., 2021, 21, 77–83 CrossRef CAS PubMed.
- S.-D. Guo, W.-Q. Mu, Y.-T. Zhu, R.-Y. Han and W.-C. Ren, J. Mater. Chem. C, 2021, 9, 2464–2473 RSC.
- X.-k. Hu, Z.-x. Pang, C.-w. Zhang, P.-j. Wang, P. Li and W.-x. Ji, J. Mater. Chem. C, 2019, 7, 9406–9412 RSC.
- C. Liu, H. Gao, Y. Li, K. Wang, L. A. Burton and W. Ren, J. Mater. Chem. C, 2020, 8, 5143–5149 RSC.
- V. Garcia and M. Bibes, Nat. Commun., 2014, 5, 1–12 CAS.
- H. Wang, P. Gopal, S. Picozzi, S. Curtarolo, M. B. Nardelli and J. Sławińska, npj Comput. Mater., 2020, 6, 1–7 CrossRef.
- B. T. Zhou, K. Taguchi, Y. Kawaguchi, Y. Tanaka and K. T. Law, Commun. Phys., 2019, 2, 1–7 CAS.
- M. Kawano, Y. Onose and C. Hotta, Commun. Phys., 2019, 2, 1–8 CAS.
- S.-D. Guo, Y.-T. Zhu, W.-Q. Mu and X.-Q. Chen, J. Mater. Chem. C, 2021, 9, 7465–7473 RSC.
- L. G. D. da Silveira, P. Barone and S. Picozzi, Phys. Rev. B, 2016, 93, 245159 CrossRef.
- P. King, R. He, T. Eknapakul, P. Buaphet, S.-K. Mo, Y. Kaneko, S. Harashima, Y. Hikita, M. Bahramy and C. Bell,
et al.
, Phys. Rev. Lett., 2012, 108, 117602 CrossRef CAS PubMed.
- A. Narayan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 220101 CrossRef.
- A. Stroppa, D. Di Sante, P. Barone, M. Bokdam, G. Kresse, C. Franchini, M.-H. Whangbo and S. Picozzi, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- D. Di Sante, P. Barone, R. Bertacco and S. Picozzi, Adv. Mater., 2013, 25, 509–513 CrossRef CAS PubMed.
- M. Liebmann, C. Rinaldi, D. Di Sante, J. Kellner, C. Pauly, R. N. Wang, J. E. Boschker, A. Giussani, S. Bertoli and M. Cantoni,
et al.
, Adv. Mater., 2016, 28, 560–565 CrossRef CAS PubMed.
- A. V. Kolobov, J. Tominaga, P. Fons and T. Uruga, Appl. Phys. Lett., 2003, 82, 382–384 CrossRef CAS.
- X. Yin and M. K. Lü, Appl. Phys. Lett., 1992, 60, 2849–2850 CrossRef CAS.
- M. A. Kader, F. El-Kabbany, H. Naguib and W. Gamal, J. Phys.: Conf. Ser., 2013, 012036 CrossRef.
- H. Kasatani, S. Aoyagi, Y. Kuroiwa, K. Yagi, R. Katayama and H. Terauchi, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 199, 49–53 CrossRef CAS.
- L. Bayarjargal, L. Wiehl, A. Friedrich, B. Winkler, E. A. Juarez-Arellano, W. Morgenroth and E. Haussuehl, J. Phys.: Condens. Matter, 2012, 24, 325401 CrossRef PubMed.
- G. Crane, Z. Kristallogr. – Cryst. Mater., 1975, 141, 312–313 CrossRef CAS.
- Y.-z. Jia, W.-x. Ji, C.-w. Zhang, P. Li, M.-j. Ren and P.-j. Wang, J. Mater. Chem. C, 2016, 4, 8750–8757 RSC.
- S.-s. Li, W.-x. Ji, C.-w. Zhang, P. Li and P.-j. Wang, J. Mater. Chem. C, 2016, 4, 2243–2251 RSC.
- G. Dresselhaus, Phys. Rev., 1955, 100, 580–586 CrossRef CAS.
- E. I. Rashba, Phys. Solid State, 1960, 2, 1109–1122 Search PubMed.
- F. T. Vas'ko, ZhETF Pisma Redaktsiiu, 1979, 30, 574 Search PubMed.
- Y. A. Bychkov and E. I. Rashba, J. Phys. C: Solid State Phys., 1984, 17, 6039–6045 CrossRef.
- L. Tao and E. Y. Tsymbal, J. Phys. D: Appl. Phys., 2021, 54, 113001 CrossRef CAS.
- L. Tao, T. R. Paudel, A. A. Kovalev and E. Y. Tsymbal, Phys. Rev. B, 2017, 95, 245141 CrossRef.
-
R. Winkler, S. Papadakis, E. De Poortere and M. Shayegan, Spin-Orbit Coupling in Two-Dimensional Electron and Hole Systems, Springer, 2003, vol. 41 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- R. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651 CrossRef CAS PubMed.
- R. Resta, Rev. Mod. Phys., 1994, 66, 899 CrossRef CAS.
- N. A. Spaldin, J. Solid State Chem., 2012, 195, 2–10 CrossRef CAS.
-
G. F. Koster, J. O. Dimmock, R. G. Wheeler and H. Statz, The Properties of the Thirty-Two Point Groups (Research Monograph), 1963 Search PubMed.
- H. T. Stokes and D. M. Hatch, J. Appl. Crystallogr., 2005, 38, 237–238 CrossRef CAS.
- M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr. - Cryst. Mater., 2006, 221, 15–27 CrossRef CAS.
- Y. Hinuma, G. Pizzi, Y. Kumagai, F. Oba and I. Tanaka, Comput. Mater. Sci., 2017, 128, 140–184 CrossRef CAS.
- Wolfram Research, Inc., Mathematica, Version 12.3.1, https://www.wolfram.com/mathematica, Champaign, IL, 2021.
- U. Herath, P. Tavadze, X. He, E. Bousquet, S. Singh, F. Munoz and A. H. Romero, Comput. Phys. Commun., 2020, 251, 107080 CrossRef CAS.
- H. J. Zhao, P. Chen, C. Paillard, R. Arras, Y.-W. Fang, X. Li, J. Gosteau, Y. Yang and L. Bellaiche, Phys. Rev. B, 2020, 102, 041203 CrossRef CAS.
- H. J. Zhao, H. Nakamura, R. Arras, C. Paillard, P. Chen, J. Gosteau, X. Li, Y. Yang and L. Bellaiche, Phys. Rev. Lett., 2020, 125, 216405 CrossRef CAS PubMed.
- C. Ederer and N. A. Spaldin, Phys. Rev. Lett., 2005, 95, 257601 CrossRef PubMed.
- D. Ricinschi, K.-Y. Yun and M. Okuyama, J. Phys.: Condens. Matter, 2006, 18, L97–L105 CrossRef CAS PubMed.
- Y. Heon Kim, A. Bhatnagar, E. Pippel, M. Alexe and D. Hesse, J. Appl. Phys., 2014, 115, 043526 CrossRef.
- Bilbao Crystallographic Server, Generators and general positions, https://www.cryst.ehu.es/cryst/get_gen.html.
- Bilbao Crystallographic Server, Point group tables, https://www.cryst.ehu.es/rep/point.html.
- S. Vajna, E. Simon, A. Szilva, K. Palotas, B. Ujfalussy and L. Szunyogh, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075404 CrossRef.
- S. Bandyopadhyay and I. Dasgupta, Phys. Rev. B, 2021, 103, 014105 CrossRef CAS.
- J. M. Rondinelli and N. A. Spaldin, Adv. Mater., 2011, 23, 3363–3381 CrossRef CAS PubMed.
- L. Tao and J. Wang, J. Appl. Phys., 2016, 120, 234101 CrossRef.
- R. Arras, J. H. Gosteau, C. Paillard, Y. Yang and L. Bellaiche, Phys. Rev. B, 2019, 100, 174415 CrossRef CAS.
- H. J. Zhao, C. Xu, Y. Yang, W. Duan, X. M. Chen and L. Bellaiche, J. Phys.: Condens. Matter, 2015, 27, 485901 CrossRef PubMed.
- H. J. Zhao, C. Xu, Y. Yang, W. Duan, X. M. Chen and L. Bellaiche, J. Phys.: Condens. Matter, 2015, 27, 485901 CrossRef PubMed.
- C. Capillas, E. S. Tasci, G. de la Flor, D. Orobengoa, J. M. Perez-Mato and M. I. Aroyo, Z. Krist., 2011, 226(2), 186–196 CrossRef CAS.
- M. Ye and D. Vanderbilt, Phys. Rev. B, 2016, 93, 134303 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma00912e |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Manish
Kumar
*,
Manish
Kumar
 ,
Preeti
Bhumla
,
Preeti
Bhumla
 and
Saswata
Bhattacharya
and
Saswata
Bhattacharya
 *
*
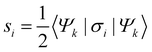
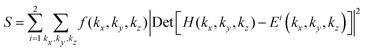
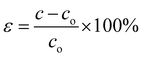
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, R3m and R3c space group symmetries. The Pm
m, R3m and R3c space group symmetries. The Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is centrosymmetric and contains an inversion center and therefore, does not show the Rashba-type splitting. Hence, we have studied the non-centrosymmetric rhombohedral phases R3m and R3c in detail for Rashba and Dresselhaus properties. The R3m phase is symmorphic as all generating symmetry operations leave one common point fixed, apart from the lattice translations. In contrast, R3c phase is non-symmorphic containing the glide planes. Fig. 1 shows the conventional hexagonal unit cells of the R3m and R3c phases of KIO. The lattice parameters of both phases are given in Table 1. The calculated lattice parameters of the R3m phase are well in agreement with experimental values (a = 6.34 Å, c = 7.94 Å).22 The lattice parameters of R3c phase coincide with the crystal structure already reported using DFT (a = 6.37 Å, c = 15.92 Å).23 At equilibrium (without considering the strain), the formation energy of the R3c phase is the lowest. Our calculated formation energy of the R3c phase is 18 meV f.u.−1 lower than that for the R3m phase. For the R3m phase, we have calculated the change in the ferroelectric polarization i.e., dipole moment per unit volume
m phase is centrosymmetric and contains an inversion center and therefore, does not show the Rashba-type splitting. Hence, we have studied the non-centrosymmetric rhombohedral phases R3m and R3c in detail for Rashba and Dresselhaus properties. The R3m phase is symmorphic as all generating symmetry operations leave one common point fixed, apart from the lattice translations. In contrast, R3c phase is non-symmorphic containing the glide planes. Fig. 1 shows the conventional hexagonal unit cells of the R3m and R3c phases of KIO. The lattice parameters of both phases are given in Table 1. The calculated lattice parameters of the R3m phase are well in agreement with experimental values (a = 6.34 Å, c = 7.94 Å).22 The lattice parameters of R3c phase coincide with the crystal structure already reported using DFT (a = 6.37 Å, c = 15.92 Å).23 At equilibrium (without considering the strain), the formation energy of the R3c phase is the lowest. Our calculated formation energy of the R3c phase is 18 meV f.u.−1 lower than that for the R3m phase. For the R3m phase, we have calculated the change in the ferroelectric polarization i.e., dipole moment per unit volume 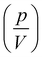 with respect to the centrosymmetric structure, of 41 μC cm−2 along the [0001] direction in a hexagonal setting (along the [111] direction in a rhombohedral setting). However, in the R3c phase, we have found a slightly smaller polarization of 29 μC cm−2 along the [0001] direction in a hexagonal setting. In previous studies on BiFeO3 thin films, it has been shown that FE polarization can be enhanced to be as large as 150 μC cm−2 using the strain.51–53 In view of this, we have also verified the enhancement in FE polarization of KIO on the application of strain (the calculated lattice parameters for different strained states are given in Section II of the ESI†). The FE polarization increases (decreases) under the application of tensile (compressive) strain and direction remains the same. The FE polarization has varied from 21 to 35 μC cm−2 and 29 to 50 μC cm−2 in R3m and R3c phases, respectively, on applying strain in the range of −5% to +5%.
with respect to the centrosymmetric structure, of 41 μC cm−2 along the [0001] direction in a hexagonal setting (along the [111] direction in a rhombohedral setting). However, in the R3c phase, we have found a slightly smaller polarization of 29 μC cm−2 along the [0001] direction in a hexagonal setting. In previous studies on BiFeO3 thin films, it has been shown that FE polarization can be enhanced to be as large as 150 μC cm−2 using the strain.51–53 In view of this, we have also verified the enhancement in FE polarization of KIO on the application of strain (the calculated lattice parameters for different strained states are given in Section II of the ESI†). The FE polarization increases (decreases) under the application of tensile (compressive) strain and direction remains the same. The FE polarization has varied from 21 to 35 μC cm−2 and 29 to 50 μC cm−2 in R3m and R3c phases, respectively, on applying strain in the range of −5% to +5%.

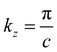 , which is perpendicular to the polarization axis (see Fig. 3a and b). In contrast, splitting is completely absent in the direction Γ–A, which is parallel to the polarization axis [0001]. It is consistent with the Rashba model, where splitting occurs in the direction perpendicular to the polarization axis. The δE for CB and VB is 27.3 and 18.1 meV, respectively. The δk for CB and VB is 0.047 and 0.054 Å−1, respectively. Within the linear approximation, these values lead to
, which is perpendicular to the polarization axis (see Fig. 3a and b). In contrast, splitting is completely absent in the direction Γ–A, which is parallel to the polarization axis [0001]. It is consistent with the Rashba model, where splitting occurs in the direction perpendicular to the polarization axis. The δE for CB and VB is 27.3 and 18.1 meV, respectively. The δk for CB and VB is 0.047 and 0.054 Å−1, respectively. Within the linear approximation, these values lead to 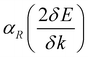 of 1.16 and 0.67 eV Å, respectively (see Section IV of the ESI†). We have observed a comparatively larger Rashba splitting at the CBm than at the VBM due to the higher contribution of I-5p orbitals at the CBm (see Fig. 2).
of 1.16 and 0.67 eV Å, respectively (see Section IV of the ESI†). We have observed a comparatively larger Rashba splitting at the CBm than at the VBM due to the higher contribution of I-5p orbitals at the CBm (see Fig. 2).
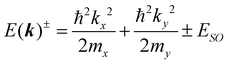
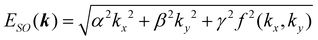 , where f(kx, ky) = (kx3 + ky3) − 3(kxky2 + kykx2). Normalized spinor wavefunctions corresponding to energy eigenvalues are given by
, where f(kx, ky) = (kx3 + ky3) − 3(kxky2 + kykx2). Normalized spinor wavefunctions corresponding to energy eigenvalues are given by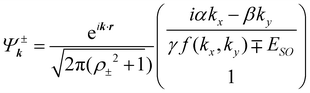
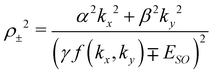 . The expectation values of spin operators are given by
. The expectation values of spin operators are given by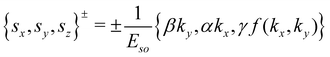
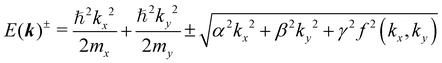 , which estimate only the magnitude of α, β and γ. The signs of α, β and γ are determined by the orientation of spins in Fourier space. Rashba and Dresselhaus coefficients are defined as
, which estimate only the magnitude of α, β and γ. The signs of α, β and γ are determined by the orientation of spins in Fourier space. Rashba and Dresselhaus coefficients are defined as 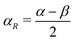 and
and 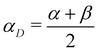 , respectively (the details can be seen in Section IV of ESI†). For the CB, α = 1.12 eV Å, β = −1.12 eV Å and γ = −21.70 eV Å3 reproduce the DFT band structure. These parameters lead to αR = 1.12 eV Å and αD = 0 eV Å, confirming that the splitting is coming mainly from the linear Rashba effect. For the VB, α = 0.63 eV Å, β = −0.63 eV Å and γ = −1.10 eV Å3 reproduce the DFT band structure leading to purely Rashba with αR = 0.63 eV Å apart from the negligible cubic contribution. The Rashba parameters calculated using the k·p model are listed in Table 2 and are fairly close to the DFT predictions.
, respectively (the details can be seen in Section IV of ESI†). For the CB, α = 1.12 eV Å, β = −1.12 eV Å and γ = −21.70 eV Å3 reproduce the DFT band structure. These parameters lead to αR = 1.12 eV Å and αD = 0 eV Å, confirming that the splitting is coming mainly from the linear Rashba effect. For the VB, α = 0.63 eV Å, β = −0.63 eV Å and γ = −1.10 eV Å3 reproduce the DFT band structure leading to purely Rashba with αR = 0.63 eV Å apart from the negligible cubic contribution. The Rashba parameters calculated using the k·p model are listed in Table 2 and are fairly close to the DFT predictions.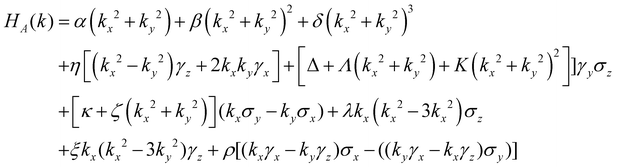
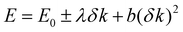 ). The CBm and VBM are in the vicinity of the k-point A, which can be brought to the k-point A using the strain for possible applications of these novel spin textures. Rashba coefficients of some selected ferroelectric materials are compared with KIO in Section VI of the ESI.†
). The CBm and VBM are in the vicinity of the k-point A, which can be brought to the k-point A using the strain for possible applications of these novel spin textures. Rashba coefficients of some selected ferroelectric materials are compared with KIO in Section VI of the ESI.†


![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, which is generated by the symmetry elements of R3m followed by an inversion. The polarization, Pz along the c-direction breaks the inversion symmetry. Thus, the R
m, which is generated by the symmetry elements of R3m followed by an inversion. The polarization, Pz along the c-direction breaks the inversion symmetry. Thus, the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is centrosymmetric and band splitting is absent. It is well known that in ferroelectric Rashba semiconductors, switching the direction of polarization leads to the reversal of the spin texture. The full reversal of the spin texture on reversing the direction of polarization is also observed in KIO. To switch the direction of polarization, transition state R
m phase is centrosymmetric and band splitting is absent. It is well known that in ferroelectric Rashba semiconductors, switching the direction of polarization leads to the reversal of the spin texture. The full reversal of the spin texture on reversing the direction of polarization is also observed in KIO. To switch the direction of polarization, transition state R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m has to be crossed, which defines the potential barrier. The parent centrosymmetric structure is generated using the program PSEUDO.63 The calculated potential barrier to switch the polarization through the R
m has to be crossed, which defines the potential barrier. The parent centrosymmetric structure is generated using the program PSEUDO.63 The calculated potential barrier to switch the polarization through the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase is 135 meV f.u.−1 for R3m. Similarly, the potential barrier for the R3c phase is found to be 112 meV f.u.−1 The calculated potential barrier is comparable to 110 meV f.u.−1 of LaWN349 and is smaller than 130 meV f.u.−1 of LiNbO3.64 The Rashba parameters are larger for KIO than BAO, despite a significantly larger ferroelectric polarization in BAO. Therefore, we infer that larger ferroelectric polarization does not directly imply the larger splitting. A thorough analysis of the symmetry and electronic structure is always required.
m phase is 135 meV f.u.−1 for R3m. Similarly, the potential barrier for the R3c phase is found to be 112 meV f.u.−1 The calculated potential barrier is comparable to 110 meV f.u.−1 of LaWN349 and is smaller than 130 meV f.u.−1 of LiNbO3.64 The Rashba parameters are larger for KIO than BAO, despite a significantly larger ferroelectric polarization in BAO. Therefore, we infer that larger ferroelectric polarization does not directly imply the larger splitting. A thorough analysis of the symmetry and electronic structure is always required.


