 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Materials prepared by Freezing-Induced Self-Assembly of Dispersed Solutes: A Review
Ranajit
Mondal
 and
Guruswamy
Kumaraswamy
and
Guruswamy
Kumaraswamy
 *
*
Soft Materials for Sustainability, Department of Chemical Engineering, Indian Institute of Technology Bombay, Mumbai-400076, India. E-mail: guruswamy@iitb.ac.in
First published on 14th February 2022
Abstract
Crystallization demands structural regularity. Therefore, when a solvent is frozen to form a crystalline solid, it forces the dispersed solute to partition out of the crystalline phase. This forms the basis of ice-templating, wherein a solvent (often water) containing dispersed particles and/or macromolecules is frozen so that the dispersed solute phase is expelled by the ice crystals and is consolidated at their boundaries, when the ice crystals impinge. Removal of the ice crystals results in the formation of a macroporous material, whose pores are bounded by walls formed by the freezing-induced self-assembly of the solute. This versatile technique can be applied to a wide variety of solutes since their expulsion and aggregation due to solvent freezing is largely independent of solute chemistry. Ice-templating has therefore become an increasingly popular synthetic tool in the materials science community. In this review, we summarize the process of freezing and the interaction of the solute with the freezing solvent. We specifically review the literature on how solute–solute interactions influence the self-assembled structure that results from ice templating, and identify lacunae in our current understanding of ice-templated materials synthesis.
1 Introduction
Self-assembly has been defined as the “autonomous organization of components into patterns or structures without human intervention”.1 Self-assembly provides an attractive route to the synthesis of materials with engineered structures and has emerged as an exciting frontier area of research. For materials comprising colloidal or macromolecular building blocks, or for composites comprising inorganic nanoparticles and organic macromolecules, several self-assembly schemes have been explored in the literature. For example, spherical particles with a monodisperse size distribution have been crystallized into three-dimensional periodic structures with precise thickness using convective deposition2 that balances interparticle interactions, capillary forces and gravitational drainage. Similarly, particle and composite films have been formed using dip coating.3,4 Electrodeposition5 where particle deposition is controlled by external electric fields, assembly at fluid–fluid interfaces,6,7 dewetting,8 evaporation9 and polymerization-induced self-assembly of polymers with varied architectures (linear, star-like, bottlebrush-like, etc.)10,11 have emerged as simple yet powerful protocols to prepare materials with control over self-assembled structures. Self-assembly around sacrificial porogen templates has been used to prepare porous materials.12–15 Among the most industrially important examples of such materials are crystalline microporous zeolites16 and mesoporous materials with ordered pores.17 Such materials are not the focus of this review. Porogens have also been used to prepare macroporous materials, such as foams, where chemical blowing agents are used to create gas bubbles as porogens.18 In aerogels19 and zerogels, a porous structure results from covalent coupling (typically of oxides). Porous materials have also been obtained by templating a variety of static20–26 and dynamic27–33 structures. In particular, there has been a revival in interest in the use of ice as a template to prepare macroporous materials using ice-templating or ice-segregation induced self-assembly. The process of self-assembly in such materials is the focus of this review. The use of water as a porogen makes ice-templating an environmentally benign strategy for material synthesis. In recent years, there has been extensive investigation of the mechanism of ice templating, leading to a deeper understanding of the methods to control structure formation using this process. This has resulted in the use of ice templating to create well controlled self-assembled structures such as colloidal chains,34,35 2D colloidal sheets,36 fibers, membranes,37–39 core–shell fibers,40 flakes,41 porous micro-spheres,42 and 3D porous monoliths based on ceramics,43–45 polymers,46 biomacromolecules,47–50 metals51–53 and carbon based materials.54–59Functional materials with remarkable properties have been prepared using ice-templating. For example, biomimetic layered structures inspired by nacre, with brittle inorganic sheets separated by dissipative layers, have been reported. Such composite materials exhibit outstanding mechanical properties despite a high loading of the brittle inorganic phase, such as a combination of rigidity and toughness.60–63 Control over the state of solvation of the macromolecular phase in ice-templated polymer–inorganic composites has been exploited to produce macroporous sponges capable of recovering from large compressive deformation.64 Such exquisite control over hierarchical structuring and over the mechanical properties of ice-templated assemblies has been exploited to prepare materials with relevance to diverse technological areas ranging from biomedical implants, energy storage, and electronics to aerospace. For example, inorganic sponges with an unprecedented combination of viscoelastic shape memory and fire retardancy (obtained without the use of environmentally hazardous flame retardant additives) have been reported,65 as have next generation electrode materials66 for lithium ion batteries tolerant of the volume phase-transitions experienced during electrochemical reactions.67–70 The growing technological importance of ice templated materials has been documented in several recent reviews that focus on several different aspects of structural control or technological relevance in specific areas.71–78
The basic premise of preparing materials using ice-templating appears deceptively straightforward. An aqueous dispersion of solute (here, we use the term solute to refer to dissolved macromolecules as well as dispersed colloidal particles) is frozen. Ice crystals nucleate and grow, expelling the solute to the liquid regions. When the ice crystals impinge, the solute is consolidated at their boundaries. At solute volume fractions of a few percent, a three-dimensionally percolated structure results, with walls comprising the self-assembled solute. If the solute in the walls is held together subsequent to the removal of the ice, then a self-standing macroporous monolith results, with the pore size and shape corresponding to those of the template ice crystals. However, this apparent simplicity masks significant complexity associated with the physics of freezing, the nature of the solid–liquid interface and the influence of the solute on this process. Freezing is associated with the evolution of latent heat, setting up a thermal gradient at the freezing interface. Furthermore, depending on the interaction of the solute with the freezing front, it can either be expelled at the boundary or the ice can grow around it, engulfing the solute particle. This can result in the setting up of a solute concentration gradient at the freezing interface. While most treatments of ice templating deal with the case of dilute solute interacting with a freezing front, in practical situations, one is confronted with phenomena that arise from solute–solute interactions, especially when the solute concentration increases as the ice-templating progresses. Understanding these processes in detail is important to achieve structural control over the self-assembled materials resulting from ice templating. In this review, we provide an overview of these critical aspects of ice-templating. In the next section, we discuss the process of freezing and the nature of the frozen interface. Then, we discuss the interaction of the solute with the freezing front. Finally, we provide a perspective of the influence of solute–solute interactions on the development of ice-templated structures and outline a few aspects that remain incompletely understood. Previous reviews have not specifically concentrated on the aspect of the control of solute–solute interactions as a means to influence the structure of ice-templated materials. We hope that this review provokes investigations into this aspect of ice templating.
2 Freezing
Freezing-induced material preparation has been performed using a variety of solvents apart from water, including camphene, terpene, tertiary butyl alcohol, etc. Several aspects of freezing-induced solute consolidation are similar for water and other solvents. For simplicity, we refer to freezing-induced self-assembly as ice-templating in this review, since most reports investigate the freezing of aqueous dispersions. Freezing of water to form ice is a first order phase transition, and is associated with a discontinuous change in the first derivative of free energy (such as the specific volume) and in molecular packing, from a phase with liquid-like order to one with crystalline symmetry. This phase transition occurs through a nucleation and growth process, in which a crystalline phase nucleus with a critical size needs to form before the phase transition can proceed. Under typical laboratory experimental conditions of atmospheric pressure, water crystallizes below 0 °C into the hexagonal form of ice, which has a density of ≈920 kg m−3, lower than that of liquid water. For ice crystals to nucleate, water needs to be supercooled below the equilibrium melting point. With an increase in the degree of supercooling, there is an increase in the nucleation density. However, it is to be noted that the nucleation of ice depends not only on the degree of supercooling, but also on the presence of heterogenous surfaces that enhance epitaxial nucleation and, on impurities that could either enhance or inhibit nucleation.80 Therefore, while it is already challenging to predict crystal nucleation rates in well-defined model systems,81 it is currently impossible to predict ice crystal nucleation densities in experimental samples. After the formation of a critical nucleus, water molecules rapidly add to the ice crystal as it grows. This addition results in the release of latent heat. For the growth of the ice crystal, water molecules need to diffuse into the growing crystal front and the liberated latent heat needs to be removed. Water is characterized by a thermal diffusivity (=k/ρCp, where k, ρ and Cp are the thermal conductivity, density and specific heat at constant pressure) of ≈0.14 mm2 s−1 at 25 °C. Since freezing is typically effected by cooling a liquid sample in a container, uniform cooling to ensure uniform sized ice crystals necessitates that the sample be thin (viz. the sample dimension,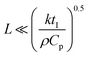 , where tI is the induction time for ice nucleation). For larger samples, temperature gradients result, leading to a spatial variation in the nucleation density and size of ice crystals and/or growth of oriented ice crystals. One strategy that has been reported65 to produce uniform size ice crystals in large samples is to induce convective flows so that temperature variations are minimized. Often, samples are frozen by intentionally imposing a temperature gradient82,83 so as to force the directional growth of ice crystals, resulting in the formation of anisotropic, oriented pores in the resultant self-assembled material. Unidirectional propagation of a crystal front is described by the classical Stefan problem that assumes diffusive heat transfer of the latent heat released for one dimensional propagation of a planar freezing front. However, the planar front is unstable and forms lamellar fingers due to the presence of a solute, as will be described in the next section. Lamellar ice crystals do not grow exactly along the temperature gradient direction, but at an angle to it and exhibit a dendritic shape. This has implications for the porous materials that result from ice-templating unidirectionally frozen samples. The imposition of a unidirectional temperature gradient results in the formation of multi-domain lamellar structures, viz. the global alignment of lamellae in the sample is not uniform. Researchers have shown84 that the samples subjected to bidirectional freezing (viz. with temperature gradients in two orthogonal directions) show lamellar morphologies that are aligned over the sample size. In addition, researchers have also explored the consequences of radial freezing85 and freezing under flow,61 to control the microstructures of ice-templated materials.
, where tI is the induction time for ice nucleation). For larger samples, temperature gradients result, leading to a spatial variation in the nucleation density and size of ice crystals and/or growth of oriented ice crystals. One strategy that has been reported65 to produce uniform size ice crystals in large samples is to induce convective flows so that temperature variations are minimized. Often, samples are frozen by intentionally imposing a temperature gradient82,83 so as to force the directional growth of ice crystals, resulting in the formation of anisotropic, oriented pores in the resultant self-assembled material. Unidirectional propagation of a crystal front is described by the classical Stefan problem that assumes diffusive heat transfer of the latent heat released for one dimensional propagation of a planar freezing front. However, the planar front is unstable and forms lamellar fingers due to the presence of a solute, as will be described in the next section. Lamellar ice crystals do not grow exactly along the temperature gradient direction, but at an angle to it and exhibit a dendritic shape. This has implications for the porous materials that result from ice-templating unidirectionally frozen samples. The imposition of a unidirectional temperature gradient results in the formation of multi-domain lamellar structures, viz. the global alignment of lamellae in the sample is not uniform. Researchers have shown84 that the samples subjected to bidirectional freezing (viz. with temperature gradients in two orthogonal directions) show lamellar morphologies that are aligned over the sample size. In addition, researchers have also explored the consequences of radial freezing85 and freezing under flow,61 to control the microstructures of ice-templated materials.
It is now accepted that there is a thin layer of quasi-liquid water at the surface of ice. Recent simulations suggest that this layer is characterized by a higher density than bulk water.86 The presence of this mobile layer at the ice interface has important implications for facilitating reactions at the ice surface, and therefore, for materials synthesis during ice templating. While the structure of this layer has attracted attention in the literature,87–90 the relevance of this to ice templating has not been considered. Freezing of water containing dissolved salts results in charge separation and trapping of ions in ice, giving rise to an electrostatic potential at the ice surface. This influences the interaction of the freezing front with solutes and could influence solute self-assembly during ice templating.
3 Interaction of the solute with the freezing front
The presence of a dissolved solute leads to a concentration-dependent decrease in the freezing point of the solvent. Since the solute is substantially excluded from the frozen solvent, there is an increase in the solute concentration over a layer of thickness Δ at the freezing front, where Δ = D/v is the ratio of the solute diffusivity D to the velocity of the growing front v. This increased solute concentration decreases the equilibrium liquidus temperature over Δ, leading to a constitutive supercooling, recognized by Rutter and Chalmers91 and by Keith and Padden.92 Thus, the growth velocity of the freezing front is determined not only by diffusion of latent heat, but also by solute-induced constitutive supercooling. This renders the freezing front unstable to perturbations, a situation that was first analysed by the celebrated paper of Mullins and Sekerka.93 They performed a linear stability analysis of a planar freezing front, assuming purely diffusive flux of the solute at the interface and obtained an analytical expression for the growth of perturbations of the freezing front. Despite the severe simplifications inherent in their analysis, this model provides a good estimate of the lamellar periodicity observed during unidirectional freezing. Dispersed colloidal particles also lead to constitutive supercooling at the freezing front94 and decrease the melting point of the solvent Tf as,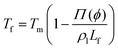 | (1) |
| Δσ = σps − (σpl + σsl) > 0 | (2) |
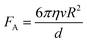 | (3) |
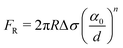 | (4) |
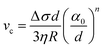 | (5) |
Below vc, the particle is rejected at the freezing front while for growth velocities that exceed vc, the particle is engulfed as the frozen phase grows around it. This represents a somewhat simplified picture of the interactions between a particle and a freezing front. A more complete picture needs to explicitly consider a variety of interactions depicted schematically in Fig. 1. Deville has recently reported95 experiments where a growing planar freezing front encounters monodisperse oil droplets of different sizes. They show that isolated droplets are rejected at the freezing front when they are smaller than a critical size while larger droplets are engulfed. However, when multiple small droplets are accumulated at the freezing front, they interact to form larger droplet clusters that are engulfed by the freezing front. Omenyi et al. identified an inversely proportional relationship between the critical solid/liquid interface velocity and particle size79 for naphthalene/nylon-6,10 and biphenyl/nylon-l2 systems as illustrated in Fig. 2. There is a critical velocity of the growing solidification front above which particles become entrapped for a given particle size. Particles are rejected at the front, only for growth below this threshold velocity. Inversely, there is a critical particle size for entrapment for a given displacement velocity: particles larger than the critical size are entrapped, whereas smaller ones are repelled. Deville et al. have also elucidated a general stability analysis for the solidification of colloidal suspensions over a range of interface velocities and particle sizes.96 Their observation revealed that small colloidal particles (of the order of microns or smaller) are rejected when they encounter a freezing front propagating at low interface velocity (<1 μm s−1). Here, the liquid freezes such that the interface proceeds as the planar front and the colloids are rejected and are concentrated in the unfrozen region. As the front velocity exceeds a critical value, it is destabilized to form lamellar structures due to constitutive supercooling, as described by Mullins and Sekerka.93 On further increasing to still higher interface velocities (>1 mm s−1) the morphology of the interface remains planar but the colloidal particles are engulfed by the growing front and show no spatial redistribution. Interesting porous morphologies where solute particles self-assemble into walls result at intermediate velocities of the freezing front (1 μm s−1 –1 mm s−1) and for intermediate solute particle sizes. Here, the particles are excluded as the solvent crystallizes and are consolidated between the growing lamellar crystals.
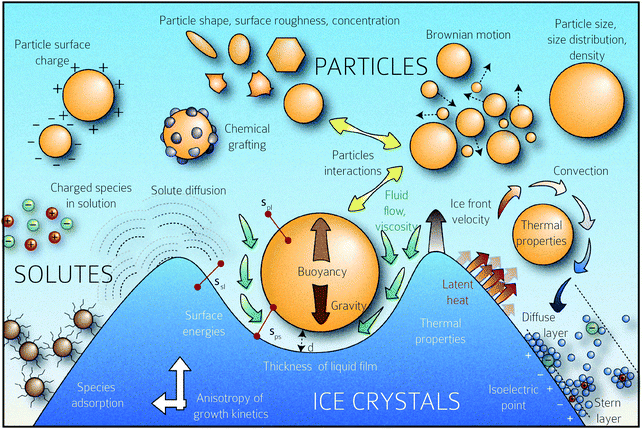 | ||
| Fig. 1 Schematic representation of the multiplicity of interactions between the freezing front and solutes (particles, polymers, charged species, etc.) The rich physics inherent in this situation, from growth instabilities of the growth front, hydrodynamic interactions between the front and solute, charging and electrostatic interactions between the species, solute–solute interactions, and species diffusion, among others, are schematically depicted. Copyright (2016) Sylvain Deville (DOI: 10.6084/m9.figshare.4012677) CC BY 4.0 https://doi.org/10.6084/m9.figshare.4012677.v1. | ||
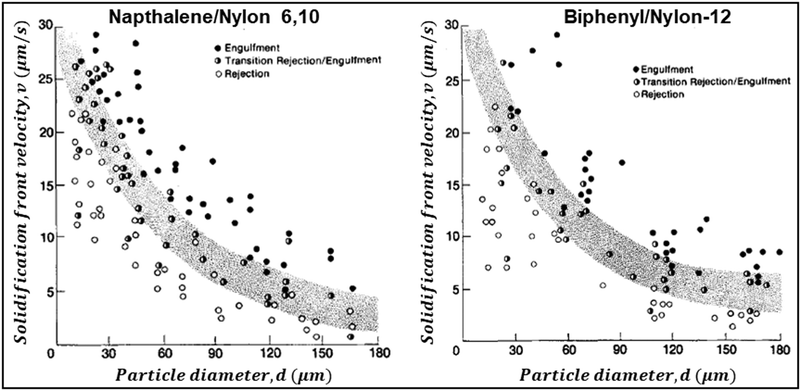 | ||
| Fig. 2 Data from experiments where dispersions of Nylon particles in naphthalene (left) and biphenyl (right) were frozen. The figures show the solidification front velocity of naphthalene (left) and biphenyl (right) versus the diameter of nylon particles. At low interface velocities, the solid–liquid interface is planar and the particles are rejected by the growing front. With an increase in velocity the interface becomes unstable. Above a particle-size dependent critical velocity, the particles are engulfed by the growing front. Reprinted with permission from ref. 79. Copyright (1981) AIP Publishing. | ||
4 Solute–solute interactions for control of self-assembled structures during freezing
As seen in the previous section, the interaction of a dispersed colloidal particle with a freezing front has been studied in depth. Often, such studies have been performed for unidirectional propagation of a freezing front, driven by a temperature gradient. If the dispersed phase colloidal particles are sufficiently small that they are Brownian, then under a wide range of practically realizable freezing conditions, they are expelled at the freezing front. Thus, their concentration in the dispersed phase increases until the ice crystals impinge after completion of freezing. The structure of the final assembly is determined by inter-particle interactions as well as by geometrical aspects of the consolidation of dispersed colloidal particles by growing ice crystals. Here, we explore the literature on how these aspects determine the structure of the assemblies. The mode of freezing the sample (uniform cooling versus unidirectional propagation of a freezing front) influences the geometry of ice crystal impingement. In recent work, dilute colloidal dispersions were frozen to form isolated colloidal clusters, and the cluster size distribution was analysed to gain insight into the mechanism of their assembly.35,36 Samples were frozen using one of the two protocols: isotropically, where no temperature gradient was imposed on the sample, or unidirectionally as schematically shown in Fig. 3(a). In both protocols, the cluster size distributions obtained were described by a power law, Pn ∼ n−ξ, where Pn represents the probability of finding a cluster comprising n particles. For isotropic freezing, experiments and simulations yielded ξ ≈ 2 over two orders of magnitude in the dispersion concentration (all sufficiently dilute that percolated structures did not form). In contrast, for unidirectional freezing, the exponent ξ decreased with concentration from about 3.5 to ≈2 over two decades of particle concentration from 0.001% to 0.1% (Fig. 3(b)). These experimental results are near quantitatively captured by simulations that invoke only the expulsion of the colloids by the growing ice front, neglecting hydrodynamics, inter-particle interactions (except hard sphere contact repulsion) and details of ice growth. Therefore, it is rationalized that the qualitative difference in cluster size distribution in the two freezing protocols arises from how the ice crystals fill space as they grow and impinge. Ice crystals that are nucleated randomly in the bulk of the dispersion grow isotropically to form pockets at late stages that trap particles, all of which must then consolidate into a single cluster. Therefore, the cluster size distribution remains the same, independent of particle concentration. In contrast, for unidirectional ice growth, colloidal particles are trapped in between walls of ice. With time, these walls thicken and grow towards each other, trapping colloidal particles between them. However, since the colloids can diffuse over the surface of the wall, the colloids between two walls do not necessarily assemble to form one cluster. Thus, differences in the cluster size distribution result from differences in the topology of liquid pockets as the ice crystals impinge, and from the distribution of particles in these pockets.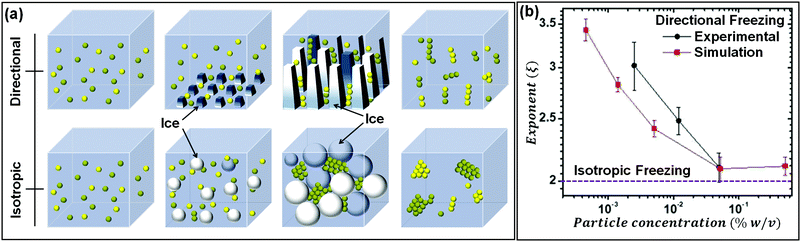 | ||
| Fig. 3 (a) Schematic representation of the time dependent structural evolution when a dilute dispersion of colloidal particles is frozen unidirectionally (top panel) and under isotropic conditions (bottom panel). Particles are expelled by the growing ice front and are assembled into isolated clusters that reflect the geometry of ice crystal impingement. (b) The size distribution of particle clusters follows a power law for both isotropic and directional freezing. The power law exponent is shown, as a function of particle concentration for directional freezing (solid black – experimental and red line – simulations) and for isotropic freezing (dashed purple line). Adapted with permission from ref. 36. Copyright (2021) Royal Society of Chemistry. | ||
The self-assembly of Brownian colloids expelled at the freezing front depends on their shape, size distribution and inter-particle interactions. Im and Park have demonstrated that freezing dispersions of a monodisperse charge-stabilized polystyrene latex resulted in the formation of three-dimensionally ordered structures, as shown in Fig. 4, that exhibit a photonic band-gap.97 They reported that rapid freezing resulted in the formation of curved or spherical assemblies (Fig. 4(b) and (c)), while slower freezing rates resulted in planar crystals (Fig. 4(a)) with fewer defects. Expulsion of Brownian monodisperse polystyrene colloids at the ice–water interface in unidirectional freezing has been shown to give rise to colloidal crystals arranged as oriented columnar domains.99
 | ||
| Fig. 4 SEM images of (a) planar, (b) curved, and (c) spherical structures obtained by the self-assembly of size-monodisperse polystyrene latex by freezing aqueous dispersions. Reprinted with permission from ref. 97. Copyright (2002) AIP Publishing. | ||
Crystallization of charge stabilized colloids expelled at a freezing front is controlled by an interplay between the particle Brownian diffusivity and the rate at which a particle attaches to and detaches from a colloidal crystal (which, in turn, depends on particle concentration and inter-particle interactions). Experiments that examined the systematic variation of the freezing front growth velocity on the ordering of monodisperse colloids have identified that colloidal crystallization is controlled by the Peclet number, Pe = dv/D, where d is the colloidal particle diameter, v is the velocity of the freezing front and D = kBT/ζ is the Brownian diffusivity of the colloid at temperature T and in a medium with hydrodynamic resistance ζ.100 However, we note that this analysis only balances the time scales for Brownian diffusivity (=d2/D) with that for convection (=d/v) and does not account for the role of inter-particle interactions. The inadequacy of this approach has been pointed out in the literature upon evaporation of colloidal dispersions.101 It is known that attractive interactions between colloids inhibit positional reorganization in particle assemblies and preclude the crystallization of even monodisperse colloids.102 For colloids that interact as hard spheres, equilibrium colloidal crystallization is determined only by the particle volume fraction.103 Brownian dynamics simulations indicate that for a hard sphere colloidal dispersion that is concentrated by a moving interface (for example, by evaporation or freezing), intermediate values of Pe promote colloidal crystallization.104 In the low Pe regime, Brownian diffusion dominates and particle crystallization is determined by their concentration, as in the equilibrium case. At high Pe, particles pile up at the freezing front and kinetic constraints on particle reorganization inhibit colloidal crystallization, as observed in the experiments on charge stabilized colloids.100 Ice templating experiments typically employ charge stabilized colloids. In charge stabilized particles, the strength and range of inter-particle interactions can be tuned by changing the ionic strength or by the addition of non-adsorbing polymers (to induce depletion interactions) or adsorbing polymers (to induce interactions as particles approach each other by charge correlations or bridging). A thorough, systematic investigation of the combined effects of particle size (that determines the Brownian diffusivity), crystallization rate (that could also determine the strength of particle consolidation in the aggregate105) and inter-particle interactions on particle ordering is still not available in the literature. When the size polydispersity of colloidal dispersions exceeds about 10%, they cannot crystallize.106 Ice templating of bidisperse colloidal dispersions comprising micron size particles and nanometer size sols has been used to produce crack-free high density ceramics with hierarchical porosity.41,107 It was reported that assemblies of micron sized inorganic particles consolidated by ice templating have insufficient strength and require freeze drying to withstand stresses generated by removal of the ice template. In contrast, objects assembled by ice-templating of bidisperse colloidal dispersions could be recovered intact by normal drying. Anisotropic rigid colloidal particles exhibit entropically driven orientational ordering with an increase in concentration, as first analysed by Onsager.108 Such lyotropic orientational ordering transitions have been experimentally observed in both rod-like and plate-like colloids that interact through hard-sphere or screened Coulombic interactions.109–112 When a dispersion containing anisotropic colloids is ice-templated, their expulsion from the frozen phase results in an increase in their local concentration such that liquid crystalline phases may form. This has important implications for the structure of the assembled colloids when they are consolidated by impingement of the frozen phase. As a rod-like colloid is approached by a moving front, the resultant hydrodynamic forces lead to particle alignment.113 For low Pe, the rod aligns with its major axis parallel to the moving front.
When a dispersion of anisotropic particles is subjected to unidirectional freezing, the particles are consolidated into lamellar structures. The majority of this research is focused on bioinspired approaches that try to mimic the structure of various natural materials. Ice templating of dispersions of high aspect ratio rod-like or fiber-like structures,114 especially bio-derived fibers such as chitin, amyloid fibers,115 cellulose nanofibers,48,116–119 keratin filaments,120,121 SiC fibres,59 platelets,61,122–127 and nanorods,128 has been reported. However, there are few investigations that systematically probe the effect of particle shape or colloid aspect ratio on freezing-induced orientational phase transitions. Thus, a comprehensive understanding of orientation development in ice templated rod-like dispersions is lacking in the literature. Depending on the nature of the anisotropy, the crystals can organize anisotropic particles with a specific favoured orientation. For example, for plate-like two dimensional colloidal suspensions, unidirectional freezing is used to produce macroporous materials with aligned platelets in the wall. Here, aligned platelets in the macroporous materials can only be achieved when the ice crystals are large enough compared to the platelet size. Densification, required to attain superior mechanical properties, remains a major challenge for ice-templating of large platelet suspensions. By controlling the anisotropy of the particles, an anisotropic functional response of the material can be achieved at the macro-sample scale. Hexagonal boron nitride anisotropic particles are characterized by different thermal conductivity in in-plane and out-of-plane orientations. Better orientation (and therefore, anisotropic response) can be obtained when samples are prepared using freezing rather than by the use of external electric or magnetic fields.122 Even if there is no functional anisotropy, the texture of the materials can also be used to improve the mechanical behavior of the materials. In one report, low concentration cellulose nanocrystal dispersions were aligned into a nematic phase in the lamellar space between ice crystals, and were consolidated into an oriented assembly.129 The same work also investigated higher concentration dispersions that already showed chiral nematic order assembly. When these were subjected to directional freezing, the nematic assemblies were further organized into lamellar structures. In another report cellulose nanofiber and nanocrystal dilute dispersions were shown to form aligned structures upon unidirectional freezing.128 The authors noted that the alignment of cellulosic structures could be disrupted by changing the ionic strength and/or pH of the original dispersion, thereby introducing attractive inter-colloid interactions. However, they also noted that alignment was not significantly affected for higher initial dispersion concentrations where the cellulose nanostructures gelled. In another report, it was observed that when a hydrogel of chiral cellulose nanocrystals is frozen, the growing ice crystals compress the nanocrystals resulting in a decrease in their helical pitch to generate photonic structures at visible wavelengths.130 Nematic liquid crystal dispersions of silver nanowires in PVA–water have also been directionally ice templated, and it was reported that the silver nanowires were oriented perpendicular to the freezing direction.114 Thus, during ice templating the orientation of the particles appears to depend on several factors, including the chemistry of the ice templated materials, their aspect ratio and inter-particle interactions.
There are important implications of particle alignment induced by the growing ice front on the properties of ice templated structures. In recent work,98 hematite dispersions of colloids with systematically varied aspect ratios (from about 1 to 4) were ice templated to form nanocomposite monoliths. The preparation protocol for ice-templated macroporous scaffolds and the microstructure of the wall comprising hematite particles with varying aspect ratios are shown in Fig. 5(a)–(f), where the hematite particles are held together in a mesh of crosslinked polymers. It was observed that monoliths comprising nearly isotropic particles (aspect ratio ∼1) showed a linear dependence of their modulus on the nominal density (E ∼ ρ) as shown in Fig. 5(g). There was no preferred local particle orientation of the anisotropic hematite particles observed, as evident from the SEM micrographs (Fig. 5(d) and (f)). However, for these monoliths, it was observed that E ∼ ρ1.4 (for aspect ratio ∼ 2.2) and E ∼ ρ2 (for aspect ratio ∼ 4), a qualitatively different dependence (Fig. 5(h) and (i)). Thus, a systematic understanding of how particle anisotropy and interactions govern their packing during ice templating has implications for the control of properties of the resultant monolith. Experiments and DEM simulations have been used to investigate the assembly of plate-like faceted colloids during unidirectional freezing.122 The particles are expelled by the growing ice and are trapped in the dispersion between the sheet-like ice. When these sheets thicken and move towards each other, particles at the moving interface are reoriented with their axis normal to the interface. As the dispersion concentration continues to increase, the particles closest to the interface become aligned while those away from the interface eventually jam into a state with a lower degree of order. They report that particle alignment is driven largely by contact repulsion and is observed even for particles with relatively low anisotropy. Similar behaviour is observed for unidirectional ice-templating of plate-like alumina colloids dispersed in aqueous chitosan/gelatin123 as shown in Fig. 6(a). Here, additionally, electrostatic interactions between the cationic chitosan/gelatin and the anionic alumina result in the formation of layered inorganic/polymer composites reminiscent of the structure of nacre as depicted in Fig. 6(b). These observations also suggest that the mechanical properties (Young's modulus, yield strength and toughness) of the ice-templated scaffolds are greatly influenced by the particle shape, size and freezing rate, as described in Fig. 6(c). However, there are also reports on the orientation of plate-like colloids that form interlamellar bridges perpendicular to the moving front in unidirectionally ice templated samples.131 Local orientational ordering of ice-templated plate like particles is also strongly influenced by interparticle interactions. Ice templating of as-prepared graphene oxide aqueous dispersions results in the random orientational ordering of the graphene oxide sheets. However, ice templating subsequent to the partial reduction of graphene oxide results in highly ordered assemblies with parallel graphene oxide sheets.57 Such monoliths have been reported to exhibit highly elastic mechanical recovery after large compression and exhibit modulus, E ∼ ρ2 (compared with ∼ρ3 for carbon nanoparticles or nanotube foams, with random interparticle orientations).
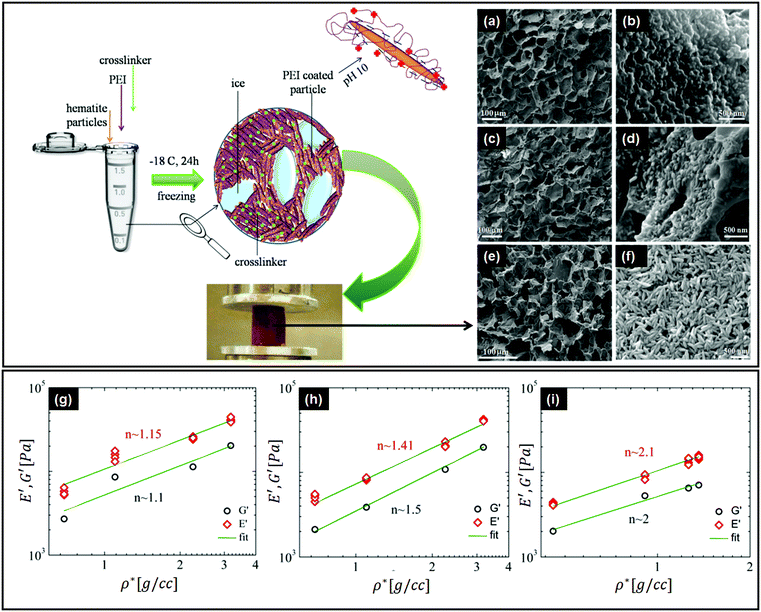 | ||
| Fig. 5 Top left panel – preparation protocol for ice-templated macroporous scaffolds, comprising walls of hematite particles held together in a mesh of crosslinked polymers. On the right, we observe the SEM micrographs of the walls of the porous monolith made using this protocol. (a and b) Monolith containing hematite particles with aspect ratios of ∼1, (c and d) ∼2.2 and (e and f) ∼4. Bottom panel – mechanical moduli from dynamic experiments in compression (E') and shear (G′) modes, as a function of nominal density (ρ*) for the hematite scaffolds with aspect ratios of (g) ∼1, (h) ∼2.2, and (i) ∼4. Note the systematic change in the power law exponents with the particle aspect ratio. Reprinted with permission from ref. 98. Copyright (2020) AIP Publishing. | ||
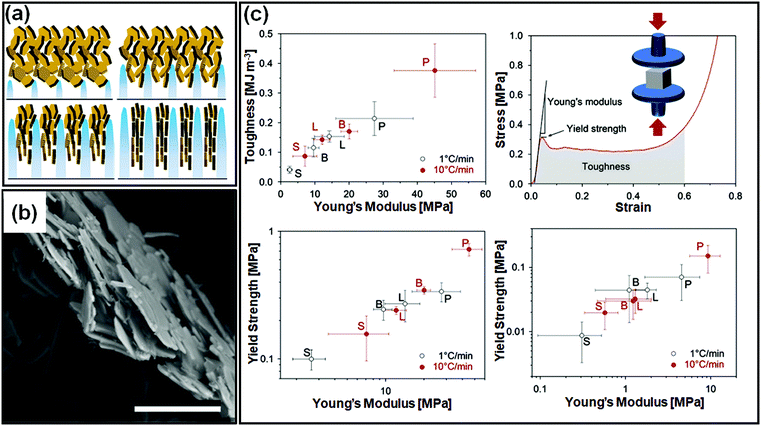 | ||
| Fig. 6 (a) Unidirectional ice templating of plate-like alumina dispersions in aqueous chitosan/gelatin results in their alignment, as indicated in the schematic. (b) An SEM image of the cross-section of the wall in the macroporous scaffold shows a nacre-like organization with aligned ceramic platelets in a composite structure. (c) Mechanical response of monoliths comprising alumina platelets [P] or isotropic particles with different sizes [S, small and L, large, or B bimodal, comprising S and L particles] prepared at two different freezing rates. The representative stress–strain curve shows that P monoliths exhibit a combination of high toughness and stiffness. Reprinted with permission from ref. 123. Copyright (2013), Elsevier. | ||
When multicomponent dispersions are ice-templated, the composite structure that results is governed by the inter-component interactions and their spatial organization. For example, in ice templated inorganic polymer nanocomposite monoliths, it has been demonstrated that the mechanical properties can be qualitatively different, depending on the processing route.132 The processing route determines the solvation state of the polymer in the composite, and thereby its ability to participate in crosslinking to mechanically stabilize the monolith. In nacre-mimetic composites, electrostatic interactions between the cationic polymer and anionic plate-like particles in the dispersion provide steric stabilization and result in one-dimensional stacking of alternating inorganic particles and the polymer.123 Therefore, in this report, the cationic polymer also acts as a dispersant, modifying the colloidal inter-particle interactions. In ice templating, the use of dispersants to stabilize colloids and binders to provide green strength to monoliths is common. These additives, could in addition, also influence the nucleation and growth of ice, and the stability of the frozen state.133,134 Electrostatic interactions between the components of a dispersion have been exploited to create self-assembled aggregates that are then ice-templated to form monolith structures.135 The imposition of external fields, such as electric, magnetic and acoustic fields, can influence inter-particle interactions at field strengths lower than that required to affect solvent freezing. This can be used to control particle assembly during ice templating, but is not the focus of this review. The literature on field-induced structural control during ice templating has been reviewed recently.136
Finally, we comment on the effect of increasing concentration during freezing on determining the self-assembled structure of amphiphiles. The structure of a dispersed phase is strongly determined by its concentration. When a dispersed phase is expelled at the freezing front, its concentration increases steadily as freezing proceeds. Close to the impingement of the frozen phase, the dispersed phase concentration is very high, with important consequences for the structure. For example, it has been shown137 that freezing aqueous solutions of amphiphilic P123 Pluronic copolymers results in the formation of ordered mesophases even when the initial solutions are below their critical micellar temperature (Fig. 7). This results from a continuous increase in the concentration of the amphiphilic copolymer to form dispersed micelles at first, followed by ordered micellar mesophases which was inferred from the time dependent evolution of temperature and concentration and SAXS patterns shown in Fig. 7(a)–(c). This is reminiscent of amphiphilic micellar ordering reported in Evaporation Induced Self-Assembly (EISA) protocols.138 Using a similar concept, an aqueous dispersion of block copolymer micelles was frozen to form a hexagonal mesophase that was subsequently templated to form mesoporous silica walls in a macroporous ice-templated monolith.139 Freezing has also been shown to result in structural changes in protein dispersions, for example, the formation of β-sheets in silk fibroin dispersions leading to gelation.140,141 Other examples in the literature have suggested using ice templating to spatially organize reactants in the walls of a macroporous monolith142 and subsequently carry out chemical transformations in the walls such as, for example, the synthesis of microporous zeolites.143 The possibility that the rate of chemical reactions can be modulated due to the confinement or increased reactant concentration during ice templating offers intriguing possibilities. For example, one anticipates that endothermic reactions such as amine-epoxy curing should proceed slowly as the temperature is decreased, through an Arrhenius rate factor. Our group has shown that polyethyleneimine (PEI) reacts with PEG-diepoxide during ice templating, viz. at temperatures as low as −18 °C.64,132 We see no evidence for any substantial progress in the PEI–diepoxide reaction in the initial dilute dispersion at room temperature over the same time period. We reason that the increase in concentration of the reactants as the water freezes more than compensates for the decrease in reaction rate due to cooling. Thus, this reaction is enabled even at low temperatures due to the freezing-induced increase in the reactant concentration. It is possible that such ice-assisted chemistry might be promoted by the existence of a mobile layer on the surface of crystalline ice (first reported by Faraday144). The formation of the crosslinked polymer mesh is not limited to the polyethylene imine–diepoxide system and several other chemistries have been demonstrated. For example, Rajamanickam et al.64 have shown that glutaraldehyde can effectively crosslink polyethyleneimine concentrated by freezing to produce self-standing monoliths. Furthermore, they prepared completely biocompatible macroporous monoliths by freezing dispersions of hydroxyapatite particles and gelatin, and by crosslinking gelatin in the frozen state using EDC coupling chemistry. Their group has demonstrated the preparation of monoliths using dispersions of colloidal particles with sizes varying from about 20 nm to several microns; for freezing dispersions in water or DMSO, and for freezing at different cooling rates (by placing in a refrigerator at −18 °C for rapid cooling by plunging in liquid nitrogen). In all these cases, crosslinking of the polymer mesh surrounding the colloidal particles resulted in the formation of monoliths capable of recovering from large compressive strains (nearly 90%). Therefore, the formation of monoliths capable of elastic recovery from compression appears to be governed by the nanocomposite structure produced – rather than the specific nature of the particle, polymer or crosslinker – with mechanical recovery governed by the rubbery crosslinked polymer mesh that surrounds the colloidal particles. Indeed, these monoliths are soft, despite their large inorganic content, pointing to the dominant role of the polymeric mesh in determining the mechanical properties. Therefore, the mechanical properties are highly sensitive to changes in the preparation protocol that affect the formation of the crosslinked polymer mesh. For example, if the frozen sample is lyophilized immediately after freezing, and before the crosslinking reaction proceeds to a substantial extent, then the dilute polymer chains are exposed to air (bad solvent conditions) rather than to water (good solvent). Under these conditions, there is a change in the conformation of the dilute polymer chains as they collapse. Crosslinking these samples at the same temperature and for the same duration as the frozen samples results in the formation of a monolith that is brittle, and that forms cracks even for small compressive strains (of the order of 5%).132 Thus, the formation of crosslinks to prepare a polymer mesh is less efficient for the case of collapsed polymer chains and produces monoliths with a qualitatively different (brittle) mechanical response. We note that for the case of effective crosslinking, intact centimeter-scale monoliths can be obtained simply by thawing and drying the ice templated samples, obviating the need for lyophilization. Such ice-assisted reactions have broad implications for materials and environmental chemistry and represent an interesting area of research.145–151
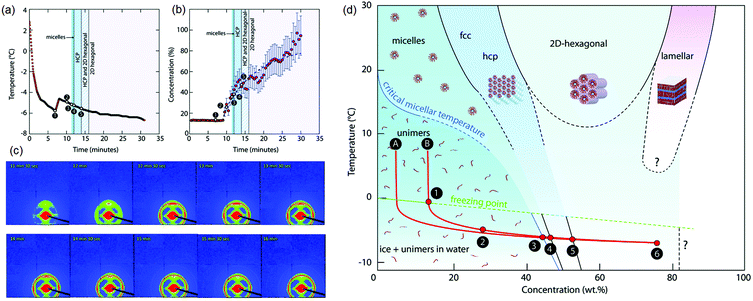 | ||
| Fig. 7 Freezing induced self-assembly of a 13 wt% aqueous P123 amphiphilic copolymer. Time dependent evolution of (a) temperature and (b) concentration, and (c) SAXS patterns are shown. (d) A concentration–temperature “phase diagram” showing structure formation during freezing-induced self-assembly of aqueous P123. Only P123 unimers are found in solution at first. When ice crystals begin to form (1–2), the concentration of P123 (in the liquid phase) increases, and self-assembled structures are observed (3–4–5). The freezing point (FP) temperature curve and the CMT curve are extrapolated (dashed lines). Reprinted with permission from ref. 137. Copyright (2017), Royal Society of Chemistry. | ||
5 Summary
There have been several recent reviews on materials synthesis using ice templating, attesting to the growing interest in this field. In this review, we focus on the role of solute–freezing front interactions, and particularly on solute–solute interactions, in determining the self-assembled structure that results from ice templating. As ice crystals grow, they expel solute to the liquid regions. The increasing solute concentrations in these regions result in strong solute–solute interactions. Therefore, self-assembled structure formation is governed by a combination of thermodynamic and kinetic factors: the range and strength of solute–solute interactions, and a balance between the rate of growth of the freezing front and solute diffusivity. While literature analyses have considered the influence of the Peclet number (a non-dimensional number that scales the velocity of the moving front with that of solute diffusion), the role of solute–solute interactions has remained underexplored. This represents an important and interesting avenue for exploration. Traditionally, stabilizers and dispersants have been used, based on experience, to keep the solute suspended until the ice crystals impinged. However, as the solute particles are concentrated during freezing, their interactions play a role in determining the structure. For example, strong attractive interactions could result in the formation of a jammed state that could influence the propagation of the freezing front. Alternately, excluded volume interactions determined by the solute shape and size could lead to crystallization or orientational ordering in the walls of ice templated monoliths. A thorough, systematic investigation of the combined effects of particle size and shape (that determine Brownian diffusivity and excluded volume interactions), crystallization rate (that could also determine the strength of particle consolidation in the aggregate) and inter-particle interactions on particle ordering is still not available in the literature. Understanding these aspects will have importance for the design of ice-templated materials with improved properties, based on appropriate choice of solute in the initial dispersion. A freezing induced increase in the solute concentration can also promote chemical reactions that can be used to create composite monoliths with exquisite control over their mechanical response. It is believed that there exists a thin mobile layer of quasi-liquid water at the ice interface which may drive the reaction even at very low temperatures. The relevance of this layer to ice-templated materials remains to be investigated. What is the importance of this molecular mobility in the progress of chemical reactions under frozen conditions? Can ordered macromolecular structures be prepared under such conditions? There are several such interesting questions that remain unanswered. The aspect of controlling the structures in monolith walls by tailoring solute–solute interactions has attracted relatively less attention in the community. By pointing to the opportunities for materials control through tailored solute–solute interactions, we hope that this aspect will be investigated more thoroughly in the near future.Conflicts of interest
The authors report no conflicts of interest related to this work.Acknowledgements
G. K. gratefully acknowledges the start-up funding from IIT-Bombay. R. M. gratefully acknowledges IIT-Bombay for the award of an Institute Postdoctoral Fellowship.References
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- P. Jiang, J. Bertone, K. S. Hwang and V. Colvin, Chem. Mater., 1999, 11, 2132–2140 CrossRef CAS.
- C. Murray, C. Kagan and M. Bawendi, Science, 1995, 270, 1335–1338 CrossRef CAS.
- Y. Mino, S. Watanabe and M. T. Miyahara, ACS Appl. Mater. Interfaces, 2012, 4, 3184–3190 CrossRef CAS PubMed.
- M. Janjua, S. Nudurupati, P. Singh and N. Aubry, Electrophoresis, 2011, 32, 518–526 CrossRef CAS PubMed.
- A. B. Subramaniam, M. Abkarian and H. A. Stone, Nat. Mater., 2005, 4, 553–556 CrossRef CAS PubMed.
- Y. Lin, H. Skaff, T. Emrick, A. Dinsmore and T. P. Russell, Science, 2003, 299, 226–229 CrossRef CAS PubMed.
- J. Huang, F. Kim, A. R. Tao, S. Connor and P. Yang, Nat. Mater., 2005, 4, 896–900 CrossRef CAS PubMed.
- E. Rabani, D. R. Reichman, P. L. Geissler and L. E. Brus, Nature, 2003, 426, 271–274 CrossRef CAS PubMed.
- Z. Li and Z. Lin, Polym. Int., 2021 DOI:10.1002/pi.6327.
- Z. Li, J. Peng and Z. Lin, Giant, 2021, 5, 100048 CrossRef CAS.
- S. Deville, Adv. Eng. Mater., 2008, 10, 155–169 CrossRef CAS.
- A. G. Slater and A. I. Cooper, Science, 2015, 348, aaa8075 CrossRef PubMed.
- A. Stein, S. G. Rudisill and N. D. Petkovich, Chem. Mater., 2014, 26, 259–276 CrossRef CAS.
- S. Deville, Freezing colloids: observations, principles, control, and use, Springer International Publishing, 2017 Search PubMed.
- R. F. Lobo, S. I. Zones and M. E. Davis, J. Inclusion Phenom. Mol. Recognit. Chem., 1995, 21, 47–78 CAS.
- C. Kresge, M. Leonowicz, W. J. Roth, J. Vartuli and J. Beck, Nature, 1992, 359, 710–712 CrossRef CAS.
- A. Barbetta, G. Rizzitelli, R. Bedini, R. Pecci and M. Dentini, Soft Matter, 2010, 6, 1785–1792 RSC.
- A. C. Pierre and G. M. Pajonk, Chem. Rev., 2002, 102, 4243–4266 CrossRef CAS PubMed.
- O. D. Velev and E. W. Kaler, Adv. Mater., 2000, 12, 531–534 CrossRef CAS.
- K. H. Rhodes, S. A. Davis, F. Caruso, B. Zhang and S. Mann, Chem. Mater., 2000, 12, 2832–2834 CrossRef CAS.
- A. Stein, F. Li and N. R. Denny, Chem. Mater., 2008, 20, 649–666 CrossRef CAS.
- R. A. Caruso and M. Antonietti, Chem. Mater., 2001, 13, 3272–3282 CrossRef CAS.
- M. Breulmann, S. Davis, S. Mann, H.-P. Hentze and M. Antonietti, Adv. Mater., 2000, 12, 502–507 CrossRef CAS.
- Y. Zhang, S. Zha and M. Liu, Adv. Mater., 2005, 17, 487–491 CrossRef CAS.
- S. A. Davis, H. M. Patel, E. L. Mayes, N. H. Mendelson, G. Franco and S. Mann, Chem. Mater., 1998, 10, 2516–2524 CrossRef CAS.
- A. Böker, Y. Lin, K. Chiapperini, R. Horowitz, M. Thompson, V. Carreon, T. Xu, C. Abetz, H. Skaff and A. Dinsmore, et al. , Nat. Mater., 2004, 3, 302–306 CrossRef PubMed.
- Y. Sakatani, C. Boissière, D. Grosso, L. Nicole, G. J. Soler-Illia and C. Sanchez, Chem. Mater., 2008, 20, 1049–1056 CrossRef CAS.
- D. Walsh, L. Arcelli, T. Ikoma, J. Tanaka and S. Mann, Nat. Mater., 2003, 2, 386–390 CrossRef CAS PubMed.
- E. M. Herzig, K. White, A. B. Schofield, W. C. Poon and P. S. Clegg, Nat. Mater., 2007, 6, 966–971 CrossRef CAS PubMed.
- V. Anderson, E. Terentjev, S. Meeker, J. Crain and W. Poon, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 4, 11–20 CrossRef CAS.
- K. P. Sharma, A. K. Ganai, S. S. Gupta and G. Kumaraswamy, Chem. Mater., 2011, 23, 1448–1455 CrossRef CAS.
- H. Zhang and A. I. Cooper, Soft Matter, 2005, 1, 107–113 RSC.
- X. Shen, L. Chen, D. Li, L. Zhu, H. Wang, C. Liu, Y. Wang, Q. Xiong and H. Chen, ACS Nano, 2011, 5, 8426–8433 CrossRef CAS PubMed.
- G. Kumaraswamy, B. Biswas and C. K. Choudhury, Faraday Discuss., 2016, 186, 61–76 RSC.
- B. Biswas, M. Misra, A. S. Bisht, S. K. Kumar and G. Kumaraswamy, Soft Matter, 2021, 17, 4098–4108 RSC.
- G. Ma, Z. Wang, J. Chen, R. Yin, B. Chen and J. Nie, New J. Chem., 2014, 38, 1211–1217 RSC.
- B. S. Kim, M. K. Lee and J. Lee, Macromol. Res., 2013, 21, 194–201 CrossRef CAS.
- A. Gondolini, E. Mercadelli, S. Casadio and A. Sanson, J. Eur. Ceram. Soc., 2022, 42, 1053–1060 CrossRef CAS.
- X. Y. Liu, J. M. Yang, L. S. Zha and Z. J. Jiang, Chin. J. Polym. Sci., 2014, 32, 1544–1549 CrossRef CAS.
- J. Laurie, C. Bagnall, B. Harris, R. Jones, R. Cooke, R. Russell-Floyd, T. Wang and F. Hammett, J. Non-Cryst. Solids, 1992, 147, 320–325 CrossRef.
- H. Zhang, D. Edgar, P. Murray, A. Rak-Raszewska, L. Glennon-Alty and A. I. Cooper, Adv. Funct. Mater., 2008, 18, 222–228 CrossRef CAS.
- X. Zeng, L. Ye, S. Yu, R. Sun, J. Xu and C.-P. Wong, Chem. Mater., 2015, 27, 5849–5855 CrossRef CAS.
- Y. Si, X. Wang, L. Dou, J. Yu and B. Ding, Sci. Adv., 2018, 4, eaas8925 CrossRef PubMed.
- B. H. Yoon, E. J. Lee, H. E. Kim and Y. H. Koh, J. Am. Ceram. Soc., 2007, 90, 1753–1759 CrossRef CAS.
- M. Barrow, A. Eltmimi, A. Ahmed, P. Myers and H. Zhang, J. Mater. Chem., 2012, 22, 11615–11620 RSC.
- X. Wu, Y. Liu, X. Li, P. Wen, Y. Zhang, Y. Long, X. Wang, Y. Guo, F. Xing and J. Gao, Acta Biomater., 2010, 6, 1167–1177 CrossRef CAS PubMed.
- J. Lee and Y. Deng, Soft Matter, 2011, 7, 6034–6040 RSC.
- M. J. Hortiguela, I. Aranaz, M. C. Gutierrez, M. L. Ferrer and F. del Monte, Biomacromolecules, 2011, 12, 179–186 CrossRef CAS PubMed.
- J. W. Kim, K. Taki, S. Nagamine and M. Ohshima, Langmuir, 2009, 25, 5304–5312 CrossRef CAS PubMed.
- P. Song, H. Qin, H.-L. Gao, H.-P. Cong and S.-H. Yu, Nat. Commun., 2018, 9, 1–9 CrossRef PubMed.
- H. L. Gao, L. Xu, F. Long, Z. Pan, Y. X. Du, Y. Lu, J. Ge and S. H. Yu, Angew. Chem., 2014, 126, 4649–4654 CrossRef.
- A. Knoìller, S. Kilper, A. M. Diem, M. Widenmeyer, T. Runcìevski, R. E. Dinnebier, J. Bill and Z. Burghard, Nano Lett., 2018, 18, 2519–2524 CrossRef PubMed.
- M. C. Gutierrez, M. J. Hortigüela, J. M. Amarilla, R. Jiménez, M. L. Ferrer and F. Del Monte, J. Phys. Chem. C, 2007, 111, 5557–5560 CrossRef CAS.
- S. Nardecchia, M. C. Serrano, M. C. Gutiérrez, M. T. Portolés, M. L. Ferrer and F. del Monte, Adv. Funct. Mater., 2012, 22, 4411–4420 CrossRef CAS.
- J. L. Vickery, A. J. Patil and S. Mann, Adv. Mater., 2009, 21, 2180–2184 CrossRef CAS.
- L. Qiu, J. Z. Liu, S. L. Chang, Y. Wu and D. Li, Nat. Commun., 2012, 3, 1–7 Search PubMed.
- H. Zhang, I. Hussain, M. Brust, M. F. Butler, S. P. Rannard and A. I. Cooper, Nat. Mater., 2005, 4, 787–793 CrossRef CAS PubMed.
- C. Ferraro, E. Garcia-Tuñon, V. G. Rocha, S. Barg, M. D. Fariñas, T. E. G. Alvarez-Arenas, G. Sernicola, F. Giuliani and E. Saiz, Adv. Funct. Mater., 2016, 26, 1636–1645 CrossRef CAS.
- S. Deville, E. Saiz, R. K. Nalla and A. P. Tomsia, Science, 2006, 311, 515–518 CrossRef CAS PubMed.
- F. Bouville, E. Maire, S. Meille, B. Van de Moortèle, A. J. Stevenson and S. Deville, Nat. Mater., 2014, 13, 508–514 CrossRef CAS PubMed.
- Q. Cheng and L. Jiang, Angew. Chem., Int. Ed., 2017, 56, 934–935 CrossRef CAS PubMed.
- A. Wat, J. I. Lee, C. W. Ryu, B. Gludovatz, J. Kim, A. P. Tomsia, T. Ishikawa, J. Schmitz, A. Meyer and M. Alfreider, et al. , Nat. Commun., 2019, 10, 1–12 CrossRef CAS PubMed.
- R. Rajamanickam, S. Kumari, D. Kumar, S. Ghosh, J. C. Kim, G. Tae, S. Sen Gupta and G. Kumaraswamy, Chem. Mater., 2014, 26, 5161–5168 CrossRef CAS.
- S. Chatterjee, K. Shanmuganathan and G. Kumaraswamy, ACS Appl. Mater. Interfaces, 2017, 9, 44864–44872 CrossRef CAS PubMed.
- J. Wang, Z. Xu, J. C. Eloi, M. M. Titirici and S. J. Eichhorn, Adv. Funct. Mater., 2022, 2110862 CrossRef.
- A. Vu, Y. Qian and A. Stein, Adv. Energy Mater., 2012, 2, 1056–1085 CrossRef CAS.
- G. Li, Z. Liu, Q. Huang, Y. Gao, M. Regula, D. Wang, L. Q. Chen and D. Wang, Nat. Energy, 2018, 3, 1076–1083 CrossRef CAS.
- S. Li, G. Tian, R. Xiong, R. He, S. Chen, H. Zhou, Y. Wu, Z. Han, C. Yu and S. Cheng, et al. , Energy Storage Mater., 2022, 46, 443–451 CrossRef.
- C. Huang and P. S. Grant, J. Mater. Chem. A, 2018, 6, 14689–14699 RSC.
- K. Qin, C. Parisi and F. M. Fernandes, J. Mater. Chem. B, 2021, 9, 889–907 RSC.
- S. Deville, Scr. Mater., 2018, 147, 119–124 CrossRef CAS.
- K. L. Scotti and D. C. Dunand, Prog. Mater. Sci., 2018, 94, 243–305 CrossRef CAS.
- G. Shao, D. A. Hanaor, X. Shen and A. Gurlo, Adv. Mater., 2020, 32, 1907176 CrossRef CAS PubMed.
- I. Nelson and S. E. Naleway, J. Mater. Res. Technol., 2019, 8, 2372–2385 CrossRef.
- J. Yang, W. Yang, W. Chen and X. Tao, Prog. Polym. Sci., 2020, 109, 101289 CrossRef CAS.
- H. Joukhdar, A. Seifert, T. Jüngst, J. Groll, M. S. Lord and J. Rnjak-Kovacina, Adv. Mater., 2021, 33, 2100091 CrossRef CAS PubMed.
- J. X. Yap, C. Leo, N. H. Mohd Yasin, P. L. Show, D. T. Chu, V. Singh and C. Derek, Bioengineered, 2022, 13, 2226–2247 CrossRef CAS PubMed.
- S. Omenyi, A. Neumann, W. Martin, G. Lespinard and R. Smith, J. Appl. Phys., 1981, 52, 796–802 CrossRef CAS.
- M. I. Gibson, Polym. Chem., 2010, 1, 1141–1152 RSC.
- S. Auer and D. Frenkel, Nature, 2001, 409, 1020–1023 CrossRef CAS PubMed.
- H. Tetik, D. Feng, S. W. Oxandale, G. Yang, K. Zhao, K. Feist, N. Shah, Y. Liao, Z. C. Leseman and D. Lin, ACS Appl. Mater. Interfaces, 2021, 13, 924–931 CrossRef CAS PubMed.
- N. Zhao, M. Li, H. Gong and H. Bai, Sci. Adv., 2020, 6, eabb4712 CrossRef CAS PubMed.
- H. Bai, Y. Chen, B. Delattre, A. P. Tomsia and R. O. Ritchie, Sci. Adv., 2015, 1, e1500849 CrossRef PubMed.
- L. Fan, J. L. Li, Z. Cai and X. Wang, ACS Nano, 2018, 12, 5780–5790 CrossRef CAS PubMed.
- H. Niinomi, T. Yamazaki, H. Nada, T. Hama, A. Kouchi, J. T. Okada, J. Nozawa, S. Uda and Y. Kimura, J. Phys. Chem. Lett., 2020, 11, 6779–6784 CrossRef CAS PubMed.
- J. Dash, A. Rempel and J. Wettlaufer, Rev. Mod. Phys., 2006, 78, 695 CrossRef CAS.
- Y. Nagata, T. Hama, E. H. Backus, M. Mezger, D. Bonn, M. Bonn and G. Sazaki, Acc. Chem. Res., 2019, 52, 1006–1015 CrossRef CAS PubMed.
- B. Slater and A. Michaelides, Nat. Rev. Chem., 2019, 3, 172–188 CrossRef CAS.
- K. Murata, H. Asakawa, K. Nagashima, Y. Furukawa and G. Sazaki, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E6741–E6748 CrossRef CAS PubMed.
- J. Rutter and B. Chalmers, Can. J. Phys., 1953, 31, 15–39 CrossRef CAS.
- H. Keith and F. Padden Jr, J. Appl. Phys., 1963, 34, 2409–2421 CrossRef CAS.
- W. W. Mullins and R. Sekerka, J. Appl. Phys., 1964, 35, 444–451 CrossRef.
- S. Peppin, J. Wettlaufer and M. Worster, Phys. Rev. Lett., 2008, 100, 238301 CrossRef CAS PubMed.
- S. Tyagi, C. Monteux and S. Deville, Sci. Rep., 2021, 11, 1–14 CrossRef PubMed.
- S. Deville, E. Maire, G. Bernard-Granger, A. Lasalle, A. Bogner, C. Gauthier, J. Leloup and C. Guizard, Nat. Mater., 2009, 8, 966–972 CrossRef CAS PubMed.
- S. H. Im and O. O. Park, Appl. Phys. Lett., 2002, 80, 4133–4135 CrossRef CAS.
- G. Kumaraswamy, K. Suresh, H. Lama, M. G. Basavaraj and D. K. Satapathy, J. Appl. Phys., 2020, 128, 034702 CrossRef CAS.
- Y. Suzuki, G. Sazaki, K. Hashimoto, T. Fujiwara and Y. Furukawa, J. Cryst. Grow., 2013, 383, 67–71 CrossRef CAS.
- J. You, J. Wang, L. Wang, Z. Wang, Z. Wang, J. Li and X. Lin, Colloids Surf., A, 2017, 531, 93–98 CrossRef CAS.
- A. Lesaine, D. Bonamy, C. L. Rountree, G. Gauthier, M. Impéror-Clerc and V. Lazarus, Soft Matter, 2021, 17, 1589–1600 RSC.
- G. Kumaraswamy, A. M. Dibaj and F. Caruso, Langmuir, 2002, 18, 4150–4154 CrossRef CAS.
- P. N. Pusey and W. Van Megen, Nature, 1986, 320, 340–342 CrossRef CAS.
- M. Wang and J. F. Brady, Soft Matter, 2017, 13, 8156–8170 RSC.
- J. Lee and Y. Cheng, J. Controlled Release, 2006, 111, 185–192 CrossRef CAS PubMed.
- P. Pusey, J. Phys., 1987, 48, 709–712 CrossRef CAS.
- J. Zheng, D. Salamon, L. Lefferts, M. Wessling and L. Winnubst, Microporous Mesoporous Mater., 2010, 134, 216–219 CrossRef CAS.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 CrossRef CAS.
- A. Mourchid, A. Delville, J. Lambard, E. Lecolier and P. Levitz, Langmuir, 1995, 11, 1942–1950 CrossRef CAS.
- H. Lekkerkerker and G. Vroege, Philos. Trans. R. Soc., A, 2013, 371, 20120263 CrossRef CAS PubMed.
- Z. Dogic and S. Fraden, Curr. Opin. Colloid Interface Sci., 2006, 11, 47–55 CrossRef CAS.
- Y. Xu, A. Atrens and J. R. Stokes, Adv. Colloid Interface Sci., 2020, 275, 102076 CrossRef CAS PubMed.
- K. P. Sharma, A. K. Ganai, D. Sen, B. Prasad and G. Kumaraswamy, J. Phys. Chem. B, 2013, 117, 12661–12668 CrossRef CAS PubMed.
- H. E. Romeo, C. E. Hoppe, M. A. Lopez-Quintela, R. J. Williams, Y. Minaberry and M. Jobbágy, J. Mater. Chem., 2012, 22, 9195–9201 RSC.
- G. Nystroìm, W.-K. Fong and R. Mezzenga, Biomacromolecules, 2017, 18, 2858–2865 CrossRef PubMed.
- L. Liu, L. Bai, A. Tripathi, J. Yu, Z. Wang, M. Borghei, Y. Fan and O. J. Rojas, ACS Nano, 2019, 13, 2927–2935 CrossRef CAS PubMed.
- F. Ram, B. Biswas, A. Torris, G. Kumaraswamy and K. Shanmuganathan, Cellulose, 2021, 1–15 Search PubMed.
- F. Martoa, T. Cochereau, P. J. Dumont, L. Orgéas, M. Terrien and M. Belgacem, Mater. Des., 2016, 104, 376–391 CrossRef.
- C. Darpentigny, S. Molina-Boisseau, G. Nonglaton, J. Bras and B. Jean, Cellulose, 2020, 27, 233–247 CrossRef CAS.
- Z. Zhao, H. M. Chua, B. H. R. Goh, H. Y. Lai, S. J. Tan, Z. K. Moay, M. I. Setyawati and K. W. Ng, J. Biomed. Mater. Res., Part A, 2022, 110, 92–104 CrossRef CAS PubMed.
- Z. Zhao, Z. K. Moay, H. Y. Lai, B. H. R. Goh, H. M. Chua, M. I. Setyawati and K. W. Ng, Macromol. Biosci., 2021, 21, 2000314 CrossRef CAS PubMed.
- F. Bouville, E. Maire and S. Deville, Langmuir, 2014, 30, 8656–8663 CrossRef CAS PubMed.
- P. M. Hunger, A. E. Donius and U. G. Wegst, J. Mech. Behav. Biomed. Mater., 2013, 19, 87–93 CrossRef CAS PubMed.
- F. Bouville, E. Maire and S. Deville, J. Mater. Res., 2014, 29, 175–181 CrossRef CAS.
- F. Bouville, E. Portuguez, Y. Chang, G. L. Messing, A. J. Stevenson, E. Maire, L. Courtois and S. Deville, J. Am. Ceram. Soc., 2014, 97, 1736–1742 CrossRef CAS.
- D. Ghosh, M. Banda, S. Akurati, H. Kang and V. O. Fakharizadeh, Scr. Mater., 2017, 138, 139–144 CrossRef CAS.
- S. Sabat, S. Sikder, S. K. Behera and A. Paul, Ceram. Int., 2022, 48, 2893–2897 CrossRef CAS.
- P. Munier, K. Gordeyeva, L. Bergstroìm and A. B. Fall, Biomacromolecules, 2016, 17, 1875–1881 CrossRef CAS PubMed.
- G. Chu, D. Qu, E. Zussman and Y. Xu, Chem. Mater., 2017, 29, 3980–3988 CrossRef CAS.
- Y. Cao, L. Lewis, W. Y. Hamad and M. J. MacLachlan, Adv. Mater., 2019, 31, 1808186 CrossRef PubMed.
- D. Ghosh, M. Banda, H. Kang and N. Dhavale, Scr. Mater., 2016, 125, 29–33 CrossRef CAS.
- K. Suresh, A. Chowdhury, S. K. Kumar and G. Kumaraswamy, Macromolecules, 2019, 52, 5955–5962 CrossRef CAS.
- J. You, J. Wang, L. Wang, Z. Wang, J. Li, X. Lin and Y. Zhu, Langmuir, 2019, 35, 10446–10452 CrossRef CAS PubMed.
- C. Pekor and I. Nettleship, Ceram. Int., 2014, 40, 9171–9177 CrossRef CAS.
- X. Yao, H. Yao and Y. Li, J. Mater. Chem., 2009, 19, 6516–6520 RSC.
- P. Niksiar, F. Y. Su, M. B. Frank, T. A. Ogden, S. E. Naleway, M. A. Meyers, J. McKittrick and M. M. Porter, Ceramics, 2019, 2, 208–234 CrossRef.
- P. Albouy, S. Deville, A. Fulkar, K. Hakouk, M. Impéror-Clerc, M. Klotz, Q. Liu, M. Marcellini and J. Perez, Soft Matter, 2017, 13, 1759–1763 RSC.
- C. J. Brinker, Y. Lu, A. Sellinger and H. Fan, Adv. Mater., 1999, 11, 579–585 CrossRef CAS.
- J. Dhainaut, G. Piana, S. Deville, C. Guizard and M. Klotz, Chem. Commun., 2014, 50, 12572–12574 RSC.
- F. Ak, Z. Oztoprak, I. Karakutuk and O. Okay, Biomacromolecules, 2013, 14, 719–727 CrossRef CAS PubMed.
- X. Li, S. Yan, J. Qu, M. Li, D. Ye, R. You, Q. Zhang and D. Wang, Int. J. Biol. Macromol., 2018, 117, 691–695 CrossRef CAS PubMed.
- J. Dhainaut, S. Deville, I. Amirouche and M. Klotz, Inorganics, 2016, 4, 6 CrossRef.
- H. Mori, K. Aotani, N. Sano and H. Tamon, J. Mater. Chem., 2011, 21, 5677–5681 RSC.
- M. Faraday, London, Edinburgh Dublin Philos. Mag. J. Sci., 1859, 17, 162–169 CrossRef.
- Z. Tan, X. Guo, Y. Yin, B. Wang, Q. Bai, X. Li, J. Liu and G. Jiang, Environ. Sci. Technol., 2019, 53, 13802–13811 CrossRef CAS PubMed.
- N. Takenaka, A. Ueda, T. Daimon, H. Bandow, T. Dohmaru and Y. Maeda, J. Phys. Chem., 1996, 100, 13874–13884 CrossRef CAS.
- K. Kitada, Y. Suda and N. Takenaka, J. Phys. Chem. A, 2017, 121, 5383–5388 CrossRef CAS PubMed.
- S. M. Agten, D. P. Suylen and T. M. Hackeng, Bioconjugate Chem., 2016, 27, 42–46 CrossRef CAS PubMed.
- J. Erlandsson, T. Pettersson, T. Ingverud, H. Granberg, P. A. Larsson, M. Malkoch and L. Wågberg, J. Mater. Chem. A, 2018, 6, 19371–19380 RSC.
- R. O. Concubhair and J. R. Sodeau, Acc. Chem. Res., 2013, 46, 2716–2724 CrossRef PubMed.
- K. Kim and M. J. Park, Nanoscale, 2020, 12, 14320–14338 RSC.
| This journal is © The Royal Society of Chemistry 2022 |
