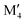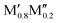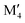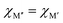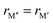Open Access Article
Open Access ArticleChemical order or disorder – a theoretical stability expose for expanding the compositional space of quaternary metal borides†
Martin
Dahlqvist
 * and
Johanna
Rosen
* and
Johanna
Rosen
 *
*
Materials Design, Department of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83 Linköping, Sweden. E-mail: martin.dahlqvist@liu.se; johanna.rosen@liu.se
First published on 11th February 2022
Abstract
Inspired by the recent discovery of Ti4MoSiB2, a quaternary phase with out-of-plane chemical order that we denote as o-MAB, we perform an extensive first-principles study to explore the attained chemical order and disorder (solid-solution) upon metal alloying of M5AB2 (T2 phases), with M from Groups 3 to 9 and A = Al, Si, P, Ga, and Ge. We show that the attainable chemistries of T2 can be significantly expanded and predict 35 chemically ordered o-MAB phases and 121 solid solutions of an 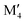 M′′AB2 stoichiometry. The possibility of realizing o-MAB or solid solution MAB phases combined with multiple elemental combinations previously not observed in these borides suggests an increased property tuning potential. Furthermore, five ternary T2 phases, yet to be synthesized, are also predicted to be stable.
M′′AB2 stoichiometry. The possibility of realizing o-MAB or solid solution MAB phases combined with multiple elemental combinations previously not observed in these borides suggests an increased property tuning potential. Furthermore, five ternary T2 phases, yet to be synthesized, are also predicted to be stable.
Introduction
The contemporary exploration of layered materials is propelled by their physical and chemical properties as well as their potential use as a precursor for conversion into 2D materials. MAX phases (M = transition metal, A = A-group element and X = C and/or N) are a family of atomically laminated hexagonal materials which combine the attributes of both metallics and ceramics, such as being machinable, excellent electrical and thermal conductivities, thermal shock and oxidation resistance.1–3 MAX phases are also the precursor materials for their two-dimensional (2D) derivatives, MXenes, realized from the selective etching of the A-element.4 MXenes have attracted huge interest due to their exceptional properties such as hydrophilicity, high electrical conductivity and volumetric capacitance, making them beneficial for numerous applications including energy storage and electromagnetic interference shielding.5–8 Recently, chemically ordered MAX phases (i-MAX and o-MAX), i.e. quaternary compounds displaying in-plane or out-of-plane chemical order for two M elements,9–11 have been converted into MXenes upon selective etching.10,12–15So-called MAB phases are also atomically laminated, though they display different crystal structures and show a wider palette of structural variations, from orthorhombic Mn+1AlB2n (with n = 1–3),16–18 MAlB17 and M4AlB4,19 hexagonal M2AB2,20,21 to tetragonal M5AB2 (T2),22 but with M mainly from Groups 6 to 9. There are a few reports on the attempted synthesis of 2D MBenes through selective etching of layered ternary MAB phases;23–25 however, the realization of individual single-layer sheets from these materials still remains a quest.
In a recent study, we considered metal alloying as a path towards expanding the attainable chemistries in orthorhombic and hexagonal M2AlB2 and discovered two in-plane chemically ordered MAB phases, Mo4/3Y2/3AlB2 and Mo4/3Sc2/3AlB2, coined i-MAB26 (analogous to i-MAX),10 along with an additional 13 i-MAB and 16 solid solution phases that were predicted to be stable. This exemplifies alloying as a prospective path to expand MAB phase chemistries which when combined with various MAB structures would allow for a range of possibilities when it comes to novel elemental combinations, bond modification, and property tuning. Bond modification in an MAB alloy could for example allow for conversion into its 2D derivative, MBene or boridene, in the same way as the conversion of i-MAX to i-MXene.27 Indeed, most recently the first 2D metal boride, named boridene, has been experimentally realized in the form of single sheets of Mo4/3B2−x, selectively etched from the i-MAB-phases (Mo2/3Sc1/3)2AlB2 and (Mo2/3Y1/3)2AlB2.28
Herein we consider the tetragonal and atomically layered T2 phases, which were discovered in 1957 when Nowotny et al. synthesized the prototypical Mo5SiB2, followed by the synthesis of Fe5SiB2 and Mn5SiB2 phases in 1960.22,29 T2 phases have an M5AB2 composition in an I4/mcm space group symmetry, where M is a transition metal from Groups 5 to 9, and A is an A-element (Si, Ge, and P). T2 phases are attractive due to their high oxidation resistance,30 nearly isotropic thermal expansion,31 superconducting properties32,33 and potential for use as rare-earth free permanent magnets.34–36
We have recently shown that metal alloying in Si-based T2 phases holds potential for a range of new compositions, including the discovered out-of-plane ordered Ti4MoSiB2, called o-MAB.37 It has been demonstrated that the bonds between the two metallic sites, Ti and Mo, are key to the stability of this specific structure.38 In the present work we use a systematic theoretical approach to demonstrate the expansion of the possible chemistries for T2 phases, beyond A = Si, both with respect to ternary and quaternary compositions. The latter by exploiting metal alloying on the two crystallographic unique metal sites by considering both the chemically ordered (out-of-plane ordered o-MAB, 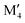 M′′AB2) and disordered (solid solution, (
M′′AB2) and disordered (solid solution, (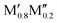 )5AB2) distribution of M′ and M′′. Guided by thermodynamic stability calculations, we confirm the stability for experimentally known ternary and quaternary T2 phases. More importantly, we also predict 35 stable o-MAB phases and 121 stable solid solutions, which are yet to be experimentally discovered.
)5AB2) distribution of M′ and M′′. Guided by thermodynamic stability calculations, we confirm the stability for experimentally known ternary and quaternary T2 phases. More importantly, we also predict 35 stable o-MAB phases and 121 stable solid solutions, which are yet to be experimentally discovered.
Furthermore, we investigate the impact of the choice of the element (M′ and M′′, and A) and the effect of the size and electronegativity of M′ and M′′ on the formation of chemically ordered (o-MAB) or solid solution MAB phases. We also propose guidelines as which elemental combination needs to be employed in the experimental discovery of a stable phase with chemical order or disorder. This study reveals that alloying is a fruitful pathway for expanding the concept of T2 phases to include novel elemental combinations which, in turn, may provide tuneable and advantageous properties as well as the potential derivation of 2D materials from chemical exfoliation.
Methods
All first-principles calculations are performed by means of density functional theory (DFT) using the Vienna ab initio simulation package (VASP) version 5.4.1.39–41 The projector augmented wave method is used with the generalized gradient approximation (GGA) as parameterized by Perdew–Burke–Ernzerhof (PBE).42–44 In systems with Cr, Mn, Fe, Co, and Ni, we used the spin-polarized GGA version and energy is taken for the lowest ferromagnetic and antiferromagnetic configurations sampled within the unit cell. Further details of the considered magnetic spin configurations can be found in Fig. S1 (ESI†). Note that while spin configurations with lower energy may exist, this approximation serves the purpose of indicating if the phase is stable or not. If found stable, a potential lower energy spin configuration will increase the stability even further.For structural relaxation, the Brillouin zone was integrated with Monkhorst–Pack special k-point sampling, with a density of 0.05 Å−1,45 with a plane-wave energy cut-off of 400 eV. The convergence of formation enthalpy with respect to the k-point density and plane-wave energy cut-off, shown in Fig. S2 (ESI†) for selected phases, demonstrates that the used settings ensure the ΔHcp values to be converged within less than 1 meV per atom. The convergence criterion for self-consistency is reached when satisfying an energy convergence of 10−6 eV per atom and a force convergence of 10−2 eV Å−1.
The T2 structure has a tetragonal I4/mcm space group symmetry in an M5AB2 composition, where M is a transition metal and A is an A-group element. In this work we have considered M from Groups 3 to 9; Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, Co, and Ni, along with traditional and non-traditional A elements; Al, Ga, Ge, Si, Ge, Sn, and P. Solid solutions, or chemical disorder, of M′ and M′′ are modelled on the M sublattices, 16l and 4c, simultaneously, using the special quasi-random structure (SQS) method.46 The convergence tests in Fig. S3 (ESI†) show that the supercells with 160 or more atoms give a qualitatively accurate representation and a quantitative convergency in terms of calculated formation enthalpies, equilibrium volumes, and lattice parameters needed for the herein presented high-throughput study.
In general, the formation energy for a phase is given by,
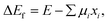 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. However, ΔEf is not an appropriate indicator for stability as demonstrated in Fig. S4 (ESI†).
K. However, ΔEf is not an appropriate indicator for stability as demonstrated in Fig. S4 (ESI†).
An alternative and a more comprehensive approach for assessing the thermodynamic stability of a phase is to compare its energy relative to competing phases in the ternary or quaternary system of interest. This will give information on whether the phase is energetically favored or prefer decomposition into other competing phases. The set of most competing phases, denoted as equilibrium simplex, is identified using a linear optimization procedure which has been proven successful to confirm the stability of already synthesized materials as well as to predict the existence of new ones.47–53 The stability of a phase is quantified in terms of the formation enthalpy ΔHcp by comparing its energy to the energy of the equilibrium simplex according to
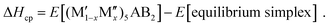 | (2) |
A phase is concluded stable when ΔHcp < 0. In the formula, 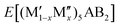 represents the M element configuration (ordered/disordered) of the lowest energy. In this work we use the notation
represents the M element configuration (ordered/disordered) of the lowest energy. In this work we use the notation 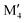 M′′AB2 for chemical order and
M′′AB2 for chemical order and 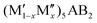 for a solid solution. In addition, when T ≠ 0 K, the contribution from configurational entropy for a disordered distribution of M′ and M′′ on the M sublattice in
for a solid solution. In addition, when T ≠ 0 K, the contribution from configurational entropy for a disordered distribution of M′ and M′′ on the M sublattice in 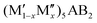 will decrease the Gibbs free energy ΔGdisordercp as approximated by
will decrease the Gibbs free energy ΔGdisordercp as approximated by
| ΔGdisordercp[T] = ΔHdisordercp − TΔS, | (3) |
ΔS = −2kB[y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(y) + (1 − y)ln(1 − y)], ln(y) + (1 − y)ln(1 − y)], | (4) |
Visualization of atomic structures was done using the VESTA code.55
Results and discussion
Stability of ternary T2 phases
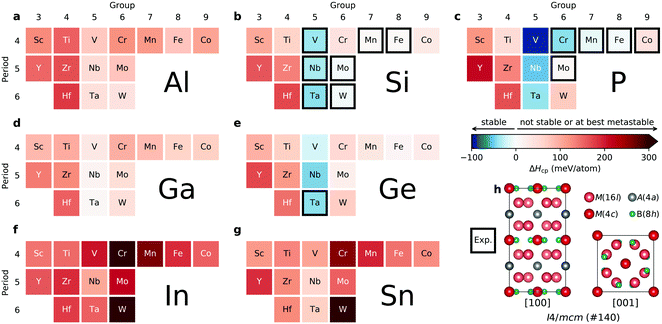
Assessment of the thermodynamic stability for the ternary T2 phases with the M5AB2 composition, where M = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co; A = Al, Ga, In, Si, Ge, Sn, and P, is presented in Fig. 1, showing the calculated formation enthalpy ΔHcp at 0 K, where the blue regions represent stable phases (ΔHcp < 0). The corresponding identified equilibrium simplex for each phase is listed in Table S1 (ESI†). Thermodynamically stable, or close to stable, M5AB2 phases are found for A = Si, P, and Ge combined with M from Groups 5 to 9 while M5AB2 phases with M from Groups 3 and 4 or with A = In and Sn are far from stable, evident from the red areas. Experimentally known T2 phases are marked by a black square (13 in total, see Table S2, ESI†), and are here identified as stable or close to stable. The consistency between synthesized phases to date and the thermodynamic phase stability calculations supports our predictions of stable T2 phases, and five novel T2 phases, yet to be synthesized, are here predicted stable, i.e., V5PB2, Nb5PB2, Ta5PB2, V5GeB2, and Nb5GeB2. These phases remain to be verified, and synthesis experiments are encouraged.Stability upon metal alloying for quaternary T2 phases – order vs. disorder
In a recent study we investigated the stability of T2 phases upon metal alloying for M5SiB2 and predicted 11 chemically ordered phases as well as 40 solid solutions to be stable, including the experimentally verified Ti4MoSiB2.37 Here we expand the possible chemistries by also considering A = Al, Ga, Ge and P upon metal alloying. We choose to not include A = In and Sn in this study due to the rather large formation enthalpy ΔHcp shown for M5InB2 and M5SnB2 in Fig. 1. We considered an M′ to M′′ ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
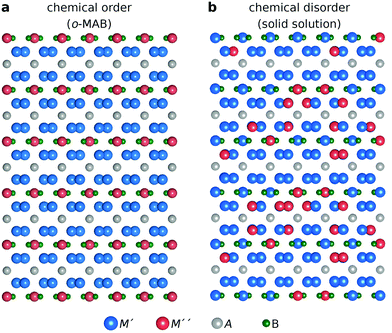
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 motivated by the two symmetrically independent M sublattices at Wyckoff sites 16l and 4c (Fig. 1h). We have considered two different distributions of M′ and M′′; (i) chemical order, denoted o-MAB, with M′ and M′′ occupying the 16l and 4c M-sites, respectively, and (ii) solid solution, obtained by mixing M′ and M′′ on both sites simultaneously in an SQS generated supercell consisting of 160 atoms. Fig. 2 depicts a schematic illustration of M′ and M′′ distributed with chemical order, o-MAB, and disorder, in a solid solution.
1 motivated by the two symmetrically independent M sublattices at Wyckoff sites 16l and 4c (Fig. 1h). We have considered two different distributions of M′ and M′′; (i) chemical order, denoted o-MAB, with M′ and M′′ occupying the 16l and 4c M-sites, respectively, and (ii) solid solution, obtained by mixing M′ and M′′ on both sites simultaneously in an SQS generated supercell consisting of 160 atoms. Fig. 2 depicts a schematic illustration of M′ and M′′ distributed with chemical order, o-MAB, and disorder, in a solid solution.
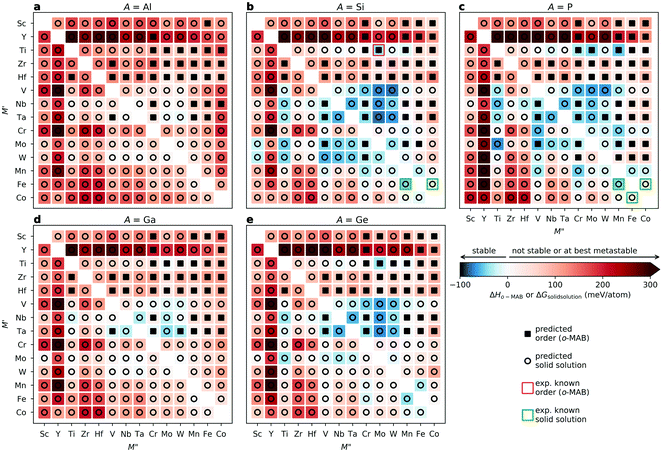
Fig. 3 shows the trends in thermodynamic stability for 910 unique compositions. For each A element (A = Al, Si, P, Ga, Ge), a heatmap is shown, where M′ and M′′ are clustered according to the periodic group of M elements. The background color represents the calculated thermodynamic stability for chemical order/disorder of the lowest energy, with the blue region representing stable phases (ΔHo-MAB or ΔGsolid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solution < 0). For the solid solution (
solution < 0). For the solid solution (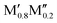 )5AB2 we evaluate ΔGsolid
)5AB2 we evaluate ΔGsolid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) solution at 2000 K, motivated by a typical temperature of 1000 to 1900 °C (1273 to 2173 K) used for the synthesis of M5AB2 (e.g. M = Mo, W, Mn) and (Fe0.8
solution at 2000 K, motivated by a typical temperature of 1000 to 1900 °C (1273 to 2173 K) used for the synthesis of M5AB2 (e.g. M = Mo, W, Mn) and (Fe0.8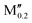 )5AB2 (M′′ = Mn, Co),35,36,56,57 by including the contribution of configurational entropy to Gibb's free energy, using eqn (3) and (4). The depicted symbol thus represents the chemical order of the lowest energy at 2000 K; filled squares for ordered
)5AB2 (M′′ = Mn, Co),35,36,56,57 by including the contribution of configurational entropy to Gibb's free energy, using eqn (3) and (4). The depicted symbol thus represents the chemical order of the lowest energy at 2000 K; filled squares for ordered 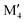 M′′AB2o-MAB and open circles for the solid solution (
M′′AB2o-MAB and open circles for the solid solution (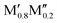 )5AB2. In addition, the experimentally reported Ti4MoSiB2o-MAB and solid solution (
)5AB2. In addition, the experimentally reported Ti4MoSiB2o-MAB and solid solution (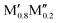 )5AB2 are marked by pink and green squares, respectively. The result obtained at 0 K, i.e., without a contribution from the configurational entropy to the solid solution phases, is shown in Fig. S5 (ESI†). The discrepancy between Fig. 3 and Fig. S5 (ESI†) highlights the importance of including the evaluation of entropy in the analysis, for reliable predictions.
)5AB2 are marked by pink and green squares, respectively. The result obtained at 0 K, i.e., without a contribution from the configurational entropy to the solid solution phases, is shown in Fig. S5 (ESI†). The discrepancy between Fig. 3 and Fig. S5 (ESI†) highlights the importance of including the evaluation of entropy in the analysis, for reliable predictions.
All five experimentally reported solid solutions (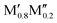 )5AB2 are predicted to be stable here,35,36,56 as well as the recently discovered Ti4MoSiB2o-MAB.37 Noteworthily, the additional 121 solid solution and 35 o-MAB phases are predicted to be stable, mainly for A = Si, P, and Ge, suggesting that metal alloying in T2 phases is a prospective path towards expanding the possible chemistries which, in turn, provide a high tunning potential of these materials. Table 1 summarizes the stable o-MAB and solid solution MAB phase compositions. The results highlight the value of computational material discoveries for accelerating exploratory synthesis in new chemical spaces. A complete list of predicted stable o-MAB and solid solution phases, with their calculated formation enthalpies and Gibbs free energies of formation, respectively, is given in Tables S5 and S6 (ESI†). Examples of phases with predicted outstanding stability, strongly motivating attempted experimental verification, are o-MAB phases Ti4M′′PB2 (M′′ = Cr, Mo or Mn), Ta4M′′AB2 (M′′ = V or Cr; A = Si, P, Ge), and Mo4M′′AB2 (M′′ = V or Cr; A = Si, P, Ge) and solid solution MAB phases (
)5AB2 are predicted to be stable here,35,36,56 as well as the recently discovered Ti4MoSiB2o-MAB.37 Noteworthily, the additional 121 solid solution and 35 o-MAB phases are predicted to be stable, mainly for A = Si, P, and Ge, suggesting that metal alloying in T2 phases is a prospective path towards expanding the possible chemistries which, in turn, provide a high tunning potential of these materials. Table 1 summarizes the stable o-MAB and solid solution MAB phase compositions. The results highlight the value of computational material discoveries for accelerating exploratory synthesis in new chemical spaces. A complete list of predicted stable o-MAB and solid solution phases, with their calculated formation enthalpies and Gibbs free energies of formation, respectively, is given in Tables S5 and S6 (ESI†). Examples of phases with predicted outstanding stability, strongly motivating attempted experimental verification, are o-MAB phases Ti4M′′PB2 (M′′ = Cr, Mo or Mn), Ta4M′′AB2 (M′′ = V or Cr; A = Si, P, Ge), and Mo4M′′AB2 (M′′ = V or Cr; A = Si, P, Ge) and solid solution MAB phases (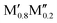 )5AB2 (M′ = V, Nb, Ta; A = Si, P, Ge) and (
)5AB2 (M′ = V, Nb, Ta; A = Si, P, Ge) and (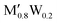 )5AB2 (M′ = V, Nb, Ta; A = Si, Ge). Detailed structural data for o-MAB phases that are predicted to be stable can be found in Table S7 (ESI†) and we encourage further exploration of various properties to find out new application possibilities for this family of materials.
)5AB2 (M′ = V, Nb, Ta; A = Si, Ge). Detailed structural data for o-MAB phases that are predicted to be stable can be found in Table S7 (ESI†) and we encourage further exploration of various properties to find out new application possibilities for this family of materials.
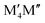 AB2) or disordered ((
AB2) or disordered ((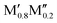 )5AB2) distribution of M′ and M′′ at a typical synthesis temperature of 2000 K
)5AB2) distribution of M′ and M′′ at a typical synthesis temperature of 2000 K
| Phase | Stability criteria | Experimentally reported phases, also predicted stable | Phases predicted stable, not yet synthesized |
|---|---|---|---|
| Stable o-MAB | ΔHo-MAB < 0 | Ti4MoSiB237 | Ti4CrAB2 (A = P) |
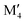 M′′AB2 M′′AB2 |
ΔGsolid solution > ΔHo-MAB | Ti4MoAB2 (A = Si, P, Ga, Ge) | |
| Ti4WAB2 (A = Ge) | |||
| Ti4MnAB2 (A = Si, P, Ge) | |||
| Nb4M′′AB2 (A = Si, P, Ge, M′′ = V, Cr) | |||
| Nb4MnAB2 (A = P) | |||
| Ta4M′′AB2 (A = Si, P, Ga, Ge, M′′ = V, Cr) | |||
| Ta4WAB2 (A = P, Ga) | |||
| Ta4MnAB2 (A = Si, P, Ge) | |||
| Mo4M′′AB2 (A = Si, P; M′′ = V, Cr, Mn) | |||
| W4CrAB2 (A = Si) | |||
Stable solid solution (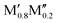 )5AB2 )5AB2 |
ΔGsolid solution < 0 | (Fe0.8Mn0.2)5AB2 (A = Si, P)56 | (Ti0.8Nb0.2)5AB2 (A = Si, P, Ge) |
| ΔGsolid solution < ΔHo-MAB | (Fe0.8Co0.2)5AB2 (A = Si, P)35,36,56 | (Ti0.8W0.2)5AB2 (A = Si, P) | |
| (Co0.8Fe0.2)5AB2 (A = P)35 | (V0.8Ti0.2)5AB2 (A = Si, P) | ||
(V0.8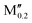 )5AB2 (A = Si, P, Ge; M′′ = Nb, Ta, Mn) )5AB2 (A = Si, P, Ge; M′′ = Nb, Ta, Mn) |
|||
(V0.8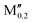 )5AB2 (A = Si, P, Ga, Ge; M′′ = Cr, Mo, W) )5AB2 (A = Si, P, Ga, Ge; M′′ = Cr, Mo, W) |
|||
| (V0.8Fe0.2)5AB2 (A = Ge) | |||
(Nb0.8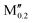 )5AB2 (A = Si, P, Ga, Ge; M′′ = Ti, Ta, Mo, W) )5AB2 (A = Si, P, Ga, Ge; M′′ = Ti, Ta, Mo, W) |
|||
| (Nb0.8Zr0.2)5AB2 (A = P) | |||
| (Nb0.8Hf0.2)5AB2 (A = Si, P, Ge) | |||
(Ta0.8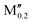 )5AB2 (A = Si, P, Ga, Ge; M′′ = Ti, Nb) )5AB2 (A = Si, P, Ga, Ge; M′′ = Ti, Nb) |
|||
| (Ta0.8Mo0.2)5AB2 (A = Al, Si, P, Ga, Ge) | |||
| (Ta0.8W0.2)5AB2 (A = Al, Si, Ge) | |||
(Cr0.8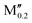 )5AB2 (A = P; M′′ = V, Mo, W, Fe, Co) )5AB2 (A = P; M′′ = V, Mo, W, Fe, Co) |
|||
| (Cr0.8Mn0.2)5AB2 (A = Si) | |||
(Mo0.8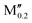 )5AB2 (A = Si; M′′ = Sc, Hf) )5AB2 (A = Si; M′′ = Sc, Hf) |
|||
(Mo0.8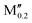 )5AB2 (A = Si, P, Ge; M′′ = Ti, Ta) )5AB2 (A = Si, P, Ge; M′′ = Ti, Ta) |
|||
| (Mo0.8V0.2)5AB2 (A = Ge) | |||
(Mo0.8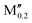 )5AB2 (A = Si, P, Ga, Ge; M′′ = Nb, W) )5AB2 (A = Si, P, Ga, Ge; M′′ = Nb, W) |
|||
(W0.8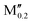 )5AB2 (A = Si; M′′ = Sc, Nb, Mo, Mn) )5AB2 (A = Si; M′′ = Sc, Nb, Mo, Mn) |
|||
(W0.8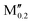 )5AB2 (A = Si, P; M′′ = Ti, V) )5AB2 (A = Si, P; M′′ = Ti, V) |
|||
| (W0.8Ta0.2)5AB2 (A = Si, Ga) | |||
(Mn0.8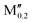 )5AB2 (A = Si, P; M′′ = V, Mo, W) )5AB2 (A = Si, P; M′′ = V, Mo, W) |
|||
(Mn0.8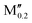 )5AB2 (A = Si, P, Ge; M′′ = Cr, Fe) )5AB2 (A = Si, P, Ge; M′′ = Cr, Fe) |
|||
| (Mn0.8Co0.2)5AB2 (A = P) | |||
(Fe0.8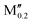 )5AB2 (A = Si, P, Ge; M′′ = Cr, Mn) )5AB2 (A = Si, P, Ge; M′′ = Cr, Mn) |
|||
| (Fe0.8Co0.2)5AB2 (A = Si, P) | |||
(Co0.8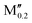 )5AB2 (A = Si, P, Ge; M′′ = Mn, Fe) )5AB2 (A = Si, P, Ge; M′′ = Mn, Fe) |
Order or disorder – impact on the size and electronegativity
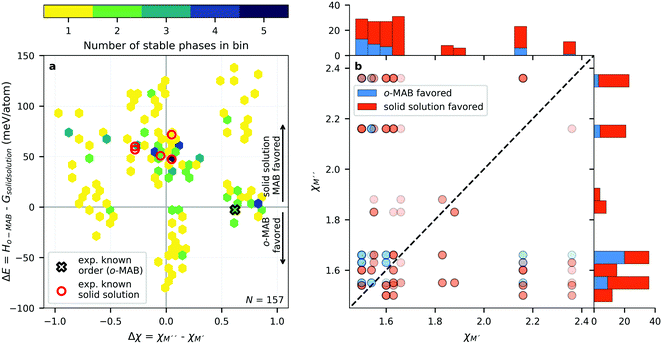
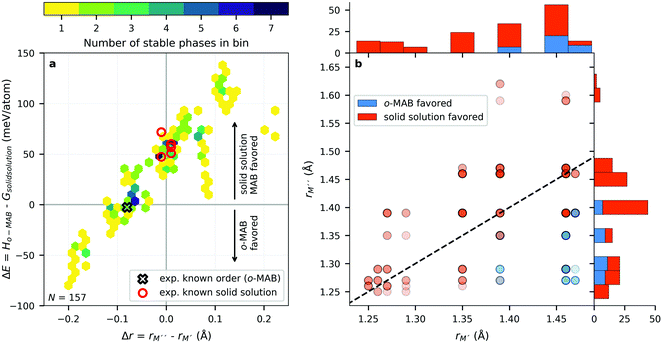
In ref. 38, the bonding characteristics of the experimentally known Ti4MoSiB2o-MAB phases were investigated and compared to those of the known Mo5SiB2 and the hypothetical Ti5SiB2. It was found that the bonding states are optimized in Ti4MoSiB2 and that the electronegativity difference of Mo and Ti could, at least in part, explain the stability of both Ti4MoSiB2 and Mo5SiB2 compared to Ti5SiB2. Recently, we demonstrated that the preference for order or solid solution upon metal alloying in 212 MAB phases is dictated by for example the size difference between the alloying metal elements,58 also shown for alloying of 211 MAX phases.59 On the other hand, out-of-plane MAX phases, o-MAX, is possible when the atomic sizes of the alloying metals are similar while the difference in electronegativity between M′ and A is large.11With these results in mind, we here aim to identify the attributes governing the preference for the formation of o-MAB or solid solution MAB by considering the electronegativity χ and atomic size r of M′ and M′′, see Table S8 (ESI†) for considered values. From the stability results in Fig. 3, it is found that out of the 910 compositions considered initially, only 157 are found to be thermodynamically stable. Out of these, 36 have the chemically ordered o-MAB as the preferred structure while 121 have the disorder solid solution as the favored distribution of M′ and M′′′. The information displayed in Fig. 3 thus only represent the chemical distribution of M′ and M′′ of the lowest energy, and thus do not explicitly show how close or far in energy the two different chemical distributions are, i.e., o-MAB vs. solid solution.
Fig. 4a shows the energy difference, ΔE = Ho-MAB – Gsolid solution MAB, between the chemically ordered o-MAB and the disordered solid solution MAB phase, as a function of the electronegativity difference of M′′ and M′, 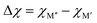 , for the 157 phases predicted stable in Fig. 3. ΔE < 0 represents the phases with chemical order (o-MAB) of the lowest energy and ΔE > 0 those phases which favor a disordered solid solution. In addition, experimentally reported quaternary MAB phases are marked. It is found that there is no clear correlation between ΔE and Δχ, as indicated by the scattering data. Furthermore, instead of looking at Δχ we also choose to present the electronegativity of the individual metals,
, for the 157 phases predicted stable in Fig. 3. ΔE < 0 represents the phases with chemical order (o-MAB) of the lowest energy and ΔE > 0 those phases which favor a disordered solid solution. In addition, experimentally reported quaternary MAB phases are marked. It is found that there is no clear correlation between ΔE and Δχ, as indicated by the scattering data. Furthermore, instead of looking at Δχ we also choose to present the electronegativity of the individual metals, 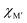 and
and 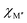 , in Fig. 4b, together with the preferred chemical distribution of M′ and M′′ in blue (o-MAB) and red (solid solution MAB). Once again, we find no clear correlation between the individual electronegativity of M′ and M′′ and any specific preference for the phase being chemically ordered or disordered. Data including all 910 compositions are shown in Fig. S6 (ESI†), which further support that electronegativity cannot be used to explain when o-MAB or solid solution MAB is to be expected.
, in Fig. 4b, together with the preferred chemical distribution of M′ and M′′ in blue (o-MAB) and red (solid solution MAB). Once again, we find no clear correlation between the individual electronegativity of M′ and M′′ and any specific preference for the phase being chemically ordered or disordered. Data including all 910 compositions are shown in Fig. S6 (ESI†), which further support that electronegativity cannot be used to explain when o-MAB or solid solution MAB is to be expected.
In Fig. 5, we instead look at ΔE for the 157 stable phases as a function of the size difference of M′′ and M′, 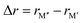 , where, once again, ΔE < 0 represents the phases with preferred chemical order (o-MAB) and ΔE > 0 represents phases which favor a disordered solid solution. First to note is that similar results are found for all A-elements indicating that the impact on the choice of A is minimal and does not influence the energy difference between order and solid solution (see Fig. S7, ESI†). From the data we find a correlation, where ΔE decreases/increases upon decreasing/increasing the Δr value. More specifically, data points with ΔE < 0, i.e., where the chemical order (o-MAB) is energetically preferred, are only found for Δr < 0 which means that the size of M′′ should be smaller than that of M′. In contrast, for Δr ≥ 0 where
, where, once again, ΔE < 0 represents the phases with preferred chemical order (o-MAB) and ΔE > 0 represents phases which favor a disordered solid solution. First to note is that similar results are found for all A-elements indicating that the impact on the choice of A is minimal and does not influence the energy difference between order and solid solution (see Fig. S7, ESI†). From the data we find a correlation, where ΔE decreases/increases upon decreasing/increasing the Δr value. More specifically, data points with ΔE < 0, i.e., where the chemical order (o-MAB) is energetically preferred, are only found for Δr < 0 which means that the size of M′′ should be smaller than that of M′. In contrast, for Δr ≥ 0 where 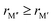 only disorder solid solution MAB phases are found as indicated by ΔE > 0. Experimentally known quaternary T2 phases are also marked in Fig. 5a where solid solutions (red circles) are all found in the region where the size of the metals is similar,
only disorder solid solution MAB phases are found as indicated by ΔE > 0. Experimentally known quaternary T2 phases are also marked in Fig. 5a where solid solutions (red circles) are all found in the region where the size of the metals is similar, 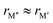 while Ti4MoSiB2o-MAB (black cross) is found at Δr = −0.08.
while Ti4MoSiB2o-MAB (black cross) is found at Δr = −0.08.
From the individual size of the metals, 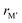 and
and 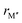 , in Fig. 5b we also find that stable o-MAB phases (blue) are comprised of M′′ with a size smaller than 1.40 Å (corresponds to M′′ typically from Groups 6 to 9) and M′ with
, in Fig. 5b we also find that stable o-MAB phases (blue) are comprised of M′′ with a size smaller than 1.40 Å (corresponds to M′′ typically from Groups 6 to 9) and M′ with 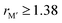 Å (corresponds to M′ typically from Group 4 or from Periods 5 and 6 combined with Groups 5 and 6). Data in favor of solid solution MAB (red) are more scattered and include a combination of metals of all sizes. An additional comparison including all 910 compositions is shown in Fig. S8 (ESI†).
Å (corresponds to M′ typically from Group 4 or from Periods 5 and 6 combined with Groups 5 and 6). Data in favor of solid solution MAB (red) are more scattered and include a combination of metals of all sizes. An additional comparison including all 910 compositions is shown in Fig. S8 (ESI†).
All of the five synthesized solid solution (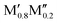 )5AB2 phases have ΔE > 0, i.e., solid solutions are favored, and are comprised of metal combinations where both the size and electronegativity of M′ and M′′ are similar. This is consistent with the Hume–Rothery rules which state that a solid solution is expected when the alloying elements have a similar size and electronegativity.60 To explain why ΔE < 0, favoring chemically ordered o-MAB, is only valid for Δr < 0, we could argue that M′′ should be smaller than M′ because M′′ is constrained in a layer together with B. M′, on the other hand, forms a layer by itself where there is somewhat more space. By looking at the individual size of the metals in Fig. 5b we find that both metals should be rather small, e.g., no large Sc or Y atoms are found among the stable o-MAB phases (see Fig. 3). The reason for this could be related to the structure, which cannot accommodate the metals if they are too large. For example, M′′ = Y would result in an overall expansion of the structure which, in turn, would lead to increased bond lengths, decreased interaction strengths and thus reduced internal stability of the structure. Indications for such arguments are visualized from a structural point-of-view in Fig. S9 and S10 (ESI†), where the large size of M′′ and M′ results in phases far from being stable and with large lattice parameters. All stable and ordered phases (o-MAB) display similar calculated lattice parameters, with 5.8 Å < a < 6.2 Å and 10.9 Å < c < 11.8 Å. This can be compared with all compositions with calculated lattice parameters in the range of 5.3 Å < a < 7.0 Å and 9.5 Å < c < 14.4 Å.
)5AB2 phases have ΔE > 0, i.e., solid solutions are favored, and are comprised of metal combinations where both the size and electronegativity of M′ and M′′ are similar. This is consistent with the Hume–Rothery rules which state that a solid solution is expected when the alloying elements have a similar size and electronegativity.60 To explain why ΔE < 0, favoring chemically ordered o-MAB, is only valid for Δr < 0, we could argue that M′′ should be smaller than M′ because M′′ is constrained in a layer together with B. M′, on the other hand, forms a layer by itself where there is somewhat more space. By looking at the individual size of the metals in Fig. 5b we find that both metals should be rather small, e.g., no large Sc or Y atoms are found among the stable o-MAB phases (see Fig. 3). The reason for this could be related to the structure, which cannot accommodate the metals if they are too large. For example, M′′ = Y would result in an overall expansion of the structure which, in turn, would lead to increased bond lengths, decreased interaction strengths and thus reduced internal stability of the structure. Indications for such arguments are visualized from a structural point-of-view in Fig. S9 and S10 (ESI†), where the large size of M′′ and M′ results in phases far from being stable and with large lattice parameters. All stable and ordered phases (o-MAB) display similar calculated lattice parameters, with 5.8 Å < a < 6.2 Å and 10.9 Å < c < 11.8 Å. This can be compared with all compositions with calculated lattice parameters in the range of 5.3 Å < a < 7.0 Å and 9.5 Å < c < 14.4 Å.
To summarize the key results governing the formation of o-MAB or solid solution, we find indications for ordered o-MAB being the preferred structure over a solid solution when the size of M′ is larger than M′′ and where M′ should not be too large. No clear corresponding correlation could be identified when the solid solution (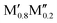 )5AB2 is the preferred structure. However, it should be noted that all of the five experimentally known solid solution MAB phases are comprised of metals of similar sizes.
)5AB2 is the preferred structure. However, it should be noted that all of the five experimentally known solid solution MAB phases are comprised of metals of similar sizes.
To date, there have been many failed attempts to convert traditional ternary metal borides (MAB phases) into their 2D counterparts.24,61,62 This contrasts to MXenes which are being successfully derived through complete etching of A from ternary metal carbides or nitrides (MAX phases).4,63 One reason for this may be the stronger interlayer bonding between metals and the A-layer in MAB phases as compared to MAX phases. Alloying can be used as an approach for modifying the interlayer interaction, which could facilitate the conversion from 3D into 2D. This has been recently demonstrated for Mo4/3Sc2/3AlB2 and Mo4/3Y2/3AlB2 which was converted into Mo4/3B2−x boridene.28 Furthermore, in a most recent study, we synthesized Ti4MoSiB2, an o-MAB phase with proven out-of-plane chemical order of Ti and Mo, from which we subsequently derived a new 2D material, TiOxCly, of high yield and in the form of delaminated sheets.37 The parent materials needed to realize these 2D materials were obtained through metal alloying of ternary MAB phases. This emphasizes that in our quest for finding novel 2D materials we must explore and enlarge the palette of materials from which they originate. In this work we demonstrate that there are numerous thermodynamically stable candidates not yet synthesized but promising for experimental realization.
Conclusion
In conclusion, we have performed a systematic theoretical study of the phase stability of quaternary T2 phases upon alloying between M′ and M′′ from Groups 3 to 9 (Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, W, Mn, Fe, and Co) for various A-elements (Al, Si, P, Ga, and Ge). We not only confirm all synthesized phases to date with chemical order (o-MAB) or disorder (solid solution) but also predict 35 stable o-MAB phases and 121 stable solid solutions. These hypothetical phases remain to be experimentally verified, and synthesis is encouraged. The preference for order or solid solution upon metal alloying in T2 phases is dictated mainly by the size difference between the alloying metal elements. Chemically ordered o-MAB (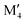 M′′AB2) is energetically favored when M′, next to the A layer, is larger than the metal M′′ in the M′′–B layer. Phases with similar sizes of M′ and M′′ or with M′ smaller than M′′ show a preference for the formation of disordered solid solution (
M′′AB2) is energetically favored when M′, next to the A layer, is larger than the metal M′′ in the M′′–B layer. Phases with similar sizes of M′ and M′′ or with M′ smaller than M′′ show a preference for the formation of disordered solid solution (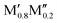 )5AB2. This study demonstrates that alloying is a viable path towards novel elemental combinations, to extend the chemical space of T2 phases which, in turn, allows for potentially tuneable and advantageous properties. Furthermore, we expand the family of potential parent phases for the derivation of 2D materials from chemical exfoliation.
)5AB2. This study demonstrates that alloying is a viable path towards novel elemental combinations, to extend the chemical space of T2 phases which, in turn, allows for potentially tuneable and advantageous properties. Furthermore, we expand the family of potential parent phases for the derivation of 2D materials from chemical exfoliation.
Author contributions
M. D. and J. R. initiated the study and wrote the manuscript. M. D. performed the ab initio calculations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. R. acknowledges the support from the Knut and Alice Wallenberg (KAW) Foundation for a Fellowship/Scholar Grant and Project funding (KAW 2020.0033), and from the Swedish Foundation for Strategic Research (SSF) for Project Funding (EM16-0004). The support from the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No 2009 00971) is also acknowledged. The calculations were carried out using supercomputer resources provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Center for High Performance Computing partially funded by the Swedish Research Council through grant agreement no. 2018-05973.References
- W. Jeitschko, H. Nowotny and F. Benesovsky, Kohlenstoffhaltige ternäre Verbindungen (H-Phase), Monatsh. Chem., 1963, 94, 672–676 CrossRef CAS.
- M. W. Barsoum, The MN+1AXN phases: A new class of solids; Thermodynamically stable nanolaminates, Prog. Solid State Chem., 2000, 28, 201–281 CrossRef CAS.
- M. W. Barsoum, MAX Phases, Properties of Machinable Ternary Carbides and Nitrides. Wiley: New York, 2013 Search PubMed.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Two-dimensional nanocrystals produced by exfoliation of Ti3AlC2, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- M. R. Lukatskaya, O. Mashtalir, C. E. Ren, Y. Dall’Agnese, P. Rozier, P. L. Taberna, M. Naguib, P. Simon, M. W. Barsoum and Y. Gogotsi, Cation Intercalation and High Volumetric Capacitance of Two-Dimensional Titanium Carbide, Science, 2013, 341, 1502–1505 CrossRef CAS PubMed.
- M. Ghidiu, M. R. Lukatskaya, M.-Q. Zhao, Y. Gogotsi and M. W. Barsoum, Conductive two-dimensional titanium carbide ‘clay’ with high volumetric capacitance, Nature, 2014, 516, 78–81 CrossRef CAS PubMed.
- F. Shahzad, M. Alhabeb, C. B. Hatter, B. Anasori, S. Man Hong, C. M. Koo and Y. Gogotsi, Electromagnetic interference shielding with 2D transition metal carbides (MXenes), Science, 2016, 353, 1137–1140 CrossRef CAS PubMed.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, 2D metal carbides and nitrides (MXenes) for energy storage, Nat. Rev. Mater., 2017, 2, 16098 CrossRef CAS.
- B. Anasori, M. Dahlqvist, J. Halim, E. J. Moon, J. Lu, B. C. Hosler, E. N. Caspi, S. J. May, L. Hultman, P. Eklund, J. Rosén and M. W. Barsoum, Experimental and theoretical characterization of ordered MAX phases Mo2TiAlC2 and Mo2Ti2AlC3, J. Appl. Phys., 2015, 118, 094304 CrossRef.
- Q. Tao, M. Dahlqvist, J. Lu, S. Kota, R. Meshkian, J. Halim, J. Palisaitis, L. Hultman, M. W. Barsoum, P. O. Å. Persson and J. Rosen, Two-dimensional Mo1.33C MXene with divacancy ordering prepared from parent 3D laminate with in-plane chemical ordering, Nat. Commun., 2017, 8, 14949 CrossRef PubMed.
- M. Dahlqvist and J. Rosen, Predictive theoretical screening of phase stability for chemical order and disorder in quaternary 312 and 413 MAX phases, Nanoscale, 2020, 12, 785–794 RSC.
- B. Anasori, Y. Xie, M. Beidaghi, J. Lu, B. C. Hosler, L. Hultman, P. R. C. Kent, Y. Gogotsi and M. W. Barsoum, Two-dimensional, ordered, double transition metals carbides (MXenes), ACS Nano, 2015, 9, 9507–9516 CrossRef CAS PubMed.
- R. Meshkian, Q. Tao, M. Dahlqvist, J. Lu, L. Hultman and J. Rosen, Theoretical stability and materials synthesis of a chemically ordered MAX phase, Mo2ScAlC2, and its two-dimensional derivate Mo2ScC2 MXene, Acta Mater., 2017, 125, 476–480 CrossRef CAS.
- I. Persson, A. e. Ghazaly, Q. Tao, J. Halim, S. Kota, V. Darakchieva, J. Palisaitis, M. W. Barsoum, J. Rosen and P. O. Å. Persson, Tailoring Structure, Composition, and Energy Storage Properties of MXenes from Selective Etching of In-Plane, Chemically Ordered MAX Phases, Small, 2018, 14, 1703676 CrossRef PubMed.
- G. Deysher, C. E. Shuck, K. Hantanasirisakul, N. C. Frey, A. C. Foucher, K. Maleski, A. Sarycheva, V. B. Shenoy, E. A. Stach, B. Anasori and Y. Gogotsi, Synthesis of Mo4VAlC4 MAX Phase and Two-Dimensional Mo4VC4 MXene with Five Atomic Layers of Transition Metals, ACS Nano, 2020, 14, 204–217 CrossRef CAS PubMed.
- H. J. Becher, K. Krogmann and E. Peisker, Über das ternäre Borid Mn2AlB2, Zeitschrift für anorganische und allgemeine Chemie, 1966, 344, 140–147 CrossRef CAS.
- M. Ade and H. Hillebrecht, Ternary Borides Cr2AlB2, Cr3AlB4, and Cr4AlB6: the First Members of the Series (CrB2)nCrAl with n = 1, 2, 3 and a Unifying Concept for Ternary Borides as MAB-Phases, Inorg. Chem., 2015, 54, 6122–6135 CrossRef CAS PubMed.
- D. Potashnikov, E. N. Caspi, A. Pesach, S. Kota, M. Sokol, L. A. Hanner, M. W. Barsoum, H. A. Evans, A. Eyal, A. Keren and O. Rivin, Magnetic properties of (Fe1−xMnx)2AlB2 and the impact of substitution on the magnetocaloric effect, Phys. Rev. Mater., 2020, 4, 084404 CrossRef CAS.
- H. Zhang, F.-Z. Dai, H. Xiang, Z. Zhang and Y. Zhou, Crystal structure of Cr4AlB4: a new MAB phase compound discovered in Cr–Al–B system, J. Mater. Sci. Technol., 2018, 35, 530–534 CrossRef.
- N. Miao, J. Wang, Y. Gong, J. Wu, H. Niu, S. Wang, K. Li, A. R. Oganov, T. Tada and H. Hosono, Computational prediction of boron-based MAX phases and MXene derivatives, Chem. Mater., 2020, 32, 6947–6957 CrossRef CAS.
- M. M. Ali, M. A. Hadi, I. Ahmed, A. F. M. Y. Haider and A. K. M. A. Islam, Physical properties of a novel boron-based ternary compound Ti2InB2, Mater. Today Commun., 2020, 25, 101600 CrossRef CAS.
- H. Nowotny, E. Dimakopoulou and H. Kudielka, Untersuchungen in den Dreistoffsystemen: Molybdän-Silizium-Bor, Wolfram-Silizium-Bor und in dem System: VSi2-TaSi2, Monatsh. Chem., 1957, 88, 180–192 CrossRef CAS.
- L. T. Alameda, C. F. Holder, J. L. Fenton and R. E. Schaak, Partial Etching of Al from MoAlB Single Crystals To Expose Catalytically Active Basal Planes for the Hydrogen Evolution Reaction, Chem. Mater., 2017, 29, 8953–8957 CrossRef CAS.
- L. T. Alameda, R. W. Lord, J. A. Barr, P. Moradifar, Z. P. Metzger, B. C. Steimle, C. F. Holder, N. Alem, S. B. Sinnott and R. E. Schaak, Multi-Step Topochemical Pathway to Metastable Mo2AlB2 and Related Two-Dimensional Nanosheet Heterostructures, J. Am. Chem. Soc., 2019, 141, 10852–10861 CrossRef CAS PubMed.
- K. Kim, C. Chen, D. Nishio-Hamane, M. Okubo and A. Yamada, Topochemical synthesis of phase-pure Mo2AlB2 through staging mechanism, Chem. Commun., 2019, 55, 9295–9298 RSC.
- M. Dahlqvist, Q. Tao, J. Zhou, J. Palisaitis, P. O. Å. Persson and J. Rosen, Theoretical Prediction and Synthesis of a Family of Atomic Laminate Metal Borides with In-Plane Chemical Ordering, J. Am. Chem. Soc., 2020, 142, 18583–18591 CrossRef CAS PubMed.
- B. Ahmed, A. E. Ghazaly and J. Rosen, i-MXenes for Energy Storage and Catalysis, Adv. Funct. Mater., 2020, 30, 2000894 CrossRef CAS.
- J. Zhou, J. Palisaitis, J. Halim, M. Dahlqvist, Q. Tao, I. Persson, L. Hultman, P. O. Å. Persson and J. Rosen, Boridene: Two-dimensional Mo4/3B2−x with ordered metal vacancies obtained by chemical exfoliation, Science, 2021, 373, 801–805 CrossRef CAS PubMed.
- B. Aronsson and I. Engström, X-Ray Investigations on M-Si-B Systems (M = Mn, Fe, Co). II. Some Features of the Fe-Si–B and Mn–Si–B Systems, Acta Chem. Scand., Ser. A, 1960, 14, 1403–1413 CrossRef CAS.
- M. K. Meyer and M. Akinc, Oxidation Behavior of Boron-Modified Mo5Si3 at 800–1300 °C, J. Am. Ceram. Soc., 1996, 79, 938–944 CrossRef CAS.
- C. J. Rawn, J. H. Schneibel, C. M. Hoffmann and C. R. Hubbard, The crystal structure and thermal expansion of Mo5SiB2, Intermetallics, 2001, 9, 209–216 CrossRef CAS.
- A. Brauner, C. A. Nunes, A. D. Bortolozo, G. Rodrigues and A. J. S. Machado, Superconductivity in the new Nb5Si3−xBx phase, Solid State Commun., 2009, 149, 467–470 CrossRef CAS.
- M. A. McGuire and D. S. Parker, Superconductivity at 9 K in Mo5PB2 with evidence for multiple gaps, Phys. Rev. B, 2016, 93, 064507 CrossRef.
- D. Hedlund, J. Cedervall, A. Edström, M. Werwiński, S. Kontos, O. Eriksson, J. Rusz, P. Svedlindh, M. Sahlberg and K. Gunnarsson, Magnetic properties of the Fe5SiB2-Fe5PB2 system, Phys. Rev. B, 2017, 96, 094433 CrossRef.
- J. Cedervall, E. Nonnet, D. Hedlund, L. Häggström, T. Ericsson, M. Werwiński, A. Edström, J. Rusz, P. Svedlindh, K. Gunnarsson and M. Sahlberg, Influence of Cobalt Substitution on the Magnetic Properties of Fe5PB2, Inorg. Chem., 2018, 57, 777–784 CrossRef CAS PubMed.
- R. Hirian, O. Isnard, V. Pop and D. Benea, Investigations on the magnetic properties of the Fe5-xCoxSiB2 alloys by experimental and band structure calculation methods, J. Magn. Magn. Mater., 2020, 505, 166748 CrossRef CAS.
- M. Dahlqvist, J. Zhou, I. Persson, B. Ahmed, J. Lu, J. Halim, Q. Tao, J. Palisaitis, J. Thörnberg, P. Helmer, L. Hultman, P. O. Å. Persson and J. Rosen, Out-Of-Plane Ordered Laminate Borides and Their 2D Ti-Based Derivative from Chemical Exfoliation, Adv. Mater., 2021, 33, 2008361 CrossRef CAS PubMed.
- P. Helmer, H. Lind, M. Dahlqvist and J. Rosen, Investigation of out-of-plane ordered Ti4MoSiB2 from first principles, J. Phys.: Condens. Matter, 2022 DOI:10.1088/1361-648X/ac51fe.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- M. Dahlqvist, B. Alling, I. A. Abrikosov and J. Rosén, Phase stability of Ti2AlC upon oxygen incorporation: A first-principles investigation, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024111 CrossRef.
- M. Dahlqvist, B. Alling and J. Rosén, Stability trends of MAX phases from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 220102 CrossRef.
- P. Eklund, M. Dahlqvist, O. Tengstrand, L. Hultman, J. Lu, N. Nedfors, U. Jansson and J. Rosén, Discovery of the ternary nanolaminated compound Nb2GeC by a systematic theoretical-experimental approach, Phys. Rev. Lett., 2012, 109, 035502 CrossRef PubMed.
- A. S. Ingason, A. Mockute, M. Dahlqvist, F. Magnus, S. Olafsson, U. B. Arnalds, B. Alling, I. A. Abrikosov, B. Hjörvarsson, P. O. Å. Persson and J. Rosen, Magnetic self-organized atomic laminate from first principles and thin film synthesis, Phys. Rev. Lett., 2013, 110, 195502 CrossRef CAS PubMed.
- A. S. Ingason, A. Petruhins, M. Dahlqvist, F. Magnus, A. Mockute, B. Alling, L. Hultman, I. A. Abrikosov, P. O. Å. Persson and J. Rosen, A nanolaminated magnetic phase: Mn2GaC, Mater. Res. Lett., 2014, 2, 89–93 CrossRef CAS.
- A. Mockute, M. Dahlqvist, J. Emmerlich, L. Hultman, J. M. Schneider, P. O. Å. Persson and J. Rosen, Synthesis and ab initio calculations of nanolaminated (Cr,Mn)2AlC compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094113 CrossRef.
- A. Mockute, P. O. Å. Persson, F. Magnus, A. S. Ingason, S. Olafsson, L. Hultman and J. Rosen, Synthesis and characterization of arc deposited magnetic (Cr,Mn)2AlC MAX phase films, Phys. Status Solidi RRL, 2014, 8, 420–423 CrossRef CAS.
- A. Thore, M. Dahlqvist, B. Alling and J. Rosén, Temperature dependent phase stability of nanolaminated ternaries from first-principles calculations, Comput. Mater. Sci., 2014, 91, 251–257 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M. A. McGuire and D. S. Parker, Magnetic and structural properties of ferromagnetic Fe5PB2 and Fe5SiB2 and effects of Co and Mn substitutions, J. Appl. Phys., 2015, 118, 163903 CrossRef.
- D. M. de Almeida, C. Bormio-Nunes, C. A. Nunes, A. A. Coelho and G. C. Coelho, Magnetic characterization of Mn5SiB2 and Mn5Si3 phases, J. Magn. Magn. Mater., 2009, 321, 2578–2581 CrossRef.
- M. Dahlqvist and J. Rosen, Predictions of Attainable Compositions of Layered Quaternary i-MAB Phases and solid solution MAB phases, Nanoscale, 2021, 13, 18311 RSC.
- M. Dahlqvist, A. Petruhins, J. Lu, L. Hultman and J. Rosen, Origin of Chemically Ordered Atomic Laminates (i-MAX): Expanding the Elemental Space by a Theoretical/Experimental Approach, ACS Nano, 2018, 12, 7761–7770 CrossRef CAS PubMed.
- W. Hume-Rothery; R. E. Smallman and C. W. Haworth, The structure of metals and alloys, The Institute of Metals, London, 1969 Search PubMed.
- L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, Topochemical Deintercalation of Al from MoAlB: Stepwise Etching Pathway, Layered Intergrowth Structures, and Two-Dimensional MBene, J. Am. Chem. Soc., 2018, 140, 8833–8840 CrossRef CAS PubMed.
- J. Wang, T.-N. Ye, Y. Gong, J. Wu, N. Miao, T. Tada and H. Hosono, Discovery of hexagonal ternary phase Ti2InB2 and its evolution to layered boride TiB, Nat. Commun., 2019, 10, 2284 CrossRef PubMed.
- A. VahidMohammadi, J. Rosen and Y. Gogotsi, The world of two-dimensional carbides and nitrides (MXenes), Science, 2021, 372, eabf1581 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ma01076j |
| This journal is © The Royal Society of Chemistry 2022 |