Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The significance of nanoparticle shape in chirality transfer to a surrounding nematic liquid crystal reporter medium
Anshul
Sharma
ab,
Taizo
Mori
 c,
Ahlam
Nemati
c,
Ahlam
Nemati
 ab,
Diana P. N.
Gonçalves
ab,
Diana P. N.
Gonçalves
 bd,
Lara
Querciagrossa
bd,
Lara
Querciagrossa
 e,
Claudio
Zannoni
e,
Claudio
Zannoni
 *e and
Torsten
Hegmann
*e and
Torsten
Hegmann
 *abdf
*abdf
aAdvanced Materials and Liquid Crystal Institute (AMLCI), Kent State University, Kent (OH) 44242-0001, USA. E-mail: thegmann@kent.edu
bMaterials Science Graduate Program, Kent State University, Kent (OH) 44242-0001, USA
cInstitute for Solid State Physics, The University of Tokyo, Tokyo, Japan
dDepartment of Chemistry and Biochemistry, Kent State University, Kent (OH) 44242-0001, USA
eDipartimento di Chimica Industriale “Toso Montanari” and INSTM, Università di Bologna, Viale Risorgimento 4, IT-40136 Bologna, Italy. E-mail: claudio.zannoni@unibo.it
fBrain Health Research Institute (BHRI), Kent State University, Kent (OH) 44242-0001, USA
First published on 4th March 2022
Abstract
Defined based on geometric concepts, the origin of biological homochirality including the single handedness of key building blocks, D-sugars and L-amino acids, is still heavily debated in many ongoing research endeavors. Origin aside, transmission and amplification of chirality across length scales are likely essential for the predominance of one handedness over the other in chiral systems and are attracting an unabated interest not only in biology but also in material science. To offer a measure for chirality and through-space chirality transfer, we here provide a report on recent progress toward the development of a suitable approach for an a priori prediction of chirality “strength” and efficacy of chirality transfer from a chiral solute to an achiral nematic solvent. We achieve this by combining an independently calculated, suitable pseudoscalar chirality indicator for the solute with another, independently calculated scalar solute–solvent shape compatibility factor. In our ongoing pursuit to put this approach to the test, we are advancing and refining a versatile experimental platform based on achiral gold nanoparticle cores varying in size, shape, and aspect ratio capped with monolayers of chiral molecules or on intrinsically chiral cellulose nanocrystals that serve as chiral solutes in an achiral nematic liquid crystal phase acting as a reporter medium. The pitch of the ensuing induced chiral nematic liquid crystal phase ultimately serves as a reporter medium that allows us to experimentally quantify and compare chirality and efficacy of chirality transfer.
1 Introduction
Chirality, defined as a geometric property of a group of points or atoms in space, or of any object that is not superimposable onto its mirror image, is ubiquitous at all scale levels1—from subatomic particles2 to galaxies in space.3 For any system to be chiral, irrespective of any physical or chemical manifestation of said chirality, all that is necessary is the complete absence of improper rotations in the symmetry group of the system. Lord Kelvin defined chirality by the absence of mirror symmetry: “I call any geometrical figure, or group of points, chiral, and say it has chirality, if its image in a plane mirror, ideally realized, cannot be brought to coincide with itself.”4 Considering its unquestionable significance in many areas of science ranging from cell–cell interactions,5 drug discovery,6 and catalysis7 to chiral optics8 and chiral nanomaterials,9–12 some key questions asked and addressed by many scientists are: Does chirality scale, can it be quantified even for abstract geometrical objects, and how does it vary solely as a function of shape? Kurt Mislow, a pioneer in this field of research, published one of the most detailed reports on purely geometric chirality metrics to quantify chirality.13 Now almost three decades ago, that report primarily focused on geometric figures in 2- and 3-D space representing molecules, rather than nanomaterials, but many of the concepts have since been applied to chiral nanostructures. Within the boundaries of each model or chirality measure, objects including molecules can be defined as “more” or “less” chiral. In due course, Mislow and colleagues concluded: “there remains the daunting challenge of bridging the gap between the results of chiral shape analysis and the world of experimental observables.”13In this perspective, we summarize recent attempts by our teams to bridge this gap by showing that an appropriate pseudoscalar chirality index can fairly accurately predict the chirality transfer efficacy in an otherwise unrelated experimental system largely by assessing shape and shape congruency. While introducing the scope of and a classification for chirality measures, Mislow and colleagues noted that any “degree of chirality” scales with shape and should be invariant with the size of the object.13
Starting with this assumption, metal nanoparticles, particularly those with a gold core, continue to be fertile ground for testing shape-chirality correlations since gold nanoparticles can now be reproducibly synthesized in a very wide range of sizes and shapes with suitably narrow size and shape polydispersity.14 For the purpose of this discussion here, we will refer to these gold nanoparticles varying in size as well as shape, capped with a monolayer of chiral molecules as chiral nanoshapes.
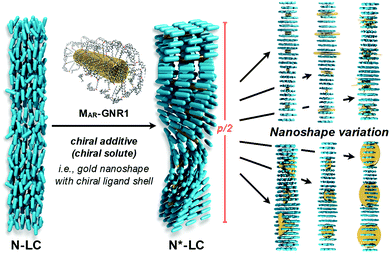
2 A chirality measure for nanoshapes
2.1 Basic concepts
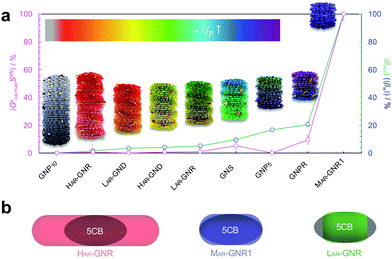
The intrinsic chirality of any given chiral shape (object or molecule) can be calculated using an absolute, as opposed to being relative to a reference, pseudoscalar chirality indicator15—termed the average chirality index 〈Gaoa〉.†,16,17 For chiral nanoshapes, such as those of interest here, this index can be derived from coarse grained (CG) representations of the chiral ligand molecules suitably distributed on the nanoshape surface as we will see later. Experimental datasets correlated to the chirality of these nanoshapes are acquired by investigating dispersions of said chiral nanoshapes in an achiral nematic liquid crystal (N-LC)18 serving as a reporter medium.19 The induced chiral nematic LC (N*-LC) phase allows a ranking of the efficacy of chirality transfer depending on the dimensions of the nanoshape via microscopically (visually)-observable and easily measurable helical pitch, p, values (Fig. 1). For any chiral nanoshape solute X in an achiral N-LC phase N, p of the induced N*-LC phase is inversely proportional to the concentration of the nanoshape,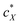 , and to the helical twisting power βXN (eqn (1)):20
, and to the helical twisting power βXN (eqn (1)):20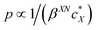 | (1) |
Thus, βXN serves as a figure of merit or measure of chirality in these systems and is assumed to be proportional to the intrinsic chirality of the nanoshape (eqn (2)):
| βXN ∝ 〈Gaoa〉 | (2) |
Early experiments by our teams focused on size effects of quasi-spherical (polyhedral) nanoparticles. Within each of the studied series of quasi-spherical gold nanoparticles (GNP), a particular GNP core diameter showed maximum values for both βXN and/or 〈Gaoa〉.19 With the chirality emanating exclusively from a combination of spatial arrangement and chiral nature of the ligand shell molecules (considering an achiral metal core based on experimental i.e., spectroscopic evidence), the molar helical twisting power βmol defined in eqn (3):
| βmol = 1/(pxLigandr) | (3) |
2.2 Early experimental nanoparticle systems
For the first set of GNPs with core diameters of about 2, 5 and 10 nm, capped with cholesterol-thiol or siloxane-networked cholesterol-thiol derivatives (Fig. 2), |βmol| was the largest (i.e., p was the tightest) for GNP5 characterized by an average core diameter of 5.5 nm (|βmol| = 178 μm−1 (we here report values for the absolute molar helical twisting power, |βmol|, since the sign of βmol indicates the handedness and not the magnitude; “+” for a right-handed and “−” for a left-handed helical distortion of the induced N*-LC phase).19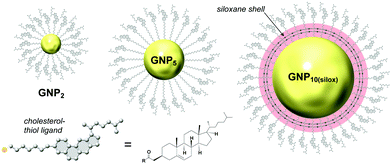 | ||
| Fig. 2 Studies focusing on the effects of core diameter and presence (absence) of a chiral bias during GNP formation. GNP2 and GNP5 (the subscript number indicating the average core diameter) are capped with cholesterol-thiol ligands; GNP10(silox) is capped with a siloxane shell using 3-mercaptopropyltrimethoxysilane (MPS) that is further end-functionalized with cholesterol. Reproduced from and adapted with permission from ref. 19 – Copyright (2014), American Chemical Society. | ||
In contrast, GNP10 with the largest core diameter did not induce an apparent N*-LC phase at any concentration judging from textural analysis data obtained by cross-polarized optical microscopy (cPOM) with the LC samples confined between substrates with varying surface boundary conditions (including homeotropic anchoring or a top surface formed by air). The observed Schlieren textures were indistinguishable from textures commonly seen for achiral N-LC phases, thus indicating p→∞ and, as a consequence, βmol → 0. GNP2 showed a value of |βmol| = 16 μm−1; about one order of magnitude lower than the value detected for GNP5 but compared reasonably well to some commercially available organic chiral additives developed to induce N*-LC phases with |βmol| values ranging from about 10 to 40 μm−1.19
Another GNP series investigated the role of axially chiral ligands. GNPs capped with three sets of (R)- and (S)-enantiomers based on axially chiral 1,1′-binaphthyl-thiol derivatives that differed only in the length of a non-tethered aliphatic chain were investigated as chiral solutes in the same N-LC host (Fig. 3).21 The variation in length of the non-tethered aliphatic chain in the 2′-position, potentially due to reasons of varying dihedral angles in solution and the resulting changes in steric demand (or due to differences in solubility) gave rise to some variation in GNP core diameter during synthesis (overall ranging from about 1.1–2.5 nm in core diameter). The binaphthyl-thiol-capped GNP with the largest core diameter of about 2.5 nm (GNPBN(R)-1) turned out to be just slightly the strongest chiral inducer of this series with |βmol| = 66 μm−1. However, in light of comparatively smaller differences in core diameter vis-à-vis the earlier series19 overall, all six GNPBN essentially showed identical |βmol| values, ranging from |βmol| = 61 μm−1 to |βmol| = 66 μm−1. Most noteworthy, all GNPs discussed thus far (with the exception of GNP10) well outperformed the free cholesterol-thiol and 1,1′-binaphthyl-thiol ligands with respect to their ability to helically distort the initially achiral N-LC, i.e., induce a significantly lower pitch (higher |βmol|) at any identical concentration of the chiral molecules in the N-LC matrix.19,21
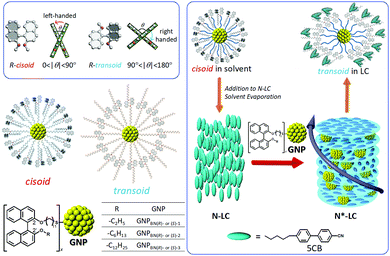 | ||
| Fig. 3 Series of GNPs capped with 1,1′-binaphthyl-thiol ligands differing in the length of the non-tethered aliphatic chain in the 2′-position ((R)- and (S)-enantiomers) tested as chiral solutes in the N-LC phase formed by 5CB (4′-pentyl-4-biphenylcarbonitrile). While cisoid-conformations were observed in organic solvents, transoid-conformations were confirmed in the induced N*-LC phase. Reproduced from and adapted with permission from ref. 21 – Copyright (2016), American Chemical Society. | ||
2.3 Desymmetrization from GNPs to GNRs (gold nanorods)
Our initial hypothesis was that the observed enhancement of this through-space chirality transfer was caused by long-range, through-space interactions between the chiral molecules and the plasmonic nanostructures exemplified by spectroscopically observed enhanced anisotropy or Kuhn's dissymmetry factors g (eqn (4)):22| g = Δε/ε | (4) |
Experimental data indeed confirmed our hypothesis,24 and each of the two GNRs differing in their aspect ratio (AR) and capped with a siloxane networked cholesterol-thiol ligand shell led to significantly higher |βmol| values (Fig. 4). MAR-GNR1 (MAR here standing for the medium aspect ratio of AR = 4.3 with the transversal cross-sectional diameter of this GNR of d = 10 nm closely matching the diameter of GNP10) produced a value of |βmol| = 1064 μm−1. Similarly, MAR-GNR2 with AR = 2.2 induced an N*-LC phase with a value of |βmol| = 895 μm−1. Remarkably, the trends of independently calculated or acquired 〈Gaoa〉 and |βmol| values, respectively, for this GNP2–10/MAR-GNR series matched almost perfectly (Fig. 5). Our, for the most part, naïve conclusions from these first couple of datasets were that desymmetrizing the shape of the nanocarrier and increasing its AR will increase 〈Gaoa〉 and |βmol|.24
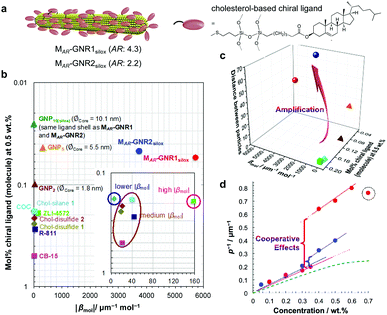 | ||
| Fig. 4 Amplification of the chirality transfer efficacy by desymmetrization. (a) GNRs with a cholesterol end-functionalized siloxane ligand shells show significantly elevated values of |βmol| in comparison to GNPs as shown in plots (b) and (c). ZLI-4572, COC, R-811, and CB15 are commercially available organic chiral dopants; the Chol-silane and Chol-disulfides are the neat organic ligand molecules tested as chiral additives, ∅Core is the core diameter of the GNP. |βmol| values here used the molar concentration of the entire ligand-capped GNR and thus the SI unit [μm−1 mol−1] (|βmol| values described in the text as well as in Table 1 use the more correct and dimensionless mole fraction of the chiral ligand shell molecules only since the GNR core is achiral; eqn (3)). (d) Cooperative effects among the admixed GNRs are supported by analyzing plots of the inverse pitch (1/p) vs. the MAR-GNR concentration; the slope increases at a threshold concentration rather than plateauing as commonly observed for chiral additives in induced N*-LC phases (green dotted curve) until a concentration when the GNRs begin the aggregate (dotted circle at cMAR−GNR1silox = 0.7 wt%). Reproduced from and adapted with permission from ref. 24 – Copyright (2018), Springer-Nature. | ||
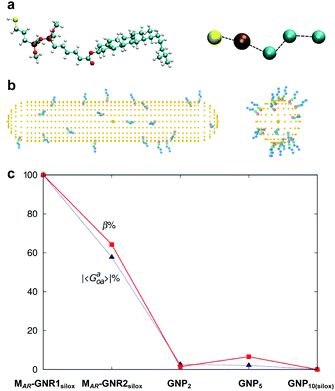 | ||
Fig. 5 (a) Atomistic and coarse-grained (CG) representation of the ligand molecule, (b) MAR-GNR1 spherocylindrical and GNP10 models each decorated with 20 CG ligands randomly distributed. (c) Trend of averaged chirality indicator |Gaoa| in comparison to the trend experimentally determined for |βmol| for GNPs2–10 as well as MAR-GNR1 and MAR-GNR2. Values of chirality have been obtained for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random configurations on the GNPs and 1800 selected configurations on the GNRs. Reproduced from and adapted with permission from ref. 24 – Copyright (2018), Springer-Nature. 000 random configurations on the GNPs and 1800 selected configurations on the GNRs. Reproduced from and adapted with permission from ref. 24 – Copyright (2018), Springer-Nature. | ||
This was further supported by the considerable amplification of the chirality transfer by MAR-GNR1 (the more effective chiral inducer of the GNRs tested thus far) capped with the identical series of axially chiral binaphthyl-thiol ligands described earlier.
For this particular MAR-GNR1BN series,25 the |βmol| values, now strongly depending on the length of the non-tethered aliphatic chain in the 2′-position on the 1,1′-binaphthyl unit, ranged from |βmol| = 192 μm−1 to a record |βmol| = 1312 μm−1. Here again, independent calculations of 〈Gaoa〉 predicted these experimental trends both with respect to magnitude of |βmol| as well as the sign (aka handedness) of the induced N*-LC phase (Fig. 6).25
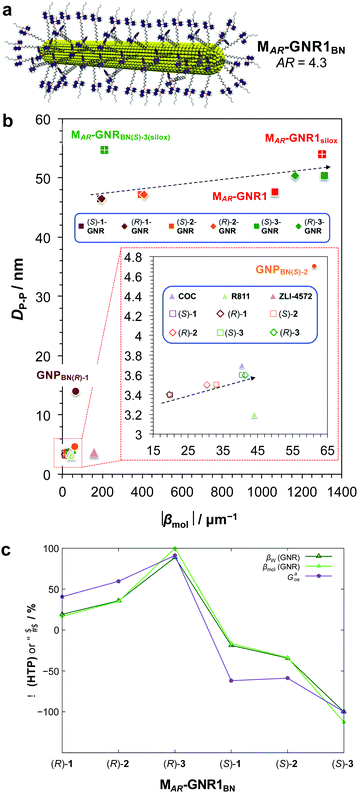 | ||
| Fig. 6 (a) Schematic depiction of the MAR-GNR1BN series with the 2,2′-substituted 1,1′-binaphthyl-thiol ligands in the transoid conformation formed in the induced N*-LC phase. (b) Chirality efficiency plot: calculated particle–particle distances, DP–P, vs. |βmol|. The most efficient chiral GNR solutes occupy the top right corner of this plot, the bottom lower corner the least efficient ones. Inset (red dashed box) shows the section highlighted in the lower left part of the plot (data points are either directly identified with the abbreviation of the nanoshape or highlighted in blue boxes. (c) Values of the chirality index, 〈Gaoa〉, for 20 binaphthyl thiol ligand molecules bound to the MAR-GNR1 compared to the values of the experimentally determined HTP data, |βw| (helical twisting power based on the weight fraction of the chiral BN ligands in the N-LC), and |βmol| (with the largest values were set to 100%). Reproduced from and adapted with permission from ref. 25 – Copyright (2019), American Chemical Society. | ||
For all the nanoshapes described so far, the working principle for any amplification of the efficacy of chirality transfer always appeared to be that the chiral ligand shell molecules act as a joined force or network, thereby amplifying chirality transfer throughout the N-LC medium both locally (to N-LC molecules in direct vicinity of the suspended GNRs) and throughout the N-LC bulk. Freeze-fracture transmission electron microscopy (TEM) experiments, showing arrays of appropriately spaced (based on simple volume fraction calculations) and seemingly twisted with respect to each other MAR-GNR2, lend support for an additional contribution to this efficacious chirality transfer (Fig. 7).24 It appeared reasonable to assume that cooperative effects among the now twisted GNRs would further amplify chirality transfer, and such cooperative effects were experimentally seen in the plots of 1/p vs. the concentration of the GNRs 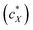 in the N-LC. At a distinct threshold value of
in the N-LC. At a distinct threshold value of 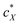 , the slope of the curve would abruptly rise with increasing
, the slope of the curve would abruptly rise with increasing 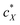 rather than plateau as normally observed for chiral additives in N-LCs.24 One may think of this contribution as a feedback loop at and above the threshold concentration: a spatially massive (when compared to the N-LC building blocks, i.e., N-LC molecules) and strong chiral inducer amplifies its own twist and thus shortens p in the surrounding matrix, which, in turn leads to an increased torque to the GNRs that shortens p and so on and so forth.
rather than plateau as normally observed for chiral additives in N-LCs.24 One may think of this contribution as a feedback loop at and above the threshold concentration: a spatially massive (when compared to the N-LC building blocks, i.e., N-LC molecules) and strong chiral inducer amplifies its own twist and thus shortens p in the surrounding matrix, which, in turn leads to an increased torque to the GNRs that shortens p and so on and so forth.
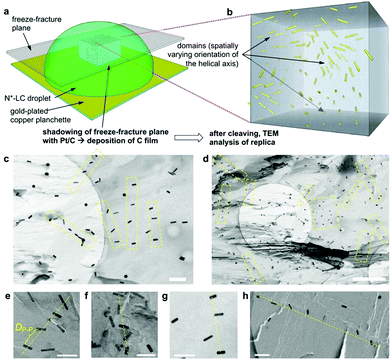 | ||
| Fig. 7 (a) Schematic depiction of the freeze-fracture (FF) method to prepare the TEM specimen. (b) A representative voxel of the N*-LC droplet showing the multi-domain structure via the embedded GNRs. (c) and (d) FF-TEM images of the induced N*-LC phase of Felix-2900-03 containing 0.5 wt% MAR-GNR2silox (scale bars: (c) 200 nm and (d) 1 μm, apparent circles are from the TEM grids). To obtain these images, it was important that the replica captured most of the MAR-GNRs on the fractured surface, thereby providing a direct visualization of the GNRs in the bulk material. Areas highlighted by a yellow box and (e–h) select areas from many of the obtained FF-TEM images show GNR arrays (often twisted) with an average separation closely matching the theoretically calculated particle–particle distances, DP–P, of ca. 90–100 nm by assuming well-dispersed GNRs in the induced N*-LC matrix (scale bars in (e–h): 100 nm). Reproduced from and adapted with permission from ref. 24 – Copyright (2018), Springer-Nature. | ||
2.4 Variations in AR, other shapes, and shape matching
Equipped with these pieces of the puzzle, the next question in our quest was: How do shape and AR of the nanocarrier of chiral information impact chirality transfer? Moreover, reflecting on our appreciation that an independently calculated 〈Gaoa〉 can predict experimental trends of |βmol|, we put this system to the test with a significant expansion of the scope of our research by focusing on more pronounced shape and AR variations.26This was ultimately accomplished by comparing calculations of a shape-corrected 〈Gaoa〉, described next, with the experimental values gathered for |βmol| for a larger set of gold nanoshapes now including nanoprisms (GNPR), nanodisks (GND), nanostars (GNS) as well as GNRs differing in AR. All gold nanoshapes were monolayer-capped with the identical cholesterol-thiol ligand shell shown in Fig. 2. The dimensions as well as |βmol| values for these and all other nanoshapes discussed in this perspective are summarized in Table 1.
| Nanoshapea | Nanoshape Core Dimensionsb (nm) (d = diameter, w = width, h = height, l = length, AR = aspect ratio) | |βmol| (μm−1) | |
|---|---|---|---|
| a All nanoshapes are capped with a thiolate ligand shell unless otherwise noted, e.g., the subscript “silox” refers to nanoshapes capped with a siloxane conjugated 3-mercaptopropylsilyloxy-ligand shell end-functionalized with aliphatic cholesteryl ester groups via a siloxane condensation reaction; BN = 1,1′-binaphthyl; all other nanoshapes are capped with a cholesterol-thiol; LAR, MAR and LAR refer to large, medium or low aspect ratio, respectively. b Calculated AR values here are not considering the thickness of the ligand monolayer. Those referred to in the text used for the calculation of the 2-D isoperimetric ratios, IPR2D, consider the ligand shell of the chiral ligand-capped nanoshapes and thus differ from those listed here for the nanoshape cores. c Assuming quasi-spherical overall shapes for polyhedral GNPs. d The AR cannot be easily calculated for GNS; thus far the only concave shape investigated. | |||
| GNP2 | d = 1.8 | AR ∼1c | 16 |
| GNP5 | d = 5.5 | 178 | |
| GNP10 | d = 10.0 | 0 | |
| GNP10(silox) | d = 10.0 | 0 | |
| GNPBN(R)-1 | d = 2.5 | 61–66 | |
| GNPBN(S)-1 | d = 1.7 | ||
| GNPBN(R)-2 | d = 2.1 | ||
| GNPBN(S)-2 | d = 1.1 | ||
| GNPBN(R)-3 | d = 1.2 | ||
| GNPBN(S)-3 | d = 1.1 | ||
| MAR-GNR1 | d = 10.0; l = 43.0 | AR = 4.3 | 1064 |
| MAR-GNR1silox | 1303 | ||
| MAR-GNR1BN(R)-1 | 196 | ||
| MAR-GNR1BN(S)-1 | 192 | ||
| MAR-GNR1BN(R)-2 | 410 | ||
| MAR-GNR1BN(S)-2 | 393 | ||
| MAR-GNR1BN(R)-3 | 1166 | ||
| MAR-GNR1BN(S)-3 | 1312 | ||
| MAR-GNR1BN(S)-3silox | 210 | ||
| MAR-GNR2silox | d = 23.5; l = 51.0 | AR = 2.2 | 896 |
| LAR-GNR | d =15.2; l = 25.0 | AR = 1.7 | 53 |
| HAR-GNR | d = 12.5; l = 87.0 | AR = 8.5 | 18 |
| LAR-GND | d = 79.0; h = 21.6 | AR = 3.7 | 37 |
| HAR-GND | d = 45.0; h = 7.4 | AR = 6.1 | 43 |
| GNS | d core = 60.0; lspikes = 69.0 | —d | 105 |
| GNPR | l edge = 50.0; h = 12.5 | AR = 5.3 | 216 |
| 5CB (N-LC) | l = 1.8; w = 0.45 | AR = 4.0 | — |
To account for a shape compatibility dependence of the chirality transfer, our new model assumed that there is a combination of the chiral solute's intrinsic chirality and its ability to twist the N-LC that contributes to the transfer chirality across length scales. For a chiral solute (nanoshape) X, we assumed that βXN can be written as:
| βXN ∝ GXSXN | (5) |
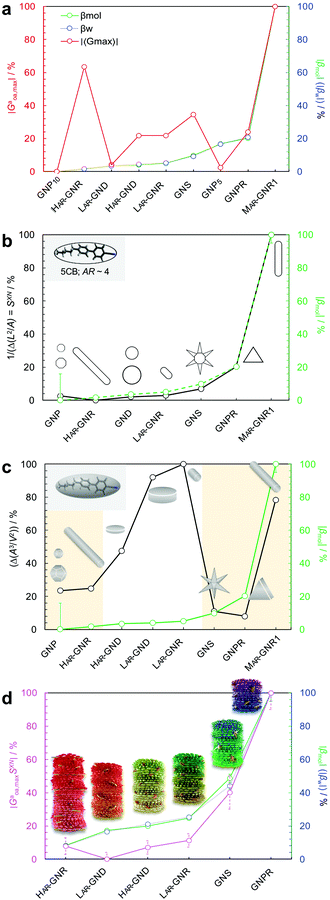 | ||
| Fig. 8 Plots showing the trends of: (a) the maximum chirality indicator |Gaoa,max| in comparison to the experimentally derived values for |βw| and |βmol| (with the largest value set to 100% and the lowest to 0%—here GNP10 with βmol = βw = 0, and every other value—and every other value weighted accordingly) for the calculated values of |βmol| see Table 1, (b) 1/(IPR2D) and (c) 1/(IPR3D) each in comparison to |βmol| (yellow shaded areas in (c) signify some correlation in trends); values for IPR2D and IPR3D use the adjusted AR values considering the thickness of the ligand shell. (d) Plot showing the trend of the shape compatibility-corrected maximum chirality indicator |Gaoa,maxSXN| for a subset of nanoshapes in comparison to |βw| and |βmol|. LAR, MAR, and HAR here refer to low, medium and high aspect ratio, respectively. Reproduced from and adapted with permission from ref. 26 – Copyright (2022), AAAS. | ||
The use of |Gaoa,max| was justified by the fact that the HTP data were calculated from experimental pitch measurements, which are particularly sensitive to the highest rather than average chirality values (particularly for a system containing various contributions of different chirality).
Hereby we further assumed that SXN is related to the inverse difference between the 2-D isoperimetric ratios (IPR2D; defined as IPR2D = ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2/A, with
2/A, with ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) being the length of the perimeter and A the 2D shape surface area) of solute and solvent, 1/IPR2DXN = 1/(IPR2DX − IPR2DN). The degree of correlation between SXN and βXN (i.e., |βmol|) will then provide direct insights into the importance of shape complementarity in chirality transfer. SXN, of course, is a scalar quantity such that the orientation of one nanoshape with respect to another is non-zero and scales invariantly under spatial transformation, even in the achiral case. We defined SXN as the absolute value of the inverse difference between the IPR2D of each nanoshape and the IPR2D of the N-LC host molecule 5CB (eqn (6)):
being the length of the perimeter and A the 2D shape surface area) of solute and solvent, 1/IPR2DXN = 1/(IPR2DX − IPR2DN). The degree of correlation between SXN and βXN (i.e., |βmol|) will then provide direct insights into the importance of shape complementarity in chirality transfer. SXN, of course, is a scalar quantity such that the orientation of one nanoshape with respect to another is non-zero and scales invariantly under spatial transformation, even in the achiral case. We defined SXN as the absolute value of the inverse difference between the IPR2D of each nanoshape and the IPR2D of the N-LC host molecule 5CB (eqn (6)):
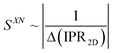 | (6) |
 | ||
| Fig. 9 (a) Plot showing trends of the shape compatibility-corrected maximum chirality indicator |Gaoa,maxSXN| for the full set of nanoshapes, now including the powerful chiral inducer MAR-GNR1, in comparison to the experimentally derived values for |βw| and |βmol|. Models of the induced N*-LC phase show a complete 360° rotation of the local director leading to a tighter pitch from left to right depending on the size, shape, and AR of the suspended nanoshape (for GNP10: p → ∞). (b) Visualization showing the varying degree of shape compatibility among GNRs featuring different AR values with the 2-D projection of 5CB scaled in size to match each GNR width. Reproduced from and adapted with permission from ref. 26 – Copyright (2022), AAAS. | ||
The importance of the shape coupling or shape compatibility factor SXN is most apparent when the AR of X is changing within a series of equal-shaped nanoshape solutes in the same N. This concept is best visualized by sketches shown in Fig. 9b, where the shape compatibility among GNRs, HAR-GNR, MAR-GNR1 and LAR-GNR proves the utility of introducing SXN.
3 Summary and outlook
Collectively, all our experimental data support the notion that size, shape, and AR of chiral ligand-capped nanoshapes affect the efficacy of chirality transfer to a surrounding reporter medium, here a nematic LC phase, in very predictable ways via independent calculations of 2-D shape compatibility corrected chirality indicators. Each of the gold nanoshapes capped with a chiral ligand shell outperforms the neat organic chiral molecules with respect to their ability to transfer chirality to the N-LC host medium. We established a very systematic correlation between purely geometric concepts and experimental chirality transfer data. This methodology provides a broadly expandable tool to a priori predict experimental chirality transfer efficacy data.In the described N-LC, this opportunity is realized by measuring the induced helical pitch and calculating the helical twisting power in an induced N*-LC medium for essentially any possible nanoshape varying in size, shape, or AR; all without much need to alter the chemical nature of the chiral molecules decorating the nanoshape surface.
But what if the nanoshape core was chiral? To elucidate the role of core chirality, we needed a system with an intrinsically chiral core. The perhaps closest match to the most potent MAR-GNR1, at least for now, appeared to be cellulose nanocrystals (CNCs). Accordingly, in another recently published study, we further studied such innately chiral CNCs, both neat and decorated with chiral or achiral molecules (Fig. 10).27 Here, a comparison between neat CNCs, CNCs-functionalized with cholesterol units (CNCs-Chol), and MAR-GNR1 revealed that the contribution to chirality transfer from a molecular and morphologically chiral core is likely considerable. The CNCs-Chol, lacking a dense chiral ligand shell present on MAR-GNR1 (translating to a 75% lower overall cholesterol content for the CNCs-Chol at a set constant weight fraction in an N-LC) showed an about eightfold decrease in |βw| in comparison to MAR-GNR1. However, replacing the chiral cholesterol units (Fig. 10b) with achiral pro-mesogenic moieties characterized by a close structural match to the N-LC host molecules (Fig. 10c) did not lead to a reduction of |βw|.
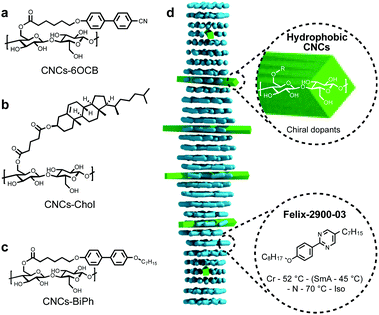 | ||
| Fig. 10 (a–c) Chemical structures of the CNC surface modifications. The CNC core displays both morphological (twist of the CNC rods) and inherent core chirality (via the glucose building blocks). (d) Schematic representation of the N*-LC phase induced by the addition of only minute amounts of the functionalized CNCs to the LC host, Felix-2900-03, in the nematic phase. Reproduced from and adapted with permission from ref. 27 – Copyright (2021), Wiley-VCH. | ||
Thus, the dense network of chiral molecules on the surface of the gold nanoshapes is the key driving force for their unusually high ability to transfer chirality to a surrounding achiral N-LC medium, fundamentally affected by shape congruency. Yet, any further enhancement of the chirality transfer efficacy can likely be accomplished by introducing nanoshapes featuring both a chiral core and an IPR2D value matching the one of the N-LC host, which is what current experiments in our labs are focusing on. Such intrinsically chiral cores have been reported for a number of anisometric nanomaterials including, for example, in a recent report by Ben-Moshe and colleagues for bipyramidal tellurium28 or Markovich et al. for rod-like Eu3+-doped terbium phosphate nanocrystals.29 Given the recently increasing number of articles citing shape compatibility arguments,30 recognized for simple molecular LC systems by Feringa and co-workers years ago,31 we foresee that the utility of the mathematical and computational concepts described here may soon be significantly advanced by machine learning and artificial intelligence (AI) strategies, and as such support familiar ‘you cannot put a square peg in a round hole’ metaphors for molecular and nanoscale chirality transfer systems. Ultimately, a further expansion of these concepts to lyotropic LC systems32,33 that are biologically significantly more relevant as well as to applications seems all but inevitable.34,35
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work by the authors’ teams described here was financially supported by the US National Science Foundation (NSF, DMR-1506018 and DMR-1904091; TH), the Ohio Third Frontier (OTF) program for Ohio Research Scholars: “Research Cluster on Surfaces in Advanced Materials” (TH), and the Italian MIUR (PRIN project 2015XJA9NT; CZ). The authors also acknowledge Hossein Mirzakhani and Diana P. N. Gonçalves for some of the graphical designs.Notes and references
- L. D. Barron, Chirality, 2012, 24, 879–893 CrossRef CAS PubMed; S. M. Morrow, A. J. Bissette and S. P. Fletcher, Nat. Nanotechnol., 2017, 12, 410–419 CrossRef PubMed.
- G. B. Gelmini and M. Roncadelli, Phys. Lett. B, 1981, 99, 411–415 CrossRef CAS; J. Gooth, A. C. Niemann, T. Meng, A. G. Grushin, K. Landsteiner, B. Gotsmann, F. Menges, M. Schmidt, C. Shekar, V. Süβ, R. Hühne, B. Rellinghaus, C. Felser, B. Yan and K. Nielsch, Nature, 2017, 547, 324–327 CrossRef PubMed.
- B. A. McGuire, P. B. Carroll, R. A. Loomis, I. A. Finneran, P. R. Jewell, A. J. Remijan and G. A. Blake, Science, 2016, 352, 1449–1452 CrossRef CAS PubMed; D. P. Glavin, A. S. Burton, J. E. Elsila, J. C. Aponte and J. P. Dworkin, Chem. Rev., 2020, 120, 4660–4689 CrossRef PubMed.
- W. T. Kelvin, Baltimore lectures on molecular dynamics and the wave theory of light, C. J. Clay and Sons, London, 1904 Search PubMed.
- M. Inaki, J. Liu and K. Matsuno, Philos. Trans. R. Soc., B., 2016, 371, 20150403 CrossRef CAS PubMed; A. S. Chin, K. E. Worley, P. Ray, G. Kaur, J. Fan and L. Q. Wan, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 12188–12193 CrossRef PubMed.
- W. H. Brooks, W. C. Guida and K. G. Daniel, Curr. Top. Med. Chem., 2001, 11, 760–770 CrossRef PubMed.
- T. P. Yoon and E. N. Jacobsen, Science, 2003, 299, 1691–1693 CrossRef CAS PubMed; A. Pfaltz and W. J. Drury III, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5723–5726 CrossRef PubMed.
- P. Gutsche, X. Garcia-Santiago, P.-I. Schneider, K. M. McPeak, M. Nieto-Vesperina and S. Burger, Symmetry, 2020, 12, 158 CrossRef.
- D. Yang, P. F. Duan, L. Zhang and M. H. Liu, Nat. Commun., 2017, 8, 15727 CrossRef CAS PubMed.
- Y. Kim, B. Yeom, O. Arteaga, S. J. Yoo, S.-G. Lee, J.-G. Kim and N. A. Kotov, Nat. Mater., 2016, 15, 461–468 CrossRef CAS PubMed.
- H.-E. Lee, H.-Y. Ahn, J. Mun, Y. Y. Lee, M. Kim, N. H. Cho, K. Chang, W. S. Kim, J. Rho and K. T. Nam, Nature, 2018, 556, 360–365 CrossRef CAS PubMed.
- K. Ariga, T. Mori, T. Kitao and T. Uemura, Adv. Mater., 2020, 32, 1905657 CrossRef CAS PubMed.
- A. B. Buda, T. auf der Heyde and K. Mislow, Angew. Chem., Int. Ed. Engl., 1992, 31, 989–1007 CrossRef.
- M. Grzelczak, J. Pérez-Juste, P. Mulvaney and L. M. Liz-Marzán, Chem. Soc. Rev., 2008, 37, 1783–1791 RSC.
- M. A. Osipov, B. T. Pickup and D. A. Dunmur, Mol. Phys., 1995, 84, 1193–1206 CrossRef CAS.
- A. Pietropaolo, L. Muccioli, R. Berardi and C. Zannoni, Proteins, 2008, 70, 667–677 CrossRef CAS PubMed.
- A. P. Almeida, L. Querciagrossa, P. E. S. Silva, F. Gonçalves, J. P. Canejo, P. L. Almeida, M. H. Goghinho and C. Zannoni, Soft Matter, 2019, 15, 2838–2847 RSC.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, Oxford, 1993 Search PubMed.
- A. Sharma, T. Mori, H.-C. Lee, M. Worden, E. Bidwell and T. Hegmann, ACS Nano, 2014, 8, 11966–11976 CrossRef CAS PubMed.
- G. Solladié and R. Zimmermann, Angew. Chem., Int. Ed. Engl., 1984, 23, 348 CrossRef.
- T. Mori, A. Sharma and T. Hegmann, ACS Nano, 2016, 10, 1552–1564 CrossRef CAS PubMed.
- W. Kuhn, Annu. Rev. Phys. Chem., 1958, 9, 417–438 CrossRef CAS.
- A. Guerrero, B. Auguié, J. Alonso-Gómez, Z. Džolić, S. Gómez-Graña, M. M. Cid and L. M. Liz-Mazán, Angew. Chem., Int. Ed., 2011, 50, 5499–5503 CrossRef PubMed.
- A. Nemati, S. Shadpour, L. Querciagrossa, L. Li, T. Mori, M. Gao, C. Zannoni and T. Hegmann, Nat. Commun., 2018, 9, 3908 CrossRef PubMed.
- A. Nemati, S. Shadpour, L. Querciagrossa, T. Mori, C. Zannoni and T. Hegmann, ACS Nano, 2019, 13, 10312–10326 CrossRef CAS PubMed.
- A. Nemati, L. Querciagrossa, C. Callison, S. Shadpour, D. P. N. Gonçalves, T. Mori, X. Cui, R. Ai, J. Wang, C. Zannoni and T. Hegmann, Sci. Adv., 2022, 8, abl4385 CrossRef PubMed.
- D. P. N. Gonçalves and T. Hegmann, Angew. Chem., Int. Ed., 2021, 60, 17344–17349 CrossRef PubMed.
- A. Ben-Moshe, A. da Silva, A. Müller, A. Abu-Odeh, P. Harrison, J. Waelder, F. Niroui, C. Ophus, A. M. Minor, M. Asta, W. Theis, P. Ercius and A. P. Alivisatos, Science, 2021, 372, 729–733 CrossRef CAS PubMed.
- U. Hananel, A. Ben-Moshe, H. Diamant and G. Markovich, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11159–11164 CrossRef CAS PubMed.
- M. Weh, J. Rühe, B. Herbert, A.-M. Krause and F. Würthner, Angew. Chem., Int. Ed., 2021, 60, 15323–15327 CrossRef CAS PubMed; S.-Y. Zhang, D. Fairen-Jimenez and M. J. Zaworotko, Angew. Chem., Int. Ed., 2020, 59, 17600–17606 CrossRef PubMed; A. B. George and K. S. Korelev, PLoS Comput. Biol., 2018, 14, e1006645 CrossRef PubMed.
- N. Katsonis, A. Minoia, T. Kudernac, T. Mutai, H. Xu, H. Uji-i, R. Lazzaroni, S. De Feyter and B. Feringa, J. Am. Chem. Soc., 2008, 130, 386–387 CrossRef CAS PubMed.
- S. Shadpour, J. P. Vanegas, A. Nemati and T. Hegmann, ACS Omega, 2019, 4, 1662–1668 CrossRef CAS PubMed.
- L. Bergquist and T. Hegmann, ChemNanoMat, 2017, 3, 863–868 CrossRef CAS.
- K. Perera, A. Nemati, E. Mann, T. Hegmann and A. Jákli, ACS Appl. Mater. Interfaces, 2021, 13, 4574–4582 CrossRef CAS PubMed.
- D. P. N. Gonçalves, M. E. Prévôt, S. Üstünel, T. Ogolla, A. Nemati, S. Shadpour and T. Hegmann, Liq. Cryst. Rev., 2021, 9, 1–34 CrossRef.
Footnote |
† This index depends only on geometric information, i.e., in this case the position and orientation of the chiral ligands with respect to the nanoparticle frame, and thus indirectly on the size, shape, and AR of the nanomaterial:16,17,24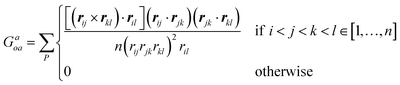 , where n is the total number of atoms (or beads), rij the vector between two atoms i and j, with modulus corresponding to their distance rij, while P indicates all permutations of i, j, k, l atoms or beads. , where n is the total number of atoms (or beads), rij the vector between two atoms i and j, with modulus corresponding to their distance rij, while P indicates all permutations of i, j, k, l atoms or beads. |
| This journal is © The Royal Society of Chemistry 2022 |