Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Confirmation of pore formation mechanisms in biochars and activated carbons by dual isotherm analysis†
L. Scott
Blankenship
 *a,
Jacek
Jagiello
*a,
Jacek
Jagiello
 b and
Robert
Mokaya
b and
Robert
Mokaya
 a
a
aSchool of Chemistry, University of Nottingham, University Park, Nottingham, NG7 2RD, UK. E-mail: leo.blankenship@nottingham.ac.uk
bMicromeritics Instrument Corporation 4356 Communications Drive, Norcross, GA 30093, USA
First published on 30th March 2022
Abstract
In this study biochars and activated carbons were synthesized either directly via the pyrolysis of sodium carboxymethyl cellulose (NC) or via hydrothermal carbonization of sawdust (SD) in an aqueous solution of KOH. The amount of porogen was varied by modulating the degree of sodium carboxymethyl substitution on NC or the amount of KOH mixed in solution with SD. Pore size distributions (PSDs) of these carbons were determined from the dual fit of kernels based on the two-dimensional version of the nonlocal density functional theory (2D-NLDFT) heterogeneous surface models to either N2 and H2 or O2 and H2 isotherms measured at −196 °C. By comparing PSDs of carbons from the same starting material at increasing degrees of activation, we show that those derived using O2 and H2 isotherms not only give more detail of variations in pore size but that the results also fit better with current understandings of porosity development in carbons derived through oxidative activation. This is likely a result of superior diffusion of O2 into ultramicropores at low pressure relative to N2.
1. Introduction
Porosimetry via the measurement of gas adsorption isotherms has provided a great depth of insight into the nature of pore channels in solids, particularly on disordered-like materials for which other techniques are not suitable for pore sizing. While N2 at −196 °C remains the dominant adsorptive used in such experiments due to its availability, studies have concluded that it is lacking in some properties required for good isotherm measurement and thus accurate determination of textural parameters.1–5 In the case of porous carbons as well as other porous materials such as conjugated microporous polymers (CMPs), it is well established that pores of width similar to the size of the N2 molecule are common. This can lead to inadequate diffusion of N2 into such pores when it is used as an adsorptive.5–7 Further, polar groups on the surface of many carbons may interact with the N2 molecule's large quadrupole moment, which obfuscates the molecular cross-sectional area used in the calculation of various measures of porosity.2,8,9 As such, alternative adsorptives have enjoyed some use in recent years, including Ar, O2, H2, CO2, CH4, CF4, and SF6 as they are either smaller in size or have a lower quadrupole moment than N2 – or both (see Table 1).10–15 Simultaneously the development of advanced DFT kernels for an array of adsorptives on carbons, in particular the 2D-NLDFT heterogeneous surface model mean that quantities such as pore size, volume, and surface area can now be more accurately determined than in the past. This model accounts for surface roughness present in the graphene sheets which make up turbostratic porous carbons by assuming a corrugated slit pore model.15,16 The nanoporous carbon structure based on curved graphene building blocks was demonstrated by using atomic resolution images taken within nanoporous carbon samples.17Nonetheless, a single isotherm cannot typically be used to accurately determine pore sizes across the entire micropore region. For example, while H2 sorption at −196 °C can probe pores as small as 3 Å its upper limit is ∼10 Å. Conversely, O2 adsorption at −196 °C is best utilized for probing pores larger than 7 Å, although it has been shown to also penetrate pores smaller than this limit to some degree.18 In order to take advantage of the information gained from measuring two isotherms, Jagiello et al. developed a method whereby appropriate kernels could be simultaneously fit to two isotherms to yield a single pore size distribution (PSD).2,5 This method was tested by using a variety of combinations of isotherms, including N2/CO2, O2/H2, and N2/H2. Generally speaking, the results derived from each of these combinations yields similar PSDs.2,4,5 However, as reported by Beda et al., N2's poor diffusion into ultramicropores means that N2 and O2 isotherms on so-called hard carbons can be quite different, and as a result PSDs may differ significantly with O2 showing much more porosity in the ultramicropore region.18 In addition, the high quadrupole moment of CO2 can lead to incorrect results due to its interaction with polar moieties which are common on activated carbons.19 The combination of O2 and H2 may provide more accurate information than the N2 and CO2 isotherms due to the former pair's lower quadrupolarity.2,4 Despite being fairly reactive gases at room temperature, under cryogenic conditions the reactivity is extremely low, so is unlikely to affect carbon surface chemistry.
Within the group of turbostratic porous carbons, there are two closely related subtypes. The first is biochar, which is produced upon the pyrolysis of biomass or other carbon-rich material.24,25 So-called activated carbon, on the other hand, differs from biochar due to the addition of an activating agent/porogen to aid in the development of porosity.25–27 This activating agent can produce porosity either through physical or chemical means. The former proceeds via gasification using an oxidizing gas such as CO2, which burns away volatile matter.26,28,29 Gasification also occurs during biomass pyrolysis as CO2 is produced from volatile carbon moieties, as such biochar can be thought of as a form of physically activated carbon.24–26 At sufficiently low temperatures (<900 °C), gasification produces very narrow pores of width <7 Å, referred to as ultramicropores.5
For chemical activation, while there is a large variety of porogens, amongst the most popular are the alkali metal hydroxides KOH and NaOH due to the fact that they facilitate a high degree of control over porosity, this being especially the case for KOH.26 Additionally, the majority of pores generated by alkali metal hydroxides have widths typically <20 Å, i.e. micropores. Such pore structures are desirable for their utility in applications such as small molecule capture and storage as well as in supercapacitors.26,30–32 In alkali metal hydroxide (MOH) activation, pores are developed via the oxidation of C to CO2, which in turn leads to further gasification. Finally, residual alkali metal atoms (M) intercalate into voids between graphitic layers resulting in further micropore development.27,33–36
| 6MOH + 2C ⇌ 2M + 3H2 + 2M2CO3 |
| 2M2CO3 → M2O + CO2↑ |
| M2O + C → 4M + CO2↑ |
The use of MOH increases the overall pore volume and broadens the PSD relative to that for carbons derived in the absence of a porogen.5,25,26 Thus so-called biochars are highly ultramicroporous, while MOH-activated carbons possess a higher degree of supermicroporosity (micropores of width >7 Å). As mentioned above, there are a variety of reasons that N2 may be unsuitable as a probe for these smaller pores present in biochars. Therefore, given the critical importance of being able to accurately determine textural properties with respect to any targeted applications, herein we investigate the use of combinations of N2, O2, and H2 isotherms and their effectiveness in assessing the porosity of biochars and activated carbons.
2. Experimental
2.1. Carbon synthesis
Carbons were synthesized with and without the use of a porogen, but keeping all other variables constant. In the case of carbons derived from sawdust, this was done by addition of KOH at the hydrothermal carbonization step. For carbons from sodium carboxymethyl cellulose the degree of substitution, i.e. the average number of carboxymethyl sodium groups per monomer was varied from 0.0 to 0.9.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sawdust ratio and T is the hydrothermal carbonization temperature.
sawdust ratio and T is the hydrothermal carbonization temperature.
2.2. Characterisation
CHN Elemental analysis of the raw sawdust precursor was performed using an Exeter Analytical CE-440 Elemental Analyser. O content is assumed to be the remaining percentage when C, H, and N are accounted for, as other elements do not occur in significant quantities.Thermogravimetric analysis was performed using a TA Q500 Thermogravimetric Analyser, in order to determine if any residual metals remained in the carbon samples (see Table S1, ESI†). All samples were analysed using a platinum pan and in the presence of air/argon. The parameters for all experiments were: Ramp 10 °C minute−1 from 20–1000 °C with an isotherm for 10 minutes at 1000 °C, gas flow: 60 mL minute−1.
H2, O2 and N2 isotherms were measured at −196 °C using a Micromeritics 3flex sorptometer. In the case of O2 and N2 isotherms were measured up to Po (∼220 and 1013 mbar, respectively), which is measured as each equilibrated point in the isotherm is recorded to account for small variations in temperature. However for H2 the isotherm Po is taken as a constant of 1013 mbar for convenience because H2 is supercritical at −196 °C. All samples were degassed at 300 °C for 16 h prior to isotherm measurement. Porosity calculations were performed via the dual-fitting of 2D-NLDFT heterogeneous surface kernels on either O2 and H2 or N2 and H2 isotherms using SAIEUS software.16,37 While 2D-NLDFT kernels account for surface roughness via the use of a corrugated slit-pore model,16 network connectivity is accounted for by the use of two differently sized probe molecules.15 All dual-fit calculations were performed using an overall pore width minimum of 3.00 Å, a minimum for the O2 or N2 kernel of 3.60 Å and the pore width maximum was set at 500.00 Å. For consistency the fitting parameter, λ38–40 is fixed at 4. For comparison, conventional determinations of pore volume (via t-plot) were obtained from N2 isotherms alone. Raw isotherms are available as human- and machine-readable AIF files in the SI.41
3. Results and discussion
3.1. Diffusion of adsorptives
During the measurement of isotherms, it became obvious that the duration of measurement of N2 isotherms on the SA0.0-T and NC0.0 (biochar) samples was impractical. Using the initial tE of 45 s for P/Po up to 10−3, only one or two points were achieved after >72 h. To avoid this problem, tE were iteratively reduced to 15 s for determination of N2 isotherms on SA0.0-T. Even with this modification, overall analysis time was up to 50 h; twice the time taken for a similarly determined O2 isotherm. This implies that the pore structure of biochars is such that N2 has difficulty diffusing into the smallest pores, possibly indicating that the pore width is similar to the kinetic diameter of the adsorptive. Alternatively, this may be a result of the interaction between polar moieties outside of the ultramicropores and N2's quadrupole moment. The attraction between N2 and such moieties may be competitive with N2's diffusion into ultramicropores. The less activated materials are also likely to have a higher oxygen content and thus more polar functional groups, meaning it is difficult to distinguish which of these phenomena is creating this effect. However, similarly slow diffusion of N2 has been observed for ultramicroporous CMPs with no polar groups.7 Regardless, the poor diffusion onto the biochar/less activated samples calls into question the accuracy of textural parameters derived from N2 isotherms.This discrepancy is most evident when comparing the time taken between isothermal points, t, as shown in Fig. 1a. While t is broadly similar for O2 and N2 isotherms of SA1.0-250 as well the O2 isotherm of SA0.0-250, t is much higher in the low relative pressure region for the N2 isotherm of SA0.0-250, with a single point taking up to 10 h to measure. This suggests that the slow diffusion may be related to compatibility of N2 with some feature of the biochar's porosity. Similarly, when comparing the time taken between points for the NCx samples synthesized with increasing amounts of Na within the cellulosic structure (Fig. 1b) it is apparent that expansion of the porosity by use of a porogen improves the ability of N2 to diffuse into the pores, and that this improvement is accelerated at some point between a degree of substitution of 0.7 and 0.9. That is, while NC0.7 allows faster diffusion than NC0.0, the improvement is only small but there is a far more marked change in t when x rises to 0.9. Indeed, while t can be extremely large (approaching 24 h) for NC0.0 and NC0.7, the maximum t for NC0.9 is closer (∼6 h) to that for the activated carbons derived from sawdust. Our observations of the lengthy measurement of N2 isotherms relative to O2 are counter to work recently published by Beda et al., wherein measurement of N2 isotherms on so-called hard-carbons was fast relative to O2.18
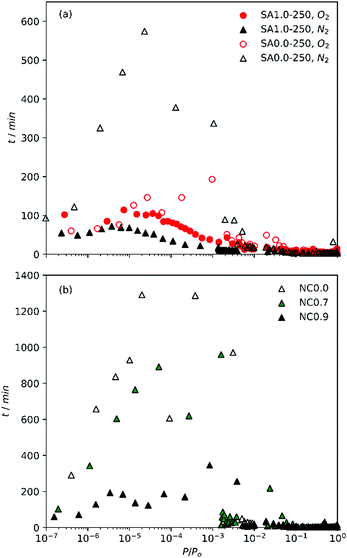 | ||
| Fig. 1 Time between points with increasing relative pressure of (a) O2 and N2 isotherms on SA1.0-250 and SA0.0-250 and (b) N2 isotherms of NCx carbons. | ||
This may be an indication of relative pore sizes i.e. that ultramicropores in biochars reported in this work are partially penetrable by N2, unlike those in hard carbons reported by Beda et al.
Table 2 shows the atomic ratios of porogen to carbon. As the principle pore development process in activated carbons begins with oxidation of carbon by the porogen, pore broadening therefore increases with increased porogen/C ratio. These ratios are much lower in the NCx samples than for SAx-T. While variables such as precursor structure and composition as well as differences in reaction kinetics of Na vs. K also play a factor,33–35 it is also clear that the higher amounts of K used in the synthesis of SAx-T samples results in porosity that is much more amenable to N2 diffusion into the pores.
| Sample | Porogen/C | Porogen/O | O/C |
|---|---|---|---|
| NC0.0 | 0.00 | 0.00 | 0.83 |
| NC0.7 | 0.09 | 0.11 | 0.86 |
| NC0.9 | 0.12 | 0.13 | 0.87 |
| SA0.0 | 0.00 | 0.00 | 0.72 |
| SA0.5 | 0.21 | 0.72 | 0.72 |
| SA1.0 | 0.43 | 1.45 | 0.72 |
Gravimetric yields of samples described in this work can be found in Table S1 (ESI†). In general, yield decreases with increasing amount of activating agent. The yield of SA0.0-300 is much higher (26%) than that of SA0.0-250 (15%). This is likely a result of greater stability of hydrochar synthesised at 300 °C on account of the lower amounts of oxygen rich-moieties.42
3.2. The isotherms
Inspection of isotherms further reveals some uncertainty in the accuracy of N2 measurements on SA0.0-T carbons (see Fig. S1, ESI†). While a characteristic plateau exists for N2 isotherms of SA0.5-T (Fig. S1(2a, b), ESI†) and SA1.0-T (Fig. S1(3a, b), ESI†) samples, indicating micropore filling, this is not the case for SA0.0-T samples (Fig. S1(1a, b), ESI†), where there is a linear increase in adsorption in the mesopore region. This is not observed in O2 isotherms, wherein monolayer completion is much more obvious. All samples also have a high H2 uptake indicating the presence of pores in the so-called ultramicropore region, which may hinder adsorption of N2.Furthermore, isotherms for NCx carbons (Fig. S2, ESI†) lend further credence to the notion that significant pore broadening does not occur until a critical ratio of porogen/C (in the range 0.09–0.12) is achieved. For both NC0.0 (Fig. S2(a), ESI†) and NC0.7 (Fig. S2(b), ESI†), the maximum H2 adsorption is similar to or greater than that of N2, indicating the presence of a high proportion of ultramicropores. For NCx samples where porogen/C ratio is increased to 0.12 (NC0.9), H2 adsorption falls significantly below the maximum for N2, indicating that porosity has broadened into the supermicropore region. Samples NC0.7 and NC0.9 also exhibit a rapid increase in adsorption for O2 and N2 as P/Po approaches 1 such that the resulting isotherms exhibit some type II character. Such shape is likely a morphological effect, either due to condensation of sorptive in macropores or large interparticle voids.1 As the materials contain no non-carbonaceous matter (within experimental error, see Table S1, ESI†) this cannot be ascribed to some chemical effect. Type II character is not observed for NC0.0, thus it can be assumed that the morphological phenomenon is a result of some action of Na+.
In the case of both NC0.0 and SA0.0-300 (Fig. S1(1b), ESI†), the H2 isotherm actually crosses the N2 isotherm which is anomalous since under the conditions used H2 is supercritical, meaning that multilayer adsorption cannot occur. As such this high level of adsorption must be due to monolayer adsorption of H2 in pores impenetrable to N2. Such pores however do appear to be penetrable by O2, which is interesting as while O2 is slightly smaller than N2 the kinetic diameters of the two molecules are quite similar – 3.46 and 3.64 Å for O2 and N2 respectively.20,21
3.3. Dual-fit analysis
Dual fits to O2/H2 and N2/H2 isotherms for SAx-T and NCx carbons are shown in Fig. S3 and S4 (ESI†), respectively. As indicated from the isotherms themselves, PSDs for SAx-T carbons (Fig. 2(1P, 2P), S5(1P, 2P), ESI†) derived using O2/H2 isotherms indicate greater porosity than when using N2/H2, and the same is true for PSDs of NCx carbons (Fig. 3(1P, 2P)). The position of the first maximum (∼4 Å) is consistent across all derived PSDs regardless of the subset of isotherms is used as this is mainly derived from the H2 isotherm. However, with regards to the second maximum, the two sets of PSDs for both SAx-T and NCx offer slightly different pictures. While N2/H2 derived PSDs show either only small differences or indeed a small decrease in pore size for the activated carbons, O2/H2 PSDs show that porosity expands out of the ultramicropore and into the supermicropore region when KOH is used as porogen. Furthermore, there is some indication of PSD broadening in the second maximum. The latter narrative fits much better with current understanding of pore formation in carbons, in that the use of alkali metal hydroxide porogens during pyrolysis leads to increases in pore size relative to those formed via gasification of biomass (i.e., pyrolysis with no added porogen). Again, this discrepancy in trends in pore size with amount of porogen according to simultaneous fitting of kernels the two isotherm pairs is likely a failing of the N2 isotherm in that ultramicropores are not adequately probed during analysis.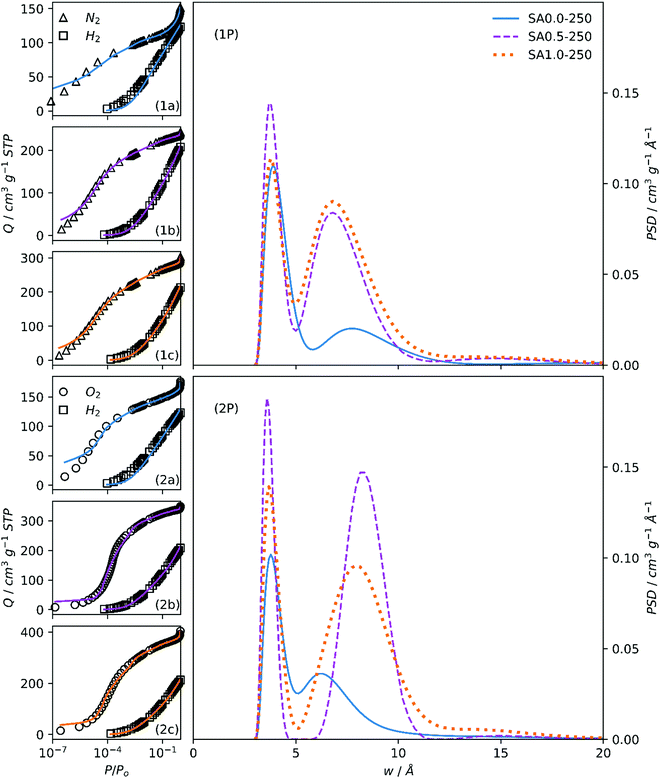 | ||
| Fig. 2 Fits to N2/H2 (1a, 1b, 1c) and O2/H2 (2a, 2b, 2c) isotherms of samples SAx-250 and resultant PSDs (1P, 2P). | ||
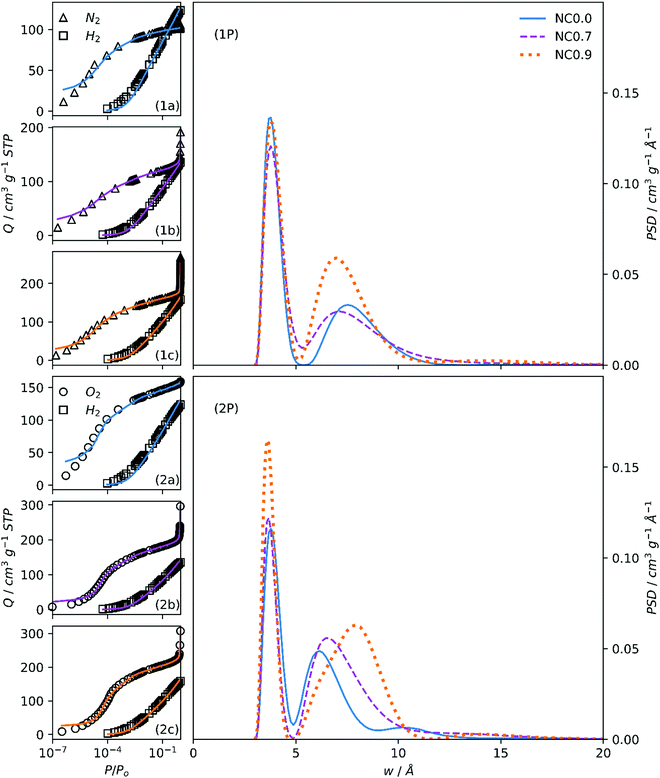 | ||
| Fig. 3 Fits to N2/H2 (1a, 1b, 1c) and O2/H2 (2a, 2b, 2c) isotherms of samples NCx and resultant PSDs (1P, 2P). | ||
While results from dual O2/H2 fitting to their respective 2D-NLDFT kernels indicate greater compliance with current understanding of porosity development in carbons, this does not alone confirm its superiority over N2/H2 for this application. On examining the fits, it is obvious that the respective 2D-NLDFT kernels struggle to account for the isotherm shape at low pressures in the case of both O2 and N2. This is particularly evident for the SA0.0-T samples, suggesting either incomplete equilibration of the system at such low pressures or inability of the O2 and N2 kernels to account for ultramicropore geometry and internal texture of in biochars, or a combination of both limitations.
O2/H2 analysis also gives far more information on differences in porosity between SA0.5-T and SA1.0-T samples. While the PSD calculated via N2/H2 indicates that the porosity of these two activated carbons is practically identical except for a slight increase in overall pore volume, O2/H2 analysis, on the other hand, shows a broadening in the second maxima, which results in the obfuscation of the two, initially distinct pore regions. A mechanistic explanation for this is that in the case of SA0.5-T, the principal route of porosity expansion comes via the formation of new pores by simple oxidation of as yet non-porous carbon, resulting in pores centred at ca. 8 Å but without significantly disturbing the ultramicropores previously formed by carbon gasification. Due to the relative increase in the quantity of K in the synthesis of SA1.0-T, the cation is able to infiltrate ultramicropores and via this intercalation expands them, resulting in the merging of the two previously distinct pore size regions.
The variation in porogen/C ratio for SAx-T carbons with increasing x is relatively large. Comparing PSDs of NCx carbons (Fig. 3(1P, 2P)) facilitates the observation of changes in porosity when the changes in porogen/C ratio are relatively small (see Table 2). Unsurprisingly, the N2/H2 calculations again show little difference between each of the three samples apart from an indication of higher overall pore volume for NC0.9.
On the other hand, there is a gradual migration of the second PSD maxima into the supermicropore region as porogen/C is increased, accompanied by a broadening of this peak. This again is a result of the oxidative effect of the (Na+) cation leading to PSD broadening. While the maximum O2 adsorption for NC0.9 and NC0.7 carbons is almost twice that of NC0.0, this is not indicated in the PSDs in the range displayed. This is because the increased porosity that causes this feature is in the macropore region.1
These inconsistencies in porosity development according to the two dual isotherm methods are further illustrated by the calculated total pore volumes, as well as the pore volume arising from micropores and ultramicropores (Table 3). Classical calculations from N2 isotherms alone reveal much smaller overall pore volumes for all samples as well as lower proportions of micropores compared to their dual-fit 2D-NLDFT counterparts for NCx and SAx-T carbons. This is because, firstly N2 alone cannot probe the smallest of ultramicropores,4,5 thus up to 32% of total pore volume (relative to N2/H2 analysis) is unaccounted for. Secondly, single point and t-plot calculations do not account for chemical and energetic heterogeneity of the internal pore surface unlike the 2D-NLDFT models.16 Additionally, determination of total- and micropore volume by classical methods is notoriously unreliable. For example, the single-point pore volume determination relies on the isotherm possessing an obvious plateau.1 As discussed above, these plateaus do not strictly exist for the N2 isotherms of the SA0.0-T samples. As such, significant errors may arise using single-point methods.
| Sample | Pore volume/cm3 g−1 | |||||||
|---|---|---|---|---|---|---|---|---|
| N2 classical | Dual N2/H2 NLDFT | Dual O2/H2 NLDFT | ||||||
| V t | V mic | V t | V mic | V umic | V t | V mic | V umic | |
| SA0.0-250 | 0.25 | 0.13 (50%) | 0.29 | 0.22 (78%) | 0.16 (54%) | 0.26 | 0.23 (90%) | 0.18 (68%) |
| SA0.0-300 | 0.17 | 0.10 (57%) | 0.25 | 0.20 (79%) | 0.14 (56%) | 0.24 | 0.22 (90%) | 0.17 (67%) |
| SA0.5-250 | 0.37 | 0.32 (87%) | 0.44 | 0.42 (97%) | 0.26 (60%) | 0.50 | 0.49 (98%) | 0.15 (30%) |
| SA0.5-300 | 0.44 | 0.38 (85%) | 0.50 | 0.47 (95%) | 0.29 (58%) | 0.53 | 0.48 (91%) | 0.21 (39%) |
| SA1.0-250 | 0.45 | 0.37 (83%) | 0.51 | 0.47 (92%) | 0.26 (52%) | 0.54 | 0.50 (92%) | 0.20 (37%) |
| SA1.0-300 | 0.54 | 0.44 (81%) | 0.63 | 0.58 (92%) | 0.32 (50%) | 0.70 | 0.63 (89%) | 0.29 (41%) |
| NC0.0 | 0.16 | 0.14 (90%) | 0.23 | 0.22 (99%) | 0.15 (65%) | 0.22 | 0.21 (95%) | 0.16 (76%) |
| NC0.7 | 0.21 | 0.16 (77%) | 0.35 | 0.25 (70%) | 0.16 (47%) | 0.38 | 0.24 (65%) | 0.14 (58%) |
| NC0.9 | 0.28 | 0.22 (80%) | 0.45 | 0.31 (69%) | 0.20 (44%) | 0.40 | 0.28 (71%) | 0.13 (44%) |
On the other hand, the dual O2/H2 fit predicts a much higher proportion of both micropores and ultramicropores than N2/H2 for SA0.0-T carbons. Again, this is likely a result of poor diffusion of N2 into ultramicropores, which limits their detection. For the so-called activated carbon samples, N2/H2 shows roughly similar proportions of ultramicroporosity compared to the aforementioned biochars, while O2/H2 shows drastic decreases. The latter picture from O2/H2 seems more likely due to known mechanisms of porosity development by KOH. Interestingly, estimates of percent microporosity are fairly consistent for calculations of both sets of isotherms for SA0.5-T and SA1.0-T samples indicating that N2 diffusion limitations are not so prevalent in supermicropores.
For NCx carbons, both overall pore volumes and absolute and percentage micropore volumes are relatively consistent across the two dual isotherm techniques. The most significant difference is in the absolute and percentage micropore volume, especially for samples NC0.0 and NC0.7. This again is an indication of the diffusion limitations encountered during measurement of N2 isotherms on these samples. While this difference in percent ultramicropore volume is 11% for these two samples, NC0.9 shows identical proportions of ultramicropores for both methods. In fact, the percentage of micropores, is the most similar here too – within 2%. While the broadening of the PSD with increasing porogen/C ratio from principally ultramicroporous into the supermicropore and larger regions is evident when using both techniques, this is far more obvious according to analysis of O2/H2 isotherms.
Interestingly, all three measures of porosity agree on one matter – that is, when comparing the relative contribution of the different pore width regions between SAx-T samples with the same KOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) SD ratio (x), but varying hydrothermal carbonization temperature (T). The hydrothermal carbonization temperature does not seem to affect what percentage of pores are made up by micropores and ultramicropores. However, total pore volumes do vary with T; in the case of the activated carbons SA0.5-T and SA1.0-T, hydrothermal carbonization at 300 °C can increase Vt by up to 30% at KOH:SD ratio 1.0 according to O2/H2 NLDFT calculations. The apparent difference decreases when classical techniques are used, and in the case of SA0.5-T, dual O2/H2 analysis shows an increase in Vt of only 6% as T increases from 250 to 300 °C. The two dual isotherm 2D-NLDFT analyses nonetheless tend to show similar differences in Vt, so perhaps this discrepancy is a result of the relative robustness of DFT methods. On the other hand, the biochars show the opposite trend, with Vt decreasing when T is raised to 300 °C. This is only by a small amount (7–14%) compared to the value derived from dual isotherm calculations, but it is evident nevertheless. This decrease in porosity of biochars with hydrothermal carbonization temperature is likely a result of a correlated decreased O/C content in the hydrochar, as well as an increase in the diameter of the characteristic microspheres.42 The latter phenomenon means that there is an increase in the proportion of stable hydrophobic aromatic moieties (in the core) relative to the more easily activated hydrophilic groups in the shell of the hydrochar microspheres. This compositional change is known to increase so-called activation resistance and therefore can result in a less porous carbon upon pyrolysis.43–45 Additionally, when KOH is included during hydrothermal carbonization it catalyses the breakdown of the activation-resistant lignin45–47 which may further explain the improvements in porosity for T = 300 °C.
SD ratio (x), but varying hydrothermal carbonization temperature (T). The hydrothermal carbonization temperature does not seem to affect what percentage of pores are made up by micropores and ultramicropores. However, total pore volumes do vary with T; in the case of the activated carbons SA0.5-T and SA1.0-T, hydrothermal carbonization at 300 °C can increase Vt by up to 30% at KOH:SD ratio 1.0 according to O2/H2 NLDFT calculations. The apparent difference decreases when classical techniques are used, and in the case of SA0.5-T, dual O2/H2 analysis shows an increase in Vt of only 6% as T increases from 250 to 300 °C. The two dual isotherm 2D-NLDFT analyses nonetheless tend to show similar differences in Vt, so perhaps this discrepancy is a result of the relative robustness of DFT methods. On the other hand, the biochars show the opposite trend, with Vt decreasing when T is raised to 300 °C. This is only by a small amount (7–14%) compared to the value derived from dual isotherm calculations, but it is evident nevertheless. This decrease in porosity of biochars with hydrothermal carbonization temperature is likely a result of a correlated decreased O/C content in the hydrochar, as well as an increase in the diameter of the characteristic microspheres.42 The latter phenomenon means that there is an increase in the proportion of stable hydrophobic aromatic moieties (in the core) relative to the more easily activated hydrophilic groups in the shell of the hydrochar microspheres. This compositional change is known to increase so-called activation resistance and therefore can result in a less porous carbon upon pyrolysis.43–45 Additionally, when KOH is included during hydrothermal carbonization it catalyses the breakdown of the activation-resistant lignin45–47 which may further explain the improvements in porosity for T = 300 °C.
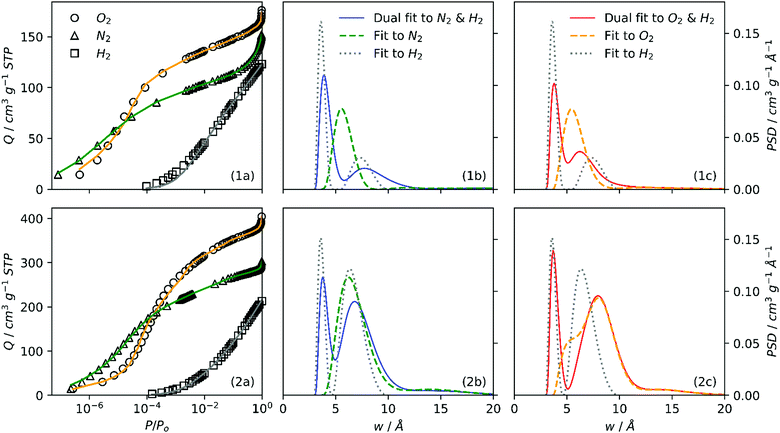
It is interesting therefore to compare PSDs derived through single and dual fits to isotherms as in Fig. 4. Further, the agreement between single and dual fits is interesting in terms of the degree to which a sample is activated, as such a low activation sample (SA0.0-250, Fig. 4(1a–c)) and highly activated sample (SA1.0-250, Fig. 4(2a–c)) were investigated. Single fit PSDs were calculated using identical parameters to those used in dual fitting, except that the maximum pore width for H2 was limited to 10 Å. Of the three individually fit adsorptives, only H2 produces a bimodal PSD similar to that found in dual fits, while N2 and O2 both show a single maximum at or above 7 Å. It appears that the position of the first maximum for H2 (∼4 Å) corresponds almost exactly in all cases to that found in dual isotherm PSDs. On the other hand, the shape and position of the second maximum (>5 Å) appears to be some combination of the two single-isotherm PSDs. This is most apparent in the case of SA0.0-250 (Fig. 4(1b, 1c)). Conversely in the case of SA1.0-250 (Fig. 4(2b, 2c)) the position and shape of the second maximum in the dual fit is approximately the same that of the sole N2 or O2 peak. These observations suggest that as PSD broadens with increasing degree of activation the fitting algorithm is able to rely more on individual isotherms for different sections of the PSD, i.e. H2 for pores 3–7 Å, N2 or O2 for pores >7Å. Whereas for so-called biochar samples, as the second maximum is lower than 7 Å
3.4. Three-way fit analysis
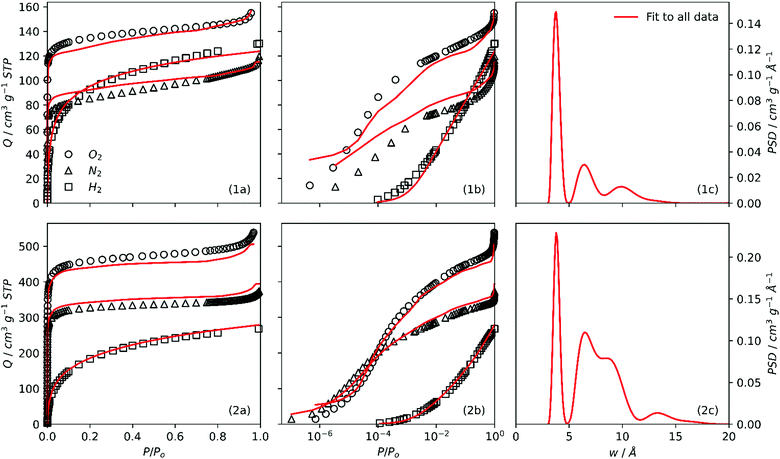
In order to further understand discrepancies between O2/H2 and N2/H2 analyses, the 2D-NLDFT heterogeneous surface kernels were simultaneously fit to all three (O2, N2, H2) isotherms for some samples. In particular, the aim here is to compare the quality of fit according to the degree of activation in each sample. The fits and PSDs achieved by this method are compared for SA0.0-300 and SA1.0-300 in Fig. 5. When the fits are examined using a logarithmic relative pressure axis (Fig. 5(1b, 2b)), it is very apparent that the fit is extremely poor for SA0.0-300, particularly in the low pressure region. While individual O2/H2 and N2/H2 analyses for SA0.0-300 had trouble with isothermal points below P/Po = 10−4 (see Fig. S3(1b, 2b), ESI†) this low quality of fit is very pronounced for the three-way fit in the entire low pressure, (i.e. micropore) region of the isotherm.On the other hand, the three-way fit for SA1.0-300 is much more satisfactory. It is also of note that for both of these samples the fit to the H2 isotherm is always good, indicating that the uncertainties are a result of disagreements between the N2 and O2 isotherms rather than H2. As for the PSDs, while peak positions for SA1.0-300 are essentially the same as those seen in either of the dual isotherm analyses (Fig. S3(1f, 2f), ESI†) the same is not apparent for SA0.0-300.
To summarise, while there is consistency between O2 and N2 fits for more highly activated samples, this is not true for less-activated, so-called biochar samples. In other words when probing ultramicropores, O2 and N2 produce different PSD results, which can be attributed to the poor diffusion of N2 into smaller pores. As porosity broadens into the supermicropore region, pores can accurately be measured by either adsorptive.
4. Conclusions
This study compares porosity in biochars and carbons activated using alkali metals as determined by two methods of dual isotherm analysis, namely using the adsorptive pairs N2/H2 and O2/H2. In particular, the reliability of using N2 in such analyses is called into question due to evident diffusion limitations in carbon samples with a low degree of activation (biochars) or where the smallest pores (ultramicropores) are prevalent. As these diffusion limitations are not present for carbons activated to a higher degree using Na+ or KOH, we conclude that the problems are associated with the size of pores found in biochars. Indeed, when using O2 (which penetrates these pores with much less difficulty) PSDs derived using the dual isotherm 2D-NLDFT method are centred at widths below 7 Å, i.e. in the ultramicropore region. Theoretically, improved ultramicropore penetration by N2 could be achieved either by allowing the system to equilibrate for longer times at low pressure, or by measuring the isotherm at a higher temperature. These modifications would however be impractical as in the first case the duration of isotherm measurements would be excessive. As for increasing temperature, this would require use of a different cryogen and/or higher pressures for ‘total’ isotherm measurement. This proves impractical on current, standard porosimetric sorptometers while the use of O2 and H2 requires the trivial task of attaching an additional cylinder to the sorptometer.Furthermore, using O2 and H2 gives a more realistic picture of porosity development with increasing degree of oxidative chemical activation as carbons are activated with an increasing amount of porogen. That is, as the ratio of porogen/C is increased we consistently observe a broadening in the PSD for samples derived both from sodium carboxymethyl cellulose and sawdust. This is in contrast to results derived using N2 and H2 wherein despite increases in overall porosity with increasing porogen/C ratio, there is little change in the widths of pores at higher levels of activation. Indeed, for some sample sets a contraction in pore width is observed as the amount of activating agent is increased. The narrative given by PSDs derived using N2 and H2 cannot be accounted for by current understanding of mechanisms of porosity development during oxidative chemical activation. The subtle effects of increasing amounts of porogen on the fine pore structure of these carbons is only detectable by the highly sensitive methods used in this work. Such sensitivity means that it is paramount to select the appropriate adsorptives for the material.
Finally, attempts at fitting the 2D-NLDFT heterogeneous surface kernels simultaneously to all three isotherms gives very poor fits to the O2 and N2 isotherms for biochars. In theory, due to the similar size of these adsorptives, fitting these two isotherms together should be facile. This lends further credence to the notion that there is in fact an inconsistency in the porosity which is probed by these two adsorptives. As these problems are not present for more highly activated samples, it is clear that above a certain pore width, O2 and N2 are equally able to probe the porosity of such carbons. In other words O2 penetrates pores in the ultramicropore region to a much greater extent.
Thus, we suggest that for carbons with a low degree of activation, N2 is an inadequate probing gas for determination of porosity as it does not adequately probe ultramicropores. When determining PSDs and other textural quantities for such carbons it is therefore advisable to look to non-traditional adsorptives such as O2. This logic should also be extended to the use of adsorptives when attempting to understand the development of porosity in carbons as the amount of activating agent is increased. Further, the understanding of porosity in non-carbonaceous ultramicroporous materials (such as CMPs) or carbonaceous materials with richer surface functionality may benefit from a similar analysis.
Author contributions
L. Scott Blankenship: conceptualisation, methodology, formal analysis, investigation, writing – original draft, visualization. Jacek Jagiello: methodology, software, validation, formal analysis, writing – review & editing. Robert Mokaya: resources, writing – review & editing, supervision, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We are thankful to the EPSRC (Low-Dimensional Materials & Interfaces DTP) for a studentship for LSB. RM thanks the Royal Society for a Royal Society Wolfson Research Merit Award.Notes and references
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CrossRef CAS.
- J. Jagiello, J. Kenvin, C. O. Ania, J. B. Parra, A. Celzard and V. Fierro, Carbon, 2020, 160, 164–175 CrossRef CAS.
- J. Jagiello and M. Thommes, Carbon, 2004, 42, 1227–1232 CrossRef CAS.
- J. Jagiello, C. Ania, J. B. Parra and C. Cook, Carbon, 2015, 91, 330–337 CrossRef CAS.
- J. Jagiello, J. Kenvin, A. Celzard and V. Fierro, Carbon, 2019, 144, 206–215 CrossRef CAS.
- F. Rodriguez-Reinoso, J. de, D. Lopez-Gonzalez and C. Berenguer, Carbon, 1982, 20, 513–518 CrossRef CAS.
- L. Qin, G.-j. Xu, C. Yao and Y.-h. Xu, Chem. Commun., 2016, 52, 12602–12605 RSC.
- J. Garrido, A. Linares-Solano, J. Martin-Martinez, M. Molina-Sabio, F. Rodriguez-Reinoso and R. Torregrosa, Langmuir, 1987, 3, 76–81 CrossRef CAS.
- A. L. McClellan and H. F. Harnsberger, J. Colloid Interface Sci., 1967, 23, 577–599 CrossRef CAS.
- A. D. Lueking, H.-Y. Kim, J. Jagiello, K. Bancroft, J. K. Johnson and M. W. Cole, J. Low Temp. Phys., 2009, 157, 410–428 CrossRef CAS.
- J. Jagiello and W. Betz, Microporous Mesoporous Mater., 2008, 108, 117–122 CrossRef CAS.
- M. Konstantakou, A. Gotzias, M. Kainourgiakis, A. K. Stubos and T. A. Steriotis, in Applications of Monte Carlo Method in Science and Engineering, ed. S. Mordechai, IntechOpen, 2011 Search PubMed.
- A. D. Buckingham, R. L. Disch and D. A. Dunmur, J. Am. Chem. Soc., 1968, 90, 3104–3107 CrossRef CAS.
- C. Nguyen and D. D. Do, J. Phys. Chem. B, 1999, 103, 6900–6908 CrossRef CAS.
- M. Lopez-Ramon, J. Jagiełło, T. Bandosz and N. Seaton, Langmuir, 1997, 13, 4435–4445 CrossRef CAS.
- J. Jagiello and J. P. Olivier, Carbon, 2013, 55, 70–80 CrossRef CAS.
- J. Guo, J. R. Morris, Y. Ihm, C. I. Contescu, N. C. Gallego, G. Duscher, S. J. Pennycook and M. F. Chisholm, Small, 2012, 8, 3283–3288 CrossRef CAS PubMed.
- A. Beda, C. Vaulot and C. M. Ghimbeu, J. Mater. Chem. A, 2021, 9, 937–943 RSC.
- M. Seredych, J. Jagiello and T. J. Bandosz, Carbon, 2014, 74, 207–217 CrossRef CAS.
- D. Lide, Handbook of Chemistry and Physics, CRC Press, 88th edn, 2017 Search PubMed.
- D. W. Breck, Zeolite molecular sieves, Wiley, New York, 1974 Search PubMed.
- B. E. Poling, J. M. Prausnitz and J. P. O’connell, Properties of gases and liquids, McGraw-Hill Education, 2001 Search PubMed.
- C. Graham, D. A. Imrie and R. E. Raab, Mol. Phys., 1998, 93, 49–56 CrossRef CAS.
- K. Weber and P. Quicker, Fuel, 2018, 217, 240–261 CrossRef CAS.
- A. Downie, A. Crosky and P. Munroe, in Biochar for Environmental Management: Science and Technology, ed. J. Lehman and S. Joseph, 2009, ch. 2, p. 14 Search PubMed.
- M. Sevilla and R. Mokaya, Energy Environ. Sci., 2014, 7, 1250–1280 RSC.
- Y. Yamashita and K. Ouchi, Carbon, 1982, 20, 41–45 CrossRef CAS.
- J. F. González, J. M. Encinar, C. M. González-García, E. Sabio, A. Ramiro, J. L. Canito and J. Gañán, Appl. Surf. Sci., 2006, 252, 5999–6004 CrossRef.
- J. Ganan, J. Gonzalez, C. Gonzalez-Garcia, A. Ramiro, E. Sabio and S. Roman, Appl. Surf. Sci., 2006, 252, 5988–5992 CrossRef CAS.
- I. Susanti and N. Widiastuti, Mal. J. Fundam. Appl. Sci., 2019, 15, 249–253 CrossRef.
- X. Fang, G. Li, J. Li, H. Jin, J. Li, V. Jegatheesan, S. Li, H. Wang and M. Yang, Desalin. Water Treat., 2017, 96, 120–127 CrossRef CAS.
- J. E. Park, G. B. Lee, S. Y. Hwang, J. H. Kim, B. U. Hong, H. Kim and S. Kim, Appl. Sci., 2018, 8, 1596 CrossRef.
- M. Lillo-Ródenas, J. Juan-Juan, D. Cazorla-Amorós and A. Linares-Solano, Carbon, 2004, 42, 1371–1375 CrossRef.
- M. Lillo-Ródenas, D. Cazorla-Amorós and A. Linares-Solano, Carbon, 2003, 41, 267–275 CrossRef.
- E. Raymundo-Pinero, P. Azaïs, T. Cacciaguerra, D. Cazorla-Amorós, A. Linares-Solano and F. Béguin, Carbon, 2005, 43, 786–795 CrossRef CAS.
- R. Xue and Z. Shen, Carbon, 2003, 41, 1862–1864 CrossRef CAS.
- J. Jagiello, Langmuir, 1994, 10, 2778–2785 CrossRef CAS.
- P. Hansen, in Computational Inverse Problems in Electrocardiology, ed. P. Johnston, WIT Press, Southampton, 2001, pp. 119–142 Search PubMed.
- P. C. Hansen and D. P. O’Leary, SIAM J. Sci. Comput., 1993, 14, 1487–1503 CrossRef.
- P. C. Hansen, SIAM Rev., 1992, 34, 561–580 CrossRef.
- J. D. Evans, V. Bon, I. Senkovska and S. Kaskel, Langmuir, 2021, 37, 4222–4226 CrossRef CAS PubMed.
- M. Sevilla and A. B. Fuertes, Chem. – Eur. J., 2009, 15, 4195–4203 CrossRef CAS PubMed.
- A. E. Ogungbenro, D. V. Quang, K. A. Al-Ali, L. F. Vega and M. R. M. Abu-Zahra, J. Environ. Chem. Eng., 2018, 6, 4245–4252 CrossRef CAS.
- A. M. Aljumialy and R. Mokaya, Mater. Adv., 2020, 1, 3267–3280 RSC.
- N. Balahmar and R. Mokaya, J. Mater. Chem. A, 2019, 7, 17466–17479 RSC.
- E. Evstigneev, Russ. J. Appl. Chem., 2011, 84, 1040–1045 CrossRef CAS.
- K. Latham, G. Jambu, S. Joseph and S. Donne, ACS Sustainable Chem. Eng., 2014, 2, 755–764 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: One table, five figures, all isotherms in human- and machine-readable.aif files. See DOI: 10.1039/d2ma00141a |
| This journal is © The Royal Society of Chemistry 2022 |