Electrocatalytic CO₂ reduction reaction on dual-metal- and nitrogen-doped graphene: coordination environment effect of active sites

Abstract

Electrochemical CO₂ reduction reaction (CO₂RR) is a promising method to convert CO₂ to CO, and developing CO₂RR electrocatalysts is essential to improve the conversion efficiency. Herein, the CO₂RR catalytic performance of dual-metal–nitrogen–carbon catalysts (M₁/M₂–N₆–Gra, Model 1, Model 2, and Model 3) with different bimetals and different coordination environments at active sites (the coordination number of metal and nitrogen ranges from 2 to 4) has been systematically studied through density functional theory (DFT). The calculated formation energies indicate that high-coordinated catalysts are thermodynamically stable. By calculating the Gibbs free energy changes of the CO₂RR pathway and the selectivity of hydrogen evolution reaction (HER), we determine that the coordination environment of the active sites of the catalysts strongly affects the activity and selectivity of CO₂ reduction to CO. The low-coordinated catalysts have strong *COOH and *CO adsorption capacity, and it is difficult for CO to desorb from the catalyst surface, resulting in the poor catalytic activity of CO₂RR; the high-coordinated catalysts have moderate *COOH and *CO adsorption capacity, and have excellent catalytic activity for reducing CO₂ to CO. In addition, the CO₂RR reduction activity of most heteronuclear M₁/M₂–N₆–Gra has been enhanced due to the synergy between heterometallic metals, and the synergy is effectively improved with the increase of the coordination number. In particular, using the limiting potential difference of CO₂RR and HER as the selective descriptor, we have screened out four catalysts, including Co/Zn, Fe/Zn, Mn/Zn, and Fe/Mn–N₆–Gra-Model 3 (the coordination number of metal and nitrogen is 4), which have favorable limiting potentials of −0.20, −0.24, −0.26, and −0.26 V, respectively. This work provides guidance for the development of effective bimetallic single-atom catalysts based on nitrogen-doped carbon materials for CO₂RR.

---

1. Introduction

Excessive emission of carbon dioxide has made the concentration of CO₂ in the atmosphere increase year by year, resulting in an increasingly serious greenhouse effect, and posing a serious threat to the ecological environment.^1–5 Converting excess CO₂ into high value-added chemicals is an effective strategy to achieve carbon neutrality and alleviate energy shortages. In recent years, the electrochemical reduction of CO₂ has gradually become a research hotspot for its controllable reaction and simple operation.^6–8 The process of electrochemical CO₂ reduction reaction (CO₂RR) involves the transition of multiple proton/electron pairs and can generate various products, such as CO, CH₄, CH₃OH, C₂H₄, C₂H₅OH, etc. Among them, the reduction of CO₂ to CO only involves two proton/electron pairs transfer (CO₂ + 2H⁺ + 2e⁻ → CO + H₂O), and greatly reduces the hindered process.^8–10

Generally, an ideal catalyst for reducing CO₂ to CO should have the following characteristics: (1) Good CO₂ adsorption activity. The strong chemical inertness of linear CO₂ molecule makes it difficult to activate the C = O bond, and efficient CO₂RR catalysts should effectively activate CO₂. (2) Weak CO binding energy. The weak CO adsorption will make it easier for CO to desorb from the catalyst surface and avoid further hydrogenation. (3) Effectively inhibit the competitive HER. High HER activity leads to low Faraday efficiency of CO₂RR.

According to previous studies, transition metals (e.g., Cu, Au, Ag, etc.) are the most widely used electrocatalysts for the reduction of CO₂ to CO,^11–15 nevertheless, they usually suffer from high overpotential, poor selectivity, and high cost.^16,17 Recently, single-atom catalysts (SAC) have attracted attention due to their high atom utilization and excellent catalytic performance.^2,10,18–21 Studies have shown that the dual-metal–nitrogen–carbon materials exhibit high catalytic activity in CO₂RR due to the synergistic effect of the bimetallic centers.^22–26 Ren et al.²² prepared a Ni/Fe–N–C catalyst with isolated diatomic Ni–Fe sites. The Faraday efficiency of CO (FE_CO) of the catalyst was 98%, which was higher than Ni–N–C and Fe–N–C. Guo et al.²⁵ also synthesized a Cu–Co bimetallic nanoparticle that was well-dispersed on porous carbon, which could reduce CO₂ to CO with high selectivity, and the FE_CO could reach 97.4%. However, so far, although bimetallic catalysts for the reduction of CO₂ to CO have been developed, their research is still in a preliminary exploration stage, finding a proper and promising catalyst to improve the activity and selectivity of CO₂RR remains a challenge.

The coordination environment of the active sites of the catalysts also has an important impact on the catalytic activity and selectivity of CO₂RR. For example, the catalytic performance of Co–N–C is affected by the coordination of Co atoms. Wang et al.²⁰ synthesized a series of Co–N_x (x = 2–4) single-atom catalysts with different N coordination numbers. The results showed that the Co–N₂ site with a lower N coordination number exhibited significant activity and selectivity for the reduction of CO₂ to CO. Pan et al.²¹ reported that the atomically dispersed Co–N₅ site could also efficiently catalyze CO₂RR with high CO Faraday efficiency (≈ 94%) and high stability. In addition, a previous study has also shown that FeCo bimetallic catalyst anchored with OH–ligand displayed unique geometric and electronic structure, and exhibited unparalleled ORR activity at the FeCoN₅–OH active site.²⁷ These works indicate that moderate regulation of the coordination environment around the active site is essential to enhance the performance of CO₂RR. Therefore, it is of great significance to investigate the effect of the coordination environment of the bimetallic active sites on the catalytic activity for the rational design of high-efficiency CO₂RR electrocatalysts.

In this work, we design a series of bimetallic single-atom catalysts embedded in N-doped graphene (M₁/M₂–N₆–Gra) by adjusting the bimetal (M = Mn–Zn) and coordination environment (the coordination number of metal and nitrogen ranges from 2 to 4) of the active sites of the catalysts, and study the CO₂RR mechanism by density functional theory (DFT). It is found that the coordination environment affects the stability of the catalysts and the catalytic performance of CO₂RR. Compared with low-coordinated catalysts, high-coordinated catalysts have more negative formation energies and are more thermodynamically stable. The research on the reduction mechanism shows that the high-coordinated catalysts have moderate *COOH and *CO adsorption capacity, resulting in excellent catalytic activity for reducing CO₂ to CO. Finally, the electrocatalysts Co/Zn, Fe/Zn, Mn/Zn, and Fe/Mn–N₆–Gra-Model 3 with high activity and selectivity for CO production are screened out, and their limiting potentials are as low as −0.20, −0.24, −0.26, and −0.26 V. This work systematically presents the theoretical stability, activity, and selectivity of M₁/M₂–N₆–Gra in three kinds of coordination environments, which inspires useful guidance for the further development of new low-cost and high-activity CO₂RR electrocatalysts.

2. Computational methods and models

All the spin-polarized calculations were carried out by the Vienna Ab initio Simulation Package (VASP 5.4.4) software package.^28–30 The GGA–PBE exchange–correlation functional was used to describe the electronic interactions.³¹ In the structural optimization, a 3 × 3 × 1 Monkhorst–Pack grid³² was used to sample the Brillouin zone, and a 12 × 12 × 1 denser k-point grid was used in the electronic structure calculations. The cutoff energy was set as 400 eV, and the energy and force convergence criteria of the self-consistent iteration were set to 10⁻⁵ eV and 0.02 eV Å⁻¹, respectively. DFT-D3 method was used to describe van der Waals (vdW) interactions.³³

To model M₁/M₂–N₆–Gra, we constructed monolayer graphene with a 4 × 3 supercell, and added a 15 Å vacuum space to reduce the interactions between adjacent layers. By removing four or six carbon atoms to create vacancies, introducing and replacing 6 N atoms around the carbon vacancies, and introducing M₁ and M₂ metal atoms in the center, M₁/M₂–N₆–Gra structures with three different coordination environments were obtained. In addition, the corresponding single metal–nitrogen–carbon (M–N₄–Gra) material models were established, in which one metal atom replaces two adjacent carbon atoms, and the four carbon atoms directly connected to the metal atom are replaced by nitrogen atoms.

The process of reducing CO₂ to CO undergoes two electron transfers, including the following three steps (1)–(3):

Step 1: CO₂ + * + H⁺ + e⁻ → *COOH (ΔG₁) (1)

Step 2: *COOH + H⁺ + e⁻ → *CO + H₂O (ΔG₂) (2)

Step 3: *CO → CO(g) + * (ΔG₃) (3)

where * refers to the adsorption site on the M₁/M₂–N₆–Gra.

The formation energies (E_f) of the M₁/M₂–N₆–Gra systems are calculated by

E_f = E_{M1/M2–N6–Gra} – E_N6–Gra – E_M1 – E_M2 (4)

where E_{M1/M2–N6–Gra} and E_N6–Gra are the total energies of M₁/M₂–N₆–Gra and substrate, respectively. E_M1 and E_M2 are the energies of the single atoms of M₁ and M₂ in the bulk phase.

The adsorption energies (E_a) of the reactive intermediates are calculated by

E_a = E_*C – E_{M1/M2–N6–Gra} – E_C (5)

where E_C and E_*C represent the energies before and after the adsorption of C species on the M₁/M₂–N₆–Gra catalyst, respectively.

The Gibbs free energy changes (ΔG) of the reaction are calculated by the computational hydrogen electrode model (CHE) proposed by Nørskov et al.:³⁴

ΔG = ΔE + ΔZPE – TΔS + ΔG_U + ΔG_pH (6)

where ΔE is the difference of electron energies calculated by DFT; ΔZPE and ΔS are the changes of zero-point energy and entropy, respectively, which are obtained from vibrational frequencies. T is the temperature (298.15 K in this work). ΔG_U = −eU, where U is the applied electrode potential. ΔG_pH = k_BT × ln 10 × pH, where k_B is the Boltzmann constant, and pH value is set to 0. The entropy of gas molecules is taken from the NIST database.

The adsorption free energies (ΔG_*C) of the reaction intermediates (*CO, *COOH) on M₁/M₂–N₆–Gra are calculated as

ΔG_*C = ΔE_a + ΔZPE – TΔS (7)

where ΔE_a represents the adsorption energy of C species (*CO, *COOH) on M₁/M₂–N₆–Gra.

The limiting potentials (U_L) of CO₂RR are defined as

U_L = −ΔG_max/e = −max{ΔG₁, ΔG₂, ΔG₃}/e (8)

where ΔG₁, ΔG₂, and ΔG₃ are the free energy changes of reaction steps (1)–(3).

Additionally, in order to examine the influence of the supercell size of graphene, the Ni/Fe–N₆–Gra models with adsorbed *COOH and *CO: (1) 4 × 3; (2) 5 × 3; (3) 6 × 4, were optimized. The optimized configurations and adsorption energies were shown in Fig. S1(ESI†), and we found that the adsorption energies of *COOH or *CO on the three supercells were relatively close. Therefore, in order to rationally utilize the computational resources, the 4 × 3 supercell models were employed in this work.

For solvation correction, starting from the random H₂O configuration, we used the Forcite module of Materials Studio 8.0 software³⁵ to run 2 nanoseconds of molecular dynamics (MD) simulations and then used VASP 5.4.4 to run 10.5 pic-second of ab initio molecular dynamics (AIMD) simulations at 298.15 K to obtain the water/catalyst equilibrium interface (Fig. S2, ESI†). In the AIMD simulations, we used the Nose–Hoover thermostat³⁶ to maintain the temperature and sampled the Brillouin zone with a cutoff energy of 300 eV³⁷ and a 3 × 3 × 1 k-point grid. The time step was set to 1.5 fs. After that, we used DFT calculations to get the adsorption energies of the intermediates in the aqueous solution, and further calculated the solvation correction values.

3. Results and discussion

3.1 Structure and Stability of M₁/M₂–N₆–Gra

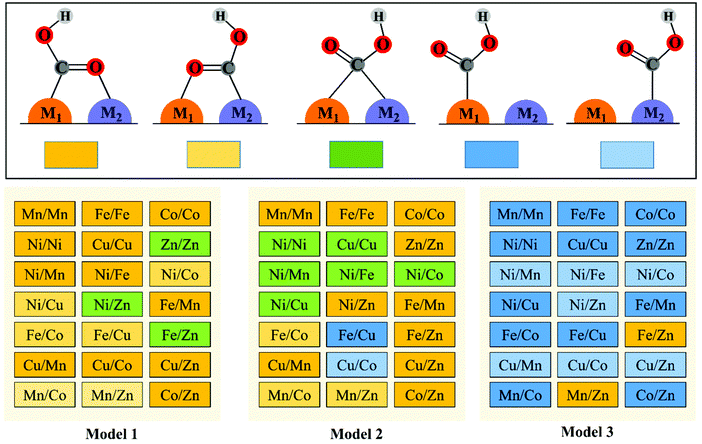
To explore the effect of the coordination environment around the active sites on CO₂RR properties, three types of M₁/M₂–N₆–Gra structures are constructed (Fig. 1(a)): the metal is bonded with two N atoms (Model 1), three N atoms (Model 2), and four N atoms (Model 3), respectively. The optimized substrate structures are given in Fig. S3 (ESI†).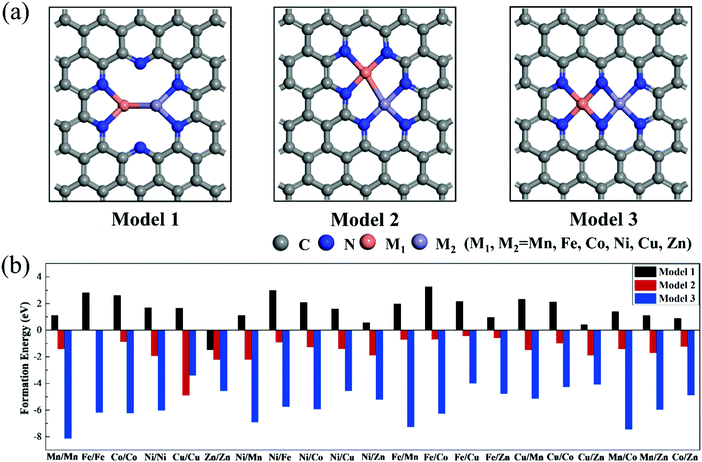

Fig. 1 (a) Geometric structures and (b) formation energies of M₁/M₂–N₆–Gra (M₁/M₂ = Mn−Zn). The gray, blue, orange, and purple atoms represent carbon, nitrogen, M₁, and M₂, respectively.

To evaluate the stability, the formation energies of M₁/M₂–N₆–Gra are calculated by eqn (4), and the calculation results are shown in Fig. 1(b) and Table S1 (ESI†). According to previous studies, the catalysts with E_f < 0 eV are considered to be thermodynamically stable.^38,39 Interestingly, from Fig. 1(b), we find that the E_f values of the three models of M₁/M₂–N₆–Gra are quite different. For Model 1, except Zn/Zn–N₆–Gra has negative formation energy, all the other catalysts have positive formation energies, which may be ascribed to the fact that the relatively more valence electron and lower energy of Zn atom than other transition metal atoms we calculated,⁴⁰ and can be more easily introduced into carbon vacancies. All the formation energies of Model 2 and Model 3 are negative. From the viewpoint of energy value, Model 3 have more negative formation energies than Model 2, indicating that Model 3 are more thermodynamically stable. This is probably due to the different coordination environments around the metals of the active sites in Model 2 and Model 3, leading to different sizes of pores surrounded by edge N atoms (Fig. S4, ESI†). The pore in Model 3 is relatively large, and the distance between the embedded two metal atoms is about 2.469 Å (half of the pore size), while that in Model 2 is about 2.029 Å (one-third of the pore size). The large pore size is more conducive to metal insertion. Additionally, the metal atoms in Model 1, Model 2, and Model 3 are coordinated with 2, 3, and 4 N atoms, respectively. The stability of the catalysts can be improved with the increase of the coordination number of metal atoms and N atoms, which is consistent with the results of previous studies.⁴¹ In general, from the perspective of thermodynamics, most M₁/M₂–N₆–Gra catalysts can be easily synthesized through experiments.

3.2 Electrocatalytic activity for CO₂RR of M₁/M₂–N₆–Gra

The reduction of CO₂ to CO process contains three steps (1)–(3) with two electron transfers. The activation of CO₂ to *COOH on the catalysts is the first step of the reaction, and *COOH is the main intermediate in the CO₂RR process. Therefore, we first study the adsorption configurations of *COOH on M₁/M₂–N₆–Gra (Model 1–Model 3), and the most stable adsorption configurations are displayed in Fig. 2 and Fig. S5–S7 (ESI†).

Fig. 2 The adsorption configurations of *COOH on M₁/M₂–N₆–Gra.

Three main adsorption configurations of *COOH on M₁/M₂–N₆–Gra are considered (Fig. 2): (a) the C and O atoms of *COOH are respectively attached to two adjacent metal atoms, that is, the two metal atoms are *C binding site and *O binding site, respectively; (b) the C atom of *COOH is attached to two metal atoms at the same time, that is, *COOH is adsorbed on the bridge site between the two metals; (c) the C atom of *COOH is only attached to one of the metal atoms, that is, *COOH is adsorbed on the metal top site.

Our calculation results demonstrate that the intermediate *COOH on Model 1 are mainly adsorbed on M₁/M₂–N₆–Gra substrate through the first type of bridge adsorption pattern. In Model 2, the most stable adsorption configurations of the intermediate *COOH on M₁/M₂–N₆–Gra substrate, all three adsorption patterns exist. In Model 3, *COOH are mainly adsorbed on the metal top site of M₁/M₂–N₆–Gra (Fig. 2). The most stable adsorption configurations of *COOH on the three models are obviously different, which is probably attributed to the combined effects of the size of carbon vacancy, the properties of bimetal, the affinity of metals to C and O, the difference in the coordination number of metal and nitrogen at the active site and the significant differences in the bond lengths between bimetals (Table S2, ESI†) caused by the difference in the atomic radius of the bimetallic atoms and many other factors. For example, for Ni/Zn–N₆–Gra, the bond lengths between bimetals on Model 1 and Model 2 are 2.294 and 2.425 Å, respectively, and the bond length of metal—C is smaller than that of metal—O bond. The *COOH of Model 1 is adsorbed on the bimetallic bridge site due to the closer bimetallic distance, and C bonds with Ni and Zn atoms. While the longer bimetallic distance of Model 2 causes the C atom of *COOH bonds with Ni atom and O atom bonds with Zn atom. For Zn/Zn–N₆–Gra-Model 1 and Mn/Zn–N₆–Gra-Model 1, *COOH is adsorbed on the bimetallic bridge site of Zn/Zn catalyst due to the lower oxophilicity of Zn atom, while the higher O-affinity on Mn atom, *COOH is adsorbed on the Mn/Zn catalyst surface in the first type of bridge adsorption pattern, O is bonded to Mn atom, and C is bonded to Zn atom.

Furthermore, on the M–N–C catalysts, *COOH can also exhibit the trans-COOH (H-down) adsorption configuration in addition to the cis-COOH (H-up) configuration.^42,43 Thus, we examine the adsorption configurations and adsorption energies of trans-COOH (H-down) on Ni/Fe–N₆–Gra and Fe/Zn–N₆–Gra. The calculation results are shown in Fig. S8 (ESI†), and the adsorption energies of cis-COOH (H-up) are more negative than that of trans-COOH (H-down). Therefore, the cis-COOH (H-up) adsorption configurations are used for all 63 bimetallic catalysts.

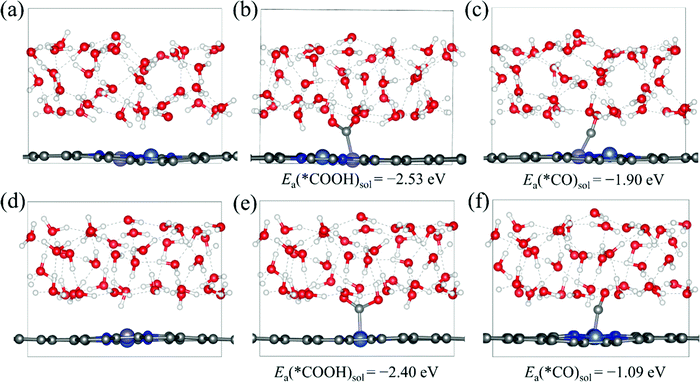
Then, we explore the electrocatalytic performance of all the homonuclear and heteronuclear M₁/M₂–N₆–Gra (Model 1–Model 3) catalysts for CO₂RR. To determine the contribution of the solvation effect to the free energies of the electrochemical CO₂ reduction reaction, we perform solvation corrections for the adsorption energies of the reaction intermediates (*COOH and *CO) calculated in vacuum. Here, we simulate the explicit aqueous-phase environment and put 37 H₂O molecules on the surfaces of Ni/Fe–N₆–Gra (Model 2 and Model 3, 10 Å vacuum layer), and estimate the magnitude of solvation based on the differences between the adsorption energies with and without water.⁴⁴Fig. 3 shows the water layer models on the surfaces of NiFe–N₆–Gra-Model 2 and Model 3, as well as the configurations and adsorption energies of *COOH and *CO in the aqueous solution. In Ni/Fe–N₆–Gra-Model 2, the calculated free energy correction values of *COOH and *CO is −0.27 eV and −0.09 eV, respectively. In Ni/Fe–N₆–Gra-Model 3, the values are −0.26 eV and −0.13 eV, respectively. In agreement with previous estimations of −0.25 eV and −0.10 eV.⁴⁵ For consistency and convenience of comparison, the average free energy correction values of *COOH and *CO on Model 2 and Model 3 are added to all 63 M₁/M₂–N₆–Gra for solvent corrections. The free energy correction values on Model 1 are not calculated because the calculation results indicate that the Model 1 catalysts have poor CO₂RR activity and high limiting potentials (See subsequent Fig. 4 and Table 1 for details). Therefore, we finally correct the adsorption energies of *COOH by −0.27 eV and *CO by −0.11 eV.

Fig. 3 The explicit solvent models of the NiFe–N₆–Gra (a) Model 2 and (d) Model 3 surface, *COOH and *CO configurations and adsorption energies at (b) and (c) water/Model 2 interface and (e) and (f) water/Model 3 interface.

Fig. 4 (a)–(g) Relative free energy profiles of CO₂RR (for CO pathway) on Model 1, Model 2, and Model 3 at 0 V vs. RHE. (h) Summary of the maximum free energy change values (ΔG_max) for CO production on M₁/M₂–N₆–Gra.

Table 1 The computational limiting potentials and elementary reaction steps with ΔG_max for CO production on M₁/M₂–N₆–Gra at 0 V vs. RHE

M1/M2–N6–Gra	Model 1		Model 2		Model 3
	U L (V)	Elementary steps	U L (V)	Elementary steps	U L (V)	Elementary steps
Mn/Mn	−1.32	*CO → CO	−1.45	*CO → CO	−0.32	*COOH → *CO
Fe/Fe	−1.50	*CO → CO	−1.22	*CO → CO	−0.48	CO2 → *COOH
Co/Co	−1.82	*CO → CO	−1.35	*CO → CO	−0.89	CO2 → *COOH
Ni/Ni	−1.65	*CO → CO	−0.62	CO2 → *COOH	−1.47	CO2 → *COOH
Cu/Cu	−1.43	*CO → CO	−1.09	CO2 → *COOH	−1.83	CO2 → *COOH
Zn/Zn	−0.81	CO2 → *COOH	−1.08	*COOH → *CO	−1.01	CO2 → *COOH
Ni/Mn	−1.56	*CO → CO	−0.39	*CO → CO	−0.31	CO2 → *COOH
Ni/Fe	−2.35	*CO → CO	−0.87	*CO → CO	−0.39	CO2 → *COOH
Ni/Co	−1.73	*CO → CO	−1.02	*CO → CO	−0.54	CO2 → *COOH
Ni/Cu	−1.46	*CO → CO	−0.73	CO2 → *COOH	−1.49	CO2 → *COOH
Ni/Zn	−1.73	*CO → CO	−0.59	*CO → CO	−1.06	CO2 → *COOH
Fe/Mn	−1.62	*CO → CO	−1.46	*CO → CO	−0.26	CO2 → *COOH
Fe/Co	−2.32	*CO → CO	−0.94	*CO → CO	−0.42	CO2 → *COOH
Fe/Cu	−1.47	*CO → CO	−0.80	*CO → CO	−0.25	*CO → CO
Fe/Zn	−1.35	*CO → CO	−1.34	*CO → CO	−0.24	*CO → CO
Cu/Mn	−2.50	*CO → CO	−0.51	*CO → CO	−0.27	*CO → CO
Cu/Co	−1.67	*CO → CO	−0.64	*CO → CO	−0.42	CO2 → *COOH
Cu/Zn	−0.65	*CO → CO	−0.40	CO2 → *COOH	−0.86	CO2 → *COOH
Mn/Co	−1.74	*CO → CO	−1.22	*CO → CO	−0.34	CO2 → *COOH
Mn/Zn	−1.99	*CO → CO	−1.08	*CO → CO	−0.26	*CO → CO
Co/Zn	−1.67	*CO → CO	−1.20	*CO → CO	−0.20	CO2 → *COOH

---

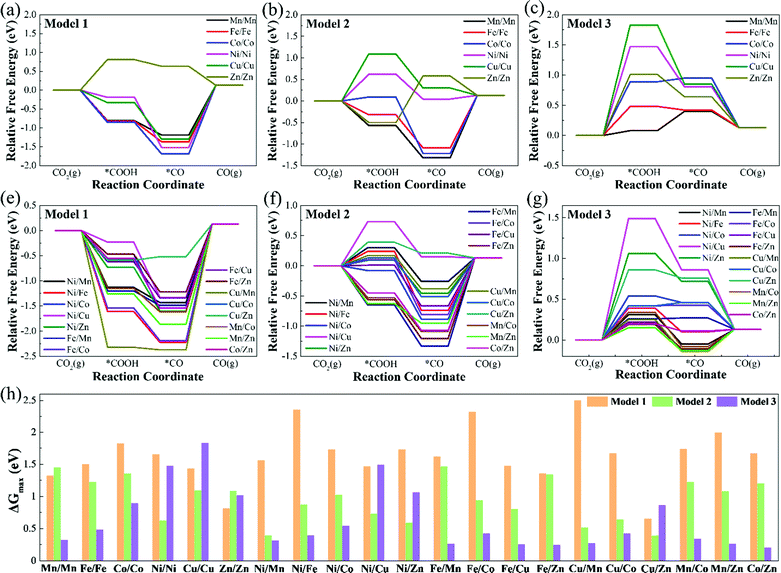
Table S3 (ESI†) lists the Gibbs free energy changes (ΔG) of each elementary reaction step of the CO₂RR. Fig. 4 displays the free energy diagrams and the maximum free energy change values (ΔG_max) of CO₂RR at 0 V. As can be seen from Fig. 4(a)–(g), for Model 1, except for Zn/Zn–N₆–Gra, the potential limiting step (PLS) of CO₂RR is CO₂ + H⁺ + e⁻ → *COOH, and the other catalysts are all *CO → CO + *. For Model 2, the potential limiting steps of most catalysts are *CO → CO + *, except for Ni/Ni, Cu/Cu, Ni/Cu, and Cu/Zn–N₆–Gra, which are CO₂ + H⁺ + e⁻ → *COOH, and Zn/Zn–N₆–Gra is *COOH + H⁺ + e⁻ → *CO + H₂O. But for Model 3, the potential limiting steps of most catalysts are CO₂ + H⁺ + e⁻ → *COOH, except for Fe/Cu, Fe/Zn, Cu/Mn, Mn/Zn–N₆–Gra, which are *CO → CO + *, and Mn/Mn–N₆–Gra is *COOH + H⁺ + e⁻ → *CO + H₂O. This is caused by the significantly different adsorption strength of *COOH and *CO on Model 1, Model 2, and Model 3.

Fig. 4(h) summarizes the maximum free energy change values (ΔG_max) on M₁/M₂–N₆–Gra along with the CO₂ reduction to CO. The larger the ΔG_max value, the more heat the reaction absorbs, and the worse the CO₂ reduction activity. For most M₁/M₂–N₆–Gra (except Mn/Mn, Ni/Ni, Cu/Cu, Zn/Zn, Ni/Cu, Ni/Zn, and Cu/Zn–N₆–Gra), as the coordination number of metal and nitrogen increases from 2 to 4 (Model 1–Model 3), the ΔG_max values greatly decrease and the CO₂ reduction activity increases. For Ni/Ni, Cu/Cu, Ni/Cu, Ni/Zn, and Cu/Zn–N₆–Gra, as the coordination number of metal and nitrogen increases from 2 to 4, the ΔG_max values show a trend of the first decrease and then increase, and the CO₂ reduction activity first increases and then decreases. However, for Zn/Zn–N₆–Gra, as the coordination number of metal and nitrogen increases, the ΔG_max values increase and the reduction activity decreases. And the ΔG_max values for the three models of Zn/Zn–N₆–Gra are 0.81, 1.08, 1.01 eV, respectively, Zn/Zn–N₆–Gra-Model 1 has the best reduction activity. Overall, we identify that Cu/Zn–N₆–Gra-Model 1, Ni/Mn–N₆–Gra-Model 2, and Co/Zn–N₆–Gra-Model 3 have the best CO₂ reduction activity on Model 1, Model 2, and Model 3 with ΔG_max values of 0.65, 0.39, and 0.20 eV, respectively. Particularly, among all the bimetallic catalysts we calculated, Co/Zn–N₆–Gra-Model 3 exhibits the highest CO₂ reduction activity.

Theoretically, the catalytic activity of the electrocatalysts is usually evaluated by the limiting potential (U_L).³⁸Table 1 lists the theoretical limiting potential values for 21 M₁/M₂–N₆–Gra on the three models and the corresponding elementary reaction steps. In general, The CO₂RR catalytic activity of Model 3 is obviously better than that of Model 1 and Model 2. Notably, most of the catalysts of Model 3 exhibit excellent activity for the reduction of CO₂ to CO, and with low U_L values of −0.20 – −0.54 V. Compared with Mn–N₄–Gra (the calculated best catalytic activity and selectivity in M–N₄–Gra, U_L = −0.36 V, Fig. S9, ESI†), Mn/Mn, Ni/Mn, Fe/Mn, Fe/Cu, Fe/Zn, Cu/Mn, Mn/Co, Mn/Zn, and Co/Zn–N₆–Gra-Model 3 have better catalytic activity. Especially, three systems, including Fe/Cu, Fe/Zn, and Co/Zn–N₆–Gra-Model 3, the U_L values of CO production are only −0.25, −0.24, and −0.20 eV, respectively.

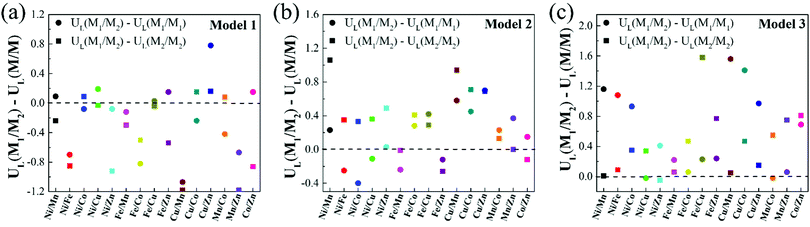
It is noteworthy that, compared with homonuclear M₁/M₁–N₆–Gra and M₂/M₂–N₆–Gra, most heteronuclear M₁/M₂–N₆–Gra have higher CO₂RR catalytic activity than at least one of the homonuclear catalysts due to the synergistic effect of bimetals (Table 1). Fig. 5 demonstrates the limiting potential difference between 15 heteronuclear M₁/M₂–N₆–Gra and their corresponding homonuclear M₁/M₁–N₆–Gra, M₂/M₂–N₆–Gra (U_L(M₁/M₂) − U_L(M/M)) on Model 1, Model 2, and Model 3. The positive (U_L(M₁/M₂) − U_L(M/M)) values correspond to the high CO₂RR activity of heteronuclear catalysts. With the increase of coordination number between metal and nitrogen (Model 1–Model 3), the catalytic activity of heteronuclear catalysts is significantly improved, which is reflected in that (U_L(M₁/M₂) − U_L(M/M)) values of more heteronuclear catalysts are greater than zero and the values are more positive. For Model 1, only Cu/Zn has higher CO₂RR activity than Cu/Cu and Zn/Zn. For Model 2, the CO₂RR activity of most heteronuclear catalysts is higher than that of homonuclear catalysts. For Model 3, except for Ni/Cu, Ni/Zn, Mn/Co, the CO₂RR activity is only higher than one of the homonuclear catalysts, and the catalytic activities of the other heteronuclear catalysts are higher than those of the two homonuclear catalysts. Overall, the increase of coordination number between metal and nitrogen effectively promotes the synergistic effect of heteronuclear bimetals, which may be due to the different adsorption energies and adsorption configurations of *COOH and *CO on the three models. The adsorption energies of *COOH and *CO of Model 1 catalysts are relatively large (Table S4, ESI†), and most of the limiting steps are CO desorption (Table 1). *COOH are mainly adsorbed on the bimetallic bridge site with C and O as binding sites, *CO are mainly adsorbed on the bimetallic bridge site (Fig. S5, ESI†). The synergistic effect of bimetals makes some heteronuclear catalysts have larger adsorption energies of *COOH and *CO (Ni/Fe, Ni/Zn, Fe/Mn, Fe/Co, Cu/Mn, Mn/Zn–N₆–Gra-Model 1), while the *CO adsorption energies of some catalysts are weakened, but CO is still difficult to desorb. For Cu/Zn, the synergistic effect of Cu and Zn atoms makes the adsorption energy of *COOH greater than Zn/Zn and Cu/Cu, while the adsorption energy of *CO is weaker than Cu/Cu (the limiting step of Cu/Cu is CO desorption, and Zn/Zn is CO₂ activation), CO₂ can be easily activated to *COOH, and *CO is also easier to desorb. The adsorption energies of *COOH and *CO of Model 3 are relatively small, *COOH and *CO are mainly adsorbed on the metal top site. The synergistic effect of bimetals makes the heteronuclear catalysts have moderate *COOH and *CO adsorption energies, and CO₂ activation and CO desorption are easier. The *COOH and *CO adsorption energies of Model 2 are between Model 1 and Model 3, the adsorption configurations of bridge site and metal top site are all existed, and the synergistic effect of bimetals are also between Model 1 and Model 3.

Fig. 5 (a)–(c) The limiting potential difference between heteronuclear M₁/M₂–N₆–Gra and homonuclear M/M–N₆–Gra (M₁/M₁–N₆–Gra, M₂/M₂–N₆–gra) for Model 1, Model 2 and Model 3. (U_L(M₁/M₂) − U_L(M/M)) > 0 means that the catalytic activity of heteronuclear M₁/M₂–N₆–Gra catalysts are higher than the homonuclear M/M–N₆–Gra.

3.3 Scaling relationship and volcano curve

Investigating the relationship between the adsorption free energies of reaction intermediates and catalytic activity is of great significance for searching for more effective catalysts. For the process of CO₂ reduction to CO, *COOH and *CO are the most important reaction intermediates for CO₂ activation and CO production. Therefore, in this study, we calculate the adsorption free energies of *COOH and *CO (Table S5, ESI†), and investigate the relationship between the Gibbs adsorption free energies of *COOH and *CO.

Fig. 6(a) shows there is a roughly linear scaling relationship between ΔG_*COOH and ΔG_*CO, and the fitting coefficient (R²) is 0.80. Our result is in line with previous research conclusions.⁴⁶ In addition, we find that most catalysts in Model 1 are located in the bottom left region of Fig. 6(a), with strong *COOH and *CO adsorption strength; and the catalysts in Model 2 are located in the middle-upper region with moderate *COOH and *CO adsorption strength; while the catalysts in Model 3 are located in the upper right region with moderate and weak *COOH and *CO adsorption strength. The larger the *COOH adsorption free energy, the smaller the free energy change value required for CO₂ activation. The greater the *CO adsorption free energy, the harder the CO desorption. These results are consistent with the previous conclusion that we calculated that the catalytic activity of CO₂RR in Model 3 is significantly better than that in Model 1 and Model 2.

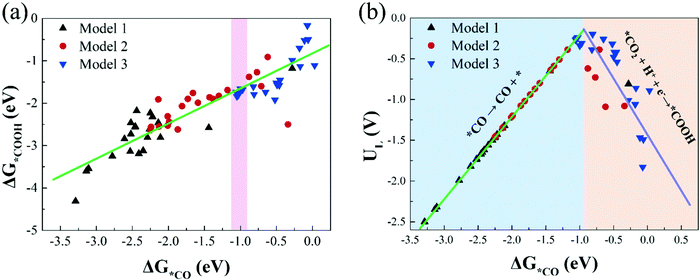Fig. 6 (a) The scaling relations of the adsorption free energies of *COOH (ΔG_*COOH) and *CO (ΔG_*CO), (b) the volcano plot between the limiting potentials (U_L) and ΔG_*CO.

Moreover, based on the scaling relationship, we construct the volcano plot between U_L and ΔG_*CO of CO₂RR on all M₁/M₂–N₆–Gra catalysts, as displayed in Fig. 6(b). The left side of Fig. 6(b) exhibits strong *CO adsorption, the larger adsorption free energy of CO molecule makes it difficult to desorb, and the potential limiting step is *CO → CO + *; while the right side of Fig. 6(b) exhibits weak *CO adsorption, the smaller adsorption free energy of CO is more conducive to its desorption from the catalyst surface, but too weak CO binding will hinder the formation of *COOH, changing the PLS to CO₂ + H⁺ + e⁻ → *COOH, and limiting the reaction activity. Notably, catalysts located near the top of the volcano have moderate adsorption strengths of *CO and *COOH, and exhibit favorable CO₂RR catalytic activity.

3.4 Competition between CO₂RR and HER

In addition to having high activity, an ideal CO₂RR catalyst should also be able to effectively inhibit the competitive side reaction—hydrogen evolution reaction (HER),^47,48 which could greatly affect the Faraday efficiency of CO production. Thus, we further study the HER catalytic activity of 21 catalysts on Model 2 and Model 3, and the results are shown in Fig. 7(a) and (c). With regard to Model 1, the previous calculation results have shown that catalysts on Model 1 have poor CO₂RR activity, and the limiting potentials of most catalysts are above −1.00 eV (Table 1). The optimal Cu/Zn–N₆–Gra-Model 1 catalyst has a limiting potential of −0.65 eV, which is significantly lower than Mn–N₄–Gra (U_L = −0.36 V). Therefore, we do not consider the calculation of HER performance on Model 1.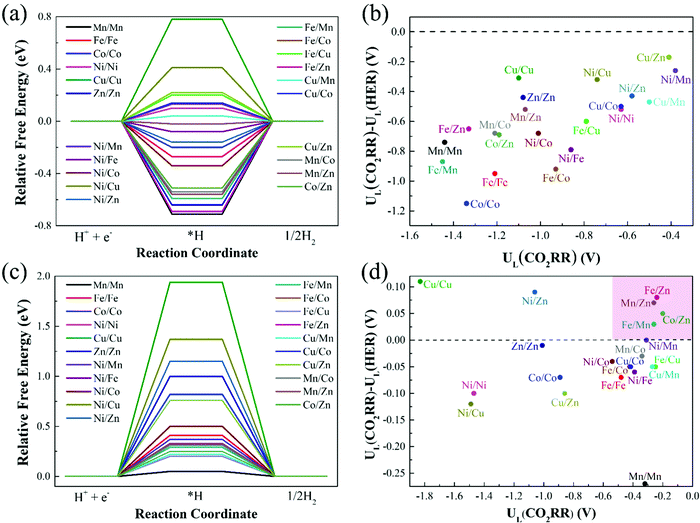

Fig. 7 Relative free energy profiles for HER on (a) Model 2 and (c) Model 3, and limiting potential difference between CO₂RR and HER for (b) Model 2 and (d) Model 3.

The catalysts with ΔG_*H values that deviate from zero are considered to be the appropriate CO₂RR electrocatalysts.^49,50 Our calculation results show that the adsorption free energies of H* species(ΔG_*H) on the catalysts of Model 2 range from −0.71 (Mn/Mn-Model 2) to 0.78 eV (Cu/Cu-Model 2), Fe/Co (ΔG_*H = −0.02 eV) and Cu/Mn (ΔG_*H = 0.04 eV) are the best HER electrocatalysts. The ΔG_*H on the catalysts of Model 3 ranges from 0.20 (Fe/Cu-Model 3) to 1.94 eV (Cu/Cu-Model 3), and Mn/Mn (ΔG_*H = 0.05 eV) is the best HER electrocatalyst. More interestingly, ΔG_*H values on the catalysts of Model 3 are all positive, while that on the catalysts of Model 2 are half positive and generally negative. This is caused by the different adsorption capacities of different bimetallic for *H. The coordination number of the metal on Model 3 is high, *H is difficult to adsorb on the catalyst surface, and usually requires additional energy. The lower coordination number of Model 2 makes the catalyst can effectively bind H. In addition, for Cu/M₂–N₆–Gra-Model 2, the fully-filled d-orbital of Cu and the less charge on the metal make the adsorption of *H weak, resulting in a positive value of ΔG_*H.

To investigate the catalytic selectivity of CO₂RR and HER on the active sites, we calculate the limiting potentials of HER on these catalysts (Model 2 and Model 3) and compare them with the limiting potentials of CO₂RR (U_L(CO₂RR) – U_L(HER)). The larger the (U_L(CO₂RR) – U_L(HER)) value, the higher the selectivity of CO₂RR.^51,52Fig. 7(b) shows the (U_L(CO₂RR) − U_L(HER)) vs. U_L(CO₂RR) of the Model 2 catalysts. The (U_L(CO₂RR) − U_L(HER)) values of the catalysts are all negative, demonstrating poor selectivity of CO₂RR. For the catalysts of Model 3, as shown in Fig. 7(d), the catalysts in the top right region (pink area) represent excellent CO₂RR catalytic activity and selectivity. Fe/Zn, Mn/Zn, Co/Zn, and Fe/Mn–N₆–Gra-Model 3 are promising CO₂RR catalysts with high activity and selectivity. In addition, the high selectivity also requires rapid desorption of CO to prevent further hydrogenation.⁵³ Therefore, we calculate the free energy change values from *CO to *CHO/*COH on the four selected catalysts, and the results are shown in Fig. S10 (ESI†). The ΔG values of *CO → *CHO/*COH on Fe/Zn, Mn/Zn, Co/Zn, and Fe/Mn–N₆–Gra-Model 3 are 0.46/2.06, 0.49/1.80, 0.12/1.86, and 0.63/1.99 eV, respectively, which are larger than the corresponding free energies of *CO → CO + * (0.24, 0.26, 0.02, and −0.14 eV). Therefore, the possibility of further hydrogenation of CO on these four catalysts is very small.

3.5 Origin of catalytic activity on M₁/M₂–N₆–Gra systems

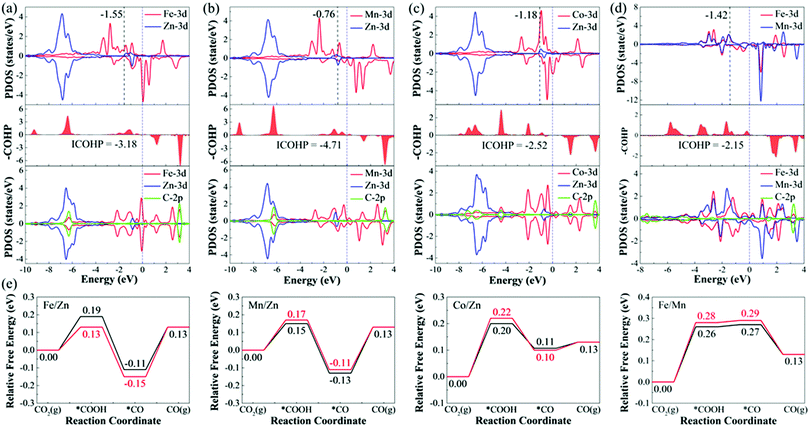
To deeply understand the origin of different catalytic activities of M₁/M₂–N₆–Gra materials, we have studied the electronic structures of several promising CO₂RR electrocatalysts (Fe/Zn, Mn/Zn, Co/Zn, and Fe/Mn–N₆–Gra-Model 3). For pure M₁/M₂–N₆–Gra surface, the charge density difference and Bader charge analysis (Fig. S11, ESI†) demonstrate that there is an electron transfer between the metal atoms and the graphene substrate. In Fe/Zn, Mn/Zn, and Co/Zn–N₆–Gra-Model 3, 1.14 e⁻ is transferred from the Zn atom to the substrate, while 1.05 e⁻, 1.28 e⁻, and 0.89 e⁻ are transferred from another metal atom (Fe, Mn, and Co) to the substrate, respectively. In Fe/Mn–N₆–Gra, 0.87 e⁻ and 1.21 e⁻ are transferred from Fe and Mn atoms to the substrate, respectively. This indicates that the metal atoms are positively charged, which can effectively activate CO₂ molecules, and promote the CO₂RR process.

For Fe/Zn and Mn/Zn–N₆–Gra-Model 3 systems, CO desorption is the limiting step, and for Co/Zn and Fe/Mn–N₆–Gra-Model 3, CO₂ activation is the limiting step. To gain further insights into the difference in catalytic performance, the partial density of states (PDOS) diagrams before and after *CO adsorption on Fe/Zn and Mn/Zn–N₆–Gra-Model 3, and before and after *COOH adsorption on Co/Zn and Fe/Mn–N₆–Gra-Model 3 are further investigated. According to previous reports,^54,55 the closer the d-band center is to the Fermi level, the higher the electron occupation of the bonding state is, and the stronger the adsorption strength of the adsorbed molecules on the catalyst surface is. As shown in Fig. 8(a) and (b), before *CO adsorption, the d-band center of Mn/Zn (ε_d(Mn), −0.76 eV) is closer to the Fermi level than Fe/Zn (ε_d(Fe), −1.55 eV), resulting in the higher CO binding strength of Mn/Zn, and CO is more difficult to desorb. Similarly, as can be seen in Fig. 8(c) and (d), before *COOH adsorption, the d-band center of Co/Zn (ε_d(Co), −1.18 eV) is closer to the Fermi level than Fe/Mn (ε_d(Fe), −1.42 eV). Co/Zn has higher *COOH binding strength, and CO₂ is more easily converted to *COOH. This is consistent with the calculated result in Fig. 4(g). After *CO and *COOH adsorption, the 3d orbital of metals is hybridized with the 2p orbital of C. To further reveal the binding strength of the metal—C bond, the crystal orbital Hamilton population (COHP) analysis is performed.^56–59 The more negative the ICOHP value (band states integrate to Fermi level), the stronger the bond between the metal and C atom. From Fig. 8(a)–(d), Mn/Zn (−4.71) has a more negative ICOHP value than Fe/Zn (−3.18), indicating that the binding strength of C and Mn is stronger than that of Fe. Co/Zn (−2.52) has a more negative ICOHP value than Fe/Mn (−2.15), indicating that the binding strength of C and Co is stronger than that of Fe. This is also consistent with the distances between the *CO, *COOH species and their corresponding catalysts (Fe/Zn is 1.721 Å, Mn/Zn is 1.765 Å, Co/Zn is 1.886 Å, and Fe/Mn is 1.882 Å, Tables S6 and S7, ESI†).

Fig. 8 The PDOS of (a) Fe/Zn and (b) Mn/Zn–N₆–Gra-Model 3 before and after *CO adsorption, (c) Co/Zn and (d) Fe/Mn–N₆–Gra-Model 3 before and after *COOH adsorption. The blue dotted lines represent the Fermi level. The black dotted lines represent the d-band center. (e) Comparison of CO₂RR pathways on Fe/Zn, Mn/Zn, Co/Zn, and Fe/Mn–N₆–Gra-Model 3 by using the default magnetic configuration values of VASP 5.4.4 software (black lines) and magnetic coupling method (red lines).

Similarly, taking Fe/Zn–N₆–Gra as an example, we study the origin of different catalytic behaviors of heteronuclear bimetallic catalysts. For Fe/Fe–N₆–Gra, the d-band center is close to the Fermi level (−1.53 eV, Table S9, ESI†), and the interaction between *COOH/*CO and the Fe/Fe–N₆–Gra surface is relatively strong, resulting in easy activation of CO₂ to *COOH. For Zn/Zn–N₆–Gra, the d-band center is far away from the Fermi level (−5.86 eV), and the interaction between *COOH/*CO and the Zn/Zn–N₆–Gra surface is relatively weak, making CO easy to desorb. Due to the synergistic effect of Fe and Zn atoms, the interaction between *COOH/*CO and Fe/Zn–N₆–Gra surface is stronger than Fe/Fe and Zn/Zn–N₆–Gra (the adsorption energy of *COOH/*CO and Fe/Zn surface is greater than that of Fe/Fe and Zn/Zn), but it makes *COOH and *CO have moderate adsorption strength, which promotes the activation of CO₂ to *COOH, while CO desorption is slightly difficult, and CO desorption is the limiting step. Therefore, the Fe/Zn–N₆–Gra catalyst shows the highest CO₂RR catalytic performance compared with Fe/Fe and Zn/Zn–N₆–Gra.

In addition, the magnetic coupling between the two metal atoms in bimetallic center catalysts also has an effect on the catalytic performance,⁶⁰ therefore, we calculate the CO₂RR pathways under the magnetic coupling, as displayed in Fig. 8(e). Although the limiting potential values calculated after considering the magnetic coupling are very close to the values calculated using the default magnetic configuration values (spin-polarized configuration) of VASP 5.4.4 software (FeZn, −0.28/−0.24 V; MnZn, −0.24/−0.26 V; CoZn, −0.22/−0.20 V; FeMn, −0.28/−0.26 V), but there is still a certain difference in energy, and magnetic coupling is an issue we need to pay attention to in our subsequent work.

4. Conclusion

In summary, by using first-principles calculations, we have comparatively studied the CO₂RR catalytic performance of M₁/M₂–N₆–Gra with different coordination environments of active sites. Our results show that: (1) the formation energies of M₁/M₂–N₆–Gra are more negative as the increase of metal and N coordination number (2–4), and M₁/M₂–N₆–Gra-Model 3 have the highest stability. (2) The reaction thermodynamics analysis indicates that from Model 1 to Model 3, the adsorption configurations of *COOH on M₁/M₂–N₆–Gra have changed from the bridge adsorption to the metal top adsorption. Most low-coordinated catalysts have strong adsorption capacity for *COOH and *CO, CO desorption is difficult, and the PLS step is the CO desorption (*CO → CO(g) + *). While most high-coordinated catalysts have weak adsorption of *COOH and *CO, CO₂ activation are difficult, and the PLS step is CO₂ + H⁺ + e⁻ → *COOH. The catalysts with moderate adsorption strength of *CO and *COOH are located on the top of the (ΔG_*CO – U_L) volcano and are conducive to CO generation. (3) Due to the synergistic effect between the two metals, most heteronuclear M₁/M₂–N₆–Gra have better CO₂RR catalytic activity than homonuclear catalysts, and the synergy increases with the increase of coordination number. (4) In all M₁/M₂–N₆–Gra systems, Co/Zn, Fe/Zn, Mn/Zn, and Fe/Mn–N₆–Gra-Model 3 (bonding with four N atoms) are the most active and selective catalysts for reducing CO₂ to CO with low limiting potentials (−0.20, −0.24, −0.26, and −0.26 V) and obvious inhibitory effect on HER. Therefore, adjusting the coordination environment of the active sites can effectively improve the catalytic performance, which will provide useful guidance for future design and development of efficient CO₂ electroreduction catalysts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 22173003 and 91741104), and the National Key R&D Program of China (2021YFC2103501).

References

1. X. Li, J. Yu, M. Jaroniec and X. Chen, Chem. Rev., 2019, 119, 3962–4179.
2. S. Liang, L. Huang, Y. Gao, Q. Wang and B. Liu, Adv. Sci., 2021, 8, 2102886.
3. Y. Zhu, J. Sokolowski, X. Song, Y. He, Y. Mei and G. Wu, Adv. Energy Mater., 2019, 10, 1902844.
4. A. Liu, M. Gao, X. Ren, F. Meng, Y. Yang, L. Gao, Q. Yang and T. Ma, J. Mater. Chem. A, 2020, 8, 3541–3562.
5. Q. Zhang and J. Guan, Adv. Funct. Mater., 2020, 30, 2000768.
6. J. Fu, K. Liu, H. Li, J. Hu and M. Liu, Environ. Chem. Lett., 2022, 20, 243–262.
7. D. D. Zhu, J. L. Liu and S. Z. Qiao, Adv. Mater., 2016, 28, 3423–3452.
8. B. Khezri, A. C. Fisher and M. Pumera, J. Mater. Chem. A, 2017, 5, 8230–8246.
9. R. Kortlever, J. Shen, K. J. P. Schouten, F. Calle-Vallejo and M. T. M. Koper, J. Phys. Chem. Lett., 2015, 6, 4073–4082.
10. A. S. Varela, N. R. Sahraie, J. Steinberg, W. Ju, H. S. Oh and P. Strasser, Angew. Chem., Int. Ed., 2015, 54, 10758–10762.
11. Y. Chen, C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 19969–19972.
12. R. Reske, H. Mistry, F. Behafarid, B. R. Cuenya and P. Strasser, J. Am. Chem. Soc., 2014, 136, 6978–6986.
13. S. Liu, H. Tao, L. Zeng, Q. Liu and Z. Xu, J. Am. Chem. Soc., 2017, 139, 2160–2163.
14. S. Mezzavilla, S. Horch, I. E. L. Stephens, B. Seger and I. Chorkendorff, Angew. Chem., Int. Ed., 2019, 58, 3774–3778.
15. D. Sun, X. Xu, Y. Qin, S. P. Jiang and Z. Shao, ChemSusChem, 2020, 13, 39–58.
16. A. Rendón-Calle, Q. H. Low, S. H. L. Hong, S. Builes, B. S. Yeo and F. Calle-Vallejo, Appl. Catal., B, 2021, 285, 119776.
17. X. Wu, Y. Guo, Z. Sun, F. Xie, D. Guan, J. Dai, F. Yu, Z. Hu, Y.-C. Huang, C.-W. Pao, J.-L. Chen, W. Zhou and Z. Shao, Nat. Commun., 2021, 12, 660.
18. C. Zhang, S. Yang, J. Wu, M. Liu, S. Yazdi, M. Ren, J. Sha, J. Zhong, K. Nie, A. S. Jalilov, Z. Li, H. Li, B. I. Yakobson, Q. Wu, E. Ringe, H. Xu, P. M. Ajayan and J. M. Tour, Adv. Energy Mater., 2018, 8, 1703487.
19. C. Lei, Y. Wang, Y. Hou, L. Pan, Y. Jian, Z. Tao, X. Zhuang, M. Chen, B. Yang and L. Lei, Energy Environ. Sci., 2019, 12, 149–156.
20. X. Wang, Z. Chen, X. Zhao, T. Yao, W. Chen, R. You, C. Zhao, G. Wu, J. Wang and W. Huang, Angew. Chem., Int. Ed., 2018, 57, 1944–1948.
21. Y. Pan, R. Lin, Y. Chen, S. Liu, W. Zhu, X. Cao, W. Chen, K. Wu, W.-C. Cheong, Y. Wang, L. Zheng, J. Luo, Y. Lin, Y. Liu, C. Liu, J. Li, Q. Lu, X. Chen, D. Wang, Q. Peng, C. Chen and Y. Li, J. Am. Chem. Soc., 2018, 140, 4218–4221.
22. W. Ren, X. Tan, W. Yang, C. Jia, S. Xu, K. Wang, S. C. Smith and C. Zhao, Angew. Chem., Int. Ed., 2019, 58, 6972–6976.
23. C. Ding, C. Feng, Y. Mei, F. Liu, H. Wang, M. Dupuis and C. Li, Appl. Catal., B, 2020, 268, 118391.
24. F. Wang, H. Xie, T. Liu, Y. Wu and B. Chen, Appl. Energy, 2020, 269, 115029.
25. W. Guo, J. Bi, Q. Zhu, J. Ma, G. Yang, H. Wu, X. Sun and B. Han, ACS Sustainable Chem. Eng., 2020, 8, 12561–12567.
26. Z. Chen, X. Liao, C. Sun, K. Zhao, D. Ye, J. Li, G. Wu, J. Fang, H. Zhao and J. Zhang, Appl. Catal., B, 2021, 288, 120021.
27. M. Xiao, Y. Chen, J. Zhu, H. Zhang, X. Zhao, L. Gao, X. Wang, J. Zhao, J. Ge, Z. Jiang, S. Chen, C. Liu and W. Xing, J. Am. Chem. Soc., 2019, 141, 17763–17770.
28. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
29. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
30. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
33. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
34. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
35. Accelrys Software. Materials Studio 8.0., Accelrys Software Inc., 2014.
36. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
37. X. Zhao and Y. Liu, J. Am. Chem. Soc., 2020, 142, 5773–5777.
38. X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, J. Am. Chem. Soc., 2020, 142, 5709–5721.
39. H. Niu, X. Wan, X. Wang, C. Shao, J. Robertson, Z. Zhang and Y. Guo, ACS Sustainable Chem. Eng., 2021, 9, 3590–3599.
40. C. Guo, T. Zhang, X. Liang, X. Deng, W. Guo, Z. Wang, X. Lu and C.-M. L. Wu, Appl. Surf. Sci., 2020, 533, 147466.
41. R. Hu, Y. Li, Q. Zeng and J. Shang, Appl. Surf. Sci., 2020, 525, 146588.
42. M. D. Hossain, Y. Huang, T. H. Yu, W. A. G. III and Z. Luo, Nat. Commun., 2020, 11, 2256.
43. Y. Wang, L. You and K. Zhou, Chem. Sci., 2021, 12, 14065–14073.
44. F. Calle-Vallejo and M. T. M. Koper, Angew. Chem., Int. Ed., 2013, 52, 7282–7285.
45. A. A. Peterson, F. Abild-Pedersen, F. Stud, J. Rossmeisla and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315.
46. F. Lia and Q. Tang, J. Mater. Chem. A, 2021, 9, 8761–8771.
47. Y. J. Zhang, V. Sethuraman, R. Michalsky and A. A. Peterson, ACS Catal., 2014, 4, 3742–3748.
48. L. Zhang, Z. J. Zhao and J. Gong, Angew. Chem., Int. Ed., 2017, 56, 11326–11353.
49. H. Wang, C. Tsai, D. Kong, K. Chan, F. A. Pedersen, J. K. Nørskov and Y. Cui, Nano Res., 2015, 8, 566–575.
50. T. Zhang, H. Zhu, C. Guo, S. Cao, C.-M. L. Wu, Z. Wang and X. Lu, Catal. Sci. Technol., 2020, 10, 458–465.
51. K. Chan, C. Tsai, H. A. Hansen and J. K. Nørskov, ChemCatChem, 2014, 6, 1899–1905.
52. Y. Ouyang, L. Shi, X. Bai, Q. Li and J. Wang, Chem. Sci., 2020, 11, 1807–1813.
53. X. Zhang, W. Wang and Z. Yang, ACS Sustainable Chem. Eng., 2020, 8, 6134–6141.
54. H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348.
55. L. Gong, D. Zhang, Y. Shen, X. Wang, J. Zhang, X. Han, L. Zhang and Z. Xia, J. Catal., 2020, 390, 126–134.
56. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
57. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
58. R. Dronskowski and P. E. Bloechl, J. Phys. Chem. B, 1993, 97, 8617–8824.
59. R. Nelson, C. Ertural, J. George, V. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
60. L. Yu, F. Li, J. Zhao and Z. Chen, Adv. Power Mater, 2020, 1, 100031.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized structures and parameters, formation energies, adsorption energies and adsorption free energies, reaction free energy change values, limiting potentials and electronic structure. See DOI: https://doi.org/10.1039/d2ma00192f

---