Pressure effect on long-term heat storage ceramics based on Mg-substituted λ-Ti₃O₅

Abstract

Waste heat energy could be effectively used if the accumulated thermal energy could be conserved. However, neither typical sensible heat-storage materials such as brick and concrete nor latent heat-storage materials such as water and polyethylene glycol can store energy for a prolonged period. Herein we report a heat-storage material, which is a ceramic that exhibits long-term storage of latent heat and release of the heat by applying pressure. This material is Mg-substituted lambda-trititanium-pentoxide (λ-Mg_xTi_3−xO₅ where 0 < x ≤ 0.053). λ-Mg_xTi_3−xO₅ shows a phase transition to Mg-substituted beta-trititanium-pentoxide (β-Mg_xTi_3−xO₅) by pressure application. Mg cation substitution can control the temperature of the heat storage originating from the β- to λ-phase transition from 196 °C (469 K) for x = 0 to 80 °C (353 K) for x = 0.053. This phase transition temperature range is suitable for heat storage from industrial waste and thermal power plants. The accumulated heat energy is maintained at a large value of 215–227 kJ L⁻¹ in the range of 0 < x ≤ 0.053. Such an eco-friendly and pressure-responsive heat-storage ceramic, which can preserve the latent heat energy for a prolonged period, is effective for the sustainable reuse of heat energy that has been wasted in industrial facilities and factories.

---

Introduction

Global warming, which is a global temperature increase due to the rise of the CO₂ concentration in the atmosphere, has become an urgent problem. Green innovations, which are technologies to solve this problem, are very important for better management of the Earth for the next generation of human beings. From the perspective of an energy problem, producing nature-friendly energy is important while simultaneously reusing generated energy effectively.^1–4 Currently, about 40% of consumed energy such as oil, gas, and coal is lost to the atmosphere as waste heat. Among the wasted heat energy, about 80% is below 200 °C (473 K). Additionally, waste heat negatively affects the environment.^5,6 Therefore, the development of high-performance heat-storage materials should be an effective solution.^7,8

Known heat-storage materials include sensible ones such as bricks and concrete, and solid–liquid latent ones such as water, paraffin, and polyethylene glycol.^9–12 In general heat-storage materials, the accumulated heat energy is released over time. Consequently, they are unsuitable for long-term storage of the accumulated heat energy. This issue is called the “time-gap problem” in the field of heat-storage materials. If the accumulated heat energy can be stored for a long period of time and released on demand, various applications should be possible.

Recently, a new concept of “long-term heat-storage ceramics” has been proposed, in which latent heat is preserved until a material is triggered by external stimuli.¹³ An example is lambda-trititanium-pentoxide (λ-Ti₃O₅), which shows a reversible phase transition to beta-trititanium-pentoxide (β-Ti₃O₅) by external stimuli such as light, heat, and pressure.^13–19 Moreover, solid–solid phase transition materials such as charge transfer phase transition materials,^20–26 spin crossover transition materials,^27–40 and metal insulator phase transition materials,^14,41,42 may also be good candidates for long-term heat storage materials. In this study, we synthesize a long-term heat-storage material based on magnesium-substituted lambda-trititanium-pentoxide, λ-Mg_xTi_3−xO₅. Synthesis of λ-Mg_xTi_3−xO₅ was first reported by our group in 2017.¹⁸ Then, the temperature-induced phase transition from λ- to α-Mg_xTi_3−xO₅ was reported.¹⁹ However, the pressure-induced phase transition of λ-Mg_xTi_3−xO₅ and its heat-storage performance have yet to be explored. Pressure-induced phase transition effect^43–48 is considered to be an essential approach for energy release because pressure applications are useful for extracting accumulated heat energy. Herein we report the crystal structure and morphology, heat-storage temperature, accumulated heat energy, pressure-responsive heat-energy release, and theoretical analyses of the heat-storage performance of λ-Mg_xTi_3−xO₅ based on a thermodynamic theory.

Results and discussion

Materials

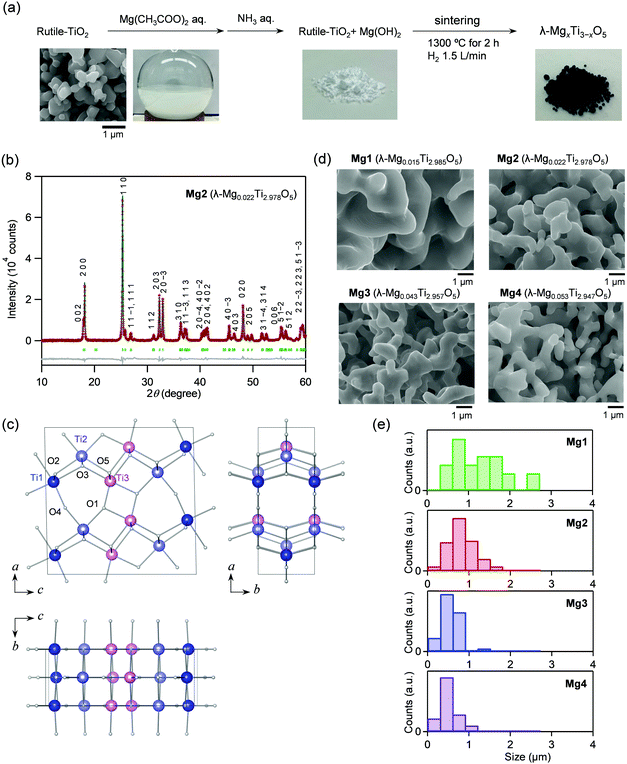
Mg-Substituted λ-Ti₃O₅ was synthesized by the following process. First, the Mg ion-covered TiO₂ precursor was prepared by adding an ammonia aqueous solution to a mixed solution of a rutile-TiO₂ particle dispersion and a magnesium acetate aqueous solution. The precursor was sintered at 1300 °C under a hydrogen atmosphere (Fig. 1a). Four samples were synthesized with different Mg feed ratios and sintering times at 1300 °C: Mg1 ([Mg]/[Mg + Ti] = 1.5%, sintering time = 6 hours), Mg2 (1.5%, 2 hours), Mg3 (3.0%, 6 hours), and Mg4 (4.0%, 6 hours). Elemental analyses were performed using X-ray fluorescence (XRF). The sample formulas are Mg_0.015Ti_2.985O₅ (Mg1), Mg_0.022Ti_2.978O₅ (Mg2), Mg_0.043Ti_2.957O₅ (Mg3), and Mg_0.053Ti_2.947O₅ (Mg4).

Fig. 1 Synthesis procedure, crystal structure, and morphology of Mg-substituted lamba-trititanium-pentoxide (λ-Mg_xTi_3−xO₅). (a) Synthesis of λ-Mg_xTi_3−xO₅. (b) PXRD patterns with Rietveld analysis for Mg2 under atmospheric pressure (0.1 MPa) with a silicon standard. Red plots, black line, and gray line are the observed pattern, the total calculated pattern, and the residual pattern, respectively. Green bars represent the calculated positions of the Bragg reflections of the λ-phase. Asterisk indicates the characteristic peaks for the silicon standard. (c) Crystal structure of λ-Mg_xTi_3−xO₅ viewed along the a, b, and c-axes. (d) SEM images of λ-Mg_xTi_3−xO₅ showing coral-like particles morphology. Acceleration voltage for the measurements is either 15 kV (Mg1, Mg2, and Mg4) or 10 kV (Mg3). All images are magnified ×10 000. (e) Diameters of the coral-structure of Mg1 (green), Mg2 (red), Mg3 (blue), and Mg4 (purple).

Crystal structure and morphology

Fig. 1b shows the powder X-ray diffraction (PXRD) pattern with Rietveld analysis of Mg2, while those of the other samples are shown in Fig. S1 (ESI†). Mg1–Mg4 consist of 100% of the λ-phase. The lattice parameters of the λ-phase are: Mg1: a = 9.8286(9) Å, b = 3.7875(2) Å, c = 9.9676(9) Å, and β = 91.173(4)°; Mg2: a = 9.8357(2) Å, b = 3.78584(4) Å, c = 9.9712(2) Å, and β = 91.1946(11)°; Mg3: a = 9.8284(4) Å, b = 3.78733(8) Å, c = 9.9709(3) Å, and β = 91.094(2)°; Mg4: a = 9.8155(3) Å, b = 3.78565(6) Å, c = 9.9680(2) Å, and β = 90.950(2)° (Table S1, ESI†). As a representative, the crystal structure of Mg2 is shown in Fig. 1c.

The morphologies of the samples were investigated by scanning electron microscopy (SEM). All samples have coral-shaped morphologies, and the diameters of the coral-structure are 0.5–2.5 μm (Mg1), 0.2–1.6 μm (Mg2), 0.2–1.5 μm (Mg3), and 0.1–1.0 μm (Mg4) (Fig. 1d). Mg substitution gradually reduces the thickness of the coral. The diameter of Mg4 is about half that of Mg1 (Fig. 1e).

Pressure-induced phase transition and released heat energy

After applying an external pressure (P) of P = 2.5, 5, 7.5, 10, 12.5, 15, 30, 45, 60, 230, 600 MPa, or 2 GPa, the pressure was released and PXRD patterns were measured. The transition pressure (P_1/2), at which the λ- and β-phase fractions are equal, is low for Mg1 (79 MPa). By contrast, P_1/2 is 450 MPa (Mg2), 700 MPa (Mg3), and over 2 GPa (Mg4) (Fig. 2).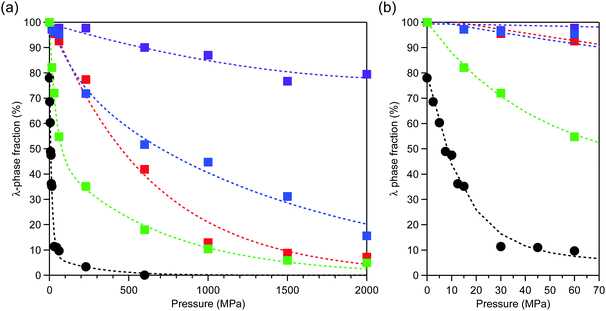

Fig. 2 (a) Pressure dependence of the λ-phase fractions of λ-Mg_xTi_3−xO₅ for Mg1 (green), Mg2 (red), Mg3 (blue), Mg4 (purple), and block-type λ-Ti₃O₅ (black, adapted from ref. 15). (b) Enlarged plot in the low pressure region. Dashed lines are to guide the eye.

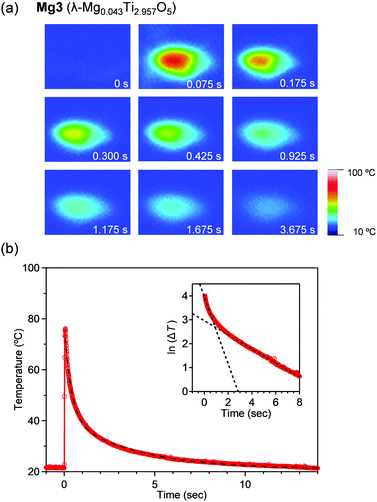
To visually measure the released heat energy at the pressure-induced phase transition, the temperature changes of the samples were measured via thermography (Fig. 3). The thermographic image is blue prior to applying pressure. The white or red point corresponds to the position pressed by applying instant pressure with a hammer. Afterward, the maximum temperature reaches 89.8 °C, 79.1 °C, 76.1 °C, and 66.8 °C for Mg1–Mg4, respectively within 75 ms (Fig. 3b and Fig. S2, ESI†). The released heat energies were evaluated under adiabatic conditions. The released heat energies are: 203 kJ L⁻¹ (Mg1), 177 kJ L⁻¹ (Mg2), 167 kJ L⁻¹ (Mg3), and 142 kJ L⁻¹ (Mg4).

Fig. 3 Heat release of λ-Mg_xTi_3−xO₅ by applying external pressure. (a) Thermographs for Mg3. Color scale of the temperature is shown on the right. (b) Decay of the maximum temperature within a square area after applying pressure to Mg3 at t = 0.

Fig. 3b shows the temperature change of the pressurized point. Heat release occurs immediately after applying pressure. A double exponential function, ΔT = A₁ exp(−t/τ₁) + A₂ exp(−t/τ₂), was fitted to the decay curves. Here, ΔT is the temperature change, t is time, τ₁ and τ₂ are decay times, and A₁ and A₂ are constants. The decay times are (τ₁, τ₂) = (0.2, 1.7), (0.5, 3.1), (0.4, 3.8), and (0.5, 2.9) seconds for Mg1–Mg4, respectively. A pressure-sensitive sheet suggests that the applied pressure is ca. 50 MPa. τ₁ is attributed to the thermal relaxation of the sample, while τ₂ is due to the thermal relaxation of acryl substrate.

Accumulated heat energy and temperature

Heat accumulation temperatures and the accumulated heat energies were measured for the pressure-produced β-phase using differential scanning calorimetry (DSC). All samples display endothermic peaks during the transition from the β-phase to the λ-phase. The DSC curves show endothermic peaks at heat storage temperatures (T_β→λ) of 178 °C (451 K), 160 °C (433 K), 108 °C (381 K), and 80 °C (353 K) for Mg1–Mg4, respectively (Fig. 4a and b). The transition enthalpy values (ΔH_β→λ) obtained from the area of the endothermic peaks are 227 kJ L⁻¹, 223 kJ L⁻¹, 215 kJ L⁻¹, and 216 kJ L⁻¹, respectively (Fig. 4c). Substitution with Mg cations decreases the T_p value from 198 °C (x = 0) to 80 °C (x = 0.053). On the other hand, exothermic peaks are not observed, indicating that the λ-phase is maintained in the cooling process.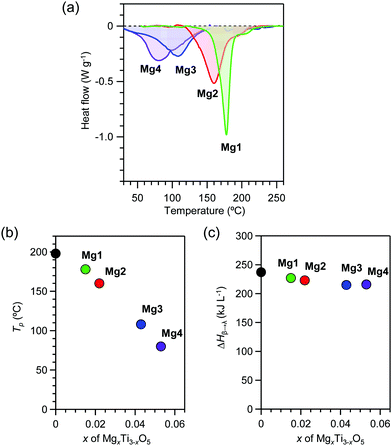

Fig. 4 Heat-storage properties of λ-Mg_xTi_3−xO₅. (a) DSC charts of Mg1 (green), Mg2 (red), Mg3 (blue), and Mg4 (purple) as the temperature increases. (b) x-Value dependence of the transition temperature. (c) x-Value dependence of the transition enthalpy. Black circle represents block-type λ-Ti₃O₅ (adapted from ref. 15).

To verify the phase transition from pressure-produced β-phase to λ-phase, variable-temperature PXRD (VT-PXRD) measurements were conducted for Mg3 and Mg4. In the heating process of Mg3, the intensity of the (2 0 4) peak due to the β-phase starts to decrease at 60 °C, drastically changes around 100 °C, and reaches a minimum at 160 °C (Fig. S3, ESI†). The differential of the (2 0 4) peak intensity versus temperature plot shows a peak at 103 °C with a full width at half maximum of 47 °C. In Mg4, the PXRD intensity of the (204) peak starts to decrease around 30 °C, changes largely around 75 °C, and reaches a minimum around 180 °C (Fig. S4, ESI†). The differential of the (204) peak intensity versus temperature plot shows a peak at 77 °C with a full width at half maximum of 87 °C. These results correspond to the endothermic peaks of Mg3 and Mg4 in the DSC measurements. These phase transition temperatures almost correspond to the previously reported values.^18,19

Appearance of the thermal hysteresis loop on phase transition

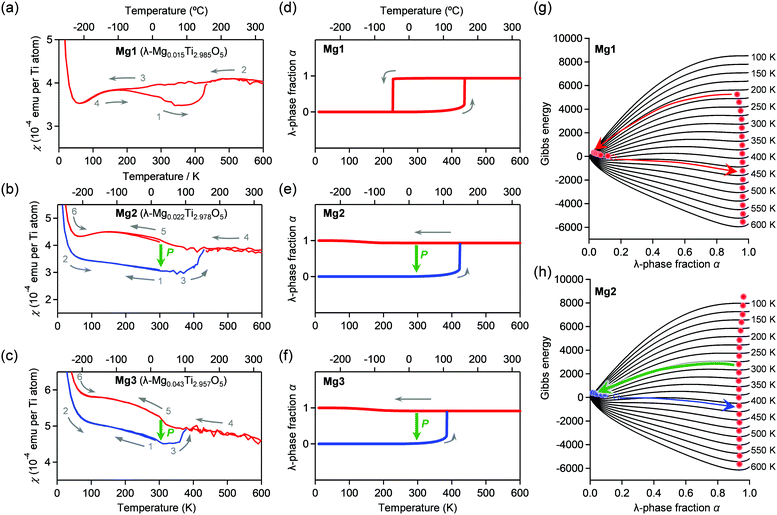
The temperature dependences of the magnetic susceptibility (χ) in Mg1–Mg3 were measured using a superconducting quantum interference device (SQUID) magnetometer (Fig. 5a–c). Mg1 displays a thermal hysteresis loop with a phase transition temperature upon cooling (T_λ→β) at 180 K and a phase transition temperature upon heating (T_β→λ) of 420 K, and a temperature width of a thermal hysteresis (ΔT ≡ T_β→λ − T_λ→β) of 240 K. On the other hand, Mg2 and Mg3 do not show such a thermal hysteresis loop at ambient pressure. Applying an external pressure transforms the λ-phase into the β-phase in the heating process. Pressurized Mg2 shows a phase transition from the β-phase to the λ-phase at T_β→λ = 433 K. Similarly, the T_β→λ value is 380 K for Mg3.

Fig. 5 Temperature dependence of magnetic susceptibility (χ) of (a) Mg1, (b) Mg2, and (c) Mg3 under an external magnetic field of 5 kOe. For Mg2 and Mg3, the samples were pressurized by 600 MPa and 2 GPa, respectively, before the measurement. Gray arrows and numbers denote the order of the measurement sequence. Calculated λ-phase fraction (α) versus temperature curves at atmospheric pressure for (d) Mg1, (e) Mg2, and (f) Mg3. Gibbs energy versus λ-phase fraction at various temperatures for (g) Mg1 and (h) Mg2.

Mechanism of the pressure-induced phase transition

Here, we discuss the reason for the decrease in T_β→λ by Mg-substitution as well as the increase in the phase transition pressure. We calculated the thermal hysteresis loops of the phase transition between the λ-phase and the β-phase using the mean-field model proposed by Slichter and Drickamer (SD model).⁴⁹ In the model, the Gibbs energy G of the system is described as G = αΔH_t + γ α(1 − α) + T{R[α ln α + (1 − α)ln(1 − α)] − αΔS_t} + G_β, where α is the λ-phase fraction, G_β is the Gibbs energy of the β-phase set as the origin of the energies. ΔH_t and ΔS_t are the transition enthalpy and the transition entropy, which are smaller than ΔH_β→λ and ΔS_β→λ, and γ is the interaction parameter between the λ- and β-phases. The γ value is the interaction parameter due to the elastic interaction inside of crystals, γ = γ_a + γ_bT. The SD model calculation reproduced the observed thermal hysteresis loop of Mg1 with T_λ→β = 232 K and T_β→λ = 440 K with ΔH_t = 11.4 kJ mol⁻¹, ΔS_t = 28.4 J K⁻¹ mol⁻¹, γ_a = 12.6 kJ mol⁻¹, and γ_b = 6.33 J K⁻¹ mol⁻¹. In addition, we reproduced T_β→λ values of 430 K and 380 K for Mg2 and Mg3, respectively (Fig. 5d–h). Details of the SD parameters for simulations are shown in the Experimental section.

To reproduce the pressure-induced phase transition from the λ-phase to the β-phase at room temperature, we calculated the temperature dependence of the Gibbs energy for the λ-and β-phases of Mg1–Mg3 using the γ value and considering pressure contribution (i.e., γ = γ_a + γ_bT + γ_cP). As examples, thermodynamic simulations of thermal hysteresis were performed at 79 MPa (Mg1), 450 MPa (Mg2), and 700 MPa (Mg3). The SD parameters are shown in the Experimental section. The T_λ→β values of Mg1–Mg3 exceed 300 K and correspond to the pressure-induced phase transition from λ-phase to β-phase (Fig. S5, ESI†). Hence, the Mg concentration should significantly influence the γ_c value, increasing the necessary pressure for the phase transition. To consider the drastic change in the γ_c value, we investigated the primary particle size of the λ-phase using high-resolution TEM images (Fig. S6, ESI†). The primary particle size of Mg1 is ca. 500 nm, whereas those of Mg2–Mg4 are 50–200 nm. Based on our previous studies,^14,15 the primary size of Mg1 and those of Mg2–Mg4 correspond to block-type λ-Ti₃O₅ and flake-type λ-Ti₃O₅, respectively. Although the particle sizes in the SEM images change only slightly, the primary particle sizes drastically decrease as the Mg concentration increases. Therefore, the increase of the necessary pressure for the pressure-induced phase transition is attributed to the decreased correlation length of the elastic interaction due to the smaller primary particle size from impurities or defects inside the crystals.

In fact, the increase of the χ value of Mg1–Mg3 in the low-temperature region is attributed to the Curie paramagnetic component due to lattice defects. The Curie constant (C) was obtained by fitting an equation of χ = C/(T − θ), where θ is the Weiss temperature, to the χ–T plot. The fitted C values are 3.3 × 10⁻³ (Mg1), 4.1 × 10⁻³ (Mg2), and 6.2 × 10⁻³ (Mg3) (Fig. S7, ESI†). The increase in the C value also suggests an increase in the lattice defects by Mg-substitution.

Conclusions

Here, we construct a long-term heat-storage system based on Mg-substituted λ-Ti₃O₅ and investigated its phase transition induced by pressure and heat-storage characteristics. The temperature of the heat storage originating from the β- to λ-phase transition can be controlled from 196 °C (469 K) for x = 0 to 80 °C (353 K) for x = 0.053 by Mg-substitution. The temperature dependence of the λ-phase fraction is well reproduced by the SD model and considering the pressure contribution to the elastic interaction inside crystals. Mg-Substituted λ-Ti₃O₅ with long-term heat-storage performance would be useful for power plants and industry-to-residential heat-waste reuse because 70% of the generated heat energy is wasted, which is below 100 °C (373 K), the boiling temperature of water. This series composed of Mg, Ti, and O should realize both economic and environmental benefits.

Experimental

Physical measurements

Elemental analyses on the prepared samples were performed using XRF (Rigaku, ZSX PrimusII). The compositions were determined to be Mg1: Mg_0.015Ti_2.985O₅ (calc.: Mg 0.17%, Ti 64.00%, O 35.84%; found: Mg 0.16%, Ti 63.72%, O 36.11%); Mg2: Mg_0.022Ti_2.978O₅ (calc.: Mg 0.24%, Ti 63.90%, O 35.86%; found: Mg 0.24%, Ti 63.64%, O 36.13%); Mg3: Mg_0.043Ti_2.957O₅ (calc.: Mg 0.47%, Ti 63.59%, O 35.94%; found: Mg 0.47%, Ti 63.11%, O 36.43%); and Mg4: Mg_0.053Ti_2.947O₅ (calc.: Mg 0.58%, Ti 63.44%, O 35.98%; found: Mg 0.58%, Ti 63.80%, O 35.61%). The TEM measurements were conducted using a JEOL JEM-2000EXII and a JEM-4000FXII. A JEOL JSM-7000F SEM measured the morphologies of the compounds with a 15 kV or 10 kV accelerating voltage. The XRD measurements were carried out on Rigaku Ultima IV (Cu Kα source, λ = 1.5418 Å). RIETAN-FP⁵⁰ and RIGAKU PDXL programs were used for Rietveld analyses. The magnetic properties were measured using a SQUID magnetometer (Quantum Design, MPMS 7). DSC measurements were conducted using a Rigaku DSC 8230. The samples for DSC measurements were prepared by pressurization, and the phase ratios for each sample were as follows: 36% of λ-phase and 64% of β-phase (Mg1), 75% of λ-phase and 25% of β-phase (Mg2), 52% of λ-phase and 48% of β-phase (Mg3), and 80% of λ-phase and 20% of β-phase (Mg4). An infrared thermal imaging camera (NIPPON AVIONICS R550Pro) acquired the thermographic images. The background temperatures were around 25 °C (Mg1), 21 °C (Mg2 and Mg4), and 28 °C (Mg3).

Thermodynamic analysis

The γ value is dependent on temperature and pressure (i.e., γ = γ_a + γ_bT + γ_cP). In the simulation of the temperature dependence of α at 0.1 MPa, γ_c was not taken into account. The parameters of the SD model simulations (ΔH, ΔS, γ_a, γ_b) for Mg1–Mg3 were (216 kJ L⁻¹, 539 J K⁻¹ L⁻¹, 239 kJ L⁻¹, −120 J K⁻¹ L⁻¹), (204 kJ L⁻¹, 524 J K⁻¹ L⁻¹, 237 kJ L⁻¹, −130 J K⁻¹ L⁻¹), and (188 kJ L⁻¹, 519 J K⁻¹ L⁻¹, 229 kJ L⁻¹, −185 J K⁻¹ L⁻¹), respectively. Based on the pressure-induced phase transition properties of Mg1–Mg3, thermodynamic simulations at 79 MPa (Mg1), 450 MPa (Mg2), and 700 MPa (Mg3) were performed using the following parameters of (ΔH, ΔS, γ_a, γ_b, γ_c): (216 kJ L⁻¹, 536 J K⁻¹ L⁻¹, 243 kJ L⁻¹, −120 J K⁻¹ L⁻¹, −168 J MPa⁻¹ L⁻¹), (204 kJ L⁻¹, 486 J K⁻¹ L⁻¹, 237 kJ L⁻¹, −130 J K⁻¹ L⁻¹, −3.8 J MPa⁻¹ L⁻¹), and (188 kJ L⁻¹, 395 J K⁻¹ L⁻¹, 229 kJ L⁻¹, −185 J K⁻¹ L⁻¹, −0.9 J MPa⁻¹ L⁻¹), respectively. The ΔH and ΔS values under pressure were determined based on first-principles calculations in which the ΔS value decreased by 12% while the ΔH value remained nearly constant at 1 GPa.

Author contributions

S. O. coordinated and designed the entire study, supervised all of the experiments and theoretical simulations, and wrote the paper. F. J. synthesized the samples and conducted the elemental analyses, SEM observations, pressure-dependence experiments, PXRD, thermography, DSC, and magnetic measurements, thermodynamic calculations, and TEM analysis. M. Y. obtained the TEM images and contributed to writing the paper. K. I. conducted the thermodynamic calculations, Rietveld analyses, and analyses of the magnetic data. H. T. contributed to the DSC and magnetic measurements. K. N. conducted the DSC, thermography, and magnetic measurements, Y. M. contributed to the synthesis, A. N. conducted the Rietveld analysis, and R. H., K. H., K. K., K. S., and T. S. contributed to the interpretation of the results. All authors commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by the Advanced Research Program for Energy and Environmental Technologies project commissioned by the New Energy and Industrial Technology Development Organization (NEDO) of METI and a JSPS Grant-in-Aid for Scientific Research (A) (Grant Number 20H00369). F. J. is grateful to JST SPRING (Grant Number JPMJSP2108). This work was partially carried out in the framework of the IM-LED LIA (CNRS). We recognize the Cryogenic Research Center and the Center for Nano Lithography & Analysis at The University of Tokyo.

References

1. D. Butler, Nature, 2007, 445, 768–769.
2. D. Lindley, Nature, 2009, 458, 138–141.
3. S. A. Rattner and S. Garimella, Energy, 2011, 36, 6172–6183.
4. D. B. Gingerich and M. S. Mauter, Environ. Sci. Technol., 2015, 49, 8297–8306.
5. C. W. King, A. S. Holman and M. E. Webber, Nat. Geosci., 2008, 1, 283–286.
6. M. D. Bartos and M. V. Chester, Nat. Clim. Change, 2015, 5, 748–752.
7. G. W. Crabtree and N. S. Lewis, Phys. Today, 2007, 60, 37–42.
8. E. Cartlidge, Science, 2011, 334, 922–924.
9. M. M. Farid, A. M. Khudhair, S. A.-K. Razack and S. Al-Hallaj, Energy Convers. Manage., 2004, 45, 1597–1615.
10. A. Sharma, V. V. Tyagi, C. R. Chen and D. Buddhi, Renewable Sustainable Energy Rev., 2009, 13, 318–345.
11. M. Barrio, D. O. López, J. Ll. Tamarit, P. Negrier and Y. Haget, J. Solid State Chem., 1996, 124, 29–38.
12. I. Gur, K. Sawyer and R. Prasher, Science, 2012, 335, 1454–1455.
13. H. Tokoro, M. Yoshikiyo, K. Imoto, A. Namai, T. Nasu, K. Nakagawa, N. Ozaki, F. Hakoe, K. Tanaka, K. Chiba, R. Makiura, K. Prassides and S. Ohkoshi, Nat. Commun., 2015, 6, 7037.
14. S. Ohkoshi, Y. Tsunobuchi, T. Matsuda, K. Hashimoto, A. Namai, F. Hakoe and H. Tokoro, Nat. Chem., 2010, 2, 539–545.
15. S. Ohkoshi, H. Tokoro, K. Nakagawa, M. Yoshikiyo, F. Jia and A. Namai, Sci. Rep., 2019, 9, 13203.
16. C. Mariette, M. Lorenc, H. Cailleau, E. Collet, L. Guérin, A. Volte, E. Trzop, R. Bertoni, X. Dong, B. Lépine, O. Hernandez, E. Janod, L. Cario, V. Ta Phuoc, S. Ohkoshi, H. Tokoro, L. Patthey, A. Babic, I. Usov, D. Ozerov, L. Sala, S. Ebner, P. Böhler, A. Keller, A. Oggenfuss, T. Zmofing, S. Redford, S. Vetter, R. Follath, P. Juranic, A. Schreiber, P. Beaud, V. Esposito, Y. Deng, G. Ingold, M. Chergui, G. F. Mancini, R. Mankowsky, C. Svetina, S. Zerdane, A. Mozzanica, A. Bosak, M. Wulff, M. Levantino, H. Lemke and M. Cammarata, Nat. Commun., 2021, 12, 1239.
17. Y. Nakamura, Y. Sakai, M. Azuma and S. Ohkoshi, Sci. Adv., 2020, 6, 5264.
18. S. Ohkoshi, Y. Maeno and T. Nasu, International Patent Number WO2017/164083, 2017.
19. M. Wang, W. Huang, Z. Shen, J. Gao, Y. Shi, T. Lu and Q. Shi, J. Alloys Compd., 2019, 774, 1189–1194.
20. A. Bleuzen, V. Marvaud, C. Mathonière, B. Sieklucka and M. Verdaguer, Inorg. Chem., 2009, 48, 3453–3466.
21. S. Ohkoshi, S. Ikeda, T. Hozumi, T. Kashiwagi and K. Hashimoto, J. Am. Chem. Soc., 2006, 128, 5320–5321.
22. Y.-Z. Zhang, P. Ferko, D. Siretanu, R. Ababei, N. P. Rath, M. J. Shaw, R. Clérac, C. Mathonière and S. M. Holmes, J. Am. Chem. Soc., 2014, 136, 16854–16864.
23. J. M. Cain, A. C. Felts, M. W. Meisel and D. R. Talham, Chem. Mater., 2021, 33, 246–255.
24. M. Magott, M. Reczyński, B. Gaweł, B. Sieklucka and D. Pinkowicz, J. Am. Chem. Soc., 2018, 140, 15876–15882.
25. F. J. Luque, I. A. Kowalik, J. P. Prieto-Ruiz, M. Á. Niño, H. Prima-García, F. M. Romero, D. Arvanitis, C. Mathonière, E. Coronado, R. Miranda and J. J. de Miguel, J. Mater. Chem. C, 2019, 7, 2305–2317.
26. S. Chorazy, T. Charytanowicz, D. Pinkowicz, J. Wang, K. Nakabayashi, S. Klimke, F. Renz, S. Ohkoshi and B. Sieklucka, Angew. Chem., Int. Ed., 2020, 59, 15741–15749.
27. P. Gütlich, Y. Garcia and T. Woike, Coord. Chem. Rev., 2001, 219, 839–879.
28. K. Ridier, A.-C. Bas, V. Shalabaeva, W. Nicolazzi, L. Salmon, G. Molnár, A. Bousseksou, M. Lorenc, R. Bertoni, E. Collet and H. Cailleau, Adv. Mater., 2019, 31, 1901361.
29. F. Renz, H. Oshio, V. Ksenofontov, M. Waldeck, H. Spiering and P. Gütlich, Angew. Chem., Int. Ed., 2000, 39, 3699–3700.
30. C. Rajnak, R. Micova, J. Moncol, L. Dlhan, C. Kruger, F. Renz and R. Boca, Dalton Trans., 2021, 50, 472–475.
31. V. Davesne, M. Gruber, M. Studniarek, W. H. Doh, S. Zafeiratos, L. Joly, F. Sirotti, M. G. Silly, A. B. Gaspar, J. A. Real, G. Schmerber, M. Bowen, W. Weber, S. Boukari, V. Da Costa, J. Arabski, W. Wulfhekel and E. Beaurepaire, J. Chem. Phys., 2015, 142, 194702.
32. S. Ohkoshi, K. Imoto, Y. Tsunobuchi, S. Takano and H. Tokoro, Nat. Chem., 2011, 3, 564–569.
33. P. N. Martninho, P. N. Gildea, M. M. Harris, T. Lemma, A. D. Naik, H. Müller-Bunz, T. E. Keyes, Y. Garcia and G. G. Morgan, Angew. Chem., Int. Ed., 2012, 51, 12597–12601.
34. S. Ohkoshi, S. Takano, K. Imoto, M. Yoshikiyo, A. Namai and H. Tokoro, Nat. Photonics, 2014, 8, 65–71.
35. H. Holovchenko, J. Dugay, M. Gimenez-Marques, R. Torres-Cavanillas, E. Coronado and H. S.-J. van der Zaant, Adv. Mater., 2016, 28, 7228–7233.
36. Y. Zan, L. Salmon and A. Bousseksou, Nanomaterials, 2021, 11, 3169.
37. J. E. Clements, P. R. Airey, F. Ragon, V. Shang, C. J. Kepert and S. M. Neville, Inorg. Chem., 2018, 57, 14930–14938.
38. M. Paez-Espejo, M. Sy and K. Boukheddaden, J. Am. Chem. Soc., 2018, 140, 11954–11964.
39. Y. Guo, S. Xue, M. M. Dirtu and Y. Garcia, J. Mater. Chem. C, 2018, 6, 3895–3900.
40. T. Boon-prab, S. J. Lee, S. J. Telfer, K. S. Murray, W. Phonsri, G. Chastanet, E. Collet, E. Trzop, G. N.-L. Jameson, P. Harding and D. J. Harding, Angew. Chem., Int. Ed., 2019, 58, 11811–11815.
41. Z. Liu, Y. Sakai, J. Yang, W. Li, Y. Liu, X. Ye, S. Qin, J. Chen, S. Agrestini, K. Chen, S.-C. Liao, S.-C. Haw, F. Baudelet, H. Ishii, T. Nishikubo, H. Ishizaki, T. Yamamoto, Z. Pan, M. Fukuda, K. Ohashi, K. Matsuno, A. Machida, T. Watanuki, S. Kawaguchi, A. M. Arevalo-Lopez, C. Jin, Z. Hu, J. P. Attfield, M. Azuma and Y. Long, J. Am. Chem. Soc., 2020, 142, 5731–5741.
42. J. Varignon, M. Bibes and A. Zunger, Nat. Commun., 2019, 10, 1658.
43. S. N. Vaidya, C. Karunakaran and S. T. Arina, High Pressure Res., 2001, 21, 79–92.
44. S. Rahman, S. Samanta, D. Errandonea, S. Yan, K. Yang, J. Lu and L. Wang, Phys. Rev. B, 2017, 95, 024107.
45. F. Bai, K. Bian, X. Huang, Z. Wang and H. Fan, Chem. Rev., 2019, 119, 7673–7717.
46. E. Coronado and G. M. Espallargas, Chem. Soc. Rev., 2013, 42, 1525–1539.
47. D. Pinkowicz, M. Rams, M. Mišek, K. V. Kamenev, H. Tomkowiak, A. Katrusiak and B. Sieklucka, J. Am. Chem. Soc., 2015, 137, 8795–8802.
48. A. B. Gaspar, G. Molnár, A. Rotaru and H. J. Shepherd, C. R. Chim, 2018, 21, 1095–1120.
49. C. P. Slichter and H. G. Drickamer, J. Chem. Phys., 1972, 56, 2142–2160.
50. F. Izumi and K. Momma, Solid State Phenom., 2007, 130, 15–20.

---

Footnote

† Electronic supplementary information (ESI) available: PXRD patterns, Rietveld analyses, pressure-induced temperature changes, high-temperature PXRD patterns, SD-model calculations, TEM images, and Curie paramagnetic component estimated from magnetic susceptibility. See DOI: https://doi.org/10.1039/d2ma00278g

---