Towards textile metamaterials: a pathway to auxeticity and tensegrity in a needle-punched nonwoven stiff felt

Abstract

Auxetics are a class of mechanical metamaterials that show a negative Poisson's ratio, which has been of interest as a mechanism to provide enhanced performance in, for example, composite materials and energy dissipation structures. Given this interest, there is a need to realize this behavior in a practical fashion. In this work, we move towards identifying and understanding such materials by examining the out-of-plane auxeticity of fiber networks contained in stiff felt nonwovens. The network contains fiber connections that provide a structure which is intermediate to a physically entangled nonwoven and a composite. The results show that these nonwovens display an out-of-plane auxetic response that is at least partially reversible. Additionally, it was found that the elastic-plastic behavior seen at larger strains can be described using concepts of multistable tensegrity structures, supporting the suggestion that tensegrity and auxeticity can coexist in some metamaterial structures.

---

Introduction

Mechanical metamaterials are those materials/structures whose properties are determined not by their specific chemical constitution but by their larger scale structural/topological organization. Among metamaterials and materials with “negative” properties,¹ auxetic materials and structures are a subcategory that has been studied extensively to elucidate the underlying structure–property relationships that drive their mechanical response.^2,3 Specifically, auxetics possess a negative Poisson's ratio,⁴ meaning that in the simplest case they show an expansion in at least one transverse direction when deformed in tension. The auxetic response is present in some natural materials like certain types of skin,⁵ in some metals along certain crystallographic directions,⁶ as well as in engineered materials in purposefully designed structures.^7,8 One of the most recognized engineered materials to display auxeticity is Lakes’ reentrant foam.⁹ Auxeticity is imparted to these foams through a post-processing heat compression step, which collapses the foam cell walls into a reentrant structure which produces an auxetic response in both transverse directions upon deformation. This mechanism for auxeticity has been described in models for reentrant honeycomb structures.^10,11 Beyond reentrant structures, several other structures have been identified that would produce auxetic behavior,² including chiral lattices,^12,13 arrays of rotating squares¹⁴ and triangles,¹⁵ and networks of fibrils and nodules.^16,17 Additionally, other types of auxetic engineered structures have been designed and fabricated including knitted structures,^18–20 polymer fibers consisting of fused particles,²¹ microporous polymers,^22–24 and helical fibers consisting of an assembly of two dissimilar fibers.^25–27 Modeling approaches have also shown pathways to producing composite materials with tunable auxeticity.^28,29 While the application space for auxetics is potentially large, many studies focus on applications in energy dissipation such as absorbing impact in sports³⁰ and acoustic dampening,^31,32 which take advantage of this unusual material response.

Within the family of auxetic materials and structures, networked fiber structures have emerged as a category of materials with robust auxeticity. While certain materials within this category have shown an in-plane auxetic response,^33,34 fiber networks often show an out-of-plane auxetic response, i.e., an increase in thickness when loaded in uniaxial tension. In these structures, the fiber arrangements and connectivities are thought to be responsible for the auxetic response. One of the first fiber networks to demonstrate this capability was paper.^35–38 This behavior has also been seen with stiffer materials. Jayanty et al. examined the auxetic character of sintered stainless steel fiber networks as well as their composites.³⁹ In the absence of a polymer matrix, the fiber network showed a negative out-of-plane Poisson's ratio that varied in magnitude as the open space in the network varied. The Poisson's ratio became more negative as the porosity in the network increased. The addition of a soft polymer matrix decreased the magnitude of Poisson's ratio, but it remained negative. Extension of these studies to a carbon nanofiber composite showed qualitatively similar results. Modeling results have shown that auxeticity can be expected for certain fiber networks and that the magnitude of this auxetic response correlates to the degree of fiber entanglement.⁴⁰

Nonwoven materials and other textile structures have also been studied as potential auxetics.⁴¹ The authors have previously investigated the auxeticity of different types of nonwovens, including needle-punched nonwovens made from polyester^42,43 and felted nonwovens made from wool.^44,45 For the needle-punched nonwovens, a heated compression treatment was used to impart an auxetic character to the fabric. Prior to the heated compression treatment, these fabrics consisted of an entangled web of polymer fibers with interspersed vertical columns of aligned fibers spanning the thickness of the fabric. Micro-computed tomography imaging showed that the heated compression treatment distorted the columns. Since the attachments of the columns to the top and bottom surfaces of the fabrics were maintained, in-plane tensile loading of the fabric acted to straighten the columns toward their original vertical orientation, leading to an auxetic response through an increase in the fabric thickness. The process variables used during the heated compression (temperature, time, and pressure) were found to affect the magnitude of Poisson's ratio, with more severe conditions producing a more negative value. Conversely, the wool felt was auxetic in its as-received condition, likely due to compression of the fiber network during its manufacture. Further treatment with heated compression enhanced the auxetic response. Since this wool felt nonwoven construction is not needle-punched, it does not contain fiber columns. We suggested that the mechanism for the auxetic response was similar to that observed for paper in that the thickness increase during tension was a cooperative effect of the network structure. As fibers oriented roughly in the loading direction straightened under load, neighboring fibers above and below these fibers moved vertically, resulting in a thickness increase under tension. While our work has shown that heated compression can enhance the auxetic effect in nonwovens, Rawal et al. have also examined the effect of process parameters during the needle punching operation for nonwovens and found that increasing the punch density (decreasing the spacing between fiber columns) can increase the auxetic effect in these fabrics.^46,47 Extending the auxetic behavior of needle-punched nonwovens, work by Dubrovski et al. have produced in-plane auxeticity in needle-punched nonwovens by using laser cutting to produce a rotating square pattern in the fabric.⁴⁸

This paper builds on what is known about auxetic nonwovens by examining the auxetic character of a stiff felt nonwoven. This type of nonwoven is of interest since its network structure includes elements of more than one type of auxetic nonwoven, and therefore, its auxeticity could result from multiple mechanisms. Stiff felts incorporate the structural characteristics of needle-punched nonwovens and paper in the sense that their network structure contains both, through-thickness fiber bundles as well as interfiber bonding. The stiffness arises from chemically bonded connections between the fibers that comprise the network. They are denser than the nonwovens previously studied and would be approaching a fully dense structure which may suggest routes for producing auxetic polymer composites. Additionally, it is of interest to investigate whether such interfiber bonding imparts tensegrity characteristics to the structure,^40,49–54 since the bonding provides continuity to a structure made up of discrete elements (fibers, fiber-bundles, fiber entanglements, etc.) that remain connected over large strain regimes. To elucidate the network deformation behavior of this material type and understand its auxetic behavior, mechanical testing and imaging studies were performed to characterize this bonded network and distinguish any unique features as compared to other nonwoven fiber networks.

Experimental

Materials

Stiff felt (PE-F-32125-48), a needle-punched nonwoven felt made of polyester fibers with a low melting component, was purchased from Sutherland Felt Company (Madison Heights, Michigan, USA). According to the manufacturer, the fibers are heat-compressed to ‘activate’ the low-melt component during processing, giving it a board-like rigidity.⁵⁵ Felts used in this study were 0.125 inches thick, obtained as a sheet with dimensions of 48 inches × 60 inches. This material was chosen for study since the low melt fibers provided a fiber network held together by physical entanglements (needle punched columns) and fused network points (melted material at fiber junctions).

Methods

Treatment protocol

Stiff felt samples were subjected to a simultaneous heat and pressure treatment, similar to the protocol used previously with polyester needle punched nonwoven fabrics^42,43 and wool felts.^44,45 Square samples measuring 6 inches × 6 inches were cut from the as-received sheet. These samples were compressed in a benchtop press (Carver auto series, model 4386) at a pressure of 2.5 MPa (a force of 6 metric tons applied over an area of 36 square inches, and assuming acceleration due to gravity to be 9.8 ms⁻²), at a temperature of 70 °C for a period of 24 hours. This temperature was near the glass transition temperature of PET, and hence was chosen for the treatment, like previous work,^42,43 in order to make the PET fibers more compliant under pressure. Heat flow data from a differential scanning calorimetry (DSC) measurement is given in Fig. S1 (ESI†) and shows the glass transition temperature of the as-received fabric. During the first heating cycle, the glass transition temperature is near 70 °C. In a subsequent heating cycle following programmed cooling, the glass transition temperature is below 70 °C. After treatment, the samples were stored in sealed plastic bags under ambient laboratory conditions. As-received samples are identified as AR, while treated samples are identified as TR.

Measurement of thickness and recovery over time

Before and after the heated compression treatment, the thickness of the material was measured. The thickness of the fabric was measured using a digital micrometer (Mitutoyo, model 369-350) having flat circular platens of diameter 2 cm. The shape and size of the platens compensated for the heterogeneity in the surface of the felt. Additionally, the platens consistently exerted a pressure of 20–25 kPa on the sample (according to the manufacturer), which was important in defining thickness of compressible materials. Thickness measurements provided information about how much compression was achieved and if any significant recovery was occurring following the heated compression. In this material, recovery would be observed through an increase in thickness, and this behavior has been observed previously.^42–45 To establish the time during which treated fabrics experienced recovery, the square sample was marked with four circles (of diameter 2 cm each) close to the corners of the square (approximately 5 cms from the edges), and the thickness was measured at each of these four locations over a period of 20 days. Samples were stored in sealed plastic bags in ambient laboratory conditions; samples were taken out for the measurement and put back into the bag after the measurement. Environmental conditions such as temperature and relative humidity were not actively monitored over the 20 day measurement period. Thickness was expressed as a percentage of original sample thickness (before treatment), averaged over the four regions, and plotted against time. Uncertainty in this measurement was given as the standard deviation of the data. From a visual observation of the plot, the number of days after which thickness recovery had sufficiently slowed to a near constant value, was noted.

Mechanical testing

Mechanical testing protocols were used to characterize several aspects of the deformation and auxetic behavior of the stiff felt materials. In all cases, a universal testing frame (Instron model 5566) was used to apply a uniaxial tensile deformation at ambient laboratory conditions. The samples tested had a gage length of 100 mm and a testing speed of 1 cm/min was used. Sample strain was measured using the crosshead displacement. These protocols are described below.

Thickness change with extension

To obtain the out-of-plane auxetic response of stiff felt samples (both AR and TR), variations in thickness with respect to axial deformation of the sample were examined. For TR samples, this experiment was performed after the sample had spontaneously recovered and attained the steady thickness value. Rectangular specimens with a length of 15 cm and a width of 2 cm were cut (with their lengths being in the long direction of the obtained sheet) and loaded into the mechanical testing frame and then subjected to uniaxial tensile deformation in displacement control. The test was paused at regular strain intervals, allowing the thickness to be measured at the center of the specimen (marked with a circle). The specimen length and the corresponding thickness values were recorded. From this data, thickness strain (with respect to thickness before loading) and axial strain (with respect to gage length) were calculated. This measurement took approximately 30 seconds. During this time, there was some drop in the applied load which was recovered when the test was started again. Instantaneous Poisson's ratios were obtained at each pause, from the ratio of thickness to axial strain with respect to those measured at the previous strain level. Six specimens for each sample type were tested, and the average value and standard deviation were calculated from the data.

Reversibility experiment

The reversible components of the deformations leading to thickness changes in TR were determined in a manner similar to that used previously for wool and polyester nonwovens.^44,45,56 Samples were allowed spontaneous thickness recovery over time before being tested for reversibility as described above. After this time period, rectangular strips were subjected to uniaxial tensile deformation to 1, 2, 3, 5, 10 or 20% strain maxima. Once the sample achieved the desired maximum strain, the test was paused, and the thickness was measured, similar to the procedure described for the thickness change experiments above. Subsequently, the sample was returned to the gage length separation of 10 cm (same 0% strain). Thickness was measured again. This process of loading and unloading the sample, along with measuring the thickness at each pause, was repeated over 5 cycles for each of the maximum strain values. Thickness changes were reported as a percentage, with respect to the original specimen thickness. Reversibility was expressed as the ratio of thickness decrease during return, to the thickness increase during loading step of the first cycle. Two samples were examined at each strain level for this experiment. These values were reported as the average of the two measured values with uncertainty given as the spread in the data.

Imaging

Scanning electron microscopy (SEM) was conducted using a Hitachi SU8010 electron microscope. Specimens were cut into a cube of a few millimeters in dimensions and mounted on an SEM stage using carbon tape. They were sputtered with about a 10 nm thick coating of gold–palladium alloy (using Quorum Q150T ES), prior to being introduced into the microscopy chamber. Additionally, micro-computed tomography (μCT) of both the AR and TR samples, was used to observe the three-dimensional arrangement of the fiber network. μCT was performed using a Scanco Medical μCT50 instrument. Disk-shaped specimens were cut using a biopsy punch (of diameter 5 mm) and positioned into a scanning tube of inner diameter 5 mm. Samples were then scanned using an X-ray source of energy 45 kVp at a resolution of 2 μm voxels. A cylindrical subsection (diameter slightly smaller than 5 mm and height of about 1 mm) of the specimen was digitally selected for scanning and subsequent computational construction yielding a 3D image, which could be viewed at various angles and sections.

Results and discussion

Fig. 1a shows the thickness recovery data for the TR sample. These results were used to establish the time frame over which significant recovery occurred and to identify the conditioning time after processing that would be needed prior to characterization experiments. Using a standard conditioning time allowed us to conduct characterization experiments at a time point where structural changes had effectively ceased, and the structure had attained a stable configuration.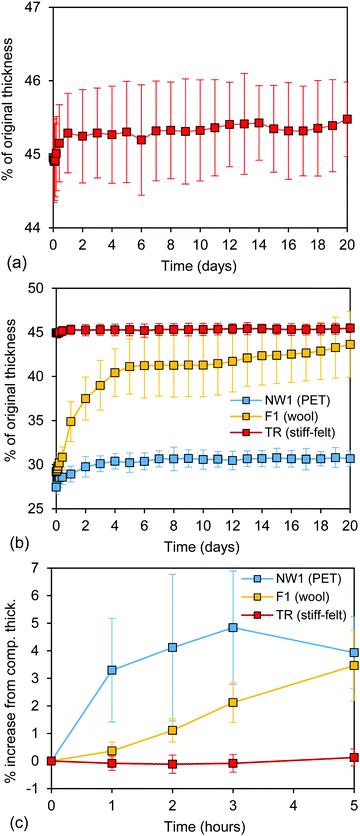

Fig. 1 (a) Thickness recovery over time for treated stiff felt (TR). Thickness has been expressed as the percentage of original (prior to treatment) sample thickness and was measured over a period of 20 days. Each datapoint represents an average of thickness measured at four corners of a square sample. Vertical bars indicate standard deviation in the measurement at these four points. (b) Comparison of thickness recovery over time (20 days) for TR (stiff felt) along with heat-compressed needle-punched PET (NW1)⁴² and wool (F1) nonwoven fabrics^44,45 – all treated similarly. (c) Initial thickness recovery comparison, where y-axis expresses the percent thickness increase from the compressed thickness after the sample was taken out of the press. Data for the first 5 hours has been shown.

For the TR sample, the initial compression achieved was approximately 45%. While the data indicated that the fabric's thickness increased slightly in the first day following the heated compression step, the change in percent compression values did not change significantly over the 20 day observation period. This trend suggested that limited structural relaxation occurred, which could have resulted from existing fiber junctions in the as-received material and possibly from additional fiber fusion caused by the heated compression process in the TR sample. Based on these results, a conditioning time of 7 days was used in further testing. In other fabric structures that we have characterized previously, heat compressed needle-punched PET nonwoven fabrics showed more relaxation, but only on the order of a few percent⁴² (Fig. 1b). In the heat-compressed wool felt, which did not have needle-punched columns, more significant relaxation was observed^44,45 (Fig. 1b). While the majority of the relaxation in the wool felt occurred by day 5, a smaller amount of relaxation continued to occur at later time points beyond ∼10 days. This small amount of relaxation at longer times could be related to the structure of the fiber network or potentially due to water absorption, though this effect was not specifically investigated. In order to compare the initial thickness recovery for these three types of nonwovens, thickness increase was calculated with respect to the compressed thickness (thickness measured right after the sample was taken out of the press) and plotted in Fig. 1c. It was observed that treated stiff felt showed the lowest thickness recovery, both, during the first few hours, and over the entire period of 20 days, indicative of the presence of inter-fiber bonding as well as distorted through-thickness fiber bundles.

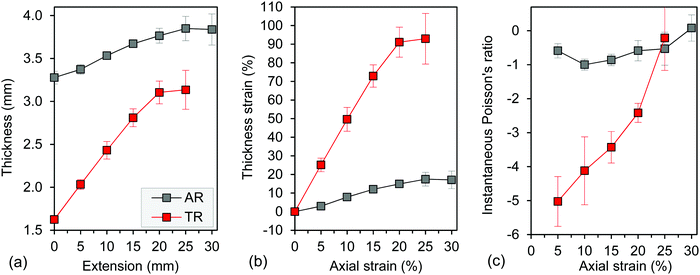
Fig. 2 shows the out-of-plane auxetic character of the AR and TR samples. Unlike other needle-punched nonwoven fabrics that we have examined previously, the stiff felt fabric was auxetic in the as-received state, and this response was enhanced with the heated compression treatment. The auxetic response was shown from the measured data as a thickness increase with uniaxial tensile deformation (Fig. 2a). While the TR sample experienced substantial thickness expansion, it did not attain the same final thickness as the AR sample, suggesting that the heated compression step imparted some permanent changes to the fiber network that limited the thickness expansion. As expected, the auxetic response was influenced by heated compression. At most axial strain values, the magnitudes of the thickness strain values and the instantaneous Poisson's ratio values, shown in Fig. 2b and c, respectively, were larger for the TR samples than the AR samples. Considering the average values of the instantaneous Poisson's ratio, both the AR and TR samples were auxetic at strain values up to 25%, but the trends observed for instantaneous Poisson's ratio were different. For the AR sample, the values for instantaneous Poisson's ratio showed less variation as the axial strain increased, suggesting that the network structure and mechanisms that were responsible for the auxetic response did not change substantially over the strain range. For the TR sample, the auxetic response decreased, as indicated by the values of the instantaneous Poisson's ratio becoming less negative and approaching zero as axial strain increased. However, at 25% axial strain, the instantaneous Poisson's ratio values were similar for the AR and TR samples. These trends are similar to those observed previously for PET needle-punched nonwovens⁴² and wool felts,^44,45 in that the value of the instantaneous Poisson's ratio was large and negative at smaller strains and became more similar to the as-received fabric at higher strains. Overall, these trends indicated that the structure of the treated sample was undergoing changes and was progressing toward its untreated structure with the application of tensile strain.

Fig. 2 (a) Thickness vs. extension plots for as-received and treated stiff felts – AR and TR. (b) Thickness strain vs. axial strain plots for AR and TR felts. (c) Instantaneous Poisson's ratio vs. axial strain for AR and TR felts. In each of (a), (b) and (c), every datapoint represents the average y-axis value of six specimens and vertical bars indicate the standard deviation in its measurement over these six specimens.

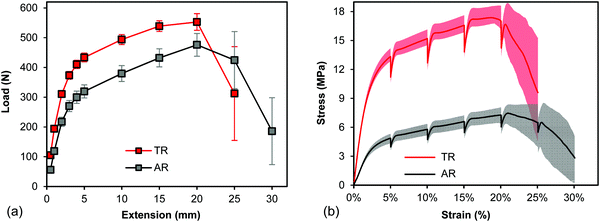
To investigate structural changes that may have occurred during the heated compression treatment, the stress–strain curves for the AR and TR samples from these experiments were also examined. As shown in Fig. 3, the TR felts required higher stresses to deform, indicating that the TR felts had a higher strength, but since the felts were not fully dense materials and the overall cross sectional area was used to calculate the stress, the load values associated with these stress values were also examined. At strain values up to 20%, the load experienced by the TR felt was higher than that for the AR sample, though the increase in load was lower than the increase in stress. For example, at 15% strain, the average load values for TR vs. AR samples were 539 (± 18) vs. 432 (± 30) N while the average (engineering) stress values were 16.6 (± 0.6) vs. 6.6 (± 0.5) MPa, respectively. Considering that increases in load were also observed and in general the strain associated with failure was reduced for the TR felt, it is likely that the heated compression step did produce some structural change in the network, such as increased interfiber entanglement/bonding. Another feature seen in the stress–strain plots is the effect of pausing the test to measure the sample thickness at prescribed strain values. For the AR and TR fabrics, the load (and corresponding stress) decreased when the experiment was paused at a fixed deformation, indicating some relaxation of the fabric during the measurement time. However, upon resuming the test, the stress increased, and after a small stress overshoot, the stress values appeared to be approximately continuous to the stress values before the pause.

Fig. 3 Load-extension data for select extensions (a) and stress–strain data (b) obtained from the thickness change with extension experiments. Error bars on load-extension plot are standard deviations calculated on load for the six specimens tested. Shaded area in the stress–strain plots envelope the maximum and minimum stress values.

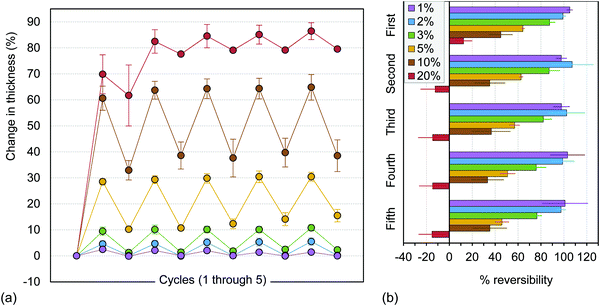
Reversibility experiments were conducted to evaluate the auxetic response with repeated tensile strain. The thickness increases observed at each strain level and at each cycle as well as the percent reversibility are shown in Fig. 4. The overall trends were consistent with what might be expected for low strain levels (1% and 2%) and strain levels in the plastic regime (3% and greater). Additionally, the results were qualitatively consistent with previous results obtained for wool felt, though some differences in the behavior at 20% strain were observed.^44,45 Elastic-plastic strain regimes were estimated from the stress–strain plots obtained during the ‘thickness change with extension’ experiments (shown in Fig. 3). In all cases tested here, the thickness increase increased with axial strain, i.e., 10% strain produced a larger thickness increase than 5% strain. This behavior was expected based on the results of the tests to measure Poisson's ratio. In those tests, the thickness of the TR samples continued to increase up to 20% strain (Fig. 2b). Strain levels of 1% and 2% demonstrated nearly full reversibility, with a larger thickness increase seen at 2% strain. For these strain levels, the thickness increased to near constant values over the course of five cycles and upon the release of deformation, the thickness returned to values near the original thickness. This behavior would be indicative of elastic deformation. It should be noted that a slack correction was not applied to these data, so the strain values include machine slack and should be considered approximate for these lower strain values.

Fig. 4 (a) Change in thickness over five loading-return cycles of TR sample. Each datapoint represents average thickness percent change at each strain and for each cycle for two specimens. Error bars denote the range of values for the two specimens. (b) Percentage of reversible component of thickness changes with respect to thickness change during the first loading. Error bars denote the range of values for the two specimens.

The next highest strain level, 3%, showed similar behavior, but the thickness remained larger than the original thickness when the strain was removed, indicating that some permanent changes to the network structure had occurred. Additionally, the reversibility decreased after the first two cycles, suggesting that damage accumulation (irreversible structural change) was occurring.

Samples tested at higher strain values (5%, 10%, and 20%) showed even larger deviations from the starting thickness as the cycles proceeded, which would be expected as the amount of plastic deformation during the first cycle increased. However, the behavior of samples tested at 5% and 10% were more similar in character. The thickness values at each of these strains were not similar in their values, but the thickness increase difference between loading and unloading was similar until the third unloading step. Both sets of samples showed a difference of about 20% in the thickness values between loading and unloading, suggesting that the same structural features might be responsible for the recovery at these strain levels. Likely, these features were the needle punched columns.

At the highest strain level used in this work, the thickness increase data indicated a different behavior. The overall thickness increase was the largest observed, but the amount of recovery in cycles 2 through 5 was small, approximately 5% of original thickness. A lesser amount of recovery suggested that the needle-punched columns were likely damaged at this strain level and the structural features which were left intact, primarily inter-fiber bonds, could only provide small amounts of recovery.

Analogous trends were observed in the percent reversibility data shown in Fig. 4b: (1) reversibility decreased as the applied strain increased, for any given cycle and (2) reversibility decreased as the number of cycles increased for any given strain level. There were a couple of exceptions where average reversibility of 2% data was higher than that of 1% strain (second and third cycles), but the error in 2% strain data was large in these instances. The negative reversibility for 20% strain (second cycle onwards) was a mathematical artefact arising from the reversibility being calculated with respect to the first cycle and, in the case of 20% strain, the minimum thickness attained for second cycle and onwards was still higher than the maximum thickness obtained during the first cycle.

Additionally, trends observed in reversibility were reflected in the trends observed in the loading stress. These data are shown as adjusted stress vs. strain plots in ESI† (Fig. S2). For 2% and higher strain level experiments, a gap between the first cycle stress and subsequent cycles appeared and kept increasing in magnitude – consistent with irreversibility trend. Furthermore, as the number of cycles increased in a particular experiment, the stress levels decreased but were also observed to approach an asymptotic value (suggesting approach towards a ‘settled’ structure) at the 5th cycle. This behavior has been observed in other porous materials such as foams and described by the Mullins effect.^57,58 The Mullins effect, which describes stress softening upon cyclic loading, was originally observed in elastomers⁵⁹ but is present in porous materials as well. In elastomers, the Mullins effect is correlated with a change in the structure of reinforcement particle clusters. For porous materials, the Mullins effect would be correlated to a change in a different structural feature or features, such as fiber entanglements or at higher strains, changes to the buckled columns. This stress softening is likely related to the trends seen in reversibility.

Structural characterization of the AR and TR fabrics was performed using SEM and μCT. The SEM imaging focused primarily on the compressed surfaces, whereas the μCT provided information about the internal structure. SEM images of the AR and TR fabrics are shown in Fig. 5. The fabric surface did not show large differences in appearance following heat compression treatment. Both fabrics showed some fusion of individual fibers, which would be expected since the fabrics were produced from fibers containing a low melting component. It appeared that additional melting occurred during the heated compression treatment. Additionally, the fibers in the TR fabric showed some flattening and exposure of the inner fiber. While this feature was also observed in the AR fabric, the effect was more pronounced after heat treatment, suggesting that additional inter-fiber bonds may have been produced by the heat treatment through fiber fusion and increased entanglement. This result is consistent with the reduced thickness recovery of the TR fabrics and overall mechanical behavior.

Fig. 5 SEM images of AR fabric (a–c) and TR fabric (d–f) The images suggested that additional inter-fiber bonding occurred during heat treatment.

The μCT imaging provided some complementary information about the structure and insight into the effect of heat compression on the structure of the needle punched columns. The images for the AR and TR fabrics are shown in Fig. 6. Considering the surface of the fabric, which in these images was an internal “surface” and not the outer surfaces as shown in the SEM imaging, the AR fabric showed the expected features. Specifically, the cross section of the needle punched columns were visible as roughly circular collections of fibers in the in-plane view and relatively vertical fiber assemblies as seen through the cross section, though some tilting of the fiber columns was seen. The TR fabrics showed a greater deformation of the needle punched columns, with rotated and distorted structures visible in the cross section. The individual fibers also appeared to be packed more densely in the TR fabric, as would be anticipated. The microstructural features observed were similar to those seen for the needle punched polyester fabrics studied by the authors previously.^42,43

Fig. 6 μCT images of the AR fabric (a) and TR fabric (b).

Considering the results of structural characterization and mechanical properties together, we propose that the stiff felt structure in its AR and TR states combines aspects of auxeticity and tensegrity in a manner similar to the reentrant tensegrity structure recently described by Oster et al.⁶⁰ Tensegrity is a structural design concept employed in engineering, science, and art and is generally described as having compressed elements contained inside of a network of tensioned elements. The elements are connected to one another, and this network is stabilized by prestress.

In Oster et al., the reentrant tensegrity structure was built and studied computationally and then subsequently validated experimentally using a 3D printed structure. While the reentrant tensegrity structure was periodic and element conformations were more regular than what would be expected for the stiff felts, the similarities in the reentrant tensegrity structure and the stiff felt structure are compelling. The reentrant tensegrity structure contained a three-dimensional, periodic arrangement of cylinders which were deformed from a linear conformation to a curvilinear conformation, though still oriented in the same direction. These fibers were connected to those around them through rigid bars. Integrating buckled/wavy elements into the prestressed network allowed for auxeticity and tensegrity to be present in a single structure.

In order to check the applicability of the model in Oster et al. to our materials, one could consider a possible mapping of its structural features to the stiff felt. The cylinders with a curvilinear conformation resembled the distorted fiber columns in the stiff felts, though the reentrant tensegrity structure had these columns regularly arranged and oriented in three orthonormal directions. The fiber columns in the stiff felt were present in the thickness direction of the fabric only and were not arranged regularly. The function of the rigid bars in the reentrant tensegrity structure would be performed by the fibers connecting columns in the felt. The fibers connecting the columns were not perfectly rigid or short, but they were constrained and connected to one another in a network of fibers, though the level of constraint may be different in different areas of the fabric. For the stiff felts, the inter-fiber bonds could be in the form of bonded connections as seen in the SEM image or physical entanglements. The former is specific to the stiff felts, while the latter could be present in most any nonwoven structure. The reentrant tensegrity model described by Oster et al. also contains structural chirality which does not seem to be present in the same way in the stiff felts. Though, some asymmetry could be present due to slight tilting of the fiber columns observed with μCT. This tilting in the AR sample is expected to occur during manufacturing since the needle-punching operation is performed on a moving fiber web. Beyond these structural features, another element of tensegrity is prestress in the structure. For the stiff felts and other nonwoven structures, prestress can be imparted to the fiber network during manufacturing and maintained since the network contains connections that prevent or hinder fibers slipping past each other when loaded.⁴⁰ The degree of prestress would be affected by the processing steps used to produce the nonwoven as well as any post-processing steps like the heated compression steps used to make the stiff felt (AR) and enhance the auxetic response (TR). Aside from the structural similarities, the modeling results for the reentrant tensegrity structure has shown that the auxeticity is reversible under cyclic loading, similar to what we have shown in this work.

The implications of these similarities in structure and performance between the stiff felt and the reentrant tensegrity structure further suggest that nonwoven and other textile structures are a powerful platform for realizing unique structures in a scalable, accessible fashion. Specifically, the current work has achieved substantial auxeticity with a common material arranged in an imprecise structure that was produced by large scale manufacturing. It is likely the small-scale network irregularity (for example: variations in fiber orientation and configuration; fiber bundle size and tilt; differing strength of fiber connectivity) in these stiff felts that contributes to their ability to undergo gradual morphing of the average network arrangement as strain is increased – at first reversible and later elastic-plastic network configurations – followed by removal of load and specimen relaxation. In the elastic-plastic regime the interplay of these factors in the locally inhomogeneous, but globally homogeneous network results in the macroscopic sample being able to realize a ‘stable’ relaxed arrangement for each maximum strain value. In this way, the behavior is analogous to what has been described as multistable tensegrity structures in which there exists a barrier to interconversion among the stable states.^61,62 In our case, we feel it is mechanical energy (subsequent strain cycle) that activates this conversion to a new network configuration. These results support the assertion that highly entangled/connected fiber networks can behave as tensegrity structures and suggest pathways for understanding how auxeticity and tensegrity can be used together in material constructs such as mechanical metamaterials and composites.

Conclusion

In this research, a stiff felt nonwoven fabric was characterized to establish its out-of-plane auxetic response in the as-received state (AR) and following post-processing treatment with heated compression (TR). This nonwoven fabric provided additional insight about the auxeticity of fiber networks since its structure was intermediate to a physically entangled nonwoven and a composite. In the stiff felt, the fibers were connected to one another through a low melting component as well as through physical entanglements (purposefully included needle-punched columns and entangled fibers between columns), but the open space in the fiber network was not completely filled by a matrix, allowing further consolidation of the fiber network with heated compression. This combination of network attributes may provide a stepping-stone or transition material to guide similarly motivated research with polymer composites.

The results of the mechanical characterization performed in this study indicated some similarities in the auxetic character of stiff felt and other nonwovens with different structures, specifically, needle-punched nonwovens and felted nonwovens. Unlike previously studied needle-punched nonwovens, the stiff felt was slightly auxetic in the as-received state, likely due to the heated compression step used to activate the low melting component in the fiber system which would impart some deformation to the needle-punched columns. As with other work with nonwovens, the heated compression step was able to impart a greater auxetic character to the fiber network, and the magnitude of Poisson's ratio at lower strains was comparable to what had been achieved previously. The effect was found to be at least partially reversible up to strain values near the fracture strain, suggesting that elements of the network that contribute to the auxetic response remained intact through the deformation.

Overall, these results provided an improved understanding of how nonwoven structures fit into the family of mechanical metamaterials and how they can be designed to produce an out-of-plane auxetic response with applications in composites and structures for multiple types of energy dissipation. While the commercially available fabrics studied so far have been made from commodity polymers and natural fibers, this manufacturing process is also applicable with high performance fibers, providing guidelines for working with high performance fibers and other materials of interest. Beyond examining the auxeticity, the stiff felt structure may also be useful to elucidate connections between auxeticity and tensegrity. This connection has been intimated by some studies and shown computationally. However, practical examples of structures that may show the connection are more difficult to obtain. Similarities between the stiff felt structure and the reentrant tensegrity structure are compelling and could be explored further to establish relationships between auxeticity and tensegrity and provide performance parameters that define when auxeticity and tensegrity are present simultaneously and when they are not.

Author contributions

Prateek Verma: conceptualization, methodology, formal analysis, investigation, data curation, writing – original draft, writing – review & editing, visualization; Casey L. Smith: conceptualization, methodology, investigation, writing – review & editing; Anselm C. Griffin: conceptualization, methodology, supervision, writing – review & editing; Meisha L. Shofner: conceptualization, methodology, supervision, writing – original draft, writing – review & editing, funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by internal funding from Georgia Tech. The authors would like to thank Robert Hughley, Angela Lin and Laxminarayanan Krishnan for their help with obtaining μCT images. This work was performed in part at the Georgia Tech Institute for Electronics and Nanotechnology, a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (ECCS-2025462)

References

1. T.-C. Lim, Mechanics of Metamaterials with Negative Parameters, Springer Nature, Singapore, 2020.
2. T.-C. Lim, Auxetic Materials and Structures, Springer, Singapore, 2015.
3. P. U. Kelkar, H. S. Kim, K.-H. Cho, J. Y. Kwak, C.-Y. Kang and H.-C. Song, Cellular auxetic structures for mechanical metamaterials: A review, Sensors, 2020, 20, 3132.
4. G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Poisson's ratio and modern materials, Nat. Mater., 2011, 10, 823–837.
5. D. R. Veronda and R. A. Westmann, Mechanical characterization of skin—Finite deformations, J. Biomech., 1970, 3, 111–124.
6. R. H. Baughman, J. M. Shacklette, A. A. Zakhidov and S. Stafström, Negative Poisson's ratios as a common feature of cubic metals, Nature, 1998, 392, 362–365.
7. Y. Hou, R. Neville, F. Scarpa, C. Remillat, B. Gu and M. Ruzzene, Graded conventional-auxetic Kirigami sandwich structures: Flatwise compression and edgewise loading, Composites, Part B, 2014, 59, 33–42.
8. F. Scarpa, M. Ouisse, M. Collet and K. Saito, Kirigami auxetic pyramidal core: Mechanical properties and wave propagation analysis in damped lattice, J. Vib. Acoust., 2013, 135, 041001.
9. R. Lakes, Foam structures with a negative Poisson's ratio, Science, 1987, 235, 1038–1040.
10. T. L. Warren, Negative Poisson's ratio in a transversely isotropic foam structure, J. Appl. Phys., 1990, 67, 7591–7594.
11. C. W. Smith, J. N. Grima and K. E. Evans, A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model, Acta Mater., 2000, 48, 4349–4356.
12. D. Prall and R. S. Lakes, Properties of a chiral honeycomb with a Poisson's ratio of—1, Int. J. Mech. Sci., 1997, 39, 305–314.
13. A. Spadoni and M. Ruzzene, Elasto-static micropolar behavior of a chiral auxetic lattice, J. Mech. Phys. Solids, 2012, 60, 156–171.
14. J. N. Grima and K. E. Evans, Auxetic behavior from rotating squares, 2000.
15. J. N. Grima and K. E. Evans, Auxetic behavior from rotating triangles, J. Mater. Sci., 2006, 41, 3193–3196.
16. A. Alderson and K. E. Evans, Microstructural modelling of auxetic microporous polymers, J. Mater. Sci., 1995, 30, 3319–3332.
17. A. Alderson and K. E. Evans, Modelling concurrent deformation mechanisms in auxetic microporous polymers, J. Mater. Sci., 1997, 32, 2797–2809.
18. M. Glazzard and P. Breedon, Weft-knitted auxetic textile design, Phys. Status Solidi B, 2014, 251, 267–272.
19. K. Alderson, A. Alderson, S. Anand, V. Simkins, S. Nazare and N. Ravirala, Auxetic warp knit textile structures, Phys. Status Solidi B, 2012, 249, 1322–1329.
20. H. Hu, Z. Wang and S. Liu, Development of auxetic fabrics using flat knitting technology, Text. Res. J., 2011, 81, 1493–1502.
21. K. L. Alderson, A. Alderson, G. Smart, V. R. Simkins and P. J. Davies, Auxetic polypropylene fibres: Part 1 – Manufacture and characterisation, Plast., Rubber Compos., 2002, 31, 344–349.
22. K. L. Alderson and K. E. Evans, The fabrication of microporous polyethylene having a negative Poisson's ratio, Polymer, 1992, 33, 4435–4438.
23. B. D. Caddock and K. E. Evans, Microporous materials with negative Poisson's ratios. I. Microstructure and mechanical properties, J. Phys. D: Appl. Phys., 1989, 22, 1877.
24. K. E. Evans and B. D. Caddock, Microporous materials with negative Poisson's ratios. II. Mechanisms and interpretation, J. Phys. D: Appl. Phys., 1989, 22, 1883.
25. S. Bhattacharya, G. H. Zhang, O. Ghita and K. E. Evans, The variation in Poisson's ratio caused by interactions between core and wrap in helical composite auxetic yarns, Compos. Sci. Technol., 2014, 102, 87–93.
26. M. Sloan, J. Wright and K. Evans, The helical auxetic yarn–A novel structure for composites and textiles; geometry, manufacture and mechanical properties, Mech. Mater., 2011, 43, 476–486.
27. G. Zhang, O. Ghita, C. Lin and K. E. Evans, Varying the performance of helical auxetic yarns by altering component properties and geometry, Compos. Struct., 2016, 140, 369–377.
28. G. W. Milton, Composite materials with Poisson's ratios close to -1, J. Mech. Phys. Solids, 1992, 40, 1105–1137.
29. T. Strek, H. Jopek and E. Idczak, Computational design of two-phase auxetic structures, Phys. Status Solidi B, 2016, 253, 1387–1394.
30. M. Sanami, N. Ravirala, K. Alderson and A. Alderson, Auxetic materials for sports applications, Procedia Eng., 2014, 72, 453–458.
31. F. Scarpa, F. Dallocchio and M. Ruzzene, Identification of acoustic properties of auxetic foams, Proc. SPIE 5052, Smart Structures and Materials 2003, 468–474.
32. B. Howell, P. Prendergast and L. Hansen, Examination of acoustic behavior of negative Poisson's ratio materials, Appl. Acoust., 1994, 43, 141–148.
33. L. J. Hall, V. R. Coluci, D. S. Galvão, M. E. Kozlov, M. Zhang, S. O. Dantas and R. H. Baughman, Sign change of Poisson's ratio for carbon nanotube sheets, Science, 2008, 320, 504–507.
34. S. Tanpichai, F. Quero, M. Nogi, H. Yano, R. J. Young, T. Lindström, W. W. Sampson and S. J. Eichhorn, Effective Young's modulus of bacterial and microfibrillated cellulose fibrils in fibrous networks, Biomacromolecules, 2012, 13, 1340–1349.
35. O. E. Öhrn, Thickness variations of paper on stretching, Sven. Papperstidn., 1965, 68, 141–149.
36. N. Stenberg and C. Fellers, Out-of-plane Poisson's ratios of paper and paperboard, Nord. Pulp Pap. Res. J., 2002, 17, 387–394.
37. G. Baum, K. Pers, D. R. Shepard and T. R. Ave'Lallemant, Wet straining of paper, Tappi, 1984, 67, 100–104.
38. P. Verma, M. L. Shofner and A. C. Griffin, Deconstructing the auxetic behavior of paper, Phys. Status Solidi B, 2014, 251, 289–296.
39. S. Jayanty, J. Crowe and L. Berhan, Auxetic fibre networks and their composites, Phys. Status Solidi B, 2011, 248, 73–81.
40. V. Negi and R. C. Picu, Tensile behavior of non-crosslinked networks of athermal fibers in the presence of entanglements and friction, Soft Matter, 2021, 17, 10186–10197.
41. Y. Chang and H. Hu, 3D fabrics with negative Poisson's ratio: A review, Appl. Compos. Mater., 2022, 29, 95–108.
42. P. Verma, M. L. Shofner, A. Lin, K. B. Wagner and A. C. Griffin, Inducing out-of-plane auxetic behavior in needle-punched nonwovens, Phys. Status Solidi B, 2015, 252, 1455–1464.
43. P. Verma, M. L. Shofner, A. Lin, K. B. Wagner and A. C. Griffin, Induction of auxetic response in needle-punched nonwovens: Effects of temperature, pressure, and time, Phys. Status Solidi B, 2016, 253, 1270–1278.
44. P. Verma, C. L. Smith, A. C. Griffin and M. L. Shofner, Wool nonwovens as candidates for commodity auxetic materials, Engineering Research Express, 2020, 2, 045034.
45. P. Verma, C. L. Smith, A. C. Griffin and M. L. Shofner, Corrigendum: Wool nonwovens as candidates for commodity auxetic materials (2020 Eng. Res. Express 2 045034), Engineering Research Express, 2022, 4, 029501.
46. A. Rawal, V. Kumar, H. Saraswat, D. Weerasinghe, K. Wild, D. Hietel and M. Dauner, Creating three-dimensional (3D) fiber networks with out-of-plane auxetic behavior over large deformations, J. Mater. Sci., 2017, 52, 2534–2548.
47. A. Rawal, S. Sharma, V. Kumar, P. V. K. Rao, H. Saraswat, N. K. Jangir, R. Kumar, D. Hietel and M. Dauner, Micromechanical analysis of nonwoven materials with tunable out-of-plane auxetic behavior, Mech. Mater., 2019, 129, 236–245.
48. P. Dobnik Dubrovski, N. Novak, M. Borovinšek, M. Vesenjak and Z. Ren, In-plane behavior of auxetic non-woven fabric based on rotating square unit geometry under tensile load, Polymers, 2019, 11, 1040.
49. R. P. Bywater, A tensegrity model for hydrogen bond networks in proteins, Heliyon, 2017, 3, e00307.
50. R. B. Fuller, Tensegrity, Portfolio and Art News Annual, 1961, vol. 4, supp. 112–127, p. 148.
51. J. H. Lee and M. L. Shofner, Tensegrity-inspired polymer nanocomposites, Polymer, 2017, 111, 9–19.
52. A. Sidorenko, T. Krupenkin, A. Taylor, P. Fratzl and J. Aizenberg, Reversible switching of hydrogel-actuated nanostructures into complex micropatterns, Science, 2007, 315, 487–490.
53. W. Ren, W. M. Kline, P. J. McMullan and A. C. Griffin, Thermal strain recovery of anelastic monodomain liquid crystalline networks: Mechanically induced strains ratios, Phys. Status Solidi B, 2011, 248, 105–110.
54. W. T. Ren and A. C. Griffin, Mechanism of strain retention and shape memory in main chain liquid crystalline networks, Phys. Status Solidi B, 2012, 249, 1379–1385.
55. Stiff felt, https://sutherlandfelt.com/felt/stiff-felt/, accessed [cited March 31, 2020.
56. P. Verma, K. B. Wagner, A. C. Griffin and M. L. Shofner, Reversibility of auxetic response in needle-punched nonwovens, in preparation.
57. G. S. Batt, J. M. Gibert and M. Daqaq, Small strain vibration of a continuous, linearized viscoelastic rod of expanded polymer cushion material, J. Sound Vib., 2015, 349, 330–347.
58. Q. Zhang, X. Yu, F. Scarpa, D. Barton, K. Rankin, Z.-Q. Lang and D. Zhang, Anisotropy in conventional and uniaxially thermoformed auxetic polymer foams, Composites, Part B, 2022, 237, 109849.
59. L. Mullins, Effect of stretching on the properties of rubber, Rubber Chem. Technol., 1948, 21, 281–300.
60. M. Oster, M. A. Dias, T. D. Wolff and M. E. Evans, Reentrant tensegrity: A three-periodic, chiral, tensegrity structure that is auxetic, Sci. Adv., 2021, 7, eabj6737.
61. P. Schorr, F. Schale, J. M. Otterbach, L. Zentner, K. Zimmermann and V. Böhm, presented in part at the IEEE International Conference on Robotics and Automation (ICRA), Virtual Conference, 2020.
62. S. Sumi, V. Böhm and K. Zimmermann, A multistable tensegrity structure with a gripper application, Mech. Mach. Theory, 2017, 114, 204–217.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00405d

---