Open Access Article
Open Access ArticleThermal hysteresis of stress and strain in spin-crossover@polymer composites: towards a rational design of actuator devices†
José Elias
Angulo-Cervera
 ,
Mario
Piedrahita-Bello
,
Baptiste
Martin
,
Seyed Ehsan
Alavi
,
William
Nicolazzi
,
Lionel
Salmon
,
Mario
Piedrahita-Bello
,
Baptiste
Martin
,
Seyed Ehsan
Alavi
,
William
Nicolazzi
,
Lionel
Salmon
 ,
Gábor
Molnár
,
Gábor
Molnár
 * and
Azzedine
Bousseksou
*
* and
Azzedine
Bousseksou
*
LCC, CNRS & University of Toulouse, 205 route de Narbonne, 31077 Toulouse, France. E-mail: azzedine.bousseksou@lcc-toulouse.fr; gabor.molnar@lcc-toulouse.fr
First published on 23rd May 2022
Abstract
Polymer composites of molecular spin crossover complexes have emerged as promising mechanical actuator materials, but their effective thermomechanical properties remain elusive. In this work, we investigated a series of iron(II)-triazole@P(VDF-TrFE) particulate composites using a tensile testing stage with temperature control. From these measurements, we assessed the temperature dependence of the Young's modulus as well as the free deformation and blocking stress, associated with the thermally-induced spin transition. The results denote that the expansion of the particles at the spin transition is effectively transferred to the macroscopic composite material, providing ca. 1–3% axial strain for 25% particle load. This strain is in excess of the ‘neat’ particle strain, which we attribute to particle-matrix mechanical coupling. On the other hand, the blocking stress (∼1 MPa) appears reduced by the softening of the composite around the spin transition temperature.
Introduction
Molecular spin crossover (SCO) complexes of 3d4–3d7 transition metal ions can be reversibly interconverted between their low spin (LS) and high spin (HS) states using different external stimuli (such as temperature, pressure and light irradiation).1,2 When switching the spin state of an SCO molecule from the LS to the HS state, the antibonding eg orbitals are populated at the detriment of the non-bonding t2g orbitals of the metal ion which is concomitant with a (reversible) elongation of the metal–ligand bond lengths.3 In molecular crystals, the LS to HS transition is therefore accompanied by a substantial expansion of the lattice: up to 22% in volume and up to 11% uniaxial.4–6 This huge transformation strain has motivated research to harness different forms of energy into useful mechanical work via the SCO phenomenon, with potential applications in robotic, biomedical and nano-technologies.7–24In this context, embedding SCO particles into polymer matrices provides a versatile means for exploiting this mechanical strain in actuating,7,8,11–13,15–17,19,20,22,23 sensing9,10,21 and energy harvesting14,18 devices. Indeed, a polymer matrix allows for convenient processing the SCO material, such as dispersions of microcrystals, nanoparticles, nanorods or molecules, to obtain functional objects with arbitrary shapes at different size scales, including both macroscopic and micro/nanoscale devices.25–28 In addition, SCO particle-matrix mechanical interactions in polymer composites may sizably alter the SCO properties and can be thus potentially used to fine-tune the spin transition behaviour. Such matrix effects have notably been reported on the spin transition temperature, hysteresis width and kinetic properties.29–33 Despite this considerable practical interest, the current knowledge about the effective thermomechanical properties of SCO@polymer composites remains largely incomplete,13,14,17,19,20,34,35 making rational material and device designs difficult. Of particular interest would be to understand how efficiently one could transform the elastic strain energy stored in SCO particles7 (up to several tenths of J cm−3) into a force or a stroke in a SCO@polymer composite material. To investigate this important question, we report here a thermomechanical analysis (TMA) of a series of Fe(II)-triazole@P(VDF70-TrFE30) particulate composites in the form of blade-casted, freestanding films. (VDF and TrFE stand for vinylidene fluoride and trifluoro-ethylene, respectively.) We use a variable-temperature tensile stage to evaluate the Young's modulus of the composites at selected temperatures as well as to assess the SCO-induced expansion and the stress under isostress and isostrain conditions, respectively. We selected iron-triazole family complexes (Fig. 1(a)) for this study for two main reasons: (i) the important volume change of the unit cell36,37 and (ii) the SCO above room temperature, which are crucial assets for technological applications in actuating devices. On the other hand, the P(VDF-TrFE) matrix (Fig. 1(b)) was used mainly for its good processability, either by solvent routes, such as blade-casting, spin- and spray-coating, or by melting.38,39
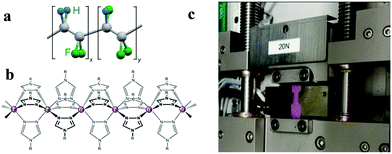 | ||
| Fig. 1 (a) Structure of the copolymer P(VDF-TrFE), (b) scheme of the iron(II)-triazole chain and (c) photo of a dog-bone-shaped sample (pink) clamped in the tensile stage. | ||
Experimental
Sample synthesis
The synthesis and characterization of nanoparticles of formulae [Fe(Htrz)2(trz)](BF4) (1), [Fe(Htrz)2.1(trz)0.8(NH2trz)0.1](BF4)1.2 (2) and [Fe(Htrz)2.05(trz)0.75(NH2trz)0.2](BF4)1.25 (3) was described in ref. 40 (trz = 1,2,4-triazolato), whereas that of [Fe(NH2trz)3]SO4 (4) particles was given in ref. 18. We shall note that among the numerous Fe(II) triazole complexes,41 we opted for compounds 1 and 4 because of their robust and well reproducible spin crossover properties and, importantly, because their crystal structure is known,36,42 which is not frequent in this family of compounds. On the other hand, compounds 2 and 3, which can be considered as derivatives of 1, were added to the study with the aim to more firmly confirm the main findings. P(VDF-TrFE) with a VDF/TrFE ratio of 70/30 was provided by Piezotech. The SCO@P(VDF-TrFE) composites were blade casted using the protocol reported in ref. 19. The films were then annealed at 105 °C for 12 h and finally brought slowly (2 h) to room temperature. The obtained composite films (1C–4C) have ca. 100 μm thickness and a few cm2 area. Since the mass densities of the polymer matrix and the SCO particles are similar (ca. 1.8–2.0 g cm−3), the weight and volume fractions of the filler can be considered approximately the same (ca. 25 wt% and 25 vol%). It should be noted that this specific particle concentration was chosen, based on our actuator device studies,24 as a compromise between small loads (i.e. weak SCO-induced effects) and high loads with increasing difficulties in homogeneous particle dispersion.Characterization methods
The SCO properties of the samples were characterized by differential scanning calorimetry (DSC) using a Thermal Analysis DSC 2920 instrument with a heating/cooling ramp of 10 °C min−1. Temperature and enthalpy were calibrated using the melting transition of indium. The particle morphology of the SCO powders was investigated by transmission electron microscopy (TEM) using a JEOL JEM-1011 instrument. TEM samples were prepared by placing a drop of the particles suspended in ethanol on a carbon-coated copper grid. Scanning electron microscopy (SEM) images of the composites were obtained by means of a HITACHI S-4800 electronic microscope operated in secondary electron mode. The composite films were fractured at liquid nitrogen temperature to study their cross-section by SEM.Thermomechanical analysis
The tensile properties of the composites were measured by cutting the films in dog-bone-shaped probes with a gage zone of typically L = 5.5 mm in length and W = 2–3 mm in width (Fig. 1(c)). The thermotensile testing was carried out using a TST350E tensile stage (Linkam Scientific). Three main tensile properties were tested: (i) the Young's modulus (E), extracted from constant temperature stress–strain curves; (ii) the strain associated with the SCO phenomenon (εSCO), extracted from temperature cycles under constant stress; and (iii) the blocking stress associated with the SCO phenomenon (σSCO), extracted from temperature cycles under constant strain. All experiments were done in the axial direction of the gage zone and we report the average values of at least five measurements.Prior to the mechanical tests, the samples were submitted to at least one heating–cooling cycle to avoid the undesirable effects of the first thermal cycle (solvent loss, stress relaxation, etc.). The Young's moduli of the samples were assessed isothermally by increasing and decreasing the strain at a constant rate of 0.2 μm s−1 and measuring the resulting force, from which the engineering stress is calculated. To measure the thermal expansion (resp. thermal stress), an initial stress (resp. strain) was applied to the sample held at 45 °C by stretching it at a rate of 0.2 μm s−1. Following further 10 minutes stabilization, a heating–cooling cycle was carried out at a rate of 1 °C min−1, while keeping the force (resp. distance) constant. The measurement output is the clamp position (resp. force), from which the strain (resp. stress) is calculated as a function of the temperature. Once the maximum temperature is reached, the probe is left at constant temperature for 5 minutes before cooling it back to the initial temperature. The thermal cycles were reiterated with small force (resp. strain) increments in the linear elastic regime allowing for extrapolation to zero force (resp. strain). During the TMA measurements, the colour change arising due to the SCO phenomenon was characterized in situ by variable-temperature optical reflectivity measurements, using an Olympus BXFM microscope equipped with a 5× magnification lens and a colour camera (Motic).
Results and discussion
Composite microstructure and spin crossover properties
Fig. 2 shows representative TEM images of the various SCO particles used in our work. Since samples 1–3 consist very similar, ca. 50 nm mean size particles with broad size distributions and irregular shapes, only sample 1 is shown (see Fig. S1 in the ESI† for TEM images of the other samples). On the contrary, sample 4 consists of rod-shaped particles with a mean length of ca. 2 μm and a mean width of ca. 0.3 μm.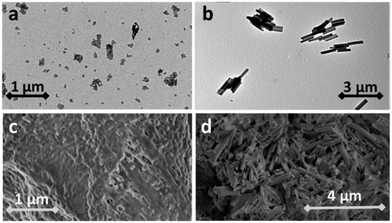 | ||
| Fig. 2 Representative TEM images showing the typical particle morphologies of sample 1 (a) and 4 (b), and representative SEM images showing the cross-sections of composites 1C (c) and 4C (d). | ||
Representative SEM images of the composites are also shown in Fig. 2 and Fig. S2 (ESI†). A homogeneous dispersion of the particles can be observed in each case, without any pronounced aggregation, thanks to a thorough ultrasonic agitation of the particle suspension before mixing with the polymer. No preferential particle orientation is apparent, though one shall note that the blade-casting process tends to align anisometric particles.20 The thermal spin crossover properties of the composites have been assessed using DSC measurements (Fig. S3, ESI†). This technique allows us to assess the spin transition temperatures (Table 1) and compare the DSC peaks to those reported for the pure powders in refs. 40 and 18. Albeit small shifts occur, overall, the spin transition properties of the particles embedded into the P(VDF-TrFE) matrix remain close to those of the neat particle powders. Each sample displays relatively abrupt SCO above room temperature with a large (ca. 10–30 °C) hysteresis loop. Hysteresis is usually a drawback for actuating purposes because it renders position control more difficult. It represents, however, a substantial advantage for our thermomechanical analysis because we can easily distinguish the effect of SCO on the measured property from ‘ordinary’ thermal expansion effects and we can compare the properties of the HS and LS forms at the same temperature (in the middle of the hysteresis).
| Sample | Particle composition | Particle shape | Particle mean size (nm) | T 1/2↑ (°C) | T 1/2↓ (°C) |
|---|---|---|---|---|---|
| 1C | [Fe(Htrz)2(trz)](BF4) | Irregular | ∼50 nm | 97 | 69 |
| 2C | [Fe(Htrz)2.1(trz)0.8(NH2trz)0.1](BF4)1.2 | Irregular | ∼50 nm | 82 | 59 |
| 3C | [Fe(Htrz)2.05(trz)0.75(NH2trz)0.2](BF4)1.25 | Irregular | ∼50 nm | 75 | 58 |
| 4C | [Fe(NH2trz)3](SO4) | Rod | 2 μm (length) | 64 | 55 |
| 0.3 μm (width) |
Young's modulus of the composites
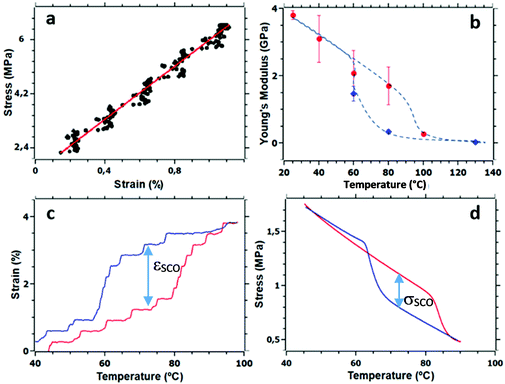
The Young's modulus (E) of the composites was extracted from the early (low strain) portion of their engineering stress (σ) vs. engineering strain (ε) curve using Hooke's law (Fig. 3(a)):| σ = Eε | (1) |
The values of E were assessed at different temperatures below the spin transition (LS state), within the hysteresis region (both in the LS and HS states) and above the spin transition (HS state). The temperature dependence of E for sample 3C is shown in Fig. 3(b), whereas the data for the other samples as well as for the pure copolymer are shown in Fig. S4, ESI† and tabulated in Table 2. At room temperature, the Young's modulus of the blade-casted P(VDF70-TrFE30) film is 4.3 ± 0.8 GPa. In agreement with recent reports,43 the Young's modulus of the copolymer drastically decreases with increasing temperature and reaches a value of 1.0 ± 0.5 GPa at 80 °C.
| Sample | E LS 25 °C (GPa) | E LS 80 °C (GPa) | E HS 80 °C (GPa) | α LS (ppm K−1) | α HS (ppm K−1) | α SCO (ppm K−1) | ε freeSCO (%) | σ SCO (MPa) |
|---|---|---|---|---|---|---|---|---|
| *Measured at 65 °C. | ||||||||
| P(VDF-TrFE) | 4.3 | 1.1 | 470 | N/A | ||||
| 1C | 2.6 | 2.0 | 0.3 | 330 | 230 | 2600 | 2.8 | >1 |
| 2C | 4.4 | 2.2 | 0.5 | 370 | 260 | 2700 | 2.2 | >1.8 |
| 3C | 3.8 | 1.7 | 0.4 | 270 | 290 | 2500 | 1.9 | 0.7 |
| 4C | 3.4 | 1.5* | 1.0* | 220 | 190 | 1500 | 1.1 | 0.4 |
Unexpectedly, the Young's modulus of the composites remains comparable, within the experimental uncertainty (approx. ±0.5 GPa), with that of the pure copolymer for the whole investigated temperature range, apparently escaping classical rules of mixture.44 (N.B. The Young's modulus of the investigated SCO particles is unknown, but from the available literature data45 we can expect to find it around 10 GPa.) Nevertheless, it is important to note that the Young's modulus of the pure P(VDF-TrFE) is actually not the same as that of the P(VDF-TrFE) matrix in the composite. In fact, the SCO filler is known to have a substantial impact on the crystallinity of the P(VDF-TrFE) matrix, depending on both the nature and the quantity of the SCO particles.19 Hence, the value of E obtained for the pure copolymer is just a crude estimation of the elastic modulus of the matrix. In addition, cooling from high temperatures, which is encountered during the synthesis of the composites, may give rise to imperfect bonding between the matrix and the particles at low temperatures, reducing thus the transferred load to the particles.
Remarkably, one can depict in Fig. 3(b) a thermal hysteresis of the Young's modulus in the temperature range of the spin transition phenomenon. However, it is important to remind that the copolymer matrix displays a ferro-paraelectric phase transition between the so-called β and α phases near 105 °C on heating and 75 °C on cooling (Fig. S3, ESI†). Hence a significant overlap between the hysteresis loops associated with the LS/HS and ferro/paraelectric phase transitions occurs, as witnessed by the DSC thermograms (Fig. S3, ESI†). As a result, the Young's modulus measured at 80 °C in the HS phase (i.e. in the cooling mode) refers to HS particles in the α phase of the matrix, explaining the drastic softening with respect to the LS particles in the β phase (measured at 80 °C on heating). We could unambiguously separate the two phase-transition phenomena only in the case of composite 4C displaying the lowest SCO temperature. As a result, for this sample the difference between the Young's moduli of the HS and LS forms (measured at 65 °C) appears less pronounced (Fig. S4, ESI†), which we can rationalize by the fact that the polymer matrix remains in the β phase through the whole thermal cycle.
Thermal expansion of the composites
The thermal expansion of the composites was analyzed by measuring the axial strain in the samples as a function of the temperature under a constant tensile force. These ‘isostress experiments’ were repeated for different applied stress values (0.01–4 MPa). Fig. 3(c) shows a representative result for sample 3C, whereas similar data for the other composites as well as for the pure copolymer are shown in Fig. S5 (ESI†). Far from the spin transition, the strain is proportional to the temperature variation allowing the assessment of the coefficients of linear thermal expansion (α) of the composite by linear regression to: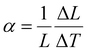 | (2) |
| εSCO = εHS – εLS | (3) |
This free expansion is a key characteristic of any actuator material as it determines the amplitude of movement and the work output that the actuator could produce. For our composites, the SCO-related free expansion (εfreeSCO) was obtained by extrapolating εSCO to zero stress (Table 2), but it is important to underline that neither the SCO strain, neither the SCO temperature displayed any pronounced dependence on the applied, relatively small forces. The obtained values of εfreeSCO range between 1.1 and 2.8%, depending on the nature of the particles. It is worth to note that this expansion is not fully reversible upon thermal cycling in each sample, which indicates deviations from the idealized elastic solid. By differentiating the ε vs. T curves, we can assess the thermal expansion peak at the spin transition, αSCO, which reaches values between 1500–2700 ppm °C−1 in the different samples (Table 2). This ‘colossal’ thermal expansion, exceeding the expansion of ‘ordinary’ materials by 2–3 orders of magnitude, is of great interest for various applications.47 To analyze these values, in a first approximation, we can simply assume that εfreeSCO is proportional to one-third of the volumetric expansion of the randomly-oriented particles at the SCO (ΔVSCO/3V), and the proportionality factor (f = 0.25) equals the particle volume fraction:
| εfreeSCO = f(ΔVSCO/3V) | (4) |
Taking into account the reported volumetric strain in particles of 1 (11.4%)36 and 4 (4.9%),37eqn (4) leads to an estimated εfreeSCO of 1% for 1C and 0.4% for 4C, which are nearly three times smaller than the measured values (2.8% and 1.1%, respectively). This result might seem surprising at first sight, but actually it derives from well-established thermoelastic theories of composites. Indeed, as discussed by McMeeking,48 when stiff transforming particles are embedded into a soft matrix the resulting effective transformation strain of the composite is expected to exceed the volume-weighted particle strain (expressed by eqn (4)). In an isotropic, biphasic composite with random particle orientation, this amplification is uniquely determined by the elastic moduli of the constituents and the composite as:49
| εfreeSCO = [KfKc−1(Kc − Km)(Kf − Km)−1](ΔVSCO/3V) | (5) |
Blocking stress of the composites
Besides the free expansion, another important characteristic of an actuator material is the blocking stress. When the material is free to move, ordinary thermal expansion will not generate any macroscopic stress. However, if the material is constrained, heating (resp. cooling) leads to compressive (resp. tensile) stresses. To investigate this phenomenon, thermomechanical measurements were performed by imposing a constant, uniaxial tensile strain on the samples and measuring the stress generated upon thermal cycling. These ‘isostrain experiments’ were repeated for different applied strain values (0.01–0.5%). As shown in Fig. 3(d), far from the spin transition, the constrained thermal expansion of the 3C composite leads to a linear decrease (resp. increase) in the stress for increasing (resp. decreasing) temperatures, whereas the spin transition gives rise to a more abrupt change of the stress. The other samples showed similar behavior (see Fig. S6, ESI†), but for samples 1C and 2C the full blocking stress could not be assessed because the initial tensile stress was cancelled by the growing compressive thermal stress. We can conveniently define the ‘SCO-induced blocking stress’ as the difference of stress between the HS and LS states in the middle of the hysteresis loop (extrapolated to zero strain) as:| σSCO = σHS − σLS | (6) |
The values of σSCO, gathered in Table 2, appear rather small (ca. 1 MPa). Indeed, one can note here that the σSCO/εSCO ratio, which corresponds to the ‘effective modulus’ of the composite near the SCO temperature, has a value of ca. 0.05 GPa, which is more than one order of magnitude lower than the Young's modulus measured by quasi-static stress–strain measurements. This observation thus denotes a softening of the material at the spin transition, explaining the relatively small blocking stress associated with the SCO. Such elastic softening is a common characteristic of numerous phase transition materials52 and was reported also for the SCO compound [Fe(abpt)2(NCS)2] (abpt = 4-amino-3,5-bis(pyridin-2-yl)-1,2,4-triazole).53 From a thermodynamical point of view, such changes of elastic constants can be linked to the coupling of strain to the order parameter of the transition, but further work will be necessary to properly assess the origin of this phenomenon.
Conclusions
We have synthesized a series of composites of the copolymer P(VDF70-TrFE30) charged with particles of four different iron-triazole family complexes. For a 25 w% particle load, we obtained statistically homogeneous, well-dispersed composites displaying abrupt, hysteretic spin transitions analogous to the neat particle powders. We have conducted a systematic investigation of the interplay between the SCO phenomenon and the thermomechanical properties of the composites using a tensile stage. These measurements revealed unambiguous signatures of the SCO phenomenon in the form of strain/stress/vs. temperature hysteresis cycles. The key experimental finding of this work is the observation of an effective transformation strain in the composites in considerable excess (by a factor of three) with respect to the volume-weighted SCO particle transformation strain. We highlighted that the amplification of the strain is a natural phenomenon if stiff, transforming particles are embedded into a soft, non-transforming matrix. This finding opens up interesting perspectives for the engineering of SCO@polymer composite actuator properties by adjusting the contrast between the particle and matrix elastic properties. On the other hand, the isostrain measurements revealed relatively small SCO-induced stress, which we attributed to the elastic softening of the material around the spin transition.This work represents the first step towards the fundamental understanding of the micromechanical behavior of this class of smart, composite materials. The main perspective here is to provide essential inputs for the rational design of mechanical devices (actuators, sensors, harvesters) using the SCO phenomenon in hybrid/composite materials. However, for quantitative predictions it will be important to establish a theoretical model, which takes into account the constitutive complexity of SCO materials. Such comprehensive models become relevant only if the thermoelastic properties of spin crossover materials could be assessed. This will be therefore a vital task for future work. Of course, the design space of such smart composites is not restricted to the effective thermo-elastic properties and volume fraction of the constituents, but implies implicitly numerous parameters, such as morphology, orientation, connectivity, interfacial bonding and so forth,54,55 providing a wealth of possibilities both for fundamental research and applications.
Author contributions
JEAC: TMA and SEM measurements, data analysis, writing – original draft. MPB: sample preparation. BM: DSC measurements. SEA and WN: data analysis. LS: TEM measurements, supervision. GM: supervision, writing – original draft. AB: project administration, funding acquisition, conceptualization, review. The manuscript has been read and approved by all named authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 101019522). JEAC thanks the CONACYT for a PhD grant (No. 471690).Notes and references
- P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054 CrossRef.
- Spin Crossover in Transition Metal Compounds I–III, ed. P. Gütlich and H. A. Goodwin, Springer, Berlin, Germany, 2004, vol. 233–235 Search PubMed.
- A. Hauser, Top. Curr. Chem., 2004, 233, 49–58 CrossRef CAS.
- P. Guionneau, Dalton Trans., 2014, 43, 382–393 RSC.
- M. Grzywa, R. Röβ-Ohlenroth, C. Muschielok, H. Oberhofer, A. Błachowski, J. Żukrowski, D. Vieweg, H.-A. Krug von Nidda and D. Volkmer, Inorg. Chem., 2020, 59, 10501–10511 CrossRef CAS PubMed.
- I. A. Gural'skiy, B. Golub, S. Shylin, V. Ksenofontov, H. J. Shepherd, P. Raithby, W. Tremel and I. Fritsky, Eur. J. Inorg. Chem., 2016, 3191–3195 CrossRef.
- M. D. Manrique-Juárez, S. Rat, L. Salmon, G. Molnár, C. M. Quintero, L. Nicu, H. J. Shepherd and A. Bousseksou, Coord. Chem. Rev., 2016, 308, 395–408 CrossRef.
- H. J. Shepherd, I. A. Gural'skiy, C. M. Quintero, S. Tricard, L. Salmon, G. Molnár and A. Bousseksou, Nat. Commun., 2013, 4, 2607 CrossRef PubMed.
- I. A. Gural'skiy, C. M. Quintero, J. S. Costa, P. Demont, G. Molnár, L. Salmon, H. J. Shepherd and A. Bousseksou, J. Mater. Chem. C, 2014, 2, 2949–2955 RSC.
- Y. S. Koo and J. R. Galán-Mascarós, Adv. Mater., 2014, 26, 6785–6789 CrossRef CAS PubMed.
- C. Chen, Y. Meng, Z. P. Ni and M. L. Tong, J. Mater. Chem. C, 2015, 3, 945–949 RSC.
- M. D. Manrique-Juarez, S. Rat, F. Mathieu, D. Saya, I. Séguy, T. Leïchlé, L. Nicu, L. Salmon, G. Molnár and A. Bousseksou, Appl. Phys. Lett., 2016, 109, 061903 CrossRef.
- M. D. Manrique-Juárez, F. Mathieu, V. Shalabaeva, J. Cacheux, S. Rat, L. Nicu, T. Leïchlé, L. Salmon, G. Molnár and A. Bousseksou, Angew. Chem., Int. Ed., 2017, 56, 8074–8078 CrossRef PubMed.
- M. D. Manrique-Juárez, F. Mathieu, A. Laborde, S. Rat, V. Shalabaeva, P. Demont, O. Thomas, L. Salmon, T. Leichle, L. Nicu, G. Molnár and A. Bousseksou, Adv. Funct. Mater., 2018, 28, 1801970 CrossRef.
- S. Rat, M. Piedrahita-Bello, L. Salmon, G. Molnár, P. Demont and A. Bousseksou, Adv. Mater., 2018, 30, 1705275 CrossRef PubMed.
- M. Urdampilleta, C. Ayela, P.-H. Ducrot, D. Rosario-Amorin, A. Mondal, M. Rouzières, P. Dechambenoit, C. Mathonière, F. Mathieu, I. Dufour and R. Clérac, Sci. Rep., 2018, 8, 8016 CrossRef PubMed.
- J. Dugay, M. Giménez-Marqués, W. Venstra, R. Torres-Cavanillas, U. Sheombarsing, N. Manca, E. Coronado and H. van der Zant, J. Phys. Chem. C, 2019, 123, 6778–6786 CrossRef CAS.
- M. Piedrahita-Bello, J. E. Angulo-Cervera, R. Courson, G. Molnár, L. Malaquin, C. Thibault, B. Tondu, L. Salmon and A. Bousseksou, J. Mater. Chem. C, 2020, 8, 6001–6005 RSC.
- M. Piedrahita-Bello, B. Martin, L. Salmon, G. Molnár, P. Demont and A. Bousseksou, J. Mater. Chem. C, 2020, 8, 6042–6051 RSC.
- M. Piedrahita-Bello, J. E. Angulo-Cervera, A. Enriquez-Cabrera, G. Molnár, B. Tondu, L. Salmon and A. Bousseksou, Mater. Horiz., 2021, 8, 3055–3062 RSC.
- J. E. Angulo-Cervera, M. Piedrahita-Bello, F. Mathieu, T. Leichle, L. Nicu, L. Salmon, G. Molnár and A. Bousseksou, Magnetochemistry, 2021, 7, 114 CrossRef CAS.
- D. Nieto-Castro, F. A. Garcés-Pineda, A. Moneo-Corcuera, I. Sánchez-Molina and J. R. Galán-Mascarós, Adv. Funct. Mater., 2021, 31, 2102469 CrossRef CAS.
- B. Tondu, M. Piedrahita-Bello, L. Salmon, G. Molnár and A. Bousseksou, Sens. Actuators, A, 2022, 335, 113359 CrossRef CAS.
- M. Piedrahita-Bello, Y. Zan, A. Enriquez-Cabrera, G. Molnár, B. Tondu, L. Salmon and A. Bousseksou, Chem. Phys. Lett., 2022, 793, 139438 CrossRef CAS.
- A. Enriquez-Cabrera, A. Rapakousiou, M. Piedrahita Bello, G. Molnár, L. Salmon and A. Bousseksou, Coord. Chem. Rev., 2020, 419, 213396 CrossRef CAS.
- M. Cavallini, Phys. Chem. Chem. Phys., 2012, 14, 11867–11876 RSC.
- L. Salmon and L. Catala, C. R. Chim., 2018, 21, 1230–1269 CrossRef CAS.
- T. Mallah and M. Cavallini, C. R. Chim., 2018, 21, 1270–1286 CrossRef CAS.
- R. Tanasa, C. Enachescu, J. Laisney, D. Morineau, A. Stancu and M.-L. Boillot, J. Phys. Chem. C, 2019, 123, 10120–10129 CrossRef CAS.
- C. Enachescu, R. Tanasa, A. Stancu, A. Tissot, J. Laisney and M.-L. Boillot, Appl. Phys. Lett., 2016, 109, 031908 CrossRef.
- A. Tissot, C. Enachescu and M.-L. Boillot, J. Mater. Chem., 2012, 22, 20451–20457 RSC.
- C. Göbel, K. Marquardt, D. Baabe, M. Drechsler, P. Loch, J. Breu, A. Greiner, H. Schmalz and B. Weber, Nanoscale, 2022, 14, 3131–3147 RSC.
- Y. Raza, F. Volatron, S. Moldovan, O. Ersen, V. Huc, C. Martini, F. Brisset, A. Gloter, O. Stéphan, A. Bousseksou, L. Catala and T. Mallah, Chem. Commun., 2011, 47, 11501–11503 RSC.
- S. Rat, V. Nagy, I. Suleimanov, G. Molnar, L. Salmon, P. Demont, L. Csoka and A. Bousseksou, Chem. Commun., 2016, 52, 11267–11269 RSC.
- Y. Bibik, J. E. Angulo-Cervera, R. Lampeka and I. A. Gural'skiy, Polymer, 2022, 238, 124410 CrossRef CAS.
- A. Grosjean, P. Négrier, P. Bordet, C. Etrillard, D. Mondieig, S. Pechev, E. Lebraud, J.-F. Létard and P. Guionneau, Eur. J. Inorg. Chem., 2013, 796–802 CrossRef CAS.
- D. Niestro Castro, PhD thesis, Universitat Rovira i Virgili, Tarragona, Spain, 2021 Search PubMed.
- C. Ribeiro, C. M. Costa, D. M. Correia, J. Nunes-Pereira, J. Oliveira, P. Martins, R. Gonçalves, V. F. Cardoso and S. Lanceros-Méndez, Nat. Protoc., 2018, 13, 681–704 CrossRef CAS PubMed.
- P. Martins, A. C. Lopes and S. Lanceros-Mendez, Prog. Polym. Sci., 2014, 39, 683–706 CrossRef CAS.
- M. Piedrahita-Bello, K. Ridier, M. Mikolasek, G. Molnár, W. Nicolazzi, L. Salmon and A. Bousseksou, Chem. Commun., 2019, 55, 4769–4772 RSC.
- O. Roubeau, Chem. – Eur. J., 2012, 18, 15230–15244 CrossRef CAS PubMed.
- V. Y. Sirenko, O. I. Kucheriv, A. Rotaru, I. O. Fritsky and I. A. Gural'skiy, Eur. J. Inorg. Chem., 2020, 4523–4531 CrossRef CAS.
- J. Hafner, M. Teuschel, M. Schneider and U. Schmid, Polymer, 2019, 170, 1–6 CrossRef CAS.
- H. Kim, S. Hong and S. Kim, J. Mater. Process. Technol., 2001, 112, 109–113 CrossRef.
- M. Mikolasek, M. D. Manrique-Juarez, H. J. Shepherd, K. Ridier, S. Rat, V. Shalabaeva, A.-C. Bas, I. E. Collings, F. Mathieu, J. Cacheux, T. Leichle, L. Nicu, W. Nicolazzi, L. Salmon, G. Molnár and A. Bousseksou, J. Am. Chem. Soc., 2018, 140, 8970–8979 CrossRef CAS PubMed.
- Advances in Shape Memory Materials, ed. Q. Sun, R. Matsui, K. Takeda, E. A. Pieczyska, Springer International Publishing AG, Cham, Switzerland, 2017 Search PubMed.
- A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S.-O. Evans, D. A. Keen, L. Petersand and M. G. Tucker, Science, 2008, 319, 754–757 CrossRef PubMed.
- R. M. McMeeking, J. Am. Ceram. Soc., 1986, 69, C-301–C-302 CrossRef.
- Z. Hashin and B. Z. Rosen, J. Appl. Mech., 1964, 31, 223–232 CrossRef.
- D. Paliwoda, et al., unpublished results.
- Z. Hashin and S. Shtrikman, J. Mech. Phys. Solids, 1963, 11, 127–140 CrossRef.
- M. A. Carpenter and E. K.-H. Salje, Eur. J. Mineral., 1998, 10, 693–812 CrossRef CAS.
- H. E. Mason, W. Li, M. A. Carpenter, M. L. Hamilton, J. A.-K. Howard and H. A. Sparkes, New J. Chem., 2016, 40, 2466–2478 RSC.
- B. Lester, T. Baxevanis, Y. Chemsky and D. Lagoudas, Acta Mech., 2015, 226, 3907–3960 CrossRef.
- J. Bhaskar, A. K. Sharma, B. Bhattacharya and S. Adhikari, Smart Mater. Struct., 2020, 29, 073001 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional TEM, SEM, DSC and TMA data. See DOI: https://doi.org/10.1039/d2ma00459c |
| This journal is © The Royal Society of Chemistry 2022 |