DOI:
10.1039/D2MA00694D
(Paper)
Mater. Adv., 2022,
3, 6826-6830
High-throughput computational evaluation of lattice thermal conductivity using an optimized Slack model
Received
16th June 2022
, Accepted 11th July 2022
First published on 16th July 2022
Abstract
High-throughput computational screening of materials with targeted thermal conductivity (κ) plays an important role in promoting the advancement of material design and enormous applications. The Slack model has been widely applied for the fast evaluation of κ with minimal time and resources, showing the potential capability of high-throughput screening of κ. However, after examining the Slack model on a large set of 353 materials, a huge discrepancy is found between the predicted κ and the correspondingly measured κ in experiments for some materials in addition to the generally overestimated κ by the Slack model. Thus, it is necessary to optimize the Slack model for efficiently and accurately evaluating κ. In this study, based on the high-throughput comparison of the κ predicted by the Slack model using elastic properties and those measured in experiments, an optimized Slack model is proposed. As a result, the κ predicted by the optimized Slack model agrees reasonably with the κ measured in experiments, which is much better than the previous prediction. The optimized Slack model proposed in this study can be used for further high-throughput computational evaluation of κ, which would be helpful for finding materials of ultrahigh or ultralow κ with broad applications.
1. Introduction
The thermal conductivity (κ) is a fundamental physical property that quantifies the ability of heat transfer.1,2 Designing new materials or modifying existing materials with a targeted κ is a long-term goal for enormous practical implications, such as phase change memories, electronic cooling, thermoelectrics, etc.1,3 For instance, high κ is of great significance to the heat dissipation in micro electric devices, while low κ could largely benefit the thermoelectric performance for converting waste heat to electricity. High-throughput computational screening of crystalline materials with ultrahigh or ultralow κ plays an important role in promoting the advancement of materials design and their applications,2,4 where fast evaluation of κ only requiring minimal time and resources is the key.
There are lots of available methods for evaluating κ. First-principles based anharmonic lattice dynamics (ALD) has been a widely employed method in the past few years.5 However, too many force calculations using large supercells are time and resource consuming although they can be partially reconstructed,6 which limits its practical applications in high-throughput computational prediction of κ. Alternately, evaluating κ using an empirical model is a more efficient and feasible (computationally cheaper) way, such as the Debye–Callaway model,7–9 the Slack model,10etc. In particular, the Slack model has been widely applied for the evaluation of κ for lots of materials,11–13 showing the potential capability of fast predicting κ and achieving insights into the thermal transport.14–16
The key point in applying the Slack model for high-throughput computations is to efficiently obtain the Debye temperature and Grüneisen parameter, where lots of efforts have been dedicated. Xiao et al.16 evaluated the Grüneisen parameter for four compounds (PbS, PbSe, PbTe, and SnSe) based on the Poisson ratio that is a function of sound velocity and elastic property, which is in reasonable agreement with the quasiharmonic lattice dynamics calculations. Recently, it was proposed by Jia et al.17 that the Grüneisen parameter can be efficiently estimated based on the elastic properties and the variation with volume change, which is a more general approach as verified by applying it to 39 compounds in three prototype structures (Rock-salt, Zincblende, and Wurtzite). The new approach overcomes the limitations of the previous Poisson ratio-based Grüneisen parameters that are only suitable for Rock-salt structures.16 However, the calculated κ using the Slack model shows a general overestimation when compared to the experimentally measured κ, despite the overall good evaluation of the Debye temperature and Grüneisen parameter [Fig. 1(a–c)].17 Furthermore, by applying the same procedure to more materials (353 materials) and comparing the predicted κ with the corresponding experimentally measured κ,4,18–23 it is found that a huge discrepancy exists between the κSlack![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) model and κExp. for some materials in addition to the general overestimation by the Slack model [Fig. 1(d)]. Such problems are detrimental to the broad applications of the Slack model in high-throughput computational prediction of κ. Thus, it is necessary to optimize the Slack model for efficiently and accurately evaluating κ.
model and κExp. for some materials in addition to the general overestimation by the Slack model [Fig. 1(d)]. Such problems are detrimental to the broad applications of the Slack model in high-throughput computational prediction of κ. Thus, it is necessary to optimize the Slack model for efficiently and accurately evaluating κ.
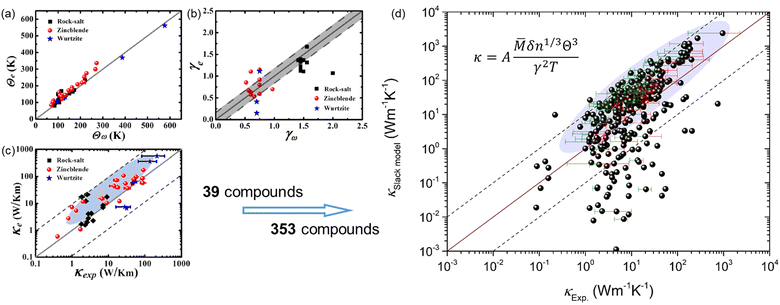 |
| | Fig. 1 The generally overestimated thermal conductivity (κ) by the Slack model using elastic properties, despite the overall good evaluation of the acoustic Debye temperature and Grüneisen parameter. (a) The acoustic Debye temperature, (b) the Grüneisen parameter, and (c) the κ for 39 compounds in the three prototype structures (Rock-salt, Zincblende, and Wurtzite) predicted by Jia et al.17 (d) The comparison between the κ calculated by the Slack model using elastic properties and the κ measured in experiments4,18–23 for 353 materials. The shaded ellipses in (c and d) mark the generally overestimated κ by the Slack model, and the error bars on some points indicate the uncertainty in experimental measurements. (a–c) Reproduced with permission from ref. 17. Copyright 2017, American Physical Society. | |
In this study, based on the high-throughput comparison of the κ predicted by the Slack model using elastic properties and those measured in experiments, an optimized Slack model is proposed. As a result, the κ predicted by the optimized Slack model agrees reasonably with the κ measured in experiments for a large set of 353 materials, which is much better than the previous prediction. The optimized Slack model can be used for further high-throughput computational evaluation of κ, which would be helpful for seeking materials of ultrahigh or ultralow κ with broad applications.
2. Methodology
2.1 First-principles
All the first-principles calculations are performed based on density functional theory (DFT) using the projector augmented wave (PAW) method24 as implemented in the Vienna ab initio simulation package (vasp).25 The Perdew–Burke–Ernzerhof (PBE)26 of generalized gradient approximation (GGA) is chosen as the exchange-correlation functional. The kinetic energy cut-off of wave functions is set as the default maximum energy cutoff. A Monkhorst–Pack27 k-mesh density of 0.4 2 π Å−1 is used to sample the Brillouin Zone (BZ). The energy convergence threshold for the self-consistent field (SCF) calculations is set as 10−5 eV. All geometries are fully optimized until the maximal Hellmann–Feynman force is smaller than 0.01 eV Å−1. The elastic constants are calculated using the density functional perturbation theory (DFPT). To evaluate the variation of elastic properties with volume change, the volume is changed from −1.5% to 1.5% (5 points in total), which is generally suitable for most calculations.28
2.2 Slack model
Considering the fact that acoustic phonon modes play an important role in the thermal transport processes of semiconductors, the lattice thermal conductivity (κ) can be obtained using the Slack model:10| | 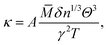 | (1) |
where ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the averaged atomic mass, δ is the cubic root of the average volume per atom, n is the number of atoms in the primitive cell that determines the number of phonon branches, Θ is the acoustic Debye temperature, γ is the Grüneisen parameter, and T is the absolute temperature. Commonly, the coefficient A in the Slack model [eqn (1)] is calculated as:17
is the averaged atomic mass, δ is the cubic root of the average volume per atom, n is the number of atoms in the primitive cell that determines the number of phonon branches, Θ is the acoustic Debye temperature, γ is the Grüneisen parameter, and T is the absolute temperature. Commonly, the coefficient A in the Slack model [eqn (1)] is calculated as:17| | 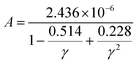 | (2) |
where γ is the Grüneisen parameter.
The formula suggested by Slack has been widely applied for the evaluation of κ for lots of materials.11–13 As for the κ evaluation, the key point is to efficiently obtain the Θ and γ in a convenient manner. Generally, the Θ and γ can be accurately determined based on the phonon dispersions and thermal expansion coefficients either from experimental measurements or (harmonic & anharmonic) lattice dynamic calculations,17 which are very expensive. Thus, lots of efforts have been dedicated to the efficient evaluation of Θ and γ that only requires moderate time and resources.
Jia et al.17 proposed that the Θ and γ can be efficiently estimated based on the elastic properties of bulk modulus (B) and shear modulus (G), which is more computationally feasible compared to the experiment or expensive lattice dynamic calculations. According to the Voigt–Reuss–Hill (VRH) theory,29–31 the elastic properties (B and G) can be evaluated from the elastic constants, which can be obtained based on accurate first-principles calculations. With the evaluated B and G, the sound velocities of the longitude (vL) and shear (vS) waves can be obtained as31
| | 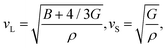 | (3) |
where
ρ is the mass density of the material. Thus, the corresponding average sound velocity
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)
can be obtained:
| | 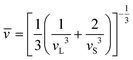 | (4) |
with the obtained sound velocity, the acoustic Debye temperature (
Θ) can be evaluated:
31| | 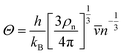 | (5) |
where
h is the Planck constant,
kB is the Boltzmann constant, and
ρn is the number of atoms per volume.
In addition to the acoustic Debye temperature (Θ), the Grüneisen parameter (γ) can also be evaluated based on the obtained elastic properties (B and G). The γ quantifies the anharmonic nature of a system, which can be characterized by the change of phonon frequency (ω) with respect to the change of volume (V):
| | 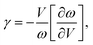 | (6) |
where
ω =
vq (
v is the sound velocity in the long-wave limit and
q is the wave vector). By substituting
ω and
v [
eqn (3)] into
eqn (6), the acoustic
γ can be derived as
17| | 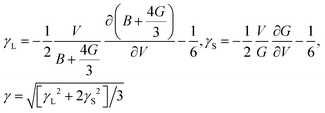 | (7) |
Thus, the γ is not only determined by the elastic properties but also determined by the derivation of the elastic properties with respect to the change of volume. With the obtained Θ [eqn (5)] and γ [eqn (7)], the κ can be simply calculated using the Slack model [eqn (1)].
3. Results and discussion
Based on the elastic properties (B and G) calculated from first-principles, both the acoustic Debye temperature (Θ) and Grüneisen parameter (γ) can be evaluated using eqn (5 and 7). In a previous study, Jia et al.17 performed calculations and evaluations for 39 compounds in the three prototype structures (Rock-salt, Zincblende, and Wurtzite). As shown in Fig. 1(a and b), the evaluated Θ and γ using elastic properties are in good agreement with the Θ and γ calculated directly from accurate first-principles phonon calculations. However, the finally calculated κ using the Slack model [eqn (1)] shows a general overestimation when compared to the experimentally measured κ [Fig. 1(c)], despite the overall good evaluation of Θ and γ [Fig. 1(a and b)]. Following the same procedure, we calculated more materials (353) with experimentally measured κ available.4,18–23 By comparing the κ of the large set of 353 materials calculated with the Slack model using elastic properties and the corresponding measured κ in experiments [Fig. 1(d)], it is found that the κ are generally overestimated by the Slack model, which has the same problem as in the previous study.17 Since the Θ and γ evaluated using elastic properties have already been confirmed to be accurate [Fig. 1(a and b)], the generally overestimated κ in both studies [Fig. 1(c and d)] must lie in the coefficient A in the Slack model [eqn (1)].
As claimed by previous studies,17,22 the coefficient A in the Slack model is in fact not a constant for different materials, which is a variable depending on the γ [eqn (2)]. Thus, the non-constant coefficient A provides a correction to the Slack model on the κ dependence of γ, which is important for the accurate prediction of thermal conductivity. Based on the large set of 353 materials, the actual values of A (AExp.) can be obtained as
| | 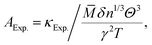 | (8) |
where the
κExp. is the experimentally measured
κ. As clearly shown in
Fig. 2, the
AExp. varies with the
γ for different materials. The original
A used in the Slack model [
eqn (1 and 2)] cannot successfully capture the variations of
AExp. for the large set of different materials. In particular, the original
A is larger than the main part of the
AExp. as shown in the shaded ellipse of
Fig. 2 (where most materials lie), which is responsible for the generally overestimated
κ in this and previous studies [
Fig. 1(c and d)]. Thus, based on the comparison between the original
A and the
AExp., the parameters of
A in the Slack model should be optimized to achieve accurate prediction of
κ.
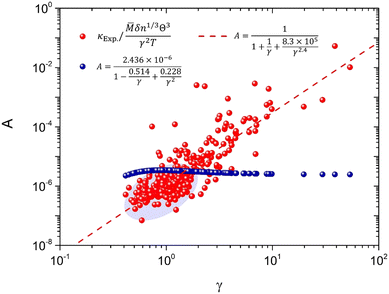 |
| | Fig. 2 The coefficient in the Slack model (A) as a function of the Grüneisen parameter (γ). The red points are the actual values of A based on the comparison with κExp. [eqn (8)]. The blue points are the original A used in the Slack model [eqn (2)]. The dashed line is the new fitting to the actual values of A (red points) [eqn (10)]. | |
A possible solution for the optimization of A in the Slack model could be simply scaling the original A by a factor, for instance:4
| | 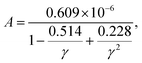 | (9) |
which is effective for correcting the generally overestimated
κ as shown in
Fig. 3(a). However, the problem is that the optimized Slack model with the scaled
A [
eqn (9)] predicts lots of really bad points as marked in
Fig. 3(a) that is similar to the original Slack model [
Fig. 1(d)], although the prediction of most materials becomes better. The reason is that the scaled
A [
eqn (9)] still cannot fully capture the feature of
AExp. as a function of
γ for the large set of 353 materials (
Fig. 2), and thus leads to the huge discrepancy between the
κSlack![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) model
model and the
κExp. for some materials with very strong or very weak phonon anharmonicity, such as boron arsenide (BAs).
32
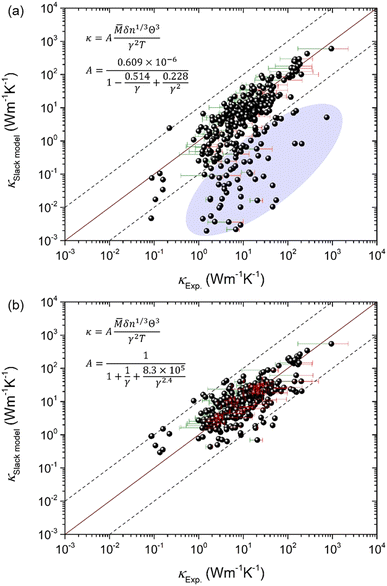 |
| | Fig. 3 The comparison between the κ calculated by the Slack model and the κ measured in experiments4,18–23 for a large set of 353 materials. (a) The coefficient in the Slack model (A) is simply scaled by a factor of 4 from the original A used in the Slack model [eqn (9)] to lower the generally overestimated κ [Fig. 1(c and d)]. The shaded ellipse marks the bad predictions. (b) With the newly fitting A [eqn (10) and Fig. 2], the κ predicted by the optimized Slack model agrees reasonably with the κ measured in experiments. The error bars on some points indicate the uncertainty in experimental measurements. | |
To achieve accurate prediction of κ for the whole set of 353 materials, the coefficient A in the Slack model should be fully optimized. The same formula as the original A [eqn (2)] is used for consistency, and all the parameters are refitted using the least square method to characterize the feature of AExp. as a function of γ:
| | 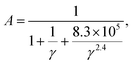 | (10) |
As shown in
Fig. 2, the newly fitted
A well captures the feature of
AExp. as a function of
γ. As a result, the
κ predicted by the optimized Slack model [
eqn (1)] with the new
A [
eqn (10)] agrees reasonably with the
κ measured in experiments as shown in
Fig. 3(b), which is much better than the previous prediction [
Fig. 1(d) and 3(a)]. Moreover, the root mean square (RMS) is calculated to quantify the improved performance of the optimized Slack model:
| | 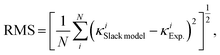 | (11) |
where
i specifies one material and
N is 353 for the data set studied here. The RMS of the optimized Slack model is calculated to be 27.6% of the RMS of the original Slack model. Thus, the optimized Slack model with the new
A is more accurate than the original Slack model for predicting
κ, indicating improved performance.
4. Conclusions
In summary, by high-throughput comparison of the κ predicted by the Slack model using elastic properties and those measured in experiments, an optimized Slack model is proposed for more accurate prediction of κ. The comparison is performed on a large set of 353 materials with all κ obtained from experiments, and it is confirmed that the coefficient A in the Slack model is not a constant for different materials, which depends on the Grüneisen parameter (γ). The original A cannot fully capture the feature of AExp. as a function of γ for the large set of different materials, leading to the generally overestimated κ and the huge discrepancy between the κSlack![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) model and κExp. To solve the problem, the A in the Slack model is refitted to characterize the feature of AExp.(γ). As a result, the κ predicted by the optimized Slack model with the new A agrees reasonably with the κ measured in experiments, which is much better than the previous prediction. With the advantages of less resource requirements and fast calculations compared to the atomic simulations, such as full first-principles and molecular dynamics, the optimized Slack model can be used for further high-throughput computational evaluation of κ with reasonable accuracy, which would be helpful for seeking materials with targeted κ with broad applications.
model and κExp. To solve the problem, the A in the Slack model is refitted to characterize the feature of AExp.(γ). As a result, the κ predicted by the optimized Slack model with the new A agrees reasonably with the κ measured in experiments, which is much better than the previous prediction. With the advantages of less resource requirements and fast calculations compared to the atomic simulations, such as full first-principles and molecular dynamics, the optimized Slack model can be used for further high-throughput computational evaluation of κ with reasonable accuracy, which would be helpful for seeking materials with targeted κ with broad applications.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
G. Q. is supported by the National Natural Science Foundation of China (Grant No. 52006057), the Fundamental Research Funds for the Central Universities (Grant No. 531119200237 and 541109010001), and the State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body at Hunan University (Grant No. 52175013). The numerical calculations in this paper have been done on the supercomputing system of the E. T. Cluster and the National Supercomputing Center in Changsha. Simulations were also partly performed with computing resources granted by RWTH Aachen University, Germany under projects of rwth0366. Z. Q. is supported by the National Natural Science Foundation of China (Grant No. 11847158, 11904324) and the China Postdoctoral Science Foundation (2018M642776). H. W. is supported by the National Natural Science Foundation of China (Grant No. 51906097). M. H. and J. H. is supported by the NSF (award number 1905775).
References
- D. G. Cahill, P. V. Braun, G. Chen, D. R. Clarke, S. Fan, K. E. Goodson, P. Keblinski, W. P. King, G. D. Mahan, A. Majumdar, H. J. Maris, S. R. Phillpot, E. Pop and L. Shi, Appl. Phys. Rev., 2014, 1, 011305 Search PubMed.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- A. A. Balandin and D. L. Nika, Mater. Today, 2012, 15, 266–275 CrossRef CAS.
- J. Carrete, W. Li, N. Mingo, S. Wang and S. Curtarolo, Phys. Rev. X, 2014, 4, 011019 CAS.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- G. Qin and M. Hu, npj Comput. Mater., 2018, 4, 1–6 CrossRef CAS.
- Y. Zhang, E. Skoug, J. Cain, V. Ozoliņš, D. Morelli and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054306 CrossRef.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS.
- D. T. Morelli, J. P. Heremans and G. A. Slack, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 195304 CrossRef.
- G. A. Slack, J. Phys. Chem. Solids, 1973, 34, 321–335 CrossRef CAS.
- D. T. Morelli, V. Jovovic and J. P. Heremans, Phys. Rev. Lett., 2008, 101, 035901 CrossRef CAS PubMed.
- E. J. Skoug, J. D. Cain and D. T. Morelli, Appl. Phys. Lett., 2010, 96, 181905 CrossRef.
- M. D. Nielsen, V. Ozolins and J. P. Heremans, Energy Environ. Sci., 2013, 6, 570–578 RSC.
- G. Qin, X. Zhang, S.-Y. Yue, Z. Qin, H. Wang, Y. Han and M. Hu, Phys. Rev. B, 2016, 94, 165445 CrossRef.
- S. Lee, K. Esfarjani, T. Luo, J. Zhou, Z. Tian and G. Chen, Nat. Commun., 2014, 5, 3525 CrossRef PubMed.
- Y. Xiao, C. Chang, Y. Pei, D. Wu, K. Peng, X. Zhou, S. Gong, J. He, Y. Zhang, Z. Zeng and L.-D. Zhao, Phys. Rev. B, 2016, 94, 125203 CrossRef.
- T. Jia, G. Chen and Y. Zhang, Phys. Rev. B, 2017, 95, 155206 CrossRef.
- S. A. Miller, P. Gorai, B. R. Ortiz, A. Goyal, D. Gao, S. A. Barnett, T. O. Mason, G. J. Snyder, Q. Lv, V. Stevanović and E. S. Toberer, Chem. Mater., 2017, 29, 2494–2501 CrossRef CAS.
- G. Petretto, S. Dwaraknath, H. P. C. Miranda, D. Winston, M. Giantomassi, M. J. van Setten, X. Gonze, K. A. Persson, G. Hautier and G.-M. Rignanese, Sci. Data, 2018, 5, 180065 CrossRef CAS PubMed.
- J. J. Plata, P. Nath, D. Usanmaz, J. Carrete, C. Toher, M. de Jong, M. Asta, M. Fornari, M. B. Nardelli and S. Curtarolo, npj Comput. Mater., 2017, 3, 1–10 CrossRef CAS.
- A. Seko, A. Togo, H. Hayashi, K. Tsuda, L. Chaput and I. Tanaka, Phys. Rev. Lett., 2015, 115, 205901 CrossRef PubMed.
- C. Toher, J. J. Plata, O. Levy, M. de Jong, M. Asta, M. B. Nardelli and S. Curtarolo, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 174107 CrossRef.
- A. van Roekeghem, J. Carrete, C. Oses, S. Curtarolo and N. Mingo, Phys. Rev. X, 2016, 6, 041061 Search PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- J. Zhao, J. M. Winey and Y. M. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 094105 CrossRef.
- D. H. Chung and W. R. Buessem, J. Appl. Phys., 1967, 38, 2535–2540 CrossRef CAS.
- J. M. J. den Toonder, J. A. W. van Dommelen and F. P. T. Baaijens, Modell. Simul. Mater. Sci. Eng., 1999, 7, 909 CrossRef CAS.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS.
- L. Yu, Y. Tian, X. Zheng, H. Wang, C. Shen and G. Qin, Int. J. Therm. Sci., 2022, 174, 107438 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
An
Huang
*a,
An
Huang
 a,
Yinqiao
Liu
bc,
Huimin
Wang
a,
Yinqiao
Liu
bc,
Huimin
Wang
 d,
Zhenzhen
Qin
d,
Zhenzhen
Qin
 *e,
Xue
Jiang
*e,
Xue
Jiang
 b,
Jijun
Zhao
b,
Jianjun
Hu
b,
Jijun
Zhao
b,
Jianjun
Hu
 f and
Ming
Hu
f and
Ming
Hu
 *c
*c
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) model and κExp. for some materials in addition to the general overestimation by the Slack model [Fig. 1(d)]. Such problems are detrimental to the broad applications of the Slack model in high-throughput computational prediction of κ. Thus, it is necessary to optimize the Slack model for efficiently and accurately evaluating κ.
model and κExp. for some materials in addition to the general overestimation by the Slack model [Fig. 1(d)]. Such problems are detrimental to the broad applications of the Slack model in high-throughput computational prediction of κ. Thus, it is necessary to optimize the Slack model for efficiently and accurately evaluating κ.
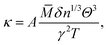
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the averaged atomic mass, δ is the cubic root of the average volume per atom, n is the number of atoms in the primitive cell that determines the number of phonon branches, Θ is the acoustic Debye temperature, γ is the Grüneisen parameter, and T is the absolute temperature. Commonly, the coefficient A in the Slack model [eqn (1)] is calculated as:17
is the averaged atomic mass, δ is the cubic root of the average volume per atom, n is the number of atoms in the primitive cell that determines the number of phonon branches, Θ is the acoustic Debye temperature, γ is the Grüneisen parameter, and T is the absolute temperature. Commonly, the coefficient A in the Slack model [eqn (1)] is calculated as:17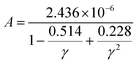
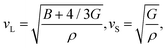
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) can be obtained:
can be obtained: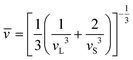
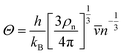
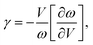
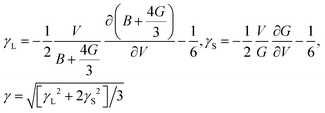
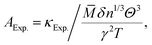

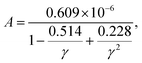
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) model and the κExp. for some materials with very strong or very weak phonon anharmonicity, such as boron arsenide (BAs).32
model and the κExp. for some materials with very strong or very weak phonon anharmonicity, such as boron arsenide (BAs).32

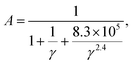
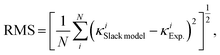
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) model and κExp. To solve the problem, the A in the Slack model is refitted to characterize the feature of AExp.(γ). As a result, the κ predicted by the optimized Slack model with the new A agrees reasonably with the κ measured in experiments, which is much better than the previous prediction. With the advantages of less resource requirements and fast calculations compared to the atomic simulations, such as full first-principles and molecular dynamics, the optimized Slack model can be used for further high-throughput computational evaluation of κ with reasonable accuracy, which would be helpful for seeking materials with targeted κ with broad applications.
model and κExp. To solve the problem, the A in the Slack model is refitted to characterize the feature of AExp.(γ). As a result, the κ predicted by the optimized Slack model with the new A agrees reasonably with the κ measured in experiments, which is much better than the previous prediction. With the advantages of less resource requirements and fast calculations compared to the atomic simulations, such as full first-principles and molecular dynamics, the optimized Slack model can be used for further high-throughput computational evaluation of κ with reasonable accuracy, which would be helpful for seeking materials with targeted κ with broad applications.
