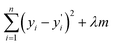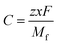Open Access Article
Open Access ArticleCapacity prediction of K-ion batteries: a machine learning based approach for high throughput screening of electrode materials†
Souvik
Manna
 ,
Diptendu
Roy
,
Diptendu
Roy
 ,
Sandeep
Das
,
Sandeep
Das
 and
Biswarup
Pathak
and
Biswarup
Pathak
 *
*
Department of Chemistry, Indian Institute of Technology (IIT) Indore, Simrol, Indore 453552, India. E-mail: biswarup@iiti.ac.in
First published on 9th August 2022
Abstract
Machine learning (ML) techniques have revolutionized the field of materials science in recent decades. ML has emerged as an excellent tool to accelerate the screening of electrode materials for alternative metal ion batteries, particularly K-ion batteries, which can outperform the conventionally used lithium-ion batteries with drawbacks of low abundance and high reactivity in air. Since specific capacity is an important metric to estimate the performance of a battery, hereby we attempt to predict the specific capacity for potassium battery electrode materials using ML based on compositional features for the first time. We have employed various ML models and Kernel Ridge Regression is identified as the most reliable model for our dataset, considering mean absolute percentage error as the performance metric. From the obtained specific capacity values, we have also determined the number of K ions that can be intercalated in the formula unit of considered electrode compounds. DFT calculations have been performed to confirm the stability of intercalated electrode materials. Our results show that the application of ML algorithms can circumvent the huge computational cost associated with DFT-based screening studies for identifying suitable electrode materials with high specific capacity, which is crucial for efficient battery technology.
1. Introduction
With the increase in energy demands, harnessing energy from renewable sources has become increasingly important for sustainable development. However, renewable energy sources are intermittent in nature as they depend on factors like weather, location, efficiency, and available infrastructure. Thus, efficient large-scale energy storage systems are required to store, transfer, and utilize the energy produced from renewable energy sources.1 Rechargeable metal-ion batteries are used extensively to store energy in the form of chemical energy, which can be converted back to electrical energy whenever required. Among all the metal-ion batteries, Li-ion batteries (LIBs) are leading the energy storage devices market, especially in portable devices such as smartphones and laptops.2,3 Li metal-ion batteries have even opened extraordinary possibilities in the automotive sector and electric vehicles market recently.4,5 The long cycle life, high efficiencies and high energy densities are the main reason behind the success of LIBs.2,6 However, for large scale energy storage, LIBs have certain shortcomings such as their relatively low energy density, and safety issues owing to their high reactivity in air.4,6–11 Very low abundance of Li sources is also a major concern, which ultimately contributes to the high price of these batteries.6,12,13 These issues demand cheap, efficient and sustainable alternatives to LIBs.Potassium (K) is one of the metal ions that could replace lithium in energy storage devices. K is more abundant compared to Li sources and hence reduces the production cost.14 K-ion batteries have a similar rocking chair mechanism like LIBs. K+ having large atomic radius (1.38 Å) has a small Stokes radius in various organic electrolytes, which results in higher ionic conductivity.15 The standard potential of K/K+ in a nonaqueous medium, especially in the most common solvent propylene carbonate, is −2.88 V, which is more negative compared to Li and Na.16 Organic electrode materials are also used as cathode materials for K ion batteries.17 K ions having low de-solvation energy possess faster diffusion over the electrode/electrolyte interface.18 Readily available and cheaper electrolyte solutions and salts of K ion batteries are also a reason for their low price compared to LIBs. For example, KPF6 is much cheaper than the similar analogues of Li and Na.19 Currently, extensive investigation is ongoing regarding the layered transition metal oxide cathode materials having larger interlayer distances and diffusion paths for K ion batteries.20 Adopting K ion battery technology can also lead to the production of cheaper Co-free batteries, often based on transition metals such as Fe, Mn, and V.21 Though the electrode materials for LIBs have been extensively explored, the same is not true for K-ion batteries. However, seeking suitable electrode materials for K ion batteries is experimentally challenging and even theoretically, requires high computational facilities. The majority of the electrode materials used for LIBs are still unexplored for K-ion batteries due to the difficulties in experimental and computational screening of a large number of electrode materials with high accuracy.22–24 Therefore, machine learning (ML) could be an advanced tool that can save both time and cost, and at the same time screen many electrodes with minimum computational cost. Among different factors affecting the success of ML, data takes the central position. Every ML model depends on the amount and quality of data needed for training. Taking advantage of different computational material databases like Materials Project, OQMD, AFLowLib, ESP, CMR, and NOMAD, applications of ML for determining battery properties are increasing day by day. Besides computational data, ICSD and COD provide data from published literature, while NASA battery datasets contain experimental battery data and so on.25–32 Although the use of DFT based data is not standard for every context, it still delivers sensible insights which ultimately help in the guidance of experimental research.33,34 ML combined with data from various databases can be used for predicting any specific property of interest for a particular battery material.23,29,35–39 Application of ML in the field of materials science can be found in the prediction of microscopic properties like band structure, formation energy, density of states, etc. which play an essential role in research areas like solar cells, batteries, and catalysis.40–55 Kernel ridge regression (KRR) and support vector regression (SVR) have been used by Seko et al. for the prediction of thermal conductivity and cohesive energy of binary and tertiary compounds.56,57 ML techniques have also been used for the prediction of different properties for their applicability as materials in photovoltaic cells and glass alloys.58–60 Application of ML on battery systems was first carried out by Salkind et al., predicting the state of charge and state of health and from then onwards investigation on the application of ML in battery monitoring has continued.61 Siqi Shi and coworkers have predicted the activation energy in cubic Li-argyrodites with hierarchically encoding crystal structure based descriptors.62 Application of ML has also been reported for the determination of interphase stability of Li-doped Li7La3Zr2O12.63 Sendek and coworkers have used the logistic regression for screening of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Li-containing solids as solid-state electrolytes for LIBs by rapid screening.52 ML has also been applied for the identification of chemical factors and descriptors affecting the reaction kinetics of Li batteries.64,65 Meredig et al. built a ML model to estimate thermodynamic stability and proposed around 4500 stable novel materials.66 The multilayer automated feature selection method has been reported to incorporate expert knowledge.67 ML has also been used as an alternative as well as faster method than DFT, for prediction of thermal, electronic and mechanical properties.29,68–70 However, certain challenges exist in applying ML to materials research, such as contradictions between high dimension and small sample data, conflict and compromise between complexity and accuracy of machine learning models, and inconsistency and collaboration between learning results and domain expert knowledge.71,72 Method development and guidelines for different ML-based publications highlighting supervised learning and its interpretability have been elaborated recently by Rodrigues and co-workers.73
000 Li-containing solids as solid-state electrolytes for LIBs by rapid screening.52 ML has also been applied for the identification of chemical factors and descriptors affecting the reaction kinetics of Li batteries.64,65 Meredig et al. built a ML model to estimate thermodynamic stability and proposed around 4500 stable novel materials.66 The multilayer automated feature selection method has been reported to incorporate expert knowledge.67 ML has also been used as an alternative as well as faster method than DFT, for prediction of thermal, electronic and mechanical properties.29,68–70 However, certain challenges exist in applying ML to materials research, such as contradictions between high dimension and small sample data, conflict and compromise between complexity and accuracy of machine learning models, and inconsistency and collaboration between learning results and domain expert knowledge.71,72 Method development and guidelines for different ML-based publications highlighting supervised learning and its interpretability have been elaborated recently by Rodrigues and co-workers.73
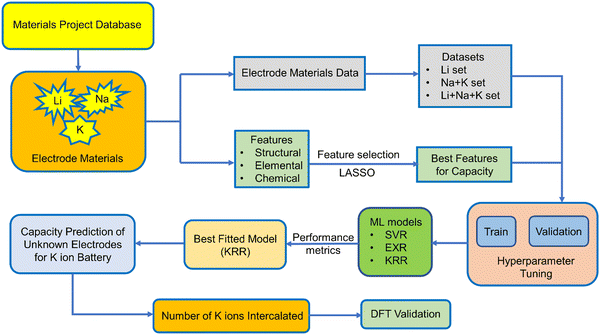
Capacity is one of the important metrics for the measurement of battery performance. The longevity of a battery mainly depends on the cycle life of a battery and the former is directly related to the capacity of a battery. The capacity can be calculated from the number of ions intercalated in electrode materials and in order to do so quantum mechanically, we need to perform time consuming DFT calculations for each individual electrode material. However, we can utilize the different advance machine learning model as a tool to speed up the screening of electrode materials based on capacity as a target variable. Very few studies have been carried out on the experimental capacity prediction on the basis of cycle life via ML for a particular electrode material.74,75 In a recent report, ML has been used for the prediction of voltage for a large number of electrode materials for metal ion batteries.76 They have considered both low and high metal ion concentration. However, we want to calculate the specific capacity of non-intercalated systems by learning from known electrode materials without the help of high ion concentration. In this study, we have utilized the Li, Na, and K ion battery data for the training of ML models in order to predict the capacity of those electrode materials for the K ion battery. To the best of our knowledge, this is the first work regarding the prediction of theoretical capacity on the basis of the structure of electrode materials for metal ion batteries. Here, we have directly predicted the capacity of a non-intercalated electrode material without knowing the number of K ions getting intercalated, i.e., without doing any DFT calculation. The capacity of different electrode materials varies rapidly, and the range of minimum capacity and maximum capacity is very high. Keeping that in mind, we have only considered the monovalent ions and not bivalent and trivalent ions for intercalation. We have also not considered the lower alkali metal ions since the radius of those ions will increase as we go down the group. Among the metal ion batteries, LIBs have been explored extensively; however, experimentally or by DFT calculation, testing all of those LIB electrode materials for K ion batteries is a lengthy process. Therefore, after considering the Li, Na and K ion battery data as the training set, we have replaced the Li and Na by K for an approximate estimation of capacity with the help of different machine learning models. Here, we have used Support Vector Machine (SVM), ExtraTrees Regression (EXR) and Kernel Ridge Regression (KRR) to fit the training dataset. In addition to our particular interest, i.e., capacity, we further used the predicted capacity for the calculation of number of K ions that could be intercalated in the electrode materials for LIBs and sodium ion batteries. In the Materials Project database, there are many instances of the same electrode with different numbers of intercalated ions and capacity. However, we have considered only the non-intercalated system for a particular ion intercalation with maximum capacity as the target variable, so that the machine can learn about the capacity by maximum intercalation of specific ions for a fixed electrode material. The performance of different ML models was assessed by mean absolute percentage error (MAPE). DFT calculation for a few unknown electrode materials has been performed to validate the machine learning model. We have provided a schematic diagram (Scheme 1), which shows the steps followed in our work.
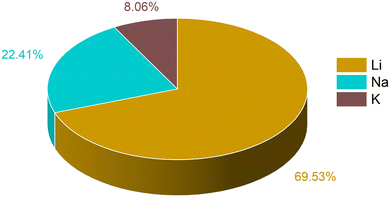
The training data for these metal ion batteries has been retrieved from the Materials Project database.30,77 Overall, 2118 data points have been considered in the training set, among which 69.53% are Li, 22.41% are Na and 8.06% are K ion battery data. We have excluded the repeating formula unit cells, as we are considering non-intercalated electrode materials for learning about the capacity. From the dataset, the ML model may overconcern with LIB electrode materials, and ignore some knowledge about those for Na/K ions, since the contribution in the overall data from LIBs is very high compared to the other two metal ion batteries. The overall known dataset is divided into training set and validation set. The training set has been used to train the ML model whereas the validation set was used to validate the performance of our machine learning models. The validation set is composed of 20% of the total data and the rest of the data is used for training. The training set remains unique for all the ML models used and the same is true for the validation set. The amount of Li, Na and K ion data used for training has been shown in Fig. 1. To describe the electrode materials, we have generated 196 unique elemental features depending on the chemical formula of individual electrode materials using choice-based feature vectorization.78 Along with these features, other structural parameters such as lattice parameter (a, b, c), lattice angle (α, β, γ), and volume of void, have also been considered, so that these features can represent each electrode material uniquely. The method for calculating the void volume has been shown in Text S1 (ESI†). In order to specify the intercalated ion, we have also included some elemental properties like ionic radius, ionization energy, and heat of atomization, among others. After the generation of features, scaling has been performed on each descriptor except on the target variable using the StandardScaler module of the python package to bring down all the features in the same scale to avoid the biasness of our data set based on the magnitude of each descriptor of electrode materials by the machine.
Furthermore, to check the importance of considered features towards the desired target variable, we have performed Lasso Regression. Using Lasso regression, we have calculated the feature importance of each individual feature and based on the magnitude of the feature importance we have screened the features. We have only considered the features having feature importance greater than zero and eliminated the rest during the fitting of the ML models. The mathematical expression of LASSO Regression is given as,
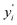 varies from i = 1 to n, where n is the number of observations. Using Lasso regression, we have calculated the slope (m) value for each descriptor. λ is a constant and considering its value equal to one, the slope for each descriptor has been established. The features having m value equal to zero were considered as irrelevant and those features were dropped. As a result, the number of considered features has shrunk from 199 to 71 i.e., 36% of features remain after Lasso regression. The selection of features based on feature importance has been shown in Table S1 (ESI†) and Fig. S1 (ESI†). From Table S1 (ESI†), it is observed that lattice parameters (a, b, c), S orbital contribution, average number of valence electrons, void volume, Allred Rochow electronegativity etc., contributed more towards the target variable specific capacity. Variance in Allred Rochow electronegativity and average number of valence electrons are found to be among the most important features.
varies from i = 1 to n, where n is the number of observations. Using Lasso regression, we have calculated the slope (m) value for each descriptor. λ is a constant and considering its value equal to one, the slope for each descriptor has been established. The features having m value equal to zero were considered as irrelevant and those features were dropped. As a result, the number of considered features has shrunk from 199 to 71 i.e., 36% of features remain after Lasso regression. The selection of features based on feature importance has been shown in Table S1 (ESI†) and Fig. S1 (ESI†). From Table S1 (ESI†), it is observed that lattice parameters (a, b, c), S orbital contribution, average number of valence electrons, void volume, Allred Rochow electronegativity etc., contributed more towards the target variable specific capacity. Variance in Allred Rochow electronegativity and average number of valence electrons are found to be among the most important features.
2. Data analysis
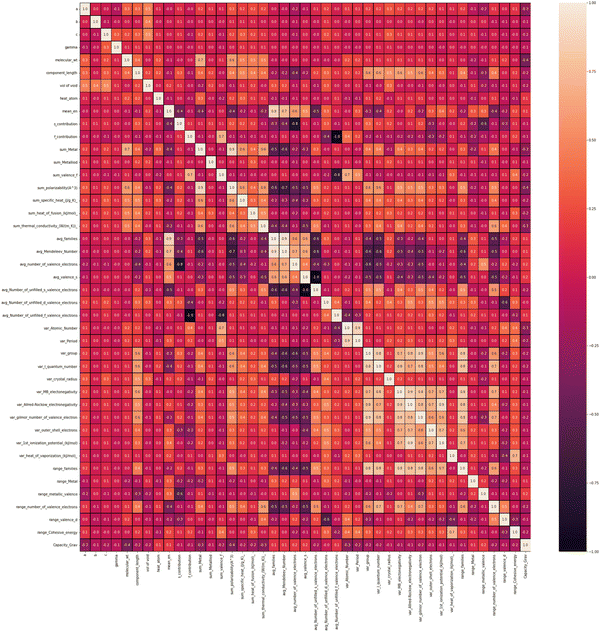
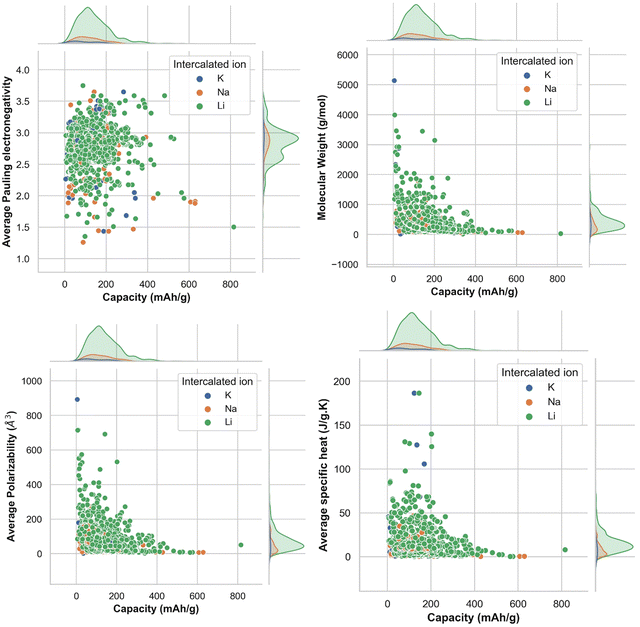
To find out the correlation among the features, the heat map is generated, as shown in Fig. 2 using the correlation function from the seaborn library. From the correlation values of different features, most of the features are found to be independent of each other. Some features are positively correlated, while some show a negative correlation. For example, Variance in Allred Rochow electronegativity is negatively correlated whereas average valence electrons are found to be positively correlated with the target variable (capacity). Hence, the choice of these features will be able to represent each electrode material uniquely. Though few elemental features are found to be dependent on each other, those features are not dropped so as to represent the intercalating ions. The elemental descriptors considered for the generation of input features are listed in Table S2 (ESI†).Understanding the nature of the dependence of features is highly important and, in this regard, a joint plot helps us to find out the density of features. From Fig. 3, it is observed that molecular weight and polarizability follow almost the same trend, whereas Pauling electronegativity values are diverse at higher magnitude. There is an indirect correlation between molecular weight and polarizability as electron density increases with the increase in atomic mass.79 Therefore, it is very likely to observe a similar trend between these two parameters. Any trend in change of capacity with respect to average Pauling electronegativity could not be identified. The high range of electronegativity for most of the electrode materials may be the cause for this. To understand how the capacity of electrode materials changes with the change in the electronic properties of these materials, average s, d and f valence electrons have been calculated by taking the average of the valence electrons of the constituent atoms of the electrode materials, which is then plotted as the contribution of valence electrons with change in specific capacity. From Fig. S2 (ESI†) it is evident that the average capacity values fall in the range of higher s electron contribution, whereas in the case of the d orbital valence electron contribution, the capacity values are on the lower side. Thus, a large number of electrode materials have more s orbital valence electrons and fewer d orbital valence electrons. However, the capacity range varies from low magnitude to high magnitude of the f-orbital valence electron. The reason behind the observed phenomenon may be that most of the electrode materials in our data consists of transition metals with valence d orbital electrons and filled s orbital electrons.
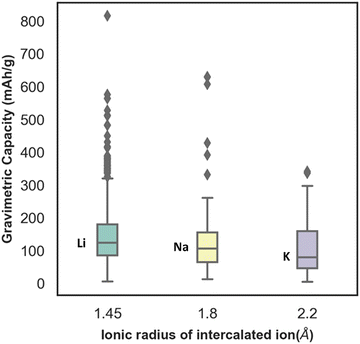
In Fig. S3 (ESI†), the distribution of capacity with the different lattice parameters (a, b, c) and lattice angle γ, of electrode materials has been presented. From the plot, the distribution ranges of a and c are found to be wide, whereas the distribution range of the lattice parameter b is found to be very limited. The capacity is found to vary considerably for similar values of lattice parameter b. Similarly, with change in gamma the capacity is found to change without any uniform trend. Though the capacity value distribution is dispersed with respect to the lattice parameter, still the consideration of lattice parameters as descriptors is important to include the domain knowledge and structural properties of the various electrode materials. For instance, there are multiple unit cell structures for the same electrode material compound in the Materials Project database and hence, lattice parameters as descriptors help in distinguishing them. The box plot between gravimetric capacity and the ionic radius of intercalated ions has been presented in Fig. 4. The mid-line in the box plot is the median, the lower line outside the box is the minimum range and the upper line outside the box is the maximum range of our property of interest. The average capacity for Li ion batteries is found to be higher followed by Na and K ion batteries. With increase in ionic radius, the number of intercalated ions within an electrode material is expected to decrease and so is the specific capacity of the electrode material.
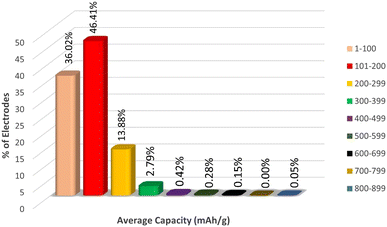
Since the target variable capacity varies rapidly with a slight change in the electrode material, in order to understand the distribution of the electrode materials across the capacity we have plotted the range of % electrodes across per 100 mA h g−1 intervals of capacity, as represented in Fig. 5.
From Fig. 5, we can observe that more than 44% of electrodes lie in the capacity range 101 to 200 mA h g−1, around 35% of electrodes lie in the capacity range 1 to 100 mA h g−1 and 15% of electrodes have capacity 200 to 299 mA h g−1. The % of electrodes having capacity greater than 299 mA h g−1 is very low compared to the first three groups of capacity ranges. Therefore, the sampling of the target variable is highly heterogeneous, which might cause a misinterpretation in the nature of data by the machine, which may lead to overestimation of capacity data in the range of 1 to 299. To avoid this overestimation, we fit the ML models in three different data sets Li, Na + K, and Li + Na + K, which has been discussed later.
3. Results and discussion
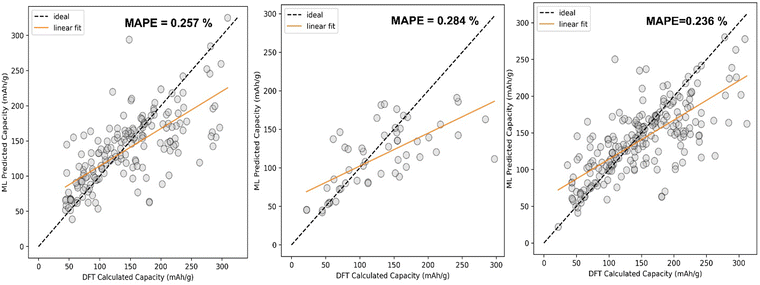
The analysis of our data set begins with fixing the target variable as capacity. The overall data set has been split into two sets, training set composed of 80% of data and validation set composed of 20% data. Here we have compared three different machine learning algorithms, namely Support Vector Machine (SVM), ExtraTress Regression (EXR) and Kernel Ridge Regression (KRR). After analyzing the complexity of the dataset, we have chosen these non-linear ML algorithms to fit the data. Different types of non-linear kernels present in each of these two ML algorithms like Radial basis function (rbf), polynomial, and Laplacian have been used for the training of the machine. Since our data set is medium in size, KRR comes in very handy as it is an advanced ML algorithm compared to SVR having an additional parameter, namely kernel trick. The KRR fitting is much faster compared to the fitting of the SVR. Therefore, first we have fitted our dataset with an SVR algorithm to see the performance. Furthermore, we have checked using KRR and our result shows that the KRR fitted well compared to SVR. An ensemble-based ML algorithm, namely ExtraTrees Regressor, which takes decisions from the combination of a large number of decision trees, has also been applied on the training data set. This algorithm has been chosen as it divides the whole data into further small datasets and each model predicts some different value and the result is basically the average result of each model. These models have been found to be applied on capacity prediction for a particular cycle life of electrode materials.80Since we are predicting continuous values via ML, it therefore belongs to a regression problem and hence we have used Support Vector Regression (SVR), which is a sub part of SVM. SVR contains two important parameters, C (penalty term) and gamma, which should be optimized before fitting of our dataset in the SVR model. We have also tested our training data considering different kernel functions within SVR, like linear function, radial basis function (RBF) and polynomial function to select the most optimized kernel through the assessment of loss function as mean absolute percentage error (MAPE). As discussed earlier, the large contribution of LIBs in the overall dataset might result in mimicking of the Li data, and the data set has been divided in three sets Li, Na + K, and Li + Na + K dataset. The training set is divided into 10 folds so that for each cross-validation test, 9 folds are used for the training whereas the remaining 1-fold is used for the assessment of the model performance in terms of MAPE as loss function. The standard deviation for each 10-fold cross-validation set has also been calculated. By the cross-validation test, we have tried to sample our data in such a way so that the machine does not overfit certain data, which could lead to a good training score but a very bad test score. The details regarding testing of different kernels for SVR are shown in Table 1. Among different kernels, the RBF kernel function is found to fit well with less error as we have assessed our SVR model performance by checking the cross-validation score (CVi).
| CVi | Linear | RBF | Polynomial |
|---|---|---|---|
| CV1 | 0.62 | 0.46 | 0.60 |
| CV2 | 0.36 | 0.36 | 0.39 |
| CV3 | 0.37 | 0.32 | 0.64 |
| CV4 | 0.49 | 0.33 | 0.55 |
| CV5 | 0.46 | 0.35 | 0.46 |
| CV6 | 0.38 | 0.40 | 0.44 |
| CV7 | 0.32 | 0.23 | 0.44 |
| CV8 | 0.29 | 0.19 | 0.31 |
| CV9 | 0.29 | 0.20 | 0.43 |
| CV10 | 0.36 | 0.35 | 0.53 |
| SD | 0.10 | 0.08 | 0.10 |
| Mean MAPE | 0.39 | 0.32 | 0.48 |
| MAPEV | 0.31 | 0.24 | 0.40 |
The cross-validation has been also performed for all three different datasets and shown in Table 1. The Mean MAPE shows the error on the training set, whereas MAPEV shows the error on the validation set. For all three datasets a similar trend has been observed with respect to training error and validation error. Though less error is expected for the Na + K data set as it contains the lowest number of data points, the less error for the Li + Na + K data set compared to the other two datasets evidences a better sampling of the data. The standard deviation for the dataset containing Li, Na and K data is lower compared to the dataset having Na and K data, which indicates that in the overall dataset the deviation mainly arises from the Na + K data and not from the Li data. However, this data set can play an important role in the prediction of the capacity for the K-ion battery as Na is the closer element of K in the alkali metal group compared to Li.
The hyperparameter tuning on C and gamma for the SVR ML model has been illustrated in Fig. 6(a and b). The best parameters for Li + Na + K and Li data are found to be the same whereas for Na + K data they are different (Table 2). After finding out the best hyperparameters for the three different data sets we have fitted the SVR model on the training set and then validated the model in terms of MAPE utilizing the validation set.
| CVi | Li (C = 100, gamma = 0.05) | Na + K (C = 75, gamma = 0.01) | Li + Na + K (C = 100, gamma = 0.05) |
|---|---|---|---|
| CV1 | 0.44 | 0.54 | 0.46 |
| CV2 | 0.36 | 0.50 | 0.36 |
| CV3 | 0.35 | 0.25 | 0.32 |
| CV4 | 0.31 | 0.38 | 0.33 |
| CV5 | 0.40 | 0.24 | 0.35 |
| CV6 | 0.32 | 0.18 | 0.40 |
| CV7 | 0.25 | 0.12 | 0.23 |
| CV8 | 0.21 | 0.19 | 0.19 |
| CV9 | 0.19 | 0.18 | 0.20 |
| CV10 | 0.34 | 0.23 | 0.35 |
| SD | 0.08 | 0.14 | 0.08 |
| Mean MAPE | 0.32 | 0.28 | 0.32 |
| MAPEV | 0.26 | 0.28 | 0.23 |
The comparison between DFT calculated capacity and ML Predicted capacity has been shown in Fig. 7. We have plotted the DFT calculated capacity vs ML predicted capacity using the best hyperparameters of SVR for all three different datasets.
Similarly, we have fitted our dataset in a tree-based ML model, ExtraTrees Regression (EXR). The cross-validation score using the EXR algorithm has been presented in Table 3. The number of trees and other parameters are optimized before fitting the EXR ML model. However, the optimized parameters remain the same for all three different datasets. We have found the same error trend as the SVR model. The Li + Na + K data have given less error on the validation set compared to the other two data sets. As we have compared the performance of the SVR model in three different sets, here also we have plotted the same plot using the EXR ML model after fitting (Fig. S5, ESI†). Thus, the overall performance of the EXR algorithm is found to be almost similar to the SVR algorithm.
| CVi | Li | Na + K | Li + Na + K |
|---|---|---|---|
| CV1 | 0.43 | 0.60 | 0.47 |
| CV2 | 0.37 | 0.31 | 0.33 |
| CV3 | 0.32 | 0.16 | 0.26 |
| CV4 | 0.36 | 0.24 | 0.32 |
| CV5 | 0.37 | 0.17 | 0.34 |
| CV6 | 0.31 | 0.16 | 0.39 |
| CV7 | 0.21 | 0.14 | 0.23 |
| CV8 | 0.20 | 0.16 | 0.19 |
| CV9 | 0.23 | 0.21 | 0.25 |
| CV10 | 0.38 | 0.25 | 0.33 |
| SD | 0.08 | 0.14 | 0.08 |
| Mean MAPE | 0.32 | 0.24 | 0.31 |
| MAPEV | 0.26 | 0.28 | 0.24 |
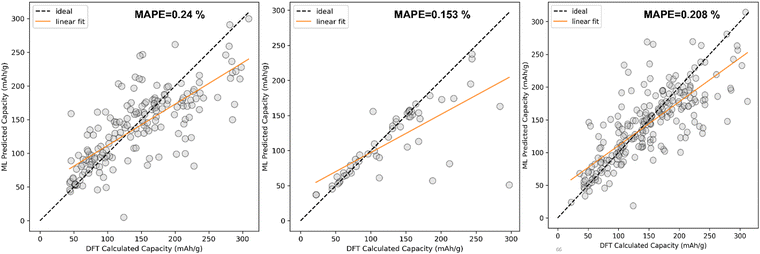
Furthermore, KRR has been used for the fitting of the data where we have again checked the 10-fold cross-validation result after choosing the optimized hyperparameters. The result of the 10-fold cross-validation test is shown in Table 4. Among all these three ML algorithms, KRR has fitted the Na + K data well compared to the others having MAPEV of 0.153%. Gamma and alpha are two important parameters for the KRR algorithm. The optimization of these parameters is shown in Fig. 6(c).
| CVi | Li | Na + K | Li + Na + K |
|---|---|---|---|
| CV1 | 0.42 | 0.50 | 0.40 |
| CV2 | 0.33 | 0.19 | 0.30 |
| CV3 | 0.31 | 0.16 | 0.22 |
| CV4 | 0.33 | 0.19 | 0.32 |
| CV5 | 0.36 | 0.12 | 0.34 |
| CV6 | 0.32 | 0.14 | 0.40 |
| CV7 | 0.24 | 0.19 | 0.25 |
| CV8 | 0.20 | 0.19 | 0.18 |
| CV9 | 0.22 | 0.13 | 0.23 |
| CV10 | 0.38 | 0.24 | 0.33 |
| SD | 0.07 | 0.11 | 0.07 |
| Mean MAPE | 0.31 | 0.21 | 0.30 |
| MAPEV | 0.24 | 0.15 | 0.21 |
The comparison between DFT calculated capacity and ML predicted capacity for three different datasets has been displayed in Fig. 8. Though the trend in training error and validation error in KRR is slightly different from the SVR and EXR ML model, the overall performance of the KRR ML model is better than the rest of the two as KRR is able to mimic the nature of Na + K data better, which is more important than to mimic Li ion data considering our goal of predicting the capacity for K ion battery electrode materials. Therefore, from overall analysis on different datasets, it is evident that KRR performs better than other considered models.
We have also fitted random forest regression (RFR). The best hyperparameters of RFR and optimized number of trees are attached in Text S2 (ESI†) and Fig. S6 (ESI†), respectively, and the cross-validation score is attached in Table S3 (ESI†). Optimized hyperparameters and mean absolute percentage error (MAPE) for decision tree regression are also given in Table S4 (ESI†).
4. DFT validation
To validate our calculated capacity for various electrode materials, we have considered five structurally different sample electrode materials (Mn4NiO8, FeO2, Fe(CoO3)2, V5O12 and CoPO4) and checked their maximum specific capacity by carrying out first principles calculations using the projector augmented wave (PAW) method as implemented in the Vienna Ab initio Simulation Package.81–86 The selected materials are taken in such a way that they belong to different crystal lattice structures and stoichiometry of constituent elements. Moreover, the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE) has been considered as the exchange correlation potential and the energy cutoff is set to 470 eV. Furthermore, the dispersion energy corrections have been considered by incorporating the DFT-D3 method of Grimme.87,88 All of the structures are relaxed until the Hellmann–Feynman force criteria of <0.01 eV Å−1 and the total energy convergence criteria of 10−4 eV is reached. The structures of the system have been taken from the Materials Project database. Using the value of specific capacity from the ML results, we obtained the number of intercalating ions using the equation,where z represents the charge on intercalating ions (1 in case of K), x represents the number of intercalating ions and F is the Faraday constant (26.8 A h mol−1). Mf represents the molecular weight of the formula unit of the electrode material. Using the ML predicted data from the KRR model we have found the number of intercalated K ions and rounded off to the nearest whole number for DFT validation, as presented in Table 5. The rounding off is carried out to decrease the computational cost as modelling fractional ion intercalation will result in heavier DFT calculations. The DFT optimized fully intercalated systems with maximum capacity are represented in Fig. 9. This proves that the number of K intercalations obtained from ML predicted data also agrees with the DFT optimized structures.
| Electrode materials | No. of intercalating K ions predicted by ML | No. of intercalating K ions considered for DFT |
|---|---|---|
| Mn4NiO8 | 3.1 | 3 |
| FeO2 | 0.6 | 1 |
| Fe(CoO3)2 | 2.5 | 2 |
| VFeO4 | 1.1 | 1 |
| CoPO4 | 0.9 | 1 |
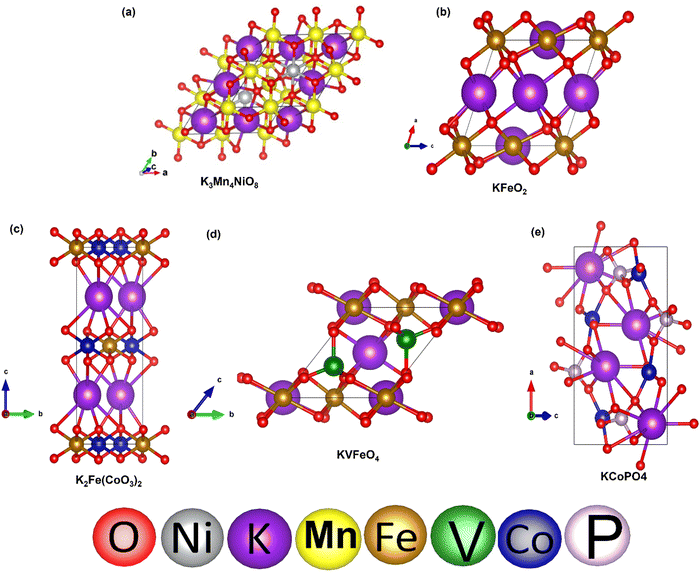 | ||
| Fig. 9 DFT optimized structures of K intercalated electrode materials: (a) Mn4NiO8, (b) FeO2, (c) Fe(CoO3)2, (d) VFeO4, and (e) CoPO4. | ||
The gradual intercalation of K has also been shown for a sample electrode material Mn4NiO8, where the negative binding energy of K insertion shows the favourability of intercalation in the considered electrode material (Fig. S7 and Table S5,ESI†). Furthermore, we have intercalated the fourth K-ion into the Mn4NiO8 in two possible ways to check if further intercalation is possible. The huge distortion in optimized structures of K4Mn4NiO8 (Fig. S8, ESI†) as well as the abrupt increase in RMSD value (Fig. S9, ESI†) of the intercalated system with respect to the non-intercalated system shows that intercalation of the fourth K-ion is not suitable. This further validates that the ML predicted capacity values correspond to the maximum intercalation of K-ions in the electrode materials.
5. Conclusion
In this work, we have predicted the specific capacity of prospective K-ion battery electrode materials based on the structural properties (e.g., lattice parameter, lattice angle, void space, etc.) and choice based feature vectorization generated from elemental properties (e.g., atomic number, electronegativity, ionic radius, valence electrons, etc.). We have considered Li, Na and K-ion electrode materials and their available battery data from the Materials Project database. The electrode materials extracted from the materials project database can be considered as stable as their formation energies are negative. Suitable features have been considered and developed to train the various machine learning algorithms. The available data has been divided into training set and validation set. The training set has been fitted using various ML algorithms like Support Vector Regression, ExtraTrees Regression and Kernel Ridge Regression to learn the nature of the data and features. Some statistical methods of data analysis like box plot and joint plot to understand the distribution of features and heatmap for the correlation metrics have been utilized. We have evaluated the performance of considered machine learning models by comparing the mean absolute percentage error between the training set and validation set in each case. Furthermore, adopting Kernel Ridge Regression we have predicted the capacity of unknown electrode materials for K-ion batteries (Table S6,ESI†). Using the value of specific capacity, the number of intercalated K ions in the formula unit of the non-intercalated electrode material compounds has been calculated. DFT calculations have been performed for sample electrode materials to verify that our ML model can give similar results. Thus, implementing the ML approach is much faster compared to the computationally demanding quantum mechanical methods for quick screening of electrode materials, which will help to guide the experiments for developing electrode materials for metal ion batteries.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank IIT Indore for the lab and computing facilities. This work is supported by DST-SERB (Project Number CRG/2018/001131), SPARC (Project Number SPARC/2018-2019/P116/SL) New Delhi, and CSIR (project 01(3046)/21/EMR-II). S. M. thanks Prime Minister's Research Fellowship (PMRF) for the research fellowship. D. R. thanks MoE for the research fellowship. S.D. thank CSIR for the research fellowship.References
- Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Electrochemical Energy Storage for Green Grid, Chem. Rev., 2011, 111, 3577–3613 CrossRef CAS PubMed.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Li-ion battery materials: present and future, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- M. Winter, B. Barnett and K. Xu, Before Li Ion Batteries, Chem. Rev., 2018, 118, 11433–11456 CrossRef CAS PubMed.
- B. Dunn, H. Kamath and J. M. Tarascon, Electrical energy storage for the grid: a battery of choices, Science (1979), 2011(334), 928–935 Search PubMed.
- F. Cheng, J. Liang, Z. Tao, J. Chen, F. Y. Cheng, J. Liang, Z. L. Tao and J. Chen, Functional Materials for Rechargeable Batteries, Adv. Mater., 2011, 23, 1695–1715 CrossRef CAS PubMed.
- J. M. Tarascon, Is lithium the new gold?, Nat. Chem., 2010, 2, 510 CrossRef CAS PubMed.
- R. P. Joshi, B. Ozdemir, V. Barone and J. E. Peralta, Hexagonal BC3: a robust electrode material for Li, Na, and K ion batteries, J. Phys. Chem. Lett., 2015, 6, 2728–2732 CrossRef CAS PubMed.
- P. Bhauriyal, A. Mahata and B. Pathak, Hexagonal BC3 Electrode for a High-Voltage Al-Ion Battery, J. Phys. Chem. C, 2017, 121, 9748–9756 CrossRef CAS.
- J. O. G. Posada, A. J. R. Rennie, S. P. Villar, V. L. Martins, J. Marinaccio, A. Barnes, C. F. Glover, D. A. Worsley and P. J. Hall, Aqueous batteries as grid scale energy storage solutions, Renewable Sustainable Energy Rev., 2017, 68, 1174–1182 CrossRef CAS.
- K. Liu, Y. Liu, D. Lin, A. Pei and Y. Cui, Materials for lithium-ion battery safety, Sci. Adv., 2018, 4(6), eaas9820 CrossRef PubMed.
- J. M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Mater. Sustainable Energy, 2010, 171–179 Search PubMed.
- C. Nithya and S. Gopukumar, Sodium ion batteries: a newer electrochemical storage, Wiley Interdisciplinary Rev.: Energy Environ., 2015, 4, 253–278 CrossRef CAS.
- D. Larcher and J. M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2014, 7, 19–29 CrossRef PubMed.
- B. Scrosati and J. Garche, Lithium batteries: Status, prospects and future, J. Power Sources, 2010, 195, 2419–2430 CrossRef CAS.
- W. Zhang, Y. Liu and Z. Guo, Approaching high-performance potassium-ion batteries via advanced design strategies and engineering, Sci. Adv., 2019, 5(5), eaav7412 CrossRef CAS PubMed.
- A. Eftekhari, Z. Jian and X. Ji, Potassium Secondary Batteries, ACS Appl. Mater. Interfaces, 2017, 9, 4404–4419 CrossRef CAS PubMed.
- W. Zhang, W. Huang and Q. Zhang, Organic Materials as Electrodes in Potassium-Ion Batteries, Chem. – Eur. J., 2021, 27, 6131–6144 CrossRef PubMed.
- R. Rajagopalan, Y. Tang, X. Ji, C. Jia, H. Wang, R. Rajagopalan, Y. Tang, X. Ji, H. Wang and C. Jia, Advancements and Challenges in Potassium Ion Batteries: A Comprehensive Review, Adv. Funct. Mater., 2020, 30, 1909486 CrossRef CAS.
- J. C. Pramudita, D. Sehrawat, D. Goonetilleke, N. Sharma, J. C. Pramudita, D. Sehrawat, D. Goonetilleke and N. Sharma, An Initial Review of the Status of Electrode Materials for Potassium-Ion Batteries, Adv. Energy Mater., 2017, 7, 1602911 CrossRef.
- W. Li, Z. Bi, W. Zhang, J. Wang, R. Rajagopalan, Q. Wang, D. Zhang, Z. Li, H. Wang and B. Wang, Advanced cathodes for potassium-ion batteries with layered transition metal oxides: a review, J. Mater. Chem. A, 2021, 9, 8221–8247 RSC.
- H. Kim, H. Ji, J. Wang and G. Ceder, Next-Generation Cathode Materials for Non-aqueous Potassium-Ion Batteries, Trends. Chem., 2019, 1, 682–692 CrossRef CAS.
- P. Kirkpatrick and C. Ellis, Chemical space, Nature, 2004, 432, 823 CrossRef CAS.
- O. A. von Lilienfeld, Quantum Machine Learning in Chemical Compound Space, Angew. Chem., Int. Ed., 2018, 57, 4164–4169 CrossRef CAS PubMed.
- A. Mullard, The drug-maker's guide to the galaxy, Nature, 2017, 549, 445–447 CrossRef PubMed.
- C. Draxl and M. Scheffler, NOMAD: The FAIR concept for big data-driven materials science, MRS Bull., 2018, 43, 676–682 CrossRef.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD), JOM, 2013, 65, 1501–1509 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, Npj. Comput. Mater., 2015, 1, 1–15 Search PubMed.
- S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, AFLOW: an automatic framework for high-throughput materials discovery, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- E. Gossett, C. Toher, C. Oses, O. Isayev, F. Legrain, F. Rose, E. Zurek, J. Carrete, N. Mingo, A. Tropsha and S. Curtarolo, AFLOW-ML: A RESTful API for machine-learning predictions of materials properties, Comput. Mater. Sci., 2017, 152, 134–145 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: a materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- S. P. Ong, S. Cholia, A. Jain, M. Brafman, D. Gunter, G. Ceder and K. A. Persson, The Materials Application Programming Interface (API): a simple, flexible and efficient API for materials data based on REpresentational State Transfer (REST) principles, Comput. Mater. Sci., 2015, 97, 209–215 CrossRef.
- C. Ling, A review of the recent progress in battery informatics, Npj. Comput. Mater., 2022, 8, 1–22 CrossRef.
- R. P. Joshi, K. Trepte, K. P. K. Withanage, K. Sharkas, Y. Yamamoto, L. Basurto, R. R. Zope, T. Baruah, K. A. Jackson and J. E. Peralta, Fermi-Löwdin orbital self-interaction correction to magnetic exchange couplings, J. Chem. Phys., 2018, 149, 164101 CrossRef PubMed.
- T. P. Kaloni, R. P. Joshi, N. P. Adhikari and U. Schwingenschlögl, Band gap tunning in BN-doped graphene systems with high carrier mobility, Appl. Phys. Lett., 2014, 104, 073116 CrossRef.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, Machine learning in materials informatics: recent applications and prospects, Npj. Comput. Mater., 2017, 3, 1–13 CrossRef.
- L. Bassman, P. Rajak, R. K. Kalia, A. Nakano, F. Sha, J. Sun, D. J. Singh, M. Aykol, P. Huck, K. Persson and P. Vashishta, Active learning for accelerated design of layered materials, Npj. Comput. Mater., 2018, 4, 1–9 CrossRef.
- Y. Zhang and C. Ling, A strategy to apply machine learning to small datasets in materials science, Npj. Comput. Mater., 2018, 4, 1–8 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, J. Phys.: Mater., 2019, 2, 032001 CAS.
- Y. Dong, C. Wu, C. Zhang, Y. Liu, J. Cheng and J. Lin, Bandgap prediction by deep learning in configurationally hybridized graphene and boron nitride, Npj. Comput. Mater., 2019, 5, 1–8 CrossRef CAS.
- Y. Zhuo, A. Mansouri Tehrani and J. Brgoch, Predicting the Band Gaps of Inorganic Solids by Machine Learning, J. Phys. Chem. Lett., 2018, 9, 1668–1673 CrossRef CAS PubMed.
- B. Kolb, L. C. Lentz and A. M. Kolpak, Discovering charge density functionals and structure–property relationships with PROPhet: a general framework for coupling machine learning and first-principles methods, Sci. Rep., 2017, 7, 1–9 CrossRef CAS PubMed.
- G. Pilania, C. Wang, X. Jiang, S. Rajasekaran and R. Ramprasad, Accelerating materials property predictions using machine learning, Sci. Rep., 2013, 3, 1–6 Search PubMed.
- G. Pilania, A. Mannodi-Kanakkithodi, B. P. Uberuaga, R. Ramprasad, J. E. Gubernatis and T. Lookman, Machine learning bandgaps of double perovskites, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed.
- K. Takahashi, L. Takahashi, I. Miyazato and Y. Tanaka, Searching for Hidden Perovskite Materials for Photovoltaic Systems by Combining Data Science and First Principle Calculations, ACS Photonics, 2018, 5, 771–775 CrossRef CAS.
- K. Sodeyama, Y. Igarashi, T. Nakayama, Y. Tateyama and M. Okada, Liquid electrolyte informatics using an exhaustive search with linear regression, Phys. Chem. Chem. Phys., 2018, 20, 22585–22591 RSC.
- Y. Okamoto and Y. Kubo, Ab Initio Calculations of the Redox Potentials of Additives for Lithium-Ion Batteries and Their Prediction through Machine Learning, ACS Omega, 2018, 3, 7868–7874 CrossRef CAS PubMed.
- R. Jalem, M. Nakayama and T. Kasuga, An efficient rule-based screening approach for discovering fast lithium ion conductors using density functional theory and artificial neural networks, J. Mater. Chem. A, 2013, 2, 720–734 RSC.
- K. Fujimura, A. Seko, Y. Koyama, A. Kuwabara, I. Kishida, K. Shitara, C. A. J. Fisher, H. Moriwake and I. Tanaka, Accelerated Materials Design of Lithium Superionic Conductors Based on First-Principles Calculations and Machine Learning Algorithms, Adv. Energy Mater., 2013, 3, 980–985 CrossRef CAS.
- N. Kireeva and V. S. Pervov, Materials space of solid-state electrolytes: unraveling chemical composition–structure–ionic conductivity relationships in garnet-type metal oxides using cheminformatics virtual screening approaches, Phys. Chem. Chem. Phys., 2017, 19, 20904–20918 RSC.
- E. D. Cubuk, A. D. Sendek and E. J. Reed, Screening billions of candidates for solid lithium-ion conductors: a transfer learning approach for small data, J. Chem. Phys., 2019, 150, 214701 CrossRef PubMed.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K. A. N. Duerloo, Y. Cui and E. J. Reed, Holistic computational structure screening of more than 12
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 candidates for solid lithium-ion conductor materials, Energy Environ. Sci., 2017, 10, 306–320 RSC.
000 candidates for solid lithium-ion conductor materials, Energy Environ. Sci., 2017, 10, 306–320 RSC. - K. T. Schütt, H. Glawe, F. Brockherde, A. Sanna, K. R. Müller and E. K. U. Gross, How to represent crystal structures for machine learning: Towards fast prediction of electronic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205118 CrossRef.
- D. Roy, S. C. Mandal and B. Pathak, Machine Learning-Driven High-Throughput Screening of Alloy-Based Catalysts for Selective CO2Hydrogenation to Methanol, ACS Appl. Mater. Interfaces, 2021, 13, 56151–56163 CrossRef CAS PubMed.
- D. Roy, S. C. Mandal and B. Pathak, Machine Learning Assisted Exploration of High Entropy Alloy-Based Catalysts for Selective CO2 Reduction to Methanol, J. Phys. Chem. Lett., 2022, 13, 5991–6002 CrossRef CAS PubMed.
- A. Seko, H. Hayashi, K. Nakayama, A. Takahashi and I. Tanaka, Representation of compounds for machine-learning prediction of physical properties, Phys. Rev. B, 2017, 95, 144110 CrossRef.
- A. Seko, T. Maekawa, K. Tsuda and I. Tanaka, Machine learning with systematic density-functional theory calculations: Application to melting temperatures of single- and binary-component solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054303 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, A general-purpose machine learning framework for predicting properties of inorganic materials, Npj. Comput. Mater., 2016, 2, 1–7 CrossRef.
- F. A. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Machine Learning Energies of 2 Million Elpasolite (ABC2D6) Crystals, Phys. Rev. Lett., 2016, 117, 135502 CrossRef PubMed.
- A. M. Deml, R. O’Hayre, C. Wolverton and V. Stevanović, Predicting density functional theory total energies and enthalpies of formation of metal-nonmetal compounds by linear regression, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 085142 CrossRef.
- S. Shi, J. Gao, Y. Liu, Y. Zhao, Q. Wu, W. Ju, C. Ouyang and R. Xiao, Multi-scale computation methods: Their applications in lithium-ion battery research and development, Chin. Phys. B, 2016, 25, 018212 CrossRef.
- Q. Zhao, M. Avdeev, L. Chen and S. Shi, Machine learning prediction of activation energy in cubic Li-argyrodites with hierarchically encoding crystal structure-based (HECS) descriptors, Sci. Bull., 2021, 66, 1401–1408 CrossRef CAS.
- B. Liu, J. Yang, H. Yang, C. Ye, Y. Mao, J. Wang, S. Shi, J. Yang and W. Zhang, Rationalizing the interphase stability of Li|doped-Li7La3Zr2O12via automated reaction screening and machine learning, J. Mater. Chem. A, 2019, 7, 19961–19969 RSC.
- A. Wang, Z. Zou, D. Wang, Y. Liu, Y. Li, J. Wu, M. Avdeev and S. Shi, Identifying Chemical Factors Affecting Reaction Kinetics in Li-air Battery via ab initio Calculations and Machine Learning, Energy Storage Mater., 2021, 35, 595–601 CrossRef.
- Q. Zhao, L. Zhang, B. He, A. Ye, M. Avdeev, L. Chen and S. Shi, Identifying descriptors for Li+ conduction in cubic Li-argyrodites via hierarchically encoding crystal structure and inferring causality, Energy Storage Mater., 2021, 40, 386–393 CrossRef.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. W. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Combinatorial screening for new materials in unconstrained composition space with machine learning, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094104 CrossRef.
- Y. Liu, J. M. Wu, M. Avdeev and S. Q. Shi, Multi-Layer Feature Selection Incorporating Weighted Score-Based Expert Knowledge toward Modeling Materials with Targeted Properties, Adv. Theory Simul., 2020, 3, 1900215 CrossRef CAS.
- F. Brockherde, L. Vogt, L. Li, M. E. Tuckerman, K. Burke and K. R. Müller, Bypassing the Kohn–Sham equations with machine learning, Nat. Commun., 2017, 8, 1–10 CrossRef CAS PubMed.
- K. Mills, M. Spanner and I. Tamblyn, Deep learning and the Schrödinger equation, Phys. Rev. A, 2017, 96, 042113 CrossRef.
- L. Li, J. C. Snyder, I. M. Pelaschier, J. Huang, U. N. Niranjan, P. Duncan, M. Rupp, K. R. Müller and K. Burke, Understanding machine-learned density functionals, Int. J. Quantum Chem., 2016, 116, 819–833 CrossRef CAS.
- Y. Liu, B. Guo, X. Zou, Y. Li and S. Shi, Machine learning assisted materials design and discovery for rechargeable batteries, Energy Storage Mater., 2020, 31, 434–450 CrossRef.
- Y. Liu, T. Zhao, W. Ju and S. Shi, Materials discovery and design using machine learning, J. Materiomics, 2017, 3, 159–177 CrossRef.
- A. Bender, N. Schneider, M. Segler, W. Patrick Walters, O. Engkvist and T. Rodrigues, Evaluation guidelines for machine learning tools in the chemical sciences, Nat. Rev. Chem., 2022, 6, 428–442 CrossRef.
- J. Wu, C. Zhang and Z. Chen, An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks, Appl. Energy, 2016, 173, 134–140 CrossRef.
- D. Cheng, W. Sha, L. Wang, S. Tang, A. Ma, Y. Chen, H. Wang, P. Lou, S. Lu and Y. C. Cao, Solid-State Lithium Battery Cycle Life Prediction Using Machine Learning, Appl. Sci., 2021, 11, 4671 CrossRef CAS.
- R. P. Joshi, J. Eickholt, L. Li, M. Fornari, V. Barone and J. E. Peralta, Machine Learning the Voltage of Electrode Materials in Metal-Ion Batteries, ACS Appl. Mater. Interfaces, 2019, 11, 18494–18503 CrossRef CAS PubMed.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, First-principles prediction of redox potentials in transition-metal compounds with LDA + U, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–8 Search PubMed.
- A. Y. T. Wang, R. J. Murdock, S. K. Kauwe, A. O. Oliynyk, A. Gurlo, J. Brgoch, K. A. Persson and T. D. Sparks, Machine Learning for Materials Scientists: An Introductory Guide toward Best Practices, Chem. Mater., 2020, 32, 4954–4965 CrossRef CAS.
- P. Atkins, P. W. Atkins and J. de Paula, Atkins' physical chemistry, Oxford University Press, 2014, ch. 16, p. 59 Search PubMed.
- G. Wang, T. Fearn, T. Wang and K. L. Choy, Machine-Learning Approach for Predicting the Discharging Capacities of Doped Lithium Nickel-Cobalt-Manganese Cathode Materials in Li-Ion Batteries, ACS Cent. Sci., 2021, 7, 1551–1560 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The supplementary information contents are the method of calculating volume of void, table of selected features based on feature importance, plot of feature importance vs. features, list of elemental properties to generate feature vectors, joint plots for the distribution plot across electronic properties, distribution of capacity with respect to different lattice parameters of electrode materials, change of explained variance with each principal component, comparison between ML predicted capacity and DFT calculated capacity for the EXR ML model, best hyperparameters found for random forest regression (RFR), estimation of optimized number of trees for the random forest ML model, cross validation score for random forest regression, optimized hyperparameters and mean absolute percentage error for decision tree regression, gradual insertion of K ions in electrode material, Mn4NiO8, (a) K0Mn4NiO8, (b) K1Mn4NiO8, (c) K2Mn4NiO8 and (d) K3Mn4NiO8, calculated binding energy per K insertion for different concentrations of K insertion in Mn4NiO8, DFT optimized structures of Mn4NiO8 upon intercalation by four K ions, root mean square displacement (RMSD) of the Mn4NiO8 structure upon intercalation of K-ions with respect to the unintercalated structure, and predicted capacity for the electrode materials. See DOI: https://doi.org/10.1039/d2ma00746k |
| This journal is © The Royal Society of Chemistry 2022 |