Open Access Article
Open Access ArticleA mechanistic view of defect engineered VFeSb half-Heusler alloys†
Nagendra S.
Chauhan
 * and
Yuzuru
Miyazaki
* and
Yuzuru
Miyazaki
 *
*
Department of Applied Physics, Graduate School of Engineering, Tohoku University, Sendai, Miyagi 980-8579, Japan. E-mail: nagendra599@gmail.com; yuzuru.miyazaki.b7@tohoku.ac.jp; Fax: +81-22-795-7971; Tel: +81-22-795-7970
First published on 20th September 2022
Abstract
Defects are ubiquitous and extensively found in a half-Heusler microstructure, and often yield a significant variation in its transport properties. There remains a critical gap in understanding the nature and origin of such prevalent defects that influence the electronic band structure and lattice dynamics of the innately disordered half-Heusler alloys. Here, we employ thermodynamics evaluation and structural characterization to understand the microscopic origin of a defect sub-structure and elucidate the critical role of stoichiometry by examining defective V1+xFe1+ySb (−0.1 < x, y < 0.1) half-Heusler compositions. It was found that microstructural metastability and an inherent tendency for atomic ordering result in vacancies/interstitials, which can be enhanced in off-stoichiometric compositions. These atomic disorders are embodied as V-segregates, Fe-rich dendrites, and V-deficient eutectic substructures within the structurally ordered half-Heusler microstructure while their concentration depends on the altered stoichiometry. A significant variation in both power factors and lattice thermal conductivity was observed, which is more favorable for V-excess and Fe-deficient compositions in low self-doping limits (0 < x < 0.05) for thermoelectric applications. These findings highlight the defective nature of cubic n-type VFeSb half-Heusler alloys and elucidate the implication of prevalent defects on thermoelectric transport properties.
1. Introduction
Energy conversion via thermoelectrics (TEs) is primarily the external manifestation of charge carriers’ flow, phonon flow, and their intercoupling, mediated by defects.1–3 Owing to the ubiquitous nature of defects and their significant impact on the physical properties of solids, defect engineering in TEs provides a unique ability to decouple their thermal and electrical transport properties, synergistically. For example, defect-related spin tuning,1,4 defect-induced energy filtering,5–7 vacancy-mediated atom or charge transfer,8–11 surface distortion,12,13 and dislocations14–16 are actively explored approaches in TE material research, which appear to be promising in overcoming the limitations of prevailing electronic and phonon structure optimization strategies. The presence of defects is categorized by their dimensionality in a material's microstructure, such as point defects (such as vacancies, interstitials, and antisites), dislocations, planar defects (such as twin boundaries, stacking faults, and grain boundaries), and volume defects (mainly precipitates and voids).1–3 The ability to manipulate the type, concentration, size, and spatial distribution of defects can provide a robust framework and additional degrees of freedom for establishing defect engineering approaches.In half-Heusler (HH) alloys, configurations with a valence electron count per unit formula (VEC) of ∼18 are thermodynamically stable and have been extensively investigated for TE applications.17–23 This is due to the remarkable electronic transport with high power factors exhibited by many of these 18 VEC alloys, which desirably can be formed with constituents within the realm of earth-abundant materials.24–31 Having a ternary equiatomic XYZ composition, most HH alloys crystallize into a cubic crystal system [space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (no. 216)] and host a rich variety of 3d, 4d, and 5d transition metal elements.19,32 Ideally, the HH structure contains four vacant tetrahedral sites in comparison to their full-Heusler XY2Z analogue, wherein these vacant sites are occupied by extra Y atoms. Interestingly, the vacant sites in HH alloys allow a limited solubility of interstitials which can effectively enhance both the phonon scattering and self-doping ability for carrier concentration optimization.33–35 During synthesis, these vacant sites available in HH alloys are highly susceptible to point defects such as the Frenkel-pair type, antisites36–39 and/or Schottky defects37,40 as a result of charge compensation effects, thereby causing an inherent interruptions of regular patterns in crystalline solids. Moreover, the presence of low melting constituent elements such as antimony and tin may cause non-homogeneity in the stoichiometry of HH alloys, as they vaporize during melting and remain in a segregated impurity phase post melting, thus making the synthesis of HH alloys highly susceptible to impurity phases.40–46
3m (no. 216)] and host a rich variety of 3d, 4d, and 5d transition metal elements.19,32 Ideally, the HH structure contains four vacant tetrahedral sites in comparison to their full-Heusler XY2Z analogue, wherein these vacant sites are occupied by extra Y atoms. Interestingly, the vacant sites in HH alloys allow a limited solubility of interstitials which can effectively enhance both the phonon scattering and self-doping ability for carrier concentration optimization.33–35 During synthesis, these vacant sites available in HH alloys are highly susceptible to point defects such as the Frenkel-pair type, antisites36–39 and/or Schottky defects37,40 as a result of charge compensation effects, thereby causing an inherent interruptions of regular patterns in crystalline solids. Moreover, the presence of low melting constituent elements such as antimony and tin may cause non-homogeneity in the stoichiometry of HH alloys, as they vaporize during melting and remain in a segregated impurity phase post melting, thus making the synthesis of HH alloys highly susceptible to impurity phases.40–46
Among the pre-existing HH alloys, structurally ordered cubic VFeSb alloys are a prospective n-type candidate for near-room temperature TE applications owing to their remarkably high-power factor near room temperature.47–51 Interestingly, VFeSb alloys are homologous compounds of NbFeSb HH alloys for which significant progress has been reported lately using microstructural engineering and substitution.27,28,30,31 However, unlike NbFeSb HH alloys, VFeSb is highly susceptible to a significant concentration of vacancies and Fe-interstitials.52–54 Thus, understanding the nature and origin of such prevalent defects remains critical towards improving the TE transport favorably in VFeSb HH alloys. It is widely recognized that the thermodynamic properties of metals and their alloys are of great significance in understanding and interpreting the phenomena such as solidification, diffusion, nucleation, and precipitation. In recent years, the calculation of phase diagram (CALPHAD) technique55–57 has been extensively used to assess the phase stability of a great number of systems by minimizing the Gibbs free energy from the experimental phase equilibrium data. However, for compositions with unavailable experimental information, theoretical models such as Miedema's method58–60 could be alternatively used to perform thermodynamic calculations.61–67 For carrying out thermodynamic calculations to design alloys, understanding the chemical activity of elemental constituents will be useful for better correlating their chemical behavior to attain favorable microstructures.
In this work, we demonstrate defective V1+xFe1+ySb (−0.1 < x, y < 0.1) HH compositions, which are structurally ordered by heat treatment and controlled nominally using stoichiometric alteration, for tuning their TE transport favorably. It was found that cubic VFeSb HH upholds the characteristic HH crystal structure despite a slight variation in off-stoichiometry. The refinement reveals the presence of Fe-interstitials and V-vacancies in all the synthesized specimens, which can be related to changes in stoichiometry. The microstructural characterization reveals the V-segregates, Fe-rich dendrites, and V-deficient eutectic substructure which can be regarded as the embodiments of Fe-interstitials and V-vacancies within the structurally ordered HH microstructure. Most defective compositions display high electrical conductivity and low thermal conductivity arising from distinct substructures, which conduct electrons and effectively scatter phonons. A maximum TE figure-of-merit (zT) of ≈ 0.2 at 523 K was achieved for optimal V1.05FeSb and VFe0.95Sb defective HH alloys due to the enhanced PF and synergistic reduction in κL, which corresponds to a 50% enhancement over pristine VFeSb. Furthermore, the thermodynamic modeling of the V–Fe–Sb system employing the extended Miedema's method was carried out, to provide a qualitative description of the activity–constitution relationship of VFeSb HH alloys.
2. Experimental details
2.1 Materials synthesis
Ingots with nominal compositions V1+xFe1+ySb (−0.1 < x, y < 0.1) were prepared by arc-melting (GMAC-1100, G.E.S Corporation, Japan) thestoichiometrically weighed high purity elements, i.e., V (3N, grains), Fe (3N, grains) and Sb (5N, grains) procured from Kojundo Chemical Laboratory Co., Ltd, Japan. To obtain homogenized ingots, arc-melting was performed multiple times under an Ar atmosphere. Next, the ingots with hexagonal phases were annealed at 873 K for 4 days, to obtain an ordered cubic phase. The annealed arc-melted ingots were then pulverized into a fine powder using a mortar and pestle. The pulverized powder was then directly loaded into a high-strength tungsten carbide die with an inner diameter of 10 mm and bulk consolidated employing SPS (LABOX-325R, NJS Co., Ltd, Japan) at 1023 K under 50 MPa for 5 min. The density (d) of sintered polycrystalline samples enlisted in Table S1 (ESI†) were determined by the Archimedes principle to be >98% of the theoretical density.2.2 Structural characterization
The powder X-ray diffraction (XRD) patterns were collected using CuKα radiation (D8 Advance, Bruker AXS, Germany). As the XRD patterns for the synthesized VFeSb HH alloys were recorded using copper radiation, which may lead to a high background,68 the fluorescence X-ray (background) removal mode setting has been employed for each measurement to achieve a higher PIB ratio (the beam ratio of the peak to the background). The crystal structure determination and phase identification were carried out using the FullProf Suite Rietveld program.69,70 The phase mapping, morphological features, and compositional homogeneity were studied over polished sample surfaces by scanning electron microscopy (SEM, JSM-IT 100, JEOL, Japan) in both secondary electron (SE) and backscattered electron (BSE) modes equipped with energy dispersive spectroscopy (EDS).2.3 Thermoelectric characterization
The temperature-dependent TE transport measurements were performed on bulk sintered samples in the temperature range of 300 K to 873 K. For thermal diffusivity (D) and specific heat (CP) measurement in a vacuum by the flash diffusivity method (LFA467HT HyperFlash, Netzsch, Germany), a circular disc specimen with a diameter of ∼10 mm and a thickness of ∼2 mm was used. The electrical conductivity (σ) and Seebeck coefficient (S) measurements were performed simultaneously using the four-probe DC method (ZEM-3, Ulvac-Riko, Japan) under a helium atmosphere on a sample cut into rectangular bars with approximate dimensions of 10 mm × 2 mm × 2 mm. The determined accuracies in the transport measurement are ±10% for thermal conductivity, ±7% for electrical conductivity, and ±7% for the Seebeck coefficient. The Hall coefficient (RH) measurement was performed using a physical property measurement system (PPMS, Quantum Design, Japan) at 300 K in the magnetic field swept range from −5.0 T to 5.0 T. The carrier concentration (nH = 1/eRH) and carrier mobility (μH = σRH) were obtained subsequently using RH.2.4 Theoretical calculations
The electronic structure calculations of nominal and defective VFeSb were performed employing the self-consistent Korringa–Kohn–Rostoker (KKR) method with the coherent potential approximation (CPA) using the AkaiKKR Package (Machikaneyama2002).71–73 For the calculation, nominal (V4a1.0Fe4b1.0Sb4c1.0) and defective (V4a1.0Fe4b1.0Sb4c1.0) compositions were considered based on experimental outcomes indicating the predominant presence of Fe-Frenkel defects and their site preference, to examine the implications of defects for the electrical transport of VFeSb HH alloys. For calculating the final crystallinity degree, the total density of states (DOS), the site decomposed DOS, and Fermi surface properties were deduced from our estimates. The convergence of the total energy was set to a numerical precision of mRy.To estimate the thermodynamic properties of the nominal VFeSb alloy, extended Miedema's model,58–60i.e. asymmetric Hillert's model74,75 for ternary alloys was employed.65–67 At a given temperature (T), the Gibbs free energy of mixing for a random solid solution was determined from the entropy of mixing (ΔSm) and enthalpy of mixing (ΔHm) as follows:
| ΔGm = ΔHm − TΔSm | (1) |
The enthalpy of mixing ΔHmVFeSb was determined employing asymmetric Hillert's model74,75 by assuming the transformation of an asymmetric ternary system into a reciprocal system. The ΔHmVFeSb values were evaluated from the mole fractions of xV, xFe, and xSb of elements V, Fe, and Sb, respectively, and the enthalpy of mixing ΔHmVFe, ΔHmVSb and ΔHmFeSb of binaries V–Fe, Fe–Sb, and V–Sb, respectively. ΔHmVFeSb is calculated as follows:67,74,75
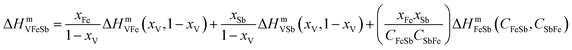 | (2) |
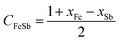 and
and 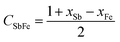 .
.
The entropy term is determined using the configurational entropy of a random solid solution as follows:
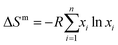 | (3) |
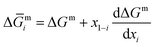 | (4) |
The activity coefficient (γi) of the elemental constituents, i.e., γV, γFe and γSb, was obtained using the tangential intercept method as 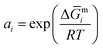 and plotted as a function of composition for annealing and sintering conditions besides room temperature to elucidate the phase formation and microstructure.76
and plotted as a function of composition for annealing and sintering conditions besides room temperature to elucidate the phase formation and microstructure.76
3. Results
The XRD patterns of polycrystalline bulk samples with varied V and Fe stoichiometries in V1+xFe1+ySb (−0.1 < x, y < 0.1) alloys are shown in Fig. 1(a and b), respectively. All peaks were well indexed to the cubic VFeSb HH (space group. F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, No. 216) structure77 with no noticeable secondary phases (within the detection limit of our XRD equipment). The refined lattice constant obtained by the Rietveld refinement of the measured XRD pattern is shown in the inset of Fig. 1(a and b). The cubic lattice constant of the HH crystal varies linearly for both deficient and excess compositions, thereby following the Vegard Law78 and suggesting the complete solubility of interstitials and vacancies within the HH microstructure as the localized and short-range order of defects. It can be inferred that off-stoichiometry in these defective compositions at low concentrations is well accommodated within the sublattice implying limited yet considerable solubility of interstitials/vacancies within the HH matrix.10,33,48,79
3m, No. 216) structure77 with no noticeable secondary phases (within the detection limit of our XRD equipment). The refined lattice constant obtained by the Rietveld refinement of the measured XRD pattern is shown in the inset of Fig. 1(a and b). The cubic lattice constant of the HH crystal varies linearly for both deficient and excess compositions, thereby following the Vegard Law78 and suggesting the complete solubility of interstitials and vacancies within the HH microstructure as the localized and short-range order of defects. It can be inferred that off-stoichiometry in these defective compositions at low concentrations is well accommodated within the sublattice implying limited yet considerable solubility of interstitials/vacancies within the HH matrix.10,33,48,79
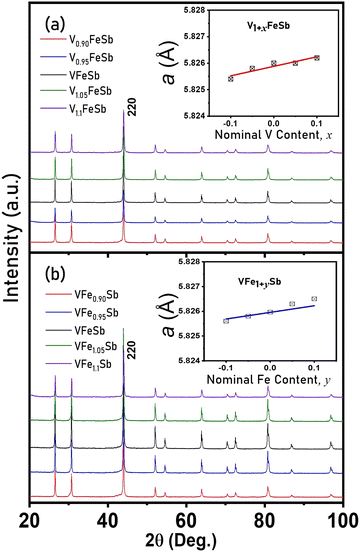 | ||
| Fig. 1 X-Ray diffraction patterns of (a) V1+xFeSb and (b) VFe1+ySb half-Heusler alloys along with a lattice constant with varying V and Fe stoichiometry (−0.1 < x, y < 0.1) are shown in the inset. | ||
The refined XRD patterns corresponding to each composition are also shown in the ESI† of Fig. S1–S9 with refined parameters enlisted in Table S1 (ESI†). Interestingly, the refined chemical compositions for all the samples were found to inherently exhibit Fe vacancies at both 4b and 4c lattice sites. For the structural refinement, isotropic atomic displacement parameters, i.e., B(iso) values, were fixed, and vacancies were refined for each atom. Although no clear relationship on occupancies was established, a prevalence of Fe-4d Frenkel-type defects intrinsically in the synthesized VFeSb HH compounds was established. Such atomic-level defects are characteristically similar to the Co-4d Frenkel-type defects reported for ZrCoSb-based HH80 and conform to the previous assertions made on the thermodynamic stability of interstitial Fe atoms at 4d sites.48,79
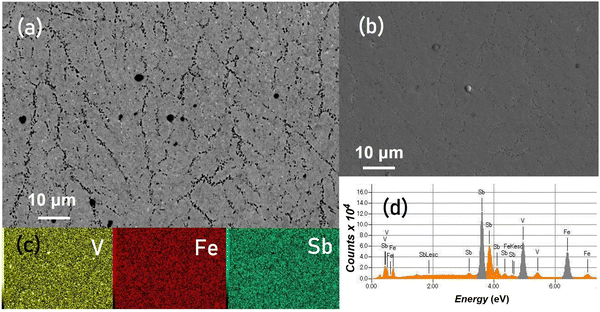
The microstructural characterization of representative excess and deficient regions within the off-stoichiometric specimens at the same magnification is shown along with the elemental mapping image in Fig. 2. The SEM images reveal a densely packed microstructure with distinct defect structures corresponding to varied stoichiometries, which are shown using both SE-SEM and BSE-SEM micrographs along with the elemental mapping image. In V-excess (Fig. 2(a)) HH compositions, V-segregation alongside Fe-rich dendrites was prominently observed, while V-deficient (Fig. 2(b)) compositions displayed an extensive formation of the V-deficient eutectic substructure. For Fe-excess (Fig. 2(c)) compositions, Fe-rich dendrites interlaced within the V-deficient eutectic substructure and V-precipitates were prominent, while Fe-deficient (Fig. 2(d)) compositions display V-segregation over the Fe-rich dendritic substructure. In all defective samples, the localized variation of Sb was also observed which interestingly led to two kinds of substructures prominently. The Sb-excess (Fig. 2(e)) regions correspond to the V-deficient eutectic substructure, while Sb-deficiency (Fig. 2(f)) is typically observed in regions where Fe-rich dendrites and V-precipitates are widespread. The elemental map shown alongside indicates a uniform distribution of constituent elements but marks the regions corresponding to V-segregation and Fe-rich dendrites more evidently. The EDX analysis shows closer agreement with the nominal stoichiometry suggesting the localized nature of these defect structures within the cubic VFeSb HH phase which despite their existence preserve the overall nominal compositions.
For comparison, nominally stoichiometric VFeSb HH alloys are presented in Fig. 3. A well-distributed network of Fe-rich dendrites alongside V-precipitates, dispersed all over and the V-deficient eutectic substructure, is shown in the BSE-SEM (Fig. 3(a)) and SE-SEM (Fig. 3(b)) images. Interestingly, the off-stoichiometric granular effects were also found as localized domains with the stoichiometric VFeSb HH microstructure. The elemental map shown in Fig. 3(c) indicates a uniform distribution of constituent elements, while the EDX map shown in Fig. 3(d) reveals signatures of the constituent elements in the spectrum. Thus, structurally ordered VFeSb with a cubic phase inherently exhibits a localized susceptibility towards the disorder and formation of granular defects. It was observed that the defect types and their concentration are sensitive and characteristic to stoichiometric alteration thereby signifying the distinct role of stoichiometry in inducing these defect substructures within the VFeSb HH matrix.
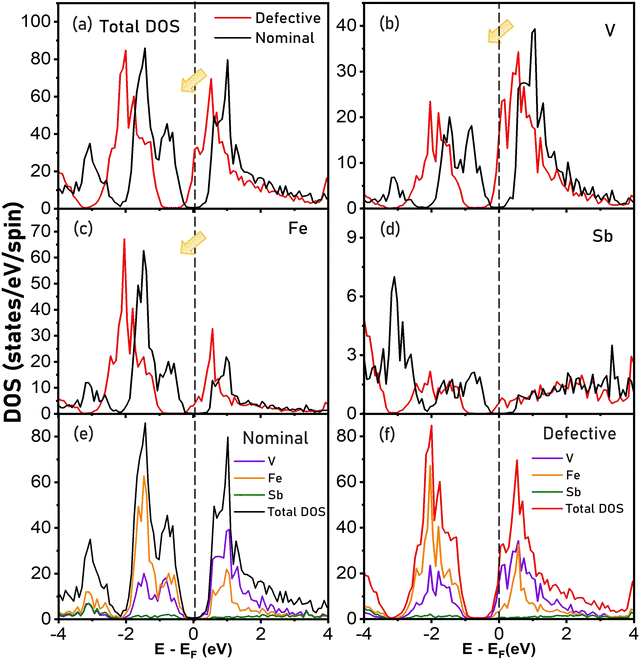
To understand the changes in the electronic band structure due to the inherently defective nature of VFeSb HH, the total and site-decomposed density of states for nominal and defective VFeSb compositions is presented in Fig. 4(a and b–d), respectively. The atomic DOS for all constituents is altered in an innately defective composition due to the Fe-interstitials which prevail widely and shift the Fermi level into the conduction band from the bandgap. As indicated, the contribution from p-states of Sb is limited to the low-lying core states in both nominal and defective band structures, while the strong hybridization of d-states contribution from the transition metal atoms (V and Fe) remains critical to the DOS near the Fermi level. The total and atom-projected density of states displayed in Fig. 4(e and f), respectively, presents the shift in the Fermi level towards the conduction band in the defective composition from the mid-gap position projected for the nominal composition. This indicates the prevailing self-doping tendencies particularly due to the presence of Fe-interstitials, which as donor impurities contribute additional electrons with inherent degeneracy in structurally ordered VFeSb HH alloys. To determine carrier characteristics, the results of the room temperature Hall data measurement are tabulated in Table 1. Interestingly, the carrier concentration (nH) of all defective samples was measured to be higher in comparison to that of pristine VFeSb and may be attributed to the increasing concentration of the defect concentration which brings inherent changes to the electronic band structure causing self-doping. Correspondingly, lower carrier mobility (μH) was obtained in all defective samples which can be ascribed to the occurrence of defect scattering.
| Compositions | R H (m3 C−1) × 10−8 | n H (cm−3) × 1019 | μ H (cm2 V−1 s−1) |
|---|---|---|---|
| 0 | −8.5 (1) | 7.4 | 60 |
| x = −0.10 | −6.3 (2) | 9.8 | 53 |
| x = −0.05 | −5.9 (1) | 10 | 50 |
| x = +0.05 | −5.5 (1) | 11 | 58 |
| x = +0.10 | −5.2 (2) | 12 | 42 |
| y = −0.10 | −3.9 (2) | 16 | 41 |
| y = −0.05 | −5.4 (1) | 11 | 46 |
| y = +0.05 | −5.8 (1) | 10 | 54 |
| y = +0.10 | −3.8 (2) | 16 | 33 |
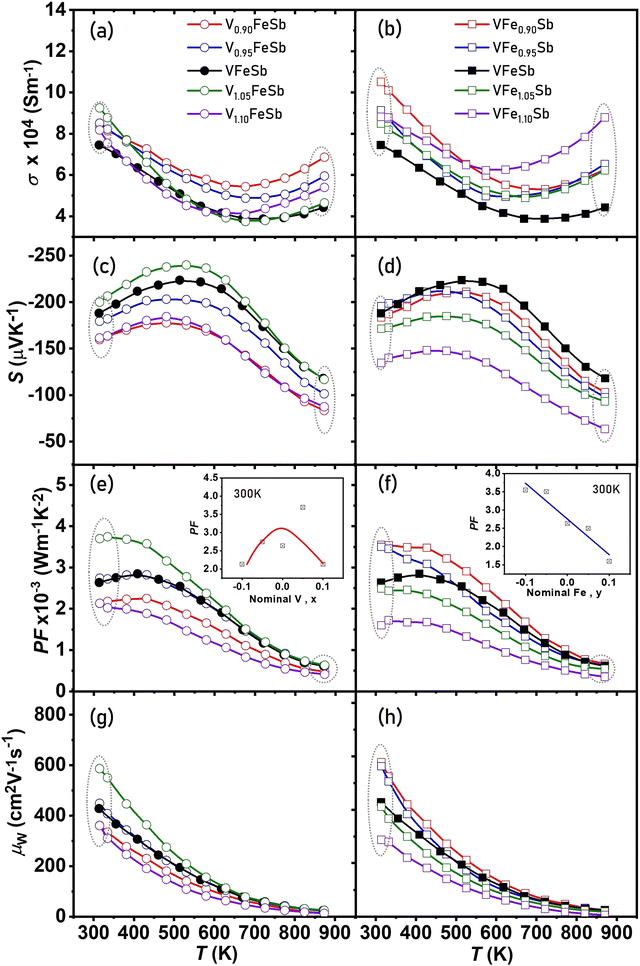
Fig. 5(a and b) show the temperature-dependent σ for V1+xFeSb and VFe1+ySb (−0.1 < x, y < 0.1) HH alloys. All samples display a degenerate semiconducting behavior up to 700 K, wherein σ decreases with increasing temperature. In both V-defective and Fe-defective samples, a considerable increase in σ was observed especially near room temperature which may be ascribed to higher nH and degenerate band structure modification particularly by the presence of Fe-interstitials. The Seebeck coefficient (S) is shown in Fig. 5(c and d), which displays n-type conduction with the electrons as the majority charge carriers for all samples. A gradual increase in |S| was observed with increasing temperature which inverses at ∼500 K for most samples. This may be ascribed to extrinsic charge carrier excitation from impurity states dominant at a lower temperature. Beyond 500 K, intrinsic excitation of minority carriers across the energy gap is anticipated to decrease S with increasing temperature.
To determine the cumulative implication of stoichiometry on the electrical transport, the temperature-dependent electrical power factor (PF = S2σ) is shown in Fig. 5(e and f). A remarkably high PF of ∼3 × 10−3 W m−1 K−2 was achieved for both stoichiometric and defective compositions which are comparatively higher near room temperature.81–84 Stoichiometric alterations can both enhance/deteriorate the power factor with variations ranging between 1–4 × 10−3 W m−1 K−2 at room temperature for the synthesized samples as shown in the inset of Fig. 5(e and f). The electron mobility weighted by the density of electronic states which is referred85 to as the weighted mobility (μw) is also displayed in Fig. 5(g and h). The large deviation in μw was observed especially at a lower temperature which indicates an inherent change in the electronic transport properties due to stoichiometric alterations.
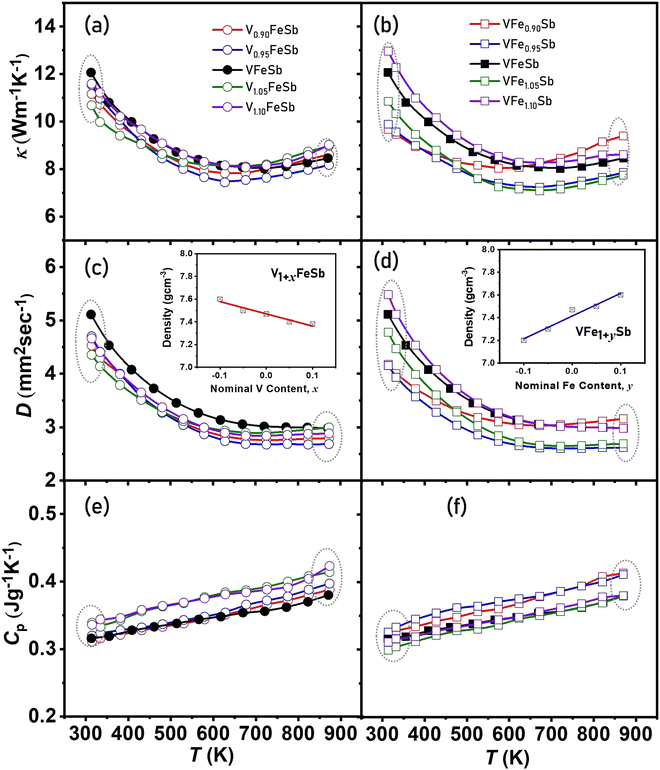
The total thermal conductivity (κ) shown in Fig. 6(a and b) was determined using the expression D × Cp × d, from measured diffusivity (Fig. 6(c and d)) and specific heat (Fig. 6(e and f)) and density (shown in the inset of Fig. 6(c and d)) for V1+xFeSb and VFe1+ySb (−0.1 < x, y < 0.1) HH alloys. κ shown is reduced at a lower temperature for all defective compositions when compared to pristine VFeSb and can be ascribed to the presence of a defective structure with the VFeSb HH microstructure. The simple cubic crystal of HH alloys offers minimal resistance to the phonon propagation within the lattice as indicated by high values of thermal diffusivity. However, the defect introduced due to off-stoichiometry tends to scatter phonons in a wide range as indicated by decreasing κ and D. The V-deficiency and Fe-excess in the VFeSb HH alloy were found to promote bipolar behavior which causes thermal excitation of minority charge carriers and is more prominent at higher temperatures. The enhanced phonon scattering in the synthesized defective samples can be ascribed to the network of defect substructures within the HH matrix which, besides high-frequency phonons, largely scatters the mid-frequency range of phonons.
4. Discussion
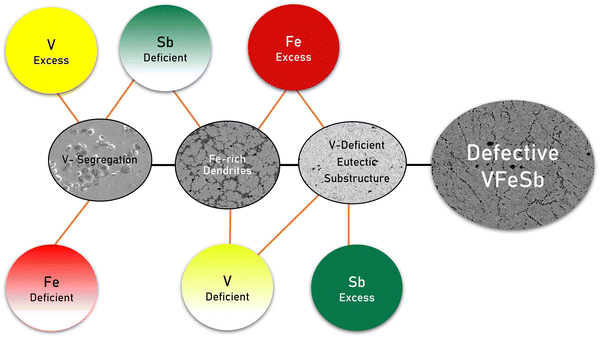
4.1 Defective microstructures corresponding to stoichiometric alterations
Defects are ubiquitous in a material, but they can be partially controlled using heat treatment and extrinsically introduced by altering stoichiometry. In the synthesized HH samples, granular defects were inevitably found; however, their type and concentrations were found to be related to stoichiometry as shown in Fig. 7 using a fishbone diagram. A plausible explanation regarding the formation of these defect substructures can be ascribed to vacant sites in the HH alloy which induces a localized tendency towards charge compensation and promotes vacancies, interstitials, and antisites inherently. Unlike the ionic crystal, where Frenkel defects or Schottky pairs are more distinctly understood and defined, vacancy and interstitial formation may propagate in HH alloys through a similar mechanism. Under equilibrium conditions, such defects get accumulated locally and are embodied into the defect substructure. The V-segregation and V-deficient eutectic substructure led to V-vacancies, while Fe-rich dendrites can be attributed to Fe-interstitials.A composition–structure–property correlation presented in the synthesized HH alloys indicates the critical role of stoichiometric alteration in stimulating characteristic defects which may vary for different thermal histories and synthesis methodologies. The defect concentration depends on the condition and duration of heat treatment owing to the underlying phase transformation and structural ordering, wherein undesirable intermediate binary phases such as binary antimonides simultaneously compete.45 The V-segregation was evident in all samples upon prolonged annealing which explains the V-deficient HH matrix even in stoichiometric VFeSb.52 Conclusively, three types of granular defects with stoichiometric alterations, i.e., V-segregation, Fe-rich dendrites, and V-deficient eutectic substructures, were prominently observed as shown in Fig. 7. Off-stoichiometric changes stimulate characteristic defect types and its concentration, revealing inherent and localized susceptibility towards disorder in VFeSb HH, which even in the stoichiometric composition contains such granular defects inevitably.
4.2 Microstructural evolution and its thermodynamic description
In the thermodynamics of alloys, the chemical activities of the different constituents are connected by various cross-differentiation relationships, which determine the phases and their extant within the microstructure. In this section, the formation of stoichiometric VFeSb HH alloys was assessed by the thermodynamic calculations of the Gibbs free energy of mixing (ΔGm). The calculations were performed at three critical temperatures, i.e., room temperature (300 K), annealing temperature (873 K), and maximum temperature of sintering (1023 K) and are shown in Fig. 8, which presents the modified Gibbs free energy in kJ mol−1 as a function of the V–Fe–Sb compositions. The ideal Gibbs free energy of mixing (ΔGm,id) is shown in the ESI† of Fig. S10 for comparison. A lower ΔGm < ΔGm,id in the whole composition range was estimated which increases with decreasing temperature suggesting a greater probability for VFeSb solid-solution formation from elemental powders. A relatively higher ΔGm value is observed at the three corners of the ternary diagram, while the smallest ΔGm prevails near the equiatomic V–Fe–Sb region at a higher temperature which shifts towards equiatomic V–Fe, which corresponds to a large homogeneity region in the V–Fe binary system.45,86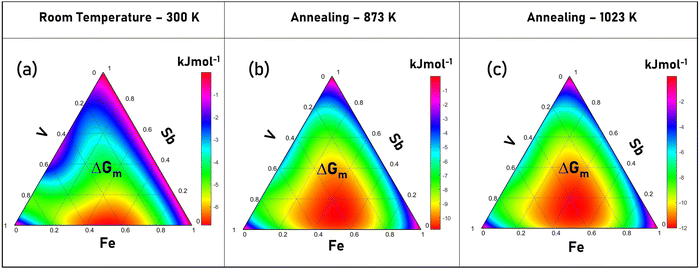 | ||
| Fig. 8 Modified Gibbs free energy at (a) room temperature (300 K), (b) annealing (873 K), and (c) sintering (1023 K) temperature for VFeSb alloys. | ||
The chemical activity coefficient as a descriptor for the chemical potential of constituents in the condensed solid solution is evaluated and shown in Fig. 9. Based on the activity coefficients of V (γV), Fe(γFe) and Sb(γSb), the microscopic interactions between constitutive elements and their solubility in the V–Fe–Sb solid solution can be evaluated. At a maximum sintering temperature of 1023 K, the activity coefficients of γV, γFe and γSb remain <1 with a greater preference of interaction towards Sb, V, and Fe, respectively. This also explains the competing existence and formation of binary phases such as antimonides.45 Alternatively, γV, γFe and γSb ∼ 1 observed at their respective corners indicate their minimal reactive tendency during sintering. At annealing temperature, i.e., 873 K, the activity coefficient undergoes marginal changes in comparison to that at room temperature.
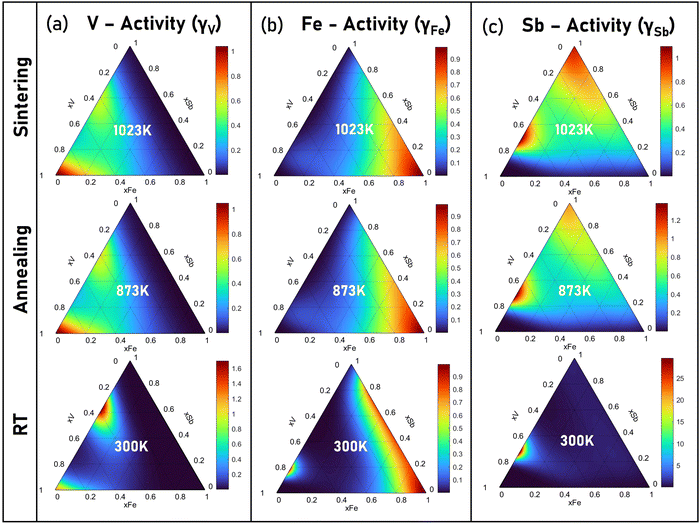 | ||
| Fig. 9 The activity coefficients of (a) V, (b) Fe, and (c) Sb at room temperature (300 K), annealing (873 K), and sintering (1023 K) temperature in VFeSb alloys. | ||
Upon solidification of arc-melted VFeSb, the thermodynamic metastability may enhance the solubility of constituents and the formation of binary phases. However, on annealing, the structural ordering and interface instability tend to reach thermodynamic equilibrium thereby promoting granular defects within the VFeSb microstructure. A higher γFe along Sb, regions were evaluated along with a relatively higher ΔGm in corresponding regions, which implies the V-deficient eutectic substructure to be energetically favorable during solidification. Similarly, γV along V having an activity coefficient of ∼1, particularly around corners is distinctly observed which can be ascribed to V-segregation. The solidification of Fe-rich dendrites implies that, upon solidification, some portion of V and Fe gets partitioned into the liquid and solidifies eventually to form Fe-rich dendrites and V-precipitates. Thus, the resulting microstructure in defective half-heusler corroborates with the thermodynamic assessment and can be favorably adapted to achieve an engineered microstructure with enhanced phonon scattering and carrier mobility.
4.3 Critical role of stoichiometry in thermoelectric transport
Stoichiometry plays a critical role in determining the intrinsic transport properties of materials and its alteration provides an inherent ability to modify both the electronic band structure and microstructure simultaneously using defect-induced disorder.34,87 Although a slight variation in nominal stoichiometry upholds the average HH crystal structure, it was found that characteristic defects were enhanced by alteration in V and Fe contents within the microstructure of the cubic VFeSb HH matrix. A remarkable high-power factor of ∼3 × 10−3 W m−1 K−2 was achieved for both stoichiometric and defective compositions which are comparable to those of state-of-the-art n-type Bi2Te3 alloys.81–84 The maxima for the power factor in all samples are attained near room temperatures, but the stoichiometry alteration can both enhance/deteriorate the power factor. Such variation ranges lie between 1–4 × 10−3 W m−1 K−2 and suggest that a lower V-excess concentration and Fe-deficient compositions are more favorable for maximizing the PF.The κL reduction at both low and high temperatures was attained when compared with the pristine counterpart in the measured temperature range. Thus, it was found that changes in the sample stoichiometry affect the type and concentration of the short and long-range defects within the microstructure for which the thermal treatment of samples remains a predominant consideration, as it can allow controlling these defects, and thereby the thermal and electrical transport, without any changes in the composition. The structurally ordered cubic VFeSb HH alloys are a promising candidate for TE power generation near room temperature owing to their remarkably high PF, which provides an estimate of the power generation ability of a TE material. zT is shown in Fig. 10(a and b) for defective V1+xFeSb and VFe1+ySb (−0.1 < x, y < 0.1) HH alloys. Benefiting from its improved electrical properties and lower thermal conductivity, a peak zT of ∼ 0.2 at ∼523 K was achieved for optimal V1.05FeSb and VFe0.95Sb defective HH alloys. The V-excess and Fe-defective compositions also correspond to a higher quality factor (QF) as shown in Fig. 10(c and d). The optimal nH ∼ 1.2 × 1021 cm−3 was measured for both these defective compositions, which is optimum for attaining the maximum power factor. Simultaneously, all-scale hierarchical type microstructure was effective in scattering phonons in all frequency ranges. The κL of these defective HH alloys can be further reduced by employing nanostructuring approaches by enhancing grain boundary scattering more profoundly near room temperature, thus making them prospective alternatives to state-of-the-art Bi2Te3 alloys for near-room temperature thermoelectric applications.81–84
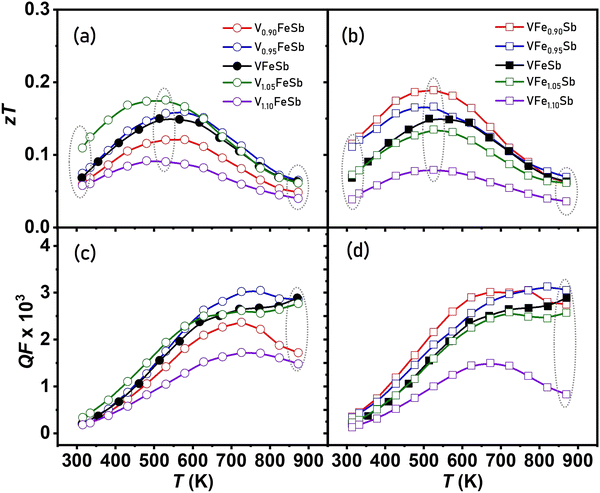 | ||
| Fig. 10 Temperature-dependent thermoelectric (a and b) figure-of-merit (zT) and (c and d) quality factor of V1+xFe1+ySb (−0.1 < x, y < 0.1) half-Heusler alloys. | ||
5. Conclusion
Stoichiometry-induced defects and their nature have predominant effects on thermoelectric transport properties. We demonstrate defective V1+xFe1+ySb (−0.1 < x, y < 0.1) HH compositions with an altered stoichiometry as prospective derivative systems for tuning the thermoelectric transport favorably. The structurally ordered HH alloys crystallize into the cubic structure [space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m (no. 216)] and were prepared to employ arc-melting, annealing, and spark plasma sintering. The defective alloys show high electrical conductivity and low thermal conductivity arising from a high concentration of defect substructures within the ordered VFeSb HH matrix that distinctively forms Fe-rich dendritic patterns and V-segregation alongside native defects, which conduct electrons and effectively scatter phonons. The ubiquitous presence of Fe/4d Frenkel point defects and V-segregation was found to facilitate the microstructural evolution in VFeSb HH alloys. The stoichiometry was found to affect the concentration and the mobility of electrical carriers, which is more favorable for V-excess and Fe-deficient compositions in low self-doping limits (0 < x < 0.05). A remarkable high-power factor and an enhanced zT were attained near room temperature for V-excess and Fe-deficient at low concentrations. The correlation of thermodynamic parameters with structural observation and their implications for the measured thermoelectric transport properties have been studied to understand the critical role of heat treatment and stoichiometry in HH alloys. The structural ordering into the cubic VFeSb phase results in V-segregation as a secondary phase that coexists with a percolated network of Fe-rich dendrites and a V-deficient eutectic substructure which effectively decouples the thermal and electrical transport. The ability to distinctively control the defect type and their concentration will allow further improving the thermoelectric properties of these systems.
3m (no. 216)] and were prepared to employ arc-melting, annealing, and spark plasma sintering. The defective alloys show high electrical conductivity and low thermal conductivity arising from a high concentration of defect substructures within the ordered VFeSb HH matrix that distinctively forms Fe-rich dendritic patterns and V-segregation alongside native defects, which conduct electrons and effectively scatter phonons. The ubiquitous presence of Fe/4d Frenkel point defects and V-segregation was found to facilitate the microstructural evolution in VFeSb HH alloys. The stoichiometry was found to affect the concentration and the mobility of electrical carriers, which is more favorable for V-excess and Fe-deficient compositions in low self-doping limits (0 < x < 0.05). A remarkable high-power factor and an enhanced zT were attained near room temperature for V-excess and Fe-deficient at low concentrations. The correlation of thermodynamic parameters with structural observation and their implications for the measured thermoelectric transport properties have been studied to understand the critical role of heat treatment and stoichiometry in HH alloys. The structural ordering into the cubic VFeSb phase results in V-segregation as a secondary phase that coexists with a percolated network of Fe-rich dendrites and a V-deficient eutectic substructure which effectively decouples the thermal and electrical transport. The ability to distinctively control the defect type and their concentration will allow further improving the thermoelectric properties of these systems.
Data availability statement
The data that support the findings of this study are available upon request from the authors.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
We thank Dr. Huang Yi and Mr Ichiro Ono of the Miyazaki Research Group at Tohoku University, Sendai, Japan for insightful discussions and Toppan Inc. for financial support.References
- Z. Li, C. Xiao, H. Zhu and Y. Xie, J. Am. Chem. Soc., 2016, 138, 14810–14819 CrossRef CAS PubMed.
- Y. Zheng, T. J. Slade, L. Hu, X. Y. Tan, Y. Luo, Z.-Z. Luo, J. Xu, Q. Yan and M. G. Kanatzidis, Chem. Soc. Rev., 2021, 50, 9022–9054 RSC.
- C. Zhao, Z. Li, T. Fan, C. Xiao and Y. Xie, Research, 2020, 2020, 9652749 CAS.
- K. Manna, Y. Sun, L. Muechler, J. Kübler and C. Felser, Nat. Rev. Mater., 2018, 3, 244–256 CrossRef CAS.
- C. Gayner and Y. Amouyal, Adv. Funct. Mater., 2020, 30, 1901789 CrossRef CAS.
- A. Bhardwaj, N. S. Chauhan, B. Sancheti, G. N. Pandey, T. D. Senguttuvan and D. K. Misra, Phys. Chem. Chem. Phys., 2015, 17, 30090–30101 RSC.
- N. S. Chauhan, A. Bhardwaj, T. D. Senguttuvan, R. P. Pant, R. C. Mallik and D. K. Misra, J. Mater. Chem. C, 2016, 4, 5766–5778 RSC.
- N. S. Chauhan, P. R. Raghuvanshi, K. Tyagi, K. K. Johari, L. Tyagi, B. Gahtori, S. Bathula, A. Bhattacharya, S. D. Mahanti, V. N. Singh, Y. V. Kolen’ko and A. Dhar, J. Phys. Chem. C, 2020, 124, 8584–8593 CrossRef CAS.
- Z. Li, C. Xiao, S. Fan, Y. Deng, W. Zhang, B. Ye and Y. Xie, J. Am. Chem. Soc., 2015, 137, 6587–6593 CrossRef CAS.
- K. Xia, P. Nan, S. Tan, Y. Wang, B. Ge, W. Zhang, S. Anand, X. Zhao, G. J. Snyder and T. Zhu, Energy Environ. Sci., 2019, 12, 1568–1574 RSC.
- Y. Zhang, S. Li, F. Liu, C. Zhang, L. Hu, W. Ao, Y. Li, J. Li, H. Xie, Y. Xiao and F. Pan, J. Mater. Chem. A, 2019, 7, 26053–26061 RSC.
- H. Miyazaki, O. M. Ozkendir, S. Gunaydin, K. Watanabe, K. Soda and Y. Nishino, Sci. Rep., 2020, 10, 1–8 CrossRef.
- S. Guo, S. Anand, Y. Zhang and G. J. Snyder, Chem. Mater., 2020, 32, 4767–4773 CrossRef CAS.
- Y. Xing, R. Liu, J. Liao, Q. Zhang, X. Xia, C. Wang, H. Huang, J. Chu, M. Gu and T. Zhu, Energy Environ. Sci., 2019, 12, 3390–3399 RSC.
- H. Zhao, B. Cao, S. Li, N. Liu, J. Shen, S. Li, J. Jian, L. Gu, Y. Pei and G. J. Snyder, Adv. Energy Mater., 2017, 7, 1700446 CrossRef.
- N. S. Chauhan, S. v Pyrlin, O. I. Lebedev, L. S. A. Marques, M. M. D. Ramos, T. Maiti, K. Kovnir, B. A. Korgel and Y. V. Kolen’Ko, J. Phys. Chem. C, 2021, 125, 20184–20194 CrossRef CAS.
- R. J. Quinn and J.-W. G. Bos, Mater. Adv., 2021, 2, 6246–6266 RSC.
- N. S. Chauhan, S. Bathula, A. Vishwakarma, R. Bhardwaj, B. Gahtori, A. Kumar and A. Dhar, ACS Appl. Energy Mater., 2018, 1, 757–764 CrossRef CAS.
- W. G. Zeier, J. Schmitt, G. Hautier, U. Aydemir, Z. M. Gibbs, C. Felser and G. J. Snyder, Nat. Rev. Mater., 2016, 1(6), 1–10 CrossRef.
- S. Chen and Z. Ren, Mater. Today, 2013, 16, 387–395 CrossRef CAS.
- Z. Liu, S. Guo, Y. Wu, J. Mao, Q. Zhu, H. Zhu, Y. Pei, J. Sui, Y. Zhang and Z. Ren, Adv. Funct. Mater., 2019, 29(44), 1905044 CrossRef CAS.
- N. S. Chauhan, S. Bathula, A. Vishwakarma, R. Bhardwaj, K. K. Johari, B. Gahtori, M. Saravanan and A. Dhar, J. Phys. Chem. Solids, 2018, 123, 105–112 CrossRef CAS.
- N. S. Chauhan, S. Bathula, A. Vishwakarma, R. Bhardwaj, K. K. Johari, B. Gahtori and A. Dhar, J. Materiomics, 2019, 5, 94–102 CrossRef.
- K. K. Johari, R. Bhardwaj, N. S. Chauhan, B. Gahtori, S. Bathula, S. Auluck and S. R. Dhakate, ACS Appl. Energy Mater., 2019, 3, 1349–1357 CrossRef.
- N. S. Chauhan, S. Bathula, B. Gahtori, Y. v Kolen’ko and A. Dhar, J. Electron. Mater., 2019, 48, 6700–6709 CrossRef CAS.
- K. K. Johari, R. Bhardwaj, N. S. Chauhan, S. Bathula, S. Auluck, S. R. Dhakate and B. Gahtori, ACS Appl. Energy Mater., 2021, 4, 3393–3403 CrossRef CAS.
- C. Fu, T. Zhu, Y. Liu, H. Xie and X. Zhao, Energy Environ. Sci., 2015, 8, 216–220 RSC.
- T. Zhu, C. Fu, H. Xie, Y. Liu and X. Zhao, Adv. Energy Mater., 2015, 5, 1500588 CrossRef.
- H. Zhu, J. Mao, Y. Li, J. Sun, Y. Wang, Q. Zhu, G. Li, Q. Song, J. Zhou, Y. Fu, R. He, T. Tong, Z. Liu, W. Ren, L. You, Z. Wang, J. Luo, A. Sotnikov, J. Bao, K. Nielsch, G. Chen, D. J. Singh and Z. Ren, Nat. Commun., 2019, 10, 1–8 CrossRef.
- G. Joshi, R. He, M. Engber, G. Samsonidze, T. Pantha, E. Dahal, K. Dahal, J. Yang, Y. Lan and B. Kozinsky, Energy Environ. Sci., 2014, 7, 4070–4076 RSC.
- C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- K. Tolborg and B. B. Iversen, Chem. Mater., 2021, 33, 5308–5316 CrossRef CAS.
- X. Li, P. Yang, Y. Wang, Z. Zhang, D. Qin, W. Xue, C. Chen, Y. Huang, X. Xie and X. Wang, Research, 2020, 2020, 4630948 CAS.
- N. S. Chauhan, B. Gahtori, B. Sivaiah, S. D. Mahanti, A. Dhar and A. Bhattacharya, Appl. Phys. Lett., 2018, 113, 013902 CrossRef.
- N. S. Chauhan, S. Bathula, B. Gahtori, S. D. Mahanti, A. Bhattacharya, A. Vishwakarma, R. Bhardwaj, V. N. Singh and A. Dhar, ACS Appl. Mater. Interfaces, 2019, 11, 47830–47836 CrossRef CAS.
- K. Kirievsky, Y. Gelbstein and D. Fuks, J. Solid State Chem., 2013, 203, 247–254 CrossRef CAS.
- K. Kirievsky, D. Fuks and Y. Gelbstein, Phys. Chem. Chem. Phys., 2020, 22, 8035–8047 RSC.
- P. Qiu, J. Yang, X. Huang, X. Chen and L. Chen, Appl. Phys. Lett., 2010, 96, 152105 CrossRef.
- G. Y. Yonggang, X. Zhang and A. Zunger, Phys. Rev. B, 2017, 95, 85201 CrossRef.
- Y. Tian, H. Zhu, W. Ren, N. Ghassemi, E. Conant, Z. Wang, Z. Ren and J. H. Ross, Phys. Chem. Chem. Phys., 2018, 20, 21960–21967 RSC.
- J. S. Young and R. G. Reddy, J. Mater. Eng. Perform., 2019, 28(10), 5917–5930 CrossRef CAS.
- K. K. Johari, D. K. Sharma, A. K. Verma, R. Bhardwaj, N. S. Chauhan, S. Kumar, M. N. Singh, S. Bathula and B. Gahtori, ACS Appl. Mater. Interfaces, 2022, 14, 19579–19593 CrossRef CAS PubMed.
- D. K. Misra, A. Rajput, A. Bhardwaj, N. S. Chauhan and S. Singh, Appl. Phys. Lett., 2015, 106, 103901 CrossRef.
- N. S. Chauhan, S. Bathula, B. Gahtori, Y. v Kolen’ko, R. Shyam, N. K. Upadhyay and A. Dhar, J. Appl. Phys., 2019, 126, 125110 CrossRef.
- V. V. Romaka, L. Romaka, Y. Stadnyk, V. Gvozdetskii, R. Gladyshevskii, N. Skryabina, N. Melnychenko, V. Hlukhyy and T. Fässler, Eur. J. Inorg. Chem., 2012,(15), 2588–2595 CrossRef CAS.
- N. S. Chauhan, S. Bathula, A. Vishwakarma, R. Bhardwaj, B. Gahtori, A. K. Srivastava, M. Saravanan and A. Dhar, Materialia, 2018, 1, 168–174 CrossRef CAS.
- Y. Huang, K. Hayashi and Y. Miyazaki, Acta Mater., 2021, 215, 117022 CrossRef CAS.
- Y. Huang, K. Hayashi and Y. Miyazaki, Chem. Mater., 2020, 32, 5173–5181 CrossRef CAS.
- A. Yamamoto and T. Takeuchi, J. Electron. Mater., 2017, 46, 3200–3206 CrossRef CAS.
- C. Fu, H. Xie, Y. Liu, T. J. Zhu, J. Xie and X. B. Zhao, Intermetallics, 2013, 32, 39–43 CrossRef CAS.
- N. S. Chauhan and Y. Miyazaki, J. Alloys Compd., 2022, 908, 164623 CrossRef CAS.
- Y. Huang, K. Hayashi and Y. Miyazaki, Chem. Mater., 2020, 32, 5173–5181 CrossRef CAS.
- D. A. Ferluccio, B. F. Kennedy, S. A. Barczak, S. R. Popuri, C. Murray, M. Pollet and J.-W. G. Bos, J. Phys.: Energy, 2021, 3, 035001 CAS.
- N. S. Chauhan and Y. Miyazaki, Materialia, 2022, 22, 101430 CrossRef CAS.
- Z.-K. Liu and Y. Wang, Computational thermodynamics of materials, Cambridge University Press, 2016 Search PubMed.
- L. Kauffman and H. Bernstein, Computer calculation of phase diagrams with special reference to refractory metals, Academic Press Inc., United States, 1970 Search PubMed.
- N. Saunders and A. P. Miodownik, CALPHAD (calculation of phase diagrams): a comprehensive guide, Elsevier, 1998 Search PubMed.
- A. R. Miedema, P. F. de Chatel and F. R. de Boer, Physica B+C, 1980, 100, 1–28 CrossRef CAS.
- A. R. Miedema, R. Boom and F. R. de Boer, J. Less-Common Met., 1975, 41(2), 283–298 CrossRef CAS.
- A. K. Niessen, F. R. de Boer, R. Boom, P. F. de Châtel, W. C. M. Mattens and A. R. Miedema, Calphad, 1983, 7(1), 51–70 CrossRef CAS.
- D. J. M. King, S. C. Middleburgh, A. G. McGregor and M. B. Cortie, Acta Mater., 2016, 104, 172–179 CrossRef CAS.
- G. Arzpeyma, A. E. Gheribi and M. Medraj, J. Chem. Thermodyn., 2013, 57, 82–91 CrossRef CAS.
- C. Li, Y. Yuan, F. Li, Q. Wei and Y. Huang, Phys. B, 2022, 627, 413540 CrossRef CAS.
- R. Boom and F. R. de Boer, Calphad, 2020, 68, 101647 CrossRef CAS.
- R. F. Zhang, S. H. Zhang, Z. J. He, J. Jing and S. H. Sheng, Comput. Phys. Commun., 2016, 209, 58–69 CrossRef CAS.
- W. C. Wang, J. H. Li, H. F. Yan and B. X. Liu, Scr. Mater., 2007, 56, 975–978 CrossRef CAS.
- C. Aguilar, P. Martin, E. Pio, C. Salvo and G. O. Neves, Comput. Phys. Commun., 2021, 259, 107573 CrossRef CAS.
- Y. M. Mos, A. C. Vermeulen, C. J. N. Buisman and J. Weijma, Geomicrobiol. J., 2018, 35(6), 511–517 CrossRef CAS.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- J. Rodríguez-Carvajal, Recent developments of the program FULLPROF, in Commission on powder diffraction (IUCr), Newsletter, 2001, vol. 26, pp. 12–19 Search PubMed.
- T. Kotani and H. Akai, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16502 CrossRef CAS PubMed.
- W. Kohn and N. Rostoker, Phys. Rev., 1954, 94, 1111 CrossRef CAS.
- J. Korringa, Physica, 1947, 13, 392–400 CrossRef.
- M. Hillert, Calphad, 1980, 4(1), 1–12 CrossRef CAS.
- M. Hillert, Calphad, 1988, 12(3), 257–259 CrossRef CAS.
- X. Ding, W. Wang and P. Fan, Metall. Mater. Trans. B, 1999, 30, 271–277 CrossRef.
- Y. Y. Noda, M. M. Shimada and M. M. Koizumi, Inorg. Chem., 1979, 18, 3244–3246 CrossRef CAS.
- A. R. Denton and N. W. Ashcroft, Phys. Rev. A, 1991, 43(6), 3161 CrossRef CAS PubMed.
- D. A. Ferluccio, B. F. Kennedy, S. A. Barczak, S. R. Popuri, C. Murray, M. Pollet and J. W. G. Bos, J. Phys. Energy, 2021, 3(3), 035001 CrossRef CAS.
- R. He, T. Zhu, Y. Wang, U. Wolff, J. C. Jaud, A. Sotnikov, P. Potapov, D. Wolf, P. Ying, M. Wood, Z. Liu, L. Feng, N. P. Rodriguez, G. J. Snyder, J. C. Grossman, K. Nielsch and G. Schierning, Energy Environ. Sci., 2020, 13, 5165–5176 RSC.
- X. Yan, B. Poudel, Y. Ma, W. S. Liu, G. Joshi, H. Wang, Y. Lan, D. Wang, G. Chen and Z. F. Ren, Nano Lett., 2010, 10, 3373–3378 CrossRef CAS.
- I. T. Witting, T. C. Chasapis, F. Ricci, M. Peters, N. A. Heinz, G. Hautier and G. J. Snyder, Adv. Electron. Mater., 2019, 5, 1–20 Search PubMed.
- N. S. Chauhan, O. I. Lebedev, K. Kovnir, S. v. Pyrlin, L. S. A. Marques, M. M. D. Ramos, B. A. Korgel and Y. V. Kolen’Ko, Nanoscale Adv., 2020, 2, 5699–5709 RSC.
- H. J. Goldsmid, Materials, 2014, 7, 2577–2592 CrossRef CAS PubMed.
- G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537 CrossRef CAS.
- H. Okamoto and T. B. Massalski, Binary alloy phase diagrams, ASM International, Materials Park, OH, USA, 1990, p. 12 Search PubMed.
- Z. Liu, S. Guo, Y. Wu, J. Mao, Q. Zhu, H. Zhu, Y. Pei, J. Sui, Y. Zhang and Z. Ren, Adv. Funct. Mater., 2019, 29, 1905044 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Hall measurement and Rietveld refined XRD patterns for V1+xFe1+ySb (−0.1< x, y < 0.1) half-Heusler alloys. See DOI: https://doi.org/10.1039/d2ma00777k |
| This journal is © The Royal Society of Chemistry 2022 |