Open Access Article
Open Access ArticleEffect of different molecular coatings on the heating properties of maghemite nanoparticles†
Marco
Sanna Angotzi‡
 ab,
Valentina
Mameli‡
ab,
Valentina
Mameli‡
 ab,
Shankar
Khanal
c,
Miroslav
Veverka
c,
Jana
Vejpravova
ab,
Shankar
Khanal
c,
Miroslav
Veverka
c,
Jana
Vejpravova
 *c and
Carla
Cannas
*c and
Carla
Cannas
 *ab
*ab
aDepartment of Chemical and Geological Sciences, University of Cagliari, S.S. 554 Bivio per Sestu, Monserrato, 09042 CA, Italy. E-mail: ccannas@unica.it
bConsorzio Interuniversitario Nazionale per la Scienza e Tecnologia dei Materiali (INSTM), Via Giuseppe Giusti 9, 50121 Firenze (FI), Italy
cDepartment of Condensed Matter Physics, Charles University, Ke Karlovu 5, 12116 Prague 2, Czech Republic. E-mail: jana@mag.mff.cuni.cz
First published on 8th November 2021
Abstract
In this work, the effect of different molecular coatings on the alternating magnetic field-induced heating properties of 15 nm maghemite nanoparticles (NPs) in water dispersions was studied at different frequencies (159–782 kHz) and field amplitudes (100–400 G). The original hydrophobic oleate coating was replaced with dimercaptosuccinic acid (DMSA) or polyethylene glycol trimethoxysilane (PEGTMS), while cetrimonium bromide (CTAB) or stearic acid-poloxamer 188 (SA-P188) was intercalated or encapsulated, respectively, to transfer the dispersions into water. Surface modification, based on intercalation processes, induced clustering phenomena with the formation of spherical-like assemblies (CTAB and SA-P188), while ligand-exchange strategies kept the particles isolated. The clustering phenomenon has detrimental effects on the heating performances compared with isolated systems, in line with the reduction of Brown relaxation times. Furthermore, broader comprehension of the heating phenomenon in this dynamic system is obtained by following the evolution of SPA and ILP with time and temperature beyond the initial stage.
Introduction
Spinel ferrite nanoparticles (NPs), thanks to the excellent control of magnetic properties through chemical manipulation, represent ideal systems for many fields, such as environmental applications1–5 and biomedicine.6–8 In particular, their ability to release heat when subjected to an alternating magnetic field (i.e., magnetic heat generation) makes them appealing for catalysis9–12 and magnetic fluid hyperthermia (MFH).13–15 When NPs are in the superparamagnetic (SPM) state, according to linear-response theory (LRT),16 heat is released through relaxation losses, which can be associated with vector magnetization reversal inside the particle (Néel relaxation time, τN, eqn (1)), and through physical rotation of the particle in a fluid (Brown relaxation time, τB, eqn (2)):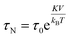 | (1) |
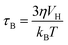 | (2) |
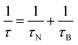 | (3) |
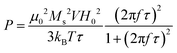 | (4) |
Other mechanisms responsible for the heat release are hysteresis losses, typical of multi-domain or blocked single-domain nanoparticles, which are associated with hysteretic magnetic responses. For these systems, the power per unit of volume is given by the product of the frequency f and the hysteresis loop area μ0∮HdM. Besides this common distinction between hysteresis and relaxation losses, other authors have highlighted that in real systems both types might occur at the same time, especially if they are nearby the transition region between the SPM and the ferromagnetic regimes.18
Nevertheless, when dealing with colloidal dispersions, NPs tend to form clusters (aggregates if the assembly is permanent or agglomerates if it is reversible), affecting their Brownian motion and, consequently, the heat response. In the literature, only a few studies have been devoted to the investigation of clustering effects, showing contradictory results in terms of improvement19–23 or deterioration23–27 of the heat response, which consequently is hardly predictable. Indeed, inter-particle interactions, predominantly of dipolar origin, can occur among the particles in the colloidal state. Thus, the magnetic response might be affected by the occurrence of the random orientation or the alignement of individual magnetic moments. Therefore, a systematic study on a suitable model system needs to be developed, where the interparticle interactions and their influence in the heat response can be disentangled, keeping a constant chemical composition, size, and shape of the original nanoparticles.
Therefore, it is of primary importance to employ a synthesis method that guarantees the NPs with a defined shape, high crystallinity, and low size dispersity for a unique magnetic response, but that also features repeatability and low environmental impact.28 These advantages have been recently found in an oleate-based solvothermal method that has been set up for the synthesis of spinel ferrite NPs, in the form of single phases,29,30 mixtures,31,32 core–shells,7,8,33 and silver–ferrite flower-like heterostructures.34
In addition, the modification of the nanoparticles' surface is fundamental to ensure good colloidal stability and modulate the interparticle distance through the formation of clusters. Therefore, several stabilizers have been proposed in the literature, such as bonding of hydrophilic molecules to the NPs' surface, such as dimercaptosuccinic acid (DMSA),35–39 functionalized silanes,40–42 and carboxylic acids,37,43–46 encapsulation of NPs in polymers such as dextran,47–49 polyethylene glycol (PEG),50–52 polyacrylic acid,53–56 biopolymers,57–60etc. (Table 1S†). Up to now, various methods have been developed for the clustering of primary NPs, exploiting a self-assembly mechanism as the result of the spontaneous control of the nanoentities that interplay through noncovalent interactions with the help of surfactants such as SDS61 or poloxamers.62
In this work, the aqueous colloidal dispersions of maghemite NPs with a diameter of 15 nm, prepared by a solvothermal method, were obtained through NPs' surface modification with commonly used molecules and polymers. DMSA, 2-[methoxy(polyethyleneoxy)6-9propyl] trimethoxysilane (PEGTMS), cetrimonium bromide (CTAB), and stearic acid (SA) combined with poloxamer 188 (P188) were employed to modify the NPs' surface through ligand-exchange, intercalation, or encapsulation procedures. The heat response of the NPs was studied as a function of the molecular coating, by varying the frequency and amplitude of the applied high-frequency magnetic field, and correlated with the magnetic and colloidal properties, paying attention to the role of cluster formation. Furthermore, the evolution of SPA and intrinsic loss power (ILP) with time and temperature was followed to better understand the heat release phenomenon also after the initial stage.
Experimental
Chemicals
Oleic acid (90%) and iron chloride tetrahydrate (98%) were purchased from Alpha Aesar. 1-Pentanol (≥99%), cetrimonium bromide (CTAB, 98%), chloroform (99.4%), dimercaptosuccinic acid (DMSA, 90%), ethanol (99.8%), iron nitrate nonahydrate (≥98%), n-hexane (≥97%), sodium hydroxide (98%), toluene (99.7%), and triethylamine (TEA, >99.5%) were purchased from Sigma Aldrich. Dimethyl sulfoxide (DMSO, ≥99.5%) was purchased from Sigma. Poloxamer 188 (P188) and sodium hydroxide (1 mol L−1) were purchased from Panreac. 2-[Methoxy(polyethyleneoxy)6–9propyl] trimethoxysilane (PEGTMS, 90%) was purchased from ABCR GmBH. Stearic acid (SA, 97%) was purchased from Acros Organics.Methods
The hydrophobic (oleate-capped) nanoparticles (Fe_Ole) were converted into hydrophilic ones by ligand exchange with DMSA and PEGTMS and by intercalation of CTAB or SA followed by encapsulation in P188.
After each post-synthesis modification, the aqueous dispersion was centrifuged to remove any unstable particle and stored in a vial. The samples were labeled Fe_DMSA, Fe_PEG, Fe_CTAB, and Fe_SA-P188, based on the employed molecules.
Characterization
The dispersions' concentrations were determined by Inductively Coupled Plasma – Optical Emission Spectrometry (ICP–OES). 0.5 mL of aqueous dispersion was digested by adding 4 mL HNO3 and stirring at ∼50 °C for two hours. The solutions were allowed to cool down, filtered, and diluted by using 2% v/v HNO3 solution. The ICP measurements were performed on an Agilent 5110 spectrometer by analyzing Fe at wavelengths 238.204 nm, 259.940 nm, and 261.187 nm, and the concentration was averaged.The samples were characterized by powder X-ray diffraction (XRD) using a Seifert X3000, equipped with a Cu anode (Kα radiation with λ = 1.5418 Å). The calibration of the peak position and instrumental width was done using powdered LaB6 from NIST. The refinement of the structural parameters66 was performed by the Rietveld method using the software MAUD67 and adopting recommended fitting procedures.68 The CIF structure COD ID used for the refinement is 1010369.69
Transmission electron microscopy (TEM) images were obtained using a JEOL JEM 1400 Plus operating at 120 kV. The particle size distribution was obtained by measuring over 1000 particles with the aid of the software Pebbles, setting a spherical shape for the elaboration.70 The weighted-mean particle diameter was calculated through the following equation:71
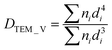 | (5) |
High-resolution TEM images were obtained through a JEOL JEM 2010 UHR equipped with a 794 slow-scan CCD camera.
Fourier Transform Infrared (FT-IR) spectra were recorded in the region from 400 to 4000 cm−1 by using a Bruker Equinox 55 spectrophotometer. Samples were measured as KBr pellets. Spectra were processed using OPUS software.
Thermogravimetric analysis (TGA) curves were obtained using a PerkinElmer STA 6000, in the 25–850 °C range, with a heating rate of 10 °C min−1 under a 40 mL min−1 O2 flow.
Room temperature (RT) 57Fe Mössbauer spectroscopy was performed on a Wissel spectrometer using a transmission arrangement and proportional detector LND-45431. α-Fe foil was used as a standard, and the fitting procedure was done by using the NORMOS program to determine the isomer shift, quadrupole splitting, hyperfine field, and full width at half maximum (FWHM) of the signals.
Dynamic light scattering (DLS) and electrophoretic light scattering (ELS) measurements were performed on colloidal dispersions through a Malvern Instrument Zetasizer Nano ZSP equipped with a He–Ne laser (λ = 633 nm and max 5 mW) and operated at a scattering angle of 173°. The Brown relaxation time was calculated from the hydrodynamic diameter calculated from the number size distribution (DDLS_N) through eqn (2), considering a temperature of 30 °C and a solvent viscosity of 7.92 × 10−4 kg m−1 s−1.
The magnetic characterization of the dispersions was performed using a SQUID magnetometer (MPMS7XL, Quantum Design). The temperature-dependent magnetization response was measured at 100 Oe using zero-field-cooled (ZFC) and field cooled (FC) protocols. The blocking temperatures (Tb) were calculated as the maximum of the derivative of the difference between the FC and ZFC magnetization curves. The anisotropy constants (K) were calculated through eqn (6):72
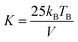 | (6) |
The heat response of NPs was recorded using a D5 system (Nano-Biomagnetic) in the frequency range 159–782 kHz with different amplitudes of the alternating magnetic field (100–400 G). The concentration of NPs in water dispersion was fixed to 1.12 mg mL−1 for all samples. A fiber-optic probe, which allows recording temperature with high accuracy, was used to monitor the solvent temperature during the experiment. Both the field and the frequency-dependent heat response was recorded under adiabatic conditions. The SPA of the NPs' dispersions was evaluated using the formula:
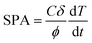 | (7) |
Results and discussion
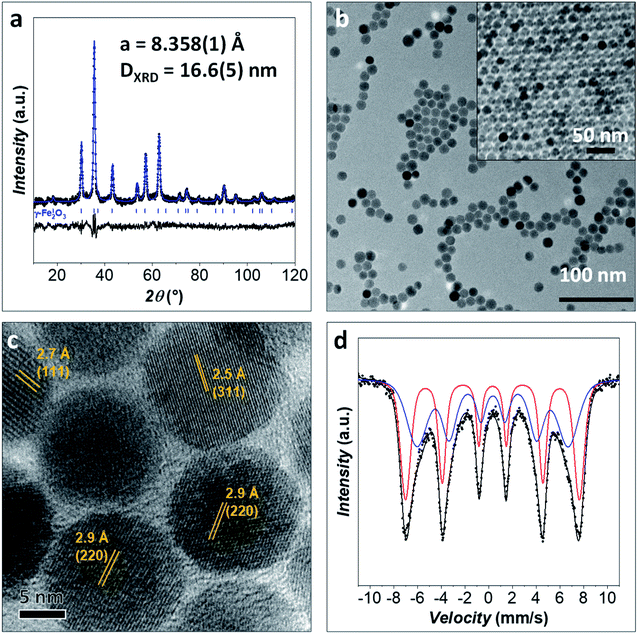
An iron oxide sample (Fe_Ole) was prepared through an oleate-based seed-mediated growth approach under solvothermal conditions and characterized from the structural and morphological points of view by XRD, TEM, HRTEM, and room temperature (RT) 57Fe Mössbauer spectroscopy.The XRD diffraction pattern of the Fe_Ole sample and the Rietveld refinement are reported in Fig. 1a. Only diffraction peaks corresponding to a nanostructured spinel iron oxide are visible. The cell parameter (a, 8.359(1) Å) suggests the presence of maghemite nanoparticles (maghemite: 8.3515 Å from PDF card 039-1346; magnetite: 8.3960 Å from PDF card: 019-0629). The crystallite size calculated from Rietveld refinement is equal to 16.6(5) nm.
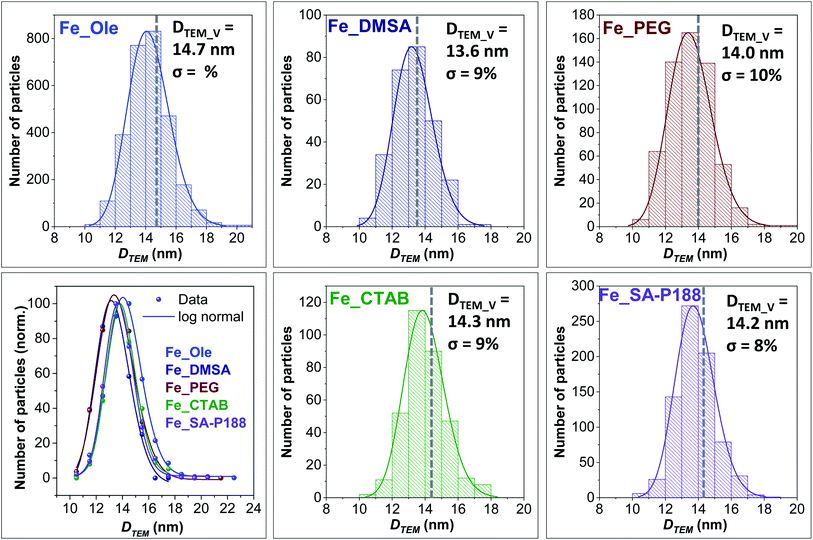
TEM images reveal well-separated spherical NPs with a particle size of 14.7 nm (Fig. 1b and 2), in fair agreement with the size obtained from XRD. The particle size dispersity is low enough (σ = 10%) to generate superlattices in the TEM grid as soon as the solvent evaporates (Fig. 1b). The HRTEM image (Fig. 1c) shows highly crystalline particles with no evidence of an amorphous part or heterojunctions, suggesting epitaxial coating of iron oxide around the pre-formed seeds. Inter-fringe distances and the associated Miller's indices confirmed the spinel ferrite structure.
RT 57Fe Mössbauer spectroscopy was performed to obtain information on the iron state (FeII/FeIII) and the magnetic properties of the spinel ferrite NPs (Fig. 1d).1,30 The spectrum of the sample Fe_Ole was fitted by using two sextets due to the expectation of the blocked state for nanoparticles of this size (i.e., around 15 nm).30 The two sextets presented hyperfine field values of 45.5 and 39.6 T, corresponding to iron cations in the tetrahedral and octahedral sites of the spinel ferrite structure.73 The isomer shift for both the sextets is in the range 0.33–0.34 mm s−1, indicating the almost complete absence of FeII, whose values are around 0.6–0.7 mm s−1.74 Since FeII–oleate was used for the synthesis, oxidation toward FeIII occurred, which is expected over time.30 The presence of maghemite is in agreement with the XRD data.
The Fe_Ole sample was modified with different organic molecules to make it hydrophilic: (i) ligand-exchange with PEGTMS (Fe_PEG) or (ii) ligand exchange with DMSA (Fe_DMSA); (iii) intercalation with CTAB (Fe_CTAB); (iv) intercalation with SA, and encapsulation in P188 (Fe_P188). The surface modification effectiveness was evaluated through FT-IR, TGA, DLS, ELS, and TEM analyses.
First of all, no changes in the size of the inorganic core and size distributions were detected upon functionalization (Fig. 2). Indeed, the slight variations in the particle sizes can be associated with possible differences in the image contrast derived from the different capping molecules.
The FTIR spectrum of Fe_Ole (Fig. 3) shows the main vibrational modes associated with the oleate molecules, as the COO− vibrational modes (νas (COO−) and νs (COO−) at about 1529 and 1415 cm−1, respectively) and those related to the hydrocarbon chain (2955 cm−1 for νas C–H(CH3), 2922 cm−1 for νas C–H(CH2), and 2852 cm−1 for νs C–H(CH2)).13,75 The bands centered at about 632 and 590 cm−1, accompanied by three shoulders at 735, 695, and 560 cm−1, are associated with the Fe–O stretching and indicate the presence of maghemite, in agreement with 57Fe Mössbauer spectroscopy and XRD data.30,33 The FT-IR spectrum of the DMSA-coated sample (Fig. 3a) revealed a series of absorption bands typical of carboxylic acids (1640–1370 cm−1 region), a shift (from 1700 cm−1 to 1740 cm−1) of the carbonyl stretching, and a metal–oxygen stretching mode at around 590 cm−1. The S–H stretching that should appear at about 2560 cm−1 is not visible due to the low amount and the weak intensity, S–H being a weak dipole.76 The sharp reduction of alkyl bands in the DMSA-coated sample indicates the almost complete removal of oleate molecules.77 The FT-IR spectrum of the PEG-coated sample is reported in Fig. 3b, showing the characteristic bands of PEGTMS in the region 1000–1100 cm−1, especially the Si–O–Si and Si–OH stretching modes at 1100 and 946 cm−1, respectively,78 as well as the Fe–O stretching mode at 590 cm−1. The FT-IR spectrum of the sample after the intercalation process with CTAB (Fig. 3c) shows the bands at 2944, 2918, and 2848 cm−1 associated with the different modes of the hydrocarbon chain (present in both oleate and CTAB), and the bands typical of CTAB in the region 1500–500 cm−1 besides the peak at 3016 cm−1 related to the N–CH3 mode.79 The band related to the Fe–O mode at 590 cm−1 is also visible; however it is very weak due to the high percentage of CTAB (95% w/w). The spectrum of the sample intercalated with stearic acid and encapsulated in poloxamer 188 is displayed in Fig. 3d, showing, besides the Fe–O mode at 590 cm−1, the typical bands of the molecules. In particular, the C–H stretching modes at about 3000 cm−1 and the bands in the fingerprint region confirm the presence of P188, while the bands associated with stearic acid are more difficult to visualize, due to the lower amount (6%) with respect to P188.
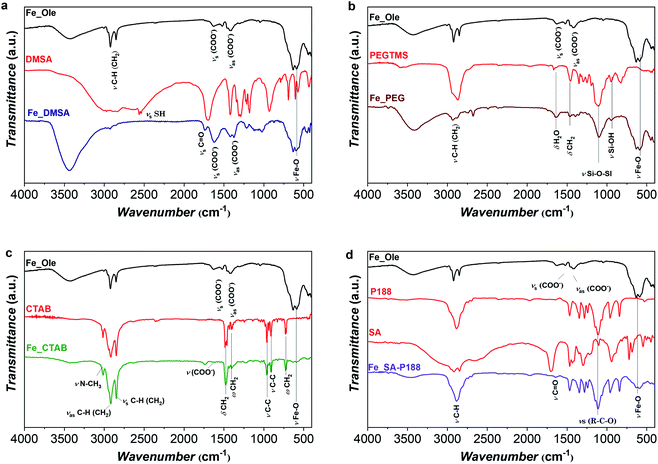 | ||
| Fig. 3 FT-IR spectra of the oleate-capped Fe_Ole sample with the corresponding ligand after surface modification: DMSA (a), PEG (b), CTAB (c), and SA-P188 (d). | ||
Thermogravimetric analyses of the oleate coated samples, the molecules used for surface modification, and the samples after post-synthesis treatment are reported in Fig. 1S and 2S† to determine the organic content (Table 1) and the decomposition temperatures. The free molecule decompositions are all in the range 220–275 °C, with DMSA and CTAB having a smaller second step at about 450–470 °C. The oleate decomposition temperature for Fe_Ole is at about 240–250 °C, in agreement with results obtained for similar particles.7,13,30,33 DMSA-coated particles undergo weight losses at 220 °C and 370 °C: the first one is close to the one of the free molecule, while the second one is shifted toward lower temperatures, indicating the bonding of DMSA to the maghemite, as also observed by other authors.80,81 The PEG-coated sample reveals a decomposition temperature of about 240 °C, slightly higher compared to that of the free PEGTMS molecule, indicating bonding between PEG and the iron oxide surface. The CTAB-modified sample displays a two-step decomposition (at 250 and 450 °C), similar to those of the free-CTAB molecule, indicating the absence of strong bonds between NPs and molecules, typical of the intercalation process. Similar behavior is observed for the samples encapsulated in P188, with a weight loss in the range 130–300 °C as the free P188, even though the first derivative is shifted to lower temperature due to the presence of the oleate and stearic acid molecules.
| Sample | D TEM_V (nm) | D DLS_N (nm) | D DLS_V (nm) | D C (μ2/s) | τ B (s) | ζ (mV) | K × 103 (J m−3) | τ N (s) | τ eff (s) | T b (K) | OC (% w/w) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe_DMSA | 13.6(1.2) | 14(3) | 17(5) | 12.8(3) | 8(2) × 10−7 | −29(1) | 3.1(3) | 6.7(6) × 10−5 | 8(2) × 10−7 | 105(2) | 7(1) |
| Fe_PEG | 14.0(1.3) | 17(5) | 22(9) | 19.3(1) | 1.5(4) × 10−6 | −30(1) | 2.3(2) | 1.5(1) × 10−5 | 1.4(4) × 10−6 | 89(2) | 18(2) |
| Fe_CTAB | 14.3(1.2) | 25(7) | 38(30) | 5.9(1) | 5(1) × 10−6 | +44(2) | 2.2(3) | 1.5(1) × 10−5 | 3.7(8) × 10−6 | 87(2) | 95(5) |
| Fe_SA-P188 | 14.2(1.2) | 59(16) | 75(26) | 6.1(1) | 6(2) × 10−5 | −10(1) | 2.2(3) | 1.5(1) × 10−5 | 1.2(4) × 10−5 | 87(2) | 82(4) |
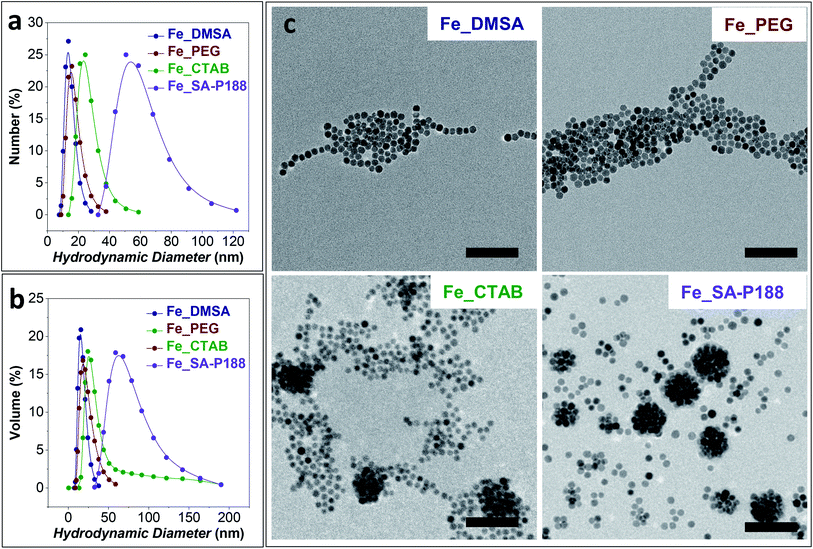
DLS analyses on the colloidal dispersions of the surface-modified samples are shown in Fig. 4a and b, while the hydrodynamic diameter and the Brown relaxation times are shown in Table 1. The Fe_SA-P188 sample presents the largest clusters, having a hydrodynamic diameter of about 60 nm and the slowest Brown relaxation (τB = 6.0 × 10−5 s). This scenario corroborates the hypothesis of the intercalation of stearic acid between the oleate molecules capping the iron oxide NP surface and the encapsulation of several of them by poloxamer 188. The other samples present a smaller hydrodynamic diameter, suggesting the presence of isolated NPs. In particular, the smallest hydrodynamic diameter (and the lowest τB) was obtained for the DMSA and PEG-coated samples produced by the ligand exchange process instead of intercalation. It is worth noting that all samples present constant values with time, a monomodal distribution, and no sedimentation, indicating the stability of the aqueous colloidal dispersions.
The TEM images of the modified samples are reported in Fig. 4c. Both DMSA- and PEG-coated samples featured isolated particles with the absence of clusters. In contrast, in the CTAB-coated sample's micrograph, some clusters of about 80 nm are visible. Nevertheless, a large number of separated particles are present. For this reason, the mean diameter estimated from DLS measurements in terms of the number of particles is in the range of 20–30 nm. The existence of the 80 nm clusters also in the aqueous dispersion is confirmed by the volume distribution of hydrodynamic diameters (Fig. 4b and Table 1) that features a long tail at higher DDLS values. Well-defined spherical clusters of NPs of about 60–70 nm are observable in the P188 modified sample due to the encapsulation of the particles inside the polymer. The low content of separated particles also enables the match between the observed TEM size and the hydrodynamic diameter calculated by DLS both by number and volume distributions.
ELS analyses were performed on the modified samples to estimate the zeta potential (ζ, Table 1). The CTAB-modified sample features positive values due to the presence of quaternary ammonium,82–88 thus confirming effective intercalation. In contrast, DMSA-coated NPs reveal negative values because of the thiol group of DMSA molecules.14,77,89 Fe_PEG also shows negative values. Even though no acidic or basic functions are present in the molecule, other authors observed the same behavior, ascribing it to incorporating hydroxide ions into the PEG layer90 or to ionizable hydroxyl groups on the iron oxide surface.64 Also, the P188-modified sample reveals a negative zeta potential value, probably for the same reasons, but no data are available in the literature for comparison.
The temperature dependence of the magnetization was studied through ZFC–FC protocols directly on the dispersions with a concentration identical to that used for the heating experiments (Fig. 3S†). Despite the minor differences among the aqueous dispersions, all samples possess a similar temperature dependence of the magnetization. The curves show a jump in the temperature range 260–280 K due to the melting of water and a maximum temperature of about 190 ± 10 K for all samples (Fig. 4Sa†). The distribution of blocking temperatures (Fig. 4Sb†) reveals a Tb centered at 88 ± 2 K for Fe_PEG, Fe_CTAB, and Fe_SA-P188 samples, while a slightly shifted distribution (Tb = 105 ± 2 K) is observed for Fe_DMSA, probably because of the shorter chain of the DMSA molecule that can cause stronger interparticle interactions. The anisotropy constants (K) calculated from Tb through eqn (6) are in the range 2 to 3 × 103 J m−3, close to the bulk maghemite (5 × 103 J m−3). The Néel relaxation times (τN), calculated utilizing eqn (1), are all in the order of 10−5 s, indicating high magnetic similarities among the samples. As a consequence, the effective relaxation time (τeff, eqn (3)) depends mainly on the τB, and it was found to be faster for Fe_DMSA (8 × 10−7 s), followed by Fe_PEG (1.5 × 10−6 s), Fe_CTAB (1.4 × 10−6 s), and Fe_SA-P188 (1.2 × 10−5 s). All FC curves feature a temperature-independent behavior up to 200 K (curve flatness), indicating strong interparticle interactions, as already observed for CTAB-intercalated core–shell spinel ferrite NPs.7 Note that the concentration of the NPs in the dispersions is rather high, and the interparticle interactions become important.
At room temperature, the samples do not exhibit hysteretic behaviour (measurements not shown), indicating a SPM regime in the DC magnetometry time window. It is important to note that superparamagnetism is a time- and frequency-dependent phenomenon. While the samples exhibit SPM behavior in the time window of DC magnetometry (0.001–1 s), if other techniques with a faster time window are used, the samples might appear in the blocked state. For instance, in the room temperature 57Fe Mössbauer spectrum of Fe_Ole a sextet is present (Fig. 1d), due to particles in the blocked state, in the measurement time window of 10−9 to 10−7 s.
Magnetic field-induced heating
The set of samples represents an ideal case study, all made up of the same non-toxic magnetic core with low size dispersity and water stability but featuring different capping molecules, aggregation states, hydrodynamic sizes, and Brown relaxation times. Therefore, all aqueous sample dispersions (1.12 mg mL−1) were tested as heat mediators under an applied alternating magnetic field of 100, 200, 316, or 400 G, and at frequencies of 159, 330, 497, 639, or 782 kHz. The heating curves at 316 G and 782 kHz are reported in Fig. 5, while ΔT, SPA, and ILP values are shown in Table 2.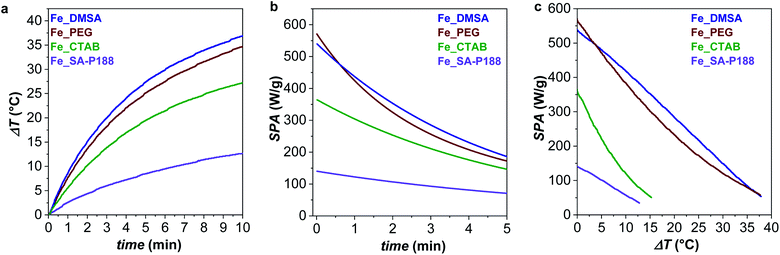 | ||
| Fig. 5 (a) Heat dissipation of the aqueous colloidal dispersion (1.12 mg mL−1) measured at 316 G and 782 kHz; (b) SPA evolution of the samples with time and temperature (c) for the curves recorded at 782 kHz and 316 G. The heat dissipation curves at various frequencies and amplitude of the applied magnetic field are reported in Fig. 5S and 6S.† | ||
| Experimental conditions | 159 kHz, 316 G | 330 kHz, 316 G | 497 kHz, 316 G | 639 kHz, 316 G | 782 kHz, 316 G | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | ΔT (°C) | SPA (W g−1) | ILP (a) | ΔT (°C) | SPA (W g−1) | ILP (a) | ΔT (°C) | SPA (W g−1) | ILP (a) | ΔT (°C) | SPA (W g−1) | ILP (a) | ΔT (°C) | SPA (W g−1) | ILP (a) |
| a nH m2 kgox−1. | |||||||||||||||
| Fe_DMSA | 4.2 | 62 | 0.61 | 11.5 | 191 | 0.91 | 19.9 | 324 | 1.02 | — | — | — | 36.9 | 539 | 1.08 |
| Fe_PEG | 2.7 | 31 | 0.31 | 9.4 | 154 | 0.73 | 17.3 | 311 | 0.98 | 25.1 | 379 | 0.93 | 34.7 | 571 | 1.14 |
| Fe_CTAB | 3.1 | 32 | 0.32 | 8.5 | 116 | 0.55 | 15.1 | 182 | 0.58 | 21.7 | 271 | 0.66 | 27.2 | 364 | 0.73 |
| Fe_SA-P188 | — | — | — | 2.8 | 27 | 0.13 | 5.6 | 62 | 0.20 | 10.6 | 151 | 0.37 | 12.7 | 140 | 0.28 |
At 782 kHz and 316 G, the highest SPA values are observed for the samples coated with DMSA and PEG molecules that reach 539 and 571 W g−1, respectively. Considering the limitations of the parameter intrinsic loss power (ILP), which can be applied only on superparamagnetic systems and in the frame of the linear response theory, it represents a helpful tool for comparing data acquired at different frequencies and amplitudes.13,39,91 The calculated ILP values are reported in Table 2, while a comparison with data reported in the literature for similar systems is shown in Table 1S.† Even though DMSA is a commonly employed coating molecule for stabilizing NPs in water, ILP values above 1.1 nH m2 kgox−1 have never been observed in the literature (Table 1S†).35–39 In contrast, Fe_SA-P188 features the lowest ΔT and SPA value (140 W g−1), which is most likely correlated with the formation of spherical clusters as recognized by TEM and DLS analyses (Fig. 4). It is known that the formation of secondary entities (clusters) affects the heating abilities7,38 due to the slower Brown relaxation time (Table 1). The CTAB-intercalated sample reveals a heating efficiency in the middle, in line with the presence of some clusters and faster τB than that of Fe_SA-P188 and slower than that of Fe_PEG and Fe_DMSA.
The initial SPA values for all samples follow the theoretical frequency dependence (eqn (4)) in the range 159–782 kHz (Fig. 6a), obtaining the best fit for Fe_DMSA (R2 = 0.998) and the worst for Fe_SA-P188 (R2 = 0.90). For some samples, e.g., Fe_DMSA and Fe_CTAB, the dependence is almost linear in the studied frequency range. Even though only minor differences can be observed in the heating abilities as a function of frequency for Fe_DMSA and Fe_PEG, it seems that Fe_DMSA is the most efficient sample at low frequencies (50% and 20% more efficient at 159 and 330 kHz, respectively). In comparison, at higher frequencies, they become comparable (4–6% differences at 497–782 kHz). One possible explanation could be related to the slower Néel relaxation time of Fe_DMSA compared to Fe_PEG (1.4 × 10−6vs. 8 × 10−7 s), which may be responsible for slightly better efficiency at low frequency. Nevertheless, it must be highlighted that both samples behave in a very similar way, in agreement with the small differences in magnetic and colloidal properties (which are reflected in τB and τN).
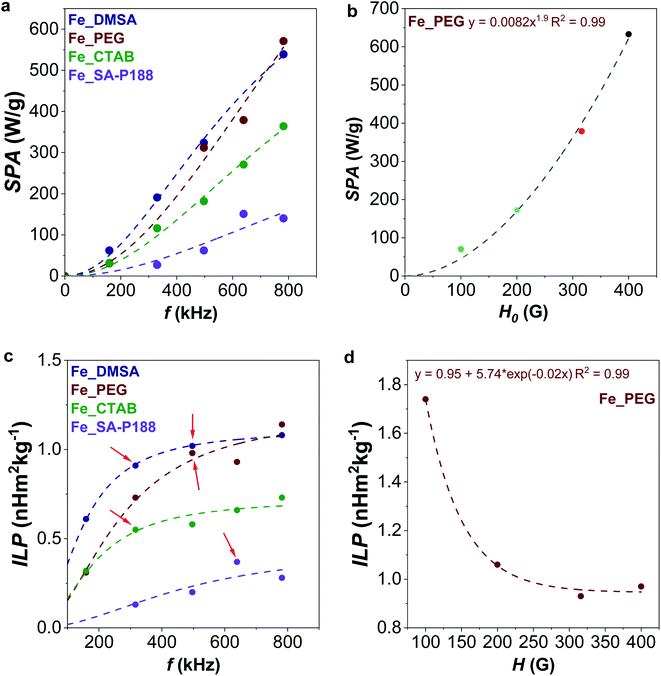 | ||
| Fig. 6 Evolution of SPA with frequency (a, at 316 G, fitted with eqn (4)) and amplitude (b, at 639 kHz, fitted with a power law) of the applied alternating magnetic field. Evolution of ILP with frequency (c, at 316 G, fitted with eqn (4)) and amplitude (d, at 639 kHz, fitted with exponential decay) of the applied alternating magnetic field. | ||
For the Fe_PEG sample, the dependency of the SPA on the amplitude of the magnetic field follows the square low SPA = αHx, where x was found to be 1.9, very close to the theoretical value of 2, as also observed by other authors (Fig. 6b).39,92
By looking at the ILP frequency dependence (Fig. 6c), one would expect no variation of ILP; instead, we observed its gradual increase with the frequency (the data were fitted with eqn (4)), clearly indicating a deviation from linear response theory. Also, other authors observed a nonlinear behavior of the susceptibility imaginary part with the frequency that can cause the nonconstant response of the ILP.93–95 For all samples except Fe_SA-P188, the maximum ILP is reached at the maximum frequency. For Fe_SA-P188, in contrast, 639 kHz is the most efficient frequency. Concerning the evolution of ILP with the applied field amplitude (Fig. 6d), the tendency is not constant. Still, it follows an exponential decay, reaching the maximum for Fe_PEG (ILP = 1.74 nH m2 kgox−1) at 100 G and becoming almost constant at 316 and 400 G (ILP = 0.95 ± 0.02 nH m2 kgox−1). In contrast, de la Presa et al. observed an initial increase of ILP with H0, and then a steady behavior in the range 40–90 G, and therefore below the range of the magnetic fields applied in this work. In this latter case, they analyzed 13 nm-uncoated maghemite nanoparticles having an aggregate size, estimated by DLS, in the range 60–75 nm.95
Magnetic field-induced heating is a complex process. In addition, for these samples, we can hypothesize both relaxations (linear response theory) and hysteresis losses as responsible for the heat release but with no information on their relative importance, considering the frequency of the alternating magnetic field. Indeed, the frequency range employed in this study for the heat dissipation (159–782 kHz) corresponds to a time window of 1 × 10−6 to 2 × 10−7 s, just above the Mössbauer measurement time window, and it is reasonable to expect that at least a part of the NPs' population was not in the SPM state. In addition, aggregation phenomena, often occurring in colloidal magnetic dispersion, can make the understanding of mechanisms even more complex. In our case, a comparison among the samples and the effect of the molecular coating can be carried out with high reliability as all samples are based on the same inorganic core and, therefore, the same size, also kept after the surface functionalization. Therefore, all the effects derived from the different organic coatings on the magnetic and colloidal properties are summed up in the obtained heat response, although it is not possible to discern the contribution of single parameters. Additional information on the heat response efficiency can also be extracted by following the evolution of the SPA with time and temperature since the colloidal dispersions of magnetic NPs are dynamic systems. Beyond the initial SPA values, the SPA dependences on time and temperature are shown, for the curves recorded at 782 kHz and 316 G, in Fig. 5; the curves recorded at the other frequencies and amplitudes are reported in Fig. 6S–8S.†
By looking at Fig. 5b, it is possible to observe that the heat release gradually decreases with increasing time and temperature. Still, clear differences can be identified between the samples. For instance, Fe_PEG shows a more pronounced initial decrease, so it features the highest SPA value in the initial phase. However, after just 30 seconds, there is an inversion with Fe_DMSA, which becomes the sample with the overall highest heat release. Similar sharp decreases can be observed for other frequencies and samples, for instance, at 639 kHz for Fe_SA-P188, at 497 kHz for Fe_PEG, 330 kHz for Fe_CTAB 330, and 497 kHz for Fe_DMSA.
Interestingly, these are also the points that deviate the most from the initial ILP vs. frequency plots (Fig. 6c, red arrows), corroborating the hypothesis that the initial heating stage does not truly represent the whole heat dissipation phenomenon. The anomalous trends are clearly visible in Fig. 8S,† where the SPA vs. temperature graphs for different frequencies of the applied alternating magnetic field are shown. Although they generally follow a straight line, a kink emerges for some frequencies specific to each sample (highlighted by black arrows). It seems that under those experimental conditions, a higher response at the beginning of the heat dissipation is observed, as in part predicted by fitting with eqn (4), where the curve bends, which then gradually decreases and follows the general linear trend of the other frequencies. The observed anomalies could also be caused by the possible occurrence of hysteretic losses, as already explained.
For this reason, the evolution of ILP with time, reported in Fig. 9S,† reveals some crucial aspects. In the beginning, there is a separation of ILP vs. time curves for the different frequencies, but the curves converge when approaching a kind of steady state. For instance, after 9 minutes, the ILP of both Fe_DMSA and Fe_PEG is equal to 0.17 ± 0.02 nH m2 kg−1, for Fe_CTAB is 0.13 ± 0.02 nH m2 kg−1, and for Fe_SA-P188 is 0.07 ± 0.02 nH m2 kg−1, considering all the frequencies. The standard deviation of the mean value for each sample (±0.02 nH m2 kg−1) would be even better if the slowest frequency is neglected since it introduces the highest uncertainty.
Therefore, the evolution of SPA vs. time and temperature permits understanding how the NPs behave at different frequencies. In contrast, the ILP vs. time curves enable an easier and more reliable comparison among the samples when each NP system acts independently of the frequency (e.g., after 9 min).
Conclusions
In this work, 15 nm oleate-capped maghemite NPs were prepared by a seed-mediated growth method under solvothermal conditions, and then made hydrophilic through modification with polyethylene glycol (PEG), dimercaptosuccinic acid (DMSA), cetrimonium bromide (CTAB), or stearic acid (SA) and poloxamer 188 (P188). Ligand exchange procedures with PEG and DMSA permitted the NPs to be kept isolated, while intercalation with CTAB and SA and encapsulation with P188 led to agglomeration into spherical clusters. The aqueous dispersions were tested for heating abilities under adiabatic conditions in an alternating magnetic field with different frequencies and amplitudes. The results showed higher initial performances for the samples with no clustering phenomena (PEG and DMSA) and lower performances for CTAB and SA-P188, in line also with the Brown relaxation times of the particles, highlighting the detrimental effect of a cluster of NPs where there is no magnetic order. Moreover, an appropriate selection of the frequency, amplitude, and time of the AMF permitted the tuning of the final temperature from room temperature to 60 °C. Furthermore, the evolution of SPA and ILP with frequency and amplitude was followed as a function of the time and the temperature. The character of the heating curves was found to help understand how the NPs behave since the kinks correspond to the inflection points of the frequency dependency of the power loss. Moreover, a convergence of the ILP vs. time curves suggests that the system behaves independently of the frequency after a certain time, allowing a direct comparison among all samples within the series. These results highlighted how a deeper understanding of the heat dissipation phenomenon is possible by analyzing in detail both the initial SPA and ILP values and their evolution with time and temperature, besides the frequency and the amplitude of the applied alternating magnetic field.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The CESA Project – RAS Piano Sulcis (CUP E58C16000080003) is gratefully acknowledged for financing the post-doctoral fellowships of M. Sanna Angotzi. PON AIM (PON Ricerca e Innovazione 2014–2020-Azione I.2-D.D. n.407 del 27 Febbraio 2018 “Attraction and International Mobility”, Cult-GeoChim project no. AIM1890410-3) is gratefully acknowledged for financing the fixed-term researcher fellowship of V. Mameli. Thanks are due to Dr Andrea Ardu and Centro Servizi di Ateneo per la Ricerca (CeSAR) for using the electron microscopes Jeol JEM 1400 Plus and Jeol JEM 2010 UHR. The Fondazione di Sardegna (FdS) is acknowledged for the financial support – Project: CUP F72F20000240007(2019): “Surface-tailored Materials for Sustainable Environmental Applications”. The authors also acknowledge the support provided by the Research Infrastructures MGML (Project no. LM2018096) and European Research Council (ERC-Stg-716265).Notes and references
- C. Cara, E. Rombi, A. Musinu, V. Mameli, A. Ardu, M. Sanna Angotzi, L. Atzori, D. Niznansky, H. L. Xin and C. Cannas, J. Mater. Chem. A, 2017, 5, 21688–21698 RSC.
- M. Vacca, C. Cara, V. Mameli, M. Sanna Angotzi, M. Scorciapino, M. G. Cutrufello, A. Musinu, V. Tyrpekl, L. Pala and C. Cannas, ACS Sustainable Chem. Eng., 2020, 8, 14286–14300 CrossRef CAS.
- C. Cara, E. Rombi, V. Mameli, A. Ardu, M. Sanna Angotzi, D. Niznansky, A. Musinu and C. Cannas, J. Phys. Chem. C, 2018, 122, 12231–12242 CrossRef CAS.
- C. Cara, V. Mameli, E. Rombi, N. Pinna, M. Sanna Angotzi, D. Nižňanský, A. Musinu and C. Cannas, Microporous Mesoporous Mater., 2020, 298, 110062 CrossRef CAS.
- M. Sanna Angotzi, V. Mameli, C. Cara, K. B. L. Borchert, C. Steinbach, R. Boldt, D. Schwarz and C. Cannas, Nanoscale Adv., 2021, 3, 6100–6113 RSC.
- N. Lee, D. Yoo, D. Ling, M. H. Cho, T. Hyeon and J. Cheon, Chem. Rev., 2015, 115, 10637–10689 CrossRef CAS PubMed.
- M. Sanna Angotzi, V. Mameli, C. Cara, A. Musinu, C. Sangregorio, D. Niznansky, H. L. Xin, J. Vejpravova and C. Cannas, Nanoscale Adv., 2020, 2, 3191–3201 RSC.
- M. Sanna Angotzi, V. Mameli, C. Cara, D. Peddis, H. L. Xin, C. Sangregorio, M. L. Mercuri and C. Cannas, Nanoscale Adv., 2021, 3, 1612–1623 RSC.
- A. Kirschning, L. Kupracz and J. Hartwig, Chem. Lett., 2012, 41, 562–570 CrossRef CAS.
- R. B. N. Baig and R. S. Varma, Chem. Commun., 2013, 49, 752–770 RSC.
- V. Polshettiwar, R. Luque, A. Fihri, H. Zhu, M. Bouhrara and J. M. Basset, Chem. Rev., 2011, 111, 3036–3075 CrossRef CAS.
- D. Zhang, C. Zhou, Z. Sun, L.-Z. Wu, C.-H. Tung and T. Zhang, Nanoscale, 2012, 4, 6244 RSC.
- V. Mameli, A. Musinu, A. Ardu, G. Ennas, D. Peddis, D. Niznansky, C. Sangregorio, C. Innocenti, N. T. K. Thanh and C. Cannas, Nanoscale, 2016, 8, 10124–10137 RSC.
- M. Avolio, A. Guerrini, F. Brero, C. Innocenti, C. Sangregorio, M. Cobianchi, M. Mariani, F. Orsini, P. Arosio and A. Lascialfari, J. Magn. Magn. Mater., 2019, 471, 504–512 CrossRef CAS.
- E. Fantechi, C. Innocenti, M. Zanardelli, M. Fittipaldi, E. Falvo, M. Carbo, V. Shullani, L. Di Cesare Mannelli, C. Ghelardini, A. M. Ferretti, A. Ponti, C. Sangregorio and P. Ceci, ACS Nano, 2014, 8, 4705–4719 CrossRef CAS PubMed.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- R. Hergt, S. Dutz and M. Zeisberger, Nanotechnology, 2010, 21, 015706 CrossRef PubMed.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 083921 CrossRef.
- C. L. Dennis, A. J. Jackson, J. A. Borchers, R. Ivkov, A. R. Foreman, J. W. Lau, E. Goernitz and C. Gruettner, J. Appl. Phys., 2008, 103, 2–5 CrossRef.
- A. Y. Zubarev, Phys. Rev. E, 2018, 98, 032610 CrossRef CAS.
- B. Mehdaoui, R. P. Tan, A. Meffre, J. Carrey, S. Lachaize, B. Chaudret and M. Respaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–10 CrossRef.
- D. Serantes, K. Simeonidis, M. Angelakeris, O. Chubykalo-Fesenko, M. Marciello, M. Del Puerto Morales, D. Baldomir and C. Martinez-Boubeta, J. Phys. Chem. C, 2014, 118, 5927–5934 CrossRef CAS.
- A. F. Abu-Bakr and A. Y. Zubarev, J. Magn. Magn. Mater., 2019, 477, 404–407 CrossRef CAS.
- C. Blanco-Andujar, D. Ortega, P. Southern, Q. A. Pankhurst and N. T. K. K. Thanh, Nanoscale, 2015, 7, 1768–1775 RSC.
- L. C. Branquinho, M. S. Carrião, A. S. Costa, N. Zufelato, M. H. Sousa, R. Miotto, R. Ivkov and A. F. Bakuzis, Sci. Rep., 2013, 3, 20–22 Search PubMed.
- C. Haase and U. Nowak, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 2–6 Search PubMed.
- B. Mehdaoui, A. Meffre, J. Carrey, S. Lachaize, L.-M. Lacroix, M. Gougeon, B. Chaudret and M. Respaud, Adv. Funct. Mater., 2011, 21, 4573–4581 CrossRef CAS.
- V. Mameli, M. Sanna Angotzi, C. Cara and C. Cannas, J. Nanosci. Nanotechnol., 2019, 19, 4857–4887 CrossRef PubMed.
- M. Fantauzzi, F. Secci, M. Sanna Angotzi, C. Passiu, C. Cannas and A. Rossi, RSC Adv., 2019, 9, 19171–19179 RSC.
- M. Sanna Angotzi, V. Mameli, C. Cara, A. Ardu, D. Nizňnanský and A. Musinu, J. Nanosci. Nanotechnol., 2019, 19, 4954–4963 CrossRef PubMed.
- M. Sanna Angotzi, V. Mameli, A. Musinu and D. Nizňnanský, J. Nanosci. Nanotechnol., 2019, 19, 5008–5013 CrossRef PubMed.
- M. Sanna Angotzi, V. Mameli, D. Zákutná, D. Kubániová, C. Cara and C. Cannas, J. Phys. Chem. C, 2021, 125, 20626–20638 CrossRef CAS.
- M. Sanna Angotzi, A. Musinu, V. Mameli, A. Ardu, C. Cara, D. Niznansky, H. L. Xin and C. Cannas, ACS Nano, 2017, 11, 7889–7900 CrossRef CAS PubMed.
- M. Sanna Angotzi, V. Mameli, C. Cara, V. Grillo, S. Enzo, A. Musinu and C. Cannas, Sci. Rep., 2020, 10, 17015 CrossRef CAS PubMed.
- V. Nandwana, S. R. Ryoo, S. Kanthala, M. De, S. S. Chou, P. V. Prasad and V. P. Dravid, ACS Appl. Mater. Interfaces, 2016, 8, 6953–6961 CrossRef CAS PubMed.
- Z. Surowiec, A. Miaskowski and M. Budzyński, Nukleonika, 2017, 62, 183–186 CrossRef CAS.
- D. F. Coral, P. Mendoza Zélis, M. Marciello, M. D. P. Morales, A. Craievich, F. H. Sánchez and M. B. Fernández Van Raap, Langmuir, 2016, 32, 1201–1213 CrossRef CAS PubMed.
- L. L. Gutiérrez, L. de la Cueva, M. Moros, E. Mazarío, S. de Bernardo, J. M. de la Fuente, M. P. Morales and G. Salas, Nanotechnology, 2019, 30, 112001 CrossRef PubMed.
- M. Avolio, A. Guerrini, F. Brero, C. Innocenti, C. Sangregorio, M. Cobianchi, M. Mariani, F. Orsini, P. Arosio and A. Lascialfari, J. Magn. Magn. Mater., 2019, 471, 504–512 CrossRef CAS.
- T. K. Oanh Vuong, T. T. Le, H. D. Do, X. T. Nguyen, X. C. Nguyen, T. T. Vu, T. L. Le and D. L. Tran, Mater. Chem. Phys., 2020, 245, 122762 CrossRef CAS.
- F. Mérida, C. Rinaldi, E. J. Juan and M. Torres-Lugo, Int. J. Nanomed., 2020, 15, 419–432 CrossRef.
- L. Storozhuk and N. Iukhymenko, Appl. Nanosci., 2019, 9, 889–898 CrossRef CAS.
- J. M. Orozco-Henao, D. Muraca, F. H. Sánchez and P. Mendoza Zélis, J. Phys. D: Appl. Phys., 2020, 53, 385001 CrossRef CAS.
- M. E. de Sousa, A. Carrea, P. Mendoza Zélis, D. Muraca, O. Mykhaylyk, Y. E. Sosa, R. G. Goya, F. H. Sánchez, R. A. Dewey and M. B. Fernández van Raap, J. Phys. Chem. C, 2016, 120, 7339–7348 CrossRef CAS.
- E. Cheraghipour and M. Pakshir, J. Environ. Chem. Eng., 2021, 9, 104883 CrossRef CAS.
- L. M. Bauer, S. F. Situ, M. A. Griswold and A. C. S. Samia, Nanoscale, 2016, 8, 12162–12169 RSC.
- A. Skumiel, K. Kaczmarek, D. Flak, M. Rajnak, I. Antal and H. Brząkała, J. Mol. Liq., 2020, 304, 0–5 CrossRef CAS.
- P. H. Linh, N. X. Phuc, L. V. Hong, L. L. Uyen, N. V. Chien, P. H. Nam, N. T. Quy, H. T. M. Nhung, P. T. Phong and I. J. Lee, J. Magn. Magn. Mater., 2018, 460, 128–136 CrossRef CAS.
- Z. Shaterabadi, G. Nabiyouni and M. Soleymani, Mater. Sci. Eng., C, 2020, 117, 111274 CrossRef CAS PubMed.
- E. Illés, M. Szekeres, I. Y. Tóth, Á. Szabó, B. Iván, R. Turcu, L. Vékás, I. Zupkó, G. Jaics and E. Tombácz, J. Magn. Magn. Mater., 2018, 451, 710–720 CrossRef.
- R. D. Piazza, W. R. Viali, C. C. dos Santos, E. S. Nunes, R. F. C. Marques, P. C. Morais, S. W. da Silva, J. A. H. Coaquira and M. Jafelicci, Mater. Res. Express, 2020, 7, 015078 CrossRef CAS.
- M. Kishimoto, R. Miyamoto, T. Oda, H. Yanagihara, N. Ohkohchi and E. Kita, J. Magn. Magn. Mater., 2016, 398, 200–204 CrossRef CAS.
- L. H. Nguyen, V. T. K. Oanh, P. H. Nam, D. H. Doan, N. X. Truong, N. X. Ca, P. T. Phong, L. V. Hong and T. D. Lam, J. Nanopart. Res., 2020, 22, 258 CrossRef CAS.
- V. Ganesan, B. B. Lahiri, C. Louis, J. Philip and S. P. Damodaran, J. Mol. Liq., 2019, 281, 315–323 CrossRef CAS.
- M. Cobianchi, A. Guerrini, M. Avolio, C. Innocenti, M. Corti, P. Arosio, F. Orsini, C. Sangregorio and A. Lascialfari, J. Magn. Magn. Mater., 2017, 444, 154–160 CrossRef CAS.
- D. Sakellari, K. Brintakis, A. Kostopoulou, E. Myrovali, K. Simeonidis, A. Lappas and M. Angelakeris, Mater. Sci. Eng., C, 2016, 58, 187–193 CrossRef CAS PubMed.
- A. F. Alves, S. G. Mendo, L. P. Ferreira, M. H. Mendonça, P. Ferreira, M. Godinho, M. M. Cruz and M. D. Carvalho, J. Nanopart. Res., 2016, 18, 1–13 CrossRef CAS.
- I. Khmara, M. Molcan, A. Antosova, Z. Bednarikova, V. Zavisova, M. Kubovcikova, A. Jurikova, V. Girman, E. Baranovicova, M. Koneracka and Z. Gazova, J. Magn. Magn. Mater., 2020, 513, 167056 CrossRef CAS.
- M. Soleymani, M. Velashjerdi, Z. Shaterabadi and A. Barati, Carbohydr. Polym., 2020, 237, 116130 CrossRef CAS PubMed.
- R. R. Koli, N. G. Deshpande, D. S. Kim, A. R. Shelke, A. V. Fulari, V. J. Fulari and H. K. Cho, Ceram. Int., 2020, 46, 24290–24301 CrossRef CAS.
- C. Cannas, A. Ardu, A. Musinu, L. Suber, G. Ciasca, H. Amenitsch and G. Campi, ACS Nano, 2015, 9, 7277–7286 CrossRef CAS PubMed.
- L. Gomez, C. De Weerd, J. L. Hueso and T. Gregorkiewicz, Nanoscale, 2017, 9, 631–636 RSC.
- F. Carlà, G. Campo, C. Sangregorio, A. Caneschi, C. de Julián Fernández and L. I. Cabrera, J. Nanopart. Res., 2013, 15, 1813 CrossRef.
- E. K. U. Larsen, T. Nielsen, T. Wittenborn, H. Birkedal, T. Vorup-Jensen, M. H. Jakobsen, L. Østergaard, M. R. Horsman, F. Besenbacher, K. A. Howard and J. Kjems, ACS Nano, 2009, 3, 1947–1951 CrossRef CAS PubMed.
- E. B. Abuin, M. A. Rubio and E. A. Lissi, J. Colloid Interface Sci., 1993, 158, 129–132 CrossRef CAS.
- T. A. S. Ferreira, J. C. Waerenborgh, M. H. R. M. Mendonça, M. R. Nunes and F. M. Costa, Solid State Sci., 2003, 5, 383–392 CrossRef CAS.
- L. Lutterotti and P. Scardi, J. Appl. Crystallogr., 1990, 23, 246–252 CrossRef CAS.
- R. A. Young and D. B. Wiles, J. Appl. Crystallogr., 1982, 15, 430–438 CrossRef CAS.
- V. Montoro, Gazz. Chim. Ital., 1938, 68, 728–733 CAS.
- S. Mondini, A. M. Ferretti, A. Puglisi and A. Ponti, Nanoscale, 2012, 4, 5356 RSC.
- R. J. Matyi, L. H. Schwartz and J. B. Butt, Particle Size, Particle Size Distribution, and Related Measurements of Supported Metal Catalysts, 1987, vol. 29 Search PubMed.
- E. F. Kneller and F. E. Luborsky, J. Appl. Phys., 1963, 34, 656–658 CrossRef CAS.
- J. M. G. Duarte and S. L. Campbell, Design, 2009, 02142, 3–7 Search PubMed.
- E. Murad and J. H. Johnston, Mössbauer Spectrosc. Appl. to Inorg. Chem., 1987, pp. 507–583 Search PubMed.
- R. De Palma, S. Peeters, M. J. Van Bael, H. Van Den Rul, K. Bonroy, W. Laureyn, J. Mullens, G. Borghs and G. Maes, Chem. Mater., 2007, 19, 1821–1831 CrossRef CAS.
- S. Bandyopadhyay and A. Dey, Analyst, 2014, 139, 2118–2121 RSC.
- Z. P. Chen, Y. Zhang, S. Zhang, J. G. Xia, J. W. Liu, K. Xu and N. Gu, Colloids Surf., A, 2008, 316, 210–216 CrossRef CAS.
- M. Yamaura, R. L. Camilo, L. C. Sampaio, M. A. Macêdo, M. Nakamura and H. E. Toma, J. Magn. Magn. Mater., 2004, 279, 210–217 CrossRef CAS.
- N. Shukla, C. Liu, P. M. Jones and D. Weller, J. Magn. Magn. Mater., 2003, 266, 178–184 CrossRef CAS.
- H. Zhai, Y. Wang, M. Wang, S. Liu, F. Yu, C. Gao, G. Li and Q. Wu, Int. J. Mol. Sci., 2018, 19, 3790 CrossRef PubMed.
- F. Xiong, Z. Zhu, C. Xiong, X. Hua, X. Shan, Y. Zhang and N. Gu, Pharm. Res., 2012, 29, 1087–1097 CrossRef CAS PubMed.
- H. Wang, X. Zhao, W. Meng, P. Wang, F. Wu, Z. Tang, X. Han and J. P. Giesy, Anal. Chem., 2015, 87, 7667–7675 CrossRef CAS PubMed.
- Z. Tang, X. Zhao, T. Zhao, H. Wang, P. Wang, F. Wu and J. P. Giesy, Environ. Sci. Technol., 2016, 50, 8640–8648 CrossRef CAS PubMed.
- J. A. Ramos Guivar, E. A. Sanches, C. J. Magon and E. G. Ramos Fernandes, J. Electroanal. Chem., 2015, 755, 158–166 CrossRef CAS.
- S. A. Elfeky, S. E. Mahmoud and A. F. Youssef, J. Adv. Res., 2017, 8, 435–443 CrossRef CAS PubMed.
- D. Joseph, R. D. Rodriguez, A. Verma, E. Pousaneh, D. R. T. Zahn, H. Lang and S. Chandra, RSC Adv., 2017, 7, 3628–3634 RSC.
- B. Bateer, C. Tian, Y. Qu, S. Du, Y. Yang, Z. Ren, K. Pan and H. Fu, Dalton Trans., 2014, 43, 9885–9891 RSC.
- P. Qiu, C. Jensen, N. Charity, R. Towner and C. Mao, J. Am. Chem. Soc., 2010, 132, 17724–17732 CrossRef CAS PubMed.
- A. G. Roca, S. Veintemillas-verdaguer, M. Port, C. Robic, C. J. Serna and M. P. Morales, J. Phys. Chem. B, 2009, 113, 7033–7039 CrossRef CAS PubMed.
- H. J. Kreuzer, R. L. C. Wang and M. Grunze, J. Am. Chem. Soc., 2003, 125, 8384–8389 CrossRef CAS PubMed.
- M. Kallumadil, M. Tada, T. Nakagawa, M. Abe, P. Southern and Q. a. Pankhurst, J. Magn. Magn. Mater., 2009, 321, 1509–1513 CrossRef CAS.
- I. Y. Tóth, D. Nesztor, L. Novák, E. Illés, M. Szekeres, T. Szabó and E. Tombácz, J. Magn. Magn. Mater., 2017, 427, 280–288 CrossRef.
- R. S. Yadav, Anju, T. Jamatia, I. Kuřitka, J. Vilčáková, D. Škoda, P. Urbánek, M. Machovský, M. Masař, M. Urbánek, L. Kalina and J. Havlica, Nanomaterials, 2021, 11, 1112 CrossRef CAS PubMed.
- V. Pilati, R. Cabreira Gomes, G. Gomide, P. Coppola, F. G. Silva, F. L. O. Paula, R. Perzynski, G. F. Goya, R. Aquino and J. Depeyrot, J. Phys. Chem. C, 2018, 122, 3028–3038 CrossRef CAS.
- P. de la Presa, Y. Luengo, M. Multigner, R. Costo, M. P. Morales, G. Rivero and A. Hernando, J. Phys. Chem. C, 2012, 116, 25602–25610 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: TGA analyses; magnetic measurements; MFH measurements; literature comparison. See DOI: 10.1039/d1na00478f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |