Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Domain wall motion driven by a wide range of current in coupled soft/hard ferromagnetic nanowires
Ziyang
Yu
 a,
Bin
Gong
a,
Lun
Xiong
a,
Bin
Gong
a,
Lun
Xiong
 *a,
Xinran
Du
b,
Chenhuinan
Wei
b,
Rui
Xiong
*a,
Xinran
Du
b,
Chenhuinan
Wei
b,
Rui
Xiong
 c,
Zhihong
Lu
c,
Zhihong
Lu
 d and
Yue
Zhang
d and
Yue
Zhang
 *e
*e
aHubei Key Laboratory of Optical Information and Pattern Recognition, School of Optical Information and Energy Engineering, Wuhan Institute of Technology, Wuhan 430205, P. R. China. E-mail: xionglun@wit.edu.cn
bHubei Provincial Key Laboratory of Green Materials for Light Industry, Hubei University of Technology, Wuhan 430068, China
cKey Laboratory of Artificial Micro- and Nano-structures of Ministry of Education, School of Physics and Technology, Wuhan University, Wuhan 430072, China
dThe State Key Laboratory of Refractories and Metallurgy, School of Materials and Metallurgy, Wuhan University of Science and Technology, Wuhan 430081, China
eSchool of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan, 430074, China. E-mail: yue-zhang@hust.edu.cn
First published on 3rd February 2022
Abstract
Racetrack memory with the advantages of small size and high reading speed is proposed based on current-induced domain wall (DW) motion in a ferromagnetic (FM) nanowire. Walker breakdown that restricts the enhancement of DW velocity in a single FM nanowire can be depressed by inter-wire magnetostatic coupling in a double FM nanowire system. However, this magnetostatic coupling also limits the working current density in a small range. In the present work, based on micromagnetic calculation, we have found that when there is a moderate difference of magnetic anisotropy constant between two FM nanowires, the critical current density for triggering the DW motion can be reduced while that for breaking the inter-wire coupling can be enhanced significantly to a magnitude of 1013 A m−2, which is far above the working current density in current electronic devices. The manipulation of working current density is relevant to the modification of DW structure and inter-wire magnetostatic coupling due to the difference of the anisotropy constants between the two nanowires and paves a way to develop racetrack memory that can work in a wide range of current.
Introduction
In racetrack memory that was proposed by Prof. Stuart S. P. Parkin of IBM in 2008,1 digital information is stored in an array of magnetic domains in a nanowire of ferromagnetic metal (FM), and the domain wall (DW) that separates the neighboring domains is able to be driven by injecting an electrical current due to the spin-transfer torque (STT) effect.2–4 When compared to a traditional hard disc driver, the racetrack memory device exhibits advantages of small size and high reading speed. Therefore, the current induced DW motion (CIDWM) in an FM nanowire has been widely investigated in experiments and in theory.5–12In CIDWM, the stability of DW structure depends on current density. When the current density exceeds a critical value, the magnetic moments in the DW precess, and the DW motion slows down. This is the so-called Walker breakdown.8,13–15 Depression of the Walker breakdown results in DW motion at a high velocity with a stable DW structure. In 2015, Purnama et al. found that in an FM/insulator/FM sandwiched nanowire with perpendicular magnetic anisotropy (PMA), the magnetostatic coupling between the DWs in the neighboring FM nanowires provides a closed magnetic line of force that stabilizes the DW structure and depresses the Walker breakdown.16 The depression of Walker breakdown by inter-wire magnetostatic coupling has also been observed experimentally very recently.17 However, the inter-wire magnetostatic coupling also restricts the range of working current, and the DW can only be induced to move with the current density between two critical values. One is the smallest current density (Ja) to overcome the pinning due to the inter-wire magnetostatic coupling.16 Lowering Ja reduces dissipation. On the other hand, when the current density is higher than another critical value (Jb), the two DWs are decoupled. When the current density is between Ja and Jb, the Walker breakdown is depressed.16 Therefore, a low Ja with a high Jb is expectable in such a double FM nanowire system. However, in a sandwiched multilayer composed of two FM nanowires with identical parameters, lowering Ja and enhancing Jb at the same time seems not easy. This is because the magnetostatic coupling acting on the two DWs is the same, and they become stronger or weaker together. As a result, the range of current density for the synchronization of DW motion is fixed in a small range.
In the present work, we have found that the small difference of the magnetic anisotropy constant between the two nanowires is able to reduce Ja and enhance Jb at the same time. As a result, the gap between Ja and Jb is significantly enlarged, and Jb becomes even higher than 1013 A m−2, which is far beyond the current density that can be injected in current electronic devices.
Methods
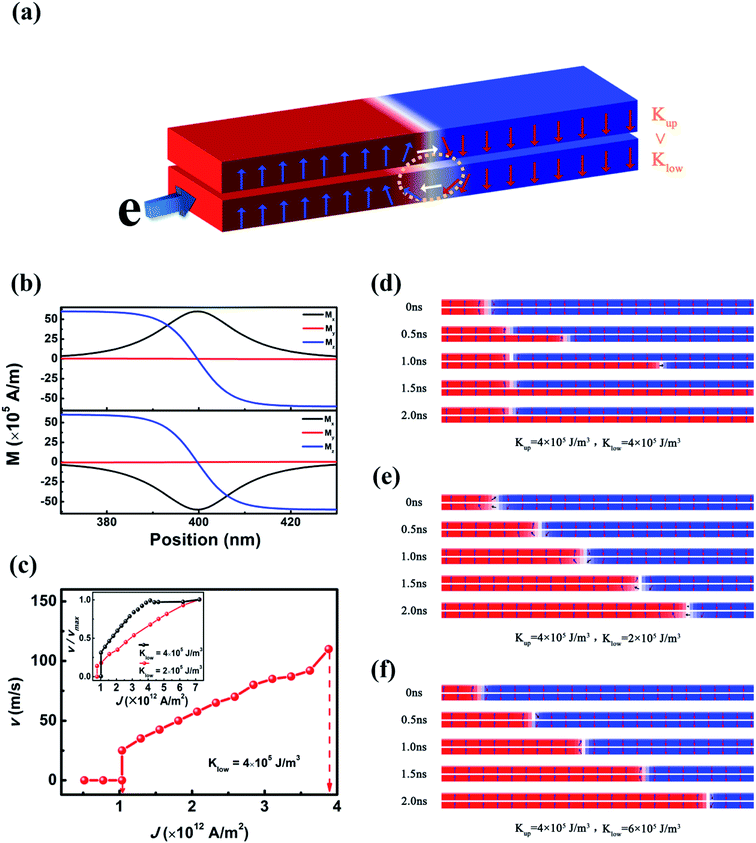
The CIDWM is simulated using the micromagnetic simulation software named Object-Oriented Micromagnetic Framework (OOMMF). In the simulation, we consider the CIDWM in a double FM nanowire system with PMA, and the magnetic anisotropy constants of the upper (Ku) and lower (Kl) nanowires are different (Fig. 1(a)). The interfacial Dzyaloshinskii–Moriya interaction (DMI) is also taken into account since it usually exists in an ultrathin FM film with PMA and contributes to stabilizing the Néel-type DW structure.17,18 The current is injected into the lower nanowire, in which the DW is driven due to the STT effect. Because of the inter-layer magnetostatic coupling, the DW in the upper one is also dragged to move to reduce the demagnetization energy till the current density is above Jb.The simulation is based on resolving the Landau–Lifshitz–Gilbert (LLG) equation containing the STT terms:8
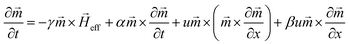 | (1) |
In eqn (1), the parameters 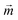 , t, and γ represent the unit vector for the orientation of magnetic moment, time, and the absolute value of gyromagnetic ratio. The first and second terms at the right side of eqn (1) contribute to the torque from the effective magnetic field
, t, and γ represent the unit vector for the orientation of magnetic moment, time, and the absolute value of gyromagnetic ratio. The first and second terms at the right side of eqn (1) contribute to the torque from the effective magnetic field 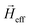 and Gilbert damping with the damping coefficient α = 0.01, respectively. The third and fourth terms are the adiabatic and non-adiabatic STT with the coefficient β = 0.04,16 respectively. Here β is significantly larger than α, which will lead to the STT-induced Walker breakdown under a small J.8u is the velocity of an electron:
and Gilbert damping with the damping coefficient α = 0.01, respectively. The third and fourth terms are the adiabatic and non-adiabatic STT with the coefficient β = 0.04,16 respectively. Here β is significantly larger than α, which will lead to the STT-induced Walker breakdown under a small J.8u is the velocity of an electron: 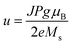 , where J is the current density, P is the polarization rate (P = 0.7), g is the Landé factor, μB is the Bohr magneton, and e is the electron charge.
, where J is the current density, P is the polarization rate (P = 0.7), g is the Landé factor, μB is the Bohr magneton, and e is the electron charge.
The model and parameters are as follows: the length and width of the nanowire are 5000 nm and 40 nm, respectively. The lower nanowire and the upper one share the same thickness (6 nm), and the inter-wire distance is 2 nm. The cell dimensions are 5 nm × 5 nm × 2 nm. The saturation magnetization (MS) is 6 × 105 A m−1. The exchange stiffness constant (A) is 1.3 × 10−11 J m−1. The absolute value of the DMI constant (D) is between 0 mJ m−2 and 1 mJ m−2, and the signs of D of the two nanowires are opposite. The Ku is fixed as 4 × 105 J m−3, and the Kl changes between 2 × 105 J m−3 and 6 × 105 J m−3.
Results and discussion
Initially, the Néel-type DWs are generated in the two nanowires (Fig. 1(b)). Because of their opposite chirality, a closed magnetic line of force can be generated between the two nanowires.16,17 When both Ku and Kl are 4 × 105 J m−3, Ja and Jb are 0.9 × 1012 A m−2 and 3.7 × 1012 A m−2, respectively (Fig. 1(c)). When J is 7.5 × 1012 A m−2, higher than this Jb, the lower DW is able to be driven by STT, but the upper DW is decoupled with the lower one (Fig. 1(d)). However, when Kl is 2 × 105 J m−3 or 6 × 105 J m−3, the upper DW can still be dragged to move together with the lower one under the same J (Fig. 1(e) and (f)). This indicates that the small difference of the magnetic anisotropy constant between the two nanowires contributes to the enhancement of Jb. Additionally, when Ku = Kl = 4 × 105 J m−3, the increase of DW velocity is depressed when J exceeds Jb, 3.7 × 1012 A m−2. Nevertheless, with Kl = 2 × 105 J m−3, the DW velocity keeps increasing when J is far beyond 4 × 1012 A m−2, indicating the depression of Walker breakdown under a higher current (the inset figure of Fig. 1(c)). And the reversal time of magnetic moments is about 0.01 ns.The variation of Ja and Jb with Kl (Ku is fixed at 4 × 105 J m−3) is different (Fig. 2(a)). When Kl increases from 2 × 105 J m−3 to 6 × 105 J m−3, Ja increases monotonically from 5 × 1011 A m−2 to around 2 × 1012 A m−2. However, Jb changes with Kl non-monotonically: Jb is close to 1 × 1013 A m−2 when Kl is 2 × 105 J m−3. It decreases with increasing Kl and reaches the minimum value when Kl = Ku and is enhanced again with further increase in Kl. When Kl and Ku are fixed at 2 × 105 J m−3 and 4 × 105 J m−3, Jb can be further modified by manipulating D (Fig. 2(b)). When D increases from 0.05 mJ m−2 to 1 mJ m−2, Ja does not change, but Jb keeps increasing to 2 × 1013 A m−2, which is far beyond the upper limit of electrical current density for current electronic devices. It is noticed that this D is reasonable in experiments for some heavy metal/FM multilayers such as Pt/Co.19,20
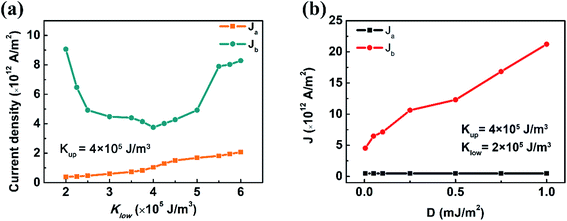 | ||
| Fig. 2 Critical current density Ja and Jb as a function of (a) the anisotropy constant of the lower layer Kl (Ku is fixed at 4 × 105 J m−3) and (b) DMI constant D. | ||
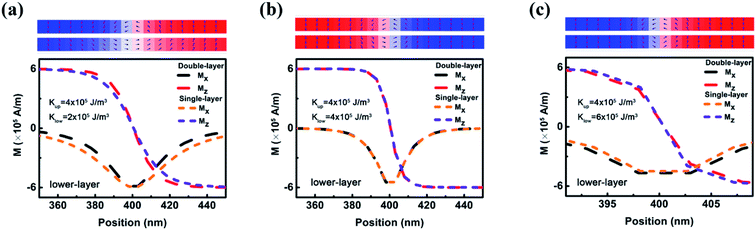
In theory, when β is larger than α, the DW in a single FM nanowire is able to be driven if only the current density is higher than zero.8,16 However, the inter-wire magnetostatic coupling in the double FM nanowire system pins the DW motion and results in a nonzero Ja.16 When Kl is different from Ku, the inter-wire magnetostatic coupling may assist or hinder the motion of the lower DW, depending on the difference between Kl and Ku. As indicated in Fig. 3, the structure of the lower DW in the double-nanowire system is modified due to the magnetostatic coupling from the upper DW. When Kl is 2 × 105 J m−3, the lower DW in the double nanowire system is narrower than that in the single nanowire with the same parameters. This means that the magnetostatic coupling rotates the magnetic moments in the left part of the lower DW towards the +z axis. In the CIDWM, the DW is triggered to move to the right through the STT-driven rotation of the magnetic moments at the left of the DW towards the +z axis. Therefore, when Kl is 2 × 105 J m−3, the magnetostatic coupling assists this rotation of magnetic moments, and the DW is able to move under a weaker current. When Kl is 6 × 105 J m−3, higher than Ku, the situation is the opposite: the magnetostatic coupling from the upper DW widens the lower DW and hinders the rotation of magnetic moments.
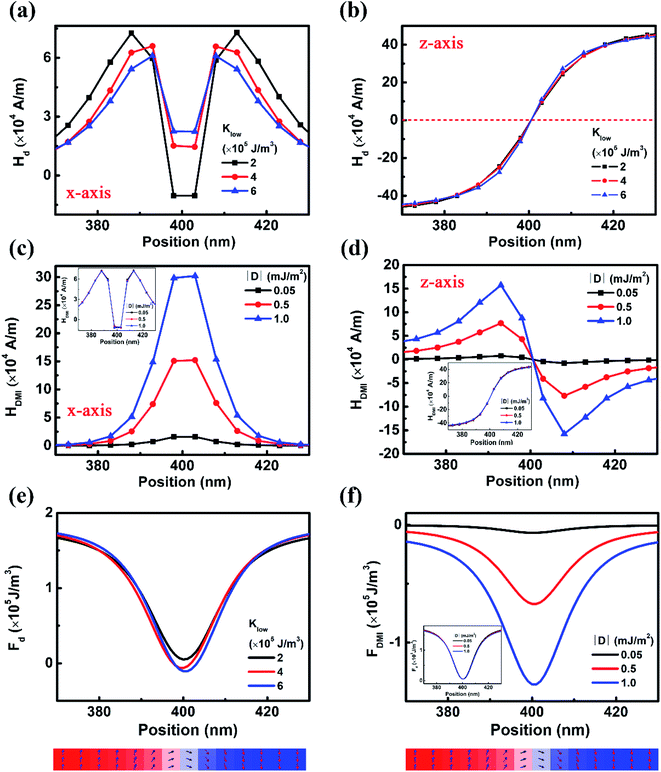
To understand the non-monotonic variation of Jb, one needs to consider the variation of the magnetostatic coupling acting on the upper DW. This may be indirectly reflected from the demagnetizing field (Hd) near the DW in the initial state. Because of the Néel-type DW structure, we only consider the Hd in the xz plane. The x and z components of Hd are extracted from the OOMMF. It is shown that changing Kl has a small effect on (Hd)z, but changes (Hd)x considerably. When Kl increases from 2 × 105 J m−3 to 6 × 105 J m−3, the (Hd)x near the centre of the DW is enhanced, while that near the DW edge decreases. This indicates that when Kl is low or high, a strong (Hd)x assists the rotation of the magnetic moments either in the centre or at the edge of the DW. Since the DMI effective field is also in the xz plane, the changing of DMI also modifies the effective field for assisting/hindering the rotation of magnetic moments near the DW region. Both x and z components of the DMI effective field ((HDMI)x and (HDMI)z) are enhanced with increasing D (Fig. 4(c) and (d)), but Hd does not change obviously (the inset figures in Fig. 4(c) and (d)). The increasing (HDMI)z at the left edge of the DW assists the rotation of magnetic moments towards the +z direction, which makes it easy for the upper DW to move to the right and enhances Jb.
The non-monotonic changing of Jb may also be understood from the aspect of free energy density. When Kl = 2 × 105 J m−3, the demagnetizing energy density (Fd) throughout the upper DW region is higher than that for Kl = 4 × 105 J m−3. When Kl = 6 × 105 J m−3, the Fd at the left side of the upper DW is also higher than that for Kl = 4 × 105 J m−3 (Fig. 4(e)). Therefore, in both cases, the magnetic moments at the left side of the upper DW have a higher demagnetizing energy, which increases the probability for the rotation and the DW motion to the right. On the other hand, the energy density of DMI near the DW region increases with increasing D (Fig. 4(f)), yet the changing of DMI has little impact on the Fd (the inset figure of Fig. 4(f)). This also confirms that in addition to demagnetizing field, DMI also contributes to the enhancement of Jb.
Conclusion
In summary, in a coupled FM nanowire system, when the current is injected into the nanowire whose magnetic anisotropy constant is moderately lower than that of the other one, the DW can be triggered to move under a weaker current with a more stable magnetostatic coupling between the DWs in the two nanowires. This inter-layer magnetostatic coupling stabilizes the DW structure, depresses the Walker breakdown, and widens the range of current density for the DW motion. This paves a way to develop a novel racetrack memory device with low dissipation and high reading speed.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the National Natural Science Foundation of China (No. 12104348, 51971098 and 11804211), the Major Research Plan of the National Natural Science Foundation of China (No. 91963207) and the Science and Technology Department of Hubei Province (No. 2019CFB435).References
- S. Parkin, M. Hayashi and L. Thomas, Science, 2008, 320, 190–194 CrossRef CAS PubMed.
- D. C. Ralph and M. D. Stiles, J. Magn. Magn. Mater., 2008, 320, 1190–1216 CrossRef CAS.
- S. Muehlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Boeni, Science, 2009, 323(5916), 915–919 CrossRef CAS PubMed.
- M. Yamanouchi, D. Chiba, F. Matsukura, T. Dietl and H. Ohno, Phys. Rev. Lett., 2006, 96, 79–92 CrossRef PubMed.
- C. Adrian, Science, 2008, 320, 166 CrossRef PubMed.
- A. Brataas, A. D. Kent and H. Ohno, Nat. Mater., 2012, 11, 372 CrossRef CAS PubMed.
- L. M. Miron, T. Moore, H. Szambolics, L. D. Buda-Prejbeanu, S. Auffret, B. Rodmacq, S. Pizzini, J. Vogel, M. Bonfim and A. Schuhl, Nat. Mater., 2011, 10, 419–423 CrossRef PubMed.
- A. Thiaville, Y. Nakatani, J. Miltat and Y. Suzuki, Europhys. Lett., 2005, 69, 990–996 CrossRef CAS.
- T. Koyama, D. Chiba, K. Ueda, K. Kondou, H. Tanigawa, S. Fukami, T. Suzuki, N. Ohshima, N. Ishiwata and Y. Nakatani, Nat. Mater., 2011, 10(3), 194–197 CrossRef CAS PubMed.
- Z. Li and S. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 2199–2208 Search PubMed.
- O. Boulle, J. G. Kimling, P. Warnicke, M. Klui and G. Faini, Phys. Rev. Lett., 2008, 101, 216601 CrossRef CAS PubMed.
- S. Krishnia and W. S. Lew, in Emerging Non-volatile Memory Technologies, Springer, 2021, pp. 103–147 Search PubMed.
- C. J. Slonczewski and, J. Appl. Phys., 1991, 69, 4590–4592 CrossRef.
- N. L. Schryer and L. R. Walker, J. Appl. Phys., 1974, 45, 5406–5421 CrossRef CAS.
- J. Moon, J. Yoon, K. Kim, S.-H. Lee, D.-Y. Kim and S.-B. Choe, Multiple Walker Breakdowns in Magnetic Multilayers, 2021, preprint, DOI:10.21203/rs.3.rs-775358/v1.
- I. Purnama, I. S. Kerk, G. J. Lim and W. S. Lew, Sci. Rep., 2015, 5(1), 8754 CrossRef CAS PubMed.
- A. Hrabec, V. Krizakova, S. Pizzini, J. Sampaio, A. Thiaville, S. Rohart and J. Vogel, Phys. Rev. Lett., 2018, 120, 227204.227201–227204.227205 CrossRef PubMed.
- S. Rohart and A. Thiaville, Physics, 2013, 88, 1352–1355 Search PubMed.
- H. Yang, A. Thiaville, S. Rohart, A. Fert and M. Chshiev, Phys. Rev. Lett., 2015, 115, 267210 CrossRef PubMed.
- W. Legrand, D. Maccariello, F. Ajejas, S. Collin, A. Vecchiola, K. Bouzehouane, N. Reyren, V. Cros and A. Fert, Nat. Mater., 2020, 19(1), 34–42 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |