Open Access Article
Open Access ArticleObservation of suppressed diffuson and propagon thermal conductivity of hydrogenated amorphous silicon films
Yingying
Zhang
 a,
Mohammad Ali
Eslamisaray
a,
Mohammad Ali
Eslamisaray
 a,
Tianli
Feng
a,
Tianli
Feng
 b,
Uwe
Kortshagen
b,
Uwe
Kortshagen
 a and
Xiaojia
Wang
*a
a and
Xiaojia
Wang
*a
aDepartment of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, USA Web: wang4940@umn.edu
bDepartment of Mechanical Engineering, University of Utah, Salt Lake City, UT 84112, USA
First published on 19th October 2021
Abstract
Hydrogenated amorphous silicon (a-Si:H) has drawn keen interest as a thin-film semiconductor and superb passivation layer in high-efficiency silicon solar cells due to its low cost, low processing temperature, high compatibility with substrates, and scalable manufacturing. Although the impact of hydrogenation on the structural, optical, and electronic properties of a-Si:H has been extensively studied, the underlying physics of its impact on the thermal properties is still unclear. Here, we synthesize a-Si:H films with well-controlled hydrogen concentrations using plasma-enhanced chemical vapor deposition and systematically study the thermal conductivity of these a-Si:H films using time-domain thermoreflectance. We find that the reduction of thermal conductivity of a-Si:H films is attributed to the suppression of diffuson and propagon contributions as the hydrogen concentration increases. At the maximum hydrogen concentration of 25.4 atomic percentage, the contributions from diffusons and propagons to the thermal conductivity are decreased by 40% (from 1.10 to 0.67 W m−1 K−1) and 64% (from 0.61 to 0.22 W m−1 K−1), respectively. Such a significant reduction in the thermal conductivity of a-Si:H originates from the hydrogen induced material softening, the decrease in density, and phonon-defect scattering. The results of this work provide fundamental insights into the thermal transport properties of a-Si:H thin films, which is beneficial for the design and optimization of amorphous silicon-based technologies including photovoltaics, large-area electronics, and thermoelectric devices.
1. Introduction
Amorphous silicon deposited via plasma-enhanced chemical vapor deposition (PECVD) contains a certain amount of hydrogen stemming from the silane (SiH4) precursor and is therefore called “hydrogenated amorphous silicon (a-Si:H)”. Compared to hydrogen-free amorphous silicon (a-Si), such as that deposited by sputtering, the hydrogen in a-Si:H greatly improves its electrical properties by terminating the dangling bonds and modifying its degree of short-range order,1–3 making it a promising material candidate for thin-film semiconductor devices.4–9 Despite its poorer electronic properties compared to those of crystalline silicon (c-Si), a-Si:H offers significant technical advantages including low manufacturing cost, low processing temperature, and great compatibility with flexible substrates and large-scale electronic manufacturing. Therefore, a-Si:H has received extensive interest leading to numerous studies focusing on its structural, optical, and electronic properties.10–14The performance and reliability of semiconductor devices largely depend on their operating temperature, dictated by their thermal properties.15–17 This is more important for amorphous materials since their low thermal conductivity18,19 can result in considerably higher operating temperatures that are detrimental for devices.20 Therefore, extensive research has been conducted to understand the thermal transport in a-Si films, which report a strong size-dependent thermal conductivity attributed to the contribution of long mean free path (MFP) propagons.21–23 Due to the presence of H atoms, the thermal properties of a-Si:H can be significantly different from those of a-Si.24,25 However, a systematic study of the impact of hydrogen on the thermal transport mechanisms and heat carrier characteristics of a-Si:H is still lacking. Although the thermal conductivity of a-Si:H films was reported in several studies,24,26,27 an in-depth understanding of the impact of H atoms on the contribution of different heat carriers to the thermal transport in a-Si:H films is still lacking.
In this work, a-Si:H films with various H concentrations (εH) are prepared in a PECVD reactor at different substrate temperatures. Fourier transform infrared spectroscopy (FTIR) is used to examine the H bonding configuration and total H concentration in the films. The thermal conductivities of these films before and after annealing are measured with the ultrafast laser-based time-domain thermoreflectance (TDTR) technique.28,29 The impact of H atoms on the contributions of different heat carriers to the thermal conductivity of a-Si:H films is discussed in detail, based on the interpretation of measurement data assisted by theoretical modelling.
2. Sample preparation and characterization
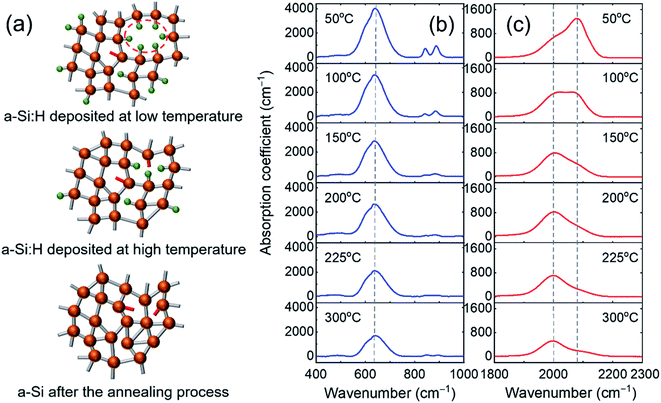
A conventional capacitively coupled PECVD reactor with an RF glow discharge of 13.56 MHz was used for film depositions. A mixture of 2 sccm (standard cubic centimeter per minute) SiH4 and 41 sccm Ar was introduced into the reactor, resulting in a chamber pressure of 210 mTorr. Plasma was triggered by applying a low RF power of 4 W (power density of ∼65 mW cm−2) at 13.56 MHz to parallel plate electrodes. A series of a-Si:H films with varying H concentrations were prepared by changing the substrate temperature systematically from 50 °C to 300 °C. Profilometric measurements (KLA-Tencor P-7 stylus profiler) show the film thicknesses (da-Si:H) in the range of 350–460 nm. At each substrate temperature studied, samples were deposited on two quartz substrates for thermal conductivity measurements and two double-sided polished c-Si wafers for FTIR. One set of samples was studied as produced, while the other set was annealed in a furnace under a nitrogen flow at 460 °C for 30 hours with heating and cooling rates of 3 °C min−1. The annealing process was intended for H effusion with little to no crystallization of the films.30,31Fig. 1(a) shows a schematic diagram of the as-produced a-Si:H deposited at different substrate temperatures as well as a-Si obtained by the post-annealing process. The H bonding configuration in the a-Si:H films was studied by FTIR (Bruker Alpha IR spectrometer) in the transmission mode. The Brodsky–Cardona–Cuomo (BCC) method was employed to convert the infrared transmittance to absorption coefficients.1Fig. 1(b) and (c) show the FTIR absorption spectra of the as-produced samples prepared at different substrate temperatures in the wagging and stretching bond regions, respectively. The stretching mode absorption could be deconvoluted into two Gaussian peaks centered at around 2000 cm−1 and 2080 cm−1, representing silicon monohydride (SiH) and dihydride ((SiH2)n) bonds, respectively. The SiH bond is assigned to isolated H in a dense network structure, while the (SiH2)n bond is attributed to the presence of clustered H at the internal surfaces of microvoids.32 For the sample prepared at 50 °C, the dihydride peak is predominant, indicating the high degree of microscopic voids at low temperatures. With increasing substrate temperature during deposition, the dihydride peak intensity decreases much faster than the monohydride peak intensity showing that a-Si:H thin films are less porous at higher temperatures.
The H concentration of the films was evaluated using the integrated absorption of the Si–H wagging bond at 640 cm−1, following:
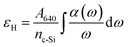 | (1) |
| T (°C) | ε H (at%) | ϕ (%) | C a-Si:H (J cm−3 K−1) | d a-Si:H (nm) | v L (m s−1) |
|---|---|---|---|---|---|
| 50 | 25.4 | 21 | 1.30 | 450 | 7100 ± 200 |
| 100 | 21.5 | 13 | 1.43 | 425 | 7800 ± 200 |
| 150 | 18.4 | 10 | 1.48 | 464 | 7500 ± 200 |
| 200 | 16.6 | 8 | 1.51 | 388 | 7600 ± 300 |
| 225 | 13.6 | 6 | 1.54 | 410 | 7700 ± 200 |
| 300 | 10.1 | 5 | 1.56 | 449 | 8000 ± 200 |
Due to the mass difference between H and Si atoms, the mass density (ρ) of a-Si:H films decreases with increasing H concentration. The relationship between the H concentration and ρ of a-Si:H films has been extensively examined in prior studies.33–35 The film porosity (ϕ) can be obtained from the film mass density following: 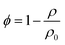 , with ρ0 being the mass density of the pure a-Si film without hydrogenation. Table 1 summarizes the structural parameters and properties of the as-produced samples necessary for the thermal analysis as detailed in Sec. 3.
, with ρ0 being the mass density of the pure a-Si film without hydrogenation. Table 1 summarizes the structural parameters and properties of the as-produced samples necessary for the thermal analysis as detailed in Sec. 3.
3. Thermal measurement results and discussion
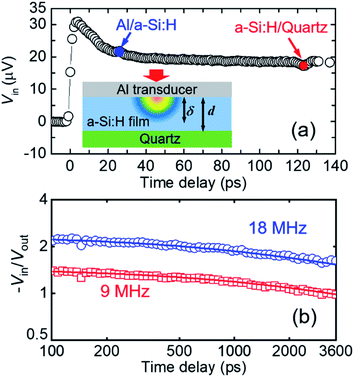
The thermal conductivities of the films were measured with TDTR,28,36 a technique that has been thoroughly validated and extensively employed in the study of thermal conductivities of thin films,37–40 nanocomposites,41,42 bulk specimens,43,44 and thermal conductance of interfaces.45 Prior to thermal measurements, a thin layer of Al was deposited onto the sample surface as a transducer and heating source, as illustrated by the schematic of the sample stack in the inset of Fig. 2(a). The thickness of the Al transducer (≈80 nm) can be determined by picosecond acoustics, based on the longitudinal speed of sound of Al46,47 and the time delay at which the acoustic wave makes a round trip within the Al layer, as shown in Fig. 2(a).48 Similarly, using the acoustic echo reflected from the a-Si:H/quartz interface and da-Si:H from profilometry, the longitudinal speed of sound (vL) of a-Si:H films can be derived.The data reduction of TDTR thermal measurements requires multiple inputs: the thickness (dAl), volumetric heat capacity (CAl), and thermal conductivity (ΛAl) of the Al transducer, and the thickness (da-Si:H) and volumetric heat capacity (Ca-Si:H) of the a-Si:H film. dAl and da-Si:H are obtained from picosecond acoustics and profilometry, respectively, as described above. ΛAl is converted from the electrical conductivity measured with the four-point probe method based on the Wiedemann–Franz Law and CAl is taken from the literature.49Ca-Si:H is taken as the heat capacity of c-Si scaled down with the film porosity (Ca-Si:H = ϕ × Cc-Si). Here, the H contribution to Ca-Si:H is neglected at room temperature since the vibrational frequency of H atoms (∼100 THz) is much higher than that of Si atoms (∼10 THz).50–54 Also, the heat capacity of c-Si is approximately equal to that of fully dense amorphous silicon.18,27 The values of vL, Ca-Si:H, and da-Si:H for the as-produced a-Si:H samples are summarized in Table 1.
By fitting the measurement data to a heat diffusion model with the aforementioned input parameters, the sample's thermal conductivity can be extracted.28Fig. 2(b) illustrates the representative TDTR signals of dual-modulation frequency measurements and associated best fitting to extract Λ for the a-Si:H film (10.1 at%) deposited on the quartz substrate. The fitted thermal conductivity is Λa-Si:H = 1.42 ± 0.16 W m−1 K−1. At the modulation frequencies of 9 and 18 MHz, the thermal penetration depth 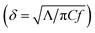 is calculated to be ∼200 nm, smaller than the film thickness. This suggests that our a-Si:H films are essentially thermally opaque, and therefore TDTR measurements are not sensitive to the quartz substrate and the thermal interface between the film and the substrate.
is calculated to be ∼200 nm, smaller than the film thickness. This suggests that our a-Si:H films are essentially thermally opaque, and therefore TDTR measurements are not sensitive to the quartz substrate and the thermal interface between the film and the substrate.
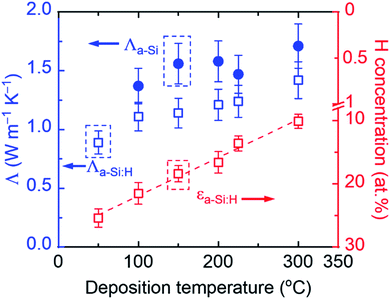
Fig. 3 summarizes the H concentration of the as-produced (εa-Si:H) samples and the thermal conductivities of both the as-produced (Λa-Si:H) and annealed (Λa-Si) samples. The total uncertainty of measured thin-film thermal conductivity consists of the random uncertainty (UA) and the systematic uncertainty (UB) via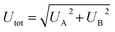 . UA takes into account the deviation of measurements at two different locations and UB is estimated based on the sensitivity analysis as detailed previously.29,40 Among individual parameters, the transducer thickness makes the dominant contribution to UB followed by the transducer heat capacity. Take the 21.5 at% a-Si:H sample as an example. A 4% uncertainty in the transducer thickness and a 3% uncertainty in the transducer heat capacity would lead to a UB of ∼10%. Combined with UA, the resulting total uncertainty of measurement results is ∼11%. Note that here all annealed samples are considered as “pure” a-Si films since their H concentrations are negligible (<1 at%) as a result of H effusion during the annealing processes. As shown in Fig. 3, εa-Si:H decreases linearly with the deposition temperature, while Λa-Si:H increases with the deposition temperature (and thus decreases with εa-Si:H). The decreasing trend of Λa-Siversus deposition temperature is also observed in annealed samples, suggesting that the initial hydrogenation can impact the thermal properties of a-Si through the annealing processes. Due to the H effusion process during heat treatment, defects are more likely to occur in samples with higher H concentrations.55–57 Likely due to the same reason, the film with a H concentration of 25.4 at% did not adhere to the substrate after annealing, despite several attempts. Therefore, there are only five data points for the annealed samples as compared to six data points for the as-produced samples.
. UA takes into account the deviation of measurements at two different locations and UB is estimated based on the sensitivity analysis as detailed previously.29,40 Among individual parameters, the transducer thickness makes the dominant contribution to UB followed by the transducer heat capacity. Take the 21.5 at% a-Si:H sample as an example. A 4% uncertainty in the transducer thickness and a 3% uncertainty in the transducer heat capacity would lead to a UB of ∼10%. Combined with UA, the resulting total uncertainty of measurement results is ∼11%. Note that here all annealed samples are considered as “pure” a-Si films since their H concentrations are negligible (<1 at%) as a result of H effusion during the annealing processes. As shown in Fig. 3, εa-Si:H decreases linearly with the deposition temperature, while Λa-Si:H increases with the deposition temperature (and thus decreases with εa-Si:H). The decreasing trend of Λa-Siversus deposition temperature is also observed in annealed samples, suggesting that the initial hydrogenation can impact the thermal properties of a-Si through the annealing processes. Due to the H effusion process during heat treatment, defects are more likely to occur in samples with higher H concentrations.55–57 Likely due to the same reason, the film with a H concentration of 25.4 at% did not adhere to the substrate after annealing, despite several attempts. Therefore, there are only five data points for the annealed samples as compared to six data points for the as-produced samples.
To reveal the impact of hydrogenation on the thermal conductivity of a-Si:H films, we first discuss the thermal conductivities of a-Si, i.e., annealed samples (Λa-Si). Due to the lack of structural periodicity in amorphous materials, adaptation of the phonon picture is no longer applicable, and therefore the concepts of ballistic and diffusive transport that are usually used in crystalline materials are not suitable here.58,59 Instead, we adopt the concepts of propagons and diffusons that are commonly used in studies of amorphous materials. As has been reported in prior studies, diffusons and propagons are the two main heat carriers contributing to the thermal conductivity of a-Si films.59–62 The diffuson contribution (Λdiff) is thickness independent and can be calculated by the minimum thermal conductivity model given by Cahill et al.:19
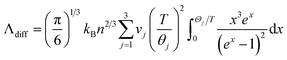 | (2) |
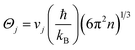 | (3) |
The propagon contribution (Λprop) increases with the film thickness, possessing similar features to phonons as a reflection of the size effect for thin films.21–23,58,63 Λprop can be modeled following Braun et al.:21
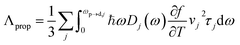 | (4) |
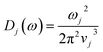 | (5) |
The relaxation time is obtained based on a three-phonon scattering model involving the boundary scattering:
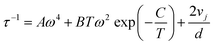 | (6) |
The thickness-dependent thermal conductivity of a-Si films has been well documented in the literature. As shown in Fig. 4(a), the measured thermal conductivities of our a-Si samples agree well with literature data.18,21,22,24,27,65 Since a-Si films were obtained from annealing the a-Si:H samples, structural defects induced by the initial hydrogenation and H effusion processes can exist in a-Si samples. Considering such defects and the small range of film thickness (∼350–450 nm), the thickness dependence of our measured Λa-Si is less apparent. The total thermal conductivity of Λa-Si is decomposed into the contributions from diffusons (Λdiff) and propagons (Λprop), based on eqn (2) and (4) with parameters taken from ref. 21, which are denoted as dotted and dashed lines in Fig. 4(b). Among the a-Si films, the 420 nm a-Si film is grown under the highest deposition temperature, leading to the lowest H concentration before annealing. For the a-Si film of 420 nm thickness, Λdiff and Λprop are calculated to be ∼1.1 and 0.7 W m−1 K−1 which account for nearly 60% and 40% of the total thermal conductivity (∼1.8 W m−1 K−1), respectively, agreeing well with our measurement data (1.71 W m−1 K−1). It is noted that the literature data of Λa-Si actually scatter.18,21,22,24,27,65 This is likely attributed to the variations of defects in a-Si prepared with different growth methods and conditions.
 | ||
| Fig. 4 (a) The comparison of experimental results of a-Si films with literature measurement data18,21,22,24,65 and model predictions. The propagon (dashed line) and diffuson (dotted line) contributions are calculated using eqn (2) and (4), respectively. (b) The comparison of measured thermal conductivity of a-Si:H films with model predictions of a-Si. It is worth noting that Λa-Si:H with higher H concentrations approaches or is even lower than the diffuson-only thermal conductivity of a-Si. | ||
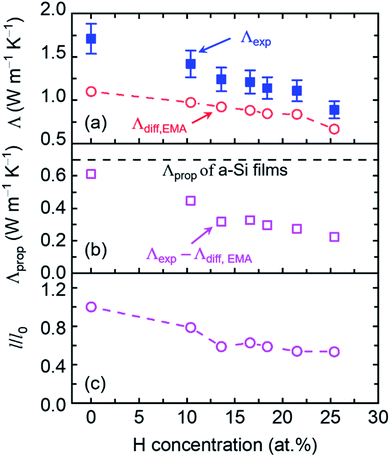
As the thermal conductivity of a-Si is understood, we proceed to the discussion of a-Si:H films. The thermal conductivities of a-Si:H films are plotted in Fig. 4 with the H concentrations denoted by percentages. It is seen that the thermal conductivity does not show any apparent dependence on the film thickness, suggesting that the size effect is not the dominant factor affecting thermal transport in these a-Si:H films. Rather, H concentration plays a much more important role in determining the thermal properties of a-Si:H films. This is reflected by the fact that for a-Si:H films with larger H concentrations, the measured thermal conductivity approaches or is even smaller than the Λdiff of a-Si films. Fundamentally, the introduction of H atoms into a-Si leads to three main changes that can affect thermal transport. The first one is the mass loss, which decreases the density and heat capacity of a-Si as shown in Table 1; the second one is the material softening induced by the voids, which lowers the sound velocity as shown in Table 1; and the last one is the enhanced heat carrier-defect scattering, where the defects include both H atoms and the voids they introduce, both of which predominantly impact propagons with low frequencies. In the latest theories,21,66,67 diffusons are described as non-propagating modes, i.e., they have zero group velocity, and therefore they are not participants in any scattering mechanism.58,66–68 Thus, the diffuson thermal conductivity is related to the first two changes, while the propagon thermal conductivity is influenced by all three changes.
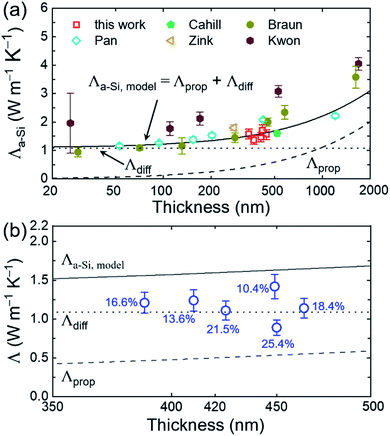
The diffuson thermal conductivity is impacted by the mass loss and material softening. Nilsson et al.69 proposed a model 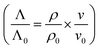 that accounts for both impacts, and this model has been extensively used in the literature.70–74 However, the factor of ρ/ρ0 in this model oversimplifies the effect of porosity (ϕ) on thermal conductivity, which can be better predicted by the effective medium approximation (EMA) approach.75–77 EMA assumes that the intrinsic properties of solid materials (e.g., sound velocity) do not change, and thus avoids double counting the effect of sound velocity reduction. The diffuson thermal conductivity calculated with the EMA approach can be written as:
that accounts for both impacts, and this model has been extensively used in the literature.70–74 However, the factor of ρ/ρ0 in this model oversimplifies the effect of porosity (ϕ) on thermal conductivity, which can be better predicted by the effective medium approximation (EMA) approach.75–77 EMA assumes that the intrinsic properties of solid materials (e.g., sound velocity) do not change, and thus avoids double counting the effect of sound velocity reduction. The diffuson thermal conductivity calculated with the EMA approach can be written as:
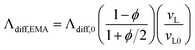 | (7) |
The propagon contribution can be obtained by subtracting Λdiff from the measured total thermal conductivity (Λprop = Λexp − Λdiff,EMA), which is plotted in Fig. 5(b). Λprop decreases from 0.61 to 0.22 W m−1 K−1 as the H concentration increases from 0 to 25.4 at%. For 0 at% H concentration, Λprop approaches the calculated value of propogon thermal conductivity for a 420 nm a-Si film based on eqn (4) (dashed line in Fig. 5(b)). We further estimate the normalized MFP (mean free path) of propagons, l/l0, with l0 being the propagon MFP of a pure a-Si film, for these a-Si:H films following the rule of Λprop ∼ cvl (Fig. 5(c)). We find that even at a low H concentration (∼10 at%), the propagon MFP is already affected by the introduction of H atoms. Propagons in amorphous silicon are long-wavelength phonons,23 which cannot discern small-size defects such as H atoms or point-defect vacancies due to the short-wavelength preference of Rayleigh scattering.79 It suggests that large voids may form due to the introduction of H atoms. Such large voids can scatter propagons with long wavelengths and lead to a clear drop in propagon MFP at ∼10 at%. The reduction of propagon MFP reaches nearly 50% as the H concentration increases to 25.4 at%.
4. Conclusions
This work experimentally investigated the impact of hydrogenation on thermal transport in a-Si:H films prepared by PECVD. Before hydrogenation, for an a-Si film of ∼400 nm thickness, the diffuson and propagon contribute 1.10 and 0.61 W m−1 K−1, which account for 64% and 36% of the total thermal conductivity, respectively. After H is introduced, the thermal conductivity decreases monotonically with increasing H concentration. At a maximum H concentration of 25.4 at%, we find that the diffuson and propagon thermal conductivities are decreased from 1.10 and 0.61 to 0.67 and 0.22 W m−1 K−1, with a decreasing ratio of 40% and 64%, respectively. Such decreases are attributed to three factors: (1) mass loss, or density decrease due to the replacement of H with Si and the introduction of nanovoids, (2) sound velocity reduction, and (3) heat carrier-defect scattering. While diffuson thermal conductivity is impacted by the first two factors, propagon thermal conductivity is impacted by all three. As a result, the impact of hydrogenation is more significant on propagon contributions to the thermal conductivity. Furthermore, we find that the propagon MFP can be affected by H atoms even at a small H concentration (∼10 at%). When H concentration further increases to 25.4 at%, the dominant propagon MFP is suppressed by ∼50%. With knowledge of the individual contributions from diffusons and propagons, the results of this work can potentially be applied to tune the thermal properties of a-Si:H and thus facilitate the design and optimization of Si-based technologies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y. Z., M. A. E., U. K., and X. W. gratefully acknowledge the funding support from the University of Minnesota MRSEC (under the NSF Award DMR-2011401) and the MN Futures award. M. A. E. would like to thank Prof. James Kakalios for helpful discussion. T. F. acknowledges the startup funding support from the Mechanical Engineering Department at the University of Utah. Portions of this work were conducted in the Minnesota Nano Center, which is supported by the National Science Foundation through the National Nanotechnology Coordinated Infrastructure (NNCI) under Award Number ECCS-2025124.References
- M. Brodsky, M. Cardona and J. Cuomo, Phys. Rev. B: Solid State, 1977, 16, 3556 CrossRef CAS.
- N. Maley and J. Lannin, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 1146 CrossRef CAS PubMed.
- R. A. Street, Hydrogenated amorphous silicon, Cambridge University Press, 2005 Search PubMed.
- M. Stuckelberger, R. Biron, N. Wyrsch, F.-J. Haug and C. Ballif, Renewable Sustainable Energy Rev., 2017, 76, 1497–1523 CrossRef CAS.
- M. Hermle, F. Feldmann, M. Bivour, J. C. Goldschmidt and S. W. Glunz, Appl. Phys. Rev., 2020, 7, 021305 CAS.
- Y. Liu, Y. Li, Y. Wu, G. Yang, L. Mazzarella, P. Procel-Moya, A. C. Tamboli, K. Weber, M. Boccard and O. Isabella, Mater. Sci. Eng., R, 2020, 142, 100579 CrossRef.
- M. Z. Rahman and S. I. Khan, Mater. Renew. Sustain. Energy, 2012, 1, 1 CrossRef CAS.
- W. Fuhs, K. Niemann and J. Stuke, AIP Conf. Proc., 1974, 20, 345–350 CAS.
- S. Dauwe, J. Schmidt and R. Hezel, Conference Record of the Twenty-Ninth IEEE Photovoltaic Specialists Conference, 2002, 1246–1249 CAS.
- W. Kessels, A. Smets, D. Marra, E. Aydil, D. Schram and M. C. M. van de Sanden, Thin Solid Films, 2001, 383, 154–160 CrossRef CAS.
- A. Mahan, J. Carapella, B. Nelson, R. Crandall and I. Balberg, J. Appl. Phys., 1991, 69, 6728–6730 CrossRef CAS.
- Y. Hishikawa, S. Tsuda, K. Wakisaka and Y. Kuwano, J. Appl. Phys., 1993, 73, 4227–4231 CrossRef CAS.
- Y.-P. Chou and S.-C. Lee, J. Appl. Phys., 1998, 83, 4111–4123 CrossRef CAS.
- C. Das, A. Dasgupta, S. Saha and S. Ray, J. Appl. Phys., 2002, 91, 9401–9407 CrossRef CAS.
- P. Singh and N. M. Ravindra, Sol. Energy Mater. Sol. Cells, 2012, 101, 36–45 CrossRef CAS.
- M. C. Wingert, J. Zheng, S. Kwon and R. Chen, Semicond. Sci. Technol., 2016, 31, 113003 CrossRef.
- S. Deng, C. Xiao, J. Yuan, D. Ma, J. Li, N. Yang and H. He, Appl. Phys. Lett., 2019, 115, 101603 CrossRef.
- B. Zink, R. Pietri and F. Hellman, Phys. Rev. Lett., 2006, 96, 055902 CrossRef CAS.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131 CrossRef CAS.
- M. H. Wong, Y. Morikawa, K. Sasaki, A. Kuramata, S. Yamakoshi and M. Higashiwaki, Appl. Phys. Lett., 2016, 109, 193503 CrossRef.
- J. L. Braun, C. H. Baker, A. Giri, M. Elahi, K. Artyushkova, T. E. Beechem, P. M. Norris, Z. C. Leseman, J. T. Gaskins and P. E. Hopkins, Phys. Rev. B, 2016, 93, 140201 CrossRef.
- Y. Pan, J. Zhou and G. Chen, Phys. Rev. B, 2020, 101, 144203 CrossRef CAS.
- K. T. Regner, D. P. Sellan, Z. Su, C. H. Amon, A. J. McGaughey and J. A. Malen, Nat. Commun., 2013, 4, 1–7 Search PubMed.
- D. G. Cahill, M. Katiyar and J. R. Abelson, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6077 CrossRef CAS.
- N. Attaf, M. Aida and L. Hadjeris, Solid State Commun., 2001, 120, 525–530 CrossRef CAS.
- X. Liu, J. Feldman, D. Cahill, R. Crandall, N. Bernstein, D. Photiadis, M. Mehl and D. Papaconstantopoulos, Phys. Rev. Lett., 2009, 102, 035901 CrossRef.
- H.-S. Yang, D. G. Cahill, X. Liu, J. Feldman, R. Crandall, B. Sperling and J. R. Abelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 104203 CrossRef.
- D. G. Cahill, Rev. Sci. Instrum., 2004, 75, 5119–5122 CrossRef CAS.
- J. Zhu, X. Wu, D. M. Lattery, W. Zheng and X. Wang, Nanosc. Microsc. Therm., 2017, 21, 177–198 CrossRef CAS.
- H. Fritzsche, M. Tanielian, C. C. Tsai and P. J. Gaczi, J. Appl. Phys., 1979, 50, 3366–3369 CrossRef CAS.
- Y. Masaki, P. LeComber and A. Fitzgerald, J. Appl. Phys., 1993, 74, 129–134 CrossRef CAS.
- T. Ruan, M. Qu, X. Qu, X. Ru, J. Wang, Y. He, K. Zheng, B. H. H. Lin, X. Xu and Y. Zhang, Thin Solid Films, 2020, 711, 138305 CrossRef CAS.
- A. Langford, M. Fleet, B. Nelson, W. Lanford and N. Maley, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13367 CrossRef CAS.
- A. Smets, W. Kessels and M. Van de Sanden, Appl. Phys. Lett., 2003, 82, 1547–1549 CrossRef CAS.
- T. Sekimoto, M. Matsumoto and A. Terakawa, Jpn. J. Appl. Phys., 2018, 57, 08RB07 CrossRef.
- J. Zhu, D. Tang, W. Wang, J. Liu, K. W. Holub and R. Yang, J. Appl. Phys., 2010, 108, 094315 CrossRef.
- Y. Zhang, Q. Su, J. Zhu, S. Koirala, S. J. Koester and X. Wang, Appl. Phys. Lett., 2020, 116, 202101 CrossRef CAS.
- X. Wu, J. Walter, T. Feng, J. Zhu, H. Zheng, J. F. Mitchell, N. Biškup, M. Varela, X. Ruan, C. Leighton and X. Wang, Adv. Funct. Mater., 2017, 27, 1704233 CrossRef.
- D. Xu, Q. Wang, X. Wu, J. Zhu, H. Zhao, B. Xiao, X. Wang, X. Wang and Q. Hao, Frontiers in Energy, 2018, 12, 127–136 CrossRef.
- J. Zhu, H. Park, J. Y. Chen, X. Gu, H. Zhang, S. Karthikeyan, N. Wendel, S. A. Campbell, M. Dawber and X. Du, Adv. Electron. Mater., 2016, 2, 1600040 CrossRef.
- X. Wu, B. L. Greenberg, Y. Zhang, J. T. Held, D. Huang, J. G. Barriocanal, K. A. Mkhoyan, E. S. Aydil, U. Kortshagen and X. Wang, Phys. Rev. Mater., 2020, 4, 086001 CrossRef CAS.
- J. Zhu, Y. Zhu, X. Wu, H. Song, Y. Zhang and X. Wang, Appl. Phys. Lett., 2016, 108, 231903 CrossRef.
- J. Zhu, T. Feng, S. Mills, P. Wang, X. Wu, L. Zhang, S. T. Pantelides, X. Du and X. Wang, ACS Appl. Mater. Interfaces, 2018, 10, 40740–40747 CrossRef CAS.
- T. Feng, X. Wu, X. Yang, P. Wang, L. Zhang, X. Du, X. Wang and S. T. Pantelides, Adv. Funct. Mater., 2020, 30, 1907286 CrossRef CAS.
- K. Zheng, F. Sun, J. Zhu, Y. Ma, X. Li, D. Tang, F. Wang and X. Wang, ACS Nano, 2016, 10, 7792–7798 CrossRef CAS.
- A. E. Lita and J. E. Sanchez Jr, J. Appl. Phys., 1999, 85, 876–882 CrossRef CAS.
- A. E. Lita and J. E. Sanchez Jr, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7692 CrossRef CAS.
- G. T. Hohensee, W.-P. Hsieh, M. D. Losego and D. G. Cahill, Rev. Sci. Instrum., 2012, 83, 114902 CrossRef.
- D. Ditmars, C. Plint and R. Shukla, Int. J. Thermophys., 1985, 6, 499–515 CrossRef CAS.
- C. G. Van de Walle, Phys. Rev. Lett., 1998, 80, 2177 CrossRef CAS.
- A. Leitch, V. Alex and J. Weber, Phys. Rev. Lett., 1998, 81, 421 CrossRef CAS.
- N. Zotov, M. Marinov, N. Mousseau and G. Barkema, J. Phys.: Condens. Matter, 1999, 11, 9647 CrossRef CAS.
- D. Ma, A. Arora, S. Deng, G. Xie, J. Shiomi and N. Yang, Mater. Today Phys., 2019, 8, 56–61 CrossRef.
- D. Ma, H. Ding, H. Meng, L. Feng, Y. Wu, J. Shiomi and N. Yang, Phys. Rev. B, 2016, 94, 165434 CrossRef.
- H. Shanks, C. Fang, L. Ley, M. Cardona, F. Demond and S. Kalbitzer, Phys. Status Solidi B, 1980, 100, 43–56 CrossRef CAS.
- R. Rüther and J. Livingstone, Thin Solid Films, 1994, 251, 30–35 CrossRef.
- A. Hadjadj, A. Beorchia, P. R. i Cabarrocas, L. Boufendi, S. Huet and J. Bubendorff, J. Phys. D: Appl. Phys., 2001, 34, 690 CrossRef.
- H. R. Seyf and A. Henry, J. Appl. Phys., 2016, 120, 025101 CrossRef.
- P. B. Allen, J. L. Feldman, J. Fabian and F. Wooten, Philos. Mag. B, 1999, 79, 1715–1731 CrossRef CAS.
- J. M. Larkin and A. J. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144303 CrossRef.
- H. R. Seyf, L. Yates, T. L. Bougher, S. Graham, B. A. Cola, T. Detchprohm, M.-H. Ji, J. Kim, R. Dupuis and W. Lv, npj Comput. Mater., 2017, 3, 1–8 CrossRef CAS.
- W. Lv and A. Henry, New J. Phys., 2016, 18, 013028 CrossRef CAS.
- S. G. Volz and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 2651 CrossRef CAS.
- J. L. Feldman, M. D. Kluge, P. B. Allen and F. Wooten, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 12589 CrossRef.
- S. Kwon, J. Zheng, M. C. Wingert, S. Cui and R. Chen, ACS Nano, 2017, 11, 2470–2476 CrossRef CAS.
- M. T. Agne, R. Hanus and G. J. Snyder, Energy Environ. Sci., 2018, 11, 609–616 RSC.
- P. B. Allen and J. L. Feldman, Phys. Rev. Lett., 1989, 62, 645 CrossRef CAS PubMed.
- P. B. Allen and J. L. Feldman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 12581 CrossRef CAS.
- O. Nilsson, G. Rüschenpöhler, J. Groß and J. Fricke, High Temperatures. High Pressures (Print), 1989, vol. 21, pp. 267–274 Search PubMed.
- F. Hu, S. Wu and Y. Sun, Adv. Mater., 2019, 31, 1801001 CrossRef.
- O.-J. Lee, K.-H. Lee, T. J. Yim, S. Y. Kim and K.-P. Yoo, J. Non-Cryst. Solids, 2002, 298, 287–292 CrossRef CAS.
- W.-P. Hsieh, M. D. Losego, P. V. Braun, S. Shenogin, P. Keblinski and D. G. Cahill, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174205 CrossRef.
- X. Xie, D. Li, T.-H. Tsai, J. Liu, P. V. Braun and D. G. Cahill, Macromolecules, 2016, 49, 972–978 CrossRef CAS.
- G. Tang, C. Bi, Y. Zhao and W. Tao, Energy, 2015, 90, 701–721 CrossRef CAS.
- J. C. Maxwell, A Treatise on Electricity and Magnetism: pt. III. Magnetism. pt. IV. Electromagnetism, Clarendon Press, 1881 Search PubMed.
- V. A. Markel, J. Opt. Soc. Am. A, 2016, 33, 1244–1256 CrossRef PubMed.
- A. Eucken, Forsch. Geb. Ingenieurwes., 1940, 11, 6–20 CrossRef.
- M. Molina-Ruiz, H. Jacks, D. Queen, Q. Wang, R. Crandall and F. Hellman, Mater. Res. Express, 2020, 7, 095201 CrossRef CAS.
- T. Feng, X. Ruan, Z. Ye and B. Cao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 224301 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |