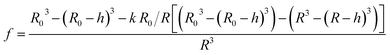Scattering versus fluorescence self-quenching: more than a question of faith for the quantification of water flux in large unilamellar vesicles?†
Received
24th July 2021
, Accepted 16th October 2021
First published on 18th October 2021
Abstract
The endeavors to understand the determinants of water permeation through membrane channels, the effect of the lipid or polymer membrane on channel function, the development of specific water flow inhibitors, the design of artificial water channels and aquaporins for the use in industrial water filtration applications all rely on accurate ways to quantify water permeabilities (Pf). A commonly used method is to reconstitute membrane channels into large unilamellar vesicles (LUVs) and to subject these vesicles to an osmotic gradient in a stopped-flow device. Fast recordings of either scattered light intensity or fluorescence self-quenching signals are taken as a readout for vesicle volume change, which in turn can be recalculated to accurate Pf values. By means of computational and experimental data, we discuss the pros and cons of using scattering versus self-quenching experiments or subjecting vesicles to hypo- or hyperosmotic conditions. In addition, we explicate for the first time the influence of the LUVs size distribution, channel distribution between vesicles and remaining detergent after protein reconstitution on Pf values. We point out that results such as the single channel water permeability (pf) depend on the membrane matrix or on the direction of the applied osmotic gradient may be direct results of the measurement and analysis procedure.
1. Introduction
Water homeostasis is of fundamental importance for life and plays a major role in human health and disease, plant growth and bacterial survival. Thereby, the permeation of water is driven by osmotic imbalances of solutes and occurs in either an unfacilitated fashion through the cell membrane or in a facilitated one through membrane spanning protein channels. Classical highly selective water channels, like aquaporins (AQPs), facilitate rapid water transport with approx. 109 water molecules per second. Additionally, different classes of membrane proteins like transporters,1 ion channels2 and receptors3 facilitate passive water flux and may assist or substitute AQPs depending on their site of expression. AQP function itself can be influenced by diverse factors. E.g. mutations causing alterations in their expression level, cellular localization, folding or permeability, are directly attributed to human diseases.4,5 Furthermore, lipid–protein interactions determine the stability6 and function7 of transmembrane proteins (MP). Thereby, protein conformation can be influenced by local interactions at the lipid–protein interface7 or global interactions such as the lateral pressure profile of the membrane,8–11 which in turn is influenced by the lipid composition of the membrane.12,13 It has already been shown that lipid-binding at weak interfaces stabilizes loosely interacting oligomers and altering the lipid composition propagates changes in the overall oligomeric state.6,14 Besides their substantial role in mammals, AQPs fulfill pivotal functions in plants, where they are also involved in the regulation of cellular water homeostasis.15 This includes a key role in transpiration sensitivity to soil drying as well as to high atmospheric vapor pressure deficit (VPD).16 Therefore, they represent the perfect target to address abiotic stresses like drought through genetic engineering.17 Hence, it is vital to understand the molecular determinants of water transport in order to optimize their performance in vivo. Recent progress in the quantification of water flux through narrow MPs18,19 already identified the number of hydrogen bonds that water molecules may form with channel lining residues as the major determinant of single-file water transport.19 Positively charged amino acids at the pore mouth potentially decrease the dehydration penalty of water molecules entering the single-file region and thereby enhance the passive water flow.20 This knowledge is exquisitely important for the design of artificial channels21–27 in material science, where the selectivity and permeability mechanism of AQPs serve as template to design artificial water channels envisioned to be used in next generation membrane-based separations and purifications. Similarly, AQPs28–35 itself or carbon nanotubes36 are potential building blocks of biomimetic membranes. These highly permeable pore structures are envisioned to determine membrane performance, selectivity and functionality. To increase the stability and chemical resistance of such biomimetic membranes, lipid bilayers are replaced by polymer layers for industrial applications.37 Furthermore, other MPs are embedded into polymer-based membranes in the emerging field of synthetic biology.38–40
To understand the impact of different factors such as point mutations, post-translational modifications, external stimuli like protons or divalent ions, and lipid interactions on water permeability of MPs embedded in lipid based membranes and further advance the understanding of the molecular determinants of water flux through narrow MPs it is necessary to assess single channel permeability (pf) values with highest accuracy. Otherwise, relative changes in MP activity in dependence of e.g. the lipid surrounding or the oligomeric state could be dismissed as measurement artefacts. Likewise, the performance of artificial and biological channels in biomimetic membranes, as well as MP stability and functionality in polymer-based membranes can only be assessed by calculating accurate pf values. Estimation of pf values involves the precise determination of (i) the overall (membrane + channels) membrane water permeability Pf and (ii) the background (lipid or polymer matrix) permeability Pm as well as (iii) channel (MP or artificial channels) counting as
| | 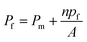 | (1) |
with
n being the average number of monomers (smallest water transporting units) per vesicle and
A the area of the lipid or polymer membrane.
Different methods exist to estimate such Pf and Pm values.18,41,42 The most widely used method involves the rapid exposure of large unilamellar vesicles (LUVs) or polymersomes (LPSs) with a diameter of around 100–150 nm to an osmotic gradient by a stopped flow device (Fig. 1). Such lipid43,44 and polymer45–47 vesicles can be directly imaged using transmission electron microscopy. From these studies it is evident that vesicle extrusion leads to a distribution of vesicle sizes which are rather spherical under isosmotic conditions.43 Thereby, the homogeneity and unilamellarity of a vesicle suspension increases using multiple extrusion cycles and smaller (e.g. 100 nm) pore sizes.43 Furthermore, their shape transforms upon application of a hyperosmotic gradient due to the increased surface to volume ratio.44–47 However, due to their small size, no method exists to directly assess the dynamically changing vesicle volume as for example by light microscopy in the case of giant unilamellar vesicles (GUVs).48 Instead the resulting change in vesicle volume can either be tracked by detecting changes in intensity of scattering light49 or fluorescence.50 In both cases, the change in vesicle volume upon application of a hyperosmotic gradient can be written as
| | 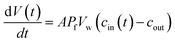 | (2) |
where
V(
t),
A,
Pf,
Vw, and
cout are the vesicle volume at time
t, the surface of the vesicle, the water permeability of the vesicular membrane, the molar volume of water and the osmotic concentration of the osmolyte in the external solution. The osmotic concentration
ci (also known as osmolarity) of substance
i is related to the molar concentration
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i
i by:
| | ci = φini![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i i | (3) |
where
φi and
ni are the osmotic coefficient and the number of particles into which molecule
i dissociates.
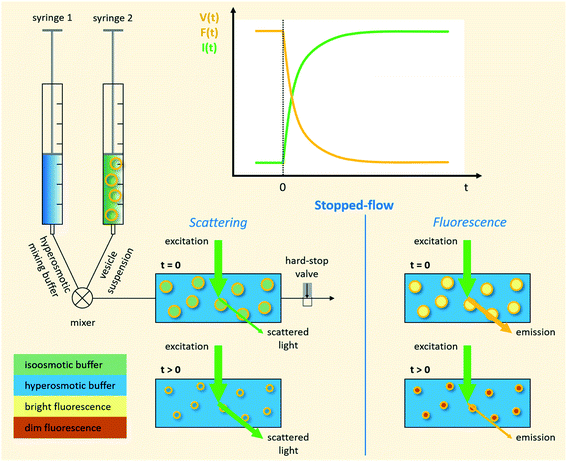 |
| | Fig. 1 Schematic representation of a stopped-flow device. Two syringes containing the vesicle suspension and hyperosmotic mixing buffer, respectively, are driven by independent stepping-motors. The content of the two syringes is rapidly mixed at the mixer and transferred into the observation chamber (cuvette). The time it takes for the solution to flow from the mixer, where the reaction starts, to the cuvette is called ‘dead time’ and is usually in the low millisecond range. A hard-stop valve abruptly stops the liquid flow, which eliminates pressure artifacts. Monochromatic light of defined wavelength illuminates the chamber and at a detection angle of 90° either the scattered light, or by introducing a longpass filter only the emitted fluorescent light is detected by a photomultiplier. | |
In case the permeation of other substances is negligible compared to water permeation the time dependent osmotic concentration of the osmolyte inside the vesicle cin(t) can be expressed as
| | 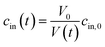 | (4) |
with
V0 and
cin,0 the initial vesicle volume and the initial osmotic concentration of the osmolyte inside the vesicle. Assuming a solute is membrane impermeable at the timescale of the experiment, internal solutes are up concentrated until the osmolarity of the internal and the external solutions match, causing a refractive index change of the vesicle during shrinkage. Whereas fluorescence self-quenching is a direct read out of the vesicle volume, the change in the scattering signal
I(
t) is influenced by the change in vesicle volume and the refractive index of the vesicle (
Fig. 2).
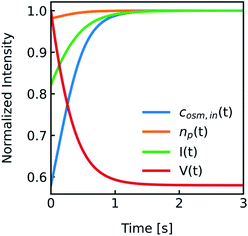 |
| | Fig. 2 Normalized measurement parameters after subjection to a hyperosmotic solution. Plot of total osmotic concentration inside the vesicle cosm,in, refractive index of the particle np, scattering intensity I(t), and volume V(t) over time. The starting values are: cosm,in(0) = 197 mOsm L−1, np(0) = 1.335, I(0) = 1.3 × 10−5 AU, V(0) = 2 × 10−13 μL. For all simulations in this paper, except explicitly mentioned, typical experimental conditions have been used: 187 mOsm L−1 NaCl and 10 mOsm L−1 buffer inside and outside the vesicles, additional 150 mOsm L−1 sucrose outside for hyperosmotic shrinkage, Pf = 6 μm s−1, membrane thickness d = 4 nm, wavelength of the illuminating monochromatic light WL = 546 nm and Weibull distribution parameters for number distribution α = 1.35, β = 12.1 and μ = 32.6 with expected values for the radius of ∼44 nm for number, 50 nm for volume and 57 nm for intensity weighted distributions (see the corresponding curves in Fig. 3A). | |
To accurately fit the volume change after subjection to a hyperosmotic solution and calculate experimentally derived Pf values it is possible to use either the analytical solution19 to eqn (2)
| | 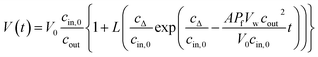 | (5) |
where
cΔ =
cout −
cin,0, or a suitable approximation
18| | 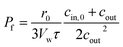 | (6) |
with
r0 and
τ the initial average radius of the vesicle population and the time constant of an exponential fit to the data. However, besides choosing correct models instead of historical but erroneous approximations, which may lead to
Pf values being orders of magnitude off,
18 it is also important to consider several other methodological peculiarities of scattering and self-quenching experiments on LUVs and LPSs. Herein, it is our intention to thoroughly discuss and review all these points necessary to contemplate when performing
Pf measurements with a stopped-flow device in general or using scattering or self-quenching experiments in particular. This section will be followed by an example of residual detergent after MP reconstitution illustrating the strengths and weaknesses of both approaches.
2. Material and methods
2.1. Protein overexpression and purification of AQP1
S. cerevisiae strain pep4 was transformed with expression vector pYES2-His-YFP-AQP1 encoding human wildtype AQP1 N-terminally fused to a 10 times His-Tag and YFP. After clonal expansion in 500 mL DOB-Ura till O.D.600 was 1.0, protein expression was induced by transferring the cells to 3l YPG medium for 16 hours. Harvested cells were resuspended in one 1/100 culture volume of ice-cold lysis buffer (100 mM K2HPO4, protease inhibitors, pH 8.0) and subjected to three lysis cycles using EmulsiFlex (Avestin) at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–25
000–25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi (4 °C). Unbroken cells and debris were separated from the cell lysate by a 20 min centrifugation at 7000 × g and discarded. Membrane fractions recovered from the supernatant by a 120 min centrifugation at 100
000 psi (4 °C). Unbroken cells and debris were separated from the cell lysate by a 20 min centrifugation at 7000 × g and discarded. Membrane fractions recovered from the supernatant by a 120 min centrifugation at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g were resuspended to the original volume in solubilization buffer [3% OG in 100 mM K2HPO4, 10% (vol/vol) glycerol, 200 mM NaCl, pH 8.0] and incubated for 1 hour at 4 °C on a roller shaker. Insoluble material was pelleted by 60 min centrifugation at 100
000 × g were resuspended to the original volume in solubilization buffer [3% OG in 100 mM K2HPO4, 10% (vol/vol) glycerol, 200 mM NaCl, pH 8.0] and incubated for 1 hour at 4 °C on a roller shaker. Insoluble material was pelleted by 60 min centrifugation at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g. The soluble fraction was mixed with 2 mL of prewashed Ni-NTA-agarose beads (Qiagen) and incubated with agitation at 4 °C for 60 min. The beads were then packed in a plastic disposable column (Stratagene) and washed with 100 bead volumes of wash buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 100 mM imidazole, pH 7.5) to remove nonspecifically bound material. Ni-NTA-agarose-bound material was eluted 5 times sequentially by adding 0.5 mL elution buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 0.5 M imidazole, pH 7.5) at each step. Typically, eluates of the 3 l expression cultures yielded pure protein at a concentration of 1.5 mg mL−1, measured by Bradford using BSA as a standard.
000 × g. The soluble fraction was mixed with 2 mL of prewashed Ni-NTA-agarose beads (Qiagen) and incubated with agitation at 4 °C for 60 min. The beads were then packed in a plastic disposable column (Stratagene) and washed with 100 bead volumes of wash buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 100 mM imidazole, pH 7.5) to remove nonspecifically bound material. Ni-NTA-agarose-bound material was eluted 5 times sequentially by adding 0.5 mL elution buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 0.5 M imidazole, pH 7.5) at each step. Typically, eluates of the 3 l expression cultures yielded pure protein at a concentration of 1.5 mg mL−1, measured by Bradford using BSA as a standard.
2.2. Reconstitution
E. coli polar lipids (PLE, Avanti Polar Lipids, Alabaster, AL, USA) was dissolved in chloroform, labeled with Atto633PPE and dried on a rotary evaporator. The dry lipid film was rehydrated with reconstitution buffer (100 mM NaCl, 10 mM MOPS, 1.33% OG, pH 7.4) to a final lipid concentration of 20 mg mL−1. After 10–15 minutes of bath sonication, the vesicle suspension was mixed with the purified protein and incubated for 1 h at room temperature. With increasing amount of Bio-Beads SM-2 resin (Bio-Rad Laboratories, Hercules, CA, USA) detergent was removed in 3 steps at 4 °C within 48 h. Proteoliposomes (PL) were pelleted by 100 min centrifugation at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g, resuspended in reconstitution buffer without OG and finally extruded through two polycarbonate filters with 100 nm pore sizes.
000 × g, resuspended in reconstitution buffer without OG and finally extruded through two polycarbonate filters with 100 nm pore sizes.
2.3. Bare lipid vesicle preparation
Large unilamellar vesicles (LUVs) were prepared from an E. coli polar lipid extract (PLE) in chloroform as previously described.51 In brief, PLE was dried on a rotary evaporator and hydrated in working buffer (100 mM NaCl, 10 mM MOPS, pH 7.4). Subsequently, the solution was extruded through 100 nm polycarbonate filters to reach a final stock solution of 10 mg mL−1. For self-quenching experiments with carboxyfluorescein (CF), if not differently stated, 10 mM CF were added during lipid rehydration. Directly before the measurements free dye was removed via PD-10 columns.
2.4. Vesicle size distribution & mean diameters
The size distribution of vesicles formed by extrusion or detergent removal is well described by the Weibull distribution.52 Thereby, the probability density function (pdf) of the general Weibull distribution is given by| | 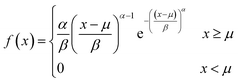 | (7) |
where α, β and μ are the shape, scale and location parameter (Fig. S1†). The corresponding cumulative density function is:| | 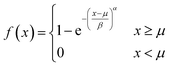 | (8) |
The most straightforward method to measure such vesicle size distributions is dynamic light scattering (DLS). We used a DelsaNano HC particle analyzer (Beckman Coulter; Brea, CA, USA) to measure the scattering distribution (green bars and line in Fig. 3) at RT and at a fixed angle of 165° and recalculated it to a volume (orange) and a number distribution (blue) with the supplied software. Notably, the RGD theory shows a blind spot for lipid vesicles with a diameter of approximately 250 nm at a detection angle of 165° (Fig. S2†). According to the Rayleigh approximation, the intensity distribution is proportional to r6 and the volume distribution to r3. Thus, the intensity weighted distribution can be converted into a volume weighted distribution with
| | 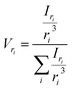 | (9) |
where
Iri and
Vri are the relative amount of scattered intensity of particles with size
ri and the volume-weighted distribution for particles with radius
ri, based on the volume of particles with size
ri.
53 The corresponding normalized number-weighted distribution
Nri for particles with radius
ri, based on the number of particles with size
ri is therefore
| | 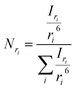 | (10) |
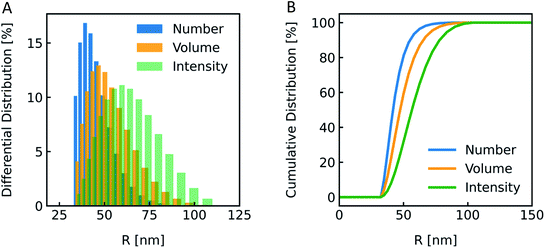 |
| | Fig. 3 Size distribution analysis by dynamic light scattering (DLS). (A) Number (blue), volume (orange) and intensity (green) weighted distributions representing the number of vesicles in % with radius R and (B) the corresponding cumulative distributions. PLE LUVs were measured with DLS after extrusion through a 100 nm filter. | |
The vesicle radius is derived from the peak of the volume (for self-quenching experiments)33 and the cumulant radius of the intensity (for scattering experiments) distribution.
Generally, volume distributions can be compared to the results of fluorescence correlation spectroscopy (FCS)54,55 whereas size distributions obtained with electron microscopy (EM)56 are closest related to the number distributions. For the transformation of intensity to volume and number weighted distributions, it is assumed that particles are spherical and homogeneous,57 the optical properties are known (e.g. refractive indices), and that the determined intensity distribution is correct. Hence, due to the assumptions inherent in the transformation, the results of volume and number distribution always need to be taken with caution.
2.5. Fluorescence correlation spectroscopy (FCS)
FCS served to measure the average radius of vesicle ensembles and the leakage of CF from lipid vesicles after subjection to an hypoosmotic gradient. In brief, the average residence time τD of Atto633-PPE labeled vesicles and the appearance of free CF visible as a second component in the autocorrelation function G(τ) of the fluorescence temporal signals from the confocal volume, was acquired using a commercial laser scanning microscope equipped with avalanche diodes (LSM 510 META Confocor 3 with a 40x-UOPLAN water immersion objective; Carl Zeiss). The confocal volume was calibrated using the residence time of rhodamine 6G in solution and its diffusion coefficient of 426 μm2 s−1,58 as previously described.59,60 To this end, we applied the standard model for one- or two-component free 3D diffusion.51,61D was determined as ω2/4τD.
2.6. Stopped-flow experiments & data analysis
PLs and LUVs are subjected to a hyperosmotic solution in a stopped-flow apparatus (SFM-300 or μ-SFM, Bio-Logic, Claix, France) at 4 °C and the intensity of scattered light is monitored at 90° at a wavelength of 546 nm if not otherwise stated.1,18–20 Water permeability values Pf are, except explicitly mentioned, calculated using our recently calculated analytical solution.19 For self-quenching experiments, monochromatic light of 480 nm wavelength is used to illuminate the sample. The emitted fluorescent light passes a 515 nm longpass filter and is detected at an angle of 90°. Averaged self-quenching curves are then fitted, according to eqn (5), to the following function:| | 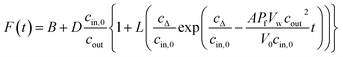 | (11) |
where F(t) is the fluorescence intensity and B and D are fitting parameters.
The normalized intensity Inorm is determined either by Inorm(t) = I(t)/Imax or, for normalization between [0,1], by Inorm(t) = (I(t) − Imin)/(Imax − Imin), where I(t) is the measured intensity at time t and Imax and Imin are the averaged maximum and minimum intensities. In all experiments, buffer osmolarities were determined with a Wescor 5500 Vapor Pressure Osmometer.
2.7.
I(t) and V(t) simulations
For simulating the scattering behavior of size distributed vesicles, we used the number distribution determined by dynamic light scattering and fitted the resulting cumulative function by the cumulative density function of the Weibull distribution (eqn (8)). The determined Weibull parameters were then used to weight I(r,t) with the Weibull probability density function (eqn (7)) of r. Subsequent integration over r ranging from 1 nm to 1000 nm results in the total scattering intensity signal of the vesicle suspension. The time dependent volume change after applying a hyperosmotic gradient is simulated according to eqn (2). The relationship between vesicle volume V(t) and scattering intensity I(t) can be described by the Rayleigh–Gans–Debye relation:19| | 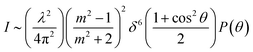 | (12) |
where λ, θ, m, δ, P(θ) are the effective wavelength (i.e. the ratio of λ0 (=546 nm in our experiments) and the refractive index ns of the surrounding aqueous solution, the angle (here 90°) at which the intensity I of scattered light was measured, the relative refractive index (m = np/ns, where np is the average refractive index of the particle), the size parameter, and the form-factor, respectively. δ is defined as δ = 2πR/λ, where R is the vesicle radius. The form factor for optically homogeneous vesicles (homogeneous sphere model) may be expressed via P(θ) = (3(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u − u
u − u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u)/u3)2 whereas P(θ) used for the hollow sphere model (see Fig. S3†) is
u)/u3)2 whereas P(θ) used for the hollow sphere model (see Fig. S3†) is 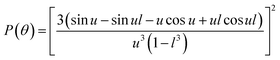 .62,63 In both cases, u = 2δ
.62,63 In both cases, u = 2δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2). Throughout this paper, except explicitly mentioned, we used the homogeneous sphere model for simulations and fits.
sin(θ/2). Throughout this paper, except explicitly mentioned, we used the homogeneous sphere model for simulations and fits.
The average refractive index np of a particle can be expressed, according to the sum rule of polarizability, from the following equation63
| | 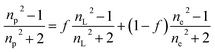 | (13) |
where
nL,
ne and
f are the refractive indices of the lipid (
nL = 1.497)
62 and the intravesicular solution and the fraction of the lipids per vesicle, which can be expressed as a function of
R0,
R, and
h, the initial vesicle radius, the radius of the osmotically shrunken vesicles and the thickness of the lipid bilayer as
| | 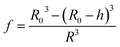 | (14) |
Thus, with eqn (13), we obtain for the average refractive index of a particle
| | 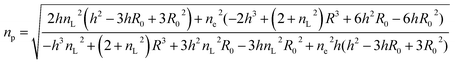 | (15) |
Vesicle shrinkage leads to an increase in internal electrolyte concentration (Fig. 4):
| | 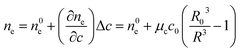 | (16) |
where
n0e,
μc and
c0 are the initial refractive index, the concentration coefficient for the refractive index and the initial solute concentration.
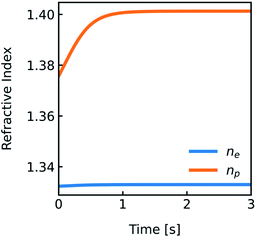 |
| | Fig. 4 Development of the refractive indices ne and np over time. Simulation conditions are described in Fig. 2. | |
The temperature dependence of the refractive indices ne and ns is taking into account with:
| | 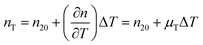 | (17) |
where
nT,
n20 and
μT = −1.2 × 10
−4 K
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64
64 are the refractive index at temperature
T, the refractive index at 20 °C and the temperature coefficient for the refractive indices, respectively.
3. Results
It is our aim to extensively examine various methodological aspects of water permeability estimation using stopped-flow spectroscopy. This should on the one hand foster the understanding of methodological peculiarities and on the other hand serve as a reference study regarding the choice and interpretation of measurement conditions and data. Therefore, we first consider scattering and self-quenching relevant details before we for the first time thoroughly assess the effect of vesicles-size-distributions, MP-distributions between PLs and the choice of osmotic measurement conditions on Pf. Finally, we use a showcase experiment demonstrating the effect of rest detergent in lipid vesicles after MP reconstitution on the scattering and self-quenching approach to measure Pf values with stopped-flow.
3.1. Scattering
3.1.1. Relation: I(t)–V(t).
As comprehensively explained in the Material and methods section “I(t) and V(t) simulations” light scattering at lipid vesicles with a size well below the optical resolution limit can be described by the RGD theory. However, these scattering intensities I(t) are only an indirect measure of vesicle volume V(t). Hence, for Pf calculations it is critical to relate V(t) to I(t). In the past this was done using a second-degree polynomial function19 and empirical approximations ranging from double logarithmic,65 over quadratic66 to simple linear relations.67 As this point of signal translation is always a point of confusion, we directly compare the differences in Pf for a second-degree polynomial function,| | | I(t) = a + bV(t) + dV2(t) | (18) |
which should be the most accurate approximation as scattered light intensities exhibit an inflection point on R,19 with a linear relation,which is the simplest approximation. The latter is commonly used together with exponential fits to the scattering data. To be able to attribute differences of both approaches on Pf we simulated I(t) for a common vesicle ensemble, related it to V(t) by both approaches and then fitted V(t) with the analytical solution (eqn (5)) and an exponential fit. Further, we used the time constant τ of the exponential fit to calculate Pfvia the most accurate approximation depicted in eqn (6). Fig. 5 illustrates that all four approaches nicely fit the simulated data with only minor deviations (<10%). Solely, estimation of Pf with an exponential fit using a 2nd order Taylor approximation leads to an error of 30% in our case (Table S1†).
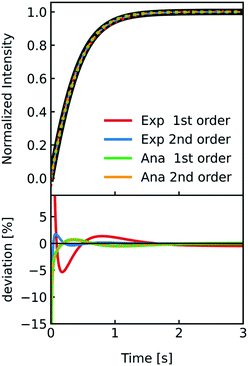 |
| | Fig. 5 Comparison of methods relating V(t) and I(t). Stopped-flow simulation of osmotic shrinkage of liposomes with Weibull distributed radii and a water permeability Pf = 6.0 μm s−1 (black curve). For the simulation, standard conditions described in Fig. 2 have been used. The simulated scattering curve was fitted with an exponential using a I(t)–V(t) relationship described by a 1st (red) and 2nd order (blue) Taylor approximation and with the analytical solution using again the 1st (green) and 2nd order (orange) Taylor approximation. The deviation of the different fitting routines to the simulated scattering curve is depicted below. With the right choice of constraints concerning the signs of the fit parameters (negative b and positive d in eqn (18)), the implementation of the 2nd order Taylor approximation leads to virtually the same results as with using the 1st order Taylor approximation for fitting with the analytical solution, whereas for the exponential fit, the 1st order Taylor approximation is the best choice (see the corresponding Pf values in table S1†). | |
3.1.2. Excitation wavelength.
According to the RGD relation (eqn (12)) scattering intensities depend on the experimentally used excitation wavelength. Furthermore, a variety of excitation wavelengths in the range of 450 nm,68 500 nm,69 546 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 to 600 nm
19 to 600 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 were exploited for scattering experiments in literature. To visualize the effect of λex on the experiment and to guide the rational selection of λex, we simulated and measured I(t) at different λex. From eqn (12) the relation of I(t) on λex is not directly obvious as λex is not only hidden in δ but also in P(θ). Generally, the RGD theory is applicable in the visible light range if the conditions |m − 1| ≪ 1 and kd|m − 1| ≪ 1 with k = 2π/λ and d the vesicle diameter are fulfilled.70 Simulation of scattering data at different wavelengths ranging from 346 nm to 846 nm reveal an increasing relative signal amplitude with smaller wavelength (Fig. 6A). Next, we chose the three main intensity peaks in our XeHg light source to verify that a similar dependence can also be seen experimentally (Fig. 6B). The discrepancies in the relative signal amplitudes between in vitro and in silico data may arise from the wavelength dependence of the refractive indices, which have not been taken into account with our simulations. Another source of error quantifying the relative amplitude change of experimental data is the background correction, where the scattering intensity signal of the background, which is determined by measuring the scattered light intensity of the mixture of buffer without vesicles and osmolyte buffer, is subtracted before normalization. Small errors in the determination of the background signal may have, due to normalization, a high impact on the relative amplitude change. Nevertheless, the kinetic and thus the Pf values are not affected by the height of the relative amplitude. Fitting the data with the analytical solution illustrates that Pf is within the error of the measurement as expected and with these experimental conditions Pf is independent of the wavelength used (Fig. S4 and Table S2†).
33 were exploited for scattering experiments in literature. To visualize the effect of λex on the experiment and to guide the rational selection of λex, we simulated and measured I(t) at different λex. From eqn (12) the relation of I(t) on λex is not directly obvious as λex is not only hidden in δ but also in P(θ). Generally, the RGD theory is applicable in the visible light range if the conditions |m − 1| ≪ 1 and kd|m − 1| ≪ 1 with k = 2π/λ and d the vesicle diameter are fulfilled.70 Simulation of scattering data at different wavelengths ranging from 346 nm to 846 nm reveal an increasing relative signal amplitude with smaller wavelength (Fig. 6A). Next, we chose the three main intensity peaks in our XeHg light source to verify that a similar dependence can also be seen experimentally (Fig. 6B). The discrepancies in the relative signal amplitudes between in vitro and in silico data may arise from the wavelength dependence of the refractive indices, which have not been taken into account with our simulations. Another source of error quantifying the relative amplitude change of experimental data is the background correction, where the scattering intensity signal of the background, which is determined by measuring the scattered light intensity of the mixture of buffer without vesicles and osmolyte buffer, is subtracted before normalization. Small errors in the determination of the background signal may have, due to normalization, a high impact on the relative amplitude change. Nevertheless, the kinetic and thus the Pf values are not affected by the height of the relative amplitude. Fitting the data with the analytical solution illustrates that Pf is within the error of the measurement as expected and with these experimental conditions Pf is independent of the wavelength used (Fig. S4 and Table S2†).
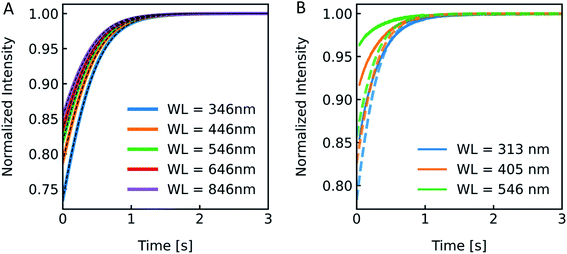 |
| | Fig. 6 Excitation wavelength influences I(t). (A) Normalized scattered light intensity upon exposure to a hyperosmotic gradient for different wavelengths WL of the illuminating monochromatic light. (B) Simulated (dashed lines) and experimental scattering data (solid lines) for different wavelengths. | |
3.1.3. Choice of osmolyte.
Different osmolytes are being exploited for measuring water permeabilities with stopped-flow. Common osmolytes include sucrose, urea, glucose and various salts to name a few. The most obvious impact of the osmolyte on the experiment is the permeability of (i) the lipid or polymer matrix or (ii) the protein itself to the osmolyte of choice. While in the first case the osmotic gradient diminishes with time, which effects Pf only indirectly, in the latter case, the osmolyte also directly impacts the water flux through the channel. Depending on the ratio of solute permeability Ps to Pf, the solute blocks or slows down the passage of water through the channel. This slow down or inhibition of Pf was shown for example for K+ in the bacterial potassium channel KcsA2 and glucose in the human sodium glucose cotransporter hSGLT1.1 However, this effect can also be exploited to measure the equilibrium dissociation constant of the osmolyte to the respective channel.2 In addition, the osmolyte influences scattering measurements due to their sensitivity to the refractive index of the particle. This increase in inner osmolarity during vesicle shrinkage increases the vesicle's refractive index, further elevating their light scattering ability. At the same time, the reduced vesicle size, counteracts this effect by diminishing its scattering ability. Fig. 7 illustrates the influence of the refractive index of the osmolyte on I(t). To increase the relative signal amplitude, it is necessary to minimize the refractive index of the vesicle np which minimizes the refractive index difference between the vesicle and the surrounding np/ns.
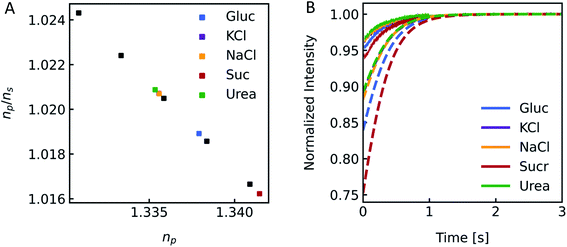 |
| | Fig. 7 Impact of the osmolyte on the refractive index and I(t). (A) Ratio of the refractive indices of vesicles np to bulk buffer ns, with 100 mM NaCl in – and outside and additional 150 mM of glucose (blue), potassium chloride (purple), sodium chloride (orange), sucrose (red) and urea (green) outside of the vesicles. (B) Simulated (dashed lines) and experimental (solid lines) scattering traces for the different osmolytes using standard conditions (see Fig. 2). | |
3.1.4. Membrane thickness.
Polymer membranes forming LPSs may be several times thicker than lipid membranes. Whereas lipid bilayers of biological membranes exhibit a membrane thickness d in the range of 3–4 nm,41,71 polymer membranes range from 5–21 nm.72,73 To illustrate the effect of such an increased d on I(t) we simulated scattering intensities for a variety of d values. As it can be seen in Fig. 8, the relative amplitudes increase with lower d values, but with the absolute values of I(t) increasing at thicker membranes. This can be rationalized by the fact that the lipid/polymer contribution to nparticle always exceeds that of the inner vesicle solution. As summarized in Table S3,†Pf and its deviation from the simulated values increase with increasing d.
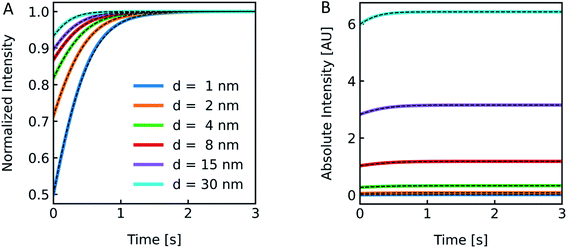 |
| | Fig. 8 Effect of membrane thickness on I(t). Normalized (A) and absolute (B) scattered light intensity of lipid vesicles upon exposure to a hyperosmotic gradient for different values of membrane thickness ranging from 1 nm (blue), 2 nm (orange), 4 nm (green), 8 nm (red), 15 nm (purple) to 30 nm (cyan). The corresponding Pf values from analytical fits to the simulated data (black dashed lines) are depicted in Table S3.† As we are only interested in qualitative comparison between different membrane thicknesses, we used a similar refractive index for the refractive index of the polymer as compared to the lipid throughout the manuscript. | |
3.1.5. Vesicle shape.
Both, the form factor P(θ) used in the RGD theory as well as the change in vesicle volume upon application of a hyperosmotic gradient (eqn (2) and (4)) assume a spherical vesicle shape. However, vesicles prepared by extrusion can exhibit shapes, such as prolate and oblate ellipsoids74 and subjection to a hyperosmotic gradient leads to a volume decrease of the vesicles by a factor of cout/cin,0. Hence, as the surface area of a lipid vesicle is assumed to stay invariant during shrinkage, vesicle shape deviates more and more from a spherical shape during shrinkage at larger hyperosmotic gradients. Still, Pf was found to be invariant in scattering experiments under hyperosmotic conditions.18 Furthermore, we simulated scattering signals for hyperosmotic shrinkage with increasing ellipticity (Fig. S5†) according to the form factor for prolate and oblate vesicles.74 These simulations clearly showed that despite an increased absolute scattering intensity at higher ellipticity the effect of vesicle deformation on the overall shape of the scattering trace (Fig. S5A†) and Pf can be neglected. Therefore, we can conclude that the vesicle shape has a marginal influence on I(t).
3.2. Self-quenching
Fluorescence self-quenching experiments assume a linear relation between V(t) and the fluorescence signal F(t). Even though the absolute number of fluorophores stays constant during vesicle shrinkage, the concentration inside the vesicles increases. This leads to a decreased average distance between the fluorophores, increasing fluorescence self-quenching and therefore reducing the overall signal intensity. Generally, F(t) of a single fluorophore due to self-quenching for a given concentration is described by the Stern–Volmer relationship| | 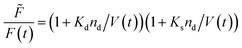 | (20) |
where ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) , Kd, Ks = 412 M−1,75nd and V are the fluorescent intensity in absence of quencher, the Stern–Volmer constant for dynamic quenching, the Stern–Volmer constant for static quenching, the amount of fluorescent molecules in mole and the volume of the vesicles, respectively. As dynamic or collisional self-quenching of CF in liposomes can be neglected,75eqn (20) reduces to
, Kd, Ks = 412 M−1,75nd and V are the fluorescent intensity in absence of quencher, the Stern–Volmer constant for dynamic quenching, the Stern–Volmer constant for static quenching, the amount of fluorescent molecules in mole and the volume of the vesicles, respectively. As dynamic or collisional self-quenching of CF in liposomes can be neglected,75eqn (20) reduces to| | 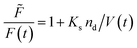 | (21) |
Thereby, the relative fluorescence signal Frel for a given [fluorophore] is (Fig. S6†)
| | 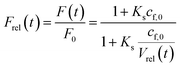 | (22) |
with
F0,
F(
t),
cf,0 and
Vrel(
t), the initial fluorescence intensity, the fluorescence intensity at time
t, the initial concentration of fluorescent molecules encapsulated in the vesicles and the relative volume
Vrel(
t) =
V(
t)/
V0, which is the quotient of the vesicle volume at time
t and the initial volume, respectively.
Fig. 9A visualizes this dependence of
Frel on different
cf,0 for five
Vrel. It can be seen that
Frel approaches a stable value linearly proportional to
Vrel at higher
cf,0. To further illustrate that this linear relation between
V(
t) and
F(
t) does not hold for low
cf,0 we plotted
Frel over
Vrel.
Fig. 9B demonstrates that the linear relation holds for
cf,0 > 10 mM with the olive curve exhibiting perfect proportionality between quenching signal and volume change. Nevertheless, smaller
cf,0 can be used to estimate
Pf values with errors <25% (inset
Fig. 9B). A similar dependence of
Pf on
cf,0 was found experimentally using DPhPC (4ME 16:0 PC, 1,2-diphytanoyl-
sn-glycero-3-phosphatidylcholine) vesicles (
Fig. 9C). The error that results from the non-linear dependence for low initial fluorophore concentration has been calculated with
| | 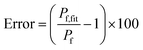 | (23) |
where
Pf and
Pf,fit are the osmotic water permeability of the simulation (shown in Fig. S6
†) and the permeability value of the corresponding analytical fit.
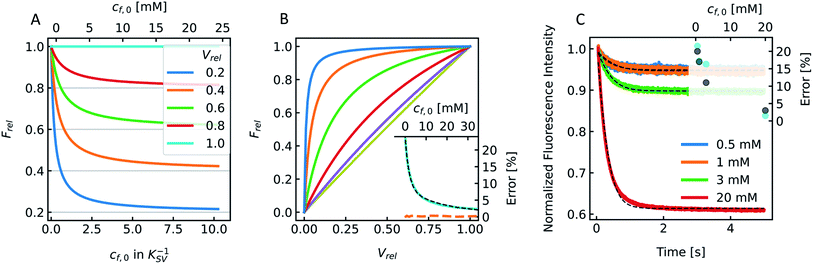 |
| | Fig. 9 Stern–Volmer relationship. (A) Relative fluorescence of a single fluorophore Frel over initial fluorophore concentration cf,0 in units KSV−1 and in mM for several values of the total relative volume change Vrel starting from 1 (cyan, no shrinkage) up to 0.2 (blue), where the final volume is 20% of the initial one. (B) Frel plotted over Vrel for 0.025 mM (blue), 0.1 mM (orange), 0.5 mM (green), 2 mM (red), 9 mM (violet) and 40 mM (olive) initial fluorophore concentration. The error in Pf (cyan) that results from the non-linear dependence of Frel on Vrel for low cf,0 is shown in the inset (osmotic shrinkage scattering curves depicted in Fig. S6† have been fitted with eqn (11) and the resulting Pf values have been used to calculate the error according to eqn (23)). The concentration dependent error has been fitted with a two-component exponential function (black dashed line) and the results have been used to correct the Pf values according to eqn (S2).† The deviation of the corrected Pf values to the simulated ones is shown in the inset (orange dashed line). (C) Measured hyperosmotic self-quenching curves for different concentrations of CF starting from 0.5 mM to 20 mM. The error in Pf compared to scattering measurements of the same samples is shown as cyan dots in the inset, whereas the grey dots represent the simulated values. | |
3.3. General methodological peculiarities
3.3.1. Hyper- or hypoosmotic conditions.
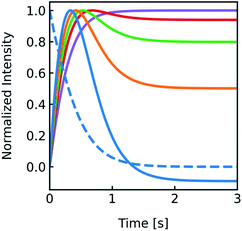
During the application of osmotic gradients to lipid- or polymer-based vesicles it is important to ensure that the integrity of the lipid or polymer membrane is guaranteed. This is the case under hyperosmotic conditions (vesicle shrinkage), but care must be taken under hypoosmotic conditions. As compared to hyperosmotic gradients, hypoosmotic gradients lead to vesicle swelling. However, lipid bilayers can only be stretched by a few percent before rupturing.76 From Fig. S7† it is obvious that at hypoosmotic conditions the protein concentration dependent kinetics get lost and the estimated Pf values deviate strongly from Pf values calculated from hyperosmotic data. The measured self-quenching data under hypoosmotic conditions can be explained by the outflow of fluorescent molecules during membrane rupture, which due to a decrease in [fluorophore] in the vesicle interior leads to a further reduction of fluorescent self-quenching additionally to its decrease caused by vesicle swelling. Even though the vesicle size hardly changes after application of a hypoosmotic gradient, scattering signals show a pronounced kinetic as during vesicle rupture the outflux of solute and solvent is accompanied by a change in the refractive index of the vesicle. As previously described, this decrease in np results in a change in I(t) like the one observed here. To corroborate our argumentation, we performed FCS experiments of CF filled LUVs which we subjected to varying hypoosmotic gradients. Fig. 10 shows quite plainly that membrane rupture takes place above a volume increase of 3.2% for PLE LUVs. Hence, vesicle rupture after subjection of LUVs to hypoosmotic conditions takes place, confirming that hypoosmotic measurement conditions cannot be chosen to estimate membrane permeability Pf without acknowledging membrane mechanics.
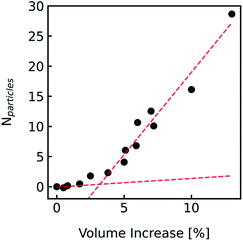 |
| | Fig. 10 Visualization of the lost membrane integrity during vesicle swelling with FCS. Vesicles loaded with 0.5 mM CF, 100 mM NaCl, 10 mM MES, pH 7.0, were exposed to hypoosmotic buffer, which was the same buffer without addition of dye and slightly diluted with Millipore water. The measured buffer osmolarities were used to calculate the total volume change. Free dye, which leaked out due to defects in the lipid membrane during swelling, was separated from the liposomes by running a PD-10 column. With FCS the number Nparticles of free CF molecules within the confocal volume was analyzed and plotted against the corresponding calculated total volume increase. Linear fits (red dashed lines) of the measured points below 2% and above 5% volume increase show a point of interception of 3.2%. | |
3.3.2. Vesicle size distribution.
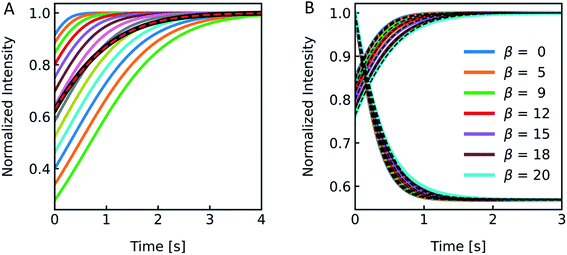
The production of LUVs and LPSs or the reconstitution of MPs into PLs or LPSs never leads to a vesicle ensemble with a unique diameter. Instead, MP reconstitution and extrusion through 100 nm polycarbonate filters lead to a unimodal vesicle distribution with its width depending on the lipid composition and eventual residual detergent after reconstitution.77 We investigated the effect of the broadness of such a vesicle size distribution on Pf using simulated I(t) and F(t) data. First we simulated a family of scattering (Fig. S8†) and self-quenching (Fig. 11A) curves with varying r0, calculated their superimposed signal (black line) and fitted it with the analytical fit (red line). A comparison of the simulated value to the fit result calculated for the average diameter revealed an error in Pf of approx. 30% compared to an error of 4% for the self-quenching counterpart.
 |
| | Fig. 11 Effect of vesicle size distribution on Pf. (A) Family of scattering curves and their average (black solid line) after exposure to a 150 mosm sucrose gradient. The initial equally populated radii of the vesicles were simulated in 10 nm steps ranging from 30 nm (blue) to 150 nm (green). With the intensity weighted (eqn (S1)†) average radius RINT = 135.3 nm, the error in Pf between simulation and analytical fit was ∼5%. (B) Difference in scattering I(t) (raising curves) and self-quenching F(t) (falling curves) of largely varying scale parameters β of Weibull distributed vesicle size distributions. While the shape parameter a was set to 1.35, the location parameter γ was adjusted to achieve an expectation value for the number-weighted radius of 43.7 nm. The conversion of number to intensity distribution was done according to eqn (S3)† and the resulting distribution was fitted with a Weibull distribution function (eqn (7)) to obtain the intensity-weighted radii RINT (see Fig. S9†). All other simulation conditions are described in Fig. 2. | |
After this rather theoretical consideration where each individual radius had an equal probability of occurrence in the vesicle population, we simulated I(t) and F(t) (Fig. 11B) with implemented Weibull distributions (Fig. 3A). The family of curves with largely different size distributions (β = 0 to 20, 0 is equal to a single radius) revealed that the overall shape looks similar, but the time dependence of the respective signals seem slower (Fig. S9†) for broader distributions (larger β) and the relative amplitude I(t) increases as well. An analytical fit to the data (black dashed line) showed that the error in Pf for both scattering and self-quenching experiments is <12% (Fig. S9†). Thereby the chosen values in β cover our experimental range of AQP PLs, (poly(butadiene)–poly(ethylene oxide) (PBD–PEO)) LPSs, OSPC liposomes, PLE liposomes and PLE liposomes with detergent (OG, DM) which varied between 9 < β < 14.5 and 1.07 < α < 1.4. Similarly, the error in estimating Pf values from simulated data varying the shape parameter α over a reasonable range is < 18% (Fig. S10†).
3.3.3. Permeability distribution.
Reconstitution of MPs into PLs results in a Poisson distribution of the number of oligomers per PLs.19 Similar distributions can be assumed for artificial channels or channel forming peptides as gramicidin. To see if the distribution of Pf values in the PL fraction has a similar marginal effect on Pf as it is the case for the size distribution shown in the previous chapter, we again simulated I(t) and F(t) stopped-flow data to investigate this experimentally scarcely addressable problem. A family of simulated I(t) curves, representing a typical reconstitution series with a bare lipid vesicle fraction of 20% (xl = 0.2) and a varying average number of MPs per PL, Nmean, between 1 and 20 is shown in Fig. 12A. Three corresponding Poisson distributions (color coded) in Fig. 12B exemplify the probability of different N's on the respective Nmean. To estimate the effect of different xl and Nmean on Pf we calculated the relative error in percent from the simulated Pf (Fig. 12C) by performing an analytical fit (dash-dotted lines), where the water permeability of liposomes, which do not contain channels, Pm, is fixed, a global analytical fit (eqn (5)) (solid lines) or an exponential fit with two components where either one time constant is fixed (dashed lines) to the respective time constant of bare lipid vesicles or both time constants are free (dotted lines) and using eqn (6) to calculate Pf. Similarly, a simulated family of F(t) curves and its error on Nmean is depicted in Fig. S11.† These simulations show that for an error in Pf below 20%, stopped-flow data should be fitted with one component fixed to the bare lipid vesicle value or a global fit, Nmean should be ≥5, and xl ≤ 0.5. At high xl and small Nmean the error in Pf may reach 100% or more in the worst case.
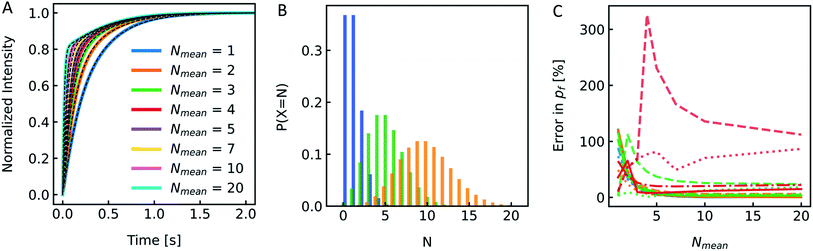 |
| | Fig. 12 Effect of MP distribution on Pf. (A) Normalized scattered light plot of osmotic vesicle shrinkage for PLs of different Nmean. The fraction of vesicles which do not contain protein xl = 0.2. For the single channel water permeability, the published value of AQP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 with pf = 3.25 × 10−13 cm3 s−1 has been taken. (B) Poisson distribution with an average number of monomers per PL Nmean of 1 (blue), 5 (green) and 10 (orange). The probability of a PL containing N numbers of monomers of the reconstituted protein is plotted over N. (C) Error in Pf depending on Nmean for xl = 0.0 (blue), xl = 0.2 (orange), xl = 0.5 (green) and xl = 0.8 (red). Dotted, dashed, dashdotted and solid lines represent the error for a two-component exponential fit with free components, a two-component exponential fit, where one component is fixed to the rate constant of liposomes containing no protein, an analytical fit and a global analytical fit, respectively. The global fit determines Pm as the average slow component (and one component for the control only) of all curves. 19 with pf = 3.25 × 10−13 cm3 s−1 has been taken. (B) Poisson distribution with an average number of monomers per PL Nmean of 1 (blue), 5 (green) and 10 (orange). The probability of a PL containing N numbers of monomers of the reconstituted protein is plotted over N. (C) Error in Pf depending on Nmean for xl = 0.0 (blue), xl = 0.2 (orange), xl = 0.5 (green) and xl = 0.8 (red). Dotted, dashed, dashdotted and solid lines represent the error for a two-component exponential fit with free components, a two-component exponential fit, where one component is fixed to the rate constant of liposomes containing no protein, an analytical fit and a global analytical fit, respectively. The global fit determines Pm as the average slow component (and one component for the control only) of all curves. | |
3.3.4. Fitting routine – global versus single.
The intensity signal of a vesicle ensemble after MP reconstitution subjected to a hyperosmotic gradient usually exhibits two components. As can be seen from eqn (1) the fast component Pf represents the overall water flux through the membrane of protein containing vesicles and Pm corresponding to the water transport through the fraction of empty vesicles not containing any channels. Both components must be considered by the fitting routines. As it can be seen by the example in the previous paragraph, despite the desire to optimize the reconstitution efficiency to minimize errors, the type of fitting routine is very important. It is advisable to use fitting routines were Pm can be fixed in control experiments with pure lipid vesicles or use global fits including a control sample as well as several PLs with different amounts of MPs which can be fitted by one global Pm and different Pfs (global fit). We advise to use the latter as MP concentration dependent measurements ensure the highest reliability compared to results from one-point measurements.
3.4. Example show-case: residual detergent after membrane protein reconstitution
To show the differences as well as the strength and weaknesses of both approaches, we oppose them in an exemplary case face-to-face. To be able to calculate pf values of MPs or artificial water channels, it is inevitable to reconstitute them into lipid- or polymer-based membranes. Especially in the case of MPs, this usually involves the use of detergents to mimic the lipid bilayer and avoid aggregation of MPs in solution. However, after detergent removal and PL formation it is hard to estimate if residual detergent remains in the sample and if so what the influence on the calculated pf is. To explore a potential effect of residual detergent on pf, we mixed different amounts of octyl-glucoside (OG) to the lipid mixture either in chloroform before evaporation (measurements shown in Fig. S13†), or in hydration buffer after evaporation (measurements shown in Fig. 13 and S12†). Note that the stated amount of detergent corresponds to the % (w/v) of OG in chloroform or in buffers used for hydration or PD-10. The final amount of detergent within the membrane is not known, as not all OG molecules have been incorporated into the lipid bilayer (see Fig. 14). After vesicle preparation the different preparations were subjected to a hyperosmotic sucrose gradient. Fig. 13A and S12† illustrate that scattering signals show a pronounced second kinetic which is elevated at higher temperatures and higher OG concentrations compared to inconspicuous F(t) data. Interestingly, even though both data sets were fitted with a two-component model to extract the first relevant time constant τ for Pf estimation also the seemingly unaltered F(t) data revealed a similar error in Pf (triangles) as calculations from the scattering intensity I(t) data (spheres) (Fig. 13A inset). Furthermore, scattering experiments with various osmolytes revealed similar OG concentration dependent secondary kinetics (Fig. S13†) as well as errors in Pf (Table S4,†Fig. 13B). To elucidate why the error in Pf suddenly drops further increasing the detergent concentration to 0.3% we looked into the corresponding intensity and number distribution (Fig. S14†). Both distributions illustrate that an increased OG concentration has an impact on the size distribution of the vesicles. This is evident for the sample with 0.3% OG. The number of small vesicles increases drastically and the deviation of the distribution from a Gaussian increases (red curve in Fig. S14†), which might bias the size determination and thus the corresponding results for Pf.53
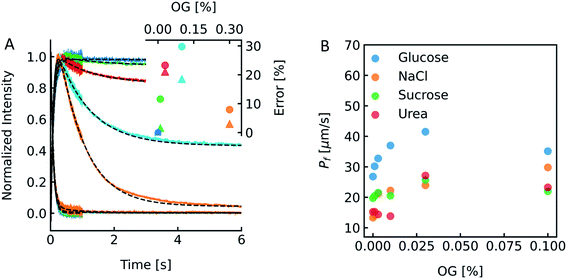 |
| | Fig. 13 Detergent effects on scattering and self-quenching data. (A) Exemplary ensemble scattering and self-quenching traces for vesicles doped with different amounts of detergent at 24 °C. Insets: error (in %) in Pf for different detergent concentrations compared to the permeability coefficient of liposomes without detergent (dark blue) in scattering (spheres) and self-quenching (triangles) experiments. For each sample, 10 mg PLE was used with 1 mL of buffer containing 10 mM CF, 100 mM NaCl and 10 mM MOPS at pH 7.4 and the OG concentration was 0% (blue curve), 0.01% (green), 0.03% (red), 0.1% (cyan) and 0.3% (orange), respectively. (B) Dependence of membrane water permeabilities on the OG concentration. Water permeabilities were calculated from two-components exponential fits (shown in Fig. S13†). | |
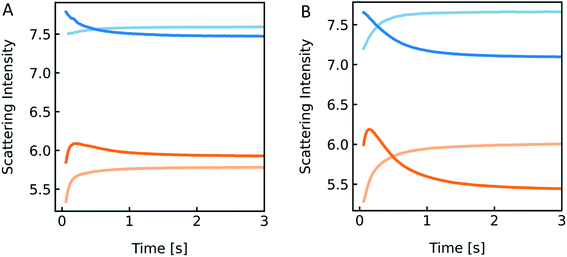 |
| | Fig. 14 Detergent effect on scattering curves. Stopped-flow measurements of PLE liposomes (with 100 mM NaCl and 10 mM MOPS) exposed to the inside buffer (100 mM NaCl, 10 mM MOPS) (blue) and hyperosmotic buffer containing 100 mM NaCl, 10 mM MOPS and 150 mM sucrose (orange), with 0.03% OG (A) and 0.3% OG (B) only inside (dark colored) and in- and outside (light-colored) of the vesicles, respectively. | |
However, the perfect plateau in self-quenching experiments suggests that the reason for the second kinetic in the scattering experiments is not an OG induced enhanced solute permeability through the lipid bilayer. Alternatively, it is known that removal of OG from the lipid bilayer after subjection to detergent-free buffer is highly temperature dependent.78 To see if our effects were indeed due to detergent extraction from the lipid vesicles, changing the membrane area during shrinkage, we mixed lipid vesicles at two different detergent concentrations with an equal buffer or a hyperosmotic buffer, with and without detergent each (Fig. 14). Most interestingly, both samples showed a pronounced kinetic even in the isosmotic case. The decreasing signals in the dark colored curves correspond to the loss of detergent molecules upon exposure of detergent-free buffer. This effect as well as the second kinetic in hyperosmotic experiments could be reversed by the addition of detergent in the mixing solution. The concentration of OG outside the vesicles is higher for the light-colored curves, as most of the detergent inside the liposomes is supposed to be integrated in the lipid membrane. Hence, the incorporated detergent molecules increase the lipid fraction, the refractive index of the particle and therefore the intensity signal. The light orange curve represents an overlay of shrinkage and detergent incorporation, which results in the largest relative amplitude change. While the relative amplitude change within the dead time can be neglected, the final scattering intensity signal for the dark orange curve in Fig. 14B is even lower as compared to the initial signal at t = 0 seconds. Osmolyte influx cannot, under any circumstances, describe this effect, as the final total osmolarity after back-swelling to the initial volume would be equal to the osmolarity of the hyperosmotic buffer. The final refractive index of the particle is dependent on the final refractive indices of the lipid, which is, after back-swelling, the same as initially, and the inside solution, which is higher, due to higher concentrations. Conclusively, the final scattering intensity must be higher than the initial intensity, if there is no loss in lipid or detergent molecules.
To further proof that the second kinetic in the scattering traces is due to detergent extraction after subjection to a hyperosmotic detergent free solution, we simulated the effect that upon mixing OG containing vesicles with buffer lacking OG, detergent molecules leave the lipid membrane. As the influence of single detergent molecules on the total scattering intensity signal is negligible, we only take the reduction of the lipid (and detergent) fraction into consideration:
| | 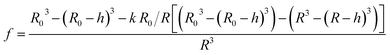 | (24) |
where the expression in the brackets is referring to the difference in lipid fraction of the initial volume and the shrunken vesicle. The prefactor
k is the fraction of the time dependent ratio
R0/
R. The results summarized in
Fig. 15 illustrate that it is indeed possible to reproduce the second kinetic seen in scattering experiments where we exposed OG containing vesicles to a hyperosmotic gradient with reduced [OG].
 |
| | Fig. 15 Hyperosmotic shrinkage simulations with a loss of detergent molecules. Simulations for different values of the prefactor k in eqn (24) starting from 0.20 (purple) to 0.21 (red), 0.215 (green), 0.22 (orange) and 0.225 (blue) are shown in scattering (solid lines) and self-quenching mode (dashed lines), whereas for the latter, the curves are perfectly overlaying. | |
4. Discussion
4.1. Hyper-/hypoosmotic conditions
LUVs or GUVs are perfect osmosensors. This osmotic sensitivity is lost in the case of very small vesicles obtained by extensive sonication.79 Hereby, the osmotic pressure seems not enough to overcome the tension in the highly curved phospholipid bilayer. The lower size limit of such vesicles is envisioned to depend on the phospholipid composition of the bilayer and is approximately 10 nm in radius for synthetic phosphatidylcholines with varying chain lengths.80 For larger vesicles hypoosmotic gradients cause vesicle swelling which results in processes strongly determined by vesicle rupture and content efflux. There is no physical basis to fit scattering or self-quenching data at hypoosmotic conditions with equations as described in this paper. Published differences in Pf between hyper- and hypoosmotic conditions23 can solely be explained by the improper measurement conditions and data evaluation procedure. Our experiments with PLE vesicles at room temperature show that the membrane integrity is lost above 3.2% volume increase or 2.1% area expansion. This is in reasonable agreement to an average maximum increase in vesicle volume until the membrane ruptures of about 8%81 or 5%76 for 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and lecithin GUVs, respectively. Fig. 16 illustrates that, in contrast to hyperosmotic conditions where V(t) decreases with time (black solid line), the vesicle undergoes multiple swelling–burst cycles under hypoosmotic conditions (red solid line). Such swelling–burst cycles could be directly visualized for GUVs,81 however at longer time scales due to their larger vesicle volume compared to LUVs.
 |
| | Fig. 16 Normalized vesicle volume after subjection to a hyper- or hypoosmotic solution. The red line illustrates that during each swelling–burst cycle the vesicle volume increases until the maximum sustainable strain is reached. Further influx of water leads to rupture of the membrane, an outflux of water and solute, vesicle shrinkage and membrane recovery, which is illustrated by the falling flank of this saw tooth like part of the signal. The swelling–burst cycle repeats until the final plateau is reached beyond the maximum volume change. | |
Clearly, these swelling–burst cycles cannot be directly visualized for LUVs in ensemble measurements. On average, they lead to scattering and self-quenching signals which on the first glance look like meaningful measurements under hyperosmotic conditions, but with inverted sign (Fig. S7†). However, at a second glance it is obvious that these kinetics do not represent the kinetics of water flux through the membrane barrier, but are limited by several unrelated parameters including the exact physical properties of the membrane that determine the exact rupture point after vesicle area expansion and the healing time as well as the buffer exchange between the vesicle interior and exterior during vesicle rupture. However, the fluorophore release assay82 performed in Fig. 10, as indication for membrane leakage, can be used to identify the maximum area expansion (2.1% for PLE) of such membranes before rupture. Moreover, this assay is suitable to study the process of membrane healing in more detail in the future. It is important to note that the accuracy of membrane expansion measurements is much higher with the micropipette pressurization method which also allows to verify elastic reversibility.83
4.2. Influence of the fluorophore concentration in self-quenching experiments on Pf
The pH dependent fluorescence properties of CF, a dye typically used for self-quenching experiments, are used to relate the changes of F(t) at low [CF] (∼0.5 mM) to proton and weak acid permeabilities.41,84,85 Usually, in such experiments with [CF] in the low mM range the self-quenching properties are neglected.86 However, our results clearly show that depending on the accompanying volume changes it is necessary to consider them also in pH experiments. Additionally, low [CF] can be used to measure both, volume changes for water flux and pH changes for proton and weak acid permeabilities with one batch of PLs. The accompanying error in Pf estimation depending on the fluorophore concentration is moderate (maximal 25%). Nevertheless, with eqn (S1) and (S2)† we herein provide a correction term for the fluorophore concentration used.
4.3. Vesicle size distribution
P
f linearly scales with the error in r0.18 It is justifiable to use the average radius of the unimodal size distributions to accurately calculate Pf values from I(t) and F(t) ensemble stopped-flow data. The average radius can either be recalculated from the scattering distribution from DLS measurements or extracted from FCS measurements. The average hydrodynamic radius accessible with FCS, is most closely related to the average radius of the volume distributions of DLS (see Materials and methods section Vesicle size distribution/average mean diameter for more details). Average radii from FCS cannot be converted to average diameters of the intensity or volume weighted distributions as the volume distribution is not accessible by FCS but only the mean radius. This average radius of the volume weighted distribution is important for the evaluation of self-quenching data. In contrast, for scattering experiments the average radius of the intensity distribution has to be used. There is no wavelength correction for the different wavelengths used in DLS and scattering experiments necessary, since there is hardly any wavelength dependence as exemplified in Fig. S4.† Obviously, these considerations cannot be directly translated to the problem of polydisperse distributions even though the considerations herein might suggest that an average radius might also be a good approximation for such experimental conditions.
4.4. Variability of Pf in a vesicle population
MP reconstitution does not result in a homogeneous distribution of MPs between all PLs, but the optimization of the reconstitution efficiency leads to a fraction of empty vesicles2,87 and a distribution of MPs within the fraction of PLs.19 Hence, I(t) and F(t), resemble a superposition of different Pf values from vesicles with varying amounts of artificial channels, channel forming peptides, or MPs and a fraction of bare lipid vesicles. Whereas, the bare lipid vesicle fractions can be described by a single Pf value, in reality the ensemble of PLs has to be described by a distribution of Pf values, corresponding to the distribution of MPs in the PLs. To estimate the effect of this distribution on Pf values we simulated a realistic reconstitution series of AQP1 in PLE, assuming varying average amounts of Poisson distributed AQP1. The in silico experiments clearly show that the error is neglectable as soon as the distribution of the number of channels in the vesicle ensemble is symmetric. In case the distribution is asymmetric as in the case of Nmean < 5 for a Poisson distribution the error in Pf estimated from an overall fit to the data compared to the Pf used for the simulation approaches 100%. Similarly important is a high fraction of protein containing vesicles as compared to empty vesicles. To keep the ‘empty’ liposome fraction below 0.5 and increase Nmean above 5 it may be necessary to enhance the reconstitution efficiency. Parameters which can be tuned and optimized are the choice of the right detergent, the initial protein to lipid ratio (and concentration), detergent removal (removal speed, temperature) and the buffer composition. The bare lipid vesicle fraction can be determined using FCS to compare the total number of vesicles (vesicles contain labelled lipids, e.g. red labelled) with the ones that contain protein (e.g. protein is labelled with a green fluorophore).1,2,19,20 A similar strategy can be used to accurately quantify protein abundance Nmean.42 Thereby the number of PLs containing labeled protein are compared to the number of individual protein oligomer containing micelles after detergent addition.
4.5. Residual detergent after protein reconstitution
During reconstitution of membrane proteins into lipid vesicles or LPSs membrane proteins are mixed with detergent and the membrane matrix material. To induce vesicle formation detergent is removed either by dialysis,88 addition of BioBeads,89,90 dilution88 or cyclodextrins.91 However, due to variable detergent affinities to BioBeads and proteins and different critical micellar concentrations of detergents, complete removal of used detergents poses a challenge and is hard to detect. We therefore investigated the influence of residual detergent after MP reconstitution on the example of the widely used detergent octyl glucoside (OG). However, we want to emphasize that detergent effects on scattering and self-quenching data in general and on Pf in particular depend on the experimental conditions. The membrane-water partition coefficient of detergent molecules as well as the flip-flop from one monolayer into the other monolayer strongly vary for different detergents and lipids.92 The results show that the presence of OG caused a relative increase in Pf of less than 60–70% depending on the osmolyte used. Therefore, we suggest performing water flux measurements always in a MP concentration dependent manner to reduce the unknown detergent effects in the preparation. Assuming that (i) detergent removal is similar between multiple samples in one preparation and (ii) it is independent on the protein concentration due to the negligible stoichiometry ratio of protein to detergent molecules, a potential detergent effect incurs in the bilayer background permeability from a fit to a Pf over Nmean plot.
Most interestingly, dilution of OG in the measurement cuvette leads to a temperature dependent extraction of OG out of the lipid bilayer into the buffer visible as a second kinetic in the scattering data, which is sensitive to the refractive index of the vesicle defined by the refractive indices and the respective volume fractions of the membrane and the interior. In contrast, application of a hyperosmotic gradient did not influence fluorescence self-quenching experiments as the process of detergent extraction, in turn decreasing the vesicle membrane area does only change the vesicle shape towards a sphere but doesn't affect the volume change which is solely defined by the osmotic gradient. At this stage it remains unclear if the rapid withdrawal of OG from the outer vesicle leaflet creates a mass imbalance between both leaflets resulting in a destabilized inner leaflet forming mixed micellar structures within the inner monolayer or if flip-flop of OG between both monolayers occurs on a similar timescale as the detergent partitioning into the aqueous phase.93 Hence, stopped-flow light scattering experiments are perfectly capable of monitoring detergent removal from lipid- or polymer-based vesicles as well as to proof the presence of detergent remaining in vesicular membrane systems.
5. Conclusion
For most applications, fluorescence self-quenching and light scattering experiments are equally well capable of delivering accurate Pf values if performed correctly. However, fluorescence self-quenching experiments are more robust and less prone to artefacts as they solely depend on the vesicle volume as the sole measurement parameter. Therefore, interference from the lipid or polymer membrane, vesicle shape or deformation and extraction of detergent from lipid vesicles can be neglected. The only drawback is that they involve two more steps during sample preparation; (i) addition of the dye during vesicle formation and (ii) removal of free dye before the experiment. Furthermore, the fluorophore used should not interact with any substance in the experiment that lead to a change in fluorescent properties. Light scattering on the other hand has an additional sensitivity towards refractive index changes, which are temperature, wavelength and concentration dependent. This on the first glance advantages property for solute permeability measurements leads to a reduced sensitivity as the refractive index of the particle is dominated by the refractive index of the membrane matrix and not the interior, which significantly reduces its amplitude compared to pure volume changes.
To ensure accurate Pf estimations it is necessary to calculate the average radius of the relevant vesicle size distribution, ensure a high reconstitution efficiency of MPs into PLs, use the models described herein (either analytical solution or approximation based on an exponential fit), use hyperosmotic measurement conditions, and avoid residual detergent in vesicles. In light scattering experiments lower excitation wavelengths and osmolytes exhibiting a large refractive index compared to the buffer solution maximize the relative signal amplitude. Yet, care has to be taken to ensure the applicability of the RGD relation, which was the case for all in silico and in vitro experiments performed throughout this study. For further estimations of pf, it is inevitable to correlate the stopped-flow data with accurate channel counting. The accuracy of pf estimations increases significantly using reconstitution series with varying amounts of channels in the PLs and using a global fitting routine were the Pf of the bare lipid vesicles fraction is fixed. A linear dependence of Pf on the average number of channels per vesicle will help to dispel any doubts on the significance of pf values which can be directly calculated from the slope of a linear regression to the data points.
Author contributions
A. H. conceived the project. J. W., A. S., T. B and A. E. performed stopped-flow and DLS experiments. T. B. performed FCS experiments. J. W. and A. S. performed simulations. J. W., C. H., A. S., T. B, A. E. and A. H. analyzed in vitro and/or in silico data. J. W. and C. S. expressed, purified and reconstituted AQP1. J. W. and A. H. wrote the manuscript. All authors commented on the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The financial support for this study is from the Austrian Science Fund (P31074) to AH.
References
- L. Erokhova, A. Horner, N. Ollinger, C. Siligan and P. Pohl, The Sodium Glucose Cotransporter SGLT1 Is an Extremely Efficient Facilitator of Passive Water Transport, J. Biol. Chem., 2016, 291(18), 9712 CrossRef CAS.
- T. Hoomann, N. Jahnke, A. Horner, S. Keller and P. Pohl, Filter gate closure inhibits ion but not water transport through potassium channels, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(26), 10842 CrossRef CAS.
- S. Yuan, S. Filipek, K. Palczewski and H. Vogel, Activation of G-protein-coupled receptors correlates with the formation of a continuous internal water pathway, Nat. Commun., 2014, 5(1), 4733 CrossRef CAS PubMed.
- P. Agre, L. S. King, M. Yasui, W. B. Guggino, O. P. Ottersen, Y. Fujiyoshi, A. Engel and S. Nielsen, Aquaporin water channels - from atomic structure to clinical medicine, J. Physiol., 2002, 542(Pt 1), 3 CrossRef CAS.
- S. Nielsen, J. Frokiaer, D. Marples, T. H. Kwon, P. Agre and M. A. Knepper, Aquaporins in the kidney: From molecules to medicine, Physiol. Rev., 2002, 82(1), 205 CrossRef CAS PubMed.
- K. Gupta, J. A. C. Donlan, J. T. S. Hopper, P. Uzdavinys, M. Landreh, W. B. Struwe, D. Drew, A. J. Baldwin, P. J. Stansfeld and C. V. Robinson, The role of interfacial lipids in stabilizing membrane protein oligomers, Nature, 2017, 541, 421 CrossRef CAS PubMed.
- A. Laganowsky, E. Reading, T. M. Allison, M. B. Ulmschneider, M. T. Degiacomi, A. J. Baldwin and C. V. Robinson, Membrane proteins bind lipids selectively to modulate their structure and function, Nature, 2014, 510(7503), 172 CrossRef CAS PubMed.
- D. Marsh, Lateral pressure profile, spontaneous curvature frustration, and the incorporation and conformation of proteins in membranes, Biophys. J., 2007, 93(11), 3884 CrossRef CAS PubMed.
- R. S. Cantor, Lateral pressures in cell membranes: A mechanism for modulation of protein function, J. Phys. Chem. B, 1997, 101(10), 1723 CrossRef CAS.
- E. van den Brink-van der Laan, J. Antoinette Killian and B. de Kruijff, Nonbilayer lipids affect peripheral and integral membrane proteins via changes in the lateral pressure profile, Biochim. Biophys. Acta, 2004, 1666(1), 275 CrossRef CAS PubMed.
- J. Gullingsrud and K. Schulten, Lipid bilayer pressure profiles and mechanosensitive channel gating, Biophys. J., 2004, 86(6), 3496 CrossRef CAS.
- R. S. Cantor, Lipid composition and the lateral pressure profile in bilayers, Biophys. J., 1999, 76(5), 2625 CrossRef CAS.
- D. Marsh, Lateral pressure in membranes, Biochim. Biophys. Acta, 1996, 1286(3), 183 CrossRef CAS.
- A. Anderluh, T. Hofmaier, E. Klotzsch, O. Kudlacek, T. Stockner, H. H. Sitte and G. J. Schutz, Direct PIP2 binding mediates stable oligomer formation of the serotonin transporter, Nat. Commun., 2017, 8, 14089 CrossRef CAS.
- C. Maurel, L. Verdoucq, D. T. Luu and V. Santoni, Plant aquaporins: membrane channels with multiple integrated functions, Annu. Rev. Plant Biol., 2008, 59, 595 CrossRef CAS.
- A. Shekoofa and T. Sinclair, Aquaporin Activity to Improve Crop Drought Tolerance, Cells, 2018, 7(9), 123 CrossRef CAS PubMed.
- S. M. Zargar, P. Nagar, R. Deshmukh, M. Nazir, A. A. Wani, K. Z. Masoodi, G. K. Agrawal and R. Rakwal, Aquaporins as potential drought tolerance inducing proteins: Towards instigating stress tolerance, J. Proteomics, 2017, 169, 233 CrossRef CAS PubMed.
- C. Hannesschlager, T. Barta, C. Siligan and A. Horner, Quantification of Water Flux in Vesicular Systems, Sci. Rep., 2018, 8(1), 8516 CrossRef.
- A. Horner, F. Zocher, J. Preiner, N. Ollinger, C. Siligan, S. A. Akimov and P. Pohl, The mobility of single-file water molecules is governed by the number of H-bonds they may form with channel-lining residues, Sci. Adv., 2015, 1(2), e1400083 CrossRef PubMed.
- A. Horner, C. Siligan, A. Cornean and P. Pohl, Positively charged residues at the channel mouth boost single-file water flow, Faraday Discuss., 2018, 209, 55 RSC.
- Y. X. Shen, W. Song, D. R. Barden, T. Ren, C. Lang, H. Feroz, C. B. Henderson, P. O. Saboe, D. Tsai and H. Yan,
et al., Achieving high permeability and enhanced selectivity for Angstrom-scale separations using artificial water channel membranes, Nat. Commun., 2018, 9(1), 2294 CrossRef.
- W. Song, Y.-M. Tu, H. Oh, L. Samineni and M. Kumar, Hierarchical optimization of high performance biomimetic and bioinspired membranes, Langmuir, 2019, 35(3), 589–607 CrossRef CAS PubMed.
- Y. X. Shen, W. Si, M. Erbakan, K. Decker, R. De Zorzi, P. O. Saboe, Y. J. Kang, S. Majd, P. J. Butler and T. Walz,
et al., Highly permeable artificial water channels that can self-assemble into two-dimensional arrays, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(32), 9810 CrossRef CAS PubMed.
- I. Kocsis, Z. Sun, Y. M. Legrand and M. Barboiu, Artificial water channels—deconvolution of natural Aquaporins through synthetic design, npj Clean Water, 2018, 1(1), 13 CrossRef.
- S. Murail, T. Vasiliu, A. Neamtu, M. Barboiu, F. Sterpone and M. Baaden, Water permeation across artificial I-quartet membrane channels: from structure to disorder, Faraday Discuss., 2018, 209, 125 RSC.
- M. Barboiu and A. Gilles, From Natural to Bioassisted and Biomimetic Artificial Water Channel Systems, Acc. Chem. Res., 2013, 46(12), 2814 CrossRef CAS.
- Y. Le Duc, M. Michau, A. Gilles, V. Gence, Y. M. Legrand, A. van der Lee, S. Tingry and M. Barboiu, Imidazole-Quartet Water and Proton Dipolar Channels, Angew. Chem., Int. Ed., 2011, 50(48), 11366 CrossRef CAS PubMed.
- M. Grzelakowski, M. F. Cherenet, Y. X. Shen and M. Kumar, A framework for accurate evaluation of the promise of aquaporin based biomimetic membranes, J. Membr. Sci., 2015, 479, 223 CrossRef CAS.
- H. Wang, T.-S. Chung and Y. W. Tong, Study on water transport through a mechanically robust Aquaporin Z biomimetic membrane, J. Membr. Sci., 2013, 445, 47 CrossRef CAS.
- P. S. Zhong, T.-S. Chung, K. Jeyaseelan and A. Armugam, Aquaporin-embedded biomimetic membranes for nanofiltration, J. Membr. Sci., 2012, 407–408, 27 CrossRef CAS.
- S. Qi, R. Wang, G. K. M. Chaitra, J. Torres, X. Hu and A. G. Fane, Aquaporin-based biomimetic reverse osmosis membranes: Stability and long term performance, J. Membr. Sci., 2016, 508, 94 CrossRef CAS.
- N. G. Çalıcıoğlu, G. Ö. Özdemir, A. Öztürk, A. Yıldız, H. Yılmaz, P. Ergenekon, M. Erbakan, E. Erhan and M. Özkan, Use of halophilic aquaporin for preparation of biomimetic thin film composite membrane, J. Membr. Sci., 2018, 568, 105 CrossRef.
- M. Kumar, M. Grzelakowski, J. Zilles, M. Clark and W. Meier, Highly permeable polymeric membranes based on the incorporation of the functional water channel protein Aquaporin Z, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(52), 20719 CrossRef CAS.
- M. Wang, Z. Wang, X. Wang, S. Wang, W. Ding and C. Gao, Layer-by-Layer Assembly of Aquaporin Z-Incorporated Biomimetic Membranes for Water Purification, Environ. Sci. Technol., 2015, 49(6), 3761 CrossRef CAS PubMed.
- H. Wang, T. S. Chung, Y. W. Tong, K. Jeyaseelan, A. Armugam, Z. Chen, M. Hong and W. Meier, Highly permeable and selective pore-spanning biomimetic membrane embedded with aquaporin Z, Small, 2012, 8(8), 1185 CrossRef CAS.
- Y. Li, Z. Li, F. Aydin, J. Quan, X. Chen, Y. C. Yao, C. Zhan, Y. Chen, T. A. Pham and A. Noy, Water-ion permselectivity of narrow-diameter carbon nanotubes, Sci. Adv., 2020, 6(38), eaba9966 CrossRef CAS.
- Y. X. Shen, P. O. Saboe, I. T. Sines, M. Erbakan and M. Kumar, Biomimetic membranes: A review, J. Membr. Sci., 2014, 454, 359 CrossRef CAS.
- L. Otrin, N. Marušič, C. Bednarz, T. Vidaković-Koch, I. Lieberwirth, K. Landfester and K. Sundmacher, Toward Artificial Mitochondrion: Mimicking Oxidative Phosphorylation in Polymer and Hybrid Membranes, Nano Lett., 2017, 17(11), 6816 CrossRef CAS.
- T. Einfalt, R. Goers, I. A. Dinu, A. Najer, M. Spulber, O. Onaca-Fischer and C. G. Palivan, Stimuli-Triggered Activity of Nanoreactors by Biomimetic Engineering Polymer Membranes, Nano Lett., 2015, 15(11), 7596 CrossRef CAS PubMed.
- J. Gaitzsch, S. Hirschi, S. Freimann, D. Fotiadis and W. Meier, Directed Insertion of Light-Activated Proteorhodopsin into Asymmetric Polymersomes from an ABC Block Copolymer, Nano Lett., 2019, 19(4), 2503 CrossRef CAS.
- C. Hannesschlaeger, A. Horner and P. Pohl, Intrinsic Membrane Permeability to Small Molecules, Chem. Rev., 2019, 119(9), 5922 CrossRef CAS.
- A. Horner and P. Pohl, Single-file transport of water through membrane channels, Faraday Discuss., 2018, 209, 9 RSC.
- J. Drazenovic, H. Wang, K. Roth, J. Zhang, S. Ahmed, Y. Chen, G. Bothun and S. L. Wunder, Effect of lamellarity and size on calorimetric phase transitions in single component phosphatidylcholine vesicles, Biochim. Biophys. Acta, 2015, 1848(2), 532 CrossRef CAS PubMed.
- E. K. Eriksson, K. Edwards, P. Grad, L. Gedda and V. Agmo Hernández, Osmoprotective effect of ubiquinone in lipid vesicles modelling the E. coli plasma membrane, Biochim. Biophys. Acta, 2019, 1861(7), 1388 CrossRef CAS.
- I. A. B. Pijpers, L. K. E. A. Abdelmohsen, D. S. Williams and J. C. M. van Hest, Morphology Under Control: Engineering Biodegradable Stomatocytes, ACS Macro Lett., 2017, 6(11), 1217 CrossRef CAS PubMed.
- R. Rikken, H. Engelkamp, R. Nolte, J. Maan, J. Van Hest, D. Wilson and P. Christianen, Shaping polymersomes into predictable morphologies via out-of-equilibrium self-assembly, Nat. Commun., 2016, 7(1), 1 Search PubMed.
- C. K. Wong, M. H. Stenzel and P. Thordarson, Non-spherical polymersomes: formation and characterization, Chem. Soc. Rev., 2019, 48(15), 4019 RSC.
- D. Boytsov, C. Hannesschlaeger, A. Horner, C. Siligan and P. Pohl, Micropipette Aspiration-Based Assessment of Single Channel Water Permeability, Biotechnol. J., 2020, 15(7), e1900450 CrossRef.
- R. Sha'Afi, G. Rich, V. W. Sidel, W. Bossert and A. Solomon, The effect of the unstirred layer on human red cell water permeability, J. Gen. Physiol., 1967, 50(5), 1377 CrossRef PubMed.
- P. Y. Chen, D. Pearce and A. S. Verkman, Membrane water
and solute permeability determined quantitatively by self-quenching of an entrapped fluorophore, Biochemistry, 1988, 27(15), 5713 CrossRef CAS.
- A. Horner, F. Goetz, R. Tampe, E. Klussmann and P. Pohl, Mechanism for targeting the A-kinase anchoring protein AKAP18delta to the membrane, J. Biol. Chem., 2012, 287(51), 42495 CrossRef CAS PubMed.
- B. A. Korgel, J. H. van Zanten and H. G. Monbouquette, Vesicle size distributions measured by flow field-flow fractionation coupled with multiangle light scattering, Biophys. J., 1998, 74(6), 3264 CrossRef CAS PubMed.
- J. Stetefeld, S. A. McKenna and T. R. Patel, Dynamic light scattering: a practical guide and applications in biomedical sciences, Biophys. Rev., 2016, 8(4), 409 CrossRef CAS PubMed.
- J. i. Pánek, L. Loukotová, M. Hrubý and P. Štěpánek, Distribution of diffusion times determined by fluorescence (Lifetime) correlation spectroscopy, Macromolecules, 2018, 51(8), 2796 CrossRef.
- N. Pal, S. Dev Verma, M. K. Singh and S. Sen, Fluorescence correlation spectroscopy: an efficient tool for measuring size, size-distribution and polydispersity of microemulsion droplets in solution, Anal. Chem., 2011, 83(20), 7736 CrossRef CAS.
- B. Coldren, R. van Zanten, M. J. Mackel, J. A. Zasadzinski and H. T. Jung, From vesicle size distributions to bilayer elasticity via cryo-transmission and freeze-fracture electron microscopy, Langmuir, 2003, 19(14), 5632 CrossRef CAS.
-
H. C. Hulst and H. C. van de Hulst, Light Scattering by Small Particles, Courier Corporation, 1981 Search PubMed.
- Z. Petrasek and P. Schwille, Precise measurement of diffusion coefficients using scanning fluorescence correlation spectroscopy, Biophys. J., 2008, 94(4), 1437 CrossRef CAS PubMed.
- Y. N. Antonenko, A. Horner and P. Pohl, Electrostatically induced recruitment of membrane peptides into clusters requires ligand binding at both interfaces, PLoS One, 2012, 7(12), e52839 CrossRef CAS PubMed.
- A. Horner, S. A. Akimov and P. Pohl, Long and short lipid molecules experience the same interleaflet drag in lipid bilayers, Phys. Rev. Lett., 2013, 110(26), 268101 CrossRef PubMed.
- D. Magde, E. L. Elson and W. W. Webb, Fluorescence correlation spectroscopy. II. An experimental realization, Biopolymers, 1974, 13(1), 29 CrossRef CAS.
- K. Matsuzaki, O. Murase, K. Sugishita, S. Yoneyama, K. Akada, M. Ueha, A. Nakamura and S. Kobayashi, Optical characterization of liposomes by right angle light scattering and turbidity measurement, Biochim. Biophys. Acta, 2000, 1467(1), 219 CrossRef CAS.
- P. N. Yi and Rc. Macdonal, Temperature-Dependence of Optical Properties of Aqueous Dispersions of Phosphatidylcholine, Chem. Phys. Lipids, 1973, 11(2), 114 CrossRef.
- W. M. M. Yunus, Temperature dependence of refractive index and absorption of NaCI, MgCI2, and Na2SO4 solutions as major components in natural seawater, Appl. Opt., 1992, 31, 2963 CrossRef CAS PubMed.
- M. P. van Heeswijk and C. H. van Os, Osmotic water permeabilities of brush border and basolateral membrane vesicles from rat renal cortex and small intestine, J. Membr. Biol., 1986, 92(2), 183 CrossRef CAS PubMed.
- N. P. Illsley and A. S. Verkman, Serial permeability barriers to water transport in human placental vesicles, J. Membr. Biol., 1986, 94(3), 267 CrossRef CAS PubMed.
- A. N. van Hoek and A. S. Verkman, Functional reconstitution of the isolated erythrocyte water channel CHIP28, J. Biol. Chem., 1992, 267(26), 18267 CrossRef CAS.
- Y. Tanimura, Y. Hiroaki and Y. Fujiyoshi, Acetazolamide reversibly inhibits water conduction by aquaporin-4, J. Struct. Biol., 2009, 166(1), 16 CrossRef CAS.
- A. Kirscht, S. S. Kaptan, G. P. Bienert, F. Chaumont, P. Nissen, B. L. de Groot, P. Kjellbom, P. Gourdon and U. Johanson, Crystal Structure of an Ammonia-Permeable Aquaporin, PLoS Biol., 2016, 14(3), e1002411 CrossRef.
- A. H. Hsieh, D. S. Corti and E. I. Franses, Rayleigh and Rayleigh-Debye-Gans light scattering intensities and spetroturbidimetry of dispersions of unilamellar vesicles and multilamellar liposomes, J. Colloid Interface Sci., 2020, 578, 471 CrossRef CAS PubMed.
- K. Pluhackova and A. Horner, Native-like membrane models of E. coli polar lipid extract shed light on the importance of lipid composition complexity, BMC Biol., 2021, 19(1), 4 CrossRef CAS.
- F. Itel, M. Chami, A. Najer, S. Lorcher, D. L. Wu, I. A. Dinu and W. Meier, Molecular Organization and Dynamics in Polymersome Membranes: A Lateral Diffusion Study, Macromolecules, 2014, 47(21), 7588 CrossRef CAS.
- F. Itel, A. Najer, C. G. Palivan and W. Meier, Dynamics of Membrane Proteins within Synthetic Polymer Membranes with Large Hydrophobic Mismatch, Nano Lett., 2015, 15(6), 3871 CrossRef CAS PubMed.
- J. Pencer and F. R. Hallett, Effects of vesicle size and shape on static and dynamic light scattering measurements, Langmuir, 2003, 19(18), 7488 CrossRef CAS.
- R. F. Chen and J. R. Knutson, Mechanism of fluorescence concentration quenching of carboxyfluorescein in liposomes: energy transfer to nonfluorescent dimers, Anal. Biochem., 1988, 172(1), 61 CrossRef CAS.
- R. Kwok and E. Evans, Thermoelasticity of large lecithin bilayer vesicles, Biophys. J., 1981, 35(3), 637 CrossRef CAS PubMed.
- M. J. Hope, M. B. Bally, G. Webb and P. R. Cullis, Production of large unilamellar vesicles by a rapid extrusion procedure: characterization of size distribution, trapped volume and ability to maintain a membrane potential, Biochim. Biophys. Acta, 1985, 812(1), 55 CrossRef CAS.
- J. L. Rigaud, D. Levy, G. Mosser and O. Lambert, Detergent removal by non-polar polystyrene beads, Eur. Biophys. J., 1998, 27(4), 305 CrossRef CAS.
- S. M. Johnson and N. Buttress, The osmotic insensitivity of sonicated liposomes and the density of phospholipid-cholesterol mixtures, Biochim. Biophys. Acta, 1973, 307(1), 20 CrossRef CAS.
- B. A. Cornell, G. C. Fletcher, J. Middlehurst and F. Separovic, The lower limit to the size of small sonicated phospholipid vesicles, Biochim. Biophys. Acta, 1982, 690(1), 15 CrossRef CAS.
-
P. Peterlin, V. Arrigler, H. Diamant and E. Haleva, in Advances in Planar Lipid Bilayers and Liposomes, Elsevier, 2012, vol. 16 Search PubMed.
- F. R. Hallett, J. Marsh, B. G. Nickel and J. M. Wood, Mechanical properties of vesicles. II. A model for osmotic swelling and lysis, Biophys. J., 1993, 64(2), 435 CrossRef CAS.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Effect of Chain Length and Unsaturation on Elasticity of Lipid Bilayers, Biophys. J., 2000, 79(1), 328 CrossRef CAS.
- C. Hannesschlaeger and P. Pohl, Membrane Permeabilities of Ascorbic Acid and Ascorbate, Biomolecules, 2018, 8(3), 73 CrossRef PubMed.
- C. Hannesschlaeger, T. Barta, H. Pechova and P. Pohl, The Effect of Buffers on Weak Acid Uptake by Vesicles, Biomolecules, 2019, 9(2), 63 CrossRef PubMed.
- J. R. Werber and M. Elimelech, Permselectivity limits of biomimetic desalination membranes, Sci. Adv., 2018, 4(6), eaar8266 CrossRef.
- N. Jahnke, O. O. Krylova, T. Hoomann, C. Vargas, S. Fiedler, P. Pohl and S. Keller, Real-time monitoring of membrane-protein reconstitution by isothermal titration calorimetry, Anal. Chem., 2014, 86(1), 920 CrossRef CAS.
- M. J. Borgnia, D. Kozono, G. Calamita, P. C. Maloney and P. Agre, Functional reconstitution and characterization of AqpZ, the E. coli water channel protein, J. Mol. Biol., 1999, 291(5), 1169 CrossRef CAS PubMed.
- J. Preiner, A. Horner, A. Karner, N. Ollinger, C. Siligan, P. Pohl and P. Hinterdorfer, High-speed AFM images of thermal motion provide stiffness map of interfacial membrane protein moieties, Nano Lett., 2015, 15(1), 759 CrossRef CAS.
- A. Karner, B. Nimmervoll, B. Plochberger, E. Klotzsch, A. Horner, D. G. Knyazev, R. Kuttner, K. Winkler, L. Winter and C. Siligan,
et al., Tuning membrane protein mobility by confinement into nanodomains, Nat. Nanotechnol., 2017, 12(3), 260 CrossRef CAS PubMed.
- M. Textor, C. Vargas and S. Keller, Calorimetric quantification of linked equilibria in cyclodextrin/lipid/detergent mixtures for membrane-protein reconstitution, Methods, 2015, 76, 183 CrossRef CAS PubMed.
- H. Heerklotz, Interactions of surfactants with lipid membranes, Q. Rev. Biophys., 2008, 41(3–4), 205 CrossRef CAS PubMed.
- D. Lichtenberg, H. Ahyayauch and F. M. Goñi, The Mechanism of Detergent Solubilization of Lipid Bilayers, Biophys. J., 2013, 105(2), 289 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00577d |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Christof
Hannesschlaeger
,
Christof
Hannesschlaeger
 ,
Armin
Speletz
,
Thomas
Barta
,
Anna
Eckerstorfer
,
Christine
Siligan
and
Andreas
Horner
,
Armin
Speletz
,
Thomas
Barta
,
Anna
Eckerstorfer
,
Christine
Siligan
and
Andreas
Horner
 *
*
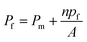
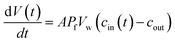
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i by:
i by:![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i
i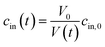

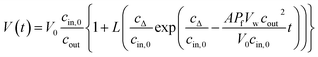
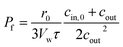
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–25
000–25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi (4 °C). Unbroken cells and debris were separated from the cell lysate by a 20 min centrifugation at 7000 × g and discarded. Membrane fractions recovered from the supernatant by a 120 min centrifugation at 100
000 psi (4 °C). Unbroken cells and debris were separated from the cell lysate by a 20 min centrifugation at 7000 × g and discarded. Membrane fractions recovered from the supernatant by a 120 min centrifugation at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g were resuspended to the original volume in solubilization buffer [3% OG in 100 mM K2HPO4, 10% (vol/vol) glycerol, 200 mM NaCl, pH 8.0] and incubated for 1 hour at 4 °C on a roller shaker. Insoluble material was pelleted by 60 min centrifugation at 100
000 × g were resuspended to the original volume in solubilization buffer [3% OG in 100 mM K2HPO4, 10% (vol/vol) glycerol, 200 mM NaCl, pH 8.0] and incubated for 1 hour at 4 °C on a roller shaker. Insoluble material was pelleted by 60 min centrifugation at 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g. The soluble fraction was mixed with 2 mL of prewashed Ni-NTA-agarose beads (Qiagen) and incubated with agitation at 4 °C for 60 min. The beads were then packed in a plastic disposable column (Stratagene) and washed with 100 bead volumes of wash buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 100 mM imidazole, pH 7.5) to remove nonspecifically bound material. Ni-NTA-agarose-bound material was eluted 5 times sequentially by adding 0.5 mL elution buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 0.5 M imidazole, pH 7.5) at each step. Typically, eluates of the 3 l expression cultures yielded pure protein at a concentration of 1.5 mg mL−1, measured by Bradford using BSA as a standard.
000 × g. The soluble fraction was mixed with 2 mL of prewashed Ni-NTA-agarose beads (Qiagen) and incubated with agitation at 4 °C for 60 min. The beads were then packed in a plastic disposable column (Stratagene) and washed with 100 bead volumes of wash buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 100 mM imidazole, pH 7.5) to remove nonspecifically bound material. Ni-NTA-agarose-bound material was eluted 5 times sequentially by adding 0.5 mL elution buffer (3% OG, 100 mM K2HPO4, 10% glycerol, 200 mM NaCl, 0.5 M imidazole, pH 7.5) at each step. Typically, eluates of the 3 l expression cultures yielded pure protein at a concentration of 1.5 mg mL−1, measured by Bradford using BSA as a standard.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g, resuspended in reconstitution buffer without OG and finally extruded through two polycarbonate filters with 100 nm pore sizes.
000 × g, resuspended in reconstitution buffer without OG and finally extruded through two polycarbonate filters with 100 nm pore sizes.
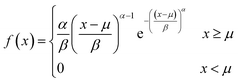
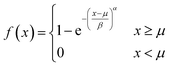
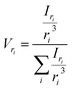
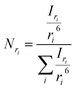
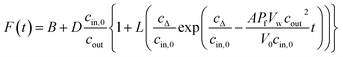
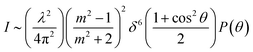
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u − u
u − u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u)/u3)2 whereas P(θ) used for the hollow sphere model (see Fig. S3†) is
u)/u3)2 whereas P(θ) used for the hollow sphere model (see Fig. S3†) is 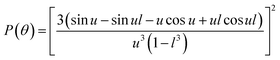 .62,63 In both cases, u = 2δ
.62,63 In both cases, u = 2δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2). Throughout this paper, except explicitly mentioned, we used the homogeneous sphere model for simulations and fits.
sin(θ/2). Throughout this paper, except explicitly mentioned, we used the homogeneous sphere model for simulations and fits.
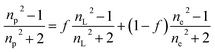
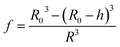
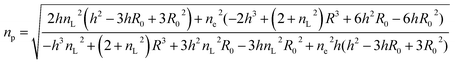
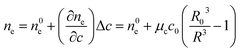

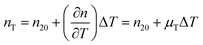
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 are the refractive index at temperature T, the refractive index at 20 °C and the temperature coefficient for the refractive indices, respectively.
64 are the refractive index at temperature T, the refractive index at 20 °C and the temperature coefficient for the refractive indices, respectively.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 to 600 nm
19 to 600 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 were exploited for scattering experiments in literature. To visualize the effect of λex on the experiment and to guide the rational selection of λex, we simulated and measured I(t) at different λex. From eqn (12) the relation of I(t) on λex is not directly obvious as λex is not only hidden in δ but also in P(θ). Generally, the RGD theory is applicable in the visible light range if the conditions |m − 1| ≪ 1 and kd|m − 1| ≪ 1 with k = 2π/λ and d the vesicle diameter are fulfilled.70 Simulation of scattering data at different wavelengths ranging from 346 nm to 846 nm reveal an increasing relative signal amplitude with smaller wavelength (Fig. 6A). Next, we chose the three main intensity peaks in our XeHg light source to verify that a similar dependence can also be seen experimentally (Fig. 6B). The discrepancies in the relative signal amplitudes between in vitro and in silico data may arise from the wavelength dependence of the refractive indices, which have not been taken into account with our simulations. Another source of error quantifying the relative amplitude change of experimental data is the background correction, where the scattering intensity signal of the background, which is determined by measuring the scattered light intensity of the mixture of buffer without vesicles and osmolyte buffer, is subtracted before normalization. Small errors in the determination of the background signal may have, due to normalization, a high impact on the relative amplitude change. Nevertheless, the kinetic and thus the Pf values are not affected by the height of the relative amplitude. Fitting the data with the analytical solution illustrates that Pf is within the error of the measurement as expected and with these experimental conditions Pf is independent of the wavelength used (Fig. S4 and Table S2†).
33 were exploited for scattering experiments in literature. To visualize the effect of λex on the experiment and to guide the rational selection of λex, we simulated and measured I(t) at different λex. From eqn (12) the relation of I(t) on λex is not directly obvious as λex is not only hidden in δ but also in P(θ). Generally, the RGD theory is applicable in the visible light range if the conditions |m − 1| ≪ 1 and kd|m − 1| ≪ 1 with k = 2π/λ and d the vesicle diameter are fulfilled.70 Simulation of scattering data at different wavelengths ranging from 346 nm to 846 nm reveal an increasing relative signal amplitude with smaller wavelength (Fig. 6A). Next, we chose the three main intensity peaks in our XeHg light source to verify that a similar dependence can also be seen experimentally (Fig. 6B). The discrepancies in the relative signal amplitudes between in vitro and in silico data may arise from the wavelength dependence of the refractive indices, which have not been taken into account with our simulations. Another source of error quantifying the relative amplitude change of experimental data is the background correction, where the scattering intensity signal of the background, which is determined by measuring the scattered light intensity of the mixture of buffer without vesicles and osmolyte buffer, is subtracted before normalization. Small errors in the determination of the background signal may have, due to normalization, a high impact on the relative amplitude change. Nevertheless, the kinetic and thus the Pf values are not affected by the height of the relative amplitude. Fitting the data with the analytical solution illustrates that Pf is within the error of the measurement as expected and with these experimental conditions Pf is independent of the wavelength used (Fig. S4 and Table S2†).


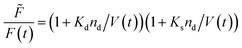
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) , Kd, Ks = 412 M−1,75nd and V are the fluorescent intensity in absence of quencher, the Stern–Volmer constant for dynamic quenching, the Stern–Volmer constant for static quenching, the amount of fluorescent molecules in mole and the volume of the vesicles, respectively. As dynamic or collisional self-quenching of CF in liposomes can be neglected,75eqn (20) reduces to
, Kd, Ks = 412 M−1,75nd and V are the fluorescent intensity in absence of quencher, the Stern–Volmer constant for dynamic quenching, the Stern–Volmer constant for static quenching, the amount of fluorescent molecules in mole and the volume of the vesicles, respectively. As dynamic or collisional self-quenching of CF in liposomes can be neglected,75eqn (20) reduces to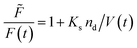
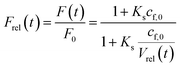
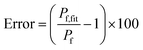



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 with pf = 3.25 × 10−13 cm3 s−1 has been taken. (B) Poisson distribution with an average number of monomers per PL Nmean of 1 (blue), 5 (green) and 10 (orange). The probability of a PL containing N numbers of monomers of the reconstituted protein is plotted over N. (C) Error in Pf depending on Nmean for xl = 0.0 (blue), xl = 0.2 (orange), xl = 0.5 (green) and xl = 0.8 (red). Dotted, dashed, dashdotted and solid lines represent the error for a two-component exponential fit with free components, a two-component exponential fit, where one component is fixed to the rate constant of liposomes containing no protein, an analytical fit and a global analytical fit, respectively. The global fit determines Pm as the average slow component (and one component for the control only) of all curves.
19 with pf = 3.25 × 10−13 cm3 s−1 has been taken. (B) Poisson distribution with an average number of monomers per PL Nmean of 1 (blue), 5 (green) and 10 (orange). The probability of a PL containing N numbers of monomers of the reconstituted protein is plotted over N. (C) Error in Pf depending on Nmean for xl = 0.0 (blue), xl = 0.2 (orange), xl = 0.5 (green) and xl = 0.8 (red). Dotted, dashed, dashdotted and solid lines represent the error for a two-component exponential fit with free components, a two-component exponential fit, where one component is fixed to the rate constant of liposomes containing no protein, an analytical fit and a global analytical fit, respectively. The global fit determines Pm as the average slow component (and one component for the control only) of all curves.