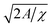Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Acoustically propelled nano- and microcones: fast forward and backward motion
Johannes
Voß
and
Raphael
Wittkowski
 *
*
Institut für Theoretische Physik, Center for Soft Nanoscience, Westfälische Wilhelms-Universität Münster, D-48149 Münster, Germany. E-mail: raphael.wittkowski@uni-muenster.de
First published on 26th October 2021
Abstract
We focus on cone-shaped nano- and microparticles, which have recently been found to show particularly strong propulsion when they are exposed to a traveling ultrasound wave, and study based on direct acoustofluidic computer simulations how their propulsion depends on the cones' aspect ratio. The simulations reveal that the propulsion velocity and even its sign are very sensitive to the aspect ratio, where short particles move forward whereas elongated particles move backward. Furthermore, we identify a cone shape that allows for a particularly large propulsion speed. Our results contribute to the understanding of the propulsion of ultrasound-propelled colloidal particles, suggest a method for separation and sorting of nano- and microcones concerning their aspect ratio, and provide useful guidance for future experiments and applications.
I. Introduction
Research on active nano- and microparticles is strongly motivated by their complex nonequilibrium behavior, which is interesting from a fundamental point of view, and by the wide range of possible future applications of such particles.1–4 Among the most important potential fields of application are medicine5–12 and materials science.13–19 However, most of the active particles that have been developed so far are mainly useful for fundamental research but not suitable for applications, e.g., since their propulsion runs quickly out of fuel, requires a very particular chemical environment, or is not biocompatible.9,20–25 A realization of active particles that is particularly useful for applications is acoustically propelled particles.26–60 Some of their advantages are that the particles can easily and permanently be supplied with energy via ultrasound, that the propulsion mechanism works in various types of fluids and soft materials, and that it is biocompatible.There exist two different types of acoustically propelled particles: rigid particles26–28,31–34,37,38,40,41,43,44,46,51,55–57,60–65 and particles with movable components.23,40,45,50,53,54,58,59,66 The rigid particles are easier to produce in large numbers and thus of special relevance with respect to future applications, where usually a large number of particles is required. There exist also some hybrid particles that combine acoustic propulsion with other propulsion mechanisms.57,62,64,65,67,68
In recent years, ultrasound-propelled nano- and microparticles have been intensively investigated.26–28,30,32,34,37–40,43–46,51–55,57–61,63–65,69–71 Besides two articles that are based on analytical approaches61,63 and an article that relies on direct computational fluid dynamics simulations,51 a large number of experimental studies have been published so far.26–28,30,32,38–40,44,45,49,50,53–55,57,60,64,65,69 It was found that the propulsion of the particles is strongly linked with an asymmetry of their shape.61,63 Also, an anisotropic mass density of the particle was found to affect its motion.63 In the previous work, mostly cylindrical particles with a concave end and a convex end were studied.26–28,30,32–34,39,45,54,55,60,65 As a limiting case, which corresponds to a very short cylindrical particle with concave and convex ends, also half-sphere cups (nanoshells) were considered.38,51,64 Recently, half-sphere-shaped particles, cone-shaped particles, and spherical-as well as conical-cup-like particles were compared with respect to their propulsion.51 In two other studies, gear-shaped microspinners44,69 were addressed, and there are a few additional publications that focus on particles with movable components.23,40,50,53,66
Among the rigid particles with mainly translational motion that have been addressed so far, cone-shaped particles and conical-cup-shaped particles showed the fastest propulsion, where the speeds of cone-shaped and conical-cup-shaped particles differed only slightly.51 Since cone-shaped particles have a simpler shape, which facilitates their fabrication, and a larger volume, which is advantageous for delivery of drugs or other substances, than conical-cup-shaped particles, the former particles have been identified as particularly suitable candidates for efficient ultrasound-propelled particles that could be used in future experiments and applications. Cone-shaped particles can be produced, e.g., by electrodeposition,42,72 or directly be found, e.g., in the form of carbon nanocones,73 in large numbers. Up to now, however, only ultrasound-propelled cone-shaped particles with a particular aspect ratio have been studied,51 although the aspect ratio can have a strong influence on the efficiency of the particles' propulsion.63 Given that previous studies found for the short spherical-cup-shaped particles motion towards the particles' convex end38,51,64 but for the longer cylindrical particles with concave and convex ends motion towards the concave end,39 also the direction of propulsion can depend on the aspect ratio.
Therefore, in this article we investigate the acoustic propulsion of cone-shaped nano- and microparticles with a constant mass density in more detail. Using direct acoustofluidic simulations, we study how the propulsion of acoustically propelled nano- and microcones depends on their aspect ratio and we determine an aspect ratio that is associated with particularly fast and thus efficient propulsion. In contrast to all but one40 previous experimental studies, we assume that the particles are exposed to a traveling ultrasound wave since this scenario is more realistic for future applications of the particles than standing ultrasound waves that are usually considered.
II. Methods
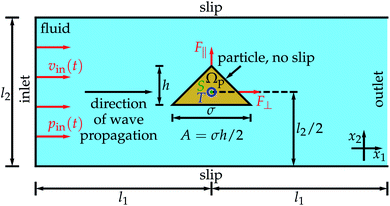
This work is based on a similar setup and procedure as ref. 51 since the methodology used there has been proven to be very suitable for studying ultrasound-propelled particles. We consider a particle that is surrounded by water and exposed to ultrasound. Using direct acoustofluidic simulations, where the compressible Navier–Stokes equations are solved numerically, the propagation of ultrasound through the water and the interaction with the particle are calculated. These calculations allow to determine the sound-induced forces and torques acting on the particle, from which in turn we calculate the particle's translational and angular propulsion velocities.Fig. 1 shows the setup in detail. We consider a particle with a conical shape in two spatial dimensions. The particle is oriented perpendicular to the direction of wave propagation, has a fixed cross-section area A, and is described by a particle domain Ωp. Its aspect ratio χ = h/σ with the particle's height h and diameter σ is varied. The position of the particle is fixed. This means that the results of the simulations are valid for a particle which is held in place. Such a particle can be seen as a free moving particle in the limiting case of an infinite mass density. This limiting case can, in turn, be considered as an upper bound for a free moving particle made of a material with a high mass density like gold, which is a widely used material for such particles.26,30,32,34,37–39,42–44,46,48,55
The particle is positioned in the middle of a water-filled rectangular domain so that the center of mass of the rectangle and the center of mass S of the particle coincide. One edge of the rectangular domain has length l2 = 200 μm and is perpendicular to the direction of ultrasound propagation. The other edge is parallel to the direction of ultrasound propagation and has length 2l1. We choose a Cartesian coordinate system such that the x1 axis is parallel to the direction of ultrasound propagation and the x2 axis is perpendicular to that direction, i.e., the coordinate axes are parallel to the edges of the rectangular domain. The ultrasound wave has frequency f = 1 MHz and enters the rectangular domain at the edge perpendicular to the sound-propagation direction. We prescribe the incoming ultrasound wave by a time-dependent inflow pressure pin(t) = Δp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft) and velocity vin(t) = Δv
sin(2πft) and velocity vin(t) = Δv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft) perpendicular to the inlet with the pressure amplitude Δp = 10 kPa, which is much lower than the normal pressure p0 = 101
sin(2πft) perpendicular to the inlet with the pressure amplitude Δp = 10 kPa, which is much lower than the normal pressure p0 = 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa and consistent with previous work,51 and the velocity amplitude Δv = Δp/(ρ0cf) = 6.75 mm s−1. Here, ρ0 = 998 kg m−3 is the mass density of the initially quiescent fluid, and cf = 1484 m s−1 is the sound velocity in the fluid. The acoustic energy density of this wave is E = Δp2/(2ρ0cf2) = 0.0227 J m−3. Both Δv and E are not prescribed directly but follow from the value chosen for the pressure amplitude Δp. Note that energy densities below Emax = 4.9 J m−3 are considered as harmless in medical applications.74 In experiments reported in the literature,39,40,55 mostly a propulsion voltage of 10 V was applied. A voltage of ≲10 V can be assumed to correspond to an energy density of 10–100 J m−3.75 Thus, in the experiments from the literature, the energy density was much larger than the energy density used in the present work and even much larger than the maximum harmless energy density Emax. After a distance l1 = λ/4, where λ is the wavelength of the ultrasound wave λ = 1.484 mm, the wave reaches the fixed rigid particle. The interaction of the ultrasound with the particle leads to time-averaged forces F∥ parallel and F⊥ perpendicular to the particle orientation as well as to a time-averaged torque T relative to the reference point S acting on the particle. After a further distance l1, the wave leaves the domain through an outlet at the edge of the water domain opposing the inlet. The full boundary of the particle is described by a no-slip condition, as it is common for treating solid–liquid interfaces in fluid dynamics, and at the edges of the water domain parallel to the direction of sound propagation we assume a slip condition to minimize the effect of these boundaries on the propagation of the ultrasound wave.
325 Pa and consistent with previous work,51 and the velocity amplitude Δv = Δp/(ρ0cf) = 6.75 mm s−1. Here, ρ0 = 998 kg m−3 is the mass density of the initially quiescent fluid, and cf = 1484 m s−1 is the sound velocity in the fluid. The acoustic energy density of this wave is E = Δp2/(2ρ0cf2) = 0.0227 J m−3. Both Δv and E are not prescribed directly but follow from the value chosen for the pressure amplitude Δp. Note that energy densities below Emax = 4.9 J m−3 are considered as harmless in medical applications.74 In experiments reported in the literature,39,40,55 mostly a propulsion voltage of 10 V was applied. A voltage of ≲10 V can be assumed to correspond to an energy density of 10–100 J m−3.75 Thus, in the experiments from the literature, the energy density was much larger than the energy density used in the present work and even much larger than the maximum harmless energy density Emax. After a distance l1 = λ/4, where λ is the wavelength of the ultrasound wave λ = 1.484 mm, the wave reaches the fixed rigid particle. The interaction of the ultrasound with the particle leads to time-averaged forces F∥ parallel and F⊥ perpendicular to the particle orientation as well as to a time-averaged torque T relative to the reference point S acting on the particle. After a further distance l1, the wave leaves the domain through an outlet at the edge of the water domain opposing the inlet. The full boundary of the particle is described by a no-slip condition, as it is common for treating solid–liquid interfaces in fluid dynamics, and at the edges of the water domain parallel to the direction of sound propagation we assume a slip condition to minimize the effect of these boundaries on the propagation of the ultrasound wave.
In the simulations, we numerically solve the continuity equation for the mass-density field of the fluid, the compressible Navier–Stokes equation, and a linear constitutive equation for the fluid's pressure field. Thus we are avoiding approximations like perturbation expansions that are used in most previous studies using analytical61,63 or numerical40,44,64 methods. For solving these equations, we used the finite volume method implemented in the software package OpenFOAM.76 We applied a structured mixed rectangular–triangular mesh with about 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells, where the cell size Δx is very small close to the particle, and larger far away from it. Concerning the time integration, an adaptive time-step method is used with a time-step size Δt such that the Courant–Friedrichs–Lewy number
000 cells, where the cell size Δx is very small close to the particle, and larger far away from it. Concerning the time integration, an adaptive time-step method is used with a time-step size Δt such that the Courant–Friedrichs–Lewy number
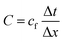 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CPU core hours. The reason for this expense is the necessary fine discretization in space and time relative to the large spatial and temporal domains.
000 CPU core hours. The reason for this expense is the necessary fine discretization in space and time relative to the large spatial and temporal domains.
Through the simulations, we calculated the time-dependent force and torque acting on the particle in the laboratory frame. Since the particle has no-slip boundary conditions and is fixed in space, the fluid velocity is zero at the fluid–particle interface. So the force and torque can be calculated by the integral of the stress tensor Σ over the particle surface. The force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p) +
(p) + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v) and torque T(p) + T(v) consist of two components, namely a pressure component (superscript “(p)”) and a viscosity component (superscript “(v)”) with77
(v) and torque T(p) + T(v) consist of two components, namely a pressure component (superscript “(p)”) and a viscosity component (superscript “(v)”) with77
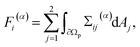 | (2) |
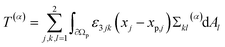 | (3) |
![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) (
(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) = (dA1(
) = (dA1(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ),dA2(
),dA2(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ))T is the normal and outwards oriented surface element of ∂Ωp at position
))T is the normal and outwards oriented surface element of ∂Ωp at position ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) when
when ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ∈ ∂Ωp, εijk the Levi-Civita symbol, and
∈ ∂Ωp, εijk the Levi-Civita symbol, and ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) p the position of S. To obtain the time-averaged stationary values, we locally averaged over one period and extrapolated towards t → ∞ using the extrapolation procedure described in ref. 51.
p the position of S. To obtain the time-averaged stationary values, we locally averaged over one period and extrapolated towards t → ∞ using the extrapolation procedure described in ref. 51.
With this procedure, we get the force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) =
= ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) p +
p + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) v with pressure component
v with pressure component ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) p = 〈
p = 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)〉 and viscous component
(p)〉 and viscous component ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) v = 〈
v = 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v)〉 as well as the torque T = Tp + Tv with components Tp = 〈T(p)〉 and Tv = 〈T(v)〉 acting on the particle, where 〈⋅〉 denotes the time average. To calculate the translational–angular velocity vector
(v)〉 as well as the torque T = Tp + Tv with components Tp = 〈T(p)〉 and Tv = 〈T(v)〉 acting on the particle, where 〈⋅〉 denotes the time average. To calculate the translational–angular velocity vector 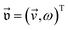 with the particle's translational velocity
with the particle's translational velocity 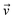 and angular velocity ω, we define the force-torque vector
and angular velocity ω, we define the force-torque vector 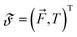 . Then the values of
. Then the values of 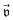 can be calculated with the Stokes law as78
can be calculated with the Stokes law as78
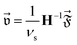 | (4) |
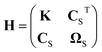 | (5) |
Since we consider a system with two spatial dimensions to keep the computational effort for the simulations manageable, we cannot use eqn (2)–(4) directly. Hence, we assign a thickness of 1 μm to the particle, so that H can be calculated.79,80 The general structure of H for a particle with a shape as we study here is
 | (6) |
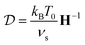 | (7) |
| χ | K 11/μm | K 22/μm | K 33/μm | C 13/μm2 | C 31/μm2 | Ω 11/μm3 | Ω 22/μm3 | Ω 33/μm3 |
|---|---|---|---|---|---|---|---|---|
| 0.25 | 8.58 | 11.29 | 8.98 | −0.38 | 0.61 | 3.44 | 4.76 | 4.75 |
| 0.5 | 8.49 | 9.72 | 8.14 | −0.14 | 0.4 | 3 | 3.36 | 2.63 |
| 0.75 | 8.76 | 9.07 | 7.94 | −0.03 | 0.11 | 3.06 | 3.03 | 2.22 |
| 1 | 9.03 | 8.77 | 7.94 | −0.01 | −0.14 | 3.18 | 2.96 | 2.27 |
| 1.5 | 9.69 | 8.57 | 8.13 | 0.25 | −0.54 | 3.68 | 2.97 | 2.68 |
| 2 | 10.15 | 8.55 | 8.39 | 0.43 | −0.9 | 4.25 | 3.08 | 3.29 |
| 2.5 | 10.61 | 8.56 | 8.59 | 0.6 | −1.21 | 4.86 | 3.17 | 3.97 |
| 3 | 11.02 | 8.64 | 8.84 | 0.77 | −1.5 | 5.53 | 3.29 | 4.69 |
| 3.5 | 11.41 | 8.75 | 9.08 | 0.95 | −1.79 | 6.23 | 3.41 | 5.47 |
| 4 | 11.67 | 8.87 | 9.33 | 1.1 | −2.07 | 6.94 | 3.51 | 6.27 |
We determine the components of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) and
and  parallel and perpendicular to the particle's orientation, i.e., parallel to the x2 and x1 axes, respectively. These components are the parallel force F∥ = (
parallel and perpendicular to the particle's orientation, i.e., parallel to the x2 and x1 axes, respectively. These components are the parallel force F∥ = (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) )2 = F∥,p + F∥,ν, with its pressure component F∥,p = (〈
)2 = F∥,p + F∥,ν, with its pressure component F∥,p = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)〉)2 and viscous component F∥,ν = (〈
(p)〉)2 and viscous component F∥,ν = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (ν)〉)2, perpendicular force F⊥ = (〈
(ν)〉)2, perpendicular force F⊥ = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ⊥〉)1 = F⊥,p + F⊥,ν with the components F⊥,p = (〈
⊥〉)1 = F⊥,p + F⊥,ν with the components F⊥,p = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)〉)1 and F⊥,ν = (〈
(p)〉)1 and F⊥,ν = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (ν)〉)1, parallel speed
(ν)〉)1, parallel speed 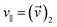 , and perpendicular speed
, and perpendicular speed 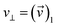 .
.
Nondimensionalization of the governing equations leads to four dimensionless numbers: the Euler number Eu corresponding to the pressure amplitude of the ultrasound wave entering the simulated system, the Helmholtz number He corresponding to the frequency of the ultrasound wave, a Reynolds number Reb corresponding to the bulk viscosity, and another Reynolds number Res corresponding to the shear viscosity. Table 2 shows the names and symbols of the parameters that are relevant for our simulations and their values that we have chosen in analogy to the values used in ref. 51. By using the parameter values from Table 2, the dimensionless numbers for our simulations have the following values:
Eu = Δp/(ρ0Δv2) ≈ 219![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919, 919, | (8) |
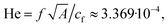 | (9) |
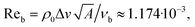 | (10) |
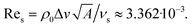 | (11) |
The Euler number Eu denotes the ratio of the pressure amplitude and the inertial force density of the liquid that corresponds to the oscillatory motion of the liquid resulting from the ultrasound wave. Since Eu ≫ 1, the inertial force density is negligible compared to the pressure amplitude. With the Helmholtz number He, the ratio of the size of the particle and the wavelength of the ultrasound is denoted. Here, He ≪ 1 since the particle is much smaller than the wavelength. The Reynolds numbers correspond to the ratio of the inertial forces and viscous forces acting on the particle. Since Reb ≪ 1 and Res ≪ 1, the viscous forces clearly dominate. Note that the Reynolds number
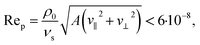 | (12) |
III. Results and discussion
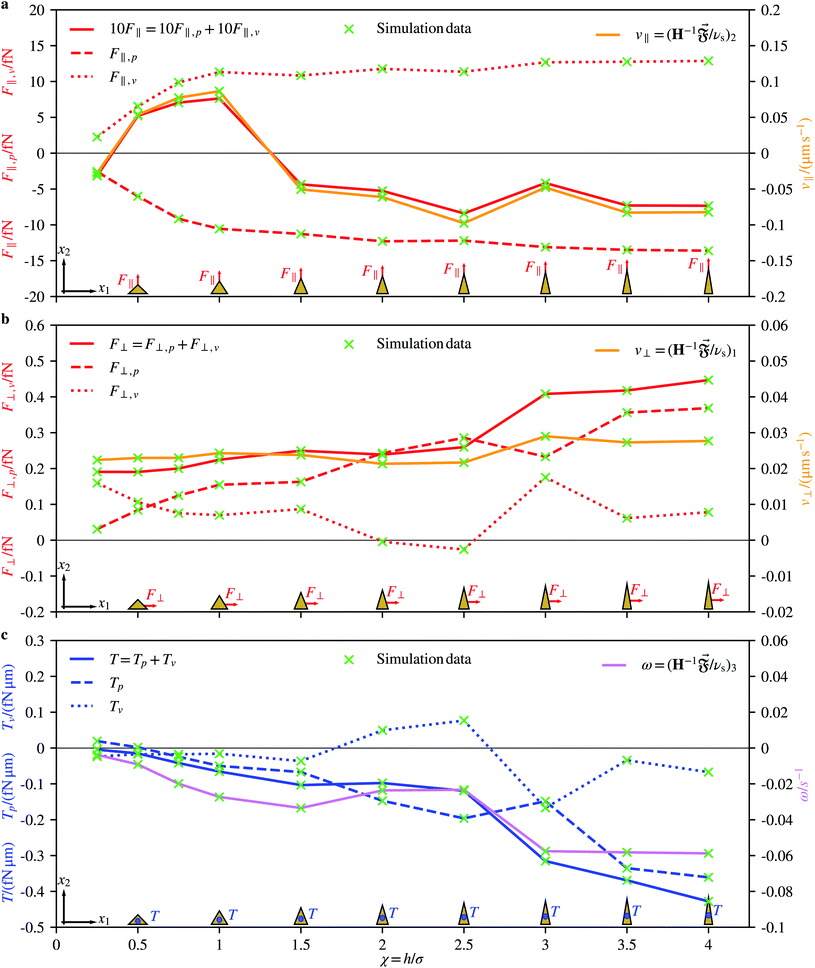
Fig. 2 shows our results for the propulsion-force components F∥ and F⊥, propulsion torque T, translational-propulsion-velocity components v∥ and v⊥, and angular propulsion velocity ω as functions of the aspect ratio χ ∈ [0.25,4].The force F∥ and velocity v∥ have a strong dependence on the aspect ratio χ. This includes even a sign change. Both curves have qualitatively the same course. They start at χ = 0.25 with negative propulsion force F∥ = −0.32 fN and velocity v∥ = −0.028 μm s−1. Increasing χ leads to a positive sign of F∥ and v∥ until about χ = 1 where the force is maximal with F∥ = 0.76 fN and also the speed reaches its maximum v∥ = 0.086 μm s−1. Afterwards, the propulsion force and velocity decrease to and remain at negative values. The globally maximal amplitude is reached at χ = 2.5, where F∥ = −0.84 fN and v∥ = −0.098 μm s−1. In the further course of the curves, the values rise until χ = 3 and then decrease again until χ = 4, where the values saturate at F∥ = −0.73 fN and v∥ = −0.082 μm s−1.
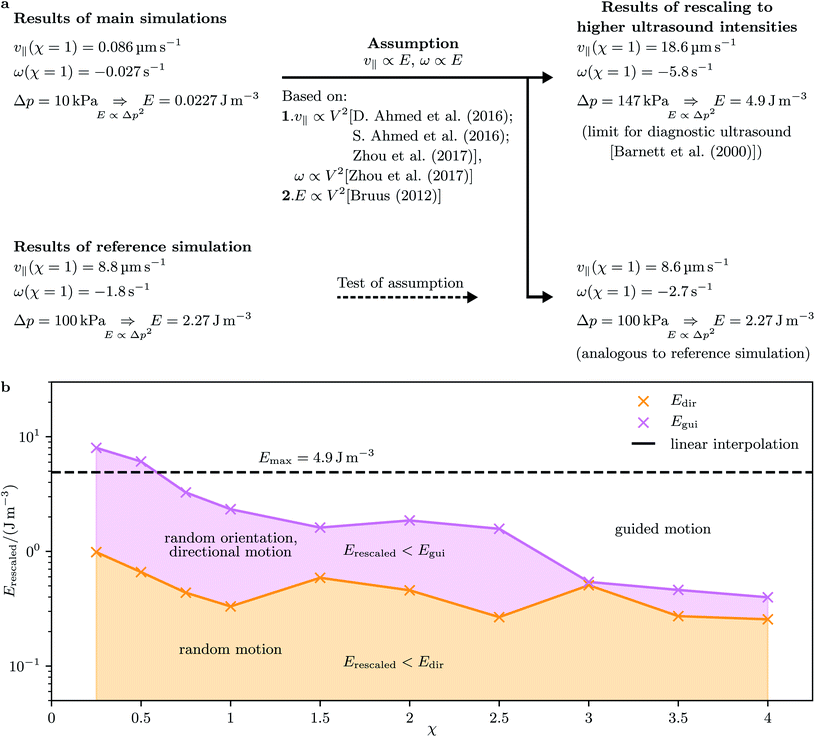
According to amount, the largest velocity v∥ = −0.098 μm s−1, found here for χ = 2.5, is about 80% larger than the velocity of cone-shaped particles with aspect ratio χ = 0.5 studied in previous work.51 Since the energy density E = 0.0227 J m−3 used in the present work is strongly smaller than the largest energy density Emax = 4.9 J m−3 allowed by the U.S. Food and Drug Administration for diagnostic applications in the human body,74 the results can be extrapolated to higher energies. To be able to do this, we need to make some assumption. In experiments, the velocity39,40,55 and energy density75 were measured to be proportional to the squared amplitude of the driving voltage. The same dependence on the amplitude of the driving voltage was observed in experiments for the angular velocity.55 Therefore, we assume that the velocities are proportional to the energy density. To confirm this assumption by direct simulations, we performed an additional simulation for χ = 1 and a 10 times larger pressure amplitude, i.e., a 100 times larger energy density, which means an energy density of the same magnitude as Emax. This reference simulation yielded an increase of the translational velocity by a factor ≈103 and an increase of the angular velocity by a factor ≈66, which is in sufficient agreement with the assumed scaling of the velocities with the pressure amplitude. See Fig. 3a for a sketch illustrating the rescaling procedure. Rescaling the highest magnitude of the translational velocity, which is attained at χ = 2.5, to the higher energy density Emax based on the assumed scaling, results in the Emax/E = 216 times higher value vrescaled = 21.2 μm s−1. For χ = 2.5, the values of the parameters describing the particle size are σ = 0.45 μm and h = 1.12 μm. With the higher energy density Emax, the particle would thus move with a speed of roughly 19 body lengths per second. For the largest positive velocity, which corresponds to χ = 1, the rescaled speed has the value vrescaled = 18.6 μm s−1. Since the size parameters are now σ = 0.71 μm and h = 0.71 μm, this speed equals 26.2 body lengths per second. Depending on the particular application, one can therefore choose an aspect ratio of χ = 2.5 or χ = 1 to reach a maximal absolute speed or a maximal speed related to the particle length, respectively. For medical applications, compact particles in a certain size range are necessary6,81,82 such that they do not block the blood flow. Therefore, the aspect ratio χ = 1 could be preferable for these types of applications.
The dependence of F∥,p and F∥,v on the aspect ratio is simpler. Both values keep their sign with F∥,p as a negative force and F∥,v as a positive force. The magnitude of both values increases until χ = 1 fast to F∥,p = −10.56 fN and F∥,v = 11.32 fN. Afterwards, the magnitude oscillates a little bit but with the tendency to increase slowly towards F∥,p = −13.60 fN and F∥,v = 12.87 fN at χ = 4.
We now consider the propulsion parallel to the direction of propagation of the ultrasound wave. The perpendicular propulsion force F⊥ increases for increasing χ slowly until χ = 1.5 to F⊥ = 0.25 fN. Then it is constant until χ = 2.5. From χ = 2.5 to χ = 3 a strong increase occurs to F⊥ = 0.41 fN. Subsequently, a slow further increase follows. The perpendicular velocity v⊥ can be seen as roughly constant with v⊥ = 0.023 μm s−1 until χ = 2.5 and then it has a small rise to χ = 3 with v⊥ = 0.03 μm s−1. Afterwards, it is roughly constant again. This behavior can be understood as follows: in the direction of ultrasound propagation, two opposing forces act on a particle. These are the acoustic radiation force and the acoustic streaming force. Typically, for a particle with a size of about a micrometer, the acoustic radiation force is the dominant one.83–85 The scaling behavior of the acoustic radiation force is nontrivial for nonspherical shapes, but for a sphere it scales linearly with the particle volume.75 Since we kept the particle volume constant, it is therefore reasonable that the velocity v⊥ shows no strong change when the aspect ratio of the particle is varied.
The value of the pressure component F⊥,p of the force F⊥ increases for increasing χ and the value of the viscous component F⊥,v decreases roughly until χ = 2.5, except for a slight intermediate growth of F⊥,v near χ = 1.5. At χ = 3, there is a downwards oriented peak in the amplitude for both components. Afterwards, the amplitude increases again for both components, and from χ = 3.5 onwards the values of both components increase slightly.
When the particle, which we assume here to be made of gold, is exposed to gravity, the additional force
| Fg = Vp(ρp − ρ0)g = 2.29 fN | (13) |
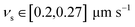 , which follows from the Stokes law (4). As one can see, the influence of gravity on the motion of the particle would not be negligible but much smaller than the propulsion speed that is achieved for suitable values of the aspect ratio χ and for the energy density Emax.
, which follows from the Stokes law (4). As one can see, the influence of gravity on the motion of the particle would not be negligible but much smaller than the propulsion speed that is achieved for suitable values of the aspect ratio χ and for the energy density Emax.
Using eqn (7), we can estimate the effect of Brownian motion on the motion of the particle. If we address translational Brownian motion along the orientation of the particle, the diffusion coefficient 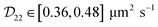 is relevant. Translational Brownian motion in this direction would therefore be of the order 1 μm s−1. This shows that Brownian motion would be visible in experiments but could be clearly dominated by the acoustic propulsion for suitable values of χ and E = Emax.
is relevant. Translational Brownian motion in this direction would therefore be of the order 1 μm s−1. This shows that Brownian motion would be visible in experiments but could be clearly dominated by the acoustic propulsion for suitable values of χ and E = Emax.
Since the time period of sound τ = 1 μs is very small and the flow velocity amplitude Δv = 6.75 mm s−1 is rather large, both sedimentation and Brownian motion would change the position of a particle only negligibly during a sound period. Therefore, we can expect that sedimentation and Brownian motion cannot affect the acoustic propulsion mechanism. Instead, they lead to independent contributions to the particle motion that can be described by additive terms. This justifies the assumption of a fixed particle in our simulations (see Methods).
The torque acting on the considered particle shapes is for all aspect ratios, according to amount, rather small. It decreases for increasing χ from T = −0.005 fN μm to T = −0.43 fN μm, where the curve has a small local maximum at χ = 2. The corresponding angular velocity decreases from ω = −0.004 s−1 at χ = 0.25 to ω = −0.033 s−1 at χ = 1.5, increases afterwards to ω = −0.023 s−1 at χ = 2.5, decreases again to ω = −0.06 s−1 at χ = 3, and remains there for larger values of χ.
We now consider the effect of rotational Brownian motion on the particle motion and how it depends on the aspect ratio χ of the particle and the energy density E of the ultrasound. Note that the acoustic propulsion of the particles depends on χ and E, whereas Brownian motion depends only on χ as long as E remains moderate. For energy densities below Emax, we can expect that there is no significant heating of water by the ultrasound so that Brownian motion is not affected. First, we study the occurrence of directional motion by the propulsion. In this case, the motion of the particle must have a preferred direction that originates from the acoustic propulsion. For this, the Brownian rotation of the particle must be very small during a time period τ of the ultrasound or, equivalently, τ must be small compared to the Brownian reorientation time τR = DR−1 with the particle's rotational diffusion coefficient 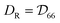 :
:
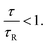 | (14) |
Since τ = 1 μs and τR ∈ [0.5,1.6]s for our setup, the first condition is fulfilled for all considered values of χ and E. Furthermore, the particle must move significantly by its propulsion during the reorientation time τR. This means that the persistence length 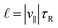 must be larger than the particle size:
must be larger than the particle size:
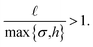 | (15) |
Assuming the scaling |v∥| ∝ E, this condition is fulfilled for energies above
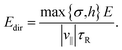 | (16) |
This condition is fulfilled, e.g., if we consider particles with aspect ratio χ = 1, where σ = h = 0.71 μm, DR = 1.78 s−1, and τR = 0.56 s apply and where we found a speed of 0.1211 body lengths per second, and increase E by a factor 15. For E < Edir, one will observe no clear directional motion but random motion. Second, we study the occurrence of guided motion. This occurs when the torque T exerted on the particle has a larger effect on its orientation than Brownian rotation has. The condition for guided motion can be written as
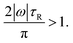 | (17) |
This condition follows from comparing the time π/(2|ω|), in which the angular velocity ω rotates the particle by 90 degrees, with the Brownian reorientation time τR. Assuming the scaling |ω| ∝ E, this condition is fulfilled for energies above
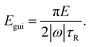 | (18) |
For the values of χ and E used in our main simulations, the condition (17) is not fulfilled since the small values of the torques that we obtained by our simulations are negligible compared to the rotational Brownian motion of the particles. This indicates that there is either no preferred orientation of the particles or a stable orientation is close to the particle orientation considered in the present work. Considering the aspect ratio χ = 4, where we found, according to the amount, the largest torque T = −0.43 fN μm and angular velocity ω = −0.06 s−1, a change of the particle orientation by 90 degrees takes roughly 26 s. On the other hand, the rotational diffusion coefficient DR = 0.68 s−1 of the particle shows that the particle orientation changes significantly by Brownian rotation on the time scale τR = DR−1 = 1.46 s. This estimate clearly shows that the torques resulting from the ultrasound are so weak that they are dominated by Brownian rotation. However, if the angular velocity is rescaled to the energy density Emax, a change of the particle orientation by 90 degrees needs only 0.12 s and is thus dominant compared to the Brownian rotation. For E < Egui, one will observe no guided motion, but random orientations of the particles that result from Brownian rotation and are typical also for active Brownian particles.86Fig. 3b gives an overview about the type of motion of the particles that can be expected for the various considered aspect ratios χ and higher energy densities Erescaled > E. As one can see, Egui is larger than Edir for all considered values of χ.
Concerning the components of the torque, the pressure component Tp decreases (with superimposed fluctuations) for increasing χ from Tp = 0.02 fN μm to Tp = −0.36 fN μm, whereas the viscous component Tv fluctuates (with stronger amplitude than for Tp) around zero.
In summary, the force and velocity perpendicular to the direction of propagation of the ultrasound wave have a sign change at a particular value of the aspect ratio of the particle, the force and velocity parallel to the propagation direction do not change sign, and the torque is very weak.
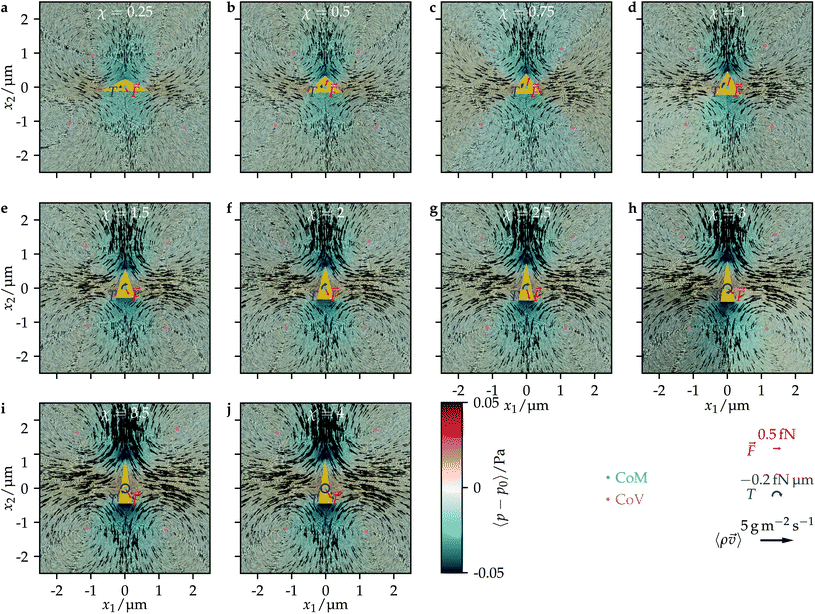
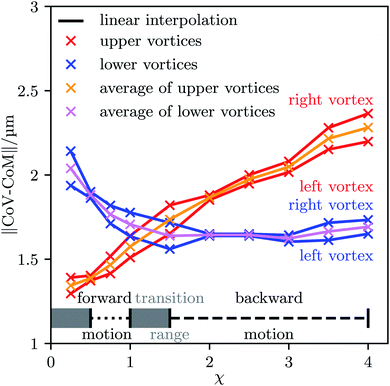
Our results are in line with the available theoretical results on ultrasound-propelled particles from the literature. In the theory of Collis et al.,63 the propulsion direction depends strongly on the acoustic Reynolds number β = ρ0σ2πf/(2νs), which ranges for our work between β = 0.2 for χ = 4 and β = 3.1 for χ = 0.25. They found that particles can change their propulsion direction up to two times when increasing the acoustic Reynolds number, which is exactly what happens here. According to their theory, this should happen for β ∼ O(1), which is perfectly in line with the interval of values for β we investigated. A similar result was found experimentally.38,39 There, long cylinders with spherical caps at the ends corresponding to an aspect ratio χ = 4.3 to χ = 17.3 are moving towards their concave end,39 whereas the short half-sphere cups with aspect ratio χ = 0.5 have a propulsion in the opposite direction.38 This is qualitatively the same behavior as for our particles, where the long ones with χ ≳ 1.5 are moving in the direction opposite to their convex end and the shorter ones with 0.5 ≲ χ ≲ 1 are moving towards the convex end. As a qualitative physical picture for the occurrence of the sign change of the propulsion direction, Collis et al.63 mentioned the χ-dependent distances of the vortices that are generated around a particle. Depending on the value of χ, either the vortices in front of a particle are closer to the particle than the vortices behind it, or vice versa. To study this consideration in the context of our work, we plotted the time-averaged flow field around a particle for each particle shape we addressed. The results are shown in Fig. 4. As one can see, the strength of the vortices increases with the particle's aspect ratio χ and also the positions of the vortices relative to the particle change with χ. There are two vortices above and below the particle. For low values of χ, the vortices in front of the particle are closer to each other and to the center of mass of the particle than the vortices behind it. The opposite applies for large values of χ. For some value 1 < χ < 1.5, both pairs of vortices have an equal distance from the center of mass. The distances of the vortices from the center of mass are plotted in Fig. 5 as functions of the aspect ratio χ. There, also the parameter ranges for which we found forward or backward motion of the particles are indicated. One can clearly see that the direction of propulsion correlates with the relative positions of the vortices. This is reasonable since the vortices lead to a suction at the particle so that those vortices that are closer to the particle determine in which direction it moves.
IV. Conclusions
We have studied the acoustic propulsion of nano- and microcones powered by a traveling ultrasound wave through direct numerical simulations. Our results show that the propulsion of the particles depends sensitively on their aspect ratio and includes both fast forward and fast backward motion. We found that the direction of motion depends on the distances of the vortices, which are generated around a particle, from the particle. These distances depend on the aspect ratio of the particle, and the particle typically moves towards the vortices that are next to it. The strong dependence of the propulsion on the aspect ratio could be used to separate and sort artificial and natural cone-shaped particles (such as carbon nanocones) in an efficient and easy way with respect to their aspect ratio. For later applications of cone-shaped ultrasound-propelled particles, e.g., in medicine, an aspect ratio of χ = 1 was identified as a very suitable choice, since it combines a compact particle shape with a large body-lengths-per-time speed. This finding also suggests to use cone-shaped particles with this aspect ratio as a more efficient particle design for future experiments.The maximum particle speed of 21.2 μm s−1, which we obtained for the still harmless energy density Emax, is of the same order of magnitude as the flow velocity 100 μm s−1 (ref. 7) that is typical for blood flow in the capillaries, which constitute by far the largest part of a human's vascular system. However, for a medical application where ultrasound-propelled particles shall transport drugs through the vascular system, this speed is a little too low. It is likely that by optimizing other parameters besides the particle shape, such as the frequency of the ultrasound, the particle speed can further be increased so that the particles can overcome blood flow for harmless ultrasound intensities. Furthermore, the studied particles can already be used in medicine when they are applied outside of the vascular system. An example is an application in the eye, where they could be used to transport drugs through the flow-free vitreous body to the retina.87
The obtained results are in good agreement with the literature and expand the understanding of acoustically propelled colloidal particles, which is helpful with regard to future experiments and applications in nanomedicine or materials science. Furthermore, the knowledge about the particle propulsion can be used to model this propulsion when describing the dynamics of the particles via Langevin equations88,89 or field theories based on symmetry-based modeling,90,91 the interaction–expansion method,92,93 classical dynamical density functional theory,94,95 or other analytical approaches on time scales that are much larger than the period of the ultrasound.
In the future, this study should be extended by considering other particle orientations and studying how the propulsion depends on the angle between the particle orientation and the direction of propagation of the ultrasound. Furthermore, the dependence of the propulsion on parameters like the ultrasound frequency, pressure amplitude, and fluid viscosity still need to be investigated. For the latter case, the results of previous experiments suggest that the propulsion speed increases for decreasing viscosity.27,29,30,46,49 It is, therefore, likely that the ratio of acoustic propulsion and Brownian motion depends on the viscosity.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Patrick Kurzeja for helpful discussions. R. W. is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – WI 4170/3-1. The simulations for this work were performed on the computer cluster PALMA II of the University of Münster.References
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Active particles in complex and crowded environments, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- P. Venugopalan, B. Esteban-Fernández de Ávila, M. Pal, A. Ghosh and J. Wang, Fantastic voyage of nanomotors into the cell, ACS Nano, 2020, 14, 9423–9439 CrossRef CAS.
- M. Fernández-Medina, M. A. Ramos-Docampo, O. Hovorka, V. Salgueiriño and B. Städler, Recent advances in nano- and micromotors, Adv. Funct. Mater., 2020, 30, 1908283 CrossRef.
- Q. Yang, L. Xu, W. Zhong, Q. Yan, Y. Gao, W. Hong, Y. She and G. Yang, Recent advances in motion control of micro/nanomotors, , Adv. Intell. Syst., 2020, 2, 2000049 CrossRef.
- T. Xu, L. Xu and X. Zhang, Ultrasound propulsion of micro-/nanomotors, Appl. Mater. Today, 2017, 9, 493–503 CrossRef.
- M. Luo, Y. Feng, T. Wang and J. Guan, Micro-/Nanorobots at work in active drug delivery, Adv. Funct. Mater., 2018, 28, 1706100 CrossRef.
- P. Erkoc, I. C. Yasa, H. Ceylan, O. Yasa, Y. Alapan and M. Sitti, Mobile microrobots for active therapeutic delivery, Adv. Ther., 2019, 2, 1800064 CrossRef.
- J. Li, B. Esteban-Fernández de Ávila, W. Gao, L. Zhang and J. Wang, Micro/Nanorobots for biomedicine: delivery, surgery, sensing, and detoxification, Sci. Robot., 2017, 2, eaam6431 CrossRef.
- F. Peng, Y. Tu and D. A. Wilson, Micro/Nanomotors towards in vivo application: cell, tissue and biofluid, Chem. Soc. Rev., 2017, 46, 5289–5310 RSC.
- F. Soto and R. Chrostowski, Frontiers of medical micro/nanorobotics: in vivo applications and commercialization perspectives toward clinical uses, Front. Bioeng. Biotechnol., 2018, 6, 170 CrossRef.
- D. Wang, C. Gao, C. Zhou, Z. Lin and Q. He, Leukocyte membrane-coated liquid metal nanoswimmers for actively targeted delivery and synergistic chemophotothermal therapy, Research, 2020, 2020, 3676954 CAS.
- W. Wang and C. Zhou, A journey of nanomotors for targeted cancer therapy: principles, challenges, and a critical review of the state-of-the-art, Adv. Healthcare Mater., 2021, 10, 2001236 CrossRef CAS.
- A. Visser, Biomixing of the oceans?, Science, 2007, 316, 838–839 CrossRef CAS PubMed.
- F. Kümmel, P. Shabestari, C. Lozano, G. Volpe and C. Bechinger, Formation, compression and surface melting of colloidal clusters by active particles, Soft Matter, 2015, 11, 6187–6191 RSC.
- B. van der Meer, M. Dijkstra and L. Filion, Removing grain boundaries from three-dimensional colloidal crystals using active dopants, Soft Matter, 2016, 12, 5630–5635 RSC.
- R. Jeanneret, D. Pushkin, V. Kantsler and M. Polin, Entrainment dominates the interaction of microalgae with micron-sized objects, Nat. Commun., 2016, 7, 12518 CrossRef CAS.
- D. Needleman and Z. Dogic, Active matter at the interface between materials science and cell biology, Nat. Rev. Mater., 2017, 2, 17048 CrossRef CAS.
- Y. Wang, W. Duan, C. Zhou, Q. Liu, J. Gu, H. Ye, M. Li, W. Wang and X. Ma, Phoretic liquid metal micro/nanomotors as intelligent filler for targeted microwelding, Adv. Mater., 2019, 31, 1905067 CrossRef CAS.
- S. Ramananarivo, E. Ducrot and J. Palacci, Activity-controlled annealing of colloidal monolayers, Nat. Commun., 2019, 10, 3380 CrossRef PubMed.
- S. J. Ebbens and J. R. Howse, In pursuit of propulsion at the nanoscale, Soft Matter, 2010, 6, 726–738 RSC.
- B. Esteban-Fernández de Ávila, P. Angsantikul, J. Li, W. Gao, L. Zhang and J. Wang, Micromotors go in vivo: from test tubes to live animals, Adv. Funct. Mater., 2018, 28, 1705640 CrossRef.
- M. Safdar, S. U. Khan and J. Jänis, Progress toward catalytic micro- and nanomotors for biomedical and environmental applications, Adv. Mater., 2018, 30, 1703660 CrossRef PubMed.
- D. Kagan, M. J. Benchimol, J. C. Claussen, E. Chuluun-Erdene, S. Esener and J. Wang, Acoustic droplet vaporization and propulsion of perfluorocarbon-loaded microbullets for targeted tissue penetration and deformation, Angew. Chem., Int. Ed., 2012, 51, 7519–7522 CrossRef CAS.
- M. Xuan, J. Shao, C. Gao, W. Wang, L. Dai and Q. He, Self-propelled nanomotors for thermomechanically percolating cell membranes, Angew. Chem., Int. Ed., 2018, 57, 12463–12467 CrossRef CAS.
- Z. Xu, M. Chen, H. Lee, S.-P. Feng, J. Y. Park, S. Lee and J. T. Kim, X-ray-powered micromotors, ACS Appl. Mater. Interfaces, 2019, 11, 15727–15732 CrossRef CAS.
- W. Wang, L. Castro, M. Hoyos and T. E. Mallouk, Autonomous motion of metallic microrods propelled by ultrasound, ACS Nano, 2012, 6, 6122–6132 CrossRef CAS PubMed.
- V. Garcia-Gradilla, J. Orozco, S. Sattayasamitsathit, F. Soto, F. Kuralay, A. Pourazary, A. Katzenberg, W. Gao, Y. Shen and J. Wang, Functionalized ultrasound-propelled magnetically guided nanomotors: toward practical biomedical applications, ACS Nano, 2013, 7, 9232–9240 CrossRef CAS PubMed.
- S. Ahmed, W. Wang, L. O. Mair, R. D. Fraleigh, S. Li, L. A. Castro, M. Hoyos, T. J. Huang and T. E. Mallouk, Steering acoustically propelled nanowire motors toward cells in a biologically compatible environment using magnetic fields, Langmuir, 2013, 29, 16113–16118 CrossRef CAS PubMed.
- Z. Wu, T. Li, J. Li, W. Gao, T. Xu, C. Christianson, W. Gao, M. Galarnyk, Q. He, L. Zhang and J. Wang, Turning erythrocytes into functional micromotors, ACS Nano, 2014, 8, 12041–12048 CrossRef CAS.
- W. Wang, S. Li, L. Mair, S. Ahmed, T. J. Huang and T. E. Mallouk, Acoustic propulsion of nanorod motors inside living cells, Angew. Chem., Int. Ed., 2014, 53, 3201–3204 CrossRef CAS.
- V. Garcia-Gradilla, S. Sattayasamitsathit, F. Soto, F. Kuralay, C. Yardımcı, D. Wiitala, M. Galarnyk and J. Wang, Ultrasound-propelled nanoporous gold wire for efficient drug loading and release, Small, 2014, 10, 4154–4159 CAS.
- A. L. Balk, L. O. Mair, P. P. Mathai, P. N. Patrone, W. Wang, S. Ahmed, T. E. Mallouk, J. A. Liddle and S. M. Stavis, Kilohertz rotation of nanorods propelled by ultrasound, traced by microvortex advection of nanoparticles, ACS Nano, 2014, 8, 8300–8309 CrossRef CAS.
- S. Ahmed, D. T. Gentekos, C. A. Fink and T. E. Mallouk, Self-assembly of nanorod motors into geometrically regular multimers and their propulsion by ultrasound, ACS Nano, 2014, 8, 11053–11060 CrossRef CAS.
- B. Esteban-Fernández de Ávila, A. Martín, F. Soto, M. A. Lopez-Ramirez, S. Campuzano, G. M. Vásquez-Machado, W. Gao, L. Zhang and J. Wang, Single cell real-time miRNAs sensing based on nanomotors, ACS Nano, 2015, 9, 6756–6764 CrossRef.
- Z. Wu, T. Li, W. Gao, W. Xu, B. Jurado-Sánchez, J. Li, W. Gao, Q. He, L. Zhang and J. Wang, Cell-membrane-coated synthetic nanomotors for effective biodetoxification, Adv. Funct. Mater., 2015, 25, 3881–3887 CrossRef CAS.
- Z. Wu, B. Esteban-Fernández de Ávila, A. Martín, C. Christianson, W. Gao, S. K. Thamphiwatana, A. Escarpa, Q. He, L. Zhang and J. Wang, RBC micromotors carrying multiple cargos towards potential theranostic applications, Nanoscale, 2015, 7, 13680–13686 RSC.
- B. Esteban-Fernández de Ávila, C. Angell, F. Soto, M. A. Lopez-Ramirez, D. F. Báez, S. Xie, J. Wang and Y. Chen, Acoustically propelled nanomotors for intracellular siRNA delivery, ACS Nano, 2016, 10, 4997–5005 CrossRef.
- F. Soto, G. L. Wagner, V. Garcia-Gradilla, K. T. Gillespie, D. R. Lakshmipathy, E. Karshalev, C. Angell, Y. Chen and J. Wang, Acoustically propelled nanoshells, Nanoscale, 2016, 8, 17788–17793 RSC.
- S. Ahmed, W. Wang, L. Bai, D. T. Gentekos, M. Hoyos and T. E. Mallouk, Density and shape effects in the acoustic propulsion of bimetallic nanorod motors, ACS Nano, 2016, 10, 4763–4769 CrossRef CAS.
- D. Ahmed, T. Baasch, B. Jang, S. Pane, J. Dual and B. J. Nelson, Artificial swimmers propelled by acoustically activated flagella, Nano Lett., 2016, 16, 4968–4974 CrossRef CAS PubMed.
- M. Uygun, B. Jurado-Sánchez, D. A. Uygun, V. V. Singh, L. Zhang and J. Wang, Ultrasound-propelled nanowire motors enhance asparaginase enzymatic activity against cancer cells, Nanoscale, 2017, 9, 18423–18429 RSC.
- B. Esteban-Fernández de Ávila, D. E. Ramírez-Herrera, S. Campuzano, P. Angsantikul, L. Zhang and J. Wang, Nanomotor-enabled pH-responsive intracellular delivery of caspase-3: toward rapid cell apoptosis, ACS Nano, 2017, 11, 5367–5374 CrossRef PubMed.
- M. Hansen-Bruhn, B. Esteban-Fernández de Ávila, M. Beltrán-Gastélum, J. Zhao, D. E. Ramírez-Herrera, P. Angsantikul, K. Vesterager Gothelf, L. Zhang and J. Wang, Active intracellular delivery of a Cas9/sgRNA complex using ultrasound-propelled nanomotors, Angew. Chem., Int. Ed., 2018, 57, 2657–2661 CrossRef CAS PubMed.
- S. Sabrina, M. Tasinkevych, S. Ahmed, A. M. Brooks, M. Olvera de la Cruz, T. E. Mallouk and K. J. M. Bishop, Shape-directed microspinners powered by ultrasound, ACS Nano, 2018, 12, 2939–2947 CrossRef CAS PubMed.
- D. Wang, C. Gao, W. Wang, M. Sun, B. Guo, H. Xie and Q. He, Shape-transformable, fusible rodlike swimming liquid metal nanomachine, ACS Nano, 2018, 12, 10212–10220 CrossRef CAS.
- B. Esteban-Fernández de Ávila, P. Angsantikul, D. E. Ramírez-Herrera, F. Soto, H. Teymourian, D. Dehaini, Y. Chen, L. Zhang and J. Wang, Hybrid biomembrane–functionalized nanorobots for concurrent removal of pathogenic bacteria and toxins, Sci. Robot., 2018, 3, eaat0485 CrossRef PubMed.
- X. Lu, H. Shen, Z. Wang, K. Zhao, H. Peng and W. Liu, Micro/Nano machines driven by ultrasound power sources, Chem. - Asian J., 2019, 14, 2406–2416 CrossRef CAS PubMed.
- J. R. Qualliotine, G. Bolat, M. Beltrán-Gastélum, B. Esteban-Fernández de Ávila, J. Wang and J. A. Califano, Acoustic nanomotors for detection of human papillomavirus-associated head and neck cancer, Otolaryngol.--Head Neck Surg., 2019, 161, 814–822 CrossRef PubMed.
- C. Gao, Z. Lin, D. Wang, Z. Wu, H. Xie and Q. He, Red blood cell-mimicking micromotor for active photodynamic cancer therapy, ACS Appl. Mater. Interfaces, 2019, 11, 23392–23400 CrossRef CAS.
- L. Ren, N. Nama, J. M. McNeill, F. Soto, Z. Yan, W. Liu, W. Wang, J. Wang and T. E. Mallouk, 3D steerable, acoustically powered microswimmers for single-particle manipulation, Sci. Adv., 2019, 5, eaax3084 CrossRef CAS PubMed.
- J. Voß and R. Wittkowski, On the shape-dependent propulsion of nano- and microparticles by traveling ultrasound waves, Nanoscale Adv., 2020, 2, 3890–3899 RSC.
- K. J. Rao, F. Li, L. Meng, H. Zheng, F. Cai and W. Wang, A force to be reckoned with: a review of synthetic microswimmers powered by ultrasound, Small, 2015, 11, 2836–2846 CrossRef CAS.
- M. Kaynak, A. Ozcelik, A. Nourhani, P. E. Lammert, V. H. Crespi and T. J. Huang, Acoustic actuation of bioinspired microswimmers, Lab Chip, 2017, 17, 395–400 RSC.
- C. Zhou, J. Yin, C. Wu, L. Du and Y. Wang, Efficient target capture and transport by fuel-free micromotors in a multichannel microchip, Soft Matter, 2017, 13, 8064–8069 RSC.
- C. Zhou, L. Zhao, M. Wei and W. Wang, Twists and turns of orbiting and spinning metallic microparticles powered by megahertz ultrasound, ACS Nano, 2017, 11, 12668–12676 CrossRef CAS.
- L. Ren, W. Wang and T. E. Mallouk, Two forces are better than one: combining chemical and acoustic propulsion for enhanced micromotor functionality, Acc. Chem. Res., 2018, 51, 1948–1956 CrossRef CAS.
- M. Valdez-Garduño, M. Leal-Estrada, E. S. Oliveros-Mata, D. I. Sandoval-Bojorquez, F. Soto, J. Wang and V. Garcia-Gradilla, Density asymmetry driven propulsion of ultrasound-powered Janus micromotors, Adv. Funct. Mater., 2020, 30, 2004043 CrossRef.
- A. Aghakhani, O. Yasa, P. Wrede and M. Sitti, Acoustically powered surface-slipping mobile microrobots, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 3469–3477 CrossRef CAS.
- J. Liu and H. Ruan, Modeling of an acoustically actuated artificial micro-swimmer, Bioinspir. Biomim., 2020, 15, 036002 CrossRef PubMed.
- G. Dumy, N. Jeger-Madiot, X. Benoit-Gonin, T. Mallouk, M. Hoyos and J. Aider, Acoustic manipulation of dense nanorods in microgravity, Microgravity Sci. Technol., 2020, 32, 1159–1174 CrossRef CAS.
- F. Nadal and E. Lauga, Asymmetric steady streaming as a mechanism for acoustic propulsion of rigid bodies, Phys. Fluids, 2014, 26, 082001 CrossRef.
- W. Wang, W. Duan, Z. Zhang, M. Sun, A. Sen and T. E. Mallouk, A tale of two forces: simultaneous chemical and acoustic propulsion of bimetallic micromotors, Chem. Commun., 2015, 51, 1020–1023 RSC.
- J. F. Collis, D. Chakraborty and J. E. Sader, Autonomous propulsion of nanorods trapped in an acoustic field, J. Fluid Mech., 2017, 825, 29–48 CrossRef CAS.
- S. Tang, et al., Structure-dependent optical modulation of propulsion and collective behavior of acoustic/light-driven hybrid microbowls, Adv. Funct. Mater., 2019, 29, 1809003 CrossRef.
- D. Zhou, Y. Gao, J. Yang, Y. C. Li, G. Shao, G. Zhang, T. Li and L. Li, Light-ultrasound driven collective firework behavior of nanomotors, Adv. Sci., 2018, 5, 1800122 CrossRef.
- D. Ahmed, M. Lu, A. Nourhani, P. E. Lammert, Z. Stratton, H. S. Muddana, V. H. Crespi and T. J. Huang, Selectively manipulable acoustic-powered microswimmers, Sci. Rep., 2015, 5, 9744 CrossRef PubMed.
- J. Li, T. Li, T. Xu, M. Kiristi, W. Liu, Z. Wu and J. Wang, Magneto-acoustic hybrid nanomotor, Nano Lett., 2015, 15, 4814–4821 CrossRef CAS PubMed.
- L. Ren, D. Zhou, Z. Mao, P. Xu, T. J. Huang and T. E. Mallouk, Rheotaxis of bimetallic micromotors driven by chemical-acoustic hybrid power, ACS Nano, 2017, 11, 10591–10598 CrossRef CAS.
- M. Kaynak, A. Ozcelik, N. Nama, A. Nourhani, P. E. Lammert, V. H. Crespi and T. J. Huang, Acoustofluidic actuation of in situ fabricated microrotors, Lab Chip, 2016, 16, 3532–3537 RSC.
- K. Kim, J. Guo, Z. Liang, F. Zhu and D. Fan, Man-made rotary nanomotors: a review of recent developments, Nanoscale, 2016, 8, 10471–10490 RSC.
- X.-Z. Chen, B. Jang, D. Ahmed, C. Hu, C. De Marco, M. Hoop, F. Mushtaq, B. J. Nelson and S. Pané, Small-scale machines driven by external power sources, Adv. Mater., 2018, 30, 1705061 CrossRef.
- J. Li, I. Rozen and J. Wang, Rocket science at the nanoscale, ACS Nano, 2016, 10, 5619–5634 CrossRef CAS.
- Z. L. Tsakadze, I. Levchenko, K. Ostrikov and S. Xu, Plasma-assisted self-organized growth of uniform carbon nanocone arrays, Carbon, 2007, 45, 2022–2030 CrossRef CAS.
- S. B. Barnett, G. R. Ter Haar, M. C. Ziskin, H. D. Rott, F. A. Duck and K. Maeda, International recommendations and guidelines for the safe use of diagnostic ultrasound in medicine, Ultrasound Med. Biol., 2000, 26, 355–366 CrossRef CAS.
- H. Bruus, Acoustofluidics 7: The acoustic radiation force on small particles, Lab Chip, 2012, 12, 1014–1021 RSC.
- H. G. Weller, G. Tabor, H. Jasak and C. Fureby, A tensorial approach to computational continuum mechanics using object-oriented techniques, Comput. Phys., 1998, 12, 620–631 CrossRef.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Landau and Lifshitz: Course of Theoretical Physics, Butterworth-Heinemann, Oxford, 2nd edn, vol. 6, 1987 Search PubMed.
- J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, Mechanics of Fluids and Transport Processes, Kluwer Academic Publishers, Dordrecht, 2nd edn, 1991, vol. 1 Search PubMed.
- J. Voß and R. Wittkowski, Hydrodynamic Resistance Matrices of Colloidal Particles with Various Shapes, preprint, arXiv:1811.01269, 2018 Search PubMed.
- J. Voß, J. Jeggle, and R. Wittkowski, HydResMat – FEM-Based Code for Calculating the Hydrodynamic Resistance Matrix of an Arbitrarily-Shaped Colloidal Particle, Zenodo, 2019, DOI:10.5281/zenodo.3541588.
- M. E. Davis, Z. Chen and D. M. Shin, Nanoparticle therapeutics: an emerging treatment modality for cancer, Nat. Rev. Drug Discovery, 2008, 7, 771–782 CrossRef CAS.
- L. Reinišová, S. Hermanová and M. Pumera, Micro/Nanomachines: what is needed for them to become a real force in cancer therapy?, Nanoscale, 2019, 11, 6519–6532 RSC.
- R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Acoustic radiation- and streaming-induced microparticle velocities determined by microparticle image velocimetry in an ultrasound symmetry plane, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056307 CrossRef PubMed.
- P. B. Muller, R. Barnkob, M. J. H. Jensen and H. Bruus, A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces, Lab Chip, 2012, 12, 4617–4627 RSC.
- M. Wiklund, R. Green and M. Ohlin, Acoustofluidics 14: Applications of acoustic streaming in microfluidic devices, Lab Chip, 2012, 12, 2438–2451 RSC.
- P. Romanczuk, M. Bär, W. Ebeling, B. Lindner and L. Schimansky-Geier, Active Brownian particles. From individual to collective stochastic dynamics, Eur. Phys. J.: Spec. Top., 2012, 202, 1–162 CAS.
- Z. Wu, et al., A swarm of slippery micropropellers penetrates the vitreous body of the eye, Sci. Adv., 2018, 4, eaat4388 CrossRef CAS PubMed.
- R. Wittkowski and H. Löwen, Self-propelled Brownian spinning top: dynamics of a biaxial swimmer at low Reynolds numbers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021406 CrossRef PubMed.
- B. ten Hagen, R. Wittkowski, D. Takagi, F. Kümmel, C. Bechinger and H. Löwen, Can the self-propulsion of anisotropic microswimmers be described by using forces and torques?, J. Phys.: Condens. Matter, 2015, 27, 194110 CrossRef PubMed.
- D. Marenduzzo, E. Orlandini and J. M. Yeomans, Hydrodynamics and rheology of active liquid crystals: a numerical investigation, Phys. Rev. Lett., 2007, 98, 118102 CrossRef CAS PubMed.
- A. Tiribocchi, R. Wittkowski, D. Marenduzzo and M. E. Cates, Active Model H: scalar active matter in a momentum-conserving fluid, Phys. Rev. Lett., 2015, 115, 188302 CrossRef.
- J. Bickmann and R. Wittkowski, Predictive local field theory for interacting active Brownian spheres in two spatial dimensions, J. Phys.: Condens. Matter, 2020, 32, 214001 CrossRef CAS.
- J. Bickmann and R. Wittkowski, Collective dynamics of active Brownian particles in three spatial dimensions: a predictive field theory, Phys. Rev. Res., 2020, 2, 033241 CrossRef CAS.
- H. H. Wensink and H. Löwen, Aggregation of self-propelled colloidal rods near confining walls, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031409 CrossRef CAS.
- M. te Vrugt, H. Löwen and R. Wittkowski, Classical dynamical density functional theory: from fundamentals to applications, Adv. Phys., 2020, 69, 121–247 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |