Phonon confinement and interface lattice dynamics of ultrathin high-k rare earth sesquioxide films: the case of Eu₂O₃ on YSZ(001)

Abstract

The spatial confinement of atoms at surfaces and interfaces significantly alters the lattice dynamics of thin films, heterostructures and multilayers. Ultrathin films with high dielectric constants (high-k) are of paramount interest for applications as gate layers in current and future integrated circuits. Here we report a lattice dynamics study of high-k Eu₂O₃ films with thicknesses of 21.3, 2.2, 1.3, and 0.8 nm deposited on YSZ(001). The Eu-partial phonon density of states (PDOS), obtained from nuclear inelastic scattering, exhibits broadening of the phonon peaks accompanied by up to a four-fold enhancement of the number of low-energy states compared to the ab initio calculated PDOS of a perfect Eu₂O₃ crystal. Our analysis demonstrates that while the former effect reflects the reduced phonon lifetimes observed in thin films due to scattering from lattice defects, the latter phenomenon arises from an ultrathin EuO layer formed between the thin Eu₂O₃ film and the YSZ(001) substrate. Thus, our work uncovers another potential source of vibrational anomalies in thin films and multilayers, which has to be cautiously considered.

---

Thin oxide films with high dielectric constants, often referred to as high-k dielectrics, are of foremost importance for the complementary metal oxide semiconductor (CMOS) device technology. They have replaced the archetypal gate dielectric material SiO₂ in the field effect transistor (FET) – the heart of central processor units (CPU), in the metal–insulator–metal (MIM) capacitors of the volatile dynamic random access memory (DRAM), and in the floating gate FET of the non-volatile flash memory devices.^1–4 This step ensured the continuation of the exponential increase of transistor packing density in integrated circuits beyond the 45 nm technology, lowering the power consumption and increasing the operation speed in every subsequent generation of devices.⁵

The substitution of SiO₂ became necessary because at a layer thickness below ca. 1.2 nm, the quantum tunneling effect resulted in an unacceptably high leakage current, and consequently, higher power losses and poor device performance. Materials with higher dielectric constants compared to SiO₂ enabled reduction of the equivalent oxide thickness (EOT) to the subnanometer range at higher physical thickness, allowing to further reduce the transistor size. For instance, in the 14 nm technology an EOT of 0.9 nm was achieved by a high-k dielectric layer thickness of 2.6 nm, whereas in the upcoming 3 nm technology the targeted EOT of 0.6 nm requires a dielectric layer with a physical thickness below 2 nm.^6–8 Despite the fact that currently HfO₂, ZrO₂, and Al₂O₃ are widely used as high-k dielectrics for CPUs, DRAMs and flash memories, respectively, there is a continuous search for new outperforming materials for these applications.^9,10

Rare earth sesquioxides (RE₂O₃) have been extensively investigated for applications as high-k dielectrics.^11–13 The favorable combination of high dielectric constants, relatively large bandgaps, high breakdown electric fields, thermal and chemical stability, and small lattice mismatch with silicon promoted this class of materials as attractive candidates for high-k dielectrics in the CMOS device technology. Among the rare earth sesquioxides, Eu₂O₃, which is the subject of the present study, demonstrated superior performance as a charge-trapping high-k dielectric with a layer thickness of 3 nm in low temperature polycrystalline silicon thin-film transistor (LTPS-TFT) nonvolatile memory devices.¹⁴

The spatial confinement of atoms in nano- and subnanometer-thick layers profoundly alters their vibrational dynamics.¹⁵ Via phonon–phonon,¹⁶ electron–phonon¹⁷ and spin–phonon¹⁸ interactions, these size effects impact important properties of nanomaterials like thermal conductivity, superconductivity, charge mobility, spin polarization and others, manifesting themselves in phenomena such as self-heating,¹⁹ increase of the critical temperature of superconductors^20–22 and spin relaxation,²³ which play a crucial role in micro-, optoelectronic and spintronic device technologies.^24–26

Common features of the phonon density of states (PDOS) of thin films are enhancement of the number of states at low and high energy as well as broadening and shift of the peaks.²⁷ Extensive studies revealed that the origin of these vibrational anomalies is tightly connected to the crystal structure and thickness of the layer. In epitaxial thin films and superlattices, the broken translational symmetry at the surface and interface constitutes a source of novel vibration dynamics, which relaxes towards the bulk behavior within a few atomic layers.^28–38 In amorphous thin films, the structural disorder induces a reduction and a broad distribution of the mean force constants, leading to a significant enhancement of the number of low-energy states.^39–41

Fundamentally, the origin of the high-k property is directly related to the vibrational spectrum of a solid, since the static dielectric constant is a sum of the electronic and lattice contributions. While the former equals to the square of the refractive index and thus is intrinsically limited to low values, the high-k values originate from the lattice component, which is inversely proportional to the square of the frequency of transverse optical phonons.^4,42 This fact, combined with the observed modifications of the PDOS of ultrathin films, calls for a study of the lattice dynamics of high-k dielectrics with thicknesses of several atomic layers.

In this Communication we present a systematic lattice dynamics study of ultrathin Eu₂O₃ films with thicknesses of 2.2, 1.3 and 0.8 nm deposited on YSZ(001) substrates. The Eu-partial PDOS, derived from nuclear inelastic scattering (NIS) on the Mössbauer-active isotope ¹⁵¹Eu, unveils strong size effects that significantly alter the vibrational thermodynamic and elastic properties of the thin films in comparison to a 21.3 nm thick film. Our analysis reveals that these effects primarily originate from an ultrathin EuO layer formed between the thin Eu₂O₃ film and the YSZ(001) substrate. In addition to the spatial confinement and structural disorder, we demonstrate that the formation of sub-nanometer-thick layers with exotic crystal phases at the interface constitutes another source of vibrational anomalies of thin films and multilayers.

Eu₂O₃ films with thicknesses of 21.3, 2.2, 1.3 and 0.8 nm, hereinafter referred to as S1, S2, S3 and S4, were deposited on YSZ(001) substrates in the UHV system,⁴³ located at the Nuclear Resonance Beamline ID18 (ref. 44) of the ESRF in Grenoble, France, with a base pressure of 5 × 10⁻¹⁰ mbar. Europium was sublimated in an effusion cell from a metallic foil enriched to 97% in the Mössbauer-active isotope ¹⁵¹Eu creating a steady flux of Eu atoms at a rate of 6.0 Å min⁻¹. High-purity (99.9995%) molecular oxygen was supplied into the growth chamber via a leak valve. Prior to the Eu deposition, the substrate was annealed at 925 K for 60 min at a pressure below 3.0 × 10⁻⁹ mbar followed by annealing for 30 min at the films deposition temperature of 823 K in an oxygen partial pressure of 1.0 × 10⁻⁶ mbar. After deposition of the Eu metal, the sample was annealed at the same conditions for 60 min in order to achieve a complete oxidation of the Eu metal and to avoid the formation of other oxide phases. To protect the sensitive Eu₂O₃ films and to mimic the spatially confined geometry of the gate dielectric in a planar FET, the samples were covered at 298 K by 4.0 nm thick Nb layer.

The ¹⁵¹Eu-partial PDOS of the samples was obtained⁴⁵ from the energy dependence of the probability for nuclear inelastic absorption^46,47 of X-rays with an energy of 21.5 keV with an energy resolution of 1.1 meV (fwhm).⁴⁸ All samples were illuminated at a grazing angle of 0.15 degree using a focused X-ray beam with dimensions: vertical × horizontal ≈ 10 × 100 μm².

The Eu-partial PDOS of the investigated samples are presented in Fig. 1(a). The PDOS of S1 exhibits a broad peak at around 13 meV, a peak at 24 meV and a high-energy cutoff at 27.5 meV. The gray solid line depicts the ab initio calculated Eu-partial PDOS of an Eu₂O₃ crystal with cubic symmetry.⁴⁹ A comparison with the theory reveals a good agreement with the number and positions of the phonon states, as well as an excess of states at energies up to 12 meV in the experimental PDOS. A reduction of the film thickness to 2.2 nm in S2 leads to an increase of the number of low-energy states and a significant broadening of the spectral features. The effect is particularly strong for the high-energy peak, which practically diminishes. The tendency of enhancement of the number of low-energy states is clearly present in the PDOS of S3 (film thickness of 1.3 nm) and S4 (film thickness of 0.8 nm).

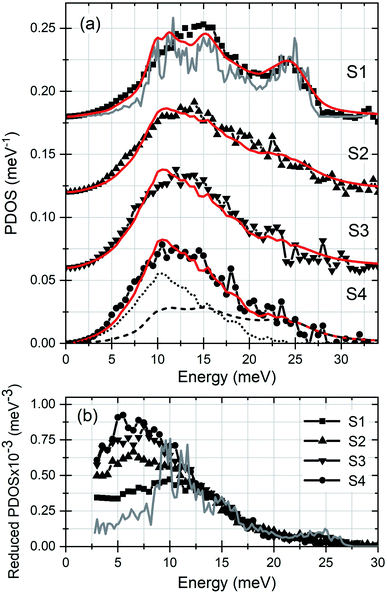Fig. 1 (a) Eu-partial PDOS of the investigated samples. The solid gray line stands for the ab initio calculated PDOS of a bulk Eu₂O₃ crystal with cubic symmetry.⁴⁹ The dashed line corresponds to the gray-line PDOS, convoluted with the DHO function with a quality factor Q = 5 (see Table 1). The dotted line stands for the Eu-partial PDOS of an EuO film with a thickness of 2.0 nm.³⁷ The solid red lines depict the model function described in the text. (b) Reduced PDOS (PDOS/E²) of S1–S4 and of Eu₂O₃ crystal with cubic symmetry (gray line).

The differences between the samples in the low-energy range of the PDOS is illustrated in Fig. 1(b), where the reduced PDOS (PDOS/E²) is plotted. This figure shows that the number of states between 5 and 7 meV in S2 and S3 exceeds that of S1 in average by factors of 1.6 and 2, respectively, wheres in S4 the excess reaches a factor of 2.3. Compared to the theoretical Debye level of an Eu₂O₃ crystal with cubic symmetry (gray line in Fig. 1(b)), the number of low-energy states in S1 is increased by a factor of 1.8.

The increase of the number of low-energy states is a generic feature of the PDOS of thin films. At epitaxial surfaces and coherent interfaces, this feature originates from surface- and interface-specific vibrational modes arising from the reduced mean force constants which is a consequence of the broken translational symmetry.^{29,30,33,34,37} The theoretically predicted sharp peaks appear significantly broader in the experimental PDOS. In addition to the finite experimental resolution, the presence of defects in the crystal lattice in form of misfit dislocations, vacancies, interstitials, or grain boundaries in polycrystalline films, leads to a reduced phonon lifetime and consequently a broadening of the PDOS features.^50,51 In amorphous thin films, the broad low-energy peak originates from the reduced mean force constants with a large width of distribution associated with the structural disorder.^39–41 In addition to these well studied effects, below we unveil another potential source of anomalies in the lattice dynamics of thin films and multilayers.

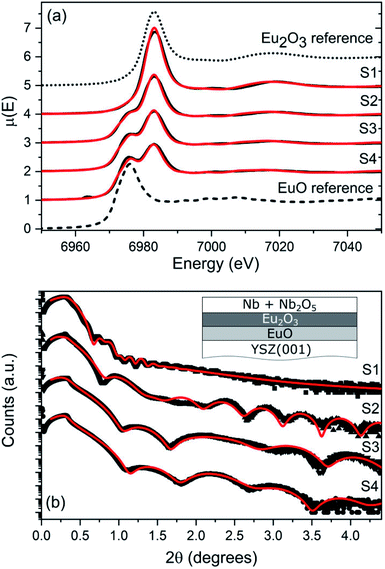
The crystal quality, thickness and composition of the films were determined by X-ray diffraction (XRD)⁵² and X-ray reflectivity (XRR) measurements using Cu-K_α energy, and by X-ray absorption near-edge structure (XANES) spectroscopy on the L₃ edge of Eu (6977 eV) at the SUL-X beamline of the KIT Light Source. The FitSuite,⁵³ ATHENA and ARTEMIS codes from the IFFEFIT⁵⁴ package were used for reduction and modeling of the experimental data.

Fig. 2(a) shows the XANES data obtained from samples S1–S4 along with a reference 100 nm thick EuO film¹⁸ and a commercial Eu₂O₃ powder sample measured in the same experiment. The XANES data show a distinct difference in the position of the absorption L₃ edge of Eu in Eu₂O₃, where the Eu atoms are in an oxidation state +3, and in EuO where the atoms, similarly to metallic europium, exhibit an oxidation state +2. Unexpectedly, Fig. 2(a) reveals, in addition to Eu³⁺, the presence of Eu²⁺ in the investigated samples. The relative amount of this phase increases with decreasing the film thickness. The presence of metallic Eu can be excluded due to the high partial oxygen pressure in the growth chamber, the elevated temperature of the substrate and the prolonged annealing time. Therefore, the Eu²⁺ peak indicates the formation of EuO, which however, is unexpected since the optimal values for the epitaxial growth of EuO on YSZ(001) were exceeded by 150 K for the substrate temperature and by one order of magnitude for the partial oxygen pressure.⁵⁵ The relative Eu²⁺ and Eu³⁺ fractions in the samples were obtained by modeling the experimental data with a linear combination of the XANES spectra of the reference samples. The best-fit results, plotted with solid/red lines in Fig. 2(a), show that this model satisfactorily reproduces the experimental data. The obtained relative amount of the EuO phase and the corresponding film thickness (assuming a homogeneous layer) are summarized in Table 1.

Fig. 2 XANES (a) and XRR (b) data of the investigated samples. The red lines mark the corresponding simulations (see text for details). The inset in (b) depicts the model used for the fit of the XRR data.

Table 1 Thickness of the oxide layer (Eu₂O₃ + EuO) and relative contribution (A)/thickness of the EuO interface layer obtained by the corresponding methods. Q is the quality factor of the DHO function (see text for details)

Sample	Thickness (nm)	XRR (%/nm)	XANES (%/nm)	NIS (%/nm)	Q
S1	21.3	4/0.9	5/1.1	6/1.3	12
S2	2.2	18/0.4	35/0.77	23/0.51	4
S3	1.3	38/0.5	47/0.61	45/0.59	4
S4	0.8	37/0.3	56/0.45	51/0.41	5

---

The formation of an EuO layer at the interface with the YSZ(001) substrate is further confirmed by the analysis of the XRR data presented in Fig. 2(b). The red lines correspond to the best-fit results assuming an EuO layer formed between the Eu₂O₃ film and the YSZ(001) substrate (see inset Fig. 2(b)).⁵² The total thickness of the oxide layer (Eu₂O₃ + EuO), the thickness and the corresponding relative volume fraction of the EuO interface layer are presented in Table 1. While the results from both methods are in a qualitative agreement on the increasing contribution of the EuO phase as the film thickness is reduced, the obtained relative contribution of this phase from the XANES experiment systematically exceeds that derived by the XRR measurement.⁵⁶ Yet the thickness of this interface layer obtained by both methods is in the sub-nanometer range except in S1 where it reaches 1 nm.

A combined experimental and theoretical study revealed strong confinement effects in the lattice dynamics of thin EuO films.³⁷ Namely, the Eu-partial PDOS of an EuO film with a thickness of 2.0 nm exhibits a broad peak at 10.5 meV and a high-energy cutoff at 25 meV. These features are very similar to those exhibited by the PDOS of S2–S4 (Fig. 1(a)). In order to thoroughly explain the experimental observations, the data were modeled by a superposition of the ab initio calculated Eu-partial PDOS of Eu₂O₃ with cubic symmetry⁵²g_th(E) (gray line in Fig. 1(a)) and the experimentally determined PDOS of a 2.0 nm thick EuO film,³⁷g_if(E) (dotted line in Fig. 1(a)), representing the interface. Furthermore, the broadening of PDOS features is a common characteristic for nanoscale materials that originates from phonon scattering at atoms located at irregular lattice sites, i.e. grain boundaries, defects and dislocations at surfaces and interfaces, as well as within the nanostructure.^57,58 This effect is satisfactorily described by the damped harmonic oscillator (DHO) function, which introduces an energy-dependent broadening of the phonon features reflecting the fact that high-frequency phonons scatter more efficiently.^59,60 The strength of phonon damping is inversely proportional to the quality factor Q of the DHO function. To account for these two sources of anomalies in the PDOS of the thin films, namely the phonon damping and the presence of an EuO interface layer, the following model function is defined:

g_model(E, Q) = Ag_if(E) + (1 − A)g_th(E, Q)

with A being the relative EuO interface atomic fraction. The experimental PDOS of S1–S4 were modeled with the function g_model(E, Q) using the least-squares method with A and Q being variable parameters.⁶¹ The results are plotted with red/solid lines in Fig. 1(a) and show that the used model satisfactorily reproduces the experimental data. The obtained values of A and Q are summarized in Table 1. The relative interface fraction falls in between the values obtained by XRR and XANES, which indicates the consistency of the results obtained by three independent experimental techniques.⁵² The corresponding EuO layer thickness is also consistent with the values derived by the other two methods. The values of Q are abruptly reduced from 12 in S1, corresponding to an almost bulk-like crystal (compare the width of the peak at 25 meV in the experimental and theoretical PDOS) to 4 in S2 and S3 and 5 in S4 (this difference we attribute to the statistical error). These values of Q unveil strong and very similar phonon damping in the thin Eu₂O₃ films, despite the fact that the total oxide layer thickness varies by a factor of 2.8 from S2 to S4. This result indicates that the investigated Eu₂O₃ ultrathin films exhibit crystal lattices of similar quality (as confirmed by the XRD study).⁵² The main difference in the PDOS arises from the increase of the relative fraction of the EuO interface layer as the total film thickness is reduced, leading to the anomalous enhancement of the number of low-energy states.

A closer comparison of the experimental PDOS to the g_model(E, Q) (Fig. 1(a)) demonstrates that the model function systematically underestimates the number of phonon states between 3 and 10 meV. Most likely this difference arises from vibrational states of Eu atoms located at the Nb/Eu₂O₃ interface, which was not included in the model.

The observed broadening of the Eu-partial PDOS of the ultrathin films, quantified with the quality factor Q, most likely applies as well for the vibrational modes of the oxygen atoms, characterized with higher frequencies⁴⁹ and being primarily responsible for the high-k property of the RE₂O₃.⁴² This suppression and even disappearance of transverse optical modes could potentially reduce the lattice contribution to the dielectric constant. Indeed, a decrease of the static dielectric constant of La₂Zr₂O₇ thin films compared to the bulk material was observed and explained by a broadening and vanishing of the infrared-active phonon modes due to structural disorder of the thin films.⁶²

The reduction of the film thickness has important implications on the elastic and thermodynamic properties. Table 2 summarizes the experimental and theoretical values of the mean force constant F, mean square atomic displacement 〈x²〉, vibrational entropy S_V, and lattice specific heat at constant volume C_V, obtained⁶³ from the Eu-partial PDOS of an Eu₂O₃ crystal with cubic symmetry⁴⁹ (calculated for the experimental lattice constant of 10.80 Å),⁵² samples S1–S4 and of a 2.0 nm thick EuO film.³⁷ A decrease of F in S2 by 6.5% compared to S1 results in an increase of 〈x²〉 by 17.6%. A further softening of the lattice by 20.8% in S3 and by 26.8% in S4 increases 〈x²〉 by 35.3% and 41.2%, respectively. S_V increases by 3.9% in S2, 8.8% in S3 and 10.9% in S4 compared to S1, whereas C_V shows only a marginal enhancement by 1.4% in S4. Since the quality factor of the DHO function remains essentially the same in S2–S4 (Table 1) and the EuO film exhibits significantly different properties from those of bulk Eu₂O₃ (Table 2), the observed anomalous behavior of the thermoelastic properties of the films originates primarily from the increase of the EuO interface fraction as the film thickness is reduced.

Table 2 Mean force constant F, mean square atomic displacement 〈x²〉, vibrational entropy S_V, and lattice specific heat C_V at constant volume calculated from the Eu-partial PDOS of the indicated samples. All values are obtained at 298 K

Sample	F (N m^−1)	〈x^2〉 (Å^2)	S V (kB per atom)	C V (kB per atom)
Eu2O3 bulk^49	208	0.01237	4.462	2.870
S1	168(5)	0.017(1)	4.68(2)	2.89(2)
S2	157(4)	0.020(1)	4.86(2)	2.90(2)
S3	133(4)	0.023(1)	5.09(2)	2.92(2)
S4	123(3)	0.024(1)	5.19(2)	2.93(2)
EuO film^37	89(7)	0.031(2)	5.58(4)	2.94(3)

---

In summary, using nuclear inelastic scattering of synchrotron radiation on the Mössbauer-active isotope ¹⁵¹Eu, we determined the Eu-partial phonon density of states in Eu₂O₃ films with thicknesses of 21.3, 2.2, 1.3 and 0.8 nm deposited on YSZ(001). The PDOSs exhibit broadening and suppression of the peaks accompanied by up to a four-fold enhancement of the number of low-energy states in the thinnest layer compared to the ab initio calculated PDOS of a perfect Eu₂O₃ crystal. Our analysis demonstrates that the former effect, which could potentially reduce the dielectric constant of ultrathin high-k films, arises from the presence of lattice defects and grain boundaries and reflects the reduced phonon lifetimes observed in thin films. The structural characterization unveiled the formation of a sub-nanometer-thick EuO layer at the interface between the Eu₂O₃ film and the YSZ(001) substrate. The spatially confined atomic vibrations of this interface layer contribute significantly to the increased number of low-energy phonon states and to the anomalies in the thermodynamic and elastic properties of the investigated samples.

The presented results demonstrate that in addition to spatial confinement,³⁵ structural disorder,⁴¹ surface-³⁰ and interface-³³ specific vibrational modes, sub-nanometer-thick layers exhibiting exotic crystal phases that might form at the interface between two materials constitute a source of novel vibrational dynamics of thin films and multilayers. Moreover, the targeted embedment of such ultrathin layers might be a successful approach towards ultimately engineered heterostructures for phononic applications.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge ESRF-The European Synchrotron for provision of synchrotron radiation facilities, the National Isotope Development Center at Oak Ridge National Lab, which is sponsored by the U.S. DOE Basic Energy Sciences, for providing the ¹⁵¹Eu source material. S. S. acknowledges the financial support by the Helmholtz Association (VH-NG-625) and BMBF (05K16VK4). P. P. acknowledges the financial support by the National Science Centre (NCN) within the project no. 2017/25/B/ST3/02586 and the access to the ESRF financed by the Polish Ministry of Science and High Education – decision number: DIR/WK/2016/19.

Notes and references

1. J. Robertson, Rep. Prog. Phys., 2005, 69, 327–396,  DOI:10.1088/0034-4885/69/2/R02.
2. J. A. Kittl, K. Opsomer, M. Popovici, N. Menou, B. Kaczer, X. P. Wang, C. Adelmann, M. A. Pawlak, K. Tomida, A. Rothschild, B. Govoreanu, R. Degraeve, M. Schaekers, M. Zahid, A. Delabie, J. Meersschaut, W. Polspoel, S. Clima, G. Pourtois, W. Knaepen, C. Detavernier, V. V. Afanas'ev, T. Blomberg, D. Pierreux, J. Swerts, P. Fischer, J. W. Maes, D. Manger, W. Vandervorst, T. Conard, A. Franquet, P. Favia, H. Bender, B. Brijs, S. Van Elshocht, M. Jurczak, J. Van Houdt and D. J. Wouters, Microelectron. Eng., 2009, 86, 1789–1795,  DOI:10.1016/j.mee.2009.03.045.
3. C. Zhao, C. Z. Zhao, S. Taylor and P. R. Chalker, Materials, 2014, 7, 5117–5145,  DOI:10.3390/ma7075117.
4. J. Robertson and R. M. Wallace, Mater. Sci. Eng., R, 2015, 88, 1–41,  DOI:10.1016/j.mser.2014.11.001.
5. M. T. Bohr, R. S. Chau, T. Ghani and K. Mistry, IEEE Spectrum, 2007, 44, 29–35,  DOI:10.1109/MSPEC.2007.4337663.
6. S. Natarajan, M. Agostinelli, S. Akbar, M. Bost, A. Bowonder, V. Chikarmane, S. Chouksey, A. Dasgupta, K. Fischer, Q. Fu, T. Ghani, M. Giles, S. Govindaraju, R. Grover, W. Han, D. Hanken, E. Haralson, M. Haran, M. Heckscher, R. Heussner, P. Jain, R. James, R. Jhaveri, I. Jin, H. Kam, E. Karl, C. Kenyon, M. Liu, Y. Luo, R. Mehandru, S. Morarka, L. Neiberg, P. Packan, A. Paliwal, C. Parker, P. Patel, R. Patel, C. Pelto, L. Pipes, P. Plekhanov, M. Prince, S. Rajamani, J. Sandford, B. Sell, S. Sivakumar, P. Smith, B. Song, K. Tone, T. Troeger, J. Wiedemer, M. Yang and K. Zhang, IEEE Int. Electron Devices Meet., Tech. Dig., 50th, 2014, 3.7.1–3.7.3,  DOI:10.1109/IEDM.2014.7046976.
7. P. Lu, B. Colombeau, S. Hung, W. Li, X. Duan, Y. Li, E. M. Bazizi, S. Natarajan and J. C. S. Woo, IEEE Trans. Electron Devices, 2021, 68, 1352–1357,  DOI:10.1109/TED.2021.3052432.
8. W. Li, J. Zhou, S. Cai, Z. Yu, J. Zhang, N. Fang, T. Li, Y. Wu, T. Chen, X. Xie, H. Ma, K. Yan, N. Dai, X. Wu, H. Zhao, Z. Wang, D. He, L. Pan, Y. Shi, P. Wang, W. Chen, K. Nagashio, X. Duan and X. Wang, 2019, arXiv:1909.09753.
9. K. Yim, Y. Yong, J. Lee, K. Lee, H.-H. Nahm, J. Yoo, C. Lee, C. S. Hwang and S. Han, NPG Asia Mater., 2015, 7, e190,  DOI:10.1038/am.2015.57.
10. T. Li, T. Tu, Y. Sun, H. Fu, J. Yu, L. Xing, Z. Wang, H. Wang, R. Jia, J. Wu, C. Tan, Y. Ling, Y. Zhang, C. Zhang, Y. Dai, C. Qiu, M. Li, R. Huang, L. Jiao, K. Lai, B. Yan, P. Gao and H. Peng, Nat. Electron., 2020, 3, 473–478,  DOI:10.1038/s41928-020-0444-6.
11. M. Leskelä, K. Kukli and M. Ritala, J. Alloys Compd., 2006, 418, 27–34,  DOI:10.1016/j.jallcom.2005.10.061.
12. K. H. Goh, A. S. M. A. Haseeb and Y. H. Wong, Mater. Sci. Semicond. Process., 2017, 68, 302–315,  DOI:10.1016/j.mssp.2017.06.037.
13. S. Li, Y. Lin, S. Tang, L. Feng and X. Li, J. Rare Earths, 2021, 39, 121–128,  DOI:10.1016/j.jre.2020.10.013.
14. T. Pan, L. Yen, S. Huang, C. Lo and T. Chao, IEEE Trans. Electron Devices, 2013, 60, 2251–2255,  DOI:10.1109/TED.2013.2261511.
15. M. Stroscio and M. Dutta, Phonons in Nanostructures, Cambridge University Press, Cambridge, 2001,  DOI:10.1017/CBO9780511534898.
16. A. Cammarata, RSC Adv., 2019, 9, 37491–37496,  10.1039/C9RA08294H.
17. N. Driza, S. Blanco-Canosa, M. Bakr, S. Soltan, M. Khalid, L. Mustafa, K. Kawashima, G. Christiani, H.-U. Habermeier, G. Khaliullin, C. Ulrich, M. Le Tacon and B. Keimer, Nat. Mater., 2012, 11, 675–681,  DOI:10.1038/nmat3378.
18. R. Pradip, P. Piekarz, A. Bosak, D. G. Merkel, O. Waller, A. Seiler, A. I. Chumakov, R. Rüffer, A. M. Oleś, K. Parlinski, M. Krisch, T. Baumbach and S. Stankov, Phys. Rev. Lett., 2016, 116, 185501,  DOI:10.1103/PhysRevLett.116.185501.
19. E. Pop, Nano Res., 2010, 3, 147–169,  DOI:10.1007/s12274-010-1019-z.
20. S. Couet, H. Peelaers, M. Trekels, K. Houben, M. Y. Hu, J. Y. Zhao, W. Bi, E. E. Alp, E. Menéndez, B. Partoens, F. M. Peeters, M. J. Van Bael, A. Vantomme and K. Temst, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045437,  DOI:10.1103/PhysRevB.88.045437.
21. D. P. Lozano, S. Couet, C. Petermann, G. Hamoir, J. K. Jochum, T. Picot, E. Menéndez, K. Houben, V. Joly, V. A. Antohe, M. Y. Hu, B. M. Leu, A. Alatas, A. H. Said, S. Roelants, B. Partoens, M. V. Milošević, F. M. Peeters, L. Piraux, J. Van de Vondel, A. Vantomme, K. Temst and M. J. Van Bael, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 064512,  DOI:10.1103/PhysRevB.99.064512.
22. K. Houben, J. K. Jochum, S. Couet, E. Menéndez, T. Picot, M. Y. Hu, J. Y. Zhao, E. E. Alp, A. Vantomme, K. Temst and M. J. Van Bael, Sci. Rep., 2020, 10, 5729,  DOI:10.1038/s41598-020-62617-4.
23. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620,  DOI:10.1038/ncomms14620.
24. J. Fabian and S. Das Sarma, Phys. Rev. Lett., 1999, 83, 1211,  DOI:10.1103/PhysRevLett.83.1211.
25. I. Žutić, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–410,  DOI:10.1103/RevModPhys.76.323.
26. D. Bozyigid, N. Yazdani, M. Yarema, O. Yarema, W. M. M. Lin, S. Volk, K. Vuttivorakulchai, M. Luisier, F. Juranyi and V. Wood, Nature, 2016, 531, 618–622,  DOI:10.1038/nature16977.
27. R. Röhlsberger, W. Sturhahn, T. S. Toellner, K. W. Quast, P. Hession, M. Hu, J. Sutter and E. E. Alp, J. Appl. Phys., 1999, 86, 584–587,  DOI:10.1063/1.370770.
28. T. Ruckert, W. Keune, W. Sturhahn, M. Y. Hu, J. P. Sutter, T. S. Toellner and E. E. Alp, Hyperfine Interact., 2000, 126, 363–366,  DOI:10.1023/A:1012670628702.
29. S. Stankov, R. Röhlsberger, T. Ślęzak, M. Sladecek, B. Sepiol, G. Vogl, A. I. Chumakov, R. Rüffer, N. Spiridis, J. Łażewski, K. Parlinski and J. Korecki, Phys. Rev. Lett., 2007, 99, 185501,  DOI:10.1103/PhysRevLett.99.185501.
30. T. Ślęzak, J. Łażewski, S. Stankov, K. Parlinski, R. Reitinger, M. Rennhofer, R. Rüffer, B. Sepiol, M. Ślęzak, N. Spiridis, M. Zając, A. I. Chumakov and J. Korecki, Phys. Rev. Lett., 2007, 99, 066103,  DOI:10.1103/PhysRevLett.99.066103.
31. B. Roldan Cuenya, W. Keune, R. Peters, E. Schuster, B. Sahoo, U. von Hörsten, W. Sturhahn, J. Zhao, T. S. Toellner, E. E. Alp and S. D. Bader, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165410,  DOI:10.1103/PhysRevB.77.165410.
32. N. Spiridis, M. Zajac, P. Piekarz, A. I. Chumakov, K. Freindl, J. Goniakowski, A. Kozioł-Rachwał, K. Parliński, M. Ślęzak, T. Ślęzak, U. D. Wilgocka-Ślęzak, D. Wilgocka-Slezak and J. Korecki, Phys. Rev. Lett., 2015, 115, 186102,  DOI:10.1103/PhysRevLett.115.186102.
33. J. Kalt, M. Sternik, I. Sergueev, J. Herfort, B. Jenichen, H.-C. Wille, O. Sikora, P. Piekarz, K. Parlinski, T. Baumbach and S. Stankov, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 121409,  DOI:10.1103/PhysRevB.98.121409.
34. O. Sikora, J. Kalt, M. Sternik, A. Ptok, P. Jochym, J. Łażewski, P. Piekarz, K. Parlinski, I. Sergueev, H.-C. Wille, J. Herfort, B. Jenichen, T. Baumbach and S. Stankov, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 134303,  DOI:10.1103/PhysRevB.99.134303.
35. A. Seiler, P. Piekarz, S. Ibrahimkutty, D. G. Merkel, O. Waller, R. Pradip, A. I. Chumakov, R. Rüffer, T. Baumbach, K. Parlinski, M. Fiederle and S. Stankov, Phys. Rev. Lett., 2016, 117, 276101,  DOI:10.1103/PhysRevLett.117.276101.
36. W. Keune, S. Hong, M. Y. Hu, J. Zhao, T. S. Toellner, E. E. Alp, W. Sturhahn, T. S. Rahman and B. Roldan Cuenya, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 024–308,  DOI:10.1103/PhysRevB.98.024308.
37. R. Pradip, P. Piekarz, D. G. Merkel, J. Kalt, O. Waller, A. I. Chumakov, R. Rüffer, A. M. Oleś, K. Parlinski, T. Baumbach and S. Stankov, Nanoscale, 2019, 11, 10968–10976,  10.1039/C9NR01931F.
38. B. Eggert, M. E. Gruner, K. Ollefs, E. Schuster, N. Rothenbach, M. Y. Hu, J. Zhao, T. S. Toellner, W. Sturhahn, R. Pentcheva, B. Roldan Cuenya, E. E. Alp, H. Wende and W. Keune, Phys. Rev. Mater., 2020, 4, 044402,  DOI:10.1103/PhysRevMaterials.4.044402.
39. W. Keune, T. Ruckert, B. Sahoo, W. Sturhahn, T. S. Toellner, E. E. Alp and R. Röhlsberger, J. Phys.: Condens. Matter, 2004, 16, S379–S393,  DOI:10.1088/0953-8984/16/5/004.
40. B. Sahoo, W. Keune, E. Schuster, W. Sturhahn, T. S. Toellner and E. E. Alp, Hyperfine Interact., 2006, 168, 1185–1190,  DOI:10.1007/s10751-006-9421-3.
41. B. Sahoo, W. Keune, E. Schuster, W. Sturhahn, J. Zhao, T. S. Toellner and E. E. Alp, Hyperfine Interact., 2006, 170, 33–46,  DOI:10.1007/s10751-006-9476-1.
42. E. Bonera, G. Scarel, M. Fanciulli, P. Delugas and V. Fiorentini, Phys. Rev. Lett., 2005, 94, 027602,  DOI:10.1103/PhysRevLett.94.027602.
43. S. Stankov, R. Rüffer, M. Sladecek, M. Rennhofer, B. Sepiol, G. Vogl, N. Spiridis, T. Slezak and J. Korecki, Rev. Sci. Instrum., 2008, 79, 045108,  DOI:10.1063/1.2906321.
44. R. Rüffer and A. I. Chumakov, Hyperfine Interact., 1996, 97, 589–604,  DOI:10.1007/BF02150199.
45. V. G. Kohn and A. I. Chumakov, Hyperfine Interact., 2000, 125, 205–221,  DOI:10.1023/A:1012689705503.
46. M. Seto, Y. Yoda, S. Kikuta, X. W. Zhang and M. Ando, Phys. Rev. Lett., 1995, 74, 3828–3831,  DOI:10.1103/PhysRevLett.74.3828.
47. W. Sturhahn, T. S. Toellner, E. E. Alp, X. Zhang, M. Ando, Y. Yoda, S. Kikuta, M. Seto, C. W. Kimball and B. Dabrowski, Phys. Rev. Lett., 1995, 74, 3832–3835,  DOI:10.1103/PhysRevLett.74.3832.
48. O. Leupold, J. Pollmann, E. Gerdau, H. D. Rüter, G. Faigel, M. Tegze, G. Bortel, R. Rüffer, A. I. Chumakov and A. Q. R. Baron, Europhys. Lett., 1996, 35, 671–676,  DOI:10.1209/epl/i1996-00169-0.
49. J. Łażewski, M. Sternik, P. T. Jochym, J. Kalt, S. Stankov, A. I. Chumakov, J. Göttlicher, R. Rüffer, T. Baumbach and P. Piekarz, Inorg. Chem., 2021, 60, 9571–9579,  DOI:10.1021/acs.inorgchem.1c00708.
50. S. Couet, M. Sternik, B. Laenens, A. Siegel, K. Parlinski, N. Planckaert, F. Gröstlinger, A. I. Chumakov, R. Rüffer, B. Sepiol, K. Temst and A. Vantomme, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094109,  DOI:10.1103/PhysRevB.82.094109.
51. K. Houben, S. Couet, M. Trekels, E. Menéndez, T. Peissker, J. W. Seo, M. Y. Hu, J. Y. Zhao, E. E. Alp, S. Roelants, B. Partoens, M. V. Milošević, F. M. Peeters, D. Bessas, S. A. Brown, A. Vantomme, K. Temst and M. J. Van Bael, Phys. Rev. B, 2017, 95, 155413,  DOI:10.1103/PhysRevB.95.155413.
52. See the ESI† for: Analysis of the XRR data assuming the formation of the EuO layer between the Eu₂O₃ film and the capping layer; XRD data of S1–S4; analysis of the PDOS of S1–S4 with trigonal and monoclinic crystal phases of Eu₂O₃; influence of the Lamb–Mössbauer factors of EuO film and Eu₂O₃ on the analysis approach.
53. http://www.fs.kfki.hu .
54. B. Ravel and N. Newville, J. Synchrotron Radiat., 2005, 12, 537–541,  DOI:10.1107/S0909049505012719.
55. R. Sutarto, S. G. Altendorf, B. Coloru, M. Moretti Sala, T. Haupricht, C. F. Chang, Z. Hu, C. Schüßler-Langeheine, N. Hollmann, H. Kierspel, H. H. Hsieh, H.-J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205318,  DOI:10.1103/PhysRevB.79.205318.
56. Most likely the discrepancy arises due to the different experimental geometry of the two measurements. While the XRR experiment is performed in the angular range 0–4.5 degrees implying a large footprint of the X-ray beam, the XANES experiment is performed at an incidence angle of the X-ray beam at 45 degrees with respect to the surface of the YSZ(001). Consequently, the first method probes the entire substrate, whereas the second method measures essentially the center of the substrate. A possible temperature gradient across the substrate could lead to a variation of the thickness and composition of the film.
57. B. Fultz, C. C. Ahn, E. E. Alp, W. Sturhahn and T. S. Toellner, Phys. Rev. Lett., 1997, 79, 937–940,  DOI:10.1103/PhysRevLett.79.937.
58. S. Stankov, Y. Z. Yue, M. Miglierini, B. Sepiol, I. Sergueev, A. I. Chumakov, L. Hu, P. Svec and R. Rüffer, Phys. Rev. Lett., 2008, 100, 235503,  DOI:10.1103/PhysRevLett.100.235503.
59. B. Fåk and B. Dorner, Institut Laue-Langevin Technical Report No. 92FA008S, 1992, unpublished.
60. B. Fultz, Prog. Mater. Sci., 2010, 55, 247–352,  DOI:10.1016/j.pmatsci.2009.05.002.
61. Note that only the ab initio calculated Eu-partial PDOS g_th(E, Q) was convoluted with the DHO function.
62. X. Cheng, Z. Qi, T. Li, G. Zhang, C. Li, H. Zhou, Y. Wang and M. Yin, Phys. Status Solidi B, 2012, 249, 854–857,  DOI:10.1002/pssb.201147313.
63. M. Y. Hu, T. S. Toellner, N. Dauphas, E. E. Alp and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 064301,  DOI:10.1103/PhysRevB.87.064301.

---

Footnote

† Electronic supplementary information (ESI) available: Analysis of the XRR data assuming the formation of the EuO layer between the Eu₂O₃ film and the capping layer; XRD data of S1–S4; Analysis of the PDOS of S1–S4 with trigonal and monoclinic crystal phases of Eu₂O₃; influence of the Lamb–Mössbauer factors of EuO film and Eu₂O₃ on the analysis approach. See DOI: 10.1039/d1na00728a

---