Open Access Article
Open Access ArticleThe electronic structure of the metal–organic interface of isolated ligand coated gold nanoparticles†
Robin
Schürmann
 *a,
Evgenii
Titov
*a,
Evgenii
Titov
 a,
Kenny
Ebel
a,
Sergio
Kogikoski
Jr
a,
Kenny
Ebel
a,
Sergio
Kogikoski
Jr
 a,
Amr
Mostafa
a,
Peter
Saalfrank
a,
Amr
Mostafa
a,
Peter
Saalfrank
 a,
Aleksandar R.
Milosavljević
b and
Ilko
Bald
a,
Aleksandar R.
Milosavljević
b and
Ilko
Bald
 *a
*a
aUniversity of Potsdam, Institute of Chemistry, 14476 Potsdam, Germany. E-mail: robin.schuermann@uni-potsdam.de; ilko.bald@uni-potsdam.de
bSynchrotron SOLEIL, 91192 GIF-sur-YVETTE CEDEX, France
First published on 2nd February 2022
Abstract
Light induced electron transfer reactions of molecules on the surface of noble metal nanoparticles (NPs) depend significantly on the electronic properties of the metal–organic interface. Hybridized metal–molecule states and dipoles at the interface alter the work function and facilitate or hinder electron transfer between the NPs and ligand. X-ray photoelectron spectroscopy (XPS) measurements of isolated AuNPs coated with thiolated ligands in a vacuum have been performed as a function of photon energy, and the depth dependent information of the metal–organic interface has been obtained. The role of surface dipoles in the XPS measurements of isolated ligand coated NPs is discussed and the binding energy of the Au 4f states is shifted by around 0.8 eV in the outer atomic layers of 4-nitrothiophenol coated AuNPs, facilitating electron transport towards the molecules. Moreover, the influence of the interface dipole depends significantly on the adsorbed ligand molecules. The present study paves the way towards the engineering of the electronic properties of the nanoparticle surface, which is of utmost importance for the application of plasmonic nanoparticles in the fields of heterogeneous catalysis and solar energy conversion.
Introduction
The electron transfer reactions of illuminated noble metal nanoparticles (NPs) play a significant role in the conversion of solar light to chemical energy.1,2 These reactions are mediated by the localized surface plasmon resonances (LSPRs) of the NPs, which are collective oscillations of the conduction band electrons that are excited by incident light.3–5 In a non-radiative decay process of the LSPR, electron–hole pairs are formed, which can be transferred directly or indirectly to molecules adsorbed on the NP surface and trigger reactions therein.6–11 The reaction of 4-nitrothiophenol (NTP) to 4′,4-dimercaptoazobenzene (DMAB) on metal surfaces is a show-case reaction for plasmon mediated chemistry.12–24 Even though the parameters determining the reaction are still under debate, it is assumed to be triggered by an electron transfer from the NPs to the adsorbed molecules forming a stable anion.12,13,15,16,18,20,25 In addition to the electron transfer also a hole transfer from the NPs to the adsorbed molecules has a significant role in the dimerization of NTP.26 The transfer probability depends significantly on the electronic properties like the density of initial and final states and work function, which are significantly influenced by the metal–organic interface.4,13,27 By tuning the properties of the metal–organic interface, the electron or hole transfer can be optimized. Self-assembled molecular monolayers of thiolated molecules like NTP significantly alter the properties of Au substrates, namely work function28,29 and electronic states,30 when the Fermi levels of the molecular layer and NPs are pinned31 due to the formation of hybridized molecular-metallic states.32 The work function of a metal can be significantly altered by molecular dipole moments, whereas the resulting work function of the system depends mainly on the adsorbed molecules.33–35 Moreover, by tailoring the molecular dipoles the electronic states at the metal–organic interface can be tuned.33,36 The properties of the NP–ligand interface can be either affected by the functional groups of the molecules or by their packing density and alignment.34 Recently, it has been demonstrated by comparing the plasmon mediated formation of diazo bonds from NTP and 4-nitrobenzylmercaptan (NBM) that the reaction kinetics are significantly influenced by the molecular geometry.37 The in-depth knowledge of the electronic properties at the molecule–NP interface allows efficient tuning of the kinetics of plasmon mediated electron transfer reactions.38 Therefore, the following needs to be understood:• How are the electronic states on the NP surface altered by the adsorption of ligand molecules?
• What is the range of the effects that alter the electronic properties at the interface?
• How are the electronic states of the adsorbed molecules affected by the adsorption on the NPs?
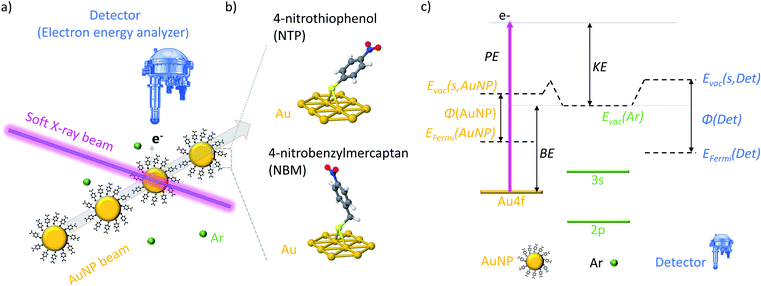
Within this work we study the electronic properties, namely work function and core level states, by XPS of isolated NTP coated AuNPs and elucidate the role of surface dipoles by comparison with NBM. By tuning the inelastic mean free path (IMFP) of the generated photoelectrons, depth dependent information is obtained.
Results and discussion
In the present experiments a focused beam of ligand coated AuNPs has been generated and transferred into a vacuum, where it is crossed with the tunable soft X-ray beam of the PLEIADES beamline at the Synchrotron SOLEIL to perform X-ray photoelectron spectroscopy (XPS) measurements (see Fig. 1(a)). In this way, both the X-ray induced photodamage to the studied NPs and the effects from a substrate are prevented.In a typical solid state XPS experiment, the sample and the detector are grounded; hence the reference energy for the binding energy (BE) is the Fermi energy, which is calibrated with well-accepted binding energies, e.g. the C 1s state of adventitious carbon or the Au 4f7/2 state of bulk gold.39,40 However, in the present experiment the AuNPs are isolated in a vacuum and the detector and sample are decoupled, which leads to the consequence that the Fermi energy of the sample and detector might differ.41 Therefore, the ionization energies of dilute Ar42 gas have been used for the calibration of the kinetic energy (KE) of the photoelectrons, and hence, the vacuum energy of Ar is the reference of the BE (see Fig. S3†). In Fig. 1(c) an energy diagram of the XPS measurements of isolated NPs is presented, showing that the vacuum energy of Ar gas and the vacuum energy at the surface of the NPs might differ due to the action of the surface dipoles of the NP sample.43,44 In consequence, the energy difference between the BEs determined in the present experiment (i.e. with respect to the vacuum level) and the BEs determined in solid state XPS experiments (i.e. with respect to the Fermi level) corresponds to the work function φ of the NP system reduced by the dipole energy of the surface. It has to be noted that, in contrast to ambient pressure XPS measurements,45 an impact of the surface dipoles of the sample on the vacuum energy of the Ar atoms can be neglected due to the small size and dilute concentration of the NPs in a vacuum (see Fig. S4† for details).
Depth dependent measurements of isolated AuNPs
XPS is a very surface sensitive technique, which allows the determination of the composition and position of electronic states in a material, as the inelastic mean free path (IMFP) of the photoelectrons is limited.46–48 The effective sampling depth in XPS is three times the IMFP of the sample, and therefore, only those photoelectrons that are generated in the outer layers of the AuNPs can escape the particle and reach the detector, even though they are produced through the entire NPs. In XPS measurements, the KE of the photoelectrons originating from an atomic shell with a certain BE depends linearly on the photon energy (PE):| KE = PE − BE. | (1) |
The IMFP λ of electrons, which gives the average path length an electron can move in a solid without an inelastic scattering event, depends significantly on their KE:49
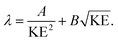 | (2) |
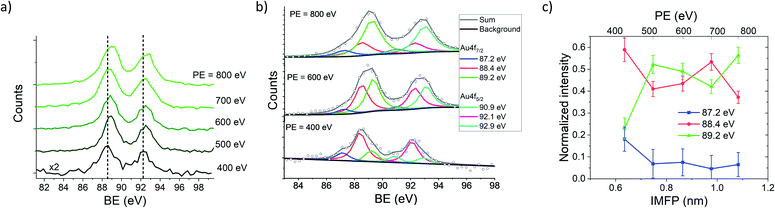
Hence, the IMFP of the generated photoelectrons can be tuned by the PE and the depth dependent information of the NP/ligand interface can be obtained. XPS measurements of AuNPs with an average diameter of 10 nm coated with NTP have been performed as a function of the PE to vary the KE and in consequence the IMFP of the photoelectrons. In Fig. 2(a) the Au 4f spectra of the NTP coated AuNPs are presented, and have been recorded at PEs between 400 eV and 800 eV, wherein special care was taken for a precise calibration of the KE of the photoelectrons at the different PEs to avoid possible effects of the PE peak position (see the Methods part for details). In solid state XPS, the Au 4f signal of bulk Au consists of two components (Au 4f7/2 and Au 4f5/2) located at 84.0 eV and 87.7 eV with respect to the Fermi level with a fixed ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 due to the spin–orbit coupling.50 Hence, the KE of the photoelectrons varies between approximately 310 eV to 710 eV, assuming a work function of the AuNPs of around 5 eV. In this case, the IMFP is varied from approximately 0.6 nm to 1.1 nm (ref. 51–53) and in consequence, only the outmost atomic layers of the ligand coated AuNPs are probed in this energy range. Fig. 2 shows that with increasing PE, the maximum of the Au 4f signal shifts from 88.5 eV at PE = 400 eV and reaches 88.9 eV at PE = 800 eV, which indicates a lower BE of the Au atoms at or close to the surface compared to those in the bulk. The Au 4f spectrum recorded at a photon energy of 400 eV reveals three components of the Au 4f7/2 peak, wherein the most intense is centered at 88.4 eV and two shoulders at 87.2 eV and 89.2 eV respectively (see Fig. 2(b)). For the fitting of the peaks the energy resolution of the photoelectrons has been used as the peak width, which has been validated by the FWHM of the Ar 2p and Ar 3s spectra recorded under the same conditions. Typically on a plane Au(111) surface, three Au species would be expected, namely bulk Au atoms, “free” surface Au atoms and surface Au atoms involved in Au–S bonding.54–57 The 89.2 eV signal shows a shift of 5.2 eV compared to the Au0 signal in the solid state located at 84.0 eV, which agrees well with the work function of bulk gold.58,59 Hence, it is concluded that the 89.2 eV signal originates from the Au atoms inside the AuNPs, where the electronic environment is comparable to that of bulk gold. The signals at 88.4 eV and 87.2 eV are assigned to surface Au atoms, which represent Au(111) facets and further Au species originating from edges or other crystalline facets present on an AuNP surface. The lower binding energy compared to bulk gold might be caused by several, possibly superimposed effects that are shortly explained in the following:
3 due to the spin–orbit coupling.50 Hence, the KE of the photoelectrons varies between approximately 310 eV to 710 eV, assuming a work function of the AuNPs of around 5 eV. In this case, the IMFP is varied from approximately 0.6 nm to 1.1 nm (ref. 51–53) and in consequence, only the outmost atomic layers of the ligand coated AuNPs are probed in this energy range. Fig. 2 shows that with increasing PE, the maximum of the Au 4f signal shifts from 88.5 eV at PE = 400 eV and reaches 88.9 eV at PE = 800 eV, which indicates a lower BE of the Au atoms at or close to the surface compared to those in the bulk. The Au 4f spectrum recorded at a photon energy of 400 eV reveals three components of the Au 4f7/2 peak, wherein the most intense is centered at 88.4 eV and two shoulders at 87.2 eV and 89.2 eV respectively (see Fig. 2(b)). For the fitting of the peaks the energy resolution of the photoelectrons has been used as the peak width, which has been validated by the FWHM of the Ar 2p and Ar 3s spectra recorded under the same conditions. Typically on a plane Au(111) surface, three Au species would be expected, namely bulk Au atoms, “free” surface Au atoms and surface Au atoms involved in Au–S bonding.54–57 The 89.2 eV signal shows a shift of 5.2 eV compared to the Au0 signal in the solid state located at 84.0 eV, which agrees well with the work function of bulk gold.58,59 Hence, it is concluded that the 89.2 eV signal originates from the Au atoms inside the AuNPs, where the electronic environment is comparable to that of bulk gold. The signals at 88.4 eV and 87.2 eV are assigned to surface Au atoms, which represent Au(111) facets and further Au species originating from edges or other crystalline facets present on an AuNP surface. The lower binding energy compared to bulk gold might be caused by several, possibly superimposed effects that are shortly explained in the following:
(i) On the one hand, the Au 4f states at a clean Au surface are typically shifted by 0.4 eV to lower BE compared to bulk gold due to a redistribution of the atomic-like valence-band states at the surface, since the coordination number of the surface atoms is lower, which affects the core level states as well.60,61 Hence, for AuNPs this effect is likely to be even more pronounced than for flat gold surfaces.62
(ii) Moreover, surface dipoles caused by ligand molecules at the metal–organic interface can significantly alter the work function and the vacuum energy of coated gold surfaces.63 Since the Au 4f core level states are localized at the individual gold atoms their BE follows the dipole induced change of the z-component of the dipole.64 The z-component of the dipole moment of a complex of NTP coupled to the (111) surface of a cluster of 30 Au atoms has been calculated by density functional theory (DFT) with the B3LYP functional and determined to be −2.88 Debye.
(iii) In addition, also an electron transfer from the metal to the molecule affects the work function, which has been described elsewhere in more detail for the present system.37
(iv) A fourth effect is a possible shift of the Au 4f signals due to the different chemical environment of the gold sulfur bond. The shift for NTP coupled to a single Au atom compared to pure Au has been calculated by DFT to be 1.3 eV to higher BE, which is in good agreement with previously reported values for Au–S65 and other hybridized Au species.55 For larger Au complexes, the calculated shift of the Au 4f orbitals decreases to 0.9 eV for Au2 and 0.4 eV for Au10, indicating a minor influence of the chemical shift for larger Au complexes with attached molecules (see Table S1† for details). Moreover, the Au 4f7/2 signal of species with higher BEs would be overlapped by the 5/2 signal and the 5/2 component would be overlapped by the Lorentzian tail of the higher BE species in a region, which is significantly impacted by the correction of the Shirley type background.
It needs to be mentioned that these four effects act in different directions and raise or lower the BE of the Au 4f states, and consequently, the resulting BE is determined by their superposition. In Fig. 2(b), the decomposition of the peaks contributing to the Au 4f signal is presented, revealing a predominant contribution of the 88.4 eV signal to the Au 4f7/2 spectrum recorded at 400 eV, whereas with increasing PE the contribution of the 88.4 eV signal decreases, and the 89.2 eV signal increases. The relative intensities of the Au 4f7/2 peaks are plotted against the IMFP in Fig. 2(c). The decrease of the 87.2 eV and 88.4 eV signals with an increasing IMFP supports the assignment of these signals to Au atoms located at or close to the surface of the AuNPs, whereas the increase of the 89.2 eV signal with the IMFP confirms that this signal originates from the inner atoms of the AuNPs.
Calculation of the Au shell thickness
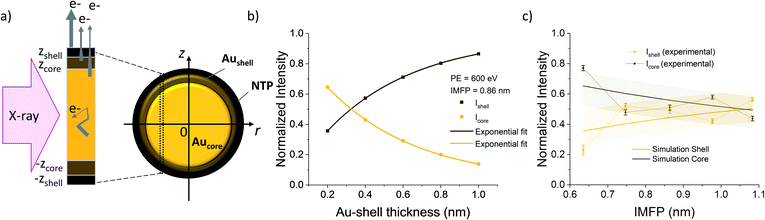
The thickness of the Au shell at the interface, where the Au 4f states vary from the bulk gold signal, can be determined from the signal intensities of the different contributions of the Au 4f states. In general, in a substrate covered with a layer of thickness d, the signal intensity I of the underlying substrate is given by:I = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−d/λ, e−d/λ, | (3) |
To calculate the relative intensities of the XPS signals, it has been assumed that the intensity of the X-ray beam passes through the AuNPs without attenuation, and only non-scattered photoelectrons emitted at a 90° angle have been taken into account. In an infinitesimal small slice, the AuNPs can be considered as a plane layer structure (see Fig. 3(a)), where the relative intensities can be calculated by assuming an exponential signal attenuation of the upper layers shown in eqn (3). By integration of the slices over the whole nanoparticle in cylindrical coordinates, the intensity of the signal originating from the core of the AuNP Icore and the signal originating from the Au shell Ishell can be obtained by:
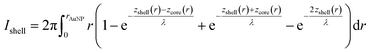 | (4) |
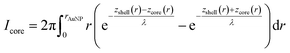 | (5) |
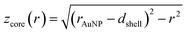 and
and 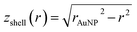 (see derivation in ESI, below Fig. S5†). The IMFP λ of the photoelectrons in gold at different KEs has been used from the NIST electron inelastic mean free path database (Version 1.2.) based on the values for gold reported by Powell and Jablonski.51,53 The contributions Ishell and Icore to the Au 4f signal have been calculated for different layer thicknesses between 0.2 nm and 1 nm for the IMFP occurring in the XPS measurements of the Au 4f states presented in Fig. 2. In Fig. 3(b) an exemplary plot of normalized Icore and Ishellversus the layer thickness dshell is presented, for an IMFP of 0.86 nm at PE = 600 eV. The plots for the PE of 400 eV, 500 eV, 700 eV and 800 eV are shown in Fig. S6.† The calculated intensities have been fitted with exponential functions to allow an assignment of intensity ratios to Au shell thicknesses at a given IMFP λ. To determine the Au shell thicknesses for the experimental data, the signal intensity of the 89.2 eV Au 4f component determined from the XPS measurements has been used as Icore and the sum of the 88.4 eV and 87.2 eV signals as Ishell. From the Au 4f spectra presented in Fig. 2(a), the Au shell thickness has been determined using the calculated exponential intensity vs. Au shell thickness plots (see Fig. 3(b) and S6†). The Au shell thickness with altered electronic properties at the surface of the NTP coated AuNPs is consequently given by dshell = 0.38 ± 0.12 nm, where the error is given by the standard deviation of the values for dshell for different PEs. In Fig. 3(c), the intensities Icore and Ishell at different IMFPs for a 10 nm AuNP with an Au shell thickness of 0.38 nm are plotted together with the measured signal intensities of the 89.2 eV, 88.4 eV and 87.2 eV signals, revealing good agreement of the experimental values with applied theoretical model results. As the thickness of the layer with altered Au 4f states is only about 3.8 Å, which corresponds to the first atomic layer of the AuNPs, it can be concluded that the adsorption of ligand molecules impacts electronic properties at the metal–organic interface within a very short range.
(see derivation in ESI, below Fig. S5†). The IMFP λ of the photoelectrons in gold at different KEs has been used from the NIST electron inelastic mean free path database (Version 1.2.) based on the values for gold reported by Powell and Jablonski.51,53 The contributions Ishell and Icore to the Au 4f signal have been calculated for different layer thicknesses between 0.2 nm and 1 nm for the IMFP occurring in the XPS measurements of the Au 4f states presented in Fig. 2. In Fig. 3(b) an exemplary plot of normalized Icore and Ishellversus the layer thickness dshell is presented, for an IMFP of 0.86 nm at PE = 600 eV. The plots for the PE of 400 eV, 500 eV, 700 eV and 800 eV are shown in Fig. S6.† The calculated intensities have been fitted with exponential functions to allow an assignment of intensity ratios to Au shell thicknesses at a given IMFP λ. To determine the Au shell thicknesses for the experimental data, the signal intensity of the 89.2 eV Au 4f component determined from the XPS measurements has been used as Icore and the sum of the 88.4 eV and 87.2 eV signals as Ishell. From the Au 4f spectra presented in Fig. 2(a), the Au shell thickness has been determined using the calculated exponential intensity vs. Au shell thickness plots (see Fig. 3(b) and S6†). The Au shell thickness with altered electronic properties at the surface of the NTP coated AuNPs is consequently given by dshell = 0.38 ± 0.12 nm, where the error is given by the standard deviation of the values for dshell for different PEs. In Fig. 3(c), the intensities Icore and Ishell at different IMFPs for a 10 nm AuNP with an Au shell thickness of 0.38 nm are plotted together with the measured signal intensities of the 89.2 eV, 88.4 eV and 87.2 eV signals, revealing good agreement of the experimental values with applied theoretical model results. As the thickness of the layer with altered Au 4f states is only about 3.8 Å, which corresponds to the first atomic layer of the AuNPs, it can be concluded that the adsorption of ligand molecules impacts electronic properties at the metal–organic interface within a very short range.
Role of ligand molecules
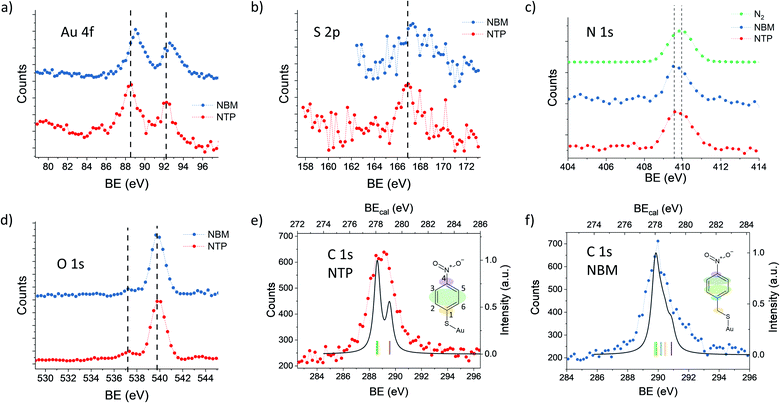
In order to elucidate the influence of the ligands on the XPS signals, we have compared NTP with NBM capped AuNPs. In Fig. 4(a) the Au 4f spectra of NTP and NBM coated AuNPs are presented, which have been recorded at a PE of 400 eV. The IMFP of the photoelectrons is 0.64 nm, and thus the measurements mainly probe the topmost layers of the AuNPs. The center of the Au 4f7/2 signal of the NBM coated AuNPs is located at 89.1 eV, which is shifted by (0.6 ± 0.2) eV compared to NTP coated AuNPs and indicates a lower work function at the interface. Even though the center of the Au 4f signal is not directly reflecting the states at the surface and is partly overlapped with the bulk signal, the strong contribution of the surface signal clearly indicates a significant shift of these states. The differences of the Au 4f states for the two ligand molecules can be explained by a different dipole moment induced by the ligand molecules. Using DFT the z-component of the dipole moment had been calculated for the complex of a molecule bound to an Au30 cluster giving −2.88 Debye for the NTP–Au30- and −3.44 Debye for NBM–Au30-complex. This would lead to a shift of the Au 4f states to higher BEs for NBM compared to NTP. The direct calculations of the Au 4f orbitals by DFT reveal a shift of the Au 4f signal of the gold complex of 0.357 eV for NTP–Au10 and 0.321 eV for NBM–Au10 (see Table S1†). Therefore, the shift of the Au 4f states caused by the different chemical environment of the molecular-metal bonds can be neglected compared to the shifts of the near surface vacuum level by molecular dipoles. Besides the surface dipoles, the differences of the work function can be explained by different packing densities of the molecules, since the adsorption of the molecules can be significantly influenced by the additional carbon linker. Moreover, the packing density can influence the alignment of the molecules and consequently affect the z-component of the surface dipole.34 The S 2p spectra shown in Fig. 4(b) reveal a maximum of S 2p3/2 of 166.9 eV for AuNPs capped with NTP and 167.3 eV capped with NBM. This corresponds to a difference of (0.4 ± 0.2) eV for the NTP capped AuNPs compared to NBM, which is in agreement with the shift of the Au 4f states.The Au 4f and S 2p spectra reflect the metal–organic interface, whereas the O 1s and N 1s signals originate from the nitro group, which is separated from the gold surface by the benzene ring. In Fig. 4(c), the N 1s spectra of NTP and NBM capped AuNPs are presented together with a spectrum recorded in the same energy range in the absence of AuNPs, when N2 is introduced into the chamber. The center of the N 1s peak of gaseous N2 is located at 409.9 eV, whereas the N 1s signals of the NTP and NBM coated AuNPs give rise to a center peak position of 409.7 eV and 409.8 eV, respectively. Moreover, due to the centered distribution of the electrons on the detector, the signal shows a significant contribution from the NP beam (see Fig. S4†). Nevertheless, due to the proximity of the peaks the decomposition of the N 1s signal of NTP and NBM from the contribution of residual N2 gas in the chamber is not precisely possible and an uncertainty remains. In XPS measurements of the NTP monolayer on an Au(111) substrate by Nielsen et al. and Waske et al., the N 1s peak has been observed at 405.5 eV and 405.4 eV, respectively, with respect to the Fermi level and consequently the expected shift of 4.5 eV due to the AuNP work function would lead to the observed overlap.66,67 The O 1s spectrum of NTP and NBM capped AuNPs is dominated by the O 1s signal of gaseous water at 539.9 eV,68,69 which has been used to precisely calibrate the binding energy. The O 1s signal originating from the nitro group of the molecules is located well separated from the water peak at 537.4 eV, for NTP and NBM likewise.
The C 1s spectrum of NTP capped AuNPs has been recorded with a high kinetic energy resolution (FWHM = 0.66 eV) to distinguish the signals of the different carbon atoms (see Fig. 4(e)). According to DFT calculations of NTP on an Au30 cluster two main signal components can be expected with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (see Fig. S7†), wherein one signal originates from the sp2 hybridized C atoms 2, 3, 5 and 6 bound to two C and one H atom and a second signal from the C atoms 1 and 4 bound to the nitro and the thiol group, respectively, which are expected to be shifted by approximately 1 eV towards higher binding energy. This is comparable to previous interpretations of XPS measurements of NTP on an Au(111) substrate.67 However, by taking into account the given experimental energy resolution, which has been verified by the 2s and 2p ionization edges of Ar gas, the experimental spectrum is significantly broadened compared to the theoretical predictions (see Fig. 4(e)). There are several effects that might explain the broadening of the C 1s spectrum of NTP on the surface of a nanoparticle. It was reported previously by Taucher et al. that in the XPS measurements of the C 1s states of molecular monolayers on gold surfaces an electrostatic environment influenced by internal dipole moments of the molecules and their intermolecular interaction must be considered in addition to the chemical environment of the C atoms.64 Besides the effect of intramolecular surface dipoles shifting the C 1s states, it is also possible that the C 1s signal is broadened by the contributions of NTP molecules bound to surface sites with different work functions. A third possibility is a broadening due to thermal atom motion and intermolecular interactions in the NTP layer as described by Ehlert et al.70 In Fig. 4(f) the C 1s spectrum of NBM on AuNPs is presented together with the calculated spectrum for NBM on an Au30 cluster (see Fig. S8†) taking into account the experimental resolution. Also in the case of NBM the experimental C 1s spectrum is broadened compared to the DFT calculations. The center of the C 1s peak for NBM, located at 290.0 eV, is shifted by 0.7 eV to higher BEs compared to the signal of NTP located at 289.3 eV. Hence, the shift of the C 1s signals of the two AuNP ligand systems is comparable to the shift of the Au 4f signals.
2 (see Fig. S7†), wherein one signal originates from the sp2 hybridized C atoms 2, 3, 5 and 6 bound to two C and one H atom and a second signal from the C atoms 1 and 4 bound to the nitro and the thiol group, respectively, which are expected to be shifted by approximately 1 eV towards higher binding energy. This is comparable to previous interpretations of XPS measurements of NTP on an Au(111) substrate.67 However, by taking into account the given experimental energy resolution, which has been verified by the 2s and 2p ionization edges of Ar gas, the experimental spectrum is significantly broadened compared to the theoretical predictions (see Fig. 4(e)). There are several effects that might explain the broadening of the C 1s spectrum of NTP on the surface of a nanoparticle. It was reported previously by Taucher et al. that in the XPS measurements of the C 1s states of molecular monolayers on gold surfaces an electrostatic environment influenced by internal dipole moments of the molecules and their intermolecular interaction must be considered in addition to the chemical environment of the C atoms.64 Besides the effect of intramolecular surface dipoles shifting the C 1s states, it is also possible that the C 1s signal is broadened by the contributions of NTP molecules bound to surface sites with different work functions. A third possibility is a broadening due to thermal atom motion and intermolecular interactions in the NTP layer as described by Ehlert et al.70 In Fig. 4(f) the C 1s spectrum of NBM on AuNPs is presented together with the calculated spectrum for NBM on an Au30 cluster (see Fig. S8†) taking into account the experimental resolution. Also in the case of NBM the experimental C 1s spectrum is broadened compared to the DFT calculations. The center of the C 1s peak for NBM, located at 290.0 eV, is shifted by 0.7 eV to higher BEs compared to the signal of NTP located at 289.3 eV. Hence, the shift of the C 1s signals of the two AuNP ligand systems is comparable to the shift of the Au 4f signals.
Conclusions
The Au 4f states of surface and bulk of ligand capped isolated AuNPs have been determined by PE dependent measurements, to modulate the escape depth of the photoelectrons. It has been shown that there is a significant shift of Au 4f states in the outer Au layer, which significantly depends on the adsorbed ligand molecule and might be caused by different dipole moments that modify the work function of the AuNP surface. The range of this effect is limited to the topmost atomic layer of the AuNPs. By the modification of the interface dipoles due to the functional groups of the molecules or different orientations to the surface, e.g. as a consequence of the packing density, the charge transfer between NPs and adsorbed molecules can be tuned. This allows for the engineering of NP systems using tightly bound ligands in plasmonic catalysis. Moreover, also the core level states of the ligands, most remarkably the C 1s states, are affected by the dipole moments or due to the binding of the molecules to different adsorption sites. These effects need to be considered by the evaluation of the XPS core level states of ligands bound to NP surfaces.Methods
Chemicals
AuHCl4, trisodium citrate (TSC), and 4-nitrobenzylmercaptan (NBM) have been purchased from Sigma Aldrich and 4-nitrothiophenol (NTP) has been purchased from Alfa Aesar. All chemicals have been used without further purification.Preparation of AuNPs
AuNPs have been synthesized by citrate reduction of HAuCl4 according to a modified version of the Turkevich protocol.71 Briefly, a 500 mL stirred aqueous solution of 1 mM HAuCl4 has been heated up in a 1 L 2 neck round bottom flask to a rolling boil under reflux in an oil bath. Subsequently, 4 mL of 500 mM TSC has been added using a syringe and the solution has been kept boiling for 20 more minutes and cooled down to room temperature and stored at 4 °C. The diameter of the AuNPs determined from SEM images is 8.7 ± 1.7 nm and the maximum of the SPR is located at λ = 518 nm (see Fig. S1†).In order to exchange the citrate ligands of the AuNPs with the analyte molecules, the AuNP solution has been incubated with NTP or NBM overnight. Using 15 mL Amicon filters (Merck Millipore) the AuNP solution has been centrifuged at 3000 g for 10 min and refilled with H2O Milli Q trice. After the final centrifugation step the concentration of the AuNP solution has been adjusted to approximately 3 mM referring to the Au atoms in the solution. Raman spectra validating the bond of the ligands to the AuNP surface are shown in Fig. S2.†
Synchrotron XPS
The XPS measurements of isolated AuNPs have been performed at the PLEIADES beamline at the synchrotron SOLEIL using a multipurpose source chamber (MPSC).72,73 The AuNPs have been brought to the gas phase from a colloidal solution using a TSI 3076 atomizer, with argon as the carrier gas at 35 Psi. The solvent (water) has been mainly removed by passing the aerosol through silica desiccators. The AuNPs then have entered the MPSC through a limiting orifice (240 μm) and have been focused with an aerodynamic lens system through a skimmer (1.5 mm) into the ionization chamber. At the entrance of the VG Scienta R4000 hemispherical electron energy analyzer the Au nanoparticle beam has been crossed with the soft X-ray photon beam produced by a permanent magnet APPLE II type undulator, with a period of 80 mm, in combination with a high-flux, 600 L mm−1 grating of the modified Petersen plane grating monochromator used to monochromatize the synchrotron radiation. The binding energy of the Au 4f energy level was calibrated according to the kinetic difference with respect to the 2p and 3s ionization edges of the carrier argon gas42 at all recorded PEs (see Fig. SI 3†). The linearity of the kinetic energy scale has been validated by using 2s, 2p, 3p and 3s ionization edges42 and KLL Auger electrons74 of the carrier argon gas, as discussed before.75 The overall uncertainty of BE due to the calibration is estimated to be 0.1–0.2 eV. It should be noted that in the PLEIADES setup, the photoelectron lines from the focused AuNPs can be resolved from those produced by residual H2O solvent molecules and Ar carrier gas, which are not focused by the aerodynamic lens.75The peaks have been distinguished using XPSPEAK 4.1 software assuming a Gaussian–Lorentzian fit function with a ratio of 80%. The FWHM has been fixed for all components to the experimentally determined FWHM from the measurements of the Ar ionization edges.
DFT
DFT calculations were performed with the quantum chemical package Gaussian 16.76 The gold–molecule complexes were optimized using the global hybrid functional B3LYP.77,78 The TZVP basis set79 was used for the H, C, N, O, and S atoms and LANL2TZ(f) effective core potential with the corresponding basis set80 (of triple zeta valence orbital quality and an f polarization function) was used for the Au atoms. Spin-unrestricted DFT was used for doublet species (neutral complexes with an even number of gold atoms; one gold atom) and spin-restricted DFT for singlet species (neutral complexes with a single gold atom; gold clusters with an even number of gold atoms).Au 4f orbital shifts were calculated with the all-electron ANO-R basis set81 (the largest one in the recent ANO-R series) for gold and TZVP for the other atoms, again employing B3LYP.
The LANL2TZ(f) and ANO-R basis sets were downloaded from the Basis Set Exchange82 website (https://www.basissetexchange.org/). The complexes of NTP and NBM with 1, 2, 10, and 30 atoms were considered. Further details of the used models are reported in ref. 37.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
IB, RS and AM acknowledge support by the European Research Council (ERC; consolidator grant no. 772752), and we acknowledge beamtime at the synchrotron SOLEIL at the beamline PLEIADES through project 20191485.References
- S. Linic, P. Christopher and D. B. Ingram, Nat. Mater., 2011, 10, 911–921 CrossRef CAS PubMed.
- S. Linic, U. Aslam, C. Boerigter and M. Morabito, Nat. Mater., 2015, 14, 567–576 CrossRef CAS PubMed.
- D. C. Ratchford, ACS Nano, 2019, 13, 13610–13614 CrossRef CAS PubMed.
- E. Kazuma and Y. Kim, Angew. Chem., Int. Ed., 2019, 58, 4800–4808 CrossRef CAS PubMed.
- M. J. Kale, T. Avanesian and P. Christopher, ACS Catal., 2014, 4, 116–128 CrossRef CAS.
- A. Manjavacas, J. G. Liu, V. Kulkarni and P. Nordlander, ACS Nano, 2014, 8, 7630–7638 CrossRef CAS PubMed.
- G. V. Hartland, L. V. Besteiro, P. Johns and A. O. Govorov, ACS Energy Lett., 2017, 2, 1641–1653 CrossRef CAS.
- P. Christopher and M. Moskovits, Annu. Rev. Phys. Chem., 2017, 68, 379–398 CrossRef CAS PubMed.
- K. Chen and H. Wang, Mol. Syst. Des. Eng., 2021, 6, 250–280 RSC.
- R. Schürmann and I. Bald, Nanoscale, 2017, 9, 1951–1955 RSC.
- A. Dutta, R. Schürmann, S. Kogikoski, N. S. Mueller, S. Reich and I. Bald, ACS Catal., 2021, 11, 8370–8381 CrossRef CAS PubMed.
- C.-F. Wang, B. T. O'Callahan, D. Kurouski, A. Krayev and P. Z. El-Khoury, J. Phys. Chem. Lett., 2020, 11, 3809–3814 CrossRef CAS PubMed.
- R. Schürmann, K. Ebel, C. Nicolas, A. R. Milosavljević and I. Bald, J. Phys. Chem. Lett., 2019, 10, 3153–3158 CrossRef PubMed.
- N. C. Brandt, E. L. Keller and R. R. Frontiera, J. Phys. Chem. Lett., 2016, 7, 3179–3185 CrossRef CAS PubMed.
- H.-K. Choi, K. S. Lee, H.-H. Shin and Z. H. Kim, J. Phys. Chem. Lett., 2016, 7, 4099–4104 CrossRef CAS PubMed.
- H.-K. Choi, W.-H. Park, C.-G. Park, H.-H. Shin, K. S. Lee and Z. H. Kim, J. Am. Chem. Soc., 2016, 138, 4673–4684 CrossRef CAS PubMed.
- Q. Ding, M. Chen, Y. Fang, Z. Zhang and M. Sun, J. Phys. Chem. C, 2017, 121, 5225–5231 CrossRef CAS.
- W. Koopman, R. M. Sarhan, F. Stete, C. N. Z. Schmitt and M. Bargheer, Nanoscale, 2020, 12, 24411–24418 RSC.
- X. Ren, E. Cao, W. Lin, Y. Song, W. Liang and J. Wang, RSC Adv., 2017, 7, 31189–31203 RSC.
- R. M. Sarhan, W. Koopman, R. Schuetz, T. Schmid, F. Liebig, J. Koetz and M. Bargheer, Sci. Rep., 2019, 9, 3060 CrossRef PubMed.
- M. Zhang, L.-B. Zhao, W.-L. Luo, R. Pang, C. Zong, J.-Z. Zhou, B. Ren, Z.-Q. Tian and D.-Y. Wu, J. Phys. Chem. C, 2016, 120, 11956–11965 CrossRef CAS.
- Q. Zhang and H. Wang, J. Phys. Chem. C, 2018, 122, 5686–5697 CrossRef CAS.
- Z. Zhang, T. Deckert-Gaudig, P. Singh and V. Deckert, Chem. Commun., 2015, 51, 3069–3072 RSC.
- Z. Zhang, D. Kinzel and V. Deckert, J. Phys. Chem. C, 2016, 120, 20978–20983 CrossRef CAS.
- R. Schürmann, T. F. M. Luxford, I. S. Vinklárek, J. Kočišek, M. Zawadzki and I. Bald, J. Chem. Phys., 2020, 153, 104303 CrossRef PubMed.
- D. Lee and S. Yoon, J. Phys. Chem. C, 2020, 124, 15879–15885 CrossRef CAS.
- C. D. Lindstrom and X.-Y. Zhu, Chem. Rev., 2006, 106, 4281–4300 CrossRef CAS PubMed.
- W. E. Ford, D. Gao, N. Knorr, R. Wirtz, F. Scholz, Z. Karipidou, K. Ogasawara, S. Rosselli, V. Rodin, G. Nelles and F. von Wrochem, ACS Nano, 2014, 8, 9173–9180 CrossRef CAS PubMed.
- X. Peng, L. Hu, F. Qin, Y. Zhou and P. K. Chu, Adv. Mater. Interfaces, 2018, 5, 1701404 CrossRef.
- H. Häkkinen, Nat. Chem., 2012, 4, 443–455 CrossRef PubMed.
- P. C. Rusu, G. Giovannetti, C. Weijtens, R. Coehoorn and G. Brocks, J. Phys. Chem. C, 2009, 113, 9974–9977 CrossRef CAS.
- R. Otero, A. L. Vázquez de Parga and J. M. Gallego, Surf. Sci. Rep., 2017, 72, 105–145 CrossRef CAS.
- E. Zojer, T. C. Taucher and O. T. Hofmann, Adv. Mater. Interfaces, 2019, 6, 1900581 CrossRef.
- S.-Y. Hong, P.-C. Yeh, J. I. Dadap and R. M. Osgood, ACS Nano, 2012, 6, 10622–10631 CrossRef CAS PubMed.
- O. T. Hofmann, D. A. Egger and E. Zojer, Nano Lett., 2010, 10, 4369–4374 CrossRef CAS PubMed.
- M. Gärtner, E. Sauter, G. Nascimbeni, A. Petritz, A. Wiesner, M. Kind, T. Abu-Husein, M. Bolte, B. Stadlober, E. Zojer, A. Terfort and M. Zharnikov, J. Phys. Chem. C, 2018, 122, 28757–28774 CrossRef.
- W. Koopman, E. Titov, R. M. Sarhan, T. Gaebel, R. Schürmann, A. Mostafa, S. Kogikoski, A. R. Milosavljević, F. Stete, F. Liebig, C. N. Schmitt, J. Koetz, I. Bald, P. Saalfrank and M. Bargheer, Adv. Mater. Interfaces, 2021, 8, 2101344 CrossRef CAS.
- J. Liu, Z.-Y. Cai, W.-X. Sun, J.-Z. Wang, X.-R. Shen, C. Zhan, R. Devasenathipathy, J.-Z. Zhou, D.-Y. Wu, B.-W. Mao and Z.-Q. Tian, J. Am. Chem. Soc., 2020, 142, 17489–17498 CrossRef CAS PubMed.
- G. Greczynski and L. Hultman, Prog. Mater. Sci., 2020, 107, 100591 CrossRef CAS.
- M. P. Seah, I. S. Gilmore and G. Beamson, Surf. Interface Anal., 1998, 26, 642–649 CrossRef CAS.
- D. R. Baer, K. Artyushkova, H. Cohen, C. D. Easton, M. Engelhard, T. R. Gengenbach, G. Greczynski, P. Mack, D. J. Morgan and A. Roberts, J. Vac. Sci. Technol., A, 2020, 38, 031204 CrossRef CAS.
- A. C. Thompson, D. T. Attwood, E. M. Gullikson, M. R. Howells, J. B. Kortright, A. L. Robinson, J. H. Underwood, K.-J. Kim, J. Kirz, I. Lindau, P. Pianetta, H. Winick, G. P. Williams and J. H. Scofield, X-Ray Data Booklet, Berkeley, 2009 Search PubMed.
- D. Cahen and A. Kahn, Adv. Mater., 2003, 15, 271–277 CrossRef CAS.
- A. Kahn, Mater. Horiz., 2016, 3, 7–10 RSC.
- S. Axnanda, M. Scheele, E. Crumlin, B. Mao, R. Chang, S. Rani, M. Faiz, S. Wang, A. P. Alivisatos and Z. Liu, Nano Lett., 2013, 13, 6176–6182 CrossRef CAS PubMed.
- M. F. Lichterman, S. Hu, M. H. Richter, E. J. Crumlin, S. Axnanda, M. Favaro, W. Drisdell, Z. Hussain, T. Mayer, B. S. Brunschwig, N. S. Lewis, Z. Liu and H.-J. Lewerenz, Energy Environ. Sci., 2015, 8, 2409–2416 RSC.
- J. Hwang, A. Wan and A. Kahn, Mater. Sci. Eng., R, 2009, 64, 1–31 CrossRef.
- J. B. Gilbert, M. F. Rubner and R. E. Cohen, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6651–6656 CrossRef CAS PubMed.
- M. P. Seah and W. A. Dench, Surf. Interface Anal., 1979, 1, 2–11 CrossRef CAS.
- C. Passiu, A. Rossi, M. Weinert, W. Tysoe and N. D. Spencer, Appl. Surf. Sci., 2020, 507, 145084 CrossRef CAS.
- C. J. Powell and A. Jablonski, J. Phys. Chem. Ref. Data, 1999, 28, 19–62 CrossRef CAS.
- H. Shinotsuka, S. Tanuma, C. J. Powell and D. R. Penn, Surf. Interface Anal., 2015, 47, 871–888 CrossRef CAS.
- C. J. Powell, J. Vac. Sci. Technol., 2020, 38, 23209 CrossRef CAS.
- M. de Anda Villa, J. Gaudin, D. Amans, F. Boudjada, J. Bozek, R. Evaristo Grisenti, E. Lamour, G. Laurens, S. Macé, C. Nicolas, I. Papagiannouli, M. Patanen, C. Prigent, E. Robert, S. Steydli, M. Trassinelli, D. Vernhet and A. Lévy, Langmuir, 2019, 35, 11859–11871 CrossRef CAS PubMed.
- M. Tchaplyguine, M.-H. Mikkelä, C. Zhang, T. Andersson and O. Björneholm, J. Phys. Chem. C, 2015, 119, 8937–8943 CrossRef CAS.
- F. Chesneau, J. Zhao, C. Shen, M. Buck and M. Zharnikov, J. Phys. Chem. C, 2010, 114, 7112–7119 CrossRef CAS.
- M. Zharnikov, J. Electron Spectrosc. Relat. Phenom., 2010, 178–179, 380–393 CrossRef CAS.
- Y. Zhang, O. Pluchery, L. Caillard, A.-F. Lamic-Humblot, S. Casale, Y. J. Chabal and M. Salmeron, Nano Lett., 2015, 15, 51–55 CrossRef CAS PubMed.
- InCRC handbook of chemistry and physics. A ready-reference book of chemical and physical data: 2012-2013, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, Boca Raton (Fla.), London, New York, 93rd edn, 2012 Search PubMed.
- P. H. Citrin, G. K. Wertheim and Y. Baer, Phys. Rev. Lett., 1978, 41, 1425–1428 CrossRef CAS.
- G. K. Wertheim, S. B. DiCenzo and S. E. Youngquist, Phys. Rev. Lett., 1983, 51, 2310–2313 CrossRef CAS.
- J. Radnik, C. Mohr and P. Claus, Phys. Chem. Chem. Phys., 2003, 5, 172–177 RSC.
- D. M. Alloway, A. L. Graham, X. Yang, A. Mudalige, R. Colorado, V. H. Wysocki, J. E. Pemberton, T. R. Lee, R. J. Wysocki and N. R. Armstrong, J. Phys. Chem. C, 2009, 113, 20328–20334 CrossRef CAS.
- T. C. Taucher, I. Hehn, O. T. Hofmann, M. Zharnikov and E. Zojer, J. Phys. Chem. C, 2016, 120, 3428–3437 CrossRef CAS PubMed.
- F. Vitale, I. Fratoddi, C. Battocchio, E. Piscopiello, L. Tapfer, M. V. Russo, G. Polzonetti and C. Giannini, Nanoscale Res. Lett., 2011, 6, 103 CrossRef PubMed.
- J. U. Nielsen, M. J. Esplandiu and D. M. Kolb, Langmuir, 2001, 17, 3454–3459 CrossRef CAS.
- P. Waske, T. Wächter, A. Terfort and M. Zharnikov, J. Phys. Chem. C, 2014, 118, 26049–26060 CrossRef CAS.
- R. Sankari, M. Ehara, H. Nakatsuji, Y. Senba, K. Hosokawa, H. Yoshida, A. de Fanis, Y. Tamenori, S. Aksela and K. Ueda, Chem. Phys. Lett., 2003, 380, 647–653 CrossRef CAS.
- B. Winter, E. F. Aziz, U. Hergenhahn, M. Faubel and I. V. Hertel, J. Chem. Phys., 2007, 126, 124504 CrossRef PubMed.
- C. Ehlert, D. Kröner and P. Saalfrank, J. Electron Spectrosc. Relat. Phenom., 2015, 199, 38–45 CrossRef CAS.
- J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55 RSC.
- O. Sublemontier, C. Nicolas, D. Aureau, M. Patanen, H. Kintz, X. Liu, M.-A. Gaveau, J.-L. Le Garrec, E. Robert, F.-A. Barreda, A. Etcheberry, C. Reynaud, J. B. Mitchell and C. Miron, J. Phys. Chem. Lett., 2014, 5, 3399–3403 CrossRef CAS PubMed.
- A. Lindblad, J. Söderström, C. Nicolas, E. Robert and C. Miron, Rev. Sci. Instrum., 2013, 84, 113105 CrossRef PubMed.
- L. O. Werme, T. Bergmark and K. Siegbahn, Phys. Scr., 1973, 8, 149–153 CrossRef CAS.
- D. Danilović, D. K. Božanić, R. Dojčilović, N. Vukmirović, P. Sapkota, I. Vukašinović, V. Djoković, J. Bozek, C. Nicolas, S. Ptasinska and A. R. Milosavljević, J. Phys. Chem. C, 2020, 124, 23930–23937 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Jr Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- L. E. Roy, P. J. Hay and R. L. Martin, J. Chem. Theory Comput., 2008, 4, 1029–1031 CrossRef CAS PubMed.
- J. P. Zobel, P.-O. Widmark and V. Veryazov, J. Chem. Theory Comput., 2020, 16, 278–294 CrossRef PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00737h |
| This journal is © The Royal Society of Chemistry 2022 |