Open Access Article
Open Access ArticleMultifunctional metasails for self-stabilized beam-riding and optical communication†
Mohammadrasoul
Taghavi
 ,
Mohammad Mahdi
Salary
,
Mohammad Mahdi
Salary
 and
Hossein
Mosallaei
*
and
Hossein
Mosallaei
*
Northeastern University, USA. E-mail: hosseinm@ece.neu.edu
First published on 3rd February 2022
Abstract
The photonic propulsion of lightsails can be used to accelerate spacecraft to relativistic velocities, providing a feasible route for the exploration of interstellar space in the human lifetime. Breakthrough Starshot is an initiative aiming to launch lightsail-driven spacecrafts accelerated to a relativistic velocity of 0.2c via radiation pressure of a high-power laser beam in order to probe the habitable zone of Alpha Centauri, located 4.2 light years away from the Earth, and transmit back the scientific data collected in the flyby mission to an Earth-based receiver. The success of such a mission requires the lightsail to provide maximal acceleration while featuring beam-riding stability under the illumination of an intense laser beam during the launch phase. Moreover, the large-area lightsail can be harnessed to improve the margin in the photon-starved downlink channel throughout the communication phase by maximizing the gain of the transmitter despite extending the acceleration period and reducing the stability margin due to the elimination of a portion of the propulsion segments. Owing to the potential of metasurfaces to serve as low-weight versatile multifunctional photonic components, metasurface-based lightsails or metasails are deemed to be ideal candidates to simultaneously address the requirements of photonic propulsion and optical communication in laser-driven deep-space probes. Here, we demonstrate the design of a multifunctional metasail for providing high acceleration and enabling the self-stabilized beam-riding of a spacecraft with a detached payload from the sail while maximizing the transmission gain in the downlink optical communication. The metasail consists of two interleaved sub-arrays of dielectric unit cells operating based on the Pancharatnam–Berry geometric phase, optimized to meet the propulsion and communication requirements, respectively. The beam-riding stability of the sail is analyzed through simulation of the motion trajectory during the acceleration phase, while taking into account the effect of the relativistic Doppler shift, and the downlink communication performance is enabled by providing the required conjugate phase by the metasail elements, resulting in beam collimation. The obtained results verify the multifunctionality of the platform and point toward the promise of metasails for extended mission applications.
1 Introduction
Since the discovery of Alpha Centauri in 1917, located approximately 4.2 light-years from the Earth as the nearest star to the solar system, humans’ dream for interstellar voyage has pushed the limits of technology in the field of space exploration, convincing engineers and scientists of the infeasibility of propulsion technologies based on chemical propellants to enable interstellar travel, as it will take hundreds of millennia to reach the target, which is not comparable with the human life span.1 Several propulsion schemes have been proposed for realizing interstellar travels over the last century. With the advent of Ruby lasers in 1960, Marx and Forward postulated the use of X-ray and microwave laser beams to propel large-area reflective mirrors to significant fractions of the speed of light for interstellar space travel.2,3 With photonic technology being in its infancy, the technical realization of such a technology seemed to be impractical. Nevertheless, the dramatic technological advances in the 21st Century have brought this goal closer within reach. In particular, the successful interplanetary space missions by JAXA and NASA using lightsails in recent years4–7 have re-sparked the interest in the use of photonic propulsion for deep space exploration.8 The concept of the lightsail was first conceived of by Tsiolkovskiy and Tsander, who proposed the use of the radiation pressure of sunlight as a propellant for spacecrafts by utilizing large reflective mirrors which would eliminate the need for reaction mass.9 The operating principle of a lightsail is based on the momentum exchange between the light and the object upon scattering, which is manifested by an optical force exerted on the object. Optical forces are currently being used in variety of applications, including the manipulation and trapping of the nanoparticles.10–13Soon after the discovery of Proxima Centauri B, the exoplanet within the habitable zone of Alpha Centauri, in 2016, the Breakthrough Starshot initiative was launched, aiming to send a swarm of lightsail-driven probes to this region for collecting scientific data in a flyby mission and transmitting information back to an Earth-based receiver. For this purpose, the Breakthrough Starshot envisions ultra-light spacecrafts consisting of a payload, called Starchip, carrying communication and sensing equipment, and a large-area lightsail which is accelerated to 20% of the speed of light under the illumination of a high-power laser beam (100 GW) generated by an Earth-based laser array, for a duration of approximately 1000 seconds. The interstellar voyage would take approximately 20 years, followed by communication with Earth, which would take an additional 4 years.1,14,15 Although this project does not violate any known physical laws, it presents significant challenges for the current state-of-the-art of engineering and requires major breakthroughs in several fields in order to succeed. The photonic design of the lightsail is one of these key challenges. An effective photonic propulsion requires the sail to exhibit an optimal tradeoff between mass and reflectivity to maximize the acceleration.16,17 Furthermore, the sail should provide restoring forces and counterbalancing torques to stabilize the beam-riding and remain within the beam area for the entire acceleration phase.18–22 In particular, these requirements should be addressed over a Doppler-broadened propulsion band due to the significant red-shift of the beam’s wavelength in the frame of the moving sail with relativistic velocities. Another requirement of the probe is the ability to communicate with an Earth-based station in order to send the collected scientific data via a photon-starved free-space channel. Given that the lightsail is the largest area of the probe, harnessing it for maximizing the gain margin by increasing the aperture size in the downlink communication is highly desirable and indispensable for lowering the requirement on the signal power and size of the Earth-based receiver. The material choice for the lightsail is another crucial aspect.16,23 The sail should survive the intense illumination of the laser beam during the acceleration phase through minimal absorption and effective radiative cooling, but also should maintain integrity under thrust in the extreme environmental conditions of space, including zero atmospheric pressure, dramatic temperature fluctuations, and cosmic radiation.
In earlier works, engineering the geometry of conformal lightsails made of opaque materials has been proposed to achieve self-stabilized beam-riding.18,19,24–26 The integration of Fresnel-zone antennas as part of a solar sail has also been envisioned for accommodating sufficient transmitter gain to satisfy the communication link requirements in solar sail missions.27,28 More recently, lightsails made of nanophotonic structures and metasurfaces have been shown to not only maximize the acceleration by providing an optimal tradeoff between mass and reflectivity,16,29,30 but also to enable the self-stabilization of beam-riding with flat macroscopic geometries.20–22,31,32 These metasails can offer complex wavefront control by relying on phase discontinuities created by their constituent nanoantennas rather than relying on a gradient propagation phase delay in conventional conformal structures.33 Metasurfaces are also ideal platforms for achieving versatile multifunctional photonic components. As such, they can be used to realize multifunctional metasails which simultaneously address the requirements of photonic propulsion and downlink optical communication in a deep space probe.
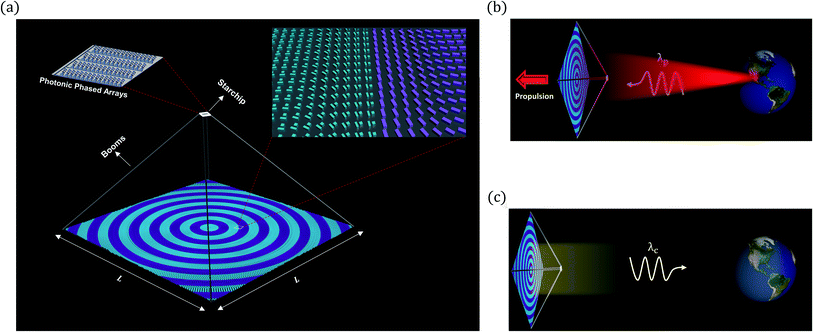
In this work, we present the design of a multifunctional metasail consisting of two sub-arrays of distinct nanoantennas made of crystalline silicon (c-Si) interleaved in a 2 × 2 m2 shared aperture backed by an ultrathin silica substrate to accommodate the requirements of stable beam-riding and optical communication at the same time. Due to the dual functionality of the sail and the concurrent presence of both of the components in the simulations, the optical properties of the propulsion and communication building blocks should be engineered in a manner that the destructive interference of their responses on one another is minimized, which can be achieved by a proper optimization process. As shown in Fig. 1 the payload carrying the communication circuitry is considered to be detached from the sail, located on the illumination side and connected to the sail via rigid booms. During the acceleration phase, the ultra-light metasail maximizes the thrust under illumination of a high-power laser beam and stabilizes the beam-riding until reaching the target relativistic velocity of 0.2c. For this purpose, it provides high reflectivity, as well as restoring forces and counter-balancing torques across the entire Doppler-broadened propulsion band of corresponding to the propulsion laser wavelength of λ0 = 1.3 μm. In the communication phase, the metasail serves as a large-area reflector for the communication payload, which collimates the highly divergent data-carrying beam generated by the small photonic chip at the communication wavelength of λc = 1065 nm and gives rise to a diffraction-limited beam at the farfield to maximize the transmission gain in the downlink communication.
The rest of the manuscript is organized as follows. In Section 2, we delineate the design procedure of the interleaved metasurface and its constituent unit cells. In Section 3, we outline the optomechanical modeling and stability analysis framework by a motion trajectory estimation. The possibility of the downlink communication and the required components and the results of the proposed communication systems, including the calculated antenna parameters, are discussed in the Section 4. Finally, the final conclusions are drawn in Section 5.
2 Interleaved geometric phase metasurface design
Throughout this work, we choose the propulsion laser wavelength as λ0 = 1.3 μm, according to the atmospheric transparency window, which yields a Doppler-broadened propulsion band of [1.3 μm, 1.586 μm] for a terminal velocity of 0.2c. The communication wavelength is also chosen to be at λc = 1065 nm, which yields a Doppler-shifted wavelength of λ0 = 1.3 μm for the beam received at the Earth-based station. This choice allows the same Earth-based phased array system to be used for both propulsion and communication in principle.In order to accommodate the stable beam-riding and optical communication requirements of the probe shown in Fig. 1, the metasail should be capable of complex wavefront control via phase discontinuities, both across the Doppler-broadened propulsion band and at the communication wavelength. The former capability should be used to create lateral restoring forces and counter-balancing torques to correct deviations of the sail’s position with respect to the beam axis during beam-riding, while the latter capability should be harnessed for collimating the data-carrying beam emitted from the Starchip to maximize transmission gain in the downlink communication. Given the independence of these functionalities, two distinct phase discontinuity profiles should be imprinted across the metasail. A common approach to achieve this goal is to use shared aperture interleaved metasurfaces, in which two or multiple sub-arrays are interspersed, each of which is associated with a different phase function.34–38 Although previous demonstrations of metasails have relied on diffraction or resonant phase tuning to enable wavefront engineering,20–22,31,32 the use of the geometric Pancharatnam–Berry (PB) phase shift seems to be a more natural choice, especially when it comes to a multifunctional design. The use of PB phase not only gives rise to a dispersionless phase discontinuity suitable for the broadband response required across the Doppler-broadened propulsion band for stable beam-riding, but also yields minimal crosstalk between the phase response of the interleaved sub-arrays in a multifunctional shared aperture platform owing to its non-resonant nature.39–42 The independence of the geometric phase from the incident angle also allows for sustaining the phase gradient under rotational deviations of the metasail with respect to the beam axis, which is crucial for generating counter-balancing torques to stabilize the beam-riding. In such a design, the constituent nanoantennas of the metasurface will convert the handedness of a circularly-polarized (CP) light upon reflection or transmission, whose local phase can be controlled simply by rotating the nanoantennas around their optical axis, independent from the incident wavelength and angle.43 Specifically, by rotating a nanoantenna by θ around its optical axis, the reflected CP light of the same handedness and the transmitted light of the opposite handedness will acquire a phase shift of 2θ, which allows the access to the full 2π span in the phase gradient profile. In the limit of adiabatic transitions and dismissing the adverse coupling effect between the unit cells, the amplitude of cross circular polarized light is maintained constant as the unit cells are rotated around their axis, which yields minimal spurious scattering.
In addition to the propulsion and communication functionalities, thermal management of the sail requires it to exhibit minimal absorption in the Doppler-broadened propulsion band while providing sufficient emissivity across the thermal mid-infrared spectrum. These requirements are shown to be satisfied, with all-dielectric platforms being a hybrid of c-Si and silica.32,44 The high refractive index of c-Si can also be harnessed to enhance the light–matter interaction via the excitation of resonant modes to increase the reflectivity of the metasail in the propulsion band.
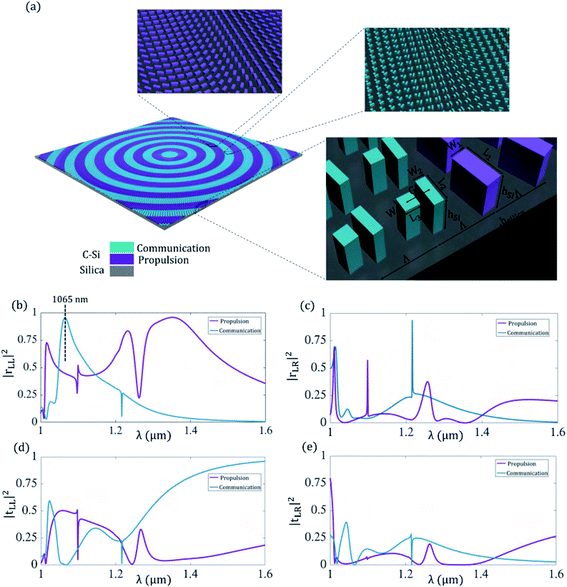
Here, we design two sets of building blocks for addressing the requirement of photonic propulsion and optical communication, respectively. The height and periodicity of both building cells are chosen to be identical to facilitate the fabrication and assembly process. The building block responsible for accommodating stable beam-riding is considered to be a c-Si nanobar while the one addressing the requirement of communication is chosen to consist of two non-identical c-Si nanobars which are placed orthogonal to one another with a distance of G for extending degrees of freedom in the constrained design space. The periodic response of the unit cells is modeled via an in-house developed solver based on rigorous coupled wave analysis (RCWA), which is one of the most powerful methods for simulating multiplayer planar periodic structures.45–50 Considering the existence of two sets of unit cells in the proposed structure, operating in different bands, we have performed separate multiobjective genetic algorithm (GA) optimizations for each of the propulsion and communication unit cells by considering the demands for an efficient photonic propulsion and optical communication performance. The geometrical dimensions of the propulsion building block are optimized taking the following objectives into consideration: (1) maximizing the acceleration by providing an optimal trade-off between mass density and circular cross-polarization conversion in reflection across the Doppler-broadened propulsion band and (2) exhibiting minimal crosstalk with the communication building block by minimizing the circular cross-polarization conversion in reflection at the communication wavelength of λc = 1065 nm. Similarly, the structural parameters of the communication building block are optimized in order to (1) maximize the transmission gain by providing maximal circular cross-polarization conversion in reflection at the communication wavelength and (2) minimize the crosstalk with the propulsion building block by minimizing the circular cross-polarization conversion in reflection across the Doppler-broadened propulsion band. The optimized structural parameters marked in Fig. 2(a) are given as: L1 = 500 nm,W1 = 252 nm, L2 = 350 nm, W2 = 125 nm, L3 = 206 nm, W3 = 195 nm, hSi = 500 nm, hsilica = 40 nm, G = 325 nm, Λ = 680 nm, which identify the designs with optimal performance within the design space. It should be noted that the propulsion and communication unit cells possess equal periodicity Λ = 680, hence we have shown one of the borders of the annular propulsion and communication portions at the edge of the metasail in the zoomed in section of Fig. 2(a).
Here, we set the polarization of incident light as a left-handed CP light, with the only difference being that the geometric phase would be conjugate for the opposite handedness. Similar results can be obtained for the right-handed polarization. Fig. 2(b) and (c) show the reflectance of the designed unit cells responsible for communication and propulsion functionalities corresponding to the reflected CP light with and without cross polarization conversion in the metasurface (rLL and rLR), respectively. Fig. 2(c) and (d) show the same for transmitted CP light. It should be emphasized that the reflection and transmission of the CP light undergoing cross-polarization conversion in the metasurface which experiences geometric phase shift are associated with rLL and tLR. This is while rLR and tLL do not acquire any geometric phase shift and their scattering is described by conventional laws of reflection and transmission, as opposed to generalized Snell’s laws governing the response of rLL and tLR in a gradient metasurface. As can be clearly observed from the results, the communication unit cell exhibits a near-unity peak for the cross-polarization conversion (rLL) at the communication wavelength of λc = 1065 nm. At the same time, it is mostly transparent and features minimal reflectivity over the Doppler-broadened propulsion band of [1.3–1.586 μm], minimizing its crosstalk with the propulsion unit cell. On the other hand, the propulsion unit cell shows a relatively high reflectivity for cross-polarization converted light (rLL) over the entire Doppler-broadened propulsion band of [1.3–1.586 μm].
In order to render the metasail as a multifunctional platform, we divide the 2 × 2 m2 aperture of the sail into 14 concentric circular regions which are assigned to the communication and propulsion building blocks alternately. Alternative configurations for interleaving can also be considered given the weak cross-talk between the sub-arrays. The orientation of the building blocks at each radial distance from the center of the sail is set according to the required phase functions for accommodating stable beam-riding and optical communication. Both of these phase functions are considered to be parabolic to yield focusing of the reflected CP light undergoing polarization conversion (rLL) at their respective operating wavelengths. For the stable beam-riding, the focal distance of the propulsion sub-array across the Doppler-broadened propulsion band should be shorter than a threshold set by the distance spacecraft’s center-of-mass from the sail, as shown previously for the parabolic sails with detached payloads.18,19,32 This allows for the creation of restoring lateral forces and sufficiently strong counter-balancing torques to compensate for deviations in the sail’s position with respect to the beam axis. On the other hand, the focal distance of the communication sub-array at the communication wavelength should be equal to the distance of the payload from the sail to allow for the collimation of the beam emitted from the Starchip, under reciprocity. Given that the location of the spacecraft’s center-of-mass depends on the distance of the payload from the sail, the phase functions for photonic propulsion and optical communication, although independent, are correlated. In the following sections, we study the performance of the interleaved metasail for both functionalities while taking into account this correlation.
3 Photonic propulsion
As highlighted earlier in the manuscript, a successful photonic design of the sail for photonic propulsion requires the sail to have a self-stabilizing optomechanical response which allows it to keep itself within the beam area for the entire duration of the acceleration phase until reaching the target relativistic velocity of 0.2c. In this section, we analyze the beam-riding stability of the multifunctional metasail with interleaved design and study its motion trajectory in the acceleration phase under the illumination of an intense laser beam with the net power of 100 GW, while taking into account the effect of the relativistic Doppler shift.We start by constructing the nanostructured geometry of the interleaved metasail according to the phase functions corresponding to the propulsion and communication sub-arrays, denoted by φp(x,y) and φc(x,y), respectively. For this purpose, the orientation of unit cells forming each sub-array across the metasail is adjusted according to the required geometric phase imprinted across the reflected light undergoing cross circular polarization conversion at their respective operating wavelengths when the metasail is illuminated by left-handed CP light. The phase functions are described by 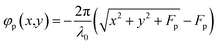 and
and 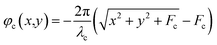 , with Fp and Fc corresponding to the focal distance of the propulsion and communication sub-arrays at λ0 = 1.3 μm and λc = 1065 nm, respectively. The mass of the 2 × 2 m2 sail is estimated as mLS = 1.405 g according to the mass density of silicon and silica. The payload mass is considered to be equal to the sail’s mass such that the total mass of the spacecraft is given by mtot = 2.81 g and the center-of-mass distance from the sail is equal to half the distance of payload from the sail or the focal distance of the communication sub-array, i.e. dCM = Fc/2.
, with Fp and Fc corresponding to the focal distance of the propulsion and communication sub-arrays at λ0 = 1.3 μm and λc = 1065 nm, respectively. The mass of the 2 × 2 m2 sail is estimated as mLS = 1.405 g according to the mass density of silicon and silica. The payload mass is considered to be equal to the sail’s mass such that the total mass of the spacecraft is given by mtot = 2.81 g and the center-of-mass distance from the sail is equal to half the distance of payload from the sail or the focal distance of the communication sub-array, i.e. dCM = Fc/2.
Given that the sail structure is extended over many light wavelengths and features subwavelength features, a full-wave simulation of the metasail structure is prohibitive due to the enormous computational complexity. As such, in order to evaluate the scattering response of the large-area interleaved metasail, we use an approximate method based on generalized Snell’s laws with the assumption of local periodicity, which describes the local scattering response of any given unit cell in a quasi-periodic gradient metasurface by its response in a periodic arrangement obtained using full-wave RCWA simulations here.32 This approach has been shown to yield fairly accurate results for large-area metasurfaces with smooth transitions between the adjacent unit cells and is capable of bringing out the essential physics with minimal computational complexity.51,52 Following predictions of the optical response using generalized Snell’s laws using RCWA simulation results for the unit cells based on local periodicity approximation, we calculate the spatial distribution of the optical forces for a given position and orientation of the sail by evaluating the flux of Maxwell’s stress tensor through small groups of unit cells across the metasail,32,53 which results in closed-form expressions in terms of the local reflection/transmission coefficients, spatial phase gradient, amplitude profile of the incident field, and angle of incidence. The components of the total force and torque imparted to the sail, as shown in Fig. 3, can be then obtained through the integration of local forces across the metasail as 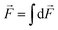 and
and 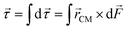 , with
, with ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) CM being the vector pointing from the center-of-mass to a location on the surface of metasail. It should be emphasized that we have taken into account co-polarized and cross-polarized scattering in both reflection and transmission to attain optical forces. Further details regarding this modeling approach and the closed-form expressions for the optical forces are provided in Section S1 of the ESI.† Moreover, the wavefront engineering capability of the designed unit cells based on the geometric phase is rigorously verified via full-wave RCWA simulations for small supercells and the results are included in Section S2 of the ESI,† which show excellent agreement with the predictions of the generalized Snell’s laws based on local periodicity.
CM being the vector pointing from the center-of-mass to a location on the surface of metasail. It should be emphasized that we have taken into account co-polarized and cross-polarized scattering in both reflection and transmission to attain optical forces. Further details regarding this modeling approach and the closed-form expressions for the optical forces are provided in Section S1 of the ESI.† Moreover, the wavefront engineering capability of the designed unit cells based on the geometric phase is rigorously verified via full-wave RCWA simulations for small supercells and the results are included in Section S2 of the ESI,† which show excellent agreement with the predictions of the generalized Snell’s laws based on local periodicity.
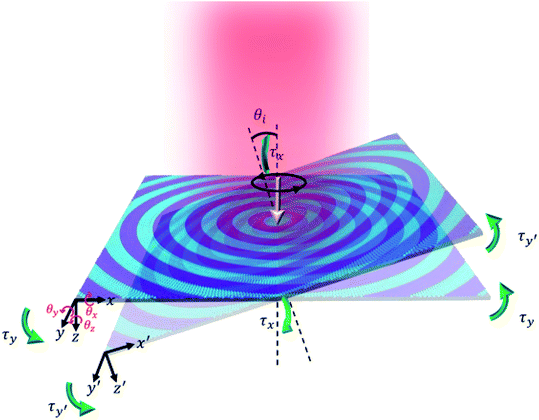 | ||
| Fig. 3 The depiction of the Euler angles, as well as the components of applied forces and torques, on the moving metasail in the local coordinate system. | ||
Assuming rigid dynamics for the spacecraft, its mechanical response is governed by Newton–Euler equations. Given the azimuthal symmetry of the phase functions and the optical response, as well as the circular polarization of incident laser beam, the metasail will experience zero torque around the beam axis (τz = 0). In such a non-spinning case, the Newton–Euler equations can be written as a nonlinear system of ordinary differential equations in the following form:19,54
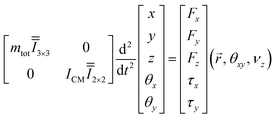 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = [x, y, z]T is the position vector for the center-of-mass in the stationary global coordinate system,
= [x, y, z]T is the position vector for the center-of-mass in the stationary global coordinate system, ![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) = [θz, θy, θx]T is the vector of Euler angles shown in Fig. 3, νz = dz/dt is the velocity of the spacecraft along the beam propagation direction, and ICM is the principal moment of inertia about the center-of-mass, which is given by ICM = mtotdCM2 when the mass of payload and the lightsail are equal. The change of the force and torque components as a function of velocity (νz) is governed by the relativistic Doppler-shift of the wavelength
= [θz, θy, θx]T is the vector of Euler angles shown in Fig. 3, νz = dz/dt is the velocity of the spacecraft along the beam propagation direction, and ICM is the principal moment of inertia about the center-of-mass, which is given by ICM = mtotdCM2 when the mass of payload and the lightsail are equal. The change of the force and torque components as a function of velocity (νz) is governed by the relativistic Doppler-shift of the wavelength 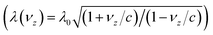 (taking into account time-dilation within the special relativity framework55) and the dispersive response of the metasail. The force and torque components also have nontrivial dependencies on the position and orientation of the sail within the global coordinate system for a given incident beam profile, which are taken into account by the change in the incident angle and illumination beam offset in the local coordinate system of the metasail (as shown in Fig. 3). In order to obtain the motion trajectory of the metasail during the acceleration phase, we use a concurrent coupling of the optical model with Newton–Euler equations. For this purpose, the nonlinear system of the Newton–Euler equations is numerically solved through forward integration in time via the Runge–Kutta method while recalculating the force and torque components depending on the position, orientation, and velocity at each time-step.
(taking into account time-dilation within the special relativity framework55) and the dispersive response of the metasail. The force and torque components also have nontrivial dependencies on the position and orientation of the sail within the global coordinate system for a given incident beam profile, which are taken into account by the change in the incident angle and illumination beam offset in the local coordinate system of the metasail (as shown in Fig. 3). In order to obtain the motion trajectory of the metasail during the acceleration phase, we use a concurrent coupling of the optical model with Newton–Euler equations. For this purpose, the nonlinear system of the Newton–Euler equations is numerically solved through forward integration in time via the Runge–Kutta method while recalculating the force and torque components depending on the position, orientation, and velocity at each time-step.
Although the motion trajectory of the sail can be used to infer the stability of the beam-riding by observing the bounded oscillatory motion of the sail within the transverse plane of the laser beam, it can be excessively time-consuming. A linear stability analysis based on the eigenvalues of the sail’s transverse dynamics can be conducted for a more efficient evaluation of the beam-riding stability, as well as gaining insight into the role of different parameters, such as the Doppler shift and chromatic dispersion on the stability condition. To this end, the dynamics of the sail can be projected into the transverse plane orthogonal to the beam propagation direction as follows:18
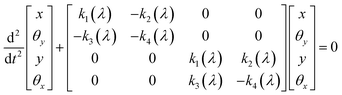 | (2) |
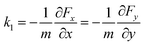 | (3) |
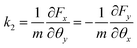 | (4) |
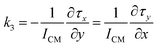 | (5) |
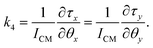 | (6) |
These partial derivatives can be evaluated numerically in the linear regime by differentiation of the force and torque components for small displacement and rotational offsets with respect to the upright position of the sail located at the center of the beam. The eigenvalues of the matrix in eqn (2) governing the transverse dynamics of the sail are given by 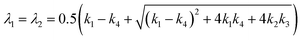 and
and 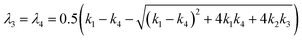 . The necessary and sufficient conditions for the marginal stability requires these eigenvalues to have positive real parts.18 From the given expressions, it can be inferred that a necessary condition for marginal stability is k1k4 + k2k3 < 0. For a parabolic metasail giving rise to restoring lateral forces and counterbalancing torques under displacement and rotational deviations with respect to the upright position, yielding k1 > 0 and k4 < 0, this condition is also a sufficient condition for marginal stability. The quantity C = k1k4 + k2k3 describes the coupling between the displacement and rotational degrees of freedom.20,31,32 A larger magnitude of the coupling between the displacement and rotation yields a lower tolerance of the beam-riding stability with respect to the displacement and rotational offsets, which results in a larger residual motion at the terminal velocity. This is while in case of a positive coupling, slightest perturbations in the position and orientation of the metasail with respect to the beam center can cause the metasail to be expelled from the beam area.19,32
. The necessary and sufficient conditions for the marginal stability requires these eigenvalues to have positive real parts.18 From the given expressions, it can be inferred that a necessary condition for marginal stability is k1k4 + k2k3 < 0. For a parabolic metasail giving rise to restoring lateral forces and counterbalancing torques under displacement and rotational deviations with respect to the upright position, yielding k1 > 0 and k4 < 0, this condition is also a sufficient condition for marginal stability. The quantity C = k1k4 + k2k3 describes the coupling between the displacement and rotational degrees of freedom.20,31,32 A larger magnitude of the coupling between the displacement and rotation yields a lower tolerance of the beam-riding stability with respect to the displacement and rotational offsets, which results in a larger residual motion at the terminal velocity. This is while in case of a positive coupling, slightest perturbations in the position and orientation of the metasail with respect to the beam center can cause the metasail to be expelled from the beam area.19,32
3.1 Linear stability analysis
Here, we use the linear stability analysis to study the required conditions for the beam-riding stability of the metasail. The incident field is assumed to have a Gaussian mode profile as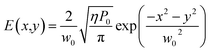 , in which η is the free-space impedance, w0 is the beam’s spot size, and P0 is the net power of the beam, assumed to be 100 GW throughout this work.
, in which η is the free-space impedance, w0 is the beam’s spot size, and P0 is the net power of the beam, assumed to be 100 GW throughout this work.
The distance of the payload from the sail defines the geometry of the communication sub-array according to its focal distance at the communication wavelength, which is set to be twice the distance of the center-of-mass from the sail. Fig. 4(a) schematically shows the reflection response of the metasail’s sub-arrays under the illumination of a laser beam in the propulsion mode. It should be noted that the reflectivity of the communication sub-array across the Doppler-broadened propulsion band is significantly lower compared to that of the propulsion sub-array.
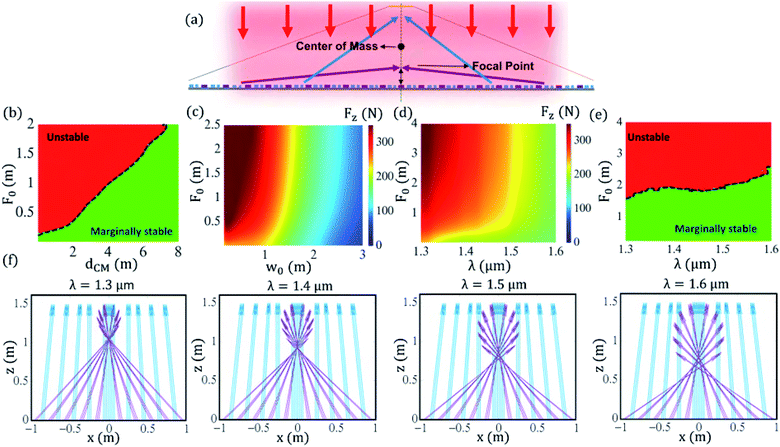
First, we evaluate the stability condition of the metasail at the incident laser wavelength as a function of the nominal focal distance of the propulsion sub-array (i.e. the focal distance at λ0 = 1.3 μm) and center-of-mass distance from the sail when the beam spot size is fixed at w0 = 80 cm. Fig. 4(b) shows the results for the marginal stability basins. As it can be seen, the metasail is marginally stable when the center-of-mass distance from the sail is larger than a threshold defined by the focal distance of the propulsion sub-array. While previous works have reported the required center-of-mass distance from a parabolic sail to achieve marginal beam-riding stability as dCM > 2F0,18,19,32 here the minimum required, dCM, is larger, which is attributed to the contribution of the communication sub-array and the specular reflections due to co-polarized scattering. Fig. 4(c) shows the net thrust imparted to the metasail along the beam propagation direction as a function of the nominal focal distance of the propulsion sub-array and the incident beam’s spot size. It should be noted that the net thrust is independent of the location of the center-of-mass, while the beam spot size weakly affects the stability condition. As it can be observed from the results, a smaller beam size yields stronger propulsion due to the higher confinement of the beam on the sail area and less energy spill-over. Moreover, the net thrust is larger for longer focal distances, which yield smaller in-plane lateral forces. Nevertheless, the absence of half of the propulsion layers comes with the cost of a significant reduction of the net thrust.
Having studied the stability condition of the metasail at the incident wavelength of the propulsion laser beam, we move on to analyze the effect of the relativistic Doppler shift on the stability condition by studying the optomechanical response of the metasail across the Doppler-broadened propulsion band. For this purpose, we fix the beam’s spot size as w0 = 80 cm and the center-of-mass distance from the sail as dCM = 6 m. Fig. 4(d) shows the net thrust imparted to the metasail as a function of the nominal focal distance of the propulsion sub-array (defined as λ0 = 1.3 μm) and the wavelength. As it can be seen from the results, the net thrust decreases as the wavelength increases, which can be attributed to two factors, namely the increase in the in-plane lateral forces caused by the dispersive response of the focusing of the propulsion sub-array and the reduction in the average reflectivity of the metasail. The marginal stability basin of the metasail is also depicted in Fig. 4(e) as a function of the nominal focal distance of the propulsion sub-array and the wavelength. It can be observed that not only can the marginal stability condition be sustained over the entire Doppler-broadened propulsion band by an appropriate choice of the nominal focal distance, but also that the stability basins expands in size as the wavelength red shifts, which is attributed to the growth in the magnitude of the in-plane lateral forces, yielding an improvement of the stability condition. In order to provide more insight into the dispersive optical response of the metasail and its effect on the stability condition, we conduct a ray tracing of the reflected CP light undergoing cross-polarization conversion in a metasail, with a nominal focal distance of Fp = 1 m for the propulsion sub-array and a center-of-mass distance of dCM = 6 m (corresponding to the focal distance of Fc = 2dCM = 12 m for the communication sub-array), based on the generalized Snell’s law. Fig. 4(f) shows the normalized reflected rays from the metasail at different wavelengths. The rays reflected from the communication and propulsion sub-arrays are denoted by distinct colors associated with the color of their corresponding unit cells. As can be seen, the reflected rays from the propulsion sub-array converge at a shorter distance compared to those reflected from the communication sub-array. Although a perfect focusing of the reflected rays from the propulsion sub-array can only be achieved at the incident laser wavelength, the anomalous reflection response is sustained over a broad bandwidth due to the dispersionless property of the geometric phase, yielding convergence of the reflected rays toward the beam axis. Despite the aberrations caused by the chromatic dispersion of the focusing performance, the circle of least confusion gets closer to the metasail as the wavelength red-shifts, which yields stronger in-plane lateral forces due to stronger anisotropy in the transverse scattering from the propulsion sub-array. It should be emphasized that, despite the dispersionless property of the geometric phase, its employment by itself cannot yield an achromatic focusing performance that requires a phase with an inverse linear proportionality to the wavelength, rather than a wavelength-independent phase.
3.2 Motion trajectory
In this subsection, we analyze the motion trajectory of the multifunctional metasail during the acceleration phase under illumination with an intense laser beam with a net power of 100 GW, subject to displacement and rotational offsets with respect to the beam axis. Such a study is essential to infer the beam-riding stability of the metasail, as its actual motion dynamics are governed by a nonlinear system whose stability depends on the relative ratios between displacement and rotational offsets which cannot be fully described through a linear stability analysis. Furthermore, obtaining the motion trajectory provides an accurate measure of the acceleration time and distance while also yielding an estimate for the residual motion at the terminal velocity.The center-of-mass distance from the metasail is set as dCM = 6 m, corresponding to a focal distance of Fc = 12 m for the communication sub-array, and the nominal focal distance of the propulsion sub-array is fixed at Fp = 1 m. These quantities ensure the marginal stability of the metasail in the linear regime across the entire Doppler-broadened propulsion band, according to the study conducted in the previous subsection. The beam spot size is fixed at w0 = 80 cm, which is assumed to be maintained over the entire acceleration phase through employing adaptive optics in the photon engine in order to ensure maximal energy efficiency by avoiding energy spill over. Considering the propulsion laser beam is diffraction limited, this requirement sets the size of the required laser array according to the acceleration distance of the metasail (i.e. the distance that the metasail has to travel to reach the terminal velocity).
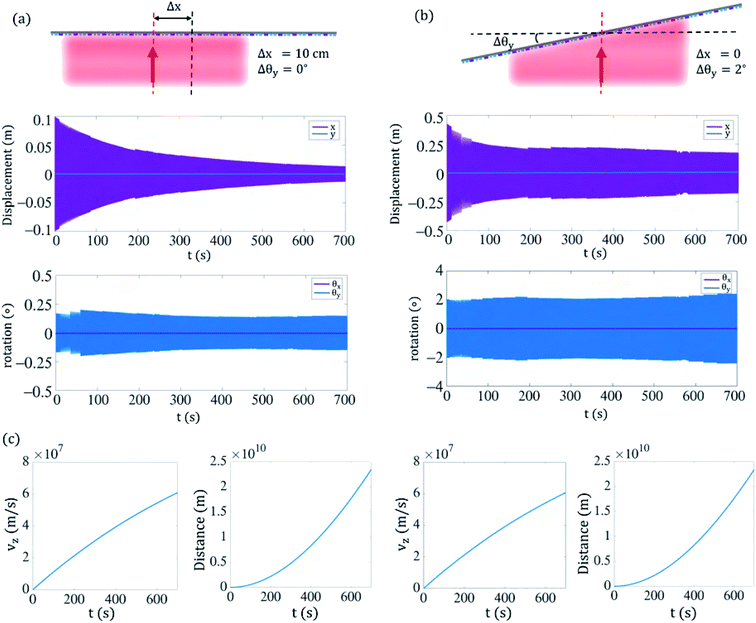
As noted in Section 3, the motion trajectory is calculated by solving the Newton–Euler equations via the Runge–Kutta method while being concurrently coupled to the optical model to take into account the dependencies of the force and torque components on the position, orientation, and velocity, with the latter being governed by the relativistic Doppler shift. In order to gain insight into the features of motion with respect to the displacement and rotational degrees of freedom, we obtain the motion trajectory of the spacecraft during the entire acceleration stage for two different cases where the metasail is subjected to an initial displacement offset relative to the beam axis with no inclination, and an initial rotational offset with no transverse displacement. Fig. 5(a) demonstrates the displacement, rotation, velocity (νz), and traveled distance of the spacecraft as functions of time for an initial displacement offset of Δx = 10 cm with respect to the center of the beam in the absence of a rotational offset. As can be observed from the results, the metasail remains within the beam area while exhibiting a bounded oscillatory motion in the transverse plane, until reaching the target velocity of 0.2c over ≈690 seconds (≈11.5 minutes) after traveling a distance of ≈23.453 × 109 m. The beam-riding in such a time-scale is afforded thanks to the satisfaction of the marginal stability condition over the entire Doppler-broadened propulsion band, which allows the metasail to remain within the beam area despite the significant red-shift of the wavelength in the frame of the moving sail as its velocity increases. The results show that the displacement offset (Δx) leads to a non-zero oscillation amplitude in the rotational offset (Δθy) as a result of the cross-coupling between displacement and rotation. Nevertheless, the amplitudes of oscillations in both the displacement and rotation remain bounded due to the negative coupling coefficient k1k4 + k2k3. Furthermore, the amplitude of the oscillation in the displacement offset with respect to the beam center reduces substantially as the sail accelerates, which is a result of the Doppler shift and the dispersive optical response of the metasail. While the non-dispersive response of a conventional lightsail renders its in-plane motion dynamics as those of an undamped oscillator, the Doppler shift in a dispersive accelerating metasail can act as a damping mechanism for the residual motion. The result presented here shows suppression of the displacement offset with respect to the center from 10 cm to less than 2 cm at the terminal velocity. Considering the rotational symmetry of incident field and the metasail’s response, similar results can be obtained for the trajectory of the metasail subject to any radial displacement offset with respect to the beam’s center. The same analysis is performed for the metasail subject to an initial rotational offset of Δθy = 2° around the y axis in the absence of the displacement offset, and the results for the displacement, rotation, velocity (νz), and traveled distance of the spacecraft as functions of time are shown in Fig. 5(b). Similar to the previous case, a stable beam-riding is observed until reaching the target velocity, which is accompanied by an oscillatory motion in lateral displacement and rotation around the beam axis. The acceleration time and distance are negligibly affected by the change in the initial position and orientation, while the residual motion is significantly increased. This observation indicates that the motion behavior of the metasail governed by a nonlinear system is strongly dependent on the relative ratios between displacement and rotation. It is noteworthy that, while the oscillatory motion of the metasail in the included results here is limited only to the (x, θy) plane due to the choice of Δy = 0 and Δθx = 0, the designed metasail, being rotationally symmetric, is capable of providing stability around the beam axis with respect to all degrees of freedom in motion.
4 Downlink optical communication of Starshot
The main purpose of the spacecraft propelled by the relativistic lightsail in the Starshot project is to serve as an interstellar probe. For this purpose, the spacecraft should be able to collect data and transmit the data back to an Earth-based station through optical communication in a flyby mission.1 The use of modulated laser beams for deep-space communication has been a subject of research for a long time and it has started to find more and more applications in recent years for both commercial applications and scientific missions.56–60 This is motivated by the lower divergence of the laser beams compared to radio-frequency waves, which can increase the reach of the signal while also allowing for the reduction in size, weight, and power (SWaP), which are highly constrained in a spacecraft. Nevertheless, there are several challenges associated with the pointing systems, as well as the development of space-qualified and energy-efficient communication systems. These challenges become more paramount for the Starshot project, since the optical communication channel is photon starved as a result of the extremely long propagation distance and divergence of the beam (approximately 4 light years away in the case of Proxima Centauri), significantly limiting the number of photons reaching the detector. The received number of photons or, equivalently, the received signal power is directly related to the bit error rate and throughput capacity in a communication scenario. The Friis transmission equation can be used to obtain the received signal power (PRx) as:61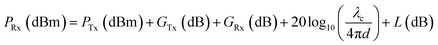 | (7) |
Here, we evaluate the performance of the multifunctional metasail in terms of directional gain. For this purpose, we set the nominal focal distance of the propulsion sub-array and the center-of-mass distance from the sail as Fp = 1 m and dCM = 6 m, respectively. The latter corresponds to a focal distance of Fc = 12 m for the communication sub-array at λc = 1065 nm. In order to obtain the farfield reflection pattern from the sail and its directivity, the local scattering response of the metasail calculated via full-wave RCWA simulations based on the assumption of local periodicity should be used to yield scattered fields at observation points in the farfield region. This can be achieved by using the field equivalence principle to obtain the equivalent electric and magnetic surface currents across the metasail as:
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) s( s(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = ) = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) × × ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) r( r(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), ), ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) s( s(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = − ) = −![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) × × ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) r( r(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) | (8) |
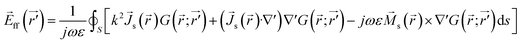 | (9) |
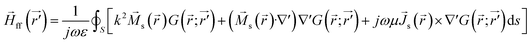 | (10) |
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) s and
s and ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) s are the equivalent surface electric and magnetic currents, respectively,
s are the equivalent surface electric and magnetic currents, respectively, ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) is the unity normal vector for the surface of the metasail facing the Starchip,
is the unity normal vector for the surface of the metasail facing the Starchip, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) r and
r and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) r are the local reflected magnetic and electric fields from the metasail obtained from the response of unit cells simulated by RCWA, respectively, ω = 2πc/λc is the angular frequency, μ and ε are the permeability and permittivity of the free-space, respectively, k = 2π/λc is the wave number, and G is the scalar Green’s function of free-space, given by
r are the local reflected magnetic and electric fields from the metasail obtained from the response of unit cells simulated by RCWA, respectively, ω = 2πc/λc is the angular frequency, μ and ε are the permeability and permittivity of the free-space, respectively, k = 2π/λc is the wave number, and G is the scalar Green’s function of free-space, given by 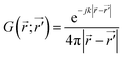 with r and r′ being the position vectors for the source and observation points, respectively.
with r and r′ being the position vectors for the source and observation points, respectively.
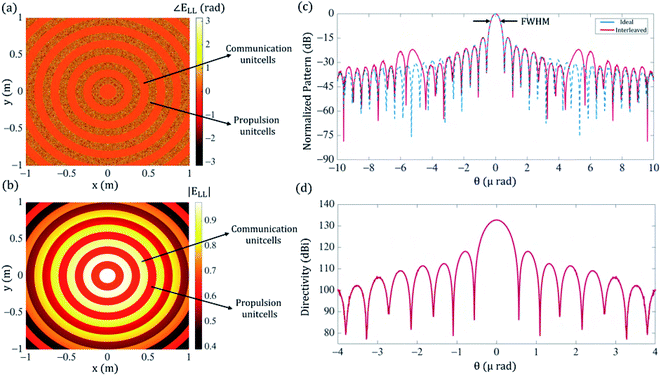
Fig. 6(a) and (b) show the distribution of the local phase and amplitude corresponding to the reflected field at λc undergoing cross circular polarization conversion (ELL). As can be observed, the reflection at λc is dominated by the communication sub-array which yields an in-phase wavefront for the reflected beam. The propulsion sub-array also contributes to the scattering, however it leads to deviation of the reflected beam from the diffraction-limited response due to the phase mismatch with the conjugated wavefront of the emitted beam from the Starchip at λc. Fig. 6(c) shows the comparison of the normalized farfield reflection pattern corresponding to an ideal 2 × 2 m2 collimator and the interleaved metasail. While the full-width at half-maximum (FWHM) of the reflected beam by the interleaved metasail is almost equal to that of the ideal collimator, being equal to 0.49 μrad, the finite size, the non-uniformity of amplitude and phase mismatch caused by the contribution of the propulsion sub-array leads to the emergence of parasitic sidelobes. It is noteworthy that both sets of the unit cells in the interleaved metasail configurations have parabolic phase profiles with different focal distances of fc = 12 and fp = 1. Therefore, when a beam with a parabolic wavefront emitting from the Starchip (conjugate of the communication sub-array’s phase) is incident on the sail, propulsion unit cells also cooperate in the reconstruction of a planar wavefront for the reflected beam. Furthermore, in this scenario, propulsion unit cells can partially alleviate the destructive effects of interleaving in which portions of the communication unit cells are eliminated, such that the results are not affected significantly.
The directivity (D) of the aperture antenna can be calculated from 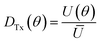 , in which U(θ) is the farfield intensity of the reflected beam and Ū is the mean reflection intensity, given by
, in which U(θ) is the farfield intensity of the reflected beam and Ū is the mean reflection intensity, given by 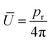 , in which pr is the total reflected power, which is estimated to be DTx = 136.46 dBi for the full-aperture and 133.46 dBi for the interleaved case.63 As shown in Fig. 6(d) the obtained maximum directivity at θ = 0 is at DTx = 132.74 dBi, which is in a good agreement with estimated directivity. The gain of the metasail antenna can also be calculated by replacing the Ū of the interleaved metasail with that of an ideal collimator to take into account the effect of insertion losses and parasitic scattering in the link budget. The gain is estimated as GTx = 128.96 dB, which indicates that the use of a multifunctional metasail for optical communication leads to a significant improvement in the link margin compared to quasi-isotropic radiation from a small communication payload.
, in which pr is the total reflected power, which is estimated to be DTx = 136.46 dBi for the full-aperture and 133.46 dBi for the interleaved case.63 As shown in Fig. 6(d) the obtained maximum directivity at θ = 0 is at DTx = 132.74 dBi, which is in a good agreement with estimated directivity. The gain of the metasail antenna can also be calculated by replacing the Ū of the interleaved metasail with that of an ideal collimator to take into account the effect of insertion losses and parasitic scattering in the link budget. The gain is estimated as GTx = 128.96 dB, which indicates that the use of a multifunctional metasail for optical communication leads to a significant improvement in the link margin compared to quasi-isotropic radiation from a small communication payload.
We have presented a multifunctional metasail for extended mission application and verified its dual functionality. There are works in progress in this area and on different aspects, including fabrication. A challenge is large-area fabrication and using efficient and lightweight materials. Although with the current technology one can enable centimeter-scale metasurfaces, larger dimensions could be achieved by assembling and sticking together small scale blocks, which requires advances in thin-film technology.16,64–68 The Starshot program is a long-term project and research on the different aspects of it is currently in progress.
5 Conclusion
In conclusion, we have demonstrated the design of a multifunctional metasail based on geometric phase sub-arrays interleaved in a shared aperture platform, which can simultaneously accommodate the requirements of photonic propulsion and optical communication for a deep-space relativistic probe, as the geometric phase nanostructures provide better control over the in-plane forces owing to their dispersionless scattering response. The large aperture size of the lightsail offers great potential for implementing multiple functionalities, owing to the interleaving technique in the metasurfaces, and the final goal is to fulfill the optomechanical requirements for successful propulsion while obtaining an efficient communication performance. Multiobjective genetic algorithm (GA) optimization was adopted to satisfy the requirements for an efficient trade-off between the mentioned objectives. In the propulsion stage, the metasail enables stable beam-riding under the illumination of an intense laser beam, thanks to the capability of the creation of restoring forces and counter-balancing torques across the entire Doppler-broadened propulsion band, which allows the sail to keep itself within the beam area until the target velocity is reached, although the missing portion of the propulsion elements and presence of the communication unit cells remarkably decreases the acceleration and in-plane restoring forces. Furthermore, by taking advantage of the large dimension of the sail, a novel downlink communication scheme is proposed. The metasail can serve as a large-area reflector for the communication payload detached from the sail, collimating its emission, which leads to a significant improvement in the downlink margin by maximizing the transmitter gain. The results obtained from the propulsion and communication simulations demonstrate the great capabilities that shared aperture platforms can offer for space-borne relativistic nanocrafts with a minimized performance degradation of each functionality by taking advantage of appropriate optimization techniques.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by the Breakthrough Initiatives, a division of the Breakthrough Prize Foundation, and in part by the U.S. Air Force Office of Scientific Research (AFOSR), #FA9550-18-1-0354. It has also benefited from the support of the Northeastern University’s Research Computing team by providing resources for high-performance computing through Discovery Cluster.References
- P. Lubin, A roadmap to interstellar flight, J. Br. Interplanet. Soc., 2016, 69, 40–72 Search PubMed.
- G. Marx, Interstellar vehicle propelled by terrestrial laser beam, Nature, 1966, 211(5044), 22–23 CrossRef.
- R. L. Forward, Starwisp-an ultra-light interstellar probe, J. Spacecr. Rockets, 1985, 22(3), 345–350 CrossRef.
- Y. Tsuda, O. Mori, R. Funase, H. Sawada, T. Yamamoto, T. Saiki, T. Endo and J. Kawaguchi, Flight status of ikaros deep space solar sail demonstrator, Acta Astronaut., 2011, 69(9–10), 833–840 CrossRef.
- O. Mori, Y. Shirasawa, Y. Mimasu, Y. Tsuda, H. Sawada, T. Saiki, T. Yamamoto, K. Yonekura, H. Hoshino, J. Kawaguchi, et al., Overview of ikaros mission, in Advances in Solar Sailing, Springer, 2014, pp. 25–43 Search PubMed.
- L. Johnson, M. Whorton, A. Heaton, R. Pinson, G. Laue and C. Adams, Nanosail-d: A solar sail demonstration mission, Acta Astronaut., 2011, 68(5–6), 571–575 CrossRef.
- C. Biddy and T. Svitek, Lightsail-1 solar sail design and qualification, in Proceedings of the 41st Aerospace Mechanisms Symposium, Jet Propulsion Lab., National Aeronautics and Space Administration, Pasadena, CA, 2012, pp. 451–463 Search PubMed.
- A. R. Davoyan, J. N. Munday, N. Tabiryan, G. A. Swartzlander and L. Johnson, Photonic materials for interstellar solar sailing, Optica, 2021, 8(5), 722–734 CrossRef.
- C. R. McInnes, Solar Sailing: Technology, Dynamics and Mission Applications, Springer Science & Business Media, 2013 Search PubMed.
- A. Ashkin, J. M. Dziedzic, J. Bjorkholm and S. Chu, Observation of a single-beam gradient force optical trap for dielectric particles, Opt. Lett., 1986, 11(5), 288–290 CrossRef CAS PubMed.
- L. K. Chin, Y. Shi and A.-Q. Liu, Optical Forces in Silicon Nanophotonics and Optomechanical Systems: Science and Applications, Adv. Devices Instrum., 2020, 2020, 1964015 Search PubMed.
- M. M. Salary, S. Inampudi, K. Zhang, E. B. Tadmor and H. Mosallaei, Mechanical actuation of graphene sheets via optically induced forces, Phys. Rev. B, 2016, 94(23), 235403 CrossRef.
- F. J. Rodríguez-Fortuño, N. Engheta, A. Martínez and A. V. Zayats, Lateral forces on circularly polarizable particles near a surface, Nat. Commun., 2015, 6, 8799 CrossRef PubMed.
- Breakthrough Initiatives, Breakthrough Starshot, https://breakthroughinitiatives.org/Initiative/3, 2018 Search PubMed.
- P. Daukantas, Breakthrough starshot, Opt. Photonics News, 2017, 28(5), 26–33 CrossRef.
- H. A. Atwater, A. R. Davoyan, O. Ilic, D. Jariwala, M. C. Sherrott, C. M. Went, W. S. Whitney and J. Wong, Materials challenges for the starshot lightsail, Nat. Mater., 2018, 17(10), 861 CrossRef CAS PubMed.
- G. A. Swartzlander, Radiation pressure on a diffractive sailcraft, J. Opt. Soc. Am. B, 2017, 34(6), C25–C30 CrossRef CAS.
- Z. Manchester and A. Loeb, Stability of a lightsail riding on a laser beam, Astrophys. J., Lett., 2017, 837(2), L20 CrossRef.
- E. Popova, M. Efendiev and I. Gabitov, On the stability of a space vehicle riding on an intense laser beam, Math. Methods Appl. Sci., 2017, 40(4), 1346–1354 CrossRef.
- J. Siegel, A. Wang, S. G. Menabde, M. A. Kats, M. S. Jang and V. W. Brar, Self-stabilizinglaser sails based on optical metasurfaces, ACS Photonics, 2019, 6(8), 2032–2040 CrossRef CAS.
- P. R. Srivastava, Y.-J. L. Chu and G. A. Swartzlander, Stable diffractive beam rider, Opt. Lett., 2019, 44(12), 3082–3085 CrossRef PubMed.
- O. Ilic and H. A. Atwater, Self-stabilizing photonic levitation and propulsion of nanostructured macroscopic objects, Nat. Photonics, 2019, 13(4), 289–295 CrossRef CAS.
- O. Ilic, Nanophotonic materials for space applications, MRS Bull., 2020, 45(9), 769–778 CrossRef.
- E. Schamiloglu, C. Abdallah, D. Georgiev, J. Benford and G. Benford, Control of microwave-propelled sails using delayed measurements, AIP Conf. Proc., 2002, 608, 452–456 CrossRef.
- J. Benford and G. Benford, Flight of microwave-driven sails: Experiments and applications, AIP Conf. Proc., 2003, 664, 303–312 CrossRef.
- E. Schamiloglu, C. T. Abdallah, K. A. Miller, D. Georgiev, J. Benford, G. Benford and G. Singh, 3-d simulations of rigid microwave-propelled sails including spin, AIP Conf. Proc., 2001, 552, 559–564 CrossRef.
- B. Khayatian and Y. Rahmat-Samii, A novel antenna concept for future solar sails: Application of fresnel antennas, IEEE Antennas Propag. Mag., 2004, 46(2), 50–63 CrossRef.
- B. Khayatian and Y. Rahmat-Samii, A dual-band dual-feed fresnel zone antenna concept: Application in solar sails missions, in IEEE Antennas and Propagation Society International Symposium (IEEE Cat. No. 02CH37313), IEEE, 2002, vol. 1, pp. 638–641 Search PubMed.
- W. Jin, W. Li, M. Orenstein, and S. Fan, Inverse design of lightweight broadband reflector for efficient lightsail propulsion, 2020, arXiv preprint arXiv:2005.04840.
- A. B. Evlyukhin, M. Matiushechkina, V. A. Zenin, M. Heurs and B. N. Chichkov, Lightweight metasurface mirror of silicon nanospheres, Opt. Mater. Express, 2020, 10(10), 2706–2716 CrossRef CAS.
- M. M. Salary and H. Mosallaei, Inverse design of diffractive relativistic meta-sails via multi-objective optimization, Adv. Theory Simul., 2021, 4(6), 2100047 CrossRef CAS.
- M. M. Salary and H. Mosallaei, Photonic metasurfaces as relativistic lightsails for doppler-broadened stable beam-riding and radiative cooling, Laser Photonics Rev., 2020, 14(8), 1900311 CrossRef CAS.
- N. Yu and F. Capasso, Flat optics with designer metasurfaces, Nat. Mater., 2014, 13(2), 139 CrossRef CAS PubMed.
- M. Yannai, E. Maguid, A. Faerman, Q. Li, J.-H. Song, V. Kleiner, M. L. Brongersma and E. Hasman, Order and disorder embedded in a spectrally interleaved metasurface, ACS Photonics, 2018, 5(12), 4764–4768 CrossRef CAS.
- D. Lin, A. L. Holsteen, E. Maguid, G. Wetzstein, P. G. Kik, E. Hasman and M. L. Brongersma, Photonic multitasking interleaved si nanoantenna phased array, Nano Lett., 2016, 16(12), 7671–7676 CrossRef CAS PubMed.
- E. Arbabi, A. Arbabi, S. M. Kamali, Y. Horie and A. Faraon, Multiwavelength metasurfaces through spatial multiplexing, Sci. Rep., 2016, 6(1), 32803 CrossRef CAS PubMed.
- E. Maguid, I. Yulevich, M. Yannai, V. Kleiner, M. L. Brongersma and E. Hasman, Multifunctional interleaved geometric-phase dielectric metasurfaces, Light: Sci. Appl., 2017, 6(8), e17027 CrossRef PubMed.
- M. Yannai, E. Maguid, A. Faerman, Q. Li, J.-H. Song, V. Kleiner, M. L. Brongersma and E. Hasman, Spectrally interleaved topologies using geometric phase metasurfaces, Opt. Express, 2018, 26(23), 31031–31038 CrossRef CAS PubMed.
- W. Zhao, B. Liu, H. Jiang, J. Song, Y. Pei and Y. Jiang, Full-color hologram using spatial multiplexing of dielectric metasurface, Opt. Lett., 2016, 41(1), 147–150 CrossRef CAS PubMed.
- D. Lin, P. Fan, E. Hasman and M. L. Brongersma, Dielectric gradient metasurface optical elements, Science, 2014, 345(6194), 298–302 CrossRef CAS PubMed.
- A. Niv, G. Biener, V. Kleiner and E. Hasman, Manipulation of the pancharatnam phase in vectorial vortices, Opt. Express, 2006, 14(10), 4208–4220 CrossRef PubMed.
- A. E. Minovich and A. V. Zayats, Geometric-phase metasurfaces based on anisotropic reflection: generalized design rules, ACS Photonics, 2018, 5(5), 1755–1761 CrossRef CAS.
- L. Huang, X. Chen, H. Muhlenbernd, G. Li, B. Bai, Q. Tan, G. Jin, T. Zentgraf and S. Zhang, Dispersionless phase discontinuities for controlling light propagation, Nano Lett., 2012, 12(11), 5750–5755 CrossRef CAS PubMed.
- O. Ilic, C. M. Went and H. A. Atwater, Nanophotonic heterostructures for efficient propulsion and radiative cooling of relativistic lightsails, Nano Lett., 2018, 18(9), 5583–5589 CrossRef CAS PubMed.
- M. Moharam, E. B. Grann, D. A. Pommet and T. Gaylord, Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings, J. Opt. Soc. Am. A, 1995, 12(5), 1068–1076 CrossRef.
- J. Cheng, S. Inampudi and H. Mosallaei, Optimization-based dielectric metasurfaces for angle-selective multifunctional beam deflection, Sci. Rep., 2017, 7(1), 1 CrossRef PubMed.
- S. Inampudi, J. Cheng, M. M. Salary and H. Mosallaei, Unidirectional thermal radiation from a sic metasurface, J. Opt. Soc. Am. B, 2018, 35(1), 39–46 CrossRef CAS.
- S. Inampudi, J. Cheng and H. Mosallaei, Graphene-based near-field optical microscopy: high-resolution imaging using reconfigurable gratings, Appl. Opt., 2017, 56(11), 3132–3141 CrossRef CAS PubMed.
- S. Inampudi and H. Mosallaei, Tunable wideband-directive thermal emission from sic surface using bundled graphene sheets, Phys. Rev. B, 2017, 96(12), 125407 CrossRef.
- S. Inampudi, M. M. Salary, S. Jafar-Zanjani and H. Mosallaei, Rigorous space-time coupled-wave analysis for patterned surfaces with temporal permittivity modulation, Opt. Mater. Express, 2019, 9(1), 162–182 CrossRef CAS.
- R. Pestourie, C. Pérez-Arancibia, Z. Lin, W. Shin, F. Capasso and S. G. Johnson, Inverse design of large-area metasurfaces, Opt. Express, 2018, 26(26), 33732–33747 CrossRef CAS PubMed.
- J. Cheng, S. Jafar-Zanjani and H. Mosallaei, All-dielectric ultrathin conformal metasurfaces: lensing and cloaking applications at 532 nm wavelength, Sci. Rep., 2016, 6, 38440 CrossRef CAS PubMed.
- J. D. Jackson, Classical electrodynamics, 1999 Search PubMed.
- A. Rao, Dynamics of Particles and Rigid Bodies: a Systematic Approach, Cambridge University Press, 2006 Search PubMed.
- L. D. Landau and E. M. Lifshitz, The classical theory of fields, 1971 Search PubMed.
- H. Hemmati, Deep Space Optical Communications. John Wiley & Sons, 2006, vol. 11 Search PubMed.
- H. Hemmati, A. Biswas and I. B. Djordjevic, Deep-space optical communications: Future perspectives and applications, Proc. IEEE, 2011, 99(11), 2020–2039 Search PubMed.
- D. M. Boroson, J. J. Scozzafava, D. V. Murphy, B. S. Robinson, and M. Lincoln, The lunar laser communications demonstration (llcd), in 2009 Third IEEE International Conference on Space Mission Challenges for Information Technology. IEEE, 2009, pp. 23–28 Search PubMed.
- D. M. Boroson, B. S. Robinson, D. V. Murphy, D. A. Burianek, F. Khatri, J. M. Kovalik, Z. Sodnik, and D. M. Cornwell, Overview and results of the lunar laser communication demonstration, in Free-Space Laser Communication and Atmospheric Propagation XXVI, International Society for Optics and Photonics, 2014, vol. 8971, p. 89710S Search PubMed.
- R. W. Kingsbury, Optical communications for small satellites, PhD dissertation, Massachusetts Institute of Technology, 2015.
- K. L. Parkin, A starshot communication downlink, 2020, arXiv preprint arXiv:2005.08940.
- S. J. Orfanidis, Electromagnetic Waves and Antennas, 2002 Search PubMed.
- C. A. Balanis, Antenna Theory: Analysis and Design. John Wiley & Sons, 2015 Search PubMed.
- D. Andren, J. Martinez-Llinas, P. Tassin, M. Kall and R. Verre, Large-scale metasurfaces made by an exposed resist, ACS Photonics, 2020, 7(4), 885–892 CrossRef CAS.
- A. She, S. Zhang, S. Shian, D. R. Clarke and F. Capasso, Large area metalenses: design, characterization, and mass manufacturing, Opt. Express, 2018, 26(2), 1573–1585 CrossRef CAS PubMed.
- L. Wondraczek, E. Bouchbinder, A. Ehrlicher, J. C. Mauro, R. Sajzew and M. M. Smedskjaer, Advancing the mechanical performance of glasses: perspectives and challenges, Adv. Mater., 2022, 2109029 Search PubMed.
- H. Zheng, Y. Zhou, C. F. Ugwu, A. Du, I. I. Kravchenko and J. G. Valentine, Large-scale metasurfaces based on grayscale nanosphere lithography, ACS Photonics, 2021, 8(6), 1824–1831 CrossRef CAS.
- P. Su, M. Shalaginov, T. Gu, S. An, D. Li, L. Li, H. Jiang, S. Joo, L. Kimerling and H. Zhang, et al., Large-area optical metasurface fabrication using nanostencil lithography, Opt. Lett., 2021, 46(10), 2324–2327 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00747e |
| This journal is © The Royal Society of Chemistry 2022 |