Open Access Article
Open Access ArticleBioinspired nanoscale hierarchical pillars for extreme superhydrophobicity and wide angular transmittance†
Cheonji
Lee‡
ab,
Seungmuk
Ji‡
c,
Sunjong
Oh
a,
Seungchul
Park
a,
Youngdo
Jung
a,
Jinkee
Lee
*b and
Hyuneui
Lim
 *ad
*ad
aDepartment of Nature-Inspired Nanoconvergence Systems, Korea Institute of Machinery and Materials, 156 Gajeongbuk-Ro, Yuseong-Gu, Daejeon, 34103, Republic of Korea. E-mail: helim@kimm.re.kr; Fax: +82-42-868-7933; Tel: +82-42-868-7106
bSchool of Mechanical Engineering, Sungkyunkwan University, 2066, Seobu-Ro, Jangan-Gu, Suwon, Gyeonggi-Do 16419, Republic of Korea. E-mail: lee.jinkee@skku.edu; Fax: +82-31-295-1937; Tel: +82-31-299-4845
cYonsei Institute of Convergence Technology, Yonsei University, 85 Songdogwahak-ro, Yeonsu-gu, Incheon 21983, South Korea
dDepartment of Nano-mechatronics, University of Science and Technology, 217 Gajeongbuk-Ro, Yuseong-Gu, Daejeon, 34113, Republic of Korea
First published on 24th December 2021
Abstract
Hierarchical structures in nature provide unique functions for living organisms that can inspire technology. Nanoscale hierarchical structured surfaces are essential to realize the dual functions of non-wetting and transparency for applications such as cover glasses and windows; however, these structures are challenging to fabricate. In this study, nano-hierarchical structured glass surfaces were fabricated using multi-step colloidal lithography and etching to obtain tunable morphology. Nanostructured surfaces of mono-pillar structures of diameter 120 and 350 nm and hierarchical-pillar structures of their combinations exhibited superhydrophobicity after perfluoropolyether coating. In particular, the hierarchical nanosurfaces showed excellent non-wetting properties with the apparent, advancing, and receding water contact angles exceeding 177° and contact angle hysteresis below 1°. Water bouncing behaviors – contact time, spreading diameter, and shape of the bouncing motion were also evaluated according to the Weber number to examine the robustness of superhydrophobicity. Hierarchical nanosurfaces showed larger spreading diameters than mono-nanosurfaces with 14 bounces, indicating minimal energy loss from friction, as can be explained by the effective slip length. Furthermore, the nano-hierarchical structures exhibited better transmittance for wide angles of incidence up to 70° than mono-nanostructures owing to their reduced scattering area and multi-periodicity.
1. Introduction
Hierarchical structures are effective in realizing smart biological behavior in nature by implementing or reinforcing various surface functionalities, such as self-cleaning, antireflection, antibiofouling, water harvesting, structural color, and drag reduction.1,2 These amazing properties enabled by hierarchical structures can be observed in the lotus leaf,3–6 pitcher plant,7–11 moth eye,12–16 butterfly wings,17 cicada wings,18 Namib desert beetle's back,19–21 and shark skin.22–25 In particular, the introduction of a hierarchical nanostructure on transparent surfaces can lead to significant performance enhancement for the developing applications such as the cover glass of photovoltaics, building and car windows and lenses of optical sensors.26–28 However, the implementation of nanoscale hierarchical structures on transparent surfaces is challenging because of the current lack of controllable and cost-effective nanofabrication techniques and lack of knowledge of the role of nano-hierarchies in wetting and optical properties.The superhydrophobic surface of lotus leaves has a micro/nano hierarchical structured wax layer that exhibits a high contact angle and a low sliding angle. The microbump- and nanopillar-based hierarchical structures enhance the wetting properties compared to the hydrophobic chemical surface by reducing the contact area and the loss of the kinetic energy of the water droplets at the interface between water and the structures.19,20 The antireflective surface of the moth eye has ordered nanopillar structures, creating an interface at which the refractive index changes gradually. Consequently, the nanopillar structures largely suppress Fresnel reflection for a broad range of wavelengths as well as wide angles of incidence compared to optical coatings based on the quarter-wavelength principle.29–31 Several studies have attempted to induce the combination of superhydrophobic and antireflective functional surfaces by fabricating the nanostructures on a transparent substrate. Park et al. demonstrated a nanotextured fused silica wafer using a multiple coating layer and subsequent etching steps. The subwavelength-tapered conical structures with high aspect ratios and large packing densities resulted in superhydrophobicity and omnidirectional transparency.32 Furthermore, Lin et al. reported transparent superhydrophobic glass surfaces with nanopatterns fabricated using a femtosecond laser with exceptional water repellency and thermostability.33 However, these surfaces were not successful in exhibiting improved non-wetting with dynamic droplets and transparency for wide angles because they utilized simple mono-structures unlike the hierarchical structures in nature. Therefore, hierarchical nanoscale surface development is required to understand extreme non-wetting properties and superior angular antireflective effects for the practical application of nanoscale dual roughness.
To date, the fabrication of hierarchical structures has been limited for the micro–nano hierarchy and has been performed via expensive, complex, and time-consuming methods such as electron beam lithography, nanoimprint lithography, photolithography, and hybrid approaches with laser or plasma treatment;34 while the hierarchical structure at the nanoscale has not been well reported owing to the delicate complicated multistep process and restriction on the preparation of nanomasks. Colloidal lithography, also called nanosphere lithography, offers great advantages due to its high throughput and low cost.35 Recently, Xu et al. reported the fabrication of periodic three-dimensional hierarchical silicon nanotubes using the selected and repeated etching of polystyrene nanospheres and deposited nickel.36 Fang et al. produced silicon metastructures using a multi-step etching of a polystyrene nanosphere layer.37 Although hierarchically aligned nanostructures have been demonstrated, the reported fabrication process is very delicate, and shows critical dependence on the etching conditions because only one size of polystyrene nanospheres was used as a mask.
In this study, we used a simple nanofabrication process to demonstrate a nanoscale hierarchical pillar-structured surface with tunable morphology and a two-tier solid fraction of low values. The manufactured hierarchical nanosurface was investigated to understand its wetting behavior and transmittance. Effectively, superhydrophobicity via water bouncing behavior after a low surface tension chemical coating as well as broadband antireflection up to an incident angle of 70° were observed, demonstrating the excellent properties of the hierarchical nanosurface. The proposed nanofabrication method and the resulting hierarchical nanostructures imply that the bioinspired nanopillar surfaces provide high-performance functionality and can be expanded for various practical applications such as solar cells, windows, lenses, exterior materials of home appliances, and bio-devices.
2. Experimental section
2.1 Fabrication process of nanostructure
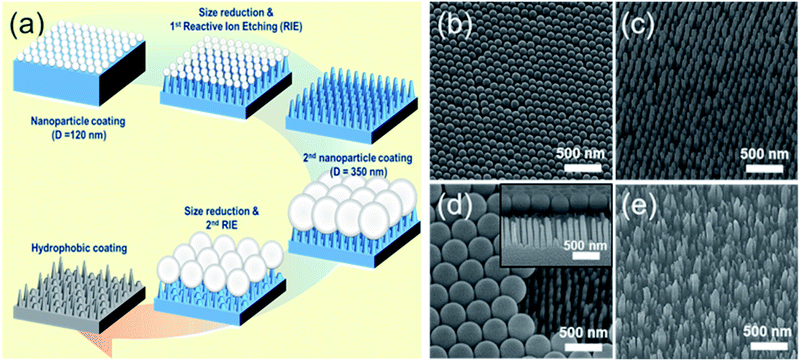
4 kinds of samples were prepared as the mono-structured nanopillars, S120 and S350, and hierarchical nanopillars, SNH1 and SNH2. S120 and S350 indicate the nanopillars made by using 120 nm PS NPs and 350 nm PS NPs, respectively. SNH1 and SNH2 indicate the hierarchical nanopillars made by using combinations of 120 nm PS NPs and 350 nm PS NPs with different size reduction times.To prepare an etching mask, 10 wt% commercial colloidal polystyrene nanoparticles solution (Polyscience, Inc.) was used by diluting with ethanol (Aldrich) in an appropriate ratio according to the size of the nanoparticle, to control the solvent evaporation. The size distributions of the NPs were 120 ± 7 and 350 ± 14 nm, respectively. The nanoparticle assembly was generated by dropping the prepared nanoparticle solution using a micropipette with a few microliters on top of a hydrophilic supporting plate partially immersed in a deionized water bath. At the three-phase contact point, the nanoparticle assembly was floated on the water surface as an evaporating solvent, and then a certain area of the assembly was picked up using a 1 × 1 inch quartz glass substrate. Then, the size of the assembled nanoparticles on quartz glass was reduced to 20% using O2 plasma inside the reactive ion etching chamber (All for System Inc.) to aid the etching by attaining the distance between the NPs. Anisotropic etching was followed in a mixture of CF4, H2, and O2 gases. After etching, the remaining nanoparticles on the structures were removed using O2 plasma. To fabricate nanoscale hierarchical structured surfaces; first, quartz was etched with 120 nm PS NPs using the same method to fabricate nanopillars. Subsequently, 350 nm-sized PS NPs were placed on the nanostructure, and the same process was repeated for size reduction of nanoparticles, glass etching, and removal of the remaining nanoparticles. The difference between the structures of SNH1 and SNH2 was determined by controlling the size reduction time of 350 nm PS NPs in the 2nd step. The size reduction time for SNH1 was 20 s, while that for SNH2 was 40 s.
2.2 Characterization of prepared surfaces
The surface morphologies were confirmed using a scanning electron microscope (SEM, Quanta 250, FEI) and the wettability of the prepared samples was determined by measuring the water contact angles (CA) and sliding angles (SA) using a contact angle meter (Model DM-50, Kyowa Interface Science Co., Ltd). The volume of a water droplet is 10.3 μl.2.3 Optical properties
The transparency and anti-reflective properties of the prepared surfaces were characterized using a UV-visible spectrometer (Cary 5000, Agilent Technologies) according to the incident angle. All prepared samples were compared with a bare quartz glass surface as a reference in the wavelength range of 350–1100 nm.2.4 Droplet impact experiment
Droplets (8.6 μl) were detached off under its weight at the tip of the needle from a syringe pump providing water, and fell onto the surfaces. Droplet impacts were recorded using a high-speed camera (Photron Ltd) at 3000 fps and shutter speed of 1/6400 s with a resolution of 512 × 420 pixels. A high-speed camera was placed on the side of the glass. The droplet impact velocity was varied by changing the height of the 22-gauge nozzle. Based on the needle height, we evaluated the impact velocities as given in Table 1.| Weber number | Height (mm) | Impact velocity (m s−1) | P WH (MPa) | P D (kPa) | Spreading motion |
|---|---|---|---|---|---|
| 6 | 10 | 0.42 | 0.12 | 0.09 | Flat disk |
| 13 | 20 | 0.62 | 0.18 | 0.19 | Flat disk |
| 48 | 80 | 1.17 | 0.35 | 0.68 | Flat disk |
| 140 | 230 | 2.01 | 0.59 | 2.00 | Wavy shape |
| 290 | 450 | 2.97 | 0.86 | 4.14 | Splash motion |
| 416 | 670 | 3.63 | 1.03 | 5.94 | Splash motion |
| 673 | 980 | 4.38 | 1.30 | 9.61 | Splash motion |
| 854 | 1330 | 5.11 | 1.47 | 12.20 | Splash motion |
Results and discussion
The fabrication process for hierarchical nanostructures involves repeating basic colloidal lithography and reactive ion etching (RIE).38 The process for fabricating hierarchical nanopillar surfaces via multiple step colloidal lithography (MS-CL) is illustrated schematically in Fig. 1(a), and the resulting surfaces of each step are shown in the associated scanning electron microscopy (SEM) images in Fig. 1(b)–(e). Polystyrene nanoparticles (PS NPs) were employed as a mask to achieve the target morphology with the desired superhydrophobicity and low reflectivity for self-cleaning and transparency. The success of the surface patterning was determined by controlling the self-assembly of PS NPs and manipulating their monolayer packing. The floating method was used to pack particles on the surface,39 enabling hexagonal packing of PS NPs at the air/water interface driven by surface tension and gravity, as shown in Fig. 1(b) and (d). We used commercial colloidal PS NPs having the sizes of 120 ± 7 and 350 ± 14 nm. This determined the 1st and 2nd base diameters of the nanopillars on the surface. Thereafter, anisotropic quartz glass etching was successively conducted in a mixture of CF4, H2, and O2 gases, as shown in Fig. 1(c). The condition are described in detail in ref. 40. Finally, the remaining polystyrene nanoparticles on the structures were removed using O2 plasma. Furthermore, to fabricate nanoscale hierarchical structures, the colloidal lithography of larger NPs than the 1st NPs was repeated using the same process. During etching, the prepared1st nanopillars located below the 2nd NPs were protected from reactive ion etching, resulting in the fabrication of a hierarchically structured surface, as shown in Fig. 1(e). In summary, quartz glass was etched with a mask of monolayered 120 nm PS NPs at first and thereafter with 350 nm PS NPs. MS-CL can be repeated continuously with increasing NPs for multistage hierarchical structures. In addition, we could control the number of short nanopillars in the nanoscale hybrid structure by adjusting the size reduction time during the 2nd RIE process.To obtain the dual functions of robust superhydrophobicity and omnidirectional broadband antireflective properties with hierarchical nanostructures, two types of samples were prepared with a combination of 120 and 350 nm NPs. Fig. 2 shows the SEM images of the mono-structured nanopillars, S120 and S350, and hierarchical nanopillars, SNH1 and SNH2. The morphology of the nanopillars was determined according to the size reduction and etching times. As the size reduction time of the PS NP is increased, sharp tip-shaped nanopillars are obtained. The height of the nanopillars was linearly related to the etching time. Among the several etching processes used, S120 resulted in truncated cone-shaped nanopillars with a height of 517 ± 21 nm, top diameter of 82 ± 6 nm top, and bottom diameter of 120 ± 7 nm, as shown in Fig. 2(a); S350 also led to truncated cone-shaped nanopillars with a height of 678 ± 28 nm, top diameter of 203 ± 13 nm, and bottom diameter of 350 ± 14 nm, as shown in Fig. 2(b). The maximum gap between the top of the nanopillars was 40 ± 5 nm for S120 and 151 ± 7 nm for S350. By contrast, the hierarchically structured samples had two different shapes of nanopillars by modulating the size reduction time of the 2nd NPs as 30 and 45 s for SNH1 and SNH2, respectively. The reason for the difference between the short and long pillars is that the long pillars were not etched by the 350 nm PS NP mask in the 2nd RIE process. As a result, hierarchically structured samples such as SNH1 and SNH2 showed dissimilar morphologies based on the change in size of the 350 nm PS NP mask owing to the varied size reduction times in the 2nd RIE process. Therefore, while SNH1 has three to five grouped pillar structures, SNH2 has two to three grouped pillar structures. Furthermore, SNH1 led to long pillars with a height of 682 ± 12 nm, top diameter of 79 ± 2 nm, and maximum gap of 154 ± 3 nm, and short pillars with a height of 272 ± 18 nm height, top diameter of 93 ± 5 nm, and maximum gap of 40 ± 3 nm, as shown in Fig. 2(c). However, SNH2 shows the long pillars with a height of 682 ± 21 nm, top diameter of 78 ± 2 nm, and maximum gap of 520 ± 12 nm, as well as the short pillars with a height of 269 ± 14 nm, top diameter of 103 ± 9 nm, and maximum gap of 40 ± 6 nm, as shown in Fig. 2(d). Then, based on the maximum gaps of the samples, the contact area fraction (ΦC) of the nanostructured samples was determined. ΦC of S120 and S350 were 0.42 and 0.29, respectively. By contrast, the hierarchically structured samples have two ΦC depending on the pillar height because the long pillars have a larger maximum gap than the short pillars. While the contact area fraction of SNH1 was 0.09 for long pillars and 0.54 for short pillars, the contact area fraction of SNH2 was 0.08 and 0.66 for long and short pillars, respectively, as listed in Table 2.
| Sample | Contact angle (CA) (°) | Advancing CA (°) | Receding CA (°) | CA hysteresis (°) | Contact area fraction (ΦC) |
|---|---|---|---|---|---|
| S120 | 170.6 ± 1.4 | 177.4 ± 2 | 163.5 ± 1.9 | 13.9 ± 2.1 | 0.42 |
| S350 | 172.4 ± 2 | 173.2 ± 1.1 | 160.6 ± 4 | 12.7 ± 1.3 | 0.29 |
| SNH1 | 177.4 ± 2.0 | 177.8 ± 1 | 177.1 ± 0.1 | 0.7 ± 0.8 | 0.09 (L), 0.54 (S) |
| SNH2 | 177.8 ± 0.9 | 177.9 ± 0.1 | 177.2 ± 1.0 | 0.7 ± 0.1 | 0.08 (L), 0.66 (S) |
The water contact angle (CA) was measured to investigate the superhydrophobicity of the hierarchy. Because the physical structure and chemical coating determine the surface wettability, the samples were coated with perfluoropolyether (PFPE) via a simple dipping method. In the contact angle measurements, the water droplet did not adhere on the surface as shown in ESI Movie S1.† After observing that the water droplet hardly attached to the surface, the water contact angle values were measured in Table 2. The static, advancing, and receding contact angles of all samples were >160°, suggesting that all cavities were filled with air. Furthermore, the surfaces with large cavity area fractions have a higher contact angle and lower hysteresis angle than the surfaces with small cavity area fractions. The contact angle hysteresis of SNH1 and SNH2 was 0.7°, which is 10° lower than the contact angle hysteresis of S120 and S350. Based on these measured CAs, nanoscale hierarchically structured samples showed excellent water repellency, and a droplet could slide easily even with a small slope (∼1°) on SNH1 and SNH2.
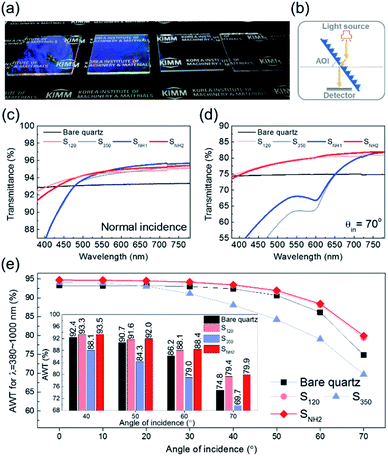
The optical properties of the nanopillar-structured surfaces were investigated considering their wide angular transmittance. The antireflection of nanostructures for photovoltaics or optical devices provides improved transmission and visual clarity in particular for a wide angle of incidence (AOI). According to Boden et al., the reflection minima of the reflectance spectrum of a nanopillar array are related to the diameter of the nanopillar depending on the wavelength.35 Moreover, because the height of the nanopillar affects the interference between the reflected light from its top and bottom, the wavelengths that cause the lowest reflection can be adjusted depending on the height.40 Therefore, the formation of nanoscale hierarchical structures with different diameters or heights can be an effective strategy to improve the antireflection effect.41,42 Furthermore, the benefits achieved by the periodic arrangement of nanostructures, such as low scattering loss in the short wavelength range, can be maintained.43 Considering these aspects, the fabricated nano-hierarchical structure offers great advantages in achieving high antireflectivity performance owing to its controllability.
Fig. 3(a) shows photographs of the quartz glass under light exposure. All samples exhibit an antireflective effect, so that the letters below the glasses are clearly observed. However, the visibility varies slightly with different characteristics according to the nanopillar morphologies. Therefore, the transmittance was measured using a spectrophotometer in the configuration shown in Fig. 3(b). Although the transmittance of SNH1 is almost identical to that of S350 in the short-wavelength range, a broadband enhancement compared to S350 is observed at normal incidence, as shown in Fig. 3(c). SNH2 that has an increased number of short pillars on the top, exhibited a significant enhancement in the transmittance for the short-wavelength range compared to SNH1 and S350. This implies that reducing the number of short nanopillars is effective in diminishing size-dependent incoherent backward scattering. In addition, SNH2 also exhibited slightly better properties than S120 at long wavelengths owing to the existence of a 350 nm size morphology. When the AOI was 70°, SNH2 still demonstrated the best antireflective effect, as shown in Fig. 3(d). Moreover, the improvement in transmittance due to the nanoscale hierarchical structure becomes more pronounced as the AOI increases. For example, SNH1 has an identical transmittance in the short-wavelength range to that of S350 for normal incidence, while the transmittance of SNH1 for an AOI of 70° is higher than that of S350. This better angular antireflective effect of the nano-hierarchical structure can be explained by the decrease in the scattering area. In the case of normal incidence, the difference in the area that produced light scattering between SNH1 and S350 was negligible, allowing a similar transmittance to be observed over the short-wavelength range. However, for an AOI of 70°, SNH1 provides a more reduced scattering area than S350; thus, its transmittance increased. In Fig. 3(e), the values of the average weighted transmittance (AWT) of the samples used in this work are presented as a function of AOIs to show a broadband improvement of the high-angle antireflective effect owing to nanoscale hierarchical structuring. The values of AWT were obtained using ∫T(λ)I(λ)AM1.5Gdλ/∫I(λ)AM1.5Gdλ, where T(λ) is the measured transmittance and I(λ)AM1.5G is the standard terrestrial solar irradiance.44 Because SNH2 has a better angular antireflective effect than SNH1 owing to its effective design that avoids undesirable scattering, only SNH2 was compared with the bare quartz and the other mono-structures as shown in Fig. 3(e). S350 exhibited a lower performance in angular antireflective effects than the other samples due to significant scattering loss in the short-wavelength region. However, S350 exhibits good antireflective properties in the infrared range because the size of the nanostructure corresponds to the subwavelength scale. Although SNH2 appears to have little difference in AWT values compared to S120, SNH2 consistently showed improved AWT values over S120 for 50–70° AOIs, as shown in the inset of Fig. 3(e). In particular, when the AOI was 70°, SNH2 showed a 0.6% improvement in AWT compared to S120. This means that SNH2 clearly shows a larger scattering than S120 for the short-wavelength region, but compensates for the scattering loss by broadband transmittance improvements using dual periodicity. Consequently, SNH2 exhibits a superior high-angle antireflective performance than S120 for broadband wavelengths. Therefore, considering the results of the above investigations on the angular antireflective effect, it is concluded that the reduced scattering area and the dual periodicity are the primary merits of the nano-hierarchical structure to achieve a better antireflective effect for the broadband wavelengths and wide AOIs.
The non-wetting property of the samples was evaluated in depth by analyzing water bouncing behavior to understand the aspect of the hierarchy. The superhydrophobic wetting state is categorized by the Wenzel state or the Cassie–Baxter state. In the Wenzel state, a water droplet follows surface asperity,45 wherein the water droplet is strongly pinned onto the contact area, specifically at the edges of the structures. By contrast, in the Cassie–Baxter state, because a water droplet sits on the top of the surface structures, the surface area in contact with the solid surface is small.45 This generates the liquid–gas interface where the adhesive force is absent, forming on a gas layer below the droplet. In addition, a water droplet in the Cassie–Baxter state can be easily removed from the surface because it has a smaller adhesive area than that in the Wenzel state. The droplet impact experiment allows for different spreading and bouncing motions according to the extent of non-wetting and mostly induces the wetting transition from the Cassie–Baxter to the Wenzel state. Therefore, the investigation of impact behavior is useful for determining the non-wetting ability, particularly for superhydrophobic surfaces with high contact angles. When an impacted droplet is in the Wenzel state, the droplet is pinned on the surface or bounces off, leaving small droplets on the surface. Alternatively, when an impacted droplet is in the Cassie–Baxter state, the structural gap creates capillary pressure that pushes water out with fast contact time and without a splash. Table 1 summarizes the spreading motion with various impact velocities and Weber numbers (We = ρv2D/σ) of the impacting droplets for different impact heights, calculated hammer pressures (PWH), and dynamic pressures (PD).46 In the definition of Weber numbers, ρ is the droplet density, v is the droplet impact velocity, D is the droplet diameter, and σ is the liquid surface tension. When the droplet is impacted, pressures are balanced on the hierarchical nanosurface, PWH, PD, and capillary pressure (PC), as described in Fig. 4(a). PWH is generated by compression waves during the droplet impact, and PD is caused by kinetic energy. To prevent the penetration of water into the gap, PC is created by the surface tension between the structures on the surface during impact. The two pressures applied at the direction normal to the surface by impact are PWH and PD and are expressed as
| PWH ≈ 0.2ρcv, | (1) |
| PD = 0.5ρv2, | (2) |
PC = −2σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/gs, θ/gs, | (3) |
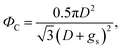 | (4) |
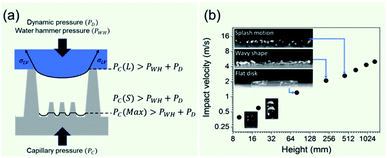 | ||
| Fig. 4 (a) Schematics of pressure balance of dynamic pressure, water hammer pressure, and capillary pressure. (b) Water bouncing behavior according to impact velocity. | ||
Then, gs and PC are
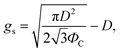 | (5) |
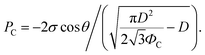 | (6) |
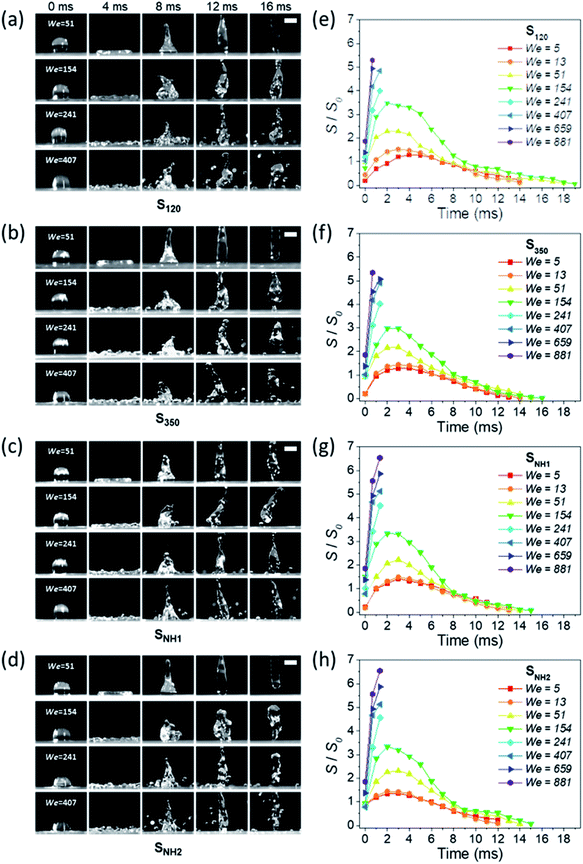
Varanasi et al. showed the wetting state by balancing the water hammer pressure, dynamic pressure, and capillary pressure.48 When the pressure condition was PWH > PD > PC, the impacted droplet was in a Wenzel state, whereas when the pressure condition was PWH > PC > PD, the impacted droplet was in a partial pinning state. Furthermore, when the pressure condition was PC > PWH > PD, the impacted droplet was in a Cassie–Baxter state. Because all surfaces have truncated conical nanostructures as a result of colloidal lithography, the capillary pressure varies depending on the height of the structure. Unlike S120 and S350, SNH1 and SNH2 have two different capillary pressures and maximum capillary pressures because they have truncated conical structures of different heights. The values of maximum capillary pressures were 8.08 MPa for S350 and 23.97 MPa for S120, SNH1, and SNH2, respectively. Based on the calculated pressure values of PWH (0.12–1.47 MPa), PD (0.12–1.47 kPa), and the maximum PC (8.08–23.97 MPa), it is inferred that the impacted water droplets were in the Cassie–Baxter state. As shown in Fig. 4(b) and Table 1, the first spreading motion of impacted droplets were of three typical types; flat disk, wavy shape, and splash motion depending on the impact velocity (i.e., Weber number), regardless of the sample. The movie of droplet impact motion on SNH2 at different dropped heights of 80, 230, and 450 mm (i.e. Weber number; 48, 140, and 290) is available in ESI Movie S2.† For a Weber number <48, the spreading shape was flat disk. When the Weber number was 140, the spreading shape changed from a flat disk to a wavy shape and for a Weber number ≥290, the spreading motions on all surfaces were wavy, and the impacted droplets then splashed. The critical velocity of the droplet breakup was 2.97 m s−1.
This behavior proves that all of the nanostructured samples showed excellent superhydrophobicity. The detailed image sequences of Weber numbers 48, 140, 290, and 416 at 4 ms intervals up to 16 ms are displayed for the analysis of the impact behavior in Fig. 5(a)–(d). Water droplets show the representative motion of impact, spreading, recoiling, and rebound. The spreading motion and diameter of the samples show different behaviors according to the Weber number and surface wetting property in 4 ms images, and all droplets recoiled and rebounded at 8 ms. Furthermore, from the images, it is observed that the extent of rebounding was slightly different, in particular, for the splash behavior at high Weber numbers of 290 and 416. Depending on the Weber number, not only the spreading motion but also the spreading diameter changed. Fig. 5(e)–(h) show the spreading diameters and contact time of the impacted droplets depending on the Weber number. As the Weber number increased, the maximum spreading diameter increased, and the contact time, which is the time required for the bouncing process, increased owing to the increase in contact area where the friction force acts. Among the surfaces, SNH2 had shorter contact times than the others. In addition, for Weber number above 290, the impacted droplets splashed and separated into small droplets and then rebounded from the surfaces with changed mass. On the SNH1 and SNH2 surfaces, larger spreading diameters of the impacted droplets were observed than those on S120 and S350.
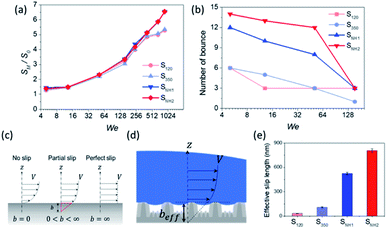
The excellent performance of the hierarchical nanostructures of SNH1 and SNH2 was investigated in terms of the maximum spreading diameter, number of bounces, and effective slip length, as shown in Fig. 6. Fig. 6(a) and (b) show the comparison of the maximum spreading diameter and the number of bounces of each sample according to the Weber number, respectively. The maximum spreading diameter decreased in the order of SNH2, SNH1, S350, and S120. When the weber number was 881, the value of maximum spreading diameter (SM) is 42.30, 42.22, 34.54, and 34.15 mm for SNH2, SNH1, S350, and S120, respectively. The maximum spreading diameter of SNH1 and SNH2 is 1.2 times larger than that of S120 and S350. Furthermore, the impacted droplets on SNH2 had the highest number of bounces; in particular, when the Weber number was 6, the water droplets bounced 14 times on SNH2, 12 times on SNH1, 6 times on S350, and 6 times on S120 as shown in ESI Movie S3.† Furthermore, as the Weber number increased, the number of bounces decreased owing to severe splash behavior. These behaviors clearly indicate that nanoscale hierarchical structures contribute to non-wetting properties, even with dynamic water droplets. The superior bouncing property of nano-hierarchical surfaces can be explained by the slip length as an indicator to elucidate the bouncing behavior on superhydrophobic surfaces. The spreading diameter of the samples is affected by friction during spreading and recoiling as the energy loss of the impacted droplet is minimized with a low friction interaction. Friction force is the force generated by the no-slip boundary condition in the liquid–solid interaction.49 On a smooth surface, the friction force is defined as
| Ff = Aηγs, | (7) |
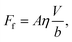 | (8) |
The spreading and recoil process on the superhydrophobic surface with the Cassie–Baxter state has two boundary conditions owing to the contact and gas areas. During the spreading and recoiling of water, the area of the pillars induces a no-slip boundary condition, whereas the gas area induces a perfect slip boundary condition on the liquid–vapor interface. The friction force on a superhydrophobic surface is defined as
Ff=AΦCη![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) s, s, | (9) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) s is the average shear rate of the solid patch. To estimate
s is the average shear rate of the solid patch. To estimate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) s, the velocity profile in the liquid is influenced by the solid zones only in a region of size 0.5D.
s, the velocity profile in the liquid is influenced by the solid zones only in a region of size 0.5D.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) s ∼2U/D, s ∼2U/D, | (10) |
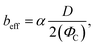 | (11) |
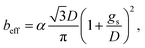 | (12) |
The previous result shows that, in the case of patterned no-slip dots, 1/π is appropriate as a prefactor, α, of the predicted relationship.50
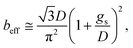 | (13) |
The results calculated using the equation are shown in Fig. 6(e) and ESI Table S1† with values of minimum and maximum capillary pressure (PC). The effective slip length of SNH2 was found to be the longest. Therefore, the friction force on SNH2 is smaller than that of the others and provides the highest number of bounces among the reported numbers. Consequentially, based on the several analyses of bouncing behavior, it is suggested that the contact time, spreading diameter, and spreading shape of the bouncing behavior do not precisely correlate with the excellence of the hierarchical structures, while the effective slip length distinguishes between the superhydrophobic samples. To date, the reports on the water impact behavior, critical velocity, number of bounces, and slip length, for understanding superhydrophobicity have been scarce. Table 3 summarizes the various superhydrophobic surfaces with different wetting characteristics. Based on the analysis of these results, nanohierarchy provides excellent superhydrophobicity, resulting in a high critical velocity and a large number of bounces with two-tier morphology for large capillary pressure and long effective slip length. Because the mechanical robustness of the nanopillar structured surfaces was confirmed against finger rubbing,65,66 these functional surfaces is promising in the practical applications.
| Structure | CA (°) | Critical velocity (m s−1) | Number of bouncing | Slip length (nm) |
|---|---|---|---|---|
| Nano-hierarchical structureThis study | 178 | 2.97 | 14 | 800 |
| Flat51 | 120 | 25–100 | ||
| Rough surface52 | 120 | 50–350 | ||
| Porous structure53 | 130 | 1.14 | ||
| Rough surface54 | 120–150 | 2–16 | ||
| Hierarchical structure55 | 154 | 1.41 | ||
| Micro structure56 | 156 | 2 | ||
| Micro structure57 | 157 | 1.34 | ||
| Rough surface58 | 160 | 2.1 | ||
| Hierarchical structure59 | 164 | 1.97 | ||
| Hierarchical structure60 | 164 | 2.95 | ||
| Nano structure61 | 165 | 0–1500 | ||
| Hierarchical structure62 | 166 | 2.24 | ||
| Porous structure63 | 169 | 7 | ||
| Porous structure64 | 175 | 14 |
Conclusions
Inspired by the lotus leaf and moth-eye, nanoscale hierarchical pillars were fabricated via multiple step colloidal lithography with 120 and 350 nm polystyrene nanoparticles. First, the smaller nanopillars were fabricated, and then the larger nanoparticles were used as a mask in the subsequent etching process. Upon repeating these steps, hierarchical structures can be obtained regardless of size. Four fabricated nanosurfaces, mono-pillared S120 and S350, and hierarchical-pillared SNH1 and SNH2, exhibited superhydrophobicity. Notably, SNH2 and SNH1 have water contact angles of 177° and a sliding angle of 1°. SNH2 with a 120 nm morphology hierarchical surface exhibited the best antireflective effect among the samples by decreasing the scattering area, in particular, when the angle of incidence increased. Therefore, SNH2 has a transmittance of 80% at an incidence angle of 70°. The water bouncing behavior of the samples demonstrated the superiority of the non-wetting behavior of the surfaces, showing the advantages of hierarchy. The values of the maximum capillary pressures were calculated as 23.97 MPa for 120 nm morphology-based samples; S120, SNH1, and SNH2. Furthermore, the impacted droplets for the Weber number above 290 were splashed and the critical velocity of droplet breakup was obtained as 2.97 m s−1 for all samples. Furthermore, the impacted droplets on SNH2 had the highest number of bounces, 14 times at Weber number 6, and largest maximum spreading diameter of 42.30 mm among the samples. These observations can be explained by the effective slip length. In particular, these results provide a valuable contribution by maintaining the transparency overcoming the hierarchy in microstructures. Therefore, the presented nanoscale hierarchical surface displays outstanding potential for superhydrophobicity and wide angular transmittance, demonstrating extreme water bouncing behavior. Hierarchy in nature results in unique multifunctionality, and multiple step colloidal lithography can potentially be used to formulate such structures, specifically at the nanoscale.Author contributions
Both authors (C. L. and S. J.) contributed equally as first authors to fabricate the sample and measure the properties. S. J. conceived and designed the experiments. C. L. performed the analysis. S. O. and S. P. provided critical suggestions. Y. J improved the manuscript. J. L. reviewed and improved the manuscript. H. L. conceived and supervised the project. All authors reviewed and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Korea Institute of Energy Technology Evaluation and Planning. Financial resources were granted by the Ministry of Trade, Industry & Energy, Republic of Korea (20193010014740), the Korea Environment Industry & Technology Institute through its Ecological Imitation-based Environmental Pollution Management Technology Development Project and funded by the Korea Ministry of Environment (2019002790005), and National Research Foundation grant by the Ministry of Education, under “Basic Science Research Program” (NRF-2017R1D1A1B04033182).Notes and references
- V. A. Ganesh, H. K. Raut, A. S. Nair and S. Ramakrishna, J. Mater. Chem., 2011, 21, 16304 RSC.
- S. Nishimoto and B. Bhushan, RSC Adv., 2013, 3, 671 RSC.
- X. Li, G. Wang, A. S. Moita, C. Zhang, S. Wang and Y. Liu, Appl. Surf. Sci., 2020, 505, 144386 CrossRef CAS.
- L. J. Chen, M. Chen, H. Di Zhou and J. M. Chen, Appl. Surf. Sci., 2008, 255, 3459 CrossRef CAS.
- B. L. Feng, S. Li and Y. Li, Adv. Mater., 2016, 14, 1857 CrossRef.
- M. Sun, C. Luo, L. Xu, H. Ji, Q. Ouyang, D. Yu and Y. Chen, Langmuir, 2005, 21, 8978 CrossRef CAS PubMed.
- I. You, T. G. Lee, Y. S. Nam and H. Lee, ACS Nano, 2014, 8, 901 Search PubMed.
- J. Yong, F. Chen, Q. Yang, Y. Fang, J. Huo, J. Zhang and X. Hou, Adv. Mater. Interfaces., 2017, 4, 1700552 CrossRef.
- X. Dai, N. Sun, S. O. Nielsen, B. B. Stogin, J. Wang, S. Yang and T. S. Wong, Sci. Adv., 2018, 4, 1 Search PubMed.
- J. Zhang, A. Wang and S. Seeger, Adv. Funct. Mater., 2014, 24, 1074 CrossRef CAS.
- T. S. Wong, S. H. Kang, S. K. Y. Tang, E. J. Smythe, B. D. Hatton, A. Grinthal and J. Aizenberg, Nature, 2011, 477, 443 CrossRef CAS PubMed.
- K. Hadobas, S. Kirsch, A. Carl, M. Acet and E. F. Wassermann, Nanotechnology, 2000, 11, 161 CrossRef CAS.
- W. K. Kuo, G. F. Kuo, S. Y. Lin and H. Yu, Bioinspiration Biomimetics, 2015, 10, 56010 CrossRef PubMed.
- W. K. Kuo, J. J. Hsu, C. K. Nien and H. H. Yu, ACS Appl. Mater. Interfaces, 2016, 8, 32021 CrossRef CAS PubMed.
- W. K. Kuo, S. Y. Lin, S. W. Hsu and H. H. Yu, Opt. Mater., 2017, 66, 630 CrossRef CAS.
- D. Yoo, S. C. Park, S. Lee, J. Y. Sim, I. Song, D. Choi, H. Lim and D. S. Kim, Nano Energy, 2019, 57, 424 CrossRef CAS.
- J. Huang, X. Wang and Z. L. Wang, Nano Lett., 2006, 6, 2325–2331 CrossRef CAS PubMed.
- W. Lee, M. K. Jin, W. C. Yoo and J. K. Lee, Langmuir, 2004, 20, 7665 CrossRef CAS PubMed.
- X. Zeng, L. Qian, X. Yuan, C. Zhou, Z. Li, J. Cheng, S. Xu, S. Wang, P. Pi and X. Wen, ACS Nano, 2017, 11, 760 CrossRef CAS PubMed.
- X. Gou and Z. Guo, Langmuir, 2020, 36, 64 CrossRef CAS PubMed.
- L. T. Nguyen, Z. Bai, J. Zhu, C. Gao, X. Liu, B. T. Wagaye, J. Li, B. Zhang and J. Guo, ACS Omega, 2021, 6, 3910 CrossRef CAS PubMed.
- Y. Liu, H. Gu, Y. Jia, J. Liu, H. Zhang, R. Wang, B. Zhang, H. Zhang and Q. Zhang, Chem. Eng. J., 2019, 356, 318 CrossRef CAS.
- X. Li, J. Deng, H. Yue, D. Ge and X. Zou, Tribol. Int., 2019, 134, 240 CrossRef CAS.
- H. W. Chien, X. Y. Chen, W. P. Tsai and M. Lee, Colloids Surf., B, 2020, 186, 110738 CrossRef CAS PubMed.
- A. G. Domel, G. Domel, J. C. Weaver, M. Saadat, K. Bertoldi and G. V. Lauder, Bioinspiration Biomimetics, 2018, 13, 056014 CrossRef PubMed.
- T. Zhu, Y. Cheng, J. Huang, J. Xiong, M. Ge, J. Mao, Z. Liu, X. Dong, Z. Chen and Y. Lai, Chem. Eng. J., 2020, 399, 125746 CrossRef CAS.
- S. S. Latthe, R. S. Sutar, V. S. Kodag, A. K. Bhosale, A. M. Kumar, K. Kumar Sadasivuni, R. Xing and S. Liu, Prog. Org. Coat., 2019, 128, 52 CrossRef CAS.
- S. P. Dalawai, M. A. Saad Aly, S. S. Latthe, R. Xing, R. S. Sutar, S. Nagappan, C. S. Ha, K. Kumar Sadasivuni and S. Liu, Prog. Org. Coat., 2020, 138, 105381 CrossRef CAS.
- H. K. Raut, V. A. Ganesh, A. S. Nair and S. Ramakrishna, Energy Environ. Sci., 2011, 4, 3779 RSC.
- S. Chattopadhyay, Y. F. Huang, Y. J. Jen, A. Ganguly, K. H. Chen and L. C. Chen, Mater. Sci. Eng., R, 2010, 69, 1 CrossRef.
- K. H. Kim and Q. H. Park, Sci. Rep., 2013, 3, 1062 CrossRef PubMed.
- K. C. Park, H. J. Choi, C. H. Chang, R. E. Cohen, G. H. McKinley and G. Barbastathis, ACS Nano, 2012, 6, 3789 CrossRef CAS PubMed.
- Y. Lin, J. Han, M. Cai, W. Liu, X. Luo, H. Zhang and M. Zhong, J. Mater. Chem. A, 2018, 6, 9049 RSC.
- W. S. Chu, C. S. Kim, H. T. Lee, J. O. Choi, J. Il Park, J. H. Song, K. H. Jang and S. H. Ahn, Int. J. Precis. Eng. Manuf. - Green Technol., 2014, 1, 75 CrossRef.
- S. A. Boden and D. M. Bagnall, Appl. Phys. Lett., 2008, 93, 1 CrossRef.
- X. Xu, Q. Yang, N. Wattanatorn, C. Zhao, N. Chiang, S. J. Jonas and P. S. Weiss, ACS Nano, 2017, 11, 10384 CrossRef CAS PubMed.
- X. Fang, C. Zheng, Z. Yin, Z. Wang, J. Wang, J. Liu, D. Luo and Y. J. Liu, ACS Appl. Mater. Interfaces, 2020, 12, 12345 CrossRef PubMed.
- H. Lim, S. Ji and W. D. Kim, (Korean Institute of Machinery & Materials) Patterning Method for Nano-Structure, KR patent 10-2009-0127387. 2009.
- S. C. Park, N. Kim, S. Ji and H. Lim, Microelectron. Eng., 2016, 158, 35 CrossRef CAS.
- S. Ji, J. Park and H. Lim, Nanoscale, 2012, 4, 4603 RSC.
- K. Watanabe, J. Yamamoto and R. Tsuchiya, J. Appl. Phys., 2015, 118, 085102 CrossRef.
- L. Yang, Q. Feng, B. Ng, X. Luo and M. Hong, Appl. Phys. Express, 2010, 3, 5 Search PubMed.
- S. Ji, K. Song, T. B. Nguyen, N. Kim and H. Lim, ACS Appl. Mater. Interfaces, 2013, 5, 10731 CrossRef CAS PubMed.
- National Renewable Energy Laboratory (NREL), Reference Air Mass 1.5 Spectra, accessed June 5, 2021, https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html Search PubMed.
- D. Quéré and M. Reyssat, Philos. Trans. R. Soc., A, 2008, 366, 1539 CrossRef PubMed.
- O. G. Engel, J. Res. Natl. Bur. Stand., 1955, 54, 281 CrossRef.
- H. Kim and S. H. Kim, Langmuir, 2018, 34, 5480 CrossRef CAS PubMed.
- K. K. Varanasi, T. Deng, M. Hsu and N. Bhate, Tech. Proc. 2009 NSTI Nanotechnol. Conf. Expo, NSTI-Nanotech 2009, vol. 3, p. 184 Search PubMed.
- L. Bocquet and J. L. Barrat, Soft Matter, 2007, 3, 685 RSC.
- C. Ybert, C. Barentin, C. Cottin-Bizonne, P. Joseph and L. Bocquet, Phys. Fluids, 2007, 19, 123601 CrossRef.
- P. Huang, J. S. Guasto and K. S. Breuer, J. Fluid Mech., 2006, 566, 447 CrossRef CAS.
- T. Schmatko, H. Hervet and L. Leger, Phys. Rev. Lett., 2005, 94, 244501 CrossRef.
- C. Y. Chiang, T. Y. Yang, A. Casandra and S. Y. Lin, Exp. Therm. Fluid Sci., 2017, 88, 444 CrossRef.
- F. J. M. Ruiz-Cabello, P. F. Ibáñez-Ibáñez, J. F. Gómez-Lopera, J. Martínez-Aroza, M. Cabrerizo-Vílchez and M. A. Rodríguez-Valverde, J. Colloid Interface Sci., 2017, 508, 129 CrossRef CAS PubMed.
- P. Hao, C. Lv, F. Niu and Y. Yu, Sci. China: Phys., Mech. Astron., 2014, 57, 1376 Search PubMed.
- R. Zhang, P. Hao, X. Zhang, F. Niu and F. He, Langmuir, 2018, 34, 7942 CrossRef CAS PubMed.
- C. Guo, D. Zhao, Y. Sun, M. Wang and Y. Liu, Langmuir, 2018, 34, 3533 CrossRef CAS PubMed.
- E. S. Quintero, G. Riboux and J. M. Gordillo, J. Fluid Mech., 2019, 870, 175 CrossRef CAS.
- L. Chen, Z. Xiao, P. C. H. Chan, Y. K. Lee and Z. Li, Appl. Surf. Sci., 2011, 257, 8857 CrossRef CAS.
- H. Kim and S. H. Kim, Langmuir, 2018, 34, 5480 CrossRef CAS PubMed.
- P. Joseph, C. Cottin-Bizonne, J. M. Benoît, C. Ybert, C. Journet, P. Tabeling and L. Bocquet, Phys. Rev. Lett., 2006, 97, 156104 CrossRef CAS PubMed.
- M. Abolghasemibizaki and R. Mohammadi, J. Colloid Interface Sci., 2018, 509, 422 CrossRef CAS PubMed.
- Z. Xu, D. Jiang, F. Wu, X. Guo, Z. Wei and J. Chen, J. Mater. Sci., 2018, 53, 5364 CrossRef CAS.
- C. R. Crick and I. P. Parkin, Chem. Commun., 2011, 47, 12059 RSC.
- J. Park, H. Lim, W.-D. Kim and J. S. Ko, J. Colloid Interface Sci., 2011, 360, 272 CrossRef CAS PubMed.
- I. D. Jung, M. C. Lee, H. Lim, E. Smela and J. S. Ko, Appl. Surf. Sci., 2015, 349, 705 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Table S1; minimum and maximum capillary pressure (PC) and the effective slip length (beff) of samples. The PC of long pillars are marked with L and that of short pillars are marked with S; Movie S1; contact angle measurement. Attaching a water droplet on samples; S120, S350, SNH1, and SNH2. Volume of droplet is 10.3 μl; Movie S2; droplet impact motion. Droplets impact on SNH2 with different dropped height; 80, 230, and 450 mm (Weber number; 48, 140, and 290). The volume of droplet is 8.6 μl. The process is recorded at 3000 frames per second (fps) and shown at 30 fps; Movie S3; number of bouncing. Droplets bounce on samples; S120, S350, SNH1, and SNH2. The dropped height is 10 mm and volume of droplet is 8.6 μl. The process is recorded at 3000 frames per second (fps) and shown at 30 fps. See DOI: 10.1039/d1na00806d |
| ‡ Both authors contributed equally as first authors. |
| This journal is © The Royal Society of Chemistry 2022 |