Open Access Article
Open Access ArticleHighly stretchable and sensitive strain sensors with ginkgo-like sandwich architectures†
Pengdong
Feng
abc,
Yi
Zheng
abc,
Kang
Li
abc and
Weiwei
Zhao
 *abc
*abc
aSauvage Laboratory for Smart Materials, School of Materials Science and Engineering, Harbin Institute of Technology, Shenzhen 518055, People's Republic of China. E-mail: wzhao@hit.edu.cn
bShenzhen Key Laboratory of Flexible Printed Electronics Technology, Harbin Institute of Technology, Shenzhen 518055, People's Republic of China
cState Key Laboratory of Advanced Welding & Joining, Harbin Institute of Technology, Harbin 150001, People's Republic of China
First published on 14th February 2022
Abstract
The development of a strain sensor that can detect tensile strains exceeding 800% has been challenging. The non-conductive stretchable Eco-flex tape has been widely used in strain sensors due to its high elastic limit. In this work, an Eco-flex-based strain sensor that was conductive until occurrence of fracture was developed. The silver nanoparticles and carbon nanotubes constituted stretchable conductive paths in the Eco-flex matrix. The maximum tensile strain of this sensor was 867%, and the resistance change rate was higher than 104, while the strain resolution was 7.9%. Moreover, the sensor is characterized by segmented logarithmic linearity. This excellent performance was attributed to the ginkgo-like pattern, the patterned strain-coordinating architecture (PSCL), and specific nanocomposites with micro-cracks. The deformation of the architecture and the evolution of the microcracks were studied. In addition, the application of this strain sensor on a wing-shaped aircraft was proposed and its feasibility was demonstrated.
1 Introduction
As the physical carriers of artificial intelligence, stretchable electronics have been developed in many fields,1 including bioelectronics,2 thin film transistors,3,4 optical fiber sensors,5 three-dimensional printing,6 human organ surgery,7 and flexible batteries.8 Strain sensors play an important role in these fields and their performance is mainly measured by their sensitivity and stretchability.9 To date, some sensors have achieved sensitivity above 103 under a tensile strain of less than 8% (ref. 10 and 11) while several studies have also demonstrated conductors with a stretchability of more than 500%, or even as high as 2000% that however have not been used to sense strain.12–15 While a large number of previous studies have achieved a stretchability of approximately 300% and a sensitivity of approximately 50, more recent studies have found it difficult to further improve the overall strain sensor performance.16–24The use of nanomaterials and deformable structures are the two most common strategies for obtaining stretchable electronics. Graphene,25 carbon nanotubes,26–28 silver flakes and nanoparticles,29 polyurethane/gold nanoparticles,30 and liquid metals31 have been widely used as conductive carriers for composites. In another approach, the PEDOT:PSS/ionic material was composited in the styrene ethylene butylene styrene (SEBS) substrate, making the composite conductive at 800% strain.32 Additionally, nanomesh,33 fiber fabric,34 kirigami structures35 and different patterns36,37 have been combined with traditional rigid metals to obtain conductive paths that are robust under tensile strains. It is clear that further development of these two strategies is highly promising for achieving excellent strain sensitivity.
Recently, some intrinsically stretchable strain sensors have attracted widespread attention.38,39 Kim et al. prepared nanocomposites by bonding multiple-wall carbon nanotube (MWCNT) forests and PU, obtaining a remarkable maximum strain of 1400%.40 It was found that the nanocomposites can sense strain until 300% with a normalized relative resistance (R/R0) of 5. Kim et al. developed a strain sensor by spinning carbon nanotube (CNT) fibers onto an Eco-flex substrate, and obtained an R/R0 of close to 360 for a tensile strain of 960%.41 The strain resolution of this sensor was 20%, and the resistance of the sensor hardly changed under 0–400% strain. Strain resolution is defined as the minimum difference between two strains that the sensor can detect accurately, with a smaller minimum difference corresponding to a higher resolution. Yu et al. fabricated NIPAM in an AgNW aerogel to prepare a sensor that could detect 800% strain.42 The R/R0 was approximately 2, and the strain resolution was 100%. Hong et al. achieved a record-breaking maximum tensile strain of 1780% by adhering silver flakes to the hydrogel\Eco-flex hybrid substrate43 and obtained a strain resolution of 100%, and an R/R0 of approximately 20 for 0–1000% strain. Lee et al. developed an excellent strain sensor by connecting silver flakes and liquid metal to an EVA tape.44 The R/R0 of this sensor was approximately 70 under 1000% strain, and the strain resolution was 50%. The above studies have significantly advanced the field of stretchable electronics. Improving the R/R0 and strain resolution under 0–2000% strain and realizing full strain spectrum detection are the current focus of research in the field of strain sensors.
The graphene foam-PDMS composite and graphene-Silly Putty have been studied, which were used as compliant, stretchable and flexible strain/pressure sensors capable of sensing even the human pulse.45–47 A sensor based on spider cracks has achieved a promising gauge factor of 1700.48 Graphene foam prepared through the two-step technique has shown a stable resistance signal.49 What's more, porous micro-structure graphene assembled films have been used in two-segment linear resistive sensors.50 The CNT-Eco-flex nanocomposite was conductive until 500% strain.51 A fully 3D printed multi-material soft bio-inspired whisker will be applied to underwater detection robots.52
Here, we report a promising strain sensor obtained using the combination of nanocomposites and architecture strategies. The ginkgo-like sandwich structure was introduced in a strain sensor for the first time and was used together with Eco-flex-based nanocomposites and patterned strain coordination layers. These features made key contributions to achieving high sensor performance with an R/R0 of higher than 104 at 867% strain, excellent cycle stability and a strain resolution reaching 7.9%. We analyzed the logarithmic linear regression equation and gauge factors. Additionally, the architecture and micro-cracks of the sensor were simulated and characterized, and an application of this sensor in smart devices was proposed and simulated.
2 Results and discussion
2.1 Patterns, architectures and nanocomposites
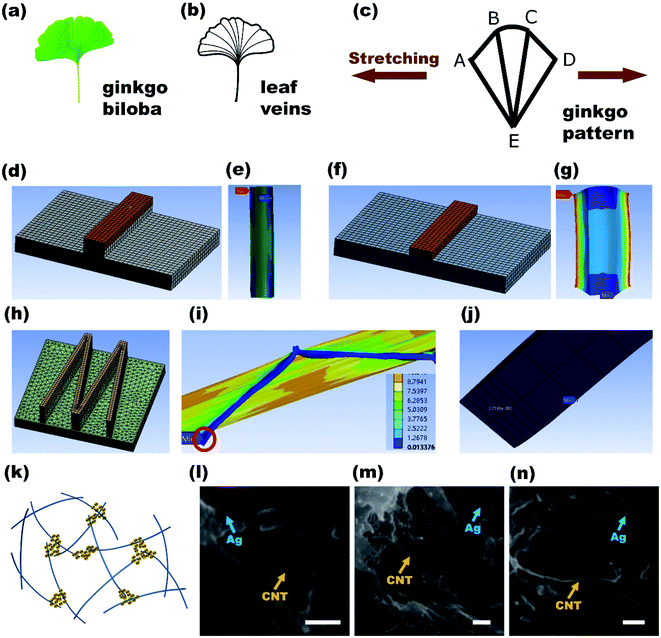
Ginkgo-like patterns, patterned strain-coordinating layers (PSCL) and specific nanocomposites make key contributions to this ultrastretchable strain sensor. In this work, the ginkgo-like pattern was applied for the first time to stretchable electronics. For the nanocomposites, the elasticity of the silicone rubber matrix was impaired by inorganic nanofillers, and thus the fracture strain of the nanocomposite was much smaller than that of Eco-flex. It was necessary to introduce a pattern to coordinate the large strain. The optical photograph of the ginkgo leaf and the schematic diagram of the leaf vein are shown in Fig. 1(a and b). The layout of these veins is similar to a symmetrical structure with the petiole as the axis. The ginkgo-like pattern in this study was evolved from this layout, as shown in Fig. 1(c). Seven lines and five nodes (A, B, C, D, and E) are included in this pattern. The line between the two nodes A and B is named LAB, and similarly, lines LBC, LCD, LAE, LBE, LCE, and LDE are obtained. The stretching direction was marked by two brown arrows. During electrical characterization, the two positive and two negative probes of the four-probe resistance measurement were connected to nodes B and C, respectively.During stretching, these lines prepared by the nanocomposites were subjected to axial and lateral strains, and the latter caused devastating damage to the pattern. In order to avoid this damage, for the first time, PSCL was introduced into the architecture of this device. The important role of PSCL was demonstrated by the results of ANSYS simulations. Fig. 1(d) and (f) show two device models with and without PSCL, respectively, where the brown block is the conductive layer and the stretching direction was perpendicular to the brown block. The strain distributions of the conductive layer in the two models for the tensile strain of 100% of the bottom layer are shown in Fig. 1(e) and (g). It is clear that the lateral strain of the conductive layer of the model with PSCL was much lower than that of the other model. The maximum strain of the conductive layer of the model without PSCL was almost 7 times higher than that of the other model.
A polyline pattern similar to “M” was introduced into a model with PSCL, as shown in Fig. 1(h). The strain distribution of the whole model for the strain of the bottom layer close to the fracture strain of Eco-flex is shown in Fig. 1(i). The conductive layer with low strain (blue) is in sharp contrast with the high-strain substrate (yellow). Although the maximum strain of the substrate was close to 900%, the strain in most areas of the conductive layer was less than 60%, and these lines were hardly affected by the lateral strain. Even better, there was almost no deformation at the shoulder position (marked by a red circle) of the pattern in the stretching direction. An enlarged view of this position is shown in Fig. 1(j). The equivalent strain at this shoulder position was only 0.2–2.7%, proved by the simulation data. Compared with the 900% strain of the substrate, the deformation of the shoulder was almost negligible. This result was because of the PSCL, which was very important for electrical testing. For electrical characterization, the cable of the instrument was a rigid metal wire, and the conductive layer of the device was a flexible elastomer. Due to the sharp difference in elastic modulus, a terrible error of the test data was caused by the mismatch of the connecting positions of the rigid metal and the flexible elastomer during the stretching process. Fortunately, this cruel problem was perfectly avoided here. Therefore, the PSCL plays a key role in the device. The novel patterned structure in this work provides an important supplement to the research on strain sensors. The maximum tensile strain that the sensor can sense is far greater than the tensile limit of advanced soft materials.
Rubber-based nanocomposites are intrinsically stretchable. Fig. 1(k) shows a schematic diagram of the spatial distribution of nanofillers. The MWCNTs (blue) are constructed in the matrix as the main conductive skeleton, and AgNPs (yellow) are dispersed in the areas near the skeleton to assist in electrical conduction. Since the conductivity of MWCNTs is lower than that of AgNPs, the obtained results indicated that both of these two kinds of nanofillers must exist in the nanocomposites. In the absence of silver, the conductivity of the nanocomposites will be too low and lower than the observed value. However, in the absence of MWCNTs and in the presence of only AgNPs, the nanocomposites will not be able to maintain their conductivity under tension, which is in disagreement with the experimental results. Thus, only the presence of both MWCNTs and AgNPs can explain the experimental results. The morphology of these two nanofillers in the nanocomposites is shown by the SEM images in Fig. 1(l–n). Because the nanofillers were deeply buried inside the matrix, it was difficult to clearly characterize them by SEM. Here, a micron-scale crack appeared in the nanocomposites by locally applying pressure, and therefore AgNPs and MWCNTs were exposed separately. The SEM images of AgNPs and MWCNTs are shown in Fig. S1(a and b) (ESI†). The elemental distribution of the nanocomposites was characterized by the EDS maps, as shown in Fig. S1(c)–(f).† The volume fraction of AgNPs was quite small and the AgNPs were distributed among the MWCNTs. Fig. S1(g)† shows the SEM image of a schismatic area with a width of 5 μm. The red and green boxes in this area are enlarged and shown in Fig. S1(h)–(j).† Both nanofillers were clearly photographed.
Carbon-based nanomaterials play an important role in nanocomposites. Considering the dispersibility and composition, carbon nanotubes were chosen as the main filler instead of graphene.
A lot of experiments were conducted to verify the most suitable composition of the nanocomposite. As shown in Fig. S2,† composition_1 corresponds to W(AgNPs) = 8.1% and W(CNT) = 9.0%, and composition_2 corresponds to W(AgNPs) = 6.6% and W(CNT) = 10.0%. Obviously, the increase in the content of silver nanoparticles can reduce the resistivity, and the increase in CNTs can improve the stretchability. In addition, the polymer matrix cannot contain an unlimited amount of nanofillers. Too high content of nanofillers leads to the deterioration of stretchability. These factors are contradictory, and it is necessary to optimize the composition, so as to obtain the required resistivity and stretchability.
According to percolation threshold theory, when the conductive filler of the nanocomposite reaches the percolation threshold, its conductivity has a leap of more than 5 orders of magnitude. When the dispersion of nanofillers in the polymer is very uniform, the relationship between the electrical conductivity and the composition and the properties of the filler conforms to a specific formula.26 However, the mechanical mismatch between agglomerated nanomaterials and polymer matrices lead to a poor dispersion state, making that specific formula no longer applicable. In this work, the actual percolation threshold was about W(CNT) = 8.0%, and the maximum content was about W(CNT) = 12%. Finally, we used two specific compositions mentioned in this article.
In conclusion, these novel patterns, structures and nanocomposites are the prerequisites for the preparation of the best strain sensors.
2.2 Fabrication
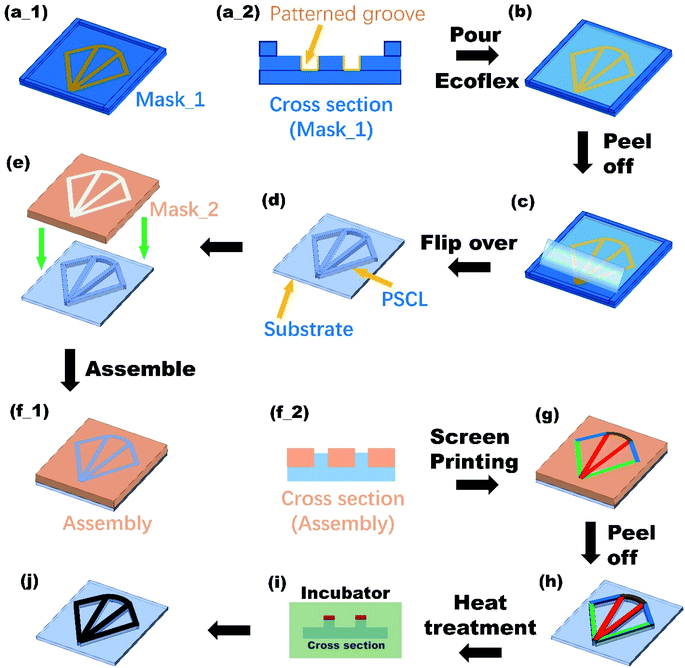
The fabrication process of the sensor is shown in Fig. 2.First, the specific size of the ginkgo-like pattern was designed, and the intaglio mold was manufactured. The schematic and cross-section of the mold are shown in Fig. 2(a_1) and (a_2). Second, liquid Eco-flex was poured into the mold, and the ginkgo-like patterned grooves were filled with Eco-flex, as shown in Fig. 2(b). Third, after the bubble removal and curing steps, the Eco-flex substrate was peeled from the mold and flipped over, as shown in Fig. 2(c) and (d). Fourth, mask 2 and the substrate were assembled, and patterned grooves appeared again, as shown in Fig. 2(e), (f1) and (f2). Then, using multiple screen printing processes, the conductive layer was connected to the PSCL. The compositions of the various lines of the conductive layer were different as shown in Fig. 2(g).
Then, the device was peeled off from mask 2, followed by heat treatment, as shown in Fig. 2(h)–(j). Finally, four probes were connected to nodes B and C. We note that other commonly used fractal patterns can also be applied in this preparation method. The optical images of the two samples are shown in Fig. S3.†
2.3 Highly stretchable sensors
The electrical properties during stretching are shown in Fig. 3. The pattern parameters and composition of ginkgo_1 are given in Table 1.| Composition of nanocomposites (weight fraction) | LBC | W(MWCNT) = 11.2% |
| W(AgNPs) = 6.8% | ||
| Others | W(MWCNT) = 9.3% | |
| W(AgNPs) = 6.9% | ||
| Included angle between two lines (°) | LAE and LDE | 48° |
| LBE and LCE | 16° | |
| LAB and LCD | 28° | |
| LAE and LAB | 142° |
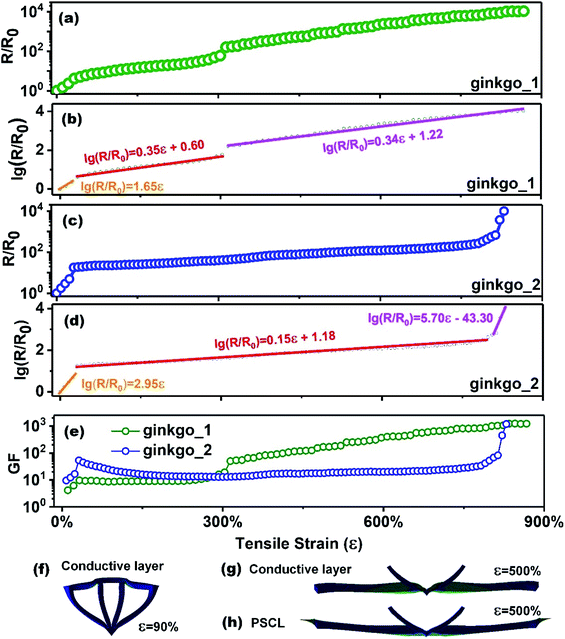
For the sensor with the ginkgo_1 pattern, as shown in Fig. 3(a), the maximum tensile strain was 867%, and the corresponding resistance growth rate (R/R0) was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 615. R0 is the resistance of the sensor at 0% strain. The resistance increased monotonically with increasing strain, and strain resolution was as low as 10.8%. The sensor was conductive until the Eco-flex substrate was fractured. Therefore, the strain sensor in this study was extremely stretchable, and highly sensitive and displayed high resolution.
615. R0 is the resistance of the sensor at 0% strain. The resistance increased monotonically with increasing strain, and strain resolution was as low as 10.8%. The sensor was conductive until the Eco-flex substrate was fractured. Therefore, the strain sensor in this study was extremely stretchable, and highly sensitive and displayed high resolution.
Linearity is one of the important parameters of strain sensors. In this study, due to the multiple induction mechanisms of the nanocomposite, the growth rate of resistance was more than 104. A series of resistance data is essentially different from an arithmetic sequence, and is not a linear increase in conventional mathematics. Here, the electrical data (R/R0) were mathematically converted to logarithm, log10(R/R0). For easy display, it was abbreviated as lg(R/R0). The performance of this sensor was converted into a logarithmic linear curve. This curve was divided into three linear segments, as shown in Fig. 3(b). In the first linear segment (orange), the strain is from 0 to 21.7%, and lg(R/R0) is from 0 to 0.37. By the least squares method, the linear fit of this segment was obtained. The linear regression equation is given as eqn (2.1),
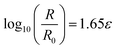 | (2.1) |
 | (2.2) |
In the second linear segment (red), the strain is from 21.7% to 303.5%, and lg(R/R0) is from 0.37 to 1.77. The second linear regression equation is given as eqn (2.3),
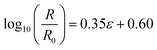 | (2.3) |
R 2 of eqn (2.3) is 0.9740.
In the third linear segment (pink), the strain is from 303.5% to 867.0%, and lg(R/R0) is from 1.77 to 4.03. The third linear regression equation is given as eqn (2.4),
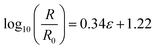 | (2.4) |
R 2 of eqn (2.4) is 0.9882.
Segmented logarithmic linearity is a potential concept for AI sensors. The regression coefficients of the above three equations are all very close to 1.0000, indicating the rigorous linear correlation between logarithmic resistance change rates and tensile strain. These calculation results have proved the excellent sensing performance of the sensor with the ginkgo_1 pattern.
However, the change of R/R0 for the sensor with the ginkgo_2 pattern was different from that of the sensor with the ginkgo_1 pattern, as shown in Fig. 3(c). The included angles between LAE and LDE, LBE and LCE, and LAB and LCD were 60°, 16°, and 108°, respectively and the resistance rose monotonically with increasing strain. The maximum tensile strain was 829%, and the strain resolution was as low as 7.9%. When the tensile strain changed from 32% to 782%, the R/R0 value only increased from 17.8 to 265.2, which was seriously inconsistent with the maximum R/R0 of this sensor of 9836.
The resistance change rates of this sensor has been logarithmic conversion and linear fitting, and the results are shown in Fig. 3(d). Similarly, this curve is divided into three linear segments. In the first linear segment (orange), the strain is from 0% to 23.7%, and lg(R/R0) is from 0 to 0.69. The first linear regression equation is given as eqn (2.5),
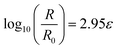 | (2.5) |
R 2 of eqn (2.5) is 0.9998.
In the second linear segment (red), the strain is from 23.7% to 805.6%, and lg(R/R0) is from 0.69 to 2.74. The second linear regression equation is given as eqn (2.6),
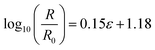 | (2.6) |
R 2 of eqn (2.6) is 0.9872.
In the third linear segment (pink), the strain is from 805.6% to 829.3%, and lg(R/R0) is from 2.74 to 3.99. The third linear regression equation is given as eqn (2.7),
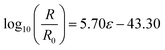 | (2.7) |
R 2 of eqn (2.7) is 0.9306.
Obviously, the segmented logarithmic linearity is also represented in the sensor with the ginkgo_2 pattern, because the regression coefficients are very close to 1.0000. However, the fly in the ointment is that compared with the first sensor, the slopes of the three linear regression equations are quite different. This phenomenon was attributed to the slight mismatch between the included angles of ginkgo_2.
The ginkgo-like pattern was deformed in the process of withstanding the strain, as shown in Fig. S4 (ESI†). The fracture occurred first in LBC, followed by LAB and LCD. When these two fractures occurred prematurely, the conductive path can only be the fold line composed of LBE and LCE. This will inevitably lead to a slow increase in the resistance, because most of the tensile deformation will be dissipated by the fold line. Therefore, the slope of the second segment is relatively low.
Sensitivity is another important parameter of strain sensors, which is generally represented by gauge factors (GF). GF can be calculated by using eqn (2.8),
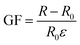 | (2.8) |
Eqn (2.8) can be written as eqn (2.9),
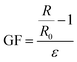 | (2.9) |
Since the resistance change rate has been logarithmically converted, eqn (2.9) is logarithmically converted into eqn (2.10),
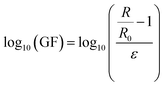 | (2.10) |
The lg(GF) is called the logarithmic sensitivity. According to the logarithm algorithm, eqn (2.10) can be written as eqn (2.11),
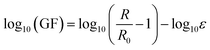 | (2.11) |
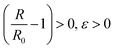 | (2.12) |
Since the resistance increases monotonously with strain, R > R0 and ε > 0 can be ensured, and inequality (2.12) can always be satisfied. The GF of the above two sensors are given in Fig. 3(e). For the sensor with the ginkgo_1 pattern, the GF changed from 4.1 to 1224.2, and for the other, the GF changed from 9.6 to 1186.0. The logarithmic sensitivity of the above two sensors is given in Fig. 3(e) and S5.† For the sensor with the ginkgo_1 pattern, the lg(GF) of the second segment basically remained at 0.95, the lg(GF) of the first segment increased from 0.61 to 0.98, and the lg(GF) of the thirdsegment increased from 1.70 to 3.09. For the sensor with the ginkgo_2 pattern, the lg(GF) of the second segment mainly remained at 1.12, the lg(GF) of the first segment increased from 0.98 to 1.73, and the lg(GF) of the third segment increased from 1.83 to 3.07. These sensitivities have unfortunately not remained stable.
The ANSYS simulation of gingko pattern deformation during stretching was studied. For the conductive layer at 90% strain, all the lines were conductive but the conductivity of LBC was already very poor, as shown in Fig. 3(f). At 500% strain, LAB, LBC, and LCD have not played a role in conductivity, and the deformation of the other lines of the conductive layer and PSCL is shown in Fig. 3(g) and (h). Comparing the deformation of the ends of these two layers, it can be seen that the large strain of the substrate was transferred to the PSCL and therefore the conductive layer was protected.
The design principle includes multiple conditions. First, the number of leaf veins (similar to LAE) needs to be determined. Different leaf veins play an important role in different strain ranges, and at the same time their deformations influence each other. Secondly, the length and included angle of different leaf veins directly affect the overall resistance change and stretchability of the device. The most suitable pattern parameters needs a lot of experiments to determine. In the end, the two patterns in this article were selected because they can keep the conductive layer with a monotonic resistance change until the substrate breaks.
Note that some leaf veins will break and restore connection during the process of stretching and recovery. The angle and the length of the line are not independent variables. They are interdependent and used to control the strain caused by the fracture of the vein. In addition, the included angle has a decisive influence on the stretching limit. Fig. S7† shows the simulation results of the 32° and 48° fold line at 500% and 270% strain. These patterns could not be stretched more. The above is the main mechanism of deformation.
The ANSYS simulation method of the structure in this work is shown in Fig. S8.† The software interface of the simulation result is shown in Fig. S8(a).† The mesh of the geometry is shown in Fig. S8(b),† where inflation layers were set near the interface between the conductive layer and the PSCL, and the specific nodes are shown in Fig. S8(c).† Fig. S8(d) shows the boundary conditions, including fix support (Fig. S8(e)), displacement (Fig. S8(f)), and frictionless support (Fig. S8(g)).† The three conditions were set on three faces of the substrate. Fix support and displacement were set on two parallel faces, perpendicular to the stretching direction.
2.4 Performance of folding line patterns
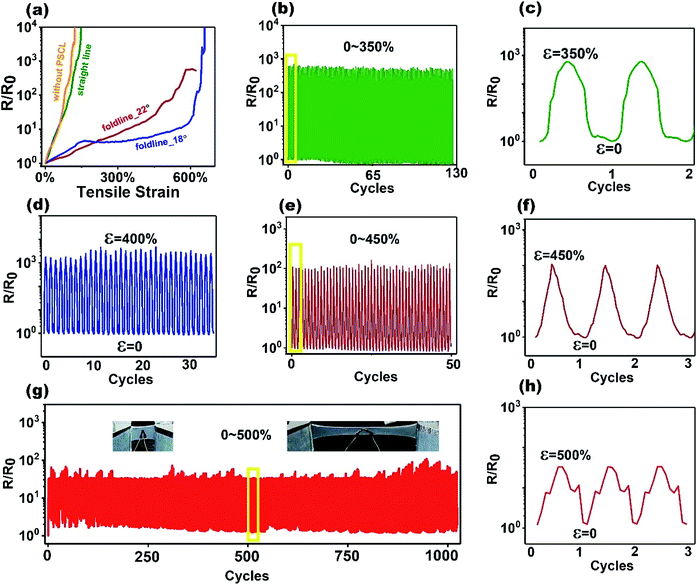
Ginkgo-like patterns are composed of basic geometric figures such as straight lines, arcs and fold lines. When the straight line was stretched axially, PSCL provided optimization for mechanical properties, as shown in Fig. 4(a). The maximum strain of the devices with straight lines was increased by 25%, and non-monotonic behavior was avoided due to PSCL. On the other hand, the change in the resistance was affected by the included angle of the fold lines, as shown in Fig. 3(a). A smaller included angle corresponded to a smaller change in the resistance within the low strain range, and even non-monotonic behavior. However, the maximum strain that could maintain conductivity decreased with increasing angle. For the fold line with an included angle of 18°, the maximum strain is only 662%, which is attributed to the too large thickness and width of the substrate. For the included angles of 32° and 48°, the ANSYS simulation results of these architectures are shown in Fig. S9.† It is clear that the strain of the conductive layer was greater than 300%, already exceeding the maximum strain at which the nanocomposite can maintain conductivity. For ginkgo-like patterns, the deformability of the fold lines is affected by other lines, as shown in Fig. S10.† Therefore, the fracture of LBC and LCD was inevitable.The cyclic stretchability of this architecture was studied. For the fold line with an included angle of 36°, the R/R0 values during the stretching cycles are shown in Fig. 4(b) and (c). It is observed that the device showed stable electrical and mechanical comprehensive performance. For the 0–350% stretching–releasing cycles, the R/R0 was approximately 595. However, for the 0–400% cycles, the R/R0 increased to more than 2000, as shown in Fig. 4(d). This proved that the resistance sensitivity of the fold line depends strongly on the strain. In the large strain range, the R/R0 changed strongly, while in the small strain range, the R/R0 increased only slightly. For another fold line with an included angle of 32°, the R/R0 was only ∼108 in the 0–450% cycles, as shown in Fig. 4(e) and (f). This proved that the strain range increased with decreasing angle for the changes in the R/R0 that determine the sensitivity.
Thousands of stretching cycles have been tested, as shown in Fig. 4(g). The angle of the fold line is 16°. For 0–500% strain cycles, the resistance change was stable. The insets are photos of samples at 0 and 500% strains, respectively. Fig. 4(h) shows the cyclic curve in the yellow rectangle in Fig. 4(g). In each cycle, the resistance change under low strain is not monotonous, due to the satisfactory coordinated deformation ability of the fold line under low strain. Therefore, for the 0–400 strain cycle, the resistance change is very unstable, as shown in Fig. S11.† Severe drift and errors are exhibited here. This once again proves that the fold line can only show a monotonous resistance change in a specific strain range.
The zero point drift has been calculated, taking the stretching cycle curves in Fig. 4 as the object. The calculation method is as follows. The initial resistance of the device is marked R0, and the resistance at 0% strain in each cycle is marked R0(n), while n is the number of each cycle. Select R0(n) with the largest deviation from R0 and mark it as R0(min). The zero drift is calculated from
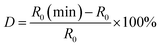 | (2.13) |
In Fig. 4(b), the zero drift of the first dozens of cycles is only 2.8%, but the decrease of the zero resistance value afterwards leads to a final zero drift of −32.2%.
In addition, the drift and error were checked through the overlap of the curves of different stretching cycles, as shown in Fig. S6.† Obviously, the coincidence degree and error of the first dozens of cycles in Fig. S6(a)† (associated with Fig. 4(c)) are quite satisfactory. However, a slight error and hysteresis was seen in Fig. S6(b)† (associated with Fig. 4(f)) due to too large strain.
2.5 Microcracks in nanocomposites
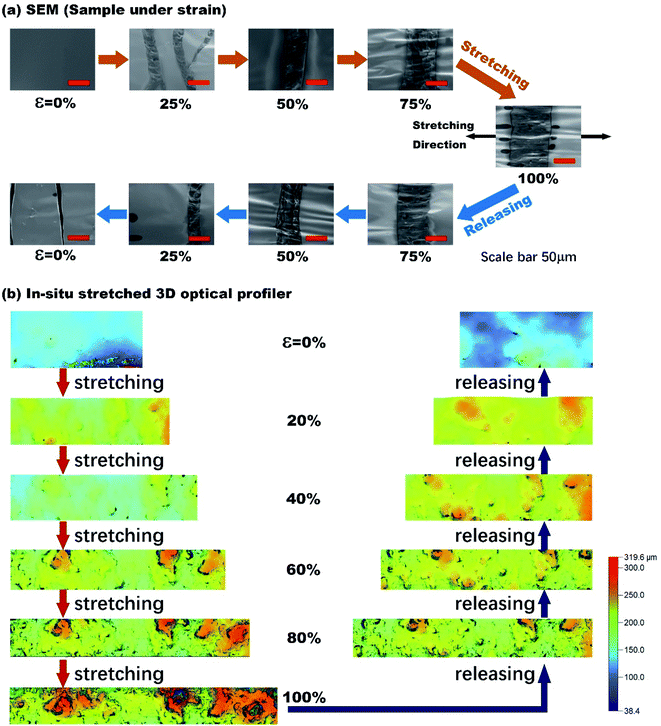
Cracks are shown in Fig. 5.The change in the sensor resistance was attributed to the microcracks of the nanocomposites under tensile strain. The size and number of microcracks grew with increasing tensile strain during the stretching process, resulting in fewer current percolation paths. By contrast, the microcracks were gradually self-healed during the release process, eventually reducing the resistance of the sensor to the initial value. The evolution of the microcrack width was confirmed by the SEM images of the nanocomposites under tensile strain, as shown in Fig. 5(a). When the strain increased from 0% to 100%, the width of the longitudinal microcracks grew to approximately 100 μm. Upon recovery, the microcracks gradually self-healed, leaving only surface traces. Furthermore, the depth propagation of the microcracks was characterized by three-dimensional surface topography of the nanocomposites, as shown in Fig. 5(b). The nanocomposites were stretched in situ under the confocal eyepiece of an optical 3D profiler. For a strain of 40%, the depth of the micro-cracks was already greater than 100 μm, as shown in the dark blue areas. The depth, width, length, and amounts of microcracks continued to increase in the subsequent stretching. During release, the microcracks gradually disappeared until the depth decreased to 0. Therefore, the evolution of the microcracks contributed strongly to the high sensitivity of the resistive strain sensor, and the self-healing ability ensured the stable recyclability of the sensor.
According to the simulation results of Fig. 1(i) and 3(g), when the strain of the substrate exceeds 500%, the strain of the conductive nanocomposite (LBE and LCE) is still far below 100%. According to the crack image in Fig. 5, when the strain of the nanocomposite is less than 20%, no obvious cracks appear. At this time, the increase in resistance is attributed to the decrease in the number of percolation networks composed of CNTs and AgNPs. The influence of tensile deformation on the percolation network has been verified.11 On the other hand, when the strain of the nanocomposite material is greater than 20%, obvious cracks appear and expand, and the successive breaks of LBC and other lines lead to an increase and abrupt change in resistance.
The ginkgo-like pattern broke twice during the stretching process, resulting in two abrupt changes of resistance, and so the resistance–strain curve was divided into three linear segments. It needs to be emphasized that all abrupt changes were not expected. For the logarithmic resistance-strain curve, the slopes of the three segments are expected to be the same. In addition, the curve of pattern 1 is not the average of multiple experimental data, but the performance of the sample itself.
A summary of the maximum detected strain, maximum R/R0, and strain resolution of seven previously reported high-performance strain sensors is given in Table 3 and Fig. S12† for comparison with the characteristics of the sensor obtained in this work. It is observed that the strain sensor of this work exhibited superior performance to the other sensors.
2.6 Application
A potential application of the sensors with large stretching limits was proposed in this study. After carefully observing the dynamics of the wings, the related tensile strain changes were simulated by a programmable stretching test machine, and the results are shown in Fig. 6.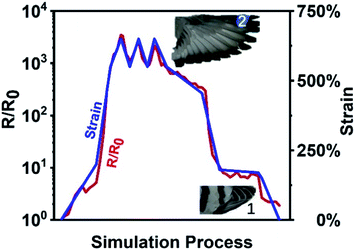 | ||
| Fig. 6 Simulation of monitoring the state of pigeon wings. (inset_1) The primary feathers of the wing in the completely folded state and (inset_2) the completely unfolded state. | ||
The wings of a bird-like bionic aircraft exhibit three states – folded, unfolded, and flapping. The wingspan of such an aircraft experiences a tensile strain of more than 600% during the change from the folding state to the unfolding state. The monitoring of these states plays an important role in the development of bionic aircraft. Here the wings of pigeons were selected as the research object. In Fig. 6, the primary feathers of the wing in the completely folded state are shown in the inset photo_1. The completely unfolded state is shown in the inset photo_2. If a strain sensor was installed on these primary feathers, the status of the wing could be monitored. The strain state is represented by the blue curve, and the resistance change of the sensor is shown by the red curve. In this dynamic simulation, the changes in the resistance detected by the sensor were almost identical to the changes in the strain. This shows that the proposed sensor is suitable for meeting the huge demand for emerging artificial intelligence equipment in the field of large strain detection.
3 Conclusions
In this study, a high-resolution sensor capable of detecting tensile strains of up to 867% was developed. The novel ginkgo-like pattern can withstand most of the tensile deformation, and PSCL provided protection for this pattern. The linear regression equation and sensitivity of the sensor were analyzed through mathematical logarithmic operations. The multi-component structure of the nanocomposites exhibited excellent electrical conductivity and cyclic stretchability, and the changes in the number and thickness of the microcracks caused the resistance change rate to be greater than 104. Both the ANSYS simulations and experimental results demonstrated the potential of ginkgo-like architectures. In the future, this approach can be used to further increase the maximum detected strain by matching the elastomer with a larger tensile limit, so as to no longer be limited by the tensile limit of Eco-flex. This super strain sensor is likely to be widely used in wing-shaped aircraft and other artificial intelligence devices.4 Experimental
4.1 Materials
Eco-flex 0030 (Smooth-on), multi-wall carbon nanotubes (MWCNTs, Aladdin, China), Ag nanoparticles (AgNPs, Aladdin, China), PVC slices, and silver wires (diameter 30 μm).4.2 Fabrication of the nanocomposites
The conductive nanocomposites were composed of Eco-flex 0030, MWCNTs and AgNPs. The parts A and B of Eco-flex were mixed uniformly in a mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to serve as the matrix. Then, the Ag nanoparticles (AgNPs) were added to the liquid matrix and stirred under ultrasonication for 2 min. Next, MWCNTs were immediately mixed into the mixture, and stirred again for 3 min. Care was taken to avoid contact of MWCNTs with water and oxygen in the air. The above three steps were completed within 10 min. The obtained nanocomposites were stored overnight in a refrigerator at −2 °C.
1 to serve as the matrix. Then, the Ag nanoparticles (AgNPs) were added to the liquid matrix and stirred under ultrasonication for 2 min. Next, MWCNTs were immediately mixed into the mixture, and stirred again for 3 min. Care was taken to avoid contact of MWCNTs with water and oxygen in the air. The above three steps were completed within 10 min. The obtained nanocomposites were stored overnight in a refrigerator at −2 °C.
4.3 Fabrication of the Eco-flex substrates
The architecture in this study was fabricated by connecting the substrate and a conductive layer. The Eco-flex substrate was composed of a bottom layer and a patterned strain coordinating layer. First, the PVC slice was pattern-engraved by a laser, and thus mask 1 was fabricated. The pattern was similar to the veins of ginkgo leaves. Then, mask 1 was welded to another PVC sheet, and a template similar to the intaglio mold was obtained. After fixing the enclosure around the PVC sheet, liquid Eco-flex was poured into the template. The whole template was placed in a vacuum chamber for 10 min to completely remove air bubbles, and then cured in a dry box for 24 h. Then, the whole template was immersed in water for 2 h so that the substrate was completely peeled from the template. Finally, the substrate was flipped over, and the patterned strain coordination layer was fabricated face up.4.4 Fabrication of the strain sensor
The pattern size of mask 2 was the same as that of mask 1, but its thickness was equal to the sum of the thicknesses of the strain-coordinating layer and the conductive layer. First, mask 2 and the patterned layer of the substrate were assembled together, and the patterned grooves appeared again. At this step, the whole template was similar to a new intaglio mold. Then, the conductive nanocomposites were printed into the grooves. We note that the different lines of the pattern must be printed in stages due to their different compositions. Third, the whole template was heat-treated in an incubator for 24 h at 30 °C. Finally, the sensor was peeled from mask 2, followed by the installation of two silver wire cables at points B and C.4.5 Characterization
The accuracy of the analytical balance was 0.0001 g and the power of the ultrasonic disperser was 100 W. The pattern on the mask was engraved by using a controllable laser. Scanning electron microscopy (SEM) images and electron dispersive spectroscopy (EDS) maps were obtained using a Hitachi field emission scanning electron microscope (Hitachi S4700, Japan). A programmable automated lead screw and fixture were assembled to facilitate the application of tensile strain to the sample. A resistivity test system (ET96, East Changing Inc) and the lead screw were combined to test and record the real-time resistance of the sample simultaneously. Moreover, the size and included angle of the sample pattern were measured using a high-resolution optical microscope (MSHOT MS60). The surface topography was scanned using an optical 3D profiler (Rtec/UP-Lambda) in the confocal mode.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Foundation of China No. 52073075 and Shenzhen Science and Technology Program (Grant No. KQTD20170809110344233). Pengdong Feng contributed to the design and implementation of all the experiments and the writing of the paper. Yi Zheng and Kang Li assisted in the implementation of the experiments. Weiwei Zhao was the manager of this project.References
- J. A. Rogers, T. Someya and Y. Huang, Materials and Mechanics for Stretchable Electronics, Science, 2010, 327(5973), 1603–1607 CrossRef CAS PubMed.
- T. Someya, Z. Bao and G. G. Malliaras, The rise of plastic bioelectronics, Nature, 2016, 540(7633), 379–385 CrossRef CAS PubMed.
- S. Wang, J. Xu, W. Wang, G.-J. N. Wang, R. Rastak and F. Molina-Lopez, et al., Skin electronics from scalable fabrication of an intrinsically stretchable transistor array, Nature, 2018, 555(7694), 83–88 CrossRef CAS.
- M. Kaltenbrunner, T. Sekitani, J. Reeder, T. Yokota, K. Kuribara and T. Takeyoshi, et al., An ultra-lightweight design for imperceptible plastic electronics, Nature, 2013, 499(7459), 458–463 CrossRef CAS.
- H. Bai, S. Li, J. Barreiros, Y. Tu, C. R. Pollock and R. F. Shepherd, Stretchable distributed fiber-optic sensors, Science, 2020, 370(6518), 848–852 CrossRef CAS PubMed.
- R. L. Truby and J. A. Lewis, Printing soft matter in three dimensions, Nature, 2016, 540(7633), 371 CrossRef CAS PubMed.
- H. Yuk, C. E. Varela, C. S. Nabzdyk, X. Mao, R. F. Padera and E. T. Roche, et al., Dry double-sided tape for adhesion of wet tissues and devices, Nature, 2019, 575(7781), 169–174 CrossRef CAS.
- Y. Xu, Z. Yang, R. Jing, Z. Ye and H. Peng, An All-Solid-State Fiber-Shaped Aluminum-Air Battery with Flexibility, Stretchability, and High Electrochemical Performance, Angew. Chem., Int. Ed. Engl., 2016, 55(28), 7979–7982 CrossRef CAS PubMed.
- T. Yamada, Y. Hayamizu, Y. Yamamoto, Y. Yomogida, A. Izadi-Najafabadi and D. N. Futaba, et al., A stretchable carbon nanotube strain sensor for human-motion detection, Nat. Nanotechnol., 2011, 6(5), 296–301 CrossRef CAS PubMed.
- C. Wang, X. Li, E. Gao, M. Jian, K. Xia and Q. Wang, et al., Carbonized Silk Fabric for Ultrastretchable, Highly Sensitive, and Wearable Strain Sensors, Adv. Mater., 2016, 28(31), 6640–6648 CrossRef CAS PubMed.
- P. Feng, Y. Yuan, M. Zhong, J. Shao, X. Liu and J. Xu, et al., Integrated Resistive-Capacitive Strain Sensors Based on Polymer-Nanoparticle Composites, ACS Appl. Nano Mater., 2020, 3(5), 4357–4366 CrossRef CAS.
- P. Feng, H. Ji, L. Zhang, X. Luo, X. Leng and P. He, et al., Highly stretchable patternable conductive circuits and wearable strain sensors based on polydimethylsiloxane and silver nanoparticles, Nanotechnology, 2019, 30(18), 185501 CrossRef CAS PubMed.
- P. Feng, M. Zhong and W. Zhao, Stretchable multifunctional dielectric nanocomposites based on polydimethylsiloxane mixed with metal nanoparticles, Mater. Res. Express, 2020, 7(1), 015007 CrossRef CAS.
- P. Feng, X. Wang, B. Lu, G. Pan, X. Leng and X. Ma, et al., Ionic liquids-filled patterned cavities improve transmittance of transparent and stretchable electronic polydimethylsiloxane films, J. Mater. Sci., 2019, 54(16), 11134–11144 CrossRef CAS.
- P. Feng, Z. Ye, Q. Wang, Z. Chen, G. Wang and X. Liu, et al., Stretchable and conductive composites film with efficient electromagnetic interference shielding and absorptivity, J. Mater. Sci., 2020, 55(20), 8576–8590 CrossRef CAS.
- L. Zhang, P. Feng, S. Xie, Y. Wang, Z. Ye and Z. Fu, et al., Low-temperature sintering of silver nanoparticles on paper by surface modification, Nanotechnology, 2019, 30(50), 505303 CrossRef CAS.
- A. Qiu, P. Li, Z. Yang, Y. Yao, I. Lee and J. Ma, A Path Beyond Metal and Silicon:Polymer/Nanomaterial Composites for Stretchable Strain Sensors, Adv. Funct. Mater., 2019, 29(17), 1806306 CrossRef.
- X. Li, R. Zhang, W. Yu, K. Wang, J. Wei and D. Wu, et al., Stretchable and highly sensitive graphene-on-polymer strain sensors, Sci. Rep., 2012, 2, 870 CrossRef PubMed.
- O. A. Araromi, M. A. Graule, K. L. Dorsey, S. Castellanos, J. R. Foster and W.-H. Hsu, et al., Ultra-sensitive and resilient compliant strain gauges for soft machines, Nature, 2020, 587(7833), 219–224 CrossRef CAS PubMed.
- S. Veerapandian, W. Jang, J. B. Seol, H. Wang, M. Kong and K. Thiyagarajan, et al., Hydrogen-doped viscoplastic liquid metal microparticles for stretchable printed metal lines, Nat. Mater., 2021, 20, 533–540 CrossRef CAS PubMed.
- S. Liu, D. S. Shah and R. Kramer-Bottiglio, Highly stretchable multilayer electronic circuits using biphasic gallium-indium, Nat. Mater., 2021, 20, 851–858 CrossRef CAS PubMed.
- Z. Ma, Q. Huang, Q. Xu, Q. Zhuang, X. Zhao and Y. Yang, et al., Permeable superelastic liquid-metal fibre mat enables biocompatible and monolithic stretchable electronics, Nat. Mater., 2021, 20, 859–868 CrossRef CAS PubMed.
- J. Lee, M. W. M. Tan, K. Parida, G. Thangavel, S. A. Park and T. Park, et al., Water-Processable, Stretchable, Self-Healable, Thermally Stable, and Transparent Ionic Conductors for Actuators and Sensors, Adv. Mater., 2020, 32(7), 1906679 CrossRef CAS PubMed.
- E. Roh, B.-U. Hwang, D. Kim, B.-Y. Kim and N.-E. Lee, Stretchable, Transparent, Ultrasensitive, and Patchable Strain Sensor for Human-Machine Interfaces Comprising a Nanohybrid of Carbon Nanotubes and Conductive Elastomers, ACS Nano, 2015, 9(6), 6252–6261 CrossRef CAS PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim and K. S. Kim, et al., Large-scale pattern growth of graphene films for stretchable transparent electrodes, Nature, 2009, 457(7230), 706–710 CrossRef CAS PubMed.
- Y. Kim, J. Zhu, B. Yeom, M. Prima, X. Su and J. G. Kim, et al., Stretchable nanoparticle conductors with self-organized conductive pathways, Nature, 2013, 500(7460), 59–63 CrossRef CAS PubMed.
- D. J. Lipomi, M. Vosgueritchian, C. K. Tee, S. L. Hellstrom, J. A. Lee and C. H. Fox, et al., Skin-like pressure and strain sensors based on transparent elastic films of carbon nanotubes, Nat. Nanotechnol., 2011, 6(12), 788–792 CrossRef CAS.
- N. Matsuhisa, D. Inoue, P. Zalar, H. Jin, Y. Matsuba and A. Itoh, et al., Printable elastic conductors by in situ formation of silver nanoparticles from silver flakes, Nat. Mater., 2017, 16(8), 834 CrossRef CAS PubMed.
- M. D. Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Carbon Nanotubes: Present and Future Commercial Applications, Science, 2013, 339(6119), 535–539 CrossRef PubMed.
- H. Wang, Y. Yao, Z. He, W. Rao, L. Hu and S. Chen, et al., A Highly Stretchable Liquid Metal Polymer as Reversible Transitional Insulator and Conductor, Adv. Mater., 2019, 31(23), 1901337 CrossRef.
- T. Yamada, Y. Hayamizu, Y. Yamamoto, Y. Yomogida, A. Izadi-Najafabadi and D. N. Futaba, et al., A stretchable carbon nanotube strain sensor for human-motion detection, Nat. Nanotechnol., 2011, 6(5), 296–301 CrossRef CAS PubMed.
- W. Yue, C. Zhu, R. Pfattner, H. Yan and Z. A. Bao, Highly Stretchable, Transparent, and Conductive Polymer, Sci. Adv., 2017, 3(3), e1602076 CrossRef PubMed.
- T. C. Shyu, P. F. Damasceno, P. M. Dodd, A. Lamoureux, L. Xu and M. Shlian, et al., A kirigami approach to engineering elasticity in nanocomposites through patterned defects, Nat. Mater., 2015, 14(8), 785–789 CrossRef CAS PubMed.
- A. Miyamoto, S. Lee, N. F. Cooray, S. Lee, M. Mori and N. Matsuhisa, et al., Inflammation-free, gas-permeable, lightweight, stretchable on-skin electronics with nanomeshes, Nat. Nanotechnol., 2017, 12(9), 907–913 CrossRef CAS.
- M. Park, J. Im, M. Shin, Y. Min, J. Park and H. Cho, et al., Highly stretchable electric circuits from a composite material of silver nanoparticles and elastomeric fibres, Nat. Nanotechnol., 2012, 7(12), 803–809 CrossRef CAS.
- C. Coulais, A. Sabbadini, F. Vink and M. van Hecke, Multi-step self-guided pathways for shape-changing metamaterials, Nature, 2018, 561(7724), 512–515 CrossRef CAS PubMed.
- J. A. Fan, W. H. Yeo, Y. Su, Y. Hattori, W. Lee and S. Y. Jung, et al., Fractal design concepts for stretchable electronics, Nat. Commun., 2014, 5, 3266 CrossRef.
- C. K. Dong, H. J. Shim, W. Lee, J. H. Koo and D. Kim, Material-Based Approaches for the Fabrication of Stretchable Electronics, Adv. Mater., 2020, 32(15), 1902743 CrossRef.
- K. Sim, Z. Rao, F. Ershad and C. Yu, Rubbery Electronics Fully Made of Stretchable Elastomeric Electronic Materials, Adv. Mater., 2020, 32(15), 1902417 CrossRef CAS.
- K. S. Min, J. Oh, M. Lima, M. E. Kozlov, S. J. Kim and R. H. Baughman, Elastomeric Conductive Composites Based on Carbon Nanotube Forests, Adv. Mater., 2010, 22(24), 2663–2667 CrossRef PubMed.
- S. Ryu, P. Lee, J. B. Chou, R. Xu and S. G. Kim, Extremely Elastic Wearable Carbon Nanotube Fiber Strain Sensor for Monitoring of Human Motion, ACS Nano, 2015, 9(6), 5929 CrossRef CAS PubMed.
- P. Song, H. Qin, H. L. Gao, H. P. Cong and S. H. Yu, Self-healing and superstretchable conductors from hierarchical nanowire assemblies, Nat. Commun., 2018, 9(1), 2786 CrossRef PubMed.
- S. H. Kim, S. Jung, I. S. Yoon, C. Lee, Y. Oh and J.-M. Hong, Ultrastretchable Conductor Fabricated on Skin-Like Hydrogel-Elastomer Hybrid Substrates for Skin Electronics, Adv. Mater., 2018, 30(26), 1800109 CrossRef PubMed.
- J. Wang, G. Cai, S. Li, D. Gao, J. Xiong and P. S. Lee, Printable Superelastic Conductors with Extreme Stretchability and Robust Cycling Endurance Enabled by Liquid-Metal Particles, Adv. Mater., 2018, 30(16), 1706157 CrossRef PubMed.
- Y. A. Samad, et al., Novel Graphene Foam Composite with Adjustable Sensitivity for Sensor Applications, ACS Appl. Mater. Interfaces, 2015, 7, 9195–9202 CrossRef CAS PubMed.
- C. S. Boland, et al., Sensitive electromechanical sensors using viscoelastic graphene-polymer nanocomposites, Science, 2016, 354, 1257–1260 CrossRef CAS PubMed.
- Z. Chen, et al., Three-dimensional flexible and conductive interconnected graphene networks grown by chemical vapour deposition, Nat. Mater., 2011, 10(6), 424 CrossRef CAS.
- D. Kang, et al., Ultrasensitive mechanical crack-based sensor inspired by the spider sensory system, Nature, 2014, 516(7530), 222 CrossRef CAS PubMed.
- Y. A. Samad, et al., Graphene Foam Developed with a Novel Two-Step Technique for Low and High Strains and Pressure-Sensing Applications, Small, 2015, 11(20), 2380 CrossRef.
- Z. Wang, et al., High conductive graphene assembled films with porous micro-structure for freestanding and ultra-low power strain sensors, Sci. Bull., 2020, 65, 1363–1370 CrossRef CAS.
- M. Amjadi, et al., Ultra-stretchable and skin-mountable strain sensors using carbon nanotubes–Ecoflex nanocomposites, Nanotechnology, 2015, 26, 375501 CrossRef PubMed.
- J. Z. Gul, et al., Fully 3D Printed Multi-Material Soft Bio-Inspired Whisker Sensor for Underwater-Induced Vortex Detection, Soft Robotics, 2018, 5, 122–132 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00817j |
| This journal is © The Royal Society of Chemistry 2022 |