Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unveiling two-dimensional magnesium hydride as a hydrogen storage material via a generative adversarial network†
Junho
Lee
ab,
Dongchul
Sung
c,
You Kyoung
Chung
a,
Seon Bin
Song
a and
Joonsuk
Huh
 *abd
*abd
aDepartment of Chemistry, Sungkyunkwan University, Suwon 16419, Korea
bSKKU Advanced Institute of Nanotechnology (SAINT), Sungkyunkwan University, Suwon 16419, Korea
cDepartment of Physics, Graphene Research Institute, GRI-TPC International Research Center, Sejong University, Seoul 05006, Korea
dInstitute of Quantum Biophysics, Sungkyunkwan University, Suwon 16419, Korea. E-mail: joonsukhuh@gmail.com
First published on 8th April 2022
Abstract
This study used an artificial intelligence (AI)-based crystal inverse-design approach to investigate the new phase of two-dimensional (2D) pristine magnesium hydride (MgxHy) sheets and verify their availability as a hydrogen storage medium. A 2D binary phase diagram for the generated crystal images was constructed, which was used to identify significant 2D crystal structures. Then, the electronic and dynamic properties of the MgxHy sheets in low-energy periodic phases were identified via density functional theory (DFT) calculations; this revealed a previously unknown phase of 2D MgH2 with a P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 space group. In the proposed structure, the adsorption behaviors of the Li-decorated system were investigated for multiple hydrogen molecules. It was confirmed that Li-decorated MgH2 has an expected theoretical gravimetric density of 6 wt%, with an average H2 adsorption energy of −0.105 eV. Therefore, it is anticipated that P
m2 space group. In the proposed structure, the adsorption behaviors of the Li-decorated system were investigated for multiple hydrogen molecules. It was confirmed that Li-decorated MgH2 has an expected theoretical gravimetric density of 6 wt%, with an average H2 adsorption energy of −0.105 eV. Therefore, it is anticipated that P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 MgH2 sheets can be employed effectively as a medium for hydrogen storage. Additionally, this finding indicates that a deep learning-based approach is beneficial for exploring unrevealed 2D materials.
m2 MgH2 sheets can be employed effectively as a medium for hydrogen storage. Additionally, this finding indicates that a deep learning-based approach is beneficial for exploring unrevealed 2D materials.
1 Introduction
Hydrogen energy is a promising clean energy source that can be utilized as a primary energy carrier with extensive applications.1,2 However, designing a crystalline material for hydrogen storage with the required high gravimetric densities for operation under ambient thermodynamic conditions remains a challenge. Consequently, numerous chemical hydrogen host materials with high hydrogen capacities have been suggested for such applications, including metal hydrides (MHs),3,4 chemical hydrides,5 and complex hydrides.6,7 Due to their specific properties of high thermal stability, low cost, reaction reversibility, and significant gravimetric hydrogen storage capacity, MHs have long been regarded as a promising material for hydrogen storage. However, they are limited by high desorption temperatures, low plateau pressure under ambient conditions, and relatively slow absorption/desorption kinetics; therefore, much research, including simulations, has been focused on enhancing the properties of MHs to enable their use in hydrogen storage applications.8Another promising approach is the use of lightweight physical adsorbents with high surface areas, reversible H2 charging (and discharging), and facile kinetics, such as carbon-based nanostructures (e.g. nanotubes9,10), metal–organic frameworks,11,12 and covalent organic frameworks.13,14 Unlike chemical storage, generally, these physical adsorbents are limited by weak van der Waals interactions between adsorbed hydrogen molecules and substrates, which significantly reduces the H2 storage capacity of these substances due to the desorption of H2 at very low temperatures. Consequently, metal ions,15,16 including alkali metals, alkali earth metals, and transition metals, have been extensively used as dopants to produce ideal H2 binding strengths (∼−15 kJ mol−1) and increase H2 storage capacities.17 In this regard, much research has been conducted on the use of two-dimensional (2D) materials with a lightweight alkali metal or alkali earth metals for storing hydrogen. For example, many potential hydrogen storage systems have been proposed using Li-, Na-, or Ca-decorated graphene,18–22 boron–nitride layers,23–25 and carbon–nitride compounds.26
Recently, much research has been conducted on the structure of 2D groups of MHs, and over 100 stable MH monolayers have been reported. These 2D MHs were explored using substitution-based systematic structural investigations. They generate known layered lattice structures by combining hydrogen with all the metals in the periodic table and offer a rich array of electronic properties for use in materials ranging from metals to wide-gap semiconductors.27 However, despite their high gravimetric hydrogen capacity in the bulk state and their large surface area for the attachment of additional hydrogen molecules, the use of MH sheets as a hydrogen storage material has not been proposed. To date, the identification of novel 2D MHs has been via substitution-based methods, although depending on the combination of crystal structural motifs and atomic elements, these approaches could omit a structure from the search area.
Considerable efforts have been made to use artificial intelligence (AI) technology to predict new material structures. Compared with existing well-known structure-prediction techniques, such as evolutionary algorithms or substitution-based methods, deep learning-based approaches allow the computational cost to be reduced by exploring scoped target chemical spaces, which are represented as a continuous latent vector. In chemistry, two of the most popular generative models are the variational autoencoder and the generative adversarial network (GAN); these are used with various chemical representations, such as graph-based encoding for crystal structures, three-dimensional (3D) grid images, and point cloud images. Recently, Xie et al. developed a CDVAE model to design the periodic structure of stable materials.28 Long et al. developed a GAN-based inverse design framework for crystal structure prediction in the binary Bi–Se system.29 Fung et al. proposed an inverse design framework MatDesINNe and applied it to MoS2 for band gap engineering.30 A compositional conditional GAN (CCCGAN) model for designing Mg–Mn–O ternary materials was devised that successfully predicted 23 new crystal structures.31 We utilized this model in our study, noting that it can generate the structural motifs of materials using point-cloud-based structural image representation without any elemental consideration.This study used a deep learning-based generative model and a systematic theoretical study using the density functional theory (DFT) to propose a new crystal structure for a 2D MgxHy sheet. In terms of hydrogen storage, 2D MgH2 with a P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 space group was identified as a promising medium, and pristine and Li-doped 2D MgH2 were investigated as potential materials for storing hydrogen. Additionally, the adsorption energy and configuration of gas molecules were analyzed, and the adsorption conditions of multiple hydrogen molecules on Li-decorated MgH2 were investigated.
m2 space group was identified as a promising medium, and pristine and Li-doped 2D MgH2 were investigated as potential materials for storing hydrogen. Additionally, the adsorption energy and configuration of gas molecules were analyzed, and the adsorption conditions of multiple hydrogen molecules on Li-decorated MgH2 were investigated.
2 Computational methodology
2.1 DFT calculations
The calculations in this study were conducted using the DFT method with spin polarization, as implemented in the Vienna Ab initio Simulation Package (VASP).32–34 Projector-augmented wave (PAW)35 potentials (as parameterized by using the Perdew–Burke–Ernzerhof (PBE)36 functional within the generalized gradient approximation) were used together with dispersion corrections obtained from Grimme's DFT-D3 method37 to capture the inherent long-range atomic and molecular interactions between MH and Li, and hydrogen molecules with the Li-MH system. All calculations used a cut-off energy of 520 eV, and the system was relaxed until the forces on each atom were below 0.01 eV Å−1. Supercells of 2 × 2 or 3 × 3 were used with a Γ-centered 12 × 12 × 1 or 8 × 8 × 1 k-point mesh. To prevent artificial interactions, the periodic supercell was separated in the z-direction by a vacuum space of over 20 Å, whereas the thermal stability of the metal hydride was verified using Ab Initio molecular dynamics (AIMD) simulations. The molecular dynamics simulations of the MgH2 sheet were conducted at room temperature (300 K), and this aspect was explored using a 5 × 5 supercell. The time step was set to 3 fs, and the simulation went up to 6 ps. The ionic temperature was controlled via a Nosé–Hoover thermostat.2.2 Generative model
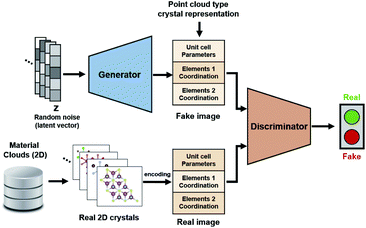
For the application of deep learning techniques for exploring materials, this study used a GAN model as the learning model for its 2D crystal structure system. A GAN comprises two network groups—a generator and discriminator—which learn in a hostile manner. The goal of the generator group is to learn the distribution of training data and create a real fake image, which it does by using the Gaussian noise vector as an input to produce a fake image. The purpose of the other GAN network—the discriminator—is to learn better discrimination between the real and the fake, and it is trained to provide improved feedback to the generator. The fake outputs produced by the generator become closer to the actual image by reducing the Wasserstein distance between the distributions of fake generation and real training data. To ensure learning stability, deconvolution layers were applied to both the generator and discriminator. The GAN model for applying point cloud input to the crystal structure was obtained from Kim et al.,31 and the compositional conditional part of the model was removed and utilized for successive training progression. The deep learning model was constructed using PyTorch 1.5.3 Results and discussion
3.1 Training of the generative model and material prediction
Before configuring a deep learning neural network for the generation of a new 2D crystal structure, it was necessary to select an appropriate representation that preserves the structural information of crystals with a reasonably sized memory. To encode the solid crystal structures into low-dimensional representations, a point-cloud-like image representation of a 2D matrix was used comprising a unit cell, lattice parameters, and fractional coordinates of each element.31 No additional processes were required since this representation is both invertible and consistent with the material structures. This representation is advantageous over graphical representations, as the inverse transformation from an image to a crystal structure is a precise correlation. Furthermore, this representation has low memory requirements compared with 3D voxel representations.31First, 2D structural data were obtained from the Material Clouds 2D structure database,38 which is a data subset of approximately 1000 easily exfoliable 2D monolayers containing less than 8 atoms per unit cell. There were 134 binary and 105 ternary system nanosheets whose stability had been confirmed previously via DFT computational exfoliation calculations. As the aim was to generate binary MHs, the initial training set contained 134 unique structures. The problems of data shortage and invariance were addressed by augmenting the data using transitional and rotational transformations for each initial original structure of about 1000 structures.31 Following data preprocessing, 134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 training data sets were available for the training of this study's model. Fig. 1 shows the complete configuration of the model.
000 training data sets were available for the training of this study's model. Fig. 1 shows the complete configuration of the model.
The model was trained for approximately 200 epochs, and following the training with the 2D binary system data, it was confirmed from the model's losses that its learning had progressed satisfactorily. A total of 500 crystal images of binary Mg–H 2D nanosheets were generated via the trained generator. To evaluate the performance of the generative model, we calculated the validity and reproduction ratio. Validity is a relatively weak criterion based on simple physical rules and was proposed by Court et al.39 According to this criterion, a structure is valid as long as the shortest distance between any pair of atoms is larger than 0.5 Å. In our model, 96.8% of structures were observed as valid structures. The reproduction ratio means how much percent of the training data was reproduced during the generation. We use StructureMatcher from pymatgen,40 which finds the best match between two structures considering all invariances of materials. The matching criterion parameter is set as stol = 0.5, angle_tol = 10, and ltol = 0.3. Totally, 87.3% of the structural motifs in the training data were reproduced in our model. Then, the structural optimization was performed using the loose convergence criterion (while fulfilling the preset material project relaxation option) for the generated material candidates, and the formation energy of each was determined (Fig. 2). The formation energies are defined as follows:
| Ef,MgH = (nMg × EMg(solid) − nH × (EH2(gas)/2))/ntot | (1) |
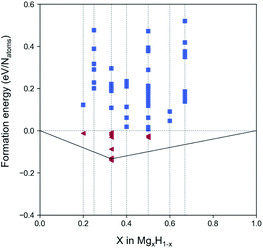 | ||
| Fig. 2 Phase diagram of the 2D MgxH1−x among the generated structures. The triangles colored red are the structures with negative formation energies. | ||
Fig. 2 shows the phase diagram of the generated MgxH1−x (the same as that of MgxHy but with a representation as a proportion of the elements in Mg), which plots the formation energies of all generated structures. In Fig. 2, the red triangles located below the level of zero formation energy indicate the selected structures that primarily satisfy thermodynamic stability. For these selected materials, additional strict criteria for the structural optimization and phonon calculations were included. Consequently, three structures of 2D magnesium hydride monolayers were filtered out: two MgH2 with P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (164) and P
m1 (164) and P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 (115) space groups and one Mg2H2 with a P1 (2) space group. For brevity, MgH2 with P
m2 (115) space groups and one Mg2H2 with a P1 (2) space group. For brevity, MgH2 with P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 and P
m1 and P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 space groups and Mg2H2 with a P1 space group are referred to as I-phase MgH2, II-phase MgH2, and III-phase Mg2H2, respectively.
m2 space groups and Mg2H2 with a P1 space group are referred to as I-phase MgH2, II-phase MgH2, and III-phase Mg2H2, respectively.
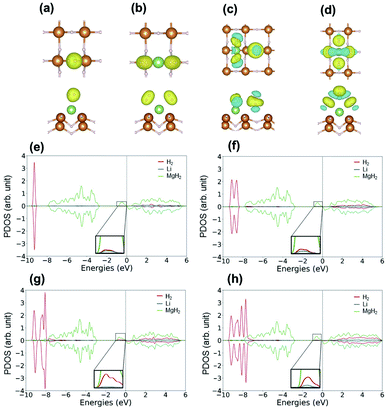
Fig. 3(a)–(c) present the top and side views of the optimized geometries of the discovered structures, and their structural details are summarized in Table 1. The lattice parameters of I-phase MgH2 are a = b = 3.001 Å, α = 89.9°, β = 89.6°, and γ = 119.9°, whereas the parameters of II-phase MgH2 are a = b = 3.198 Å and α = β = γ = 90°. I-phase Mg2H2 has parameters of a = b = 3.083 Å, α = 87.4°, β = 101.3°, and γ = 120°. In Fig. 3(d)–(f), the electronic band structures of each nanosheet are plotted with the edges of the valence and conduction bands marked in green and red dots, respectively. I-phase MgH2 has an indirect bandgap of 4.88 eV (Fig. 3(d)), II-phase MgH2 has an indirect bandgap of 4.74 eV (Fig. 3(e)), and I-phase Mg2H2 has an indirect bandgap of 0.50 eV (Fig. 3(f)). As can be seen in Fig. 3(g)–(i), these MgxHy structures are stable depending on their phonon band structures with a nonimaginary frequency.
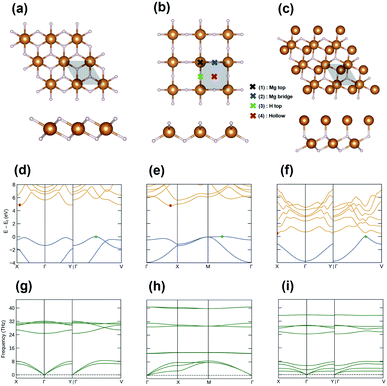 | ||
| Fig. 3 The 2 × 2 supercell of the explored structures: (a) I-phase MgH2, (b) II-phase MgH2, and (c) III-phase Mg2H2. The electronic band structures of (d) I-phase MgH2, (e) II-phase MgH2, and (f) III-phase Mg2H2. The phonon band structures of (g) I-phase MgH2, (h) II-phase MgH2, and (i) III-phase Mg2H2. All band structures were plotted using the Sumo package.41 | ||
| Name | Space group | a (Å) | α (°) | β (°) | γ (°) | E f (eV) | ΔHd (eV) |
|---|---|---|---|---|---|---|---|
| I-phase MgH2 |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
3.001 | 89.9 | 89.6 | 119.9 | −0.130 | 0.41 |
| II-phase MgH2 |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 m2 |
3.198 | 90.0 | 90.0 | 90.0 | −0.01 | 0.05 |
| III-phase Mg2H2 | P1 | 3.083 | 87.4 | 101.3 | 120 | −0.03 | 0.13 |
The dehydrogenation enthalpy for each compound (ΔHd in Table 1) was also calculated. All dehydrogenation enthalpies were calculated with a zero-point energy correction. The lowest value is shown by the II-phase MgH2 at 0.05 eV, whereas the values for the I-phase MgH2 and III-phase Mg2H2 are 0.41 and 0.13 eV, respectively. These values are relatively lower than the value of α-phase bulk MgH2 (0.80 eV).42 The lower dehydrogenation enthalpy facilitates easier removal of hydrogen atoms from Mg–H MHs. Therefore, 2D Mg–H MHs were expected to release H2 gas at a lower temperature than the α-phase bulk MgH2.
The I-phase MgH2 structure was discovered previously using a substitution-based crystal-prediction model,27 whereas III-phase Mg2H2 possesses an asymmetric structure in which one side is covered with a metal (a polymorph of Mg-decorated I-phase MgH2). However, II-phase MgH2 has a previously unproposed symmetrical structure with hydrogen covering both of its sides.27 So, this paper focuses on the analysis of II-phase MgH2. According to the available data from the Materials Project webpage (https://www.materialsproject.org), the most stable structure for MgH2 at 0 K is a tetragonal phase MgH2 (ID: mp-23710) with 6 atoms in the unit cell and with the symmetry of P42/mnm (136) (named α-phase MgH2), Fig. S1(a).† On the other hand, the layered bulk structure of the 2D II-phase of MgH2 with a tetragonal symmetry of P42/nmc (137), is only 0.038 eV per atom less stable than the α-phase, Fig. S1(b).† So the slight energy difference of 0.038 eV per atom could be readily compensated for by the energetic fluctuation in a thermally excited statistical system.
To investigate the thermal stability of MgH2, (note: MgH2 used without a phase modifier essentially means 2D II-phase MgH2) AIMD simulations were performed at 300 K up to 6 ps. Top- and side-view photographs of the structures at 0, 3, and 6 ps, respectively, are provided in Fig. S2(a), (b), and (c).† No distortions or defects were identified in the initial pristine structure, which indicates the thermodynamic stability of MgH2 under room temperature conditions.
Therefore, it is confirmed that the approach presented herein, which combines a deep learning-based crystal generative model with DFT calculations, can identify unrevealed 2D MgH2. Solid crystals can be defined by unit cells, atomic coordinates (structural motifs), and types of elements, although the crystal representation used in this study did not contain information about the latter. Although this model did not generate a new structural motif that was absent in the training data, it was successful in generating the unrevealed structures that were omitted from the classical substitution-based method. With the future development of AI technology in the field of materials, the crystal representation containing information about types of elements and structural motifs will facilitate more effective explorations of new materials.
3.2 Decoration of Li atoms on the surface of MgH2 and the adsorption of H2 molecules
Next, we considered the transition metal (TM) doped MgH2. Since it has already been investigated that TM-doped MgH2 (α-phase MgH2) materials have improved hydrogen adsorption and cycle performance,43 TM doping was expected to help improve performances in our 2D MgH2 structure. Furthermore, thanks to the characteristics of the 2D layered structure, the doped TMs were expected to serve as nuclei to hold additional H2 molecules. Among TMs, such as Al, Ca, K, Li, and Na metals, Li metal was the most stable when doped into the 2D MgH2 structure. So, the Li atoms on the surface of MgH2 (Li–MgH2) were considered to examine the hydrogen storage properties of a single-layer MgH2 surface. As shown in Fig. 3(b), four different highly symmetric sites (Mg top, H top, Mg bridge, and hollow) were selected to determine the most stable position. The most stable site for adsorbed Li atoms was found to be located at the site of the Mg bridge by −0.94 eV per unit cell. The binding energy of each Li atom on the MgH2 – (2 × 2) supercell is defined as follows:| Eb = Etot − EMgH2 − ELi | (2) |
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 MgH2
m2 MgH2
| Binding site | E bind,Li (eV) |
|---|---|
| Mg top | −0.412 |
| Mg bridge | −0.924 |
| H top | −0.293 |
| Hollow | −0.731 |
To clarify the mechanism for H2–host interactions, this section considers the adsorption behavior of H2 molecules on a single Li-atom-decorated MgH2 surface. The adsorption energies are defined as follows:
| Ead = (Etot − ELi−MgH2 − nH2 × EH2)/nH2 | (3) |
H2 molecules were adsorbed on the surface of Li–MgH2. The average adsorption energies, distances between the Li atoms and hydrogen molecules (dLi–H), and bond length of the adsorbed H2 molecules (dH–H) as a function of the number of adsorbed H2 molecules are summarized in Table 3. The H2 bond length is elongated as the number of adsorbed H2 molecules increases due to the weakening of the interior H–H bond in the H2 molecules resulting from the polarization caused by Li atoms. Multiple potential configurations were considered for the first H2 molecule with H2 at different angles to the MgH2 plane. The optimized ground state structure with an Ead of −0.104 eV and a corresponding dH–H of 0.754 Å is shown in Fig. 4(a). In this figure, the electrons can be seen to accumulate in H2 close to the Li side, whereas the other side demonstrates the contribution to adsorption by the polarization mechanism. This polarization weakens the H–H bond with an elongated dH–H of 0.754 Å and aids in subsequent H2 adsorption via an induction force. To image the process of H2 adsorption, additional H2 was added in a stepwise manner. As shown in Fig. 4(b), when the second H2 approaches the host, H2–H2 repulsive interactions cause the first one to move to Mg. Here the binding energy per H2 molecule is −0.105 eV, and the average H2 bond length (dH–H) is increased from 0.755 to 0.763 Å, as indicated in Table 3. The optimized structure of three H2 molecules adsorbed onto Li–MgH2 is illustrated in Fig. 4(c). When the third H2 is added, the Ead increases to −0.111 eV and the average H2 bond length increases to 0.763 Å. Then, as shown in Fig. 4(d), the fourth H2 is added with an Ead of −0.082 eV and a preference to be located opposite to the third one. However, the adsorption behavior of the fourth H2 does not follow the same trend; its Ead decreases further to −0.082 eV, and the dH–H value is reduced further from 0.763 to 0.754 Å. As shown in Fig. 4(c) and (d), in accordance with the adsorption results, there are significantly lower charge-density differences on the third (fourth) H2 molecule than on the first and second ones. Thus, up to four hydrogen molecules can exist on one Li-decorated MgH2 structure with an adequate adsorption energy (Ead) of −0.082 eV. The theoretical gravimetric hydrogen density (Gtheor) can be estimated using Gtheor = MH2/(Mhost + MH2), where Mhost and MH2 indicate the quality of the host material and the H2 molecules, respectively. Consequently, the Li–MgH2 (4H2) system can be expected to produce a remarkable Gtheor of 6 wt%.
| Number of H2 molecules | E ad,H2 (eV) | d Li–H2 (Å) | d H–H (Å) |
|---|---|---|---|
| 1 | −0.104 | 2.113 | 0.754 |
| 2 | −0.105 | 2.244 | 0.755 |
| 3 | −0.111 | 2.556 | 0.763 |
| 4 | −0.082 | 2.911 | 0.754 |
Next, the hydrogen-binding mechanism was clarified by investigating the electronic properties of the surface of the H2/Li–MgH2 structure. Fig. 4(e) and (f) show the PDOS of Li–MgH2 with one and two H2 molecules. With a single H2 molecule, the states of H and Li are hybridized around the peaks at −9.4 and −0.4 eV in Fig. 4(e). As shown in Fig. 4(f), for two H2 molecules, the hybridized peak at −9.4 eV divides into two at −9.6 and −8.6 eV, respectively. With the addition of the third and fourth H2 molecules, the hybridization peak at −9.4 eV splits into three and four peaks according to the number of H2 molecules, as shown in Fig. 4(g) and (h). In the system with three adsorbed H2 molecules (Fig. 4(g)), the split hybridized peaks are located at −9.6, −8.6, and −8.0 eV, respectively. As shown in Fig. 4(g), (four H2 molecules), the split hybridized peaks are located at −9.5, −8.5, −8.1, and −7.8 eV, respectively. The division of the hybridization peaks reduces the intensity of the individual peaks, which indicates a reduced bond strength between the H2 molecule and host material in accordance with the previous analysis.
Consequently, four additional H2 molecules could be stored by Li-decorated 2D MgH2 with an Ead of −0.105 eV and a Gtheor of 6 wt%. Considering that the host material in this study is 2D MH, which contains a chemisorbed hydrogen source, it can be said to possess additional hydrogen storage capacity, which makes it competitive against other Li-decorated 2D hydrogen host materials, including h-BN (∼6 wt%)23 and borophene (6.80–11.49 wt%).44,45 Therefore, the Li-decorated system of a 2D MgH2 sheet with a P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 space group is anticipated to be a viable medium for substantial hydrogen storage.
m2 space group is anticipated to be a viable medium for substantial hydrogen storage.
4 Conclusions
This study successfully demonstrated that a deep learning-based crystal structure-prediction model can generate reliable 2D materials with the potential for effective and substantial hydrogen storage. The GAN model in this study effectively explored the structural space of the 2D material and identified an unknown structure, which has not been proposed previously using classical substitution-based methods. The 2D MgH2 material with a P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 space group was confirmed to be a thermally stable structure with the potential for significant hydrogen storage. The hydrogen storage properties of the pristine and Li-decorated P
m2 space group was confirmed to be a thermally stable structure with the potential for significant hydrogen storage. The hydrogen storage properties of the pristine and Li-decorated P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 MgH2 monolayer were investigated using the DFT method, and it was revealed that pristine MgH2 can act as a source of chemisorbed hydrogen with a dehydrogenation enthalpy of 0.05 eV. Additionally, four additional H2 molecules are capable of being physisorbed onto the surface of 2D Li-decorated MgH2 to produce efficient hydrogen storage materials with an average H2 molecular adsorption energy of −0.105 eV and a gravimetric hydrogen capacity of 6 wt%.
m2 MgH2 monolayer were investigated using the DFT method, and it was revealed that pristine MgH2 can act as a source of chemisorbed hydrogen with a dehydrogenation enthalpy of 0.05 eV. Additionally, four additional H2 molecules are capable of being physisorbed onto the surface of 2D Li-decorated MgH2 to produce efficient hydrogen storage materials with an average H2 molecular adsorption energy of −0.105 eV and a gravimetric hydrogen capacity of 6 wt%.
This study's findings indicate that the combined approach of AI and DFT calculations can be used to predict 2D crystal structures efficiently; consequently, 2D P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 MgH2 is proposed as a novel hydrogen storage medium. It is anticipated that this study's findings will accelerate the development of hydrogen storage materials and other desired functional materials both theoretically and experimentally.
m2 MgH2 is proposed as a novel hydrogen storage medium. It is anticipated that this study's findings will accelerate the development of hydrogen storage materials and other desired functional materials both theoretically and experimentally.
Code and data availability
As mentioned, all DFT calculations were performed using the VASP package. Furthermore, the original code of the generative deep learning model was obtained from https://github.com/kaist-amsg/Composition-Conditioned-Crystal-GAN. We modified the code to suit the purpose of our study. The code and data used in this study are provided along with the ESI† in the code_data.zip.Author contributions
Junho Lee: conceptualization, data curation, investigation, methodology, visualization, validation, writing – original draft, writing – review & editing. Dongchul sung: methodology, validation, supervision, writing – review & editing. You Kyoung Chung: validation, writing review & editing. Seon Bin Song: validation, visualization. Joonsuk Huh: project administration, supervision, funding acquistion, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the National Research Foundation (NRF) of Korea grant-funded by the Korean government (NRF-2021M3H4A4079153 and NRF-2021R1F1A1053283).References
-
L. Schlapbach and A. Züttel, in Hydrogen-storage Materials for Mobile Applications, World Scientific, 2011, pp. 265–270 Search PubMed
.
- J. Tollefson, Nature, 2010, 464, 1262–1264 CrossRef CAS PubMed
.
- N. Rusman and M. Dahari, Int. J. Hydrogen Energy, 2016, 41, 12108–12126 CrossRef CAS
.
- B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Int. J. Hydrogen Energy, 2007, 32, 1121–1140 CrossRef CAS
.
- Q.-L. Zhu and Q. Xu, Energy Environ. Sci., 2015, 8, 478–512 RSC
.
- M. B. Ley, L. H. Jepsen, Y.-S. Lee, Y. W. Cho, J. M. B. Von Colbe, M. Dornheim, M. Rokni, J. O. Jensen, M. Sloth and Y. Filinchuk, Mater. Today, 2014, 17, 122–128 CrossRef CAS
.
- S.-i. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed
.
- H. Wang, H. Lin, W. Cai, L. Ouyang and M. Zhu, J. Alloys Compd., 2016, 658, 280–300 CrossRef CAS
.
- A. Dillon, K. Jones, T. Bekkedahl, C. Kiang, D. Bethune and M. Heben, Nature, 1997, 386, 377–379 CrossRef CAS
.
- D. S. Pyle, E. M. Gray and C. Webb, Int. J. Hydrogen Energy, 2016, 41, 19098–19113 CrossRef CAS
.
- M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782–835 CrossRef CAS PubMed
.
- P. Suksaengrat, V. Amornkitbamrung, P. Srepusharawoot and R. Ahuja, ChemPhysChem, 2016, 17, 879–884 CrossRef CAS PubMed
.
- Y. Pramudya and J. L. Mendoza-Cortes, J. Am. Chem. Soc., 2016, 138, 15204–15213 CrossRef CAS PubMed
.
- X. Zhan, Z. Chen and Q. Zhang, J. Mater. Chem. A, 2017, 5, 14463–14479 RSC
.
- D. Durbin and C. Malardier-Jugroot, Int. J. Hydrogen Energy, 2013, 38, 14595–14617 CrossRef CAS
.
- J. Ren, N. M. Musyoka, H. W. Langmi, M. Mathe and S. Liao, Int. J. Hydrogen Energy, 2017, 42, 289–311 CrossRef CAS
.
- J. Yang, A. Sudik, C. Wolverton and D. J. Siegel, Chem. Soc. Rev., 2010, 39, 656–675 RSC
.
- S. Seenithurai, R. K. Pandyan, S. V. Kumar, C. Saranya and M. Mahendran, Int. J. Hydrogen Energy, 2014, 39, 11016–11026 CrossRef CAS
.
- F. Wang, T. Zhang, X. Hou, W. Zhang, S. Tang, H. Sun and J. Zhang, Int. J. Hydrogen Energy, 2017, 42, 10099–10108 CrossRef CAS
.
- C. Ataca, E. Aktürk, S. Ciraci and H. Ustunel, Appl. Phys. Lett., 2008, 93, 043123 CrossRef
.
- Y. Zhou, W. Chu, F. Jing, J. Zheng, W. Sun and Y. Xue, Appl. Surf. Sci., 2017, 410, 166–176 CrossRef CAS
.
- Z. Ao and F. Peeters, Phys. Rev. B, 2010, 81, 205406 CrossRef
.
- P. Banerjee, B. Pathak, R. Ahuja and G. Das, Int. J. Hydrogen Energy, 2016, 41, 14437–14446 CrossRef CAS
.
- Z.-Y. Hu, X. Shao, D. Wang, L.-M. Liu and J. K. Johnson, J. Chem. Phys., 2014, 141, 084711 CrossRef PubMed
.
- E. M. Kumar, S. Sinthika and R. Thapa, J. Mater. Chem. A, 2015, 3, 304–313 RSC
.
- J. Long, J. Li, F. Nan, S. Yin, J. Li and W. Cen, Appl. Surf. Sci., 2018, 435, 1065–1071 CrossRef CAS
.
- X. Zhou, Y. Hang, L. Liu, Z. Zhang and W. Guo, J. Am. Chem. Soc., 2019, 141, 7899–7905 CrossRef CAS PubMed
.
-
T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, arXiv, 2021
.
- T. Long, N. M. Fortunato, I. Opahle, Y. Zhang, I. Samathrakis, C. Shen, O. Gutfleisch and H. Zhang, npj Comput. Mater., 2021, 7, 66 CrossRef CAS
.
- V. Fung, J. Zhang, G. Hu, P. Ganesh and B. G. Sumpter, npj Comput. Mater., 2021, 7, 200 CrossRef
.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, ACS Cent. Sci., 2020, 6, 1412–1420 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse, J. Furthmüller and J. Hafner, Phys. Rev. B, 1994, 50, 13181 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef PubMed
.
- J. P. Perdew, Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed
.
- C. J. Court, B. Yildirim, A. Jain and J. M. Cole, J. Chem. Inf. Model., 2020, 60, 4518–4535 CrossRef CAS PubMed
.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS
.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, J. Open Source Softw., 2018, 3, 717 CrossRef
.
- H. Shao, M. Felderhoff, F. Schüth and C. Weidenthaler, Nanotechnology, 2011, 22, 235401 CrossRef CAS PubMed
.
- H. Yu, S. Bennici and A. Auroux, Int. J. Hydrogen Energy, 2014, 39, 11633–11641 CrossRef CAS
.
- L. Wang, X. Chen, H. Du, Y. Yuan, H. Qu and M. Zou, Appl. Surf. Sci., 2018, 427, 1030–1037 CrossRef CAS
.
- S. Haldar, S. Mukherjee and C. V. Singh, RSC Adv., 2018, 8, 20748–20757 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1na00862e |
| This journal is © The Royal Society of Chemistry 2022 |