Open Access Article
Open Access ArticleA numerical study on the interplay between the intra-particle and interparticle characteristics in bimagnetic soft/soft and hard/soft ultrasmall nanoparticle assemblies
Franciscarlos Gomes da
Silva
 *a,
Marianna
Vasilakaki
*a,
Marianna
Vasilakaki
 b,
Rafael
Cabreira Gomes
ac,
Renata
Aquino
d,
Alex Fabiano Cortez
Campos
b,
Rafael
Cabreira Gomes
ac,
Renata
Aquino
d,
Alex Fabiano Cortez
Campos
 d,
Emmanuelle
Dubois
d,
Emmanuelle
Dubois
 e,
Régine
Perzynski
e,
Régine
Perzynski
 e,
Jérôme
Depeyrot
a and
Kalliopi
Trohidou
e,
Jérôme
Depeyrot
a and
Kalliopi
Trohidou
 b
b
aInstituto de Física, Universidade de Brasília, Caixa Postal 04455, 70919-970, Brasília, Brazil. E-mail: franciscarlos@fis.unb.br
bInstitute of Nanoscience and Nanotechnology, NCSR “Demokritos”, Athens 15310, Greece
cDepartamento de Física, Universidade Federal de Santa Catarina, 88040-900, Florianópolis, Brazil
dLaboratory for Environmental and Applied Nanoscience, Faculty UnB – Planaltina, University of Brasília, 73345-010, Brasília, Brazil
eSorbonne Université, Laboratoire PHENIX, 4 Place Jussieu, Case 51, 75005, Paris, France
First published on 4th August 2022
Abstract
A mesoscopic scale approach and the Monte Carlo (MC) method have been employed to study the exchange bias behaviour of MnFe2O4 (soft)/maghemite (soft) and CoFe2O4 (hard)/maghemite (soft) nanoparticles (NPs) of size ∼ 3 nm in dense and diluted assemblies at low temperatures. The analysis of our MC results clearly shows that in the powder samples the contribution to the exchange bias field (Hex) and the coercivity (Hc) comes mainly from the intraparticle core/shell structure in the hard/soft sample and that the interplay between the internal characteristics and the interparticle interactions is more important in the soft/soft samples where the dipolar strength is enhanced. In the diluted frozen ferrofluid samples where interparticle exchange interactions are absent and the role of the dipolar interactions is not significant the exchange bias effects are reduced, and they come from the intra particle structure. The variation of Hex and Hc with the applied cooling field well reproduces the experimental findings and sheds light on the key mechanisms of the observed magnetic behaviour. Our results demonstrate the possibility to control the magnetic behaviour of nanostructures by using properly chosen core/shell bimagnetic nanoparticles.
1. Introduction
The exchange bias (EB) effect was discovered in 1956 on Co/CoO core/shell (CS) nanoparticles.1–3 Later, this effect has been investigated in detail by many research groups from both theoretical1–4 and experimental5–9 points of view. The reason for this thorough investigation is that bimagnetic core/shell nanoparticles are becoming progressively more attractive in diverse fields such as hard magnets or magnetic recording media and biomedical applications.10–12In addition, thanks to the progress in controlled chemical synthesis and to the advances in technical instruments for the study of the structural–morphological and magnetic properties, it is possible to explore EB in a wide range of nanoparticle systems, such as doubly inverted nanoparticles,13,14 core/shell nanoparticles with different compositions,15,16 and nanocomposites.17,18 The experimental results on nanocomposites based on the hexaferrite hard/soft ferrite interface have shown that the magnetic properties depend on the hard/soft phase ratios.19,20 López-Ortega et al. gave a detailed study of the magnetic behaviour and applications of exchange coupled bimagnetic hard/soft and soft/hard magnetic core/shell nanoparticles.11 In addition, Monte Carlo studies have shed light on the role of interface and surface spins on the exchange bias properties,1,2,21–23 in various nanoparticle systems.
The cooling field dependence of the exchange bias field and the coercivity in core/shell nanoparticles has been studied by several authors.2,17,21–26 In these studies, it has been observed that as the applied field increases the exchange bias phenomena are increasing. This is attributed to the competition between the Zeeman energy and the exchange anisotropy energy for a range of applied fields. Further increase of the applied field leads to the reduction of the exchange bias effects because the Zeeman energy starts to dominate and tends to direct the interface spins along the field.
In assemblies of magnetic nanoparticles, interparticle interactions play an important role in the exchange bias behaviour of the systems. It has been demonstrated that the interplay between internal nanoparticle characteristics and interparticle interactions determines the magnetic response of the nanoparticles to an externally applied field.22,27–29 Indeed, in previous experimental studies, we have investigated the effect of core and shell composition on the exchange bias properties of MnFe2O4@γ-Fe2O3 and CoFe2O4@γ-Fe2O3 core/shell NPs of size ∼ 3 nm at low temperature (a few Ks).24,30–32 By studying dilute and dense dispersions as well as powders, it has been demonstrated experimentally that inter and intraparticle interactions play an important role in the EB properties. Our finding showed that in concentrated frozen dispersions, the dipolar interparticle interaction reduced the exchange bias field. Interparticle exchange bias was found to dominate in powder nanoparticle samples. An open question is the role of the composition and the mechanism of the observed behaviour in MnFe2O4@γ-Fe2O3 (soft/hard) and CoFe2O4@γ-Fe2O3 (hard/soft) nanoparticle systems.
In the present work, we systematically investigate by Monte Carlo simulations the role of the intraparticle characteristics and their interplay with interparticle interactions in the exchange bias behaviour of ferrofluids and powder NPs. These assemblies consisted of complex ultra-small magnetic nanoparticles (of size ∼ 3 nm) that can be used for environmental (e.g. increasing magnetoelectric performance33) and biomedical applications (e.g. magnetic hyperthermia as nanoheaters34).
In particular, the cooling field dependence of Hc and Hex is analysed in dense and in very diluted assemblies (frozen ferrofluids) using mesoscopic scale modelling. Since in the diluted dispersions, interparticle interactions play a minor role the influence of the intraparticle characteristics is clearly revealed. In all cases we discuss the numerical results in the context of our experimental findings.24,30,31,35,36
2. The model
To model spherical MnFe2O4/γ-Fe2O3 nanoparticle (of diameter d ∼ 3.3 nm and γ-Fe2O3 shell thickness tsh = 0.4 nm) assemblies and spherical CoFe2O4/γ-Fe2O3 nanoparticle (of d ∼ 3.1 nm and γ-Fe2O3 shell thickness tsh = 0.5 nm) assemblies in frozen ferrofluids (very dilute samples) and powders (dense samples), we consider systems of N ultra-small spherical nanoparticles with a ferrimagnetic (FiM) core/FiM shell morphology. We perform the Monte Carlo simulations technique with the implementation of the Metropolis algorithm to calculate the magnetic behaviour of these assemblies at low temperature T = 0.01 in our units which corresponds to 5 K.The particles are located randomly on the nodes of a cubic lattice inside a box of dimensions 10α × 10α × 10α for the dense assembly and of dimension 20α × 20α × 20α for the diluted one, where α is the lattice spacing for the sample and it is equal to the particle diameter D, and therefore there is no overlapping of the nanoparticles. It is important to note that the choice of this model is the appropriate one to capture the internal structure and to describe the interparticle characteristics, as discussed in ref. 37.
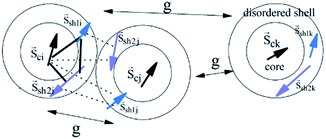
A set of three classical spin vectors is used to describe each of the nanoparticles in the assembly: one spin for the core ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) ci and two spins
ci and two spins ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) sh1i and
sh1i and ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) sh2i for the two sublattices of the shell with magnetic moments
sh2i for the two sublattices of the shell with magnetic moments 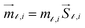 with i = 1, …, N and
with i = 1, …, N and 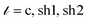 and
and 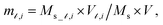 where
where 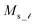 is the saturation magnetization and
is the saturation magnetization and 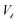 is the volume of each nanoparticle region. Ms is the total saturation magnetization of the nanoparticle and V is the particle volume (Fig. 1). We have considered one spin for the FiM core giving its net magnetic moment with uniaxial anisotropy and two for the shell because of the ultra-small size of the nanoparticle and the very small shell thickness. The two magnetic moments of the shell are randomly oriented. Therefore, in the model, the core is well-ordered retaining some of the bulk characteristics and the shell is disordered, spin-glass like.22 We introduce short range intra-particle exchange interaction between the Mn or Co ferrite core spin and each of the two maghemite shell spins (interface coupling Jc1 and Jc2) and between the two shell spins (shell coupling Jshell). Long-range inter-particle dipolar interactions among all spins in the assemblies are considered. In the case of the dense assembly (powder sample) for the particles that are in contact, because of the very small shell thickness,31 the particle core spin interacts with the nearest neighbor shell spins via exchange interactions (Jcsh1, Jcsh2).37 The shell spins of the nearest neighbours are also exchange coupled (Jsh1sh2).
is the volume of each nanoparticle region. Ms is the total saturation magnetization of the nanoparticle and V is the particle volume (Fig. 1). We have considered one spin for the FiM core giving its net magnetic moment with uniaxial anisotropy and two for the shell because of the ultra-small size of the nanoparticle and the very small shell thickness. The two magnetic moments of the shell are randomly oriented. Therefore, in the model, the core is well-ordered retaining some of the bulk characteristics and the shell is disordered, spin-glass like.22 We introduce short range intra-particle exchange interaction between the Mn or Co ferrite core spin and each of the two maghemite shell spins (interface coupling Jc1 and Jc2) and between the two shell spins (shell coupling Jshell). Long-range inter-particle dipolar interactions among all spins in the assemblies are considered. In the case of the dense assembly (powder sample) for the particles that are in contact, because of the very small shell thickness,31 the particle core spin interacts with the nearest neighbor shell spins via exchange interactions (Jcsh1, Jcsh2).37 The shell spins of the nearest neighbours are also exchange coupled (Jsh1sh2).
The total energy of the system for the N nanoparticles is given by:
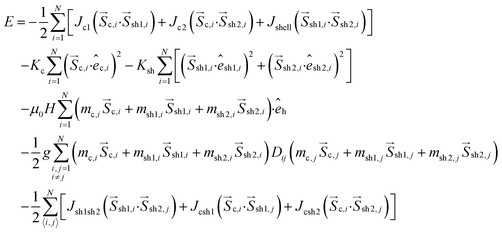 | (1) |
In eqn (1), the first three energy terms inside the brackets describe the intra-particle Heisenberg exchange interaction between the spins in each nanoparticle, the core (c) with shell spin1 (sh1), the core with shell spin2 (sh2) and between the shell spins respectively. The fourth and the fifth terms give the anisotropy energy of the core and the shell spins (êi is the random anisotropy easy-axis direction), respectively. The sixth term is the Zeeman energy (êh is the direction of the magnetic field). The next term gives the dipolar interactions among all the spins in the assembly, where Dij is the dipolar interaction tensor which in our case takes the values of the Ewald matrix.37
The last three terms exist only in the case of the powder sample and describe the inter-particle exchange interactions between the neighboring shells and between the core of each nanoparticle with the neighboring shell spins respectively. There is no exchange interparticle term in the frozen ferrofluid sample.
The dipolar strength is g = μ0(MsV)2/4πd3, where d is the diameter of the particle. The anisotropy constant of the core is Kc and of the shell Ksh, the external magnetic field is μ0H and the thermal energy is kBT (where T is the temperature). The particle volume concentration φ is taken as 27% for the powder samples and 0.4% for the frozen ferrofluids.
The magnetic moments of the core and of the shell are extracted from an atomic scale model of the spinel ferrite structure that explicitly takes into account the size of the shell and the core of the MnFe2O4/γ-Fe2O3 and CoFe2O4/γ-Fe2O3 nanoparticles and calculates their volumes and their saturation magnetization.
In the MnFe2O4/γ-Fe2O3 nanoparticle (of size d ∼ 3.3 nm) assemblies, the energy parameters are normalized by the volume anisotropy of the shell Ksh × Vsh so they are dimensionless. The normalized magnetic moments are: mc = 0.15 for the core and msh1 = 0.50 and msh2 = 0.58 for the shell. In this atomic scale model, the saturation magnetization has been taken 1.5 times higher than the core magnetization in agreement with the experimental results of ref. 32 (Mscore = 210 kA m−1 and Ms = 320 kA m−1). We consider the bulk value of MnFe2O4 for the core anisotropy (Kc = 3 × 103 J m−3) and the shell anisotropy ∼ 10 times higher than the bulk maghemite anisotropy (Kc = 5 × 103 J m−3). The reduced parameters entered into our simulations for the anisotropy strength are for the core Kc = 0.04 and for the shell Ksh = 1.0. Our atomic scale simulations show that in the core the B sublattice is the dominant one, therefore we set the core macrospin as a “B” spin. For the intraparticle exchange coupling constant strengths between the core spin and the shell spins of the two sublattices A and B we use their bulk values for the MnFe2O4 (JAB = −22.7 K and JBB = 11.5 K, sA = sB = 5/2) spinel structure and the exchange coupling constants of the maghemite (JAB = −25.9 K and JBB = 12.7 K, sA = sB = 5/2) spinel structures. From the atomic scale modeling the exchange coupling constant between the A and B shell spins is found to be 1.44 times larger than the corresponding core value and by rescaling them we find that Jc1 = −1.6, Jc2 = 0.8, and Jshell = −2.3. There is no exact microscopic model for the calculation of the exchange coupling constant strengths between the nanoparticles, and thus we consider the inter-particle exchange interactions between the shell spins of particles in contact with the JAB of the bulk maghemite and in our model the rescaled value is Jsh1sh2 = −0.5. The values of the core spins with the neighboring shell spins are Jcsh1 = 0.15 and Jcsh2 =−0.18. From the experimental values of Ms = 320 kA m−1 for the dilute sample with φ = 0.4%, the dipolar strength is found to be g = 0.16. In the powder sample the experimental hysteresis loop gives enhanced saturation magnetization by a factor of 1.095 compared to the frozen ferrofluid samples. This increase in the magnetization in the dense sample is attributed to the inter-particle exchange interactions between the particles in contact. Therefore, for the powder samples we find that g = 0.16 × 1.2 = 0.19.
The energy parameters of the CoFe2O4/γ-Fe2O3 nanoparticles (of d ∼ 3.1 nm) are also normalized by the factor Ksh × Vsh used in the previous system, so that we can compare the two types of samples. In this case, from our experimental findings we have found that the CoFe2O4 core magnetization is lower (∼5%) than that of the MnFe2O4 core and thus the normalized magnetic moment of this core is taken as mc = 0.14. We take msh1 = 0.15 and msh2 = 0.8 for the maghemite shell since its volume size (tsh = 0.5 nm) and the pinning parameter (p = 0.03) are larger than those of the shell of the MnFe2O4/γ-Fe2O3 nanoparticles (tsh = 0.4 nm and p = 0.01) in agreement with the experimental results. The bulk exchange coupling constant strengths of CoFe2O4 are JAB = −25 K JBB = 18 K, sA = 5/2, and sB = 2, and using these values in our atomic scale model we find that Jc1 = −1.76, Jc2 = 1.25, and Jshell = −2.87. The interparticle exchange coupling strengths between the core spins and the neighboring shell spins in the CoFe2O4/γ-Fe2O3 nanoparticle systems are Jcsh1 = 0.165 and Jcsh2 = −0.28. The value of the exchange coupling constant between the shell spins of nanoparticles in contact as above is taken from the JAB bulk value of maghemite and in our model this becomes Jsh1sh2 = −0.62. These interparticle exchange constant values are lower than the intra-particle ones (∼10, 4, and 5 times respectively as in the system of MnFe2O4/γ-Fe2O3 nanoparticles).
In ref. 28, it has been demonstrated that the anisotropy field of the CoFe2O4/γ-Fe2O3 assembly is 3 times larger than the anisotropy field of MnFe2O4/γ-Fe2O3 as it was estimated from the virgin magnetization curves of both systems. Therefore, if we consider that the core anisotropy has the bulk value Kc = 2 × 105 J m−3 for CoFe2O4, the increase in the effective anisotropy of the system comes from the shell. Therefore, the shell anisotropy is three times larger than that of the MnFe2O4/γ-Fe2O4 system. So, the anisotropy strengths are Kc = 1.6 for the core and Ksh = 3.0 for the shell. The dipolar strength of the frozen ferrofluid sample is found to be g = 0.034, much smaller than that of the MnFe2O4/γ-Fe2O3 assemblies, due to the smaller Ms = 160 kA m−1 as estimated from the experimental hysteresis loop. In the powder samples, assuming the same enhancement of the saturation magnetization as in MnFe2O4/γ-Fe2O3 nanoparticles assemblies, we find g = 0.041 larger by a factor of 1.2.
There is experimental evidence that all the nanoparticle assemblies are polydisperse following a log-normal distribution. Therefore, by introducing in our model the same particle volume polydispersity, we recalculate the corresponding volume dependent parameters, namely the magnetizations mc, msh1, and msh2 and the anisotropies Kc and Ksh for each nanoparticle of the polydisperse assembly.
3. Results and discussion
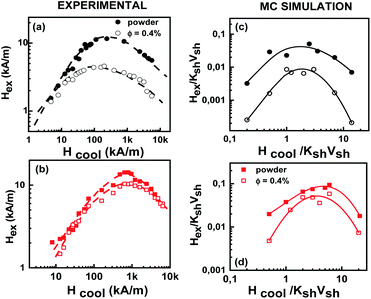
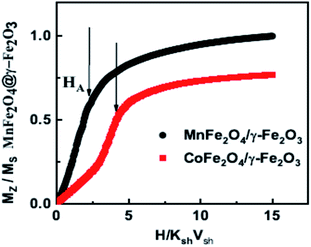
Fig. 2 shows the experimental results on the cooling field dependence of the exchange bias field Hex (Fig. 2(a and b)) together with the data of the Monte Carlo simulations (Fig. 2(c and d)) for frozen ferrofluid (0.4%) (open symbols) and powders (closed symbols) of the MnFe2O4@γ-Fe2O3 (Fig. 2(a and c)) and CoFe2O4@γ-Fe2O3 (Fig. 2(b and d)) core/shell nanoparticles respectively. In all simulations, the particle size polydispersity is included.The calculated curves (Fig. 2(c and d)) of the cooling field dependence of Hex show a maximum (peak) in both samples in agreement with the experimental findings (Fig. 2(a and b)). The peak position is located at Hcool/KshVsh ∼ 1.5 and ∼3.5 for MnFe2O4@γ-Fe2O3 and CoFe2O4@γ-Fe2O3 core/shell nanoparticles, respectively. These values are close to the half of the anisotropy fields given by Ha/KshVsh ∼ 3 and Ha/KshVsh ∼ 5 as is estimated from the calculated virgin curves of powder samples (see Fig. 3) in qualitative agreement with the experimental results.31,36 We must note here that the deviation is due to the structural difference between the experimental situation and the model. In the case of dilute dispersions (almost isolated particles) both the MC results and the experimental measurements show that the maximum of Hex is smaller than in powder. Moreover, the value of Hex maximum is more than two times larger for the CoFe2O4@γ-Fe2O3 sample than for the MnFe2O4@γ-Fe2O3 one. This result has been attributed to a stronger pinning of the more anisotropic cores in ref. 31 and indicates that the shell spin pinning through the core/shell interface depends on the hardness of the core ferrite.31
Monte Carlo simulation findings indeed give larger Hex values for CoFe2O4@γ-Fe2O3 core/shell nanoparticles in good agreement with the experimental results. For both types of samples, the measured values of Hex are found to be larger in powders than in the diluted frozen dispersions for all the investigated range of cooling fields. This has been attributed to a collective interparticle exchange interaction acting through the multi-connected shells, which are in contact with powder samples, and are behaving as a spin glass-like matrix where the FI cores are embedded.36,38 As can be seen in Fig. 2(c and d) Monte Carlo simulation data well reproduce this feature. This will be further illustrated in the discussion below where we separately study the contribution from the dipolar and exchange interparticle interactions.
The simulation results also confirm that the interface interaction between the Co ferrite core and the spin-glass like maghemite shell, which is the origin of the Hex, is rather insensitive to interparticle interactions. For CoFe2O4@γ-Fe2O3 nanoparticles, the ratio of the maximum Hex values in both the powder and the diluted frozen liquid samples is indeed 1.3 (close to the experimental ratio of 1.4) and is smaller than the corresponding value found for MnFe2O4@ γ-Fe2O3 core/shell nanoparticles in agreement with the experimental findings.
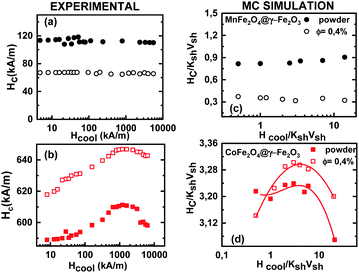
Fig. 4 illustrates the cooling field dependence of the coercivity Hc as deduced from the hysteresis loops after field cooling. Experimental data (Fig. 4(a and b)) are compared with those obtained from Monte Carlo simulations (Fig. 4(c and d)) for frozen ferrofluid (0.4%) (open symbols) and powder (closed symbols) of MnFe2O4@γ-Fe2O3 (upper panel) and CoFe2O4@γ-Fe2O3 (lower panel) core/shell nanoparticles.
The observed behaviour is slightly different in the two types of core/shell nanoparticle samples. The coercivity of MnFe2O4@γ-Fe2O3 core/shell nanoparticles does not vary within the studied cooling field range, whereas the Hc curves obtained for CoFe2O4@γ-Fe2O3 core/shell nanoparticles exhibit a small increase (4–5%) in a broad range of high cooling field values (0.6–3 × 103 kA m−1). These experimental findings (Fig. 4(a and b)) are well reproduced by Monte Carlo simulations (Fig. 4(c and d)). Also, in agreement with the experimental results, for MnFe2O4@γ-Fe2O3 core shell nanoparticles, the calculations show that the coercivity of the frozen liquid samples is more than 2 times smaller than that of the powder ones.
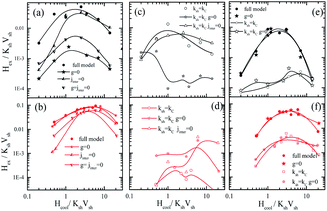
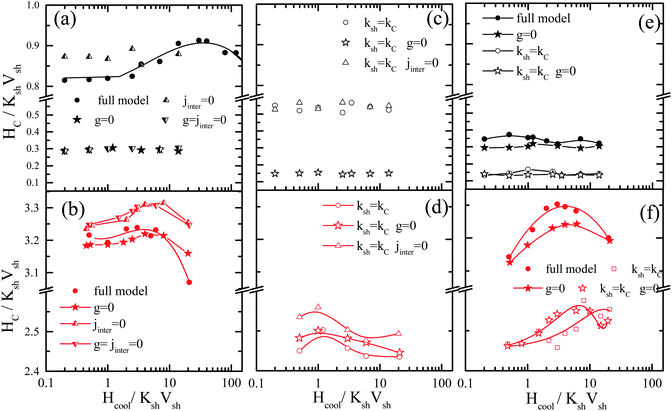
In order to further investigate the contribution of the interparticle interactions, the intraparticle characteristics and their interplay in the observed magnetic behaviour, MC simulations are performed for very diluted frozen ferrofluids (almost non-interacting Jinter = Jsh1sh2 = Jcsh1 = Jcsh2 = 0.0), where we: (a) switch off the dipolar interactions (g = 0) or (b) the shell anisotropy is taken equal to the core one (setting Ksh = Kc) or (c) we set both (Ksh = Kc and g = 0). In addition, in dense nanoparticle assemblies (powder samples) we also switch off either (c) the exchange interparticle interaction (Jinter = 0) or (d) all the interparticle interactions (g = Jinter = 0). Fig. 2 and 4 illustrate the behaviour of the exchange bias field and the coercivity as a function of the cooling field respectively, for the powder samples (a–d) and the frozen diluted ferrofluids (e and f) of the MnFe2O4@γ-Fe2O3 (upper panel) and CoFe2O4@γ-Fe2O3 (lower panel) CS nanoparticles.
In Fig. 5(a, b) and 6(a and b), the results of Hex and Hcvs. the cooling field for g = 0 (closed stars), Jinter = 0 (up triangles) and g = Jinter = 0 (down triangles) are compared with the full models MnFe2O4@γ-Fe2O3 and CoFe2O4@γ-Fe2O3 (full circles). In Fig. 5(c, d) and 6(c and d), the Hex and Hcvs. the cooling field results for Ksh = Kc (open circles), Ksh = Kc and g = 0 (open stars), Ksh = Kc and Jinter = 0 (open up triangles) are presented. Finally, in Fig. 5(e, f), 6(e and f) the cases of diluted frozen ferrofluids with g = 0 (closed stars), Ksh = Kc (open circles) and Ksh = Kc and g = 0 (open stars) are compared with the full models MnFe2O4@γ-Fe2O3 and CoFe2O4@γ-Fe2O3 (full circles).
In MnFe2O4@γ-Fe2O3 powders (Fig. 5(a and c)), Hex depends significantly on the dipolar interactions because they have a large dipolar strength compared to the anisotropy strength. The role of the intraparticle interface is not significant because of the low Kc (25 times smaller than Ksh); therefore the shell with the higher k is dragging the core spin. For the maximum of the Hex curve, they are close to the field where the Zeeman energy competes with the shell anisotropy (because this gives the dominant contribution) and the anisotropy induced by the dipolar interactions. On the other hand, in the CoFe2O4@γ-Fe2O3 powders, Fig. 6(b and d) shows that the exchange bias mainly comes from the intraparticle interface (core/shell) and from the competition between neighbouring shells due to the interparticle exchange interactions. However, the dipolar interaction does not significantly influence the intensity of the exchange bias field Fig. 5(b) (stars). The maximum Hex is in the field region where the Zeeman energy competes with the shell anisotropy energy. Then when the Zeeman energy overcomes the shell anisotropy energy the spins start to align towards the field and the Hex gradually reduces.
In the frozen diluted ferrofluids shown in Fig. 5(e and f) the role of dipolar interaction is not very significant because of the low concentration. In this case, the role of Jinter is negligible. Moreover, if we set Ksh = Kc in both types of nanoparticles the EB field is at least one order of magnitude lower. This does suggest that the anisotropy contrast at the interface between core and shell materials is one of the key parameters that govern exchange bias behaviour. In the case of the hard core the interface competition is stronger, in good agreement with experimental findings that show a larger bias for CoFe2O4@γ-Fe2O3 CS nanoparticles.
Fig. 6 shows the coercivity as a function of the cooling field, for the simulated powder samples (a–d) and the frozen ferrofluids (e and f) of MnFe2O4@γ-Fe2O3 (upper panel) and CoFe2O4@γ-Fe2O3 (lower panel) CS nanoparticles.
In the powder assembly of manganese ferrite/maghemite nanoparticles (Fig. 6(a and c)), the strong character of the dipolar strength that induces a strong anisotropy results in the observed large Hc and when they are switched off (g = 0 closed stars) the Hc drastically reduces, as seen in Fig. 6(a). On the other hand, the absence of interparticle exchange interactions (Jinter = 0 up triangles) results in a small increase in Hc. It is important to note that the absence of cooling field dependence of Hc in the experimentally studied cooling field range (in Fig. 4(a)) is due to the fact that the contribution from both shell anisotropy and dipolar interactions require a higher cooling field to compete with. Therefore, we expect the maximum to appear at a field higher than that available for the measurements. Indeed, this is the situation in Fig. 6(a) (full circles) where coercivity Hcversus the cooling field plot is shown for a more extended cooling field range. For higher cooling field values the curve is reduced after a maximum.
In cobalt ferrite based nanoparticle samples (Fig. 6(b, d and f)), Hc has a maximum value near the point that the Zeeman energy competes with the shell anisotropy energy. Then, it reduces for the same reason as in the Hex variations (Zeeman coupling of disordered shell spins). In the case of powder assembly, the dipolar strength is small; therefore it does not have significant influence on the Hc (Fig. 6(b), stars). Because of the high density of the assembly (powder), the dipolar interactions induce an extra anisotropy (nose to tail dipoles) and when they are switched off the coercivity Hc reduces. On the other hand, the absence of Jinter enhances Hc (up triangles or down triangles) because of the non-coherent rotation of the neighbouring spins. Therefore, the more significant contribution in both Hc and Hex comes from the intraparticle structure and in particular from the interplay of the particle shell anisotropy with the interparticle interactions. This can be clearly seen if we set Ksh = Kc eliminating the shell anisotropy contribution either with (Fig. 6(d) open circles) or without interparticle interactions (Fig. 6(d) open triangles and open stars).
For the frozen diluted ferrofluid samples the influence of dipolar interactions on Hc is not significant due to the low concentration of magnetic CS nanoparticles. Their absence results in a decrease in Hc (Fig. 6(e and f) closed stars). Finally, if the shell anisotropy is taken to be equal to the core one (Ksh = Kc) evidently the coercivity Hc decreases in both MnFe2O4 and CoFe2O4 based CS nanoparticles (Fig. 6(e and f) open symbols).
4. Conclusions
We have employed a mesoscopic scale approach to study the low temperature hysteresis behaviour of soft/soft and hard/soft ultra-small bimagnetic nanoparticles composed of a MnFe2O4 or CoFe2O4 core surrounded by a thin maghemite shell. A dense assembly and a very diluted ferrofluid are considered for both types of nanoparticles. In all cases, inter-particle and intra-particle interactions together with particle size polydispersity are included in our studies. Our numerical results are given together with the experimental results and interpret the observed experimental behaviour.Our results show that the cooling field dependence of the Hex is non-monotonic for both diluted and dense assemblies. The Hex is higher for the dense assemblies of bimagnetic nanoparticles due to the collective interparticle exchange interactions acting through the multi-connected shells. The maximum exchange bias field appears at a cooling field value equal to half the corresponding anisotropy field as indicated by the virgin curves. On the other hand, the coercive field does not vary significantly in a broad range of cooling fields for the soft/soft nanoparticle assemblies, and it is larger in the case of the dense assemblies as expected due to the enhanced inter-particle interactions. Surprisingly, the above Hc behaviour is different for the hard/soft assemblies where the coercive field takes higher values in the case of diluted ferrofluids and exhibits a peak at higher cooling field values for both dense and diluted assemblies attributed to the large anisotropy of particles. This variation of Hex and Hc with the applied cooling field is in good qualitative agreement with the experimental findings.
The overall analysis of our results clearly demonstrates that the more significant contribution to Hex and Hc of the CoFe2O4@γ-Fe2O3 nanoparticles comes from the intraparticle structure with the interparticle interactions playing a minor role in both ferrofluids and powders. The interplay is much stronger in manganese ferrite/maghemite nanoparticle dense assemblies where the dipolar interactions play the dominant role, because of their larger contribution compared to the particles anisotropy. In the diluted ferrofluids, the dipolar contribution is not significant because of the low particle concentration.
Our results demonstrate the possibility to control the magnetic behaviour of nanostructures by using appropriate core/shell bimagnetic nanoparticles.
5. Experimental section
5.1 NP synthesis and XRD characterization
The synthesis and characterization of the MnFe2O4@γFe2O3 or CoFe2O4@γFe2O3 core–shell NPs, probed here either in dilute colloidal dispersions or in powders, have been extensively described in ref. 31. We recall here the main important aspects.The very small NPs are obtained by coprecipitation of stoichiometric aqueous solutions of divalent metals X2+ (X2+ is either Mn2+ or Co2+) and Fe3+ ions in a NH3 buffer at pH 11, under vigorous stirring at 100 °C.39 In order to reduce the concentrations of free ions in the solution and to clean the particle surfaces, the precipitate is washed with a 2 mol l−1 aqueous HNO3 solution. A hydrothermal treatment of the NPs with a Fe(NO3)3 solution at 100 °C produces a thin maghemite (γ-Fe2O3) shell around the core of XFe2O4. This shell avoids chemical degradation of the core in an acidic medium and tunes the chemical stability of NPs. Its thickness tsh (see Table 1) is obtained by chemical titration.40 This maghemite shell also imparts the NPs with an electrostatic superficial charge, allowing their stable dispersion in aqueous media at room temperature.40
| Core–shell NPs | d (nm) | t sh (nm) | H a (kA m−1) | p |
|---|---|---|---|---|
| a d: mean crystalline NP diameter deduced from powder X-ray diffraction; tsh: shell thickness deduced from chemical titrations; Ha: anisotropy field deduced from the first magnetization curve obtained at 5 K in ref. 31; p: NPs surface pinning parameter as deduced in ref. 31. | ||||
| MnFe2O4@γFe2O3 | 3.3 | 0.4 | 4 × 102 | 0.01 |
| CoFe2O4@γFe2O3 | 3.1 | 0.5 | 1.2 × 103 | 0.03 |
Powder X-ray diffraction experiments at the Brazilian Synchrotron Light Laboratory-LNLS confirm the spinel structure of the NPs. The Scherrer equation applied to the [311] most intense line of the diffractograms allows the deduction of the mean crystalline NP diameter d, given in Table 1. The roughly spherical shape and the size distribution of the NPs were also investigated by transmission electron microscopy (TEM) at UPMC-Paris 6 with a JEOL JEM-100 CX II microscope.31
5.2 Magnetic measurements
DC magnetization measurements are performed at low temperature using a PPMS (Physical Property Measurement System) from UnB and SU with a Vibrating Sample Magnetometer set-up. Their superconducting coil produces magnetic fields in the range of 7.7 × 104 kA m−1, down to a temperature of T = 2 K. The magnetic field dependence of the magnetization is measured either in zero-field-cooled (ZFC) and or in field-cooled (FC) modes, for the latter in progressive increasing fields.For the investigation of the coupling between the NP cores and their disordered surface spins, we mainly focus here on the study of the FC magnetic hysteresis loops. The samples are first frozen in a zero field, down to T = 250 K (below the temperature of solvent freezing) to avoid any sample texture, both for dilute dispersions and for powders, of respective NP volume fractions of 0.4% and 27%. This procedure ensures that, in all the measurements carried out, the same spatial organization and randomness of the magnetic anisotropy axis of the various NPs takes place. A static magnetic field is then applied while the temperature is decreased from 250 K down to low temperature, and after this field cooling process the magnetic hysteresis is recorded. Between two loop measurements the temperature is increased back to 250 K, far above the NP blocking temperature.31 For more details on the magnetic measurement procedures see ref. 31.
Single particle behaviours, averaged over the assembly, are observed in frozen dilute dispersions, as the NPs are far away from each other, without contact. In contrast in powders, NPs are in direct contact and collective behaviours can be observed.36
The loops are observed to be H-shifted along negative fields, in FC measurements. The exchange bias (Hex) and the coercive field (Hc) are then quantified by the following relations:
| Hex = (Hc+ + Hc−)/2 | (2) |
| Hc = (Hc+ − Hc−)/2 | (3) |
Author contributions
Franciscarlos Gomes da Silva: conceptualization, methodology, data curation, resources, writing—original draft, writing—review & editing. Marianna Vasilakaki: conceptualization, theoretical model, methodology, writing—review & editing. Rafael Cabreira Gomes: conceptualization, methodology, data curation, validation. Renata Aquino: sample preparation, methodology, data curation. Alex Fabiano Cortez Campos: methodology, writing—review & editing. Emmanuelle Dubois: methodology, writing—review & editing. Régine Perzynski: conceptualization, methodology, resources, writing—review & editing. Jérôme Depeyrot: conceptualization, methodology, resources, writing—original draft, writing—review & editing. Kalliopi Trohidou: conceptualization, theoretical model, methodology, writing—review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors greatly acknowledge the European Union's Horizon 2020 Research and Innovation Programme under grant agreement no. 731976 (MAGENTA) and the Dean of Research and Innovation at UnB for their finnacial support. The authors of UnB and Sorbonne Université also acknowledge support by the Brazilian/French contract CAPES/COFECUB no. 88881.370915/2019-01. Authors also gratefully acknowledge the financial support of the Brazilian agencies CNPq through contract INCT-FCx (Grant 2014/50983-3) and PRONEX-FAPDF (2017–2021) no. 0193.001194/2016.References
- E. Eftaxias and K. N. Trohidou, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 134406 CrossRef.
- M. Vasilakaki and K. N. Trohidou, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 144402 CrossRef.
- Y. Hu, Y. Liu and A. Du, J. Magn. Magn. Mater., 2011, 323, 2613–2621 CrossRef CAS.
- S. P. Tsopoe, C. Borgohain, R. Fopase, L. M. Pandey and J. P. Borah, Sci. Rep., 2020, 10, 18666 CrossRef CAS PubMed.
- R. Skomski and J. M. D. Coey, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 15812–15816 CrossRef CAS PubMed.
- H. Khurshid, M.-H. Phan, P. Mukherjee and H. Srikanth, Appl. Phys. Lett., 2014, 104, 072407 CrossRef.
- L. del Bianco, A. Hernando, M. Multigner, C. Prados, J. C. Sánchez-López, A. Fernández, C. F. Conde and A. Conde, J. Appl. Phys., 1998, 84, 2189–2192 CrossRef CAS.
- G. C. Lavorato, E. Lima, H. E. Troiani, R. D. Zysler and E. L. Winkler, Nanoscale, 2017, 9, 10240–10247 RSC.
- D. Das and A. Alam, Phys. Rev. Mater., 2021, 5, 044404 CrossRef CAS.
- V. Skumryev, S. Stoyanov, Y. Zhang, G. Hadjipanayis, D. Givord and J. Nogués, Nature, 2003, 423, 850–853 CrossRef CAS PubMed.
- A. López-Ortega, M. Estrader, G. Salazar-Alvarez, A. G. Roca and J. Nogués, Phys. Rep., 2015, 553, 1–32 CrossRef.
- S. Noh, S. H. Moon, T.-H. Shin, Y. Lim and J. Cheon, Nano Today, 2017, 13, 61–76 CrossRef CAS.
- I. v. Golosovsky, G. Salazar-Alvarez, A. López-Ortega, M. A. González, J. Sort, M. Estrader, S. Suriñach, M. D. Baró and J. Nogués, Phys. Rev. Lett., 2009, 102, 247201 CrossRef CAS PubMed.
- G. Salazar-Alvarez, J. Sort, S. Suriñach, M. D. Baró and J. Nogués, J. Am. Chem. Soc., 2007, 129, 9102–9108 CrossRef CAS PubMed.
- E. Lima, E. L. Winkler, D. Tobia, H. E. Troiani, R. D. Zysler, E. Agostinelli and D. Fiorani, Chem. Mater., 2012, 24, 512–516 CrossRef CAS.
- K. Sartori, G. Cotin, C. Bouillet, V. Halté, S. Bégin-Colin, F. Choueikani and B. P. Pichon, Nanoscale, 2019, 11, 12946–12958 RSC.
- N. Flores-Martinez, G. Franceschin, T. Gaudisson, S. Haj-Khlifa, S. G. Derouich, N. Yaacoub, J.-M. Grenèche, N. Menguy, R. Valenzuela and S. Ammar, Sci. Rep., 2019, 9, 19468 CrossRef PubMed.
- M. A. Almessiere, Y. Slimani and A. Baykal, J. Alloys Compd., 2018, 767, 966–975 CrossRef CAS.
- N. A. Algarou, Y. Slimani, M. A. Almessiere, A. Baykal, S. Guner, A. Manikandan and I. Ercan, J. Magn. Magn. Mater., 2020, 499, 166308 CrossRef CAS.
- N. A. Algarou, Y. Slimani, M. A. Almessiere, F. S. Alahmari, M. G. Vakhitov, D. S. Klygach, S. V. Trukhanov, A. V. Trukhanov and A. Baykal, J. Mater. Res. Technol., 2020, 9, 5858–5870 CrossRef CAS.
- M. Vasilakaki, G. Margaris, E. Eftaxias and K. N. Trohidou, Sci. Rep., 2015, 5, 9609 CrossRef CAS PubMed.
- M. Vasilakaki, G. Margaris, E. Eftaxias, and K. N. Trohidou, Exchange Bias from Thin Film to Nanogranular and Bulk Systems, CRC Press, Taylor & Francis Group, Boca Raton, FL, 1st edn, 2017, vol. 1, ch. 6 Search PubMed.
- X. He, Y. Xu, X. Yao, C. Zhang, Y. Pu, X. Wang, W. Mao, Y. Du and W. Zhong, RSC Adv., 2019, 9, 30195–30206 RSC.
- F. G. Silva, J. Depeyrot, Yu. L. Raikher, V. I. Stepanov, I. S. Poperechny, R. Aquino, G. Ballon, J. Geshev, E. Dubois and R. Perzynski, Sci. Rep., 2021, 11, 5474 CrossRef CAS PubMed.
- L. del Bianco, D. Fiorani, A. Testa, E. Bonetti and L. Signorini, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 052401 CrossRef.
- V. Narayanaswamy, I. A. Al-Omari, A. S. Kamzin, B. Issa and I. M. Obaidat, Nanomaterials, 2022, 12, 262 CrossRef CAS PubMed.
- G. C. Lavorato, D. Peddis, E. Lima, H. E. Troiani, E. Agostinelli, D. Fiorani, R. D. Zysler and E. L. Winkler, J. Phys. Chem. C, 2015, 119, 15755–15762 CrossRef CAS.
- N. Domingo, D. Fiorani, A. M. Testa, C. Binns, S. Baker and J. Tejada, J. Phys. D: Appl. Phys., 2008, 41, 134009 CrossRef.
- M. S. Andersson, R. Mathieu, S. S. Lee, P. S. Normile, G. Singh, P. Nordblad and J. A. de Toro, Nanotechnology, 2015, 26, 475703 CrossRef PubMed.
- F. G. da Silva, Magnetical properties, surface disorder and Exchange bias of magnetic nanoparticle, University of Brasília/Sorbonne Université, 2013 Search PubMed.
- R. Cabreira-Gomes, F. G. Silva, R. Aquino, P. Bonville, F. A. Tourinho, R. Perzynski and J. Depeyrot, J. Magn. Magn. Mater., 2014, 368, 409–414 CrossRef CAS.
- R. C. Gomes, F. G. da Silva, T. Q. Muniz, G. Gomide, V. Pilati, R. Aquino, J. Geshev, R. Perzynski and J. Depeyrot, J. Alloys Compd., 2020, 153646 CrossRef.
- T. J. Salez, M. Kouyaté, C. Filomeno, M. Bonetti, M. Roger, G. Demouchy, E. Dubois, R. Perzynski, A. Cēbers and S. Nakamae, Nanoscale Adv., 2019, 1, 2979–2989 RSC.
- A. G. Leonel, A. A. P. Mansur, S. M. Carvalho, L. E. F. Outon, J. D. Ardisson, K. Krambrock and H. S. Mansur, Nanoscale Adv., 2021, 3, 1029–1046 RSC.
- R. Cabreira Gomes, F. G. da Silva, T.-Q. Silva, G. Gomide, V. Pilati, R. Aquino, J. Geshev, R. Perzynski and J. Depeyrot, J. Alloys Compd., 2020, 824, 153646 CrossRef CAS.
- F. G. Silva, R. Aquino, F. A. Tourinho, V. I. Stepanov, Y. L. Raikher, R. Perzynski and J. Depeyrot, J. Phys. D: Appl. Phys., 2013, 46, 285003 CrossRef.
- G. Margaris, K. N. Trohidou and J. Nogués, Adv. Mater., 2012, 24, 4331–4336 CrossRef CAS PubMed.
- G. Margaris, M. Vasilakaki, D. Peddis, K. N. Trohidou, S. Laureti, C. Binns, E. Agostinelli, D. Rinaldi, R. Mathieu and D. Fiorani, Nanotechnology, 2017, 28, 035701 CrossRef CAS PubMed.
- R. Aquino, F. A. Tourinho, R. Itri, M. C. F. L. e Lara and J. Depeyrot, J. Magn. Magn. Mater., 2002, 252, 23–25 CrossRef CAS.
- J. A. Gomes, M. H. Sousa, F. A. Tourinho, R. Aquino, J. Depeyrot, E. Dubois and R. Perzynski, J. Phys. Chem. C, 2008, 112, 6220–6227 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |