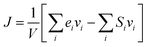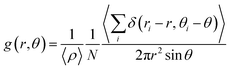Open Access Article
Open Access ArticleAligned structures of mesogenic motifs in epoxy resin and their thermal conductivities†
Minhwan
Lee
 a,
Min Young
Ha
a,
Mooho
Lee
b,
Ju Hyun
Kim
b,
Sung Dug
Kim
b,
In
Kim
*b and
Won Bo
Lee
a,
Min Young
Ha
a,
Mooho
Lee
b,
Ju Hyun
Kim
b,
Sung Dug
Kim
b,
In
Kim
*b and
Won Bo
Lee
 *a
*a
aSchool of Chemical and Biological Engineering, Seoul National University, Seoul 08826, Republic of Korea. E-mail: wblee@snu.ac.kr
bMaterial Research Center, Samsung Advanced Institute of Technology, Samsung Electronics Co., Ltd, Gyeonggi-do 16678, Republic of Korea. E-mail: in1.kim@samsung.com
First published on 2nd March 2022
Abstract
The epoxy-based crosslinked polymer with the mesogenic group has been studied as a candidate resin material with high thermal conductivity due to the ordered structure of the mesogenic groups. In this study, we conducted all atomic molecular dynamics simulations with iterative crosslinking procedures on various epoxy resins with mesogenic motifs to investigate the effect of molecular alignment on thermal conductivity. The stacked structure of aromatic groups in the crosslinked polymer was analyzed based on the angle-dependent radial distribution function (ARDF), where the resins were categorized into three groups depending on their monomer shapes. The thermal conductivities of resins were higher than those of conventional polymers due to the alignment of aromatic groups, but no distinct correlation with the ARDF was found. Therefore, we conducted a further study about two structural factors that affect the alignment and the TC by comparing the resins within the same groups: the monomer with an alkyl spacer and functional groups in hardeners. The alkyl chains introduced in the epoxy monomers induced more stable stacking of aromatic groups, but thermal conductivity was lowered as they inhibited phonon transfer on the microscopic scale. In the other case, the functional groups in the hardener lowered the TC when the polar interaction with other polar groups in the monomer was strong enough to compete with the pi–pi interaction. These results represent how various chemical motifs in mesogenic groups affect their alignment on the atomistic scale, and also how they have effects on the TC consequently.
1. Introduction
There is a growing demand for polymer materials with high thermal conductivity (TC) as electronic products are getting smaller, requiring rapid dissipation of the heat generated by miniaturized electric circuits. Thermosetting epoxy resins with crosslinked structures are widely used as packaging materials for electronic devices, due to their ability to insulate electrical current, easy processability, chemical resistance, etc.1–3 Conventionally, nano-scale fillers such as graphene or carbon nanotubes are incorporated into epoxy resins to enhance their thermal or electric conductivity.4–9 As an alternative approach, mesogenic epoxy monomers were recently introduced, since they can considerably increase the TC due to their tendency to be aligned along one direction to provide an additional route for phonon transfer, in addition to the transfer along covalent bonds.10–13 Lin et al. reviewed a variety of epoxy thermoset resins with mesogenic groups which can form highly ordered domains, increasing the TC up to 1.05 W m−1 K−1.14To facilitate the intelligent design of mesogenic epoxy polymers with high thermal conductivity, it is crucial to develop a microscopic understanding of the correlation between molecular alignment and the transport of thermal energy. Molecular dynamics (MD) simulation can be a very advantageous tool to analyze the epoxy-based crosslinked polymers because it yields the atomistic details in the crosslinked structure and the macroscopic properties of the materials. A major obstacle in epoxy MD simulation is the proper construction of the crosslinked polymer network in a periodic simulation box: one-shot polymerization of randomly mixed monomers and hardener molecules might result in an unrealistic structure. In this regard, several reports suggested simulation procedures to construct stable atomistic configurations of resins where we utilized the method described by Varshney et al.15–17 They proposed numerical procedures to obtain stable crosslinked EPON-862/DETDA resin from iterative runs of MD simulations to gradually equilibrate the system. Furthermore, they showed the correlation between the TC and the structure in the other papers.16,18 Li et al. performed MD simulation with a similar procedure to study the thermal conductivities of ordered epoxy resin according to external strain.19 In respect of a variety of chemistry, simulation results from various epoxy resins have been reported, especially with more attention to the high-TC epoxy resin-based nanocomposites augmented with fillers such as graphene and boron nitrate.20–22
However, there are few computational studies focusing on the thermal conductivity of the epoxy resins generated from mesogenic monomers. Skačej et al. conducted Monte-Carlo simulation studies with the coarse-grained model to investigate the structure of a liquid crystal elastomer but did not deal with its thermal conductivity.23,24 Koda et al. compared experimental TC data of epoxy resin and intentionally ordered structures of liquid-crystalline epoxy monomers from MD simulation.25 However, their study lacks an explanation about how the MD configuration represents the microscopic structure of the material from which the TC results were measured. Especially, as Varshney et al. showed, generating structures by iterative crosslinking procedures is crucial for the accurate evaluation of thermal conductivities but the process was omitted in the previous reports.18 To the best of the authors' knowledge, there is no systematic study correlating the mesogenic structures and the resultant thermal conductivities in crosslinked polymer resins.
In this paper, we studied various kinds of cross-linked polymers using all-atomic MD simulation to reveal the effect of their molecular architectures on the TC. We performed iterative annealing and crosslinking simulations to generate realistic network structures. Then, we investigated the aligned structure of cross-linked polymers by calculating the angle-dependent radial distribution function (ARDF) among aromatic groups and measuring the thermal conductivities using the Green–Kubo relation. As aligning behavior showed distinct characteristics according to chemical motifs, we classified the studied epoxy resins into three different groups. Meanwhile, the TCs of resins were higher than that of conventional polymer materials as expected from the aligned structure noticed in the ARDF but no quantitative correlation was found between them. Therefore, two additional structural factors were studied by comparing resins within the same group; the first is a flexible alkyl chain that is introduced into monomers as a spacer and the second is the functional groups in hardeners whose polarity affects interaction with monomers. The results indicated that the aligning behavior of epoxy monomers and the TC of resins were both affected by those geometric factors complicatedly. Consequently, the detailed atomistic investigation by MD simulation gives a direction to enhance the thermal conductivities by exploiting the relationship between the chemical structure of molecules, the resultant aligned structure, and the thermal conductivity.
2. Computational methods
2.1 Crosslinked polymer construction
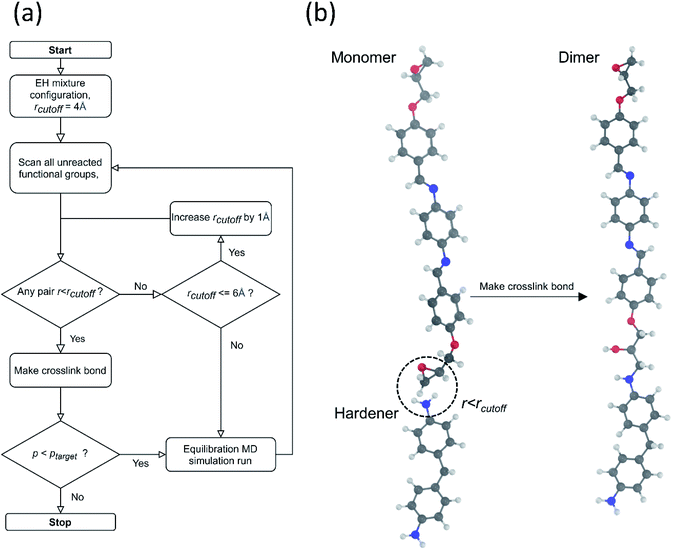
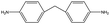
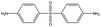
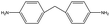
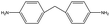
The crosslinked polymer structure was constructed from the epoxy and hardener molecules where the overall procedure is presented in Fig. 1(a). The initial mixture of the epoxy (E) and hardener (H) was made by randomly distributing the molecules with the Packmol software package to get an initial coordinate of the amorphous structure.26 The molecular representations of the studied EH pairs are listed in Table 1. The number of the total molecules was determined so that the initial density would be 1 g mL−1 in a cubic simulation box with a side length of 50 Å where the E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H ratio was set to 2
H ratio was set to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to consume all reactants when the reaction is completed. The initial configuration of the EH mixture was equilibrated by following several steps of procedures as explained in the next section.
1 to consume all reactants when the reaction is completed. The initial configuration of the EH mixture was equilibrated by following several steps of procedures as explained in the next section.
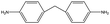
To generate epoxy crosslinking from an equilibrated EH mixture, all pairs of epoxy and amine functional groups were scanned, and the pairs closer than a prescribed cut-off distance were converted to crosslink bonds. The cut-off distance for the reaction was initially set to 4 Å but if no functional group pair was found the cut-off was increased by 1 Å. In addition, to prevent the formation of unphysically long bonds with extreme forces, the cut-off distance was not increased beyond the maximum cut-off of 6 Å. The positions and interaction parameters of atoms in the selected functional groups were modified to make a crosslinked bond structure mimicking the real ring-opening reaction of epoxy and amine groups as depicted in Fig. 1(b). The equilibrating MD procedures were then conducted again to stabilize the modified configuration. The MD simulation and crosslink formation with adaptive cut-off were iterated until the target crosslink ratio (ptarget) was reached, where the crosslink ratio p was defined by the ratio of the number of the reacted epoxy groups, ncross, to the entire initial number of the epoxy groups, nepoxy(1).
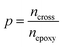 | (1) |
For all the EH pairs studied in this work, the ptarget was set as 0.6 to compromise computational cost and also to be above the percolation threshold, pc = 0.577, of the epoxy resins made from diamine and diepoxide assuming a random reaction.27 As expected, the TC was affected by the crosslink ratio as represented in Fig. S4† and it is noteworthy that the TC went up rapidly after p = 0.7. It also corresponds with the previous study by Vasilev et al. about TC of crosslinked polyisoprene and polybutadiene.28 However highly cross-linked polymers are considered to have unstable structures from the unphysically connected topology as most reaction sites are exhausted in the later stages of crosslinking iterations. Therefore, it is reasonable to set the ptarget to be just above the pc to prevent numerical artifacts in calculating TC. The supplementary simulation results for choosing parameters other than the crosslink ratio can be found in the ESI.†
2.2 MD simulation
The initial configuration of the E and H mixture was equilibrated before going to the iterative MD simulation step to make the crosslinked structure. First, energy minimization was performed to adjust the positions of atoms, bond lengths, angles, and dihedrals. The steepest descent and the conjugate gradient method were conducted consecutively. Then we performed annealing MD simulations in the NPT ensemble, with the thermostat and barostat set to 500 K and 1 atm, respectively, for 250 ps. The system was further equilibrated at the decreased temperature of 300 K for an additional 100 ps. The high temperature of 500 K was to relax the internal constraints from the unstable location of molecules.During the crosslinking iterations, a similar series of simulations were conducted to equilibrate the mixture containing newly formed crosslinking bonds. After searching for the epoxy–amine pairs and generating the crosslink bonds, the energy minimization was conducted with the steepest descent, conjugate gradient, and fire algorithms, consecutively.29 Then five steps of NVT simulations were followed: the system was equilibrated at 300 K, 400 K, and 500 K, where the temperature was linearly ramped between the equilibration runs, where each equilibration and ramping stage was 10 ps long. Finally, we conducted two rounds of NPT simulations at 1 atm, each 20 ps long, with the thermostat temperature set to 500 K and 300 K.
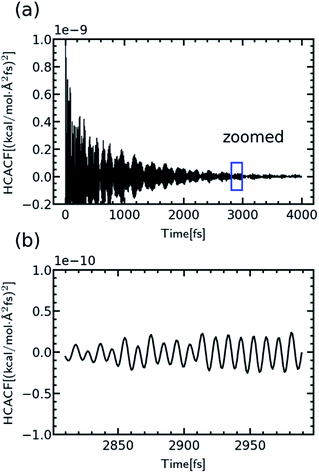
Starting from the equilibrated network structure, the TC of the crosslinked polymer was calculated using the Green–Kubo equilibrium simulation. The network was initially equilibrated for 200 ps in the NPT ensemble, and the production NVE simulation was conducted for 1 ns. The heat flux was computed and saved at every step to calculate the thermal conductivity from its time correlation function. The heat current autocorrelation function (HCACF) was obtained from 10 repeated independent runs with different initial velocities to get proper statistics.
The TC of the crosslinked polymer, κ, could be calculated by integrating the HCACF over the lag time t according to the Green–Kubo relationship where the heat flux J was from the history of energy flow (2).
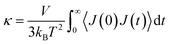 | (2) |
where ei, vi and Si are the per-atom energy, the velocity, and atomic stress of the ith atom, respectively. The HCACF of EH1 in Table 1 according to lag time is shown in Fig. 2 as an example to show the convergence of the simulation.
All simulations were conducted using LAMMPS software.30 The timestep of integration was set to 1 fs in the crosslinking step and 2 fs in the TC calculation step. All bonds associated with hydrogen atoms were constrained by the SHAKE algorithm.31 The OPLS-AA forcefield with 1.14*CM1A partial atomic charges was used to describe interactions among the atoms as obtained from the LigParGen server.32–34 Moltemplate software was used to tabulate interaction parameters from LigParGen and the initial system topology file.35 The interaction parameters for the crosslinked structure were from the topology files of monomer, hardener, dimer (one epoxy monomer + one hardener), and trimer (two epoxy monomers + one hardener) molecules where the original monomer and hardener parameters were replaced with the crosslinked structure. We assumed that the reaction changes only the interaction parameters related to crosslinking bond groups; therefore, only the products from one amine reaction site, which are a dimer with a secondary amine and an alcohol, and a trimer with a tertiary amine and two alcohol groups, were considered. The Nose–Hoover thermostat and MTK barostat were used to maintain the system temperature and pressure at the desired value.36–40
3. Results and discussion
3.1 Monomer effect
Before delving into the analysis of thermal conductivities, we first examined the molecular alignment of the crosslinked polymers at the molecular level. We calculated the pairwise distances r and the mutual angles θ between all aromatic group pairs in the system including both monomer and hardener molecules, where r is the Euclidean distance between the centers of mass of the phenyl groups, and θ is defined as the angle between the normal vectors of the 6-carbon planes. As shown in Fig. 3(a), we plot the angle-dependent radial distribution function g(r,θ),where N is the number of aromatic groups and ρ is the number density of aromatic groups.
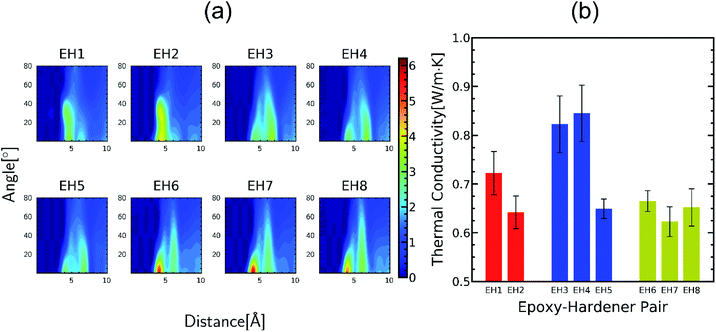
The peaks near r = 4–7 Å and θ = 0–40° were observed commonly throughout different resins, implying that there exist aligned structures in constructed crosslinked polymer MD configurations where the representative snapshot of the aligned aromatic group is inserted in Fig. S5.† The specific structure of the r − θ distributions differed among the choices of monomers and hardeners, which can be attributed to the chemical environment of the aromatic groups in each molecule. Merging the information of Fig. 3(a) and chemical features of the monomers and hardeners, the EH pairs in Table 1 were classified into three groups for explanation based on the connection group between two aromatic groups in monomers: first, monomers with biphenyl groups (EH1, EH2); second, monomers with imine groups (EH3, EH4, EH5); third, monomers whose aromatic groups are separated by ester groups (EH6, EH7, EH8). On the other hand, the hardeners have similar structures connected with two or three bonds which have fewer effects on the ARDF results compared to the monomers.
First, EH1 and EH2 resins with biphenyl groups in the monomer exhibited a single peak as shown in Fig. 3(a) near r = 4 Å, whereas all other resins showed a separation of the peak, which also featured a broad-angle peak in the narrow distance area. The narrow distance peak distribution is attributed to the similar inter-distance of two aromatic groups of the biphenyl group and hardener. Whereas the angular distribution can be explained by the structural mismatch of the straightly connected biphenyl groups and the two aromatic rings connected by two bent bonds in the hardener, where one pair of aromatic rings in the hardener and monomer should be stacked obliquely when the other pair is stacked in parallel.
EH3, EH4, and EH5 showed two vividly split peaks along the distance axis in r − θ distribution which is attributed to the imine group among the three aromatic groups in the monomer where it is also non-rotatable but the distance between two aromatic groups is farther than the biphenyl group. This difference in the inter-distance between aromatic groups also affects angle distribution; if one pair of aromatic groups of a monomer and a hardener are staked, the other aromatic group in the hardener should be located at a farther distance from another aromatic group of the monomer obliquely. Therefore, the former pair is comparatively stable due to less competition with the latter pair which results in contributing to the first narrow peak in the θ axis, while the second peak comes from the latter pair with broad-angle distribution due to their mismatch of the connected bond angle between the monomer and hardener like EH1 and EH2.
Finally, the aromatic groups in EH6, EH7, and EH8 monomers are separated by ester groups which have similar structures to imine groups resulting in double peaks in the distance axis in the same manner as in EH3, EH4, and EH5. A distinct characteristic of this third group was the intense peak near r = 4 Å which is attributed to rotatable bonds in ester groups, unlike biphenyl or imine groups. Without planar restriction, the aromatic groups could be stacked easily in parallel by changing configurations.
In summary, it was presented from the ARDF results the aligning behavior of aromatic groups in crosslinked polymers and how it was affected by the molecular structure. As a next step, we tried to correlate the microscopic stacked structure of aromatic groups with the TC results as shown in Fig. 3(b). The thermal conductivities of the resins were from 0.62 to 0.85 W m−1 K−1 and were higher than those of commonly used polymer materials which can be expected from the alignment peaks in Fig. 3(a). It is also in accord with well-known physics that crystalline likelystacked aromatic groups contribute to faster phonon transport than those stacked through the bond of polymers.41 However, any aligning parameter that quantitatively correlates the TC and the ARDF was not found and quite large deviations in the TC were noticed even in the same group. This is because different molecular structures other than the connecting parts of aromatic groups in epoxy monomers also affect the crosslinked polymer complicatedly. Therefore, we conducted further comparative analysis for several cases affected only by each factor which resulted in finding two structural factors affecting TC; one is flexible chains included in the epoxy monomer as spacers and the other one is the functional groups of hardeners connecting two aromatic groups. In the following sections, it is described how the molecular motifs affect TC considering their chemical properties from further analysis.
3.2 Flexible chain spacer effect
Among the molecules in Table 1, EH2 and EH7 are modifications of EH1 and EH6 molecules, respectively, introduced to study the effect of alkyl spacers. In our results as presented in Fig. 3(b), the TC of EH2 was 0.64 W m−1 K−1, lower than that of EH1 which was 0.72 W m−1 K−1 whereas the EH6/EH7 cases showed the same trend for TC where the TC of EH7 was 0.62 W m−1 K−1 and the TC of EH6 was 0.66 W m−1 K−1. Otherwise, in respect of alignment it was noticed that the spacer increased stacked structures of aromatic groups as presented in Fig. 4; the g(r,θ = 0) peaks have higher values as shown in Fig. 4(a) and (b) which means there are more stable stacked aromatic group pairs in parallel, and also the zoomed ARDF heatmaps in Fig. 4(c) indicate that overall aligning behavior was facilitated by alkyl spacers. Unfortunately, the TC results seemed to contradict the previous reports that the spacers in an epoxy monomer with mesogenic groups derive an ordered phase which could increase the TC.42–45 The difference could result from the small length scale of the MD simulations which is about a few nanometers long, whereas the size of the ordered domains in experiments was an order of magnitude larger than our MD simulation box. Therefore, it can be said that the flexibility of the spacer gives more chance for a stable alignment of the mesogenic groups, but in the MD scale without large ordered domains, the contributions from the alkyl spacers dominated the stability of the alignments, resulting in an overall lowering of TC. Furthermore, the connecting group chemistry among epoxies also affected the opposite trends in the molecular alignment of spacers depending on their types. The monomer of EH7 including ester groups that can rotate freely makes it relatively easy to be entangled with the alkyl chain resulting in fewer effects on aligning behavior but the EH2 biphenyl occupied linear volume straightly which prevents the structure from being disordered. The results give a microscopic understanding of how a spacer can be used to enhance the TC of a crosslinked polymer. In other respects, it is remarkable that the spacer can also increase the processability of polymer resin by decreasing glass transition temperature which broadens the applicability of our results.46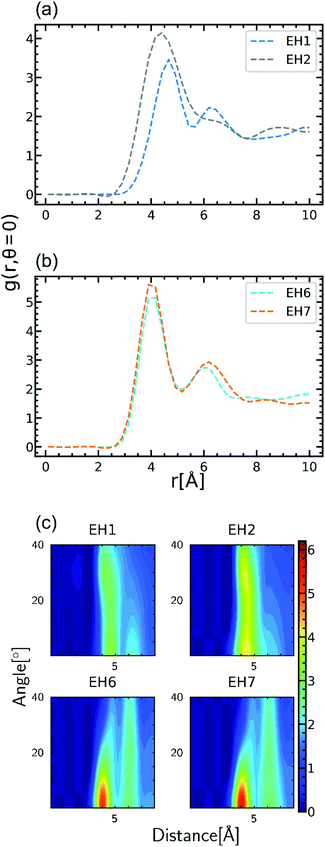 | ||
| Fig. 4 Comparative representation to show the effect of the spacer in the epoxy monomer on aligning behavior. Radial distribution functions, g(r,θ = 0), of aromatic group pairs when the angle between normal vectors is zero are represented for EH1/EH2 (a) and EH6/EH7 (b). The ARDF density maps of Fig. 3 for EH1/EH2 and EH6/EH7 cases are zoomed in to show the peak level increment in EH2 and EH7 (c). | ||
3.3 Hardener effect
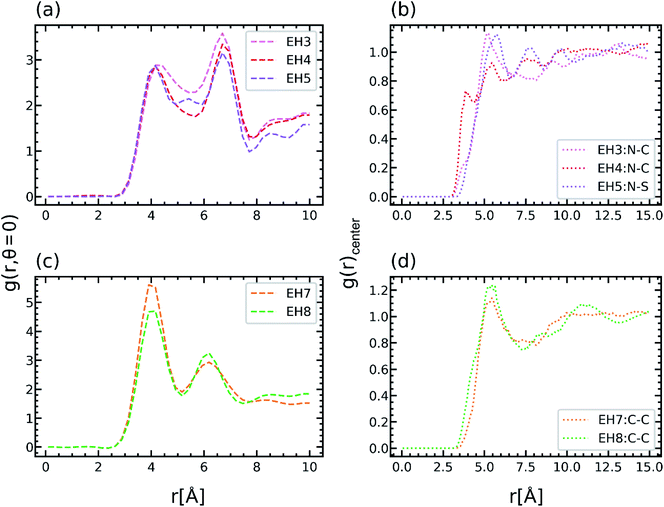
As shown in Fig. 3(b), the TC of EH5 was much lower than that of EH3 and EH4 by about 0.2 W m−1 K−1 which was a distinctly large deviation considering the similarity of the molecular structures of the epoxy and hardener in this group. Because the difference between them is mainly from the connecting parts of hardeners it can be inferred that the properties of the connecting motifs affect the structure and TC of the crosslinked polymer. Therefore, in this section, the effect of the hardener structure was investigated in detail. In Fig. 5(a), EH3, EH4, and EH5 feature two peaks in g(r,θ = 0) near r ≅ 4 Å and r ≅ 7 Å in common, whereas another small peak was observed in EH5 between the two peaks. As explained in the previous section, the common two peaks are from the two pairs of aligned aromatic groups such that one is stacked straight up and the other is distanced relatively far; therefore, another peak in EH5 implies a hardener can be located at the intermediate position which makes aromatic group pairs be distanced farther than the former pair and closer than the latter pair (Fig S6†). This coordination of the hardener to the epoxy in EH5 is attributed to the strong polar interaction between the sulfone group in the hardener and the imine group in the epoxy which is noticed from Fig. 5(b) as sulfur atoms were coordinated near the nitrogen atoms in imine groups. Consequently, the lower TC of EH5 is explained as a result of the polar interaction between polar connecting groups in the hardener and epoxy which hinders the aligning tendency by competing with the pi–pi interaction of aromatic groups.In the same manner, the ester groups of the hardener in EH3 and the EH8 were also expected to have polar interaction with the imine group and the ester group in epoxy. In the case of EH3, the g(r,θ = 0) at r ≅ 5.5 Å which is the location of the peak in EH5 derived by the polar interaction was even higher than the peak value though there was no distinct peak as presented in Fig. 5(a). Also, from Fig. 5(b), it was observed that carbon atoms in the hardener also coordinated to nitrogen atoms in the epoxy. However, as the TC of EH3 was not as low asthat of EH5, it can be inferred that the polar interaction between the ester and the imine groups is not enough to affect heat transport. Furthermore, the ester–ester interaction which is included in EH8 had more subtle effects on the crosslinked polymer; a lower value at the first peak in g(r,θ = 0) and slightly higher value of the g(r)center between the carbons in ester group are noticed as presented in Fig. 5(b) and (d). As the small disadvantage of the polar interaction is offset by the structural similarity between the epoxy and hardener, the TC of EH8 was a little higher than that of EH7. Conclusively, it was noticed that the chemical structure of the hardener also has effects on the aligning behavior of mesogenic groups but is less important than other factors except for the EH5 case where there is strong polar interaction. This result suggests that it is important to take into account the characteristics of chemical motifs in monomers and hardeners carefully since they affect the alignment and TC of the crosslinked polymer complicatedly.
4. Conclusions
The TC of various epoxy-based crosslinked polymers with mesogenic motifs was studied to elucidate the relation between the structural alignment of the aromatic groups and the enhancement of thermal conductivity. A stable atomistic configuration of crosslinked polymers was constructed by gradually converting pairs of epoxy and amine functional groups to crosslink bonds, followed by extensive equilibration. The structural analysis provided microscopic evidence that there exists molecular alignment regardless of the EH pairs used, where the aromatic groups were aligned with the most probable pair distance and angle of r = 4–7 Å and θ = 0–40°. Furthermore, the EH pairs were categorized into three groups by analyzing the ARDF peaks which explains how the molecular structure of mesogenic groups affects aligning behavior. Due to the contribution of stacking of aromatic groups, the TCs of resins were higher than those of conventional polymers, but no distinct overall correlation with the aligned structure was found. However, by comparing EH pairs within the same groups, two structural factors were found to affect the aligning behavior of crosslinked polymers: a flexible chain spacer in the monomer and a chemical motif in the connecting part in the hardener. First, the flexible chains improved the stability of the stacked structure while decreasing the TC of the crosslinked polymers on the MD scale. This result seems to originate from the limited length scale of the MD simulation, where the contribution of alkyl chains dominated the gain of TC from the ordering of mesoscopic domains as reported in experiments. Second, the polar group in the hardener lowered the TC of the resin when it has strong interaction with other polar groups in the monomer as the interaction competes with the pi–pi interaction. These computational results provide a physical understanding of the high-TC crosslinked polymers with mesogenic groups, especially in respect of the microscopic length scale that is accessible by atomistic MD simulation. It could give insights into the efficient design of thermosetting polymers with superior thermal dissipation performance by modifying the molecular structure.Author contributions
Conceptualization: In Kim and Won Bo Lee; methodology: Minhwan Lee, Min Young Ha, and Mooho Lee; formal analysis: Minhwan Lee and Min Young Ha; data curation: Minhwan Lee and Min Young Ha; validataion: Mooho Lee, Ju Hyun Kim, Sung Dug Kim, and In Kim; project administration: In Kim, Won Bo Lee, and Mooho Lee; writing – original draft: Minhwan Lee; writing – review & editing: Won Bo Lee and Min Young Ha; all authors approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Samsung Electronics Co. Ltd and the National Research Foundation of Korea (NRF) Grant funded by the Korea government (MSIT) (NRF-2018M3D1A1058633, NRF-2018H1A2A1061260, and NRF-2019R1A2C1085081).References
- L.-L. Lin, T.-H. Ho and C.-S. Wang, Polymer, 1997, 38, 1997–2003 CrossRef CAS.
- T.-H. Ho and C.-S. Wang, Polymer, 1996, 37, 2733–2742 CrossRef CAS.
- F.-L. Jin, X. Li and S.-J. Park, J. Ind. Eng. Chem., 2015, 29, 1–11 CrossRef CAS.
- M. J. Biercuk, M. C. Llaguno, M. Radosavljevic, J. K. Hyun, A. T. Johnson and J. E. Fischer, Appl. Phys. Lett., 2002, 80, 2767–2769 CrossRef CAS.
- F. Du, C. Guthy, T. Kashiwagi, J. E. Fischer and K. I. Winey, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 1513–1519 CrossRef CAS.
- S. I. Hussein, A. M. Abd-Elnaiem, T. B. Asafa and H. I. Jaafar, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 475 CrossRef.
- Q. Li, Y. Guo, W. Li, S. Qiu, C. Zhu, X. Wei, M. Chen, C. Liu, S. Liao, Y. Gong, A. K. Mishra and L. Liu, Chem. Mater., 2014, 26, 4459–4465 CrossRef CAS.
- F. Wang, L. T. Drzal, Y. Qin and Z. Huang, J. Mater. Sci., 2014, 50, 1082–1093 CrossRef.
- C. Xiao, L. Chen, Y. Tang, X. Zhang, K. Zheng and X. Tian, Composites, Part A, 2019, 116, 98–105 CrossRef CAS.
- S.-h. Song, H. Katagi and Y. Takezawa, Polymer, 2012, 53, 4489–4492 CrossRef CAS.
- A. M. Islam, H. Lim, N.-H. You, S. Ahn, M. Goh, J. R. Hahn, H. Yeo and S. G. Jang, ACS Macro Lett., 2018, 7, 1180–1185 CrossRef CAS.
- M. Harada, D. Morioka and M. Ochi, J. Appl. Polym. Sci., 2018, 135, 46181 CrossRef.
- X. Yang, X. Zhong, J. Zhang and J. Gu, J. Mater. Sci. Technol., 2021, 68, 209–215 CrossRef.
- Y. Lin, X. Huang, J. Chen and P. Jiang, High Voltage, 2017, 2, 139–146 CrossRef.
- C. Wu and W. Xu, Polymer, 2006, 47, 6004–6009 CrossRef CAS.
- V. Varshney, S. S. Patnaik, A. K. Roy and B. L. Farmer, Macromolecules, 2008, 41, 6837–6842 CrossRef CAS.
- N. B. Shenogina, M. Tsige, S. S. Patnaik and S. M. Mukhopadhyay, Macromolecules, 2012, 45, 5307–5315 CrossRef CAS.
- V. Varshney, S. S. Patnaik, A. K. Roy and B. L. Farmer, Polymer, 2009, 50, 3378–3385 CrossRef CAS.
- S. Li, X. Yu, H. Bao and N. Yang, J. Phys. Chem. C, 2018, 122, 13140–13147 CrossRef CAS.
- A. Lakshmanan, S. Srivastava, A. Ramazani and V. Sundararaghavan, Appl. Phys. Lett., 2018, 112, 151902 CrossRef.
- Z. Liu, J. Li, C. Zhou and W. Zhu, Int. J. Heat Mass Transfer, 2018, 126, 353–362 CrossRef CAS.
- M. Zhu, J. Li, J. Chen, H. Song and H. Zhang, Comput. Mater. Sci., 2019, 164, 108–115 CrossRef CAS.
- G. Skačej and C. Zannoni, Soft Matter, 2011, 7(21), 9983–9991 RSC.
- G. Skacej, Soft Matter, 2018, 14, 1408–1416 RSC.
- T. Koda, T. Toyoshima, T. Komatsu, Y. Takezawa, A. Nishioka and K. Miyata, Polym. J., 2012, 45, 444–448 CrossRef.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- K. Dušek, M. Ilavský and S. Luňák, J. Polym. Sci., Polym. Symp., 1975, 53(1), 29–44 CrossRef.
- A. Vasilev, T. Lorenz and C. Breitkopf, Polymers, 2021, 13(3), 315 CrossRef CAS PubMed.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665 CrossRef CAS PubMed.
- L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870 CrossRef CAS PubMed.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 054102 CrossRef.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- M. E. Tuckerman, J. Alejandre, R. López-Rendón, A. L. Jochim and G. J. Martyna, J. Phys. A: Math. Gen., 2006, 39, 5629–5651 CrossRef CAS.
- N. Burger, A. Laachachi, M. Ferriol, M. Lutz, V. Toniazzo and D. Ruch, Prog. Polym. Sci., 2016, 61, 1–28 CrossRef CAS.
- Y. Takezawa, M. Akatsuka and C. Farren, 2003.
- M. Akatsuka, Y. Takazawa and K. Sugaware, US20060276568, 2006.
- K. Fukushima, H. Takahashi, Y. Takezawa, M. Hattori, M. Itoh and M. Yonekura, The 17th Annual Meeting of the IEEE Lasers and Electro-Optics Society, 2004, pp. 340–343 Search PubMed.
- Q. Zhang, G. Chen, K. Wu, J. Shi, L. Liang and M. Lu, J. Appl. Polym. Sci., 2020, 137, 49143 CrossRef CAS.
- M. Harada, N. Okamoto and M. Ochi, J. Appl. Polym. Sci., 2016, 133, 44244 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1na00896j |
| This journal is © The Royal Society of Chemistry 2022 |