Open Access Article
Open Access ArticleMonolayer H-MoS2 with high ion mobility as a promising anode for rubidium (cesium)-ion batteries†
Baichuan
Lu
 a,
Xiaochi
Liu
*ab,
Jifeng
Qu
*a and
Zesheng
Li
a,
Xiaochi
Liu
*ab,
Jifeng
Qu
*a and
Zesheng
Li
 c
c
aCenter for Advanced Measurement Science, National Institute of Metrology, Beijing, 100029, China. E-mail: liuxc@apm.ac.cn; qujf@nim.ac.cn
bKey Laboratory of Atomic Frequency Standards, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan, 430071, China
cKey Laboratory of Cluster Science of Ministry of Education, Beijing Key Laboratory of Photoelectronic/Electro-photonic Conversion Materials, School of Chemistry and Chemical Engineering, Beijing Institute of Technology, Beijing, 100081, China
First published on 21st July 2022
Abstract
Secondary ion batteries rely on two-dimensional (2D) electrode materials with high energy density and outstanding rate capability. Rb- and Cs-ion batteries (RIBs and CIBs) are late-model batteries. Herein, using first-principles calculations, the potential performance of H-MoS2 as a 2D electrode candidate in RIBs and CIBs has been investigated. The M-top site on 2D H-MoS2 possesses the most stable metal atom binding sites, and after adsorbing Rb and Cs atoms, its Fermi level goes up to the conduction band, indicating a semiconductor-to-metal transition. The maximal theoretical capacities of RIBs and CIBs are 372.05 (comparable to those of commercial graphite-based LIBs) and 223.23 mA h g−1, respectively, due to the strong adsorption capability of H-MoS2 for Rb and Cs ions. Noticeably, the diffusion barriers of Rb and Cs on H-MoS2 are 0.037 and 0.036 eV, respectively. Such a low diffusion barrier gives MoS2-based RIBs and CIBs high rate capability. In addition, H-MoS2 also has the characteristics of suitable open-circuit voltage, low expansion, good cycle stability, low cost, and easy experimental realization. These results indicate that MoS2-based RIBs and CIBs are innovative batteries with great potential, and may provide opportunities for cross-application of energy storage and multiple disciplines.
1 Introduction
Electrochemical storage of alkali metal technology has shown great application prospects in the field of energy storage with a reversible, efficient and convenient electrochemical process.1–4 Representative devices are batteries and capacitors. With continuous in-depth research and innovative breakthroughs, Li, Na and K ion batteries (LIBs, SIBs and KIBs) have been successfully realized, and LIBs and SIBs have been commercialized.5–7 However, rubidium (Rb) and caesium (Cs), also as alkali metals, have low theoretical energy density due to their large relative atomic mass, so there is almost no research on Rb or Cs (Rb/Cs) energy storage devices. Recently, Kang and McGilligan reported Rb ion batteries (RIBs) as the Rb-atom source of the cold-atom physics systems.8–11 It is regarded as one of the key technologies for miniaturization of cold-atom physics systems due to its features such as reversibility, low power consumption, and small size.8,12 Cs, like Rb, has a precise transition frequency and is frequently utilized in the field of cold-atom precision measurement. Cs ion batteries (CIBs), which were inspired by RIB research, appear to be feasible as well. Importantly, the successful application of RIBs demonstrates that RIBs and CIBs are both promising and deserving of further research. The following are some of the potential advantages of RIBs and CIBs: (1) because the diffusion coefficient of alkali metal ions can increase as the atomic number increases,13,14 Rb and Cs ions may have higher diffusion coefficients. On the one hand, the greater the diffusion coefficient (low diffusion barrier) of the electrode material, the better its rate capability in general;15,16 on the other hand, a high diffusion coefficient makes dendrite formation harder17,18 (alkali metals are more likely to accumulate and deposit to form dendrites when the electrode surface has a large diffusion barrier; LIBs, SIBs, and KIBs all suffer from this disadvantage); (2) RIBs and CIBs are attractive because the standard redox potential of Rb+/Rb (−2.98 V vs. SHE) and Cs+/Cs (−3.026 V vs. SHE) in electrolyte is lower than that of Na+/Na (−2.71 V vs. SHE) and K+/K (−2.93 V vs. SHE), even comparable to Li+/Li (−3.04 V vs. SHE), which allows RIBs and CIBs to sustain higher cell voltages.19 (3) At present, most miniaturized cold-atom standards and sensors use Rb and Cs, and such battery-type alkali sources can make these quantum standards and sensors more environmentally adaptable.9,12 All the aforementioned characteristics bode well for the development of RIBs and CIBs as promising battery systems.The principle and structure of RIBs and CIBs can also follow alkali ion batteries (AIBs, including LIBs, SIBs and KIBs).9 Anode materials have always been considered as one of the key factors restricting the performance of AIBs.20 Ideal RIB and CIB anode materials should also have high energy density, fast charge and discharge rates, and high stability in order to suit the needs of RIBs and CIBs.21 Graphite is a common anode material in commercial batteries, and it has also been demonstrated to work as an anode in RIBs.8,9 However, graphite is not a good anode material for RIBs and CIBs. This is due to a mismatch between the interlayer spacing of graphite (3.35 Å) and the atomic radius of Rb and Cs (2.48 and 2.65 Å, respectively), which makes intercalation and deintercalation of Rb and Cs extremely difficult, and Rb/Cs forcibly intercalating in graphite may also cause problems such as a considerable drop in ion diffusion performance (due to too small interlayer gap) and volume expansion. For example, the results of Ma et al.14 showed that excessively short interlayer spacing would hinder the diffusion of alkali metals between graphite layers. Biby et al.13 demonstrated that intercalation of Rb into bulk MoS2 would cause the layer spacing to expand by 39.3% to 47.4%.
Two-dimensional (2D) materials have a larger specific surface area, a shorter diffusion distance, and good structural properties when compared to their bulk.22,23 2D materials, in theory, have more adsorption sites, better ion transport performance, and greater resistance to volume expansion, all of which are beneficial to anode materials' capacity, rate capability, and cycle stability.24,25 For example, it has been discovered that typical 2D materials like graphene and transition metal dihalides (TMDs) represented by monolayer MoS2 have lower migration barriers and higher capacity than their bulk.14,26 However, we have yet to come across any relevant research studies on the anode materials for RIBs and CIBs. The advantages of TMDs are ease of synthesis, low cost, and environmental friendliness. Importantly, they exhibit outstanding stability and performance in AIBs.27–29 Therefore, we will study the effect of monolayer TMDs as anode materials for RIBs and CIBs.
2 Computational methods
All geometric and electronic structures were studied by DFT calculations using the Vienna Ab initio Simulation Package (VASP).30,31 We choose the generalized gradient approximation of Perdew, Burke, and Ernzerhof (GGA-PBE)32 as the exchange–correlation functional with the plane wave basis set to calculate the geometric structures of all TMDs and graphene. The van der Waals (vdW) interactions were corrected by using the DFT-D3 (Grimme) approach in all systems.33,34 The cut-off energy was set to 500 eV. The Brillouin zone was regulated with a grid spacing of about 2π × 0.03 Å−1 of k-point meshes for all TMDs and graphene. It is worth noting that the electronic properties of all systems which contain heavy metal elements (Rb, Cs, Mo, W and Te) are considered to include the spin-orbit-coupling (SOC) calculation. All the geometry structures were fully relaxed until the convergence criteria of energy (10−5 eV) and force (0.01 eV Å−1) are satisfied. The climbing image nudged elastic band (CI-NEB) method was also implemented in the VASP transition state tools to calculate the diffusion barriers of Rb/Cs ions.35 To provide a relatively smooth diffusion route between the original and final structures for all CI-NEB calculations, seven intermediate images were made. Each image's structure was relaxed until the tangential force imposed on each of them was converged to 0.01 eV Å−1. The periodic boundary condition was applied to minimize the edge effect in a finite system. Vacuum space with at least 20 Å was constructed perpendicular to the layer plane of each TMD and graphene systems.3 Results and discussion
3.1 Phase selection of monolayer MX2
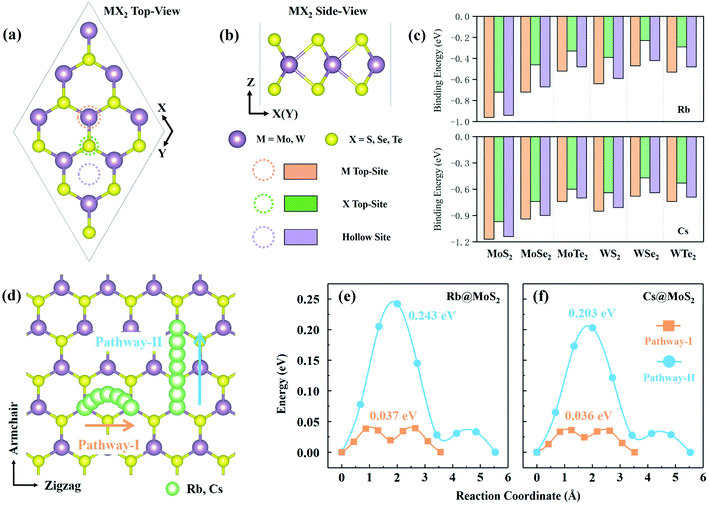
MX2 is the chemical formula for TMDs, where M stands for transition metals and X stands for chalcogen elements. In this paper, six representative MX2 monolayers are considered as anode materials, i.e., M = Mo or W; X = S, Se or Te (as shown in Fig. 1a and b). Monolayer TMDs have only two polymorphs based on the various coordination modes of transition metal atoms,36viz., trigonal prismatic (H) and octahedral (T) phases, one of which is thermodynamically stable while the other usually exists as a metastable phase. According to previous studies, the six MX2 monolayers' stable phases are all H phases.37 We also need to further investigate the stability of these two phases as anode materials. Using monolayer MoS2 as a representative, the PBE + D3 method32,33 was used to optimize the H-MoS2 and T-MoS2 structure (named *Rb/Cs@MX2, where * means adsorption quantity; when * = 1, it will not be displayed), which adsorbs Rb and Cs ions. The results indicate that the H-MoS2 adsorbing Rb/Cs ions can still exist in a stable state, whereas T-MoS2 undergoes distortion and finally becomes T′-MoS2 (as shown in Fig. S1c†). We also investigated the diffusion constants of Rb/Cs ions on H-MoS2 and T′-MoS2 surfaces (Fig. 1 and S2, and Table S1†). The diffusion constant of metal-ions can be estimated using the Arrhenius equation:7,38,39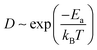 | (1) |
3.2 Adsorption ability of Rb/Cs atoms on the surface of monolayer H-MX2
The unit-cell of monolayer H-MX2 is a rhombic lattice with the lattice constants a and b being equal. We geometrically optimized the six TMDs using the PBE + D3 method, and the estimated lattice constant a (b) is remarkably similar to the previous report37 (Table S2†). On the monolayer H-MX2 surface, there are three distinct adsorption sites. As shown in Fig. 1a, Rb/Cs ions can be adsorbed on the M-top site, X-top site, or the hollow site. The binding energy (Eb) can be defined as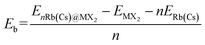 | (2) |
3.3 Diffusion of Rb/Cs ions on the surface of monolayer H-MX2
The ability of Rb/Cs ions to diffuse and migrate on the anode material is closely related to the battery's charge–discharge rate capability. The lower the diffusion barrier, the faster the cation migration, so the rate capacity of the battery is better.40 Rb/Cs ion diffusion takes place between the most stable adsorption sites that are next to each other. To check the accuracy of the calculation, we determined the diffusion barrier of Li ions on the graphene surface to be 0.301 eV (Fig. S3†), which is consistent with previous work.41 For H-MX2, there are two possible diffusion pathways (Fig. 1d) and corresponding barriers (Table S1†). The diffusion path along the zigzag direction is pathway-I, which is an arc-shaped path generated by two transition states (near hollow-sites) and hollow-sites. Diffusion pathway-II is a linear diffusion that passes through the transition state S-top site and follows the armchair direction. Obviously, in Table S1,† the *Rb/Cs@H-MX2 diffusion barrier of pathway-I is 4–6 times smaller than that of pathway-II. Despite the fact that pathway-II has a shorter diffusion distance (approximately 5.49–6.21 Å) than pathway-I (roughly 6.62–7.58 Å for two diffusions), the diffusion constant (by eqn (1)) of pathway-I is generally 102 to 103 times higher than that of pathway-II. This means that pathway-I is the better option. In reality, Rb/Cs ion diffusion on H-MX2 is isotropic, because pathway-II can be completed twice by pathway-I via diffusion. Interestingly, the diffusion barriers of pathway-I all exhibit an increasing tendency as the atomic number of elements represented by X increases (i.e. S, Se, and Te), such as, the diffusion barriers of Rb(Cs)@H-MoS2, Rb(Cs)@H-MoSe2 and Rb(Cs)@H-MoTe2 are 0.037 (0.036), 0.039 (0.039) and 0.042 (0.042) eV, respectively, and this can be explained by charge density difference.Charge density difference (Δρ) provides insight into the interaction of Rb/Cs ions upon diffusion on the monolayer H-MX2 surface. Δρ is defined as Δρ = ρRb(Cs)@MX2 − ρMX2 − ρRb(Cs), where ρRb(Cs)@MX2, ρMX2 and ρRb(Cs) represent the charge density values of Rb(or Cs)-adsorbed H-MX2, H-MX2, and a Rb(or Cs) ion, respectively. According to Δρ (Fig. S4†), all the charges accumulated on the X atoms are on the side where Rb/Cs ions are adsorbed, with no change on the other side, showing that electrons are transferred from Rb/Cs to the H-MX2 surface. The range of Rb charge transferred to the X atom on the same side of H-MX2 steadily diminishes as the atomic numbers of S, Se, and Te increase. For example, when X is S, the Rb charge can be transferred to all S atoms on the same side. And just a portion of the Se and Te atoms have gathered charges when X is Se and Te. This is because S is more electronegative than Se and Te, so the interaction range between MS2 and Rb/Cs is broader, allowing Rb/Cs to be more susceptible to diffuse on the surface of MS2.
Fascinatingly, in all H-MX2, the diffusion barrier of Rb/Cs ions on H-MoS2 is the smallest, only 0.037 and 0.036 eV, respectively (in Fig. S5†), which are significantly lower than that of common energy storage anode materials, such as Li@graphite (0.45–1.20 eV),42 Li@graphene (0.301 eV),41 Li@H-MoS2 (0.21 eV),42 Na@H-MoS2 (0.28 eV),43 Na@TiO2-B (0.48 eV),44 K@graphite (about 0.18–0.22 eV),14etc. Here, we used the Bader charge analysis method45 to quantitatively calculate the charge transfer between Rb/Cs ions and H-MX2 to further investigate the diffusion interaction. The charge transfer for Rb/Cs ions on stable (eS) and transition (eT) sites, as well as the difference between them (Δed = eT − eS), is shown in Table S4.† It can be shown that the magnitude of Δed almost completely determines the barrier height of Rb/Cs ion transport, and that the barrier grows as Δed grows. As a result, one of the major impediments to Rb/Cs ion migration is charge transfer. According to the above results, Rb@H-MoS2 and Cs@H-MoS2 have the smallest Δed (0.0031 and 0.0043e), respectively, which implies the least charge transfer between their stable and transition states. In addition, the results for Δρ have indicated a larger range of interactions between S and Rb/Cs. These two factors may make Rb/Cs ions have the smallest diffusion barrier on H-MoS2. Notably, the diffusion barriers of Rb/Cs ions on graphene were calculated to be 0.043 and 0.033 eV (Fig. S3 and Table S1†), respectively. Obviously, Rb@H-MoS2 has a lower diffusion barrier (0.037 eV) than Rb@graphene (0.043 eV), and Cs@H-MoS2 is just 0.003 eV higher than Cs@graphene. It is possible to deduce that Rb/Cs ions on H-MoS2 have a better diffusion performance than graphite (based on the diffusion results of H-MoS2 and graphene) due to the interlayer interaction of graphite. Thus, H-MoS2 has a remarkable capacity for transporting Rb/Cs ions.
3.4 Rb/Cs ion storage capacity of monolayer H-MX2
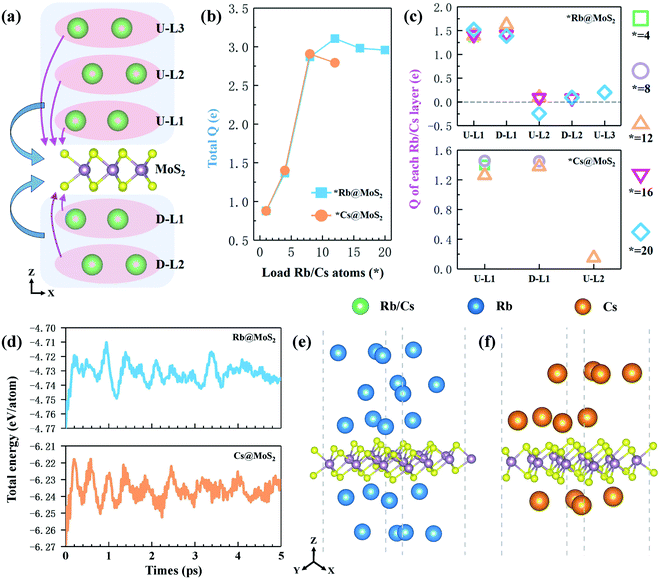
The theoretical capacity of anode materials is one of the most important performance parameters, affecting the battery's energy storage capacity, open circuit voltage, and adsorption density.46 Calculating the average adsorption energy (Eave) of the H-MX2 monolayer on Rb/Cs obtained the maximum theoretical capacity (Cmax). When Eave jumps from a negative to a positive value, the number of chemisorbed alkali metal atoms on the monolayer reaches a maximum.47 The adsorption energy of single Rb/Cs ions in monolayer H-MX2 is in the range of −0.47 to −1.17 eV (Table S3†), indicating that not only is Rb/Cs storage an exothermic and spontaneous process, but that monolayer H-MX2 may have the capacity to store more Rb/Cs due to the higher adsorption energy. The adsorbed Rb/Cs ions were stacked in the form of body-centered cubes (bcc) in a model for the adsorption of Rb/Cs by 3 × 3 × 1 supercells of H-MX2. The maximum number of Rb/Cs ions per layer for 3 × 3 × 1 supercell H-MX2 adsorption was 4. Adsorption of different concentrations of Rb/Cs is carried out with each layer as a unit, and each layer of Rb/Cs adsorbed is named U-LN and D-LN (as shown in Fig. 2a, U denotes up, D denotes down, and N is the number of layers close to H-MX2). The average adsorption energy of H-MX2 for different Rb/Cs layers is listed in Tables S5 and S6.† The results reveal that H-MoS2 exhibits excellent Rb and Cs adsorption capacity, capable of adsorbing 5 layers of Rb (20 atoms) or 3 layers of Cs (12 atoms), respectively, i.e., 20Rb@H-MoS2 and 12Cs@H-MoS2 (Fig. S6†). Although H-MoSe2 also has a good Cs adsorption capacity, the theoretical capacity is substantially lower than that of monolayer H-MoS2 (Table S6†), hence we only employ monolayer MoS2 as the anode material of CIBs.To fully evaluate the stability of 20Rb@H-MoS2 and 12Cs@H-MoS2, we performed ab initio molecular dynamics (AIMD) simulations using VASP on them at 300 K. All the AIMD simulations were carried out under the NVT ensemble. The temperature was controlled by the weak coupling of a Nose–Hoover thermostat.48 All the simulation time for each system with the 3 × 3 H-MoS2 supercell (i.e. 20Rb@H-Mo9S18 and 12Cs@H-Mo9S18) was 5 ps with a time step of 1 fs. The snapshots were saved by a time interval of 1 fs to collect data for analysis. The snapshot structures of 20Rb@H-MoS2 and 12Cs@H-MoS2 at 5 ps (Fig. 2e and f) still illustrate good integrity at 300 K. Specifically, monolayer H-MoS2 scarcely deformed, and there was no mixed-layer between Rb (or Cs) single-layers during the entire process, as well as the detachment of Rb/Cs ions, so the bcc structure was finally preserved. This demonstrates that each Rb/Cs atom vibrates only slightly in its original position and can be adsorbed on the H-MoS2 surface stably. Furthermore, as shown in Fig. 2d, the potential energies of 20 Rb@H-MoS2 and 12 Cs@H-MoS2 swiftly achieved equilibrium after about 1 ps, after which the energy oscillated slightly near the equilibrium point, with each atom's fluctuation range being only 0.03 eV. As a result, the stable theoretical maximum adsorption capacity of the H-MoS2 monolayer (3 × 3 × 1 supercell) is proven to be 20 Rb and 12 Cs.
In order to study the charge properties of the few-layer Rb/Cs adsorbed by monolayer H-MoS2, we further analyzed the Bader charge. First, the total charge (total Q; blue area and arrow in Fig. 2a) transferred from all Rb/Cs layers to H-MoS2 is shown in Fig. 2b. At the beginning, as the number of adsorbed Rb/Cs layers increases, the total Q increases dramatically. After the adsorption reached 12 Rb or 8 Cs, the total Q decreased and tended to converge. This also demonstrates that when the number of adsorption layers grows, the total Q will essentially remain stable or even drop. However, this will result in a significant reduction in the charge transfers per Rb/Cs ion, thereby weakening the interaction between adsorbed ions and H-MoS2. Especially for the adsorbed outer ion layer, the weak Coulomb effect cannot maintain the stable adsorption of more Rb/Cs ions. Secondly, Fig. 2c shows the charge transferred from each layer of adsorbed ions to H-MoS2 in the *Rb@H-MoS2 and *Cs@H-MoS2 systems with different adsorption capacities (Q; the pink area and arrow in Fig. 2a). The relevant data are listed in Table S7.† The findings reveal that the Rb/Cs ion layer closest to H-MoS2 (i.e. U-L1 and D-L1 layers) may transfer the most electrons, but the Rb/Cs ion layer far away from H-MoS2 is almost neutral, even gaining electrons (e.g. U-L2 layer in 20Rb@ H-MoS2). Furthermore, as the number of adsorption layers grows, the interaction between the outer layer of ions and the material gradually lessens, making Rb/Cs adsorption on both sides of the material preferable to adsorption on one side. The aforementioned results indicate that charge transfer is one of the most important mechanisms influencing theoretical capacity.
C max can be obtained from the equation7,38,46
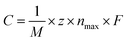 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 801 mA h mol−1). The Cmax values of *Rb@H-MX2 and *Cs@H-MX2 are presented in Fig. 3a, Tables S5 and S6.† The ratio of Li to C in graphite (commercial LIBs anode) is 1
801 mA h mol−1). The Cmax values of *Rb@H-MX2 and *Cs@H-MX2 are presented in Fig. 3a, Tables S5 and S6.† The ratio of Li to C in graphite (commercial LIBs anode) is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
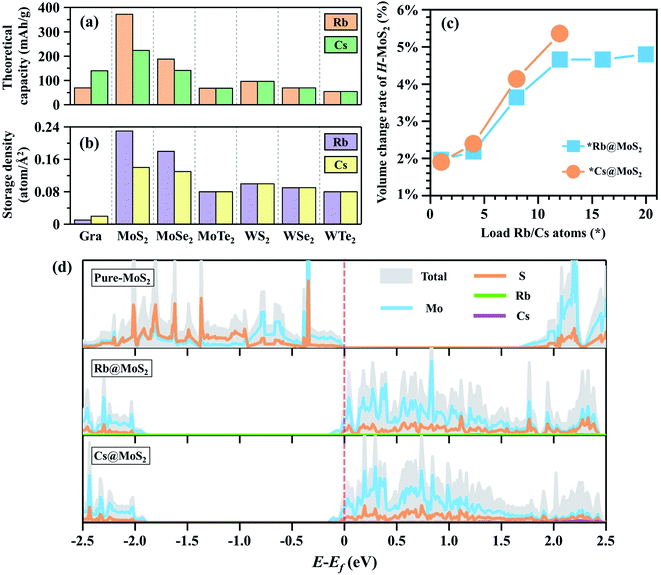
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 (i.e. Li@C6 structure), which is a widely accepted concept.46,49–51 Using eqn (3)Cmax was calculated to be 372 mA h g−1 for Li@C6, which is perfectly compatible with the experimental value.41–43 First, we estimated the Cmax of *Rb@H-MX2 and *Cs@H-MX2 based on this method (Fig. 3a), and the results demonstrate that H-MoS2 has a distinct advantage in Cmax of Rb/Cs in all H-MX2 (20Rb@H-MoS2 and 12Cs@H-MoS2 reaching 372.05 and 223.23 mA h g−1, respectively). Secondly, according to the maximum adsorption capacity of graphene (4 × 4 × 1 supercell) as the anode material for RIBs and CIBs (i.e. 1Rb@C32 and 2Cs@C32), the calculated Cmax is 69.79 and 139.59 mA h g−1, respectively, which is significantly less than that of H-MoS2. Therefore, Rb/Cs on H-MoS2 has a higher Cmax than the graphite anode. Remarkably, the Cmax of 20Rb@H-MoS2 is even comparable to that of commercial Li@graphite (372.05 vs. 372 mA h g−1). Furthermore, the successful implementation of RIBs (graphite anodes) in cold-atom physics systems can substantially accelerate the miniaturization process, which necessitates consideration of the anodes' Rb (or Cs) atomic storage density. Fig. 3b and Tables S5 and S6† summarize that the Rb and Cs storage densities of H-MoS2 are 23 times and 7 times that of graphene, respectively. Therefore, H-MoS2 has excellent Rb/Cs storage capacity.
6 (i.e. Li@C6 structure), which is a widely accepted concept.46,49–51 Using eqn (3)Cmax was calculated to be 372 mA h g−1 for Li@C6, which is perfectly compatible with the experimental value.41–43 First, we estimated the Cmax of *Rb@H-MX2 and *Cs@H-MX2 based on this method (Fig. 3a), and the results demonstrate that H-MoS2 has a distinct advantage in Cmax of Rb/Cs in all H-MX2 (20Rb@H-MoS2 and 12Cs@H-MoS2 reaching 372.05 and 223.23 mA h g−1, respectively). Secondly, according to the maximum adsorption capacity of graphene (4 × 4 × 1 supercell) as the anode material for RIBs and CIBs (i.e. 1Rb@C32 and 2Cs@C32), the calculated Cmax is 69.79 and 139.59 mA h g−1, respectively, which is significantly less than that of H-MoS2. Therefore, Rb/Cs on H-MoS2 has a higher Cmax than the graphite anode. Remarkably, the Cmax of 20Rb@H-MoS2 is even comparable to that of commercial Li@graphite (372.05 vs. 372 mA h g−1). Furthermore, the successful implementation of RIBs (graphite anodes) in cold-atom physics systems can substantially accelerate the miniaturization process, which necessitates consideration of the anodes' Rb (or Cs) atomic storage density. Fig. 3b and Tables S5 and S6† summarize that the Rb and Cs storage densities of H-MoS2 are 23 times and 7 times that of graphene, respectively. Therefore, H-MoS2 has excellent Rb/Cs storage capacity.
3.5 Open circuit voltage, cycling stability and conductivity
The anode material's low open circuit voltage (OCV) aids in increasing energy density, but too low an OCV can result in metal plating. When we neglect the pressure, volume and entropy effects, the average voltage of the H-MX2 in the concentration range of n1 < n < n2 can be calculated as7,46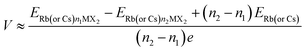 | (4) |
The electrode material's structural deformation in the reversible charge/discharge process is particularly sensitive, and considerable expansion can result in electrode powdering, which can contribute to rapid capacity decay and poor cycle stability.55 Thus, the cycle stability of H-MoS2 as an electrode material of RIBs and CIBs must be taken into account. We calculated the volume expansion of H-MoS2 adsorbing Rb/Cs. In Fig. 3c, as the amount of Rb/Cs adsorbed increases, the volume gradually increases. The maximum volume expansion was 4.80% and 5.36% when the maximum adsorption of Rb and Cs ions is reached, respectively (Table S8†). Generally, alkali metal elements' expansion rate will increase dramatically as their radius increases, notably for elements with large radius like Rb/Cs. However, when compared to the expansion rate of various LIB anode materials, H-MoS2 when used as the anode of RIBs and CIBs has a substantially lower expansion rate. For example, the volume expansion rate of the silicon-based anode of LIBs is 400%,56 and the volume change of various alloy reaction anodes of LIBs is >150%.57 The foregoing results suggest that H-MoS2 as the anode of RIBs and CIBs has a good charge and discharge stability due to its low expansion rate.
Since the electrical conductivity of the electrode material is also closely related to the rate capability of AIBs, we calculated the density of states (DOS) of H-MoS2, Rb@H-MoS2, and Cs@H-MoS2. As shown in Fig. 3d, monolayer H-MoS2 is a semiconductor material, with the Fermi level (set to zero) at the valence band maximum (VBM). When only one Rb/Cs atom is absorbed by H-MoS2, the Fermi level increases to the conduction band and crosses the conduction band minimum (CBM), resulting in a semiconductor-to-metal transition. Furthermore, the Fermi levels of Rb@H-MoS2 and Cs@H-MoS2 exhibit substantial electron carrier density, resulting in good conductivity for RIB and CIB charge and discharge cycles.
4 Conclusions
In summary, we used first-principles calculations to investigate the characteristics of six H-MX2 (M = Mo or W; X = S, Se or Te) monolayers as an anode material for RIBs and CIBs. Studies have shown that monolayer H-MoS2 appears to be an ideal anode material for RIBs and CIBs, and its great properties are as follows: (1) MoS2 has extremely low Rb and Cs ion diffusion barriers (0.037 and 0.036 eV), compared to most AIB anode materials. It also has good electronic conductivity. Thus, MoS2-based RIBs and CIBs exhibit outstanding rate capability potential advantages; (2) because of the suitable OCV and high diffusion constant, it is difficult to generate dendrites in MoS2-based RIBs and CIBs, and the battery safety may be satisfactory; (3) H-MoS2 not only has strong stability in the full load Rb/Cs state, but also has low expansion rate, indicating that H-MoS2 has good cycle stability during charge and discharge; (4) the theoretical capacity of MoS2-based RIBs is 372.05 mA h g−1, which is comparable to that of commercial graphite-based LIBs. Besides, MoS2-based CIBs have a theoretical capacity of 223.23 mA h g−1; (5) because the storage density of Rb and Cs atoms in MoS2 is 23 times and 7 times that of graphite (refer to graphene), it is better suited for battery-type Rb and Cs sources in cold-atom physics systems; (6) the experimental preparation of MoS2 is relatively mature, low-cost, and environmentally friendly. These benefits could be readily realized in RIB and CIB experiments. Thus, this work opens up the possibility of developing an improved H-MoS2 anode for RIBs and CIBs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China [grant number 61975194].Notes and references
- X. Wang, M. Salari, D.-e. Jiang, J. Chapman Varela, B. Anasori, D. J. Wesolowski, S. Dai, M. W. Grinstaff and Y. Gogotsi, Nat. Rev. Mater., 2020, 5, 787–808 CrossRef CAS.
- S. Gao, J. Hao, X. Zhang, L. Li, C. Zhang, L. Wu, X. Ma, P. Lu and G. Liu, Comput. Mater. Sci., 2021, 200, 110776 CrossRef CAS.
- C. Liu, F. Li, L. P. Ma and H. M. Cheng, Adv. Mater., 2010, 22, E28–E62 CrossRef CAS PubMed.
- L. Zhou, M. K. Tufail, Y. Liao, N. Ahmad, P. Yu, T. Song, R. Chen and W. Yang, Adv. Fiber Mater., 2022, 4, 487–502 CAS.
- X. X. Ma, X. Chen, Y. K. Bai, X. Shen, R. Zhang and Q. Zhang, Small, 2021, 2007142 CrossRef CAS PubMed.
- J. W. Choi and D. Aurbach, Nat. Rev. Mater., 2016, 1, 1–16 Search PubMed.
- T. Yu, Z. Zhao, L. Liu, S. Zhang, H. Xu and G. Yang, J. Am. Chem. Soc., 2018, 140, 5962–5968 CrossRef CAS PubMed.
- J. P. McGilligan, K. R. Moore, S. Kang, R. Mott, A. Mis, C. Roper, E. A. Donley and J. Kitching, Phys. Rev. Appl., 2020, 13, 044038 CrossRef CAS.
- S. Kang, R. P. Mott, K. A. Gilmore, L. D. Sorenson, M. T. Rakher, E. A. Donley, J. Kitching and C. S. Roper, Appl. Phys. Lett., 2017, 110, 244101 CrossRef.
- S. Kang, K. R. Moore, J. P. McGilligan, R. Mott, A. Mis, C. Roper, E. A. Donley and J. Kitching, Opt. Lett., 2019, 44, 3002–3005 CrossRef CAS PubMed.
- S. Kang, R. P. Mott, A. V. Mis, C. S. Roper, E. A. Donley and J. Kitching, Opt. Express, 2018, 26, 3696–3701 CrossRef CAS PubMed.
- J. P. McGilligan, K. R. Moore, A. Dellis, G. D. Martinez, E. de Clercq, P. F. Griffin, A. S. Arnold, E. Riis, R. Boudot and J. Kitching, Appl. Phys. Lett., 2020, 117, 054001 CrossRef CAS.
- A. H. Biby, B. A. Ali and N. K. Allam, Mater. Adv., 2021, 2, 5052–5056 RSC.
- J. Ma, C. Yang, X. Ma, S. Liu, J. Yang, L. Xu, J. Gao, R. Quhe, X. Sun and J. Yang, Nanoscale, 2021, 13, 12521–12533 RSC.
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed.
- Y. Wu, W. Wang, J. Ming, M. Li, L. Xie, X. He, J. Wang, S. Liang and Y. Wu, Adv. Funct. Mater., 2019, 29, 1805978 CrossRef.
- J. Xiao, Science, 2019, 366, 426–427 CrossRef CAS PubMed.
- X. Zhang, A. Wang, X. Liu and J. Luo, Acc. Chem. Res., 2019, 52, 3223–3232 CrossRef CAS PubMed.
- S. G. Bratsch, J. Phys. Chem. Ref. Data, 1989, 18, 1–21 CAS.
- M. Obrovac and V. Chevrier, Chem. Rev., 2014, 114, 11444–11502 CAS.
- N. Wang, Z. Bai, Y. Qian and J. Yang, Adv. Mater., 2016, 28, 4126–4133 Search PubMed.
- B. Lu, X. Zheng and Z. Li, ACS Appl. Mater. Interfaces, 2020, 12, 53731–53738 Search PubMed.
- B. Lu, X. Zheng and Z. Li, ACS Appl. Mater. Interfaces, 2019, 11, 10163–10170 CAS.
- S.-H. Bae, H. Kum, W. Kong, Y. Kim, C. Choi, B. Lee, P. Lin, Y. Park and J. Kim, Nat. Mater., 2019, 18, 550–560 CAS.
- X. Tang and L. Kou, J. Phys. Chem. Lett., 2019, 10, 6634–6649 CAS.
- P. p. Wang, H. Sun, Y. Ji, W. Li and X. Wang, Adv. Mater., 2014, 26, 964–969 CAS.
- X. Ren, Q. Zhao, W. D. McCulloch and Y. Wu, Nano Res., 2017, 10, 1313–1321 CAS.
- C. Park, Y. H. Kim, H. Lee, H. S. Kang, T. Kim, S. W. Lee, K. Lee, K.-B. Kim and C. Park, Adv. Energy Mater., 2021, 11, 2003243 CAS.
- E. Yang, H. Ji and Y. Jung, J. Phys. Chem. C, 2015, 119, 26374–26380 CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CAS.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154122 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CAS.
- A. V. Kolobov and J. Tominaga, Two-dimensional Transition-Metal Dichalcogenides, Springer, 2016 Search PubMed.
- C. Ataca, H. Sahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983–8999 CAS.
- X. Zhang, C. Yang, Y. Pan, M. Weng, L. Xu, S. Liu, J. Yang, J. Yan, J. Li and B. Shi, J. Mater. Chem. A, 2019, 7, 14042–14050 CAS.
- B. Zhao, Z. Ren, G. Tan, Z. Li and J. Xie, Acta Mater., 2022, 226, 117632 CAS.
- M. Wu, B. Xin, W. Yang, B. Li, H. Dong, Y. Cheng, W. Wang, F. Lu, W.-H. Wang and H. Liu, ACS Appl. Energy Mater., 2020, 3, 10695–10701 CAS.
- X. Fan, W. Zheng and J.-L. Kuo, ACS Appl. Mater. Interfaces, 2012, 4, 2432–2438 CAS.
- J. Jia, B. Li, S. Duan, Z. Cui and H. Gao, Nanoscale, 2019, 11, 20307–20314 CAS.
- Z. Hu, L. Wang, K. Zhang, J. Wang, F. Cheng, Z. Tao and J. Chen, Angew. Chem., Int. Ed., 2014, 53, 12794–12798 CAS.
- Q. Zhang and P. Kaghazchi, J. Phys. Chem. C, 2016, 120, 22163–22168 CAS.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CAS.
- C. Yang, X. Zhang, J. Li, J. Ma, L. Xu, J. Yang, S. Liu, S. Fang, Y. Li, X. Sun, X. Yang, F. Pan, J. Lu and D. Yu, Electrochim. Acta, 2020, 346, 136244 CAS.
- Y. Ding, C. You, Y. Xu, L. Zhong, Q. Deng, J. Li and B. Xiao, Appl. Surf. Sci., 2021, 559, 149849 CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 Search PubMed.
- M. Winter, J. O. Besenhard, M. E. Spahr and P. Novak, Adv. Mater., 1998, 10, 725–763 CAS.
- J.-M. Tarascon and M. Armand, Materials for sustainable energy: a collection of peer-reviewed research and review articles from Nature Publishing Group, World Scientific, 2011, vol. 414, pp. 171–179 Search PubMed.
- K. Toyoura, Y. Koyama, A. Kuwabara, F. Oba and I. Tanaka, Phys. Rev. B, 2008, 78, 214303 Search PubMed.
- C. Eames and M. S. Islam, J. Am. Chem. Soc., 2014, 136, 16270–16276 CAS.
- M. V. Koudriachova, N. M. Harrison and S. W. de Leeuw, Solid State Ionics, 2002, 152, 189–194 Search PubMed.
- W. Li, Y. Yang, G. Zhang and Y.-W. Zhang, Nano Lett., 2015, 15, 1691–1697 CAS.
- S. Guo, J. Yi, Y. Sun and H. Zhou, Energy Environ. Sci., 2016, 9, 2978–3006 CAS.
- C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31–35 CAS.
- Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang and T. Chen, Chem. Rev., 2020, 121, 1623–1669 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00001f |
| This journal is © The Royal Society of Chemistry 2022 |