Open Access Article
Open Access ArticleExtraordinary lattice thermal conductivity of gold sulfide monolayers†
Armin
Taheri
a,
Simone
Pisana
 *ab and
Chandra Veer
Singh
*ab and
Chandra Veer
Singh
 *cd
*cd
aDepartment of Electrical Engineering and Computer Science, York University, Toronto, Ontario M3J1P3, Canada. E-mail: pisana@yorku.ca
bDepartment of Physics and Astronomy, York University, Toronto, Ontario M3J1P3, Canada
cDepartment of Materials Science and Engineering, University of Toronto, Toronto, Ontario M5S 3E4, Canada. E-mail: chandraveer.singh@utoronto.ca
dDepartment of Mechanical and Industrial Engineering, University of Toronto, Toronto, Ontario M5S 3G8, Canada
First published on 31st May 2022
Abstract
Gold sulfide monolayers (α-, β-Au2S, α-, β-, γ-AuS) have emerged as a new class of two-dimensional (2D) materials with appealing properties such as high thermal and dynamical stability, oxidation resistance, and excellent electron mobility. However, their thermal properties are still unexplored. In this study, based on first-principles calculations and the Peierls–Boltzmann transport equation, we report the lattice thermal conductivity (κ) and related phonon thermal properties of all members of this family. Our results show that gold sulfide monolayers have lattice thermal conductivity spanning almost three orders of magnitude, from 0.04 W m−1 K−1 to 10.62 W m−1 K−1, with different levels of anisotropy. Particularly, our results demonstrate that β-Au2S with ultralow κaa = 0.06 W m−1 K−1 and κbb = 0.04 W m−1 K−1 along the principal in-plane directions, has one of the lowest κ values that have been reported for a 2D material, well below that of PbSe. This extremely low lattice thermal conductivity can be attributed to its flattened phonon branches and low phonon group velocity, high anharmonicity, and short phonon lifetimes. Our results may provide insight into the application of gold sulfide monolayers as thermoelectric materials, and motivate future κ measurements of gold sulfide monolayers.
1 Introduction
The successful exfoliation of graphene from graphite in 2004 (ref. 1) has triggered the idea that materials with lower dimensions can have promising properties superior to their three-dimensional (3D) counterparts. Graphene combines unique properties such as extremely high electron mobility (∼200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm2 V−1 s−1),2,3 thermal conductivity (∼5300 W m−1 K−1),4 and modulus of elasticity (∼1 TPa).5 However, graphene's zero band gap and low current on/off ratio pose obstacles to its applications in electronics. Two-dimensional transition-metal dichalcogenides (TMDs) and 2D materials of group VA (e.g., black phosphorene) are two well-known families of 2D materials beyond graphene that have been widely studied. Although 2D TMDs (e.g., MoS2 and WSe2) have nonzero electronic band gap (∼1–2 eV),6 their relatively low electron mobility (∼100 cm2 V−1 s−1)6 jeopardizes their applications in electronics. Black phosphorene, on the other hand, has both a direct band gap of about ∼1.5 eV as well as a desirably high electron mobility over 1000 cm2 V−1 s−1.7,8 However, the ambient stability of black phosphorene is challenging as each phosphorus atom has two uncoupled electrons that can lead to oxidation and results in chemical degradation.9 Thus, searching for stable 2D materials beyond graphene with desirable electronic, thermal, and mechanical properties to address technological challenges is still an important research topic in many disciplines ranging from materials science and condensed matter physics to engineering.
000 cm2 V−1 s−1),2,3 thermal conductivity (∼5300 W m−1 K−1),4 and modulus of elasticity (∼1 TPa).5 However, graphene's zero band gap and low current on/off ratio pose obstacles to its applications in electronics. Two-dimensional transition-metal dichalcogenides (TMDs) and 2D materials of group VA (e.g., black phosphorene) are two well-known families of 2D materials beyond graphene that have been widely studied. Although 2D TMDs (e.g., MoS2 and WSe2) have nonzero electronic band gap (∼1–2 eV),6 their relatively low electron mobility (∼100 cm2 V−1 s−1)6 jeopardizes their applications in electronics. Black phosphorene, on the other hand, has both a direct band gap of about ∼1.5 eV as well as a desirably high electron mobility over 1000 cm2 V−1 s−1.7,8 However, the ambient stability of black phosphorene is challenging as each phosphorus atom has two uncoupled electrons that can lead to oxidation and results in chemical degradation.9 Thus, searching for stable 2D materials beyond graphene with desirable electronic, thermal, and mechanical properties to address technological challenges is still an important research topic in many disciplines ranging from materials science and condensed matter physics to engineering.
Recently, based on theoretical first-principles calculations, a new class of 2D materials consisting of gold (Au) and sulfur (S) elements10 have been claimed to be dynamically and thermally stable.10 This new family of 2D materials includes two phases of Au2S (including α-Au2S and β-Au2S) and three phases of AuS (namely, α-, β-, and γ-AuS). Based on density functional theory (DFT) calculations, α-Au2S is a semiconductor with a highly desirable direct band gap of 1.0 eV.10 Based on ab initio Born–Oppenheimer molecular dynamic simulations this structure is also thermally stable at temperatures as high as 1500 K.11 Other gold sulfide monolayers are also semiconductors with indirect band gaps ranging from 1.6 eV to 3.6 eV. The electron mobility of α-Au2S is predicted to be 8.45 × 104 cm2 V−1 s−1,10 which for example is about three orders of magnitude higher than MoS2 and two orders of magnitude higher than black phosphorene. Furthermore, unlike black phosphorene, based on ab initio molecular dynamics simulations (AIMD) gold sulfide monolayers show a strong oxidation resistance10 which is promising for their synthesis using techniques such as chemical vapor deposition (CVD).12 Due to their ionic bond, gold sulfide monolayers have a low Young modulus, predicted to be about 35 N m−1 for α-Au2S.10 This low Young modulus gives gold sulfide extra flexibility compared to other 2D materials.
Based on a very recent study,13 β-AuS possesses a highly anisotropic electron mobility (zigzag: 1.9 × 104 cm2 V−1 s−1, armchair: 0.17 cm2 V−1 s−1). Very surprisingly, these values can be highly tuned when β-AuS is under 4% compressive strain, reaching to 1.9 × 106 cm2 V−1 s−1 and 2.9 × 105 cm2 V−1 s−1 along the zigzag and armchair directions, respectively. Moreover, an indirect to direct band gap transition in β-AuS has been reported to occur for an 8% compressive biaxial strain. The solar to hydrogen (STH) efficiency of β-AuS is also predicted to be 17.21% which is only slightly less than the theoretical maximum of 18%. This high value of STH makes β-AuS a promising photocatalyst for water splitting.
Despite the fact that previous studies provide insightful information on the stability and electronic properties of gold sulfide monolayers, their thermal properties remain unexplored. Due to their ionic bonds11 and large atomic mass, gold sulfide monolayers should have low lattice thermal conductivity. A potentially low lattice thermal conductivity together with their high electron mobility can make them ideal candidates for applications in thermoelectric power generators and Peltier refrigerators, possessing a high “figure-of-merit” defined as 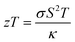 , where σ is electrical conductivity, S is Seebeck coefficient, T is temperature, and κ is the thermal conductivity.
, where σ is electrical conductivity, S is Seebeck coefficient, T is temperature, and κ is the thermal conductivity.
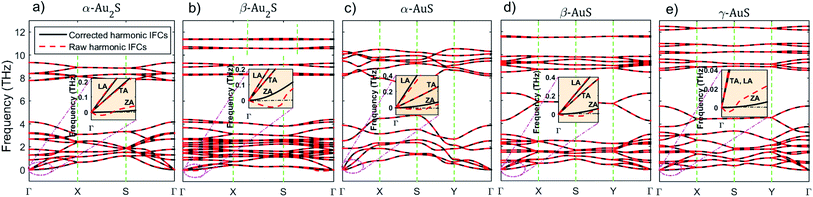
It is known that a very effective theoretical approach to predict the thermal properties of novel nanostructures is solving the Peierls–Boltzmann transport equation (PBTE) using inputs from density functional theory (DFT).14–16 However, one of the steps is to obtain a physically correct phonon dispersion curve for the material under study. Based on the continuum elasticity theory,17–19 as a universal feature, the acoustic out-of-plane flexural (ZA) phonon branch close to the Γ-point in 2D monolayers has to be purely quadratic. However, due to the complex structure, obtaining such a physically correct ZA phonon branch for gold sulfide monolayers from DFT is a challenging task. The ZA phonon dispersion presented for this class of materials by prior studies10,11 has either linear components or a small U-shaped region with imaginary frequencies close to the Γ-point, both of which can lead to huge errors in estimation of lattice thermal conductivity in the PBTE/DFT κ calculation framework.20
Here, we systematically study the phonon thermal transport properties of currently known phases of gold sulfide monolayers including α-, β-Au2S and α-, β-, and γ-AuS based on the iterative solution using the PBTE/DFT framework. To address the potential accuracy issue with the ZA mode, we impose the Born–Huang rotational invariance constraints on the harmonic interatomic force constants (IFCs) obtained from DFT, to recover the purely quadratic shape of the ZA branch close to the Γ-point. Our results provide a rich picture of the correlation between structural complexity and lattice thermal conductivity in gold sulfide monolayers which is a necessary component to examine their practical feasibility.
2 Computational methods
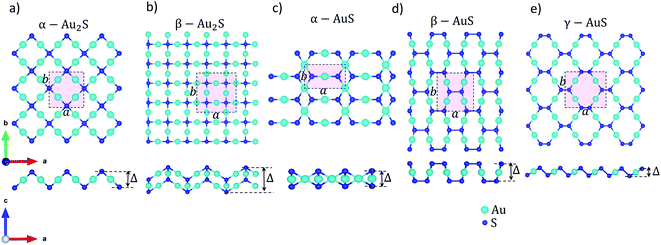
We start by structure optimization of gold sulfide monolayers to obtain the relaxed lattice constants and atomic positions. All DFT calculations are performed using the Quantum Espresso package,21 with a projected augmented wave (PAW) pseudopotential and the Perdew Burke Ernzerhof (PBE) approximation to exchange and correlation.22 The van der Waals interactions which are known to highly affect the relaxed structural properties of gold sulfide monolayers10 are also included by using the “DFT-D3” scheme. The electronic wave functions are expanded with plane waves up to an energy cutoff of 110 Ry (≈1496 eV). A fully converged electronic k-point mesh of 31 × 31 × 1 centered at Γ is used for reciprocal space integration of the Brillouin zone (BZ). The energy and force convergence thresholds for the geometry relaxation are set to 10−5 a.u. (≈0.136 meV) and 10−3 a.u. (≈26 meV Å−1), respectively. A vacuum spacing of 20 Å is imposed perpendicular to the monolayers to eliminate artificial interactions between neighbouring layers. Fig. 1 shows the optimized unit cell and a supercell of the different gold sulfide monolayers considered in this work. Listed in Table 1 are also the main geometry features including in-plane lattice parameters (a and b), the puckering/buckling distance (Δ) of each monolayer, and their space group. Our results are in fair agreement with those reported by prior studies.10,13| Material | a (Å) | b (Å) | Δ (Å) | Space group |
|---|---|---|---|---|
| α-Au2S | 5.75 | 5.75 | 2.59 | p4/nmm |
| β-Au2S | 7.95 | 7.95 | 5.06 | p4/nmm |
| α-AuS | 6.19 | 3.54 | 2.32 | p2/m |
| β-AuS | 6.12 | 6.78 | 3.06 | pmmn |
| γ-AuS | 8.15 | 7.19 | 1.48 | c2/m |
We then obtain the harmonic (second-order) interatomic force constants (IFCs) of each structure using the Phonopy package. After a careful convergence test for each system, we use supercell sizes of 5 × 5 × 1, 4 × 4 × 1, 7 × 7 × 1, 5 × 5 × 1, and 5 × 5 × 1 for α-Au2S, β-Au2S, α-AuS, β-AuS, and γ-AuS monolayers, respectively. Throughout this paper, the harmonic IFCs obtained at this step with no further corrections are referred to as “raw” harmonic IFCs. We note that usually the raw harmonic IFCs do not fully satisfy the rotational invariance conditions, and using them to obtain the dispersion curve of many 2D monolayers leads to a ZA branch that contains either a small “U-shaped” region of negative frequencies or linear components close to the Γ-point. This artifact can negatively affect the thermal conductivity prediction in terms of its value, anisotropy, and convergence behavior resulting in incorrect values, as discussed in detail in our previous study.20,23 Here we use the HiPhive package24 and an in-house code to enforce the rotational invariance as a post processing step, and obtain the “corrected” harmonic IFCs.
Next, we calculate the cubic anharmonic IFCs which are used to determine the phonon lifetime restricted by three-phonon scattering processes. After a careful convergence test, we use the thirdorder.py script25 to create supercell sizes of 3 × 3 × 1, 3 × 3 × 1, 4 × 4 × 1, 3 × 3 × 1, and 3 × 3 × 1 for α-Au2S, β-Au2S, α-AuS, β-AuS, and γ-AuS monolayers, respectively. The cutoff for interatomic interactions is also set at 10th, 8th, 7th, 11th, and 13th nearest neighbors for α-Au2S, β-Au2S, α-AuS, β-AuS, and γ-AuS monolayers, respectively. Due to their structural complexity, we note that the calculation of anharmonic IFCs in gold sulfide monolayers is noticeably more computationally expensive than other 2D monolayers. For example, for the case of β-Au2S, the chosen supercell size and cutoff value leads to 2224 DFT runs, each containing 108 atoms.
As the last step, the lattice thermal conductivity of each system is calculated with the ShengBTE package using the full (iterative) solution of PBTE as
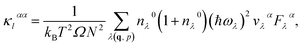 | (1) |
| Fλ = τ0λ(vλ + Δλ), | (2) |
3 Results and discussion
The relaxed structure of gold sulfide monolayers are illustrated in Fig. 1. We emphasize that although all monolayers have the same elemental constitution, they show distinct geometrical features. For example, there are two types of nonequivalent Au atoms in the structure of α-AuS (Fig. 1(c)); in one type, each Au atom is bonded with two S atoms. In the other type, each is tetracoordinated with S atoms.10 This can lead to different bonding and phonon properties compared to, for example, γ-AuS, in which all gold atoms have similar bonding environments (Fig. 1(e)). Similarly, one can observe other differences for the sulfur atoms in α-Au2S and β-Au2S monolayers (Fig. 1(a) and (b)).Now we investigate the phonon dispersion curves of gold sulfide monolayers. There are 6, 12, 4, 8, and 8 atoms in the unit cells of α-Au2S, β-Au2S, α-AuS, β-AuS, and γ-AuS, respectively. This leads to a total of 18 (α-Au2S), 36 (β-Au2S), 12 (α-AuS), 24 (β-AuS), and 24 (γ-AuS) phonon branches in the phonon dispersion curve of these systems; three of which are acoustic modes known as flexural (ZA), transverse (TA), and longitudinal (LA), and the rest are optical modes. Fig. 2 shows the dispersion curves of gold sulfide monolayers along the high symmetry points obtained using corrected and raw harmonic IFCs. The insets in Fig. 2(a)–(e) are also a closer inspection of the region close to the Γ point along the Γ–X direction. It can be seen that, in each monolayer, using the raw harmonic IFCs directly obtained from DFT to calculate the dispersion curve results in a small U-shaped region of negative frequency for the ZA mode close to the Γ point which limits the accuracy and convergence of subsequent phonon thermal transport calculations. This feature can originate from imperfect structure relaxation, hybridization between the polarization of the TA/LA modes with the ZA mode, using periodic boundary conditions along different axes, and numerical inaccuracies caused by insufficient cutoff values or insufficiently large supercell. In most cases these inaccuracies are hardly noticeable in the overall view of the dispersion curve. However, after imposing the rotational invariance constraints on the raw harmonic IFCs, the ZA mode becomes purely quadratic, while all other modes practically remain unchanged. The corrected harmonic IFCs are then used for the rest of the calculations.
The highest optical frequencies are found to be 9.35 THz, 11.40 THz, 10.5 THz, 11.6 THz, and 12.5 THz in α-Au2S, β-Au2S, α-AuS, β-AuS, and γ-AuS, respectively. These values are about five times lower than the corresponding value in graphene (≈50 THz) as a result of phonon-softening caused by larger atomic masses and weaker bonds in gold sulfide monolayers. As can be seen in Fig. 2(a)–(e), generally, the large mass difference between Au and S atoms 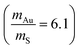 results in strong overlap between low frequency optical phonons and acoustic phonons which increases three-phonon scattering channels such as acoustic + acoustic → optical and acoustic + optical → optical, leading to an increase in the scattering rates and a decrease in the thermal conductivity. This situation is similar to the case of Tl2O monolayer which has an ultralow κ.27
results in strong overlap between low frequency optical phonons and acoustic phonons which increases three-phonon scattering channels such as acoustic + acoustic → optical and acoustic + optical → optical, leading to an increase in the scattering rates and a decrease in the thermal conductivity. This situation is similar to the case of Tl2O monolayer which has an ultralow κ.27
On a superficial level, it can be seen that there is less proximity between phonon branches in α-AuS, which can decrease the probability of three-phonon scattering, thus leading to a higher thermal conductivity compared to other gold sulfide monolayers. This effect will be discussed in detail later by considering the three-phonon scattering phase space. Based on eqn (1), the group velocity defined as 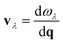 is one of the important parameters that determines thermal conductivity. Fig. 2(b) suggests that phonon branches are highly flattened in β-Au2S, which can result in lower group velocity and thermal conductivity. This can be due to the strength and importance of the van der Waals interactions. Although the gold sulfide monolayers are not layered structures, it is known that van der Waals interactions can hugely affect their structural properties, bonding and consequently phonon properties, leading to flattened dispersion branches and low group velocities.10 Also, a pronounced anisotropy in the slope of the TA and LA modes along the Γ–X and Γ–Y directions can be seen clearly in α-AuS, and to some extent in β-AuS and γ-AuS. This can lead to anisotropic thermal conductivity values along the aa- and bb-directions similar to puckered phosphorene28 and arsenene.29
is one of the important parameters that determines thermal conductivity. Fig. 2(b) suggests that phonon branches are highly flattened in β-Au2S, which can result in lower group velocity and thermal conductivity. This can be due to the strength and importance of the van der Waals interactions. Although the gold sulfide monolayers are not layered structures, it is known that van der Waals interactions can hugely affect their structural properties, bonding and consequently phonon properties, leading to flattened dispersion branches and low group velocities.10 Also, a pronounced anisotropy in the slope of the TA and LA modes along the Γ–X and Γ–Y directions can be seen clearly in α-AuS, and to some extent in β-AuS and γ-AuS. This can lead to anisotropic thermal conductivity values along the aa- and bb-directions similar to puckered phosphorene28 and arsenene.29
Fig. 3 shows the computed lattice thermal conductivity of gold sulfide monolayers in a temperature range varying from 200 K to 800 K obtained using the full solution of the PBTE (see ESI† for comparison between the iterative and the RTA solutions of the BTE). The typical 1/T temperature dependence is observed for all monolayers which highlights the dominance of Umklapp scattering in this temperature range. Table 2 also summarizes the room temperature thermal conductivity of gold sulfide monolayers as well as some other 2D materials obtained from the DFT/PBTE framework. As shown, α-Au2S has an isotropic thermal conductivity (κaa = κbb), while other gold sulfide monolayers exhibit different degrees of anisotropy in their thermal conductivity. The room temperature thermal conductivities of α-Au2S, β-Au2S, α-AuS, β-AuS, and γ-AuS along the aa-direction (bb-direction) are found to be 1.25 (1.25) W m−1 K−1, 0.06 (0.04) W m−1 K−1, 3.75 (10.62) W m−1 K−1, 1.44 (1.86) W m−1 K−1, and 1.65 (2.19) W m−1 K−1, respectively. Our calculated κ of 1.25 W m−1 K−1 for α-Au2S is in a fair agreement with a previously reported value of about 2.6 W m−1 K−1.11 However, a careful inspection of the dispersion curve in ref. 11 reveals possible breakdown of the rotational invariance and presence of small negative frequencies in the ZA mode close to the Γ point. We also use a larger supercell and cutoff distance in our harmonic and anharmonic IFCs calculation compared to ref. 11, which enables better convergence of the calculated values.
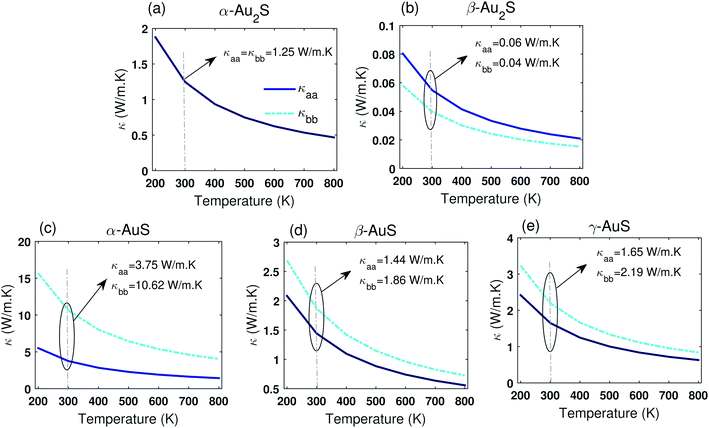 | ||
| Fig. 3 Thermal conductivity of (a) α-Au2S, (b) β-Au2S, (c) α-AuS, (d) β-AuS, and (e) γ-AuS in a temperature range from 200 K to 800 K along the aa and bb directions. | ||
| Material | κ aa (W m−1 K−1) | κ bb (W m−1 K−1) | Thickness (Å) | Ref. |
|---|---|---|---|---|
| α-Au2S | 1.25 | 1.25 | 6.19 | This work |
| β-Au2S | 0.06 | 0.04 | 8.66 | This work |
| α-AuS | 3.75 | 10.62 | 5.92 | This work |
| β-AuS | 1.44 | 1.86 | 6.66 | This work |
| γ-AuS | 1.65 | 2.19 | 5.08 | This work |
| Graphene | 5450 | 5450 | 3.35 | 31 |
| C3N | 348 | 348 | 3.20 | 32 |
| Silicene | 28.3 | 28.3 | 4.20 | 33 |
| α-Phosphorene | 36 | 110 | 5.25 | 28 |
| α-Arsenene | 5.6 | 26.1 | 5.5 | 34 |
| PbSe | 0.26 | 0.26 | Not mentioned | 30 |
| Ag2S | 0.82 | 3.81 | 3.48 | 35 |
| Tl2O | 0.8 | 0.65 | 6.58 | 27 |
| PO | 2.42 | 7.08 | 8.00 | 36 |
| 2D tellurium | 2.16 | 4.08 | 6.16 | 37 |
| MoO3 | 1.57 | 1.26 | 6.31 | 38 |
| SnSe | 2.95 | 2.59 | 5.88 | 39 |
Based on Table 2, it can be seen that gold sulfide monolayers are among the 2D materials with the lowest thermal conductivity, very appealing for thermoelectric applications. Remarkably, the room temperature thermal conductivity obtained for β-Au2S of about 0.06 W m−1 K−1, is, to the best of our knowledge, far lower than any other value reported for 2D monolayers (∼5× lower than PbSe,30 and ∼2× higher than air). This ultralow thermal conductivity, along with its high electron mobility,10,13 may point to very high thermoelectric efficiency for β-Au2S.
It can be seen that for all AuS monolayers the thermal conductivity along the zigzag direction is higher than that along the armchair direction. Based on our results, the highest anisotropy among gold sulfide monolayers is observed in α-AuS, with κbb (zigzag) being 2.8 times higher than κaa (armchair). This high anisotropy can be attributed to noticeably higher slope and group velocity of the TA and LA branches along the zigzag direction compared to the armchair direction, as observed in Fig. 2(c).
To better understand the role of the different modes in the total thermal conductivity we also plot the contribution from ZA, TA, LA, and optical modes to the total κ along the aa- and bb-directions in Fig. 4. Very interestingly, as opposed to what is typically found, the optical modes are the dominant heat carriers in gold sulfide monolayers. High optical mode contribution to heat transport has also previously observed in monolayer Ag2S.35 This feature can be attributed to the complex structure of gold sulfide monolayers and the overlap of low frequency optical phonons with the LA mode (see Fig. 2). Also, except for α-Au2S, where the ZA mode has a contribution of 29%, the contribution of this mode in all other gold sulfide monolayers is less than 10%, much smaller than that in graphene (≈80%).31 The reason stems from the fact that the planar structure of graphene gives it a mirror (reflection) symmetry which restricts many three-phonon scattering processes that involve ZA phonons.40 This makes the lifetime of the ZA phonons significantly longer, giving rise to their enhanced contribution. However, the buckled/puckered structure of gold sulfide monolayers (see Fig. 1) breaks the mirror symmetry and gives rise to the enhanced scattering of ZA phonons, reducing their contribution to transport.
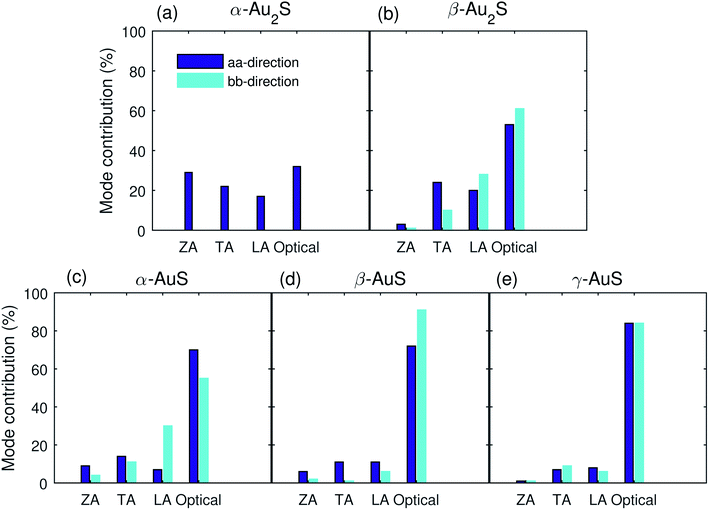 | ||
| Fig. 4 Contribution from the ZA, TA, LA, and optical modes to the room temperature thermal conductivity of (a) α-Au2S, (b) β-Au2S, (c) α-AuS, (d) β-AuS, and (e) γ-AuS along the aa and bb directions. | ||
Next, we consider the mode-dependent phonon group velocity of gold sulfide monolayers shown in Fig. 5. First, we note that the group velocity of the ZA mode at Γ vanishes for all monolayers, a telltale sign of the pure quadraticity of the ZA dispersion at the long-wavelength limit. As can be interpreted also from the phonon dispersion curves, β-Au2S and α-AuS generally have the lowest and highest group velocity among gold sulfide monolayers, respectively. The highest group velocities of the LA (TA) modes at the Γ-point are found to be 2.75 (1.84) km s−1, 2.16 (1.78) km s−1, 4.11 (2.12) km s−1, 2.12 (1.61) km s−1, 3.49 (2.92) km s−1 in α-Au2S, β-Au2S, α-AuS, β-AuS, and γ-AuS, respectively. Also, different levels of anisotropic group velocity for TA and LA modes at the Γ-point can be seen in Fig. 5. The highest anisotropy is seen in α-AuS, with the Γ-point group velocity of the LA mode along the Γ–X direction being 4.11 km s−1, about two times higher than that along the Γ–Y direction (2.14 km s−1). This can justify the high anisotropy of the thermal conductivity of α-AuS observed in Fig. 3(c). Another noticeable feature in Fig. 5 is the relatively large group velocity of the optical modes, particularly in the lower frequency region (less than 6 THz), which explains their high contribution to the total thermal conductivity discussed earlier. In summary, the evidence from phonon group velocity points to β-Au2S having the lowest and α-AuS having the highest thermal conductivity in gold sulfide monolayers which agrees well with the order of calculated thermal conductivity values observed in Fig. 3 and Table 2. Given our finding that κ of β-Au2S is much lower than many other studied 2D materials (see Table 2), it can also be interesting to compare its phonon group velocity to that of a few 2D monolayers that also have ultralow thermal conductivities. Based on ref. 38, MoO3 has κaa = 1.57 W m−1 K−1 and κbb = 1.26 W m−1 K−1. The group velocity of the TA and LA modes at the Γ-point along the aa-direction in MoO3 are reported to be 3.19 km s−1 and 3.80 km s−1,38 respectively. These values are both lower than the corresponding values in β-Au2S. Monolayer Tl2O is another 2D material with ultralow thermal conductivity, having κaa = 0.80 W m−1 K−1 and κbb = 0.65 W m−1 K−1.27 The group velocity of the LA and TA modes at the Γ-point in Tl2O are about 2.48 km s−1 and 1.80 km s−1,27 both higher than the corresponding values in β-Au2S. So, this group velocity comparison can partially suggest lower thermal conductivity for β-Au2S than MoO3 or Tl2O.
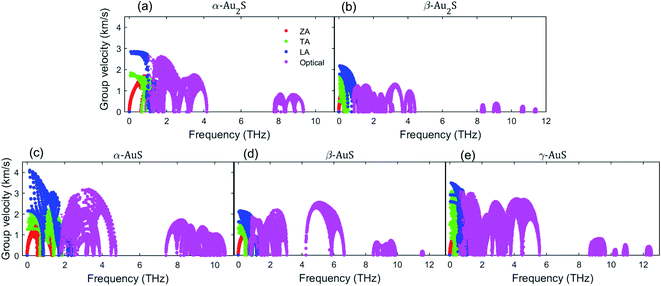 | ||
| Fig. 5 Phonon group velocity as a function of frequency in (a) α-Au2S, (b) β-Au2S, (c) α-AuS, (d) β-AuS, and (e) γ-AuS. | ||
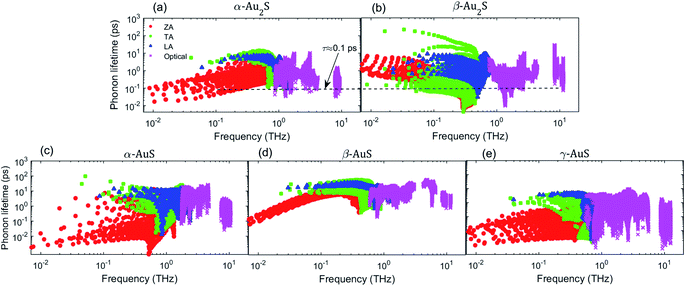
We analyze next the mode-dependent phonon relaxation times of different gold sulfide monolayers as plotted in Fig. 6. First, we note that in gold sulfide monolayers, the TA and LA modes have overall longer phonon lifetimes than the ZA mode. This situation is different from graphene, as the reflection symmetry in the structure of graphene makes the lifetime of the ZA mode considerably longer than the TA and LA mode. For an easier comparison between the phonon lifetimes in α-Au2S and β-Au2S, we include a dashed line in Fig. 6(a) and (b) as guide to the eye at τ = 0.1 ps. As can be seen, almost all the acoustic phonons in α-Au2S in the frequency range of 0.1 THz < ω < 1.0 THz have a lifetime longer than 0.1 ps. However, the lifetime of many acoustic modes of β-Au2S including the ZA, TA, and LA phonons in the same frequency region is shorter than 0.1 ps, by as much as an order of magnitude. Also note that while some ZA phonons in β-Au2S at very low-frequencies (less than 0.1 THz) have longer lifetimes than those in α-Au2S, their low group velocity implies that those modes do not contribute much to the thermal conductivity. So, the shorter phonon lifetimes in β-Au2S combined with lower group velocity (Fig. 5) can explain the lower thermal conductivity of β-Au2S compared to α-Au2S. Comparing the AuS phases plotted in Fig. 6(c) to (e), we find that generally the phonon lifetimes in γ-AuS are slightly shorter than those in α-AuS and β-AuS. For example, the longest lifetime of the LA mode in γ-AuS is about 5 ps while it is about 16 ps and 10 ps in α-AuS and β-AuS, respectively. The same observation can be made for the optical modes. The relatively long lifetime of α-AuS together with its larger group velocity results in α-AuS having the highest thermal conductivity between all gold sulfide monolayers. However, the situation is slightly different when comparing β-AuS and γ-AuS. The comparatively higher group velocity of γ-AuS more than compensates for its shorter lifetime leading to slightly higher thermal conductivity relative to β-AuS.
Similar to the discussion on group velocity, we compare the phonon lifetimes of β-Au2S with some other monolayers exhibiting ultralow thermal conductivity as listed in Table 2. First we consider the phonon scattering rates of monolayer Ag2S presented in ref. 35. In the frequency region that contributes to κ, most of the acoustic and optical phonons have scattering rates lower than 10 ps−1, which corresponds to a lifetime longer than 0.1 ps. However, as shown in Fig. 6(b), there are many acoustic and optical modes in β-Au2S with phonon lifetimes shorter than 0.1 ps. Comparing further with Tl2O, one can also find that the phonon lifetime of almost all the acoustic modes is longer than 0.1 ps. Combining these observations with our earlier discussion about phonon group velocities, we may therefore conclude that β-Au2S can offer even a lower thermal conductivity than other monolayers with an ultralow thermal conductivity.
Generally, it is known that two factors are important in determining the phonon lifetime in a system; (i) the phase space available for three-phonon scattering processes allowed by the energy and momentum conservation rules, and (ii) the strength of these scattering channels, which is usually determined by the Grüneisen parameters (γ) as measure of the anharmonic interaction matrix elements. Typically, a bigger phonon scattering phase space means larger probability of three-phonon scattering events, which results in lower lifetime and thermal conductivity. Fig. 7 compares the total scattering phase space in gold sulfide monolayers. It can be seen that α-Au2S has a total phase space of about 0.0085, slightly larger than that of 0.0082 in β-Au2S. So, the scattering phase space on its own fails to explain the longer lifetimes observed for phonons in α-Au2S as compared to β-Au2S. The total scattering phase space in α-AuS, β-AuS, and γ-AuS are found to be 0.0072, 0.0079, and 0.0084 suggesting an order of α-AuS > β-AuS > γ-AuS for the lifetime of phonons in theses monolayers, which agrees well with the trend seen in Fig. 6. The smaller phase space in α-AuS compared to other monolayers can be attributed to the greater energetic separation of its phonon branches (Fig. 2(c)), and also a larger gap between high- and low-lying optical phonons.
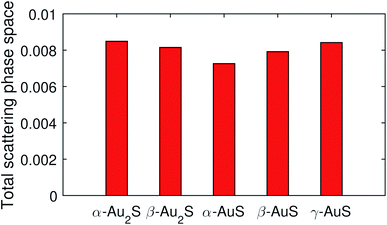 | ||
| Fig. 7 Total phase space available for three-phonon scattering processes in gold sulfide monolayers. | ||
Turning back to the important parameters that determine the phonon lifetime of a structure, we compare the anharmonicity of different gold sulfide monolayers. Fig. 8 shows the Grüneisen parameters of different modes in Au2S and AuS monolayers. First, as can be seen in Fig. 8(a) and (d) we note that the ZA branch of all gold sulfide monolayers at the long-wavelength limit show large negative γ values which is a typical feature shared between many 2D systems.41,42 This means that the frequency of the ZA phonons increases upon expansion of the crystal. Fig. 8(b) compares the Grüneisen parameters of the TA and LA modes in α-Au2S and β-Au2S. Based on our findings, β-Au2S has overall a higher γ compared to α-Au2S, particularly in the low frequency region of ω < 0.5 THz where γ of TA and LA modes in β-Au2S displays values up to 2.6 times higher than that β-Au2S. This shows that the TA and LA modes of β-Au2S in the low frequency region are subject to strong anharmonicity. Remarkably, this is the frequency region in which lifetimes of TA and LA phonons of β-Au2S are shorter than those in β-Au2S (see Fig. 6(b)). So, the higher anharmonicity of the TA and LA phonons in β-Au2S can validate its shorter lifetime and thermal conductivity of compared to α-Au2S. Based on Fig. 8(e), we did not find a noticeable difference between the Grüneisen parameters of TA and LA modes in α-AuS, β-AuS, and γ-AuS, interpreting the same level of anharmonicity for these phonon modes in AuS monolayers. Also, Fig. 8(c) and (f) reveal no significant differences between Grüneisen parameters of optical phonons in Au2S and AuS monolayers.
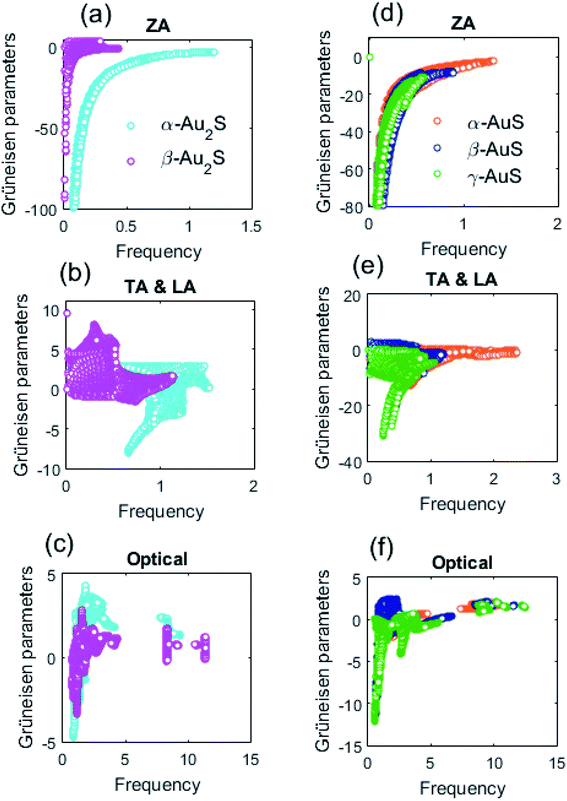 | ||
| Fig. 8 The Grüneisen parameters of different phonon modes in Au2S (left panel) and AuS (right panel) monolayers as a function of frequency. | ||
To explore the effects of nanostructuring on κ in gold sulfide monolayers we next consider the normalized thermal conductivity accumulation function versus phonon mean free path (MFP), Fig. 9. One interesting metric is the MFP which corresponds to 50% of the total thermal conductivity, Λ*. We find that the value of Λ* in all monolayers is almost isotropic, which can be found in Fig. 9. Based on our results, phonons with extremely low MFP of about 0.1 nm contribute to the lattice thermal conductivity of β-Au2S, while in other gold sulfide monolayers the lowest phonon MFP that contribute to κ is about 1.0 nm. Contribution from phonons with such low phonon MFP is previously seen in Ag2S, which also has an ultralow κ,35 and is characteristic of low thermal conductivity amorphous structures.43 However, as such low phonon MFPs are comparable or even smaller than the unit cell size of these systems, the definition of phonons with such low MFPs can be questionable.
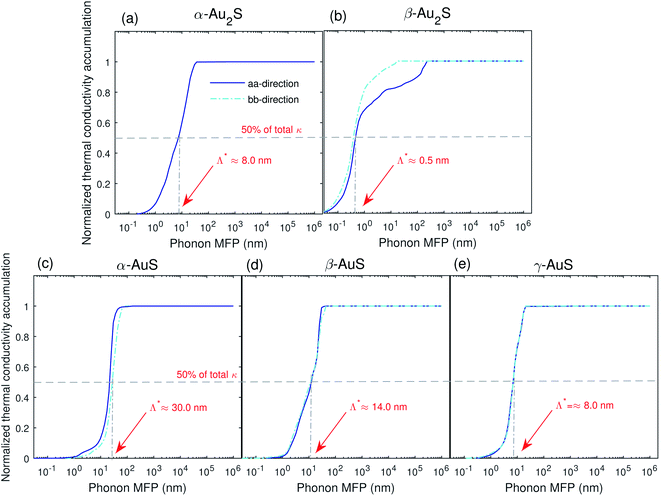 | ||
| Fig. 9 Normalized thermal conductivity accumulation along the aa- and bb-directions in (a) α-Au2S, (b) β-Au2S, (c) α-AuS, (d) β-AuS, and (e) γ-AuS as a function of phonon MFP at T = 300 K. | ||
We also find that, except for β-Au2S, the thermal conductivity of all gold sulfide monolayers saturates to its ultimate value at phonon MFP lower than about 75 nm. However, in β-Au2S, there are still contributions to κ from phonons with phonon MFP of about 200 nm, showing that size reduction can be a practical strategy to tune the lattice thermal conductivity of β-Au2S to even lower values.
4 Summary and conclusion
In conclusion, our detailed study of phonon thermal transport based on first-principles calculations and the PBTE reveals that gold sulfide monolayers generally have ultralow thermal conductivities that together with their rich electronic transport properties, can make them promising candidates for thermoelectric applications. The ultralow thermal conductivity of gold sulfide monolayers is generally a repercussion of huge mass difference between Au and S atoms, weak bonds, lack of an optical–acoustic gap, low group velocities, and high scattering rates. Different degrees of anisotropy is also observed in their thermal conductivities, with α-Au2S showing no anisotropy, whereas for α-AuS we find the highest anisotropy of about 2.8. Particularly, the results show that monolayer β-Au2S can be a contender for the 2D material with lowest thermal conductivity, having κaa = 0.06 W m−1 K−1 and κbb = 0.04 W m−1 K−1. This ultralow conductivity compared to other gold sulfide monolayers is attributed to its flattened phonon branches resulting in much lower group velocities, and also higher structure anharmonicity resulting in shorter phonon lifetimes. Our results are a promising stimulus for the synthesis and use of gold sulfide monolayers for thermoelectric applications with high figure of merit, and also motivate further experimental measurements of the thermal properties of this family of monolayers.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC). Computations were performed on the Niagara supercomputer at the SciNet HPC Consortium. SciNet is funded by the Canada Foundation for Innovation under the auspices of Compute Canada; the Government of Ontario; Ontario Research Fund-Research Excellence; and the University of Toronto.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306(5696), 666–669 CrossRef CAS PubMed.
- K. I. Bolotin, K. J. Sikes, Z. Jiang, M. Klima, G. Fudenberg, J. Hone, P. Kim and H. L. Stormer, Ultrahigh electron mobility in suspended graphene, Solid State Commun., 2008, 146(9–10), 351–355 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Two-dimensional gas of massless Dirac fermions in graphene, Nature, 2005, 438(7065), 197–200 CrossRef CAS.
- A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Superior thermal conductivity of single-layer graphene, Nano Lett., 2008, 8(3), 902–907 CrossRef CAS PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321(5887), 385–388 CrossRef CAS PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Electronics and optoelectronics of two-dimensional transition metal dichalcogenides, Nat. Nanotechnol., 2012, 7(11), 699–712 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, Phosphorene: an unexplored 2D semiconductor with a high hole mobility, ACS Nano, 2014, 8(4), 4033–4041 CrossRef CAS PubMed.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Black phosphorus field-effect transistors, Nat. Nanotechnol., 2014, 9(5), 372 CrossRef CAS PubMed.
- A. Favron, E. Gaufrès, F. Fossard, A.-L. Phaneuf-L'Heureux, N. Y. W. Tang, P. L. Lévesque, A. Loiseau, R. Leonelli, S. Francoeur and R. Martel, Photooxidation and quantum confinement effects in exfoliated black phosphorus, Nat. Mater., 2015, 14(8), 826–832 CrossRef CAS PubMed.
- Q. Wu, W. W. Xu, D. Lin, J. Wang and X. C. Zeng, Two-dimensional gold sulfide monolayers with direct band gap and ultrahigh electron mobility, J. Phys. Chem. Lett., 2019, 10(13), 3773–3778 CrossRef CAS.
- X. Chen, D. Wang, X. Liu, L. Li and B. Sanyal, Two-dimensional square-A2B (A = Cu, Ag, Au, and B = S, Se): auxetic semiconductors with high carrier mobilities and unusually low lattice thermal conductivities, J. Phys. Chem. Lett., 2020, 11(8), 2925–2933 CrossRef CAS PubMed.
- Z. Cai, B. Liu, X. Zou and H.-M. Cheng, Chemical vapor deposition growth and applications of two-dimensional materials and their heterostructures, Chem. Rev., 2018, 118(13), 6091–6133 CrossRef CAS PubMed.
- L. Lv, Y. Shen, X. Gao, J. Liu, S. Wu, Y. Ma, X. Wang, D. Gong and Z. Zhou, Strain engineering on the electrical properties and photocatalytic activity in gold sulfide monolayer, Appl. Surf. Sci., 2021, 546, 149066 CrossRef CAS.
- L. Lindsay, C. Hua, X. L. Ruan and S. Lee, Survey of ab initio phonon thermal transport, Mater. Today Phys., 2018, 7, 106–120 CrossRef.
- A. Taheri, C. Da Silva and C. H. Amon, Effects of biaxial tensile strain on the first-principles-driven thermal conductivity of buckled arsenene and phosphorene, Phys. Chem. Chem. Phys., 2018, 20(43), 27611–27620 RSC.
- A. Taheri, C. Da Silva and C. H. Amon, Phonon thermal transport in β-NX (X = P, As, Sb) monolayers: a first-principles study of the interplay between harmonic and anharmonic phonon properties, Phys. Rev. B, 2019, 99(23), 235425 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Pergamon, Oxford, 1995 Search PubMed.
- Y. Kuang, L. Lindsay, Q. Wang and L. He, Lattice chain theories for dynamics of acoustic flexural phonons in nonpolar nanomaterials, Phys. Rev. B, 2020, 102(14), 144301 CrossRef CAS.
- J. Carrete, W. Li, L. Lindsay, D. A. Broido, L. J. Gallego and N. Mingo, Physically founded phonon dispersions of few-layer materials and the case of borophene, Mater. Res. Lett., 2016, 4(4), 204–211 CrossRef CAS.
- A. Taheri, S. Pisana and C. V. Singh, Importance of quadratic dispersion in acoustic flexural phonons for thermal transport of two-dimensional materials, Phys. Rev. B, 2021, 103(23), 235426 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., Quantum espresso: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- A. Taheri, C. Da Silva and C. H. Amon, First-principles phonon thermal transport in graphene: effects of exchange-correlation and type of pseudopotential, J. Appl. Phys., 2018, 123(21), 215105 CrossRef.
- A. Taheri and C. V. Singh, Anisotropic phonon thermal transport in nitrophosphorene monolayer, Phys. Rev. Mater., 2021, 5(3), 034009 CrossRef CAS.
- F. Eriksson, E. Fransson and P. Erhart, The hiphive package for the extraction of high-order force constants by machine learning, Adv. Theory Simul., 2019, 2(5), 1800184 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Shengbte: a solver of the Boltzmann transport equation for phonons, Comput. Phys. Commun., 2014, 185(6), 1747–1758 CrossRef CAS.
- See ESI† for convergence of thermal conductivity with respect to phonon q-point grid sampling, and comparison between iterative and RTA solutions of the BTE.
- H. H. Huang, G. Xing, X. Fan, D. J. Singh and W. T. Zheng, Layered Tl2O: a model thermoelectric material, J. Mater. Chem. C, 2019, 7(17), 5094–5103 RSC.
- A. Jain and A. J. H. McGaughey, Strongly anisotropic in-plane thermal transport in single-layer black phosphorene, Sci. Rep., 2015, 5(1), 1–5 Search PubMed.
- M. Zeraati, S. M. V. Allaei, I. A. Sarsari, M. Pourfath and D. Donadio, Highly anisotropic thermal conductivity of arsenene: an ab initio study, Phys. Rev. B, 2016, 93(8), 085424 CrossRef.
- P.-F. Liu, T. Bo, J. Xu, W. Yin, J. Zhang, F. Wang, O. Eriksson and B.-T. Wang, First-principles calculations of the ultralow thermal conductivity in two-dimensional group-IV selenides, Phys. Rev. B, 2018, 98(23), 235426 CrossRef CAS.
- Y. Kuang, L. Lindsay, S. Shi, X. Wang and B. Huang, Thermal conductivity of graphene mediated by strain and size, Int. J. Heat Mass Transfer, 2016, 101, 772–778 CrossRef CAS.
- A. Taheri, C. Da Silva and C. H. Amon, Highly tunable thermal conductivity of C3N under tensile strain: a first-principles study, J. Appl. Phys., 2020, 127(18), 184304 CrossRef.
- B. Peng, D. Zhang, H. Zhang, H. Shao, G. Ni, Y. Zhu and H. Zhu, The conflicting role of buckled structure in phonon transport of 2D group-IV and group-V materials, Nanoscale, 2017, 9(22), 7397–7407 RSC.
- G. Zheng, Y. Jia, S. Gao and S.-H. Ke, Comparative study of thermal properties of group-VA monolayers with buckled and puckered honeycomb structures, Phys. Rev. B, 2016, 94(15), 155448 CrossRef.
- S. Sharma, A. Shafique and U. Schwingenschlögl, Monolayer Ag2S: ultralow lattice thermal conductivity and excellent thermoelectric performance, ACS Appl. Energy Mater., 2020, 3(10), 10147–10153 CrossRef CAS.
- S. Lee, S.-H. Kang and Y.-K. Kwon, Low lattice thermal conductivity of a two-dimensional phosphorene oxide, Sci. Rep., 2019, 9(1), 1–9 CrossRef PubMed.
- Z. Gao, F. Tao and J. Ren, Unusually low thermal conductivity of atomically thin 2D tellurium, Nanoscale, 2018, 10(27), 12997–13003 RSC.
- Z. Tong, T. Dumitrică and T. Frauenheim, Ultralow thermal conductivity in two-dimensional MoO3, Nano Lett., 2021, 21, 4351–4356 CrossRef CAS PubMed.
- G. Qin, Z. Qin, W.-Z. Fang, L.-C. Zhang, S.-Y. Yue, Q.-B. Yan, M. Hu and G. Su, Diverse anisotropy of phonon transport in two-dimensional group IV–VI compounds: a comparative study, Nanoscale, 2016, 8(21), 11306–11319 RSC.
- L. Lindsay, D. A. Broido and N. Mingo, Flexural phonons and thermal transport in graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(11), 115427 CrossRef.
- C. H. Lee and C. K. Gan, Anharmonic interatomic force constants and thermal conductivity from Grüneisen parameters: an application to graphene, Phys. Rev. B, 2017, 96(3), 035105 CrossRef.
- X.-J. Ge, K.-L. Yao and J.-T. Lü, Comparative study of phonon spectrum and thermal expansion of graphene, silicene, germanene, and blue phosphorene, Phys. Rev. B, 2016, 94(16), 165433 CrossRef.
- W.-X. Zhou, Y. Cheng, K.-Q. Chen, G. Xie, T. Wang and G. Zhang, Thermal conductivity of amorphous materials, Adv. Funct. Mater., 2020, 30(8), 1903829 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00019a |
| This journal is © The Royal Society of Chemistry 2022 |