Open Access Article
Open Access ArticleField-induced rheological characterization of nano/micro-scaled suspensions based on a multi-peak fitting method
Yang
Ming
,
Xiangming
Huang
 *,
Dongdong
Zhou
and
Yinghui
Ren
*,
Dongdong
Zhou
and
Yinghui
Ren
Hunan University, College of Mechanical and Vehicle Engineering, Changsha 410082, China. E-mail: h_xiangming@aliyun.com
First published on 21st March 2022
Abstract
Nano/micro-scaled suspensions used in damping systems, bulletproof materials and flexible machining regions are developing towards external energy field control and multi-type and multi-scale dispersed phase particles. However, the above-mentioned changes make the rheological properties of the fluid more complex, which cannot be characterized efficiently with high quality by traditional constitutive equations. In order to solve the above-mentioned problems, based on the multi-peak fitting characterization method of the Gaussian function, the field-induced rheological constitutive equation of a multi-scale particle suspension turbidity system (MRSTPF as an example) was established. Under the condition of shear distribution and external magnetic field affection, the rheological characteristic curves of the dispersion system were measured using an Antompa MCR301 rheometer. The Origin software was used to fit and characterize the above-mentioned rheological data. The results indicate that the method can effectively establish field-induced constitutive equations of different dispersed systems, and the fitting goodness evaluation parameters are above 95% (R-square) and 90% (adjusted R-square) respectively.
1 Introduction
Magnetorheological shear thickening polishing fluid (MRSTPF) is a kind of nano/micro-scaled suspension material that can realize the dual control of fluid viscosity under the action of magnetic field and shear. The researchers1,2 found that the shear thickening fluid (STF) doped with magnetic particles can obtain higher shear stress under certain magnetic field conditions, so it is widely used in engineering fields such as dampers, bulletproof materials and flexible machining, and has a good application prospect.In a damping system, the nano/micro-scaled suspension can achieve damping effects on the external vibration by virtue of good system stability and active and passive control rheological characteristics. Researchers used traditional constitutive models,3–5 such as Bingham model and B–W model, to characterize the rheological properties of the damping fluid. In addition, based on the idea of phenomenological representation, the finite difference method and Poiseuille's laminar flow hypothesis were used to solve the differential equation for arbitrary rheology.6,7 The above-mentioned study of fluid constitutive characterization provides a theoretical basis for the performance simulation and prediction of damping characteristics, velocity characteristics and system design optimization.8
In the field of bulletproof materials, the nano/micro-scaled suspension can be used for the preparation of bulletproof composite materials.9 When the dispersive system with shear thickening property is injected into a Kevlar bulletproof fiber, the kinetic energy of collision can be effectively absorbed by virtue of its inherent rheological properties.10 At the same time, the impregnation effect of the fluid on the fiber structure greatly enhanced the friction effect of the composite material in the puncture process. The effects of the STF concentration, composite fabric layer number, composite structure, Kevlar-fiber type and other factors on impact resistance and energy absorption during impact were investigated.11–15 The properties of the composite were tested by various impact methods and impact velocity. In order to further explore the mechanism and process of energy absorption during impact resistance, the coupled Lagrange method was adopted, and the dynamic response of materials under different impact rates was simulated by introducing the STF constitutive equation.16 The results indicate that the composite material can be used to achieve greater impact resistance with a lighter mass.17
In the field of flexible machining, the nano/micro-scaled suspension was introduced into non-contact machining methods such as abrasive flow machining18 and bonnet polishing,19 in order to realize high-efficiency and non-destructive self-adaptive polishing of hard and brittle materials.20–22 When the fluid moves relative to the workpiece surface, the dispersed phase particles are affected by the disturbance of the convex peak on the rough surface of the workpiece, and quickly gather into composite clusters when the abrasive particles impact the convex peak. It then carries the abrasive particles into collision with the convex peak. Under the accumulation of impact kinetic energy, the surface finishing is finally completed.23 The microscopic behavior of the above-dispersed phase particles results in shear thickening at the macroscopic view. In order to further explore the microscopic mechanism of material removal, based on the assumption of the N–S equation and Reynolds equation, the velocity and stress distribution models of the flow field in the polishing zone were established, and then the prediction model of the material removal rate was obtained.24,25 The rheological constitutive model is the key factor to the accuracy of the predict model. Therefore, it is necessary to characterize the field rheological properties of the dispersion system.
In this study, two kinds of MRSTPFs commonly used in industries, which are nano-silica based and micro-polyhydroxy polymer based (micro-PP based), were prepared. Then, the viscosity–shear rate rheological characteristic curves of the MRSTPFs were tested under different magnetic field intensities. A multi-peak fitting method based on the Gaussian function is proposed and described. The high efficiency and high-quality fitting characterizations of rheological characteristics at different magnetic field intensities and shear rate intervals were completed.
2 Materials and experiments
2.1 Materials
In the study, the parameters of dispersed phase particles and continuous-phase base carrier liquid required by the prepared dispersion system are shown in Tables 1 and 2.| Particle type | Silica | Polyhydroxy polymer | Carbonyl iron | Diamond | Alumina | Silicon carbide |
| Average particle size | 7–40 nm | 10 μm | 3–5 μm | 3 μm | 3 μm | 3 μm |
| Manufacturer | 300 m2 g−1, Nanjing Cook Biotechnology Co., Ltd, China | Guangzhou Jingtang Biotechnology Co., Ltd, China | Yuhuan CNC Machine Tool Co., Ltd, China | Zhecheng Zhongyuan Super Hard Abrasives Co., Ltd, China | Jiangxi Ketai New Material Co., Ltd, China | Chuangying Metal Material Co., Ltd, China |
| Continuous phase carrier | Organic dispersant | Inorganic dispersant | Additive |
| Type | PEG-200 | DI water | Sodium polyacrylate |
| Manufacturer | China National Pharmaceutical Group Chemical Testing Co., Ltd, China | High-tech Group Environmental Protection Biotechnology Co., Ltd, China | Juhe Biotechnology Co., Ltd, China |
2.2 Preparation methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 by mechanical agitation to obtain a nano-silica-based STF. It was then poured into a vacuum device and left for 1 hour to drain bubbles from the fluid. Then, a certain mass fraction of silicon carbide particles and carbonyl iron particles (CIPs) were added to the above STF, and the process of mechanical stirring and vacuum exhaust was repeated. Finally, nano-silica-based composite dispersion system with different CIP mass fractions (5, 10, and 15%) was obtained, as shown in Table 3. The composite cluster morphology of the magnetic pole chain in nano-silica cluster is shown in Fig. 1(a), which is due to the fact that free magnetic particles in the dispersed system polarize into chains under the action of a weak magnetic field, thus forming the chain structure in the nano-particle cluster.
5 by mechanical agitation to obtain a nano-silica-based STF. It was then poured into a vacuum device and left for 1 hour to drain bubbles from the fluid. Then, a certain mass fraction of silicon carbide particles and carbonyl iron particles (CIPs) were added to the above STF, and the process of mechanical stirring and vacuum exhaust was repeated. Finally, nano-silica-based composite dispersion system with different CIP mass fractions (5, 10, and 15%) was obtained, as shown in Table 3. The composite cluster morphology of the magnetic pole chain in nano-silica cluster is shown in Fig. 1(a), which is due to the fact that free magnetic particles in the dispersed system polarize into chains under the action of a weak magnetic field, thus forming the chain structure in the nano-particle cluster.
| Sample | Nano-silica + PEG200 (wt%) | CIP (wt%) | Silicon carbide (wt%) |
|---|---|---|---|
| CIP-5 wt% | 85 | 5 | 10 |
| CIP-10 wt% | 80 | 10 | 10 |
| CIP-15 wt% | 75 | 15 | 10 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 51) of polyhydroxy polymer particles into a continuous phase carrier (deionized water, DI water) and stirring the mixture mechanically for 20 min. Then, CIPs and hard particles (diamond, C/alumina, Al2O3) were added and mechanically stirred for 20 min. Then, the prepared fluid was poured into a vacuum device and the bubbles were discharged. Finally, a micro-PP-based composite dispersion system with different hard particles was obtained, as shown in Table 4. In this system, short chains of free magnetic particles formed under the action of a certain magnetic field gather with other dispersed phase particles, and the micro-structure of composite clusters formed is shown in Fig. 1(b).
51) of polyhydroxy polymer particles into a continuous phase carrier (deionized water, DI water) and stirring the mixture mechanically for 20 min. Then, CIPs and hard particles (diamond, C/alumina, Al2O3) were added and mechanically stirred for 20 min. Then, the prepared fluid was poured into a vacuum device and the bubbles were discharged. Finally, a micro-PP-based composite dispersion system with different hard particles was obtained, as shown in Table 4. In this system, short chains of free magnetic particles formed under the action of a certain magnetic field gather with other dispersed phase particles, and the micro-structure of composite clusters formed is shown in Fig. 1(b).
| Sample | Micro-PP + DI water (wt%) | CIP (wt%) | Hard particle (wt%) |
|---|---|---|---|
| Al2O3 | 85 | 5 | 10 |
| C | 85 | 5 | 10 |
2.3 Rheological test
In order to obtain the field-rheological properties of the composite dispersion system, samples of the dispersion system were tested using a rotary magnetorheometer (Anton Paar/MCR301, Antonpa, Austria). Selecting a diameter of 20 mm parallel plate test head, test clearance was set to 1 mm. Then, an appropriate amount of test samples was slowly poured into the test tank. Pre-shearing was performed at a constant shear rate (100 s−1) for 30 s at a set magnetic field intensity to ensure the uniform distribution of dispersed phase particles and the stable formation of the magnetic chain structure. Under the condition that the temperature in the test area was kept at 25 °C using a cooling cycle system, the dynamic shear mode was adopted to test the rheological properties of samples at the corresponding shear rate range under different magnetic field intensities, as shown in Table 5.| Sample name | Magnetic field intensity (mT) | Shear rate interval (s−1) | Test group naming |
|---|---|---|---|
| CIP-5 wt% | 100, 200, 300 | 10–1000 | For example, CIP-5 wt% – 100 mT |
| CIP-10 wt% | 100, 200, 300 | ||
| CIP-15 wt% | 100, 200, 300 | ||
| Al2O3 | 55, 95, 135, 175 | 100–1000 | For example, Al2O3 – 55 mT |
| C | 55, 95, 135, 175 | 100–1000 | For example, C – 55 mT |
3 Constitutive characterization method
3.1 Traditional constitutive characterization methods
Constitutive equation is a mathematical model that reflects the macroscopic properties of materials, also known as constitutive relations. The functional relationship between stress and strain rates or stress tensor and strain tensor is usually called the constitutive equation. The variation in viscosity with the shear rate can be used to describe the rheological properties of rheological materials. Shear rate, also known as velocity gradient, refers to the gradient distribution of the velocity field generated by internal friction when the fluid flows between interfaces. As the shear rate is a second-order tensor, it can be defined by additive decomposition, as given in eqn (1), where, Dij and Wij are the deformation rate and rotation rate tensors respectively.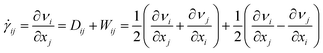 | (1) |
Power law constitutive models are commonly used to characterize the rheological properties of non-Newtonian fluids,26 as shown in eqn (2):
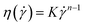 | (2) |
However, as the rheological research gradually considers the influence of the suspension preparation method and external energy field on rheological properties, the traditional power law constitution is no longer applicable. Wyart et al.27 gave DST (discontinuous shear thickening) and CST (continuous shear thickening) descriptions of a dispersed suspended turbidity system, and investigated the constitutive characteristics and microscopic mechanism of the dense suspended turbidity system. In addition, because the rheological properties of the magnetorheological shear thickening fluid are obviously affected by the mass fraction of magnetic particles and magnetic field intensity, it has also certain Bingham characteristics,28,29 as shown in eqn (3):
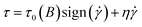 | (3) |
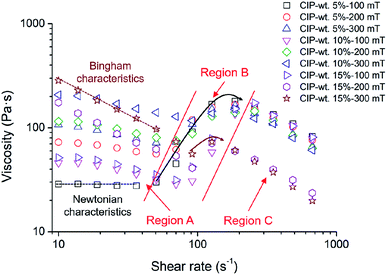
With the increase in magnetic particle mass fraction and magnetic field intensity, the initial viscosity of the fluid increases sharply, and the power law of shear thickening interval is inhibited. Thus, the Bingham characteristics of fluid are enhanced.30 Therefore, the traditional power law model and Bingham model are difficult to characterize the above-mentioned complex rheological characteristics.
The shear thickening fluid used in relevant studies mainly includes three rheological characteristics:31 low-speed shear thinning interval A, shear thickening interval B, and high-speed shear thinning interval C. The traditional power-law constitutive model only applies to the representation of shear thickening interval B, and the divergence of the function cannot describe the transition between shear thinning and shear thickening. In order to solve the problems, based on the cross constitutive model,32 Galindo-Rosales et al.33,34 constructed a segmented and continuous function constitutive model for the three above-mentioned constitutive features, whose correlation coefficient R-square value is greater than 90%, as shown in eqn (4):
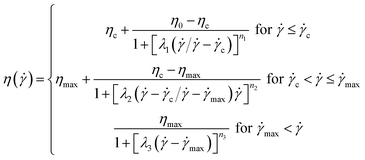 | (4) |
Unfortunately, there are as many as 11 related parameters in this model, which leads to complex fitting of constitutive equation and requires a large number of experimental data. Therefore, Wei et al.35 proposed a simplified prediction model to predict the rheological properties of the multi-dispersed phase system, which realized the high precision fitting of the silica-based shear thickening system, and the correlation coefficient R-square reached 99.7%, as shown in eqn (5):
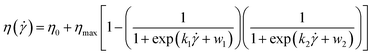 | (5) |
In the meantime, the fitting degree of this model is poor in the low shear rate interval, and it cannot be fitted when the mass fraction of dispersed phase particles is too large. Selim et al.36 improved eqn (5) by using genetic algorithm based on the Matlab optimization toolbox and obtained a high fitting accuracy (R-square value reached more than 98%), but its characterization accuracy was still affected by particle mass fraction and temperature. In addition, based on Doolittle's free volume theory, Steller et al.37 established an empirical constitutive equation describing the complex rheological behavior of high mass fraction dispersion systems, which was used to explain and simulate the time–temperature-dependent viscosity function of polymers in the liquefaction process. However, in summary, there are still problems such as complex constitutive parameters,33,34 partial interval characterization failures,35 and large characterization limitations.34
3.2 Numerical fitting characterization method
Approximating discrete data through ideal functions is the basic idea of characterizing natural systems.38 For example, the finite element method is used to approximate solving partial differential equations. Inspired by this idea, this study intends to use the Gaussian function to approximate the discrete rheological property data and obtain the constitutive equation of the dispersed system. Gaussian function is a density function of normal distribution in probability statistics, which is widely used in natural and social sciences. The Gaussian function expression used in Origin is shown in eqn (6):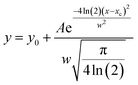 | (6) |
It is one of the basic methods in the field of fluid materials to explore the constitutive equation of dispersed systems based on phenomenology. For example, the finite deformation of the nanocrystalline layer material39 and the mechanical response of fibrous cell flow40,41 were observed to obtain the stress–strain function of the research object, and then the constitutive equation of the material was constructed. In this study, data points of rheological parameter curves (such as viscosity–shear rate) were fitted based on a multi-peak fitting method of the Gaussian function, and then the rheological properties of composite dispersed systems were characterized. The constitutive equations generated by this method have continuity and derivability, and are in accordance with the basic characteristics of the phenomenological method. Meanwhile, compared with the shear rate-dependent branch of equations proposed by Galindo-Rosales et al.,33,34 this study avoids solving a large number of constitutive parameters and has higher characterization efficiency. Compared with the simplified prediction model proposed by Wei et al.,35 it significantly improves the fitting accuracy in the low shear rate interval. In addition, the adaptability of this method is significantly better than any traditional constitutive characterization method or algorithm-based modified constitutive characterization method,34 which can meet the characterization requirements of different dispersed systems under different field conditions and maintain a high characterization accuracy.
3.3 Multi-peak fitting method
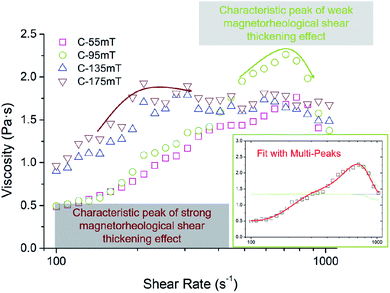
Using the peak analysis function of the Origin data analysis software and the nonlinear least square method based on the Levernberg–Marquardt algorithm (LMA), the rheological characteristics of the dispersed system were fitted. First, the arithmetic mean value of data points is selected as the baseline of the peak fitting function. Second, local extreme values in data points were selected as the peak point of the Gaussian function, as shown in Fig. 2. In particular, because the rheological characteristics of the system were “shear thinning–shear thickening–shear thinning”, two peak anchor points can be obtained. Based on the above-mentioned point selection, the method to obtain the fitting function of constitutive characteristics is called double-peak fitting.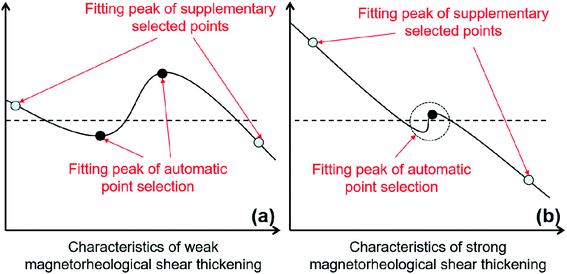 | ||
| Fig. 2 Peak point selection for peak fitting. (a) Characteristics of weak magnetorheological shear thickening. (b) Characteristics of strong magnetorheological shear thickening. | ||
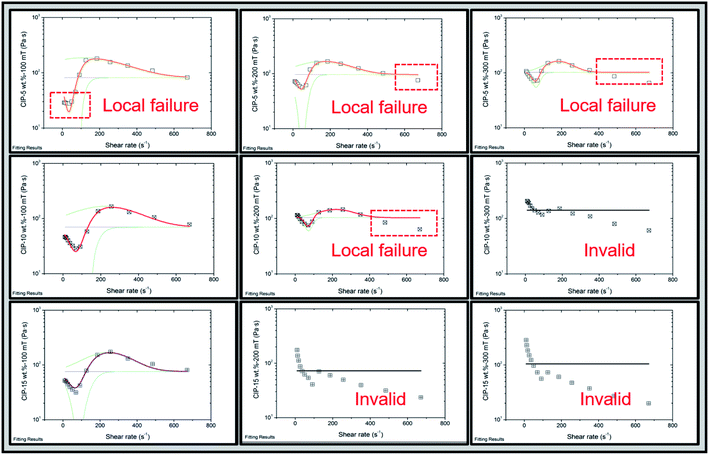
On the basis of the above-mentioned automatic selection of peak points, the rheological parameter points on the initial interval (interval A) and the terminal interval (interval C) were selected for anchoring, and then multiple fitting peaks were obtained. Among them, when the rheological characteristics are close to weak magnetorheological shear thickening (weak magnetic field + low mass fraction CIP), the automatically selected characteristic peak is far away, as shown in Fig. 2(a). However, when the rheological characteristics are close to the strong magnetorheological shear thickening (high magnetic field + high mass fraction CIP), the thickening interval is compressed, and the two automatically selected features lead to the failure of fitting. In order to complete and correct the fitting characterization of rheological properties of the system under different conditions, only one peak point was selected when interval B was narrow, and the peak points were supplemented in interval A and C, as shown in Fig. 2(b). In this study, the method of anchoring multiple Gaussian function feature peak points for constitutive feature fitting is called multi-peak fitting.
4 Result and discussion
4.1 Nano–micro composite dispersion system
The above-mentioned rheological characteristics are summarized and defined. The rheological characteristic shows “weak shear thinning–strong shear thickening–shear thinning” characteristics under the condition of a weak magnetic field and low mass fraction CIP. It is named “weak magnetorheological shear thickening characteristic”, which is similar to cross segmented power-law characteristic.42 The rheological characteristics under the condition of high magnetic field and high mass fraction CIP show “strong shear thinning–weak shear thickening–shear thinning” characteristic. It is named the strong magnetorheological shear thickening characteristic, which is similar to the Bingham characteristic.29,30
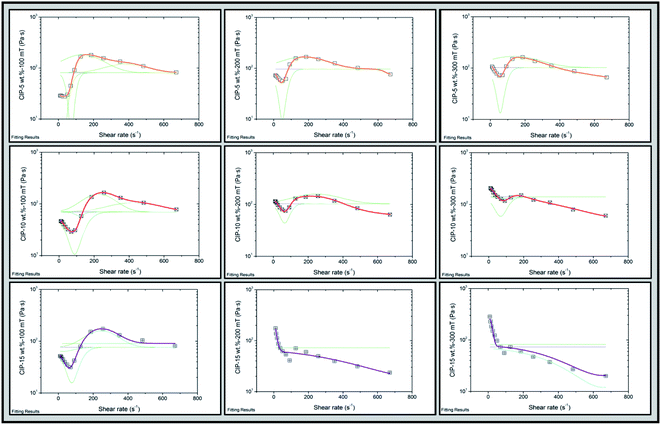
Existing studies have shown that in magnetorheological shear thickening fluids, the constitutive characteristics of the fluid change from weak magnetorheological shear thickening to strong magnetorheological shear thickening with the increase in the magnetic particle proportion and the applied magnetic field intensity.43 Specifically, the initial viscosity of the dispersed system increased sharply at interval A (shear thinning). Interval B (shear thickening) narrowed and the thickening amplitude decreased obviously. Interval C (shear thinning) was affected by the thickening effect in the aforementioned interval. The average viscosity of weak magnetorheological shear thickening is significantly higher than that of strong magnetorheological shear thickening. In particular, the obvious Bingham feature (shear thinning) on interval C leads to the serious failure of the double peak fitting, which leads to the failure of the whole function fitting. Therefore, it is necessary to supplement this part by introducing more fitting peaks.
| Evaluation parameters | CIP-5 wt% | CIP-10 wt% | CIP-15 wt% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 100 mT | 200 mT | 300 mT | 100 mT | 200 mT | 300 mT | 100 mT | 200 mT | 300 mT | |
| COD (R-square) | 98.6% | 96.3% | 85.0% | 98.8% | 72.0% | — | 97.8% | — | — |
| Adj. R-square | 97.7% | 94.0% | 75.6% | 98.0% | 54.4% | — | 96.4% | — | — |
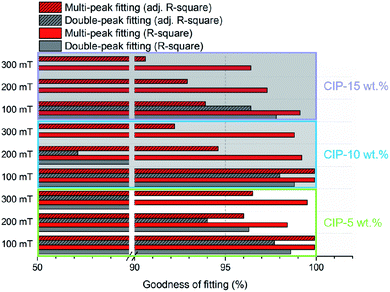 | ||
| Fig. 6 Comparative analysis of fitting goodness for rheological characterization of the composite dispersion system. | ||
| Parameter | CIP-5 wt% – 100 mT | CIP-5 wt% – 200 mT | CIP-5 wt% – 300 mT | CIP-10 wt% – 100 mT | CIP-10 wt% – 200 mT | CIP-10 wt% – 300 mT | CIP-15 wt% – 100 mT | CIP-15 wt% – 200 mT | CIP-15 wt% – 300 mT | |
|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | y 0 | 81.2 | 96.4 | 102.4 | 69.8 | 103.2 | 140.4 | 76.0 | 72.5 | 104.3 |
| x c | 37.7 | 49.1 | 62.4 | 81.5 | 71.5 | −49564.6 | 84.1 | 94.3 | −4087.1 | |
| Peak 1 | A | −19988.3 | −9185.1 | −3058.2 | −18561.6 | −2577.3 | 492![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 025.0 025.0 |
−10778.4 | 226![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175.8 175.8 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 479.9 479.9 |
| w | 117.7 | 91.7 | 60.1 | 158.5 | 55.9 | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797.7 797.7 |
139.3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 427 427![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580.0 580.0 |
42.2 | |
| x c | 115.6 | 162.0 | 181.0 | 221.2 | 219.1 | 2361.9 | 242.2 | 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 025 025![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0 000.0 |
153.2 | |
| Peak 2 | A | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511.7 511.7 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385.1 385.1 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184.2 184.2 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 282.3 282.3 |
9961.3 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242.0 242.0 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947.9 947.9 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 872 872![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0 000.0 |
−8514.6 |
| w | 475.8 | 319.4 | 174.7 | 393.0 | 222.5 | 22.0 | 281.9 | 616![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 762 762![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0 000.0 |
213.5 | |
| Evaluation parameters | CIP-5 wt% | CIP-10 wt% | CIP-15 wt% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 100 mT | 200 mT | 300 mT | 100 mT | 200 mT | 300 mT | 100 mT | 200 mT | 300 mT | |
| COD (R-square) | 99.9 | 98.4 | 99.5 | 99.9 | 99.2 | 98.8 | 99.1 | 97.3 | 96.4 |
| Adj. R-square | 99.9 | 96.0 | 96.5 | 99.9 | 94.6 | 92.2 | 93.9 | 92.9 | 90.6 |
| Parameter | CIP-5 wt% – 100 mT | CIP-5 wt% – 200 mT | CIP-5 wt% – 300 mT | CIP-10 wt% – 100 mT | CIP-10 wt% – 200 mT | CIP-10 wt% – 300 mT | CIP-15 wt% – 100 mT | CIP-15 wt% – 200 mT | CIP-15 wt% – 300 mT | |
|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | y 0 | 81.2 | 96.4 | 102.4 | 69.8 | 103.2 | 140.4 | 76.0 | 60.9 | 73.2 |
| x c | 73.3 | 174.0 | 57.1 | 89.1 | 65.0 | 68.1 | 77.2 | 68.6 | 55.6 | |
| Peak 1 | A | −5653.9 | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393.9 393.9 |
−8260.0 | −9330.7 | −5150.0 | −8809.6 | −8032.7 | −3526.8 | 177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649.7 649.7 |
| w | 67.4 | 294.7 | 87.2 | 148.0 | 81.3 | 101.6 | 124.9 | 92.8 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680.5 680.5 |
|
| x c | 136.4 | 49.0 | 134.9 | 226.0 | 249.8 | 103.7 | 247.3 | 69.0 | 7.3 | |
| Peak 2 | A | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658.9 658.9 |
−7879.0 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658.5 658.5 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544.7 544.7 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 009.4 009.4 |
−1035.2 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218.2 218.2 |
6781.7 | 6530.2 |
| w | 255.8 | 85.2 | 330.1 | 203.9 | 303.1 | 107.6 | 205.2 | 227.2 | 33.9 | |
| x c | 14.2 | 680.1 | −208.6 | 116.0 | −95.9 | −48.7 | 25.4 | −9.6 | 656.6 | |
| Peak 3 | A | −10613.9 | −1976.2 | 131.5 | −730.0 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 973.6 973.6 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 145.3 145.3 |
−2008.6 | 7564.9 | −44463.3 |
| w | 102.3 | 90.2 | 441.1 | 63.2 | 383.9 | 325.4 | 151.9 | 41.8 | 682.5 | |
| x c | 386.7 | — | 934.2 | 431.4 | 1083.1 | 773.8 | 370.5 | 568.3 | — | |
| Peak 4 | A | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 037.9 037.9 |
— | −41577.1 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 787.2 787.2 |
−75944.3 | −69922.6 | 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250.3 250.3 |
−19616.0 | — |
| w | 256.2 | — | 833.4 | 327.2 | 1471.6 | 775.2 | 3580.4 | 515.3 | — | |
4.2 Micro-PP-based composite dispersion systems
Referring to the shear thickening polishing method,20–22,24,25 a variety of micron particle dispersion systems were prepared. Based on the multi-peak fitting method, the field rheological properties of the composite dispersion system were fitted and characterized, and the corresponding constitutive function was constructed.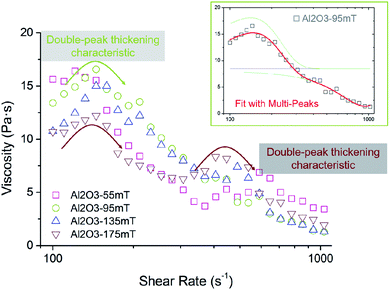 | ||
| Fig. 7 Rheological properties and constitutive characterization of the micron dispersed system (alumina). | ||
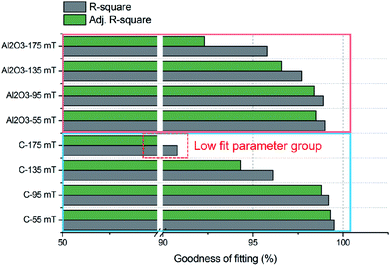 | ||
| Fig. 9 Fitting degree analysis of the constitutive characterization of the micron composite dispersion system. | ||
| Evaluation parameter | Al2O3-55 mT | Al2O3-95 mT | Al2O3-135 mT | Al2O3-175 mT | C-55 mT | C-95 mT | C-135 mT | C-175 mT |
|---|---|---|---|---|---|---|---|---|
| COD (R-square) | 99.0 | 98.9 | 97.7 | 95.8 | 99.5 | 99.2 | 96.1 | 90.8 |
| Adj. R-square | 98.5 | 98.4 | 96.6 | 92.3 | 99.3 | 98.8 | 94.3 | 86.4 |
| Parameter | Al2O3-55 mT | Al2O3-95 mT | Al2O3-135 mT | Al2O3-175 mT | C-55 mT | C-95 mT | C-135 mT | C-175 mT | |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | y 0 | 7.9 | 8.5 | 8.1 | 7.2 | 1.1 | 1.3 | 1.5 | 1.6 |
| x c | 389.5 | 140.8 | 144.3 | 145.1 | 890.3 | 705.1 | 265.7 | 220.6 | |
| Peak 1 | A | −871.4 | 1964.7 | 1182.4 | 186.0 | 573.3 | 449.4 | 47.3 | 28.4 |
| w | 228.5 | 191.3 | 135.1 | 49.2 | 837.0 | 444.6 | 153.5 | 243.9 | |
| x c | 120.5 | 87.8 | 90.2 | 431.1 | 87.4 | 98.3 | 55.9 | 95.9 | |
| Peak 2 | A | 863.4 | −642.2 | −481.7 | 72.8 | −188.4 | −189.4 | −143.1 | −94.3 |
| w | 96.4 | 242.2 | 141.4 | 339.3 | 257.3 | 213.0 | 217.4 | 122.3 | |
| x c | 983.6 | 946.2 | 935.4 | 100.0 | 1060.2 | 991.7 | 624.8 | 777.9 | |
| Peak 3 | A | −2873.6 | −6607.0 | −4783.9 | 268.3 | −163.2 | −51.8 | 86.5 | 355.5 |
| w | 598.7 | 877.6 | 653.1 | 91.3 | 265.1 | 283.3 | 365.0 | 3168.9 | |
| x c | — | — | — | 940.7 | — | — | — | — | |
| Peak 4 | A | — | — | — | −2930.3 | — | — | — | — |
| w | — | — | — | 528.0 | — | — | — | — | |
5 Conclusion
Based on the phenomenological theory, the Gaussian function was used to characterize the field-induced rheological properties of composite multi-scale dispersed systems. The method of peak fitting characterization was proposed, and the constitutive equation of the above-mentioned system was established. The fitting characterization results indicate that:(1) The multi-peak fitting method has higher fitting goodness than that of the double-peak fitting method.
(2) The multi-peak fitting method can more effectively characterize the rheological properties of different dispersion systems (nano-silica based and micro-PP based).
(3) The multi-peak fitting method can realize the consStitutive characterization of micro–nano-scale and micro-scale composite dispersed systems.
(4) The multi-peak fitting can realize the constitutive characterization of rheological characteristics under different magnetic field intensities.
(5) Under different conditions, the fitting degree of the constructed rheological constitutive function can reach R-square more than 95% and adjusted R-square more than 90%.
Outlook
● Based on the data analysis module of the Origin software, the fluid constitutive function with a high fitting degree can be obtained simply and effectively.● The fitting degree of the constitutive function to rheological characterization is less affected by the preparation scheme of the composite dispersion system and external energy field.
● This study is beneficial to the setting of fluid custom material properties in fluid simulation and greatly improves the accuracy of the complex flow field simulation.
Funding
The authors would like to acknowledge the financial support from the National Natural Science Foundation of China (Grant No. 51975203), and Natural Science Foundation of Hunan Province (2021JJ30113).Conflicts of interest
There are no conflicts to declare.References
- Y. Tian, J. L. Jiang, Y. G. Meng and S. Z. Wen, A shear thickening phenomenon in magnetic field controlled-dipolar suspensions Appl, Phys. Lett., 2010, 97(15), 329 Search PubMed.
- G. Bossis, Y. Grasselli and A. Meunier, et al., Outstanding magnetorheological effect based on discontinuous shear thickening in the presence of a superplastifier molecule, Appl. Phys. Lett., 2016, 109(11), 111902-1–111902-4 CrossRef.
- Q. H. Nguyen and S. B. Choi, Optimal design of a vehicle magnetorheological damper considering the damping force and dynamic range, Smart Mater. Struct., 2008, 18(1), 015013 CrossRef.
- Z. A. Qian, Y. A. Jing and A. Hj, et al., Vibration control of a rotor system by shear thickening fluid dampers - ScienceDirect, J. Sound Vib., 2020, 494, 115883 Search PubMed.
- Z. Qian, Y. He and H. Yao, et al., Dynamic performance and mechanical model analysis of a shear thickening fluid damper, Smart Mater. Struct., 2018, 27(7), 075021 CrossRef.
- P. Nagy-Gyrgy and C. Hs, Predicting the damping characteristics of vibration dampers employing generalized shear thickening fluids, J. Sound Vib., 2021, 506(3), 116116 CrossRef.
- G. A. Dimock and J. E. Lindler, Wereley N M Bingham biplastic analysis of shear thinning and thickening in magnetorheological dampers, Proc. SPIE, 2000, 3985, 444–455 CrossRef.
- A. Kl, B. Az and A. Hl, et al., Shear thickening fluid damper and its application to vibration mitigation of stay cable - ScienceDirect, Struct., 2020, 26, 214–223 CrossRef.
- A. Srivastava, A. Majumdar and B. S. Butola, Improving the impact resistance performance of Kevlar fabrics using silica based shear thickening fluid, Mater. Sci. Eng. A, 2011, 529, 224–229 CrossRef CAS.
- A. Khodadadi, G. Liaghat and S. Vahid, et al., Ballistic performance of Kevlar fabric impregnated with nanosilica/PEG shear thickening fluid, Composites, Part B, 2019, 162(APR.1), 643–652 CrossRef CAS.
- Q. Y. He and S. Cao, et al., Impact resistance of shear thickening fluid/Kevlar composite treated with shear-stiffening gel, Composites, Part A, 2018, 106, 82–90 CrossRef CAS.
- S. Cao, Q. Chen and Y. Wang, et al., High strain-rate dynamic mechanical properties of Kevlar fabrics impregnated with shear thickening fluid, Composites, Part A, 2017, 100, 161–169 CrossRef CAS.
- J. Qin, B. Guo and L. Zhang, et al., Soft armor materials constructed with Kevlar fabric and a novel shear thickening fluid, Composites, Part B, 2020, 183(Feb.15), 107686.1–107686.13 Search PubMed.
- A. Majumdar and B. S. Butola, Srivastava A Development of soft composite materials with improved impact resistance using Kevlar fabric and nano-silica based shear thickening fluid, Mater. Des., 2014, 54(Feb), 295–300 CrossRef CAS.
- N. Asija, H. Chouhan and S. A. Gebremeskel, et al., High strain rate characterization of shear thickening fluids using Split Hopkinson Pressure Bar technique, Int. J. Impact Eng., 2017, 110, 365–370 CrossRef.
- S. Sen, B. Noushad and A. Shaw, et al., Numerical Investigation of Ballistic Performance of Shear Thickening Fluid (STF)-Kevlar Composite, Int. J. Mech. Sci., 2019, 164, 105174 CrossRef.
- M. Liu, S. Zhang and S. Liu, et al., CNT/STF/Kevlar-based Wearable Electronic Textile with Excellent Anti-impact and Sensing Performance, Composites, Part A, 2019, 126, 105612 CrossRef CAS.
- N. Dixit and V. Sharma, Kumar P Research trends in abrasive flow machining: A systematic review, J. Manuf. Process., 2021, 64, 1434–1461 CrossRef.
- W. L. Zhu and A. Anthony Beaucamp, Non-Newtonian fluid based contactless sub-aperture polishing, CIRP Ann., 2020, 69(1), 293–296 CrossRef.
- Y. Ming, X. M. Huang and D. D. Zhou, A novel Non-Newtonian fluid polishing technique for zirconia ceramics based on the weak magnetorheological strengthening thickening effect, Ceram. Int., 2021, 48(507), 192–7203 Search PubMed.
- D. D. Zhou, X. M. Huang and Y. Ming, Material removal characteristics of magnetic-field enhanced shear thickening polishing technology, J. Mater. Res. Technol., 2021, 15, 2697–2710 CrossRef CAS.
- Y. H. Ren, S. F. Yang, X. M. Huang, Y. Ming and W. Li, Research on the rheological characteristic of magnetorheological shear thickening fluid for polishing process, Int. J. Adv. Manuf. Technol., 2021, 117, 413–423 CrossRef.
- T. Wang, D. Chen and W. Zhang, et al., Study on key parameters of a new abrasive flow machining (AFM) process for surface finishing, Int. J. Adv. Manuf. Technol., 2019, 101, 39–54 CrossRef.
- L. Min, A. Bl and B. Jya, et al., Shear-thickening polishing method, Int. J. Mach. Tool Manufact., 2015, 94, 88–99 CrossRef.
- M. Li, B. Lyu and J. Yuan, et al., Evolution and equivalent control law of surface roughness in shear-thickening polishing, Int. J. Mach. Tool Manufact., 2016, 108, 113–126 CrossRef.
- A. Nejat, A. Jalali and M. Sharbatdar, The flow of Newtonian and power law fluids in elastic tubes, J. Non-Newtonian Fluid Mech., 2011, 166, 1158–1172 CrossRef CAS.
- M. Wyart and M. Cates, Discontinuous shear thickening without inertia in dense nonbrownian suspensions, Phys. Rev. Lett., 2014, 112(9), 098302 CrossRef CAS PubMed.
- L. Stein, Viscoelastic properties of concentrated shear-thickening dispersions, J. Colloid Interf. Sci., 1992, 149(1), 10–22 CrossRef.
- W. H. Li and X. Z. Zhang, Rheology of Magnetorheological Shear Thickening Fluids, Adv. Mater. Res., 2012, 32, 161–164 Search PubMed.
- W. Li, M. Nakano and T. Tian, et al., Viscoelastic properties of MR shear thickening fluids, J. Fluid Sci. Technol., 2014, 9(2), JFST0019 CrossRef.
- F. J. Galindo-Rosales, F. J. Rubio-Hernández, A. Sevilla and R. H. Ewoldt, How Dr Malcom M. Cross may have tackled the development of An apparent viscosity function for shear thickening fluids, J. Non-Newtonian Fluid Mech., 2011, 166(23–24), 1421–1424 CrossRef CAS.
- M. M. Cross, Rheology of non-newtonian fluids: a new flow equation for pseudoplastic systems, J. Colloid Sci., 1965, 20(5), 417–437 CrossRef CAS.
- F. J. Galindo-Rosales, F. J. Rubio-Hernández and A. Sevilla, An apparent viscosity function for shear thickening fluids, J. Non-Newtonian Fluid Mech., 2011, 166, 321–325 CrossRef CAS.
- F. J. Galindo-Rosales, F. J. Rubio-Hernández and J. F. Velázquez-Navarro, Shear thickening behavior of Aerosil® R816 nanoparticles suspensions in polar organic liquids, Rheol. Acta, 2009, 48, 699–708 CrossRef CAS.
- M. Wei, L. Sun and P. Qi, et al., Continuous phenomenological modeling for the viscosity of shear thickening fluids, Nanomater. Nanotechnol., 2018, 8, 184798041878655 CrossRef.
- S. Gürgen, M. A. Sofuoğlu and M. C. Kuşhan, Rheological compatibility of multi-phase shear thickening fluid with a phenomenological model Smart, Mater. Struct., 2019, 28(3), 035027 CrossRef.
- R. Steller and J. Iwko, New generalized newtonian fluid models for quantitative description of complex viscous behavior in shear flows Polym, Eng. Sci., 2018, 58(8), 1446–1455 CAS.
- E. Samaniego, C. Anitescu and S. Goswami, et al., An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications, Comput. Methods Appl. Sci., 2020, 362(M), 112790 CrossRef.
- M. Sinha, A. Izadi and R. J. Anthony, et al., A novel approach to finding mechanical properties of nanocrystal layers, Nanoscale, 2019, 11(15), 7520–7526 RSC.
- P. D. Garcia and C. R. Guerrero, Garcia R Nanorheology of living cells measured by AFM-based force-distance curves, Nanoscale, 2020, 12 RSC.
- B. Rajabifar, A. Bajaj and R. Reifenberger, et al., Discrimination of adhesion and viscoelasticity from nanoscale maps of polymer surfaces using bimodal atomic force microscopy, Nanoscale, 2021, 13, 17428–17441 RSC.
- W. H. Li and X. Z. Zhang, Rheology of magnetorheological shear thickening fluids, Adv. Mater. Res., 2012, 32, 161–164 Search PubMed.
- G. Bossis, Y. Grasselli and A. Meunier, et al., Outstanding magnetorheological effect based on discontinuous shear thickening in the presence of a superplastifier molecule Appl, Phys. Lett., 2016, 109(11), 111902-1–111902-4 Search PubMed.
- G. Selim and W. H. Li, et al., The rheology of shear thickening fluids with various ceramic particle additives Mater, Design, 2016, 104, 312–319 Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |