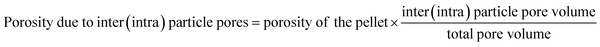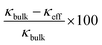Open Access Article
Open Access ArticlePreparation of mesoporous nitrogen-doped titania comprising large crystallites with low thermal conductivity†
Yuta
Shimasaki
a,
Takamichi
Matsuno
 a,
Quansheng
Guo
b,
Atsushi
Shimojima
a,
Quansheng
Guo
b,
Atsushi
Shimojima
 ac,
Hiroaki
Wada
ac,
Takao
Mori
ac,
Hiroaki
Wada
ac,
Takao
Mori
 bd and
Kazuyuki
Kuroda
bd and
Kazuyuki
Kuroda
 *ac
*ac
aDepartment of Applied Chemistry, School of Advanced Science and Engineering, Waseda University, 3-4-1 Okubo, Shinjuku-ku, Tokyo 169-8555, Japan
bInternational Center for Materials Nanoarchitectonics (WPI-MANA), National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan
cKagami Memorial Research Institute for Materials Science and Technology, Waseda University, 2-8-26 Nishiwaseda, Shinjuku-ku, Tokyo 169-0051, Japan
dGraduate School of Pure and Applied Sciences, University of Tsukuba, 1-1-1 Tennodai, Tsukuba, Ibaraki 305-8577, Japan
First published on 9th May 2022
Abstract
Reducing the thermal conductivity (κ) of mesoporous N-doped titania (TiO2) is crucial for the development of TiO2-based materials that exhibit excellent electronic, photochemical, and thermoelectric properties. Mesopores can contribute to the reduction of κ via phonon scattering, and the scattering effect due to the randomness of crystal interfaces should be significantly reduced to clarify the role of mesopores in reducing thermal conductivity. Highly ordered mesoporous N-doped TiO2 comprising large crystallites was prepared with silica colloidal crystals as a template into which a Ti source was introduced, followed by calcination with urea. N-doped samples comprising large crystallites exhibiting random mesopores were also prepared and used for the investigation of the effects of the shape and arrangement of the mesopore on phonon scattering. The mesostructures of the two separately prepared N-doped TiO2 samples were retained after sintering at 873 K and 80 MPa to fabricate pellets. Furthermore, the effective suppression of the long mean-free-path phonon conduction by the thin pore walls at a nanometer scale thickness significantly reduced the thermal conductivities of both samples. The presence of ordered mesopores further contributed to the reduction of κ, which was probably due to the enhanced contribution of the backscattering of phonons caused by ordered pore wall surfaces.
Introduction
Titania (TiO2) is one of the most attractive materials from a practical viewpoint because of its unique optical and electrical properties, nontoxicity, resource abundance, and inexpensiveness. These features have ensured its practical applications as photocatalysts, dye-sensitized solar cells, fuel cells, and lithium-ion batteries, and further applications are anticipated.1–6 To aid the applications of TiO2, different elements (dopants) are introduced into the compound to increase its light absorption wavelength range and impart it with electrical conductivity (σ). Among the various dopants, the effectiveness of N at narrowing the band gap has been frequently reported.7,8 Additionally, TiO2-based thermoelectric materials with high Seebeck coefficients (S) have been reported.9,10 The performances of thermoelectric materials are evaluated by a dimensionless thermoelectric figure of merit, ZT = S2σT/κ, where S, σ, T, and κ are the Seebeck coefficient, electrical conductivity, absolute temperature, and thermal conductivity, respectively. In addition, materials with high electrical and low thermal conductivities are generally required.11,12 However, since TiO2 exhibits low σ, its ZT will also be low. Therefore, it is necessary to increase the ZT value of TiO2 by doping it with different elements to increase σ and by reducing κ toward its utilization as a thermoelectric material. The improved thermoelectric performances of sintered N-doped TiO2 nanoparticles13,14 and Nb-doped15 or Pt-loaded16 mesoporous TiO2 thin films have been reported.There are various methods for reducing κ based on heat transfer mechanisms (conduction, convection, and radiation).17–22 From the materials design viewpoint, it is essential to suppress the conduction heat transfer based on the phonon conduction in semiconductors. Phonon scattering using various approaches, such as the introduction of grain boundaries and the formation of defects in the crystal lattice, is a necessary strategy for suppressing conduction heat transfer.19,20 The introduction of a porous structure can also contribute to the substantial reduction of conduction heat transfer. Furthermore, the introduction of nanopores with pore sizes shorter than the mean free path (MFP) of air (∼60 nm) is an effective strategy for reducing convection heat transfer.21,22 The introduction of pores with controlled pore shapes, sizes, and arrangements23 is very advantageous regarding the materials design for low-κ materials for the following reasons: (1) the pore wall with nanometer-level thickness (the phonon conduction path), that is defined between pores, can suppress long MFP phonon conduction, and (2) the ordered arrangement of pores regarding the direction of heat transfer (temperature gradient) can induce a phonon backscattering at pore wall surfaces.24,25 Yu et al. reported that the extensive reduction in κ of single-crystal Si exhibiting both nanomesh and nanowire morphologies, compared with that of thin-film Si, was attributed to the long MFP phonon conduction suppression in nanosized Si.26 The κ value of a material with nanomesh morphology is lower than that with nanowire one, and as discussed by Ravichandran et al.24 and Lee et al.,25 the reason is that the pore wall surface of the nanomesh is not parallel to the direction of heat transfer (temperature gradient), and this results in more frequent phonon backscattering. In terms of thermoelectric performance, it was previously shown for a skutterudite thermoelectric that >100% enhancement in ZT could be obtained without employing the conventional rattling phenomenon, and attributed to porous architecture containing nano- to micro-meter size irregularly shaped and randomly oriented pores.27 This strategy was similarly utilized for p-type thermoelectric (Bi, Sb)2Te3 to enhance ZT.28
The heat conduction in nanoporous TiO2 by long MFP phonons can be effectively suppressed by reducing the pore wall thickness thinner than 10 nm.29 Therefore, it is necessary to control the sizes and arrangements of pores to define the pore wall thickness.30 Thus, a porous material with pores that are arranged in a close-packed structure is desirable to form many pore wall surfaces which cause further phonon backscattering. Ha et al. reported that an irregular pore array exerts a weaker effect on the reduction of κ compared with a two-dimensional hexagonal array with same pore sizes;31 this is attributed to the presence of longer heat transfer paths that do not hinder the heat transfer in the irregular pore array, although there are short heat transfer paths that significantly contribute to the reduction of κ. Therefore, the pore arrangement of the hexagonal structure can further reduce κ, and mesoporous TiO2 exhibiting a regular pore arrangement can effectively reduce κ. However, the reduction of the κ of mesoporous TiO2 exhibiting a regular pore arrangement was only measured in thin films,15,16,30,31 and additional findings employing bulk samples, such as pellets, are required for further studies and applications. Furthermore, the temperature dependence of κ above room temperature has not been investigated. The effect of periodically arranged mesopore walls on phonon scattering in such a high-temperature region has not been investigated. It is also important to increase the crystallite size to reduce the effect of grain boundaries because the mesoporous TiO2 in previous studies was formed with polycrystalline materials, and the phonon scattering at grain boundaries, as well as mesopores, cannot be neglected as factors that determine the reduction of κ.
To discuss the phonon scattering arising from mesopore walls and wall surfaces, mesoporous materials with large crystallite sizes and highly ordered pores are required, as mentioned above. The thermal conductivity of such materials has only been measured for nanoporous indium tin oxide (ITO) by us.32 A significant reduction of κ above room temperature via phonon scattering in mesopores was observed in nanoporous ITO with large crystallites containing spherical pores that are regularly arranged in a face-centered cubic (fcc) structure. Therefore, the demonstration of the phonon scattering behavior of mesoporous TiO2 with large crystallite sizes (single crystalline) and highly ordered pore arrangement presents a useful insight into the κ-reduction behavior of metal oxide mesoporous materials of various compositions. Furthermore, the measurement of κ of mesoporous materials with varied pore arrangements will contribute to the precise understanding of the effect of pore arrangement on phonon scattering, which will be useful for the design of materials with low κ.
In the synthesis of single-crystalline mesoporous TiO2, aggregates of silica nanoparticles were used as templates,33–35 but the resulting pores exhibited disorderliness. To resolve this issue, we previously reported the hydrothermal preparation of single-crystalline mesoporous TiO2 with highly ordered pore arrangements using silica colloidal crystals as templates.36 Similarly, single-crystalline mesoporous Nb-doped TiO2 exhibiting highly ordered pore arrangements was prepared from the mixed precursors of Ti and Nb to improve σ.36 However, because the crystal phase and shape of the mesostructure of TiO2 changed depending on the amount of Nb source added, it was very challenging to satisfy the following conditions: doping with foreign elements, high crystallinity, and the precise control of the mesostructure.
To solve the foregoing issues, we developed a method for doping N atoms into TiO2 using a gas–solid reaction after the preparation of highly ordered mesoporous TiO2 with large crystallites and a pore wall thickness thinner than 10 nm (Scheme 1). The doping of N into TiO2 with the gas–solid reaction between TiO2 and NH3 generated from urea has been previously reported,14,37–39 and the N/Ti ratio was in the range of 0.017–0.047. It was also reported that N-doped TiO2 whose N concentration was in this range exhibited good σ in the range of 102–103 S m−1.14 The thermodynamically stable rutile phase was selected as the crystalline phase of TiO2 to measure κ in the medium and the high-temperature range. Mesoporous N-doped TiO2 powders were sintered such that mesopores and their regular arrangement were retained. As a reference, TiO2 with rod-like crystals exhibiting disordered mesopores along the rods was also prepared to investigate the effects of the different shapes and arrangements of the mesopores on phonon scattering. The thermal conductivity results indicated that the presence of very thin pore walls arising from ordered mesopores effectively suppressed long MFP phonon conduction and that the regular ordering of mesopores is thought to be effective for the induction of phonon backscattering on the mesopore surfaces from room temperature to medium and high temperatures.
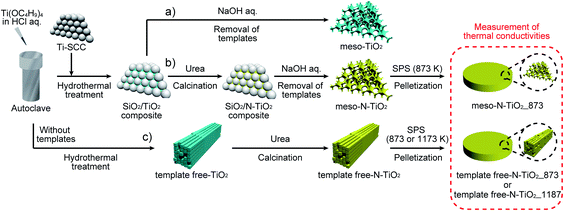 | ||
| Scheme 1 Preparation of (a) highly ordered mesoporous non-doped TiO2, (b) highly ordered mesoporous N-doped TiO2, and (c) rod-shaped N-doped TiO2 with random mesopores. | ||
Experimental section
Materials
Tetraethoxysilane (TEOS; Wako Pure Chemical Industries Ltd.; >98%) and tris(hydroxymethyl)aminomethane (THAM; Wako Pure Chemical Industries Ltd.; >99%) were used to prepare silica colloidal crystals.40 Titanium tetrachloride (TiCl4; Wako Pure Chemical Industries Ltd.; >99%) was used to prepare Ti-containing silica colloidal crystals. Tetrabutoxytitanium (TBOT; Wako Pure Chemical Industries Ltd.; >95%) was used as Ti precursors, and concentrated hydrochloric acid (HCl; Wako Pure Chemical Industries Ltd.) was used for the hydrothermal process. Urea (Wako Pure Chemical Industries Ltd., >99%) was used as the N dopant.Preparation of Ti-containing silica colloidal crystals (Ti–SCCs) as a template
SCCs were prepared according to a previously reported method.40 THAM (12.1 g, 1.0 × 10−2 mol) was dissolved in deionized water (500 mL), after which the solution was stirred for 10 min at 353 K. After confirming the satisfactory dissolution of THAM in deionized water, TEOS (100 mL, 0.45 mol) was added to the aqueous solution of THAM, and the mixture was stirred for 24 h at 353 K. Thereafter, a dispersion of silica nanoparticles with a diameter of approximately 19 nm was obtained by cooling the solution at room temperature, as evidenced by its dynamic light scattering (DLS) profile (Fig. S1a†) and transmission electron microscopy (TEM) images (Fig. S1b†). Silica nanoparticles were uniformly grown by repeating the above procedure (seed growth method). Further, an aqueous solution of THAM (375 mL, 0.20 M) was added to the obtained dispersion of silica nanoparticles (125 mL), and the mixture was stirred for 10 min at 353 K. Subsequently, TEOS (175 mL, 0.79 mol) was added to the mixture, and the mixture was stirred for 24 h at 353 K. Afterward, the DLS profile (Fig. S2a†) and TEM images (Fig. S2b†) confirmed that a dispersion of silica nanoparticles with a diameter of approximately 35 nm was obtained by cooling the solution at room temperature. The flake-like SCCs were prepared by air-drying the obtained colloidal solution at 323 K, followed by calcination in air for 6 h at 823 K.Ti-containing SCCs (denoted as Ti–SCCs) used as a template were prepared as follows33–36 (please note that the incorporation of the Ti species into SCCs was necessary to exclusively deposit TiO2 into the template using the hydrothermal process, as previously reported).33–36 A stock solution of TiCl4 (2 M) was prepared by adding conc. HCl (20 μL) and TiCl4 (2 mL) to deionized water (7 mL) in an ice bath. Further, an aqueous solution of TiCl4 (15 mM) was prepared by adding the stock solution to deionized water. Thereafter, the prepared SCCs (5 g) were immersed in a 15 mM TiCl4 solution (33 mL) for 1 h at 343 K. Afterward, the SCCs were collected by filtration and washed with deionized water. The flake-like Ti–SCCs were obtained by calcination for 30 min at 773 K. Scanning electron microscopy (SEM) images (Fig. S3a†) and small-angle X-ray scattering (SAXS) patterns (Fig. S3b†) of Ti–SCCs showed that silica nanoparticles, with a diameter of approximately 35 nm, were arranged in an fcc lattice. The N2 adsorption–desorption isotherms of Ti–SCCs (Fig. S4†) revealed the presence of mesopores as interstitial voids in silica nanoparticles.
Preparation of highly ordered mesoporous N-doped TiO2 with large crystallites (meso-N–TiO2)
Highly ordered mesoporous N-doped TiO2 with large crystallites (denoted as meso-N–TiO2) was prepared, as follows (Scheme 1b): TBOT was vacuum-distilled at 463 K for purification. The reaction solution was prepared by adding the purified TBOT (2.4 mL) to a mixture of conc. HCl (28 mL) and deionized water (28 mL). Subsequently, the flake-like Ti–SCCs (2.16 g) were added to the reaction solution in a Teflon-lined autoclave (100 mL) and hydrothermally treated for 12 h at 423 K to precipitate TiO2 in the mesopores of Ti–SCCs (denoted as the silica/TiO2 composite).36 The flake-like silica/TiO2 composite was ground into a powder in an agate mortar. After the silica/TiO2 composite powder was mixed with a urea powder in the urea-to-TiO2 mass ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and subsequent calcination was conducted in air at 873 K for 45 min, a yellow powder was obtained (denoted as silica/N–TiO2 composite). Finally, the silica/N–TiO2 composite was stirred in an aqueous solution of NaOH (2 M, 40 mL) for 2 h at 353 K to remove the silica template. After the sample was centrifuged and washed with water several times, the obtained yellow powder was denoted as meso-N–TiO2. For a comparison with the meso-N–TiO2 for characterization, a highly ordered mesoporous non-doped TiO2 with large crystallites (denoted as meso-TiO2) was prepared by removing the silica template from the silica/TiO2 composite (Scheme 1a).
1, and subsequent calcination was conducted in air at 873 K for 45 min, a yellow powder was obtained (denoted as silica/N–TiO2 composite). Finally, the silica/N–TiO2 composite was stirred in an aqueous solution of NaOH (2 M, 40 mL) for 2 h at 353 K to remove the silica template. After the sample was centrifuged and washed with water several times, the obtained yellow powder was denoted as meso-N–TiO2. For a comparison with the meso-N–TiO2 for characterization, a highly ordered mesoporous non-doped TiO2 with large crystallites (denoted as meso-TiO2) was prepared by removing the silica template from the silica/TiO2 composite (Scheme 1a).
Preparation of rod-shaped N-doped TiO2 crystals with random mesopores (template free-N-doped TiO2)
TiO2, which is an aggregate of rod-shaped crystals (denoted as template free-TiO2), was prepared under the same hydrothermal treatment conditions as those of meso-TiO2, without the silica template (Scheme 1c). After template free-TiO2 was mixed with the same amount of urea powder as that in the case of meso-N–TiO2, and calcination was conducted in air at 873 K for 45 min, a yellow powder was obtained (denoted as template free-N–TiO2). Table 1 shows the list of the above samples.| Sample name | Use of the template (Ti–SCCs) | Shape of mesopores | N/Ti molar ratio in the starting reaction mixture | N/Ti molar ratio of the samplea | Si/Ti molar ratio of the sampleb |
|---|---|---|---|---|---|
| a The values of the N/Ti molar ratio are based on the X-ray photoelectron spectroscopy (XPS) profiles (Fig. 2 and S6). b The Si/Ti molar ratios were calculated on the basis of the energy-dispersive X-ray (EDX) spectroscopy data (Fig. S7). | |||||
| Meso-TiO2 | Use | Spherical (ordered) | 0.0 | 0.0 | 2.0 × 10−2 |
| Meso-N–TiO2 | Use | Spherical (ordered) | 7.9 | ∼2 × 10−2 | 4.8 × 10−2 |
| Template free-TiO2 | Not use | Rod-like (disordered) | 0.0 | 0.0 | 0.0 |
| Template free-N–TiO2 | Not use | Rod-like (disordered) | 7.9 | ∼2 × 10−2 | 0.0 |
Preparation of sintered pellets of meso-N–TiO2 and template free-N-doped TiO2
A powdery sample was loaded into a graphite die (diameter = 10 mm) and sintered using spark plasma sintering (SPS) with an SPS-1080 system (SPS SYNTEX INC.) to obtain a pellet (diameter = 10 mm, thickness = ∼1 mm). A pellet of sintered meso-N–TiO2 (denoted as meso-N–TiO2_873) was prepared by SPS for 5 min in a N2 atmosphere at 873 K and 80 MPa. The sintering temperature of 873 K was selected because the mesostructures collapsed when sintered at higher temperatures than 873 K (Fig. S5†). A sample of template free-N–TiO2 was sintered for 5 min in an N2 atmosphere at 873 or 1173 K and 80 MPa, and the obtained pellets were denoted as template free-N–TiO2_873 and template free-N–TiO2_1173, respectively. The pellets were sintered at 1173 K to achieve densification. All three N-doped pellets exhibited a yellowish-gray color, which was probably attributed to the oxygen defects.32,41–44Characterization
TEM images, selected-area electron diffraction (SAED) patterns, and EDX profiles were obtained on a JEM-2010 microscope (JEOL Ltd.) at an accelerating voltage of 200 kV. Bright-field scanning transmission electron microscopy (BF-STEM) images and EDX spectral mappings were obtained on a JEOL JEM-2100F microscope using an accelerating voltage of 200 kV. SEM images were obtained on an S-5500 microscope (Hitachi High-Technologies Co.) at an accelerating voltage of 2.0 kV to observe SCCs and at 15.0 kV to observe TiO2-based materials. The powdery samples for TEM, SAED, EDX, and SEM analyses were dispersed in ethanol, and the resulting suspensions were drop-casted onto carbon-coated microgrids (Okenshoji Co.). The sintered pellets for SEM analyses were cleaved and then mounted on a carbon tape. The particle size of the silica nanoparticles in the silica colloidal solution was determined using DLS measurements (HORIBA nanopartica SZ-100-S). SAXS patterns were obtained using a NANO-Viewer (Rigaku Co.) with Cu Kα radiation under the operating conditions of 40 kV and 30 mA and a Pilatus 2D X-ray detector (Dectris). N2 adsorption–desorption isotherms were obtained using a MicrotracBEL BELSORP-max at 77 K. Prior to the measurements, samples were heated at 393 K under vacuum. Powder X-ray diffraction (XRD) patterns were obtained using a Rigaku RINT-Ultima III diffractometer with Cu Kα radiation under the operating conditions of 40 kV and 40 mA. XPS profiles were recorded with a PHI 5000 VersaProbe II (ULVAC-PHI, Inc.) with monochromated Al Kα radiation. Ultraviolet-visible diffuse reflectance spectroscopy (UV-vis DRS) profiles were obtained using a HITACHI F-4500 spectrometer with an integrating sphere. The absorption intensities of UV-vis DRS profiles, F(R), were calculated using the Kubelka–Munk equation: F(R) = (1 − R)2/2R, where R is the diffuse reflectance. Furthermore, σ and Seebeck coefficient (S) were simultaneously measured using an Ulvac-Riko ZEM-2 instrument at 300–673 K in a He atmosphere. Thermal conductivity (κ) was calculated as follows: κ = DCpρ, where D, Cp, and ρ are the thermal diffusivity, specific heat capacity, and pellets density, respectively. Thermal diffusivity (D) was measured using a Lazer Flash ULVAC-Riko TC-7000 instrument in a N2 flow at 300–673 K. Specific heat capacity (Cp) was measured using a DSC8500 (PerkinElmer) apparatus in a N2 flow at 300–673 K. The density (ρ) and the porosity of the pellets were calculated from eqn (1) and (2), respectively. The densities (ρ) of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 were 2.48, 2.67, and 3.67 g cm−3, respectively, and their porosities were 0.42, 0.37, and 0.14, respectively, considering 4.25 g cm−1 as the ρ of rutile TiO2.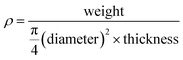 | (1) |
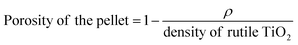 | (2) |
Results and discussion
Characterizations of meso-TiO2 and template free-TiO2 with/without N-doping
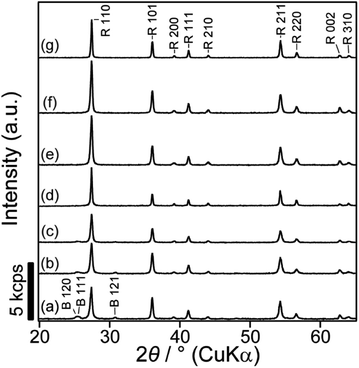
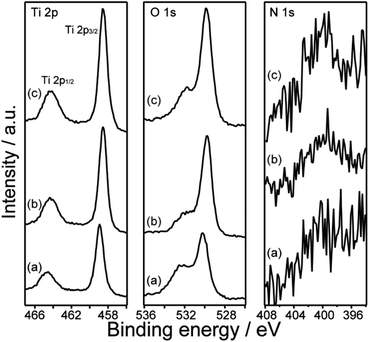
The XRD pattern of meso-TiO2 (Fig. 1a) shows that the major diffraction peaks assignable to rutile-type TiO2 appeared and were consistent with reported data (JCPDS #76-1940). The formation of the rutile phase is reasonable and is supported by previous reports employing hydrothermal treatments (393–473 K) in conc. hydrochloric acid.34,45–47 A few small peaks, which were assigned to brookite TiO2 (JCPDS #29-1360), were also observed and were consistent with the results of our previous report on highly ordered mesoporous TiO2 exhibiting large crystallites.36 Rutile-type TiO2 was also observed in meso-N–TiO2, and small peaks, which were assigned to brookite-type TiO2, were also observed (Fig. 1b), indicating the absence of phase transition when meso-TiO2 was calcined with urea. The brookite phase was not observed in template free-TiO2 and template free-N–TiO2, and only peaks that corresponded to the rutile phase were observed (Fig. 1d and e). The formation of the brookite phase in meso-TiO2 and meso-N–TiO2 may be due to the interactions with silanol groups on the SCCs surfaces,48 volumetric confinement effects of SCCs pores,48 and conditions of the TiO2 precursor solution such as pH49 and TBOT concentration.50Fig. 2 shows the XPS profiles of meso-TiO2 and meso-N–TiO2. The core level peaks of Ti 2p3/2 were observed at 458.9 and 458.6 eV for meso-TiO2 and meso-N–TiO2, respectively. The slightly lower binding energy of Ti 2p3/2 in meso-N–TiO2 than that in meso-TiO2 can be attributed to the presence of Ti–N bonds. It is known that the electron density around a cation increases when the electronegativity of the anion decreases.51–53 Because the electronegativity of N is lower than that of O, the electron density around Ti atoms increases when O is replaced with N in the TiO2 lattice. This tendency of the peak shift is consistent with previous studies on N-doped TiO2.51,52,54,55
The core level peaks of O 1s were observed at 530.2 and 529.8 eV for meso-TiO2 and meso-N–TiO2, respectively. The lower binding energy of O 1s in meso-N–TiO2 than that in meso-TiO2 was due to the increased electron density around Ti atoms owing to the substitution of O with N in the TiO2 lattice, which was similar to the reason for the aforementioned Ti 2p3/2 peak shift. The tendency of the O 1s peak shift also correlated with the findings of the previous studies on N-doped TiO2.51,54,56
The core level peak of N 1s was observed in the range of 399–403 eV for meso-N–TiO2; however, it was not observed for meso-TiO2. It is known that the peaks of N 1s arising from chemisorbed N2 and the N–Ti–N bonds of TiN are observed at lower than 397.5 eV, while the peaks of N 1s originating from NO and NO2 are observed at higher than 400 eV.41,51,53 It is also reported that the N 1s peak arising from the N–Ti–O bond is observed at 399.6 eV.55 Therefore, the core level peak of N 1s observed in this study probably originated from the substitution of N at the O site of TiO2. The calculated N/Ti ratio of meso-N–TiO2 was approximately 0.02 based on peak areas (Table 1). J. Wang et al. reported that the core level peak of Ti 2p shifted to the lower energy region by 0.2 eV at an N/Ti ratio of approximately 0.02.55 Therefore, the N/Ti ratio and the degree of peak shift in this study are reasonable. The Si/Ti ratios of meso-TiO2 and meso-N–TiO2 were approximately 0.02 and 0.048 (Table 1), respectively, which were due to the Ti–SCCs. Therefore, it is probably considered that silica is present on the pore wall surfaces of TiO2 particles in meso-TiO2 and meso-N–TiO2.
The core level peaks of Ti 2p3/2 of the template free-TiO2 and template free-N–TiO2, which are assemblies of rod-like crystals, were 459.0 and 458.6 eV, respectively, and the core level peaks of O 1s were 530.3 and 529.9 eV, respectively (Fig. S6†). The peak shifts of Ti 2p3/2 and the O 1s in template free-N–TiO2 were similar to those in meso-N–TiO2. The N 1s spectrum of template free-N–TiO2 was also similar to that of meso-N–TiO2 (Fig. S6†). These data indicate that the O in the TiO2 lattice was replaced with N in template free-N–TiO2, as well as in meso-N–TiO2.
A strong absorption in the UV region and an absorption edge at a wavelength of 400 nm were observed for meso-TiO2 and meso-N–TiO2 in the UV-vis DRS profiles (Fig. 3A). The absorption in the visible light region was observed for meso-N–TiO2 at a wavelength of 500 nm. It has been reported that N-doping causes the formation of an impurity level band on the high-energy side of the upper valence band, which results in the narrowing of the band gap and the absorption in the visible light region.41,42,51,53,57–60 This tendency was also observed for template free-TiO2 and template free-N–TiO2 (Fig. S8A†). The narrowing of the band gap of meso-N–TiO2 compared with that of meso-TiO2 is also shown in the Tauc plots (Fig. 3B), and they were calculated from the UV-vis DRS profiles. The calculated band gaps of meso-TiO2 and meso-N–TiO2 were 2.93 and 2.84 eV, respectively. These values are within the range of the reported values for rutile TiO2 (ref. 61–63) and N-doped rutile TiO2,61,62,64 respectively. The calculated band gaps of template free-TiO2 and template free-N–TiO2 were 2.92 and 2.87 eV, respectively (Fig. S8B†), indicating that meso-N–TiO2 and template free-N–TiO2 were doped with N.
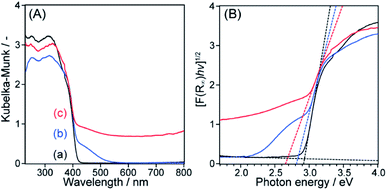 | ||
| Fig. 3 (A) UV-vis DRS profiles and (B) Tauc plots of (a) meso-TiO2, (b) meso-N–TiO2, and (c) meso-N. | ||
The SEM images of meso-N–TiO2 (Fig. 4a and b) exhibited highly ordered three-dimensionally arranged mesopores replicated from Ti–SCCs. The estimated average size of spherical pores was approximately 35 nm, which is in good agreement with the diameter of silica nanoparticles (Fig. S2†). The thinnest pore wall thickness was estimated to be approximately 6 nm, as obtained from the data of 50 different areas. No ring-like patterns were observed in the SAED pattern (Fig. 4d) of the whole particle observed in the TEM image (Fig. 4c), and spot-like patterns, which were attributed to rutile TiO2, were observed, but with slightly streaked spots. This result indicated that one meso-N–TiO2 particle was basically composed of one large crystallite or large crystallites of several hundreds of nanometers at least. High-magnification TEM images (Fig. S9b†) also show that the pore walls were composed of rutile TiO2. The TEM image of meso-TiO2 without N-doping (Fig. S10a†) and the corresponding SAED pattern (Fig. S10b†) revealed that meso-TiO2 comprised rutile TiO2 with large crystallites, indicating that the mesostructure and crystal phase of both samples were retained regardless of N-doping.
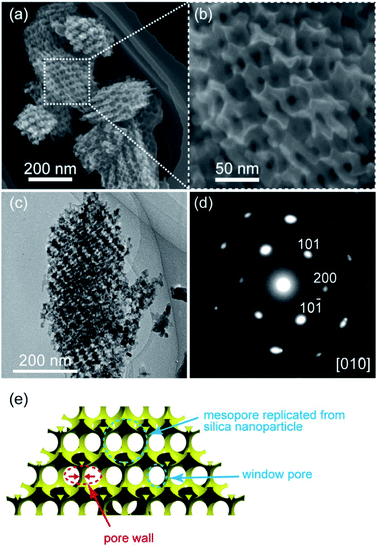 | ||
| Fig. 4 (a) and (b) SEM images, (c) TEM image, (d) corresponding SAED pattern with the assignment of indices of the rutile phase, and (e) schematic representation of meso-N–TiO2. | ||
The steep increase and decrease in the N2 adsorption–desorption isotherms of meso-N–TiO2 (Fig. S11A†) indicate the formation of ordered mesopores. Because the pore size, as calculated using the Barrett–Joyner–Halenda (BJH) method with an adsorption branch, was 38 nm (Fig. S11B†), the formation of mesopores via the replication of silica nanoparticles was indicated. The pore size, as calculated using the BJH method with a desorption branch, was 19 nm (Fig. S11B†), indicating the presence of window pores, which were observed in the SEM image (Fig. 4b and S9a†). The Brunauer–Emmett–Teller (BET) specific surface area was 17 m2 g−1, and the pore volume was 1.2 × 10−1 cm3 g−1.
The SAXS pattern of meso-N–TiO2 (Fig. S12†) revealed that the peaks were observed at the same q values as those of Ti–SCCs, although the broadened peak intensities were lower than those of Ti–SCCs (Fig. S13†).65 This result indicates the successful formation of meso-N–TiO2 with a regular fcc arrangement of spherical pores via the replication of the mesostructure of Ti–SCCs.
Rod-like crystals were observed in the TEM image of template free-N–TiO2 (Fig. S14a†). The crystals were split into rods from the center to the tip (Fig. S14b and d†), and the width of these rods was in the range of 5–8 nm (Fig. S14c†). The SAED pattern (Fig. S14e†) of the whole particle observed in the TEM image (Fig. S14a†) revealed intense spots that were attributable to the single-crystalline rutile phase, indicating that one particle of template free-N–TiO2 was almost composed of one single crystallite. Furthermore, the spots, which were streaked perpendicularly along the direction of rod elongation (Fig. S14e†), indicate that the defects between the rods were formed parallel to the direction of elongation.47 Various external rod shapes were observed (Fig. S14f†), and a few bulk crystals were also observed (Fig. S14g†).
Characterizations of the sintered samples
The XRD patterns of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 (Fig. 1c, f and g) indicated that the crystalline phase did not change during sintering and that the crystallite sizes were almost the same before and after sintering, indicating that there was no crystal growth after sintering. The XPS profiles of meso-N–TiO2_873 (Fig. 2c), template free-N–TiO2_873, and template free-N–TiO2_1173 (Fig. S6†) revealed that the core level peaks of Ti 2p3/2 were observed at 458.6, 458.6, and 458.7 eV, respectively, and those of O 1s were observed at 529.9, 529.9, and 529.8 eV, respectively. The N/Ti ratios of meso-N–TiO2_873, template free-N–TiO2_873 and template free-N–TiO2_1173, as calculated from the XPS peak area ratio, were approximately 0.02, indicating that the N/Ti ratio did not change after sintering. The UV-vis DRS profile of meso-N–TiO2_873 (Fig. 3A) revealed the absorption in the wavelength range of 400–800 nm. The absorption range was wider than that of meso-N–TiO2 before sintering, and this can be attributed to the N-doping into the TiO2 framework, as well as the presence of oxygen defects and Ti3+.41,42 This is probably because sintering was conducted in a N2 atmosphere below the atmospheric pressure.32,66 Similar UV-vis DRS profiles were observed for template free-N–TiO2_873 and template free-N–TiO2_1173 (Fig. S8A†). Tauc plots reveal that the band gaps of meso-N–TiO2_873 (Fig. 3B), template free-N–TiO2_873, and template free-N–TiO2_1173 (Fig. S8B†) were 2.69, 2.68, and 2.64 eV, respectively. Because the band gap values of these three samples were almost the same, the differences in their κ among the three samples can be compared on the basis of the difference in their internal structures, which will be discussed in the thermal conductivity section.The mesostructure of meso-N–TiO2_873 was characterized using SEM, N2 adsorption–desorption, and SAXS. The low-magnification SEM image of meso-N–TiO2_873 (Fig. 5a) shows the presence of submicrometer spaces between particles. The high-magnification SEM image (Fig. 5b) shows the presence of highly ordered three-dimensionally arranged mesopores. The image clearly indicates that the pore surfaces of meso-N–TiO2_873 are concave. The estimated average pore wall thickness was approximately 6 nm, which was the same as that of meso-N–TiO2. The steep increase and decrease in the N2 adsorption–desorption isotherm of meso-N–TiO2_873 (Fig. S11A†) indicated the presence of mesopores, and this finding is similar to that of meso-N–TiO2. The pore sizes, which were calculated using the BJH method employing the adsorption and desorption branches, were approximately 38 and 17 nm, respectively (Fig. S11B†).
The BET specific surface area was 19 m2 g−1, and the pore volume was 1.0 × 10−1 cm3 g−1. These values were almost the same as those of meso-N–TiO2, indicating that the mesoporous structure was retained after sintering. The SAXS pattern of meso-N–TiO2_873 (Fig. S12†) revealed the appearances of peaks at the same q values as those of meso-N–TiO2, indicating that the periodicity of the pore arrangement was successfully retained after sintering. The retention of the mesostructure is probably due to much larger crystallite size of the pore walls, significantly surpassing the size of mesopores. Relaxation, which was due to the presence of mesopores, against the structural deformation during sintering might also mitigate structural collapse.
The mesostructure of template free-N–TiO2_873 was characterized using SEM and N2 adsorption–desorption. The low-magnification SEM image of template free-N–TiO2_873 (Fig. S15a†) shows the presence of submicrometer spaces between particles. The highly-magnified SEM image (Fig. S15b†) shows the retention of originally present rod-like TiO2 crystals and the defects between rods. The width of each rod was in the range of 5–8 nm, which is the same as that of template free-N–TiO2. Additionally, pores with sizes of a few tens of nanometers were newly observed (Fig. S15c†). The TEM image of the sample containing the newly observed pores (Fig. S15d†) reveals that the observed contrast in the rods indicated that they were partly deformed, inducing the formation of new pores in addition to those that were originally present due to the grain growth during sintering. Therefore, the pore surfaces of template free-N–TiO2_873 are basically flat. The steep increase and decrease in the N2 adsorption–desorption isotherm of template free-N–TiO2_873 (Fig. S16a†) indicate the formation of mesopores. The BJH pore size distribution, as calculated from the adsorption branch, revealed broad peaks larger than 30 nm (Fig. S16b†). Further, the calculation employing the desorption branch revealed a peak at 20 nm and a broad peak larger than 40 nm. These data are consistent with the formation of pores, as mentioned above. The BET specific surface area was 8 m2 g−1, and the pore volume was 6.3 × 10−2 cm3 g−1.
The SEM images of template free-N–TiO2_1173 (Fig. S17†) show the disappearance of both rods and disordered mesopores, as well as the formation of macropores in the submicrometer range, indicating that the shape of crystals changed because of grain growth during sintering at 1173 K.
Interparticle and intraparticle pores in the sintered samples
The thermal conductivity is significantly affected by the presence of pores in the sintered samples. There are two types of pores: interparticles and intraparticle pores. The porosity values owing to the inter- and intraparticle pores were calculated by the following equation:The porosities of pellets and calculated porosities due to the inter- and intraparticle pores of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 are listed in Table 2. The details of calculations are presented in the ESI (p. S17).†
| Sample name | Porosity of the pellet | Porosity due to interparticle pores | Porosity due to intraparticle pores |
|---|---|---|---|
| Meso-N–TiO2_873 | 0.42 | 0.17 | 0.25 |
| Template free-N–TiO2_873 | 0.37 | 0.20 | 0.17 |
| Template free-N–TiO2_1173 | 0.14 | 0.14 | 0 |
Thermal conductivities of the pellets
Fig. 6 shows that the κ values of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 in the measured temperature range were 0.79–0.82, 1.0–1.1, and 2.9–3.8 W m−1 K−1, respectively. The κ values of these samples were lower than that of the nonporous pellet of rutile TiO2 (4.0–5.2 W m−1 K−1),67 which was prepared by sintering rutile TiO2 nanoparticles with a grain size of 500 nm. In particular, the κ values of meso-N–TiO2_873 and template free-N–TiO2_873 were significantly reduced.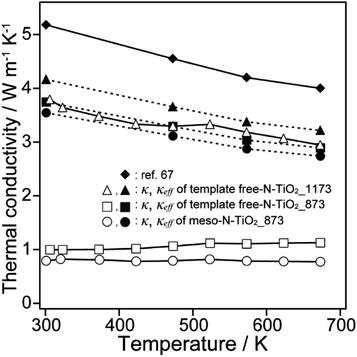 | ||
| Fig. 6 Thermal conductivities of meso-N–TiO2_873, template free-N–TiO2_873, template free-N–TiO2_1173, and ref. 67. | ||
Although the reduction in κ of all three samples is related to their total pore volume (=interparticle pore volume + intraparticle pore volume), the reduction in κ caused by the interparticle and intraparticle pores should be discussed separately. This is because the presence of interparticle pores contributes to the reduction in κ by both radiation and convection through the pores.68 Therefore, the contributions of both pore types are separately discussed in the following section. The effective thermal conductivities reduced by the interparticle pores (κeff) were calculated from the Eucken model: κeff = κbulk(2 − 2ϕ)/(2 + ϕ),69 where κbulk is the thermal conductivity of bulk rutile TiO2 (κbulk = 5.2 W m−1 K−1 at 300 K),67 and ϕ is the porosity due to interparticle pores. The calculated values of κeff of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 at 300 K were 4.0, 3.8, and 4.2 W m−1 K−1, respectively (Table 3). The measured κ value of template free-N–TiO2_1173 exhibiting only interparticle pores was lower than the κbulk value of bulk TiO2, indicating the contribution of existing interparticle pores. This result is supported by the fact that the calculated κeff value (4.2 W m−1 K−1) of template free-N–TiO2_1173 was close to the measured κ value (3.8 W m−1 K−1) of this sample. Then, the measured κ values of meso-N–TiO2_873 and template free-N–TiO2_873 were 0.79 and 1.00 W m−1 K−1, respectively, and the values were much lower than the calculated κeff values of those samples by hypothesizing that only interparticle pores existed. The degrees of reduction of κeff of these two samples compared with the κbulk value were 24% ((5.2–4.0) W m−1 K−1/5.2 W m−1 K−1) and 27% ((5.2–3.8) W m−1 K−1/5.2 W m−1 K−1) for meso-N–TiO2_873 and template free-N–TiO2_873, respectively, owing to the presence of interparticle pores. The drastic reduction of κ of the two samples can be explained by the presence of intraparticle pores, and the estimated reduction degree of the contribution by the intraparticle pores is 80% ((4.0–0.79) W m−1 K−1/4.0 W m−1 K−1) and 74% ((3.8–1.00) W m−1 K−1/3.8 W m−1 K−1) for meso-N–TiO2_873 and template free-N–TiO2_873, respectively. Therefore, the presence of intraparticle pores plays a major role in reducing the κ of meso-N–TiO2_873 and template free-N–TiO2_873.
| Sample name | Measured κ/W m−1 K−1 | κ eff /W m−1 K−1 | ||
|---|---|---|---|---|
| a The κeff values were calculated based on only the contribution by the presence of interparticle pores using the thermal conductivity of bulk TiO2 (κbulk = 5.2 W m−1 K−1).67 b Degree of reduction in the thermal conductivities by the presence of interparticle pores. c Degree of reduction in the thermal conductivities by the presence of intraparticle pores. | ||||
| Meso-N–TiO2_873 | 0.79 | 4.0 | 24% | 80% |
| Template free-N–TiO2_873 | 1.00 | 3.8 | 27% | 74% |
| Template free-N–TiO2_1173 | 3.8 | 4.2 | 20% | 9% |
The reduction of the κ of meso-N–TiO2_873 and template free-N–TiO2_873 owing to the presence of intraparticle pores, which is induced by the following factors, is discussed here: (1) nanosized pore walls can suppress long MFP phonon conduction, and (2) pore wall surfaces can induce phonon scattering. These two factors are discussed separately in the following paragraphs.
The first discussion is related to the suppression of the long MFP phonon conduction by nanosized pore walls. The pore wall thickness of meso-N–TiO2_873 was approximately 6 nm, and the rod width of template free-N–TiO2_873 was 5–8 nm, as mentioned above. In both samples, it is considered that the conduction of phonon with a shorter MFP than that of the single nanometer order contributes to conduction heat transfer.20 On the other hand, the conduction of phonon with a long MFP above the single nanometer order is suppressed by nanosized pore walls.20 In fact, the κ values of meso-N–TiO2_873 and template free-N–TiO2_873 were lower than the reported κ values of the N-doped Ti-based oxide nanoparticles with particle sizes of hundreds of nanometers, i.e., 1.6–1.8 W m−1 K−1 for N-doped TiO2−x (ref. 13) and 2.0–2.6 W m−1 K−1 for N and Nb codoped TiO2.14 Although it was reported that the κ value of a TiO2 nanotube with the wall thickness of 2–3 nm was 0.40–0.84 W m−1 K−1,70 which was lower than those of meso-N–TiO2_873 and template free-N–TiO2_873, it should be noted that the nanotube comprised only nanocrystals, and the material was inadequate for understanding the role of arranged pores.
The suppression of the long MFP phonon conduction by nanosized pore walls can be explained by focusing on the disappearance of the temperature dependence of the κ of meso-N–TiO2_873 and template free-N–TiO2_873. In the same measured temperature range as that employed in this study, the κ of bulk rutile TiO2 generally decreases with an increasing temperature71 because the MFP of phonon becomes shorter owing to the increase in the probability of the umklapp scattering with the temperature.19 On the other hand, the κ values of meso-N–TiO2_873 and template free-N–TiO2_873 were low and constant regardless of the measured temperature from 300 to 673 K, indicating that only a short MFP existed in the temperature range because of the thin pore walls at a single nanometer scale.
Next, the contribution of the phonon scattering at the pore wall surfaces to the reduction of κ is discussed on the basis of the results that the κ value of meso-N–TiO2_873 was lower than that of template free-N–TiO2_873. The κ of meso-N–TiO2_873 and template free-N–TiO2_873 were reduced by 80% and 74%, respectively, as mentioned above, because of the presence of intraparticle pores. It is considered that the difference between the degrees of reduction of the κ of the two samples was affected by the fraction of backscattering of phonons at the pore wall surfaces, though the effect of the difference in the pore volume cannot be completely excluded. This consideration is further explained in the ESI (p. S19).† The concave pore surfaces of meso-N–TiO2_873 were not parallel to heat transfer paths because they exhibited a regular arrangement of the spherical pores in an fcc arrangement. Therefore, it is considered that the fraction of backscattering of the phonons in meso-N–TiO2_873 was higher than that in template free-N–TiO2_873, possessing flat pore surfaces and random arrangement of the pores, which resulted in a reduced κ of meso-N–TiO2_873 compared to that of template free-N–TiO2_873. Theoretically, the thermal conductivity of porous materials is also related to the emissivity of the surface, the size, shape, and distribution of the pores.68 In addition, pore orientation has been found to affect profoundly the thermal conductivity of a given pore.72 Therefore, the arrangement of intraparticle pores will really affect the thermal conductivity. The BET specific surface area of meso-N–TiO2_873 (19 m2 g−1) was larger than that of template free-N–TiO2_873 (8 m2 g−1). This result is also consistent with the higher fraction of phonon backscattering in meso-N–TiO2_873.
To ensure the relationship between phonon conduction and κ, as mentioned above, it is necessary to consider the ratios of κph/κ and κe/κ, where κph is the lattice thermal conductivity due to phonon transport and κe is the electronic thermal conductivity due to carrier transport, as described by the following equation: κ = κph + κe. The calculated κe values73 of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 were negligibly small compared to the measured κ values (Fig. S18b†), indicating that κ almost entirely comprised κph. Therefore, it is highly likely that the κ values of the three samples essentially depend on phonon conduction.
This study clarifies that the reduction of κ above room temperature is attributed to the suppression of long MFP phonon conduction and the phonon backscattering by nanosized pore walls and ordered pore wall surfaces, respectively. These two structural factors can be defined by the sizes, shapes, and arrangements of pores. In our previous report,32 the significant reduction of κ of a highly ordered nanoporous ITO with large crystalline frameworks was attributed to the suppression of the long MFP phonon conduction at nanosized pore walls and the phonon scattering at pore wall surfaces. The findings in this paper indicate that the phonon backscattering at pore wall surfaces also contributes to the reduction of κ of highly ordered mesoporous materials, as evidenced by the comparison of TiO2 with randomly arranged rod-like pores. Although the ZT values of the samples in this study were low (Fig. S18d†) owing to the relatively low σ caused by the weak contact between TiO2 particles under relatively mild sintering conditions, the preparative method reported here ensured the combined doping of foreign elements, high crystallinity, and a precise control of mesostructures. Thermoelectric performance would be improved by preparing and employing highly ordered mesoporous metal oxides, such as ITO,74–77 ZnO,78–82 and Co-based layered oxides,83–85 with larger crystallites. In addition, σ would be improved if the sintering conditions can be explored to strengthen the contact between particles while retaining the mesostructure, which will be one of the future issues to be tackled.
Conclusions
Highly ordered mesoporous N-doped TiO2 with large crystallites was prepared by the deposition of TiO2 in the interstices of silica colloidal crystals as a template, followed by calcination with urea. N-doped TiO2 with rod-like random mesopores and large crystallites was also prepared to investigate the effect of the pore wall thicknesses and surfaces on the reduction of thermal conductivities. Additionally, the pellets retaining the mesostructures of samples were successfully fabricated by sintering at 873 K and 80 MPa. The thermal conductivities of these pellets were significantly reduced, compared with those of bulk TiO2. Further, the values of the thermal conductivities of both pellets containing mesopores were constant in the measured temperature range of 300–673 K, which is quite different from the generally observed behavior, where the thermal conductivity due to phonon conduction decreases with an increasing temperature. These results indicate that long MFP phonon conduction was suppressed by nanosized pore walls defined between mesopores. The thermal conductivity of N-doped TiO2 with highly ordered mesopore arrangements was lower than that of N-doped TiO2 with disordered mesopore arrangements, and this was attributed to the higher fraction of phonon backscattering at the pore wall surfaces in N-doped TiO2 with highly ordered mesopore arrangements. The results reported here will benefit the development of thermal management materials via the precise control of promising materials on a nanometer scale.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Mr T. Gotoh and Dr N. Sugimura (Material Characterization Center Laboratory, Waseda University) for their kind assistance with the XPS and DSC measurements, respectively. We also acknowledge Mr S. Enomoto (Waseda University) for the STEM observation and the corresponding EDX spectral mapping. This work was supported by a Grant-in-Aid for Scientific Research (A) (grant number JP19H00833). T. Mori and Q. Guo acknowledge the support from JST-Mirai JPMJMI19A1, and Y. Shimasaki acknowledges a Grant-in-Aid for JSPS Fellows (grant number JP16J08643).Notes and references
- K. Nakata, T. Ochiai, T. Murakami and A. Fujishima, Electrochim. Acta, 2012, 84, 103–111 CrossRef CAS.
- K. Nakata and A. Fujishima, J. Photochem. Photobiol., A, 2012, 13, 169–189 CrossRef CAS.
- A. Meng, L. Zhang, B. Cheng and J. Yu, Adv. Mater., 2019, 31, 1807660 CrossRef PubMed.
- M. K. Nowotny, L. R. Sheppard, T. Bak and J. Nowotny, J. Phys. Chem. C, 2008, 112, 5275–5300 CrossRef CAS.
- P. Roy, D. Kim, K. Lee, E. Spiecker and P. Schmuki, Nanoscale, 2010, 2, 45–59 RSC.
- D. V. Bavykin, J. M. Friedrich and F. C. Walsh, Adv. Mater., 2006, 18, 2807–2824 CrossRef CAS.
- S. A. Bakar and C. Ribeiro, J. Photochem. Photobiol., A, 2016, 27, 1–29 CrossRef.
- R. Asahi, T. Morikawa, H. Irie and T. Ohwaki, Chem. Rev., 2014, 114, 9824–9852 CrossRef CAS PubMed.
- S. Walia, S. Balendhran, H. Nili, S. Zhuiykov, G. Rosengarten, Q. H. Wang, M. Bhaskaran, S. Sriram, M. S. Strano and K. Kalantar-zadeh, Prog. Mater. Sci., 2013, 58, 1443–1489 CrossRef CAS.
- G. Kieslich, G. Cerretti, I. Veremchuk, R. P. Hermann, M. Panthöfer, J. Grin and W. Tremel, Phys. Status Solidi A, 2016, 213, 808–823 CrossRef CAS.
- T. Mori, Small, 2017, 13, 1702013 CrossRef PubMed.
- Z. Liu, J. Mao, T.-H. Liu, G. Chen and Z. Ren, MRS Bull., 2018, 43, 181–186 CrossRef.
- M. Mikami and K. Ozaki, J. Phys.: Conf. Ser., 2012, 379, 012006 CrossRef.
- C. Liu, L. Miao, J. Zhou, R. Huang, C. A. J. Fisher and S. Tanemura, J. Phys. Chem. C, 2013, 117, 11487–11497 CrossRef CAS.
- S.-Y. Jung, T.-J. Ha, W.-S. Seo, Y. S. Lim, S. Shin, H. H. Cho and H.-H. Park, J. Electron. Mater., 2011, 40, 652–656 CrossRef CAS.
- T.-J. Ha, Y.-J. Choi, S.-Y. Jung, W.-S. Seo, Y. S. Lim, S. Shin, H. H. Cho and H.-H. Park, Jpn. J. Appl. Phys., 2011, 50, 075001 CrossRef.
- T.-Y. Wei, T.-F. Chang, S.-Y. Lu and Y.-C. Chang, J. Am. Ceram. Soc., 2007, 90, 2003–2007 CrossRef CAS.
- T. Coquil, C. Reitz, T. Brezesinski, E. J. Nemanick, S. H. Tolbert and L. Pilon, J. Phys. Chem. C, 2010, 114, 12451–12458 CrossRef CAS.
- T. M. Tritt, Thermal Conductivity: Theory, Properties, and Applications, Springer, US, 2005 Search PubMed.
- K. Koumoto and T. Mori, Thermoelectric Nanomaterials: Materials Design and Applications, Springer, Berlin, Heidelberg, 2013 Search PubMed.
- Y. Belmoujahid, M. Bonne, Y. Scudeller, D. Schleich, Y. Grohens and B. Lebeau, Microporous Mesoporous Mater., 2015, 201, 124–133 CrossRef CAS.
- M. Fuji, C. Takai, H. Watanabe and K. Fujimoto, Adv. Powder Technol., 2015, 26, 857–860 CrossRef CAS.
- S. Yazdani and M. T. Pettes, Nanotechnology, 2018, 29, 432001 CrossRef PubMed.
- N. K. Ravichandran and A. J. Minnich, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205432 CrossRef.
- J. Lee, W. Lee, G. Wehmeyer, S. Dhuey, D. L. Olynick, S. Cabrini, C. Dames, J. J. Urban and P. Yang, Nat. Commun., 2017, 8, 14054 CrossRef CAS PubMed.
- J. K. Yu, S. Mitrovic, D. Tham, J. Varghese and J. R. Heath, Nat. Nanotechnol., 2010, 5, 718–721 CrossRef CAS PubMed.
- A. U. Khan, K. Kobayashi, D.-M. Tang, Y. Yamauchi, K. Hasegawa, M. Mitome, Y. Xue, B. Jiang, K. Tsuchiya, D. Golberg, Y. Bando and T. Mori, Nano Energy, 2017, 31, 152–159 CrossRef CAS.
- H.-L. Zhuang, H. Hu, J. Pei, B. Su, J.-W. Li, Y. Jiang, Z. Han and J.-F. Li, Energy Environ. Sci., 2022 10.1039/D2EE00119E.
- D. Mitra, P. Howli, B. K. Das, N. S. Das, P. Chattopadhyay and K. K. Chattopadhyay, J. Mol. Liq., 2020, 302, 112499 CrossRef CAS.
- J. Fang, C. Reitz, T. Brezesinski, E. J. Nemanick, C. B. Kang, S. H. Tolbert and L. Pilon, J. Phys. Chem. C, 2011, 115, 14606–14614 CrossRef CAS.
- T.-J. Ha, S.-Y. Jung, J.-H. Bae, H.-L. Lee, H. W. Jang, S.-J. Yoon, S. Shin, H. H. Cho and H.-H. Park, Microporous Mesoporous Mater., 2011, 144, 191–194 CrossRef CAS.
- Y. Saito, T. Matsuno, Q. Guo, T. Mori, M. Kashiwagi, A. Shimojima, H. Wada and K. Kuroda, ACS Appl. Mater. Interfaces, 2021, 13, 15373–15382 CrossRef CAS PubMed.
- E. J. Crossland, N. Noel, V. Sivaram, T. Leijtens, J. A. Alexander-Webber and H. J. Snaith, Nature, 2013, 495, 215–219 CrossRef CAS PubMed.
- W. Jiao, Y. Xie, R. Chen, C. Zhen, G. Liu, X. Ma and H. M. Cheng, Chem. Commun., 2013, 49, 11770–11772 RSC.
- X. Zheng, Q. Kuang, K. Yan, Y. Qiu, J. Qiu and S. Yang, ACS Appl. Mater. Interfaces, 2013, 5, 11249–11257 CrossRef CAS PubMed.
- M. Kitahara, Y. Shimasaki, T. Matsuno, Y. Kuroda, A. Shimojima, H. Wada and K. Kuroda, Chem.–Eur. J., 2015, 21, 13073–13079 CrossRef CAS PubMed.
- J. Yuan, M. Chen, J. Shi and W. Shangguan, Int. J. Hydrogen Energy, 2006, 31, 1326–1331 CrossRef CAS.
- D. Mitoraj and H. Kisch, Angew. Chem., Int. Ed., 2008, 47, 9975–9978 CrossRef CAS PubMed.
- M. Nasirian and M. Mehrvar, J. Environ. Sci., 2018, 66, 81–93 CrossRef CAS PubMed.
- K. M. Choi and K. Kuroda, Chem. Commun., 2011, 47, 10933–10935 RSC.
- Y. Cao, Z. Xing, Y. Shen, Z. Li, X. Wu, X. Yan, J. Zou, S. Yang and W. Zhou, Chem. Eng. J., 2017, 325, 199–207 CrossRef CAS.
- A. Naldoni, F. Riboni, M. Marelli, F. Bossola, G. Ulisse, A. Di Carlo, I. Píš, S. Nappini, M. Malvestuto, M. V. Dozzi, R. Psaro, E. Selli and V. Dal Santo, Catal. Sci. Technol., 2016, 6, 3220–3229 RSC.
- A. Naldoni, M. Allieta, S. Santangelo, M. Marelli, F. Fabbri, S. Cappelli, C. L. Bianchi, R. Psaro and V. Dal Santo, J. Am. Chem. Soc., 2012, 134, 7600–7603 CrossRef CAS PubMed.
- C. Di Valentin, E. Finazzi, G. Pacchioni, A. Selloni, S. Livraghi, M. C. Paganini and E. Giamello, Chem. Phys., 2007, 339, 44–56 CrossRef CAS.
- K. Yanagisawa and J. Ovenstone, J. Phys. Chem. B, 1999, 103, 7781–7787 CrossRef CAS.
- H. Cheng, J. Ma, Z. Zhao and L. Qi, Chem. Mater., 1995, 7, 663–671 CrossRef CAS.
- A. Wisnet, S. B. Betzler, R. V. Zucker, J. A. Dorman, P. Wagatha, S. Matich, E. Okunishi, L. Schmidt-Mende and C. Scheu, Cryst. Growth Des., 2014, 14, 4658–4663 CrossRef CAS.
- D. G. Gregory, Q. Guo, L. Lu, C. J. Kiely and M. A. Snyder, Langmuir, 2017, 33, 6601–6610 CrossRef CAS PubMed.
- Z. Yang, B. Wang, H. Cui, H. An, Y. Pan and J. Zhai, J. Phys. Chem. C, 2015, 119, 16905–16912 CrossRef CAS.
- L. Wang, Z. Xiao, Y. Liu, S. Cao, Z. Ma and L. Piao, Sci. China Mater., 2020, 63, 758–768 CrossRef CAS.
- M. Sathish, B. Viswanathan, R. P. Viswanath and C. S. Gopinath, Chem. Mater., 2005, 17, 6349–6353 CrossRef CAS.
- J. Fang, F. Wang, K. Qian, H. Bao, Z. Jiang and W. Huang, J. Phys. Chem. C, 2008, 112, 18150–18156 CrossRef CAS.
- K. Sivaranjani and C. S. Gopinath, J. Mater. Chem., 2011, 21, 2639–2647 RSC.
- X. Chen and C. Burda, J. Phys. Chem. B, 2004, 108, 15446–15449 CrossRef CAS.
- J. Wang, W. Zhu, Y. Zhang and S. Liu, J. Phys. Chem. C, 2007, 111, 1010–1014 CrossRef CAS.
- H. Tian, L. Hu, C. Zhang, W. Liu, Y. Huang, L. Mo, L. Guo, J. Sheng and S. Dai, J. Phys. Chem. C, 2010, 114, 1627–1632 CrossRef CAS.
- X. Liu, Z. Xing, Y. Zhang, Z. Li, X. Wu, S. Tan, X. Yu, Q. Zhu and W. Zhou, Appl. Catal., B, 2017, 201, 119–127 CrossRef CAS.
- W. Fang, Y. Zhou, C. Dong, M. Xing and J. Zhang, Catal. Today, 2016, 266, 188–196 CrossRef CAS.
- T. Wang, X. Yan, S. Zhao, B. Lin, C. Xue, G. Yang, S. Ding, B. Yang, C. Ma, G. Yang and G. Yang, J. Mater. Chem. A, 2014, 2, 15611–15619 RSC.
- G. Yang, Z. Jiang, H. Shi, T. Xiao and Z. Yan, J. Mater. Chem., 2010, 20, 5301–5309 RSC.
- O. Diwald, T. L. Thompson, T. Zubkov, S. D. Walck and J. T. Yates, J. Phys. Chem. B, 2004, 108, 6004–6008 CrossRef CAS.
- A. R. Gandhe and J. B. Fernandes, J. Solid State Chem., 2005, 178, 2953–2957 CrossRef CAS.
- A. Folger, P. Ebbinghaus, A. Erbe and C. Scheu, ACS Appl. Mater. Interfaces, 2017, 9, 13471–13479 CrossRef CAS PubMed.
- S. Livraghi, A. M. Czoska, M. C. Paganini and E. Giamello, J. Solid State Chem., 2009, 182, 160–164 CrossRef CAS.
- The reason for the lower peak intensities is considered to be partially due to the presence of nonporous TiO2 deposited outside the template. In fact, a small portion of nonporous TiO2 was observed in the SEM image of meso-N–TiO2. The reason for the broadening of the peaks is considered to be due to the smaller size of the continuous domain of regular arranged spherical pores in meso-N–TiO2 than that of regular arranged silica nanoparticles in Ti–SCC.
- C.-J. Ting and H.-Y. Lu, J. Am. Ceram. Soc., 1999, 82, 841–848 CrossRef CAS.
- S. Harada, K. Tanaka and H. Inui, J. Appl. Phys., 2010, 108, 083703 CrossRef.
- A. L. Loeb, J. Am. Ceram. Soc., 1954, 37, 96–99 CrossRef CAS.
- A. Eucken, Forschung auf dem Gebiet des Ingenieurwesens A, 1940, 11, 6–20 CrossRef.
- T. Gao and B. P. Jelle, J. Phys. Chem. C, 2013, 117, 1401–1408 CrossRef CAS.
- W. R. Thurber and A. J. H. Mante, Phys. Rev., 1965, 139, A1655–A1665 CrossRef.
- J. Francl and W. D. Kingery, J. Am. Ceram. Soc., 1954, 37, 99–107 CrossRef CAS.
- The κe values of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 were calculated from the Wiedemann–Frantz law: κe = σLT, where σ is the electrical conductivity, L is the Lorenz number (2.45 × 10−8 V2 K−2), and T is the temperature. The σ values of meso-N–TiO2_873, template free-N–TiO2_873, and template free-N–TiO2_1173 were 0.9–7.8, 0.7–4.5, and 83.4–111.1 S m−1, respectively (Fig. S18a†).
- S. J. Wen, G. Couturier, G. Campet, J. Portier and J. Claverie, Phys. Status Solidi A, 1992, 130, 407–414 CrossRef CAS.
- S. V. Pammi, A. Chanda, J.-K. Ahn, J.-H. Park, C.-R. Cho, W.-J. Lee and S.-G. Yoon, J. Electrochem. Soc., 2010, 157, H937–H941 CrossRef CAS.
- G. Korotcenkov, V. Brinzari and B. K. Cho, Solid State Sci., 2016, 52, 141–148 CrossRef CAS.
- M. Thirumoorthi and J. T. J. Prakash, J. Asian Ceram. Soc., 2016, 4, 124–132 CrossRef.
- M. Ohtaki, K. Araki and K. Yamamoto, J. Electron. Mater., 2009, 38, 1234–1238 CrossRef CAS.
- L. Brockway, V. Vasiraju, M. K. Sunkara and S. Vaddiraju, ACS Appl. Mater. Interfaces, 2014, 6, 14923–14930 CrossRef CAS PubMed.
- P. Jood, R. J. Mehta, Y. Zhang, T. Borca-Tasciuc, S. X. Dou, D. J. Singh and G. Ramanath, RSC Adv., 2014, 4, 6363–6368 RSC.
- R. V. R. Virtudazo, Q. Guo, R. Wu, T. Takei and T. Mori, RSC Adv., 2017, 7, 31960–31968 RSC.
- R. V. R. Virtudazo, B. Srinivasan, Q. Guo, R. Wu, T. Takei, Y. Shimasaki, H. Wada, K. Kuroda, S. Bernik and T. Mori, Inorg. Chem. Front., 2020, 7, 4118–4132 RSC.
- I. Terasaki, Y. Sasago and K. Uchinokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R12685–R12687 CrossRef CAS.
- J. W. Fergus, J. Eur. Ceram. Soc., 2012, 32, 525–540 CrossRef CAS.
- V. Vulchev, L. Vassilev, S. Harizanova, M. Khristov, E. Zhecheva and R. Stoyanova, J. Phys. Chem. C, 2012, 116, 13507–13515 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00083k |
| This journal is © The Royal Society of Chemistry 2022 |