Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A novel study on the preferential attachment of chromophore and auxochrome groups in azo dye adsorption on different greenly synthesized magnetite nanoparticles: investigation of the influence of the mediating plant extract's acidity
Kaouthar
Ahmouda
 *ab,
Moussa
Boudiaf
ac and
Boubaker
Benhaoua
d
*ab,
Moussa
Boudiaf
ac and
Boubaker
Benhaoua
d
aDepartment of Process Engineering and Petrochemistry, Faculty of Technology, University of El Oued, El Oued, 39000, Algeria. E-mail: ahmouda-kaouthar@univ-eloued.dz; drssmoussa@yahoo.fr
bRenewable Energy Research Unit in Arid Zones, University of El Oued, El Oued, 39000, Algeria
cLCIMN, Laboratory, Department of Process Engineering, Faculty of Technology, University Ferhat, Abbas Setif, 19000, Sétif, Algeria. E-mail: benhaouab@yahoo.fr
dDepartment of Physics, Faculty of Exact Sciences, University of El Oued, El Oued, 39000, Algeria
First published on 13th July 2022
Abstract
In this paper, the adsorption of Evans blue (EB) and methyl orange (MO) azo dyes on four greenly synthesized magnetite nanoparticles has been studied to investigate the effect of the mediating plant extract's acidity on magnetite surface reactivity in azo dye adsorption. Magnetite surface reactivity has been studied through the analysis of preferential attachment of dye chromophore and auxochrome groups on magnetite nanoparticles, and adsorption yields. According to the contents of chromophore and auxochrome groups in dye structures, the mediating plant extract's acidity effect on acid site types and densities was also deduced. Used plants for the green synthesis were: Artemisia herba-alba (L), Matricaria pubescens (L), Juniperus phoenicea (L), and Rosmarinus officinalis (L), and their extract pHs were respectively 5.25, 5.05, 4.63, and 3.69. The four greenly synthesized samples of magnetite were characterized by XRD, SEM, ATR-FTIR, and UV-Vis techniques. The novelty of this paper lies in highlighting the influence of the mediating plant extract's acidity on the greenly synthesized magnetite surface reactivity towards the preferential attachment of chromophore and auxochrome functional groups in azo dye adsorption, where obtained results show that the mediating plant extract's acidity has a clear effect on the preferential attachment of chromophore and auxochrome groups on magnetite surfaces as well as on azo dyes' adsorption yields and capacities. Indeed, the decrease in the plant extract's acidity leads to an increase in the attachment of chromophore groups and a decrease in the attachment of auxochrome groups. So, it leads to an increase in Lewis acid site density and a decrease in Brønsted acid site density of magnetite surfaces. Also, the decrease of the plant extract's acidity leads to an increase in the studied dye adsorption yields, and this is because the majority of functional groups of MO and EB dyes are chromophores that attach to Lewis acid sites. The difference found in adsorption yields of EB and MO on all four magnetite samples is due to the fact that the ratio of chromophore/auxochrome groups in EB is remarkably greater than that in MO. The linear and non-linear pseudo-first-order and pseudo-second-order kinetics of the adsorption as well as the intra-particle diffusion mechanism have been analyzed. Obtained results indicate that in all adsorption processes the adsorption kinetics followed a linear pseudo-first-order kinetic model, and film diffusion is the step that controlled adsorption mechanisms. The thermodynamic studies of EB and MO adsorption processes on the four magnetite surfaces have been analyzed in the temperature range of 303.15–318.15 K. Obtained results reveal the endothermic nature of the adsorption in all cases.
1 Introduction
Dyes are present in the effluent water of several industries, including textile, leather, paper, rubber, plastics, printing, cosmetics, pharmaceutical, and food industries. Dyes contribute to water toxicity and represent an increasing danger for the environment, humans, and animals.1–3 They are generally resistant to light, oxidizing agents, and many chemicals and therefore difficult to degrade once released into aquatic systems. Thus, one of the major environmental problems related to the numerous industrial applications of dyes is their removal from effluents.3Dyes are composed of chromophores that are commonly electron withdrawing and auxochromes that are usually electron-releasing groups.4 The most important chromophores, as defined in this way, are: N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, –CH
O, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, NO2, NO, NOH, C
N, NO2, NO, NOH, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C groups and ionizing auxochromes mainly include: SO3H, OH, COOH, NH2, NH3, NHCH3, and N(CH3)2 groups.4,5
C groups and ionizing auxochromes mainly include: SO3H, OH, COOH, NH2, NH3, NHCH3, and N(CH3)2 groups.4,5
Adsorption is one of the most effective processes for the removal and recovery of colored materials and dyes from effluents.6–9 Nanomaterials are widely used in the purification of aqueous media due to their advantages, such as high surface area and increased number of active sites.10–13 They therefore allow a rapid thermodynamic equilibrium between adsorbent and adsorbate during the adsorption process and selective removal of pollutants.7–9 Several factors influence the adsorption process, mainly the solution chemistry,7,14 the characteristics of the dye (adsorbate)7,15 and the adsorbent surface properties.16–22 Saha et al.7 studied the preferential adsorption of seven different dyes on magnetite NPs. They reported that the magnetite surface preferred adsorbing dyes containing higher OH content. Xiao et al.15 studied the preferential adsorption of different cationic and anionic dyes on iron nanoparticles. They reported that iron NPs preferred removing cationic dyes more than anionic dyes.
Other authors studied the effect of changing the adsorbent surface properties by binding ligands on the adsorbent surface. Khurshid et al.17 found that the use of amine-functionalized cobalt–iron NP surface enhanced the removal of anionic azo dyes. Mahmoodi et al.22 synthesized a titania/silica nano-hybrid (TSNH) and an amine-functionalized titania/silica nano-hybrid (AFTSNH) to use them in Reactive Red 198 and Acid Red 14 removal from wastewater. They found that the AFTSNH adsorbent showed high dye adsorption capacities compared to the TSNH adsorbent. The authors of ref. 23 prepared silica nanoparticles (SN) and amine-functionalized silica nanoparticles (AFSN) and then used them in Acid Red 14, Acid Black 1 and Acid Blue 25 removal. They reported that AFSN preferred adsorbing the studied dyes than SN. Meanwhile, the study of Madrakian et al.24 reported that magnetite-modified activated carbon preferred adsorbing cationic dyes than anionic dyes. Moreover, a comparative study on adsorption of methylene blue on sericin-modified and unmodified magnetite NPs25 reported that sericin-modified magnetite NPs were approximately 40% more effective than the unmodified magnetite NPs. Furthermore, in the study of the preferential adsorption of magnetite NP loaded fig leaves (MNLFL) and magnetite NP loaded azolla (MNLA) to remove crystal violet and methylene blue,26 the authors found that MNLFL preferred adsorbing crystal violet more than MNLA.
Surface acid site types and densities were also found to impact the adsorption process. Indeed, a study of the adsorption of organic contaminants on both natural and synthesized magnetite20 found that the adsorption on natural magnetite was more efficient than that on the synthesized one, and this is because of its higher surface site density. Moreover, Gogoi et al.27 studied the degradation of catechol using an Fe3O4–CeO2 nanocomposite as a Fenton-like heterogeneous catalyst. They reported that the increase of Brønsted acid site density of this nanocomposite increased the degradation of catechol.
The impact of changing the mediating plants on the behavior of greenly synthesized metal oxide NPs in dye adsorption was studied in several works. The effect of three different tea extracts on the capacity of greenly synthesized iron oxide surfaces in the removal of methyl green dye from aqueous solution has been studied by Huang et al.16 They reported that the plant extract had an effect on the adsorption yields of methyl green dye on the three iron oxide NPs, where yields varied from 81.2% to 75.6 to 67.1%. Duyen et al.28 synthesized metal oxide NPs using the extracts of flowers, bark, and leaf of Tecoma stans in order to use them in the removal of Congo red (CR) and crystal violet (CV) dyes. They reported that the adsorbent derived from flower extract gave better adsorption efficiency than those derived from other extracts. Islam et al.29 synthesized magnetite NPs using six plant extracts in order to use them in the removal of methyl orange (MO) and crystal violet (CV) dyes. They reported that plant extract had an effect on magnetite NP surface reactivity in the adsorption, where magnetite NPs synthesized using tea extract showed the highest performance (MO 92.34%, CV 96.1%). Ahmouda et al.30 used different greenly synthesized magnetite NPs in the removal of methyl green (MG) dye via the adsorption process. They reported that the mediating plant extract's acidity had an effect on the preferential adsorption of MG on the magnetite NP surface. Indeed, magnetite NPs synthesized using plant extract having the lowest acidity exhibited the highest acid site density (OH groups) and hence the highest performance in the removal of MG.
As it is known that the adsorption of dyes from wastewater is directly affected by the reactivity of the adsorbent surface towards the attachment of dyes' functional groups, looking for parameters that could control the greenly synthesized magnetite NP surface reactivity is always of importance. In this way, this paper looks for mediating plant extract parameters that could, in the case of green synthesis, impact the magnetite NP surface reactivity in azo dye adsorption.
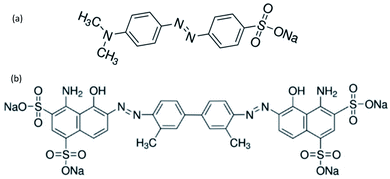
Azo dyes are the largest and most versatile class of organic dyes.31 These dyes contain one or more azo bonds (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N). The complex aromatic structures of azo dyes make them more stable and more difficult to remove from the effluents discharged into water bodies.31 The used dyes in this study are: methyl orange (MO) and Evans blue (EB) azo dyes, and their chemical structures are illustrated in Fig. 1. The EB molecule is composed of chromophore groups such as benzene, phenyl, phenyldiazonium, toluene, N
N). The complex aromatic structures of azo dyes make them more stable and more difficult to remove from the effluents discharged into water bodies.31 The used dyes in this study are: methyl orange (MO) and Evans blue (EB) azo dyes, and their chemical structures are illustrated in Fig. 1. The EB molecule is composed of chromophore groups such as benzene, phenyl, phenyldiazonium, toluene, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N groups linked to the benzene ring, and of auxochrome groups such as sulphonic acid (SO−3), phenol, and aniline groups. Meanwhile, the MO molecule is composed of chromophore groups such as benzene, phenyl, phenyldiazonium, N
N groups linked to the benzene ring, and of auxochrome groups such as sulphonic acid (SO−3), phenol, and aniline groups. Meanwhile, the MO molecule is composed of chromophore groups such as benzene, phenyl, phenyldiazonium, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, and of auxochrome groups such as sulphonic acid (SO−3) and dimethylamine (N(CH3)2).
N, and of auxochrome groups such as sulphonic acid (SO−3) and dimethylamine (N(CH3)2).
The attachment of these functional groups on the adsorbent surface is based on functional group properties (chromophore or auxochrome) towards the surface acid site type (Lewis or Brønsted). In the case of EB and MO dyes, SO−3,32 dimethylamine,33 phenol,34 and aniline35 auxochrome groups are electron donating, and their attachment on the adsorbent surface is based on their ionic interaction with the developed positively charged Brønsted acid sites of the surface. Meanwhile, the chromophore groups phenyldiazonium, phenyl,36 benzene, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N,32 and toluene37 are electron withdrawing, and their attachment on the adsorbent surface is based on their interactions with the Lewis acid sites of the adsorbent surface.
N,32 and toluene37 are electron withdrawing, and their attachment on the adsorbent surface is based on their interactions with the Lewis acid sites of the adsorbent surface.
In this paper, the effect of the mediating plant extract's acidity on the greenly synthesized magnetite surface reactivity in the adsorption of methyl orange (MO) and Evans blue (EB) azo dyes has been investigated through the analysis of MO and EB adsorption on four greenly synthesized magnetite samples, with the aim of studying the effect of the mediating plant extract's acidity on the preferential attachment of the studied dye chromophores and auxochromes (functional groups) on greenly synthesized magnetite NPs, and adsorption yields. For this purpose, after the accomplishment of adsorption experiments, the free functional groups that are not attached on magnetite surfaces have been deeply analyzed in all dye residual solutions using ATR-FTIR spectroscopy, so as to perceive their preferential attachment on the four magnetite surfaces. Based on the analysis of preferential attachments of chromophore and auxochrome groups, it was possible to compare between Brønsted and Lewis acid site densities on each magnetite surface and their influence on adsorption yields and capacities. To the best of our knowledge, there is no study in the literature that has dealt with the influence of the mediating plant extract's acidity on magnetite surface reactivity towards the preferential attachment of dye functional groups, and thus on surface acid site type and density. The used plants are Artemisia herba-alba (L), Matricaria pubescens (L), Juniperus phoenicea (L), and Rosmarinus officinalis (L). Their extract pHs are respectively 5.25, 5.05, 4.63, and 3.69. The synthesized Fe3O4 samples are respectively denoted in this paper by ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4 and JUN–Fe3O4. They were characterized by XRD, SEM, FTIR-ATR, and UV-Vis techniques.
2 Materials and methods
This section focuses on listing needed materials and used apparatuses. It also provides methods utilized to perform adsorption experiments and characterization of iron oxide NPs.2.1 Materials
2.2 Methods
In this section, used methods for solution preparation are described. Used protocols in adsorption and desorption experiments of dyes from magnetite NPs and characterization techniques are described as well.All experiment sets are sonicated in an ultrasonic bath for 15 minutes and they were then stirred continually for 60 minutes until a steady state was reached. All adsorption experiments were carried out under ambient conditions in batch mode, and they were performed in triplicate for data consistency.
Kinetic experiments were performed by withdrawing samples of dye/Fe3O4 solutions at a regular time interval to obtain, after centrifugation, adequate aliquots for the purpose of quantifying residual dye concentrations and the adsorbed amounts. The concentrations of residual dye aqueous solutions were quantified using a UV-Vis spectrophotometer at absorbance maxima of EB (λmax = 602 nm) and MO (λmax = 463 nm). Furthermore, the adsorbed amounts of EB and MO molecules are calculated from the calibration curve for all adsorption experiments (Y = 67.02X + 0.0442, R2 = 0.9987 and Y = 31.39X + 0.0346, R2 = 0.9985, respectively). On another side, after the adsorption was accomplished and steady state reached, the aliquots were centrifuged to separate liquid solutions and solid phases. The liquid solutions, which represent MO/magnetite and EB/magnetite residual solutions, were then analyzed using ATR-FTIR spectroscopy.
To calculate the adsorption capacity (qe in mg g−1) and the amount of MO and EB ions adsorbed per unit mass (qt in mg g−1) of JUN–Fe3O4, MAT–Fe3O4, ROS–Fe3O4 and ARM–Fe3O4 at equilibrium contact time, the following equations were used:
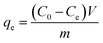 | (1) |
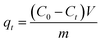 | (2) |
Adsorption yield was calculated using the following equation:
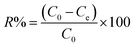 | (3) |
ln(qe − qt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe − K1t qe − K1t | (4) |
| qt = qe(1 − e−K1t) | (5) |
If the active surface of the adsorbent is regarded as invariable, the reaction could be treated as pseudo-first-order kinetic. However, once the active sites have been saturated, the transfer at the adsorbate/adsorbent particle interface may be limited by mass transfer.44
The pseudo second-order (PSO) model is proposed by Ho and McKay.40 It is based on the adsorption capacity expressed as follows:
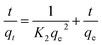 | (6) |
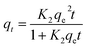 | (7) |
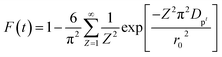 | (8) |
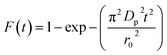 | (9) |
A further formula manipulation gives the following:
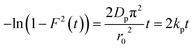 | (10) |
Additionally, eqn (11) can be used when the rate of adsorption is controlled by liquid film diffusion.46
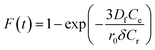 | (11) |
| −ln(1 − F) = kft | (12) |
The values of kf = 3DfCe/r0δCr for the adsorption of MO and EB on ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4, and JUN–Fe3O4 are obtained from the slopes of the fitted lines (plots of −ln(1 − F) vs. time), and the values of effective diffusion coefficient, Df (m2 s−1), can then be obtained from Df = kfr0Cr/3Ce.
The linearity test of Boyd plots −ln(1 − F) and −ln(1 − F2) versus time plots is employed to distinguish between the film diffusion and particle diffusion-controlled adsorption mechanism. If the plot of −ln(1 − F) versus time is a straight line passing through the origin, then the adsorption rate is governed by the particle diffusion mechanism, otherwise if −ln(1 − F2) versus time is a straight line passing through the origin then the adsorption is governed by film diffusion.
To calculate the desorption yields (R%) of MO and EB ions at contact time t = 60 min from JUN–Fe3O4, MAT–Fe3O4, ROS–Fe3O4 and ARM–Fe3O4 surfaces, the following equation was used:
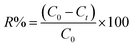 | (13) |
The adsorption capacity, qeT (mg g−1), was calculated using the following equations:
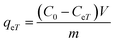 | (14) |
Adsorption yield was calculated using the following equation:
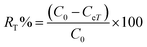 | (15) |
The activation enthalpy (ΔH0) of EB and MO adsorption processes on the magnetite NP surface was determined using the Arrhenius equation as follows:
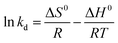 | (16) |
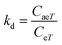 | (17) |
The values of activation enthalpy ΔH0 (kcal mol−1) and entropy ΔS0 (cal mol−1 K−1) were respectively calculated from the slope and intercept of plots between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd and 1/T. ΔG0 (kcal mol−1) was then calculated using the following equation:
kd and 1/T. ΔG0 (kcal mol−1) was then calculated using the following equation:
ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kd kd | (18) |
The free energy change indicates the degree of spontaneity of the adsorption process. The higher negative value reflects more energetically favorable adsorption. The activation energy, ΔEa (kcal mol−1), of EB and MO adsorption processes on magnetite surfaces was determined using Arrhenius's equation:
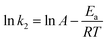 | (19) |
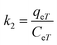 | (20) |
3 Results and discussion
3.1 X-ray analysis of magnetite nanoparticle samples
X-ray patterns of all synthesised samples are presented in Fig. 2. It is found that all synthesized samples have crystalline structures. The X-ray diffraction pattern in Fig. 2(A) exhibits Bragg reflection peaks at around 2θ = 16.20°, 20.30°, 22.39°, 25.60°, 29.72°, 32.30°, 41.05°, 41.39°, 42.48°, and 52.69°. All Bragg peaks are in agreement with orthorhombic Fe3O4 powder and correspond to Miller indices 021, 212, 030, 400, 314, 001, 250, 251, 522, and 644, respectively (JCPDS file 01-076-0958).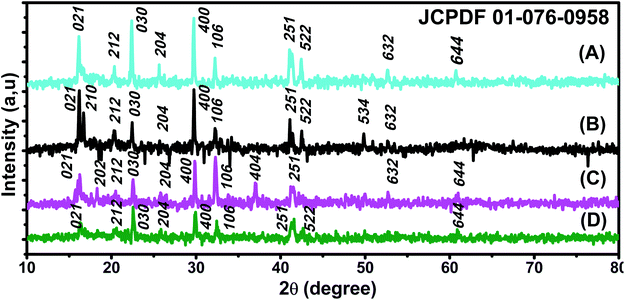 | ||
| Fig. 2 XRD patterns of (A) ROS–Fe3O4, (B) ARM–Fe3O4, (C) MAT–Fe3O4, and (D) JUN–Fe3O4 NPs (JCPDS file 01-076-0958). | ||
The X-ray diffraction pattern in Fig. 2(B) exhibits Bragg reflection peaks at around 2θ = 16.20°, 16.70°, 20.39°, 22.42°, 29.75°, 30.80°, 32.30°, 41.10°, 42.53°, 49.82°, and 52.72°. All Bragg peaks are in agreement with orthorhombic Fe3O4 powder and correspond to Miller indices 021, 210, 212, 030, 400, 041, 106, 251, 522, 534, and 644, respectively (JCPDS file 01-076-0958).
The X-ray diffraction pattern in Fig. 2(C) exhibits Bragg reflection peaks at around 2θ = 16.20°, 22.56°, 26.04°, 32.28°, 37.11°, 41.59°, 49.98°, and 52.69°. All Bragg peaks are in agreement with orthorhombic Fe3O4 powder and correspond to Miller indices 021, 030, 400, 106, 404, 251, 534, and 644, respectively (JCPDS file 01-076-0958).
The X-ray diffraction pattern in Fig. 2(D) exhibits Bragg reflection peaks at around 2θ = 16.35°, 20.58°, 22.60°, 25.77°, 29.94°, 32.47°, 41.59°, 42.69°, 49.98°, and 52.69°. All Bragg peaks are in agreement with orthorhombic Fe3O4 powder and correspond to Miller indices 021, 212, 030, 400, 001, 106, 251, 522, 534, and 644, respectively (JCPDS file 01-076-0958).
The average diameters of different magnetite samples, presented in Table 1, are calculated from XRD patterns using Scherrer's equation:48
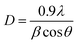 | (21) |
| Samples | Average diameter (nm) |
|---|---|
| ARM–Fe3O4 | 41.49 |
| ROS–Fe3O4 | 39.89 |
| MAT–Fe3O4 | 33.13 |
| JUN–Fe3O4 | 29.27 |
3.2 ATR-FTIR spectroscopy analysis
FTIR spectra of the synthesized Fe3O4 nanoparticle powders recorded between 4000 and 500 cm−1 are presented in Fig. 3. Fig. 3 shows that all IR spectra (A, B, C, and D) exhibit peaks in different ranges as is summarized in Table 2. The peaks at 3223.41–3266.69 cm−1 correspond to the O–H stretching vibration, while the peaks at 2930.18–2932.06 cm−1 correspond to C–H vibrations. The peaks at 1590.07–1594.63 cm−1 correspond to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching in aromatic rings and anti-symmetric stretching of the carboxylate group (COO−), whereas peaks at 1033.45–1044.36 cm−1 are assigned to the symmetric stretching vibration of the C–O–C functional group of the phenolic groups.49 The peak at around 592 cm−1 corresponds to the Fe–O stretching band of Fe3O4 NPs.50
C stretching in aromatic rings and anti-symmetric stretching of the carboxylate group (COO−), whereas peaks at 1033.45–1044.36 cm−1 are assigned to the symmetric stretching vibration of the C–O–C functional group of the phenolic groups.49 The peak at around 592 cm−1 corresponds to the Fe–O stretching band of Fe3O4 NPs.50
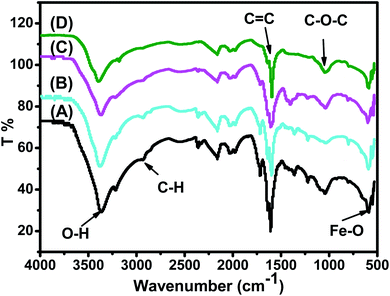 | ||
| Fig. 3 FTIR spectra of the synthesized (A) ARM–Fe3O4, (B) ROS–Fe3O4, (C) MAT–Fe3O4, and (D) JUN–Fe3O4 samples. | ||
| Sample | O–H cm−1 | C–H cm−1 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C cm−1 C cm−1 |
C–O–C cm−1 | Fe–O cm−1 |
|---|---|---|---|---|---|
| ARM–Fe3O4 | 3266.69 | 2932.06 | 1590.07 | 1036.36 | 592.64 |
| ROS–Fe3O4 | 3249.77 | 2930.18 | 1590.83 | 1038.75 | 591.83 |
| MAT–Fe3O4 | 3235.57 | 2929.75 | 1591.21 | 1039.54 | 592.46 |
| JUN–Fe3O4 | 3223.41 | 2928.82 | 1594.63 | 1039.45 | 592.69 |
Fig. 3 shows that the peaks of hydroxyl groups appear in remarkably different areas. Meanwhile, the hydroxyl group peak area appears to be the broadest on the ARM–Fe3O4 surface, next on ROS–Fe3O4, then on MAT–Fe3O4, and finally on JUN–Fe3O4. This reveals that the density of functional OH groups is higher on the ARM–Fe3O4 surface, next on ROS–Fe3O4, then on MAT–Fe3O4, and finally on JUN–Fe3O4.
3.3 UV-vis spectroscopy analysis
The optical absorbance spectra of all the synthesized Fe3O4 are measured in the wavelength range of 200–900 nm, to deduce their band gap energies. The band gap Eg and the optical absorption coefficient (α) of a direct band gap semiconductor are related through the known following equation:51| αhν = A(hν − Eg)n | (22) |
E g of the direct transition of all samples were obtained from plotting (αhν)2 as a function of αhν by the extrapolation of the linear portion of the curve (Fig. 4). However, Eg of the indirect transition of all samples were obtained from plotting (αhν)1/2 as a function of αhν by the extrapolation of the linear portion of the curve (Fig. 5).
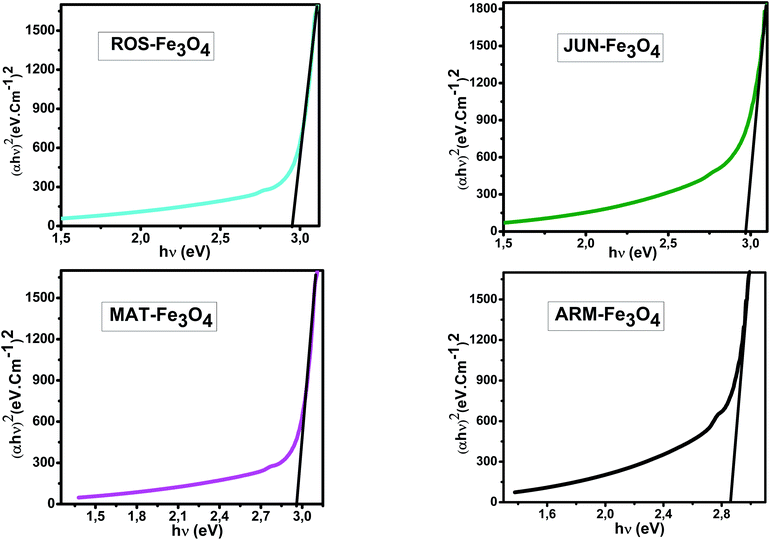 | ||
| Fig. 4 Plots of (αhν)2versus (αhν) for direct transition of synthesized Fe3O4 samples sonicated in acetone for 15 minutes. | ||
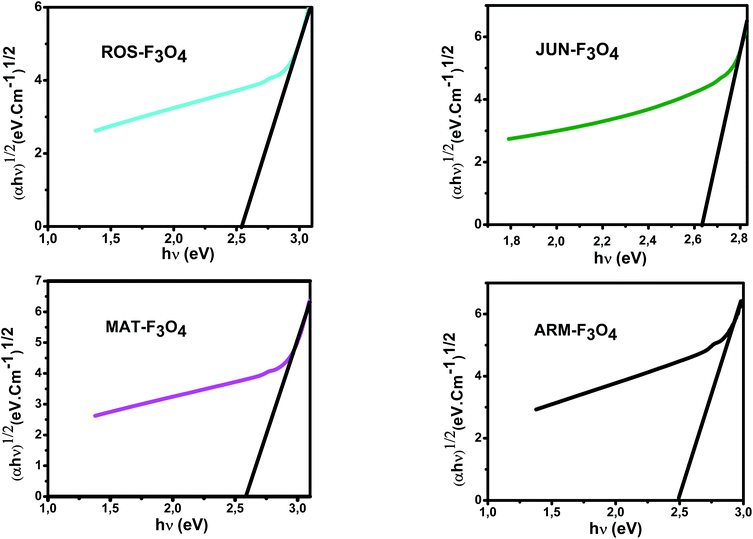 | ||
| Fig. 5 Plots of (αhν)1/2versus (αhν) for indirect transition of synthesized Fe3O4 samples sonicated in acetone for 15 minutes. | ||
Estimated direct band gap energies of JUN–Fe3O4, MAT–Fe3O4, ROS–Fe3O4, and ARM–Fe3O4 samples were found to be 2.97, 2.96, 2.95 and 2.87 eV, respectively, which are close to that found by El Ghandoor et al.52 They found that direct gap energy for Fe3O4 equals Eg = 2.87 eV.
The estimated indirect band gap energies of ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4 and JUN–Fe3O4 phases were found to be 2.51, 2.55, 2.60 and 2.64 eV, respectively, which are higher than reported by other authors.52 They found that indirect gap energy for Fe3O4 equals Eg = 1.92 eV.
It is clear that the direct gap energy is closer to the theoretical value than the indirect gap energy. The values of all direct band gap energies of magnetite samples classify them as semiconductors. The energy band gap of the semiconductors is between 0 and 3 eV.53
3.4 SEM images of the plant–Fe3O4 samples
SEM images of the plant–Fe3O4 samples are presented in Fig. 6. It is clearly shown that the morphology of all four magnetite NPs depends on the plant extract. Different irregular rock-like shapes are observed in all samples. For ROS–Fe3O4 NPs, it is clear that a few agglomerations like rocks are present as shown in Fig. 6a. Meanwhile, for JUN–Fe3O4 NPs, bigger rocks that look like mountains are visible, as shown in Fig. 6b. However, for MAT–Fe3O4 a decrease in the dimensions of the mountains with more adherence to its structure is observed (Fig. 6c). Finally, the ARM–Fe3O4 SEM image sometimes contains large-structured single bipyramid crystal as mentioned in Fig. 6d. | ||
| Fig. 6 SEM images of greenly synthesized (a) JUN–Fe3O4, (b) MAT–Fe3O4, (c) ROS–Fe3O4 and (d) ARM–Fe3O4 NPs. | ||
3.5 Adsorption experiment equilibrium, kinetics analysis, and thermodynamic study
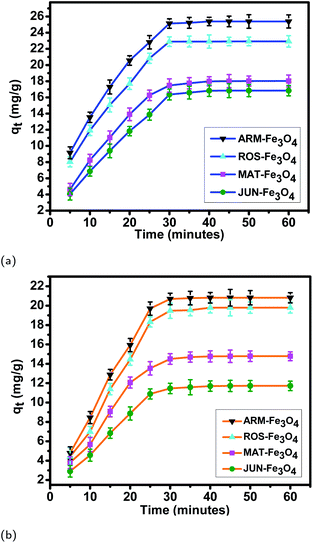 | ||
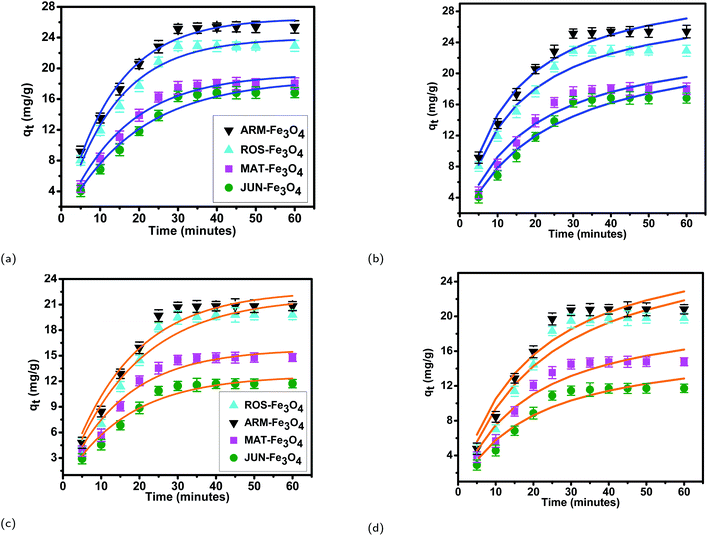
| Fig. 7 Adsorption capacities of (a) EB and (b) MO on ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4, and JUN–Fe3O4 surfaces. Error bars represent the standard deviation of three replicates. | ||
| Sample | t (min) | q t (mg g−1) | STD | t (min) | q t (mg g−1) | STD | t (min) | q t (mg g−1) | STD | t (min) | q t (mg g−1) | STD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EB/ARM–Fe3O4 | 05 | 09.15 | 0.73 | 10 | 13.54 | 0.64 | 15 | 17.29 | 0.71 | 20 | 20.55 | 0.59 |
| EB/ROS–Fe3O4 | 05 | 08.03 | 0.64 | 10 | 11.92 | 0.59 | 15 | 15.06 | 0.69 | 20 | 17.69 | 0.72 |
| EB/MAT–Fe3O4 | 05 | 04.62 | 0.75 | 10 | 08.24 | 0.72 | 15 | 11.03 | 0.73 | 20 | 13.90 | 0.78 |
| EB/JUN–Fe3O4 | 05 | 04.05 | 0.74 | 10 | 06.86 | 0.59 | 15 | 09.40 | 0.62 | 20 | 11.83 | 0.78 |
| EB/ARM–Fe3O4 | 25 | 22.82 | 0.81 | 30 | 25.22 | 0.59 | 35 | 25.29 | 0.65 | 40 | 25.33 | 0.52 |
| EB/ROS–Fe3O4 | 25 | 20.84 | 0.63 | 30 | 22.75 | 0.57 | 35 | 22.80 | 0.52 | 40 | 22.84 | 0.72 |
| EB/MAT–Fe3O4 | 25 | 16.25 | 0.64 | 30 | 17.87 | 0.78 | 35 | 17.95 | 0.67 | 40 | 17.99 | 0.56 |
| EB/JUN–Fe3O4 | 25 | 13.87 | 0.68 | 30 | 16.71 | 0.65 | 35 | 16.76 | 0.72 | 40 | 16.78 | 0.71 |
| EB/ARM–Fe3O4 | 45 | 25.35 | 0.66 | 50 | 25.37 | 0.74 | 60 | 25.39 | 0.78 | |||
| EB/ROS–Fe3O4 | 45 | 22.87 | 0.52 | 50 | 22.90 | 0.53 | 60 | 22.92 | 0.71 | |||
| EB/MAT–Fe3O4 | 45 | 18.00 | 0.81 | 50 | 18.01 | 0.61 | 60 | 18.03 | 0.63 | |||
| EB/JUN–Fe3O4 | 45 | 16.79 | 0.80 | 50 | 16.81 | 0.71 | 60 | 16.83 | 0.74 |
| Sample | t (min) | q t (mg g−1) | STD | t (min) | q t (mg g−1) | STD | t (min) | q t (mg g−1) | STD | t (min) | q t (mg g−1) | STD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MO/ARM–Fe3O4 | 05 | 04.78 | 0.65 | 10 | 08.44 | 0.65 | 15 | 12.88 | 0.55 | 20 | 15.93 | 0.66 |
| MO/ROS–Fe3O4 | 05 | 04.42 | 0.89 | 10 | 06.99 | 0.55 | 15 | 11.39 | 0.59 | 20 | 14.45 | 0.50 |
| MO/MAT–Fe3O4 | 05 | 03.80 | 0.61 | 10 | 05.67 | 0.63 | 15 | 09.07 | 0.54 | 20 | 12.06 | 0.57 |
| MO/JUN–Fe3O4 | 05 | 02.90 | 0.59 | 10 | 04.57 | 0.52 | 15 | 06.84 | 0.52 | 20 | 08.87 | 0.68 |
| MO/ARM–Fe3O4 | 25 | 19.70 | 0.69 | 30 | 20.70 | 0.54 | 35 | 20.73 | 0.70 | 40 | 20.75 | 0.69 |
| MO/ROS–Fe3O4 | 25 | 18.32 | 0.52 | 30 | 19.70 | 0.61 | 35 | 19.73 | 0.58 | 40 | 19.75 | 0.54 |
| MO/MAT–Fe3O4 | 25 | 13.54 | 0.69 | 30 | 14.70 | 0.55 | 35 | 14.71 | 0.53 | 40 | 14.73 | 0.58 |
| MO/JUN–Fe3O4 | 25 | 10.89 | 0.52 | 30 | 11.66 | 0.51 | 35 | 11.68 | 0.78 | 40 | 11.70 | 0.52 |
| MO/ARM–Fe3O4 | 45 | 20.79 | 0.83 | 50 | 20.81 | 0.74 | 60 | 20.82 | 0.53 | |||
| MO/ROS–Fe3O4 | 45 | 19.78 | 0.85 | 50 | 19.79 | 0.74 | 60 | 19.80 | 0.50 | |||
| MO/MAT–Fe3O4 | 45 | 14.74 | 0.64 | 50 | 14.76 | 0.54 | 60 | 14.78 | 0.46 | |||
| MO/JUN–Fe3O4 | 45 | 11.71 | 0.58 | 50 | 11.72 | 0.56 | 60 | 11.73 | 0.49 |
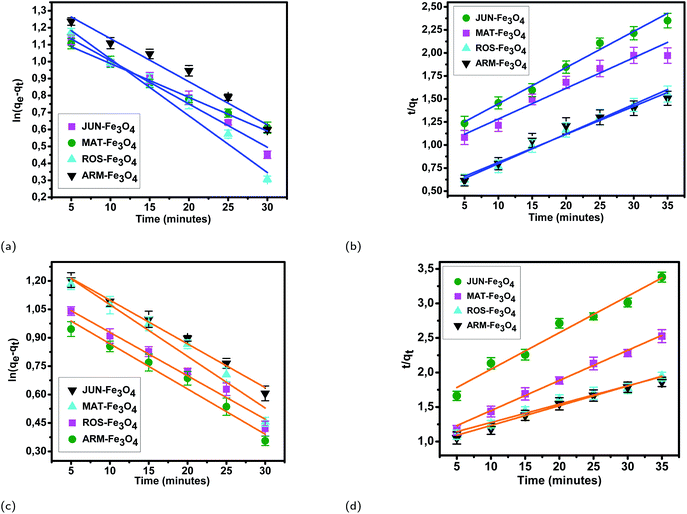
3.5.2.1 Linear and non-linear pseudo-first-order and pseudo-second-order kinetics. The results of linear and non-linear pseudo-first-order (PFO) and pseudo-second-order (PSO) kinetics analysis of MO and EB adsorption processes on the four magnetite surfaces (Tables 5 and 6, and Fig. 8 and 9) indicate a good linearity and a good fit of the experimental data to linear pseudo-first-order. However, the comparison with the pseudo-second-order model indicates a poor linearity and a poor fit to the experimental data of this model. Indeed, the equilibrium adsorption capacities qe,cal computed from linear pseudo-first-order kinetics plots are in very close agreement with the empirical qe,exp, unlike qe,cal calculated from linear pseudo-second-order plots which are far from empirical qe,exp.
| Sample | q e,exp (mg g−1) | q e,cal (mg g−1) | K 1 (min−1) | R 2 | q e,cal (mg g−1) | K 2 (g mg−1 min−1) | R 2 |
|---|---|---|---|---|---|---|---|
| EB/ARM–Fe3O4 | 25.39 | 23.85 | 0.0008 | 0.983 | 33.84 | 0.0016 | 0.972 |
| EB/ROS–Fe3O4 | 22.92 | 22.93 | 0.0011 | 0.989 | 31.52 | 0.0020 | 0.985 |
| EB/MAT–Fe3O4 | 18.03 | 18.61 | 0.0009 | 0.982 | 30.94 | 0.0010 | 0.946 |
| EB/JUN–Fe3O4 | 16.83 | 15.50 | 0.0007 | 0.991 | 26.11 | 0.0014 | 0.983 |
| MO/ARM–Fe3O4 | 20.82 | 21.52 | 0.0008 | 0.988 | 32.25 | 0.0008 | 0.965 |
| MO/ROS–Fe3O4 | 19.80 | 22.85 | 0.0009 | 0.987 | 30.76 | 0.0007 | 0.961 |
| MO/MAT–Fe3O4 | 14.78 | 14.50 | 0.0007 | 0.996 | 22.50 | 0.0020 | 0.994 |
| MO/JUN–Fe3O4 | 11.73 | 12.27 | 0.0008 | 0.989 | 18.47 | 0.0019 | 0.969 |
| Sample | q e,exp (mg g−1) | q e,cal (mg g−1) | K 1 (min−1) | R 2 | q e,cal (mg g−1) | K 2 (g mg−1 min−1) | R 2 |
|---|---|---|---|---|---|---|---|
| EB/ARM–Fe3O4 | 25.39 | 27.53 | 0.077 | 0.973 | 32.56 | 0.0026 | 0.964 |
| EB/ROS–Fe3O4 | 22.92 | 23.96 | 0.075 | 0.975 | 29.97 | 0.0025 | 0.955 |
| EB/MAT–Fe3O4 | 18.03 | 19.31 | 0.063 | 0.975 | 25.14 | 0.0023 | 0.952 |
| EB/JUN–Fe3O4 | 16.83 | 18.62 | 0.052 | 0.967 | 25.07 | 0.0018 | 0.952 |
| MO/ARM–Fe3O4 | 20.82 | 22.62 | 0.060 | 0.948 | 29.88 | 0.0018 | 0.924 |
| MO/ROS–Fe3O4 | 19.80 | 23.89 | 0.055 | 0.925 | 29.69 | 0.0015 | 0.923 |
| MO/MAT–Fe3O4 | 14.78 | 15.79 | 0.064 | 0.952 | 21.05 | 0.0026 | 0.926 |
| MO/JUN–Fe3O4 | 11.73 | 12.88 | 0.060 | 0.948 | 17.02 | 0.0030 | 0.931 |
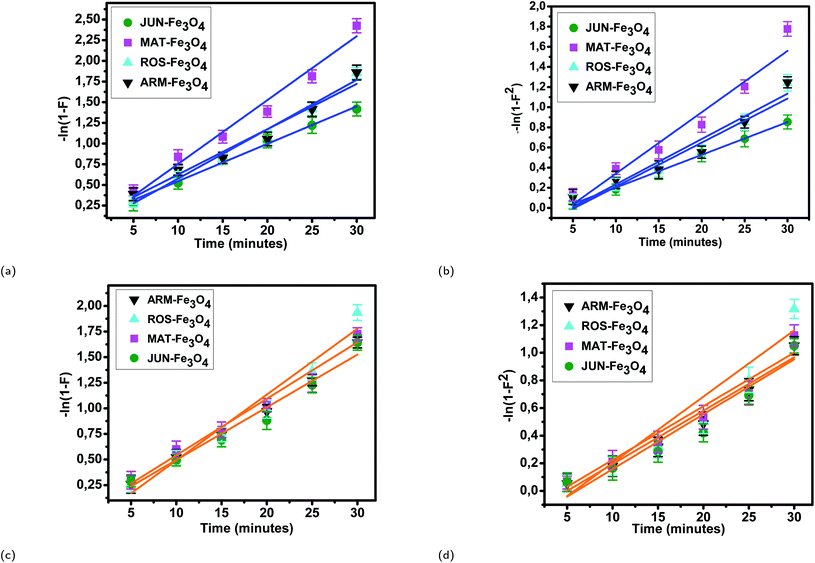
3.5.2.2 Intra-particle diffusion mechanism analysis. The linearity tests of Boyd plots (−ln(1 − F) and −ln(1 − F2)) versus time are presented in Fig. 10. The kinetic data correlate well with the homogeneous particle diffusion model as confirmed by the high R2 values. The results of linear regression analysis for eqn (10) and (12) are presented in Table 7. Film diffusion coefficients Df are found to be in the order of 10−11 m2 s−1, while intra-particle diffusion coefficients Dp are found to be in the order of 10−20 m2 s−1. Michelson et al.55 reported that the adsorption mechanism is controlled by film diffusion and that film diffusion is in control at Df ranging from 10−10 to 10−12 m2 s−1, while intra-particle diffusion is the rate-limiting step at Dp in the range of 10−15 to 10−18 m2 s−1. Indeed, the obtained results indicate that film diffusion is the step that controls the adsorption mechanism of MO and EB on magnetite surfaces, which is in agreement with the pseudo-first-order kinetic model.
| Sample | r 0 × 10−9 (m) | k p × 10−3 (1/s) | R 2 | D p × 10−19 (m2 s−1) | k f × 10−3 (1/s) | R 2 | D f × 10−12 (m2 s−1) |
|---|---|---|---|---|---|---|---|
| EB/ARM–Fe3O4 | 41.94 | 2.18 | 0.963 | 3.89 | 1.44 | 0.953 | 03.38 |
| EB/ROS–Fe3O4 | 39.89 | 2.26 | 0.985 | 3.68 | 1.51 | 0.962 | 05.91 |
| EB/MAT–Fe3O4 | 33.13 | 2.51 | 0.977 | 2.80 | 2.08 | 0.956 | 14.97 |
| EB/JUN–Fe3O4 | 29.27 | 1.89 | 0.993 | 1.65 | 1.08 | 0.998 | 08.13 |
| MO/ARM–Fe3O4 | 41.94 | 1.79 | 0.990 | 3.67 | 1.30 | 0.965 | 07.67 |
| MO/ROS–Fe3O4 | 39.89 | 2.12 | 0.963 | 3.43 | 1.60 | 0.930 | 10.62 |
| MO/MAT–Fe3O4 | 33.13 | 1.77 | 0.977 | 1.98 | 1.32 | 0.951 | 14.28 |
| MO/JUN–Fe3O4 | 29.27 | 1.75 | 0.970 | 1.46 | 1.28 | 0.970 | 18.97 |
| Sample | T (K) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD KD |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K2 K2 |
E a (kcal mol−1) | ΔH0 (kcal mol−1) | ΔS0 (cal mol−1 K−1) | ΔG0 (kcal mol−1) |
|---|---|---|---|---|---|---|---|
| EB/ARM–Fe3O4 | 303.15 | 1.82 | 9.71 | 2.79 | 2.85 | 13.03 | −1.09 |
| 308.15 | 1.92 | 9.81 | −1.18 | ||||
| 313.15 | 1.98 | 9.84 | −1.23 | ||||
| 318.15 | 2.05 | 9.94 | −1.29 | ||||
| EB/ROS–Fe3O4 | 303.15 | 1.54 | 9.43 | 3.21 | 3.32 | 14.04 | −0.93 |
| 308.15 | 1.65 | 9.54 | −1.00 | ||||
| 313.15 | 1.75 | 9.61 | −1.09 | ||||
| 318.15 | 1.80 | 9.68 | −1.14 | ||||
| EB/MAT–Fe3O4 | 303.15 | 0.61 | 8.49 | 5.59 | 5.96 | 20.86 | −0.36 |
| 308.15 | 0.76 | 8.65 | −0.47 | ||||
| 313.15 | 0.93 | 8.73 | −0.58 | ||||
| 318.15 | 1.07 | 8.94 | −0.67 | ||||
| EB/JUN–Fe3O4 | 303.15 | 0.59 | 8.48 | 6.29 | 6.54 | 22.70 | −0.35 |
| 308.15 | 0.70 | 8.59 | −0.43 | ||||
| 313.15 | 0.90 | 8.71 | −0.56 | ||||
| 318.15 | 1.07 | 8.95 | −0.66 |
| Sample | T (K) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD KD |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K2 K2 |
E a (kcal mol−1) | ΔH0 (kcal mol−1) | ΔS0 (cal mol−1 K−1) | ΔG0 (kcal mol−1) |
|---|---|---|---|---|---|---|---|
| MO/ARM–Fe3O4 | 303.15 | 1.14 | 9.03 | 3.27 | 3.31 | 13.24 | −0.69 |
| 308.15 | 1.28 | 9.17 | −0.78 | ||||
| 313.15 | 1.33 | 9.21 | −0.83 | ||||
| 318.15 | 1.41 | 9.30 | −0.89 | ||||
| MO/ROS–Fe3O4 | 303.15 | 1.07 | 8.96 | 3.66 | 3.78 | 14.63 | −0.65 |
| 308.15 | 1.20 | 9.09 | −0.74 | ||||
| 313.15 | 1.30 | 9.16 | −0.81 | ||||
| 318.15 | 1.37 | 9.26 | −0.87 | ||||
| MO/MAT–Fe3O4 | 303.15 | 0.13 | 8.02 | 6.28 | 6.75 | 22.54 | −0.078 |
| 308.15 | 0.31 | 8.20 | −0.19 | ||||
| 313.15 | 0.53 | 8.30 | −0.33 | ||||
| 318.15 | 0.64 | 8.53 | −0.41 | ||||
| MO/JUN–Fe3O4 | 303.15 | −0.27 | 7.62 | 8.45 | 8.67 | 27.27 | +0.16 |
| 308.15 | −0.13 | 7.76 | +0.08 | ||||
| 313.15 | +0.12 | 8.00 | −0.07 | ||||
| 318.15 | +0.39 | 8.28 | −0.24 |
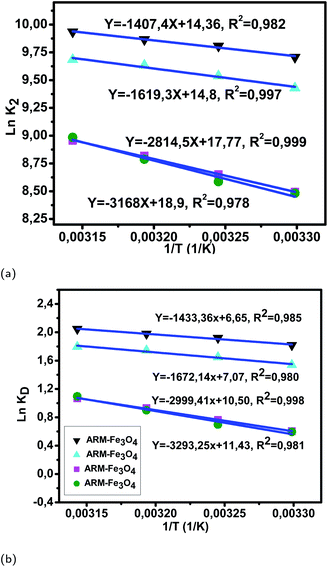 | ||
Fig. 11 (a) Plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K2versus 1/T of EB adsorption on Fe3O4 surfaces. (b) Plots of ln K2versus 1/T of EB adsorption on Fe3O4 surfaces. (b) Plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KDversus 1/T of EB adsorption on Fe3O4 surfaces. KDversus 1/T of EB adsorption on Fe3O4 surfaces. | ||
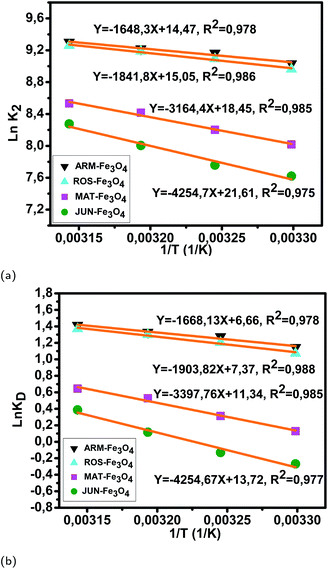 | ||
Fig. 12 (a) Plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K2versus 1/T of MO adsorption on Fe3O4 surfaces. (b) Plots of ln K2versus 1/T of MO adsorption on Fe3O4 surfaces. (b) Plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KDversus 1/T of MO adsorption on Fe3O4 surfaces. KDversus 1/T of MO adsorption on Fe3O4 surfaces. | ||
The activation entropies in all EB/plant–Fe3O4 and MO/plant–Fe3O4 systems are positive, which reveals the affinity of Fe3O4 surfaces for EB and MO molecules. The increasing randomness at the EB/plant–magnetite and MO/plant–magnetite solution interfaces indicates that significant changes in the number of surface active hydroxyl groups occurred in the internal structure of Fe3O4 surfaces. However, activation entropies of EB/JUN–Fe3O4 (22.70 cal mol−1 K−1) and MO/JUN–Fe3O4 (27.27 cal mol−1 K−1) systems are the highest ones, and those of EB/ARM–Fe3O4 (13.03 cal mol−1 K−1) and MO/ARM–Fe3O4 (13.24 cal mol−1 K−1) systems are the lowest ones. This indicates that the changes occurring in the structure of the JUN–Fe3O4 surface are the greatest ones, followed by those of MAT–Fe3O4, then ROS–Fe3O4, and finally ARM–Fe3O4 surfaces.56,57
The activation free energies of EB/ARM–Fe3O4 (−1.09, −1.17, −1.23, and −1.29 kcal mol−1), EB/ROS–Fe3O4 (−0.93, −1.00, −1.09, and −1.14 kcal mol−1), EB/MAT–Fe3O4 (−0.36, −0.47, −0.58, and −0.67 kcal mol−1), and EB/JUN–Fe3O4 (−0.35, −0.43, −0.56, and −0.66 kcal mol−1) systems are negative. However, activation energies of the EB/ARM–Fe3O4 system are more negative than those of EB/ROS–Fe3O4, EB/MAT–Fe3O4 and EB/JUN–Fe3O4 systems, which indicates the feasibility of the EB adsorption process and its spontaneous nature with more EB adsorption on ARM–Fe3O4, then on ROS–Fe3O4, next on MAT–Fe3O4, and finally on JUN–Fe3O4 surfaces.
The activation free energies of MO/ARM–Fe3O4 (−0.69, −0.78, −0.83, and −0.89 kcal mol−1), MO/ROS–Fe3O4 (−0.65, −0.74, −0.81, and −0.87 kcal mol−1), and MO/MAT–Fe3O4 (−0.078, −0.19, −0.33, and −0.41 kcal mol−1) systems are negative. However, activation energies of the MO/ARM–Fe3O4 system are more negative than those of MO/ROS–Fe3O4 and MO/MAT–Fe3O4 systems, which indicates the feasibility of the MO adsorption process and its spontaneous nature with more MO adsorption on ARM–Fe3O4 than on ROS–Fe3O4 surfaces. In the MO/JUN–Fe3O4 system, the values of activation free energy are negative only at 313.15 K and 318.15 K (−0.072 and −0.24 kcal mol−1, respectively), while positive values are found at 303.15 K and 308.15 K (0.16 and 0.079 kcal mol−1, respectively) revealing that activated MO/Fe3O4 complexes are in an excited form in the transition state.56 This leads to the spontaneity of MO adsorption at 313.15 K and 318.15 K.
As presented in Table 8, the found activation energies (Ea) for EB adsorption on ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4, and JUN–Fe3O4 surfaces are respectively: 2.79, 3.21, 5.59, and 6.29 kcal mol−1. Ea is calculated from the slopes of the Arrhenius linear plots ln K2versus 1/T (Fig. 11a). As presented in Table 9, the found activation energies (Ea) for MO adsorption on ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4, and JUN–Fe3O4 surfaces are respectively: 3.27, 3.66, 6.28, and 8.45 kcal mol−1. Ea is calculated from the slopes of Arrhenius linear plots ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K2versus 1/T (Fig. 12a). The found low Ea suggests that EB and MO adsorption processes on all plant–Fe3O4 surfaces proceeded with low energy barriers and can be achieved at relatively low temperatures. As it is known that the activation energy Ea of physical adsorption ranges from 1.2 to 12 kcal mol−1, and from 14.3 to 191 kcal mol−1 for chemical adsorption,58 the adsorption processes of EB and MO on all plant–Fe3O4 are physical in nature.
K2versus 1/T (Fig. 12a). The found low Ea suggests that EB and MO adsorption processes on all plant–Fe3O4 surfaces proceeded with low energy barriers and can be achieved at relatively low temperatures. As it is known that the activation energy Ea of physical adsorption ranges from 1.2 to 12 kcal mol−1, and from 14.3 to 191 kcal mol−1 for chemical adsorption,58 the adsorption processes of EB and MO on all plant–Fe3O4 are physical in nature.
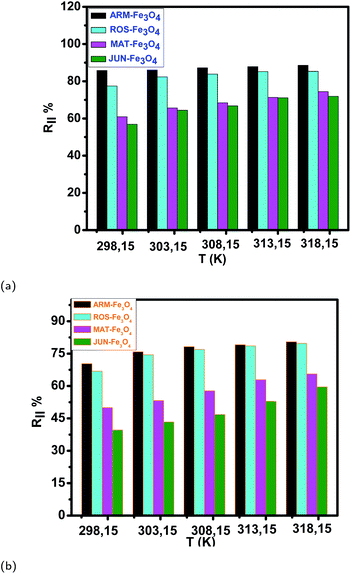 | ||
| Fig. 13 (a and b) Temperature effect on EB and MO adsorption yields on plant–Fe3O4 surfaces in the range of 303.15–318.15 K over 20 minutes, respectively. | ||
| Sample | 298.15 K | 303.15 K | 308.15 K | 313.15 K | 318.15 K | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| q e (mg g−1) | R (%) | q eT (mg g−1) | R T (%) | q eT (mg g−1) | R T (%) | q eT (mg g−1) | R T (%) | q eT (mg g−1) | R T (%) | |
| EB/ARM–Fe3O4 | 25.39 | 86.05 | 25.47 | 86.24 | 25.91 | 87.21 | 26.00 | 87.84 | 26.21 | 88.56 |
| EB/ROS–Fe3O4 | 22.92 | 77.44 | 24.37 | 82.34 | 24.83 | 83.87 | 25.2 | 85.14 | 25.09 | 85.77 |
| EB/MAT–Fe3O4 | 18.03 | 60.91 | 19.44 | 65.66 | 20.24 | 68.38 | 21.12 | 71.35 | 22.19 | 74.95 |
| EB/JUN–Fe3O4 | 16.83 | 56.88 | 19.07 | 64.41 | 19.76 | 66.76 | 21.04 | 71.08 | 21.52 | 72.70 |
| MO/ARM–Fe3O4 | 20.82 | 70.32 | 21.92 | 74.05 | 22.29 | 75.32 | 22.43 | 75.76 | 22.58 | 76.31 |
| MO/ROS–Fe3O4 | 19.80 | 66.88 | 20.59 | 69.55 | 20.93 | 70.72 | 21.65 | 73.15 | 22.05 | 74.50 |
| MO/MAT–Fe3O4 | 14.78 | 49.94 | 15.76 | 53.24 | 17.09 | 57.75 | 18.61 | 62.88 | 19.41 | 65.59 |
| MO/JUN–Fe3O4 | 11.72 | 39.61 | 12.82 | 43.33 | 13.84 | 46.76 | 15.65 | 52.88 | 17.63 | 59.55 |
The tendency of adsorption capacities and yields on the four magnetite surfaces is the same in EB and MO adsorption processes at 298.15 K and after increasing the temperature from 303.15 to 318.15 K. In EB and MO adsorption processes (298.15 K), the highest adsorption capacities were on ARM–Fe3O4, then on ROS–Fe3O4, next on MAT–Fe3O4, and finally on JUN–Fe3O4 NPs. After the exposure of EB/plant–magnetite and MO/plant–magnetite systems to heat in the temperature range of 303.15–318.15 K for 20 minutes, the order of adsorption capacities was the same.
3.6 Influence of the mediating plant extract's acidity on preferential attachment of chromophore and auxochrome groups of MO and EB on magnetite NPs
To study the adsorption of MO and EB on these four magnetite samples, all adsorption experiments were conducted under the same conditions including solution pH = 4 so as to eliminate solution pH effect on the adsorption.7,14,19
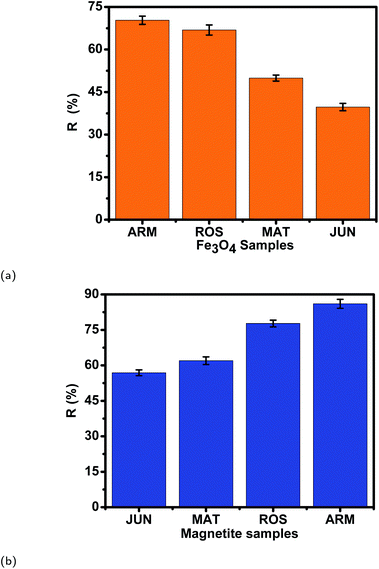
Table 11 and Fig. 14 show that the adsorption yields and capacities of dyes differed on the four Fe3O4 NPs according to the pH of plant extracts used in magnetite sample synthesis. EB and MO anions were highly adsorbed on the ARM–Fe3O4 surface with achieved adsorption yields and capacities of 86.05%, 25.39 mg g−1 and 70.31%, 20.82 mg g−1, respectively, then on the ROS–Fe3O4 surface with achieved adsorption yields of 77.71%, 22.92 mg g−1 and 66.88%, 19.80 mg g−1, respectively, next on the MAT–Fe3O4 surface with achieved adsorption yields of 61.98%, 18.03 mg g−1 and 49.94%, 14.78 mg g−1, respectively, and finally, on the JUN–Fe3O4 surface where the adsorption yields and capacities of EB and MO achieved values of only 56.88%, 16.83 mg g−1 and 39.61%, 11.73 mg g−1, respectively.When magnetite is immersed in an aqueous acidic solution, it develops its surface charge via the protonation and deprotonation of ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) FeOH sites on its surface according to the following equation:59
FeOH sites on its surface according to the following equation:59
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) FeOH+2 ↔ FeOH+2 ↔ ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) FeOH0 + H+sol (pka1 = 5.1) FeOH0 + H+sol (pka1 = 5.1) | (23) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) FeOH+2 and
FeOH+2 and ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) FeOH0 are respectively the protonated positively charged surface group with two dissociable H+, and the neutral surface group with one dissociable H+. pKa1 = 5.1 is the intrinsic acidity constant determined by Davis et al.59 for magnetite.
FeOH0 are respectively the protonated positively charged surface group with two dissociable H+, and the neutral surface group with one dissociable H+. pKa1 = 5.1 is the intrinsic acidity constant determined by Davis et al.59 for magnetite. ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) FeOH+2 known as the Brønsted acid site is an electron-pair acceptor and it is able to transfer H+ from the solid to the adsorbed molecule, implying an H-bond with the surface. Meanwhile,
FeOH+2 known as the Brønsted acid site is an electron-pair acceptor and it is able to transfer H+ from the solid to the adsorbed molecule, implying an H-bond with the surface. Meanwhile, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) FeOH0 known as the Lewis acid site is an electron-pair acceptor from the adsorbed molecule, implying a coordinated bond with the surface.59
FeOH0 known as the Lewis acid site is an electron-pair acceptor from the adsorbed molecule, implying a coordinated bond with the surface.59
| Adsorbent | q e (EB) (mg g−1) | R (EB) (%) | q e (MO) (mg g−1) | R (MO) (%) | pH of plant extract |
|---|---|---|---|---|---|
| ARM–Fe3O4 | 25.39 | 86.05 | 20.82 | 70.31 | 5.25 |
| ROS–Fe3O4 | 22.92 | 77.71 | 19.80 | 66.88 | 5.05 |
| MAT–Fe3O4 | 18.03 | 61.98 | 14.78 | 49.94 | 4.63 |
| JUN–Fe3O4 | 16.83 | 56.88 | 11.73 | 39.61 | 3.69 |
 | ||
| Fig. 14 Adsorption yields of (a) MO and (b) EB dyes on different magnetite surfaces. Error bars represent the standard deviation of three replicates. | ||
In order to study how the plant extract's acidity impacted preferential attachment of dyes' chromophore and auxochrome groups on synthesized magnetite surfaces, the free chromophore and auxochrome groups that were not attached to magnetite surfaces have been deeply analyzed in all dyes' residual solutions using FTIR spectroscopy, so as to perceive preferential attachment of chromophore and auxochrome groups on each surface and hence determine Brønsted and Lewis acid site densities. Based on this analysis, it was possible to infer Brønsted and Lewis acid site densities on each magnetite surface. For this purpose, after the accomplishment of the adsorption in all experiments, the solid and liquid fractions were separated using a centrifuge. In the next sections, the analysis of residual dye chemistry changes of MO and EB will be studied in detail by comparison between FTIR spectra of MO and EB reference solution chemistry, and the chemistry of their residual solutions.
In the rest of this paper, MO residual solutions will be denoted as MO/ARM–Fe3O4, MO/ROS–Fe3O4, MO/MAT–Fe3O4, and MO/JUN–Fe3O4. Meanwhile, EB residual solutions will be denoted as EB/ARM–Fe3O4, EB/ROS–Fe3O4, EB/MAT–Fe3O4, and EB/JUN–Fe3O4.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C at 2300–2100 cm−1, N
C at 2300–2100 cm−1, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N at 2100.95 cm−1,61 aromatic C
N at 2100.95 cm−1,61 aromatic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C ring stretching at 1655.87 cm−162 and at 1522.60 cm−1,63 N
C ring stretching at 1655.87 cm−162 and at 1522.60 cm−1,63 N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N at 1569.87 cm−1 and at 1416.02 cm−1,62,64 C–N at 1355.01 cm−1 and 1160.08 cm−1,62,64 C
N at 1569.87 cm−1 and at 1416.02 cm−1,62,64 C–N at 1355.01 cm−1 and 1160.08 cm−1,62,64 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N at 1304.74 cm−1,64 S
N at 1304.74 cm−1,64 S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 1112.02 cm−1,63 and C–H bending vibrations of the aromatic ring at 1047.03 cm−164 and at 1000–550 cm−1.65
O at 1112.02 cm−1,63 and C–H bending vibrations of the aromatic ring at 1047.03 cm−164 and at 1000–550 cm−1.65
 | ||
| Fig. 15 FTIR spectra of (A) the MO reference solution, (B) MO/JUN–Fe3O4, (C) MO/MAT–Fe3O4, (D) MO/ROS–Fe3O4, and (E) MO/ARM–Fe3O4 residual solutions. | ||
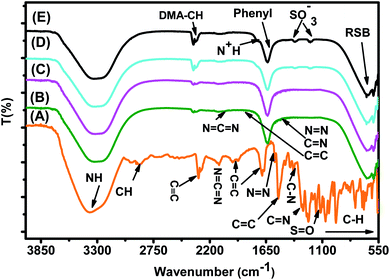
In Fig. 15, spectra (B)–(E) present the FTIR spectra of MO/JUN–Fe3O4, MO/MAT–Fe3O4, MO/ROS–Fe3O4, and MO/ARM–Fe3O4 residual solutions, respectively. The disappearance of certain peaks and the appearance of new ones indicate that the MO/plant–magnetite residual solution chemistry was changed as a result of MO adsorption on magnetite surfaces. The newly appeared peaks correspond to SO−3, 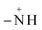 , asymmetric CH, phenyl, and the ring skeleton of benzene groups (RSB). More details about the identification of these peaks in MO/plant–magnetite residual solutions will be given in the next paragraphs, for the purpose of investigating the preferential attachment of chromophore and auxochrome groups on all four magnetite surfaces.
, asymmetric CH, phenyl, and the ring skeleton of benzene groups (RSB). More details about the identification of these peaks in MO/plant–magnetite residual solutions will be given in the next paragraphs, for the purpose of investigating the preferential attachment of chromophore and auxochrome groups on all four magnetite surfaces.
The decomposition of the dye is significantly accelerated by the presence of acidic centers at the surface.66
3.6.1.1 Analysis of preferential attachment of chromophore groups in the adsorption of MO. New peaks of the NH bond of phenyldiazonium groups shifted from 3378.48 cm−1 to around 3308 cm−1 in all four residual solutions (Fig. 15), with however different peak areas. Furthermore, all spectra in Fig. 15 show that new peaks, with however different areas, appear at around 1633 cm−1. These peaks correspond to the C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of not attached phenyl groups.67 Additionally, new peaks appear, with different areas, at around 646 cm−1, which correspond to the CH of the ring skeleton of benzene.21 The peaks of these groups in the FTIR spectrum of MO/ARM–Fe3O4 are the narrowest ones, followed by those of MO/ROS–Fe3O4, then those of MO/MAT–Fe3O4, and finally, the broadest one is in the FTIR spectrum of MO/JUN–Fe3O4. This indicates that phenyldiazonium, phenyl, and benzene groups were more attached on ARM–Fe3O4, next on ROS–Fe3O4, then on MAT–Fe3O4, and finally, on JUN–Fe3O4.
C bond of not attached phenyl groups.67 Additionally, new peaks appear, with different areas, at around 646 cm−1, which correspond to the CH of the ring skeleton of benzene.21 The peaks of these groups in the FTIR spectrum of MO/ARM–Fe3O4 are the narrowest ones, followed by those of MO/ROS–Fe3O4, then those of MO/MAT–Fe3O4, and finally, the broadest one is in the FTIR spectrum of MO/JUN–Fe3O4. This indicates that phenyldiazonium, phenyl, and benzene groups were more attached on ARM–Fe3O4, next on ROS–Fe3O4, then on MAT–Fe3O4, and finally, on JUN–Fe3O4.
Minor peaks corresponding to N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N groups, linked to the benzene ring, appear in the FTIR spectra of MO/MAT–Fe3O4 and MO/JUN–Fe3O4. Those peaks appearing in the FTIR spectrum of MO/JUN–Fe3O4 are slightly more intense than in that of MO/MAT–Fe3O4, while they do not appear in the FTIR spectra of MO/ROS–Fe3O4 and MO/ARM–Fe3O4 (Fig. 15). The lack of these groups in MO/ROS–Fe3O4 and MO/ARM–Fe3O4 indicates their complete attachment on ROS–Fe3O4 and ARM–Fe3O4 surfaces. However, these groups were almost completely attached on MAT–Fe3O4 and they were less attached on the JUN–Fe3O4 surface.
N groups, linked to the benzene ring, appear in the FTIR spectra of MO/MAT–Fe3O4 and MO/JUN–Fe3O4. Those peaks appearing in the FTIR spectrum of MO/JUN–Fe3O4 are slightly more intense than in that of MO/MAT–Fe3O4, while they do not appear in the FTIR spectra of MO/ROS–Fe3O4 and MO/ARM–Fe3O4 (Fig. 15). The lack of these groups in MO/ROS–Fe3O4 and MO/ARM–Fe3O4 indicates their complete attachment on ROS–Fe3O4 and ARM–Fe3O4 surfaces. However, these groups were almost completely attached on MAT–Fe3O4 and they were less attached on the JUN–Fe3O4 surface.
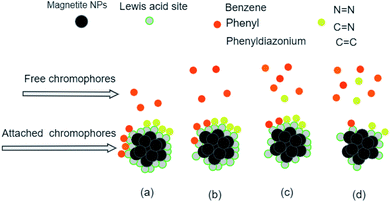
The analysis of preferential attachment of chromophore groups shows, as summarized in Fig. 16, that:
• On JUN–Fe3O4, all MO chromophore groups were less attached compared to on the three other magnetite NPs.
• On MAT–Fe3O4, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N groups were almost completely attached while other groups were more attached compared to on JUN–Fe3O4 and less attached compared to on ARM–Fe3O4 and ROS–Fe3O4.
N groups were almost completely attached while other groups were more attached compared to on JUN–Fe3O4 and less attached compared to on ARM–Fe3O4 and ROS–Fe3O4.
• On ROS–Fe3O4, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N were completely attached, while other groups were less attached than on ARM–Fe3O4 and more attached than on MAT–Fe3O4 and JUN–Fe3O4.
N were completely attached, while other groups were less attached than on ARM–Fe3O4 and more attached than on MAT–Fe3O4 and JUN–Fe3O4.
• On ARM–Fe3O4, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N were completely attached, whereas phenyldiazonium, phenyl, and benzene groups were more attached on ARM–Fe3O4 than on the other magnetite NPs.
N were completely attached, whereas phenyldiazonium, phenyl, and benzene groups were more attached on ARM–Fe3O4 than on the other magnetite NPs.
As it is known that chromophore groups prefer to attach to Lewis acid sites, it is possible to infer that the density of Lewis acid sites of ARM–Fe3O4 is the highest one, followed by that of ROS–Fe3O4, then that of MAT–Fe3O4, and finally, that of JUN–Fe3O4.
The functional group attachment analysis results are consistent with MO adsorption yields, being the highest on ARM–Fe3O4 (70.31%), then on ROS–Fe3O4 (66.98%), next on MAT–Fe3O4 (49.94%), and finally on JUN–Fe3O4 (39.61%). This is due to the fact that most of the MO functional groups are chromophores.
3.6.1.2 Analysis of preferential attachment of auxochrome groups in the adsorption of MO. As illustrated in Fig. 15, FTIR spectra of MO/ARM–Fe3O4 and MO/ROS–Fe3O4 show new peaks at 1367.14 and 1202.44 cm−1, and at 1365.24 and 1203.61 cm−1, respectively. These peaks correspond to SO−3 sulfonic acid groups.62 It is remarked that these peaks are slightly more intense in the FTIR spectrum of MO/ARM–Fe3O4 than in that of MO/ROS–Fe3O4. However, these peaks do not appear in the spectra of MO/MAT–Fe3O4 and MO/JUN–Fe3O4. This indicates that SO−3 groups were completely attached on MAT–Fe3O4 and JUN–Fe3O4 surfaces, whereas they were more attached on ROS–Fe3O4 compared to the ARM–Fe3O4 surface.
Furthermore, FTIR spectra of all four residual solutions (Fig. 15) show that new peaks of asymmetric vibration of CH of CH3 in ionized dimethylamine (DMA) 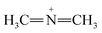 groups appear at around 2342 cm−1,68 and their N
groups appear at around 2342 cm−1,68 and their N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and
N and 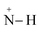 stretching bonds at around 2090 cm−1 and 1739.94 cm−1, respectively, with however remarkably different areas. The broadest peak area appears in the FTIR spectrum of MO/ARM–Fe3O4, next in that of MO/ROS–Fe3O4, then in that of MO/MAT–Fe3O4, and finally, the narrowest ones are in the FTIR spectrum of MO/JUN–Fe3O4. This leads to the conclusion that
stretching bonds at around 2090 cm−1 and 1739.94 cm−1, respectively, with however remarkably different areas. The broadest peak area appears in the FTIR spectrum of MO/ARM–Fe3O4, next in that of MO/ROS–Fe3O4, then in that of MO/MAT–Fe3O4, and finally, the narrowest ones are in the FTIR spectrum of MO/JUN–Fe3O4. This leads to the conclusion that 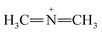 groups were more attached on JUN–Fe3O4, then on MAT–Fe3O4, next on ROS–Fe3O4, and finally, on ARM–Fe3O4.
groups were more attached on JUN–Fe3O4, then on MAT–Fe3O4, next on ROS–Fe3O4, and finally, on ARM–Fe3O4.
The analysis of preferential attachment of auxochrome groups shows that:
• On ARM–Fe3O4, all MO auxochrome groups were less attached compared to on the three other magnetite NPs.
• On ROS–Fe3O4, sulphonic acid and dimethylamine groups were more attached compared to on ARM–Fe3O4.
• On MAT–Fe3O4, sulphonic acid groups were completely attached; however, dimethylamine groups were less attached compared to on JUN–Fe3O4.
• On JUN–Fe3O4, sulphonic acid groups were completely attached, and dimethylamine groups were more attached compared to on MAT–Fe3O4.
This leads to the conclusion that the density of Brønsted acid sites of JUN–Fe3O4 is the highest one, followed by that of MAT–Fe3O4, then that of ROS–Fe3O4, and finally, that of ARM–Fe3O4.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C at 2300–2100 cm−1,61 aromatic C
C at 2300–2100 cm−1,61 aromatic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C ring stretching at 1943.10 cm−1, 1658.11 cm−1,62 and 1519.25 cm−1,63 N
C ring stretching at 1943.10 cm−1, 1658.11 cm−1,62 and 1519.25 cm−1,63 N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond at 1569.75 cm−1 and 1418.76 cm−1,62,64 C–N at 1351.98 cm−1 and 1164.01 cm−1,62,64 C
N bond at 1569.75 cm−1 and 1418.76 cm−1,62,64 C–N at 1351.98 cm−1 and 1164.01 cm−1,62,64 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N at 1306.03 cm−1,64 S
N at 1306.03 cm−1,64 S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 1114.67 cm−1,63,64 and C–H bending vibration of the aromatic ring at 1042.40 cm−164 and 1000–550 cm−1.65
O at 1114.67 cm−1,63,64 and C–H bending vibration of the aromatic ring at 1042.40 cm−164 and 1000–550 cm−1.65
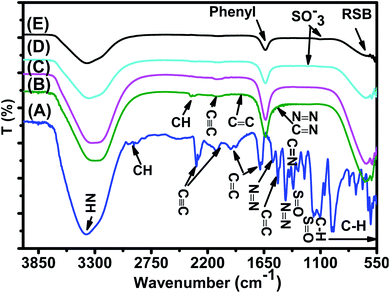 | ||
| Fig. 17 FTIR spectra of (A) the EB reference solution, (B) EB/JUN–Fe3O4, (C) EB/MAT–Fe3O4, (D) EB/ROS–Fe3O4, and (E) EB/ARM–Fe3O4 residual solutions. | ||
FTIR spectra of EB/JUN–Fe3O4, EB/MAT–Fe3O4, EB/ROS–Fe3O4, and EB/ARM–Fe3O4 are presented in Fig. 17. The disappearance of peaks and the appearance of new peaks indicate that the EB/plant–magnetite residual solution chemistry was changed due to EB adsorption on ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4, and JUN–Fe3O4 surfaces. The newly appeared peaks correspond to not attached (residual) SO−3, phenol, aniline, and phenyl groups, and the ring skeleton of benzene groups. More details about the identification of these peaks in EB/plant–magnetite residual solutions will be given in the next paragraphs, for the purpose of investigating the preferential attachment of the EB chromophore and auxochrome groups on all four magnetite surfaces.
3.6.2.1 Analysis of preferential attachment of chromophore groups in EB adsorption. The spectra of all four EB/plant–magnetite residual solutions (Fig. 17) show that the NH bond peak of not attached phenyldiazonium groups shifted from 3387.56 in the EB aqueous reference solution to around 3302 cm−1, with however different peak bond areas. Additionally, new peaks, with different areas, appear at around 1634 cm−1 which correspond to the vibration of C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of phenyl groups.67 Furthermore, the peaks of the ring skeleton of benzene groups appear, with different areas, in all four FTIR spectra at around 642 cm−1.21 It is worth noting that peak areas of NH of phenyldiazonium, C
C of phenyl groups.67 Furthermore, the peaks of the ring skeleton of benzene groups appear, with different areas, in all four FTIR spectra at around 642 cm−1.21 It is worth noting that peak areas of NH of phenyldiazonium, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C of phenyl, and CH of benzene groups vary in the same manner, where the peak area in the FTIR spectrum of EB/ARM–Fe3O4 is the narrowest one, followed by that of EB/ROS–Fe3O4, then that of EB/MAT–Fe3O4, and finally, the broadest one is that of EB/JUN–Fe3O4. This indicates that phenyldiazonium, phenyl, and benzene groups were more attached on ARM–Fe3O4, next on ROS–Fe3O4, then on MAT–Fe3O4, and finally, on the JUN–Fe3O4 surface.
C of phenyl, and CH of benzene groups vary in the same manner, where the peak area in the FTIR spectrum of EB/ARM–Fe3O4 is the narrowest one, followed by that of EB/ROS–Fe3O4, then that of EB/MAT–Fe3O4, and finally, the broadest one is that of EB/JUN–Fe3O4. This indicates that phenyldiazonium, phenyl, and benzene groups were more attached on ARM–Fe3O4, next on ROS–Fe3O4, then on MAT–Fe3O4, and finally, on the JUN–Fe3O4 surface.
Fig. 17 shows that the peak of the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond appears with different peak areas in the FTIR spectra of EB/MAT–Fe3O4 and EB/JUN–Fe3O4 (in the FTIR spectrum of EB/JUN–Fe3O4 it is broader than that of EB/MAT–Fe3O4 and attached on MAT–Fe3O4 more than in JUN–Fe3O4). In contrast, no peak corresponding to the C
C bond appears with different peak areas in the FTIR spectra of EB/MAT–Fe3O4 and EB/JUN–Fe3O4 (in the FTIR spectrum of EB/JUN–Fe3O4 it is broader than that of EB/MAT–Fe3O4 and attached on MAT–Fe3O4 more than in JUN–Fe3O4). In contrast, no peak corresponding to the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond appears in the FTIR spectra of EB/ROS–Fe3O4 and EB/ARM–Fe3O4 which confirms that C
C bond appears in the FTIR spectra of EB/ROS–Fe3O4 and EB/ARM–Fe3O4 which confirms that C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bonds were completely attached on ROS–Fe3O4 and ARM–Fe3O4 surfaces, and almost completely attached on MAT–Fe3O4; however, these groups were less attached on the JUN–Fe3O4 surface.
C bonds were completely attached on ROS–Fe3O4 and ARM–Fe3O4 surfaces, and almost completely attached on MAT–Fe3O4; however, these groups were less attached on the JUN–Fe3O4 surface.
Furthermore, the spectrum of EB/JUN–Fe3O4 shows minor peaks of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (linked to the benzene ring) groups, whereas no peak corresponding to them appear in other FTIR spectra. This reveals that these groups were completely attached on MAT–Fe3O4, ROS–Fe3O4, and ARM–Fe3O4; however, these groups were less attached on the JUN–Fe3O4 surface.
N (linked to the benzene ring) groups, whereas no peak corresponding to them appear in other FTIR spectra. This reveals that these groups were completely attached on MAT–Fe3O4, ROS–Fe3O4, and ARM–Fe3O4; however, these groups were less attached on the JUN–Fe3O4 surface.
It is also remarked that new peaks of the CH bond of CH3 of toluene groups appear at around 2343.82 cm−168 in the FTIR spectrum of EB/JUN–Fe3O4 and a minor peak of toluene groups appears in the FTIR spectrum of EB/MAT–Fe3O4. Meanwhile, no peak corresponding to toluene groups appears in the FTIR spectra of EB/ARM–Fe3O4 and EB/ROS–Fe3O4. This reveals that toluene groups were completely attached on ROS–Fe3O4 and ARM–Fe3O4, and almost completely attached on MAT–Fe3O4; however, these groups were less attached on the JUN–Fe3O4 surface.
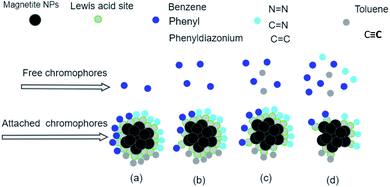
The analysis of preferential attachment of chromophore groups on magnetite surfaces shows, as summarized in Fig. 18, that:
• On JUN–Fe3O4, all EB chromophore groups were less attached compared to on the three other magnetite NPs.
• On MAT–Fe3O4, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, and C
C, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N were completely attached, whereas C
N were completely attached, whereas C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C and toluene groups were almost completely attached while other groups were more attached compared to on JUN–Fe3O4 and less attached compared to on ARM–Fe3O4 and ROS–Fe3O4.
C and toluene groups were almost completely attached while other groups were more attached compared to on JUN–Fe3O4 and less attached compared to on ARM–Fe3O4 and ROS–Fe3O4.
• On ROS–Fe3O4, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, toluene, and C
N, toluene, and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C were completely attached, while other groups were less attached than on ARM–Fe3O4 and more attached than on MAT–Fe3O4 and JUN–Fe3O4.
C were completely attached, while other groups were less attached than on ARM–Fe3O4 and more attached than on MAT–Fe3O4 and JUN–Fe3O4.
• On ARM–Fe3O4, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, toluene, and C
N, toluene, and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C were completely attached, while phenyldiazonium, phenyl, and benzene groups were more attached than on other magnetite surfaces.
C were completely attached, while phenyldiazonium, phenyl, and benzene groups were more attached than on other magnetite surfaces.
As it is known that chromophore groups prefer to attach to Lewis acid sites, it is possible to infer that the density of Lewis acid sites of ARM–Fe3O4 is the highest one, followed by that of ROS–Fe3O4, then that of MAT–Fe3O4, and finally that of JUN–Fe3O4.
The functional group attachment analysis results are consistent with EB adsorption yields, being the highest on ARM–Fe3O4 (86.05%), then on ROS–Fe3O4 (77.71%), next on MAT–Fe3O4 (61.98%), and finally on JUN–Fe3O4 (56.88%). This is due to the fact that most of the EB functional groups are chromophores.
3.6.2.2 Analysis of preferential attachment of auxochrome groups in EB adsorption. FTIR spectra of EB/ARM–Fe3O4 and EB/ROS–Fe3O4 show that new peaks corresponding to SO−3,62 to the bending vibration of OH of phenol69 and to the bending vibration of NH of aniline groups70 appear at 1099.04 and 1204.58 cm−1, respectively (Fig. 17). In the FTIR spectrum of EB/ARM–Fe3O4, this peak is slightly more intense than in that of EB/ROS–Fe3O4. Meanwhile, no peaks corresponding to these groups appear in the FTIR spectra of EB/MAT–Fe3O4 and EB/JUN–Fe3O4 (Fig. 17).
The analysis of preferential attachment of auxochrome groups shows that:
• On ARM–Fe3O4, all EB auxochrome groups were less attached compared to on the three other magnetite NPs.
• On ROS–Fe3O4, sulphonic acid, phenol, and aniline groups were almost completely attached.
• On MAT–Fe3O4, all auxochrome groups were completely attached.
• On JUN–Fe3O4, all auxochrome groups were completely attached.
This leads to the conclusion that the densities of Brønsted acid sites of JUN–Fe3O4 and MAT–Fe3O4 surfaces are higher than those of ARM–Fe3O4 and ROS–Fe3O4 surfaces.
The analysis of the preferential attachment of chromophore and auxochrome groups in EB and MO adsorption leads to the conclusion that the Lewis acid site density is the highest on ARM–Fe3O4, next on ROS–Fe3O4, then on MAT–Fe3O4, and finally on the JUN–Fe3O4 surface. Moreover, EB and MO adsorption yields and capacities were highest on ARM–Fe3O4 (86.05%, 25.39 mg g−1 and 70.31%, 20.82 mg g−1, respectively), next on ROS–Fe3O4 (77.71%, 22.92 mg g−1 and 66.88%, 19.80 mg g−1), then on MAT–Fe3O4 (61.98%, 18.03 mg g−1 and 49.94%, 14.78 mg g−1), and finally on JUN–Fe3O4 (56.88%, 16.83 mg g−1 and 39.61%, 11.73 mg g−1), respectively. Accordingly, the adsorption yields and Lewis acid site densities varied in the same manner. Seeing that plant extracts used in the synthesis of ARM–Fe3O4, ROS–Fe3O4, MAT–Fe3O4 and –Fe3O4 NPs have respectively pH 5.25, 5.05, 4.63, and 3.69, one can conclude that plant extract pH has a clear effect on the preferential attachment of dye chromophore and auxochrome groups, magnetite nanoparticle acid sites, and adsorption yields. Indeed, the decrease of the mediating plant extract's acidity leads to the increase of Lewis acid site densities and the decrease of Brønsted acid site densities on magnetite NPs and hence an increase in the attachment of chromophore groups and a decrease in the attachment of auxochrome groups of dyes. As most of the MO and EB functional groups are chromophores, the decrease of the mediating plant extract's acidity also leads to an increase in adsorption yields. The remarked difference in adsorption yields of EB and MO on all four magnetite NPs is due to the fact that the ratio of chromophore/auxochrome groups in EB is remarkably greater than that in MO.
Thus, the plant extract's acidity could provide a preconceived idea about the densities of Brønsted and Lewis acid sites of magnetite NPs to be greenly synthesized and therefore about azo dye adsorption yields. Dye adsorption yield can be predicted according to the content of chromophore and auxochrome groups in the azo dye structure.
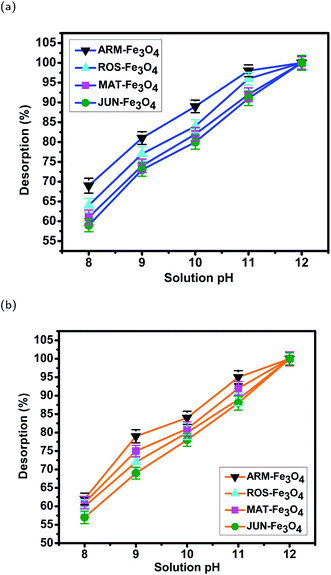
3.7 Desorption efficiency of dyes from magnetite surfaces and their stability after 3 cycles of reuse
| Sample | pH | EB des. (%) | STD | MO des. (%) | STD |
|---|---|---|---|---|---|
| JUN–Fe3O4 | 8 | 59.35 | 1.65 | 57.91 | 1.71 |
| MAT–Fe3O4 | 8 | 61.35 | 1.83 | 60.38 | 1.69 |
| ROS–Fe3O4 | 8 | 64.62 | 1.75 | 61.72 | 1.83 |
| ARM–Fe3O4 | 8 | 69.05 | 1.88 | 62.05 | 1.59 |
| JUN–Fe3O4 | 9 | 73.25 | 1.67 | 69.45 | 1.62 |
| MAT–Fe3O4 | 9 | 74.15 | 1.78 | 72.74 | 1.57 |
| ROS–Fe3O4 | 9 | 77.42 | 1.70 | 75.42 | 1.61 |
| ARM–Fe3O4 | 9 | 81.15 | 1.62 | 79.05 | 1.85 |
| JUN–Fe3O4 | 10 | 80.73 | 1.78 | 78.88 | 1.96 |
| MAT–Fe3O4 | 10 | 81.25 | 1.69 | 80.82 | 1.55 |
| ROS–Fe3O4 | 10 | 84.44 | 1.65 | 81.84 | 1.78 |
| ARM–Fe3O4 | 10 | 89.09 | 1.57 | 84.79 | 1.77 |
| JUN–Fe3O4 | 11 | 91.05 | 1.81 | 85.75 | 1.79 |
| MAT–Fe3O4 | 11 | 92.19 | 1.68 | 88.11 | 1.74 |
| ROS–Fe3O4 | 11 | 95.77 | 1.59 | 89.01 | 1.85 |
| ARM–Fe3O4 | 11 | 97.10 | 1.49 | 93.90 | 1.87 |
| JUN–Fe3O4 | 12 | 100.0 | 1.89 | 100.0 | 1.71 |
| MAT–Fe3O4 | 12 | 100.0 | 1.59 | 100.0 | 1.61 |
| ROS–Fe3O4 | 12 | 100.0 | 1.55 | 100.0 | 1.88 |
| ARM–Fe3O4 | 12 | 100.0 | 1.54 | 100.0 | 1.63 |
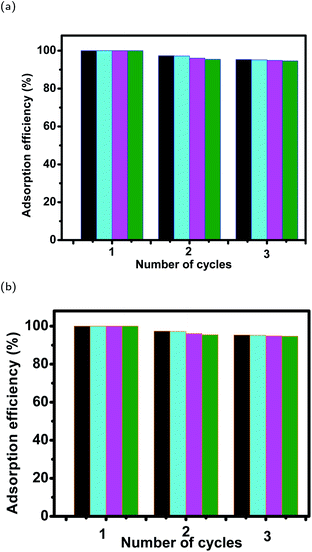 | ||
| Fig. 19 Stability of magnetite samples in (a) EB and (b) MO adsorption experiments after 3 cycles of reuse. | ||
4 Conclusion
The adsorption of methyl orange (MO) and Evans blue (EB) azo dyes on four greenly synthesized magnetite NPs has been studied. The pHs of plant extracts used for the green synthesis were 5.25, 5.05, 4.63, and 3.69. The aim of the study was the investigation of the plant extract's acidity effect on the magnetite surface reactivity through the analysis of the preferential attachment of the dyes' chromophore and auxochrome groups on magnetite nanoparticles, and adsorption yields, and therefore determination of the plant extract pH effect on acid site types and densities. To do so, the free chromophore and auxochrome groups that are not attached to magnetite surfaces have been deeply analyzed in all dye residual solutions using FTIR spectroscopy, so as to perceive preferential attachment of dye chromophore and auxochrome groups on the four magnetite surfaces.Obtained results show that the mediating plant extract's acidity has a clear effect on preferential attachment of dye chromophore and auxochrome groups, magnetite nanoparticle acid sites, and adsorption yields. Indeed, the decrease of plant extract acidity leads to the increase of Lewis acid site densities and the decrease of Brønsted acid site densities on magnetite NPs and hence an increase in the attachment of chromophore dye groups and a decrease in the attachment of auxochrome dye groups. As most of the MO and EB functional groups are chromophores, the decrease of the mediating plant extract's acidity also leads to an increase in adsorption yields.
The linear and non-linear pseudo-first-order and pseudo-second-order kinetics of the adsorption as well as the intra-particle diffusion mechanism have also been analyzed. Obtained results indicated that the adsorption kinetic followed a linear pseudo-first-order kinetic model. Meanwhile, film diffusion was found to be the step that controlled the adsorption mechanism of MO and EB adsorption processes. The thermodynamic studies of EB and MO adsorption processes have been analyzed in the temperature range of 303.15–318.15 K. They reveal the physical and endothermic nature of the adsorption in all cases.
Author contributions
Kaouthar Ahmouda: writing – original draft, resources, investigation, visualization, methodology, and revision. Moussa Boudiaf: visualization and revision. Boubaker Benhaoua: visualization.Conflicts of interest
There are no conflicts to declare.Notes and references
- M. Tsuboy, J. Angeli, M. Mantovani, S. Knasmüller, G. Umbuzeiro and L. Ribeiro, Toxicol. In Vitro, 2007, 21, 1650–1655 CrossRef CAS PubMed.
- K. Golka, S. Kopps and Z. W. Myslak, Toxicol. Lett., 2004, 151, 203–210 CrossRef CAS PubMed.
- H. Zollinger, Color Chemistry, VCH. Inc., New York, 1987, pp. 25–41 Search PubMed.
- R. Christie, Colour Chemistry, Royal Society of Chemistry, 2014 Search PubMed.
- A. Gürses, M. Açıkyıldız, K. Güneş and M. S. Gürses, Dyes and Pigments, Springer, 2016, pp. 13–29 Search PubMed.
- S. Giri, N. Das and G. Pradhan, Colloids Surf., A, 2011, 389, 43–49 CrossRef CAS.
- B. Saha, S. Das, J. Saikia and G. Das, J. Phys. Chem. C, 2011, 115, 8024–8033 CrossRef CAS.
- S. Pirillo, M. L. Ferreira and E. H. Rueda, Ind. Eng. Chem. Res., 2007, 46, 8255–8263 CrossRef CAS.
- S. Pirillo, L. Cornaglia, M. L. Ferreira and E. H. Rueda, Spectrochim. Acta, Part A, 2008, 71, 636–643 CrossRef PubMed.
- M. Amin, A. Alazba and U. Manzoor, Adv. Mater. Sci. Eng., 2014, 2014, 825910 Search PubMed.
- M. M. Khin, A. S. Nair, V. J. Babu, R. Murugan and S. Ramakrishna, Energy Environ. Sci., 2012, 5, 8075–8109 RSC.
- A. M. Elgarahy, K. Z. Elwakeel, A. Akhdhar and M. F. Hamza, Nanotechnol. Environ. Eng., 2021, 6, 1–24 CrossRef.
- A. A. Yaqoob, T. Parveen, K. Umar and M. N. Mohamad Ibrahim, Water, 2020, 12, 495 CrossRef CAS.
- S. Pirillo, M. L. Ferreira and E. H. Rueda, J. Hazard. Mater., 2009, 168, 168–178 CrossRef CAS PubMed.
- C. Xiao, H. Li, Y. Zhao, X. Zhang and X. Wang, J. Environ. Manage., 2020, 275, 111262 CrossRef CAS PubMed.
- L. Huang, X. Weng, Z. Chen, M. Megharaj and R. Naidu, Spectrochim. Acta, Part A, 2014, 130, 295–301 CrossRef CAS PubMed.
- S. Khurshid, Z. Gul, J. Khatoon, M. R. Shah, I. Hamid, I. A. T. Khan and F. Aslam, et al. , RSC Adv., 2020, 10, 1021–1041 RSC.
- H.-P. Li, Z. Dou, S.-Q. Chen, M. Hu, S. Li, H.-M. Sun, Y. Jiang and Q.-G. Zhai, Inorg. Chem., 2019, 58, 11220–11230 CrossRef CAS PubMed.
- Z. Zhang and J. Kong, J. Hazard. Mater., 2011, 193, 325–329 CrossRef CAS PubMed.
- H. Hongping, Y. Zhong, X. Liang, T. Wei, Z. Jianxi and C. Y. Wang, Sci. Rep., 2015, 5, 1–10 Search PubMed.
- H. Valdés, V. A. Solar, E. H. Cabrera, A. F. Veloso and C. A. Zaror, Chem. Eng. J., 2014, 244, 117–127 CrossRef.
- N. M. Mahmoodi and F. Najafi, Microporous Mesoporous Mater., 2012, 156, 153–160 CrossRef CAS.
- N. M. Mahmoodi, S. Khorramfar and F. Najafi, Desalination, 2011, 279, 61–68 CrossRef CAS.
- T. Madrakian, A. Afkhami, H. Mahmood-Kashani and M. Ahmadi, J. Iran. Chem. Soc., 2013, 10, 481–489 CrossRef CAS.
- K. Chamchoy, T. Inprasit, C. Vanichvattanadecha, A. Thiangtrong, P. Anukunwithaya and P. Pisitsak, J. Polym. Environ., 2021, 29, 484–491 CrossRef CAS.
- N. Alizadeh, S. Shariati and N. Besharati, Int. J. Environ. Res., 2017, 11, 197–206 CrossRef CAS.
- A. Gogoi, M. Navgire, K. C. Sarma and P. Gogoi, Chem. Eng. J., 2017, 311, 153–162 CrossRef CAS.
- D. T. C. Nguyen, H. H. Dang, D.-V. N. Vo, L. G. Bach, T. D. Nguyen and T. Van Tran, J. Hazard. Mater., 2021, 404, 124146 CrossRef CAS PubMed.
- T. Islam, C. Peng, I. Ali and I. A. Abbasi, Indian J. Geo-Mar. Sci., 2018, 47, 598–603 Search PubMed.
- K. Ahmouda and B. Benhaoua, RSC Adv., 2022, 12, 14593–14609 RSC.
- G. Crini, Bioresour. Technol., 2006, 97, 1061–1085 CrossRef CAS PubMed.
- M. Wawrzkiewicz, M. Wiśniewska, V. M. Gun’ko and V. I. Zarko, Powder Technol., 2015, 278, 306–315 CrossRef CAS.
- D. Chen, L. Zhang, C. Yi and J. Dumesic, J. Catal., 1994, 146, 257–267 CrossRef CAS.
- W. Song, Y. Liu, E. Baráth, C. Zhao and J. A. Lercher, Green Chem., 2015, 17, 1204–1218 RSC.
- I. I. Ivanova, E. B. Pomakhina, A. I. Rebrov, M. Hunger, Y. G. Kolyagin and J. Weitkamp, J. Catal., 2001, 203, 375–381 CrossRef CAS.
- Y. Mao, S. Pankasem and J. K. Thomas, Langmuir, 1993, 9, 1504–1512 CrossRef CAS.
- H. Pan, Z. Chen, M. Ma, T. Guo, X. Ling, Y. Zheng, C. He and J. Chen, J. Colloid Interface Sci., 2022, 607, 1189–1200 CrossRef CAS PubMed.
- K. Ahmouda, B. Benhaoua, S. E. Laouini and A. Labbi, Sustainable Chem. Pharm., 2022, 25, 100563 CrossRef CAS.
- S. K. Lagergren, Sven. Vetenskapsakad. Handingarl., 1898, 24, 1–39 Search PubMed.
- Y.-S. Ho and G. McKay, Process Biochem., 1999, 34, 451–465 CrossRef CAS.
- H. Yuh-Shan, Scientometrics, 2004, 59, 171–177 CrossRef.
- Y.-S. Ho, J. Hazard. Mater., 2006, 136, 681–689 CrossRef CAS PubMed.
- J. Lin and L. Wang, Front. Environ. Sci. Eng. China, 2009, 3, 320–324 CrossRef CAS.
- S. M. Ponder, J. G. Darab and T. E. Mallouk, Environ. Sci. Technol., 2000, 34, 2564–2569 CrossRef CAS.
- G. Boyd, A. Adamson and L. Myers Jr, J. Am. Chem. Soc., 1947, 69, 2836–2848 CrossRef CAS PubMed.
- C. Valderrama, X. Gamisans, X. De las Heras, A. Farran and J. Cortina, J. Hazard. Mater., 2008, 157, 386–396 CrossRef CAS PubMed.
- L. Yu and Y.-M. Luo, J. Environ. Chem. Eng., 2014, 2, 220–229 CrossRef CAS.
- U. Holzwarth and N. Gibson, Nat. Nanotechnol., 2011, 6, 534 CrossRef CAS PubMed.
- B. Kumar, K. Smita, L. Cumbal, A. Debut, S. Galeas and V. H. Guerrero, Mater. Chem. Phys., 2016, 179, 310–315 CrossRef CAS.
- P. K. Dhar, P. Saha, M. K. Hasan, M. K. Amin and M. R. Haque, Cleaner Engineering and Technology, 2021, 3, 100117 CrossRef.
- R. A. Smith, Semiconductors, 1978 Search PubMed.
- H. El Ghandoor, H. Zidan, M. M. Khalil and M. Ismail, Int. J. Electrochem. Sci., 2012, 7, 5734–5745 CAS.
- W. Strehlow and E. L. Cook, J. Phys. Chem. Ref. Data, 1973, 2, 163–200 CrossRef CAS.
- C.-H. Weng and Y.-F. Pan, Colloids Surf., A, 2006, 274, 154–162 CrossRef CAS.
- D. L. Michelsen, J. A. Gideon, G. P. Griffith, J. E. Pace and H. L. Kutat, 1975.
- M. Alkan, Ö. Demirbaş and M. Doğan, Microporous Mesoporous Mater., 2007, 101, 388–396 CrossRef CAS.
- Z. Aksu, A. İ. Tatlı and Ö. Tunç, Chem. Eng. J., 2008, 142, 23–39 CrossRef CAS.
- M. Doğan, H. Abak and M. Alkan, J. Hazard. Mater., 2009, 164, 172–181 CrossRef PubMed.
- J. A. Davis and J. O. Leckie, J. Colloid Interface Sci., 1980, 74, 32–43 CrossRef CAS.
- T. P. Kasih, J. Ecol. Eng., 2017, 18, 1–6 CrossRef.
- S. A. Sandford, F. Salama, L. J. Allamandola, L. M. Trafton, D. F. Lester and T. F. Ramseyer, Icarus, 1991, 91, 125–144 CrossRef CAS PubMed.
- A. B. D. Nandiyanto, R. Oktiani and R. Ragadhita, Indones. J. Sci. Technol., 2019, 4, 97–118 CrossRef.
- N. Bahrudin, M. Nawi, A. H. Jawad and S. Sabar, J. Polym. Environ., 2020, 28, 1901–1913 CrossRef CAS.
- T. Shen, C. Jiang, C. Wang, J. Sun, X. Wang and X. Li, RSC Adv., 2015, 5, 58704–58712 RSC.
- A. Katritzky, Q. Rev., Chem. Soc., 1959, 13, 353–373 RSC.
- J. E. Moser, D. Noukakis, U. Bach, Y. Tachibana, D. R. Klug, J. R. Durrant, R. Humphry-Baker and M. Grätzel, J. Phys. Chem. B, 1998, 102, 3649–3650 CrossRef CAS.
- A. Jantasee, K. Thumanu, N. Muangsan, W. Leeanansaksiri and D. Maensiri, Food Anal. Methods, 2014, 7, 389–399 CrossRef.
- J. Suresh, R. G. R. Gandhi, S. Gowri, S. Selvam and M. Sundrarajan, E-J. Chem., 2012, 9, 1336–1341 CrossRef.
- P. E. Fanning and M. A. Vannice, Carbon, 1993, 31, 721–730 CrossRef CAS.
- S. Kai-yi, T. Xiu-xiang, Y. Su-dong, D. Ying and L. Zuo-peng, Procedia Earth Planet. Sci., 2009, 1, 627–633 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |