Open Access Article
Open Access ArticleGraphene BioFET sensors for SARS-CoV-2 detection: a multiscale simulation approach†
A.
Toral-Lopez
 *a,
D. B.
Kokh
*a,
D. B.
Kokh
 b,
E. G.
Marin
b,
E. G.
Marin
 a,
R. C.
Wade
a,
R. C.
Wade
 bcd and
A.
Godoy
bcd and
A.
Godoy
 a
a
aDepartamento de Electrónica y Tecnología de Computadores, Facultad de Ciencias, Universidad de Granada, Spain. E-mail: atoral@ugr.es; agodoy@ugr.es
bMolecular and Cellular Modeling Group, Heidelberg Institute for Theoretical Studies, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany
cCenter for Molecular Biology (ZMBH), DKFZ-ZMBH Alliance, Heidelberg University, Im Neuenheimer Feld 282, 69120 Heidelberg, Germany
dInterdisciplinary Center for Scientific Computing (IWR), Heidelberg University, Im Neuenheimer Feld 205, Heidelberg, Germany
First published on 17th June 2022
Abstract
Biological Field-Effect Transistors (BioFETs) have already demonstrated enormous potential for detecting minute amounts of ions and molecules. The use of two-dimensional (2D) materials has been shown to boost their performance and to enable the design of new applications. This combination deserves special interest in the current pandemic caused by the SARS-CoV-2 virus which demands fast, reliable and cheap detection methods. However, in spite of the experimental advances, there is a lack of a comprehensive and in-depth computational approach to capture the mechanisms underlying the sensor behaviour. Here, we present a multiscale platform that combines detailed atomic models of the molecules with mesoscopic device-level simulations. The fine-level description exploited in this approach accounts for the charge distribution of the receptor, its reconfiguration when the target binds to it, and the consequences in terms of sensitivity on the transduction mechanism. The results encourage the further exploration of improved sensor designs and 2D materials combined with diverse receptors selected to achieve the desired specificity.
I. Introduction
The world health emergency caused by the Severe Acute Respiratory Syndrome Corona Virus-2 (SARS-CoV-2) has originated an urgent necessity to develop early detection tools to limit and mitigate its uncontrolled spread. Current detection methods for SARS-CoV-2 are mainly based on the extraction of biological samples (e.g. nasopharyngeal or oropharyngeal swabs, blood samples, etc.) for their later analysis with techniques like serology or real-time Reverse Transcription Polymerase Chain Reaction (RT-PCR).1,2 Alternative methods are being investigated based on imaging procedures, like Computed Tomography (CT),2,3 X-ray,4 or DNA amplification as LAMP (loop-mediated isothermal amplification method).5,6 However, these techniques require a protocol for sample preparation, hours for obtaining a conclusive outcome or sophisticated facilities. Biosensing devices based on field-effect transistors (BioFETs) represent an advanced technology with potential to overcome all these drawbacks.7BioFETs take advantage of the same operation principle of well-established Metal-Oxide-Semiconductor FETs (MOSFETs) to detect ions or biomolecules immersed in a solution. In a regular MOSFET, the charge in the semiconductor channel is modulated by the bias applied to the metal gate over it, which is electrostatically coupled through an oxide. Thus, the gate tunes the channel conductivity, electrically joining/isolating the two contacts located at its edges, i.e. source and drain, and consequently controlling the current flow between both ends. In a BioFET, instead, the gate metal is substituted by a liquid solution containing the ions or molecules to be detected, while the insulator in direct contact with the electrolyte is functionalized to enhance the sensitivity and selectivity of the sensor. Then, the charged analytes attached onto the surface induce a change in the semiconductor surface potential that is transduced by a variation of the source-to-drain current. Ultimately, any alteration in the charge adhered to this layer could be detected as a modification in the device output current. Although this operation principle dates back to the 70s,8 huge research efforts in the last decade have significantly improved its performance, and this along with a continuous price reduction has facilitated BioFETs' widespread use.
These efforts have recently been boosted by the surge in interest in graphene and two-dimensional materials (2DMs), which has had a profound impact on sensor design, showing enormous potential to boost sensor performance.9 However, in order to leverage the combination of both technologies and in particular their use for a fast, reliable and cheap detection of ions and molecules, numerous challenges still need to be overcome. While from the fabrication and experimental perspective, a wide variety of results are readily available,10–14 there is a noticeable lack of theoretical understanding concerning the mechanisms and principles ruling their performance. There are several approaches based on both ad hoc and TCAD solutions, but these are focused on nanowire BioFETs (NW-BioFETs)15–17 or planar devices relying on bulk semiconductors.18–20 Only a few are meant to explore 2DM-based BioFETs.21–23 In addition, most of them are based on coarse approximations, such as: (i) treating the sensing layer as a uniformly charged layer or discrete box-shaped charged blocks for the biomolecules, or (ii) analytical or simplified models are employed for the electrolyte. The main reason behind this theoretical gap is the lack of a multidisciplinary and multiscale description of the device operation, necessary to achieve a holistic picture able to consistently capture features ranging from molecular interactions at the solid–liquid interface to the extracted characteristics. This is of particular importance to comprehend the subtleties associated to the sensing target, and predict in an accurate way the sensitivity of the BioFET for the specific objective.
In this context, this work presents a novel multiscale scheme that combines a precise modelling of the receptor and target molecules at the sensor surface and a sophisticated description of the semiconductor device and the liquid electrolyte. Our approach pursues the integration of information from detailed computations of protein electrostatic properties at the atomic level into the device level numerical simulations. This approach provides a potentially powerful tool to understand in detail the operation principle and unveil the optimization keys of Graphene based BioFETs (GBioFETs) for the early detection of SARS-CoV-2.
The rest of the paper is organized as follows. First, we introduce the multiscale methodology exploited to simulate the device with special attention to the sensing layer. Next, we focus on the atomistic modelling of the molecules involved in the detection of SARS-CoV-2. Finally, the results obtained for the GBioFET are presented and analysed and the main conclusions are drawn.
II. Methods
The proposed multiscale simulation platform for BioFET treats the two regions that encompass the device, i.e. the graphene and the electrolyte, making use of different descriptions connected through the Poisson equation solved in a two-dimensional cross-section of the structure.In particular, in the channel, the continuity equation is solved in the diffusive regime assuming a common pseudo-Fermi level for electrons and holes due to the short recombination times measured in graphene.24–26 The drift-diffusion scheme provides the most appropriate description according to the dimensions of state-of-the-art experimental 2D BioFETs, where carrier transport properties are dominated by scattering processes. The source-to-drain current IDS can be expressed as:
| IDS = q(nμn + pμp)∇VEF | (1) |
At the electrolyte, we solve the modified Poisson–Boltzmann equation that takes into account the finite size of the ions that are present in the electrolyte region, limiting the maximum ion concentration.28 Using the standard Poisson–Boltzmann equation, on the contrary, can give rise to non-physical values, particularly for large ions. We complete this approach with a sophisticated model for the interactions between the solution and the device surface that encompasses a position-dependent water permittivity εw near the solid–liquid interface and Potentials of Mean Force (PMFs)29,30 as well as the electrolyte complex reactions (see ESI†). The position-dependent εw profile is included in the solution of the Poisson–Boltzmann equation, while the PMF profiles are integrated in the calculation of the concentration of the i-th ion type:
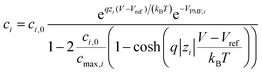 | (2) |
In addition to the ions contained in the solution, the electrolyte–device interface is charged with the receptor molecules attached to the device surface. Each receptor can be in one of two states: idle, i.e. no target molecule is attached to them, or activated, i.e. the target molecule is captured. In both cases the molecule charge is treated taking into consideration its shape and spatial distribution, employing an atomic level description of the molecular structure. This charge is later accurately mapped at the biosensor level. The model of the complex electrolyte combined with small charged receptor molecules has been evaluated against experimental data on the surface potential for a histidine–aspartic acid peptide and Green Fluorescent Protein taken from ref. 32 showing an excellent capability to reproduce them as discussed in the ESI 3.† The integration of the molecules shape, as here described, improves the possibilities to reproduce the experimental selectivity, reducing the equivalence between similarly charged molecules at the device computational level.
In the specific case addressed here, i.e. the detection of SARS-CoV-2, prior to the extraction of the molecule shape and charge distribution in the idle (ρidle) and activated (ρact) states, it is worth recalling the infection mechanism of this virus so to define the receptor-target pair of the biosensor. The structure of this virus is determined by a lipid membrane encasing its genetic load. The most remarkable element in this membrane is a set of spike proteins that surround the whole structure, and give rise to the characteristic appearance of the virus, a circular body enclosed by a halo that looks like a corona. These spike proteins, as indicated in Fig. 1, are composed of two subunits, named S1 and S2, respectively. The former is meant to bind the virus to the cell surface while the latter enables the virus core envelope to join the cell membrane releasing its genetic load.33
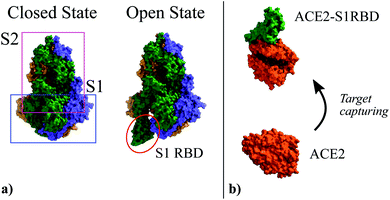 | ||
| Fig. 1 (a) Three-dimensional structure of the Spike glycoprotein head in its closed state (PDBe ID:6vxx34) and open state (PDBe ID:6vyb34). It is composed by two subunits named S1 and S2. In the open state the S1 Receptor Binding Domain (S1RBD) is exposed so that the virus can be attached to the cell surface. (b) Structure of the human Angiotensin Converting Enzyme 2 (ACE2) (PDBe ID:1o86 (ref. 35)) used as attachment point by SARS-CoV-2; and its complex with the S1RBD (PDBe ID:6m0j36). | ||
The main entry point to the cell used by SARS-CoV-2 is the Angiotensin Converting Enzyme 2 (ACE2),37–39 (see Fig. 1). The ACE2 molecule interacts with the S1 Receptor Binding Domain (S1RBD) so that the virus attaches to the cell surface. After this capturing process, the S1 unit is cleaved from the main body of the spike protein leaving the S2 unit exposed, making possible the fusion of the cell and virus membranes.33 According to the aforementioned infection mechanism, here we focus on the ACE2-S1RBD pair, where the ACE2 acts as receptor molecule.
To achieve an accurate description of the electrostatic properties of the ACE2 and ACE2-S1RBD complex, they are modelled in atomic detail. To do so, we employed structures with PDBe ID: 1o86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 and PDBe ID: 6m0j36 for the ACE2 and ACE2-S1RBD complex respectively. Glycans (NAG) were removed from the structures and missing loops were built using MODBASE web site.40 One Zn2+ and one or two (complex and ACE2, respectively) Cl− ions were retained in calculations. The proteins were protonated at pH 7.4 and partial charges at each atom were generated using PDB2PQR server41 (ions were omitted at this step). The total charge of the ACE2 protein and the complex is −12e and −22e, respectively. Zn2+ and Cl− were added back to the structures.
35 and PDBe ID: 6m0j36 for the ACE2 and ACE2-S1RBD complex respectively. Glycans (NAG) were removed from the structures and missing loops were built using MODBASE web site.40 One Zn2+ and one or two (complex and ACE2, respectively) Cl− ions were retained in calculations. The proteins were protonated at pH 7.4 and partial charges at each atom were generated using PDB2PQR server41 (ions were omitted at this step). The total charge of the ACE2 protein and the complex is −12e and −22e, respectively. Zn2+ and Cl− were added back to the structures.
The resulting charge distribution of the unbound (idle state) ACE2 receptor (ρidle) and the bound (activated state) ACE2-S1RBD pair (ρact) were then mapped in a spatial grid of 0.5 nm × 0.5 nm (Fig. 2) and included in the 2D biosensor simulation (see Fig. S3 in ESI†). These charge profiles were replicated along the device in accordance with the state and positions defined for the receptor molecules.
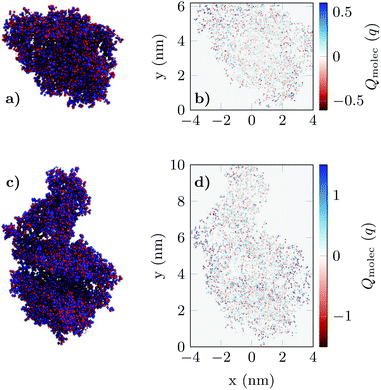 | ||
| Fig. 2 The charge distribution of apo-ACE2 (a) and the ACE2-S1RBD (b) complex viewed from the projection plane. Blue dots indicate positively charged elements while red dots indicate negatively charged elements in the molecule structure. Figures (c) and (d) shows the final result of the projection of the 3D charge distributions (see Fig. S.3 in ESI†) prior to their integration in the simulation of the GBioFET device. | ||
III. Results
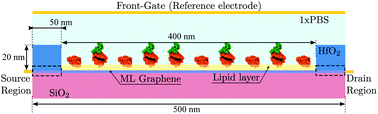
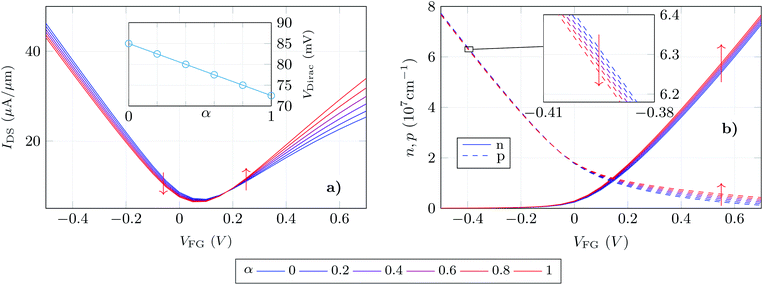
We exploit the previously described approach to study the sensitivity of GBioFETs as sensors for the detection of SARS-CoV-2, capturing the finest details in the interaction between the molecules at the sensing interface and the graphene channel. For this purpose, we have considered a graphene monolayer 500 nm-long on top of a SiO2 substrate. Source and drain regions span 50 nm from the edges of the structure and each of them is covered by a 20 nm thick HfO2 layer. In the 400 nm-long remaining region, a 3 nm thick lipid layer that hosts the receptor molecules is considered. Despite the importance of contact resistance in the context of 2DM-based FETs,42–46 we have consider ohmic contacts focusing on the intrinsic physics of the sensor and how it is impacted by the molecule features. Simulations are carried out with 10 receptors uniformly distributed along the structure. A liquid electrolyte covering the top surface of the sensor is defined by a 1× PBS (Phosphate Buffered Saline) solution. Finally, a reference electrode is immersed on the liquid electrolyte to set a reference voltage. Fig. 3 depicts a schematic of the considered GBioFET.Thus, we test the sensitivity of the GBioFET to the presence of ACE2-S1RBD pairs by determining through self-consistent simulations the transfer response of the device (IDS − VFG) assuming different percentages of activated receptors, α (Fig. 4a).
The device response can be qualitatively split into three regions: (i) the gate bias around the point of minimum conductivity, i.e. the Dirac voltage VDirac, (ii) the p-type branch, corresponding to negative gate biases, i.e. to the left of VDirac, and (iii) the n-type branch, corresponding to positive gate biases, i.e. to the right of VDirac. As can be observed at VDirac, the channel has the lowest conductivity and the GBioFET does not show noticeable changes when the S1RBD molecules are attached to the ACE2 receptors, indicating that this bias region is poorly responsive to detect the presence of the virus. Concerning the p-type branch, a slight modification in the output current is observed as α varies: the transfer response spreads out as the gate bias gets more negative, but within a limited range. The n-type branch reveals itself as the most sensitive operation region: the magnitude of the output current is lower than the p-type branch, but it exhibits a higher sensitivity to changes in α.
More importantly, the transfer characteristic manifests a counter-intuitive behaviour with the activation percentage. Both the ACE2 receptor and the S1RBD are negatively charged. Thus, when the receptors are activated (i.e. the ACE2-S1RBD complex is formed), they contribute with a higher amount of negative charge to the electrolyte than in the idle state (ACE2 receptor only). As a consequence, as α augments one would expect an increase in the output current in the p-branch due to a higher hole concentration induced by the activated receptors and, conversely, a reduction of the output current in the n-branch due to a diminished electron concentration. On the contrary, we observe that IDS decreases (increases) for higher α values in the p-branch (n-branch). A similar behaviour has been also reported in a very recent experimental realization in ref. 7 where the capture of the negatively charged spike protein does not result in a direct increase (decrease) of the p-branch (n-branch) sensor current. In this case the receptor is a spike-protein antigen, positively charged, but the capturing of the negative spike protein should, in principle, reduce the net positive charge at the sensing interface and have the same intuitive consequences above explained.
We can further analyse this behaviour leading our attention to the actual electron and hole densities in the graphene layer for different occupation percentages as a function of VFG (see Fig. 4b). As expected, below VDirac holes are the majority carriers in the channel but their concentration barely changes with α. The inset exhibits a zoom of this p − VFG profiles indicating a slight reduction of the hole concentration as the number of activated receptors increases. On the other hand, above VDirac electrons are dominant, but a non-negligible amount of holes are still present in the n-branch. In addition to this, the amount of electrons in the graphene layer is modulated in a larger extent by α when compared with the holes in the p-branch, so that we can associate both facts with the larger change in IDS observed for the n-type branch. Thus, the electron and hole concentrations, although coherent with the IDS results, still show trends with α that are not intuitive: i.e. the hole (electron) density decreases (increases) as more receptors become activated and therefore more negative charge is present in the electrolyte.
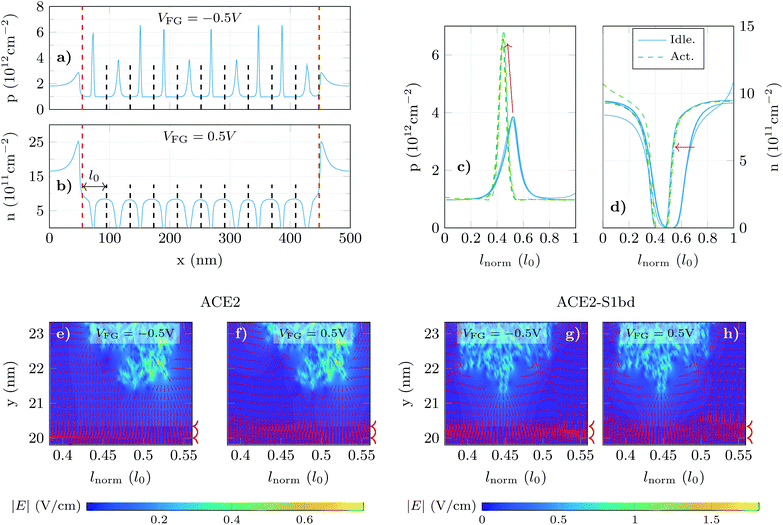
In order to shed light on this issue, we have analysed the longitudinal charge profiles under each receptor with α = 0.6 at two gate biases, one in the p-branch (VFG = −0.5 V) and another in the n-branch (VFG = 0.5 V) (Fig. 5a and b respectively). The charge varies along the channel mimicking locally the changes due to the molecule activation. To analyse in detail these variations, we selected the region under the sensing layer and split it into 10 sub-regions, in correspondence to the 10 receptors, and plot the resulting localized charged profiles, evaluating the impact that a change in the receptor state has on the main carrier distribution (Fig. 5c and d for holes and electrons, respectively). In these plots, dashed (solid) lines correspond to the carrier distribution under activated (idle) receptors. The profiles for each state overlap with small differences associated to the subtleties of the channel local changes. The hole density (Fig. 5c) shows a noticeable increase when the S1RBD (negatively charged) is captured by the ACE2 receptor. Although the peak in the hole concentration under the activated pair is higher, its profile is narrowed and the resulting overall hole concentration (i.e. the integral of these profiles) decreases. For the electron density in the channel (Fig. 5d) the situation is reversed: under the negatively charged receptors the concentration drops significantly (solid lines), but after the complexation of the receptors (dashed lines) the extension of the depleted region becomes narrower, giving rise to a net increase in the electron concentration.
The previous analysis is also supported by the electric field distribution under the molecules. Fig. 5e–h show it for both molecule states (idle at Fig. 5e and f and activated at Fig. 5g and h) and both VFG values in the p- and n-branch (Fig. 5e, g and f, h, respectively). The edges of the graphene layer are indicated by arrow heads aside each plot. The regions where the electric field is normal to the graphene layer correspond to those locations where the carrier concentration changes by a larger extent. When switching from idle (Fig. 5e and f) to activated (Fig. 5g and h) those regions with higher electric field shift from right to left, which is consistent with the charge profiles depicted in Fig. 5c and d. The present analysis evidences the necessity of a fine-grained treatment of the molecular shape and its charge distribution to capture the subtleties of the electrostatic interaction between the receptor and the graphene channel.
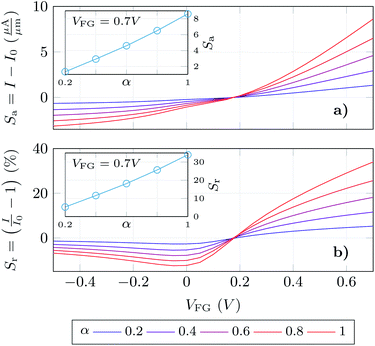
Finally, we have determined the absolute and relative change of the GBioFET output current for different values of the receptor occupation (Fig. 6a and b respectively). We opted for this read-out in the sensor response as our results depict high changes in both the p- and n-branch currents. It is worth noting, however, that the contact resistance might saturate and obscure these changes in the on-state current, and the variation in VDirac can alternatively be exploited to define the sensor response in such a case. The sensor presents a noticeable sensitivity and ability to detect SARS-CoV-2 when it is bound to the corresponding ACE2 receptor which assures its specificity. The sensitivity is higher in the n-branch than in the p-branch, reaching relative changes in the output current of 30% in the former case when all the molecules are activated. Its dependence on the gate bias also varies in both cases: while in the p-branch it reaches a maximum (around VFG = 0 V), then decreases and eventually saturates; in the n-branch the sensitivity increases monotonically with VFG indicating that higher positive biases favour the sensing capabilities of the GBioFET. Indeed, the maximum sensitivity within the range of biases simulated here occurs for VFG = 0.7 V. The inset shows the sensor response at this particular bias as a function of the occupation percentage. Interestingly, the sensitivity increases linearly with α, also guaranteeing the linearity of the sensor response at this bias point.
IV. Conclusions
We present a pioneering multiscale numerical characterization of graphene-based BioFETs incorporating the description of the charge distribution of the ACE2 receptor and of the ACE2-S1RBD complex that is formed after the virus spike protein anchors to the ACE2 receptor on the sensor surface. The molecular charge distribution is mapped in atomic detail and incorporated into macroscopic device level simulations to assess the GBioFET response to the presence of the target analytes on the sensor surface. The fine-grained level of description proposed here, which is possible due to a multiscale approach to the electrolyte device physics, results in an exceptional level of detail to capture the sensor response. The computational cost at the device level is still high and further improvements would be required to consider larger structures, like the complete spike protein or even the virus. Furthermore, the upgrade of the whole platform towards 3D simulations would be desirable to avoid the projection mapping of the molecular charge into the device configuration. Despite these initial limitations, this work demonstrated the potential of GBioFET to achieve a reliable detection of SARS-CoV-2, particularly when it operates in the n-branch. A detailed study of the electron and hole density variations due to the electric field generated by the ACE2 and the ACE2-S1RBD pair charge distributions, namely when the receptors are idle or activated, enabled us to explain what is, in principle, a counter-intuitive behaviour of the sensor response, that would be obscured by more simplistic computational treatments, rationalizing the observed behaviour in experimentally fabricated sensors. In this case, the ACE2-S1RBD pair has been considered, but future works can explore the combination of this receptor with other molecules to evaluate the impact of these changes in the response of the device. This can be also extended to any other receptor-target pair, and in particular to the investigation of sensor selectivity. Although a selectivity study would require a previous dedicated biochemical investigation of the relevant receptor-target pairs, we believe that the proposed platform constitutes a powerful tool to close the gap between the theoretical predictions and experimental selectivity measurements as it reduces the equivalence between molecules at the device computational level to those with similar electric charge distributions. In summary, we reported a multiscale approach that advances the state-of-the-art of computational tools for the study of biosensors, and which can be exploited in the design of future sensors, including, for example, the analysis of different 2DMs and oxides along with atomic level particularities of the material47 or the assessment of the impact of the device geometry on its sensitivity. Moreover, the present study might serve as a basis for further detailed investigations, including the impact on the sensor response non-idealities like charge traps,48 contact resistances, or defects in graphene.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by MCIN/AEI through the project PID2020-116518GB-I00, by FEDER/Junta de Andalucía-Consejería de Transformación Económica, Industria, Conocimiento y Universidades through the Projects PY20_00633 and B-RNM-375-UGR18; and the European Union's Horizon 2020 Framework Programme for Research and Innovation through the Project Wearable Applications Enabled by Electronic Systems on Paper (WASP) under Contract 825213. The work of A. Toral-Lopez was supported by the FPU program (FPU16/04043). D. B. Kokh and R. C. Wade acknowledge the support of the Klaus Tschira Foundation and the European Union's Horizon 2020 Framework Programme for Research and Innovation under Grant Agreement 945539 (Human Brain Project SGA3).References
- Yi-W. Tang, J. E. Schmitz, D. H. Persing and C. W. Stratton, The laboratory diagnosis of COVID-19 infection: Current issues and challenges, J. Clin. Microbiol., 2020, 58(6), e00512–20 CrossRef PubMed.
- X. Li, M. Geng, Y. Peng, L. Meng and S. Lu, Molecular immune pathogenesis and diagnosis of COVID-19, J. Pharm. Anal., 2020, 10(2), 102–108 CrossRef PubMed.
- Y. Fang, H. Zhang, J. Xie, M. Lin, L. Ying, P. Pang and W. Ji, Sensitivity of Chest CT for COVID-19: Comparison to RT-PCR, Radiology, 2020, 200432 Search PubMed.
- L. Wang and A. Wong, COVID-Net: A tailored deep Convolutional neural network design for detection of COVID-19 Cases from Chest x-ray images, Preprint (ArXiv), 2020 Search PubMed.
- Y. Zhang, O. Nelson, X. Jin, L. Sun, R. Ohuru Nyaruaba, H. Wei, and N. A. Tanner, Rapid molecular detection of SARS-CoV-2 (COVID-19) virus RNA using Colorimetric LAMP, Prepring (MedRxiv), feb 2020 Search PubMed.
- J. Kashir and Y. Ahmed, Loop mediated isothermal amplification (LAMP) assays as a rapid diagnostic for COVID-19, Med. Hypotheses, 2020, 141, 109786 CrossRef CAS PubMed.
- G. Seo, G. Lee, Mi J. Kim, S.-H. Baek, M. Choi, K. B. Ku, C.-S. Lee, S. Jun, D. Park, H. G. Kim, S.-J. Kim, J.-O. Lee, B. T. Kim, E. C. Park and S. Il Kim, Rapid detection of COVID-19 causative virus (SARS-CoV-2) in human nasopharyngeal swab specimens using field-effect transistor-based biosensor, ACS Nano, 2020, 14(4), 5135–5142 CrossRef CAS PubMed.
- P. Bergveld, Development of an ion-sensitive solid-state device for neurophysiological measurements, IEEE Trans. Biomed. Eng., 1970,(1), 70–71 CAS.
- S. Mao, J. Chang, H. Pu, G. Lu, Q. He, H. Zhang and J. Chen, Two-dimensional nanomaterial-based field-effect transistors for chemical and biological sensing, Chem. Soc. Rev., 2017, 46(22), 6872–6904 RSC.
- B. Ryu, E. Yang, Y. Park, K. Kurabayashi and X. Liang, Fabrication of prebent MoS2 biosensors on flexible substrates, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2017, 35(6), 06G805 Search PubMed.
- M. T. Hwang, M. Heiranian, Y. Kim, S. You, J. Leem, T. Amir, V. Faramarzi, Y. Jing, I. Park, A. M. van der Zande, S. Nam, N. R. Aluru and R. Bashir, Ultrasensitive detection of nucleic acids using deformed graphene channel field effect biosensors, Nat. Commun., 2020, 11(1), 1543 CrossRef CAS PubMed.
- Z. Jiang, Bo Feng, J. Xu, T. Qing, P. Zhang and Z. Qing, Graphene biosensors for bacterial and viral pathogens, Biosens. Bioelectron., 2020, 166, 112471 CrossRef CAS PubMed.
- D. San Roman, R. Garg and T. Cohen-Karni, Bioelectronics with graphene nanostructures, APL Mater., 2020, 8(10), 100906 CrossRef CAS.
- A. Béraud, M. Sauvage and M. Claudia, Bazán, Monique Tie, Amira Bencherif, and Delphine Bouilly. Graphene field-effect transistors as bioanalytical sensors: design, operation and performance, Analyst, 2021, 146(2), 403–428 RSC.
- X. Yang, W. R. Frensley, D. Zhou and W. Hu, Performance analysis of Si nanowire biosensor by numerical modeling for charge sensing, IEEE Trans. Nanotechnol., 2012, 11(3), 501–512 Search PubMed.
- In-Y. Chung, H. Jang, J. Lee, H. Moon, S. M. Seo and D. H. Kim, Simulation study on discrete charge effects of SiNW biosensors according to bound target position using a 3D TCAD simulator, Nanotechnology, 2012, 23(6), 065202 CrossRef PubMed.
- N. Shafi, J. Singh Parmaar, A. Porwal, A. Mohammad Bhat, C. Sahu and C. Periasamy, Gate all around junctionless dielectric modulated BioFET based hybrid biosensor, Silicon, 2020 Search PubMed.
- D. Passeri, A. Morozzi, K. Kanxheri and A. Scorzoni, Numerical simulation of ISFET structures for biosensing devices with TCAD tools, BioMedical Engineering OnLine, 2015, 14(2), S3 CrossRef PubMed.
- N. Kannan and M. Jagadesh Kumar, Charge-modulated underlap i-MOS transistor as a label-free biosensor: A simulation study, IEEE Trans. Electron Devices, 2015, 62(8), 2645–2651 Search PubMed.
- F. Pittino, P. Palestri, P. Scarbolo, D. Esseni and L. Selmi, Models for the use of commercial TCAD in the analysis of silicon-based integrated biosensors, Solid-State Electron., 2014, 98, 63–69 CrossRef CAS.
- K. Datta, A. Shadman, E. Rahman and D. M. Quazi, Khosru. Trilayer TMDC heterostructures for MOSFETs and nanobiosensors, J. Electron. Mater., 2016, 46(2), 1248–1260 CrossRef.
- A. Shadman, E. Rahman, D. Quazi and M. Khosru, Monolayer MoS2 and WSe2 double gate field effect transistor as super nernst pH sensor and nanobiosensor, Sensing and Bio-Sensing Research, 2016, 11, 45–51 CrossRef.
- A. Toral-Lopez, E. G. Marin, J. M. Gonzalez-Medina, F. J. Romero, F. G. Ruiz, D. P. Morales, N. Rodriguez and A. Godoy, Assessment of three electrolyte–molecule electrostatic interaction models for 2D material based BioFETs, Nanoscale Adv., 2019, 1(3), 1077–1085 RSC.
- J. G. Champlain, A first principles theoretical examination of graphene-based field effect transistors, J. Appl. Phys., 2011, 109(8), 084515 CrossRef.
- F. Rana, P. A. George, J. H. Strait, J. Dawlaty, S. Shivaraman, M. Chandrashekhar and M. G. Spencer, Carrier recombination and generation rates for intravalley and intervalley phonon scattering in graphene, Phys. Rev. B, 2009, 79(11), 115447 CrossRef.
- J. M. Dawlaty, S. Shivaraman, M. Chandrashekhar, F. Rana and M. G. Spencer, Measurement of ultrafast carrier dynamics in epitaxial graphene, Appl. Phys. Lett., 2008, 92(4), 042116 CrossRef.
- P. C. Feijoo, D. Jiménez and X. Cartoixà, Short channel effects in graphene-based field effect transistors targeting radio-frequency applications, 2D Materials, 2016, 3(2), 025036 CrossRef.
- I. Borukhov, David Andelman and H. Orland, Steric effects in electrolytes: a modified Poisson–Boltzmann equation, Phys. Rev. Lett., 1997, 79(3), 435–438 CrossRef CAS.
- N. Schwierz, D. Horinek and R. R. Netz, Reversed anionic hofmeister series: the interplay of surface charge and surface polarity, Langmuir, 2010, 26(10), 7370–7379 CrossRef CAS PubMed.
- N. Schwierz, D. Horinek and R. R. Netz, Anionic and cationic hofmeister effects on hydrophobic and hydrophilic surfaces, Langmuir, 2013, 29(8), 2602–2614 CrossRef CAS PubMed.
- A. Toral-Lopez, E. G. Marin, A. Medina, F. G. Ruiz, N. Rodriguez and A. Godoy, Simulation of 2D-material based BioFETs targeting single-molecule detection applications, in Single-Molecule Sensors and Nanosystems International Conference (SI3C), 2019 Search PubMed.
- S. Q. Lud, M. G. Nikolaides, I. Haase, M. Fischer and A. R. Bausch, Field effect of screened charges: Electrical detection of peptides and proteins by a thin-film resistor, ChemPhysChem, 2006, 7(2), 379–384 CrossRef CAS PubMed.
- A. C. Walls, M. A. Tortorici, S. Joost, X. Xiong, B.-J. Bosch, F. A. Rey and D. Veesler, Tectonic conformational changes of a coronavirus spike glycoprotein promote membrane fusion, Proc. Natl. Acad. Sci., 2017, 114(42), 11157–11162 CrossRef CAS PubMed.
- A. C. Walls, Y.-J. Park, M. Alejandra Tortorici, A. Wall, A. T. McGuire and D. Veesler, Structure, function, and antigenicity of the SARS-CoV-2 spike glycoprotein, Cell, 2020, 181(2), 281–292 CrossRef CAS PubMed.
- R. Natesh, L. Sylva, U. Schwager, E. D. Sturrock and K. Ravi Acharya, Crystal structure of the human angiotensin-converting enzyme–lisinopril complex, Nature, 2003, 421, 551–554 CrossRef CAS PubMed.
- J. Lan, J. Ge, J. Yu, S. Shan, H. Zhou, S. Fan, Qi Zhang, X. Shi, Q. Wang, L. Zhang and X. Wang, Structure of the SARS-CoV-2 spike receptor-binding domain bound to the ACE2 receptor, Nature, 2020, 581(7807), 215–220 CrossRef CAS PubMed.
- J. Lan, J. Ge, J. Yu, S. Shan, H. Zhou, S. Fan, Qi Zhang, X. Shi, Q. Wang, L. Zhang and X. Wang, Structure of the SARS-CoV-2 spike receptor-binding domain bound to the ACE2 receptor, Nature, 2020, 581(7807), 215–220 CrossRef CAS PubMed.
- D. Wrapp, N. Wang, K. S. Corbett, J. A. Goldsmith, C.-L. Hsieh, O. Abiona, B. S. Graham and J. S. McLellan, Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation, Science, 2020, 367(6483), 1260–1263 CrossRef CAS PubMed.
- M. Hussain, N. Jabeen, F. Raza, S. Shabbir and A. Ayesha, Baig, Anusha Amanullah, and Basma Aziz. Structural variations in human ACE2 may influence its binding with SARS-CoV-2 spike protein, J. Med. Virol., 2020, 1580–1586 CrossRef CAS PubMed.
- U. Pieper, MODBASE, a database of annotated comparative protein structure models, and associated resources, Nucleic Acids Res., 2004, 32(90001), 217D–222D CrossRef PubMed.
- T. J. Dolinsky, J. E. Nielsen, J. A. McCammon and N. A. Baker, PDB2pqr: an automated pipeline for the setup of poisson-boltzmann electrostatics calculations, Nucleic Acids Res., 2004, 32, W665–W667 CrossRef CAS PubMed.
- K. Bhargava and V. Singh, Electrical characterization and parameter extraction of organic thin film transistors using two dimensional numerical simulations, J. Comput. Electron., 2014, 13(3), 585–592 CrossRef CAS.
- S. B. Mitta, M. S. Choi, A. Nipane, F. Ali, C. Kim, J. T. Teherani, J. Hone and W. Jong Yoo, Electrical characterization of 2D materials-based field-effect transistors, 2D Materials, 2020, 8(1), 012002 CrossRef.
- A. Allain, J. Kang, K. Banerjee and A. Kis, Electrical contacts to two-dimensional semiconductors, Nat. Mater., 2015, 14(12), 1195–1205 CrossRef CAS PubMed.
- C. Kim, I. Moon, D. Lee, M. S. Choi, F. Ahmed, S. Nam, Y. Cho, H.-J. Shin, S. Park and W. Jong Yoo, Fermi level pinning at electrical metal contacts of monolayer molybdenum dichalcogenides, ACS Nano, 2017, 11(2), 1588–1596 CrossRef CAS PubMed.
- S.-H. Tseng, H.-Yi Chen, W.-T. Hsu, H.-C. Wang, Y.-Y. Li, W.-H. Chang, M.-P. Lu and M.-Y. Lu, Influences of contact metals on the performances of MoS2 devices under strains, J. Phys. Chem. C, 2019, 123(50), 30696–30703 CrossRef CAS.
- A. Toral-Lopez, H. Santos, E. G. Marin, F. G. Ruiz, J. Jose Palacios and A. Godoy, Multi-scale modeling of 2D GaSe FETs with strained channels, Nanotechnology, 2021, 33(10), 105201 CrossRef PubMed.
- A. Toral-Lopez, F. Pasadas, E. G. Marin, A. Medina-Rull, J. M. Gonzalez-Medina, F. J. G. Ruiz, D. Jiménez and A. Godoy, Multi-scale analysis of radio-frequency performance of 2D-material based field-effect transistors, Nanoscale Adv., 2021, 3(8), 2377–2382 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00357k |
| This journal is © The Royal Society of Chemistry 2022 |