Effect of albumin coating on the magnetic behavior of Mn ferrite nanoclusters

Abstract

The effect of clustering induced by albumin coating on the magnetic behaviour of ultra-small MnFe₂O₄ nanoparticles has been systematically investigated and compared with that in pure Mn ferrite nanoparticle dense assembly, using a mesoscopic scale approach and numerical simulations reproducing the experimental findings well. Our results provide evidence that in the coated system, the interplay between intra-particle and intra-cluster exchange interactions strongly affects the exchange bias and coercive field values, with the dipolar interactions playing a minor role. Instead, the albumin coating does not affect the thermal stability of the observed superspin glass phase, the freezing temperature being similar in the coated and uncoated systems.

---

Introduction

The technological demand for biodegradable and ecological nanostructured materials has promoted long ago the effective strategy of the coverage of the surface of magnetic nanoparticles (MNPs), during or after their preparation, with an organic coating material.¹ There is a large number of studied coating materials nowadays which allow the control of the strength of the inter-particle interactions and the degree of colloidal stability in liquid carriers.² It has also been demonstrated^3–12 that these materials can modify the intra-particle characteristics (e.g. magnetisation, surface charge, and anisotropy). In addition, there are studies lately reporting the change of the assembly's morphology during the coating process due to the formation of agglomerates of magnetic nanoparticles.^13,14 This fact has been proved to generate additional modifications in the magnetic behaviour of the nanoparticle system (e.g. decrease of the saturation magnetisation).¹¹ Therefore, the organic coating can be used as a tool that offers the ability to control and optimize those magnetic properties of the nanoparticle system which are necessary to achieve high-performance magnetic applications.

The study of ultra-small MnFe₂O₄ nanoparticles has attracted a lot of scientific interest because of their peculiar magnetic properties, such as high saturation magnetisation resulting in strong inter-particle interactions responsible for collective magnetic states, such as superspin glass (SSG). Moreover, the ultra-small size induces strong surface/interface effects (e.g. core/shell interface exchange coupling) which in turn are responsible for the observed exchange bias (EB) phenomenon.^15–17

Albumin, a protein of the human blood, has been regarded as a promising material to cover nanoparticles for bio-imaging and drug delivery.^18–23 In our recent study on the effect of the albumin coating on the structural and magnetic properties of an assembly of ultra-small (∼2 nm) Mn ferrite nanoparticles, it has been clearly demonstrated¹⁴ that the albumin coating process induces some clustering between the nanoparticles that decreases their magnetisation and the surface anisotropy. As a result, the coercive field (H_C) decreases. It is worth pointing out that the coated system exhibits SSG behaviour with a freezing temperature (T_f) similar to that of the uncoated one. On the other hand, the irreversibility temperature is much higher for the coated system, indicating large size distribution of clusters. This outcome has been attributed to the interplay of the inter-particle and intra-particle interactions in the albumin coated system.¹⁴

There are still open questions concerning the role of the clustering in the magnetic properties of the particle assembly, in particular the H_C and the exchange bias field (H_ex) values and their temperature dependence. Therefore, a thorough investigation of the effect of clustering on the magnetic properties of ultra-small MnFe₂O₄ nanoparticles, induced by the albumin coating, is necessary. In addition, the fact that the characteristics observed in the magnetic behaviour of clustered systems are different from those observed in the single coated nanoparticle systems¹⁵ opens new perspectives for the use of nanoparticles in high performance applications. Indeed, the magnetic properties of such nanoparticle systems can be tailored by selecting appropriate coating agents as well as appropriate coating procedures.

In view of this, we performed a systematic study of the clustering effect on the magnetic properties of an assembly of ultra-small MnFe₂O₄ nanoparticles (∼2 nm diameter) covered with albumin molecules, and we compared it to that on the uncoated assembly. We calculated the exchange bias properties and their temperature dependence. We used for our study the model and the simulation parameters which are based on a combined DFT and Monte Carlo approach developed in ref. 14 and 15.

Experimental and theoretical calculations

Synthesis, characterisation and magnetic measurements of albumin coated MnFe₂O₄ nanoparticles

The detailed synthesis and the chemical and physical characterisation of MnFe₂O₄ uncoated particles (labelled sample MFO) and after their coating with albumin (labelled MFO_BSA) have been reported in ref. 14, 24 and 25.

Field and temperature dependent magnetization measurements were performed on selected samples by using a quantum design superconducting quantum interference device (SQUID) magnetometer, equipped with a superconducting coil producing a magnetic field in the range of [−5 T, 5 T]. Powder samples were immobilized in an epoxy resin to prevent any nanoparticle movement during measurements. Hysteresis loops were obtained in a −5/+5 T applied magnetic field at temperatures from 5 K to 50 K after a field-cooling procedure (H_cool = 10 kOe), and ZFC/FC magnetisation curves vs. temperature for the applied field H_app = 10 Oe were obtained.

Numerical calculations

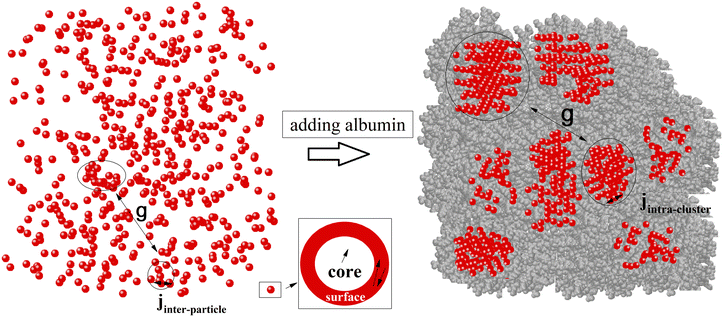
In order to investigate clustering effects on the exchange bias behaviour of the random assemblies of Mn ferrite nanoparticles, in the presence of the albumin coating, we have used a multiscale modelling approach. Starting from the atomic level, we performed DFT calculations to investigate the effect of the albumin molecules attached on the Mn ferrite particle surface, as described in ref. 14, where it has been demonstrated that the coated nanoparticles have a smaller magnetic moment per atom for both Mn and Fe atoms, resulting in a 3% reduction of the total magnetic moment and a 7.6% reduction of the magneto-crystalline anisotropy (MAE) with respect to the uncoated system.

A mesoscopic model of a manganese spinel ferrite nanoparticle of a diameter of 2 nm was consequently developed for the description of the core/surface morphology for each nanoparticle and the long range dipolar inter-particle interactions.^13,14,26,27 The parameters used for the magnetic moments, the exchange coupling constants and the anisotropy for each nanoparticle are calculated using input from the DFT calculations. In our simulation, the effect of clustering and the variation of the cluster sizes has been described in ref. 14. A schematic representation of both models is shown below (Fig. 1), and a short description of the models and the parameters is given in the ESI.†

Fig. 1 Schematic representation of the nanoparticle assemblies before and after the addition of the albumin coating. The dipolar inter-particle interactions (g) among all particles, the exchange inter-particle interactions (j_{inter-particle}) between uncoated nanoparticles in contact forming small clusters and the exchange intra-cluster interactions (j_{intra-cluster}) between nanoparticles in contact – partially covered with albumin – inside larger isolated clusters are selectively indicated. (Inset) The model of the core/surface morphology of each nanoparticle is presented.

It is worth noting that clustering does exist even in the uncoated system (as we reported in our previous work in ref. 15). The albumin coating produces an extra clustering, i.e. changing the cluster morphology and broadening their size and shape distribution, as shown by the much larger irreversibility temperature.¹⁴ In the coated system, the clusters weakly interact. They are separated by albumin molecules, and then there are no exchange interactions between them, while the nanoparticles in the clusters can be in physical contact and then exchange coupled. The dipolar interaction between the total moments of the clusters is weak, due to the random orientations of particle moments within a cluster that reduce the total moment. The bonding between albumin molecules and the surface of particles, tending to restore missing bonds at the particle surface, reduces the particle anisotropy. Such bonds deal only with the particles at the external border of the clusters surrounded by albumin, and then the reduction of the total anisotropy of the nanoparticles within the cluster is smaller than that in a single albumin coated nanoparticle.¹⁴

The above considerations have been taken into account in the introduction of the mesoscopic parameters for the anisotropy and exchange coupling strengths in our model (see the ESI).†

Monte Carlo simulations with the implementation of the Metropolis algorithm²⁸ have been performed, and we calculated the exchange bias properties at different temperatures and the ZFC/FC magnetisation curves for the coated and uncoated assemblies of the Mn ferrite nanoparticles. The hysteresis loops were calculated after a field cooling process under H_cool = 2.5 along the z-direction. The ZFC/FC magnetisation curves were calculated under a static magnetic field (H_app = 0.03).

Results and discussion

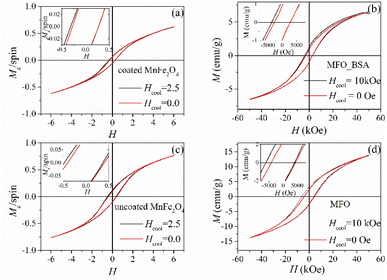
In Fig. 2, we show the Monte Carlo simulation results and the experimental results of hysteresis loops after the application of a magnetic field (black lines) and without the applied field (red lines) for the albumin coated Mn ferrite nanoparticle assemblies (Fig. 2(a and b)) and the uncoated (Fig. 2(c and d)), respectively. The simulated curves reproduce the experimental ones well.

Fig. 2 Monte Carlo simulation results at T = 0.01 (left panels) and experimental results at T = 5 K (right panels) for the hysteresis loops with (black lines) and without (red lines) a cooling field H_cool for the albumin coated system (a and b) and the uncoated system (c and d). The insets show the enlarged loop area around the H_C.

We then discuss the temperature dependence of the exchange bias field and the coercive field of the albumin coated ultra-small Mn ferrite nanoparticle assembly, and we compare it to that of the uncoated assembly.¹⁴

In Fig. 3(a) we show the Monte Carlo simulation results, and Fig. 3(b) shows the corresponding experimental results (MFO_BSA) for the temperature dependence of the coercive field H_C and the exchange bias field H_ex after a field cooling procedure for the albumin coated Mn ferrite nanoparticle dense assemblies. For comparison, Fig. 3(c) and (d) show the corresponding Monte Carlo and experimental results for the uncoated Mn ferrite nanoparticle (MFO) dense assemblies, respectively. The insets of Fig. 3(a–d) show the temperature dependence of the zero field and field cooled (ZFC/FC) magnetisation for the numerical and the experimental results, respectively.^14,15 We observe that the calculated curves reproduce the experimental findings well. In Fig. 3(a) and (b), we see that the presence of the albumin coating reduces both the H_ex and H_C of the uncoated system. We observe that in the low temperature regime, the experimental and calculated exchange bias fields are about ten times lower than the H_C for both albumin coated and uncoated nanoparticle assemblies. The reduction of H_ex is due to the fact that the strong intra-cluster exchange coupling reduces the spin disorder at the surface of the nanoparticles in contact (then reduces H_C), affecting the interface core/surface particle exchange coupling.

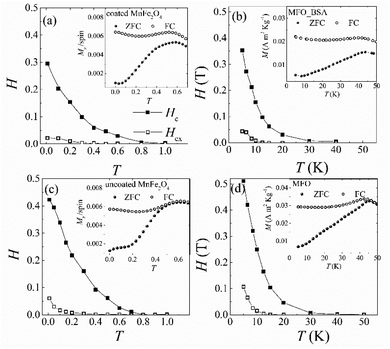Fig. 3 Monte Carlo simulation results (left panel) and experimental results (right panel) of the temperature dependence of the coercive field (H_C) after a field cooling procedure (full squares) and the corresponding exchange bias field (H_ex) (open squares) for dense assemblies coated with albumin (a and b) and uncoated (c and d) MnFe₂O₄ nanoparticles, respectively. The insets show the corresponding ZFC/FC susceptibility curves.^14,15

For both systems, we observe that H_C decreases exponentially with the temperature and vanishes at around the freezing temperature (maximum of the ZFC magnetisation curve). The temperature at which H_C becomes negligible depends on the cluster size distribution. Larger clusters in the coated sample delay the H_C decrease. It is noteworthy that the H_ex temperature dependence of the coated system is different from the uncoated one. In the case of the uncoated system, it decreases exponentially with temperature, whereas in the presence of the albumin coating, it shows weak temperature dependence in the low temperature regime (0.01–0.1), and then a faster decrease with temperature follows. This is due to the fact that the strong intra-cluster exchange coupling, induced by the clustering, keeps the surface spins of the albumin coated nanoparticles tight and masks the thermal fluctuations at low temperature.

In what follows, we study the factors that influence the exchange bias effect and its relation to the SSG state in the albumin coated nanoparticle system.

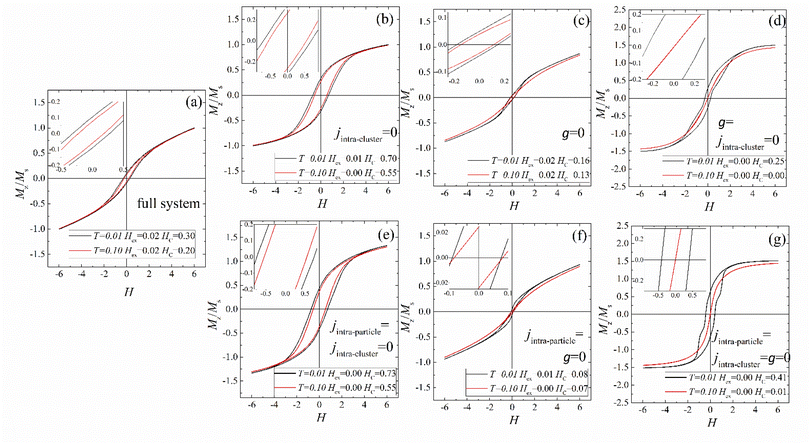
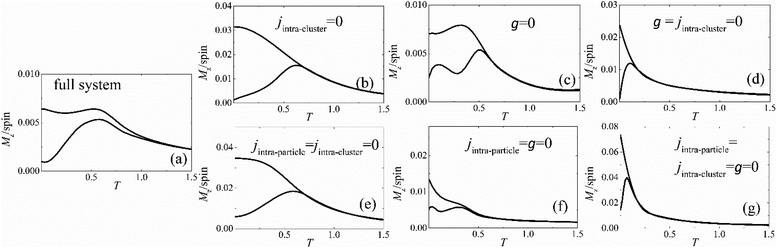
In order to investigate the effect of the clustering on the exchange bias effect of the albumin coated Mn ferrite nanoparticle assembly, we first switch off in the Hamiltonian (see eqn (S1) in the ESI†) the exchange intra-cluster interaction (j_{intra-cluster}) between nanoparticles in contact within each cluster; next, we switch off only the dipolar inter-particle interactions term (g), and then we switch off both. We have also investigated the cases of switching off the intra-particle interactions together with the intra-cluster or together with the dipolar interactions. Finally, we switch off all the intra/inter-particle and the intra-cluster interactions in the system. In Fig. 4, we show the Monte Carlo simulation results for the hysteresis loops for these six cases (Fig. 4: (b) j_{intra-cluster} = 0, (c) g = 0, (d) g = j_{intra-cluster} = 0, (e) j_{intra-particle} = j_{intra-cluster} = 0, (f) j_{intra-particle} = g = 0, and (g) j_{intra-particle} = j_{intra-cluster} = g = 0) together with the hysteresis loops for the full system for comparison (Fig. 4(a)) at the two low temperatures (T = 0.01, 0.10). The magnetisation in the hysteresis loops is normalised to the saturation magnetisation of the full system.

Fig. 4 Monte Carlo simulation results for the hysteresis loops at two temperatures T = 0.01 (black line) and T = 0.1 (red line), after applying a cooling field procedure, for the full albumin coated system (a) and the system without: (b) the intra-cluster interactions between particles in contact in each cluster (j_{intra-cluster} = 0), (c) the dipolar inter-particle interactions (g = 0), (d) both dipolar interactions and intra-cluster (g = j_{intra-cluster} = 0), (e) all the exchange interactions (j_{intra-particle} = j_{intra-cluster} = 0), (f) both the intra-particle interactions and the dipolar inter-particle interactions (j_{intra-particle} = g = 0) and (g) all the inter-particle and intra-particle and intra-cluster interactions (j_{intra-particle} = j_{intra-cluster} = g = 0). The insets show the enlarged shifted loop area around the H_C.

In Fig. 4(b), we observe that when exchange intra-cluster interactions are absent (j_{intra-cluster} = 0), we have a ∼50% decrease in the H_ex and a 233% increase in the H_C from their values in the full system (Fig. 4(a)) at T = 0.01. This shows that the exchange coupling between particles within a cluster affects the EB effect significantly, contributing to H_ex. Indeed, the lack of the intra-cluster coupling reduces H_ex, and even a small increase in the temperature causes H_ex to vanish.

Turning to H_C, a similar enhancement has been observed in the uncoated system in ref. 15 by switching off inter-particle exchange interactions. In the coated sample, the effect on H_C is much stronger because of the vanishing of the much stronger exchange intra-cluster exchange interactions. In their absence, nanoparticle's surface disorder is recovered, resulting in a much larger increase of H_C.

In the absence of dipolar inter-particle interactions, i.e. g = 0 (Fig. 4(c)), H_ex is not affected, but only H_C decreases by ∼47% from the corresponding values of the full system (Fig. 4(a)) at T = 0.01. We see that dipolar interactions do not affect the EB. Contrary to the decrease in H_ex reported for the uncoated system for g = 0 in ref. 15, in the presence of the albumin coating, the strength of the exchange intra-cluster interactions is larger, and this is the dominant contribution to the exchange bias field even at higher temperature T = 0.1.

The contact between particles produces a thicker surface layer with reduced anisotropy. The decrease of H_C is due to the lack of the contribution of dipolar interactions to the effective anisotropy of the nanoparticle assembly. However, because of the existence of the intra-particle and intra-cluster coupling, the nanoparticles are tightly bound, and they resist the change of temperature. This accounts for the small temperature dependence of H_C.

In Fig. 4(d), where both the exchange intra-cluster and the dipolar inter-particle interactions are absent, the exchange bias field is suppressed. The strong surface disorder is recovered in the absence of intra-cluster exchange interactions, and as a result, it masks the EB while the coercive field shows an increase from g = 0. As the temperature increases, thermal fluctuations mask H_C which decreases rapidly.

Finally, as can be seen in Fig. 4(e)–(g), we investigate the role of the exchange intra-particle interactions and their interplay with the inter-particle interaction terms. We observe that:

(1) When we remove both the intra-particle interactions (j_c1 = j_c2 = j_srf = 0) (see the ESI†) between the macrospins of each core/surface nanoparticle and the intra-cluster interactions (Fig. 4(e)), the exchange bias vanishes, indicating that the EB comes entirely from these interactions. The behaviour of H_C is almost similar to the case of vanishing intra-cluster interactions described above (Fig. 4(b)).

(2) In the case where we switch off the dipolar interactions and the intra-particle interactions (Fig. 4(f)), the EB decreases by 50%, whereas in the absence of all interactions (inter-particle, intra-cluster and intra-particle), the EB becomes negligible (Fig. 4(g)). Therefore, the ensemble of simulations provides a confirmation that intra-cluster exchange interactions strongly contribute to the EB effect, which is very weakly affected by dipolar interactions. In the presence of only the exchange intra-cluster interactions (Fig. 4(f)), which tend to orient the macrospins, H_C becomes very small, but with weak temperature dependence because of the presence of the strong intra-cluster interactions, as we discussed above. Finally, in the absence of all interaction energy terms (Fig. 4(g)), the non-interacting assembly of randomly oriented anisotropic macrospins results in a measurable H_C but with high temperature dependence.

To further investigate the clustering effect on the interplay between exchange intra-cluster and dipolar inter-particle interactions and its contribution to the SSG state formation, we have performed Monte Carlo simulations (Fig. 5) of the ZFC/FC magnetisation temperature dependence curves, under a low applied magnetic field, in the case of switching off separately only the exchange intra-cluster interactions (j_{intra-cluster} = 0) (Fig. 5(b)) and only the dipolar interactions (g = 0) between the coated nanoparticles (Fig. 5(c)) and in the case of switching off both the dipolar interactions and the exchange intra-cluster interactions (g = j_{intra-cluster} = 0) (Fig. 5(d)). We have also investigated the effect of switching off the intra-particle interactions together (a) with the intra-cluster ones or (b) together with the dipolar interactions or (c) all the interactions (inter-particle, intra-particle and intra-cluster) (Fig. 5(e)–(h)). The ZFC/FC magnetisation curves for the full system are also presented for comparison in Fig. 5(a).

Fig. 5 Monte Carlo simulation results for the ZFC/FC magnetisation curves as a function of temperature for the albumin coated system¹⁴ (a) and for the cases where we switch off: only the exchange intra-cluster interactions among all the nanoparticles in a cluster (j_{intra-cluster} = 0) (b), only the dipolar inter-particle interactions among all the nanoparticles (g = 0) (c), the dipolar and intra-cluster interactions (g = j_{intra-cluster} = 0) (d), and switching off all the exchange interactions (j_{intra-particle} = j_{intra-cluster} = 0) (e) or both the intra-particle and the dipolar interactions (j_{intra-particle} = g = 0) (f) and all the inter-particle, intra-cluster and intra-particle interactions (j_{intra-particle} = j_{intra-cluster} = g = 0) (g).

In Fig. 5(a), the ZFC/FC magnetisation curves of the full system show a clear SSG behaviour. It's noteworthy that the maximum of the ZFC magnetisation, indicating the freezing temperature,¹⁴ is the same in the uncoated and in the albumin coated system. As can be seen in Fig. 5(d) and (g), in the nanoparticle assemblies without intra-cluster and dipolar coupling and non-interacting particles, respectively, the SSG behaviour is absent, as shown by the continuous increase of the FC magnetisation with decreasing temperature. The same holds for the case when the exchange intra-particle interactions are removed together with dipolar inter-particle interactions (Fig. 5(f)). The non-continuous increase of the FC magnetisation for the cases where g is non-zero (Fig. 5(b) and (e)) reveals the presence of interacting particles due to dipolar interactions that tend to create disorder in the assembly.

In the case where only the dipolar interactions are switched off (Fig. 5(c)), the SSG character is retained²⁹ being the disordered collective freezing due to the interplay between the intra-particle random anisotropy and the intra-cluster interactions. Thus, it comes out that the SSG freezing is basically an intra-cluster phenomenon, with the exchange coupling between particles within clusters playing an important role. The second peak that appears in the ZFC curve (Fig. 5(c) and (f)) at a lower temperature, when dipolar interactions or both dipolar and intra-particle interactions are removed, is attributed to the blocking of the moments of smaller clusters or isolated nanoparticles. This was also observed in weakly interacting binary systems where two peaks for the two constituents are observed in the ZFC susceptibility curve.³⁰

The results of Fig. 4 and 5 demonstrate that when the albumin coating is added to the system, the intra-cluster interactions play the most important role in both the exchange bias and superspin glass phenomena. The same value of the freezing temperature in the two systems indicates that the change of cluster morphology and their size distribution, induced by the albumin coating, does not affect the interplay between inter-particle and intra-particle interactions, as also confirmed in ref. 14, by the analysis of the remanence ΔM plots for the numerical and the experimental systems, showing that the total strength of interactions is the same in the two types of nanoparticle assembly.

Conclusions

This paper provides an analysis of the effects of the clustering induced by the albumin coating on the magnetic behaviour of ultra-small MnFe₂O₄ nanoparticles and in particular on the exchange bias effect, the anisotropy and the superspin glass state. The results indicate that the difference in the H_C and H_ex values between the uncoated and albumin coated nanoparticle assemblies is mainly determined by the type of clustering induced by the coating. The exchange bias effect, intrinsically an intra-particle phenomenon, due to the core/shell interface coupling, is found to be strongly affected by the exchange interactions between the particles within a cluster. Such interplay between intra-particle and intra-cluster effects plays a major role on the H_C value too, with the dipolar interactions playing a minor role in the above values. Our findings show that the thermal stability of the SSG phase, i.e. the freezing temperature, resulting from the interplay of both dipolar and exchange inter-particle interactions, is not affected by the albumin mediated clustering.

Our results contribute to gain a better insight into the interplay between intra-particle and inter-particle effects and provide evidence that the choice of an appropriate coating agent and coating procedure can provide a tool to tailor the magnetic properties of nanoparticle based materials and improve their performance for technological applications.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. All authors contributed equally.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support from the Horizon Europe EIC Pathfinder Open Programme: under grant agreement No. 101046909 (REMAP) and computational time granted from the Greek Research & Technology Network (GRNET) in the National HPC facility ARIS (https://hpc.grnet.gr) under projects FMAGNA (pr8020) and BALCONY (pr 10005).

References

1. M. Abdolrahimi, M. Vasilakaki, S. Slimani, N. Ntallis, G. Varvaro, S. Laureti, C. Meneghini, K. N. Trohidou, D. Fiorani and D. Peddis, J. Nanomater., 2021, 11, 1787.
2. K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630.
3. B. Bittova, J. Poltierova-Vejpravova, A. G. Roca, M. P. Morales and V. Tyrpekl, J. Phys.: Conf. Ser., 2010, 200, 072012.
4. P. Biehl, M. von der Lühe, S. Dutz and F. H. Schacher, Polymers, 2018, 10, 91.
5. Y. Köseoǧlu, J. Magn. Magn. Mater., 2006, 300, 327–330.
6. G. Baldi, D. Bonacchi, M. C. Franchini, D. Gentili, G. Lorenzi, A. Ricci and C. Ravagli, Langmuir, 2007, 23, 4026–4028.
7. Y. Hu, S. Mignani, J. P. Majoral, M. Shen and X. Shi, Chem. Soc. Rev., 2018, 47, 1874–1900.
8. M. Muñoz de Escalona, E. Sáez-Fernández, J. C. Prados, C. Melguizo and J. L. Arias, Int. J. Pharm., 2016, 504, 11–19.
9. L. S. Arias, J. P. Pessan, A. P. M. Vieira, T. M. T. De Lima, A. C. B. Delbem and D. R. Monteiro, J. Antibiot., 2018, 7, 46.
10. A. Heuer-Jungemann, N. Feliu, I. Bakaimi, M. Hamaly, A. Alkilany, I. Chakraborty, A. Masood, M. F. Casula, A. Kostopoulou, E. Oh, K. Susumu, M. H. Stewart, I. L. Medintz, E. Stratakis, W. J. Parak and A. G. Kanaras, Chem. Rev., 2019, 119, 4819–4880.
11. M. Vasilakaki, N. Ntallis, N. Yaacoub, G. Muscas, D. Peddis and K. N. Trohidou, Nanoscale, 2018, 10, 21244–21253.
12. N. Ntallis, M. Vasilakaki, D. Peddis and K. N. Trohidou, J. Alloys Compd., 2019, 796, 9–12.
13. A. Kostopoulou, K. Brintakis, M. Vasilakaki, K. N. Trohidou, A. P. Douvalis, A. Lascialfari, L. Manna and A. Lappas, Nanoscale, 2014, 6, 3764–3776.
14. M. Vasilakaki, N. Ntallis, M. Bellusci, F. Varsano, R. Mathieu, D. Fiorani, D. Peddis and K. N. Trohidou, Nanotechnol., 2020, 31, 025707.
15. M. Vasilakaki, G. Margaris, D. Peddis, R. Mathieu, N. Yaacoub, D. Fiorani and K. Trohidou, Phys. Rev. B, 2018, 97(6), 094413.
16. B. Aslibeiki, P. Kameli, H. Salamati, M. Eshraghi and T. Tahmasebi, J. Magn. Magn. Mater., 2010, 322, 2929–2934.
17. B. Aslibeiki, P. Kameli and H. Salamati, J. Appl. Phys., 2016, 119, 063901.
18. M. M. Najafpour, D. J. Sedigh, C. K. King'Ondu and S. L. Suib, RSC Adv., 2012, 2, 11253–11257.
19. A. V. Bychkova, M. V. Lopukhova, L. A. Wasserman, Y. N. Degtyarev, A. L. Kovarski, S. Chakraborti and V. A. Mitkevich, Biol. Macromol., 2021, 194, 654–665.
20. F. F. An and X. H. Zhang, Theranostics, 2017, 7, 3667–3689.
21. A. Aires, S. M. Ocampo, D. Cabrera, L. D. La Cueva, G. Salas, F. J. Teran and A. L. Cortajarena, J. Mater. Chem. B, 2015, 3, 6239–6247.
22. S. Yu, A. Perálvarez-Marín, C. Minelli, J. Faraudo, A. Roig and A. Laromaine, Nanoscale, 2016, 8, 14393–14405.
23. M. Qasim, K. Asghar, G. Dharmapuri and D. Das, Nanotechnol., 2017, 28, 18.
24. M. Bellusci, S. Canepari, G. Ennas, A. La Barbera, F. Padella, A. Santini, A. Scano, L. Seralessandri and F. Varsano, J. Am. Ceram. Soc., 2007, 90, 3977–3983.
25. M. Bellusci, B. Aurelio La, S. Luca, P. Franco, P. Antonella and V. Francesca, Polym. Int., 2009, 58, 1142–1147.
26. E. H. Sanchez, M. Vasilakaki, S. S. Lee, P. S. Normile, G. Muscas, M. Murgia, M. S. Andersson, G. Singh, R. Mathieu, P. Nordblad, P. C. Ricci, D. Peddis, K. N. Trohidou, J. Nogue and J. A. De Toro, Chem. Mater., 2020, 32, 969–981.
27. G. Margaris, K. N. Trohidou and J. Nogués, Adv. Mater., 2012, 24, 4331–4336.
28. K. Binder, Applications of the Monte-Carlo Method in Statistical Physics, Springer-Verlag, NY, 1987.
29. G. Margaris, M. Vasilakaki, D. Peddis, K. N. Trohidou, S. Laureti, C. Binns, E. Agostinelli, D. Rinaldi, R. Mathieu and D. Fiorani, Nanotechnol., 2017, 28, 1–8.
30. N. Daffé, J. Zecevic, K. N. Trohidou, M. Sikora, M. Rovezzi, C. Carvallo, M. Vasilakaki, S. Neveu, J. D. Meeldijk, N. Bouldi, V. Gavrilov, Y. Guyodo, F. Choueikani, V. Dupuis, D. Taverna, P. Sainctavit and A. Juhin, Nanoscale, 2020, 12, 11222–11231.

---

Footnote

† Electronic supplementary information (ESI) available: Short description of the mesoscopic model and the parameters. See https://doi.org/10.1039/d2na00458e

---