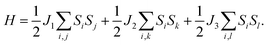A multiferroic vanadium phosphide monolayer with ferromagnetic half-metallicity and topological Dirac states

Abstract

Ferroelasticity, ferromagnetism, half-metallicity, and topological Dirac states are properties highly sought in two-dimensional (2D) materials for advanced device applications. Here, we report first-principles prediction of a dynamically and thermally stable tetragonal vanadium phosphide (t-VP) monolayer that hosts all these desirable properties. This monolayer is substantially ferromagnetic with polarized spins aligned in the in-plane direction via a d–p–d super-exchange coupling mechanism; meanwhile, its tetragonal lattice enables an intrinsic in-plane ferroelasticity with a reversible strain of 23.4%. As a result, the ferroelasticity is strongly coupled with ferromagnetism via spin–orbit coupling to enable deterministic control over the magnetocrystalline anisotropy by an applied elastic strain. More interestingly, this multiferroic t-VP monolayer possesses half-metallicity with an anisotropic, topological Dirac cone residing in the majority-spin channel. We also predict a multiferroic t-CrN monolayer, whose ferromagnetism features a high Curie temperature of up to 478 K but is weakly coupled to its in-plane ferroelasticity. These results suggest a tetragonal 2D lattice as a robust atomic-scale scaffold on the basis of which fascinating electronic and magnetic properties can be rationally created by a suitable combination of chemical elements.

---

New concepts

Two-dimensional (2D) multiferroic materials enable the control of one ferroic property by changing the other. For example, a magetoelectric material allows for the control of magnetism by means of an electric field or electric polarization by means of a magnetic field. Previously reported 2D multiferroic materials are largely limited to magetoelectric monolayers with coexisting magnetic and electric polarizations. As an alternative, 2D materials with coupled ferromagnetism and ferroelasticity permit the control of magnetism by applied mechanical strain and, thus, promise an extension of the spectrum of applications for multiferroic materials. Yet, it is surprising that 2D multiferroic monolayers with intrinsic coexistence of ferroelasticity and ferromagnetism are extremely rare. Here, we report first-principles evidences of a structurally, thermally and dynamically stable tetragonal vanadium phosphide (t-VP) monolayer, which simultaneously hosts intrinsic ferromagnetism and in-plane ferroelasticity. The ferroelasticity and ferromagnetism strongly couple with each other via spin–orbit coupling interaction of vanadium. More interestingly, the t-VP monolayer is also distinguished by a coexistence of ferromagnetic half-metallicity and topological Dirac fermions. These results highlight the potential of 2D tetragonal materials in creating novel mechanical, electronic and magnetic properties hard to achieve in other types of 2D materials, such as those with familiar honeycomb lattices.

As the key components in information devices are continuously miniaturized to nanometers, the development of non-volatile memories with high density for integration and high speed for operation is in urgent need. Atomically thin, two-dimensional (2D) ferromagnetic, ferroelectric and ferroelastic materials have been potential candidates for fabricating non-volatile memories since they all possess at least two different phases required for information storage.^1–3 However, writing in ferromagnetic memory is subject to large energy consumption, reading in ferroelectric memory tends to be destructive, while data in ferroelastic memory do not facilitate conversion into electric signals. 2D multiferroic materials with at least two coexisting ferroic properties can potentially overcome these issues. Among different kinds of multiferroic materials, magnetoelectric multiferroics with coexisting ferroelectricity and magnetism have attracted particular research interests, since these materials enable an “electric writing plus magnetic reading”⁴ mode toward achieving high-performance memory devices. Unfortunately, magnetoelectric materials are inherently rare due to the conflicting origins of ferroelectricity and ferromagnetism: the former requires empty d/f orbitals, while the latter is commonly associated with partially filled d/f orbitals.⁵ As such, reported 2D magnetoelectric materials are limited to CrN,⁶ Hf₂VC₂F₂,⁷ (CrBr₃)₂Li,⁸ CuMP₂X₆ (M = Cr, V; X = S, Se),⁹ phosphorene-halogen,¹⁰ Ge–CH₂OCH₃,¹¹ C₆N₈H,¹² VS₂,¹³ multiferroic heterostructures,¹⁴etc. These multiferroic materials can be categorized into two types: the type I multiferroics, in which the magnetism and ferroelectricity have different origins and, thus, are weakly coupled with each other, as occurring in CrN,⁶ CuMP₂X₆⁹ and (CrBr₃)₂Li;⁸ and the type II multiferroics, in which ferroelectricity originates from a specific magnetic order, and which are plagued by small electric polarization, as exemplified by Hf₂VC₂F₂.⁷

Alternatively, it is appealing to design new multiferroics, especially based on a combination of magnetism and ferroelasticity that permit an operation via the “mechanical writing plus magnetic reading” mode. The first reported 2D multiferroic material of this sort, to our knowledge, is the hole-doped α-SnO monolayer,¹⁵ but its ferroelastic and magnetic ordering are loosely coupled to each other. In addition, the two ferroic properties can only coexist in a specific range of hole carrier densities in this monolayer. Compared with the doping-induced multiferroics, it is of practical importance to search for 2D materials with coexisting intrinsic magnetism and ferroelasticity. To this end, we pay attention to rare earth metal pnictides¹⁶ and manganese pnictides,¹⁷ in light of their unique tetragonal lattice for hosting ferroelasticity and variable transition metal elements for introducing magnetism.

In this work, we find that a tetragonal vanadium phosphide (t-VP) monolayer is just such a 2D material with intrinsic ferromagnetism and in-plane ferroelasticity, as supported by intensive first-principles calculations. More surprisingly, the magnetic easy-axis of the t-VP monolayer is strongly coupled with the ferroelastic strain due to strong spin–orbit coupling (SOC), allowing for mechanical manipulation of the ferromagnetism. Besides the two coexisting ferroic properties, the t-VP monolayer is distinguished by its intrinsic half-metallicity and topological Dirac fermions near the Fermi level. We also find a multiferroic chromium nitride (t-CrN) monolayer wherein the intrinsic ferromagnetism is estimated to be sustained against a temperature of up to 478 K. These results open a new opportunity of employing the tetragonal lattice to design functional 2D materials with unprecedentedly versatile functionalities.

The calculations were performed using density functional theory described by the generalized gradient approximation of the Perdew–Burke–Ernzerhof (PBE) functional,¹⁸ implemented in VASP code,^19,20 in which the projector augmented wave²¹ method was employed to describe the core electron. A vacuum region with a thickness of 15 Å was added in the models to isolate neighboring periodic images. The plane-wave kinetic cutoff energy was set at 500 eV, and the Brillouin zone was sampled by a 12 × 12 × 1 k-point mesh. All atomic structures were fully relaxed until the force on each atom was less than 0.01 eV Å⁻¹. The HSE06 functional²² was employed to confirm the magnetic ground states and obtain electronic structures. The magnetocrystalline anisotropy energy was evaluated with SOC at a denser k-point 40 × 40 × 1 by the DFT+U (U = 3 eV) method. The selection of U = 3 eV is based on a comparison of band structures with those obtained from the HSE06 method. The phonon spectra were calculated using the PHONOPY code with the finite displacement method.²³ The ab initio molecular dynamics simulations were performed in the NVT ensemble, lasting 10 ps with a time step of 1.0 fs.

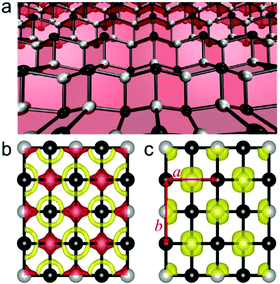
The unit cell of the t-VP monolayer possesses a pmmn space group with two V atoms and two P atoms, where each V atom is surrounded by four P atoms forming a tetrahedron. The P atoms are located in two planes of different heights, which sandwich the slightly buckled plane of V atoms. The t-VP monolayer has a rectangular unit cell, with lattice constants a (short-axis direction) and b (long-axis direction) of 3.42 and 4.22 Å, respectively (see Fig. 1c). Its thickness h, defined as the distance between two P planes, reaches 2.56 Å, slightly larger than 2.10 Å of 2D black phosphorous but smaller than 3.13 Å of MoS₂. The V–P bond length is 2.35 Å along the a direction and shortened to 2.32 Å along the b direction, suggesting symmetry-breaking of the P tetrahedra.

Fig. 1 (a) Structure of the t-VP monolayer. The black and grey balls represent P and V atoms, respectively. (b) Isosurface plots (0.01 e Å⁻³) of deformation electronic density. Charge accumulation and depletion regions are in yellow and red, respectively. (c) Isosurface plots (0.02 e Å⁻³) of spin density distribution. The lattice constants a and b are illustrated in (c).

To investigate the thermodynamic stability of the t-VP monolayer, we calculate the formation energy E_f, defined as

E_f = (E_VP − 2E_V − 2E_P)/4

where E_VP is the total energy of the t-VP monolayer in a unit cell, and E_V and E_P are the energies per atom in bulk V and P, respectively. The calculated E_f of the t-VP monolayer is −196 meV per atom, lower than −62.8 meV per atom of the experimentally realized Fe₃GeTe₂ monolayer,²⁴ supporting the thermodynamic feasibility of synthesizing the t-VP monolayer in experiments.

We then study the stability of the t-VP monolayer by analyzing its deformation electron density, which shows charge transfer from the V to P atoms (Fig. 1b). Bader charge analysis estimates a transfer of 0.68 electrons from a V to a P atom. The transferred electrons in the t-VP monolayer are mainly from V 3 d_xy orbitals and delocalized around P atoms in 3 p_x,y orbitals, different from a previously reported t-TiC monolayer where the transferred electrons are mainly from Ti 3 d_z² orbitals.²⁵ These transferred electrons are crucial for stabilizing the t-VP monolayer by strengthening the in-plane V–P bonds. The kinetic stability of the t-VP monolayer is also confirmed by the phonon dispersion spectrum shown in Fig. S1a (ESI†), where no imaginary frequency is observed. To further test the thermal stability of the t-VP monolayer, an ab initio molecular dynamics simulation was carried out for 10 ps at a temperature of 500 K using a 5 × 5 supercell. The structure snapshot plotted in Fig. S1c (ESI†) shows that there is no sign of any structural disruption or bond breaking, which indicates that the t-VP monolayer can be freestandingly stable well above room temperature.

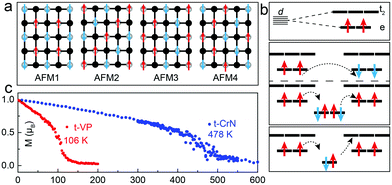
Having established the stability of the t-VP monolayer, we proceed to study its magnetism. The magnetic ground-state of the t-VP monolayer is evaluated by considering five different states: one ferromagnetic configuration, denoted as FM, and four antiferromagnetic configurations, denoted as AFM1, AFM2, AFM3 and AFM4, respectively (Fig. 2a). Results with the HSE06 functional (Table 2) show that the t-VP monolayer has a ferromagnetic ground state with a magnetic moment of 2.0 μ_B per V atom, where magnetic moments are mainly concentrated on V atoms as shown by the spin density distribution in Fig. 1c. The FM state is 15.3 meV per V atom more stable than the AFM1 state, 35.0 meV per V atom than the AFM2 state, 83.5 meV per V atom than the AFM3 state and 26.4 meV per V atom than the AFM4 state. To understand the exchange mechanism of ferromagnetism, we first analyse the orbital occupation of V atoms. As each V atom is surrounded by four P atoms that form a tetrahedron, the crystal field results in e–t₂ splitting of d orbitals. Although an isolated V atom has a valence electronic configuration of 4s²3d³, Bader charge analysis shows that the t-VP monolayer has only two unpaired d electrons in each V atom. Therefore, this e–t₂ splitting of d orbitals gives each V atom a magnetic moment of 2 μ_B (Fig. 2b), as also confirmed by the results from the HSE06 functional. The occupation of the d orbital of e²t⁰₂ results in two exchange channels between the nearest-neighboring V atoms: (i) the antiferromagnetic d–d direct exchange; (ii) the ferromagnetic d–p_x/p_y–d super-exchange. Moreover, a ferromagnetic d–p–d super-exchange occurs in the exchange channel between two second nearest-neighboring V atoms (Fig. 2b). This ferromagnetic d–p–d super-exchange and the competition between the antiferromagnetic d–d direct exchange and ferromagnetic d–p_x/p_y–d super-exchange together lead to a ferromagnetic ground-state for the t-VP monolayer.

Fig. 2 Magnetic properties of the t-VP and t-CrN monolayers. (a) Different magnetic configurations for the two monolayers. (b) Schematic diagram of 3d orbital occupations for the V atoms and kinetic exchange coupling between V atoms in the t-VP monolayer. (c) Magnetic moments in the monolayers as functions of temperature obtained from the Monte Carlo simulations based on the Heisenberg model.

Table 1 Calculated lattice constants a and b, vertical thickness h, lattice constant a_TS in the transition state, reversible strain ε, and formation energy E_f of the t-VP and t-CrN monolayers

	a (Å)	b (Å)	h (Å)	a TS (Å)	ε FE (%)	E f (meV per atom)
t-VP	3.42	4.22	2.56	3.94	23.4	−196
t-CrN	3.34	3.73	1.40	3.62	11.7	−164

---

Table 2 Total energies (meV per transition metal atom) for different magnetic configurations, magnetic moments M (μ_B u.c.⁻¹) calculated with the HSE06 functional, and magnetic anisotropic energies (μeV per transition metal atom) of the t-VP and t-CrN monolayers, calculated with DFT+U (U_eff = 3 eV) with SOC

	FM (meV)	AFM1 (meV)	AFM2 (meV)	AFM3 (meV)	AFM4 (meV)	M (μB u.c.^−1)	MAE[100] (μeV)	MAE[010] (μeV)	MAE[110] (μeV)	MAE[001] (μeV)
t-VP	0	15.3	35.0	83.5	26.4	4.0	86	0	43	69
t-CrN	0	78.3	294.0	81.1	58.8	5.0	162	123	143	0

---

Magnetocrystalline anisotropy plays a crucial role in thermally stabilizing the 2D long-range magnetic ordering, because a 2D magnetic system within the isotropic Heisenberg model cannot exist at finite temperatures according to the Mermin–Wagner theorem.²⁶ The magnetocrystalline anisotropy of 2D materials mainly stems from the SOC interaction and can be measured by the magnetocrystalline anisotropy energy (MAE). We consider the SOC interaction to obtain the relative stabilities along the [100] (i.e. the a direction), [010] (i.e. the b direction), and [110] and [001] (out-of-plane) directions in the t-VP monolayer, as summarized in Table 2. The results show that the easy-axis of the t-VP monolayer is along the b direction, different from the CrI₃,²⁷ Fe₃GeTe₂,²⁸ and MnX monolayers;¹⁷ the easy-axes of these monolayers are oriented out-of-plane. The MAE of the t-VP monolayer along the b direction is lower than those along the a, [110], and out-of-plane directions by 86, 43 and 69 μeV per V atom, respectively. To quantitatively estimate the Curie temperature (T_c) of the t-VP monolayer, a Monte Carlo simulation based on the Heisenberg model is performed. The Hamiltonian is defined as

Using the energy difference of different magnetic configurations and assuming that S = 1, we obtain the first nearest-neighbor exchange parameter J₁, the second nearest-neighbor exchange parameter J₂ and the third nearest-neighbor exchange parameter J₃ to be −3.81, −6.84 and −0.83 meV, respectively. The simulated magnetic moment versus temperature (Fig. 2c) shows that T_c of the t-VP monolayer is 106 K, which is distinctly higher than 45 K for CrI₃ monolayers²⁷ and 30 K for Cr₂Ge₂Te₆ bilayers,²⁹ and comparable to that of Fe₃GeTe₂ (130 K),²⁸ but is lower than those of the MnP (495 K), MnAs (711 K),¹⁷ 2D AXenes (484–1180 K),³⁰ Cr doped g-GeC (376 K)³¹ and CoGa₂X₄ (190–570 K) monolayers.³²

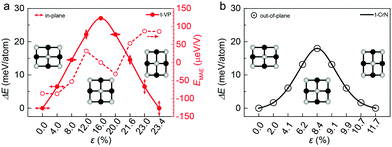
The rectangular lattice of the t-VP monolayer motivated us to further explore its ferroelasticity, which is assessed by computing the transition path and activation energy barrier. The initial and final states are degenerate, sharing the same structure but with the lattice rotated by 90° from each other as shown in Fig. 3. The transition state of the t-VP monolayer has a square lattice with lattice parameters a = b = 3.94 Å, where all the V atoms are coplanar. Ideally, the activation energy barrier should be larger than 10 meV per atom to make sure that the ferroelastic phase will not transform to a paraelastic phase at room temperature. The maximum stress during the ferroelastic switching should be less than that determined by the Young's modulus at the same strain to make sure that the structure will not undergo elastic instability. The energy profile of the t-VP monolayer with an applied uniaxial strain (Fig. 3) shows an activation energy barrier of 27 meV per atom. The ferro-elastic strain ε_FE, defined as (b − a)/a × 100%, reaches 23.4%. This activation energy barrier is much lower than those of black phosphorene (200 meV per atom),³³ MnNX (31–336 meV per atom),³⁴ GaTeCl (476 meV per atom),³⁵ and α-MPI (130–141 meV per atom),³⁶ comparable to the rare earth metal pnictides (3–48 meV per atom),^16,37 and AgF₂ (51 meV per atom)³⁸ but is higher than that of α-SnO (0.37 meV per atom).¹⁵ The maximum stress reaches 0.22 N m⁻¹ at ε = 4%, less than 1.57 N m⁻¹ as determined by the Young's modulus, indicating that the ferroelastic switching should be reachable in experiments.

Fig. 3 Calculated minimum energy pathways for ferroelastic switching of the t-VP (a) and t-CrN (b) monolayers, along with the magnetocrystalline anisotropic energy (E_MAE) for ferroelastic switching of the t-VP monolayer. Insets illustrate the evolution of lattice structures with the applied strains. The in-plane easy-axis directions of the monolayers are marked by arrows, while the out-of-plane easy-axis directions are marked by point circles.

According to the lattice symmetry, the in-plane easy-axis of the t-VP monolayer along the b direction will be reoriented to the a direction after ferroelastic switching, which means that we can control the ferromagnetism by an external strain. To investigate how the strain affects the easy-axis direction, we examine the change in MAE per V atom along the b direction with respect to that along the a direction with the applied strain (Fig. 3a). The strain increases the MAE from −87 μeV at ε = 4.0% to −53 μeV at ε = 8.0%, suggesting that the magnetization keeps oriented along the b direction. With further increasing ε to 12.0%, the MAE becomes positive to switch the magnetization along the a direction. At ε = 16.0%, the monolayer reaches an AFM transition state with isotropic in-plane MAE. Beyond the transition state, the MAE follows the same variation trend as that in the process from the initial to the transition state, but with an opposite sign. It reaches 86 μeV at the final state, confirming a complete switching of the magnetization direction from the b to the a direction. These results delineate an explicit coupling between the ferroelasticity and the ferromagnetism.

We then examine the electronic properties of the t-VP monolayer, based on results from the HSE06 functional. The spin-polarized band structure in the ferromagnetic ground state is shown in Fig. 4a. Two conductive bands in the majority-spin channel cross the Fermi level, while an indirect bandgap of 1.28 eV appears in the minority-spin channel. Therefore, the t-VP monolayer is an intrinsic ferromagnetic half-metal that can produce a completely spin-polarized current.

Fig. 4 (a) Spin-polarized electronic band structures of the t-VP monolayer. The inset shows a zoomed-in view of the 3D energy-momentum plot of the Dirac cone near the Fermi level. The red and blue lines represent band structures of the spin-up and spin-down channels, respectively. (b) The Dirac cone (dashed lines) opens a gap of 47 meV (black lines) when considering the SOC. (c) Spin-polarized band structure of the [100] edge of a t-VP nanoribbon, with the edge-contributed flat bands highlighted in colors. The bands in the majority- and minority-spin channels are shown in the left and right panels, respectively.

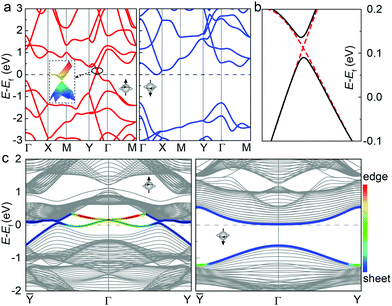
More interestingly, the two conductive bands cross to form a Dirac cone, with linear dispersion around the crossing point located at 0.18 eV above the Fermi level. A three-dimensional energy-momentum plot of the Dirac cone shows that the two states only cross at a single point as illustrated by the inset of Fig. 4, like graphene. The electron and hole carriers share the same anisotropic Fermi velocities, reaching 4.45 × 10⁵ along the Y–Γ direction and 3.25 × 10⁵ m s⁻¹ along the Γ–Y direction, comparable to the isotropic value of 8 × 10⁵ m s⁻¹ in graphene. Using the LDA+U (with U_eff = 3 eV) method and including the SOC effect, a gap of 47 meV is opened at the crossing point (Fig. 4b). The valence band states contribute a quantum Berry phase of π for each gapped Dirac cone, so that the two Dirac cones in the whole Brillouin zone correspond to a Chern number C = 1.³⁹ To confirm whether the edge was protected by the topological states, we have calculated the band structure of a semi-infinite t-VP ribbon with the edge oriented along the a direction (see Fig. 1c), as shown in Fig. 4c. The Dirac cone in the minority-spin channels produces two degenerated flat edge states when projected onto this edge. The combined ferromagnetic half-metallicity and nontrivial topological properties suggest the t-VP monolayer as a promising candidate to explore the quantum anomalous Hall effect.

In addition, we also identify a highly stable t-CrN monolayer that has the same atomic structure as the t-VP monolayer, as listed in Table 1. The formation energy of the t-CrN monolayer is −164 meV per atom, indicating that it promises to be experimentally synthesized as well. The phonon dispersion spectrum (Fig. S1b, ESI†) and ab initio molecular dynamics simulations (Fig. S1d, ESI†) confirm the high kinetic and thermal stability of the t-CrN monolayer.

The t-CrN monolayer possesses similar ferroelasticity to the t-VP monolayer. The t-CrN monolayer shares the same transition pathway and transition state structure as those of the t-VP monolayer. The obtained total energy as a function of the applied uniaxial strain shows a ferroelastic transition barrier of 18 meV per atom, lower than that of the t-VP monolayer. Its ferroelastic strain becomes ε_FE = 11.7% (Fig. 3b). The maximum stress during the ferroelastic switching is 0.46 N m⁻¹ at ε = 4.3%, less than 1.69 N m⁻¹ determined by the Young's modulus. These parameters are conducive to experimental manipulation of the ferroelasticity.

The t-CrN monolayer also possesses an FM ground-state, with a magnetic moment of 5.0 μ_B in the unit cell (Table 2). The magnetization densities are concentrated on metal atoms, as shown by the spin density distribution in Fig. S3 (ESI†). The FM state is more stable than the AFM1, AFM2, AFM3 and AFM4 states by 78.3, 294.0, 81.1 and 58.8 meV per Cr atom, respectively. These energy differences are considerably larger than the corresponding values of the t-VP monolayer, while comparable to those of a MnX monolayer.¹⁷ The Monte Carlo simulation (Fig. 2c) estimates an unusually high T_c of 478 K for the t-CrN monolayer. Different from the case of the t-VP monolayer, the easy-axis of the t-CrN monolayer is oriented out-of-plane (Table 2), which means that the ferroelastic switching cannot turn its easy-axis direction.

The t-CrN monolayer shows fractional magnetic moments per Cr atom, indicative of its itinerant magnetism. This is confirmed by spin-polarized band structures shown in Fig. S4 (ESI†). Therefore, the Stoner model can be employed to understand the mechanism underlying the FM ordering. In this model, the ferromagnetism is favored if ID(E_f) > 1, where I is the Stoner parameter and D(E_f) is the density of states at the Fermi level. Using the relation 〈ε_k〉 = IM_avg,²⁴ where 〈ε_k〉 is the average exchange splitting for the two band structures, we obtain I = 1.04. Fig. S4 (ESI†) shows that the non-spin-polarized density of states at the Fermi level is 0.99 states eV⁻¹ per Cr atom. Therefore, the Stoner criterion ID(E_f) > 1 is satisfied to induce the ferromagnetic ordering in the t-CrN monolayer.

These multiferroic materials may be synthesized on Si/SiO₂ substrates using a chemical vapor deposition approach under ambient pressure. The vanadium chloride and chromium chloride can be chosen as solid precursors of metal elements for synthesizing the t-VP and t-CrN monolayers, respectively. We propose to use NH₃ as the gas precursor for the t-CrN monolayer, while P powers as a solid precursor for the t-VP monolayer. To keep out the oxygen and other impurities, the growth process can be performed under an Ar atmosphere. With this method, tetragonal FeTe monolayers of similar structure to those of the t-VP and t-CrN monolayers have been successfully synthesized.⁴⁰

Conclusions

We report a 2D multiferroic t-VP monolayer that possesses a ferromagnetic ground-state with an estimated Curie temperature of 106 K. Meanwhile, the rectangular lattice structure of the t-VP monolayer gives rise to in-plane ferroelasticity with a moderate activation energy barrier of 27 meV per atom and a reversible strain of 23.4%. As the easy-axis of magnetization in the t-VP monolayer is along the b direction, the ferromagnetism is strongly coupled with the ferroelastic transition by the lattice-dependent magnetocrystalline anisotropy, and, thereby, can be controlled by an applied elastic strain. Moreover, the t-VP monolayer is half-metallic with a Dirac cone residing in the majority-spin channel, while an insulating bandgap in the minority-spin channel. The Fermi velocities of completely spin-polarized electrons can reach 4.45 × 10⁵ m s⁻¹. We also predict a multiferroic t-CrN monolayer that possesses itinerant ferromagnetism, with a high Curie temperature of up to 478 K. Yet, its easy-axis is oriented out-of-plane, making the ferromagnetism loosely coupled with its ferroelasticity. The ferroelastic energy barrier and reversible strain become 18 meV per atom and 11.7% for the t-CrN monolayer, respectively. The tetragonal 2D materials with an intriguing collection of electronic and magnetic properties provide new candidates for fabricating nonvolatile memories and a platform for exploring multiferroics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (2019YFA0705400), the National Natural Science Foundation of China (11772153, 22073048), the Research Fund of State Key Laboratory of Mechanics and Control of Mechanical Structures (MCMS-E-0420K01), the Natural Science Foundation of Jiangsu Province (BK20190018, BK20212008), the Fundamental Research Funds for the Central Universities (NJ2020003), and a Project by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

Notes and references

1. C. Xiao, F. Wang, S. A. Yang, Y. Lu, Y. Feng and S. Zhang, Adv. Funct. Mater., 2018, 28, 1707383.
2. C. Huang, J. Guan, Q. Li, F. Wu, P. Jena and E. Kan, Phys. Rev. B, 2021, 103, L140410.
3. J.-H. Feng, G. Li, X.-F. Meng, X.-D. Jian, Z.-H. Dai, Y.-C. Zhao and Z. Zhou, Front. Phys., 2019, 14, 43604.
4. Z. Tu and M. Wu, Adv. Electron. Mater., 2019, 5, 1800960.
5. N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694–6709.
6. W. Luo, K. Xu and H. Xiang, Phys. Rev. B, 2017, 96, 235415.
7. J. J. Zhang, L. Lin, Y. Zhang, M. Wu, B. I. Yakobson and S. Dong, J. Am. Chem. Soc., 2018, 140, 9768–9773.
8. C. Huang, Y. Du, H. Wu, H. Xiang, K. Deng and E. Kan, Phys. Rev. Lett., 2018, 120, 147601.
9. T. Zhong, X. Li, M. Wu and J.-M. Liu, Natl. Sci. Rev., 2020, 7, 373–380.
10. Q. Yang, W. Xiong, L. Zhu, G. Gao and M. Wu, J. Am. Chem. Soc., 2017, 139, 11506–11512.
11. L. Kou, Y. Ma, T. Liao, A. Du and C. Chen, Phys. Rev. Appl., 2018, 10, 024043.
12. Z. Tu, M. Wu and X. C. Zeng, J. Phys. Chem. Lett., 2017, 8, 1973–1978.
13. X. Liu, A. P. Pyatakov and W. Ren, Phys. Rev. Lett., 2020, 125, 247601.
14. Y. Zhao, J. J. Zhang, S. Yuan and Z. Chen, Adv. Funct. Mater., 2019, 29, 1901420.
15. L. Seixas, A. S. Rodin, A. Carvalho and A. H. Castro Neto, Phys. Rev. Lett., 2016, 116, 206803.
16. J. H. Yuan, G. Q. Mao, K. H. Xue, J. Wang and X. S. Miao, Nanoscale, 2020, 12, 14150–14159.
17. B. Wang, Y. Zhang, L. Ma, Q. Wu, Y. Guo, X. Zhang and J. Wang, Nanoscale, 2019, 11, 4204–4209.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
19. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
20. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
21. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
22. J. Paier, M. Marsman, K. Hummer, G. Kresse, I. C. Gerber and J. G. Angyan, J. Chem. Phys., 2006, 124, 154709.
23. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
24. H. L. Zhuang, P. R. C. Kent and R. G. Hennig, Phys. Rev. B, 2016, 93, 134407.
25. Z. Zhang, X. Liu, B. I. Yakobson and W. Guo, J. Am. Chem. Soc., 2012, 134, 19326–19329.
26. N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136.
27. B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273.
28. Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J. H. Chu and X. Xu, Nat. Mater., 2018, 17, 778–782.
29. C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269.
30. X. Jiang, Q. Liu, J. Xing and J. Zhao, J. Phys. Chem. Lett., 2019, 10, 7753–7759.
31. X. Fan, J. Jiang, R. Li and W. Mi, J. Phys. Chem. C, 2021, 125, 13688–13695.
32. S. Zhang, R. Xu, W. Duan and X. Zou, Adv. Funct. Mater., 2019, 29, 1808380.
33. M. Wu and X. C. Zeng, Nano Lett., 2016, 16, 3236–3241.
34. M. Hu, S. Xu, C. Liu, G. Zhao, J. Yu and W. Ren, Nanoscale, 2020, 12, 24237–24243.
35. S. H. Zhang and B. G. Liu, Nanoscale, 2018, 10, 5990–5996.
36. T. Zhang, Y. Ma, L. Yu, B. Huang and Y. Dai, Mater. Horiz., 2019, 6, 1930–1937.
37. B. Xu, H. Xiang, J. Yin, Y. Xia and Z. Liu, Nanoscale, 2017, 10, 215–221.
38. X. Xu, Y. Ma, T. Zhang, C. Lei, B. Huang and Y. Dai, Nanoscale Horiz., 2020, 5, 1386–1393.
39. Y. Li, J. Li, Y. Li, M. Ye, F. Zheng, Z. Zhang, J. Fu, W. Duan and Y. Xu, Phys. Rev. Lett., 2020, 125, 086401.
40. L. Kang, C. Ye, X. Zhao, X. Zhou, J. Hu, Q. Li, D. Liu, C. M. Das, J. Yang, D. Hu, J. Chen, X. Cao, Y. Zhang, M. Xu, J. Di, D. Tian, P. Song, G. Kutty, Q. Zeng, Q. Fu, Y. Deng, J. Zhou, A. Ariando, F. Miao, G. Hong, Y. Huang, S. J. Pennycook, K. T. Yong, W. Ji, X. Renshaw Wang and Z. Liu, Nat. Commun., 2020, 11, 3729.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00353d

---