Open Access Article
Open Access ArticleInsect-inspired nanofibrous polyaniline multi-scale films for hybrid polarimetric imaging with scattered light†
Ji
Feng
 a,
Xiaojing
Weng
a,
Miguel A. G.
Mandujano
a,
Baurzhan
Muminov
a,
Gaurav
Ahuja
a,
Eugenio R.
Méndez
b,
Yadong
Yin
a,
Xiaojing
Weng
a,
Miguel A. G.
Mandujano
a,
Baurzhan
Muminov
a,
Gaurav
Ahuja
a,
Eugenio R.
Méndez
b,
Yadong
Yin
 c and
Luat T.
Vuong
c and
Luat T.
Vuong
 *a
*a
aDepartment of Mechanical Engineering, University of California, Riverside, Riverside, CA 92521, USA. E-mail: Luatv@ucr.edu
bDivisión de Física Aplicada, CICESE, Carretera Ensenada-Tijuana 3918, Ensenada, BC 22860, Mexico
cDepartment of Chemistry, University of California Riverside, Riverside, CA 92521, USA
First published on 15th February 2022
Abstract
We demonstrate a bio-inspired coating for novel imaging and sensing designs: the coating sorts different colors and linear polarizations. This coating, composed of conducting, nanofibrous polyaniline in an inverse opal film (PANI-IOF), is inexpensive and can feasibly be deposited over large areas on a range of flexible and non-flat substrates. With PANI IOFs, light is scattered into azimuthally polarized Debye rings. Subsequently, the diffracted speckle patterns carry compressed representations of the polarized illumination, which we reconstruct using shallow neural networks.
New conceptsPolarimetric color sensors, although they are increasingly in demand, remain expensive. Inexpensive alternatives to compact polarimetric sensors may lie in computer vision algorithms, which extract and deconvolve information from conventional sensor data with optical encoders. This research, for the first time, demonstrates novel optical physics associated with multi-scaled, ordered polymers, and its promising prospects in computer vision applications. Our work connects self-assembled materials to metasurfaces, which shape scattering from subwavelength conducting domains in combination with periodically-patterned geometries and diffraction. Unlike metasurfaces that are usually fabricated by using top-down methods, our multi-scale polymers with photonic crystal structures and vertically aligned nanofibers are synthesized in bottom-up approaches, which greatly reduce the cost. The highly ordered periodic structure not only provides strong structural color, but polarization sorting, which occurs largely via the dipole scattering of vertically-aligned nanofibers. To provide insight on the potential applications, we demonstrate non-coaxial polarimetric imaging with neural networks using our multi-scale materials as an optical encoder, to separate color and polarization. Our work points to numerous opportunities for self-assembled multi-scale materials for hybrid optical computing and imaging applications. |
Introduction
Many insect species have evolved complex, light-sensing structures that span multiple scales of order;1–4 these structures filter specific colors and are sensitive to different degrees of light polarization in ways that confer advantages in particular environmental niches.5–8 For example, locusts and other flying insects sense the horizontally polarized light from water surfaces, which aids navigation.9 Although humans do not sense the vector quality of light, polarized light patterns are shaped and filtered by anisotropic materials and oblique-angled light scattering, reflection, and refraction.10 As such, polarization-sensitive optics offer novel sensing capabilities. For example, polarization information can be used to enhance the resolution of and enable the image reconstruction in turbid or cloudy environments.7,11–14Generally, insects’ sensitivity to light polarization coincides with the presence of polarization-sensitive detectors.5–8 This sensitivity is analogous to conventional optical analyzers that achieve polarization detection, which requires either an integration of sensors for different polarization measurements or one camera with a moving polarizer. Although some commercial products carry spectral and polarization-sensitive pixels to extrapolate polarization without bulky or moving optics, these camera sensors require a high degree of complexity in both fabrication and calibration techniques.15,16 An alternative solution is to introduce computer vision algorithms, which extract and deconvolve information from conventional sensor data.17–19 However, in order for computational approaches to be utilized efficiently, information must be filtered or compressed. Optical diffusers, metamaterials, or other optical encoders serve this purpose and are advantageous, if not necessary for computation-based image reconstruction.20–26 Using both optics and computation reduces time, power, memory, and complexity requirements; this hybrid approach may also provide additional information via a single sensor shot, which is useful for image enhancement.27–30
In this communication, we show that multi-scaled structures with both material anisotropy and surface patterning may be employed for polarization-sensitive computer vision applications. Our insect-inspired design stems from knowledge of the corneal nanostructures on compound eyes,2–4 which would optically shape and sort light via scattering. Such structures would enable polarization sensitivity without polarization-sensitive analyzers. While the existence of polarization sensitivity with polarization-insensitive sensors and image preprocessing in an insect superposition compound eye have been suggested,4,5,31,32 our work indicates that this implementation is not only possible but feasible.
Here, instead of purely dielectric or metal metasurfaces, we show that conducting polymer nanowire assemblies have tremendous potential, especially for large-surface applications: e.g., surfaces with areas the size of camera lenses. We select polyaniline (PANI) as the material and fabricate multi-scale features in photonic crystal films via a bottom-up approach. PANI is a linear polymer with rich chemistry and tunable electrical and optical properties.33–36 The low cost, low toxicity, ease of synthesis, high stability (compared to other conducting polymers), and good compatibility (with a variety of material types) make PANI a promising candidate for energy storage, optoelectronics, spintronics, sensing, and biomedical applications.35,37,38
We harness PANI's capacity to form nanofibers when the monomers are distributed freely in solution. When aligned, these nanofibers respond actively to switch the absorbed polarization of light.39 With self-assembled PANI multi-scale structures, there are numerous opportunities for inexpensive, large-area fabrication over flexible and non-flat substrates. To our knowledge, although multi-scale photonic crystals are widely found in nature,40,41 the production of multi-scale photonic structures capable of filtering color and polarization has not been demonstrated in a synthetic material fabricated by bottom-up methods.
When PANI nanowires are aligned and organized into periodic lattice structures, the color and polarization features of an image are spatially “pooled” together and separated in the scattered diffraction patterns. This pooling is important for sensing the scattered light as it increases the intensity measured by a sensor. In our approach, we produce two-dimensional (2D) PANI inverse-opal films (IOFs) with open-pore structures where the PANI nanowires are aligned radially to the polystyrene (PS). The ordering of PANI nanowire structures in combination with the ordering of the larger-scale periodic lattice yields an imaging point spread function that separates polarization (azimuthally) and color (radially).42
The unique, polarization-sensitive diffraction of the PANI IOF may find a variety of applications for enhanced and non-coaxial imaging with scattered light. “Enhanced” refers to the fact that the PANI IOF is a transparent subwavelength monolayer coating through which direct, high-resolution conventional imaging is still possible. In this way, the additional dimension of the image (i.e., polarization in our case) drawn from the diffraction may simultaneously be used to infer additional information about a conventional image or scene.43–45 “Non-coaxial” refers to a geometry where the object, imaging lens, and a sensor are not aligned. One distinct motivation for achieving non-coaxial image reconstruction with an optical film is high-field-of-view computational cameras, which are not limited by the camera pupil function.46–48 Our PANI IOF directs scattered light into a diffractive mode, which may be captured by a sensor for high-field-of-view imaging.
The strength of the PANI IOF diffraction is notable: although the angular separation of color follows that of a multi-layered Bragg feature, light only interacts with a sub-wavelength monolayer grating structure. In this way, the strong light interactions with the conducting polymer assemblies are analogous to metasurfaces with sub-wavelength, semi-metallic domains, though with low transmission losses. With PANI IOFs, we reconstruct the illuminated polarized patterns from a small sample of the diffracted light speckle using simple, shallow neural networks. The image compression and color filtering from the speckle,49 which is only visible with the lattice structure, reduces the number of pixels needed in postprocessing. Therefore, the implementation of multi-scaled scattering structures such as PANI IOFs can reduce the precision required of sensors, or the algorithmic complexity (the number of neural network layers) required for image reconstruction.
Results
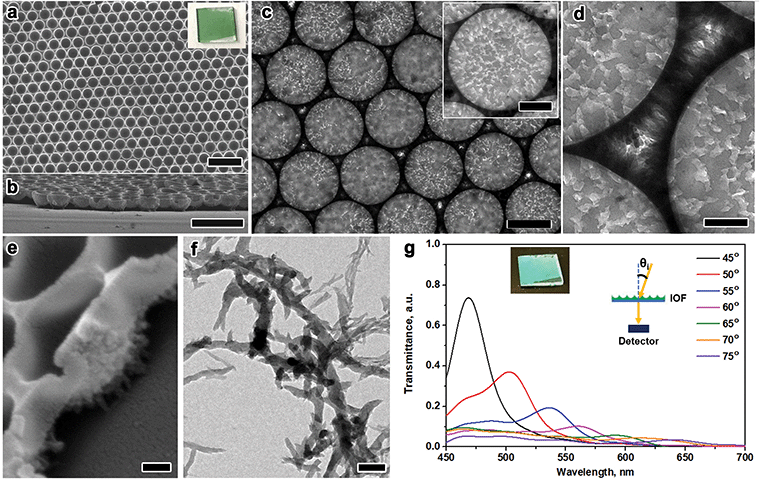
PANI IOFs are generally synthesized through hard-templating strategies.50,51 In this work, 2D PS nanosphere assemblies are formed at the air–water interface; then, PANI grows around those PS nanospheres via chemical oxidative polymerization, which leads to the open-pore structures.52 The PS film of close-packed nanospheres is formed by slowly dripping a suspension of 5 wt% PS nanospheres in ethanol and H2O (v/v = 1/1) onto the air–water interface. Adsorption of the PS nanospheres at the air–water interface is thermodynamically favorable and solvent convection squeezes the nanospheres into the close-packed assemblies.53 The PS film is collected on a glass substrate, left to dry, and transferred to the PANI synthesis solution. During the transfer, due to the minimization of the surface energy, the PS film peels off the substrate and settles on top of the solution. After polymerization and removal of the PS templates, a green film is collected on a glass slide (Fig. 1a, inset). Although there has been research with polyaniline in two-dimensional photonic crystal structures, the synthesis of monolayer polyaniline and its multi-scale, hierarchical structure are rarely mentioned. Additionally, previous work generally focuses on the structural color without mentioning its polarization-responsive properties.54–56 The optical characteristics of PANI's multi-scale structure are underexplored.The multi-scale morphology of the PANI IOF is evident from its electron microscopy characterization (Fig. 1). The top-view and cross-section SEM images (Fig. 1a and b) show the single-layer, hexagonally packed nanocup arrays with openings of 670 nm in diameter. The radial alignment of the nanofibers is observed in TEM and SEM images (Fig. 1c–e). The nanofibers around the nanocups maintain a similar shape but are narrower compared to the nanofibers in solution (Fig. 1f). The PANI IOFs have nanofibers in the middle (Fig. 1c) and spiny nanofibers around the sides of the nanocups (Fig. 1d). These images indicate that the nanofibers are radially aligned. The alignment of the nanofibers is also observable from the SEM images (Fig. 1e), which show the spiny protrusions pointing from the nanobowl to the substrate. The vertical growth of the nanofibers is due to the low concentration of the aniline monomers absorbed on the PS surface. Others have utilized this alignment to engineer surface hydrophobic interactions and energy-related devices.57–59 By contrast, we achieve two scales of order: IOFs composed of closed-packed spherical nanovoids and the radial packing of nanofibers around the pores. PANI IOF shows structural color as a 2D photonic crystal (Fig. 1g, inset). When fixing the detector at the sample normal and measuring the diffraction through the sample with an increasing incident angle, the peak continuously redshifts in the visible light range (Fig. 1g).
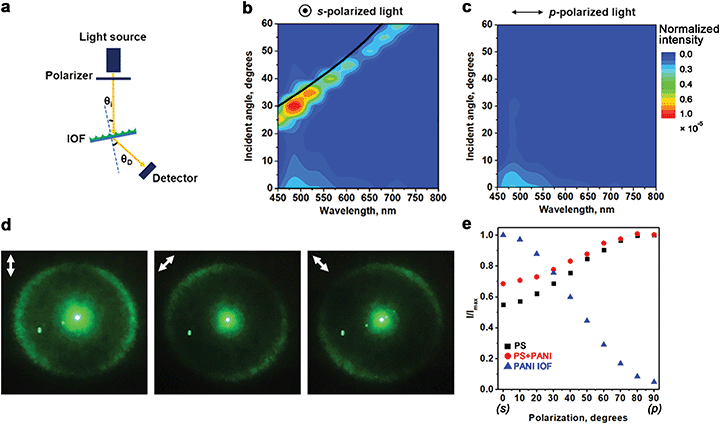
The structural color of the PANI IOF exhibits strong polarization dependence. Fig. 2a–c shows a comparison of the diffraction spectra with s- and p-polarized light irradiation. In our setup (Fig. 2a), a polarizer is placed in front of a white light source. The polarized light is incident on the PANI IOF at an angle of (θi), and the scattered light in the transmission direction is collected by an optical fiber that is placed at a specific angle to the sample normal (θD). Fig. 2b and c show the corresponding dispersion spectra, when θD is fixed at 15° and θi is increased from 0° to 60°. With s-polarized light illumination, the transmission peak shifts with the angle θi in a manner that is governed by diffraction and the lattice period. The −1 order appears for angles of incidence determined by the grating equation:
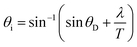 | (1) |
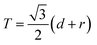 where d = 670 nm and r = 25 nm are the sizes of the pore and the edge respectively. A black line in Fig. 2b shows this relation for a lattice spacing of 645 nm, which follows the diffraction peak measured in the experiments. Without a periodic lattice structure i.e., with a random PANI film, the diffracted light from s-polarized light illumination from the PANI IOF has lower intensity.
where d = 670 nm and r = 25 nm are the sizes of the pore and the edge respectively. A black line in Fig. 2b shows this relation for a lattice spacing of 645 nm, which follows the diffraction peak measured in the experiments. Without a periodic lattice structure i.e., with a random PANI film, the diffracted light from s-polarized light illumination from the PANI IOF has lower intensity.
The p-polarized transmitted diffraction peak is not observed in-plane when the PANI IOF is illuminated with p-polarized light. Instead, the p-polarized light is scattered and measured outside of the plane of incidence. Fig. 2d shows the polarization-dependent diffraction of the PANI IOF. This Debye ring of the photonic structure is produced with a 532 nm laser at normal incidence (Fig. 2e) and is also the point spread function for a point that is located at a far distance from the sample. Here, the ring is shown on a piece of white paper, and the photos are taken from the back side of the paper. In contrast to the complete ring produced by self-assembled solid spheres,60 the light scattered from PANI IOF exhibits incomplete rings. The parts of the ring on the axis of the light polarization are missing. The Debye ring is largely azimuthally polarized when the incident light is unpolarized, circularly polarized, or carries components of both s- and p-polarizations. Spaces in the Debye ring are observed when the light polarization is linearly polarized.
A comparison of the polarization-dependent transmission characteristics of the PANI IOF with other periodic nanostructures further reveals its unique properties (Fig. 2e). Here we vary the angle between the linear polarization axis and the plane of incidence from s (transverse-electric) to p (transverse-magnetic). We measure the relative intensity for a fixed incident angle (θi = 30°) and fixed detection angle (θD = 15°). We plot the transmitted intensity, normalized by the maximum intensity (Imax) that is measured in this range. The extinction ratio between s and p-polarized light is calculated to be 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 according to Imax/Imin: 1 where Imin is the minimum intensity measured in this range. Hexagonally packed PS nanospheres (PS) and composite films of PANI over PS (PS-PANI) show a higher ratio of transmission I/Imax for p-polarized light than for s-polarized light, which is a trend that would be expected and associated with simple refraction and Fresnel equations. However, the Debye rings from hexagonally packed PS and PS-PANI composite films are round or exhibit three-fold symmetry associated with the close-packed geometry; the Debye rings for PS and PS-PANI (Fig. S1, ESI†) are not broken as they are for PANI IOFs. The curves in Fig. 2e point to the contrast in the polarization trends associated with light refraction and light scattering.
1 according to Imax/Imin: 1 where Imin is the minimum intensity measured in this range. Hexagonally packed PS nanospheres (PS) and composite films of PANI over PS (PS-PANI) show a higher ratio of transmission I/Imax for p-polarized light than for s-polarized light, which is a trend that would be expected and associated with simple refraction and Fresnel equations. However, the Debye rings from hexagonally packed PS and PS-PANI composite films are round or exhibit three-fold symmetry associated with the close-packed geometry; the Debye rings for PS and PS-PANI (Fig. S1, ESI†) are not broken as they are for PANI IOFs. The curves in Fig. 2e point to the contrast in the polarization trends associated with light refraction and light scattering.
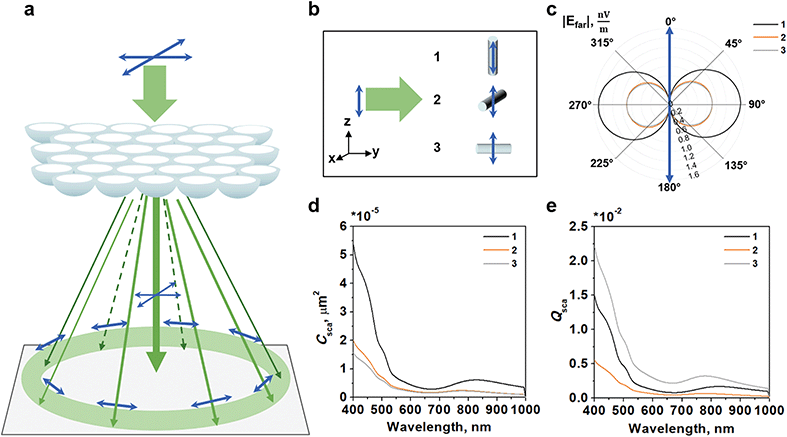
We attribute the polarization-dependent structural color of the PANI-IOF to its multi-scaled structure: the ordered nanovoids and the alignment of the PANI nanofibers function in concert to produce the azimuthally polarized Debye ring (Fig. 3). In the absence of the nanowires or with a nanosphere-dominated structure (with ordered PS nanospheres or PS-PANI nanospheres), the Debye ring is uniformly polarized and almost unchanged with polarization (Fig. S1, ESI†); therefore, there is minimal spatial filtering of the polarization. On the other hand, in the absence of a periodic lattice structure (with an unpatterned layer of randomly oriented nanowires), the dipole scattering is randomly directed and diffuse.
The underlying mechanism of the polarization-dependent dipole scattering of the PANI is expected to stem from both dielectric and semi-metallic optical properties of the 20 to 100 nm diameter nanowires.61,62 We simulate the light scattering from a single nanowire (30 nm diameter × 120 nm length) with 3 orthogonal geometries (Fig. 3b). The far-field electric field distribution of the PANI nanowires in this range of frequencies indicates that the dominant oscillation for charges is a dipole excitation. Fig. 3c shows the far-field distribution when the PANI IOF is illuminated with 532 nm light and 1 V m−1 electric fields. This dominant mode and dipole scattering from a single nanowire explains why the experimentally-measured Debye ring is broken where the polarization vector intersects with the ring.
The role of the nanowire alignment is subject to interpretation. With the 3 geometries studied, the calculated scattering cross-section Csca is greatest when light is polarized along the length of the nanowire in geometry 1 (Fig. 3d). However, Csca is a measure of the power scattered by a single nanowire and in this geometry, the transversal area is also larger since the wire is aligned perpendicular to the direction of light. When we normalize and calculate the scattering efficiency Qsca = Csca/A, where A is the transversal area normal to the direction of light, the calculated scattering efficiency Qsca is greatest when light travels along the length of the nanowire in geometry 3 (Fig. 3e). In other words, the PANI scattering is strongest for geometry 1 when we normalize by number of nanowires, but strongest for geometry 3 when we normalize by the sample surface area.
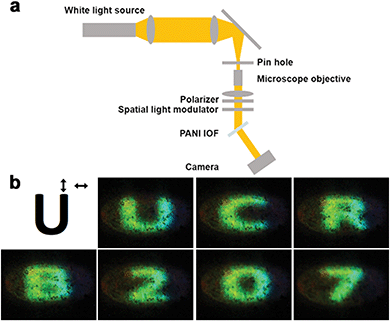
To demonstrate the usefulness of the PANI IOF structure for polarimetric imaging, we choose two non-coaxial imaging geometries that employ the PANI IOF as the optical encoder for spectral and polarization filtering. White light from a stabilized tungsten-halogen lamp (Thorlabs SLS301) is collimated and imprinted with a polarized pattern using a liquid-crystal spatial light modulator SLM (HOLOEYE LC 2012). A polarizer is used in front of the SLM. The beam is 7 mm in diameter and is imaged on the PANI IOF sample. No further polarization or spectral filter is used. The basic setup is shown in Fig. 4a.
In the first demonstration, we capture light with a digital single-lens reflex (DSLR) camera with a narrow aperture setting and long shutter time: we image the plane of the PANI IOF. As shown in the upper-left inset of Fig. 4b for the letter “U” (a 200 × 200-pixel image), the background (white) and the letter shape (black) are s- and p-polarized, respectively. Since the image is not amplitude-modulated, the pattern is not observed when imaging the light transmitted through the PANI IOF, either when viewed directly or imaged on a screen. However, when looking at the sample from the angle where the scattered light is captured, the letters and numbers are detected clearly and with high contrast. The clarity of the shapes confirms the sensitive response of the PANI-IOFs to polarized light.
In this first experiment, the DSLR camera isolates the polarization-encoded patterns that illuminate the polyaniline film. Additionally, the camera imaging system requires a narrow-aperture multi-lens system with a long shutter time. This camera provides additional spatial filtering and fine adjustment of depth of field and focus plane, which is necessary in order to remove the diffractive artifacts from the SLM pixel grid. To move towards inexpensive and lightweight alternatives for polarimetric imaging, we employ the PANI IOF as a diffractive encoder in a second experiment.
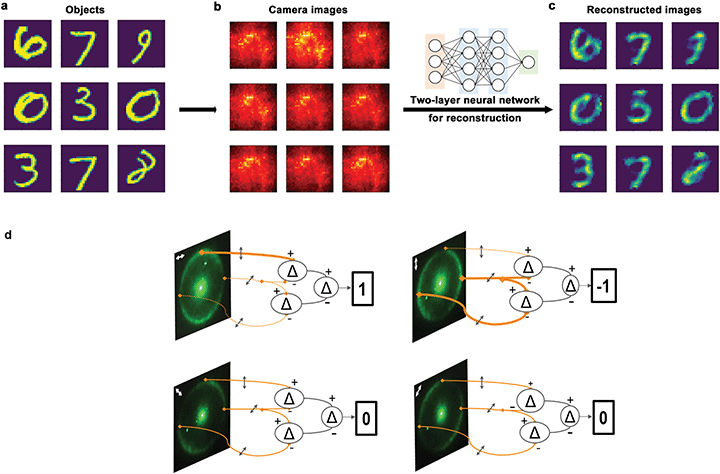
In this second experiment, we use the PANI IOF as a polarimetric encoder for lensless imaging with a shallow neural network. Here, the combination of polarization-dependent light absorption and scattering in the PANI IOF provides spatial correlations of the illuminated patterns.63 The setup is similar to that shown in Fig. 4a with a few changes. First, instead of imprinting the beam with typeset letters and numbers, we imprint 5000 images of the MNIST handwritten dataset (Fig. 5a) and train a neural network to learn from 80% of these 5000 images. Second, instead of imaging with a DSLR camera in the plane of the PANI IOF, we use a simple convex lens and bare CCD sensor (Thorlabs DCU224M) to image a plane that is 4 millimeters from the PANI IOF. At this location, the camera captures speckle patterns, which do not resemble the objects. These speckles vary slightly depending on the polarized pattern. From the 1024 × 1280 pixel images containing speckle patterns, a block of 600 × 600 pixels is acquired by the camera and downsized to 28 × 28 pixels (Fig. 5b). This array of 8-bit integer numbers is normalized to a range of 0 to 1, reshaped into a 1-D vector, and provided as an input to the neural network.
This neural network is a simple, dense, 2-layer model.27 Both layers of the model use a rectified linear-unit (‘relu’) activation function, a mean-squared-error (‘mse’) loss function, and adaptive moment estimation (‘adam’) strategy for updating the weights. The reconstructed images (Fig. 5c) agree well with the ground truth images (Fig. 5a) and the numbers are distinguishable. Fig. 5d illustrates our rationale and shows how the azimuthally-polarized Debye ring could be used to calculate the first Stokes value with a 2-layer shallow neural network. With a similar, 2-layer neural network—but with logistic regression for the final neural network layer—we achieve a classification accuracy of 87%. Although the accuracy of this approach may not be impressive compared to other lensless imaging approaches, this is the first demonstration, to our knowledge, of non-coaxial polarimetric imaging. This proof-of-concept experiment with PANI IOF demonstrates viability for polarimetric lensless imaging in low-power, real-time applications.
Discussion and conclusion
The PANI IOF's nanowire alignment within a periodic pattern leads to scattered light being directed into azimuthally polarized rings with different radii depending on the color (Fig. S2, ESI† and eqn (1)). In our experimental demonstrations using a non-coaxial white-light source and CCD camera sensor (to capture a portion of this ring), we demonstrate conventional and lensless polarimetric imaging. In both cases, the multi-scaled structure is critical for the polarimetric image reconstruction.That is, when we replace a flat, unstructured PANI film for the PANI IOF, it is not possible to repeat the polarimetric image reconstruction from either experiment. In the first experiment (Fig. 4), there is no diffracted mode or Debye ring: the camera does not have the sensitivity to image the polarization-dependent scattering. In the second experiment (Fig. 5), the measured speckle patterns are faint, small, and barely visible; following the previously used process but using a longer camera integration time, we are unsuccessful at reconstructing images using the PANI flat film. With a variety of dense model architectures, we find that lensless imaging is not available with flat PANI films as it is with the PANI IOFs.
While polarization-dependent scattering and absorption is present in the speckle patterns of an unstructured PANI flat film, the scattered light is too diffuse to be imaged with a conventional 8-bit camera. Our results therefore identify important considerations when pairing optical encoders and detector/sensors for hybrid computer vision approaches. We anticipate that polarimetric imaging is possible with PANI flat films if a more sensitive detector or camera sensor is used. Non-line-of-sight imaging through scattering environments is achieved with single-photon avalanche detectors, for example.64–66 We note that the degree of order in a PANI IOF influences the diffraction and measured speckle intensity. Given connections to insect sensing,67 we consider that the degree of order in optical encoders is an important consideration for lensless imaging applications.
The structural color and spectral filtering may further be tuned by the PANI environment in future efforts. While the diffraction cone angle closely follows a Bragg relation [eqn (1)], the optical properties of PANI may be chemically tuned. Acid-doped PANI is highly absorbing at 435 nm and 875 nm due to polaron transitions. After deprotonation, the 875 nm band blueshifts. This chemical tunability does not affect the structure of the PANI IOF, which is fixed; however, the angle of the transmitted light changes when the PANI spectra changes. This chemical tunability of PANI's properties in a multi-scale structure would spatially filter a broad band of colors and may enable hyperspectral computational imaging with a conventional broadband sensor.
In conclusion, we report on the polarization-dependent diffraction of multi-scale structured monolayer PANI IOFs. The highly ordered 2D pore arrays and the PANI nanofibers around the pores contribute to spatially separate colors and different linear polarizations of light. The insect-inspired PANI IOF hexagonal structure is arguably more versatile than any linear grating due to this radially symmetric geometry. The lattice structure redirects scattered light and does not simply filter via absorption. To get a sense of the possible applications, consider an insect with a similarly structured PANI-IOF-coated lens as part of its visual apparatus; for this insect lens, both s- and p-polarizations are preserved and spatially separated regardless of the relative rotation of the insect with respect to the object. In other words, the main advantage of our structure, which utilizes scattering-based diffraction, is that it transmits and shapes more information than a linear polarizer that operates purely with absorption.
When PANI IOFs serve as the polarization-filtering layer, we are able to image polarized patterns conventionally and reconstruct the image from the speckle with shallow neural networks. The degree of order of the PANI IOF influences the intensity of the diffracted ring as well as these speckle patterns. Further research will explore how PANI IOFs may provide the full Stokes characterization for detecting polarization ellipticity. We believe the robust preparation of the IOF and the tunability of the PANI itself will make it a promising material in various areas such as compact polarimetric imaging, multimodal sensing, and computing applications.
Author contributions
J. F. completed the synthesis and all measurements. X. W. provided the assistance with Fig. 4 and 5. M. A. G. M., G. A., and B. M. completed the simulations to provide intuition for the analysis. E. M., and Y. Y. in aided discussions. J. F. wrote the first draft of the manuscript and revised the manuscript with L. T. V., who supervised the project.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge DARPA YFA Grant #D19AP00036, editing support from Ben Stewart <linkedin:benjamin-w-stewart >, and insightful discussions with Doekele Stavenga. M. A. G. M. is funded by a UC MEXUS-Conacyt postdoctoral fellowship (FE-20-139).References
- R. O. Prum, J. A. Cole and R. H. Torres, J. Exp. Biol., 2004, 207, 3999 CrossRef PubMed.
- A. Blagodatski, A. Sergeev, M. Kryuchkov, Y. Lopatina and V. L. Katanaev, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 10750 CrossRef CAS PubMed.
- K. C. Lee, Q. Yu and U. Erb, Sci. Rep., 2016, 6, 28342 CrossRef CAS PubMed.
- D. G. Stavenga, A. Meglič, P. Pirih, H. Koshitaka, K. Arikawa, M. F. Wehling and G. Belušič, J. Comp. Physiol., 2017, 203, 23 CrossRef CAS PubMed.
- T. Heinloth, J. Uhlhorn and M. F. Wernet, Front. Cell. Neurosci., 2018, 12, 50 CrossRef PubMed.
- T. Labhart and E. P. Meyer, Microsc. Res. Tech., 1999, 47, 368 CrossRef CAS PubMed.
- N. J. Marshall, S. B. Powell, T. W. Cronin, R. L. Caldwell, S. Johnsen, V. Gruev, T.-H. S. Chiou, N. W. Roberts and M. J. How, J. Exp. Biol., 2019, 222, jeb134213 CrossRef PubMed.
- A. Meglič, M. Ilić, P. Pirih, A. Škorjanc, M. F. Wehling, M. Kreft and G. Belušič, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 21843 CrossRef PubMed.
- N. Shashar, S. Sabbah and N. Aharoni, Biol. Lett., 2005, 1, 472 CrossRef CAS PubMed.
- G. Zheng, G. Liu, M. G. Kenney, Z. Li, P. A. He, S. Li, Z. Ren and Q. Deng, Opt. Express, 2016, 24, 6749 CrossRef CAS PubMed.
- H. Hu, L. Zhao, X. Li, H. Wang, J. Yang, K. Li and T. Liu, Opt. Express, 2018, 26, 25047 CrossRef PubMed.
- Y. Li, H. Lu, J. Li, X. Li, Y. Li and S. Serikawa, Comput. Electr. Eng., 2016, 54, 68 CrossRef.
- Y. Y. Schechner, Philos. Trans. R. Soc., B, 2011, 366, 638 CrossRef PubMed.
- T. Treibitz and Y. Y. Schechner, IEEE Trans. Pattern Anal. Mach. Intell., 2009, 31, 385 Search PubMed.
- D. Rebhan, M. Rosenberger and G. Notni, Proc. SPIE, 2019, 11144, 111440A Search PubMed.
- N. A. Rubin, G. D’Aversa, P. Chevalier, Z. Shi, W. T. Chen and F. Capasso, Science, 2019, 365, eaax1839 CrossRef CAS PubMed.
- Y. Li, Y. Xue and L. Tian, Optica, 2018, 5, 1181 CrossRef.
- N. Antipa, G. Kuo, R. Heckel, B. Mildenhall, E. Bostan, R. Ng and L. Waller, Optica, 2018, 5, 1 CrossRef.
- M. S. Asif, A. Ayremlou, A. Sankaranarayanan, A. Veeraraghavan and R. G. Baraniuk, IEEE Trans. Comput. Imaging, 2017, 3, 384 Search PubMed.
- J. P. Balthasar Mueller, K. Leosson and F. Capasso, Optica, 2016, 3, 42 CrossRef.
- A. Basiri, X. Chen, J. Bai, P. Amrollahi, J. Carpenter, Z. Holman, C. Wang and Y. Yao, Light: Sci. Appl., 2019, 8, 78 CrossRef PubMed.
- J. Sung, G.-Y. Lee, C. Choi, J. Hong and B. Lee, Nanoscale Horiz., 2020, 5, 1487 RSC.
- S.-D. Liu, X. Qi, W.-C. Zhai, Z.-H. Chen, W.-J. Wang and J.-B. Han, Nanoscale, 2015, 7, 20171 RSC.
- F. Ding, R. Deshpande, C. Meng and S. I. Bozhevolnyi, Nanoscale, 2020, 12, 14106 RSC.
- Q. Jiang, B. Du, M. Jiang, D. Liu, Z. Liu, B. Li, Z. Liu, F. Lin, X. Zhu and Z. Fang, Nanoscale, 2020, 12, 5906 RSC.
- B. C. Marin, J. Ramírez, S. E. Root, E. Aklile and D. J. Lipomi, Nanoscale Horiz., 2017, 2, 311 RSC.
- B. Muminov and L. T. Vuong, Optica, 2020, 7, 1079 CrossRef.
- S. Jutamulia and F. T. S. Yu, Opt. Laser Technol., 1996, 28, 59 CrossRef.
- J. Chang, V. Sitzmann, X. Dun, W. Heidrich and G. Wetzstein, Sci. Rep., 2018, 8, 12324 CrossRef PubMed.
- G. Wetzstein, A. Ozcan, S. Gigan, S. Fan, D. Englund, M. Soljačić, C. Denz, D. A. B. Miller and D. Psaltis, Nature, 2020, 588, 39 CrossRef CAS PubMed.
- Roger C. Hardie, Curr. Biol., 2012, 22, R12 CrossRef CAS PubMed.
- M. Kryuchkov, V. Savitsky, B. D. Wilts, E. Gray and V. L. Katanaev, ACS Appl. Mater. Interfaces, 2021, 13, 23481 CrossRef CAS PubMed.
- I. Fratoddi, I. Venditti, C. Cametti and M. V. Russo, Sens. Actuators, B, 2015, 220, 534 CrossRef CAS.
- V. Kumar, A. Mirzaei, M. Bonyani, K.-H. Kim, H. W. Kim and S. S. Kim, Trends Anal. Chem., 2020, 129, 115938 CrossRef CAS.
- E. N. Zare, P. Makvandi, B. Ashtari, F. Rossi, A. Motahari and G. Perale, J. Med. Chem., 2020, 63, 1 CrossRef CAS PubMed.
- C. O. Baker, X. Huang, W. Nelson and R. B. Kaner, Chem. Soc. Rev., 2017, 46, 1510 RSC.
- N. R. Tanguy, M. Thompson and N. Yan, Sens. Actuators, B, 2018, 257, 1044 CrossRef CAS.
- J. Banerjee, K. Dutta, M. A. Kader and S. K. Nayak, Polym. Adv. Technol., 2019, 30, 1902 CrossRef CAS.
- P. Andersson, M. Berggren and T. Kugler, Appl. Phys. Lett., 2003, 83, 1307 CrossRef CAS.
- I. Rashid, M. U. Hassan, M. Nazim, M. Elsherif, Q. Dou, D. Hu, M. Kamran, Q. Dai and H. Butt, Nanoscale, 2020, 12, 21409 RSC.
- H. Butt, A. K. Yetisen, D. Mistry, S. A. Khan, M. U. Hassan and S. H. Yun, Adv. Opt. Mater., 2016, 4, 497 CrossRef CAS.
- V. I. Zakomirnyi, S. V. Karpov, H. Ågren and I. L. Rasskazov, J. Opt. Soc. Am. B, 2019, 36, E21 CrossRef CAS.
- C. Zhou and S. K. Nayar, IEEE Trans. Image Process., 2011, 20, 3322 Search PubMed.
- A. Greengard, Y. Y. Schechner and R. Piestun, Opt. Lett., 2006, 31, 181 CrossRef PubMed.
- O. Katz, P. Heidmann, M. Fink and S. Gigan, Nat. Photonics, 2014, 8, 784 CrossRef CAS.
- D. G. Dansereau, G. Schuster, J. Ford and G. Wetzstein, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, 3757.
- W. Pang and D. J. Brady, Appl. Opt., 2018, 57, 6999 CrossRef PubMed.
- Y. Peng, Q. Sun, X. Dun, G. Wetzstein, W. Heidrich and F. Heide, ACM Trans. Graph., 2019, 38, 219 Search PubMed.
- A. Liutkus, D. Martina, S. Popoff, G. Chardon, O. Katz, G. Lerosey, S. Gigan, L. Daudet and I. Carron, Sci. Rep., 2014, 4, 5552 CrossRef CAS PubMed.
- D. Wang and F. Caruso, Adv. Mater., 2001, 13, 350 CrossRef CAS.
- S. Tian, J. Wang, U. Jonas and W. Knoll, Chem. Mater., 2005, 17, 5726 CrossRef CAS.
- L. Wang, L. Jin, G. Shi, Y. Liu, B. Yao, C. Li and Y. Li, New J. Chem., 2018, 42, 12960 RSC.
- D. Liu, W. Cai, M. Marin, Y. Yin and Y. Li, ChemNanoMat, 2019, 5, 1338 CrossRef CAS.
- S. Han, A. L. Briseno, X. Shi, D. A. Mah and F. Zhou, J. Phys. Chem. B, 2002, 106, 6465 CrossRef CAS.
- L.-Y. Yang and W.-B. Liau, Synth. Met., 2010, 160, 1809 CrossRef CAS.
- C. Liu, G. Gao, Y. Zhang, L. Wang, J. Wang and Y. Song, Macromol. Rapid Commun., 2012, 33, 380 CrossRef CAS PubMed.
- N.-R. Chiou, C. Lu, J. Guan, L. J. Lee and A. J. Epstein, Nat. Nanotechnol., 2007, 2, 354 CrossRef CAS PubMed.
- L. Tan, L. Cao, M. Yang, G. Wang and D. Sun, Polymer, 2011, 52, 4770 CrossRef CAS.
- J. Xu, K. Wang, S.-Z. Zu, B.-H. Han and Z. Wei, ACS Nano, 2010, 4, 5019 CrossRef CAS PubMed.
- N. L. Smith, A. Coukouma, S. Dubnik and S. A. Asher, Phys. Chem. Chem. Phys., 2017, 19, 31813 RSC.
- P. R. Wiecha, A. Cuche, A. Arbouet, C. Girard, G. Colas des Francs, A. Lecestre, G. Larrieu, F. Fournel, V. Larrey, T. Baron and V. Paillard, ACS Photonics, 2017, 4, 2036 CrossRef CAS.
- H. Ruda and A. Shik, Polarization-sensitive optical properties of metallic and semiconducting nanowires, SPIE BiOS, 2006, 6099, PW8 Search PubMed.
- E. Khoram, A. Chen, D. Liu, L. Ying, Q. Wang, M. Yuan and Z. Yu, Photonics Res., 2019, 7, 823 CrossRef.
- D. B. Lindell, M. O. Toole and G. Wetzstein, IEEE International Conference on Computational Photography (ICCP), 2018, 1 DOI:10.1109/ICCPHOT.2018.8368466.
- M. Buttafava, J. Zeman, A. Tosi, K. Eliceiri and A. Velten, Opt. Express, 2015, 23, 20997 CrossRef CAS PubMed.
- I. Gyongy, S. W. Hutchings, A. Halimi, M. Tyler, S. Chan, F. Zhu, S. McLaughlin, R. K. Henderson and J. Leach, Optica, 2020, 7, 1253 CrossRef.
- E. Moyroud, T. Wenzel, R. Middleton, P. J. Rudall, H. Banks, A. Reed, G. Mellers, P. Killoran, M. M. Westwood, U. Steiner, S. Vignolini and B. J. Glover, Nature, 2017, 550, 469 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00465d |
| This journal is © The Royal Society of Chemistry 2022 |