In situ controlled and conformal coating of polydimethylsiloxane foams with silver nanoparticle networks with tunable piezo-resistive properties

Abstract

Nanoparticle–polymer composites hold promise in enabling material functionalities that are difficult to achieve otherwise, yet are hampered to date by the scarce control and tunability of the nanoparticle collective properties on the polymer surface, especially for polymer foams featuring a complex three-dimensional pore network. Here we report on the controlled and conformal in situ coating of polydimethylsiloxane (PDMS) foams with silver nanoparticles (AgNPs) with surface coverage finely tunable over a large range, from 0 to 75%, via the one-step room temperature reduction of AgF directly on the PDMS surface. This enables the design of AgNP electrical networks on the PDMS foam surface with piezo-resistive properties tunable up to a factor of 1000. We leveraged the control of the piezoresistive properties of the AgNP electrical network formed on PDMS foams to fabricate flexible and wearable pressure sensors with sensitivity of 0.41 kPa⁻¹, an operation range >120 kPa, and a detection limit of 25 Pa. As a proof-of-concept application in wearable biomedical electronics, we successfully used the sensors to monitor the real-time radial artery pulse wave on the human wrist of a young male with high resolution.

---

New concepts

Here we demonstrate the in situ controlled and conformal coating of porous polymers, namely, polydimethylsiloxane (PDMS) foams, with silver nanoparticles (AgNPs) with tunable surface coverage from 0 to 75%, via the one-step room temperature reduction of AgF directly on the PDMS surface. The control of the NP collective organization enables us to design AgNP networks on the PDMS foam with electrical and piezoresistive properties tunable over 3 orders of magnitude. We leveraged the control of the piezoresistive properties of the AgNP network to design flexible and wearable pressure sensors with sensitivity of 0.41 kPa⁻¹, an operation range >120 kPa, and a detection limit of 25 Pa. This work represents a key advancement in the materials science of nanoparticle–polymer composites, which has been hampered to date by the scarce control and tunability of the NP collective organization on the polymer surface, providing access to the design of novel optical, electrical, and mechanical functionalities of nanocomposites. The proposed method can be immediately extended to other polymers and metals, besides PDMS and Ag used in this study, to gain novel properties and applications of metal–polymer nanocomposites in wearable sensing, stretchable electronics, environment cleaning, and water remediation, among others.

Introduction

Nanoparticle–polymer composites, also known as nanocomposites, have enabled material multifunctionalities that are difficult to achieve otherwise. The distinctive properties of nanocomposites strongly depend on the collective organization of the nanoparticles (NPs) in the hosting material.^1,2 Thus, controlling the size and distribution of NPs on the hosting material is crucial to provide access to novel optical, electrical, and mechanical functionalities.^3–7 This is even more challenging on polymer foams, for which the conformal coating of the inner surface of the pore network with NPs is further required. The scarce control of the collective organization of NPs on polymeric materials achieved with state-of-the-art approaches has hampered the optimization of nanocomposite functionalities to date.

Recently, polymer foams made with polyurethane (PU),^8–10 polymethyl methacrylate (PMMA),^11,12 polydimethylsiloxane (PDMS),^13,14 and others have attracted great attention owing to the effective tuning of the porosity, pore size, and surface-to-volume ratio, which enables, in turn, the control of the mechanical, thermal, and fluidic properties of these materials. Conformal coating of polymer foams with continuous metal films has been reported using different multi-step electroless approaches.^15–17 For instance, the polymer-assisted metal deposition (PAMD)¹⁸ is a three-step coating technique that exploits the modification of the target substrate with anchoring polymers, immobilization of catalytic moieties in the polymer layer, and the electroless deposition of a metal film from a solution containing the metal salt. However, the coating of polymer foams with metal films via electroless deposition has been limited to the preparation of stretchable interconnections and electrodes with applications in flexible and wearable electronics.^15–17 On the other hand, the coating of the inner surface of polymer foams with nanoscopic fillers has been leveraged to modify the physio-chemical,^19–25 mechano-electrical,^17,26–32 and topological^26–28 properties of the foams and gain, in turn, novel features. Applications of such nanocomposites include sensing structures,^26–34 stretchable electronics,^17,20,35 environmental cleaning,^{19,21,36–38} and biomedical devices.^39–42 Two main routes have been used to decorate polymer foams with nanofillers, namely, ex situ and in situ approaches. Ex situ approaches are based on pre-formation of the nanofillers, i.e. NPs, nanowires (NWs), nanotubes (NTs), and nanosheets (NSs), which are then integrated on the surface of the porous hosting material by drop-casting^26,27,31 or dip coating^{8,21,22,24,25,29,32,42–44} methods. These approaches permit fine-tuning of the size and morphology of the nanofillers through wet and vapor phase processes, though they suffer from sophisticated and costly preparation of the nanofillers, limited adhesion of the nanofillers to the polymer surfaces, severe aggregation at high concentrations, and uneven coating of the inner surfaces of the pore network.^45,46 Conversely, in situ approaches leverage the growth of the nanofillers/nanocoatings directly on the surface of the porous hosting material, whose pores were previously infiltrated with the wet metal solution^{15,17,45,47–51} or metal vapor phase.⁵² Uniformity, conformability, and adhesion of the nanofillers are improved over ex situ approaches, though in situ approaches still fail to control the surface coverage of the pore network with the nanofillers, thus hampering the design of novel functionalities of the nanoparticle–polymer composite.

Pressure sensors have been largely investigated over the last decade using different approaches.^53–59 Among these, polymer foams coated with conductive nanofillers have been intensively studied as pressure sensors due to their large strain range operation, high sensitivity and gauge factor, and low detection limit.^{26,52,60–67}

Here, we report on the one-step controlled, conformal, and in situ coating of PDMS foams with a network of AgNPs with tunable surface coverage from 0 to 75%, using a fluoride-rich AgF ethanolic solution. The proposed method exploits the formation of metal NPs directly on the PDMS surface by in situ redox reactions occurring between unreacted Si–H bonds available at the PDMS surface and metallic cations Ag⁺ available in the solution. The control of the surface coverage enables us to design the piezo-resistive properties of the AgNP-decorated PDMS foams by finely tuning the resistance of the AgNP network over 3 orders of magnitude at zero-strain and up to 2 orders of magnitude with deformation. We eventually leveraged the fine-tuning of the piezoresistive properties of the AgNP–PDMS foams to demonstrate wearable pressure sensors with sensitivity (0.41 kPa⁻¹), detection limit (25 Pa), operation range (>120 kPa), and endurance (>1500 cycles) comparable to those of the best state-of-the-art pressure sensors based on polymeric foams. Pressure sensors based on microstructured polymers and metallic foams have higher sensitivity values, though the operation range of these sensors is smaller (<10 and <2 kPa, respectively) (Table S1, ESI†). As a proof-of-concept application in wearable biomedical electronics, the sensors were successfully used to measure the real-time radial artery pulse wave on the human wrist of a young male with high resolution.

Results and discussion

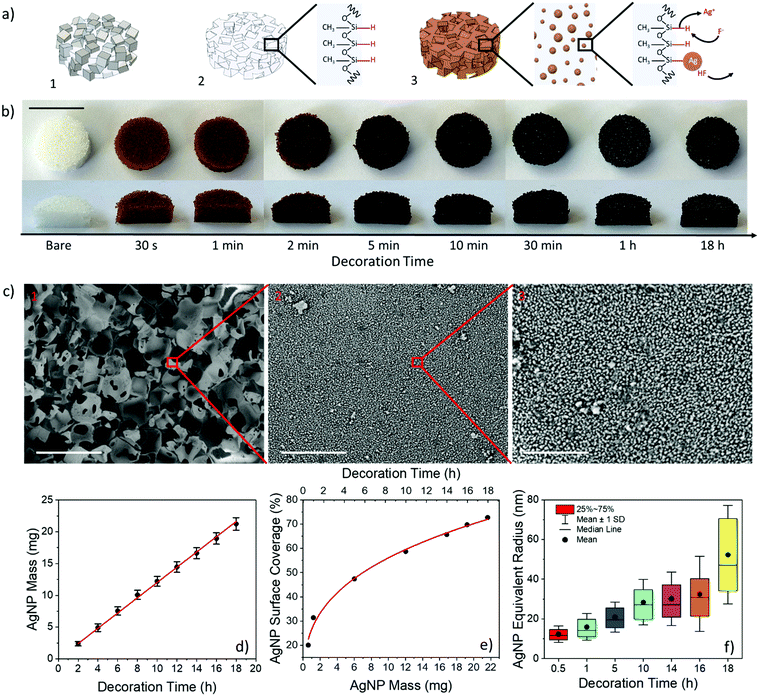
AgNP-coated PDMS foams were prepared according to the steps sketched in Fig. 1a. NaCl grains (278 ± 63 μm in size) were compressed within a syringe to achieve a cylindrical sacrificial template with a diameter and height of 20 and 65 mm, respectively. The template (in the syringe) was infiltrated with the PDMS pre-polymer (base : curing 10 : 1 w/w) using a vacuum-assisted process, and then cured at 90 °C for 5 hours to ensure complete PDMS polymerization. After curing, ten PDMS-filled NaCl disks with a diameter of 15 mm and a thickness of 5 mm were achieved by carefully sectioning the cylinder (Fig. 1a.1). The disks were immersed in water for 24 hours to ensure full dissolution of the NaCl template and achieve PDMS foams with a porosity of 68.21 ± 0.58%, pore sizes of 279 ± 50 μm, comparable to those of the NaCl grains of the template, an interpore distance of 41 ± 11 μm, and a weight of 274.6 ± 5.9 mg (Fig. 1a.2).^26,68 The grain size of the template and, in turn, the pore size and porosity of the foam⁶⁹ were chosen to ensure an extended strain range of the foam under compression, on the basis of our former results on PDMS foams.²⁶ Decoration of the PDMS foams with AgNPs was carried out by infiltration of the as-prepared foam with an ethanolic solution of 45 mM AgF at room temperature (i.e., 20 °C) for different incubation times from 30 s to 18 hours. AgNPs are formed on the PDMS surface by in situ redox reaction occurring between unreacted Si–H bonds (of the curing agent) available at the PDMS surface and metallic cations Ag⁺ available in the solution.^6,7 Eventually, the AgNP-decorated foam was thoroughly rinsed with ethanol and dried (Fig. 1a.3).

Fig. 1 Fabrication and morphological characterization of PDMS foams decorated with AgNP networks. (a) Main preparation steps of PDMS foams and decoration with AgNPs: (1) PDMS infiltration in the sacrificial cylindrical NaCl template; (2) PDMS thermal curing and NaCl dissolution in water; the inset highlights the Si–H bonds available at the PDMS surface; (3) PDMS foam decoration by in situ reduction of AgNPs using an ethanolic solution of AgF 45 mM; the inset shows the AgNP formation at the curing agent molecules on the PDMS surface: (i) a H⁺ ion is released upon Ag⁺ reduction to Ag⁰ at the Si–H bond of the PDMS surface; (ii) the released H⁺ ion binds to an F⁻ ion available in the solution generating HF molecules. (b) Top and cross-section pictures of PDMS foams decorated with AgNPs by immersion in an ethanolic solution of AgF 45 mM for 0 s (i.e., bare), 30 s, 1 min, 2 min, 5 min, 10 min, 30 min, 1 h, and 18 h. (c) Cross-section SEM images at different magnifications of AgNP-coated PDMS foams after 14 hours of decoration in an ethanolic solution of AgF 45 mM: (1) 100×; (2) 50000×, and (3) 100000×. The scale bar is (1) 1 mm, (2) 2 μm, and (3) 1 μm. (d) AgNP mass on PDMS foams at different decoration times. Data are reported as the average value measured over more than 5 foams for each decoration time, with error bars representing the standard deviation. (e) AgNP surface coverage and (f) size distribution of the AgNP-coated PDMS foams, for different Ag masses and decoration times.

Fig. 1b shows the top-view and cross-section pictures of the PDMS foams before (i.e., as-prepared) and after in situ synthesis of AgNPs at different incubation times from 30 s to 18 hours. The color of the foams varies from copper to brown, and eventually becomes black as the amount of AgNPs on the PDMS surface increases with the decoration time.⁷⁰ Remarkably, the color intensity is very uniform throughout the foams, thus indicating an excellent uniformity and conformability of the NP synthetic process within the high porosity material, regardless of the decoration time. This was further confirmed through scanning electron microscopy (SEM) analysis, from which a uniform and conformal distribution of AgNPs is visible on the pore surface of PDMS foams at any of the decoration times investigated (Fig. 1c, Fig. S1, ESI†).

The AgNP mass increases linearly with time at a rate of 1.2 mg h⁻¹ (about 22 mg of Ag deposited at 18 h) (Fig. 1d). Consistently, the surface coverage also increases with time up to about 75% in 18 h, due to physical aggregation of nearest neighbor NPs as the synthesis time increases, in agreement with the larger size (from about 12 to 43 nm) and lower surface density (from 381 to 76 NPs per μm²) of AgNPs with time (Fig. 1e, f, Fig. S2a and b, ESI†). A power-law relationship s_cov = am_NP^b with a = 26.68% and b = 0.32 between surface coverage (s_cov) and mass (m_NP, in mg, normalized to 1 mg) of AgNPs is achieved from the best-fitting (R² = 0.993) of experimental data (Fig. 1e). On the other hand, the porosity value (void to total volume fraction) of the AgNP-decorated PDMS foams reduced by only ∼0.2% after 18 hours when compared to bare foams (Fig. S2c, ESI†). This well agrees with the formation of a conformal nm-thick AgNP coating on the pore surface of the foam, consistently with the SEM observations.

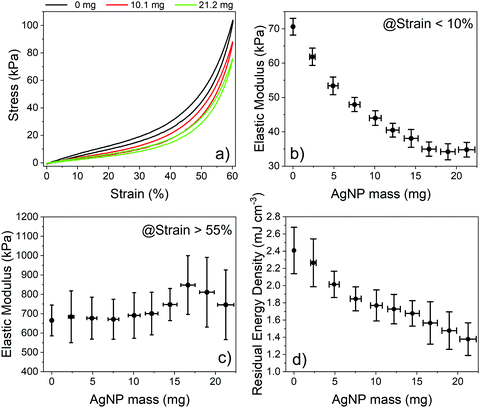
AgNP-decorated PDMS foams were subjected to cyclic stress–strain analysis to gain insights into the mechanical properties of the nanostructured composite material. Fig. 2a shows the typical stress–strain curves of bare PDMS foams and those decorated with 10.1 and 21.2 mg of AgNPs, i.e. with a surface coverage of 56 and 72%, measured under uniaxial loading/unloading cycles at a strain rate of 0.5 mm min⁻¹. The curves are in good agreement with those achieved under steady-state conditions (Fig. S3a, ESI†). The stress–strain curves show a nonlinear behavior with hysteresis, which is typical of porous elastomeric materials.^26,67,71,72 Both bare and AgNP-decorated PDMS foams completely recover to their original state without plastic deformation after a full loading–unloading cycle. The stress–strain curve of the foams is unchanged over several cycles, regardless of the AgNP mass, testifying the good adhesion of NPs to the PDMS surface. Linear regions are apparent at strain values <10% and >55%, with slopes corresponding to the elastic modulus of the composite material at low and high strain values, respectively (Fig. S3b and c, ESI†).^26,71,72 The elastic modulus of the AgNP-decorated foams at low strain steadily decreases with the AgNP mass, from ∼70 kPa for the bare foam to ∼35 kPa as the AgNP mass increases to 16.6 mg and beyond (Fig. 2b). This corresponds to a maximum reduction of the elastic modulus of the composite material of about 50%. Such a behavior well agrees with experimental data on AgNP–PDMS composites achieved pre-mixing AgNPs and PDMS pre-polymer, before curing.⁷³

Fig. 2 Mechanical characterization of PDMS foams decorated with AgNP networks. (a) Stress–strain curves of PDMS foams with different AgNP masses. Data are measured under uniaxial loading/unloading cycles at a strain rate of 0.5 mm min⁻¹. (b) Elastic modulus at strain level <10%, (c) elastic modulus at strain level >55%, and (d) residual energy density of PDMS foams on increasing AgNP mass. Data are reported as the average value measured over at least 3 foams (3 cycles per foam) for each AgNP mass, with error bars representing the standard deviation.

Reduction of the elastic modulus due to the loss of AgNPs during the mechanical characterization was ruled out by monitoring possible weight changes of the foams before and after the characterization, using a precision balance with 0.1 mg resolution; no weight changes were observed, thus proving that there is no significant release of AgNPs due to compression/release cycles and that the NPs are firmly anchored to the PDMS surface. This is in agreement with experimental results achieved on the synthesis of AgNPs on flat PDMS slabs using AgF ethanolic solutions,⁶ where tape tests successfully demonstrated that the NPs were tightly anchored to the polymer surface. We next ruled out possible changes in the elastic modulus of bare PDMS foams after immersion for 18 hours (maximum time tested for AgNP synthesis) in pure EtOH (i.e., the decoration solvent) and in 45 mM HF in EtOH (i.e., the maximum quantity of byproducts that can be produced during AgNP formation in a 45 mM AgF ethanolic solution in the ideal case that all AgF molecules are reduced to metallic Ag). We observed a 2.1 and 9.5% reduction of the elastic modulus after 18 hours of immersion in the two solutions, respectively, which is significantly smaller than the 51.6% reduction achieved after 18 hours of decoration in the AgF solution. The control experiments rule out a significant contribution of solvent rinsing and/or byproduct etching on the reduction of the elastic modulus of AgNP-decorated foams. Thus, we can reasonably conclude that the AgNPs formed on the surface of PDMS foams play a major role in the control of the elastic properties of the nanocomposite material. We speculate that the metal NPs act as a network of surface defect points from the mechanical point of view, reducing the rigidity of the PDMS foams at low strain/stress values. Notice that the elastic modulus of the decorated PDMS foams at higher strain/stress values, where the material bulk dominates the mechanical properties of the foam, is about 600–800 kPa regardless of the NP surface coverage/density (Fig. 2c). This value is consistent with the elastic modulus of a bulk-like PDMS material formed when the air gaps in the pores of the foam vanish at high compression values, considering that the AgNPs contribute for a maximum weight fraction of 7.7%.^74,75 The residual energy density of the PDMS foams also reduces as the AgNP mass increases, from 2.41 ± 0.27 mJ cm⁻³ of bare foams to 1.38 ± 0.19 mJ cm⁻³ for foams decorated with 21.2 ± 1 mg of AgNPs, with a maximum change of 42% (Fig. 2d, Fig. S3d, ESI†). We speculate that the reduction can be ascribed to a decreased adhesion of the inner pore surface of AgNP-decorated PDMS foams⁷⁶ as the NP surface coverage increases from 0 to 75%, which enables a quicker return of the compressed foams to its original state during the unloading phase.^77,78

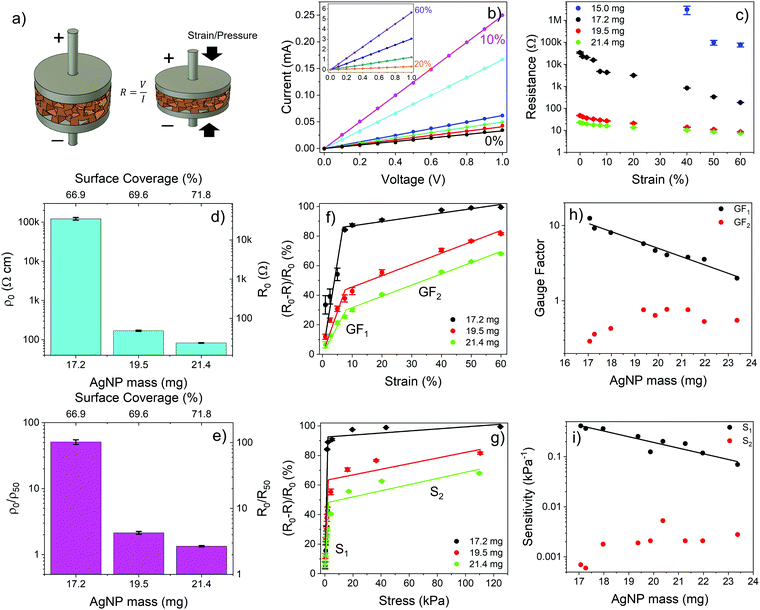
We next investigated the electrical properties of PDMS foams decorated with AgNP networks with different surface coverages/masses. The foams were provided with two copper electrodes on opposite sides and the I–V curve was measured at zero strain (i.e., no deformation) and upon compression (in static conditions) at different strain levels up to 60% (Fig. 3a). Fig. 3b shows typical I–V curves of a PDMS foam decorated with AgNPs with mass and surface coverage above the percolation threshold, namely, about 17 mg and 67%, respectively. The linear relationship between current and voltage at zero strain clearly indicates the presence of a resistive path between the electrodes arising from the physical/electrical contact of NPs over the surface of the foam. The resistance value of the foam at different strain levels was retrieved through best-fitting of the experimental I–V curves (R² > 0.99). At zero strain, the higher the NP mass the lower the resistance of the AgNP-decorated foams, consistently with the increased number of conductive paths formed on the foam as the NP surface coverage increases beyond the percolation threshold. A 3 orders of magnitude variation, from 35 kΩ to 20 Ω, of the resistance of the AgNP–PDMS foam at zero strain is achieved as the AgNP mass increases from 17.2 to 21.4 mg (surface coverage from 66.9 to 71.8%) (Fig. 3c and d). The smaller resistance variation as the AgNP mass increases beyond 19.5 mg is consistent with the saturation of the percolation paths formed on the foam as the NP surface coverage increases above 69.6%. As the strain level increases beyond zero, more AgNPs get in contact due to foam compression and additional conductive paths are formed, thus steadily reducing the resistance value of the foam with respect to the case of zero strain and providing a means to sense strain (and stress) signals with AgNP-decorated PDMS foams. The way the resistance of the foam is affected by the strain level strongly depends on the loaded AgNP mass and, in turn, on the surface coverage at zero strain. Fig. 3c shows the resistance value vs. strain level of PDMS foams decorated with different AgNP masses above the percolation threshold. The lower the NP mass the higher the resistance variation with strain. A resistance change of more than 2 orders of magnitude, from 35 kΩ to 200 Ω, is achieved for the foam decorated with 17.2 mg of AgNPs (surface coverage of 66.9%) upon compression at 60% strain, with respect to the zero-strain case; the resistance change reduces to a factor of 2 for the same strain level if the AgNP mass increases to 21.4 mg, leading to a higher surface coverage of 71.8%.

Fig. 3 Static piezoresistive properties of PDMS foams decorated with AgNP networks. (a) Sketch of a PDMS foam decorated with AgNPs provided with electrical copper contacts and operation mode of the AgNP-decorated PDMS foam as a strain/pressure sensor. (b) Current–voltage curves of a PDMS foam decorated with 17.2 mg of AgNPs measured in the range 0–1 V at different strain levels from 0 to 10%; the inset shows the current–voltage curves at strain levels ranging from 20 to 60%. (c) Resistance–strain curves of PDMS foams decorated with different AgNP masses. (d) Resistance and resistivity values at zero strain, namely R₀ and ρ₀, of PDMS foams decorated with different AgNP masses. (e) Resistance and resistivity ratios at 0 and 50% strain, namely, R₀/R₅₀ and ρ₀/ρ₅₀, of PDMS foams decorated with different AgNP masses. Data in (c–e) are reported as the average value measured over at least 3 compression cycles for each AgNP mass, with error bars representing the standard deviation. (f) Normalized resistance variation vs. strain of PDMS foams decorated with different AgNP masses (dots); the solid lines represent the piecewise linear fitting performed to retrieve the foam sensitivity to strain, i.e. the gauge factor (GF). (g) Normalized resistance variation vs. stress of PDMS foams decorated with different AgNP masses (dots); the solid lines represent the piecewise linear fitting performed to retrieve the foam sensitivity to stress (S). Data in (f, g) are reported as the average value measured over at least 3 compression cycles for each strain level and AgNP mass, with error bars representing the standard deviation. (h) Gauge factors of PDMS foams decorated with different AgNP masses, retrieved from the best fitting of normalized resistance variation–strain curves (dots). (i) Sensitivity to stress of PDMS foams decorated with different AgNP masses, retrieved from the best fitting of normalized resistance variation–stress curves (dots). The solid lines in (h, i) represent the best-fitting of the experimental data for GF₁ and S₁ with a power-law function.

Notice that below the percolation threshold the AgNPs do not form a continuous electrical path at zero strain, so that no measurable current flows through the foam. Nonetheless, the piezoresistive behavior can still be observed upon compression of the foam beyond a given strain value that leads to a dynamic increase of the surface coverage in the compressed state with formation of a NP conductive path between the electrodes. For instance, for PDMS foams decorated with 15 mg of AgNPs and having a surface coverage of 64.0%, below the percolation threshold, the piezoresistive behavior is observed at strain levels beyond 40% (Fig. 3c).

To gain insights into the effect of the AgNP network on the piezoresistive properties of AgNP–PDMS foams we calculated the resistivity and resistance ratios at 0 and 50% strain, namely, ρ₀/ρ₅₀ and R₀/R₅₀, at different surface coverages above the percolation threshold (Fig. 3d and e). The resistivity ρ can be calculated from the measured resistance values as ρ = R(S/L), once the cross-section area S and length L of the foam at any given strain value are known. Given the small Poisson's ratio of our PDMS foams measured at strain levels from 1 to 60% under uniaxial compression, namely, about 0.04 for a strain of 50%, a variation of the cross-section area S of the foam of only 4.4% occurs under compression at a strain of 50%, with respect to its value at zero strain (Fig. S4, ESI†). This leads to a 4.4% error of the resistivity value if the cross-section S is retained constant with strain. Fig. 3e shows ρ₀/ρ₅₀ and R₀/R₅₀vs. AgNP mass for different AgNP–PDMS foams. Notice that in case R₀/R₅₀ = 2 at a strain of 50%, the resistivity of the material does not change upon compression, i.e., ρ₀/ρ₅₀ = 1. Remarkably, a value of R₀/R₅₀ ∼ 100 is achieved for foams with an AgNP surface coverage of 66.9% (mass of 17.2 mg), which is close to the percolation threshold. This is a clear indication of a major resistivity change (ρ₀/ρ₅₀ ∼ 50) of the composite material upon compression, due to the formation of additional conductive paths in the NP network. On the other hand, R₀/R₅₀ ∼ 2.7 (ρ₀/ρ₅₀ ∼ 1.3) is achieved for foams with an AgNP surface coverage of 71.8% (mass of 21.4 mg), highlighting that saturation of the conductive paths in the NP network occurs with compression when a much higher NP surface coverage/mass than the percolation threshold is used. In this case the piezoresistive behavior of the composite materials is mainly dominated by changes in the length of the foam with strain.

Fig. 3f and g shows the normalized resistance changes vs. strain and stress levels of PDMS foams coated with different masses of AgNPs. The curves feature two regions, namely, a high sensitivity region at small strain (<7.5%) and stress (<5 kPa) levels and a lower sensitivity region beyond these values, regardless of the AgNP mass. Piezoresistive nanocomposites are indeed characterized by a high sensitivity region at low strain/stress and a low sensitivity region (saturation region) at higher strain/stress values. This is apparent in Table S1 (ESI†), which summarizes the most relevant works on piezoresistive polymer foams filled with nanomaterials, where high and low sensitivity regions for the different materials are highlighted. In our case, the higher sensitivity region is explained with the formation of new conductive paths in the NP network as the foam is slightly deformed from its rest position, upon application of an external force. As strain and pressure become larger than 7.5% and 5 kPa, respectively, the number of additional NP conductive paths formed with deformation reduces, limiting, in turn, resistance changes. This is in agreement with the state-of-the-art literature on piezoresistive porous materials.^26,60,72,73 The reduced sensitivity and increased rigidity of AgNP–PDMS foams at higher strain and stress values allow increasing the operation range up to 60% and 120 kPa, respectively.

The AgNP mass impacts on the sensitivity of the foam to strain and stress, which steadily reduces as the NP diameter and surface coverage increase, at small strain/stress levels. The sensitivity to strain, namely, gauge factor 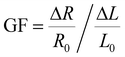, was calculated from the normalized resistance change vs. strain curves of PDMS foams decorated with different AgNP masses by best fitting the experimental data with a piecewise linear function to extrapolate the slopes corresponding to GF₁ at strain level <7.5% and GF₂ at strain level >7.5% (Fig. 3f). A gauge factor GF₁ of about 12.5 is achieved with an AgNP mass of 17.2 mg (surface coverage ∼67%), steadily reducing down to about 2 as the NP mass increases to 23.4 mg (surface coverage ∼74%) (Fig. 3h). A power-law relationship (GF₁ = cd^m_NP, with c = 813.7 and d = 0.77) between GF₁ and AgNP mass (m_NP, in mg, normalized to 1 mg) values is achieved by best-fitting the experimental data in Fig. 3h. On the other hand, a slight increase of GF₂ (between 0.3 and 0.6) with the NP mass is observed (Fig. 3h). A similar behavior is achieved for the foam sensitivity to stress, namely, 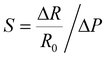; a high sensitivity S₁ of about 0.41 kPa⁻¹ is obtained at stress level <5 kPa with an AgNP mass of 17.2 mg (surface coverage ∼67%), which reduces to a value of 0.23 kPa⁻¹ as the NP mass increases to 23.4 mg (surface coverage ∼74%) following a power law (S = hd^m_NP, with h = 35.75 kPa⁻¹ and d = 0.77) (Fig. 3i). The sensitivity value S₂ at stress levels >5 kPa ranges between 0.001 and 0.003 kPa⁻¹ regardless of the AgNP mass. Current changes vs. strain and stress, and relative sensitivity values to strain 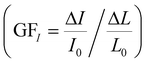and stress 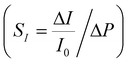are given in Fig. S5 (ESI†). Remarkably, values of GF_I and S_I up to about 1000 and 2 kPa⁻¹, respectively, are achieved with an AgNP mass close to the percolation threshold.

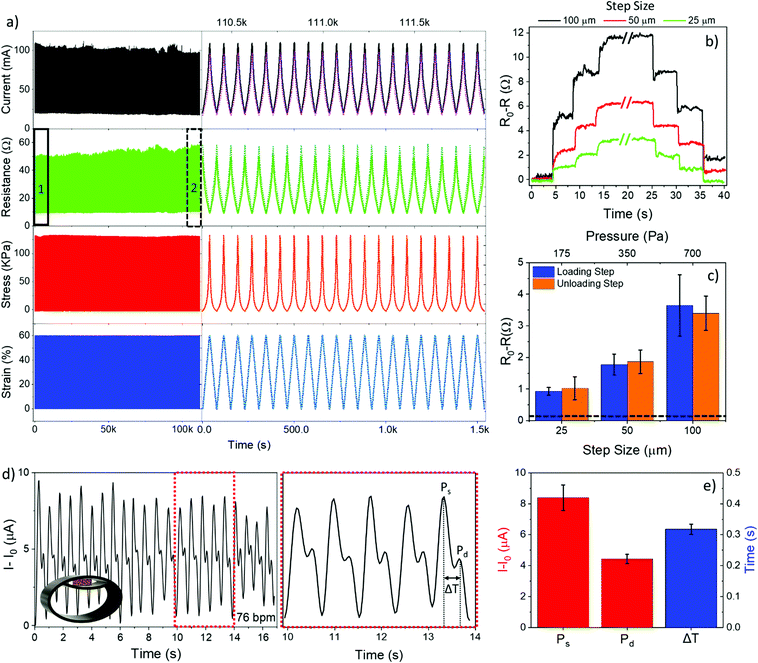
Long-term stability of the sensing performance of a pressure sensor is a critical parameter for piezoresistive micro and nano-composites.^79–82 We next investigated the dynamic piezoresistive performance of the PDMS foam with an AgNP surface coverage of about 70% (mass about 19.5 mg) by real-time monitoring of resistance and current changes, at a constant bias of 1 V, upon uniaxial compression/release cycles over the strain range 0 to 60% at a rate of 5 mm min⁻¹ for more than 24 hours of continuous operation. We chose this foam to evaluate endurance and for proof-of-concept application as it represents the best trade-off between large AgNP content and high sensitivity value. Fig. 4a shows time-resolved values of current, resistance, and pressure recorded on the AgNP-decorated foam upon application of 1500 strain cycles. Specifically, the full 1500 cycles are reported in Fig. 4a (left), whereas Fig. 4a (right) shows the details of 20 cycles acquired at the beginning of the experiment (region 1) superposed to 20 cycles acquired about 24 h later (region 2). An excellent reliability of the piezoresistive properties of the AgNP-decorated foam is apparent. A maximum current/resistance variation of ∼10% and %CV = 3.5% are obtained over the whole measurement time, with no significant changes in the recorded stress values (Fig. S8a, ESI†), confirming that the AgNPs are tightly anchored to the PDMS surface. In fact, losses of AgNPs would have led to a significant change of both the elastic modulus (Fig. 2b) and the electrical resistance (Fig. 3d), given the high sensitivity of these parameters to the AgNP mass.

Fig. 4 Dynamic piezoresistive properties of PDMS foams decorated with AgNP networks and application to radial arterial pulse monitoring. (a) Time-resolved current, resistance, and stress signals acquired on a PDMS foam decorated with about 19.5 mg of AgNPs upon application of 1500 strain cycles at a rate of 5 mm min⁻¹: (left) full 1500 cycles; (right) details of 20 cycles acquired at the beginning (region 1) and at the end (region 2) of the experiment. (b) Time-resolved resistance variation measured on the AgNP–PDMS foam in (a) subjected to compressive and release steps of 25, 50, and 100 μm (175, 350, and 700 Pa). (c) Steady-state resistance variation versus displacement and pressure extrapolated from (b). Data in (c) are reported as the average value measured over at least 5 compression and release cycles for each displacement and pressure value with error bars representing the standard deviation. (d) Time-resolved current variation revealing the radial arterial pulse signal recorded on the wrist of a young male using a PDMS foam decorated with 19.5 mg of AgNPs. The inset shows a sketch of the AgNP-decorated PDMS foam within the plastic bracelet used to perform the experiment. (e) Current variation of the systolic and diastolic peaks (left), and the time interval between them (right). Data are reported as the average value measured over at least 5 pulses with error bars representing the standard deviation.

Investigation of the performance of piezoresistive sensors at different strain ranges and rates is important for real-world applications.^80,81,83 We tested the foam over different strain ranges, namely, from 0 to 20, 40, and 60%, using a constant strain rate of 5 mm min⁻¹. Both electrical and mechanical properties of the piezoresistive foam consistently and linearly scaled with the strain range (Fig. S6 and S8b, ESI†). We then investigated the effect of the strain rate on the piezoresistive performance of the foam, namely, 0.5 and 5 mm min⁻¹ over the strain range 0–60%. No significant impact of the strain rate on current, resistance, and stress signals was evident (Fig. S7, ESI†). This was further corroborated by the value of the elastic modulus of the foam at a strain level <10% (35 kPa for both 0.5 and 5 mm min⁻¹) and >55% (about 1100 kPa for 0.5 and 5 mm min⁻¹) that was unchanged with the strain rate (Fig. S8c, ESI†).

Further experiments were carried out to investigate piezoresistive properties of the foam at small strain (<2%) and pressure (<700 Pa) levels, by real-time measurement of the current flowing through the foam, at a bias of 1 V, upon application of repetitive loading and unloading displacement steps of 25, 50, and 100 μm (i.e., strain of 0.5, 1, and 2%, pressure of 175, 350, and 700 Pa). Typical time-resolved curves of resistance and current variations measured upon application of displacement steps are shown in Fig. 4b and Fig. S9a–c (ESI†), respectively. Loading and unloading displacement steps of 25 μm and greater are reliably and quickly resolved over the noise floor with a good signal-to-noise ratio (SNR = 7 at 25 μm steps). Fig. 4c shows resistance changes (steady-state values measured over 5 replicates) versus both displacement (strain) and pressure values; a consistent variation of the resistance of the foam after both loading and unloading steps was found for all the displacement steps, with response and recovery times of 330 ± 120 ms and 180 ± 60 ms, respectively.

A linear relationship between resistance changes and strain/stress levels was achieved, which is consistent with the static curves in Fig. 3f and g. By best fitting the experimental data in Fig. 4c and Fig. S9d (ESI†) with a linear equation (R² = 0.999), we were able to calculate strain and pressure limit of detection (LOD) values, that are the minimum displacement and pressure values that the foam can reliably sense over the noise floor 3.3σ₀, with σ₀ = 44 mΩ (19 μA) standard deviation of the resistance (current) signal at zero strain/pressure. The achieved LOD values are very low, being 4 μm for displacement (i.e., strain 0.08%) and 25 Pa for pressure, in spite of the large working range of the foams, namely, 60% for strain (i.e., 3 mm in displacement) and 120 kPa for pressure. This is consistent with the high sensitivity of the AgNP network formed on the PDMS surface at very small strains, as well as with the dynamic increase of the elastic modulus of the foam at large strains owing to the large size of the pores, namely, about 280 μm.

To investigate possible aging effects on the piezoresistive performance of AgNP-decorated PDMS foams we performed a set of experiments after 6 months from fabrication. Exposure of AgNPs to O₂ in the ambient air results in the self-limiting growth of a silver oxide shell with a thickness of about 1–2 nm on the AgNP surface.^84–86 Moreover, contamination of AgNPs with carbon and sulphur compounds was also observed after exposure of AgNPs to the ambient air.⁸⁷ No impact of the ambient air on porous PDMS has been reported.^13,88 Fig. S10 (ESI†) shows the results achieved on the piezoresistive characterization of a PDMS foam coated with 19.5 mg of AgNPs after 6 months from fabrication, compared to those achieved on the as-prepared foam. The excellent superposition of current, resistance, and stress curves (resistance and current variation ∼5%, stress variation <1%) confirms the long-term stability and reduced aging of the AgNP-coated PDMS foam in piezoresistive applications.

We eventually used the PDMS foam decorated with 19.5 mg of AgNPs in a series of wearable sensing experiments aimed at measuring the radial artery pulse wave on the right wrist of a 26-year-old man, which is a common practice in the clinical setting for arterial tonometry. The radial artery pulse wave results from the mechanical stress induced by the systolic wave in the arteries upon injection of blood into the aorta during systole (approximately 60–80 ml); it is caused by dilation and next relaxation of the blood vessel walls.^{53,65,89–93} Its line-shape depends on the age of the patient.^89,94,95 For a healthy adult male 26 years old and 178 cm tall, which is the case of this work, two characteristic peaks appear in the radial artery pulse wave.^53,65,92

The AgNP–PDMS foam was packaged in a commercial plastic bracelet modified so that the foam was located in correspondence of the radial artery when worn on the wrist (inset, Fig. 4d). Although the foam was not optimized in terms of thickness and geometry for wearable applications, it easily and conformably adapted to the body features owing to its intrinsic porous nature and high flexibility. A constant voltage of 10 mV was applied to the foam and the resulting current was recorded over time (sampling time 30 ms) under both rest and stress conditions. Fig. 4d shows the acquired time-resolved radial artery pulse under rest conditions. The signal exhibits a double-peaked waveform with a periodicity of 76 beats per minute (bpm), which is consistent with the rest state of the subject under examination and in agreement with the literature.^53,65,92 The first peak, known as the systolic pressure peak (P_s), is due to the forward blood wave originating at the left ventriculus and traveling through large arteries down to the peripheral blood vessels of the body; the second peak, known as the diastolic pressure peak (P_d), is the reflected blood wave traveling back. Given the amplitude and position of P_s and P_d (Fig. 4e), the reflection index (R.I. = P_d/P_s × 100) is commonly used as a measure of the vascular tone, the transit time (ΔT = T_d − T_s) to estimate the time needed for the pulse wave to propagate along large arteries to the lower body and back to the root of the subclavian artery; the stiffness index (S.I. = subject height/ΔT) is used for the evaluation of the artery stiffness. For the test performed under rest conditions, the R.I., ΔT, and S.I. values are 55.25 ± 5.64%, 0.32 ± 0.02 s, and 5.62 ± 0.32 m s⁻¹, respectively, which are consistent with the values expected for a healthy adult male 178 cm tall and 26 years old.^94–96 The pulse artery wave was also successfully monitored under stress activity, from which a bpm value of 92, 98, and 115 increasing with the training time was consistently retrieved (Fig. S11, ESI†).

Conclusions

In this work we demonstrated the in situ conformal coating of PDMS foams with AgNPs using a fluoride-rich chemistry, with surface coverage fine-tunable over a large range, namely, from 0 to 75%. The accurate control of the NP surface coverage enabled the design of AgNP–PDMS foams with NP electrical networks on the inner surface with resistance tunable up to a factor of 1000 at zero-strain, from about 10k to 10 Ω, and up to a factor of 100 with deformation, from about 10k to 100 Ω. We leveraged the control of the piezoresistive properties of the AgNP electrical network synthesized on the foam to fabricate flexible and wearable pressure sensors with sensitivity to deformation (GF) and pressure (S) of 12.46 and 0.41 kPa⁻¹, respectively, enabling the detection of subtle displacement (4 μm) and pressure (25 Pa), coupled with a large dynamic range (up to 60% for strain, 120 kPa for pressure) and long-term operation (>1500 cycles). The sensors were successfully used to monitor the real-time radial artery pulse wave on the human wrist of a young male with high resolution, from which we extracted typical parameters of clinical relevance.

When compared to the best state-of-the-art pressure sensors based on polymeric foams our pressure sensor features comparable (or better) sensitivity values with similar operation range (>120 kPa). Best pressure sensors based on microstructured polymers and metallic foams features higher sensitivity values, though with a smaller operation range (<10 and <2 kPa, respectively) (Table S1, ESI†).

The proposed fluoride-rich method is room temperature, low cost, and highly reliable, and enables the coating of polymeric materials and foams with a conformal thin layer of metal NPs with controlled density and strong adhesion to the hosting material. The method can be immediately extended to other polymers and metals, besides PDMS and Ag that were the subject of this study, to gain novel properties and applications of metal–polymer nanocomposites in wearable sensing, stretchable electronics, environment cleaning, and water remediation, among others.

Note after first publication

The sensitivity value to pressure has been changed to account for a miscalculation identified by authors after first publication. The description pertaining to the sensitivity to pressure and the comparative analysis with other state-of-the-art pressure sensors have been revised to reflect this change. Fig. 3i has also been revised to account for the corrected sensitivity values.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

G. B. acknowledges the support of Italian Ministry of Education, University and Research (MIUR) in the framework of the CrossLab project (Departments of Excellence). The authors acknowledge Dr. L. M. Strambini for helping with the control software of the electromechanical measurement setup.

References

1. Z. Nie, A. Petukhova and E. Kumacheva, Properties and emerging applications of self-assembled structures made from inorganic nanoparticles, Nat. Nanotechnol., 2010, 5(1), 15–25.
2. S. Kango, S. Kalia, A. Celli, J. Njuguna, Y. Habibi and R. Kumar, Surface modification of inorganic nanoparticles for development of organic-inorganic nanocomposites - A review, Prog. Polym. Sci., 2013, 38(8), 1232–1261.
3. G. Schmid and U. Simon, Gold nanoparticles: Assembly and electrical properties in 1-3 dimensions, Chem. Commun., 2005,(6), 697–710.
4. E. K. W. Tan, et al., Density Modulation of Embedded Nanoparticles via Spatial, Temporal, and Chemical Control Elements, Adv. Mater., 2019, 31(51), 1–7.
5. D. Coetzee, M. Venkataraman, J. Militky and M. Petru, Influence of nanoparticles on thermal and electrical conductivity of composites, Polymers, 2020, 12(4), 742.
6. S. Mariani, A. A. La Mattina, A. Paghi, L. Strambini and G. Barillaro, Maskless Preparation of Spatially-Resolved Plasmonic Nanoparticles on Polydimethylsiloxane via In Situ Fluoride-Assisted Synthesis, Adv. Funct. Mater., 2021, 31(26), 2100774.
7. S. Mariani, et al., 4D Printing of Plasmon-Encoded Tunable Polydimethylsiloxane Lenses for On-Field Microscopy of Microbes, Adv. Opt. Mater., 2021, 2101610.
8. P. Jain and T. Pradeep, Potential of silver nanoparticle-coated polyurethane foam as an antibacterial water filter, Biotechnol. Bioeng., 2005, 90(1), 59–63.
9. M. C. Saha, M. E. Kabir and S. Jeelani, Enhancement in thermal and mechanical properties of polyurethane foam infused with nanoparticles, Mater. Sci. Eng., A, 2008, 479(1–2), 213–222.
10. Z. Yang, H. Peng, W. Wang and T. Liu, Crystallization behavior of poly(ε-caprolactone)/layered double hydroxide nanocomposites, J. Appl. Polym. Sci., 2010, 116(5), 2658–2667.
11. B. Notario, J. Pinto and M. A. Rodríguez-Pérez, Towards a new generation of polymeric foams: PMMA nanocellular foams with enhanced physical properties, Polymer, 2015, 63, 116–126.
12. D. Zhou, et al., Synthesis and compressive behaviors of PMMA microporous foam with multi-layer cell structure, Composites, Part B, 2019, 165, 272–278.
13. D. Zhu, S. Handschuh-Wang and X. Zhou, Recent progress in fabrication and application of polydimethylsiloxane sponges, J. Mater. Chem. A, 2017, 5(32), 16467–16497.
14. M. P. Wolf, G. B. Salieb-beugelaar and P. Hunziker, Progress in Polymer Science PDMS with designer functionalities—Properties, modifications strategies, and applications, Prog. Polym. Sci., 2018, 83, 97–134.
15. Y. Yu, et al., Three-Dimensional Compressible and Stretchable Conductive Composites, Adv. Mater., 2014, 26(5), 810–815.
16. B. Jiang, C. He, N. Zhao, P. Nash, C. Shi and Z. Wang, Ultralight metal foams, Sci. Rep., 2015, 5, 1–8.
17. S. Liang, et al., 3D Stretchable, Compressible, and Highly Conductive Metal-Coated Polydimethylsiloxane Sponges, Adv. Mater. Technol., 2016, 1(7), 1–6.
18. Y. Yu, C. Yan and Z. Zheng, Polymer-Assisted Metal Deposition (PAMD): A Full-Solution Strategy for Flexible, Stretchable, Compressible, and Wearable Metal Conductors, Adv. Mater., 2014, 26(31), 5508–5516.
19. D. N. H. Tran, S. Kabiri, T. R. Sim and D. Losic, Selective adsorption of oil-water mixtures using polydimethylsiloxane (PDMS)-graphene sponges, Environ. Sci.: Water Res. Technol., 2015, 1(3), 298–305.
20. S. Liang, et al., Liquid metal sponges for mechanically durable, all-soft, electrical conductors, J. Mater. Chem. C, 2017, 5(7), 1586–1590.
21. D. H. Kim, et al., UV-responsive nano-sponge for oil absorption and desorption, Sci. Rep., 2015, 5, 1–12.
22. M. N. Biutty, J. M. Koo, M. Zakia, P. L. Handayani, U. H. Choi and S. Il Yoo, Dielectric control of porous polydimethylsiloxane elastomers with Au nanoparticles for enhancing the output performance of triboelectric nanogenerators, RSC Adv., 2020, 10(36), 21309–21317.
23. S.-U. Victor, C. U. Yendry Regina and V.-B. J. Roberto, Immobilization of Gold and Silver on a Biocompatible Porous Silicone Matrix to Obtain Hybrid Nanostructures, J. Biomater. Nanobiotechnol., 2018, 09(01), 41–50.
24. E. Park and J. Hur, Three-dimensionally interconnected porous PDMS decorated with poly(dopamine) and Prussian blue for floatable, flexible, and recyclable photo-Fenton catalyst activated by solar light, Appl. Surf. Sci., 2021, 545, 148990.
25. M. N. Biutty and S. Il Yoo, Enhanced Performance of Triboelectric Nanogenerator by Controlled Pore Size in Polydimethylsiloxane Composites with Au Nanoparticles, Macromol. Res., 2021, 29(1), 98–104.
26. R. Iglio, S. Mariani, V. Robbiano, L. Strambini and G. Barillaro, Flexible Polydimethylsiloxane Foams Decorated with Multiwalled Carbon Nanotubes Enable Unprecedented Detection of Ultralow Strain and Pressure Coupled with a Large Working Range, ACS Appl. Mater. Interfaces, 2018, 10(16), 13877–13885.
27. D. Cho, et al., Three-Dimensional Continuous Conductive Nanostructure for Highly Sensitive and Stretchable Strain Sensor, ACS Appl. Mater. Interfaces, 2017, 9(20), 17369–17378.
28. S. Wu, et al., Novel Electrically Conductive Porous PDMS/Carbon Nanofiber Composites for Deformable Strain Sensors and Conductors, ACS Appl. Mater. Interfaces, 2017, 9(16), 14207–14215.
29. Y. Jung, et al., Wearable piezoresistive strain sensor based on graphene-coated three-dimensional micro-porous PDMS sponge, Micro Nano Syst. Lett., 2019, 7(1), 20.
30. W. Luo, M. Charara, M. C. Saha and Y. Liu, Fabrication and characterization of porous CNF/PDMS nanocomposites for sensing applications, Appl. Nanosci., 2019, 9(6), 1309–1317.
31. J. W. Han, B. Kim, J. Li and M. Meyyappan, Flexible, compressible, hydrophobic, floatable, and conductive carbon nanotube-polymer sponge, Appl. Phys. Lett., 2013, 102(5), 051913.
32. M. Chen, L. Zhang, S. Duan, S. Jing, H. Jiang and C. Li, Highly stretchable conductors integrated with a conductive carbon nanotube/graphene network and 3D porous poly (dimethylsiloxane), Adv. Funct. Mater., 2014, 24(47), 7548–7556.
33. S. Jung, et al., Reverse-Micelle-Induced Porous Pressure-Sensitive Rubber for Wearable Human-Machine Interfaces, Adv. Mater., 2014, 26(28), 4825–4830.
34. S. Kang, et al., Highly Sensitive Pressure Sensor Based on Bioinspired Porous Structure for Real-Time Tactile Sensing, Adv. Electron. Mater., 2016, 2(12), 1600356.
35. J. Park, et al., Three-dimensional nanonetworks for giant stretchability in dielectrics and conductors, Nat. Commun., 2012, 3(1), 916.
36. S.-J. Choi, et al., A Polydimethylsiloxane (PDMS) Sponge for the Selective Absorption of Oil from Water, ACS Appl. Mater. Interfaces, 2011, 3(12), 4552–4556.
37. X. Zhao, L. Li, B. Li, J. Zhang and A. Wang, Durable superhydrophobic/superoleophilic PDMS sponges and their applications in selective oil absorption and in plugging oil leakages, J. Mater. Chem. A, 2014, 2(43), 18281–18287.
38. A. Zhang, M. Chen, C. Du, H. Guo, H. Bai and L. Li, Poly(dimethylsiloxane) Oil Absorbent with a Three-Dimensionally Interconnected Porous Structure and Swellable Skeleton, ACS Appl. Mater. Interfaces, 2013, 5(20), 10201–10206.
39. E. Pedraza, et al., Macroporous Three-Dimensional PDMS Scaffolds for Extrahepatic Islet Transplantation, Cell Transplant., 2013, 22(7), 1123–1135.
40. J. Shi, H. Zhang, J. Jackson, A. Shademani and M. Chiao, A robust and refillable magnetic sponge capsule for remotely triggered drug release, J. Mater. Chem. B, 2016, 4(46), 7415–7422.
41. R. Zargar, J. Nourmohammadi and G. Amoabediny, Preparation, characterization, and silanization of 3D microporous PDMS structure with properly sized pores for endothelial cell culture, Biotechnol. Appl. Biochem., 2016, 63(2), 190–199.
42. J. Li, X. Liu, J. M. Crook and G. G. Wallace, Development of a porous 3D graphene-PDMS scaffold for improved osseointegration, Colloids Surf., B, 2017, 159, 386–393.
43. H. Zhang, et al., Piezoresistive Sensor with High Elasticity Based on 3D Hybrid Network of Sponge@CNTs@Ag NPs, ACS Appl. Mater. Interfaces, 2016, 8(34), 22374–22381.
44. V. V. Apyari, et al., Towards the development of solid-state platform optical sensors: aggregation of gold nanoparticles on polyurethane foam, Talanta, 2016, 161, 780–788.
45. A. M. Khalil, et al., Gold-decorated polymeric monoliths: In-situ vs ex-situ immobilization strategies and flow through catalytic applications towards nitrophenols reduction, Polymer, 2015, 77, 218–226.
46. Y. Ding, T. Xu, O. Onyilagha, H. Fong and Z. Zhu, Recent advances in flexible and wearable pressure sensors based on piezoresistive 3D monolithic conductive sponges, ACS Appl. Mater. Interfaces, 2019, 11(7), 6685–6704.
47. G. Ciobanu, S. Ilisei and C. Luca, Hydroxyapatite-silver nanoparticles coatings on porous polyurethane scaffold, Mater. Sci. Eng., C, 2014, 35(1), 36–42.
48. J. Y. Song, E. Y. Kwon and B. S. Kim, Antibacterial latex foams coated with biologically synthesized silver nanoparticles using Magnolia kobus leaf extract, Korean J. Chem. Eng., 2012, 29(12), 1771–1775.
49. C. H. Deng, J. L. Gong, P. Zhang, G. M. Zeng, B. Song and H. Y. Liu, Preparation of melamine sponge decorated with silver nanoparticles-modified graphene for water disinfection, J. Colloid Interface Sci., 2017, 488, 26–38.
50. J. Pinto, et al., Antibacterial Melamine Foams Decorated with in Situ Synthesized Silver Nanoparticles, ACS Appl. Mater. Interfaces, 2018, 10(18), 16095–16104.
51. J. Pinto, et al., Melamine foams decorated with in-situ synthesized gold and palladium nanoparticles, Polymers, 2020, 12(4), 1–13.
52. Y. Wu, et al., Channel Crack-Designed Gold@PU Sponge for Highly Elastic Piezoresistive Sensor with Excellent Detectability, ACS Appl. Mater. Interfaces, 2017, 9(23), 20098–20105.
53. C. L. Choong, et al., Highly stretchable resistive pressure sensors using a conductive elastomeric composite on a micropyramid array, Adv. Mater., 2014, 26(21), 3451–3458.
54. J. Park, et al., Giant tunneling piezoresistance of composite elastomers with interlocked microdome arrays for ultrasensitive and multimodal electronic skins, ACS Nano, 2014, 8(5), 4689–4697.
55. L. Lv, P. Zhang, T. Xu and L. Qu, Ultrasensitive Pressure Sensor Based on an Ultralight Sparkling Graphene Block, ACS Appl. Mater. Interfaces, 2017, 9(27), 22885–22892.
56. C. Hou, H. Wang, Q. Zhang, Y. Li and M. Zhu, Highly conductive, flexible, and compressible all-graphene passive electronic skin for sensing human touch, Adv. Mater., 2014, 26(29), 5018–5024.
57. B. Lee, et al., Ultraflexible and transparent electroluminescent skin for real-time and super-resolution imaging of pressure distribution, Nat. Commun., 2020, 11(1), 1–11.
58. M. Jian, et al., Flexible and Highly Sensitive Pressure Sensors Based on Bionic Hierarchical Structures, Adv. Funct. Mater., 2017, 27(9), 1606066.
59. X. Xu, et al., Copper Nanowire-Based Aerogel with Tunable Pore Structure and Its Application as Flexible Pressure Sensor, ACS Appl. Mater. Interfaces, 2017, 9(16), 14273–14280.
60. H. Bin, Yao et al., A flexible and highly pressure-sensitive graphene-polyurethane sponge based on fractured microstructure design, Adv. Mater., 2013, 25(46), 6692–6698.
61. S. Chun, A. Hong, Y. Choi, C. Ha and W. Park, A tactile sensor using a conductive graphene-sponge composite, Nanoscale, 2016, 8(17), 9185–9192.
62. Y. Luo, Q. Xiao and B. Li, Highly compressible graphene/polyurethane sponge with linear and dynamic piezoresistive behavior, RSC Adv., 2017, 7(56), 34939–34944.
63. Z. Ma, et al., Lightweight, compressible and electrically conductive polyurethane sponges coated with synergistic multiwalled carbon nanotubes and graphene for piezoresistive sensors, Nanoscale, 2018, 10(15), 7116–7126.
64. A. Tewari, S. Gandla, S. Bohm, C. R. McNeill and D. Gupta, Highly Exfoliated MWNT-rGO Ink-Wrapped Polyurethane Foam for Piezoresistive Pressure Sensor Applications, ACS Appl. Mater. Interfaces, 2018, 10(6), 5185–5195.
65. X. Wu, Y. Han, X. Zhang, Z. Zhou and C. Lu, Large-Area Compliant, Low-Cost, and Versatile Pressure-Sensing Platform Based on Microcrack-Designed Carbon Black@Polyurethane Sponge for Human–Machine Interfacing, Adv. Funct. Mater., 2016, 26(34), 6246–6256.
66. G. Ge, et al., A flexible pressure sensor based on rGO/polyaniline wrapped sponge with tunable sensitivity for human motion detection, Nanoscale, 2018, 10(21), 10033–10040.
67. Y. Ding, J. Yang, C. R. Tolle and Z. Zhu, Flexible and Compressible PEDOT:PSS@Melamine Conductive Sponge Prepared via One-Step Dip Coating as Piezoresistive Pressure Sensor for Human Motion Detection, ACS Appl. Mater. Interfaces, 2018, 10(18), 16077–16086.
68. R. Iglio, S. Mariani, L. M. Strambini and G. Barillaro, Macroporous PDMS foam decorated with carbon nanotubes for conductometric pressure and strain sensors, Proc. IEEE Sensors, 2017, 1–3.
69. C. Yu, et al., Facile Preparation of the Porous PDMS Oil-Absorbent for Oil/Water Separation, Adv. Mater. Interfaces, 2017, 4(3), 1600862.
70. J. Y. Yao, A. H. Fostier and E. B. Santos, In situ formation of gold and silver nanoparticles on uniform PDMS films and colorimetric analysis of their plasmonic color, Colloids Surf., A, 2020, 607, 125463.
71. K. J. Cha and D. S. Kim, A portable pressure pump for microfluidic lab-on-a-chip systems using a porous polydimethylsiloxane (PDMS) sponge, Biomed. Microdevices, 2011, 13(5), 877–883.
72. Y. Qin, et al., Lightweight, Superelastic, and Mechanically Flexible Graphene/Polyimide Nanocomposite Foam for Strain Sensor Application, ACS Nano, 2015, 9(9), 8933–8941.
73. S. Zhao and R. Zhu, High Sensitivity and Broad Range Flexible Pressure Sensor Using Multilayered Porous PDMS/AgNP Sponge, Adv. Mater. Technol., 2019, 4(9), 1–7.
74. Z. Wang, A. A. Volinsky and N. D. Gallant, Crosslinking effect on polydimethylsiloxane elastic modulus measured by custom-built compression instrument, J. Appl. Polym. Sci., 2014, 131(22), 1–4.
75. I. D. Johnston, D. K. McCluskey, C. K. L. Tan and M. C. Tracey, Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering, J. Micromech. Microeng., 2014, 24(3), 035017.
76. M. A. Eddings, M. A. Johnson and B. K. Gale, Determining the optimal PDMS-PDMS bonding technique for microfluidic devices, J. Micromech. Microeng., 2008, 18(6), 067001.
77. S. Vlassov, et al., Adhesion and mechanical properties of PDMS-based materials probed with AFM: A review, Rev. Adv. Mater. Sci., 2018, 56(1), 62–78.
78. W. Koetniyom, T. Suhatcho, A. Treetong and T. Thiwawong, AFM force distance curve measurement for surface investigation of polymers compound blend with metal nanoparticles, Mater. Today: Proc., 2017, 4(5), 6205–6211.
79. R. Yin, et al., Flexible conductive Ag nanowire/cellulose nanofibril hybrid nanopaper for strain and temperature sensing applications, Sci. Bull., 2020, 65(11), 899–908.
80. X. Wu, Z. Li, Y. Zhu, J. Wang and S. Yang, Ultralight GO-Hybridized CNTs Aerogels with Enhanced Electronic and Mechanical Properties for Piezoresistive Sensors, ACS Appl. Mater. Interfaces, 2021, 13(22), 26352–26361.
81. H. Liu, et al., Lightweight, Superelastic, and Hydrophobic Polyimide Nanofiber/MXene Composite Aerogel for Wearable Piezoresistive Sensor and Oil/Water Separation Applications, Adv. Funct. Mater., 2021, 31(13), 2008006.
82. X. Li, et al., Wearable, Washable, and Highly Sensitive Piezoresistive Pressure Sensor Based on a 3D Sponge Network for Real-Time Monitoring Human Body Activities, ACS Appl. Mater. Interfaces, 2021, 13(39), 46848–46857.
83. Y. Bu, et al., Ultrasensitive strain sensor based on superhydrophobic microcracked conductive Ti3C2Tx MXene/paper for human-motion monitoring and E-skin, Sci. Bull., 2021, 66(18), 1849–1857.
84. A. de Rooij, Oxidation of silver by atomic oxygen, ESA J., 1989, 13(4), 363–382.
85. H. Qi, D. Alexson, O. Glembocki and S. M. Prokes, The effect of size and size distribution on the oxidation kinetics and plasmonics of nanoscale Ag particles, Nanotechnology, 2010, 21(21), 215706.
86. Y. Han, R. Lupitskyy, T. M. Chou, C. M. Stafford, H. Du and S. Sukhishvili, Effect of oxidation on surface-enhanced Raman scattering activity of silver nanoparticles: A quantitative correlation, Anal. Chem., 2011, 83(15), 5873–5880.
87. A. Matikainen, et al., Atmospheric oxidation and carbon contamination of silver and its effect on surface-enhanced Raman spectroscopy (SERS), Sci. Rep., 2016, 6, 4–9.
88. T. Trantidou, Y. Elani, E. Parsons and O. Ces, Hydrophilic surface modification of pdms for droplet microfluidics using a simple, quick, and robust method via pva deposition, Microsyst. Nanoeng., 2017, 3, 16091.
89. M. F. O’Rourke and A. P. X. J. Jiang, Pulse wave analysis, Br. J. Clin. Pharmacol., 2001, 51(6), 507–522.
90. D. A. Duprez, et al., Determinants of radial artery pulse wave analysis in asymptomatic individuals, Am. J. Hypertens., 2004, 17(8), 647–653.
91. G. Schwartz, et al., Flexible polymer transistors with high pressure sensitivity for application in electronic skin and health monitoring, Nat. Commun., 2013, 4, 1859.
92. H. Park, et al., Stretchable Array of Highly Sensitive Pressure Sensors Consisting of Polyaniline Nanofibers and Au-Coated Polydimethylsiloxane Micropillars, ACS Nano, 2015, 9(10), 9974–9985.
93. J. He, et al., A Universal high accuracy wearable pulse monitoring system via high sensitivity and large linearity graphene pressure sensor, Nano Energy, 2019, 59, 422–433.
94. S. C. Millasseau, R. P. Kelly, J. M. Ritter and P. J. Chowienczyk, Determination of age-related increases in large artery stiffness by digital pulse contour analysis, Clin. Sci., 2002, 103(4), 371–377.
95. W. W. Nichols, Clinical measurement of arterial stiffness obtained from noninvasive pressure waveforms, Am. J. Hypertens., 2005, 18(1 SUPPL.), 3–10.
96. V. Prabha, P. Buhutkar, M. Bhutkar and G. Sivagami, A comparative study of arterial stiffness indices between smokers & non smokers, Int. J. Med. Res. Heal. Sci., 2013, 2(3), 533.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nh00648g

---