Open Access Article
Open Access ArticleIncorporating plasmonic featurization with machine learning to achieve accurate and bidirectional prediction of nanoparticle size and size distribution†
Emily Xi
Tan‡
 a,
Yichao
Chen‡
b,
Yih Hong
Lee‡
a,
Yong Xiang
Leong
a,
Shi Xuan
Leong
a,
Chelsea Violita
Stanley
a,
Chi Seng
Pun
*b and
Xing Yi
Ling
a,
Yichao
Chen‡
b,
Yih Hong
Lee‡
a,
Yong Xiang
Leong
a,
Shi Xuan
Leong
a,
Chelsea Violita
Stanley
a,
Chi Seng
Pun
*b and
Xing Yi
Ling
 *a
*a
aDivision of Chemistry and Biological Chemistry, School of Physical and Mathematical Sciences, Nanyang Technological University, 21 Nanyang Link, 637371, Singapore. E-mail: xyling@ntu.edu.sg; cspun@ntu.edu.sg
bDivision of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University, 21 Nanyang Link, 637371, Singapore
First published on 4th May 2022
Abstract
Determination of nanoparticle size and size distribution is important because these key parameters dictate nanomaterials’ properties and applications. Yet, it is only accomplishable using low-throughput electron microscopy. Herein, we incorporate plasmonic-domain-driven feature engineering with machine learning (ML) for accurate and bidirectional prediction of both parameters for complete characterization of nanoparticle ensembles. Using gold nanospheres as our model system, our ML approach achieves the lowest prediction errors of 2.3% and ±1.0 nm for ensemble size and size distribution respectively, which is 3–6 times lower than previously reported ML or Mie approaches. Knowledge elicitation from the plasmonic domain and concomitant translation into featurization allow us to mitigate noise and boost data interpretability. This enables us to overcome challenges arising from size anisotropy and small sample size limitations to achieve highly generalizable ML models. We further showcase inverse prediction capabilities, using size and size distribution as inputs to generate spectra with LSPRs that closely match experimental data. This work illustrates a ML-empowered total nanocharacterization strategy that is rapid (<30 s), versatile, and applicable over a wide size range of 200 nm.
New conceptsWe demonstrate the use of domain knowledge-driven featurization to extract key plasmonic information from the raw extinction spectra to boost machine learning. In contrast to conventional data-driven feature selection, we effectively transform and condense the raw spectra into four key plasmonic features to eliminate redundancy and enhance data interpretability to overcome challenges of size anisotropy and sample size limitations. By incorporating plasmonic featurization with machine learning, we observe a consistent 3–6 times decrease in prediction errors for all machine learning models tested, compared to previously reported ML and Mie approaches, showing that this strategy is superior. In addition to its speed (<30 s), accuracy, and generalizability, our approach is also applicable to AuNSs of a wide range of 20–220 nm. We further demonstrate predictions of both size and size distribution, showing that our approach allows complete characterization of nanoparticle ensembles in real samples. Finally, we would like to highlight the versatility of our bidirectional ML model. Besides forward predictions, we also achieve inverse prediction of extinction spectra with accurate LSPRs that closely match experimental data. Our work will no doubt inspire subsequent applications that capitalize on domain knowledge-based featurization and machine learning for predictive analytics based on spectroscopic data. |
Introduction
Determination of plasmonic nanoparticles’ size and size distribution is important because these parameters dictate the nanoparticles’ optical, catalytic and photothermal properties for targeted applications in sensing, therapeutics, and electronics.1–4 Electron microscopy has conventionally been used due to its unparalleled resolving power. However, its small field of view may not fully reflect the overall size and distribution of nanoparticles.5–7 Furthermore, it involves non-trivial sample preparation, measurement, and image analysis which typically take >1 hour to complete, making it non-ideal for high-throughput nanocharacterization.5–7 Extinction spectroscopy is a promising alternative because it provides rapid measurements (<10 s) and captures ensemble information, such as localized surface plasmon resonances (LSPRs), to generate an accurate representation of the global population within a sample.5,7–9 However, extinction data alone is insufficient to conclusively determine the size of nanoparticles and is typically combined with analytical frameworks such as Mie theory which operate under restrictive assumptions of homogeneity and sphericity and thus suffer from substantial errors of 6–20%.8–12 Moreover, these frameworks cannot account for size distributions in real samples and have not been employed to study nanoparticles larger than 100 nm, which absorb at longer wavelengths and are extensively used for in vivo photoacoustic imaging.8–13Instead of these traditional analytical frameworks, machine learning (ML) algorithms demonstrate immense potential to analyze plasmonic nanoparticles’ optical spectra and achieve accurate estimations of their dimensional parameters.14–18 ML algorithms can (1) uncover functions that connect inputs with outputs and in the process elucidate complex underlying trends/patterns within a dataset and (2) continuously learn in every iteration to improve prediction accuracy.19–21 The key to ML success is the quality of input data (features) that are used in the algorithm.19–21 Current ML-UV-vis studies employ statistical feature selection methods to compute the contribution of each datapoint (feature) towards prediction report significant errors of ∼10%.16,18 This is because each datapoint in the spectra (assuming 1 datapoint/nm, we will have ∼600 datapoints/spectra) encodes very little information. It is also challenging to find the optimal number and permutation of datapoints (feature) within the dataset for nanoparticle size prediction.16,18,22,23 We hypothesize that feature engineering based on established plasmonic knowledge can better complement ML predict nanoparticle size and size distribution. Besides extracting primary information such as LSPR positions, featurization allows us to derive secondary spectral information, such as LSPR full width at half maximum (FWHM) that is not readily obtainable from the ∼600 original datapoints, as inputs for the ML model. By judiciously extracting and transforming the raw spectra into meaningful features (LSPR peak descriptors) that correlate directly to the output (nanoparticles’ size and size distribution), we can simultaneously eliminate noise, increase data interpretability, reduce dimensionality, and enable the algorithms to detect patterns. Subsequently, we can construct generalizable, efficient, and accurate ML models that can reliably predict new data using these highly relevant and meaningful LSPR features. Through feature engineering, we can enrich the input and lower the computation cost, complexity, and the overall number of datasets required, which is especially pertinent given the challenging nature of nanoparticle synthesis.24–27
Herein, we demonstrate that plasmonic-knowledge-driven featurization combined with ML can bidirectionally predict the size and size distribution of gold nanospheres (Au NSs) over a large 20–220 nm size range, achieving low errors of 2.3% and ± 1.0 nm, respectively. Our two-pronged strategy first transforms 94 sets of experimentally acquired extinction spectra consisting of ∼600 datapoints each into 4 key inputs, namely the peak position and FWHM of individual dipolar and quadrupolar LSPR peaks. Next, we employ ML models, including basis-spline (Bspline), random forest (RF), and extreme-gradient boosting (XGB), to perform multiplex correlative data analysis and correlate the underlying relationships between size, size distribution, and LSPR features. Overall, we achieve a 2.3–2.8% error for size prediction of Au NSs between 100–220 nm using both dipole and quadrupole resonance features and 3.9–5.0% for Au NSs between 20–220 nm in size using only dipole features. We further demonstrate that our approach can account for size anisotropy in real samples through the unprecedented prediction of size distribution from extinction spectra with low error rates of ±1.0 nm for all 3 models. Knowledge elicitation from the plasmonic domain and its subsequent translation into featurization and machine learning allow us to predict the size and size distribution over a wide size range and achieve the lowest reported errors for all models, which is 3–6 times lower than conventional machine learning and Mie approaches. (Scheme 1). Importantly, our versatile ML approach allows bidirectional predictions, where an input of size and size distribution can inversely yield extinction spectra with accurate LSPRs that closely match that of experimental results. Notably, we overcome small sample size limitations by strategically increasing interpretability and reducing the dimensionality of the input data for ML model construction. We anticipate that our rapid (<30 s) and streamlined protocol can be coupled with high-throughput UV-vis spectroscopy to monitor nanoparticles’ size and shape-changing reactions in real-time. Our ML-powered optical approach for nanospheres characterization also demonstrates the potential to be extended to plasmonic nanomaterials with more complex morphologies.
 | ||
| Scheme 1 Schematic of our bidirectional machine learning (ML) method incorporating plasmonic featurization (blue and purple arrow) and the comparison with previously reported methods, such as data-driven feature selection with ML (dotted dark grey arrow), UV-vis and Mie theory (grey arrow) and multi-step electron microscopy (light grey arrow).8,9,18 The use of plasmonic knowledge to guide feature engineering (FE) allows us to achieve bidirectional prediction of gold nanosphere size and size distribution from experimentally acquired UV-vis extinction spectra with unprecedented speed (seconds) and accuracy (∼96 to 98%). | ||
Results and discussion
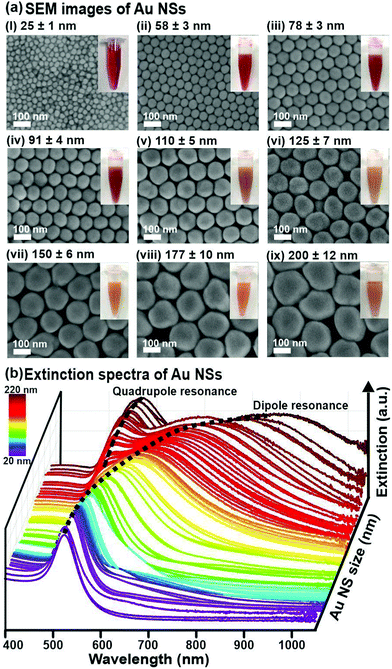
To establish our ML approach for accurate and rapid determination of nanoparticles’ size and size distribution, we first experimentally synthesize 94 batches of Au NSs using the seed-mediated method and acquire their extinction spectra.28 Electron microscopy (EM) characterization reveals that the size of Au NSs ranges between 20 and 220 nm and size distribution ranges from 1.1 nm to 14.6 nm for the smallest to largest Au NSs. The Au NSs are also homogeneously spherical, with an elongation ratio between 1 to 1.2 (Fig. 1a, ESI† 1). The corresponding extinction spectra of Au NS with diameters between 20–110 nm show a single dipole peak, which broadens and redshifts from 520 to ∼600 nm with increasing size, ascribed to the dominant dipole resonance excitation upon irradiation (Fig. 1b).29–32 Larger Au NSs >110 nm exhibit a subsidiary peak due to the excitation of higher-order plasmonic resonance modes such as the quadrupolar resonance (Fig. 1b).29–32 Our extinction signatures and behaviors are in good concordance with both theories and previously reported empirical data, which ascertains that LSPRs red-shifting and broadening are size-dependent.2,8,9,29–32Plasmonic featurization
To describe the extinction spectra in terms of their LSPR features, we perform feature engineering to extract both primary (peak positions) and secondary (FWHMs) plasmonic information from the raw extinction spectra (Fig. 2a). Critically, this transformation mitigates noise and redundant features from unstructured raw spectra (∼600 datapoints) and prepares structured data (4 LSPR features) that captures all the relevant information for subsequent correlation analysis and ML exploration.24–27 Moreover, the organized architecture of structured data is instrumental for ML success as data within a column (e.g. dipole position) can be compared directly with one another and to the output which prevents mismatches and eases query during ML data exploration.24–27 In contrast, a mismatch can easily occur with unstructured spectral data where a datapoint that corresponds to a dipole peak in one spectrum is noise in another spectrum. To eliminate bias and inconsistency associated with manual, user-defined spectral deconvolution of these overlapped peaks (i.e. dipole and quadrupole), we use an automated Gaussian spectral deconvolution routine in R to swiftly (within milliseconds) resolve and extract them (ESI† 2). Overall, plasmonic featurization is necessary to circumvent the curse of dimensionality, improve data interpretability and enhance model efficiency to alleviate the need for large datasets which remains challenging in the context of nanoparticle synthesis.24–26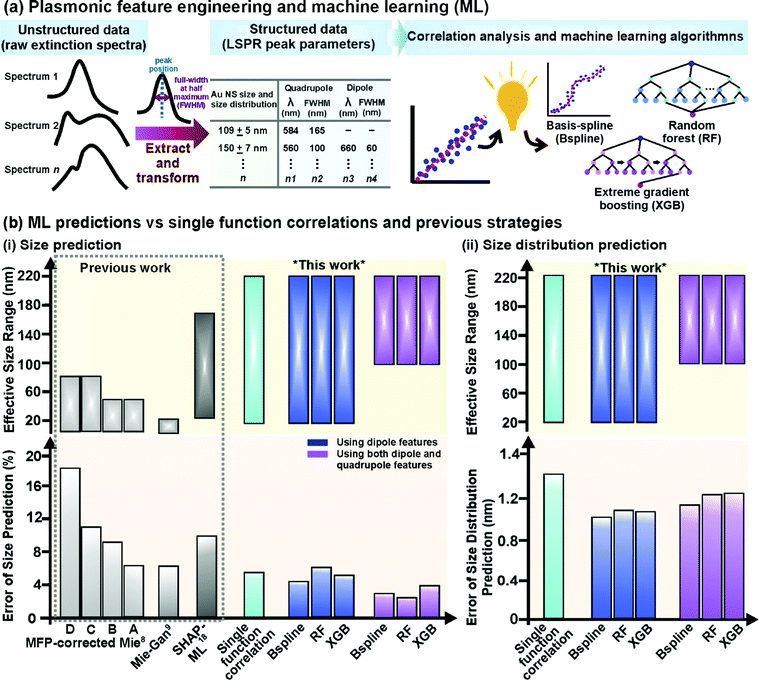 | ||
| Fig. 2 Plasmonic-knowledge-driven feature engineering, machine learning algorithms, and their prediction accuracy. (a) Schematic illustration of the feature-engineering process where raw extinction spectra are transformed into structured data consisting of LSPR features and subsequent data exploration using both single-function correlative analysis and machine learning. Machine learning algorithms used are basis-spline (Bspline), random forest (RF), and extreme gradient boosting (XGB). (b) Evaluating the predictive capabilities and effective size ranges of single-function correlation with the lowest prediction error and various machine learning algorithms in predicting Au nanospheres' (NSs) (i) size and (ii) size distribution compared to previously reported strategies, including data-driven ML models which rely on SHAP feature engineering,18 Mie-Gan model9 and other mean free path (MFP)-corrected Mie theory calculations with known nanoparticle concentration (based on experimental A, and theoretical B data) and unknown nanoparticle concentration (based on experimental C, and theoretical D data).8 | ||
Single function correlations and machine learning (ML)
To examine the extent of different peak feature size and size distribution dependencies over the entire size range of 20–220 nm, we systematically perform correlation analysis using single best-fit functions to study them separately (ESI† 3). The extracted LSPR positions and FWHMs show the obvious size and size distribution dependencies over the size range of 20–220 nm. However, the relationships between LSPR feature and particle size and size distributions cannot be easily explained using single functions, with large percentage errors of 5–28% for size and relative error of 1.2–3.3 nm for size distribution, respectively (Fig. S5b and c, ESI†). This can be attributed to size anisotropy in real samples and its confounding optical effects, which distorts the relationship between LSPR with either size or size distribution.29,30 Size anisotropy is also the major reason Mie approaches are limited in their accuracy when applied to real samples, although they offer perfect solutions to the Maxwell equations.1,9,29,30To improve prediction accuracy and better infer the non-linear relationships between size, size distribution, and LSPR, we employ non-linear ML models capable of recognizing hidden patterns and utilizing multiple correlations to predict nanoparticle size, and size distributions.19–21,31–38 In addition to rapid multiplex correlative data processing, ML can increase prediction accuracy by (1) reprojecting variables into higher-dimensional spaces for regression and (2) continuously find predictive patterns to decrease error in each iteration19–21,31–38 We train 3 ML algorithms, namely basis-spline (Bspline), random forest (RF), and extreme gradient boosting (XGB) because they are commonly used to analyze spectroscopic data for regression problems, and use the mean square error of all validations (test) sets as a metric for prediction accuracy (Fig. 2a, ESI† 4).18–21,33–38 For all the models, we employ a random stratified sampling algorithm to split the datasets into 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 train-test, perform random k-fold cross-validation and repeat the process over 100 iterations to prevent selection bias, chance error and model overfit.
20 train-test, perform random k-fold cross-validation and repeat the process over 100 iterations to prevent selection bias, chance error and model overfit.
Dipole features for Au NS size prediction
To determine the ensemble-averaged size of Au NSs, we first use the dipole features (position and FWHM) because it is a common plasmon peak present in extinction spectra of Au NSs of all sizes. By training the ML models with dipole features as input, we achieve mean errors of 3.9%, 4.3%, and 5.0% for Bspline, RF, and XGB, respectively (Fig. 2b(i), ESI† 5). All 3 models significantly surpass other previously reported methods, such as SHAP-ML (∼10%), the Mie-Gan model (6%), and mean free path-corrected Mie calculations (6–18%), in terms of accuracy.8,9,18 In terms of the effective size range, all 3 ML models are applicable over an unprecedented size range of 20–220 nm, which is larger than SHAP-ML (25–174 nm) and Mie approaches (5–50 nm). In contrast to single functions (5% error), the Bspline model performs exceedingly well to capture the non-linearity in input data using embedded piecewise step functions to fit the dataset rather than imposing an overarching linear or high-order polynomial function as the global structure.32,38 Moreover, to prevent over-or underfitting of curves, the model also optimizes and regulates a very general and flexible family of transformers known as basis functions, which are typically linear, or low-degree polynomials fitted based on the least squared error metric.32,38Dipole and quadrupole features for Au NS size prediction
To further investigate the use of multiple plasmon modes to improve accuracy, we also construct ML models including both dipole and quadrupole features for Au NSs >100 nm (Fig. 2b(i), ESI† 5). This is because Maxwell equations indicate that the higher order of plasmonic modes is size-dependent, therefore we postulate that they are meaningful inputs for the prediction of larger Au NSs with more complex LSPR features.11,12,29,30 When we increase the number of input features to 4, all models return the lowest error rates of just 2.3–2.8% for larger Au NSs between 100 and 220 nm (Fig. 2b(i), ESI† 6). The improved accuracy exemplifies the importance of inputting quadrupole features in predicting size, demonstrating the ability of models to learn and capture multiplex correlations between inputs and outputs. When inputting all four LSPR features, RF performs better than other models (2.3% error), owing to its ability to map complex dependencies in multiplex correlative problems to find the optimal fit for this dataset.35,36 Furthermore, ensemble techniques such as RF average the outcome of multiple individual decision trees (in this case, 1000) to reduce the chances of overfitting and random errors for stable predictions.33,34 Overall, we demonstrate that all our ML models can attain 3–6 times lower error rates for Au nanoparticle size prediction compared to previously reported approaches, including ML models constructed with artificial spectra.8,9,16,18 This underlines the importance of incorporating plasmonic featurization to reduce raw spectra into meaningful features for predictive analytics.Au NS size distribution prediction
In addition to size prediction, we demonstrate that our 3 ML models can also predict the size distributions of Au NSs for a complete characterization of the ensemble. Currently, there is no analytical solution to predict the size distribution of nanoparticle ensembles. Yet, the size distribution of a nanoparticle ensemble will influence their optical-based applications because a slight deviation in size can cause LSPR displacement and broadening.5–7 Our results indicate that both two-feature and four-feature ML models can provide a good estimation of the size distribution with ±1.0 to 1.3 nm accuracy, which is comparable with the resolution of electron microscopy (Fig. 2b(ii), ESI† 5). Using dipole positions as inputs for the Bspline model generates the lowest errors of ±1.0 nm for size distribution out of all the models, due to its superior ability to model the non-linearity and capture the complexity within this dataset.Overall, our ML-powered approach allows us to determine both the size and size distribution with the lowest reported predictive errors of 2.3–3.9% and ±1.0 nm, respectively, over the largest reported size range of 20–220 nm. The large effective size range and low error rates emphasize the generalizable nature of ML models, owing to its capability to cumulatively make use of multiple relationships to overcome size anisotropy which inevitably exists in a real sample. Notably, we successfully shorten the time required for the complete nanocharacterization (size and size distribution) to under 30 seconds using a single-cell spectrometer, indicating the potential for real-time analysis.
Inverse predictions
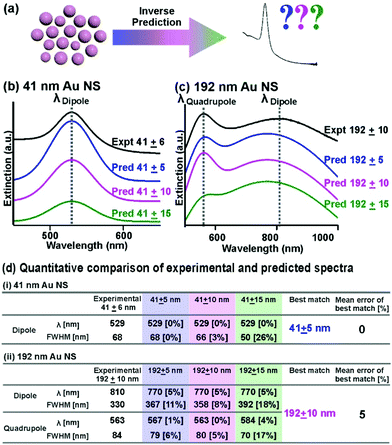
In addition to forward predictions, we demonstrate the multifunctionality of our ML model by inversely predicting the expected extinction spectrums, using size and size distribution as inputs, with accurate LSPR(s) that correspond to experimental data (Fig. 3a). The versatility to predict nanoparticle size and size distribution from extinction spectra and vice versa is important in nanooptics to guide nanoparticles’ targeted applications in bioimaging and sensing.1–4,29,30 For our inverse prediction model, we use Bspline as a representative algorithm. In brief, we first train our inverse Bspline model using Au NSs size and size distributions as inputs to predict Gaussian coefficients, which are directly proportional to LSPR positions and FWHM for spectra regeneration. To demonstrate our model's robustness, we compare the predicted and experimentally obtained extinction spectra of four nanoparticle solutions (41 ± 6, 109 ± 5, 139 ± 8, and 192 ± 10 nm) with size and size distributions ascertained by electron microscopy (ESI† 7). We affirm that the model works well across the wide size range of 40 nm to 190 nm with percentage mean errors of 0–5% (ESI† 7). For small Au NSs, the predicted spectrum (41 ± 5 nm as input) well reproduces the experimental spectrum (41± 6 nm) with 0% deviation for both LSPR position and FWHM (Fig. 3b and d(i)). Notably, our model demonstrates good accuracy in accounting for size distribution, whereby we observe an increase in mean error to 2 and 14% when the size distribution inputs deviate from the experimentally acquired spectrum to ± 10 and 15 nm, respectively (Fig. 3b and d(i)). For larger Au NSs, our inverse Bspline model also successfully regenerates spectra showing both plasmon resonances that corroborate well with experimental data of similar size distribution. The predicted spectrum of 192 ± 10 nm is consistent with the experimental spectrum (5% mean error), with 0–8% error rates for the 4 individual LSPR features (Fig. 3c and d(ii)). In contrast, the mean error increases to 6 and 11% when we input incorrect size distributions of ±5 and 15 nm, respectively (Fig. 3c and d(ii)). Comparing the overall spectral fit for all 4 sizes tested, we observe that larger nanoparticles with two plasmon peaks have higher mean error compared to smaller nanoparticles with only one peak. We also observe that for all the best-matched predicted spectra, the LSPR positions are well predicted with low errors of 0–5% while the FWHM have slightly higher errors ranging from 0–8% (ESI† 7). Notably, the series of predicted spectra display the well-documented spectral evolution trend: the LSPR modes red-shift and broaden with increasing nanoparticle size, thus indicating the accuracy of our bidirectional model (Fig. 3b and c, ESI† 7).2,8,9,29,30 Overall, our bidirectional Bspline model provides good inverse prediction capabilities because it can generate both “simple” and “complicated” spectra exhibiting only dipolar resonances and overlapping dipolar and quadrupolar resonances spectra that closely match experimental data.Conclusions
In conclusion, we demonstrate that featurization built on plasmonic insights enables us to transform and condense raw spectral data into structured data to leverage ML models for accurate, bidirectional, and robust prediction of Au NS size and size distribution over a wide size range of 20–220 nm. We use 3 different ML algorithms to predict the size of Au NSs and attain the lowest reported mean errors of 2.3–2.8% for larger Au NSs between 100–220 nm using dipole and quadrupole features. Our highly generalizable Bspline model also returns an error of just 3.9% for the entire studied size range of 20–220 nm using dipole features. Additionally, we establish a Bspline model to determine the size distribution with an error of ±1.0 nm, due to its ability to capture non-linearity within this dataset. Furthermore, we demonstrate the multi-functionality and robustness of our predictive models through the inverse generation of extinction spectra with LSPRs that match closely with experimental data using only NP size and size distribution as inputs. The accuracy, generalizability, and applicability over a wide size range, as well as rapid computing speed (<milliseconds) offered by these ML models, outperform analytical Mie approaches and offer a paradigm shift in the approach to nanoparticle characterization. Notably, we envisage that simultaneous prediction of both size and size distribution can be achieved by embedding optimized models in a single predictive algorithm to parallelize prediction for real-life applications. These models can also complement high throughput multicell spectrometers for parallelization of sample measurements to achieve multi-fold improvements in efficiency to further boost research productivity. We envision that the findings can be extended to more complex nanoparticle morphologies such as nanocubes that possess multipole resonances in their extinction spectra.Abbreviations
| Au NSs | Gold nanospheres |
| Bspline | Basis spline |
| FE | Feature engineering |
| LSPR | Localized surface plasmon resonance |
| ML | Machine learning |
| RF | Random forest |
| SHAP | Shapley additive explanations |
| XGB | Extreme gradient boosting |
Author contributions
Conceptualization, Y. H. L., X. Y. L.; methodology, E. T. X., Y. C., Y. H. L., C. S. P., X. Y. L.; investigation, E. T. X., Y. C., Y. H. L., C. V. S.; data curation and visualization, E. T. X., Y. C., Y. H. L., C. S. P., X. Y. L; writing, E. T. X., Y. H. L, Y. X. L, S. X. L., C. S. P., X. Y. L.; funding acquisition and supervision, X. Y. L. The manuscript was written with the contributions of all authors. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is supported by the Singapore Ministry of Education Academic Research Fund Tier 1 (RG97/19), and NTUitive Gap Fund (NGF-2019-07-009) grants, A*STAR AME. Individual Research Grant (A20E5c0082), Singapore National Research Foundation Central Gap Fund (NRF2020NRF-CG001-010), and Max Planck Institute -Nanyang Technological University Joint Lab. E. T. X., Y. X. L. and S. X. L. acknowledge scholarship support from Nanyang Technological University.References
- D. V. Talapin and E. V. Shevchenko, Introduction: nanoparticle chemistry, Chem. Rev., 2016, 116(18), 10343–10345 CrossRef CAS PubMed.
- S. Eustis and M. A. El-Sayed, Why gold nanoparticles are more precious than pretty gold: noble metal surface plasmon resonance and its enhancement of the radiative and nonradiative properties of nanocrystals of different shapes, Chem. Soc. Rev., 2006, 35(3), 209–217 RSC.
- Y. Mantri and J. V. Jokerst, Engineering plasmonic nanoparticles for enhanced photoacoustic imaging, ACS Nano, 2020, 14(8), 9408–9422 CrossRef CAS PubMed.
- H. Wang, D. W. Brandl, P. Nordlander and N. J. Halas, Plasmonic nanostructures: artificial molecules, Acc. Chem. Res., 2007, 40(1), 53–62 CrossRef CAS PubMed.
- S. Mourdikoudis, R. M. Pallares and N. T. Thanh, Characterization techniques for nanoparticles: comparison and complementarity upon studying nanoparticle properties, Nanoscale, 2018, 10(27), 12871–12934 RSC.
- M. M. Modena, B. Rühle, T. P. Burg and S. Wuttke, Nanoparticle characterization: what to measure?, Adv. Mater., 2019, 31(32), 1901556 CrossRef PubMed.
- D. Titus, E. J.-J. Samuel and S. M. Roopan, Nanoparticle characterization techniques, Green Synthesis, Characterization and Applications of Nanoparticles, Elsevier, 2019, pp. 303–319 Search PubMed.
- W. Haiss, N. T. Thanh, J. Aveyard and D. G. Fernig, Determination of size and concentration of gold nanoparticles from UV-Vis spectra, Anal. Chem., 2007, 79(11), 4215–4221 CrossRef CAS PubMed.
- V. Amendola and M. Meneghetti, Size evaluation of gold nanoparticles by UV− vis spectroscopy, J. Phys. Chem. C, 2009, 113(11), 4277–4285 CrossRef CAS.
- Q. Fu and W. Sun, Mie theory for light scattering by a spherical particle in an absorbing medium, Appl. Opt., 2001, 40(9), 1354–1361 CrossRef CAS PubMed.
- M. Quinten, Optical properties of nanoparticle systems, Mie and Beyond, John Wiley & Sons, 2010 Search PubMed.
- T. Wriedt, Mie theory: a review, Mie Theory, 2012, 53–71 Search PubMed.
- H. Yu, Y. Peng, Y. Yang and Z.-Y. Li, Plasmon-enhanced light–matter interactions and applications, npj Comput. Mater., 2019, 5(1), 1–14 CrossRef.
- J. He, C. He, C. Zheng, Q. Wang and J. Ye, Plasmonic nanoparticle simulations and inverse design using machine learning, Nanoscale, 2019, 11(37), 17444–17459 RSC.
- S. So, T. Badloe, J. Noh, J. Bravo-Abad and J. Rho, Deep learning enabled inverse design in nanophotonics, Nanophotonics, 2020, 9(5), 1041–1057 Search PubMed.
- H. Tao, T. Wu, M. Aldeghi, T. C. Wu, A. Aspuru-Guzik and E. Kumacheva, Nanoparticle synthesis assisted by machine learning, Nat. Rev. Mater., 2021, 1–16 Search PubMed.
- P. R. Wiecha and O. L. Muskens, Deep learning meets nanophotonics: a generalized accurate predictor for near fields and far fields of arbitrary 3D nanostructures, Nano Lett., 2019, 20(1), 329–338 CrossRef PubMed.
- K. Shiratori, L. D. Bishop, B. Ostovar, R. Baiyasi, Y.-Y. Cai, P. J. Rossky, C. F. Landes and S. Link, Machine-Learned Decision Trees for Predicting Gold Nanorod Sizes from Spectra, J. Phys. Chem. C, 2021, 125(35), 19353–19361 CrossRef.
- K. A. Brown, S. Brittman, N. Maccaferri, D. Jariwala and U. Celano, Machine learning in nanoscience: big data at small scales, Nano Lett., 2019, 20(1), 2–10 CrossRef PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559(7715), 547–555 CrossRef CAS PubMed.
- X.-D. Zhang, Machine learning, A Matrix Algebra Approach to Artificial Intelligence, Springer, 2020, pp. 223–440 Search PubMed.
- S. Cohen, E. Ruppin and G. Dror, Feature selection based on the shapley value, Other Words, 2005, 1, 98Eqr Search PubMed.
- F. Mokdad, D. Bouchaffra, N. Zerrouki and A. Touazi, In Determination of an optimal feature selection method based on maximum shapley value, 2015 15th International Conference on Intelligent Systems Design and Applications (ISDA), IEEE, 2015, pp. 116–121.
- G. Dong and H. Liu, Feature Engineering for Machine Learning and Data Analytics, CRC Press, 2018 Search PubMed.
- A. Zheng and A. Casari, Feature engineering for machine learning: principles and techniques for data scientists, O'Reilly Media, Inc., 2018 Search PubMed.
- J. Heaton, An empirical analysis of feature engineering for predictive modeling, SoutheastCon 2016, IEEE, 2016, 1–6 Search PubMed.
- C. R. Turner, A. Fuggetta, L. Lavazza and A. L. Wolf, A conceptual basis for feature engineering, J Syst. Softw., 1999, 49(1), 3–15 CrossRef.
- Q. Ruan, L. Shao, Y. Shu, J. Wang and H. Wu, Growth of monodisperse gold nanospheres with diameters from 20 nm to 220 nm and their core/satellite nanostructures, Adv. Opt. Mater., 2014, 2(1), 65–73 CrossRef.
- P. B. Johnson and R.-W. Christy, Optical constants of the noble metals, Phys. Rev. B: Solid State, 1972, 6(12), 4370 CrossRef CAS.
- V. Amendola, R. Pilot, M. Frasconi, O. M. Maragò and M. A. Iatì, Surface plasmon resonance in gold nanoparticles: a review, J. Phys.: Condens. Matter, 2017, 29(20), 203002 CrossRef PubMed.
- S. Guo, J. Popp and T. Bocklitz, Chemometric analysis in Raman spectroscopy from experimental design to machine learning–based modeling, Nat. Protoc., 2021, 16(12), 5426–5459 CrossRef CAS PubMed.
- S. Park and J. Lee, Multivariate Lévy Adaptive B-Spline Regression. arXiv preprint arXiv:2108.11863 2021.
- T. M. Oshiro, P. S. Perez and J. A. Baranauskas, How many trees in a random forest? International Workshop on Machine Learning and Data Mining in Pattern Recognition, Springer, 2012, pp. 154–168 Search PubMed.
- M. R. Segal, Machine Learning Benchmarks and Random Forest Regression, 2004 Search PubMed.
- T. Chen, T. He, M. Benesty, V. Khotilovich, Y. Tang and H. Cho, Xgboost: extreme gradient boosting, R Package version 0.4–2, 2015, 1(4), 1–4 Search PubMed.
- D. Bzdok, N. Altman and M. Krzywinski, Statistics versus machine learning, Nat. Methods., 2018, 15(4), 233–234 CrossRef CAS PubMed.
- N. M. Ralbovsky and I. K. Lednev, Towards development of a novel universal medical diagnostic method: Raman spectroscopy and machine learning, Chem. Soc. Rev., 2020, 49(20), 7428–7453 RSC.
- L. Jing and L. Sun, in: Fitting B-spline curves by least squares support vector machines, 2005 International Conference on Neural Networks and Brain, IEEE, 2005, pp. 905–909.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental procedures, supplementary information 1–7. Fig. S1–S10 and Tables S1–S13. See DOI: https://doi.org/10.1039/d2nh00146b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |