Polariscopy with optical near-fields

Abstract

Polarisation analysis of light–matter interactions established for propagating optical far-fields is now extended into an evanescent field as demonstrated in this study using an attenuated total reflection (ATR) setup and a synchrotron source at THz frequencies. Scalar intensity E², rather than a vector E-field, is used for absorbance analysis of the s- and p-components of the linearly polarised incident light. Absorption and phase changes induced by the sample and detected at the transmission port of the ATR accessory revealed previously non-accessible anisotropy in the absorption–dispersion properties of the sample probed by the evanescent optical near-field. Mapping of the sample's anisotropy perpendicular to its surface by the non-propagating light field is validated and the cos² θ absorbance dependence was observed for the angle θ, where θ = 0° is aligned with the sample's surface. A four-polarisation method is presented for the absorbance mapping and a complimentary retardance spectrum is retrieved from the same measurement of the angular dependence of transmittance in structurally complex poly-hydroxybutyrate (PHB) and poly-L-lactic acid (PLLA) samples with amorphous and banded-spherulite (radially isotropic) crystalline regions. A possibility of all 3D mapping of anisotropy (polarisation tomography) is outlined.

---

New concepts

The new phase and amplitude mapping technique based on optical near-fields was introduced. Anisotropy of real and imaginary parts of the refractive index at the absorbance bands can be determined. Polarization analysis of attenuated total reflection (ATR) was carried out for structurally complex polyhydroxybutyrate (PHB) and poly-L-lactic acid (PLLA) samples using a synchrotron-based THz light source. So far, the anisotropy of absorbance and birefringence is measured at the UV-IR-THz spectral ranges using propagating far-fields. Simultaneous measurement of absorption anisotropy and birefringence at the IR-THz spectral range was not previously accessible. 3D mapping of anisotropy can be made by rotating the sample or ATR prism using evanescent optical near-fields for nano-micro-scale characterization. Such measurements will provide information about the alignment of the absorbers and patterns inside optically sectioned nano-micro-volumes.

1. Introduction: polarisation as an analytical tool

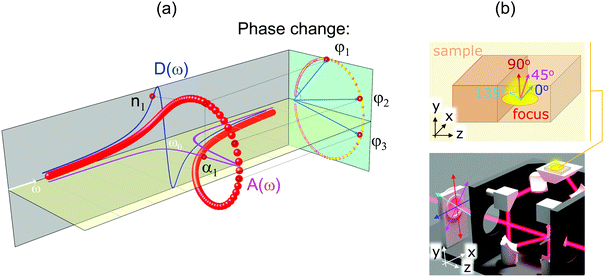
Polarisation of light in different wavelength ranges has become an essential analytical tool in a diverse range of applications, such as those used for probing material's anisotropy in infrared (IR) wavelengths,^1,2 cataclysmic gravitational astronomical events by the imaging X-ray polarimetry explorer (IXPE),³ the chirality of matter (or interaction),^4,5 and for multi-dimensional optical memory inscription to control optical retardance at nanoscales.^6,7 Linear polarisation probes the orientation of absorption, scattering and reflectance, and their anisotropies, via non-destructive and remote utility. Super-resolution (6 nm) was recently demonstrated within visible wavelengths using a radially polarised beam to map the absorption of carbon nanotubes.⁸ A propagating light is a transverse wave and has an electrical field E-vector perpendicular to the direction of propagation (k-vector). A non-propagating evanescent E-field, however, can possess a longitudinal component, e.g., upon a total internal reflection (TIR) or around a nano-absorber/scatterer. Although the evanescent light, which extends only a sub-wavelength ∼λ/4 distance into the sample, has limited use in material characterisation in the case of long wavelengths in the IR and THz spectral regions or in nano-thin films and structures. In X-ray (neutron) scattering, the grazing incidence diffraction, which is based on field (particle) scattering at close to the critical angles of the substrate and film, features prominently among surface and interface characterisation techniques.⁹

In the spectral range of long IR-THz wavelengths, analysis of the absorption anisotropy has the utility of optical biopsy for the detection of structural anisotropy directly related to medical conditions¹⁰ and can be performed beyond 1 mm depths.¹¹ Usually only two orthogonal s- and p-polarisations are utilised in the attenuated total reflection (ATR) mode. Recently, we hypothesised that polarisation analysis similar to that with propagating optical far-fields can be realised with near-fields in the ATR setting.¹² It was also recently demonstrated that polarisation far-field steering of the near-field delivers directional control over nano-ablation for nanoscale direct-write lithography down to 20 nm resolution and duty cycle.¹³ We showed that strong coupling between polymer IR absorption bands and the nanoscale cavity of a metamaterial (near-field) can be used as a narrow band absorber or emitter,¹⁴ which can be tailored to have a defined polarisation by the design of a metasurface motif. Hence, the orientation of the optical non-propagating near-field can be controlled in the transverse (in the sample's plane) direction,¹³ which is extended to the longitudinal near-field (out-of-plane) in this study.

For a linear case of low light intensity, the light-matter interaction is defined solely by the complex refractive index ñ = n + iκ within the focal volume inside a material at the wavelength of light λ. Both refractive index n and extinction coefficient κ should be known to account for portions of the absorbed, reflected, and transmitted light A + R + T = 100%. While absorption is usually directly measured from transmittance T = (1 − R)e^−αd, where α = 4πκ/λ = 2kκ is the absorption coefficient (for intensity) and d is the axial extent of light–matter interaction volume, determination of the refractive index n is more complex. It can be determined from an angular dependence of reflectance R using Fresnel formulas or retrieved numerically via the Kramers–Kronig (K–K) relation from the measured spectral dependence of absorption as 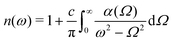where ω = kc; the reverse relation 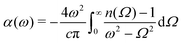.¹⁵ Directly relevant to ATR, the K–K relation for the reflectivity ρ(ω) and phase upon reflection ϕ(ω) or r̃(ω) =ρ(ω)e^iϕ(ω) (for E-field) is given as 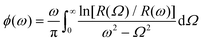for the experimentally measured reflectance spectrum R(ω) (for intensity).^16–18 The K–K calculations work well for qualitative analysis; however, they have limited applicability for the determination of n(ω) and α(ω) (or ρ(ω), ϕ(ω)), especially for measurements carried out over a limited spectral range, where the K–K integral is affected by an unknown material response at the shorter wavelengths (ω → ∞) and/or due to a change of dispersion mechanism, e.g. electronic, ionic, etc.¹⁹ Currently, there is no method available to determine n(ω) and α(ω) (ρ(ω), ϕ(ω)) simultaneously, especially in the IR chemical fingerprint region where refractive index anisotropy affects the orientation of the linearly polarised probe. The lack of spectral characterisation prompted this study to measure anisotropy of absorbance – dichroism – Δα and birefringence Δn = n_e − n_o defined by the ordinary and extraordinary refractive indices n_o,e, respectively.

In this study, we used a high brilliance synchrotron radiation, which is indispensable for material characterisation at frequencies lower than 10 THz (300 cm⁻¹ or ∼33 μm), as well as at higher frequencies in the mid-IR spectral range due to typically an order of magnitude better signal-to-noise ratio. The light source with high brilliance is valuable for polarized spectroscopy due to high intensity/power even after the polarizer. Phase transitions can be monitored spectroscopically by emission and absorption at the vibrational, rotational, and phonon spectral range from volumes comparable to the wavelength of light^20,21 as well as by diffraction of synchrotron X-rays or free-electron lasers (X-FELs).^22–24

Here, we validate the hypothesis of polarisation analysis using non-propagating evanescent light. Anisotropy of absorbance is determined by measuring the difference between two perpendicular s- and p-polarisation components, in amplitude and phase, from the fit of the angular dependence of transmittance through an ATR setup. The feasibility of determining a 3D absorbance anisotropy in ATR mode was demonstrated using organic micro-crystals which are in-plane isotropic and out-of-plane anisotropic. The anisotropy was revealed following cos² θ angular dependence. This opens the possibility for polarisation tomography. Direct measurement of optical response spectra Δα(ω) and Δn(ω) over a spectral range of an arbitrary extent is introduced.

2. Results: polariscopy with optical near-fields

In order to fully harness polarisation analysis using the ATR mode of measurements, its polarisation response should be understood, especially due to the complex linear-circular combination of polarisations originating from the synchrotron. Moreover, polarisation composition of the THz beam is different between the longer and shorter wavelength windows: 90% linear and 10% circular at <100 cm⁻¹, while the ratio of linear-to-isotropic becomes 20%-to-80% for the wavenumbers higher than 100 cm⁻¹.

2.1. Polarisation response of the ATR unit

The polarisation of the synchrotron THz beam does not translate to the same ratio of s- and p-polarisation on the sample due to the multi-reflection beam delivery of the ATR unit (Fig. 1). From the IN-port, the THz beam is reflected by a series of mirrors before being reflected from the sample-prism interface and then further experiences several reflections until it reaches the OUT-port of the ATR unit. In total from the IN to OUT port, there are ten reflections including one from the sample in Fig. 1. The beam inside the ATR unit is focused by parabolic mirrors and experiences change of s-/p-portions of the beam due to the change of direction of propagation inside the unit. Due to focusing on the sample (a 3 mm window), a range of incidence angles is covered, which contributes to different Fresnel reflection coefficients and the change of the phase.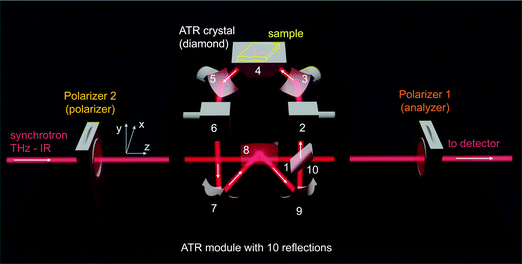

Fig. 1 ATR accessory (Pike Technologies) used in this study with ten reflections from the port-IN (synchrotron side) to OUT (detector side).

First, the polarisation response of the ATR unit without a sample (in air ambient) was analysed (Fig. 2). A mesh grid polariser was set at the IN-port and analyser at the OUT-port. Linear (horizontal) polarisation was set to enter the ATR unit, which corresponds to the linear polarisation of the synchrotron-IR radiation (θ_in = 0° in Fig. 2). A spectral window of 30–630 cm⁻¹ was selected with a suitable beamsplitter, and the detector was a Si bolometer. Mesh-grid polarisers-1,2 had the same extinction ratio 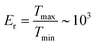over the range of the wavelengths used in this study. T_max,min is the transmission at the maximum and minimum orientation of the polariser, respectively. The detected ATR reference signal without a sample is only affected by the THz active absorbers/scatterers in air; hence, only the characteristic feature of atmospheric water is present in this spectral region. The evanescent field protrudes ∼λ/4 into the air and experiences absorption and phase changes at s-/p-polarisation corresponding to the refractive index ratio n₂/n₁ ≈ 1/2.42 (without the sample with n^(air)₂ = 1). The intensity change between s- and p-polarisations caused by the ATR unit (x-/y-polarisation lab frame of reference) and due to beam focusing at the ATR crystal surface (a range of incidence angles) led to an overall low measured extinction ratio over the entire ATR unit E_r ≈ 2.5. There was strong light leakage from the ATR unit, even under crossed polariser–analyser conditions (a cross-Nicol intensity is non-zero at minimum; Fig. 2(a)).

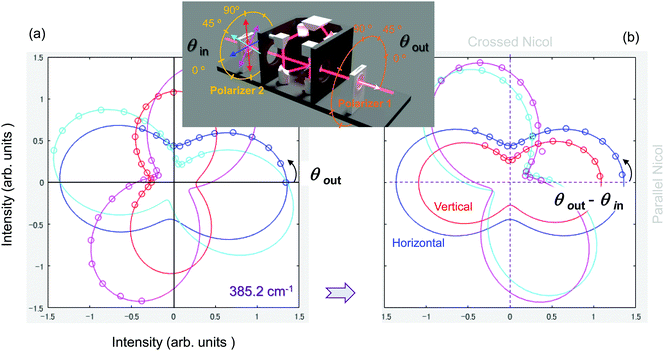Fig. 2 Polarisation analysis of the ATR signal of air (no sample) at 385.2 cm⁻¹ (11.55 THz or 25.96 μm in wavelength) in the xy-plane (see Fig. 1). This wavenumber is close to an absorption band of the PHB sample. (a) Polarisation analysis of the transmitted signal with Polariser-1 (OUT-port) for four different input polarisations 0, π/4, π/2, and 3π/4 set at the input by Polariser-2 (IN-port). Experimentally measured values in 15° steps are represented by dots, and the lines are best fits by eqn (1). The inset shows the geometry of the experiment and conventions. (b) The same data as in (a) plotted as a function of the difference between the set angles of the two polarisers (θ_out − θ_in). The error of polariser alignment was smaller than ±5°.

A perfect fit of the output signal (at OUT-port) can be obtained by the combined amplitudes A_x and A_y of orthogonal components (A_s and A_p at the ATR-sample interface) following the intensity (power) addition:

Power_OUT(θ) = A_x × cos²(θ − ψ_x) + A_y × sin²(θ − ψ_y), (1)

where A_x,y are the arbitrary amplitudes accounting for both absorption (losses) and changes in amplitude due to reflection; ψ_x,y are the phases for s- and p-polarisations, respectively. The angle θ defines the orientation of the linear polarisation in the incident beam, i.e., for θ = 0° only E_s polarisation is present and θ = 90° corresponds to pure E_p. When pure E_s polarisation is incident on the sample and there are no changes in the phase of the reflected beam, the orientational output power has a horizontally aligned Fig. 8 and, consequently, for the pure E_p case a vertical Fig. 8. A_x × cos²(θ − ψ_x) can also be defined as the in-phase contribution to the transmitted ATR signal, while A_y × sin²(θ − ψ_y) the out-of-phase. Intensity, rather than an E-field addition (eqn (1)), is used to fit the near-field absorbance in an evanescent field. Anisotropy of ñ in terms of dichroism Δα and birefringence Δn is measured at two orthogonal linear polarisations. The change in amplitude ΔA = A_x − A_y and phase Δψ = ψ_x − ψ_y for a spectral window within 3–30 THz was measured for poly-crystalline organic samples (the reference background transmittance spectra were measured in air (Appendix A)).

The entire ATR unit acts as an optical retarder with slow (or fast) axis aligning in the X or Y axis (Fig. 1). Transmittance through the crossed polariser–analyser setup with a retarder in between at angle θ is given by T(θ) = sin² 2(θ − θ_ATR) sin²(πΔnd/λ), where θ_ATR ≈ 0° (along x-axis) is the orientation of the slow (or fast) axis of the ATR unit and the phase retardance π Δnd/λ ≈ 0.1 rad over the entire spectral range (Fig. S1, ESI†), and a Δnd is the equivalent retardance birefringence × thickness of the ATR unit. The physical reason for this effective retardance in this ATR unit is due to interchanges between s- and p-polarisations upon reflections and reflectivity differences due to changes of angle of incidence due to focusing in the ATR unit.

2.2. Polarisation analysis of poly-hydroxybutyrate (PHB) and poly-L-lactic acid (PLLA)

A poly-hydroxybutyrate (PHB)²⁵ micro-film sample was placed on the ATR prism for transmission measurements with four-angle polarisation input and polarisation analysis at the OUT-port for the hyperspectral data analysis in Fig. 3. Smaller ΔA is consistent with the larger refractive index of PHB (compared to air), which results in lower reflectivity from the prism-sample interface. Distinct spectral features of PHB are apparent in the amplitude ΔA and phase Δψ spectra. Large negative Δψ values are consistent with the reflection at the ATR-sample interface where the x-component (Transverse electric-mode, TE) experiences a negative value, while the y-component (Transverse magnetic-mode, TM) indicates a positive phase jump. This would add up as a negative phase since it is plotted as phases TE-TM (b). Sharp phase changes are present at the absorption bands. The same data analysis for PLLA is presented in Appendix A (Fig. S3, ESI†) and shows overall similar tendencies: (1) there is a large baseline shift in Δψ for H- and V-polarisation at the IN-port due to the change of refractive index ratio at the ATR-sample interface n₂/n₁, and (2) abrupt phase changes clearly define the absorption bands shown in Fig. 4. To model polarisation independent transmittance T of the sample, transmittance of the ATR setup with the sample was measured at four angular settings of IN and OUT-ports as S̃ = HH + HV + VV + VH ≡ (0, 0) + (0, π/2) + (π/2, π/2) + (π/2, 0). As a reference, the transmittance of the ATR setup (without sample) S_air was measured the same way (see Fig. S2, ESI†^26,27). Then, the transmittance of the sample was calculated as T_Sample = S̃_sample/S̃_air and they were plotted for PHB and PLLA samples in Fig. 4. Interestingly, even at [small nu, Greek, tilde] >630 cm⁻¹ wavenumbers where the synchrotron signal was very weak, spectral signatures characteristic to PHB²⁸ and PLLA were distinguishable²⁹ (Fig. 4). Experimentally and numerically assigned bands parallel (‖) and perpendicular (⊥) to the main axis of the bio-polymers²⁸ were well matched (Fig. 4).

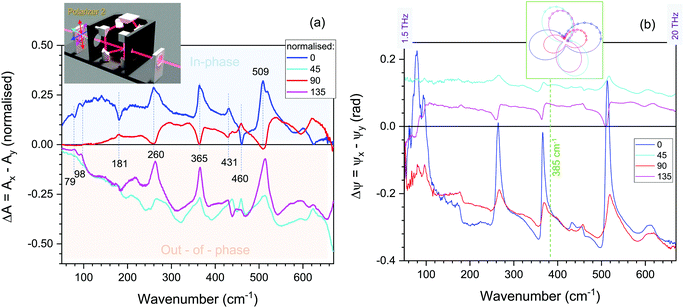Fig. 3 ATR transmittance spectra of poly-hydroxybutyrate (PHB) plotted as the difference in absorbance amplitude ΔA = A_x − A_y normalised to the total S̃ =HH + HV + VV + VH transmission spectrum (a) and retardance phase Δψ =ψ_x − ψ_y (b) calculated from the best fit by eqn (1). The inset in (a) shows color conventions for input polarisation.

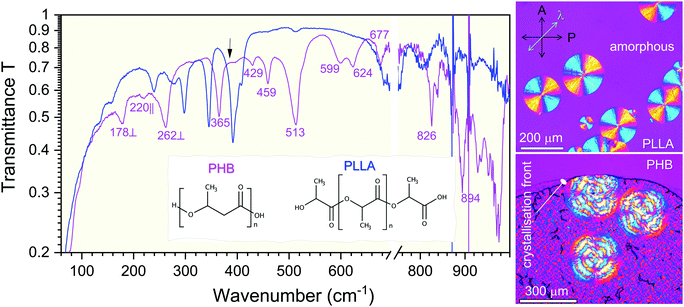Fig. 4 Non-polarized ATR transmittance, T (absorbance A = −lg T), spectra of poly-hydroxybutyrate (PHB) and poly-L-lactic acid (PLLA) normalised to the T of air (no sample; Fig. S2, ESI†). The spectra were calculated as a sum S̃ = HH + HV + VV + VH ≡ (0, 0) + (0, π/2) + (π/2, π/2) + (π/2, 0); arrow marks [small nu, Greek, tilde] = 385.2 cm⁻¹ spectral position where ΔA and Δψ were calculated. The signal was increasingly noisy out of the spectral window of measurement 30–630 cm⁻¹ defined by the beam-splitter and the sensitivity spectrum of the Si bolometer. Optical images (visible light) of typical banded spherulites of PHB and PLLA with amorphous and crystalline regions were observed under cross-polarized microscopy. Spherulites have ∼50 μm height (defined by separation between CaF₂ plates during growth). Arrows indicate analyzer (A) and polarizer (P) orientations, λ = 530 nm waveplate at π/4-orientation was used in cross-Nicol imaging.

2.3. Four-angle polarisation method in the ATR geometry

The absorbance of the sample along the x-axis can be calculated as A^Sample_x = − lg([T_XX + T_XY]/T_all), where T_all = S̃, while the absorbance along the evanescent field of the y-axis is A^Sample_y = −lg([T_YY + T_YX]/T_all) with a pair of indices corresponding to the (IN:OUT) ports. Absorbance of the sample along the z-axis can be accessed by rotating the sample on the ATR prism. It is possible to envisage an ATR prism changed by azimuthally rotating the hemisphere, which would increase the versatility of measurements in absorption anisotropy. The depth probed with p-polarisation is double that of the s-polarisation at π/4-incidence, hence A_y is determined from double the depth compared to A_x.

The measured ΔA and Δψ (Fig. 3) are related to the dichroism Δκ and birefringence Δn, which are, in turn, linked to the common nature (via K–K relation) of the refractive index κ and n at the absorption band. Fig. 5(a) shows the absorption A(ω) and dispersion D(ω) lineshapes of a Lorentzian oscillator in a complex plane presentation with Re-axis A(ω) and Im-axis D(ω).³⁰ This presentation visualises a π-phase change as the frequency ω passes through the resonance at ω₀ (a circle projection on the phase plane in Fig. 5(a)). The measured ΔA and Δψ (Fig. 3) are directly linked to anisotropy in κ and n and defined by changes of absorbance and phase difference between x- and y-orientations. This anisotropy can be determined in the ATR mode of operation using the measurement of transmission at 4-angle polarisations of the incident light (Fig. 5(b)). The xy-plane of the sample is probed by the evanescent fields which follows eqn (1). In the case of the far-field (propagating light) version of the 4-angle polarisation method, the absorbance A is measured at the four polarisation angles increasing in π/4 steps. For the simplest case, a measurement of transmitted power (energy) was carried out using one polariser, which can be considered equivalent to one fixed incident polarisation (by polariser) and a cumulative power of all analyser resolved measurements at different analyser angles. For the ATR mode, this corresponds to the ΔA averaged over all possible (θ_out − θ_in) angles for the selected polarisation of incidence (by polariser), i.e., the area enclosed in the Fig. 8 for the specific incident polarisation.

Fig. 5 (a) Absorption A(ω) = τ/(1 + (ω − ω₀)²τ²) and dispersion D(ω) = (ω − ω₀)τ²/(1 + (ω − ω₀)²τ²) lineshapes for the Lorentzian oscillator near resonance ω₀; τ is the relaxation time. Real part of the refractive index n and imaginary part κ are inter-related; absorption coefficient α ∝ κ. (b) Concept of the 4-angle polarisation method in the ATR geometry: the sample is mapped by near-fields of incident light polarised at four selected polarisation angles 0, π/4, π/2, 3π/4.

The PHB and PLLA samples with amorphous regions and spherulite inclusions are isotropic in the xz-plane (Fig. 1; the plane of optical image in Fig. 4). Their anisotropy is, on the other hand, presented in the xy-plane (Fig. 1), which is probed by the evanescent 4-angle polarisation method introduced above. Fig. S4 (ESI†) shows 4-angle polarisation fitted by the Amp × cos²(θ − θ_xy) + const function of ATR transmittance at selected spectral bands, where θ_xy is the orientation direction of the polymer main chain in the xy-plane, which is probed by the evanescent intensity. The observed ∝cos² θ dependence is typical for the absorbance; however, here it is measured with the evanescent light field in ATR mode in the sub-surface volume (out-of-plane). The anisotropy of absorbance and phase of the ATR reflected light is directly measured by the proposed method based on eqn (1) over the selected spectral range (without the need of K–K evaluation). A multi-dimensional data analysis with an added polarisation dependence increases the data set size and its complexity; however, tools for image, spectrum and polarisation analysis are developing fast.^31–34

3. Conclusions and outlook: polarisation tomography

Polariscopy with evanescent non-propagating fields is demonstrated using the ATR mode for measurements. The evanescent 4-angle polarisation method was realised by applying polariser-analyser measurements in the 30–1000 cm⁻¹ THz-IR spectral window. PHB and PLLA samples, which are in-plane isotropic and have out-of-plane anisotropy due to the presence of a spherulite structure, were measured. Their absorption bands identified experimentally and theoretically were resolved using non-propagating optical near-fields in the ATR geometry within the THz/Far-IR spectral range. A method to determine anisotropy in absorbance Δα and reflected phase Δψ by eqn (1) was validated. It is shown that both anisotropies can be determined without reliance on the K–K formalism, and it is based on a generic relation between absorption and dispersion. By adding in-plane rotation of the ATR prism, all 3D anisotropy of the sample can be determined. Such polarisation tomography could be extended to other spectral regions and will be the focus of further studies.

4. Samples and procedures

When the absorption of the evanescent wave is negligible in the sample placed onto an ATR prism, the penetration depth of the evanescent E-field (1/e-level) into the sample is given by:³⁵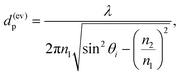where λ is the wavelength, n₁ and n₂ are the real parts of the refractive index of the ATR crystal and sample, respectively, and θ is the angle of incidence of the incoming radiation; for the intensity E² the penetration depth becomes d^(ev)_p/2.

4.1. Samples

PHB and PLLA spherulite samples were prepared between two IR-transmitting CaF₂ windows with separation ∼50 μm with alignment fixed over the entire thickness. PLLA³⁶ has a radial structure of spherulite micro-crystals, while PHB²⁵ spherulites had twisted bands in the radial direction with a 10 μm period. PHB and PLLA microcrystallites were grown from an amorphous molten phase by lowering the temperature below that of melting (T^PHB_m = 175 °C and T^PHB_m ≈ 160 °C).²⁵ Samples were thermally quenched to have a mixture of crystalline and amorphous phases. For measurements on the ATR prism, one side of the CaF₂ window was removed to allow direct contact of the PHB and PLLA with the surface of the ATR prism.

The area of characterisation on the ATR-sample interface was defined by the projection of a ∼3 mm-diameter THz beam; at π/4 angle of incidence. The area of measurement was an ellipsis with a 1/cos(π/4) ∼ 1.43 times longer axial width (along reflection; z-axis in Fig. 1) as compared to the width (x-axis in Fig. 1).

4.2. Synchrotron-based THz radiation and ATR setup

The THz/Far-IR beamline at the ANSTO-Australian Synchrotron (Clayton, Victoria) was used in this study. Polarisation of the synchroton THz radiation has the combination of linear (horizontal; along the extraction mirror slit) and circular polarisations.³⁷ The two components originate from dipole-emission inside the bending magnet and at its edge (at the entrance/exit). The THz/far-IR beamline receives more of the edge-emission compared to the dipole-emission. Coherent synchrotron radiation (CSR) at 15–25 cm⁻¹ (0.45–0.75 THz; 667–400 μm) can be produced to provide the highest brilliance for this specific spectral range.

Polarisation is defined as x and y-polarisations in the room frame of reference (Fig. 1) along the direction of propagation (z-axis). At the interface of the ATR prism and sample, standard conventions were used for the plane of incidence on the sample as E_s and E_p, which are ⊥ and ‖ to the plane (or TE and TM modes), respectively.

A Bruker IFS 125/HR Fourier transform infrared (FTIR) spectrometer with a Si bolometer (Bruker Optik GmbH, Ettlingen, Germany) was used in this study. The ATR unit (Pike Technologies, Fitchburg, WI) was equipped with a diamond prism stage (refractive index of n₁ = 2.42), which had the capability of controlling the temperature by a heater/cooler placed around the diamond ATR prism. Its sample compartment was designed to be suitable for cooling by a liquid (such as liquid nitrogen). Data analysis was carried out with OPUS 8.0 software (Bruker Optik GmbH, Ettlingen, Germany).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the JST CREST Grant JPMJCR19I3 (Japan), and the ARC Discovery Grant DP190103284 (Australia). The project was carried out during the beamtime proposal EU16010 and M15121 at the Australian Synchrotron, part of ANSTO. SJ and SHN are grateful for the financial support via ARC Linkage LP190100505 project.

Notes and references

1. M. Ryu, R. Honda, A. Balcytis, J. Vongsvivut, M. Tobin, S. Juodkazis and J. Morikawa, Nanoscale Horiz., 2019, 4, 1443–1449.
2. F. Zaera, Chem. Soc. Rev., 2014, 43, 7624–7663.
3. NASA, 2021, Press release: https://ixpe.msfc.nasa.gov.
4. G. Tkachenko and E. Brasselet, Nat. Commun., 2014, 5, 3577.
5. A. Altaqui, P. Sen, H. Schrickx, J. Rech, J.-W. Lee, M. Escuti, W. You, B. Kim, R. Kolbas, B. O’Connor and M. Kudenov, Sci. Adv., 2021, 7, eabe3196.
6. E. Brasselet, G. Gervinskas, G. Seniutinas and S. Juodkazis, Phys. Rev. Lett., 2013, 111, 193901.
7. Y. Lei, M. Sakakura, L. Wang, Y. Yu, H. Wang, G. Shayeganrad and P. Kazansky, Optica, 2021, 8, 1365–1371.
8. X. Ma, Q. Liu, N. Yu, D. Xu, S. Kim, Z. Liu, K. Jiang, B. Wong, R. Yan and M. Liu, Nat. Commun., 2021, 12, 6868.
9. J. Levine, J. Cohen, Y. Chung and P. Georgopoulos, J. Appl. Crystallogr., 1989, 22, 528–532.
10. P. Campagnola and L. Loew, Nat. Biotechnol., 2003, 21, 1356–1360.
11. T. Wang and J. V. Dam, Clin. Gastroenterol. Hepatol., 2004, 2, 744–753.
12. M. Ryu, S.-H. Ng, V. Anand, S. Lundgaard, J. Hu, T. Katkus, D. Appadoo, Z. Vilagosh, A. Wood, S. Juodkazis and J. Morikawa, Appl. Sci., 2021, 11, 7632.
13. Z.-Z. Li, L. Wang, H. Fan, Y.-H. Yu, Q.-D. Chen, S. Juodkazis and H.-B. Sun, Light: Sci. Appl., 2020, 9, 41.
14. Y. Nishijima, S. Morimoto, A. Balcytis, T. Hashizume, R. Matsubara, A. Kubono, N. To, M. Ryu, J. Morikawa and S. Juodkazis, J. Mater. Chem. C, 2022, 10, 451–462.
15. C. Bohren, Eur. J. Phys., 2010, 31, 573–577.
16. M. Kozak, V. Zhikharev, P. Puga and V. Y. Loya, Int. J. Innov. Sci. Eng. Technol., 2017, 4, 152–159.
17. K. Yamamoto and A. Masui, Appl. Spectrosc., 1995, 49, 639–644.
18. B. Czapla and L. Hanssen, Proc. Reflection, Scattering, and Diffraction from Surfaces VII, 2020, p. 114850D.
19. P. Grosse and V. Offermann, Appl. Phys. A: Solids Surf., 1991, 52, 138–144.
20. H. Terraschke, M. Rothe, A.-M. Tsirigoni, P. Lindenberg, L. Ruiz Arana, N. Heidenreich, F. Bertram and M. Etter, Inorg. Chem. Front., 2017, 4, 1157–1165.
21. K. Sato, Chem. Eng. Sci., 2001, 56, 2255–2265.
22. S. Vaucher, R. Nicula, J.-M. Catalá-Civera, B. Schmitt and B. Patterson, J. Mater. Res., 2008, 23, 170–175.
23. S. Liu, A. DeFilippo, M. Balasubramanian, Z. Liu, S. G. Wang, Y. Chen, S. Chariton, V. Prakapenka, X. Luo, L. Zhao, J. S. Martin, Y. Lin, Y. Yan, S. Ghose and T. Tyson, Adv. Sci., 2021, 8, 2003046.
24. J. Rossbach, J. R. Schneider and W. Wurth, Phys. Rep., 2019, 808, 1–74.
25. G. Lugito, E. Woo and W.-T. Chuang, Crystals, 2017, 7, 56.
26. R. Honda, M. Ryu, M. Moritake, A. Balcytis, V. Mizeikis, J. Vongsvivut, M. Tobin, D. Appadoo, J.-L. Li, S.-H. Ng, S. Juodkazis and J. Morikawa, Nanomaterials, 2019, 9, 732.
27. Y. Nishijima, N. To, A. Balcytis and S. Juodkazis, Opt. Express, 2022, 30, 4058–4070.
28. S. Yamamoto, Y. Morisawa, H. Sato, H. Hoshina and Y. Ozaki, J. Phys. Chem. B, 2013, 117, 2180–2187.
29. A. M. El-Hadi, Polym.-Plast. Technol. Eng., 2018, 58, 1–9.
30. A. G. Marshall, Chemom. Intell. Lab. Syst., 1988, 3, 261–275.
31. G. Atkinson and J. Ernst, Mach. Vision Appl., 2018, 29, 1171–1189.
32. C. Schneider, W. Rasband and K. Eliceiri, Nat. Methods, 2012, 9, 671–675.
33. M. Toplak, S. Read, C. Sandt and F. Borondics, Cells, 2021, 10, 2300.
34. M. Toplak, G. Birarda, S. Read, C. Sandt, S. Rosendahl, L. Vaccari, J. Demšar and F. Borondics, Synchrotron Rad. News, 2017, 30, 40–45.
35. G. Ramer and B. Lendl, Attenuated Total Reflection Fourier Transform Infrared Spectroscopy, John Wiley and Sons, Ltd., Berlin, Germany, 2013.
36. Y. Li, Z. Wang and T. He, Crystals, 2017, 7, 115.
37. M. Ryu, D. Linklater, W. Hart, A. Balcytis, E. Skliutas, M. Malinauskas, D. Appadoo, Y. Tan, E. P. Ivanova, J. Morikawa and S. Juodkazis, J. Opt., 2018, 20, 035101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00187j

---