Tuning photoelectron dynamic behavior of thiolate-protected MAu24 nanoclusters via heteroatom substitution†
Xueke
Yu
a,
Yuanze
Sun
a,
Wen-wu
Xu
 b,
Junyu
Fan
c,
Junfeng
Gao
b,
Junyu
Fan
c,
Junfeng
Gao
 a,
Xue
Jiang
a,
Xue
Jiang
 a,
Yan
Su
a,
Yan
Su
 *a and
Jijun
Zhao
*a and
Jijun
Zhao
 a
a
aKey Laboratory of Materials Modification by Laser, Ion and Electron Beams (Dalian University of Technology), Ministry of Education, Dalian 116024, China
bDepartment of Physics, School of Physical Science and Technology (Ningbo University), Ningbo 315211, China
cDepartment of Physics, (Taiyuan Normal University), Jinzhong 030619, China. E-mail: su.yan@dlut.edu.cn
First published on 12th August 2022
Abstract
Heteroatom substitution of gold nanoclusters enables precise tuning of their physicochemical properties at the single-atom level, which has a significant impact on the applications related to excited states including photovoltaics, photocatalysis and photo-luminescence. To this end, understanding the effect of metal exchange on the structures, electronic properties and photoexcited dynamic behavior of nanoclusters is imperative. Combining density functional theory with time-domain nonadiabatic molecular dynamics simulations, herein we explored the effect of metal replacement on the electronic and vibrational properties as well as excited-state dynamics of ligand-protected MAu24(SR)18 (M = Pd, Pt, Cd, and Hg) nanoclusters. At the atomistic level, we elucidate hot carrier relaxation and recombination dynamic behavior with various doping atoms. Such distinct excited-state behavior of MAu24(SR)18 nanoclusters is attributed to different energy gaps and electron–phonon coupling between the donor and acceptor energy levels, owing to the perturbation of nanoclusters by a single foreign atom. The specific phonon modes involved in excited-state dynamics have been identified, which are associated with the MAu12 core and ligand rings. This time-dependent excited-state dynamic study fills the gap between structure/composition and excited-state dynamic behavior of MAu24(SR)18 nanoclusters, which would stimulate the exploration of their applications in photoenergy storage and conversion.
New conceptsTo date, many thiolate-protected alloying nanoclusters have been prepared and their excited-state behavior has been characterized, but the correlation between structure/composition and physical properties remains to be unveiled. Herein, we present a comprehensive theoretical picture of MAu24(SR)18 nanoclusters, from structural stability, electronic structure, vibrational properties to hot-electron relaxation dynamics. Distinct energy gaps and vibrational properties can be achieved by modulating the sp–d and d–d orbital hybridization strengths between Au and M dopants, which in turn determines the photocarrier dynamics. We further elucidate the relaxation pathway and lifetime by simulating the excited-state dynamics of MAu24(SR)18 nanoclusters, emphasizing the important role of electron–phonon coupling in the dynamic processes. This theoretical study highlights metal exchange as a superior strategy to tune the photocarrier lifetimes of nanoclusters at single-atom levels for optoelectronics. |
Introduction
Atomically precise gold nanoclusters have always captured the imagination of scientists due to their optical, magnetic, biological and physicochemical properties.1–4 Due to the quantum size effects, small gold nanoclusters below a certain size (i.e., 2.2 nm) exhibit molecule-like optical properties rather than bulk-like properties,1 which are manifested by the quantized energy levels of molecules and plasmon absorption of large-sized nanoparticles, respectively.5 Excitingly, the physical and chemical properties of nanoclusters can be modulated by their size, shape and composition,6 which makes them promising in the design of functional materials, such as in catalysis, sensors, drug delivery, bioimaging, and solar cells.7–9 As a versatile approach to control composition, doping and alloying foreign atoms into the parent nanoclusters has been developed as an effective strategy to optimize the structure and properties of nanoclusters and broaden their applications.6,10 It has been demonstrated that alloying nanoclusters can enhance the luminescence, modify the optical absorption, improve the catalytic performance and thermal stability, and tune the electronic structures.11–14Among small-sized gold nanoclusters, Au25(SR)18 has been extensively studied in terms of optical, catalytic, magnetic and chiral properties owing to its early discovery, high stability, easy preparation and functionalization,15–20 thereby boosting its characteristic-oriented applications ranging from catalysis through chemical sensing to biomedicine.21,22 The structure of Au25(SR)18 consists of an icosahedral Au13 core and six Au2(SR)3 staple motifs on the surface.23 Inspiringly, Au25(SR)18 nanoclusters can also act as an alloying template, and their alloy nanoclusters have been widely investigated. To date, rich types of doped MAu24(SR)18 nanoclusters have been successfully synthesized, in which the hetero-metals Cu and Ag adopt the multiple heteroatom doping mode, and Pd, Pt, Cd, and Hg follow the single-atom doping mode.24–28 Subsequently, the alloying effects have been successfully utilized to improve the performance of Au25(SR)18 nanoclusters, e.g., CuxAu25−x(SR)18 with enhanced stability in comparison with Au25(SR)18, the Ag13Au12(SR)18 nanocluster exhibiting notably higher quantum yields (QY ≈ 40.1%) than AgxAu25−x(SR)18 with x ≤ 12 (QY ≈ 0.2%), and the PtAu24(SR)18 nanocluster showing enhanced stability and better catalytic performance relative to Au25(SR)18.11,26,29,30 Impressively, studies of the excited state dynamics indicated that the introduction of single hetero-atoms can produce different electronic structures so as to induce distinct excited state behavior of the entire nanocluster.31,32 In particular, Zhou et al. carried out the transient absorption spectroscopy measurement to investigate the excited-state behavior of MAu24(SR)18 (abbreviated as MAu24; M = Pd, Pt, Cd, Hg) nanoclusters, in which Pd or Pt doping gives rise to different excited-state behaviors compared with that of Cd or Hg doping.32 That is, PdAu24 and PtAu24 exhibited sub-picosecond relaxation between the core states and charge transfer from the core to shell within 3–5 ps, followed by nanosecond electron–hole (e–h) recombination,31 while CdAu24 and HgAu24 present internal conversion within 1 ps and core–shell decay of 2–4 ps, followed by e–h recombination up to 50–200 ns.32
Almost all previous works, including the studies of the excited-state behavior by Zhou et al., assumed that the foreign-metal atoms are located at the center of the icosahedron.32 Contrarily, Maran et al. demonstrated that both Cd and Hg dopants prefer to stay on the icosahedral shell, which is independent of the ligand.27,33 These divergences indicate the incomplete understanding about the structure and electronic properties of the MAu24 nanoclusters, as well as the dependence of the vibrational properties on composition. Despite previous studies, the underlying mechanisms of excited carrier relaxation and recombination, and the phonon modes participating in the dynamics of MAu24 nanoclusters have not been clarified, thereby calling for an atomistic description of the excited state dynamics.
In this paper, we carry out first-principles calculations and time-dependent nonadiabatic molecular dynamics (NAMD) simulations to establish a complete theoretical picture of MAu24 (M = Pd, Cd, Pt, Hg) nanoclusters, from structural stability, electronic structure, and vibrational properties to photocarrier relaxation and recombination. By comparing the electronic and vibrational properties of MAu24 nanoclusters doped with different elements in the ground state and excited states, the interplay between the electronic structure, electron–phonon (e–p) coupling and specific excited electron dynamic processes has been clarified. These theoretical explorations not only reveal the underlying mechanism of the excited state dynamic behavior of MAu24 nanoclusters, but also illuminate the essential clues for designing alloy nanoclusters and regulating the carrier lifetime.
Computational methods
Density functional theory calculations
Density functional theory (DFT) calculations were performed with the Vienna ab initio simulation package (VASP)34 utilizing projector augmented wave (PAW) potentials for electron–ion interactions and planewave basis with an energy cutoff of 500 eV.35 Perdew–Burke–Ernzerhof (PBE) parameterization within generalized gradient approximation (GGA) was adopted to describe the exchange and correlation interactions.36 A cubic supercell with a large dimension of 30 Å was used for each MAu24 nanocluster, and the Γ point was used to sample the Brillouin zone.37 All the structures of MAu24 were fully relaxed for the ionic and electronic degrees of freedom with the convergence criteria of 10−4 eV for the total energy and 10−2 eV Å−1 for the force on each atom. Furthermore, vibration analysis was performed with the Amsterdam Density Functional program (ADF 2018.104)38 incorporating scalar corrections using zero-order regular approximation (ZORA),39 which employed TZ2P Slater-type basis sets with a large frozen electron core40 and the GGA-PBE functional. The simulation of excited-carrier relaxation and recombination dynamics of MAu24 nanoclusters was carried out with the Hefei-NAMD code,41 which augments the VASP with NAMD capability within the framework of time-domain density functional theory (TD-DFT) (details are given in Section S1 of the ESI†).42,43Structural models
The Au25(SR)18 nanocluster considered here consists of an Au13 icosahedral core protected by six “V-shaped” –S–Au–S–Au–S– semiring motifs, and each sulfur atom is bonded with one –C2H4Ph group.18,23 To simplify and reduce the computational cost, the –C2H4Ph group was replaced by a hydrogen atom (–H) in our nanocluster models. A comparative calculation of Au25(SC2H4Ph)18 and Au25(SH)18 confirmed the rationality of our ligand simplification scheme. As revealed by the computed electronic density of states (DOS) in Fig. S1 (ESI†), the peak shape and relative energy levels of Au25(SH)18− and Au25(SH)180 nanoclusters are in line with those of Au25(SC2H4Ph)18− and Au25(SC2H4Ph)180 nanoclusters, respectively. Moreover, the gap between the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of Au25(SH)18− is moderately narrower than that of Au25(SH)180 (1.34 eV vs. 1.06 eV), which agrees with the trend of HOMO–LUMO gaps between Au25(SC2H4Ph)18− and Au25(SC2H4Ph)180 nanoclusters (1.21 eV vs. 1.03 eV from our theoretical calculations, and 1.81 eV vs. 1.78 eV from experiment, respectively),44 suggesting that it is reasonable to simplify the ligand from –C2H4Ph to –H.Results and discussion
Structures and stability of MAu24 (M = Pd, Pt, Cd, and Hg)
Atomically precise alloy nanoclusters have been successfully synthesized by the metal exchange method in laboratory. As a representative of these synthetic templates, the Au25(SR)18 nanocluster has been considered, which possesses one central atom doping position, as well as the icosahedron shell and staple doping positions with 12-fold equivalency (Fig. 1).28,33 To examine the doping position of M in MAu24 nanoclusters from the thermodynamic point of view, the formation energy is defined as| Eform = EMcoh + 24EAucoh + 18EScoh + 18EHb − EMAu24 | (1) |
| System | E form (eV) | E HL (eV) | d M–Au (Å) | ||
|---|---|---|---|---|---|
| Core | Icosahedron | Staple | |||
| PdAu24 | 3.83 | 3.51 | 3.19 | 0.59 | 2.84 |
| CdAu24 | 3.99 | 4.50 | 4.03 | 1.30 | 2.84 |
| PtAu24 | 3.70 | 3.20 | 2.78 | 0.51 | 3.00 |
| HgAu24 | 3.31 | 3.89 | 3.26 | 1.16 | 3.08 |
The HOMO–LUMO gaps for stable structures are summarized in Table 1, in which doping of Pd and Pt leads to a narrower gap of the MAu24 nanocluster (0.59 and 0.51 eV, respectively) than that of the Cd- or Hg-doped cluster (1.30 and 1.16 eV, respectively). The doping position of M in MAu24 nanoclusters and the trend of HOMO–LUMO gap upon alloying coincide well with experimental reports,33,45 and the measured HOMO–LUMO gaps for Pd-, Pt-, Cd-, and Hg-doped MAu24 nanoclusters are 1.00, 0.80, 1.46, and 1.41 eV, respectively. Indeed, the systematic underestimation of the HOMO–LUMO gap is a well-known limitation of the PBE functional, whereas the ligand simplification scheme also slightly affects the amplitude of the HOMO–LUMO gap. Therefore, our DFT calculations can reproduce the atomic and electronic structures of MAu24 with various dopants, further confirming that the current theoretical approach provides reasonable descriptions for MAu24 nanoclusters.
Electronic and vibrational properties of MAu24
Fig. 2 plots the Kohn–Sham orbitals of MAu24 nanoclusters colored with the valence orbital components of each atom. For PdAu24 and PtAu24 nanoclusters, their LUMOs are mainly composed of Au(5d) and Au(6s6p) orbitals and the former contributes more, whereas the contribution of Au(6s6p) orbitals is stronger than that of Au(5d) orbitals in the LUMOs of CdAu24 and HgAu24. Moreover, the contribution of M(sp) orbitals in the LUMOs of CdAu24 and HgAu24 is obviously more pronounced than that of PdAu24 and PtAu24. The participation of more M(sp) and Au(6s6p) orbitals in CdAu24 and HgAu24 nanoclusters also explains the relatively long M–Au bonds (i.e., the average M–Au bond lengths in CdAu24 and HgAu24 are 3.00 and 3.08 Å, respectively, in comparison to 2.84 and 2.84 Å for PdAu24 and PtAu24, respectively), the higher LUMO energy and the wider energy gaps (i.e., the energy gaps in CdAu24 and HgAu24 are 1.30 and 1.16 eV, in contrast to 0.59 and 0.51 eV in PdAu24 and PtAu24, respectively), as summarized in Table 1. The HOMO of the PdAu24 nanocluster consists of Pd(4d) and Au(5d) orbitals, while the HOMO of PtAu24, CdAu24, and HgAu24 nanoclusters is contributed by Au(5d) and Au(6s6p) orbitals. The contribution of the HOMO reflects stronger d–d hybridization between the dopant and Au atoms in PdAu24 than the other three nanoclusters.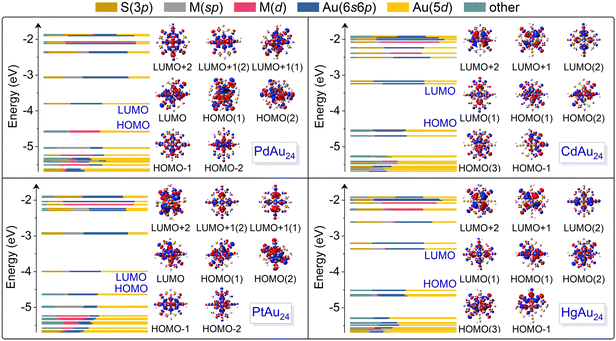 | ||
| Fig. 2 Components of the Kohn–Sham (KS) orbitals of MAu24 nanoclusters from DFT calculations and the corresponding charge density distributions in the range of HOMO−2 to LUMO+2. | ||
To directly visualize the effect of alloying on the nanoclusters, the electron densities for the HOMO−2 to LUMO+2 orbitals of MAu24 are illustrated in the insets of Fig. 2. The LUMO+2 and doubly degenerate LUMO+1 of PdAu24 and PtAu24 nanoclusters delocalize and display superatomic D-type orbitals, while the LUMO and doubly degenerate HOMO present superatomic P-type orbitals, and the HOMO−1 and HOMO−2 orbitals are localized on the atoms. For CdAu24 and HgAu24 nanoclusters, the orbitals from LUMO+2 to LUMO exhibit superatomic D-type orbitals, the triply degenerate HOMOs form superatomic P-type orbitals, and the HOMO−1 orbitals are localized on the atoms far away from the Cd and Hg atoms. The different characters of superatomic orbitals associated with the LUMO of MAu24 nanoclusters can be attributed to the effective number of valence electrons with alloying,32 that is, PdAu24 and PtAu24 nanoclusters are six-electron systems, while CdAu24 and HgAu24 are eight-electron systems. The metal exchange effect on the absorption of MAu24 nanoclusters is also displayed in Fig. 3a. In the case of PdAu24 and PtAu24 nanoclusters, the absorption peaks are significantly red-shifted with regard to those of the CdAu24 and HgAu24 nanoclusters, consistent well with the smaller HOMO–LUMO gaps in the former two clusters.
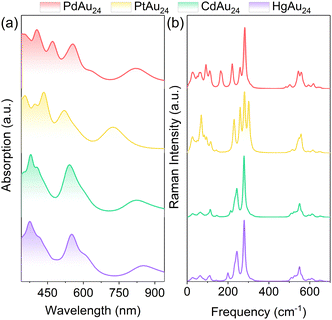 | ||
| Fig. 3 (a) The absorption spectra of MAu24 (M = Pd, Pt, Cd, and Hg) nanoclusters. (b) Raman spectra of MAu24 (M = Pd, Pt, Cd, and Hg) nanoclusters from DFT calculations. The representative vibrational modes in curves are available in the movies of the ESI.† | ||
In contrast to the intensive study of the vibrational modes of pristine Au25 nanoclusters,46–48 the knowledge about the vibrational properties is insufficient for the doped MAu24 nanoclusters, which is even more complicated. The simulated Raman spectra of MAu24 nanoclusters are plotted in Fig. 3b, where the spectral feature below 200 cm−1 evidently changes with dopant. Since the low-frequency vibrational modes are mainly related to the MAu12 core,48 the difference in Raman spectra can be attributed to the heteroatom substitution from two aspects: (i) the doping position of foreign atoms leads to different geometric symmetries of the MAu12 core; (ii) the sp–d and d–d orbital hybridization between M and Au atoms results in different M–Au bond lengths. To further discriminate the intrinsic vibrational modes of MAu24, the vibrational modes are displayed in the ESI† in the form of animation movies. Generally speaking, the four MAu24 nanoclusters considered here share a similar pattern of vibrational modes, that is, the 0–100 cm−1 region hosts the Au–Au and M–Au stretching modes and the Au–S–Au–S–Au wagging modes; MAu12 core breathing modes are around 110 cm−1; the Au–S stretching modes vary from Au(core)–S to Au(staple)–S in the range of 200–400 cm−1; and the peaks at 500–600 cm−1 come solely from the R groups (simplified by H in this work). Note that the vibrations around 150 cm−1 are assigned to M–Au stretching modes for PdAu24 and PtAu24 and to Au–Au and M–Au stretching modes for CdAu24 and HgAu24, respectively. The above picture of vibration modes is closely related to the nature of excited-state dynamics of MAu24 nanoclusters, which will be discussed below.
Excited-electron relaxation processes of MAu24
It was reported that MAu24 exhibits three dominant relaxation processes (see Fig. 5b): ① sub-picosecond relaxation from higher-energy (HE) states to LUMO+1; ② few picosecond relaxation from LUMO+1 to LUMO; and ③ nanosecond e–h recombination between the LUMO and HOMO.32,47,49 To identify the key states involved in the dynamics, the projected densities of states (PDOS) of MAu24 nanoclusters are shown in Fig. 4. The semiring ligands of MAu24 nanoclusters make noticeable contributions to the PDOS around −1.80 eV, suggesting the participation of the semiring ligands in the excited-electron dynamics. Therefore, the HE states around −1.80 eV are chosen as the initial states of hot electron relaxation of MAu24 nanoclusters. According to PDOS analysis, the HOMO, LUMO, and LUMO+1 states of MAu24 nanoclusters are mainly contributed by the MAu12 core, which, in turn, would participate in the excited-electron relaxation dynamics.To gain straightforward insight into the hot electron relaxation dynamics, NAMD simulations were carried out and the time-dependent evolutions of Kohn–Sham energy states are shown in Fig. 5a. According to the energy evolution and three relaxation processes mentioned above, the MAu24 nanoclusters can be classified into two types—type I (PdAu24 and PtAu24) and type II (CdAu24 and HgAu24). Compared with type I, type II nanoclusters present stronger orbital coupling between LUMO+1 and LUMO+n (n = 2, 3), a narrower energy gap between LUMO+1 and LUMO, and a wider HOMO–LUMO gap (see Fig. 5b), which may further lead to different dynamic behaviors. Since quantum decoherence has a significant effect on the dynamic processes with energy gap, the decoherence induced surface hopping (DISH)50 method was utilized to simulate processes ② and ③, and the fewest-switches surface-hopping (FSSH)51 method was adopted to calculate process ①.
After the photoexcitation of nanoclusters, hot electrons start to relax from HE states LUMO+1 (process ①). Here, PdAu24 and CdAu24 nanoclusters are used as representatives to compare the relaxation processes of two types of nanoclusters in terms of the electron distribution on the key states, as plotted in Fig. 6a, and those of PtAu24 and HgAu24 are given in Fig. S2a (ESI†). The time scales for the population decay of HE states are fitted by an exponential function of f(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ). The excited electrons of type I nanoclusters relax from HE states to lower-energy levels in 190 fs (PdAu24) and 380 fs (PtAu24), respectively, while they relax to the doubly degenerate LUMO+1 in about 1 ps (see Fig. S3, ESI†). For CdAu24 and HgAu24 (type II), the excited electrons suddenly equilibrate between HE states and lower energy levels within 83 and 35 fs, and then relax to LUMO+1 at 0.7 and 0.5 ps, respectively (see Fig. S3, ESI†). The difference in relaxation behavior between these two types of nanoclusters agrees well with previous experimental reports, in which process ① of type I nanoclusters occurs slower than that of type II nanoclusters.32
exp(−t/τ). The excited electrons of type I nanoclusters relax from HE states to lower-energy levels in 190 fs (PdAu24) and 380 fs (PtAu24), respectively, while they relax to the doubly degenerate LUMO+1 in about 1 ps (see Fig. S3, ESI†). For CdAu24 and HgAu24 (type II), the excited electrons suddenly equilibrate between HE states and lower energy levels within 83 and 35 fs, and then relax to LUMO+1 at 0.7 and 0.5 ps, respectively (see Fig. S3, ESI†). The difference in relaxation behavior between these two types of nanoclusters agrees well with previous experimental reports, in which process ① of type I nanoclusters occurs slower than that of type II nanoclusters.32
The striking difference in excited-state dynamic behavior between the two types of nanoclusters elicits further investigation of MAu24 nanoclusters. As a key factor of the excited-carrier dynamics, the nonadiabatic coupling (NAC) is defined as43,52,53
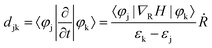 | (2) |
The e–p coupling and nuclear velocity also play a decisive role in NAC, which are closely related to phonon modes. To characterize the phonon modes involved in the excited-electron relaxation dynamics, the Fourier transforms (FT) of autocorrelation functions for the energy gap fluctuations between the donor and acceptor states are investigated and presented in Fig. 7e. For electron transfer from HE states to LUMO+1, the dominant phonon peaks of the four nanoclusters emerge in the frequency range of 33–280 cm−1 (see Table S1, ESI†), which correspond to the low-frequency vibrational modes of MAu12 cores, the staple Au–S bond-stretching and wagging vibrations.48 Besides, the weak phonon modes at high frequency, i.e., 400 and 550 cm−1 of HgAu24 and 517 cm−1 of CdAu24 (see Table S1, ESI†), are attributed to the vibration of ligands.48,54 The process ① of type II nanoclusters is coupled with stronger low-frequency and high-frequency phonon modes compared to those of type I nanoclusters, leading to faster electron migration from HE states to LUMO+1.
Since the gap between LUMO+1 and LUMO of MAu24 nanoclusters ranges from 0.4 to 1.0 eV, the electron migration of process ② takes place longer than process ①, as shown in Fig. 6b and Fig. S2b (ESI†). The excited electrons of type I nanoclusters suddenly equilibrate between the two degenerate LUMO+1 states and then relax to the LUMO within 250 ps (PdAu24) and 483 ps (PtAu24), respectively. In contrast, the electron transfer from LUMO+1 to LUMO in type II nanoclusters takes 86 ps (CdAu24) and 139 ps (CdAu24), respectively. For process ②, the NAC values between the doubly degenerate states (LUMO+1 of type I nanoclusters and LUMO of type II nanoclusters) lie between 15 and 25 meV (see Tables S2–S5, ESI†), which has little effect on the electron relaxation from LUMO+1 to LUMO. As listed in Tables S2–S5 (ESI†), PdAu24 and PtAu24 nanoclusters possess weaker NAC elements of 1.32 and 0.85 meV between LUMO+1 and LUMO than that of CdAu24 (2.44 meV) and HgAu24 (2.25 meV), which leads to slower relaxation between LUMO+1 and LUMO in the former two systems.
The FT spectra reveal that process ② of all MAu24 nanoclusters is mainly coupled with the low-frequency phonon modes below 100 cm−1 (see Fig. 7e and Table S1, ESI†), which are assigned to the stretching and breathing modes in MAu12 cores.48 Moreover, the phonon modes around 200 cm−1 of HgAu24 arise from the Hg–Au and Hg–S bond stretching.48,55 Although the low-frequency phonon modes of type I nanoclusters are stronger than those of type II nanoclusters, the NAC elements are still smaller due to the wider energy gaps between LUMO+1 and LUMO. Apart from NAC, quantum decoherence has a significant impact on the dynamics with energy gap, which can be characterized by pure-dephasing time. A shorter decoherence time generally causes slower quantum dynamics, which even stop when the decoherence time approaches zero.56 The stronger electron–vibration interaction in type I nanoclusters illustrates that doping of Pd or Pt leads to stronger elastic scattering, which is responsible for the faster loss of quantum of coherence.57 Specifically, as seen from Tables S6–S9 (ESI†), PdAu24 and PtAu24 possess shorter dephasing times of 3.88 and 4.53 fs than CdAu24 (11.11 fs) and HgAu24 (14.14 fs), respectively, which further prolongs the electron relaxation time in type I nanoclusters.
The time-resolved e–h recombination dynamics between the LUMO and HOMO of MAu24 nanoclusters are presented in Fig. 6c and Fig. S2c (ESI†). Different fitting functions were utilized here due to the difference between the time scale of e–h recombination for MAu24 nanoclusters, that is, the exponential fitting of curves was adopted for the type I nanoclusters whose recombination time was faster, whereas the population curves of type II nanoclusters were fitted by a linear function. The e–h recombination occurs within 126 ps and 233 ps for type I nanoclusters, while that of type II nanoclusters takes 8.03 ns and 7.55 ns, respectively. Although the e–h recombination times are underestimated, the simulations still reproduce the experimental results that the carrier lifetimes of CdAu24 and HgAu24 doped nanoclusters are longer than those of PdAu24 and PtAu24 nanoclusters,31,32 further demonstrating the reliability of our simulation. It is worth noting that the underestimation of the recombination time may be due to the underestimation of the LUMO in the DFT calculation, which also leads to the overestimation of the electron relaxation time from LUMO+1 to LUMO (process ②).
As shown in Fig. 7 and Tables S2–S5 (ESI†), the NAC values between the HOMO and LUMO of type I nanoclusters (1.21 and 1.48 meV) are stronger than that of type II nanoclusters (0.73 and 0.88 meV). The e–h recombination dynamics of MAu24 nanoclusters is coupled with the phonon modes in the range of 0–100 cm−1 (see Table S1, ESI†), which originate from bond-stretching and breathing of the MAu12 core.46,58 The e–p interaction coupled with low-frequency phonon modes was reported to suppress the e–h recombination dynamics in perovskites and black phosphorus, which is crucial for prolonging the carrier lifetimes.59–62 This phenomenon was attributed to the fact that the coupling between excited-electrons and low-frequency vibrations would reduce NAC and decoherence time and thus the e–h recombination events. Compared to the CdAu24 and HgAu24 nanoclusters, the phonon modes with stronger intensity for PdAu24 and wider intensity for PtAu24 nanoclusters would raise the nuclear velocity and enhance the e–p coupling, leading to stronger NACs, which, in turn, would facilitate the faster e–h recombination dynamics. Moreover, the faster e–h recombination process also originates from the stronger e–p coupling of the LUMO states of PdAu24 and PtAu24 than those of CdAu24 and HgAu24. Compared with type II nanoclusters, the shorter M–Au bonds caused by the fewer M(sp) and Au(6s6p) orbitals in the LUMO of type I nanoclusters enhance the vibrations of the MAu12 core, which dominates the low-frequency phonon modes participating in dynamic processes, suggesting a stronger e–p coupling.
The pure-dephasing time of type II nanoclusters (6.51 and 8.56 fs) is longer than that of the type I nanoclusters (3.13 and 6.38 fs) (see Tables S6–S9, ESI†), which can be ascribed to the elastic e–p scattering being suppressed by the weaker phonon modes of CdAu24 and HgAu24 nanoclusters. Since the e–h recombination dynamics are governed synergistically by NAC and decoherence time, the e–h recombination time of the former is longer than that of the latter one, although the pure-dephasing time of type II nanoclusters is longer than that of the type I nanoclusters. In other words, NAC dominates the e–h recombination process, while the decoherence time has little impact on the recombination dynamics of MAu24 nanoclusters.
The MAu24 nanoclusters, as a typical example of metal exchange nanoclusters, exhibit different hot electron relaxation and e–h recombination dynamics behaviors with various doping atoms. Attractively, the sub-nanosecond relaxation of excited electrons from LUMO+1 to LUMO effectively suppresses the energy loss of hot carriers. More impressively, the LUMO+1 state of MAu24 presents diffuse superatomic D-type orbitals, which could lead to strong hybridization with interfacial atoms when combined with two-dimensional (2D) materials, thereby facilitating the transfer of hot electrons in space. The slow hot electron relaxation of nanoclusters and fast charge transfer at the interface suggest that the LUMO+1 states of MAu24 nanoclusters are ideal charge separated states in carefully designed 0D/2D heterojunctions like Au9(PPh3)8/MoS2, C60/MoS2 and QDs(CdSe)/WS2.63–65 This highlights the important role of alloying monolayer-protected Au nanoclusters to reduce energy loss and control the photogenerated carrier lifetime, which are crucial for photovoltaic devices and other optoelectronic applications.
Conclusion
In summary, the effect of metal exchange on the stability, electronic and vibrational properties, and excited-state photophysical behavior of MAu24 nanoclusters has been systematically investigated using the TD-DFT method combined with NAMD simulations. Our results clearly demonstrate that the energy gap, e–p coupling, phonon modes, and decoherence time collectively affect the excited electron dynamics in MAu24 nanoclusters. Although the excited-electron relaxation pathways of MAu24 nanoclusters are similar, the change of energy gap upon single-atom substitution leads to different energy decays and carrier lifetimes of various MAu24 nanoclusters. Phonon mode analyses reveal that the transition between higher-energy states and LUMO+1 is dominated by the low-frequency vibrational modes of the MAu12 core and the staple Au–S bond-stretching vibrations, while the relaxation from LUMO+1 to LUMO and the e–h recombination from the LUMO to HOMO are coupled with the breathing vibrations and bond stretching modes of the MAu12 core. The photocarrier dynamics of nanoclusters are, to a large extent, associated with the gap between energy levels, which can be used to investigate the alloying effect on their carrier lifetimes. The time-dependent atomistic insights from the present study provide key guidance for precise design of doped metal nanoclusters with desired performance in optoelectronics and photocatalysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (91961204 and 12174045). The computational resources were provided by the Supercomputing Center of Dalian University of Technology and Shanghai Supercomputer Center.References
- G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887 CrossRef CAS PubMed.
- J. U. Reveles, P. A. Clayborne, A. C. Reber, S. N. Khanna, K. Pradhan, P. Sen and M. R. Pederson, Nat. Chem., 2009, 1, 310–315 CrossRef CAS PubMed.
- A. Cantelli, G. Guidetti, J. Manzi, V. Caponetti and M. Montalti, Eur. J. Inorg. Chem., 2017, 5068–5084 CrossRef CAS.
- R. W. Murray, Chem. Rev., 2008, 108, 2688–2720 CrossRef CAS PubMed.
- M. Zhou, T. Higaki, Y. Li, C. Zeng, Q. Li, M. Y. Sfeir and R. Jin, J. Am. Chem. Soc., 2019, 141, 19754–19764 CrossRef CAS PubMed.
- R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
- G. Li and R. Jin, Acc. Chem. Res., 2013, 46, 1749–1758 CrossRef CAS PubMed.
- R. J. Newhouse, H. Wang, J. K. Hensel, D. A. Wheeler, S. Zou and J. Z. Zhang, J. Phys. Chem. Lett., 2011, 2, 228–235 CrossRef CAS.
- R. R. Nasaruddin, T. Chen, N. Yan and J. Xie, Coord. Chem. Rev., 2018, 368, 60–79 CrossRef CAS.
- Q. Du, X. Wu, P. Wang, D. Wu, L. Sai, R. B. King, S. J. Park and J. Zhao, J. Phys. Chem. C, 2020, 124, 7449–7457 CrossRef CAS.
- S. Wang, X. Meng, A. Das, T. Li, Y. Song, T. Cao, X. Zhu, M. Zhu and R. Jin, Angew. Chem., Int. Ed., 2014, 53, 2376–2380 CrossRef CAS PubMed.
- S. Zhou, W. Pei, Q. Du and J. Zhao, Phys. Chem. Chem. Phys., 2019, 21, 10587–10593 RSC.
- Y. Sun, W. Pei, M. Xie, S. Xu, S. Zhou, J. Zhao, K. Xiao and Y. Zhu, Chem. Sci., 2020, 11, 2440–2447 RSC.
- M. Zhou and R. Jin, Annu. Rev. Phys. Chem., 2021, 72, 121–142 CrossRef CAS PubMed.
- T. G. Schaaff, G. Knight, M. N. Shafigullin, R. F. Borkman and R. L. Whetten, J. Phys. Chem. B, 1998, 102, 10643–10646 CrossRef CAS.
- J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, J. Am. Chem. Soc., 2008, 130, 3756–3757 CrossRef CAS PubMed.
- M. Zhu, E. Lanni, N. Garg, M. E. Bier and R. Jin, J. Am. Chem. Soc., 2008, 130, 1138–1139 CrossRef CAS PubMed.
- M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130, 5883–5885 CrossRef CAS PubMed.
- M. Zhu, C. M. Aikens, M. P. Hendrich, R. Gupta, H. Qian, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2009, 131, 2490–2492 CrossRef CAS PubMed.
- S. Antonello, N. V. Perera, M. Ruzzi, J. A. Gascón and F. Maran, J. Am. Chem. Soc., 2013, 135, 15585–15594 CrossRef CAS PubMed.
- S. H. Yau, O. Varnavski and T. Goodson, Acc. Chem. Res., 2013, 46, 1506–1516 CrossRef CAS PubMed.
- B. Du, X. Jiang, A. Das, Q. Zhou, M. Yu, R. Jin and J. Zheng, Nat. Nanotechnol., 2017, 12, 1096–1102 CrossRef CAS PubMed.
- M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, J. Am. Chem. Soc., 2008, 130, 3754–3755 CrossRef CAS PubMed.
- Y. Negishi, T. Iwai and M. Ide, Chem. Commun., 2010, 46, 4713–4715 RSC.
- Y. Negishi, K. Munakata, W. Ohgake and K. Nobusada, J. Phys. Chem. Lett., 2012, 3, 2209–2214 CrossRef CAS PubMed.
- W. Kurashige, K. Munakata, K. Nobusada and Y. Negishi, Chem. Commun., 2013, 49, 5447–5449 RSC.
- S. Wang, Y. Song, S. Jin, X. Liu, J. Zhang, Y. Pei, X. Meng, M. Chen, P. Li and M. Zhu, J. Am. Chem. Soc., 2015, 137, 4018–4021 CrossRef CAS PubMed.
- L. Liao, S. Zhou, Y. Dai, L. Liu, C. Yao, C. Fu, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 9511–9514 CrossRef CAS PubMed.
- E. Gottlieb, H. Qian and R. Jin, Chem. – Eur. J., 2013, 19, 4238–4243 CrossRef CAS PubMed.
- H. Qian, D.-e Jiang, G. Li, C. Gayathri, A. Das, R. R. Gil and R. Jin, J. Am. Chem. Soc., 2012, 134, 16159–16162 CrossRef CAS PubMed.
- M. Zhou, H. Qian, M. Y. Sfeir, K. Nobusada and R. Jin, Nanoscale, 2016, 8, 7163–7171 RSC.
- M. Zhou, C. Yao, M. Y. Sfeir, T. Higaki, Z. Wu and R. Jin, J. Phys. Chem. C, 2018, 122, 13435–13442 CrossRef CAS.
- W. Fei, S. Antonello, T. Dainese, A. Dolmella, M. Lahtinen, K. Rissanen, A. Venzo and F. Maran, J. Am. Chem. Soc., 2019, 141, 16033–16045 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- Q. Zheng, W. Chu, C. Zhao, L. Zhang, H. Guo, Y. Wang, X. Jiang and J. Zhao, WIREs Comput. Mol. Sci., 2019, 9, e1411 CAS.
- B. Rüdiger and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef.
- C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001 CrossRef PubMed.
- M. A. Tofanelli, K. Salorinne, T. W. Ni, S. Malola, B. Newell, B. Phillips, H. Hakkinen and C. J. Ackerson, Chem. Sci., 2016, 7, 1882–1890 RSC.
- K. Kwak and D. Lee, Acc. Chem. Res., 2019, 52, 12–22 CrossRef CAS PubMed.
- A. Tlahuice-Flores, Mol. Simul., 2013, 39, 428–431 CrossRef CAS.
- X. Chen, O. V. Prezhdo, Z. Ma, T. Hou, Z. Guo and Y. Li, Phys. Stateus Solidi B, 2015, 253, 458–462 CrossRef.
- Z. Liu, Y. Li, W. Shin and R. Jin, J. Phys. Chem. Lett., 2021, 12, 1690–1695 CrossRef CAS PubMed.
- V. D. Thanthirige, M. Kim, W. Choi, K. Kwak, D. Lee and G. Ramakrishna, J. Phys. Chem. C, 2016, 120, 23180–23188 CrossRef CAS.
- H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545 CrossRef PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972 CrossRef CAS PubMed.
- W. Chu, Q. Zheng, A. V. Akimov, J. Zhao, W. A. Saidi and O. V. Prezhdo, J. Phys. Chem. Lett., 2020, 11, 10073–10080 CrossRef CAS PubMed.
- A. Tlahuice-Flores, R. L. Whetten and M. Jose-Yacaman, J. Phys. Chem. C, 2013, 117, 12191–12198 CrossRef CAS.
- J. Akola, K. A. Kacprzak, O. Lopez-Acevedo, M. Walter, H. Grönbeck and H. Häkkinen, J. Phys. Chem. C, 2010, 114, 15986–15994 CrossRef CAS.
- S. V. Kilina, A. J. Neukirch, B. F. Habenicht, D. S. Kilin and O. V. Prezhdo, Phys. Rev. Lett., 2013, 110, 180404 CrossRef PubMed.
- Z. Zhou, J. Liu, R. Long, L. Li, L. Guo and O. V. Prezhdo, J. Am. Chem. Soc., 2017, 139, 6707–6717 CrossRef CAS PubMed.
- M. J. Guberman-Pfeffer, J. Ulcickas and J. A. Gascón, J. Phys. Chem. C, 2015, 119, 27804–27812 CrossRef CAS.
- L. Zhang, W. Chu, Q. Zheng, A. V. Benderskii, O. V. Prezhdo and J. Zhao, J. Phys. Chem. Lett., 2019, 10, 6151–6158 CrossRef CAS PubMed.
- L. Zhang, A. S. Vasenko, J. Zhao and O. V. Prezhdo, J. Phys. Chem. Lett., 2019, 10, 1083–1091 CrossRef CAS PubMed.
- W. Chu, W. A. Saidi, J. Zhao and O. V. Prezhdo, Angew. Chem., Int. Ed., 2020, 59, 6435–6441 CrossRef CAS PubMed.
- W. Chu, Q. Zheng, O. V. Prezhdo, J. Zhao and W. A. Saidi, Sci. Adv., 2020, 6, eaaw7453 CrossRef CAS PubMed.
- H. Guo, C. Zhao, Q. Zheng, Z. Lan, O. V. Prezhdo, W. A. Saidi and J. Zhao, J. Phys. Chem. Lett., 2018, 9, 3485–3490 CrossRef CAS PubMed.
- X. Yu, Y. Su, W.-W. Xu and J. Zhao, J. Phys. Chem. Lett., 2021, 12, 2312–2319 CrossRef CAS PubMed.
- A. Boulesbaa, K. Wang, M. Mahjouri-Samani, M. Tian, A. A. Puretzky, I. Ivanov, C. M. Rouleau, K. Xiao, B. G. Sumpter and D. B. Geohegan, J. Am. Chem. Soc., 2016, 138, 14713–14719 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00281g |
| This journal is © The Royal Society of Chemistry 2022 |