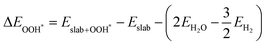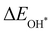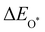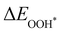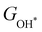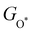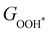DOI:
10.1039/D2NH00318J
(Communication)
Nanoscale Horiz., 2022,
7, 1404-1410
Strain-mediated oxygen evolution reaction on magnetic two-dimensional monolayers†
Received
5th July 2022
, Accepted 17th August 2022
First published on 18th August 2022
Abstract
By screening 56 magnetic 2D monolayers through first-principles calculations, it was found that 8 magnetic 2D monolayers (CoO2, FeO2, FeSe, FeTe, VS2, VSe2, VTe2 and CrSe2) can bind O*, OH* and OOH* intermediates of the oxygen evolution reaction (OER), in which the overpotentials of CoO2, FeO2, VSe2, and VTe2 monolayers are 0.684, 1.107, 0.863 and 0.837 V, respectively. After applying suitable biaxial tensile strains, the overpotentials of CoO2, FeO2 and VTe2 monolayers are reduced over 40%. In particular, the overpotentials of CoO2 and VTe2 monolayers decrease to 0.372 V and 0.491 V under the biaxial tensile strains of 4.0% and 3.0%, respectively, which are comparable to the reported overpotentials of noble metal and low-dimensional materials. Tensile strains modify the potential determining step for the OER and enhance the catalytic activity of metal atoms of magnetic 2D monolayers. Magnetic 2D monolayers could be activated by strain engineering as catalysts for the OER.
New concepts
Using two-dimensional (2D) materials as catalysts to improve the chemical reaction activity and efficiency has attracted great scientific interest and attention. The oxygen evolution reaction (OER) plays an important role in sustainable and renewable energy-conversion and -storage technologies. However, the catalytic capability of the basal surfaces of magnetic 2D materials for the OER has seldom been considered. Here, by screening 56 predicted magnetic 2D monolayers through extensive first-principles calculations we show that 8 magnetic 2D monolayers (CoO2, FeO2, FeSe, FeTe, VS2, VSe2, VTe2 and CrSe2) can bind O*, OH* and OOH* intermediates that are key reaction steps in the OER. After applying suitable biaxial tensile strain values, the overpotentials of the CoO2, FeO2 and VTe2 monolayers are reduced over 40%. In particular, the overpotentials of CoO2 and VTe2 monolayers decrease to 0.372 V and 0.491 V under biaxial tensile strain values of 4.0% and 3.0%, respectively, which are comparable to the reported overpotentials of noble metal and low-dimensional materials. Tensile strain modifies the potential determining step of the OER and significantly enhances the catalytic activity of the metal atoms of magnetic 2D monolayers. Our results highlight a possible route for utilizing strain engineering to activate magnetic 2D monolayers as catalysts for the OER.
|
Introduction
Sustainable and renewable energy-conversion and -storage technologies, including electrocatalytic water splitting,1 fuel cells2 and metal–air batteries,3 have been widely applied in clean and green energy fields.4–6 The oxygen evolution reaction (OER) plays an important role in enabling the chemical process and efficiency in those energy-storage technologies.7,8 The multistep proton-coupled electron-transfer process in the OER usually leads to a high overpotential and sluggish reaction kinetics.9 Traditional noble metal catalysts like IrO210 and RuO211,12 have state-of-the-art chemical activity for improving the efficiency of the OER, but noble metal elements and their compounds are rare in the Earth, which results in high exploitation costs and limits their widespread application. Therefore, seeking low-cost, stable and high-efficiency catalysts is critical for the OER and the development of green and clean energy-storage technologies.
In recent years, graphene and transition metal dichalcogenides (TMDs) as typical two-dimensional (2D) van der Waals (vdW) materials have exhibited excellent chemical properties,13,14 and can be good catalysts for water splitting15–17 and the hydrogen evolution reaction (HER).18–20 For the OER, the adsorption capability of O*, OH* and OOH* intermediates that are critical reaction steps of the OER is different on perfect graphene21 and TMDs.22 The relatively high adsorption energies of the intermediates give rise to higher overpotentials in the OER on the basal planes of graphene23 and TMDs.24 Further experimental and theoretical studies have shown that the adsorption sites and energies of the O*, OH* and OOH* intermediates can be altered and controlled by introducing defects or single-atom metals such as Fe, Co, Mn or Ni on the graphene and TMDs surfaces, upon which the OER overpotentials are decreased accordingly.25 For example, the electrochemical overpotential of mononuclear Mn embedded in nitrogen-doped graphene is only 0.337 V, which is better than traditional noble metal catalysts.26 Using structural engineering or combining active single-atom metals, 2D vdW materials could play the role of a catalyst in enhancing the OER.27,28 Except from non-magnetic 2D materials, magnetic 2D materials have been successfully obtained and have also attracted a great deal of scientific attention and interest because of their potential spintronics and valleytronics applications.29 The heterostructures formed by magnetic 2D materials show good catalytic activity for the OER.30–32 Different from experimental synthesis and exfoliation for achieving magnetic 2D materials,33,34 a recent theoretical study based on high-throughput computation predicted 56 possible magnetic 2D materials that are held by weak vdW interactions in their bulk states.35 Magnetic 2D materials possess a flat atomic structure and a high surface-to-volume ratio, making an ideal platform for catalytic reactions.36 On the other hand, mechanical deformation and loading have been proved to be an effective way to change and improve the chemical properties of 2D materials, which can also render 2D materials with novel physical effects.37 However, the OER on the basal surfaces of magnetic 2D materials and the influence of mechanical deformation on the catalytic activity of magnetic 2D materials have seldom been investigated.
In this study, 56 magnetic 2D monolayers that were theoretically predicted are considered as possible OER catalysts via first-principles calculations. Our calculation results show that O*, OH* and OOH* intermediates can only adsorb on the basal surfaces of 8 magnetic 2D monolayers, in which the overpotentials of the CoO2, FeO2, VSe2, and VTe2 monolayers for the OER are 0.684, 1.107, 0.863 and 0.837 V, respectively. When the biaxial tensile strain of 4.0%, 6.0%, 5.0% and 3.0% is applied on the CoO2, FeO2, VSe2 and VTe2 monolayers, their overpotentials decrease to the lowest values of 0.372, 0.600, 0.796 and 0.491 V, respectively. For the CoO2 monolayer, the overpotential of 0.372 V is comparable to that of the noble metal catalyst RuO2. The biaxial tensile strain changes the potential determining step (PDS) of the OER, strengthens the adsorption of intermediates on the 2D monolayers and reduces the energy barriers of intermediate transition. Strain engineering can enhance the chemical activity of magnetic 2D monolayers, which makes them suitable as catalysts in the OER.
Model and method
According to theoretical prediction and experimental results,35,38,39 56 magnetic 2D monolayers were considered (see Table S1 in the ESI†) and constructed in rectangular unit cells, the lengths of which in the x and y directions are both larger than 15 Å. In Fig. 1, the atomic structures of three 2D monolayers are given. The periodic boundary conditions were applied in the x and y directions and the vacuum regions were set as 20 Å in the z direction. The O*, OH* and OOH* intermediates that are involved in the OER adsorb on the center of basal surfaces. All spin-polarized calculations were performed within the framework of density functional theory (DFT) as implemented in the Vienna ab initio simulation package (VASP) using the projector augmented wave method with the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.40–42 The influence of van der Waals interactions was considered using DFT-D3 correction, which was developed by Grimme et al.43 The plane wave energy cutoff was set to 500 eV and the special Γ-centered k points sampled on a 3 × 3 × 1 mesh were employed after the convergence test. Biaxial tensile strain was applied by gradually increasing the unit cell lengths in the x and y directions. Then those systems were relaxed using a conjugate-gradient algorithm until the force on each atom was less than 0.01 eV Å−1.
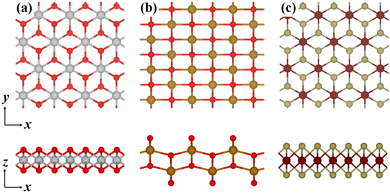 |
| | Fig. 1 Top (upper) and side (lower) views of the atomic configurations of three magnetic 2D monolayers: (a) CoO2, (b) FeO2, and (c) VTe2. | |
In the electrochemical reaction, the overall OER can be written as:44
| | | 2H2O(l) → O2(g) + 4H+ + 4e− | (1) |
The overall reaction involves four elementary reaction steps, and each step involves the transfer of one electron. The specific expressions are as follows:
44| | | H2O(l) + * → OH* + H+ + e− | (2a) |
| | | O* + H2O(l) → OOH* + H+ + e− | (2c) |
| | | OOH* → * + O2(g) + H+ + e− | (2d) |
where * represents an active site on the basal surface of the magnetic 2D monolayers. H
2O(l) and O
2(g) are a liquid-phase water molecule and a gas-phase oxygen molecule, respectively, and O*, OH* and OOH* are the three different adsorbed intermediates in the OER. H
+ and e
− are a proton and electron, respectively.
The binding energies of different adsorbed intermediates are calculated using the following equations:45
| | 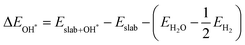 | (3a) |
| | 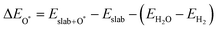 | (3b) |
where
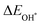
,
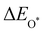
and
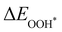
are the binding energies of the OH*, O* and OOH* intermediates, respectively.
Eslab is the ground-state energy of the magnetic 2D monolayer.
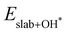
,
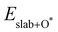
and
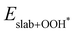
are the total energies of the magnetic 2D monolayer binding with the OH*, O* and OOH* intermediates, respectively.
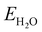
and
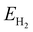
are the energies of H
2O and H
2 molecules in the liquid and gas phase, respectively.
At zero electrode potential and pH = 0, the Gibbs free energy of the adsorbed intermediates is obtained using the following equation:45
| | | Gads = ΔEads + ΔEZPE − TΔS | (4) |
where Δ
Eads is the binding energy, Δ
EZPE is the difference in zero point vibrational energy,
T is the thermodynamic temperature (298.15 K), and Δ
S is the change in entropy of the intermediates adsorbed on the magnetic 2D monolayer at one standard atmospheric pressure (101.325 kPa).
For each elementary reaction step, the Gibbs free energy difference ΔGi(i = 1, 2, 3, 4) is given by these equations:45,46
| | 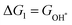 | (5a) |
| | 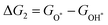 | (5b) |
| | 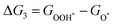 | (5c) |
| | 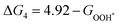 | (5d) |
where the value of 4.92 eV is the total change in the Gibbs free energy for the overall reaction 2H
2O → O
2 + 2H
2 at 298.15 K. After that, the theoretical overpotential
η for the OER is obtained using:
45| | | ΔGmaxi = max[ΔG1,ΔG2,ΔG3,ΔG4] | (6) |
In the OER, the PDS is an important reaction step that dominates the overall catalytic performance of catalysts,
47 which can be obtained from Δ
Gmaxi.
Results and discussion
The OER includes four elementary steps in which oxygen-containing intermediates (O*, OH* and OOH*) adsorb on the surfaces of magnetic 2D monolayers. After screening the 56 magnetic 2D monolayers via first-principles calculations, eight magnetic 2D monolayers on which all the intermediates can adsorb were selected, and they are CoO2, FeO2, FeSe, FeTe, VS2, VSe2, VTe2 and CrSe2. The Gibbs free energy differences ΔGi and overpotentials η of the eight monolayers for the OER were calculated according to eqn (5)–(7). For the 8 magnetic 2D monolayers, monolayer CoO2 possesses the lowest overpotential of 0.684 V, see Table S2 in the ESI.† An ideal catalyst for the OER is one in which all Gibbs free energy differences between two adjacent elementary reactions are 0 eV at 1.23 V external potential, and a lower overpotential means a better catalytic capability. In order to improve the catalytic properties for the OER, in-plane biaxial tensile strain was applied on the eight magnetic 2D monolayers. Our results show that the overpotential of monolayer CoO2 decreases from 0.684 V to the lowest value of 0.372 V when a 4.0% biaxial tensile strain εxy was applied, which is close to that of RuO2.44 Meanwhile, the overpotentials of monolayer FeO2, VSe2 and VTe2 decrease to the lowest values of 0.600, 0.796 and 0.491 V when 6.0%, 5.0% and 3.0% biaxial tensile strain εxy is applied, respectively. For the other four magnetic monolayers, their overpotentials are all larger than 1 V, even in the presence of tensile strain, see Table S2 (ESI†). Reduction of the overpotential demonstrates the validity of tensile strain in enhancing the catalytic performance of magnetic 2D materials for the OER. Moreover, Table 1 shows a comparison of the overpotentials of magnetic 2D materials for the OER with other low-dimensional materials. The overpotentials of 0.372 V for the strained CoO2 monolayer and 0.491 V for the strained VTe2 monolayer are comparable to the theoretically predicted overpotentials of non-magnetic nanomaterials and nanostructures. This means that magnetic 2D CoO2 and VTe2 combined with strain engineering can be used as catalysts for the OER on their basal planes.
Table 1 Theoretical predicted overpotentials for the OER using low-dimensional materials as catalysts
| Material |
Overpotential (V) |
Ref. |
| 2D-CoO2 (4.0% εxy) |
0.372 |
This work |
| 2D-VTe2 (3.0% εxy) |
0.491 |
This work |
| Fe–MoS2 nanosheets |
0.328 |
28
|
| Mn-NG |
0.337 |
26
|
| RuO2 (110) |
0.370 |
44
|
| Zn@MoSi2N4 |
0.380 |
48
|
| Armchair N-doped graphene |
0.405 |
49
|
| Ni-NHGF |
0.420 |
25
|
| Pd-GeC |
0.440 |
50
|
| Pt-MoS2 edge |
0.460 |
51
|
Fig. 2(a) shows the Gibbs free energy diagram of the adsorbed intermediates on monolayer CoO2 for the OER. The PDS of the OER on monolayer CoO2 without strain is the first step ΔG1 (H2O → *OH) with a value of 1.914 eV, but the PDS changes to the second step ΔG2 (*OH → *O) and decreases to 1.602 eV under a biaxial tensile strain of 4.0%, as shown in Fig. 2(a). By contrast, it can be seen from Fig. 2(b) that the PDSs of monolayer FeO2, VSe2 and VTe2 under biaxial tensile strain values of 6.0%, 5.0% and 3.0%, respectively, are all the third step ΔG3 (*O → *OOH). To further elucidate the effect of tensile deformation on the PDS, the variation in the Gibbs free energy difference (ΔGi) of the four magnetic 2D monolayers with biaxial tensile strain are shown in Fig. 3. Excluding 4.0% biaxial strain, the PDSs of the OER on monolayer CoO2 are all the first step ΔG1 in the absence or presence of biaxial tensile strain. For monolayer FeO2, the PDSs of the OER are the first step ΔG1 before the biaxial strain is lower than 3% but become the third step ΔG3 under larger biaxial strain values. The PDSs of the OER on monolayer VSe2 and VTe2 are the third step ΔG3 without any strain or in the presence of biaxial tensile strain but become the fourth step ΔG4 (*OOH → O2) when the strain is larger than 6% and 5%, respectively. The tensile strain imposes a significant modification and change on the PDSs of the OER, which could be used accordingly to decrease the overpotentials of the magnetic 2D monolayers.
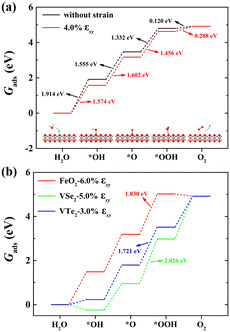 |
| | Fig. 2 Gibbs free energy diagrams of the adsorbed intermediates for the OER on (a) monolayer CoO2 without strain and under 4.0% biaxial tensile strain, and (b) monolayer FeO2, VSe2 or VTe2 under 6.0%, 5.0% and 3.0% biaxial tensile strain, respectively. The inset in (a) shows the reaction steps in which the O*, OH* and OOH* intermediates adsorb on monolayer CoO2, where the red, gray and white spheres denoted O, Co and H atoms, respectively. | |
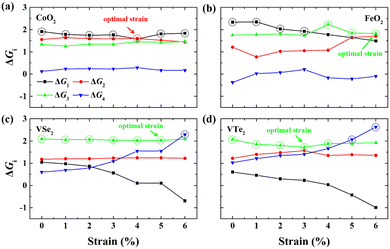 |
| | Fig. 3 Gibbs free energy differences (ΔGi) in the elementary reaction steps for (a) CoO2, (b) FeO2, (c) VSe2 and (d) VTe2 monolayers under different biaxial tensile strains. The PDSs are circled by dash lines and the optimal strains for the lowest overpotentials are marked by arrows. | |
Moreover, the relationship between biaxial tensile strain and the binding energies of the intermediates on monolayer CoO2 is shown in Fig. 4(a). The variation in the binding energies is non-monotonic with biaxial tensile strain εxy. Under 4.0% biaxial tensile strain, the binding energies of all the intermediates decrease to their lowest, indicating the strongest binding between the intermediates and the CoO2 surface. On the other hand, it can be seen from Fig. 4(b) that the binding energies 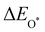 and
and 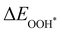 obtained under different biaxial tensile strain are approximately linear functions of
obtained under different biaxial tensile strain are approximately linear functions of 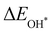 . The scaling relation between
. The scaling relation between 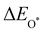 or
or 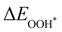 with
with 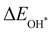 is fitted as
is fitted as 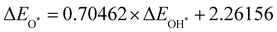 or
or 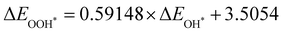 . Furthermore, the variation in the Gibbs free energies of the adsorbed intermediates under different biaxial tensile strain values shown in Fig. 4(c) is similar to that of the binding energies. There still exists approximately linear scaling relations between
. Furthermore, the variation in the Gibbs free energies of the adsorbed intermediates under different biaxial tensile strain values shown in Fig. 4(c) is similar to that of the binding energies. There still exists approximately linear scaling relations between 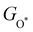 or
or 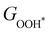 with
with 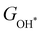 :
: 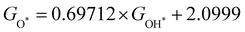 and
and 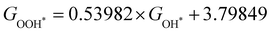 , see Fig. 4(d). As a result,
, see Fig. 4(d). As a result, 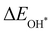 and
and 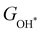 can be used to predict the binding energies and Gibbs free energies of the *O and *OOH intermediates on the CoO2 surface. For the FeO2, VSe2 and VTe2 monolayers, their Gibbs free energies
can be used to predict the binding energies and Gibbs free energies of the *O and *OOH intermediates on the CoO2 surface. For the FeO2, VSe2 and VTe2 monolayers, their Gibbs free energies 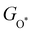 and
and 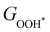 under different biaxial tensile strain also exhibit approximately linear relations with
under different biaxial tensile strain also exhibit approximately linear relations with 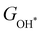 , see Fig. S1 and S2 (ESI†). These linear scaling relations between
, see Fig. S1 and S2 (ESI†). These linear scaling relations between 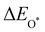 or
or 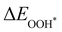 with
with 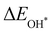 and between
and between 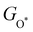 or
or 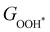 with
with 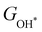 are consistent with previous studies.44,45,48,49,51
are consistent with previous studies.44,45,48,49,51
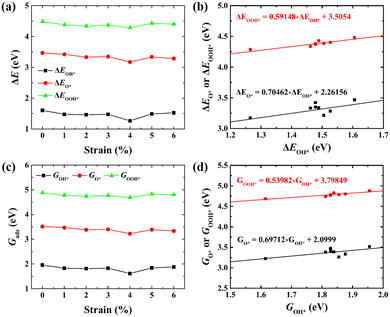 |
| | Fig. 4 (a) Binding energies of the three intermediates on the CoO2 monolayer under different biaxial tensile strain, and (b) the scaling relation between 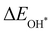 and and 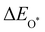 or or 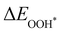 . (c) Adsorption Gibbs free energies of the three intermediates on CoO2 under different biaxial tensile strain, and (d) the scaling relations between . (c) Adsorption Gibbs free energies of the three intermediates on CoO2 under different biaxial tensile strain, and (d) the scaling relations between 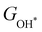 and and 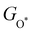 or or 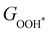 . The solid lines in (b) and (d) are fitting lines. . The solid lines in (b) and (d) are fitting lines. | |
The metal atoms of 2D materials play a key catalytic role in the OER and HER.50,51 To reveal the mechanism of tensile strain that modifies the catalytic properties of the metal atoms, Fig. 5 shows the density of states (DOS) of the metal atoms (Co, Fe and V) of the CoO2, FeO2, VSe2 and VTe2 monolayers without strain and under the biaxial tensile strain that leads to the lowest overpotential. It is shown from Fig. 5(a) and (b) that the DOS around the Fermi level of both spin-up and spin-down for the Co and Fe atoms is increased by the biaxial tensile strain, but the increasing magnitude of spin-down for the Fe atom is much higher than that of its spin-up counterpart. For the VSe2 and VTe2 monolayers, the DOS around the Fermi level of only spin-up for the V atoms is increased by the biaxial tensile strain, as shown in Fig. 5(c) and (d). Moreover, the d-band centers εd of the metal atoms of the four magnetic monolayers were calculated using 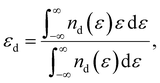 where nd(ε) is the density of states projected onto the d-states and ε is the energy.52,53 The closer the d-band center is to the Fermi level, the stronger the binding with the intermediates and the better chemical activity of the metal atom.54 For the CoO2 and FeO2 monolayers, biaxial tensile strain makes the d-band centers for spin-down of the metal atoms closer to the Fermi level, where the d-band center of the Co atom moves from −1.05 to −0.88 eV, and that for the Fe atom moves from −0.76 to −0.42 eV. By contrast, the d-band centers for spin-up of the V atoms for VSe2 and VTe2 monolayers are closer to the Fermi level when under biaxial tensile strain, where the d-band center of the V atom of VSe2 moves from −0.33 to −0.26 eV, and that of VTe2 moves from −0.37 to −0.32 eV. The tensile strain imposes a stronger improvement on the spin-down d-band centers of Co and Fe atoms, and on the spin-up d-band centers of V atoms. Furthermore, the spin-down charge densities ρspin-down around the Fermi level of the CoO2 and FeO2 monolayers and the spin-up charge densities ρspin-up around the Fermi level of the VSe2 and VTe2 monolayers are shown in Fig. 6. Clearly, more charges move to the metal atoms in the presence of biaxial tensile strain, which indicates the chemical activity enhancement of metal atoms and also coincides with the movement of the d-band centers to the Fermi level.
where nd(ε) is the density of states projected onto the d-states and ε is the energy.52,53 The closer the d-band center is to the Fermi level, the stronger the binding with the intermediates and the better chemical activity of the metal atom.54 For the CoO2 and FeO2 monolayers, biaxial tensile strain makes the d-band centers for spin-down of the metal atoms closer to the Fermi level, where the d-band center of the Co atom moves from −1.05 to −0.88 eV, and that for the Fe atom moves from −0.76 to −0.42 eV. By contrast, the d-band centers for spin-up of the V atoms for VSe2 and VTe2 monolayers are closer to the Fermi level when under biaxial tensile strain, where the d-band center of the V atom of VSe2 moves from −0.33 to −0.26 eV, and that of VTe2 moves from −0.37 to −0.32 eV. The tensile strain imposes a stronger improvement on the spin-down d-band centers of Co and Fe atoms, and on the spin-up d-band centers of V atoms. Furthermore, the spin-down charge densities ρspin-down around the Fermi level of the CoO2 and FeO2 monolayers and the spin-up charge densities ρspin-up around the Fermi level of the VSe2 and VTe2 monolayers are shown in Fig. 6. Clearly, more charges move to the metal atoms in the presence of biaxial tensile strain, which indicates the chemical activity enhancement of metal atoms and also coincides with the movement of the d-band centers to the Fermi level.
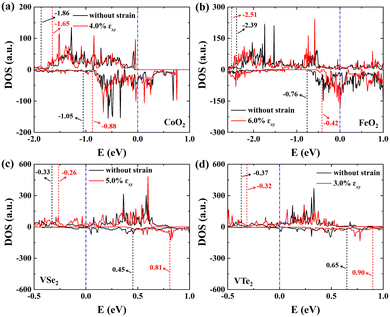 |
| | Fig. 5 DOS (in units of a.u.) of spin-up (top) and spin-down (bottom) for the metal atoms (Co, Fe and V) of (a) CoO2, (b) FeO2, (c) VSe2 and (d) VTe2 monolayers without strain and under the biaxial tensile strain that leads to the lowest overpotential. Here, the red and black dashed lines denote the d-band centers of spin-up and spin-down for the metal atoms, and the Fermi level is set to zero. | |
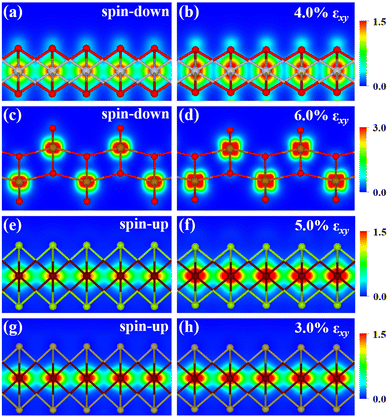 |
| | Fig. 6 2D projections of the charge densities (in units of e·Å−3) of (a and b) spin-down for monolayer CoO2 in the energy range from −0.15 to 0.15 eV, (b and c) spin-down for monolayer FeO2 in the energy range from −0.30 to 0.30 eV, (e and f) spin-up for monolayer VSe2 in the energy range from −0.30 to 0.30 eV, and (g and h) spin-up for monolayer VTe2 in the energy range from −0.20 to 0.20 eV in the absence and presence of biaxial tensile strain. | |
Different from the metal atoms, the changes in the DOS around the Fermi level of non-metal atoms (O, Se and Te) of the CoO2, FeO2, VSe2 and VTe2 monolayers are relatively slight under tensile strain, as shown in Fig. S3 (ESI†). We compared the influence of uniaxial tensile strain (in the x or y direction) on the overpotential with that of biaxial tensile strain. It can be seen from the overpotentials of the CoO2 or VTe2 monolayers in Fig. S4 (ESI†) that the lowest overpotentials occur under biaxial tensile strain. Furthermore, the overpotentials of four of the 2D magnetic monolayers (CoO2, FeO2, VSe2 and VTe2) were calculated using the PBE+U method.55 As shown in Fig. S5 (ESI†), the difference in the obtained overpotentials between the PBE and PBE+U methods is slight. For comparison with the 2D magnetic monolayers, three 2D non-magnetic monolayers NiO2, MoTe2 and MoSe2 were considered as catalysts for the OER using the same DFT calculation procedure. It can be seen from Fig. S6–S8 (ESI†) that the non-magnetic NiO2, MoSe2 and MoTe2 monolayers are unable to bind the OOH* intermediate, and biaxial tensile strain imposes a slight influence on the DOS around the Fermi level and the Gads. Clearly, the strain-induced improvement in catalytic capability of the magnetic 2D monolayers for the OER is much stronger than that for the non-magnetic 2D monolayers.
In experiments, utilizing interfacial lattice mismatch,56,57 elastic modulus mismatch58,59 and thermal expansion mismatch60–62 between the 2D materials and the substrates, as well as bending of the underlying substrates, are feasible ways to apply strain to 2D materials.63,64 Using thermal expansion mismatch between 2D materials and substrates of high Young's modulus can generate homogenous biaxial strain on 2D materials.60–62 In our work, the DFT results on the catalytic activity of magnetic 2D monolayers are all obtained from the homogenous tensile deformation of 2D monolayers. Therefore, in a practical situation it is better to apply homogenous strain on magnetic 2D monolayers for improving their catalytic activity for the OER.
Conclusions
In summary, our extensive first-principles calculations show that 8 magnetic 2D monolayers (CoO2, FeO2, FeSe, FeTe, VS2, VSe2, VTe2 and CrSe2) screened from 56 predicted magnetic 2D monolayers can bind O*, OH* and OOH* intermediates that are involved in the OER. The overpotentials of the CoO2, FeO2, VSe2 and Vte2 monolayers for the OER can be reduced to lower than 1.0 V by applying a suitable biaxial tensile strain. In particular, the overpotentials of the CoO2 and VTe2 monolayers decrease to 0.372 V and 0.491 V under biaxial tensile strain values of 4.0% and 3.0%, respectively, which are comparable to the reported overpotentials of low-dimensional materials. The reduction of overpotentials is attributed to the tensile-strain-induced modification of the PDSs and adsorption strengthening of the intermediates. Tensile strain could improve the catalytic activity of metal atoms of magnetic 2D monolayers by increasing the charge distribution around the metal atoms and moving the d-band centers of metal atoms closer to the Fermi level. These results provide a possible route for utilizing strain engineering to activate magnetic 2D monolayers as catalysts for the OER.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (11972186, 11890674, and 51921003), and the Western Light Project of CAS (xbzg-zdsys-202118), a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
References
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 0003 CrossRef CAS
 .
.
- E. Antolini, ACS Catal., 2014, 4, 1426–1440 CrossRef CAS
 .
.
- Y. C. Lu, Z. C. Xu, H. A. Gasteiger, S. Chen, K. Hamad-Schifferli and Y. Shao-Horn, J. Am. Chem. Soc., 2010, 132, 12170–12171 CrossRef CAS PubMed
 .
.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. B. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, 1–12 CrossRef PubMed
 .
.
- M. S. Dresselhaus and I. L. Thomas, Nature, 2001, 414, 332–337 CrossRef CAS PubMed
 .
.
- S. Chu, Y. Cui and N. Liu, Nat. Mater., 2016, 16, 16–22 CrossRef PubMed
 .
.
- N. T. Suen, S. F. Hung, Q. Quan, N. Zhang, Y. J. Xu and H. M. Chen, Chem. Soc. Rev., 2017, 46, 337–365 RSC
 .
.
- M. Tahir, L. Pan, F. Idrees, X. W. Zhang, L. Wang, J. J. Zou and Z. L. Wang, Nano Energy, 2017, 37, 136–157 CrossRef CAS
 .
.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS PubMed
 .
.
- S. M. Alia, S. Shulda, C. Ngo, S. Pylypenko and B. S. Pivovar, ACS Catal., 2018, 8, 2111–2120 CrossRef CAS
 .
.
- T. Reier, M. Oezaslan and P. Strasser, ACS Catal., 2012, 2, 1765–1772 CrossRef CAS
 .
.
- J. T. Zhang, Z. H. Zhao, Z. H. Xia and L. M. Dai, Nat. Nanotechnol., 2015, 10, 444–452 CrossRef CAS PubMed
 .
.
- D. J. Akinwande, C. J. Brennan, J. S. Bunch, P. Egberts, J. R. Felts, H. J. Gao, R. Huang, J. S. Kim, T. Li, Y. Li, K. M. Liechti, N. S. Lu, H. S. Park, E. J. Reed, P. Wang, B. I. Yakobson, T. Zhang, Y. W. Zhang, Y. Zhou and Y. Zhu, Ext. Mech. Lett., 2017, 13, 42–77 CrossRef
 .
.
- D. Jariwala, V. K. Sangwan, L. J. Lauhon, T. J. Marks and M. C. Hersam, ACS Nano, 2014, 8, 1102–1120 CrossRef CAS PubMed
 .
.
- B. You, M. T. Tang, C. Tsai, F. Abild-Pedersen, X. L. Zheng and H. Li, Adv. Mater., 2019, 31, 1807001 CrossRef PubMed
 .
.
- Y. N. Guo, T. Park, J. W. Yi, J. Henzie, J. Kim, Z. L. Wang, B. Jiang, Y. Bando, Y. Sugahara, J. Tang and Y. Yamauchi, Adv. Mater., 2019, 31, 1807134 CrossRef PubMed
 .
.
- Y. J. Ji, M. Y. Yang, H. P. Lin, T. J. Hou, L. Wang, Y. Y. Li and S. T. Lee, J. Phys. Chem. C, 2018, 122, 3123–3129 CrossRef CAS
 .
.
- H. Li, C. Tsai, A. L. Koh, L. L. Cai, A. W. Contryman, A. H. Fragapane, J. H. Zhao, H. S. Han, H. C. Manoharan, F. Abild-Pedersen, J. K. Nørskov and X. L. Zheng, Nat. Mater., 2016, 15, 48–53 CrossRef CAS PubMed
 .
.
- T. Yang, J. Zhou, T. T. Song, L. Shen, Y. P. Feng and M. Yang, ACS Energy Lett., 2020, 5, 2313–2321 CrossRef CAS
 .
.
- J. F. Xie, J. J. Zhang, S. Li, F. Grote, X. D. Zhang, H. Zhang, R. X. Wang, Y. Lei, B. C. Pan and Y. Xie, J. Am. Chem. Soc., 2013, 135, 17881–17888 CrossRef CAS PubMed
 .
.
- C. L. Wang, H. G. Tong, J. Lu, B. Liu, F. C. Zheng, W. W. Tao, W. J. Zhang and Q. W. Chen, Carbon, 2020, 170, 414–420 CrossRef CAS
 .
.
- G. T. Hai, H. Y. Gao, G. X. Zhao, W. J. Dong, X. B. Huang, Y. Li and G. Wang, iScience, 2019, 20, 481–488 CrossRef CAS PubMed
 .
.
- G. Murdachaew and K. Laasonen, J. Phys. Chem. C, 2018, 122, 25882–25892 CrossRef CAS PubMed
 .
.
- E. German and R. Gebauer, Appl. Surf. Sci., 2020, 528, 146591 CrossRef CAS
 .
.
- H. L. Fei, J. C. Dong, Y. X. Feng, C. S. Allen, C. Z. Wan, B. Volosskiy, M. F. Li, Z. P. Zhao, Y. L. Wang, H. T. Sun, P. F. An, W. X. Chen, Z. Y. Guo, C. Lee, D. L. Chen, I. Shakir, M. J. Liu, T. D. Hu, Y. D. Li, A. I. Kirkland, X. F. Duan and Y. Huang, Nat. Catal., 2018, 1, 63–72 CrossRef CAS
 .
.
- J. Q. Guan, Z. Y. Duan, F. X. Zhang, S. D. Kelly, R. Si, M. Dupuis, Q. G. Huang, J. Q. Chen, C. H. Tang and C. Li, Nat. Catal., 2018, 1, 870–877 CrossRef CAS
 .
.
- H. J. Lee, S. Back, J. H. Lee, S. H. Choi, Y. Jung and J. W. Choi, ACS Catal., 2019, 9, 7099–7108 CrossRef CAS
 .
.
- B. S. Tang, Z. G. Yu, H. L. Seng, N. D. Zhang, X. X. Liu, Y. W. Zhang, W. F. Yang and H. Gong, Nanoscale, 2018, 10, 20113–20119 RSC
 .
.
- O. Gutfleisch, M. A. Willard, E. Bruck, C. H. Chen, S. G. Sankar and J. P. Liu, Adv. Mater., 2011, 23, 821–842 CrossRef CAS PubMed
 .
.
- Z. R. Xiong, C. Hu, X. F. Luo, W. D. Zhou, Z. Z. Jiang, Y. Yang, T. Yu, W. Lei and C. L. Yuan, Nano Lett., 2021, 21, 10486–10493 CrossRef CAS PubMed
 .
.
- X. M. Hu, S. L. Zhang, J. W. Sun, L. Yu, X. Y. Qian, R. D. Hu, Y. N. Wang, H. G. Zhao and J. W. Zhu, Nano Energy, 2019, 56, 109–117 CrossRef CAS
 .
.
- C. L. Qin, A. X. Fan, X. Zhang, S. Q. Wang, X. L. Yuan and X. P. Dai, J. Mater. Chem. A, 2019, 7, 27594–27602 RSC
 .
.
- S. Q. Zhang, R. Z. Xu, N. N. Luo and X. L. Zou, Nanoscale, 2021, 13, 1398–1424 RSC
 .
.
- M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Nat. Nanotechnol., 2019, 14, 408–419 CrossRef CAS PubMed
 .
.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246 CrossRef CAS PubMed
 .
.
- H. Y. Jin, C. X. Guo, X. Liu, J. L. Liu, A. Vasileff, Y. Jiao, Y. Zheng and S. Z. Qiao, Chem. Rev., 2018, 118, 6337–6408 CrossRef CAS PubMed
 .
.
- P. F. Li, Z. Kang, Z. Zhang, Q. L. Liao, F. Rao, Y. Lu and Y. Zhang, Mater. Today, 2021, 51, 247–272 CrossRef CAS
 .
.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. D. Xu, Nature, 2017, 546, 270 CrossRef CAS PubMed
 .
.
- C. Gong, L. Li, Z. L. Li, H. W. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Z. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265 CrossRef CAS PubMed
 .
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
 .
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
 .
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
 .
.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed
 .
.
- J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS
 .
.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS
 .
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
 .
.
- X. F. Liu, Y. F. Zhang, W. T. Wang, Y. Z. Chen, W. J. Xiao, T. Y. Liu, Z. Zhong, Z. J. Luo, Z. Ding and Z. F. Zhang, ACS Appl. Mater. Interfaces, 2022, 14, 1249–1259 CrossRef CAS PubMed
 .
.
- S. Lu, Y. Zhang, F. L. Lou, K. Guo and Z. X. Yu, Appl. Surf. Sci., 2022, 579, 152234 CrossRef CAS
 .
.
- M. T. Li, L. P. Zhang, Q. Xu, J. B. Niu and Z. H. Xia, J. Catal., 2014, 314, 66–72 CrossRef CAS
 .
.
- X. Chen, H. Zhang and Y. Z. Zhang, Colloids Surf., A, 2021, 630, 127628 CrossRef CAS
 .
.
- X. P. Xu, H. X. Xu and D. J. Cheng, Nanoscale, 2019, 11, 20228–20237 RSC
 .
.
- B. Hammer and J. K. Nørskov, Nature, 1995, 376, 238–240 CrossRef CAS
 .
.
- B. Hammer and J. K. Nørskov, Surf. Sci., 1995, 343, 211–220 CrossRef CAS
 .
.
- A. Ruban, B. Hammer, P. Stoltze, H. L. Skriver and J. K. Nørskov, J. Mol. Catal. A: Chem., 1997, 115, 421–429 CrossRef CAS
 .
.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef
 .
.
- M. Y. Li, Y. M. Shi, C. C. Cheng, L. S. Lu, Y. C. Lin, H. L. Tang, M. L. Tsai, C. W. Chu, K. H. Wei, J. H. He, W. H. Chang, K. Suenaga and L. J. Li, Science, 2015, 349, 524–528 CrossRef CAS PubMed
 .
.
- C. D. Zhang, M. Y. Li, J. Tersoff, Y. M. Han, Y. S. Su, L. J. Li, D. A. Muller and C. K. Shih, Nat. Nanotechnol., 2018, 13, 152–158 CrossRef CAS PubMed
 .
.
- K. P. Dhakal, S. Roy, H. Jang, X. Chen, W. S. Yun, H. Kim, J. Lee, J. Kim and J. H. Ahn, Chem. Mater., 2017, 29, 5124–5133 CrossRef CAS
 .
.
- S. X. Yang, C. Wang, H. Sahin, H. Chen, Y. Li, S. S. Li, A. Suslu, F. M. Peeters, Q. Liu, J. B. Li and S. Tongay, Nano Lett., 2015, 15, 1660–1666 CrossRef CAS PubMed
 .
.
- G. Plechinger, A. Castellanos-Gomez, M. Buscema, H. S. J. van der Zant, G. A. Steele, A. Kuc, T. Heine, C. Schuller and T. Korn, 2D Mater., 2015, 2, 015006 CrossRef
 .
.
- P. Gant, P. Huang, D. P. de Lara, D. Guo, R. Frisenda and A. Castellanos-Gomez, Mater. Today, 2019, 27, 8–13 CrossRef CAS
 .
.
- G. H. Ahn, M. Amani, H. Rasool, D. H. Lien, J. P. Mastandrea, J. W. Ager, M. Dubey, D. C. Chrzan, A. M. Minor and A. Javey, Nat. Commun., 2017, 8, 608 CrossRef PubMed
 .
.
- C. R. Zhu, G. Wang, B. L. Liu, X. Marie, X. F. Qiao, X. Zhang, X. X. Wu, H. Fan, P. H. Tan, T. Amand and B. Urbaszek, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 121301 CrossRef
 .
.
- Z. W. Li, Y. W. Lv, L. W. Ren, J. Li, L. A. Kong, Y. J. Zeng, Q. Y. Tao, R. X. Wu, H. F. Ma, B. Zhao, D. Wang, W. Q. Dang, K. Q. Chen, L. Liao, X. D. Duan, X. F. Duan and Y. Liu, Nat. Commun., 2020, 11, 1151 CrossRef CAS PubMed
 .
.
Footnote |
† Electronic supplementary information (ESI) available: 56 easily exfoliated magnetic 2D monolayers, table of overpotentials of 8 magnetic 2D monolayers for the OER without strain and under the optimal biaxial tensile strains, the Gibbs free energies of adsorbed intermediates on FeO2, VSe2 and VTe2 monolayers under different biaxial tensile strains, the variations of  with with  or or 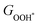 for FeO2, VSe2 and VTe2, the DOS of non-metal atoms (O, Se and Te) for CoO2, FeO2, VSe2 and Vte2 under different biaxial tensile strains, and the overpotentials of CoO2 and Vte2 under uniaxial tensile strains, the overpotentials by the PBE+U method, and the results of non-magnetic 2D monolayers. See DOI: https://doi.org/10.1039/d2nh00318j for FeO2, VSe2 and VTe2, the DOS of non-metal atoms (O, Se and Te) for CoO2, FeO2, VSe2 and Vte2 under different biaxial tensile strains, and the overpotentials of CoO2 and Vte2 under uniaxial tensile strains, the overpotentials by the PBE+U method, and the results of non-magnetic 2D monolayers. See DOI: https://doi.org/10.1039/d2nh00318j |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  * and
Wanlin
Guo
*
* and
Wanlin
Guo
*

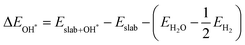
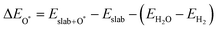
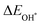 ,
, 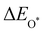 and
and 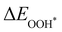 are the binding energies of the OH*, O* and OOH* intermediates, respectively. Eslab is the ground-state energy of the magnetic 2D monolayer.
are the binding energies of the OH*, O* and OOH* intermediates, respectively. Eslab is the ground-state energy of the magnetic 2D monolayer. 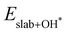 ,
, 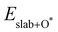 and
and 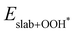 are the total energies of the magnetic 2D monolayer binding with the OH*, O* and OOH* intermediates, respectively.
are the total energies of the magnetic 2D monolayer binding with the OH*, O* and OOH* intermediates, respectively. 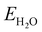 and
and 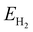 are the energies of H2O and H2 molecules in the liquid and gas phase, respectively.
are the energies of H2O and H2 molecules in the liquid and gas phase, respectively.
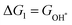
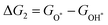
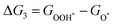
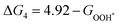
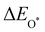 and
and 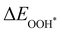 obtained under different biaxial tensile strain are approximately linear functions of
obtained under different biaxial tensile strain are approximately linear functions of 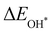 . The scaling relation between
. The scaling relation between 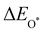 or
or 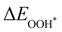 with
with 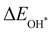 is fitted as
is fitted as 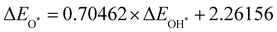 or
or 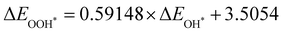 . Furthermore, the variation in the Gibbs free energies of the adsorbed intermediates under different biaxial tensile strain values shown in Fig. 4(c) is similar to that of the binding energies. There still exists approximately linear scaling relations between
. Furthermore, the variation in the Gibbs free energies of the adsorbed intermediates under different biaxial tensile strain values shown in Fig. 4(c) is similar to that of the binding energies. There still exists approximately linear scaling relations between 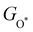 or
or 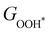 with
with 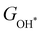 :
: 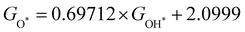 and
and 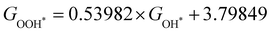 , see Fig. 4(d). As a result,
, see Fig. 4(d). As a result, 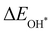 and
and 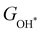 can be used to predict the binding energies and Gibbs free energies of the *O and *OOH intermediates on the CoO2 surface. For the FeO2, VSe2 and VTe2 monolayers, their Gibbs free energies
can be used to predict the binding energies and Gibbs free energies of the *O and *OOH intermediates on the CoO2 surface. For the FeO2, VSe2 and VTe2 monolayers, their Gibbs free energies 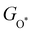 and
and 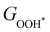 under different biaxial tensile strain also exhibit approximately linear relations with
under different biaxial tensile strain also exhibit approximately linear relations with 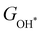 , see Fig. S1 and S2 (ESI†). These linear scaling relations between
, see Fig. S1 and S2 (ESI†). These linear scaling relations between 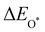 or
or 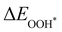 with
with 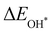 and between
and between 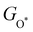 or
or 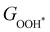 with
with 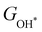 are consistent with previous studies.44,45,48,49,51
are consistent with previous studies.44,45,48,49,51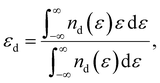 where nd(ε) is the density of states projected onto the d-states and ε is the energy.52,53 The closer the d-band center is to the Fermi level, the stronger the binding with the intermediates and the better chemical activity of the metal atom.54 For the CoO2 and FeO2 monolayers, biaxial tensile strain makes the d-band centers for spin-down of the metal atoms closer to the Fermi level, where the d-band center of the Co atom moves from −1.05 to −0.88 eV, and that for the Fe atom moves from −0.76 to −0.42 eV. By contrast, the d-band centers for spin-up of the V atoms for VSe2 and VTe2 monolayers are closer to the Fermi level when under biaxial tensile strain, where the d-band center of the V atom of VSe2 moves from −0.33 to −0.26 eV, and that of VTe2 moves from −0.37 to −0.32 eV. The tensile strain imposes a stronger improvement on the spin-down d-band centers of Co and Fe atoms, and on the spin-up d-band centers of V atoms. Furthermore, the spin-down charge densities ρspin-down around the Fermi level of the CoO2 and FeO2 monolayers and the spin-up charge densities ρspin-up around the Fermi level of the VSe2 and VTe2 monolayers are shown in Fig. 6. Clearly, more charges move to the metal atoms in the presence of biaxial tensile strain, which indicates the chemical activity enhancement of metal atoms and also coincides with the movement of the d-band centers to the Fermi level.
where nd(ε) is the density of states projected onto the d-states and ε is the energy.52,53 The closer the d-band center is to the Fermi level, the stronger the binding with the intermediates and the better chemical activity of the metal atom.54 For the CoO2 and FeO2 monolayers, biaxial tensile strain makes the d-band centers for spin-down of the metal atoms closer to the Fermi level, where the d-band center of the Co atom moves from −1.05 to −0.88 eV, and that for the Fe atom moves from −0.76 to −0.42 eV. By contrast, the d-band centers for spin-up of the V atoms for VSe2 and VTe2 monolayers are closer to the Fermi level when under biaxial tensile strain, where the d-band center of the V atom of VSe2 moves from −0.33 to −0.26 eV, and that of VTe2 moves from −0.37 to −0.32 eV. The tensile strain imposes a stronger improvement on the spin-down d-band centers of Co and Fe atoms, and on the spin-up d-band centers of V atoms. Furthermore, the spin-down charge densities ρspin-down around the Fermi level of the CoO2 and FeO2 monolayers and the spin-up charge densities ρspin-up around the Fermi level of the VSe2 and VTe2 monolayers are shown in Fig. 6. Clearly, more charges move to the metal atoms in the presence of biaxial tensile strain, which indicates the chemical activity enhancement of metal atoms and also coincides with the movement of the d-band centers to the Fermi level..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
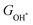 with
with 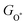 or
or 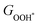 for FeO2, VSe2 and VTe2, the DOS of non-metal atoms (O, Se and Te) for CoO2, FeO2, VSe2 and Vte2 under different biaxial tensile strains, and the overpotentials of CoO2 and Vte2 under uniaxial tensile strains, the overpotentials by the PBE+U method, and the results of non-magnetic 2D monolayers. See DOI: https://doi.org/10.1039/d2nh00318j
for FeO2, VSe2 and VTe2, the DOS of non-metal atoms (O, Se and Te) for CoO2, FeO2, VSe2 and Vte2 under different biaxial tensile strains, and the overpotentials of CoO2 and Vte2 under uniaxial tensile strains, the overpotentials by the PBE+U method, and the results of non-magnetic 2D monolayers. See DOI: https://doi.org/10.1039/d2nh00318j